Economic Dispatch between Distribution Grids and Virtual Power Plants under Voltage Security Constraints

Abstract

Due to the high penetration of virtual power plants (VPPs), the bi-directional power flow between VPPs and active distribution grids makes the grid operation complex. Without congestion management, the operation schedule only considers the economic benefits, and power flow constraints might be violated. Hence, it is necessary to conduct power interaction within the operation constraints. This paper proposes a coordinated economic dispatch method under voltage security constraints. The linear expressions were derived by simplifying the AC power flow equations to reduce the computation complicity. Then, optimal economic dispatch models with voltage security constraints were established for the active distribution grid and VPPs, respectively. Meanwhile, the transacted power and clearing price were set as the communication variables, and a coordinated strategy was proposed for the overall optimal goal. The modified IEEE 33-node and PG&E-node distribution grids were utilized for the simulations, and the results affirmed the validity of the proposed method.

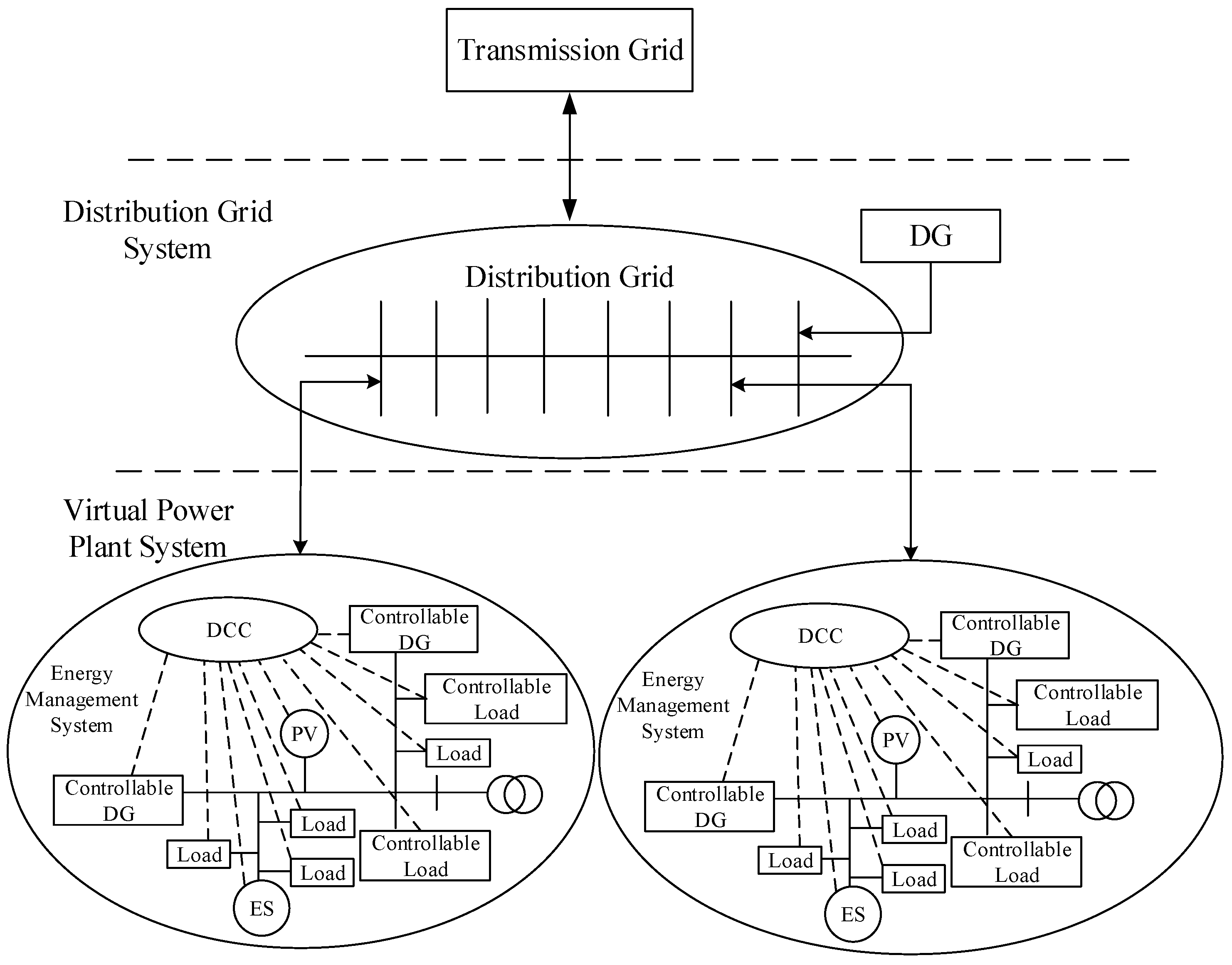
1. Introduction

As the penetration rate of distributed generation (DG) in the power grid continuously increases, multiple devices provide a valuable means for dispatching the distribution grid operation and increasing the number of decision variables. However, it also brings some problems to the power grid operation. For example, the curtailment of wind and solar resources occasionally occurs in areas with a high proportion of DGs. The power fluctuation of DGs aggravates the uncertainty of the user side and further increases the grid operation risk. Therefore, it is necessary to propose a proper coordination method for DG operation. However, when applying the centralized mode, the dispatch center must deal with the operation data of the entire grid, making the optimal model complex [1,2,3,4]. Hence, the concept of virtual power plants (VPPs) has been proposed to improve operational efficiency. In [5], VPPs aggregated the power generation resources, which could be managed through the central control system. In [6], VPPs aggregated the load-side resources, which could be connected to any node of the distribution grid. In [7], the VPPs were clusters of distributed power sources, controllable loads, and energy storage systems, and they operated as special power plants. According to the international standards for virtual electricity approved by the International Electrotechnical Commission (IEC) [8], VPPs are intelligent control technologies and business models that aggregate various DERs within a region to participate in the energy market. In other words, by integrating various DGs and controllable devices, VPPs can manage zonal energy dispatch and transact active power with the connected distribution grid [9,10,11,12].

VPPs belonging to different owners can also participate in market activities in the actual power market. Hence, it is necessary to coordinate the operation of VVPs by considering the security constraints of the distribution grid [13,14,15,16,17]. There are two kinds of coordination methods between the distribution grid and VPPs. One type is the master–slave optimization method [18,19]. The distribution grid dispatches instructions as a master, and the VPPs react passively. In general, the initiative of consumers in VPPs cannot be motivated. The other type is the decentralized optimization method. The active distribution grid and VVPs dispatch their devices independently and exchange boundary information (including the transacted clearing price) with each other. In [20], the transacted electricity price was scheduled to adjust the supply and demand situation of the VVPs. In [21], considering the transaction and congestion costs, the transacted clearing price was set to dispatch the controllable resource in the active distribution grid. In [22], the line current security constraints were considered, and the transacted clearing price was calculated using the DC power flow equations. However, the previous research mainly focused on line current congestion management and ignored the violation of the node voltage constraints caused by integrating large-scale VPPs.

With the high penetration of DGs and other controllable devices in power grids, the decision variables in the active distribution grid and VPPs are various and massive [23,24]. Meanwhile, the corresponding optimization models are nonlinear due to the AC power flow constraints, which are challenging to solve [24,25,26]. In [27], based on the DC power flow equations, a quadratic optimization model for the optimal operation was established. However, the optimal results could not be obtained without the node voltage constraints. In [28,29], convex quadratic models were established by second-order cone and semi-definite programming, respectively. By introducing new variables, the nonlinear constraints became quadratic constraints, but the optimization model was still complex due to the increasing decision variables [30]. Therefore, it is necessary to propose an optimization algorithm for low-decision spaces.

In addition, to improve the coordination efficiency between the active distribution grid and VPPs, the existing coordinated methods can be roughly divided into two types: Lagrangian decomposition-based methods [31] and Karush–Kuhn–Tucker (KKT) condition-based methods [32]. While the Lagrangian decomposition-based approach is simple, its convergence speed becomes slow because of the duality gap. While the KKT-based method eliminates the step of the manual modifications of coefficients, the variables are implicitly combined by the power flow equations, which slows the optimization speed. Hence, a coordinated method with good convergence is needed to interact with the active distribution grid and VVPs.

This paper researched the economic dispatch problem under voltage security constraints and proposed a novel coordinated method for the active distribution grid and VVPs. The features of the proposed method include the following.

(1)

According to the exchanged boundary information and the respective operation points of the distribution grid and VPPs, the approximate linear expressions constructed by node power injections were established for the node voltage security constraints. Furthermore, for the distribution grid and VPPs with relatively stable topologies, coefficients of linear expressions were generated offline and applied online. Due to the transformation of the constraints into a combination of linear combinatorial inequalities involving decision variables, and the variables in both the objective function and constraints were consistent, and the optimization model was easy to solve.

(2)

The quadratic integrated mathematic model was established to minimize the overall operating cost, and a distributed algorithm was proposed based on the KKT conditions for the global optimality. Only the boundary node voltages of the distribution grid, tie-line powers, and clearing prices were exchanged during the iterative communication.

The remainder of the paper is structured as follows: Section 2 provides a linearized way for the voltage security constraints. Section 3 establishes an integrated optimization model for the distribution grid and VPPs under the voltage security constraints, aiming for a minimal operation cost. Section 4 proposes the iterative computing method for coordination based on the KKT conditions. In Section 5, simulations for a modified IEEE 33-node distribution grid with three VPPs are presented. The conclusion is presented in Section 6.

2. Linearization for the Node Voltage Security Constraints

Considering that the current margin of the cable capacity was sufficient to meet the power demand, this paper neglected the current constraints and focused on the voltage violation caused by DGs. Suppose there are n nodes in the distribution grid. $\mathit{P}={(P_1,P_2,\dots ,P_n)}^{\mathrm{T}}$, $\mathit{Q}={(Q_1,Q_2,\dots ,Q_n)}^{\mathrm{T}}$, $\mathit{U}={(U_1,U_2,\dots ,U_n)}^{\mathrm{T}}$, and $\mathsf{\theta }={({\theta }_1,{\theta }_2,\dots ,{\theta }_n)}^{\mathrm{T}}$ are the active power injection, reactive power injection, voltage magnitude, and phase angle vectors, respectively.

The equations for the AC power flow are as follows.

$$P_i=U_i{\displaystyle \sum _{j=1}^n{U}_j(G_{ij}\cos ({\theta }_i-{\theta }_j)+B_{ij}\sin ({\theta }_i-{\theta }_j))}$$

(1)

$$Q_i=U_i{\displaystyle \sum _{j=1}^n{U}_j(G_{ij}\sin ({\theta }_i-{\theta }_j)-B_{ij}\cos ({\theta }_i-{\theta }_j))}$$

(2)

where $G_{ij}+\mathrm{j}{B}_{ij}$ is the admittance between node i and j.

The correction equation can be obtained from the above node power balance equation [33], as shown in Equation (3).

$$\mathsf{\Delta }\mathit{U}={\mathit{J}}^{-1}\left[\begin{array}{l}\mathsf{\Delta }\mathit{P}\\ \mathsf{\Delta }\mathit{Q}\end{array}\right]=[\mathsf{\alpha }\mathsf{\beta }]\left[\begin{array}{l}\mathsf{\Delta }\mathit{P}\\ \mathsf{\Delta }\mathit{Q}\end{array}\right]=\mathsf{\alpha }\mathsf{\Delta }\mathit{P}+\mathsf{\beta }\mathsf{\Delta }\mathit{Q}$$

(3)

where $\mathsf{\Delta }\mathit{U}$ is the voltage deviation variable, $\mathit{J}$ is the Jacobian matrix, And $\mathsf{\alpha }={({\alpha }_{ij})}_{n\times n}$ and $\mathsf{\beta }={({\beta }_{ij})}_{n\times n}$ are the coefficient matrices corresponding to the active power and reactive power injections, respectively. The expression of ${\alpha }_{ij}$ and ${\beta }_{ij}$ are as follows.

$$\left\{\begin{array}{l}{\alpha }_{ij}=\frac{\partial U_i}{\partial P_j}\\ {\beta }_{ij}=\frac{\partial U_i}{\partial Q_j}\end{array}\right.$$

(4)

Suppose $U_{i,\max }$ and ${\tilde{U}}_i$ are the upper limit and current state of the voltage magnitude at node i. $({\dot{\mathit{P}}}^{\mathrm{T}},{\dot{\mathit{Q}}}^{\mathrm{T}})$ is the critical operation point corresponding to $U_i=U_{i,\max }$. Then, for node i, we can achieve the following.

$$\mathsf{\Delta }{U}_{i,\max }=U_{i,\max }-{\tilde{U}}_i=\dot{\mathsf{\alpha }}\mathsf{\Delta }\mathit{P}+\dot{\mathsf{\beta }}\mathsf{\Delta }\mathit{Q}$$

(5)

where $\dot{\mathsf{\alpha }}={({\dot{\alpha }}_{ij})}_{n\times n}$ and $\dot{\mathsf{\beta }}={({\dot{\beta }}_{ij})}_{n\times n}$ can be calculated at the critical operation point $({\dot{\mathit{P}}}^{\mathrm{T}},{\dot{\mathit{Q}}}^{\mathrm{T}})$ using Equation (4). $\mathsf{\Delta }{U}_{i,\max }$ represents the difference between the maximum and current voltage magnitudes.

When $\mathsf{\Delta }{U}_{i,\max }=0$, we can achieve the following approximate expression for $U_{i,\max }$.

$$\dot{\mathsf{\alpha }}\mathsf{\Delta }\mathit{P}+\dot{\mathsf{\beta }}\mathsf{\Delta }\mathit{Q}=0$$

(6)

Considering $\mathsf{\Delta }\mathit{P}=\mathit{P}-\dot{\mathit{P}}$ and $\mathsf{\Delta }\mathit{Q}=\mathit{Q}-\dot{\mathit{Q}}$, we can achieve the following.

$$\dot{\mathsf{\alpha }}\mathit{P}+\dot{\mathsf{\beta }}\mathit{Q}={\dot{\chi }}_i$$

(7)

where ${\dot{\chi }}_i={\displaystyle \sum _{j=1}^n({\dot{\alpha }}_{ij}{\dot{P}}_j+{\dot{\beta }}_{ij}{\dot{Q}}_j)}$. For a given $({\dot{\mathit{P}}}^{\mathrm{T}},{\dot{\mathit{Q}}}^{\mathrm{T}})$, ${\dot{\chi }}_i$ is a constant variable, and Equation (7) is the linear equation for the upper limit of the voltage magnitude at node i.

Similarly, regarding the lower limit of the voltage magnitude at node i, that is, $U_i=U_{i,\min }$, $({\ddot{\mathit{P}}}^{\mathrm{T}},{\ddot{\mathit{Q}}}^{\mathrm{T}})$ is the corresponding critical operation point. Then, we can achieve the following.

$$\ddot{\mathsf{\alpha }}\mathit{P}+\ddot{\mathsf{\beta }}\mathit{Q}={\ddot{\chi }}_i$$

(8)

where $\dot{\mathsf{\alpha }}={({\dot{\alpha }}_{ij})}_{n\times n}$ and $\dot{\mathsf{\beta }}={({\dot{\beta }}_{ij})}_{n\times n}$ can be calculated at the critical operation point $({\ddot{\mathit{P}}}^{\mathrm{T}},{\ddot{\mathit{Q}}}^{\mathrm{T}})$ using Equation (4). ${\ddot{\chi }}_i={\displaystyle \sum _{j=1}^n({\ddot{\alpha }}_{ij}{\ddot{P}}_j+{\ddot{\beta }}_{ij}{\ddot{Q}}_j)}$. For a given $({\ddot{\mathit{P}}}^{\mathrm{T}},{\ddot{\mathit{Q}}}^{\mathrm{T}})$, ${\ddot{\chi }}_i$ is a constant variable, and Equation (8) is the linear equation for the lower limit of the voltage magnitude at node i.

Based on Equations (7) and (8), the linear expressions constructed by the power injections for the voltage security constraints can be depicted as follows.

$${\displaystyle \sum _{j=1}^n({\dot{\alpha }}_{ij}{P}_j+{\dot{\beta }}_{ij}{Q}_j)\le {\dot{\chi }}_i}$$

(9)

$${\displaystyle \sum _{j=1}^n({\ddot{\alpha }}_{ij}{P}_j+{\ddot{\beta }}_{ij}{Q}_j)}\ge {\ddot{\chi }}_i$$

(10)

where ${\dot{\alpha }}_{ij}$, ${\dot{\beta }}_{ij}$, ${\dot{\chi }}_{ij}$, ${\ddot{\alpha }}_{ij}$, ${\ddot{\beta }}_{ij}$, and ${\ddot{\chi }}_{ij}$ are the constants for the given critical points, which can be calculated offline and recalled online. We can see that establishing the linear expression needs critical points on the static voltage region boundaries. The method for identifying the critical points can be found in [34].

3. Integrated Economic Dispatch Model of the Distribution Grid and VPPs

In the operation structure of the active distribution grid and VPPs, as shown in Figure 1, the decision variables for the VPPs are the active power injections of the distributed generations (DGs) and energy storages (ESs), and for the distribution grid, are the active power injections of the direct-controlled DGs. The active distribution can exchange power with the transmission grid and VPPs, and the power flow among them is bi-directional. Under this energy structure, this paper proposes an integrated model for the economic dispatch of the active distribution grid and VPPs.

3.1. Optimization Model in a Distribution Grid

Suppose the sets of nodes and DGs in the distribution grid are $N_d$ and $G_d$, respectively. The operational objective of the distribution grid is to obtain the maximum market revenue, which can be expressed as follows.

$$\min f_d=\pi P_T+{\displaystyle \sum _{\forall i\in G_d}{C}_i^d(P_i)}=\pi P_T+{\displaystyle \sum _{\forall i\in G_d}(a_i{P}_i^2+b_i{P}_i+c_i)}$$

(11)

where $\pi$ is the clearing price between the transmission and distribution grids and $P_T$ is the power injected from the transmission grid. $P_i(\forall i\in G_d)$ is the power of the i-th DG; $C_i^d(P_i)$ is the operation cost of the i-th DG; and $a_i$, $b_i$, and $c_i$ are the cost coefficients.

Then, the linear expressions for the voltage security constraints of node $i\in N_d$ can be depicted as follows.

$${\displaystyle \sum _{\forall j\in N_d}({\dot{\alpha }}_{ij}^d{P}_j+{\dot{\beta }}_{ij}^d{Q}_j)}\le {\dot{\chi }}_i^d$$

(12)

$${\displaystyle \sum _{\forall j\in N_d}({\ddot{\alpha }}_{ij}^d{P}_j+{\ddot{\beta }}_{ij}^d{Q}_j)}\ge {\ddot{\chi }}_i^d$$

(13)

where ${\dot{\alpha }}_{ij}^d$ and ${\dot{\beta }}_{ij}^d$ are the coefficients derived from the Jacobian matrix of the distribution grid corresponding to the critical point $({({\dot{\mathit{P}}}^d)}^{\mathrm{T}},{({\dot{\mathit{Q}}}^d)}^{\mathrm{T}})$; ${\dot{\chi }}_i^d={\displaystyle \sum _{\forall i\in N_d}({\dot{\alpha }}_{ij}^d{\dot{P}}_j^d+{\dot{\beta }}_{ij}^d{\dot{Q}}_j^d)}$; and ${\ddot{\alpha }}_{ij}^d$ and ${\ddot{\beta }}_{ij}^d$ are the coefficients derived from the Jacobian matrix of the distribution grid corresponding to the critical point $({({\ddot{\mathit{P}}}^d)}^{\mathrm{T}},{({\ddot{\mathit{Q}}}^d)}^{\mathrm{T}})$; ${\ddot{\chi }}_i^d={\displaystyle \sum _{\forall i\in N_d}({\ddot{\alpha }}_{ij}^d{\ddot{P}}_j^d+{\ddot{\beta }}_{ij}^d{\ddot{Q}}_j^d)}$.

Meanwhile, the capacity constraints of the power injection at node i can be depicted as follows.

$$P_{i,\min }\le P_i\le P_{i,\max },\forall i\in N_d$$

(14)

where $P_{i,\max }$ and $P_{i,\min }$ are the maximum and minimum values of the power injection at node i, respectively.

In addition, the exchanged power constraint between the distribution grid and transmission gird can be depicted as follows.

$$P_{T,\min }\le P_T\le P_{T,\max }$$

(15)

where $P_{T,\max }$ and $P_{T,\min }$ are the maximum and minimum values of the exchanged power between the transmission and distribution grids.

Suppose there is no grid loss in the distribution grid, then we could achieve the following.

$$P_T+{\displaystyle \sum _{\forall i\in N_d}{P}_i}=0$$

(16)

In summary, Equations (11)–(16) form the quadratic optimization model, and the decision variables are the node power injections in the objective and constraints. Then, the proposed model can be rapidly solved using the quadratic programming method.

3.2. Optimization Model in VPPs

In an active distribution grid, the number of VPPs is $n_v$, and the VPP at node k is denoted as VPP_k. The sets of nodes, DGs, and ESs in VPP_k are $N_k$, $G_k$, and $E_k$. The controllable variables of VPP_k are the output $P_i(\forall i\in G_d^k)$ at the i-th DG, the output $P_i(\forall i\in E_d^k)$ at the i-th ES, and the tie-line power $P_k$ with the distribution grid at node k. For the operation cost and sales revenue, the optimization model of VPP_k is as follows.

$$\min f_k={\displaystyle \sum _{\forall i\in G_k}{C}_i^V(P_i)}+{\displaystyle \sum _{\forall i\in E_k}{C}_i^E(|P_i|)}-{\pi }_k{P}_k={\displaystyle \sum _{\forall i\in G_k}(a_i{P}_i^2+b_i{P}_i+c_i)}+{\displaystyle \sum _{\forall i\in E_k}{d}_i|P_i}|-{\pi }_k{P}_k$$

(17)

where ${\pi }_k$ is the clearing price of VPP_k, which is determined by the distribution grid, and $C_i^V(P_i)$ is the cost function of the i-th DG in VPP_k.

Then, the linear expressions for the node voltage security constraints of VPP_k can be expressed as follows.

$${\displaystyle \sum _{\forall j\in N_k}({\dot{\alpha }}_{ij}^k{P}_j+{\dot{\beta }}_{ij}^k{Q}_j)}\le {\dot{\chi }}_i^k$$

(18)

$${\displaystyle \sum _{\forall j\in N_k}({\ddot{\alpha }}_{ij}^k{P}_j+{\ddot{\beta }}_{ij}^k{Q}_j)}\ge {\ddot{\chi }}_i^k$$

(19)

where ${\dot{\alpha }}_{ij}^k$ and ${\dot{\beta }}_{ij}^k$ are the coefficients derived from the Jacobian matrix of VPP_k corresponding to the critical point $({({\dot{\mathit{P}}}^k)}^{\mathrm{T}},{({\dot{\mathit{Q}}}^k)}^{\mathrm{T}})$; ${\dot{\chi }}_i^k={\displaystyle \sum _{\forall i\in N_k}({\dot{\alpha }}_{ij}^k{\dot{P}}_j^k+{\dot{\beta }}_{ij}^k{\dot{Q}}_j^k)}$; and ${\ddot{\alpha }}_{ij}^k$ and ${\ddot{\beta }}_{ij}^k$ are the coefficients derived from the Jacobian matrix of the distribution grid corresponding to the critical point $({({\ddot{\mathit{P}}}^k)}^{\mathrm{T}},{({\ddot{\mathit{Q}}}^k)}^{\mathrm{T}})$; ${\ddot{\chi }}_i^k={\displaystyle \sum _{\forall i\in N_k}({\ddot{\alpha }}_{ij}^k{\ddot{P}}_j^k+{\ddot{\beta }}_{ij}^k{\ddot{Q}}_j^k)}$.

Meanwhile, the capacity constraint of the power injection at node i can be depicted as follows.

$$P_{i,\min }\le P_i\le P_{i,\max },\forall i\in N_k$$

(20)

Considering the state of charge, the capacity constraints of ES can be depicted as follows.

$$S_{i,\min }\le {\tilde{S}}_i-\frac{1}{W_i}((\frac{{\eta }_c}{2}+\frac{1}{2{\eta }_d})P_i-(\frac{{\eta }_c}{2}-\frac{1}{2{\eta }_d})|P_i|)\le S_{i,\max },\forall i\in E_k$$

(21)

where ${\tilde{S}}_i$ is the current charge state of the i-th ES and $S_{i,\max }$ and $S_{i,\min }$ are the maximum and minimum charge states of the i-th ES, respectively. ${\eta }_c$ and ${\eta }_d$ are the charging and discharge efficiency of the i-th ES, respectively and $W_i$ is the capacity of the i-th ES.

Suppose there is no grid loss in VPP_k, then the power flow constraint can be depicted as follows.

$${\displaystyle \sum _{\forall i\in N_k}{P}_i}-P_k=0$$

(22)

In addition, the tie-line power constraint can be considered as follows.

$$P_{k,\min }\le P_k\le P_{k,\max }$$

(23)

Thus, Equations (17)–(23) construct a quadratic optimization model of VPP_k, amenable to resolution through quadratic programming techniques. Equations (11)–(23) construct an integrated optimization model of the distribution grid and VPPs.

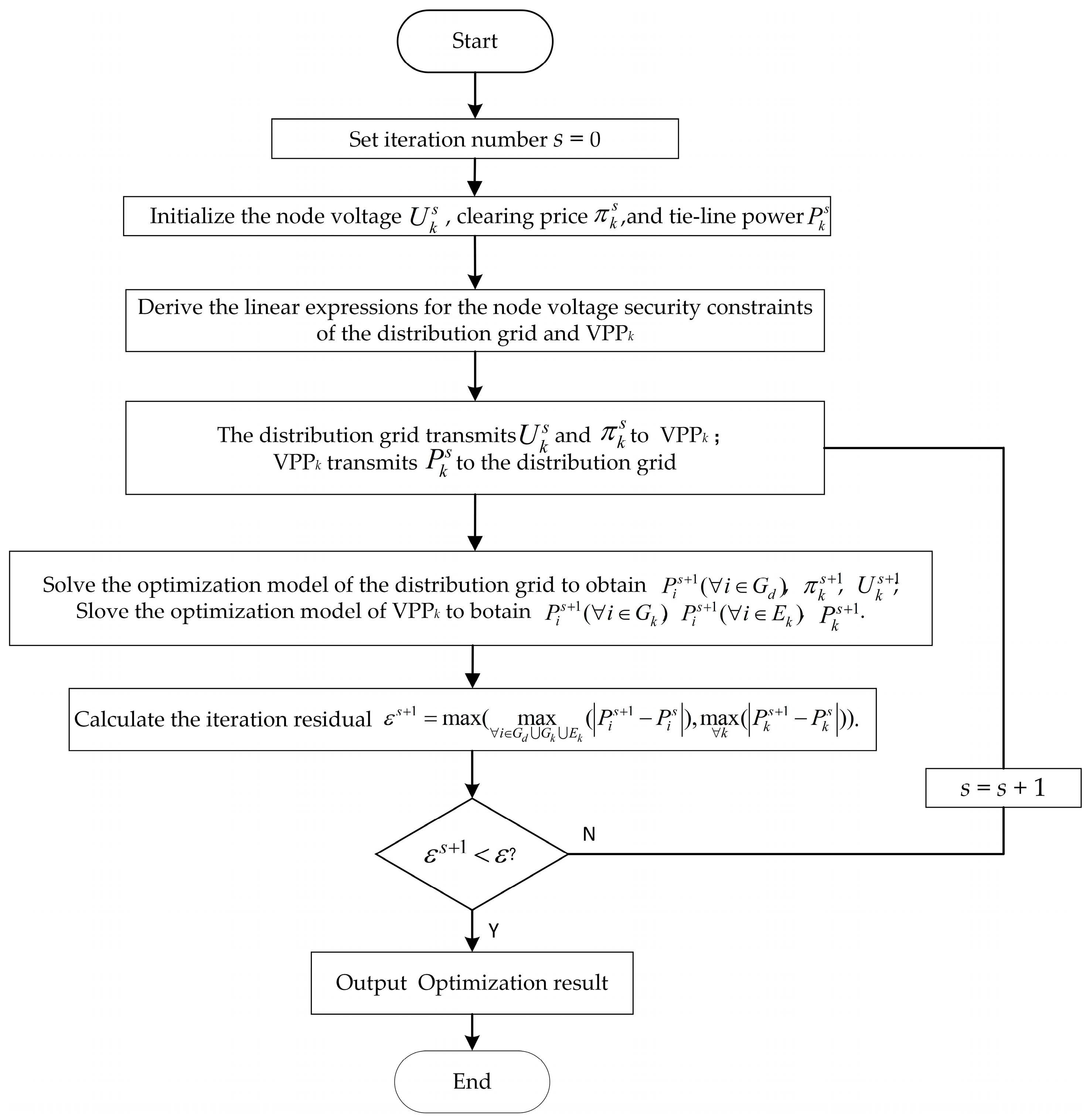
4. Coordinated Method Based on KKT Conditions

To obtain a globally optimized result, this paper proposes a KKT-based calculation method for the clearing price between the distribution grid and VPPs.

If the KKT conditions of the integrated optimization model are met, the condition related to the tie-line power $P_k$ can be shown as follows.

$${\displaystyle \sum _{\forall i\in N_d}({\mu }_{i,\max }{\dot{\alpha }}_{ik}-{\mu }_{i,\min }{\ddot{\alpha }}_{ik})}+{\nu }_{k,\max }-{\nu }_{k,\min }+{\lambda }_k-{\rho }_k=0$$

(24)

where ${\mu }_{i,\max }$ and ${\mu }_{i,\min }$ are the multipliers corresponding to the maximum and minimum voltage magnitude of node i, respectively; ${\nu }_{k,\max }$ and ${\nu }_{k,\min }$ are the multipliers corresponding to the maximum and minimum tie-line power, respectively; and ${\lambda }_k$ and ${\rho }_k$ are the multipliers corresponding to the power flow constraints of the distribution grid and VPP_k, respectively.

Then, if the KKT conditions of the optimization model of VPP_k are met, the condition related to $P_k$ can be formulated as follows.

$${\pi }_k+{\nu }_{k,\max }-{\nu }_{k,\min }-{\rho }_k=0$$

(25)

By combining Equations (24) and (25), we can see that if the clearing price meets the following equation, the KKT conditions of the global model are met.

$${\pi }_k={\displaystyle \sum _{\forall i\in N_d}({\mu }_{i,\max }{\dot{\alpha }}_{ik}-{\mu }_{i,\min }{\ddot{\alpha }}_{ik})}+{\lambda }_k$$

(26)

Equation (26) is the proposed calculation expression.

Afterward, this paper proposes a coordinated algorithm for the distribution grids and VPPs, which is shown in Figure 2. During the iteration, $U_k^s$, ${\pi }_k^s$, and $P_k^s$ are exchanged between the active distribution grid and VPP_k, and the residual is calculated as follows.

$${\epsilon }^{s+1}=\max (\underset{\forall i\in G_d\cup G_k\cup E_k}{\max }(\left|P_i^{s+1}-P_i^s\right|),\underset{\forall k}{\max }(\left|P_k^{s+1}-P_k^s\right|))$$

(27)

If

$${\epsilon }^{s+1}<\epsilon$$

(28)

where $\epsilon$ is the threshold, the proposed coordinated algorithm converges.

5. Simulation Results

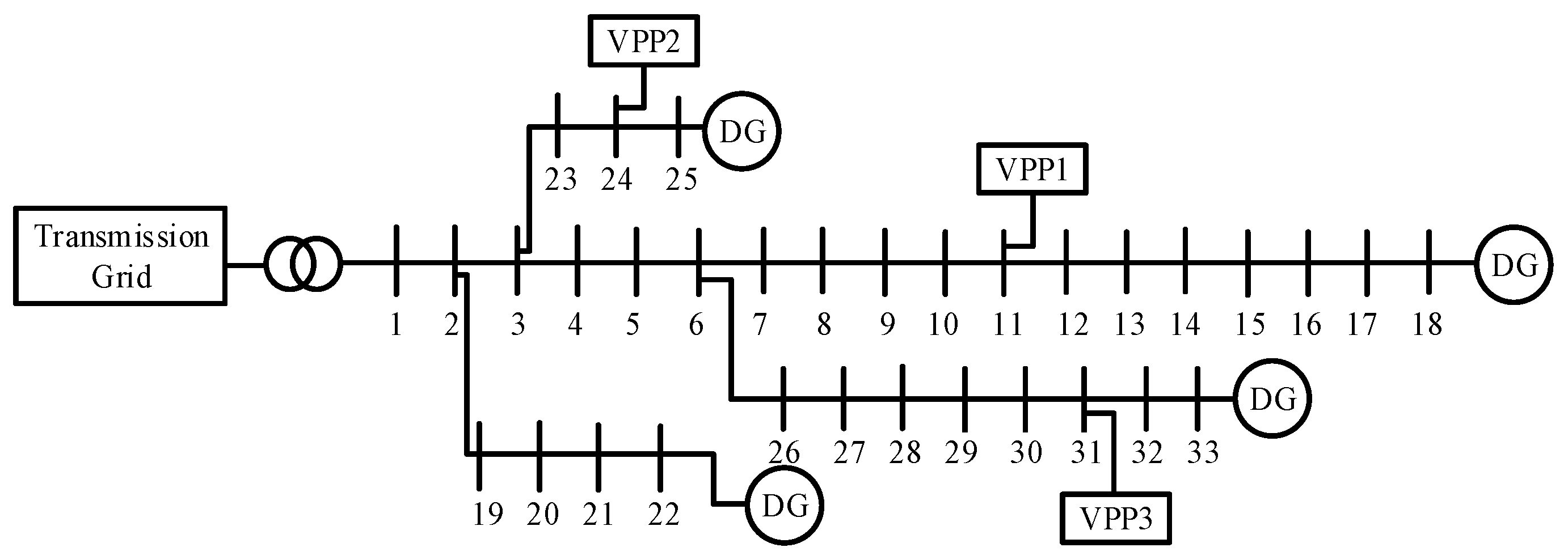
Considering the node voltage security violation caused by VPPs in the distribution grid, this paper proposed a coordinated algorithm for the distribution grid and VPPs. Here, a modified IEEE 33-node grid with three VPPs and a modified PG&E 69-node grid with five VPPs were used for the simulations, as shown in Figure 3 and Figure 4, respectively. For the IEEE 33-node grid, three integrated VPPs had the same configuration and were connected to nodes 11, 24, and 31, respectively, and the controllable DGs in the distribution grid were at nodes 18, 22, 25, and 33. For the PG&E 69-node grid, five integrated VPPs had the same configuration and were connected to nodes 9, 18, 44, 52 and 67, respectively, and the controllable DGs in the distribution grid were at nodes 6, 14, 23, 30, 37, 48, 60, and 63. The unit parameters of the above two grids are shown in

Table 1. Unit parameters of the IEEE 33-node grid.

DG Number	Pmin/kW	Pmax/kW
18	0	1500
22	50	1500
25	50	1500
33	100	1500

and

Table 2. Unit parameters of the PG&E 69-node grid.

DG Number	Pmin/kW	Pmax/kW
6	0	1500
14	50	1500
23	50	1500
30	100	1500
37	100	1500
48	100	1500
60	50	1500
63	50	1500

, respectively. The load distribution in the distribution grid can be seen in [8,35], respectively. The scheduling period of economic dispatch was 24 h.

5.1. Simulation Results for the IEEE 33-Node Grid

5.1.1. Comparison with the Centralized Method Based on the AC Power Flow Equations

To reflect the advantages of the proposed method in calculation speed and accuracy,

Table 3. Comparison results of the centralized and proposed methods for IEEE 33.

Method	Total Calculation Time (s)	Overall Cost (¥)
Proposed method	5.04	3478
Centralized method	163.7	3433

shows the comparison results with a centralized method based on the AC power flow equations, where power losses existed. We can see that the calculation time of the proposed and the centralized methods were 5.04 s and 163.7 s, respectively. The error rate of the proposed method was 1.36% compared to the traditional AC power flow equation, which was within the allowable range of engineering. Therefore, the method proposed in this paper had practical engineering application value.

In terms of economic benefits, the economic costs of the coordinated and independent modes are shown in

Table 4. Cost comparison of the different operating modes in IEEE 33.

Operation Mode	Overall Cost
Coordinated mode	3478
Independent mode	3961

. Due to the coordinated strategy proposed in this paper, the operating costs of the VPPs were lower than those of the independent mode, enhancing the economic benefit of the power grid.

5.1.2. Comparison with the Existing Decentralized Method

The decentralized method based on the alternating direction method of multipliers (ADMM) was used for the comparisons to demonstrate the convergence advantage, where a nonlinear optimization model was established.

Table 5. Compared optimization results.

Method	Average Calculation Time at Each Iteration	Number of Iterations	Total Calculation Time
Proposed method	1.61 s	3	5.04 s
ADMM	3.97 s	35	142.44 s

presents the optimization results for these two methods. Compared to ADMM, the proposed method diminished the average calculation time per iteration and the required number of iterations, i.e., both the efficiency and convergence characteristics were enhanced.

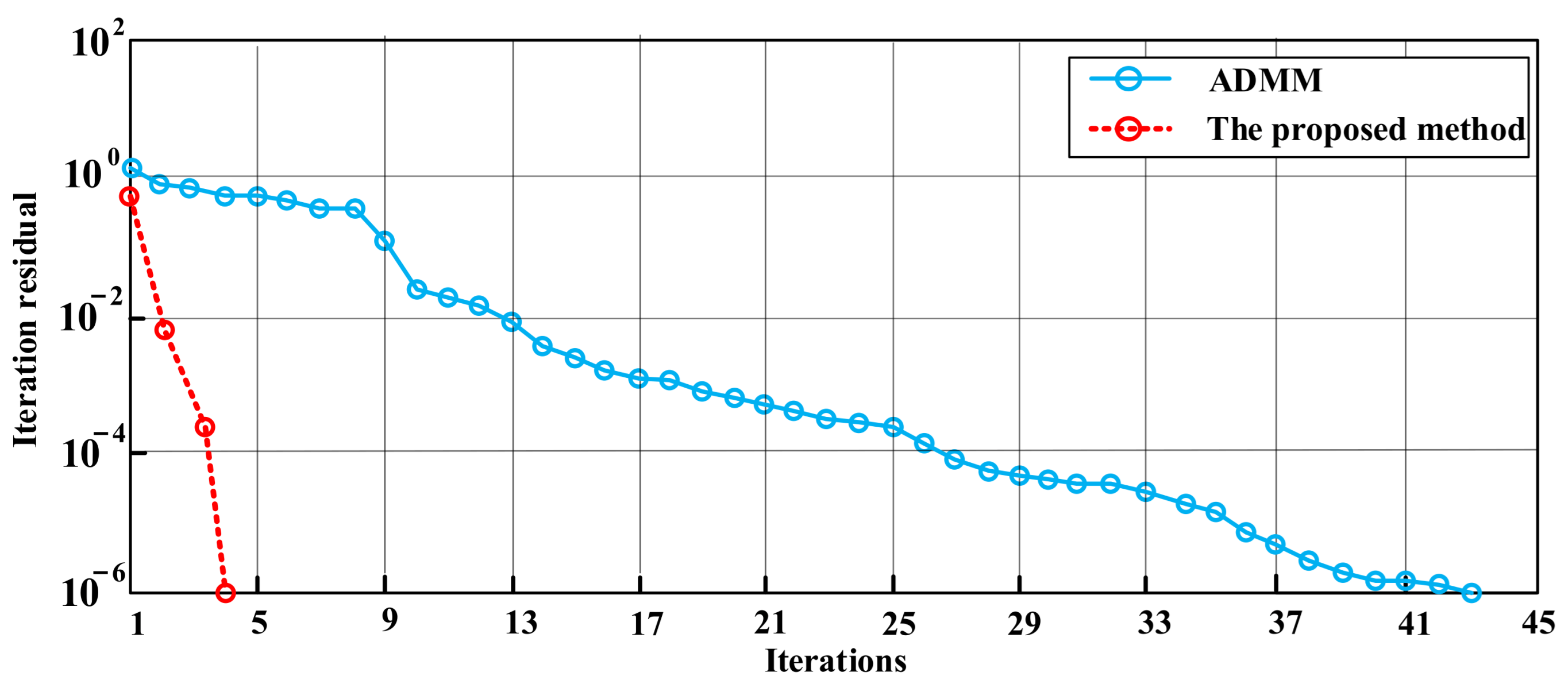
Figure 5 shows the change in the residuals with the number of iterations in the eighth hour to verify the fast convergence of the proposed method. After five iterations, the method proposed in this paper converged, while the ADMM required approx. 35 iterations. Since the proposed method used the Jacobian matrix to transform the nonlinear voltage constraint form into a linear combination of node power injection inequality, we can see that the objective function was the same as the variables in the constraint conditions. Determining the optimal conditions between each VPP and the distribution grid in the optimization process became extremely simple.

5.1.3. Comparison with Economic Dispatch without Voltage Constraints

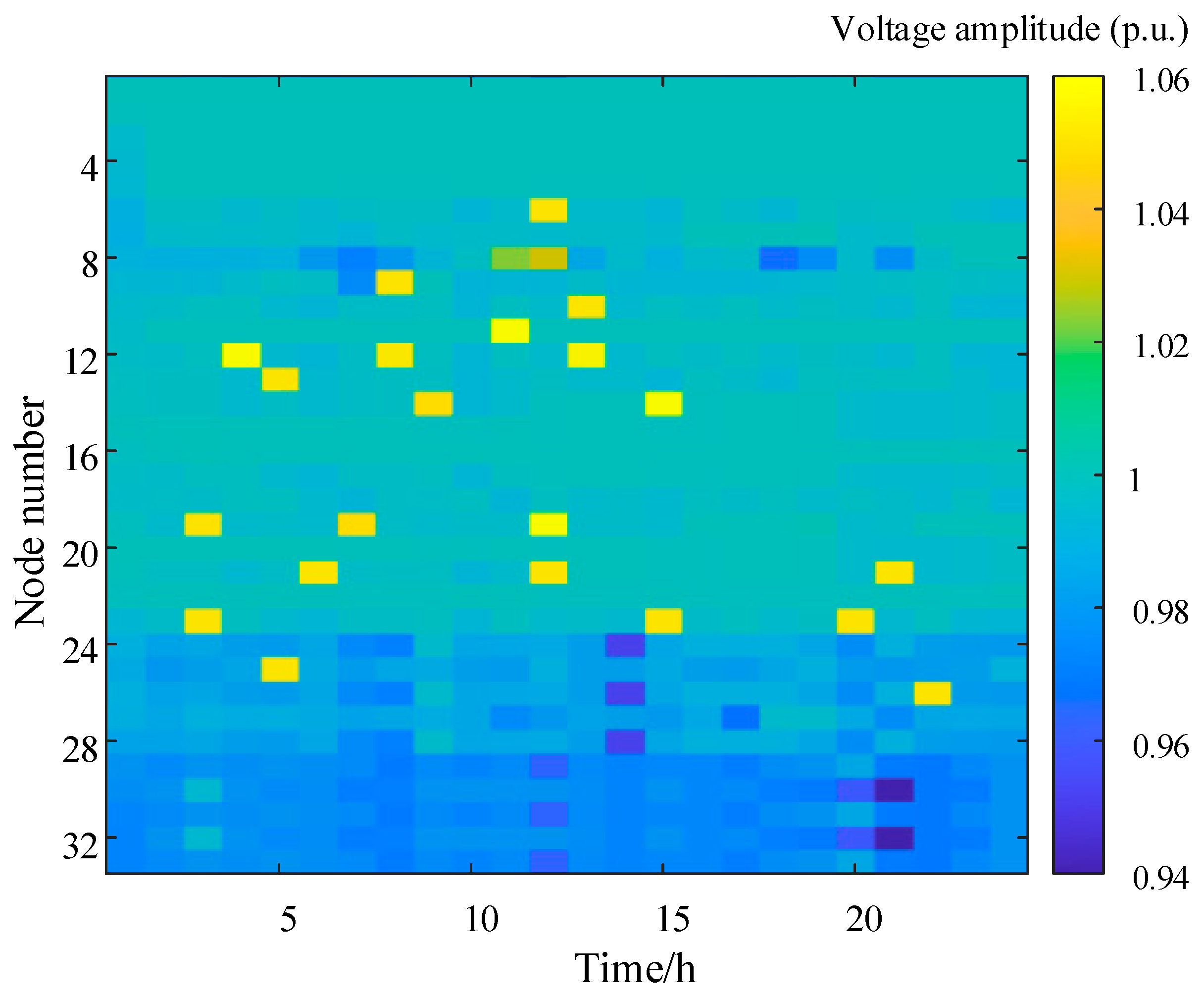
The voltage distribution of all the nodes after the economic dispatch without the voltage constraints of the distribution grid is shown in Figure 6. We can see that without congestion management, voltage violations existed after the economic dispatch, and the optimal results could not meet the requirements of the actual distribution grid.

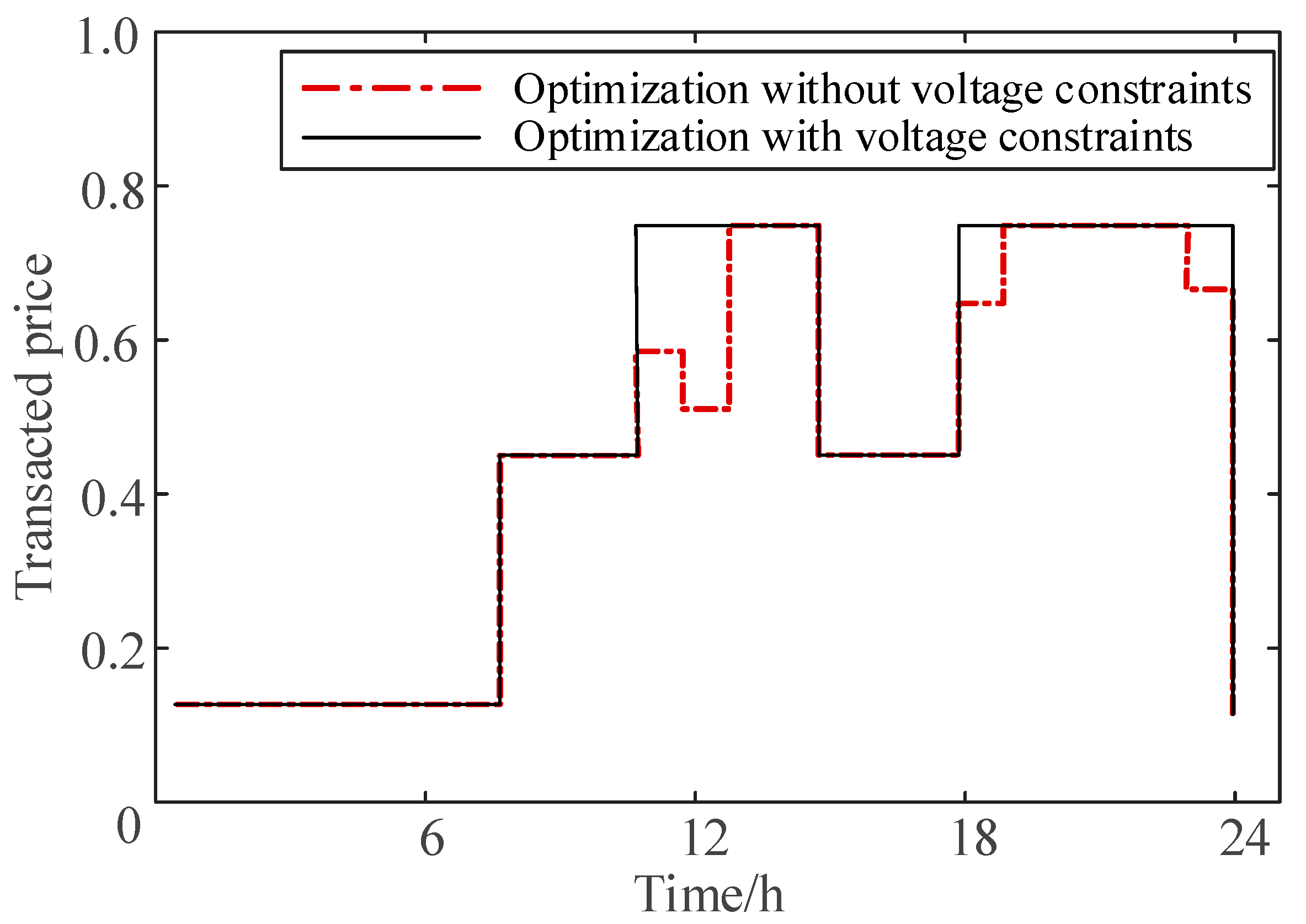
The electricity clearing prices in the economic dispatch with and without voltage constraints are shown in Figure 7. We can see that at 11, 12, 18, 23, and 24 h, the electricity prices between VPP1 and the distribution grid were affected by node voltage congestion. The transacted electricity prices were reduced to eliminate the node voltage violation, and the power injection was adjusted subsequently. We can see that the proposed method ensured the f voltage constraints in the distribution grid with the updated clearing price.

Furthermore, the optimal results of VPP1 without voltage constraints are shown in Figure 8. We can see that at 11, 12, 18, 23, and 24 h, the DER power generation capacities were sufficient, and the prices of transacted electricity were high. As a result, VPP1 actively sold electricity to the distribution grid for profit, and the voltage of node 11 in the distribution grid violated the limits. Applying the proposed method decreased the transacted electricity price between VPP1 and the distribution grid. For the scheduling results of VPP1 with voltage constraints, as shown in Figure 9, we can see that VPP1 correspondingly reduced the amount of electricity based on the updated transacted clearing price. Meanwhile, at 9, 19, 20, and 22 h, VPP1 chose to discharge energy from the ES, reduce the output of DGs, and sell electricity to the distribution grid for profit. In summary, guided by the transacted electricity price with node voltage constraints, VPP1 can actively dispatch the optimal schedule of internal DERs to alleviate node voltage congestion in the distribution grid.

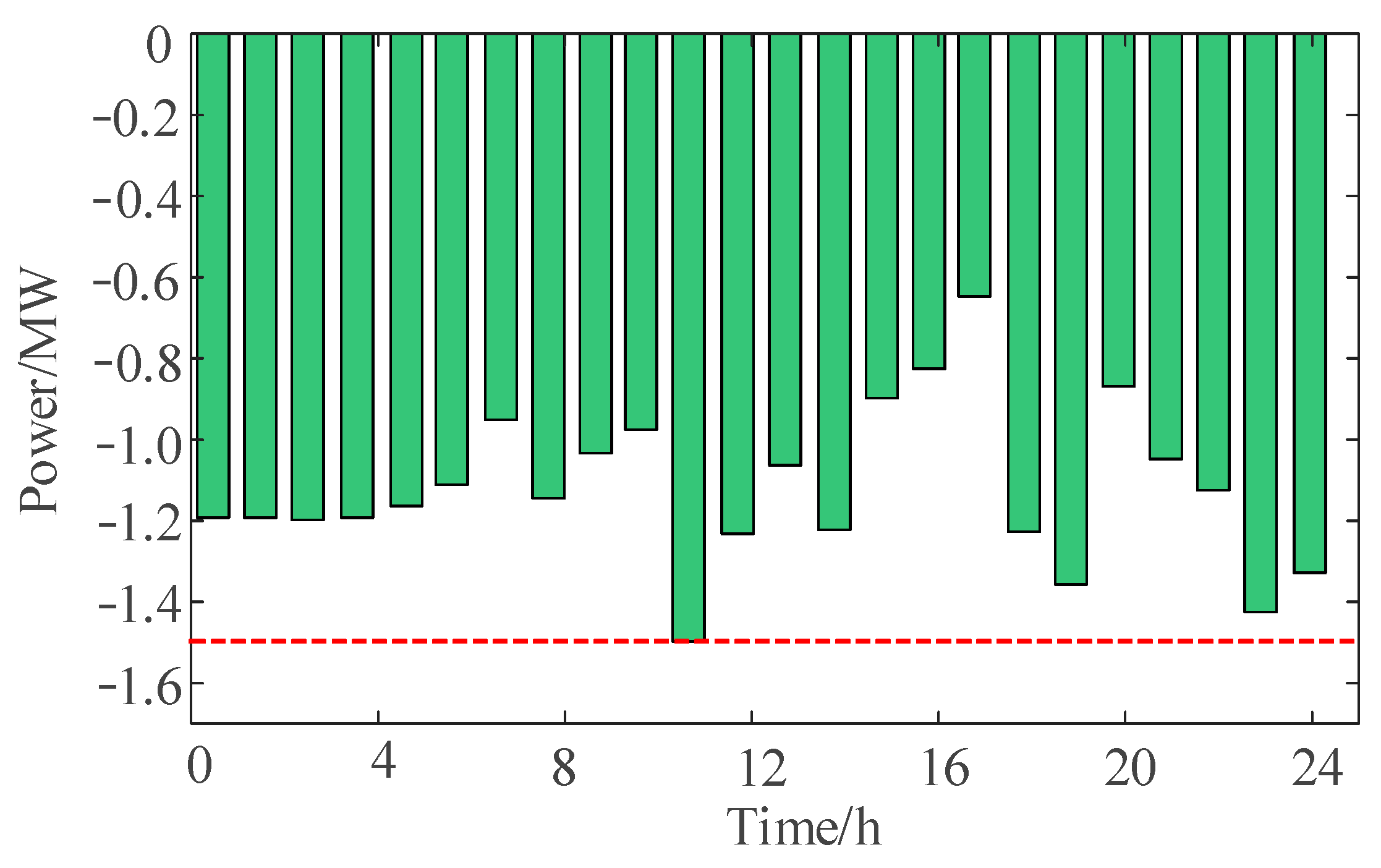
In addition, Figure 10 and Figure 11 show the power flow after the economic dispatch without/with constraints, respectively. The red dash line in Figure 10 and Figure 11 represents the lower limit of tie-line power $P_k$. We can see that the power flow on line 11 had congestion at 11, 12, 18, 23, and 24 h.

With the exchange of boundary information, the distribution grid updated the clearing price, and the VPPs adjusted the purchase and sale of power in conjunction with the clearing price. The contrast of the two figures showed that the power flow violation was effectively alleviated due to the application of the proposed method.

5.2. Simulation Results for the PG&E 69-Node Grid

5.2.1. Comparison with a Centralized Method Based on the AC Power Flow Equations

To further demonstrate the effectiveness of the proposed method, the PG&E 69-node grid was used for the simulations. The cost comparisons of the different operating modes are shown in

Table 6. Cost comparison of different operating modes for PG&E 69.

Operation Mode	Overall Cost
Coordinated mode	3478
Independent mode	3961

. Due to the coordinated strategy proposed in this paper, the operating costs of VPPs were lower than those of the independent mode, enhancing the economic benefit of the power grid.

Table 7. Comparison results of the centralized and proposed methods for PG&E 69.

Method	Total Calculation Time (s)	Overall Cost (¥)
Proposed method	7.46	8391
Centralized method	218.2	8224

shows the comparison results with a centralized method based on the AC power flow equations, where power losses existed. Similar to the simulations in the IEEE 33-node grid, the proposed method took 7.46 s, which was only 3.42% of the calculation time of the centralized method, and the error rate was only 2.01%. In addition, as the number of system nodes increased, the calculation time did not increase exponentially. In summary, the IEEE 33-node grid and PG&E 69-node grid simulations showed that the proposed method could significantly improve the calculation speed while ensuring precision.

5.2.2. Comparison with the Existing Decentralized Method

The optimization results for the PG&E 69-node grid are shown in

Table 8. Compared optimization results of the PG&E 69-node grid.

Method	Average Calculation Time at Each Iteration	Number of Iterations	Total Calculation Time
Proposed method	1.98 s	4	7.46 s
ADMM	5.03 s	43	183.63 s

and Figure 12. Similar to the IEEE 33-node grid, the proposed method only needed four iterations to converge, while the ADMM needed 43 iterations. Meanwhile, as shown in Table 8, we can see that when the system was transformed from 33 nodes to 69 nodes, the total calculation time of the method proposed in this paper increased by 48.02%, and the average calculation time at each iteration increased by 22.98%. For the ADMM method, when the system was transformed from 33 to 69 nodes, the total calculation time increased by 62.69%, and the average calculation time at each iteration increased by 84.38%, which means the proposed method was more suitable for the application in the power grid with multiple nodes.

6. Conclusions

This paper constructed linear expressions for the node voltage security constraints based on the respective topological structures and boundary information of the distribution grid and VPPs. Then, a linear coordinated economic dispatch method was proposed for the distribution grid with VPPs. Since the constraints were linear and the established model was quadratic, the optimization process and the clearing price determination were simplified. The results from the simulation showed the following.

(1)

Since the proposed method used the Jacobian matrix to transform the nonlinear voltage constraints into the linear combination of the node power injection, the objective function had the same variables as those in the constraint conditions, simplifying the optimal model. In contrast to the current distributed methods, the calculation time was reduced several times due to the fast speed in solving the quadratic optimization model and determining the electricity clearing price.

(2)

Based on the boundary information, including the amount and price of electricity transacted, the distribution grid and the VPPs can adjust their controllable devices to maximize economic returns. The proposed economic dispatch method effectively alleviated the power flow violation limits and facilitated friendly collaborative interaction between the VPPs and the distribution grid.