New Strategy on Power Absorption of a Concentric Two-Body Wave Energy Converter

Abstract

The wave energy converter (WEC) system, which extracts electricity through the relative heave motion of two concentric cylinders, comprises an inner cylinder and a torus-type outer cylinder sliding along the inner cylinder. To maximize the relative heave motion between two cylinders, the natural frequencies of the two cylinders must be precisely tuned to resonate and be situated on each side of the peak frequency of the wave spectrum. However, the demerit of this strategy is that it demands a deep draft of each cylinder for tuning, and a large-scale PTO damping device is necessary for mechanical power amplified by resonance. As an alternative to efficient and stable WECs, we adopt a new strategy in which the outer cylinder follows the incoming waves and the motion of the inner one is restricted to be minimal using a heave disk. The viscous damping due to formation of vortices at the disk edge is realized by the drag force in the Morison equation. The developed hydrodynamic model of two-body WEC based on a matched eigenfunction expansion method (MEEM) is applied to irregular waves characterized by significant wave height and peak period. It is found that the present two-body WEC with heave disk produces wave energy stably across a wide range of wave frequencies compared to the previous two-body WECs using resonance.

1. Introduction

Wave energy, being a clean and inexhaustible source of energy, has the potential to become one of the most promising renewable and environmentally friendly energy options in the future [1,2]. From the beginning of wave energy research, a significant emphasis among researchers has been directed towards tuning the WEC system to resonate with the incoming wave [3,4,5,6]. A widely accepted fact is that a point absorber system that resonates with the incoming wave experiences greater amplitude and velocity, resulting in higher transfer of wave energy compared to a system operating out of resonance. Thus, the general strategy would be to choose the natural frequency of the point absorber to be in resonance with the dominant wave frequencies at the installation sea site. This has led to the idea of a point absorber system with two bodies. By choosing two resonant frequencies existing in a two-body WEC system apart from the peak frequency of the incident wave spectrum, the extraction of wave energy can be maximized [7,8]. The authors of [7] presented a strategy of intentional mismatching of the heave natural frequencies of the inner and outer body and the peak frequency of the target spectrum. This can result in greater extraction of high-quantity power across a wider range of wave conditions. If there is a gap between two concentric bodies, gap resonance might affect motion response and wave loads. In [9], the authors presented a numerical analysis of the transient fluid resonance phenomenon inside a narrow gap between two adjacent boxes excited by the incident waves. In [10], numerical and experimental investigations were carried out into fluid resonance in a narrow gap between two side-by-side vessels.

Heave plates have primarily been used to stabilize the motion of floating offshore structures. Heave plates were first installed on spar-type drilling platforms in the late 1990s, and have proven to be an effective measure of reducing the motion responses of offshore platforms in harsh waves [11]. Much research has subsequently been performed considering the application of heave plates for motion reduction of offshore structures. The hydrodynamic performance of an attached heave plate can be described in terms of damping and added mass. The heave natural frequency of the system decreases as the added mass by the heave plate increases. In general, the viscous damping is experimentally and numerically determined by the free-decay test. It is common to model viscous damping due to edge vortices formed on the heave plate’s edge using the drag force in the Morison equation. In this way, the performance of the heave plate can be quantified by the drag coefficient of the heave plate. Several studies [12,13,14,15] have attempted to identify design parameters that affect the drag coefficient of heave plates. The drag force is generated by the creation of vortices around sharp edges; thus, the drag coefficient of a heave plate is dependent on the ratio of the edge length to the surface area, the thickness of the plate, and the shape of the edges. It has been found that thinner plates generate stronger vortices, increasing the drag coefficient of the plate. The authors of [12] performed a comprehensive analysis in which they systematically tested the effect of key design parameters on hydrodynamic performance at varying KC (Keulegan–Carpenter) numbers and values of the frequency parameter β. The varied parameters included the submerged distance from the free surface, plate porosity, porous hole size, plate thickness-to-width ratio, edge shape, and the spacing of stacked heave plates. The authors of [16] reported numerical and experimental hydrodynamic assessments of a heaving porous disk and presented the drag coefficient in terms of KC and porosity. The existing literature on heave plates provides a strong base for further research on the use of heave plates for wave energy conversion.

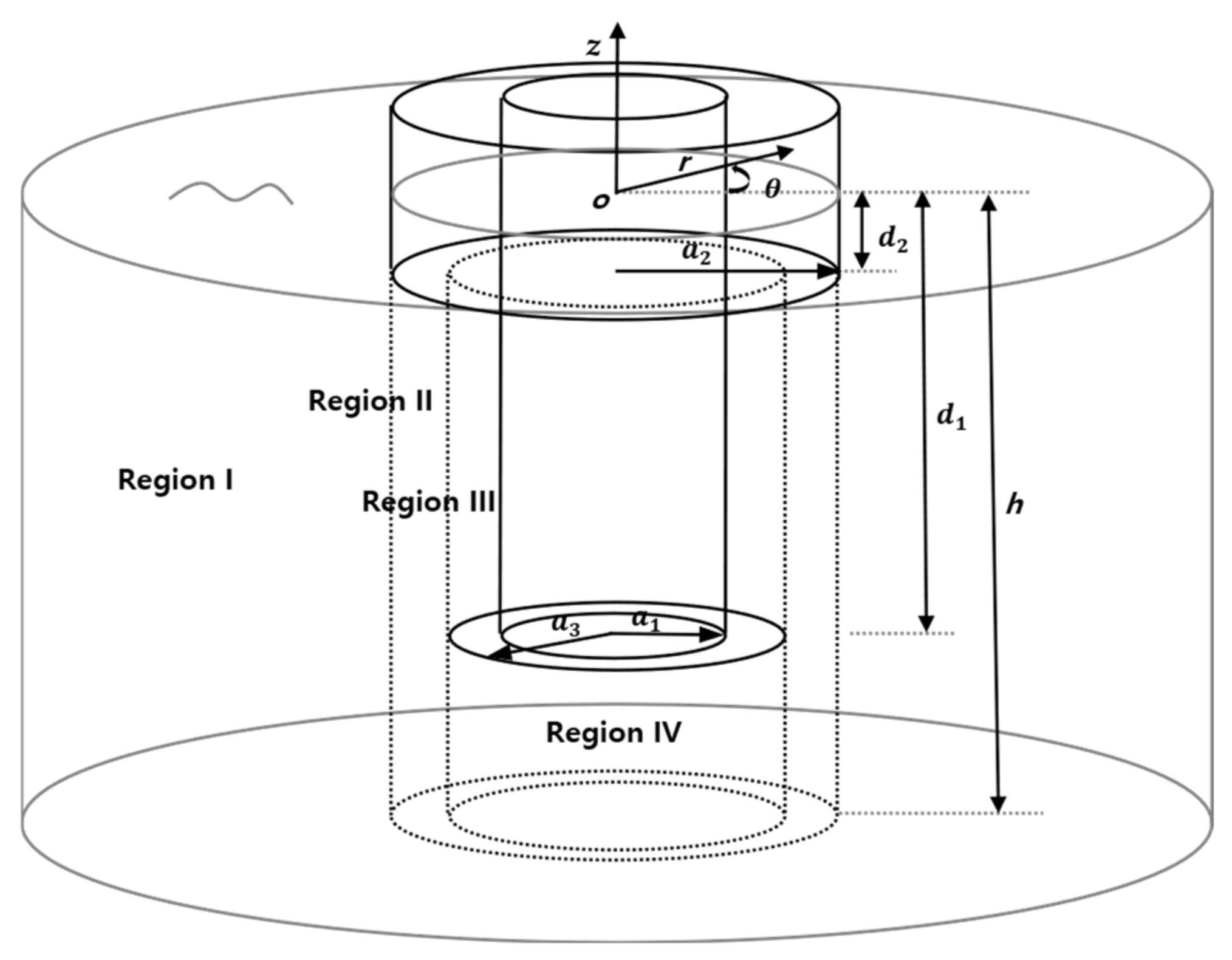
The present study focuses on determining the hydrodynamic coefficients (i.e., added mass and radiation damping) using a MEEM-based analytical method for a heaving two-cylinder system. The system is composed of an inner cylinder with a heave disk attached at the bottom and a torus-shaped outer cylinder with a minimal gap. Figure 1 shows the conceptual design of the presented two-body WEC system; the inner cylinder moves vertically with minimal friction by sliding through rollers that are connected to the outer cylinder. The authors of [17,18] reported hydrodynamic parameters for similar two-body axisymmetric heaving compound cylinders for the UC Berkeley wave energy device. The relative heave motion of two bodies has been used to extract wave energy. A similar study was first performed in [19] and reported hydrodynamic coefficients of two concentric surface-piercing truncated circular cylinders using the eigenfunction expansion method under the linear potential theory. The authors of [7] presented the hydrodynamic forces using the matched eigenfunction expansion method for the radiation and diffraction problem of coupled two-body systems.

In this study, under the assumption of linear wave theory, the radiation and diffraction problems are solved using the method of eigenfunction expansions [7,19,20,21,22,23,24,25]. The presented two-body WEC model is achieved by designing the outer body in the shape of a torus, which floats on the water with a larger waterplane area and a relatively shallower draft. Meanwhile, the inner body can have a smaller waterplane area and a lower resonance frequency by attaching a heave plate to the bottom. This design allows the outer body to follow the waves without resonance during WEC operation as well as for the inner body to have reduced heave motion due to the attached heave plate. In this way, the relative motion is enhanced over a wider frequency range and the need for site-specific design choices, such as aligning the natural frequency of the WEC system with the peak frequency of a sea site to achieve resonance, is eliminated. In addition, the peak-to-average power ratio is greatly reduced, helping to reduce mechanical and electrical PTO (Power Take-off) device overrating. Another merit is the capability to extend the available frequency range, though with some loss of extracted power. To realize the effect of the heave disk, the viscous damping dominated by the formation of vortices at the edge of the disk is modeled using the equivalent linearized drag force with the Morison equation. The drag coefficient is empirically expressed as a function of the KC number by experiments [16]. The optimal power of a two-body WEC has been extensively investigated for various design parameters in irregular-wave conditions.

2. Mathematical Formulation

Here, we have investigated the extracted power from two concentric heaving bodies (inner cylindrical body and torus outer body) with radius $a_1,a_2$ and draft $d_1$, $d_2$ floating in water of uniform depth $h$. The gap between the two bodies is very small, and the friction between them is neglected. A solid heave disk with a radius of $a_3$ is attached to the bottom of the inner body. The two-body WEC model is assumed to move in the heave direction. Let $w_j\left(t\right), \left(j=1,2\right)$ be the velocities of the heaving motion of the inner and outer bodies. The definition sketch for the two concentric bodies is shown in Figure 1. The cylindrical coordinates are chosen with the origin at the center of the inner body on the free surface and the z-axis pointing vertically upward. Assuming harmonic motion of frequency $\omega$ and supposing that the fluid is inviscid, incompressible, and its motion is irrotational, the fluid velocity can be described by the gradient of the velocity potential: $\Phi (r,\theta ,z,t)=\mathrm{Re}\left\{\varphi (r,\theta ,z)e^{-i\omega t}\right\}$. From the linear potential theory, the velocity potential can be decomposed as $\varphi (r,\theta ,z)=-\frac{igA}{\omega }{\varphi }_3(r,\theta ,z)+{\displaystyle \sum _{j=1}^2{w}_j{\varphi }_j(r,\theta ,z)}$, where $A$ is the incident wave amplitude, $w_j$ is the amplitude of the generalized body velocity of each body (j = 1, inner body, j = 2, outer body), ${\varphi }_3^{}$ is the scattering potential representing the wave scattering by the stationary body in incident waves, which is expressed by the sum of the incident wave potential (${\varphi }_0^{}$) and diffraction potential (${\varphi }_4^{}$), and ${\varphi }_j$ is the radiation potential due to the heaving motion of each body with unit body velocity.

The wave field can be described by the velocity potentials ${\varphi }_j\left(r,\theta ,z\right),j=1,2,3$, which satisfy the following boundary-value problem:

$$\begin{array}{l}{\nabla }^2{\varphi }_j=0, \mathrm{in} \mathrm{the} \mathrm{fluid} \mathrm{domain}\\ \frac{\partial {\varphi }_j}{\partial z}-\frac{{\omega }^2}{g}{\varphi }_j=0, \mathrm{on} z=0.\\ \frac{\partial {\varphi }_j}{\partial z}=0, \mathrm{on} z=-h.\\ \left\{\begin{array}{l}\frac{\partial {\varphi }_j}{\partial n}=n_z, j=1,2 \mathrm{on} \mathrm{the} \mathrm{body}\\ \frac{\partial {\varphi }_4}{\partial n}=-\frac{\partial {\varphi }_0}{\partial n}, \mathrm{on} \mathrm{the} \mathrm{body}\end{array}\right.\\ \underset{r\to \infty }{\lim }\sqrt{r}\left[\frac{\partial {\varphi }_j}{\partial r}-i{k}_1{\varphi }_j\right]=0.\end{array}$$

(1)

2.1. Velocity Potentials

The radiation problem corresponds to the case in which each body is forced to oscillate vertically in the absence of incident waves, while the diffraction problem means the case in which the body is held fixed in the incident waves. The radiation and scattering potential can be expressed by ${\varphi }_j(r,\theta ,z)={\displaystyle \sum _{l=0}^{\infty }{\varphi }_{jl}(r,z)\cos (l\theta )}, j=1,2,3$ by means of the variable separation method. The term $l=0$ among infinite series provides a contribution to the wave exciting force and hydrodynamic force in the vertical direction.

To apply the matched eigenfunction expansion method (MEEM) to the present radiation problem, the fluid is divided into the regions (I), (II), (III), and (IV). Region (I) is defined by $r\ge a_2,-h\le z\le 0$, region (II) by $a_3\le r\le a_2,-h\le z\le -d_2$, region (III) by $a_1\le r\le a_3,-d_1\le z\le -d_2$, and region (IV) by $0\le r\le a_3,-h\le z\le -d_1$.

The velocity potential (${\varphi }_j^{(1)}$) in region (I) can be written as the sum of the particular (${\widehat{\varphi }}_{j0}^{(1)}$) and homogeneous (${\tilde{\varphi }}_{j0}^{(1)}$) solutions, and can be expressed by

$$\begin{array}{cc}\hfill {\varphi }_{j0}^{(1)}(r,z)& ={\widehat{\varphi }}_{j0}^{(1)}(r,z)+{\tilde{\varphi }}_{j0}^{(1)}(r,z),\hfill \\ & =J_0(k_{1}r)\frac{f_{10}(z)}{f_{10}(0)}{\delta }_{j3}+{\displaystyle \sum _{n=0}^{\infty }{A}_{jn}^{}\frac{K_0(k_{1n}r)}{K_0(k_{1n}{a}_2)}{f}_{1n}(z)},\hfill \end{array}$$

(2)

where $n=0$ denotes propagating mode, $n\ge 1$ represents evanescent modes, and $K_0$ is a modified Bessel function.

The eigenvalues ($k_{10}=-i{k}_1 , k_{1n}, n=1,2,\dots$) in region (I) satisfy the dispersion relation $k_{1n}\tan k_{1n}h=-{\omega }^2/g$, and the normalized eigenfunctions can be written as

$$\begin{array}{l}{f}_{1n}(z)=N_{1n}^{-1}\cos k_{1n}(z+h), n=0,1,2,\dots \\ {\left(N_{1n}\right)}^2=\frac{1}{2}\left(1+\frac{\sin 2k_{1n}h}{2k_{1n}h}\right).\end{array}$$

(3)

The eigenfunctions $f_{1n}(z)$ satisfy the following orthogonal relation:

$$\frac{1}{h}{\displaystyle {\int }_{-h}^0{f}_{1m}(z)f_{1n}(z)dz}={\delta }_{mn},$$

(4)

where ${\delta }_{mn}$ is the Kronecker delta function, defined by ${\delta }_{mn}=1$ if $m=n$ and ${\delta }_{mn}=0$ if $m\ne n$.

The velocity potential in region (II) can be written as the sum of the particular (${\widehat{\varphi }}_{j0}^{(2)}$) and homogeneous (${\tilde{\varphi }}_{j0}^{(2)}$) solutions.

$$\begin{array}{ll}\hfill {\varphi }_{j0}^{(2)}(r,z)& ={\widehat{\varphi }}_{j0}^{(2)}(r,z)+{\tilde{\varphi }}_{j0}^{(2)}(r,z),\hfill \\ & =\frac{1}{2(h-d_2)}\left({(z+h)}^2-\frac{r^2}{2}\right){\delta }_{2j}+{\displaystyle \sum _{n=0}^{\infty }{\epsilon }_n\left[R_n^{}(r)B_{jn}^{}+{\tilde{R}}_n^{}(r){\tilde{B}}_{jn}^{}\right]\cos {\mu }_n(z+h)},\hfill \end{array}$$

(5)

with

for $n=0$

$$\begin{array}{l}{R}_0^{}(r)=\frac{\ln (r/a_3)}{\ln (a_2/a_3)},\\ {\tilde{R}}_0^{}(r)=\frac{\ln (a_2/r)}{\ln (a_2/a_3)}.\end{array}$$

for $n\ge 1$

$$\begin{array}{l}{R}_n^{}(r)=\frac{K_0({\mu }_n{a}_3)I_0({\mu }_{n}r)-K_0({\mu }_{n}r)I_l({\mu }_n{a}_3)}{K_0({\mu }_n{a}_3)I_0({\mu }_n{a}_2)-K_0({\mu }_n{a}_2)I_0({\mu }_n{a}_3)},\\ {\tilde{R}}_n^{}(r)=\frac{K_0({\mu }_{n}r)I_0({\mu }_n{a}_2)-K_0({\mu }_n{a}_2)I_0({\mu }_{n}r)}{K_0({\mu }_n{a}_3)I_0({\mu }_n{a}_2)-K_0({\mu }_n{a}_2)I_0({\mu }_n{a}_3)}.\end{array}$$

where ${\epsilon }_n=1$ if $n=0$ and ${\epsilon }_n=2$ if $n\ge 1$; moreover, ${\mu }_n=n\pi /(h-d_2),n=0,1,2,\dots$.

The velocity potential in region (III) can be written as the sum of the particular (${\widehat{\varphi }}_{j0}^{(3)}$) and omogeneous (${\tilde{\varphi }}_{j0}^{(3)}$) solutions.

$$\begin{array}{l}{\varphi }_{j0}^{(3)}(r,z)={\widehat{\varphi }}_{j0}^{(3)}(r,z)+{\tilde{\varphi }}_{j0}^{(3)}(r,z),\\ =\frac{1}{2(d_1-d_2)}\left\{[{(z+d_1)}^2-\frac{r^2}{2}+a_1^2\ln r]{\delta }_{2j}-[{(z+d_2)}^2-\frac{r^2}{2}+a_1^2\ln r]{\delta }_{1j}\right\}\\ +{\displaystyle \sum _{n=0}^{\infty }{\epsilon }_n{C}_{jn}\left[I_0({\lambda }_{n}r)-\frac{I_0{}^{\prime }({\lambda }_n{a}_1)}{K_0{}^{\prime }({\lambda }_n{a}_1)}{K}_0({\lambda }_{n}r)\right]\cos {\lambda }_n(z+d_1)}.\end{array}$$

(6)

where ${\lambda }_n=n\pi /(d_1-d_2),n=0,1,2,\dots$.

Finally, the radiation potential in region (IV) is provided by

$$\begin{array}{l}{\varphi }_{j0}^{(4)}(r,z)={\widehat{\varphi }}_{j0}^{(4)}(r,z)+{\tilde{\varphi }}_{j0}^{(4)}(r,z),\\ =\frac{1}{2(h-d_1)}\left({(z+h)}^2-\frac{r^2}{2}\right){\delta }_{1j}+{\displaystyle \sum _{n=0}^{\infty }{\epsilon }_n{D}_{jn}\frac{I_0({\nu }_{n}r)}{I_0({\nu }_n{a}_3)}\cos {\nu }_n(z+h)}.\end{array}$$

(7)

where ${\nu }_n=n\pi /(h-d_1),n=0,1,2,\dots$.

2.2. Matching Procedure

The velocity potential and radial velocity must be matched on the vertical boundary $r=a_2 ,a_3$.

$${\varphi }_{j0}^{(1)}={\varphi }_{j0}^{(2)},\hspace{1em}-h\le z\le -d_2, r=a_2$$

(8)

$$\frac{\partial {\varphi }_{j0}^{(1)}}{\partial r}=\left\{\begin{array}{l}0,\hspace{1em}-d_2\le z\le 0\\ \frac{\partial {\varphi }_{j0}^{(2)}}{\partial r},\hspace{1em}-h\le z\le -d_2\end{array}\right.,r=a_2$$

(9)

$${\varphi }_{j0}^{(2)}=\left\{\begin{array}{l}{\varphi }_{j0}^{(3)},\hspace{1em}-d_1\le z\le -d_2\\ {\varphi }_{j0}^{(4)},\hspace{1em}-h\le z\le -d_1\end{array}\right. ,r=a_3$$

(10)

$$\frac{\partial {\varphi }_{j0}^{(2)}}{\partial r}=\left\{\begin{array}{l}\frac{\partial {\varphi }_{j0}^{(3)}}{\partial r},\hspace{1em}-d_1\le z\le -d_2\\ \frac{\partial {\varphi }_{j0}^{(4)}}{\partial r},\hspace{1em}-h\le z\le -d_1\end{array}\right.,r=a_3$$

(11)

After substituting Equations (2) and (5) into Equations (8) and (9), then multiplying both sides by $\{\cos {\mu }_m(z+h),m=0,1,2,\dots \}$ and $\{f_{1m}(z),m=0,1,2,\dots \}$, we integrate the resulting expression over their regions of validity. When using the orthogonality of the eigenfunctions of each region, the following sets of equations that relate the unknown coefficients of adjacent fluid regions can be obtained

$$B_{jm}^{}={\displaystyle \sum _{n=0}^{\infty }{T}_{mn}{A}_{jn}^{}}+{\alpha }_{jm}, m=0,1,2,\dots$$

(12)

$$q_m{A}_{jm}^{}={\gamma }_{jm}+{\displaystyle \sum _{n=0}^{\infty }{\epsilon }_n\left[W_{ n}^{}(a_2)B_{jn}^{}+{\tilde{W}}_{ n}^{}(a_2){\tilde{B}}_{jn}^{}\right]T_{nm}},\hspace{1em}m=0,1,2,\dots$$

(13)

where

$$q_m=k_{1m}h\frac{K_0{}^{\prime }(k_{1m}{a}_2)}{K_0^{}(k_{1m}{a}_2)},$$

$$T_{mn}=\frac{1}{(h-d_2)}{\displaystyle {\int }_{-h}^{-d_2}{f}_{1n}(z)\cos {\mu }_m(z+h)dz},$$

$$\begin{array}{l}{\alpha }_{jm}=\left\{\begin{array}{l}0, j=1\\ -\frac{1}{2{(h-d_2)}^2}{\displaystyle {\int }_{-h}^{-d_2}\left({(z+h)}^2-\frac{a_2^2}{2}\right)\cos {\mu }_m(z+h)dz}, j=2\\ \frac{J_0(k_1{a}_2)}{f_{10}(0)}{T}_{m0}, j=3\end{array}\right.,\\ {\gamma }_{jm}=\left\{\begin{array}{l}0, j=1\\ -\frac{a_2}{2(h-d_2)}{\displaystyle {\int }_{-h}^{-d_2}{f}_{1m}(z)dz}, j=2\\ -\frac{k_{1}h{J}_0{}^{\prime }(k_1{a}_2)}{f_{10}(0)}{\delta }_{m0}, j=3\end{array}\right..\end{array}$$

After substituting Equations (5)–(7) into Equation (10), then multiplying both sides by $\{\cos {\lambda }_m(z+d_1),m=0,1,2,\dots \}$ and $\{\cos {\nu }_m(z+h),m=0,1,2,\dots \}$, we integrate the resulting expression over their regions of validity. The following sets of equations can be obtained relating the unknown coefficients of adjacent fluid regions:

$$\begin{array}{l}{C}_{jm}^{}=\frac{{\displaystyle \sum _{n=0}^{\infty }{\epsilon }_n{G}_{mn}{\tilde{B}}_{jn}^{}}+{\sigma }_{jm}}{s_m},\\ D_{jm}^{}={\displaystyle \sum _{n=0}^{\infty }{\epsilon }_n{H}_{mn}{\tilde{B}}_{jn}^{}}+{\beta }_{jm},\end{array}$$

(14)

where

$$G_{mn}=\frac{1}{(d_1-d_2)}{\displaystyle {\int }_{-d_1}^{-d_2}\cos {\mu }_n(z+h)\cos {\lambda }_m(z+d_1)dz},$$

$$H_{mn}=\frac{1}{(h-d_1)}{\displaystyle {\int }_{-h}^{-d_1}\cos {\mu }_n(z+h)\cos {\nu }_m(z+h)dz},$$

$$s_m=I_0({\lambda }_m{a}_3)-\frac{I_0{}^{\prime }({\lambda }_m{a}_1)}{K_0{}^{\prime }({\lambda }_m{a}_1)}{K}_0({\lambda }_m{a}_3),$$

$${\sigma }_{jm}=\left\{\begin{array}{l}\frac{1}{2{(d_1-d_2)}^2}{\displaystyle {\int }_{-d_1}^{-d_2}\left({(z+d_2)}^2-\frac{a_3^2}{2}+a_1^2\ln a_3\right)\cos {\lambda }_m(z+d_1)dz}, j=1\\ \frac{1}{2(h-d_2)(d_1-d_2)}{\displaystyle {\int }_{-d_1}^{-d_2}\left({(z+h)}^2-\frac{a_3^2}{2}\right)\cos {\lambda }_m(z+d_1)dz}\\ -\frac{1}{2{(d_1-d_2)}^2}{\displaystyle {\int }_{-d_1}^{-d_2}\left({(z+d_1)}^2-\frac{a_3^2}{2}+a_1^2\ln a_3\right)\cos {\lambda }_m(z+d_1)dz}, j=2\\ 0,\hspace{1em}j=3\end{array}\right.$$

$${\beta }_{jm}=\left\{\begin{array}{l}-\frac{1}{2{(h-d_1)}^2}{\displaystyle {\int }_{-h}^{-d_1}\left({(z+h)}^2-\frac{a_3^2}{2}\right)\cos {\nu }_m(z+h)dz}, j=1\\ \frac{1}{2(h-d_1)(h-d_2)}{\displaystyle {\int }_{-h}^{-d_1}\left({(z+h)}^2-\frac{a_3^2}{2}\right)\cos {\nu }_m(z+h)dz}, j=2\\ \\ 0, j=3\end{array}\right.$$

When substituting Equations (5)–(7) into Equation (11), multiplying both sides by the eigenfunction $\{\cos {\mu }_m(z+h),m=0,1,2,\dots \}$, and integrating from −h to $-d_2$, the following equation is obtained:

$$W_m(a_3)B_{jm}^{}+{\tilde{W}}_m(a_3){\tilde{B}}_{jm}^{}={\tau }_{jm}+{\displaystyle \sum _{n=0}^{\infty }{\epsilon }_n{w}_n{C}_{jn}^{}{G}_{nm}}+{\displaystyle \sum _{n=0}^{\infty }{\epsilon }_n{p}_n{D}_{jn}^{}{H}_{nm}},$$

(15)

$$\mathrm{where} p_{ n}={\nu }_n(h-d_1)\frac{I_0{}^{\prime }({\nu }_n{a}_3)}{I_0({\nu }_n{a}_3)}, w_{ n}={\lambda }_n(d_1-d_2)\left[I_0{}^{\prime }({\lambda }_n{a}_3)-\frac{I_0{}^{\prime }({\lambda }_n{a}_1)}{K_0{}^{\prime }({\lambda }_n{a}_1)}{K}_0{}^{\prime }({\lambda }_n{a}_3)\right].$$

$${\tau }_{jm}=\left\{\begin{array}{l}-\frac{a_3}{2(h-d_1)}{\displaystyle {\int }_{-h}^{-d_1}\cos {\mu }_m(z+h)dz}+\frac{1}{2(d_1-d_2)}\left(\frac{a_3^2-a_1^2}{a_3}\right){\displaystyle {\int }_{-d_1}^{-d_2}\cos {\mu }_m(z+h)dz}, j=1\\ \frac{a_3}{2(h-d_2)}{\displaystyle {\int }_{-h}^{-d_2}\cos {\mu }_m(z+h)dz}-\frac{1}{2(d_1-d_2)}\left(\frac{a_3^2-a_1^2}{a_3}\right){\displaystyle {\int }_{-d_1}^{-d_2}\cos {\mu }_m(z+h)dz}, j=2\\ \\ 0, j=3\end{array}\right.$$

The solutions of the infinite system obtained with Equations (12)–(15) provide the unknown coefficients in each fluid region. For the numerical calculation, infinite series are truncated after N. When eliminating $A_{jn}^{},C_{jn}^{},D_{jn}^{}$, we obtain the simultaneous algebraic equations for the unknown coefficients $B_{jn}^{},{\tilde{B}}_{jn}^{}$ for the radiation problem by the heaving motion of the inner body ($j=1$) and outer body ($j=2$) and for the diffraction problem ($j=3$) when the body is held fixed in incoming waves.

$$\begin{array}{l}{B}_{jm}^{}-{\displaystyle \sum _{k=0}^N{\epsilon }_k\left({\displaystyle \sum _{n=0}^N\frac{T_{mn}^{}{T}_{kn}^{}{W}_k(a_2)}{q_n}}\right)B_{jk}^{}}-{\displaystyle \sum _{k=0}^N{\epsilon }_k\left({\displaystyle \sum _{n=0}^N\frac{T_{mn}^{}{T}_{kn}^{}{\tilde{W}}_k(a_2)}{q_n}}\right){\tilde{B}}_{jk}^{}}\\ ={\alpha }_{jm}+{\displaystyle \sum _{n=0}^N\frac{{\gamma }_{jn}{T}_{mn}^{}}{q_n}},\hspace{1em}\mathrm{for} m=0,1,2,\dots ,N\end{array}$$

(16)

$$\begin{array}{l}{W}_m(a_3)B_{jm}^{}+{\tilde{W}}_m(a_3){\tilde{B}}_{jm}^{}-{\displaystyle \sum _{k=0}^N{\epsilon }_k{\displaystyle \sum _{n=0}^N{\epsilon }_n\left(\frac{w_n{G}_{nk}^{}{G}_{nm}^{}}{s_n}+p_n{H}_{nk}^{}{H}_{nm}^{}\right)}{\tilde{B}}_{jk}^{}}\\ ={\tau }_{jm}+{\displaystyle \sum _{n=0}^N{\epsilon }_n\left(\frac{w_n{\sigma }_{jn}{G}_{nm}^{}}{s_n}+p_n{\beta }_{jn}{H}_{nm}^{}\right)},\hspace{1em}\mathrm{for} m=0,1,2,\dots ,N\end{array}$$

(17)

The unknown coefficients $B_{jn}^{},{\tilde{B}}_{jn}^{},(j=1,2,3;n=1,2,\dots ,N)$ can be readily obtained by solving the above algebraic equation. The remaining unknown coefficients $A_{jn}^{},C_{jn}^{},D_{jn}^{}$ can be readily obtained from Equations (13) and (14).

2.3. Hydrodynamic Forces

For the diffraction problem, the vertical wave exciting force $F_i^E=\mathrm{Re}\left\{A{f}_i^E{e}^{-i\omega t}\right\}$ on the fixed inner body ($i=1$) and outer body ($i=2$) can be found by integrating the dynamic pressure over the surface of the body.

$$\begin{array}{l}{f}_1^E=2\rho g\pi \left\{{\displaystyle {\int }_0^{a_3}r{\varphi }_{30}^{(4)}(r,-d_1)dr}-{\displaystyle {\int }_{a_1}^{a_3}r{\varphi }_{30}^{(3)}(r,-d_1)dr}\right\},\\ f_2^E=2\rho g\pi \left\{{\displaystyle {\int }_{a_3}^{a_2}r{\varphi }_{30}^{(2)}(r,-d_2)dr}+{\displaystyle {\int }_{a_1}^{a_3}r{\varphi }_{30}^{(3)}(r,-d_2)dr}\right\}.\end{array}$$

(18)

The hydrodynamic vertical forces ($F_{ij}^R(t)=\mathrm{Re}\left\{w_j{f}_{ij}^R{e}^{-i\omega t}\right\}$) acting on the inner body ($i=1$) and outer body ($i=2$) due to the heaving motion of the body ($j=1,2$) are found by integrating the corresponding pressure over each body surface.

$$\begin{array}{l}{f}_{1j}^R=2\pi i\omega \rho \left\{{\displaystyle {\int }_0^{a_3}r{\varphi }_{j0}^{(4)}(r,-d_1)dr}-{\displaystyle {\int }_{a_1}^{a_3}r{\varphi }_{j0}^{(3)}(r,-d_1)dr}\right\},\\ f_{2j}^R=2\pi i\omega \rho \left\{{\displaystyle {\int }_{a_3}^{a_2}r{\varphi }_{j0}^{(2)}(r,-d_2)dr}+{\displaystyle {\int }_{a_1}^{a_3}r{\varphi }_{j0}^{(3)}(r,-d_2)dr}\right\}.\end{array}$$

(19)

It is convenient to further decompose the hydrodynamic forces into real and imaginary parts. The real part ($a_{ij}$) and imaginary part ($b_{ij}$) are termed the added mass and radiation damping coefficient.

$$a_{ij}=\mathrm{Im}\left\{f_{ij}^R/\omega \right\},b_{ij}=-\mathrm{Re}\left\{f_{ij}^R\right\},\hspace{1em}(i,j=1,2)$$

(20)

Using the Haskind relation, we can obtain the approximate solution for the wave exciting forces with the radiation potential ${\varphi }_i^{},(i=1,2)$,

$$\begin{array}{ll}\hfill f_i^E& =i\omega \rho {\displaystyle \underset{S_B}{\iint }\left({\varphi }_0+{\varphi }_4\right)n_{i }}dS\hfill \\ & =i\omega \rho {\displaystyle \underset{S_B}{\iint }\left({\varphi }_0\frac{\partial {\varphi }_i^{}}{\partial n}+{\varphi }_i^{}\frac{\partial {\varphi }_4}{\partial n}\right)}dS\hfill \\ & =-i\omega \rho {\displaystyle \underset{S_{\infty }}{\iint }\left({\varphi }_0\frac{\partial {\varphi }_i^{}}{\partial n}-{\varphi }_i^{}\frac{\partial {\varphi }_0}{\partial n}\right)}dS=-\frac{4i\omega \rho }{k_1}{C}_g{\tilde{A}}_i, (i=1,2)\hfill \end{array}$$

(21)

where $C_g=\frac{\omega }{2k_1}\left(1+\frac{2k_{1}h}{\sinh (2k_{1}h)}\right)$ is the group velocity and ${\tilde{A}}_i=\frac{\cosh \left(k_{1}h\right)A_{i0}}{H_0^{(1)}(k_1{a}_2)N_{10}}$ represents the radiated wave amplitude in the far field caused by the heaving inner and outer bodies.

2.4. Equation of Motion

A two-body WEC system generates electricity from the relative heave motion of two concentric bodies. In this case, each body has to function as a magnet or amateur (coil) in a wet condition. In the present study, we installed a heave disk at the bottom of the inner body to reduce the heave motion of the inner body. The PTO system can be simplified as an equivalent linear damping force.

The dynamic responses of the two-body WEC are obtained by solving the coupled equations of the heave motion of two bodies. These coupled equations include the hydrostatic restoring forces, wave exciting forces, radiation forces, PTO forces, and viscous damping forces. They may be written as

$$\begin{array}{l}\left[-i\omega (m_1+a_{11})+(b_{11}+b_{PTO}+b_{\nu 1}+\Delta b)-\frac{c_{11}}{i\omega }\right]w_1+\left[-i\omega a_{12}+(b_{12}-b_{PTO})\right]w_2=A{f}_1^E\\ \left[-i\omega a_{21}+(b_{21}-b_{PTO})\right]w_1+\left[-i\omega (m_2+a_{22})+(b_{22}+b_{PTO}+b_{\nu 2})-\frac{c_{22}}{i\omega }\right]w_2=A{f}_2^E\end{array}$$

(22)

where $m_1,m_2$ are the masses of the inner and outer body, respectively, $c_{11}(=\rho g\pi a_1^2)$ and $c_{22}(=\rho g\pi (a_2^2-a_1^2))$ are the heave restoring force coefficients of the inner and outer body, $a_{ij},b_{ij}$ are the frequency-dependent added mass and radiation damping coefficient, $b_{PTO}$ is the PTO damping coefficient, and $f_{vi}=b_{\nu i}{w}_i (i=1,2)$ are the viscous damping forces for each body, where $b_{\nu i}$ is the viscous damping coefficient. The viscous damping coefficients are expressed by $b_{\nu i}=\frac{2{\kappa }_i{c}_{ii}}{{\omega }_{Ni}}-b_{ii}({\omega }_{Ni})$, where the undamped natural frequency is provided by ${\omega }_{Ni}=\sqrt{\frac{c_{ii}}{m_i+a_{ii}({\omega }_{Ni})}},\hspace{1em}(i=1,2)$. The damping factor ${\kappa }_i$ can be determined from a free-decay test in still water.

The coupled equations of motion are solved to determine the complex heave velocity amplitude ($w_j,j=1,2$) of each body. The corresponding complex heave amplitude of each body is determined by ${\xi }_j=i{w}_j/\omega$.

2.5. Viscous Damping

As mentioned above, viscous damping can be commonly considered by conducting a free-decay test. However, when the viscous damping is dominantly attributed to vortices formation at the outer edge of the heave disk, as in the present model, the viscous damping is added by the drag force, inspired by the Morison equation. The drag force on the heave disk attached to the inner body is expressed as

$$\Delta f^V=\frac{1}{2}\rho C_d{S}_1\left|w_r\right|w_r,$$

(23)

where $\rho$ is the water density, $S_1=\pi a_3^2$ is the projected area of the heave disk, $w_r(=w_1-A{w}_z)$ is the relative heave velocity of the heave disk with respect to an incident wave, and $w_z$ is the vertical water particle velocity of an incident wave at the edge of a heave plate having a unit amplitude

$$w_z=-\frac{ig{k}_1}{\omega }\frac{\sinh k_1(h-d_1)}{\cosh k_{1}h}{J}_0(k_1{a}_3).$$

(24)

Using Lorenz’s principle of equivalent work, the quadratic velocity term in Equation (23) can be linearized as

$$\Delta f^V=\Delta b w_r, \mathrm{with} \Delta b=\frac{4}{3\pi }\rho C_d{S}_1\left|w_r\right|,$$

(25)

where $\Delta b$ is the added damping coefficient due to the installation of the heave disk.

To implement the effect of viscous damping due to the edge vortices of the heave disk, an empirical formula for the drag coefficient $C_d$ in Equation (23) should be determined. The empirical formula for $C_d$ is obtained through curve fitting of the experimental data in the form of $C_d=6.5{\left(KC\right)}^{-1/3}$, as presented in [16], where the $KC$ number is defined as $KC=\pi \left|{\xi }_1\right|/a_3$.

2.6. Extracted Power

Equation (22) can now be rewritten as

$$\begin{array}{l}\left[(b_{11}+b_{PTO}+b_{v1}+\Delta b)-i\omega A_{11}\right]w_1+\left[(b_{12}-b_{PTO})-i\omega a_{12}\right]w_2=A(f_1^E+\Delta b{w}_z),\\ \left[(b_{21}-b_{PTO})-i\omega a_{21}\right]w_1+\left[(b_{22}+b_{PTO}+b_{v2})-i\omega A_{22}\right]w_2=A{f}_2^E,\end{array}$$

(26)

where $A_{11}=(m_1+a_{11})-\frac{c_{11}}{{\omega }^2},A_{22}=(m_2+a_{22})-\frac{c_{22}}{{\omega }^2}$, and $b_{\nu i}(i=1,2)$ can be obtained from the free-decay test without the heave disk.

The solutions of Equation (26) can be written as

$$\begin{array}{l}\frac{w_1}{A}=\frac{(f_1^E+\Delta b{w}_z)G_{22}-f_2^E{G}_{12}}{G_{11}{G}_{22}-G_{12}{G}_{21}},\\ \frac{w_2}{A}=\frac{f_2^E{G}_{11}-(f_1^E+\Delta b{w}_z)G_{21}}{G_{11}{G}_{22}-G_{12}{G}_{21}}.\end{array}$$

(27)

where

$$\begin{array}{l}{G}_{11}=b_{11}+b_{PTO}+b_{v1}+\Delta b-i\omega A_{11},\\ G_{12}=b_{12}-b_{PTO}-i\omega a_{12},\\ G_{21}=b_{21}-b_{PTO}-i\omega a_{21},\\ G_{22}=b_{22}+b_{PTO}+b_{v2}-i\omega A_{22}.\end{array}$$

The relative heave velocity of two bodies can be expressed by

$$\frac{w_1-w_2}{A}=\frac{(f_1^E+\Delta b{w}_z)(G_{22}+G_{21})-f_2^E(G_{12}+G_{11})}{G_{11}{G}_{22}-G_{12}{G}_{21}}.$$

(28)

The nonlinear coupled Equation (26) is solved with an iteration method to determine the heave motion velocity ($w_j,(j=1,2)$) of each body.

The time-averaged extracted power can be obtained as

$$\begin{array}{ll}\hfill \overline{P}& =\frac{1}{2}{b}_{PTO}{\left|w_1-w_2\right|}^2,\hfill \\ & =\frac{1}{2}{A}^2{b}_{PTO}{\left|\frac{(f_1^E+\Delta b{w}_z)(G_{22}+G_{21})-f_2^E(G_{12}+G_{11})}{G_{11}{G}_{22}-G_{12}{G}_{21}}\right|}^2.\hfill \end{array}$$

(29)

For maximization of the extracted power, the PTO damping coefficient requires

$$\frac{d\overline{P}}{d{b}_{PTO}}=0,$$

(30)

which leads to

$${\tilde{b}}_{PTO}=\sqrt{\frac{Y_1^2+{\omega }^2{Y}_3^2}{Y_2^2+{\omega }^2{Y}_4^2}},$$

(31)

where

$$\begin{array}{l}{Y}_1=(b_{11}+b_{v1}+\Delta b)(b_{22}+b_{v2})-b_{12}{b}_{21}-{\omega }^2(A_{11}{A}_{22}-a_{12}{a}_{21}),\\ Y_2=(b_{11}+b_{v1}+\Delta b)+(b_{22}+b_{v2})+b_{12}+b_{21},\\ Y_3=(b_{11}+b_{v1}+\Delta b)A_{22}+(b_{22}+b_{v2})A_{11}-b_{21}{a}_{12}-b_{12}{a}_{21},\\ Y_4=A_{11}+A_{22}+a_{12}+a_{21}.\end{array}$$

As a measure for evaluating the performance of a two-body WEC, the capture width ($CW$) representing the WEC’s efficiency is generally used. The capture width has a length dimension and is expressed as the ratio of the time-averaged extracted power by a WEC to the time-averaged power per unit width of the incident wave.

$$CW=\frac{{\overline{P}}_{opt}}{{\overline{P}}_w}.$$

(32)

where ${\overline{P}}_w(=\frac{1}{2}\rho g{A}^2{C}_g)$ is the time-averaged power per unit width of a regular wave and $C_g$ is the group velocity.

The capture width normalized by the diameter of the outer body, referred to as the capture width ratio ($CWR$), is a measure of the extracted power efficiency in the WEC system. The capture width ratio can be calculated by

$$CWR=\frac{CR}{2a_2}=\frac{{\overline{P}}_{opt}}{2a_2{\overline{P}}_w}.$$

(33)

2.7. Irregular Waves

In the present frequency domain analysis, the root mean square (RMS) value of the relative heave velocity and motion response in irregular waves can be obtained through the following equation [26]:

$$\begin{array}{l}{w}_{1/2}^{RMS}=\sqrt{{\displaystyle {\int }_0^{\infty }\frac{{\left|w_1-w_2\right|}^2}{A^2}\cdot S_{\varsigma }(\omega )d\omega }},\\ {\xi }_{1/2}^{RMS}=\sqrt{{\displaystyle {\int }_0^{\infty }\frac{{\left|{\xi }_1-{\xi }_2\right|}^2}{A^2}\cdot S_{\varsigma }(\omega )d\omega }}.\end{array}$$

(34)

The mean power absorbed in irregular waves can be determined by the following equation [27,28]:

$${\overline{P}}_{irr}={\displaystyle {\int }_0^{\infty }\frac{2\overline{P}(\omega )}{A^2}\cdot S_{\varsigma }(\omega )d\omega }.$$

(35)

where $\overline{P}(\omega )$ is provided by Equation (29) with the particular PTO damping coefficient or optimal PTO values such as ${\tilde{b}}_{PTO}(\omega )$ or ${({\tilde{b}}_{PTO})}_{\max }$. For the incident wave spectrum $S_{\zeta }(\omega )$, the JONSWAP spectrum is used [29]

$$S_{\varsigma }(\omega )=\beta \frac{H_{1/3}^2{\omega }_P^4}{{\omega }^5}\exp \left[-1.25{\left(\frac{\omega }{{\omega }_P}\right)}^{-4}\right]{\gamma }^{\exp \left[-\frac{{(\omega -{\omega }_P)}^2}{2{\sigma }^2{\omega }_P^2}\right]},$$

(36)

$$\mathrm{with} \beta =\frac{0.0624}{0.23+0.0336\gamma -0.185{(1.9+\gamma )}^{-1}}(1.094-0.01915\ln \gamma ),$$

where $H_{1/3}$ is the significant wave height and ${\omega }_P(=2\pi /T_P)$ is the peak frequency. The peakedness factor $\gamma =3.3$, $\sigma =0.07$ for $\omega <{\omega }_P$, and $\sigma =0.09$ for $\omega \ge {\omega }_P$.

In addition, the characteristic periods (energy period, spectral mean period, and zero up-crossing period) are defined as

$$T_e=2\pi \frac{m_{-1}}{m_0},T_{01}=2\pi \frac{m_0}{m_1},T_z=2\pi \sqrt{\frac{m_0}{m_2}},$$

(37)

where $m_n(={\displaystyle {\int }_0^{\infty }{S}_{\varsigma }(\omega ){\omega }^{n}d\omega })$ is the nth-order spectral moment.

With the PTO damping coefficient, we can obtain the nondimensional optimal capture width ratio in irregular waves:

$${\left(CWR\right)}_{irr}=\frac{{\overline{P}}_{irr}}{2a_2{\overline{P}}_{w,irr}},$$

(38)

where the denominator ${\overline{P}}_{w,irr}$ is the irregular wave power per unit width and is provided by

$${\overline{P}}_{w,irr}=\rho g{\displaystyle {\int }_0^{\infty }{S}_{\zeta }(\omega )C_{g}d\omega \approx \frac{1}{64\pi }}\rho g^2{H}_{1/3}^2{T}_e$$

(39)

3. Experiments

The experiment was conducted in a glass-walled two-dimensional wave flume at Jeju National University. The schematic experimental setup of the WEC model is shown in Figure 2. It is 20 m long, 0.8 m wide, and the water depth is 0.6 m. At one end of the tank, a piston-type wavemaker is installed which can generate regular and irregular waves. The other end of the tank has a wave absorber to attenuate the waves and minimize the wave reflection. The two-body WEC is placed at a distance of 8.7 m from the wavemaker. A capacity-type wave gauge is placed 2.3 m from the wavemaker to measure the incident waves. The model is held in place with the help of four slack mooring lines to avoid model drift. The mooring lines have negligible effects on motion response.

The two-body WEC model consists of two independent cylinders made of acrylic material. The inner cylinder has a radius ($a_1$) of 0.06 m, a draft ($d_1$) of 0.267 m, and a mass ($m_1$) of 2.86 kg, while the outer cylinder has a radius ($a_2$) of 0.12 m, a draft ($d_2$) of 0.05 m, and a mass ($m_2$) of 1.55 kg. The inside surface of the outer cylinder has eight small ball rollers arranged to ensure that it slides smoothly along the inner cylinder. Heave plates made of steel with different radii ($a_3$) of 0.09 and 0.12 m were attached to the bottom of the inner cylinder by a bolt.

The heave motion of the inner cylinder and torus outer cylinder was measured with the aid of image tracking of markers on the model. Video clips of the experiments were processed with help of Python code to extract the heave motions of each cylinder and the relative heave motion between them as time series.

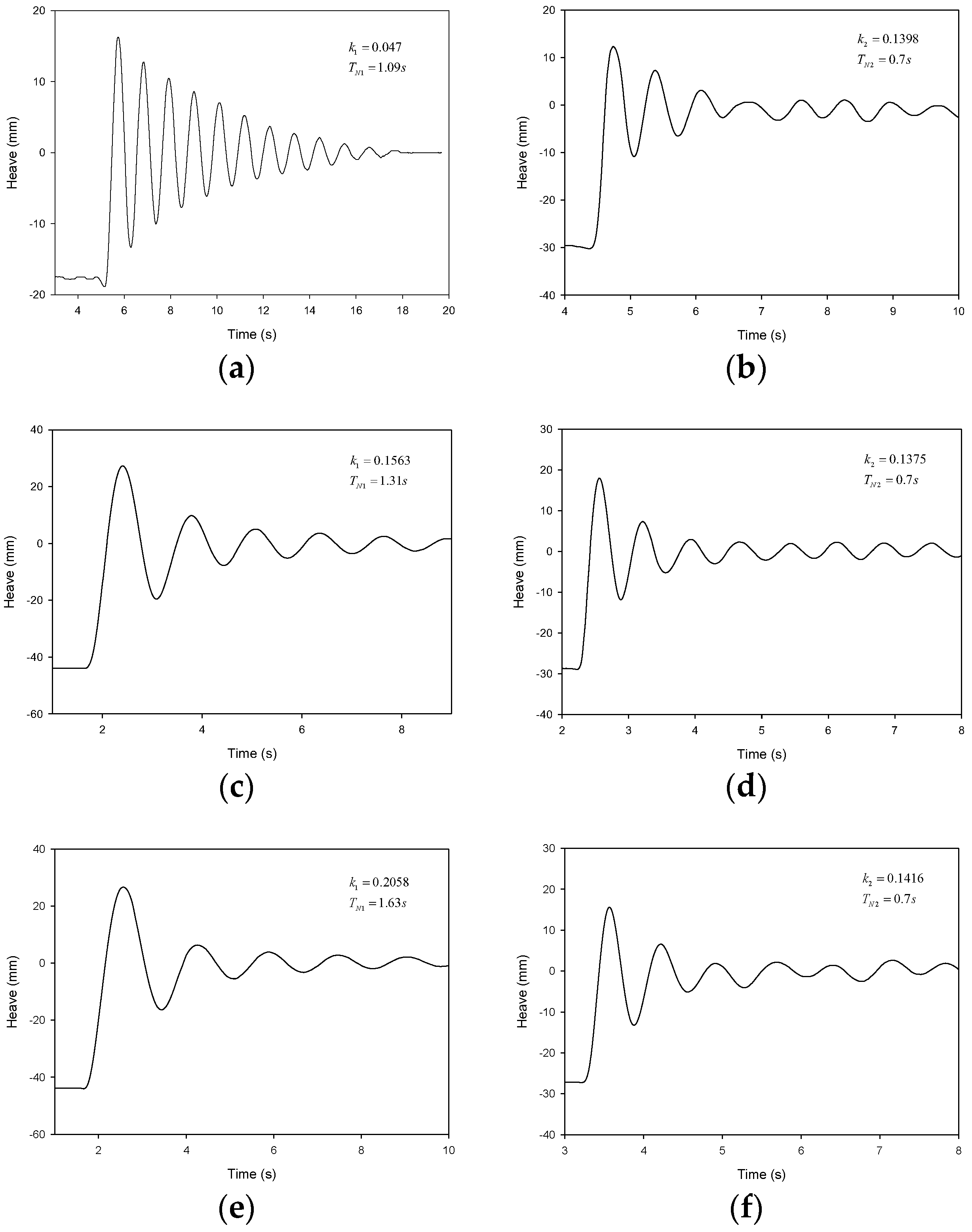
The experiments were conducted for three cases: one without a heave disk ($a_3/a_1=1.0$) and two and three with a heave disk ($a_3/a_1=1.5$, 2.0). First, the viscous damping of each cylinder including the edge vortices of the heave disk was obtained from the free-decay test, as plotted in Figure 3. The measured heave natural periods $T_{N1}$ of the inner cylinder for $a_3/a_1=1.0, 1.5, 2.0$ were 1.09 s, 1.31 s, and 1.63 s, and for the outer cylinder was 0.7 s. The corresponding damping factor ${\kappa }_i$ is depicted in the plots. It can be observed that the heave motion of the inner cylinder is drastically decreased with the increase of $a_3/a_1$ due to the higher viscous damping provided by the heave disk. The viscous damping of the outer cylinder shows no change for different cases, as was expected.

4. Results and Discussions

The analytical solutions formulated in Section 2 were validated with the panel-based commercial program WAMIT, which is a commercial software program used to compute wave loads and motions of offshore structures, floating bodies, and vessels. The design parameters considered were $d_1/a_1=4.45,d_2/d_1=0.187,a_2/a_1=2.0$. 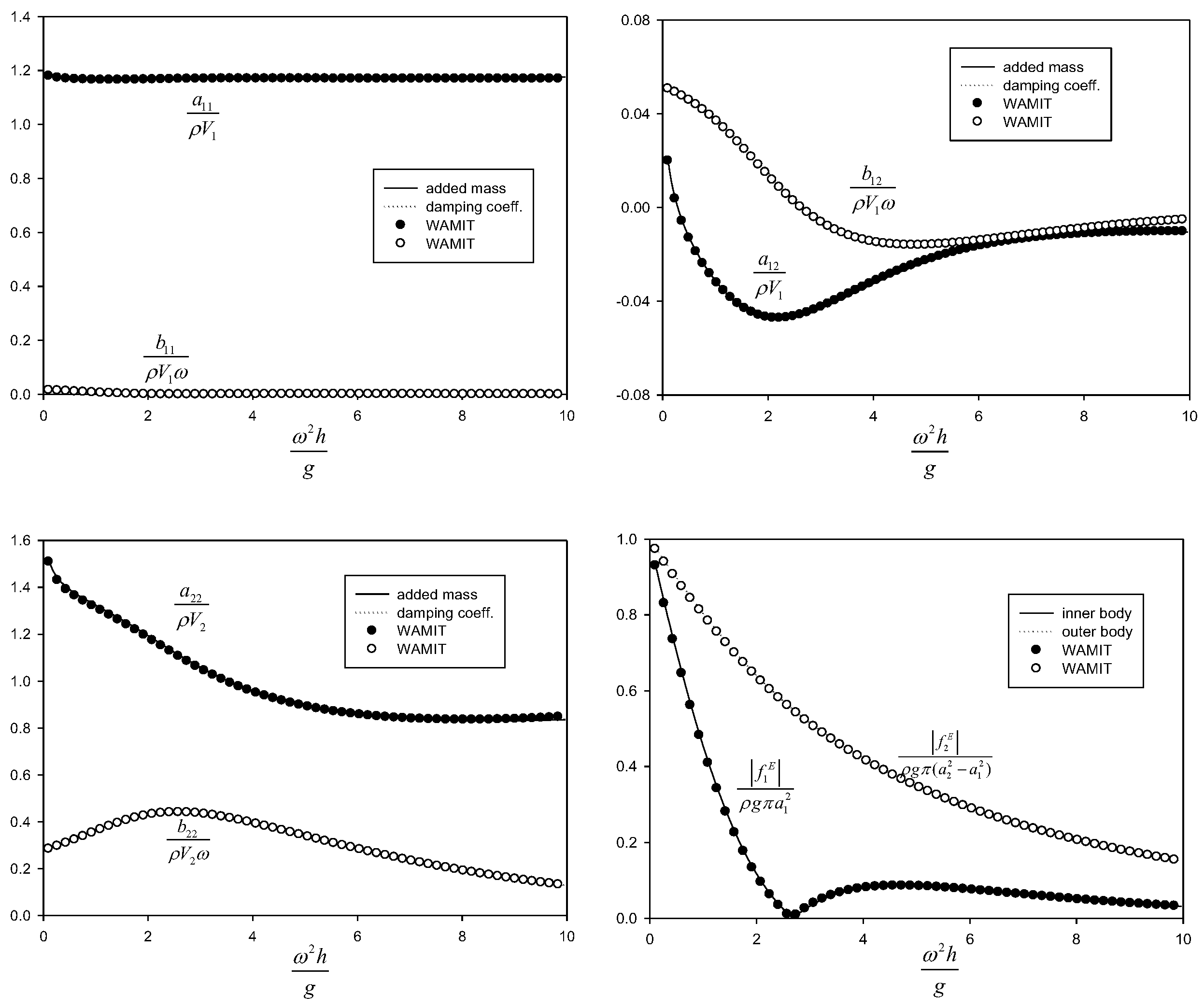The added mass, radiation damping, and wave excitation force are nondimensionalized by $\rho V_j, \rho V_j\omega$ (j = 1,2), $\rho g\pi a_1^2, \rho g\pi (a_2^2-a_1^2)$ respectively, where $V_j$ is the submerged volume of each cylinder. The added mass and radiation damping are presented for the inner and outer cylinder including cross-terms only for the heaving motion mode. 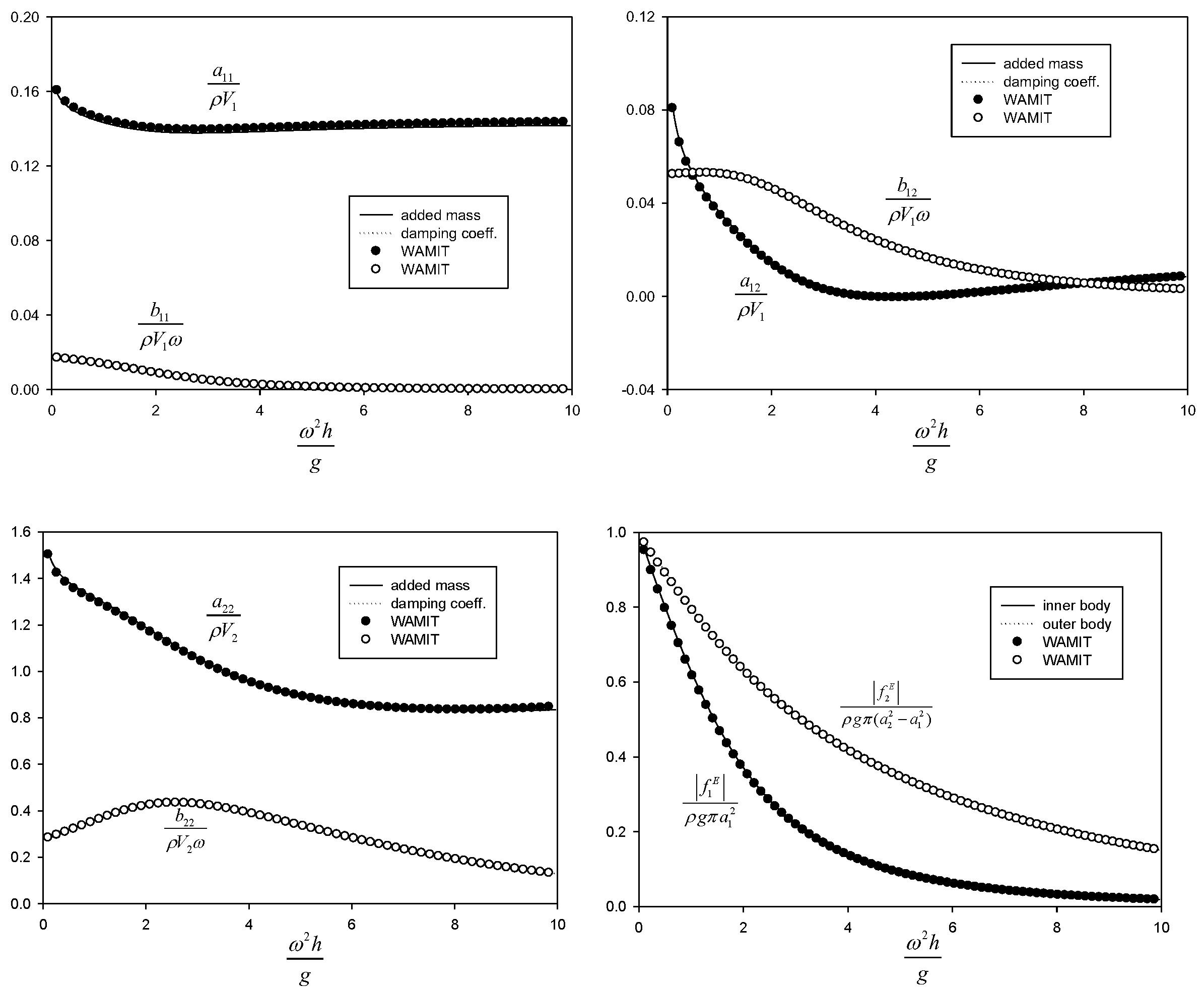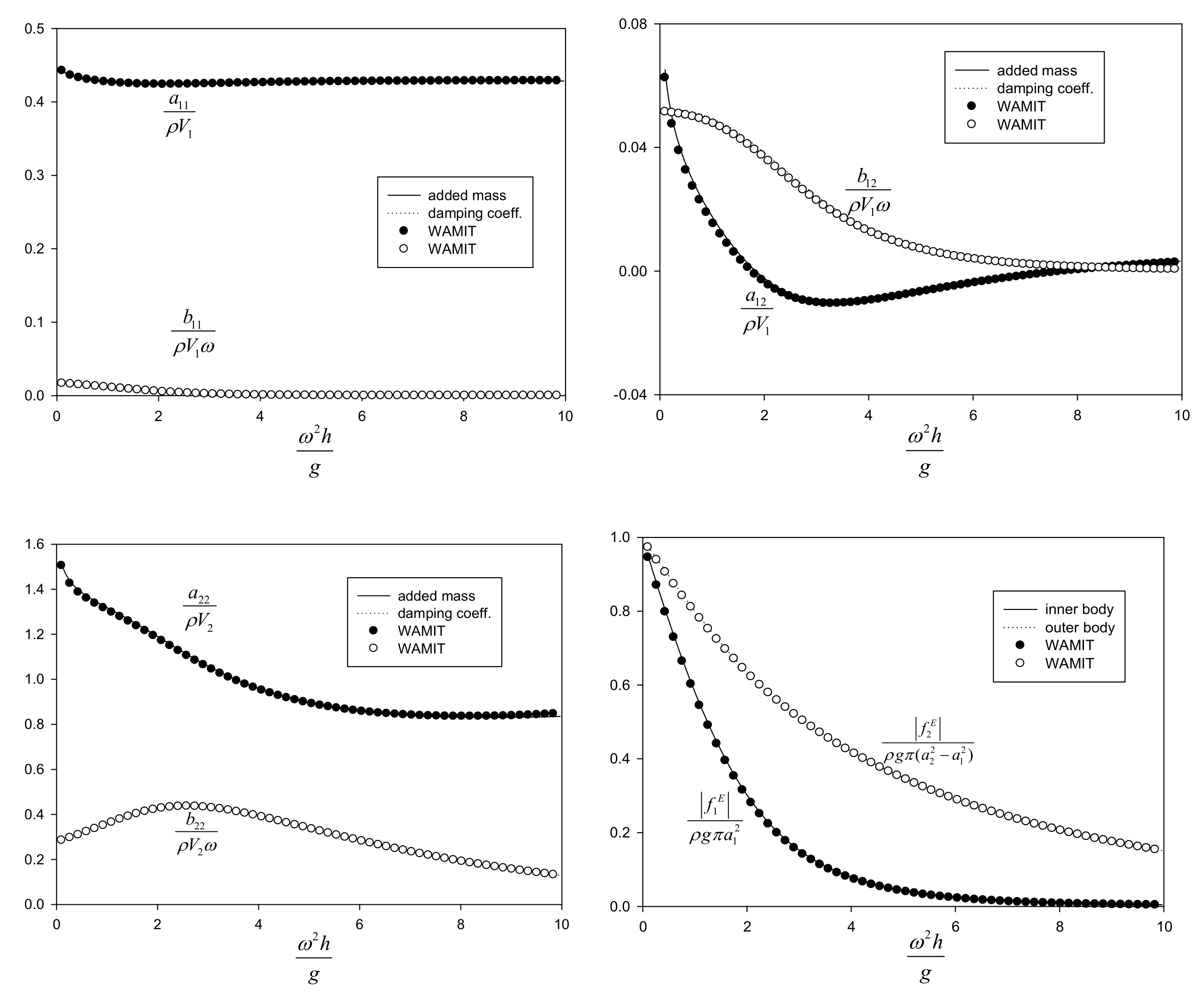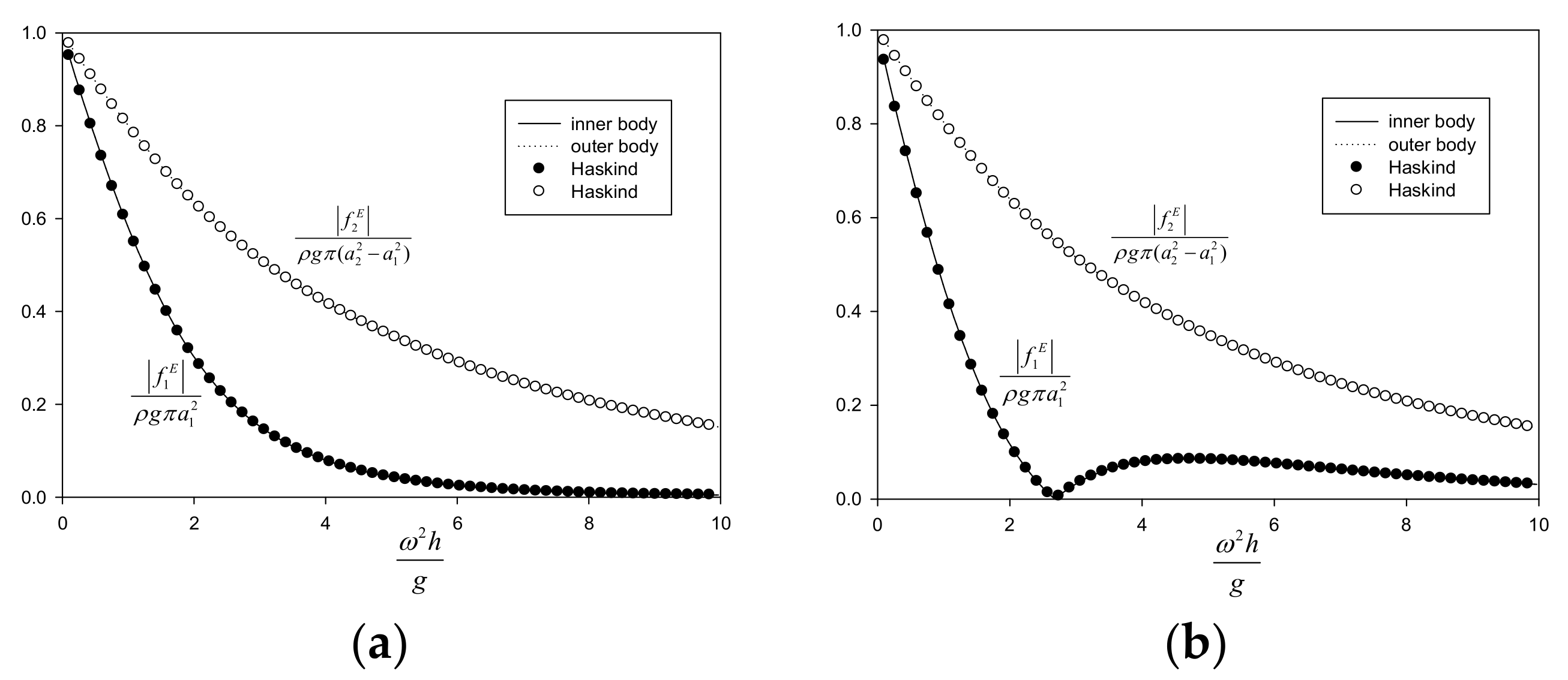Figure 4, Figure 5 and Figure 6 show comparisons between the analytical solutions and WAMIT numerical results as a function of the radius ($a_3/a_1=1.0, 1.5, 2.0$) of the heave disk, and are excellent agreement. As a double-check of analytical solutions, the wave excitation forces are compared with the Haskind results expressed in terms of radiation parameters in Figure 7, and are again in excellent agreement. Even if the number of eigenfunctions is truncated at some suitable number, the MEEM analytical solutions show excellent truncation characteristics and good agreement with WAMIT numerical results. The number of eigenfunctions (N = 60) used in Figure 4, Figure 5, Figure 6 and Figure 7 is taken in all subsequent calculations.

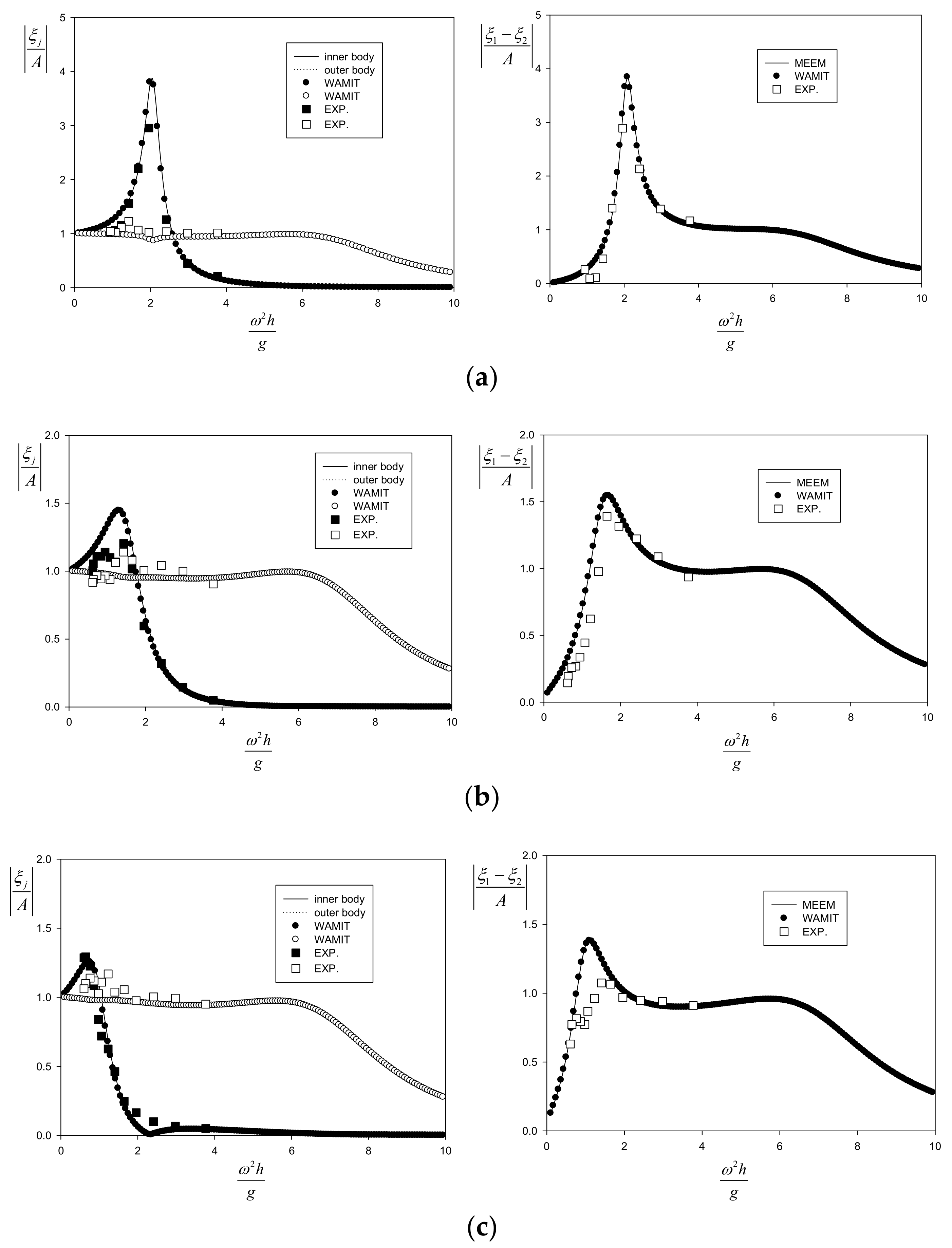
Figure 8 shows the comparison of the heave RAO (Response Amplitude Operator) of the inner cylinder and outer cylinder between the analytical (MEEM) and numerical (WAMIT) predictions and experimental results without and with a heave disk. The analytical and numerical predictions with viscous damping from the free-decay test are in reasonably good correlation with the experimental measurements, especially without a heave plate. The slight deviations for the case with a heave plate might be attributed to roller friction effects, nonlinear effects, slack mooring effects, etc. Additionally, these discrepancies could be attributed to the inaccurate prediction of viscous damping due to the formation of vortices at the disk edge being incorporated into the model. These discrepancies can be reduced by consideration of the drag force inspired by the Morison equation, as in Section 2.5, instead of using the results of the free-decay test. It can be observed that the heave RAO of the inner cylinder is significantly amplified at its natural frequency ($\frac{{\omega }_{N1}^{2}h}{g}=2.03,1.41,0.91$), while the outer cylinder conforms to the waves ($\left|{\xi }_2/A\right|\approx 1.0$). The reduction of the nondimensional natural frequency is caused by the increase in added mass according to the size of the heave plate. The heave motion response of the inner cylinder without a heave disk is about four times that of the outer cylinder, which is drastically reduced to 1.5 times owing to the increase in viscous damping caused by the presence of the heave disk. The peaks of the relative heave motion are close to the natural frequencies of the inner cylinder. With the heave disk, the frequency range of the relative heave motion, which is greater than 1.0, is widened to the low-frequency region even if the peak value is reduced. Installation of the heave disk contributes to extracting the wave energy belonging to the low-frequency range in the real sea. In addition, this approach can save the cost of protecting the WEC system against excessive motion of the WEC as well as the cost of manufacturing a large PTO system to accommodate amplified mechanical power in resonance.

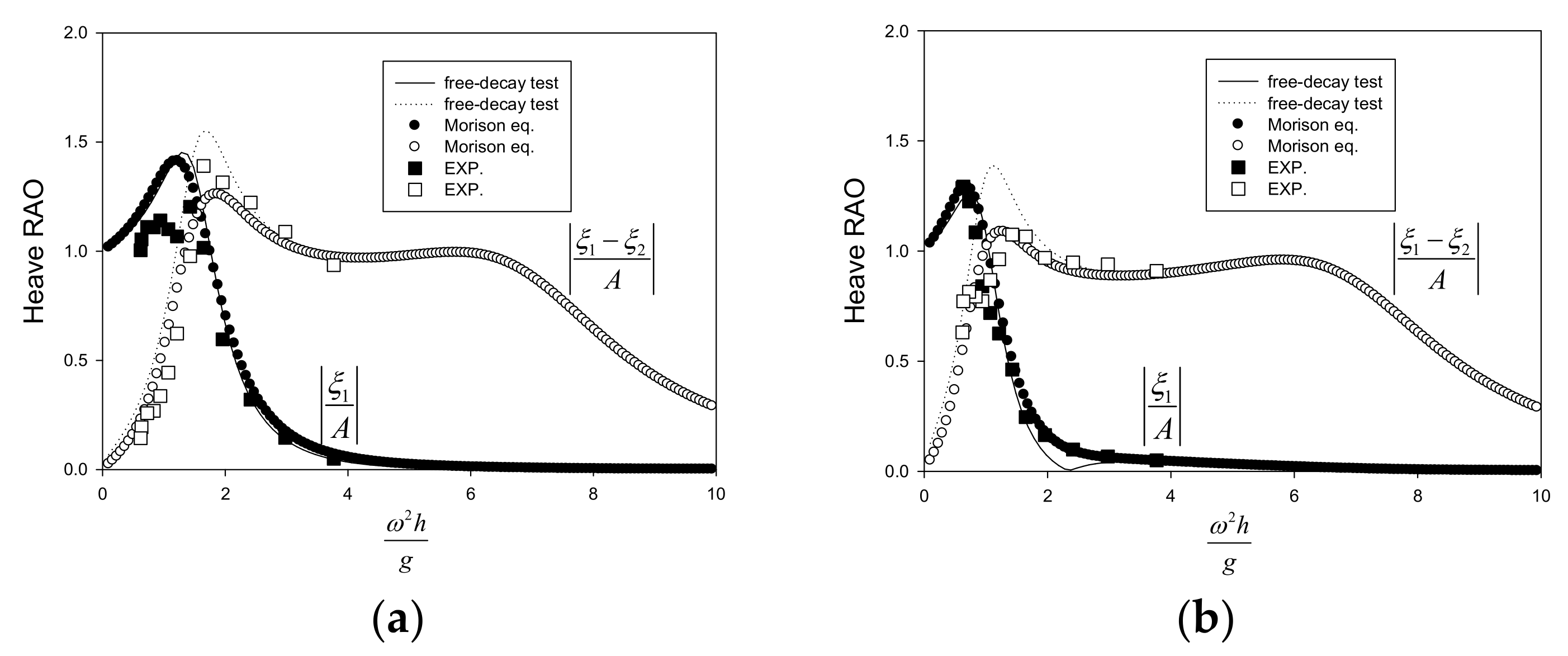
As described in Section 2.5, the viscous damping due to the formation of vortices at the disk edge can be implemented by the drag force inspired by the Morison equation, with the drag coefficient determined by curve fitting of the experimental data in the form of $C_d=6.5{\left(KC\right)}^{-1/3}$ [16], where $KC={\pi \left|{\xi }_1\right|/a}_3$. In Figure 9, the heave RAO obtained from the viscous damping from the drag force shows better predictions than that from the free-decay test near the resonance frequency. In all subsequent calculations, the viscous damping due to the edge vortices of the heave disk is added to the skin frictional damping, which is determined by the free-decay test without the heave disk ($a_3/a_1=1.0$).

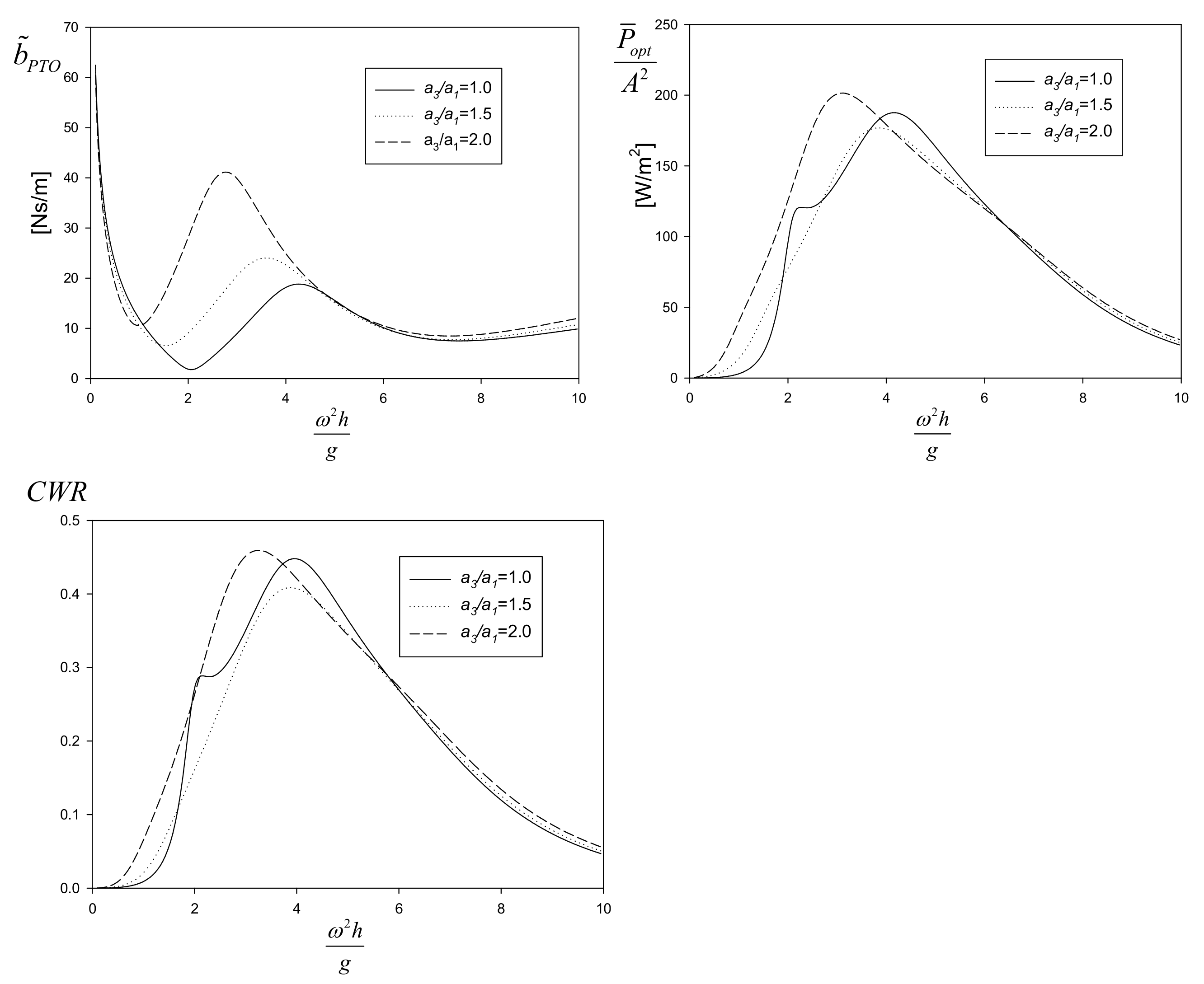
Figure 10 shows the optimal PTO damping coefficient, optimal extracted power, and capture width ratio as a function of the radius $a_3/a_1$ of the heave plate. The curve of the optimal PTO damping has valleys at two frequencies, which coincide with the natural frequencies of the inner and outer cylinders. Interestingly, the peak of the optimal extraction power is situated at the frequency representing the hump of the PTO damping curve, which is halfway between the natural frequencies of the cylinders. The optimal capture width ratio shows a similar trend to the optimal extracted power. Practically, it is impossible to control the PTO damping coefficients according to Equation (31) by responding to varying frequencies in irregular waves. In general, either the optimal value of the PTO damping coefficient at the natural frequency of the bodies or the peak frequency is selected.

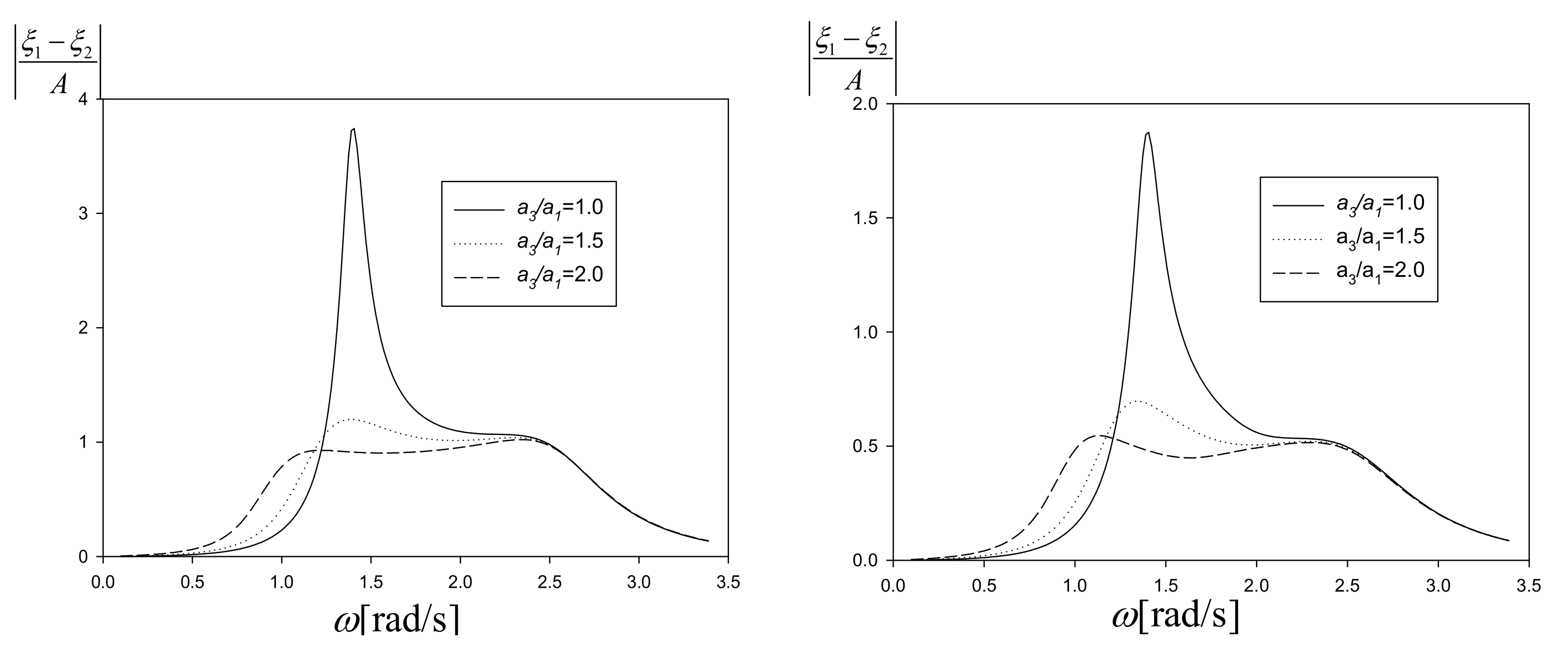
A scaled-up prototype WEC system with parameters of $h/a_1=30,d_1/a_1=4.45,d_2/a_1=0.83,a_2/a_1=2,a_1=1\mathrm{m}$ is considered in the next analysis. Figure 11 shows a comparison of the relative heave RAOs without and with the optimal PTO damping coefficient. The relative heave RAO decreases to half with the application of PTO damping. The reduced part of the mechanical energy is transferred to the electrical energy. 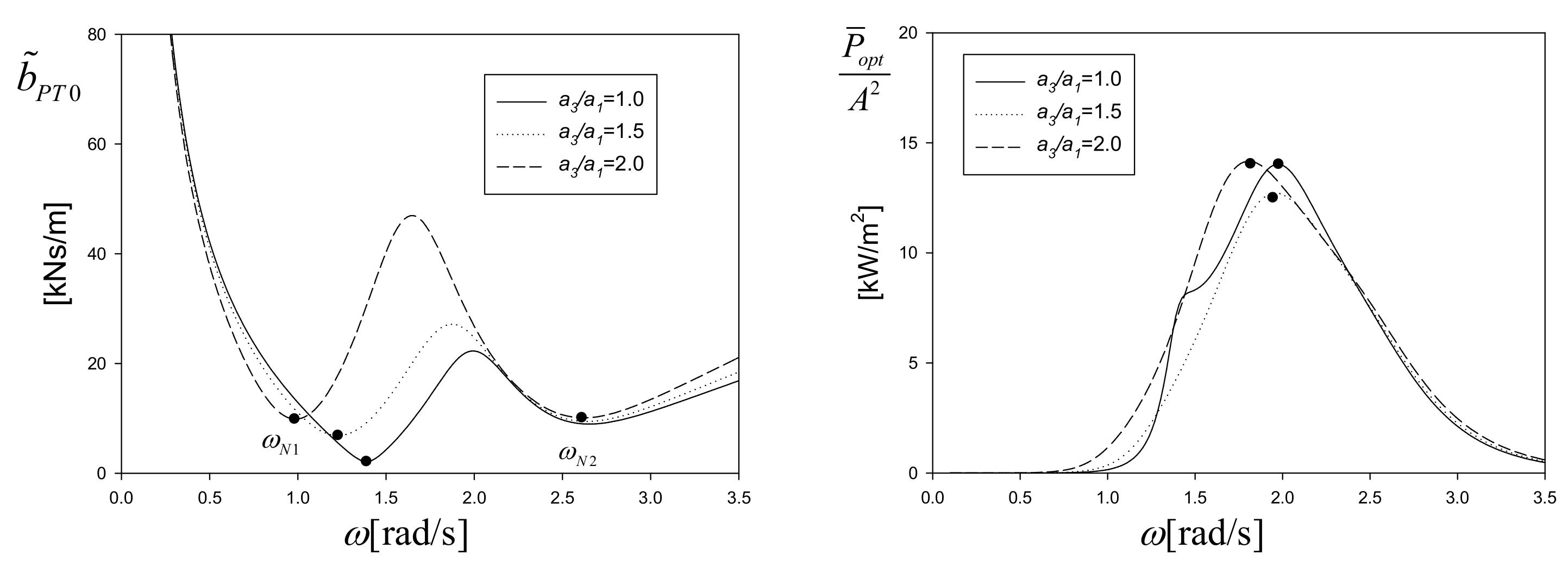Figure 12 shows the optimal PTO damping coefficient and corresponding extracted power as a function of the radius of the heave plate. The observation is similar to the previous model-scale results (see Figure 10).

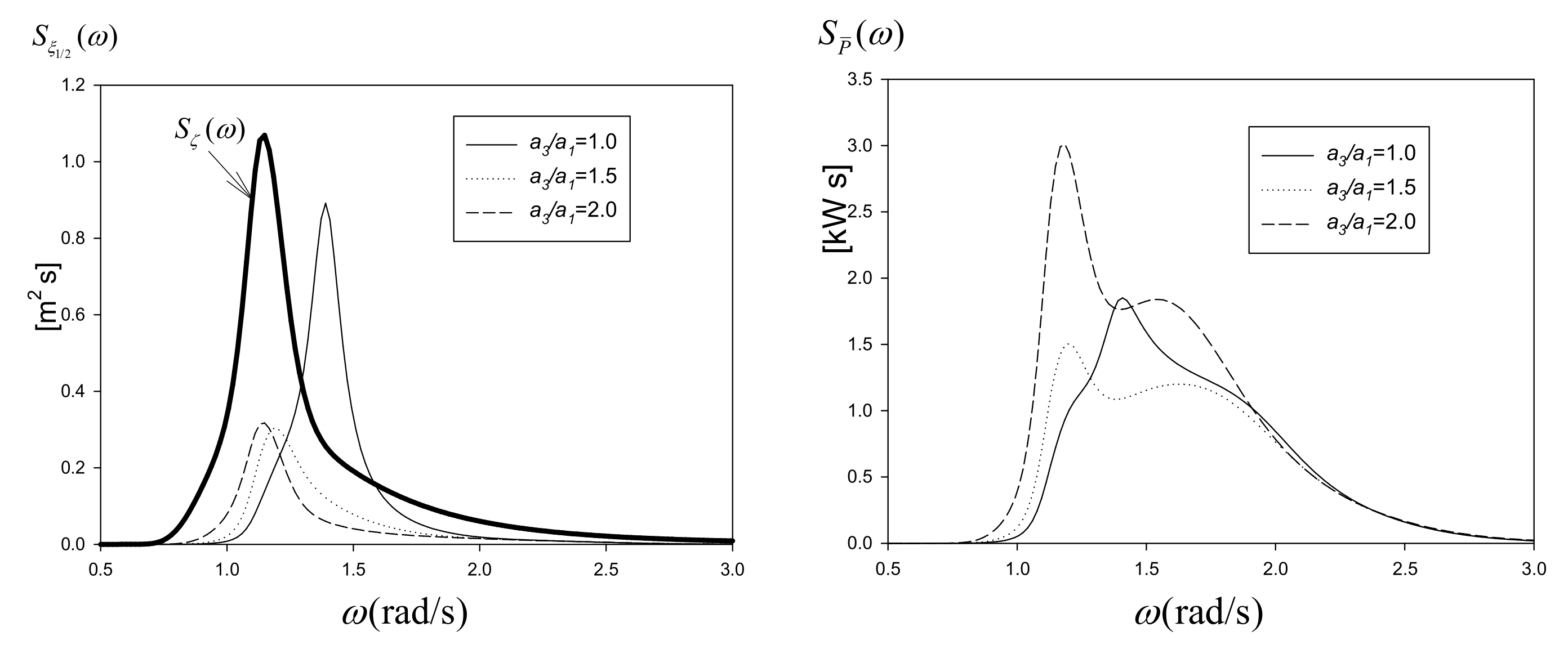
The prototype model was run for irregular waves based on the JONSWAP spectrum with $H_{1/3}=3.0\mathrm{m},T_P=5.5\mathrm{s}$. Figure 13 shows the relative heave motion spectrum and power spectrum with applied optimal PTO damping coefficients of ${\tilde{b}}_{PTO}(\omega )$ as a function of the radius of the heave plate. It can be noted that the peak frequency of the relative heave motion spectrum aligns well with the peak frequency of the wave spectrum when a heave disk is installed. It can be explained that the outer body, which follows the incident waves, dominates the relative heave motion when the inner body’s heave motion is minimized by the heave disk. As a result of minimizing the motion of the inner cylinder, the area under the power spectrum is at its maximum when $a_3/a_1=2.0$, as mentioned in Figure 13.

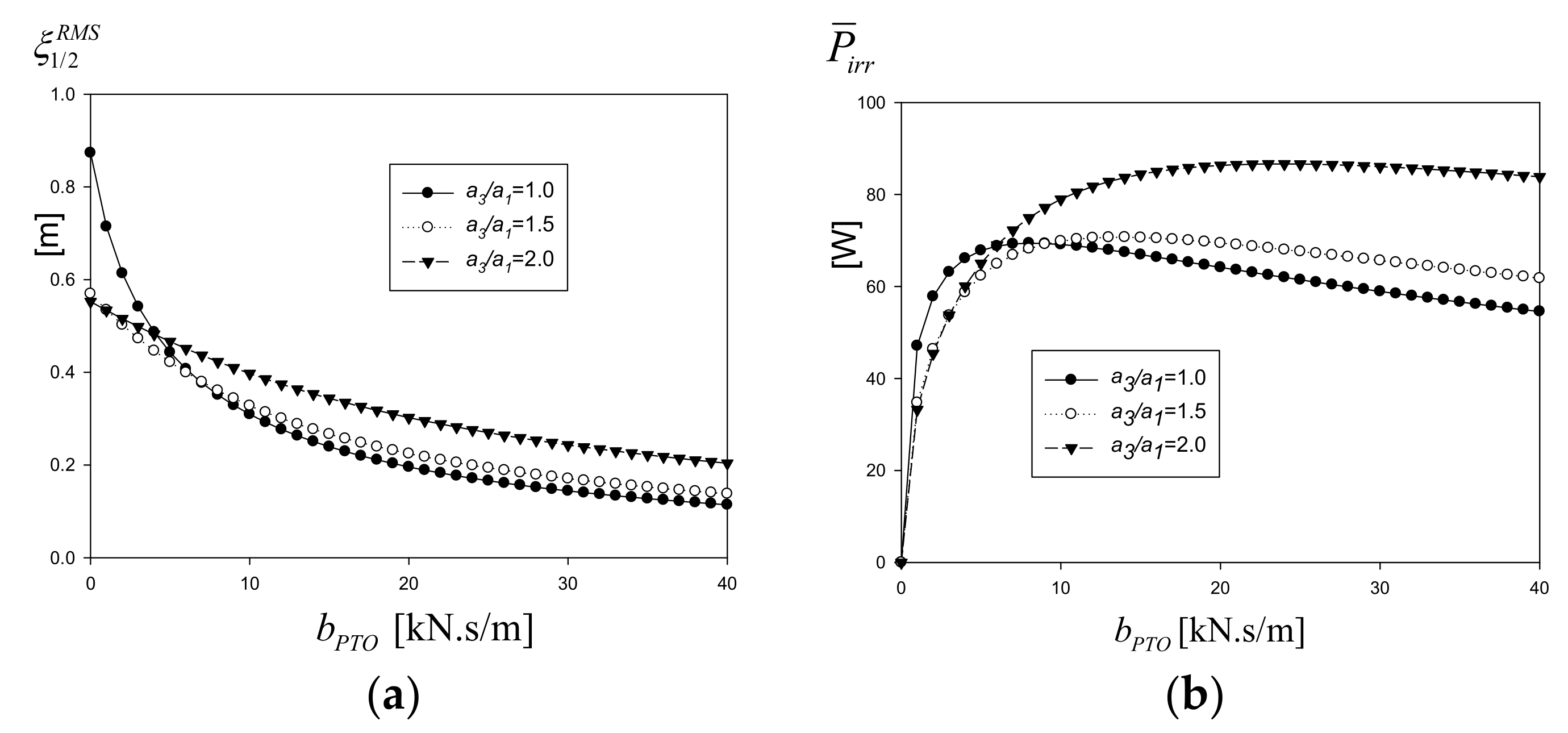
While application of the optimal PTO damping coefficient ${\tilde{b}}_{PTO}(\omega )$ to the WEC system might yield good theoretical predictions, it may be impossible to practically adjust the PTO damping from time to time in real time for varying irregular waves. Thus, the selection of one PTO damping coefficient is desirable. Figure 14 shows the root mean square of the relative heave motion and extracted power in irregular waves as a function of the PTO damping coefficient with heave plates of three different radii. While increasing PTO damping steadily decreases the relative heave motion, the extracted power increases to a maximum, then slightly decreases. The heave plate with a radius of $a_3/a_1=2.0$ shows higher relative heave motion and extracted power than $a_3/a_1=1.0,1.5$ after $b_{PTO}>5.0 \mathrm{kNs}/\mathrm{m}$.

It is possible to choose the optimal PTO damping coefficient at the natural frequency of the inner or outer cylinders or the value yielding the maximum extracted power. It is notable that the frequency of the maximum extracted power lies between the natural frequencies of the inner and outer cylinders, as shown in Figure 10. Thus, the average of these two natural frequencies is considered as ${\omega }_1=({\omega }_{N1}+{\omega }_{N2})/2$. The optimal value at the natural frequency of the outer cylinder, ${\omega }_2={\omega }_{N2}$, which moves more actively than the inner cylinder, is another candidate for optimal design. The irregular waves at a particular sea site have a peak frequency where the wave energy is concentrated. Thus, the optimal PTO value at the peak frequency of the irregular wave spectrum, ${\omega }_3={\omega }_P$, could be another selection.

Table 1. Extracted power in irregular waves for different PTO damping values.

${\mathit{a}}_3/{\mathit{a}}_1$	1.0	1.5	2.0
${\omega }_1=({\omega }_{N1}+{\omega }_{N2})/2$	1.96	1.89	1.77
${\tilde{b}}_{PTO}({\omega }_1)$ [kNs/m]	22.03	27.12	42.74
${\overline{P}}_{irr}$ [W]	63	66	83
${\omega }_2={\omega }_{N2}$ [rad/s]	2.52	2.52	2.52
${\tilde{b}}_{PTO}({\omega }_1)$ [kNs/m]	9.50	9.88	10.43
${\overline{P}}_{irr}$ [W]	69	69	79
${\omega }_3={\omega }_P$ [rad/s]	1.14	1.14	1.14
${\tilde{b}}_{PTO}({\omega }_1)$ [kNs/m]	8.11	7.51	13.31
${\overline{P}}_{irr}$ [W]	69	67	83

shows the extracted power from irregular waves for three different design PTO damping values ${\omega }_1,{\omega }_2,{\omega }_3$ for different radii of the heave plate. It is noted that the optimal heave disk is $a_3/a_1=2.0$ and the optimal PTO value corresponds to the optimal PTO damping coefficient at both ${\omega }_1=({\omega }_{N1}+{\omega }_{N2})/2$ and ${\omega }_3={\omega }_P$. If we are forced to choose one between them, the PTO damping having a smaller value is desirable, which means the smaller PTO damping device.

5. Conclusions

The performance of a two-body heaving WEC system that extracts wave energy through relative heave motion has been investigated through parametric study according to the radius of the heave disk attached to the bottom of the inner cylinder. The hydrodynamic forces on the WEC are obtained by an analytical solution based on the linear potential theory, and the viscous damping force on the heave disk is considered using the drag forces in the Morison equation. The analytical results have been validated with WAMIT numerical results and experiments self-conducted in a 2D wave tank.

Through intensive study, it was found that by allowing the outer cylinder to follow the waves and by reducing the motion of the inner cylinder using a heave disk, the two-body WEC with heave disk produces wave energy stably across a wide range of wave frequencies. This can be achieved by designing the outer body as a floating torus with a large waterplane area and a small draft, enabling it to move in harmony with the waves. Meanwhile, the inner body can have a smaller waterplane area and a low resonance frequency, which can be achieved by attaching a heave plate to the bottom. Because this design strategy does not rely on resonance, large-scale PTO damping devices and site-specific design features such as aligning the natural frequency of the system with the peak frequency of the sea site to achieve resonance are not necessary. In addition, by shifting the natural frequency of the inner cylinder to the low-frequency regime due to the increase in added mass with the heave disk, the frequency range for the extraction of the wave power is extended. This proposed WEC system concept with heave disk eliminates the need to have a large draft regardless of the incoming wave condition; thus, it is cost-effective, and can be installed even at shallower water depths. Cost savings can be achieved by eliminating the need for excessive motion protection measures for safety of the WEC system and by avoiding the manufacturing costs associated with a large Power Take-Off (PTO) system to accommodate amplified mechanical power during resonance. Thus, the proposed system has many merits over previous WECs using resonance, even at some loss of energy extraction.