A Comprehensive Comparative Analysis of Energetic and Exergetic Performance of Different Solar-Based Organic Rankine Cycles

Abstract

In this work, a comprehensive energetic and exergetic comparative assessment is presented for the simple solar organic Rankine cycle (SORC), regenerative solar organic Rankine cycle (RORC), and dual-loop solar organic Rankine cycle (DORC), considering parameters such as the net power produced, exergy destruction, exergy, and energy efficiency in four zones located in Colombia due to their high solar irradiation potential. The energetic and exergetic balances were applied for each system component, using toluene as the working fluid. The RORC system showed a 2% increase in efficiency over the SORC, while the DORC cycle was lower than the SORC (45.85%) and RORC (46.90%) systems. Finally, for the exergy analysis, the results revealed that the SORC (5.3%) and RORC (5.2%) systems had the highest efficiency compared to DORC systems. Additionally, the highest exergy destruction (89%) was related to the collector, followed by the evaporators (1–2%), pumps (0.1%), and turbines (1.12%).

1. Introduction

The continuous development of society has led to an increase in fossil fuel consumption for electricity generation as a primary source for industrial, commercial, and residential activities [1]. This has caused a decline in energy resources worldwide [2] and an increase in greenhouse gas emissions which causes global warming [3]. Given the abovementioned problems, different alternatives have been put forward to overcome them. One route is developing and implementing renewable energy sources, and the second is adopting policies and regulations for efficient energy usage [4].

Renewable energies are considered sustainable and environmentally friendly [5], as the ecological footprint is lower than that of conventional energy systems [6]. In this regard, solar collectors are technologies that transform solar radiation into thermal energy, employing natural or forced circulation for later use [7]. The collector systems are widely researched and applied in organic Rankine (ORC) systems [8,9].

On the other hand, ORC technologies are being widely applied due to the reduction of the working temperature using organic fluids and its easy operation [10]. This trend was reflected in the increase of ORC use by almost 400% between 2010 and 2015 [7]. The constant development of this technology implies multiple variations and applications in low-temperature heat recovery, such as biomass, solar, geothermal, and industrial waste heat [11,12,13]. Additionally, this technology is very efficient in converting solar energy into power. Therefore, some research has been oriented toward developing and optimizing small-scale ORCs [14].

Regarding studies on the integration of ORCs in solar fields, the one carried out by Wang et al. [15] was a comparative study of a conventional ORC system and a small-scale ORC based on thermal driven pump system integrated by an evacuated flat-plate collector coupled to a thermal storage tank. Generally, the application of the solar organic Rankine cycle (SORC) configuration based on TDP showed the best results, indicating an increase in net power (3.3%), energy efficiency (3.27%), and exergy efficiency (3.5%) in comparison with the conventional SORC configuration. They did not consider hourly variations of solar radiation in the system.

Baccioli et al. [16] analyzed the behavior of a low-concentration parabolic collector (PC) solar plant coupled to a SORC. They simulated the system in transient conditions for three zones within a year. They compared the effect of the latitude of the sites and found that the specific power output was increased when latitude was decreased. Sonsaree et al. [17] studied a small-scale ORC by considering three types of non-concentrating solar thermal collectors: compound parabolic concentrators (CPCs), flat-plate, and evacuated tube collectors. They concluded that these systems are a viable solution for energy production from low-temperature heat. Moreover, the CPC-ORC system had a higher energy production rate than the other two technologies mentioned above. In the same scenario presented by Pinto et al. [18], they studied a hybrid solar module (PV/T) composed of photovoltaic panels (PV) and solar collectors (T) coupled to a low-temperature SORC cycle (PV/T-ORC). They found that the PV/T-ORC system increased energy and exergy efficiency by 13% and 4%, respectively, compared to the PV/T system.

On the other hand, studies on the regenerative organic Rankine cycle (RORC) have also been reported. In this scenario, Bellos et al. [19] investigated the application of nanoparticles in the solar field, aiming to increase total energy efficiency. The system consisted of a regenerative organic Rankine cycle RORC driven by parabolic trough collectors (PTCs) using four working fluids (toluene, MDM, cyclohexane, and n-pentane). The results revealed that combining toluene as a working fluid with nanoparticles (CuO) increased thermal efficiency by 1.25% compared to thermal oils. Ashouri et al. [20] conducted a thermodynamic evaluation of RORCs integrated with PTCs, considering benzene, butane, pentane isopentane, R123, and R245fa as working fluids. They concluded that the RORC system had better performance. In addition, benzene was the most efficient fluid (26.55%). However, the RORC–Solar system was integrated directly into the cycle without a thermal storage tank, limiting the performance of the RORC to only hours of radiation. Additionally, Arteconi et al. [21] analyzed a small-scale ORC. The system was adapted to a solar system using an evacuated tube collector with an area of 146 m², coupled to a thermal storage tank of 2 kWe. The impact of the electrical and thermal performance of the ORC system was considered on the electricity demand of end users using an integrated plant-building model. It was found that variations in resident time mainly impact the energetic performance of the ORC system.

Comparing the performance of organic cycles under different working fluids is a crucial step in designing these systems. In this regard, Ustaoglu et al. [22] evaluated the energy performance of a RORC coupled with an evacuated compound parabolic-involute concentrator, considering dry, wet, and isentropic fluids. The results showed that R-141b (isentropic fluids) produced the highest energy due to its low specific heat and boiling point. In contrast, R-113 (dry fluid), methanol (wet), water (wet), and benzene (isentropic) ranked 2nd to 5th, respectively, with similar values. However, the researchers considered the energy performance of the integrated system and did not use a thermal storage unit. Therefore, the study was conducted in constant daytime conditions.

Tiwari et al. [23] compared the performance of SORC and RORC systems. The results showed that the RORC configuration obtained the best energy efficiency (11.9%), exergy efficiency (51.88%), and exergy destruction (1749 kW). Comparable research was done by Yang et al. [24], who studied the energy performance of SORC and RORC configurations using a parabolic trough collector (PTC) as a solar thermal source with two thermal storage units. In addition, they evaluated the performance of four working fluids (toluene, cyclohexane, pentane, and MM). The system was operated under daily radiation conditions, showing that the RORC configuration can reach up to 17.9% energy efficiency using toluene as a working fluid. Maali et al. [25] compared the energy efficiency of hybrid RORC and SORC systems driven by solar and geothermal energy. They concluded that the solar–geothermal RORC system performed better with an energy efficiency of 15.77% and a net power of 1089 kW for the winter seasons. Zare et al. [26] integrated a high-temperature Kalina cycle conducted by PTC. Chai et al. [27] studied the dimensioning of parabolic trough solar collectors in ORC applications. Kerme et al. [28] evaluated a SORC system with distillation and absorption units coupled to a PTC from an energy and exergy point of view. They concluded that the PTC is the appropriate equipment impacting the overall system irreversibility (76%) and had a potential improvement of 64.8%. On the other hand, dynamic modeling is currently being used to better understand the parameters resulting in the plant solar behavior evaluation reported by Ghazouani et al. [29] and Delgado-Torres and García-Rodríguez [30].

Recent studies simultaneously evaluated the ORC configuration, the working fluid selection, and the type of solar collector. Zhang et al. [31] evaluated two different configurations of the solar ORC, the difference being that the ejector is arranged in parallel with the turbine for one configuration. In addition, five working fluids were selected (R236ea, R123, R245fa, R365mfc, and R141b), where R236ea showed better results with a net power output efficiency of 6.58% and an exergy efficiency of 42.24%, while the parallel type cycle net power output increased by 5.08%. Aghaziarati and Aghdam [32] studied the effect of ORC working fluid change, collector type, and ambient temperature. The parabolic trough collector (PTC), linear Fresnel reflector, and parabolic dish collector were compared. The PTC was the best option considering the energy, exergy, and exergo-economic evaluation due to its higher optical efficiency and lower solar field area needs. Regarding working fluid, cyclohexane from energy and exergy evaluation and octane from exergoeconomic evaluation were more efficient, while increasing ambient temperature reduced the solar field area. Alvi et al. [33] compared the performance of a direct solar ORC system and conventional indirect solar ORC, where R245fa and water were chosen as heat transfer fluids for both configurations. The results showed that the direct configuration’s annual efficiency and output power were higher, 71.96% and 64.38%, respectively, than the indirect configuration.

According to the literature, most studies are related to SORC and RORC systems operating in steady-state and transient solar systems. However, there is a lack of exploratory studies considering the dual-loop organic Rankine cycle (DORC) using solar radiation as an energy source. In addition, most studies do not evaluate the effect of irradiance from different locations, especially from Latin American countries. Thus, in this work, the single organic Rankine cycle (SORC), regenerative organic Rankine cycle (RORC), and dual-loop organic Rankine cycle (DORC) are analyzed under four strategic locations in the Colombian Caribbean region with high potential for solar power generation due to its high solar radiation and sunshine. A thermal storage tank is integrated into the proposed configurations, allowing it to temporarily assess the system and guarantee hourly energy production in particular operating conditions. It is worth noting that the reviewed literature presents no energetic and exergetic comparative assessment of these three ORC configurations in different Colombian locations, which emphasizes the novelty of the current contribution.

2. Materials and Methods

This section presents the different thermodynamically evaluated systems, the parameters considered, and the equations used.

2.1. Description of System

The system presented is an ORC, which was selected due to its high capacity to efficiently generate energy from low-temperature heat sources. Figure 1 shows the structure of the different low-grade ORC configurations used in this study. Figure 1a shows the single ORC configuration (SORC) coupled to a solar cycle.

The radiation hitting the collector surface initially generates useful heat gain (Qcol). This heat is transferred to the thermal oil (state 9a); which was used due to its inherent advantages, including its stability at high temperatures, which helps to prevent system corrosion and improves system reliability. In turn, the thermal oil is sent to the storage tank driven by the pump (P1). There, the tank operates as a heat accumulator, which allows the output temperature of the system to be maintained (state 5a) under specified conditions (T5a > 115 °C). The fluid then exits the tank (state 5a) to the SORC system, which then enters the evaporator (ITC1). Stream 10 (state 10) leaves the tank and then repeats the heating process. In the steam generator (ITC1), the thermal fluid gives up heat to toluene (working fluid), causing a phase change, and is then fed to the turbine (T1) as saturated steam (State 3). In the turbine, the working fluid expands, generating power through a coupled electric generator. Then, the output stream of the turbine is fed to the condenser (state 4). The condenser (ITC2) uses cooling water (state 7) to condense the working fluid to the specified condensing temperature (state 1). The working fluid leaves the ITC1 as a saturated liquid driven by the pump (P1).

Figure 1b shows the RORC cycle. In this configuration, the process is analogous to that described in the SORC system. Unlike the SORC system, the RORC configuration counts as a regenerator or heat recovery unit within the cycle (ITC2). This equipment is installed to take advantage of the internal heat of the process and reduce the heat demand from the thermal source. In this case, the output stream of turbine 1 (T1) is introduced to ITC2, which yields energy in the form of heat to stream 2 (state 2) by increasing its temperature. In this way, the stream entering the evaporator (state 2r) increases its temperature and decreases the heat required for evaporation in the ITC1.

Figure 1c shows the DORC configuration, where the addition of two evaporators to the system can be seen. These two evaporators allow two different evaporation pressures and contribute to better use of the exergy coming from the thermal source (Solar Collector). Initially, the working fluid leaves the condenser as a saturated liquid (ITC3), which is subsequently driven by a pump (P4). The output flow (state 2) is divided. The first flow (state 3) is fed to the low evaporator (ITC1), which evaporates the fluid to the minimum temperature difference (10 °C). Then, the output flow (state 6) is fed to turbine 1 (T1) to be expanded. On the other hand, stream 4 is driven by the pump (P3) with a higher pressure ratio than P1 to be introduced to the high evaporator (ITC2). The output flow from ITC2 comes out as saturated steam and expands in the high turbine (T2). Then, the stream leaving Turbine 2 (state 8) mixes with the flow from ITC1 (state 6), forming state 9. This mixed flow is fed to turbine 1 (T1) to generate work through a coupled generator. Finally, flow 10 is provided to the condenser (ITC3) that uses cooling water to condense and cool the working fluid to its given condensation temperature (40 °C).

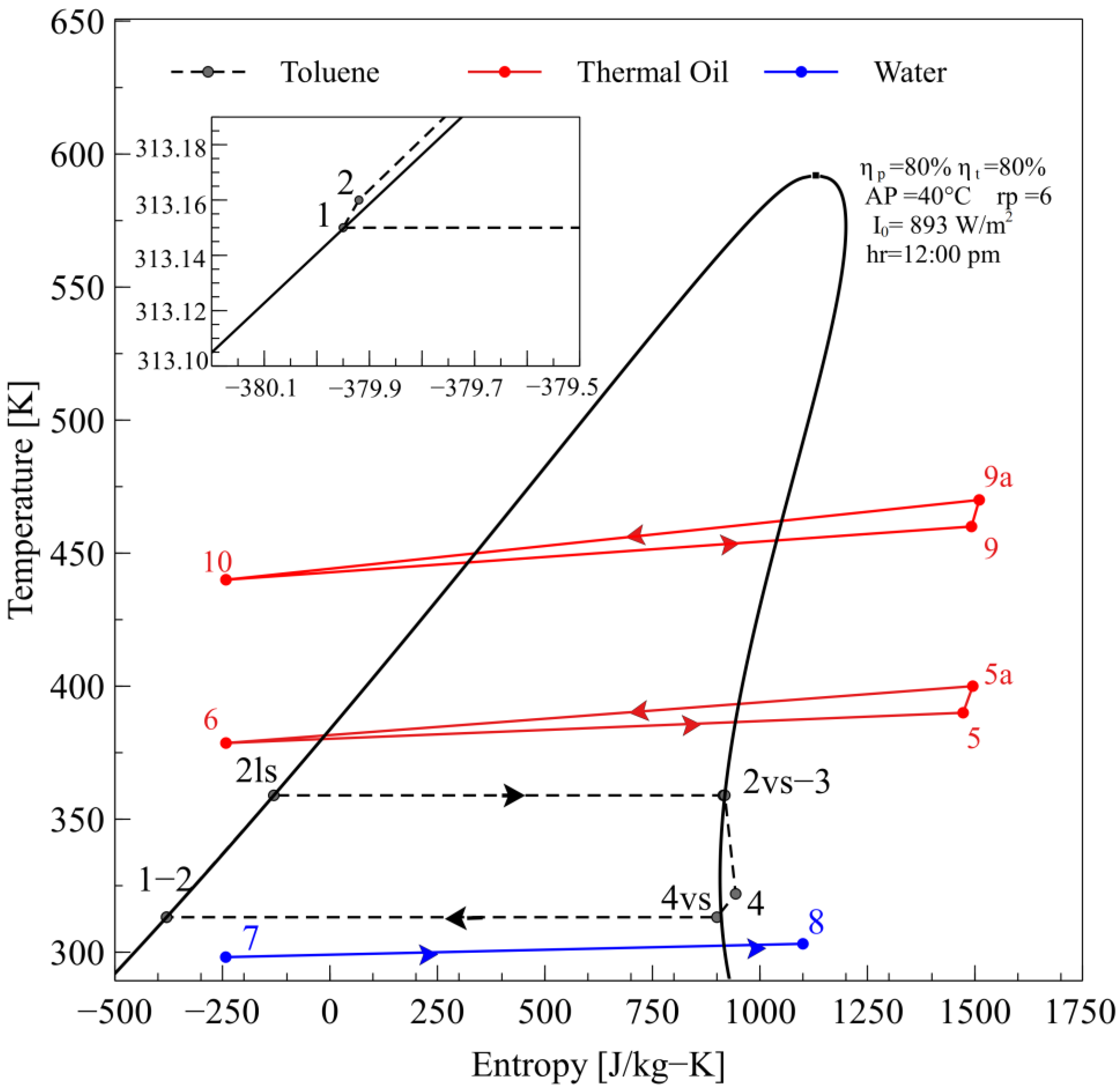
Figure 2 represents the T–S diagram of the process in the SORC cycle. According to Figure 1a, the organic fluid starts at state 1 as a saturated liquid. It then experiences a slight increase in entropy due to the temperature change in pump 1 (P1). Subsequently, the organic fluid increases its temperature to point 2ls. Then, it evaporates, increasing its entropy at a constant temperature until it reaches point 3 (evaporator outlet).

Between points 3 and 4, an expansion is experienced in the turbine, which causes a decrease in its temperature. Afterward, the fluid enters the condenser (point 4), which is taken to saturated steam (4vs) to be later condensed by decreasing its entropy at a constant temperature until state 1. Points 7–8 represent an increase in the cooling water temperature in the condenser. At the same time, states 10–9–9a and 6−5−5a represent the entropy change of the thermal oil in the solar cycle.

Figure 3 shows the T–S diagram of the RORC configuration. The process is similar to that described in the SORC configuration. However, adding the heat recovery unit (ITC2) allows heat recovery from the 4-4r state. This heat recovery is reflected in the 2-2r stages of the process through an increase in temperature and, therefore, a reduction in the energy requirements for the phase change of the toluene in the 2rls-3 states.

Finally, Figure 4 shows the T–S diagram of the DORC process. It shows the passage of the fluid through the phases of saturated liquid (5ls), saturated steam (5vs), and superheated steam (7). The high-pressure steam (state 7) enters the turbine, which expands in an isentropic way reducing its temperature (state 8). On the other hand, the low-pressure state goes through the saturated liquid phases (3ls) up to saturated steam (6). Flow 6 is mixed with flow 8, resulting in a decrease in temperature to be later expanded in the turbine (T2). Finally, the condensation process is carried out at constant pressure to bring it to a saturated liquid state in an isobaric way (10−1).

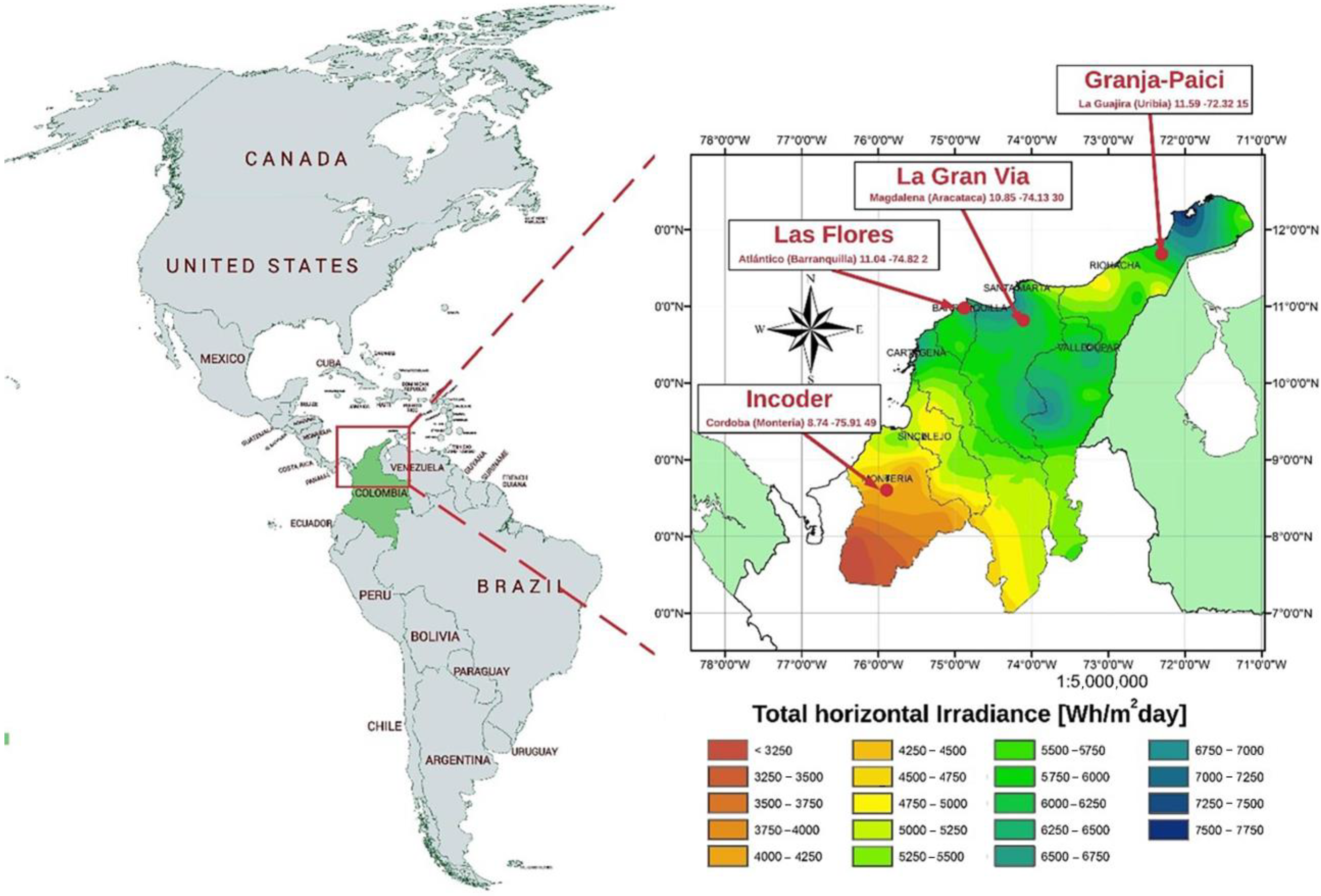
2.2. Description of the Locations

Figure 5 shows the locations of the four zones considered in this study. These zones are located in the Colombian Caribbean region and the different radiation values (Figure 5). Granja-Paici has an average value of 5500 Wh/m²-day, Gran-Vía 6300 Wh/m²-day, Incoder 3800/m²-day, and Flores 6500 Wh/m²-day.

2.3. ORC Thermodynamic Modeling

When analyzing a process thermodynamically, it is essential to consider the differences in the quality of energy. This characteristic depends on how the considered form of energy is stored. Storage can be ordered or disordered to a greater or lesser degree [34]. Since entropy reflects the disorder of a system, it is expected that it will also serve to determine the extent to which an ordered form of energy occurs and therefore can be used to assess the amount of usable energy that can be obtained [35].

Thus, exergy is a parameter that measures the quality of energy. This parameter can be used to analyze the energy efficiency of different processes. Exergy analysis can compare various alternatives to observe which one has the highest energy efficiency [36]. Therefore, exergy is the maximum useful work that can be obtained from a given energy flow, in any of its forms that are stored or transferred; it can also be observed as the minimum necessary energy required to obtain a final product [37].

For the methodology development, an energetic and exergetic balance by component was carried out. Each component was considered a control volume. The simulation was performed using Matlab^® and the thermophysical properties were obtained using Refpro^® developed by NIST.

The following assumptions were adopted [38,39]:

• All the components were considered an open system;
• Changes in potential and kinetic energy were not considered;
• Pressure losses were neglected;
• All components operate in steady state.

The above assumptions are valid for practical applications within these ORC layouts; the percentage of error that can be expected in these cases ranges from 10% to 20% [22,38].

The mass balance is given according to Equation (1).

$$\sum {\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}-\sum {\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=0$$

(1)

where ${\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}$ and ${\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{u}\mathrm{t}}$ are the incoming mass flow and the outgoing mass flow in kg/s, respectively. Similarly, the energy balance is governed by Equation (2).

$${\dot{\mathrm{Q}}}_{\mathrm{c}\mathrm{v}}-{\dot{\mathrm{W}}}_{\mathrm{c}\mathrm{v}}+\sum {\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}·{\mathrm{h}}_{\mathrm{i}\mathrm{n}}-\sum {\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{u}\mathrm{t}}·{\mathrm{h}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=0$$

(2)

where $\dot{\mathrm{Q}}$ represents the heat transfer in kW, ${\dot{\mathrm{W}}}_{\mathrm{c}\mathrm{v}}$ is the work done on the component, and $\dot{\mathrm{m}}$ and $\mathrm{h}$ represent the mass flow rate in kg/s and the enthalpy specified in kJ/kg $\mathrm{K}$, respectively.

The balance of exergy for a control volume is indicated in Equation (3).

$$\sum \left(1-\frac{{\mathrm{T}}_0}{{\mathrm{T}}_{\mathrm{k}}}\right)·{\dot{\mathrm{Q}}}_{\mathrm{k}}-\dot{\mathrm{W}}+\sum _{\mathrm{i}\mathrm{n}}\dot{\mathrm{m}·}\mathrm{e}-\sum _{\mathrm{o}\mathrm{u}\mathrm{t}}\dot{\mathrm{m}}·\mathrm{e}-{\dot{\mathrm{X}}}_{\mathrm{d}}=0$$

(3)

where the first term on the left is the exergy of heat, the second term is the mechanical work transferred, and the third and fourth terms are the difference between the input and output exergies, respectively. Finally, the ${\mathrm{T}}_0$ and ${\mathrm{T}}_{\mathrm{k}}$ terms represent the reference and k-component temperatures of the system, respectively.

The exergy flow per unit mass for the fluid flow is defined in Equation (4) [40]

$$\mathrm{e}=\left(\mathrm{h}-{\mathrm{h}}_0\right)-{\mathrm{T}}_0·\left(\mathrm{s}-{\mathrm{s}}_0\right)$$

(4)

where $\mathrm{s}$ and $\mathrm{h}$ are the entropy and specific enthalpy and ${\mathrm{h}}_0$ and ${\mathrm{s}}_0$ are the specific enthalpy and entropy to the reference conditions. Equation (5) expresses the balance of entropy generated that can be applied to any device in the system, where ${\dot{\mathrm{S}}}_{\mathrm{g}\mathrm{e}\mathrm{n}}$ is the entropy generation rate [41].

$${\dot{\mathrm{S}}}_{\mathrm{g}\mathrm{e}\mathrm{n}}=\sum {\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{u}\mathrm{t}}·{\mathrm{s}}_{\mathrm{o}\mathrm{u}\mathrm{t}}-\sum {\dot{\mathrm{m}}}_{\mathrm{i}\mathrm{n}}{·\mathrm{s}}_{\mathrm{i}\mathrm{n}}-\sum \frac{{\dot{\mathrm{Q}}}_{\mathrm{k}}}{{\mathrm{T}}_{\mathrm{k}}}$$

(5)

whereby ${\mathrm{s}}_{\mathrm{o}\mathrm{u}\mathrm{t}}$ and ${\mathrm{s}}_{\mathrm{i}\mathrm{n}}$ are the input and output entropies, respectively.

The total power produced by the cycle is expressed according to Equation (6).

$${\dot{\mathrm{W}}}_{\mathrm{n}\mathrm{e}\mathrm{t}}=\sum {\dot{\mathrm{W}}}_{\mathrm{t}}-\sum {\dot{\mathrm{W}}}_{\mathrm{P}}$$

(6)

where ${\dot{\mathrm{W}}}_{\mathrm{t}}$ and ${\dot{\mathrm{W}}}_{\mathrm{p}}$ are the power produced and consumed by the turbines and pumps, respectively. According to the thermodynamic first law, the efficiency is expressed by Equation (7).

$${\mathsf{\eta }}_{\mathrm{I},\mathrm{O}\mathrm{R}\mathrm{C}}=\frac{{\dot{\mathrm{W}}}_{\mathrm{n}\mathrm{e}\mathrm{t}}}{{\dot{\mathrm{Q}}}_{\mathrm{i}\mathrm{n}}}$$

(7)

where ${\dot{\mathrm{Q}}}_{\mathrm{i}\mathrm{n}}$ is the heat at the entrance of ORC system. The main energetic and exergetic equations of each component are summarized in

Table 1. Energy and exergy balance for the components of each configuration.

Component	SORC	RORC	DORC
ITC1	$$\begin{gathered} {\mathrm{Q}}_{\mathrm{I}\mathrm{T}\mathrm{C}1}={\dot{\mathrm{m}}}_2·({\mathrm{h}}_3-{\mathrm{h}}_2) \\ {\dot{(\mathrm{E}}}_{5\mathrm{a}}-{\dot{\mathrm{E}}}_6)-({\dot{\mathrm{E}}}_3-{\dot{\mathrm{E}}}_2)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{I}\mathrm{T}\mathrm{C}1} \end{gathered}$$	$$\begin{gathered} {\mathrm{Q}}_{\mathrm{I}\mathrm{T}\mathrm{C}1}={\dot{\mathrm{m}}}_{2\mathrm{r}}·({\mathrm{h}}_3-{\mathrm{h}}_{2\mathrm{r}}) \\ {\dot{(\mathrm{E}}}_{5\mathrm{a}}-{\dot{\mathrm{E}}}_6)-({\dot{\mathrm{E}}}_3-{\dot{\mathrm{E}}}_{2\mathrm{r}})={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{I}\mathrm{T}\mathrm{C}1} \end{gathered}$$	$$\begin{gathered} {\mathrm{Q}}_{\mathrm{I}\mathrm{T}\mathrm{C}1}={\dot{\mathrm{m}}}_{12}·({\mathrm{h}}_{12}-{\mathrm{h}}_{13}) \\ {\dot{(\mathrm{E}}}_{12}-{\dot{\mathrm{E}}}_{13})-({\dot{\mathrm{E}}}_6-{\dot{\mathrm{E}}}_3)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{I}\mathrm{T}\mathrm{C}1} \end{gathered}$$
ITC2	-	$$\begin{gathered} {\mathrm{Q}}_{\mathrm{I}\mathrm{T}\mathrm{C}2}={\dot{\mathrm{m}}}_{2\mathrm{r}}·({\mathrm{h}}_{2\mathrm{r}}-{\mathrm{h}}_2) \\ {\dot{\mathrm{E}}}_4-{\dot{\mathrm{E}}}_{4\mathrm{r}}-({\dot{\mathrm{E}}}_{2\mathrm{r}}-{\dot{\mathrm{E}}}_2)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{I}\mathrm{T}\mathrm{C}2} \end{gathered}$$	$$\begin{gathered} {\mathrm{Q}}_{\mathrm{I}\mathrm{T}\mathrm{C}2}={\dot{\mathrm{m}}}_{11}·({\mathrm{h}}_{11\mathrm{a}}-{\mathrm{h}}_{12}) \\ {\dot{(\mathrm{E}}}_{11\mathrm{a}}-{\dot{\mathrm{E}}}_{12})-({\dot{\mathrm{E}}}_7-{\dot{\mathrm{E}}}_5)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{I}\mathrm{T}\mathrm{C}2} \end{gathered}$$
ITC3	$$\begin{gathered} {\mathrm{Q}}_{\mathrm{I}\mathrm{T}\mathrm{C}3}={\dot{\mathrm{m}}}_4·({\mathrm{h}}_4-{\mathrm{h}}_1) \\ {\dot{(\mathrm{E}}}_4-{\dot{\mathrm{E}}}_1)-({\dot{\mathrm{E}}}_8-{\dot{\mathrm{E}}}_1)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{I}\mathrm{T}\mathrm{C}3} \end{gathered}$$	$$\begin{gathered} {\mathrm{Q}}_{\mathrm{I}\mathrm{T}\mathrm{C}3}={\dot{\mathrm{m}}}_{4\mathrm{r}}·({\mathrm{h}}_{4\mathrm{r}}-{\mathrm{h}}_1) \\ {\dot{(\mathrm{E}}}_{4\mathrm{r}}-{\dot{\mathrm{E}}}_1)-({\dot{\mathrm{E}}}_8-{\dot{\mathrm{E}}}_1)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{I}\mathrm{T}\mathrm{C}3} \end{gathered}$$	$$\begin{gathered} {\mathrm{Q}}_{\mathrm{I}\mathrm{T}\mathrm{C}3}={\dot{\mathrm{m}}}_{10}·({\mathrm{h}}_{10}-{\mathrm{h}}_1) \\ {\dot{(\mathrm{E}}}_{10}-{\dot{\mathrm{E}}}_1)-({\dot{\mathrm{E}}}_{15}-{\dot{\mathrm{E}}}_{14})={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{I}\mathrm{T}\mathrm{C}3} \end{gathered}$$
T1	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{T}1}={\dot{\mathrm{m}}}_4·({\mathrm{h}}_3-{\mathrm{h}}_4) \\ {\dot{(\mathrm{E}}}_3-{\dot{\mathrm{E}}}_4)-{\dot{\mathrm{W}}}_{\mathrm{T}1}={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{T}1} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{T}1}={\dot{\mathrm{m}}}_3·({\mathrm{h}}_3-{\mathrm{h}}_4) \\ {\dot{(\mathrm{E}}}_3-{\dot{\mathrm{E}}}_4)-{\dot{\mathrm{W}}}_{\mathrm{T}1}={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{T}1} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{T}1}={\dot{\mathrm{m}}}_9·({\mathrm{h}}_9-{\mathrm{h}}_{10}) \\ {\dot{(\mathrm{E}}}_9-{\dot{\mathrm{E}}}_{10})-{\dot{\mathrm{W}}}_{\mathrm{T}1}={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{T}1} \end{gathered}$$
P1	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{p}1}={\dot{\mathrm{m}}}_{9\mathrm{a}}·({\mathrm{h}}_{9\mathrm{a}}-{\mathrm{h}}_9) \\ {\dot{\mathrm{W}}}_{\mathrm{p}1}-({\dot{\mathrm{E}}}_{9\mathrm{a}}-{\dot{\mathrm{E}}}_9)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}1} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{p}1}={\dot{\mathrm{m}}}_9·({\mathrm{h}}_{9\mathrm{a}}-{\mathrm{h}}_9) \\ {\dot{\mathrm{W}}}_{\mathrm{p}1}-{\dot{(\mathrm{E}}}_{9\mathrm{a}}-{\dot{\mathrm{E}}}_9)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}1} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{p}1}={\dot{\mathrm{m}}}_{16\mathrm{a}}·({\mathrm{h}}_{16\mathrm{a}}-{\mathrm{h}}_{16}) \\ {\dot{\mathrm{W}}}_{\mathrm{p}1}-{(\dot{\mathrm{E}}}_{16\mathrm{a}}-{\dot{\mathrm{E}}}_{16})={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}1} \end{gathered}$$
T2	-	-	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{T}2}={\dot{\mathrm{m}}}_7({\mathrm{h}}_7-{\mathrm{h}}_8) \\ {\dot{(\mathrm{E}}}_7-{\dot{\mathrm{E}}}_8)-{\dot{\mathrm{W}}}_{\mathrm{T}1}={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{T}2} \end{gathered}$$
P2	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{P}2}={\dot{\mathrm{m}}}_{5\mathrm{a}}·({\mathrm{h}}_{5\mathrm{a}}-{\mathrm{h}}_5) \\ {\dot{\mathrm{W}}}_{\mathrm{P}2}-({\dot{\mathrm{E}}}_{5\mathrm{a}}-{\dot{\mathrm{E}}}_5)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}2} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{P}2}={\dot{\mathrm{m}}}_5·({\mathrm{h}}_{5\mathrm{a}}-{\mathrm{h}}_5) \\ {\dot{\mathrm{W}}}_{\mathrm{P}2}-({\dot{\mathrm{E}}}_{5\mathrm{a}}-{\dot{\mathrm{E}}}_5)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}2} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{P}2}={\dot{\mathrm{m}}}_{11}·({\mathrm{h}}_{11\mathrm{a}}-{\mathrm{h}}_{11}) \\ {\dot{\mathrm{W}}}_{\mathrm{P}2}-({\dot{\mathrm{E}}}_{5\mathrm{a}}-{\dot{\mathrm{E}}}_5)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}2} \end{gathered}$$
P3	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{P}3}={\dot{\mathrm{m}}}_2·({\mathrm{h}}_2-{\mathrm{h}}_1) \\ {\dot{\mathrm{W}}}_{\mathrm{P}3}-({\dot{\mathrm{E}}}_2-{\dot{\mathrm{E}}}_1)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}3} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{P}3}={\dot{\mathrm{m}}}_2·({\mathrm{h}}_2-{\mathrm{h}}_1) \\ {\dot{\mathrm{W}}}_{\mathrm{P}3}-({\dot{\mathrm{E}}}_2-{\dot{\mathrm{E}}}_1)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}3} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{P}3}={\dot{\mathrm{m}}}_6·({\mathrm{h}}_6-{\mathrm{h}}_4) \\ {\dot{\mathrm{W}}}_{\mathrm{P}3}-({\dot{\mathrm{E}}}_6-{\dot{\mathrm{E}}}_4)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}3} \end{gathered}$$
P4	-	-	$$\begin{gathered} {\dot{\mathrm{W}}}_{\mathrm{P}4}={\dot{\mathrm{m}}}_2·({\mathrm{h}}_2-{\mathrm{h}}_1) \\ {\dot{\mathrm{W}}}_{\mathrm{p}4}-({\dot{\mathrm{E}}}_2-{\dot{\mathrm{E}}}_1)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{P}4} \end{gathered}$$
Solar Collector (CS)	$$\begin{gathered} {\dot{\mathrm{Q}}}_{\mathrm{C}\mathrm{S}}={\mathrm{I}}_0·{\mathsf{\eta }}_{\mathrm{c}}{·\mathrm{A}}_{\mathrm{c}} \\ {\dot{\mathrm{E}}}_{\mathrm{x},\mathrm{i}\mathrm{n}}-\left({\dot{\mathrm{E}}}_9-{\dot{\mathrm{E}}}_{10}\right)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{C}\mathrm{S}} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{Q}}}_{\mathrm{C}\mathrm{S}}={\mathrm{I}}_0·{\mathsf{\eta }}_{\mathrm{c}}{·\mathrm{A}}_{\mathrm{c}} \\ {\dot{\mathrm{E}}}_{\mathrm{x},\mathrm{i}\mathrm{n}}-\left({\dot{\mathrm{E}}}_9-{\dot{\mathrm{E}}}_{10}\right)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{C}\mathrm{S}} \end{gathered}$$	$$\begin{gathered} {\dot{\mathrm{Q}}}_{\mathrm{C}\mathrm{S}}={\mathrm{I}}_0·{\mathsf{\eta }}_{\mathrm{c}}{·\mathrm{A}}_{\mathrm{c}} \\ {\dot{\mathrm{E}}}_{\mathrm{x},\mathrm{i}\mathrm{n}}-\left({\dot{\mathrm{E}}}_{16}-{\dot{\mathrm{E}}}_{17}\right)={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{C}\mathrm{S}} \end{gathered}$$
Thermal storage (TK)	$\left({\dot{\mathrm{E}}}_6+{\dot{\mathrm{E}}}_{9\mathrm{a}}\right)-\left({\dot{\mathrm{E}}}_5+{\dot{\mathrm{E}}}_{10}\right)-{\dot{\mathrm{E}}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{T}\mathrm{K}}$	$\left({\dot{\mathrm{E}}}_6+{\dot{\mathrm{E}}}_{9\mathrm{a}}\right)-\left({\dot{\mathrm{E}}}_5+{\dot{\mathrm{E}}}_{10}\right)-{\dot{\mathrm{E}}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{T}\mathrm{K}}$	$\left({\dot{\mathrm{E}}}_{16}+{\dot{\mathrm{E}}}_{13}\right)-\left({\dot{\mathrm{E}}}_{17}+{\dot{\mathrm{E}}}_{11}\right)-{\dot{\mathrm{E}}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{T}\mathrm{K}}$

.

2.4. Solar Field Modeling

The different radiation values were obtained from temperature and humidity data from different weather stations. The radiation on a surface can be calculated from ${\mathrm{I}}_{\mathrm{s}\mathrm{c}}$, which expresses the incident energy in one hour, according to Equation (8).

$${\mathrm{I}}_{\mathrm{s}\mathrm{c}}=3.6\mathsf{\gamma }\left(\frac{\mathrm{k}\mathrm{J}}{{\mathrm{m}}^2\mathrm{h}}\right)$$

(8)

On the other hand, the combination of solar and diffuse energy incidents on a horizontal plane on the earth’s surface is known as the earth’s overall energy, and these quantities are linked according to Equation (9).

$${\mathrm{I}}_{\mathrm{o}}={\mathrm{I}}_{\mathrm{o}\mathrm{n}} \mathrm{c}\mathrm{o}\mathrm{s}{\mathsf{\theta }}_{\mathrm{z}}+{\mathrm{I}}_{\mathrm{d}}$$

(9)

where ${\mathrm{I}}_{\mathrm{o}}$ is the overall radiation that impacts a horizontal surface (W/m²), ${\mathrm{I}}_{\mathrm{d}}$ and ${\mathrm{I}}_{\mathrm{o}\mathrm{n}}$ are the diffuse and direct radiation on a perpendicular surface on a horizontal plane, and ${\mathsf{\theta }}_{\mathrm{z}}$ is the zenith angle of the sun given by Equation (10).

$${\mathrm{I}}_{\mathrm{o}}={\mathrm{I}}_{\mathrm{o}\mathrm{n}} \mathrm{c}\mathrm{o}\mathrm{s}{\mathsf{\theta }}_{\mathrm{z}}+{\mathrm{I}}_{\mathrm{d}}$$

(10)

where L is the latitude of the location in degrees, $\mathsf{\delta }$ is the declination angle of the earth’s axis (23.45° approximately), and $\mathrm{w}$ is the hour angle. So, for a given day, ${\mathrm{I}}_{\mathrm{o}\mathrm{n}}$ can be the extra radiation (energy rate) on a surface normal to the sun’s rays, according to Equation (11).

$${\mathrm{I}}_{\mathrm{o}\mathrm{n}}={\mathrm{I}}_{\mathrm{s}\mathrm{c}}{\mathrm{E}}_0={\mathrm{I}}_{\mathrm{s}\mathrm{c}}\left(1+0.033·\mathrm{c}\mathrm{o}\mathrm{s}\frac{2\mathsf{\pi }{\mathrm{d}}_{\mathrm{n}}}{365}\right)$$

(11)

Substituting Equations (8) and (9) into (11), we obtained Equation (12).

$${\mathrm{I}}_{\mathrm{o}}={\mathrm{I}}_{\mathrm{s}\mathrm{c}}\left(1+0.033·\mathrm{c}\mathrm{o}\mathrm{s}\frac{2\mathsf{\pi }{\mathrm{d}}_{\mathrm{n}}}{365}\right)\left(\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{w}·\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\delta }·\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{L}+\mathrm{s}\mathrm{e}\mathrm{n}\mathsf{\delta }·\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{L}\right)$$

(12)

Based on the expression of radiation obtained in Equation (11), it is possible to determine the amount of useful gain of the heat collector, expressed by Equation (13).

$${\dot{\mathrm{Q}}}_{\mathrm{c}\mathrm{o}\mathrm{l}}={\mathrm{I}}_0·{\mathsf{\eta }}_{\mathrm{c}}{·\mathrm{A}}_{\mathrm{c}}$$

(13)

where ${\mathrm{I}}_0$ is the total solar radiation on the collector surface in $\mathrm{W}/{\mathrm{m}}^2$, ${\mathsf{\eta }}_{\mathrm{c}}$ is the instantaneous efficiency of the collector, and ${\mathrm{A}}_{\mathrm{c}}$ is the collector area in ${\mathrm{m}}^2$. The instantaneous efficiency of the collector (${\mathsf{\eta }}_{\mathrm{c}}$) can be calculated according to Equation (14).

$${\mathsf{\eta }}_{\mathrm{c}}={\mathrm{F}}_{\mathrm{R}}·\mathsf{\alpha }·\mathsf{\tau }-{\mathrm{F}}_{\mathrm{R}}·{\mathrm{U}}_{\mathrm{L}}·\frac{\left({\mathrm{T}}_{\mathrm{o}\mathrm{i}\mathrm{l},\mathrm{i}\mathrm{n}}-{\mathrm{T}}_{\mathrm{a}}\right)}{{\mathrm{I}}_0}$$

(14)

where ${\mathrm{F}}_{\mathrm{R}}$ is the heat elimination factor of the collector, the transmittance ($\mathsf{\tau }$) is the part of the incident solar radiation transmitted by the collector cover plates, the absorbance ($\mathsf{\alpha }$) is the portion of the solar radiation absorbed by the collector, ${\mathrm{U}}_{\mathrm{L}}$ is the overall heat transfer coefficient, ${\mathrm{T}}_{\mathrm{a}}$ is the reference temperature, and ${\mathrm{T}}_{\mathrm{o}\mathrm{i}\mathrm{l},\mathrm{i}\mathrm{n}}$ is the temperature at which the thermal oil enters the collector. The values of ${\mathrm{F}}_{\mathrm{R}}\left(\mathsf{\tau }\mathsf{\alpha }\right)$ and ${\mathrm{F}}_{\mathrm{R}}{\mathrm{U}}_{\mathrm{L}}$ used in this work are shown in

Table 2. Initial values for the modeling of the solar field.

Description	Value	Units	Ref.
Collector area	100	m2
Evacuated, selective surface type A			[42]
${\mathrm{F}}_{\mathrm{R}}·{\mathrm{U}}_{\mathrm{L}}$	3.3	W/m2	[42]
${\mathrm{F}}_{\mathrm{R}}·\mathsf{\alpha }·\mathsf{\tau }$	0.70	-	[42]
Overall heat transfer coefficient tank	11.1	W/k	[39]
Tank volume	50	m3	[39]
Thermal oil flow rate	1	kg/s
Initial tank temperature (${\mathrm{T}}_{\mathrm{s},\mathrm{i}}$)	130	°C
Collector thermal oil inlet temperature	90	°C

.

For all the systems (or cases) modeled in this study, it was assumed the fluid in the heat storage tank was uniformly mixed. The temperature variation as a function of time is presented below:

$${\left({\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{i}\mathrm{l}}{·\mathrm{C}\mathrm{p}}_{\mathrm{o}\mathrm{i}\mathrm{l}}\right)}_{\mathrm{s}}\frac{{\mathrm{d}\mathrm{T}}_{\mathrm{s}}}{\mathrm{d}\mathrm{t}}={\dot{\mathrm{Q}}}_{\mathrm{c}\mathrm{o}\mathrm{l}}-{\dot{\mathrm{Q}}}_{\mathrm{O}\mathrm{R}\mathrm{C}}-{\left(\mathrm{U}\mathrm{A}\right)}_{\mathrm{s}}·\left({\mathrm{T}}_{\mathrm{s}}-{\mathrm{T}}_{\mathrm{a}}\right)$$

(15)

where ${\mathrm{m}}_{\mathrm{o}\mathrm{i}\mathrm{l}}$ and ${\mathrm{C}}_{\mathrm{p},\mathrm{o}\mathrm{i}\mathrm{l}}$ are the mass and heat capacity of the thermal oil, respectively; ${\dot{\mathrm{Q}}}_{\mathrm{c}\mathrm{o}\mathrm{l}}$ denotes the effective energy gain of the solar collector; ${\dot{\mathrm{Q}}}_{\mathrm{O}\mathrm{R}\mathrm{C}}$ is the minimum energy required for ORC system, which is determined as the minimum heat required by the evaporator to convert the organic fluid from saturated liquid at the evaporator inlet to saturated steam; ${\left(\mathrm{U}\mathrm{A}\right)}_{\mathrm{s}}$ is the storage tank loss coefficient; ${\mathrm{T}}_{\mathrm{s}}$ is the initial temperature of the tank; and ${\mathrm{T}}_{\mathrm{a}}$ is the room temperature. Thus, Equation (16) can be rewritten as

$${\mathrm{T}}_{\mathrm{s},\mathrm{n}\mathrm{e}\mathrm{w}}={\mathrm{T}}_{\mathrm{s},\mathrm{i}}+\frac{∆\mathrm{t}}{{{\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{i}\mathrm{l}}·\mathrm{C}\mathrm{p}}_{\mathrm{o}\mathrm{i}\mathrm{l}}}\left[{\dot{\mathrm{Q}}}_{\mathrm{c}\mathrm{o}\mathrm{l}}-{\dot{\mathrm{Q}}}_{\mathrm{O}\mathrm{R}\mathrm{C}}-{\left(\mathrm{U}\mathrm{A}\right)}_{\mathrm{s}}·\left({\mathrm{T}}_{\mathrm{s}}-{\mathrm{T}}_{\mathrm{a}}\right)\right]$$

(16)

where ${\mathrm{T}}_{\mathrm{s},\mathrm{n}\mathrm{e}\mathrm{w}}$ is the thermal oil temperature in the storage tank at the end of the Δt (1 h), which will be supplied into the ORC system.

The total exergy input to the solar ORC system is the exergy of the solar radiation falling on the solar collector surface. The solar exergy is a function of the external temperature of the sun (${\mathrm{T}}_{\mathrm{s}\mathrm{u}\mathrm{n}}=6000 \mathrm{K})$ and is governed by Equation (17).

$${\dot{\mathrm{E}}}_{\mathrm{x},\mathrm{i}\mathrm{n}}={\mathrm{A}}_{\mathrm{c}}{·\mathrm{I}}_0·\left[1+\frac{1}{3}·{\left(\frac{{\mathrm{T}}_0}{{\mathrm{T}}_{\mathrm{s}\mathrm{u}\mathrm{n}}}\right)}^4-\frac{4}{3}·\left(\frac{{\mathrm{T}}_0}{{\mathrm{T}}_{\mathrm{s}\mathrm{u}\mathrm{n}}}\right)\right]$$

(17)

The ratio of the irreversibility of the components of the solar ORC system is defined by Equation (18).

$$\mathrm{I}\mathrm{R}=\frac{{\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{K}}}{{\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}$$

(18)

whereby ${\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{K}}$ is the exergy destruction of the component k, and ${\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$ is the total exergy of the system. Therefore, the exergy destruction of each component is calculated according to Equation (19). The exergy balance of each component is summarized in Table 1.

$${\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{K}}={\dot{\mathrm{E}}}_{\mathrm{f}}-{\dot{\mathrm{E}}}_{\mathrm{P}}$$

(19)

Another essential term to evaluate the system from the exergy point of view is the exergy fuel depletion ratio (FDR), which can be calculated using Equation (20) [39].

$$\mathrm{F}\mathrm{D}\mathrm{R}=\frac{{\dot{\mathrm{X}}}_{\mathrm{D},\mathrm{K}}}{{\dot{\mathrm{E}}}_{\mathrm{x},\mathrm{i}\mathrm{n}}}$$

(20)

where ${\dot{\mathrm{E}}}_{\mathrm{x},\mathrm{i}\mathrm{n}}$ is the amount of exergy entering the collector (Equation (17)). Finally, the exergetic efficiency of the ORC cycle can be defined as the ratio between the net power produced and the amount of exergy entering the system, according to Equation (21) [35].

$${\mathsf{\eta }}_{\mathrm{e}\mathrm{x}\mathrm{e}\mathrm{r},\mathrm{O}\mathrm{R}\mathrm{C}}=\frac{{\dot{\mathrm{W}}}_{\mathrm{n}\mathrm{e}\mathrm{t}}}{{\dot{\mathrm{E}}}_{\mathrm{i}\mathrm{n}}}$$

(21)

where ${\dot{\mathrm{E}}}_{\mathrm{i}\mathrm{n}}$ is the amount of exergy entering the ORC in kJ/s.

2.5. Heat Exchanger Modeling: Evaporator, Condenser, and Regenerator

The evaporator heat exchanger analysis involved dividing the equipment into three distinct zones based on the organic working fluid’s process and the heat exchanger involved: preheating, evaporation, and superheating. Equations (22)–(24) were used to calculate the heat rate associated with each of the three zones.

$${\dot{\mathrm{Q}}}_{\mathrm{P}\mathrm{r}\mathrm{e}}={\dot{\mathrm{m}}}_{\mathrm{w}\mathrm{f}}·({\mathrm{h}}_{2\mathrm{r}\mathrm{l}\mathrm{s}}-{\mathrm{h}}_{2\mathrm{r}\mathrm{v}\mathrm{s}})$$

(22)

$${\dot{\mathrm{Q}}}_{\mathrm{E}\mathrm{v}\mathrm{a}\mathrm{p}}={\dot{\mathrm{m}}}_{\mathrm{w}\mathrm{f}}·\left({\mathrm{h}}_{2\mathrm{r}}-{\mathrm{h}}_{2\mathrm{r}\mathrm{v}\mathrm{s}}\right)$$

(23)

$${\dot{\mathrm{Q}}}_{\mathrm{S}\mathrm{o}\mathrm{b}}={\dot{\mathrm{m}}}_{\mathrm{w}\mathrm{f}}·\left({\mathrm{h}}_{2\mathrm{r}\mathrm{v}\mathrm{s}}-{\mathrm{h}}_3\right),$$

(24)

Equation (25) provides the calculation for the heat transfer area, while the mass flow rate of the working fluid is represented by ${\dot{\mathrm{m}}}_{\mathrm{w}\mathrm{f}}$.

$$\mathrm{A}=\dot{\mathrm{Q}}/\mathrm{U}{·\mathsf{\Delta }\mathrm{T}}_{\mathrm{m}\mathrm{l}}$$

(25)

The overall heat transfer coefficient, denoted as U, is computed by taking into account the thermal resistance circuit that goes from the hot fluid to the cold fluid. This can be determined using Equation (26).

$$\frac{1}{\mathrm{U}}=\frac{1}{{\mathrm{h}}_{\mathrm{t}\mathrm{o}}}+{\mathrm{R}}_{\mathrm{w}}+\frac{1}{{\mathrm{h}}_{\mathrm{w}\mathrm{f}}}$$

(26)

The convective heat transfer coefficient for the thermal oil side is represented by ${\mathrm{h}}_{\mathrm{t}\mathrm{o}}$, while the wall resistance is denoted as ${\mathrm{R}}_{\mathrm{w}}$. The convective heat transfer coefficient for the working fluid side is represented by ${\mathrm{h}}_{\mathrm{w}\mathrm{f}}$. Equation (27) calculates the heat transfer area by summing up the areas needed for each phase.

$$\mathrm{A}={\mathrm{A}}_{\mathrm{P}\mathrm{r}\mathrm{e}}+{\mathrm{A}}_{\mathrm{E}\mathrm{v}\mathrm{a}\mathrm{p}}+{\mathrm{A}}_{\mathrm{S}\mathrm{o}\mathrm{b}}$$

(27)

The number of plates in the evaporator is calculated by Equation (28), where the height and width of the plates are denoted by L and W, respectively.

$${\mathrm{N}}_{\mathrm{p}}={\mathrm{A}}_{\mathrm{P}\mathrm{r}\mathrm{e}}/(\mathrm{L}·\mathrm{W})+{\mathrm{A}}_{\mathrm{E}\mathrm{v}\mathrm{a}\mathrm{p}}/(\mathrm{L}·\mathrm{W})+{\mathrm{A}}_{\mathrm{S}\mathrm{o}\mathrm{b}}/(\mathrm{L}·\mathrm{W})$$

(28)

Equation (29) provides the heat transfer coefficient values for the working fluid and thermal oil in the single-phase region [43].

$$\mathrm{N}\mathrm{u}=\frac{\mathrm{h}·{\mathrm{D}}_{\mathrm{h}}}{\mathrm{k}}=0.78{·\mathrm{R}}_{\mathrm{e}}^{0.5}{·\mathrm{P}}_{\mathrm{r}}^{1/3}$$

(29)

where k is the thermal conductivity, h is the heat transfer coefficient, ${\mathrm{R}}_{\mathrm{e}}$ is the Reynolds number, ${\mathrm{D}}_{\mathrm{h}}$ is the hydraulic diameter, and ${\mathrm{P}}_{\mathrm{r}}$ is the Prandtl number.

Equation (30) was used to model the heat transfer coefficient of the working fluid in the two-phase region [44].

$$\mathrm{N}\mathrm{u}=\frac{\mathrm{h}·{\mathrm{D}}_{\mathrm{h}}}{\mathrm{k}}=0.00187·{\left(\frac{\mathrm{q}·{\mathrm{d}}_0}{{\mathrm{k}}_{\mathrm{f}}}\right)}^{0.56}·{\left(\frac{{\mathrm{d}}_0·{\mathrm{h}}_{\mathrm{f}\mathrm{g}}}{{\mathsf{\alpha }}_{\mathrm{i}}^2}\right)}^{0.31}·{\mathrm{P}}_{\mathrm{r}}^{0.35}$$

(30)

The equation expresses the relationship between the heat flux (q) in $\mathrm{W} {\mathrm{m}}^{-1}$, the bubble departure diameter ${\mathrm{d}}_0$ in meters, the thermal conductivity of the liquid phase ${\mathrm{k}}_{\mathrm{f}}$ ($\mathrm{W} {\mathrm{m}}^{-1} {\mathrm{K}}^{-1}$), the latent heat of evaporation ${\mathrm{h}}_{\mathrm{f}\mathrm{g}}$ (${\mathrm{J} \mathrm{k}\mathrm{g}}^{-1}$), and the thermal diffusivity ${\mathsf{\alpha }}_{\mathrm{i}}$ (${\mathrm{m}}^2 {\mathrm{S}}^{-1}$).

Additionally, the heat exchanger for the condenser was segmented into two distinct regions: the cooling zone and the condensing zone. The corresponding amounts of heat in each zone are determined by Equations (31) and (32).

$${\dot{\mathrm{Q}}}_{\mathrm{C}\mathrm{o}\mathrm{o}\mathrm{l}}={\dot{\mathrm{m}}}_{\mathrm{w}\mathrm{f}}·\left({\mathrm{h}}_{4\mathrm{r}}-{\mathrm{h}}_{4\mathrm{r}\mathrm{v}\mathrm{s}}\right)$$

(31)

$${\dot{\mathrm{Q}}}_{\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}}={\dot{\mathrm{m}}}_{\mathrm{w}\mathrm{f}}·\left({\mathrm{h}}_{4\mathrm{r}\mathrm{v}\mathrm{s}}-{\mathrm{h}}_1\right)$$

(32)

The overall heat transfer coefficient is modeled by Equation (33).

$$\frac{1}{\mathrm{U}}=\frac{1}{{\mathrm{h}}_{\mathrm{r}\mathrm{f}}}+{\mathrm{R}}_{\mathrm{w}}+\frac{1}{{\mathrm{h}}_{\mathrm{w}\mathrm{f}}}$$

(33)

The convective heat transfer coefficient on the cooling fluid side is denoted by ${\mathrm{h}}_{\mathrm{r}\mathrm{f}}$, while ${\mathrm{R}}_{\mathrm{w}}$ represents the wall resistance, and ${\mathrm{h}}_{\mathrm{w}\mathrm{f}}$ refers to the convective heat transfer coefficient on the working fluid side.

The heat transfer coefficient in the two-phase zone of the condenser is determined through Equations (34) and (35):

$$Nu=\frac{h·D_h}{k}=4.118·{\left({Re}_{eq}\right)}^{0.4}·P_{r,l}^{0.33}$$

(34)

$${Re}_{eq}=G·\left[1-x_m+x_m{\left(\frac{{\rho }_l}{{\rho }_v}\right)}^{0.5}\right]·\frac{D}{{\mu }_l}$$

(35)

This equation calculates the two-phase heat transfer coefficient in the condenser, and it involves several variables, including the Reynolds number for the equivalent mass flow rate, the Prandtl number of the liquid phase, the vapor quality, the densities of the liquid and vapor phases, and the dynamic viscosity of the liquid phase.

The area required for the condenser heat transfer is obtained by summing up its individual areas using Equation (36).

$$\mathrm{A}={\mathrm{A}}_{\mathrm{C}\mathrm{o}\mathrm{o}\mathrm{l}}+{\mathrm{A}}_{\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}}$$

(36)

The calculation for determining the number of plates in the condenser heat exchanger is expressed by the following Equation (37).

$${\mathrm{N}}_{\mathrm{p}}={\mathrm{A}}_{\mathrm{C}\mathrm{o}\mathrm{o}\mathrm{l}}/(\mathrm{L}·\mathrm{W})+{\mathrm{A}}_{\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}}/(\mathrm{L}·\mathrm{W})$$

(37)

where L and W are the height and width of the plate, respectively. Nusselt number correlation used for the condensing and cooling phases are shown in Equations (38) and (39) [45,46].

$${\mathrm{N}\mathrm{u}}_{\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{d}}=4.18{·\mathrm{R}}_{\mathrm{e}\mathrm{q}}^{0.4}{·\mathrm{P}}_{\mathrm{r}}^{0.3}$$

(38)

$${\mathrm{N}\mathrm{u}}_{\mathrm{C}\mathrm{o}\mathrm{o}\mathrm{l}}=0.78{·\mathrm{R}}_{\mathrm{e}}^{0.5}{·\mathrm{P}}_{\mathrm{r}}^{1/3}$$

(39)

where ${\mathrm{P}}_{\mathrm{r}}$ is the Prandtl number and ${\mathrm{R}}_{\mathrm{e}\mathrm{q}}$ is the Reynolds number for the equivalent mass expenditure.

3. Results and Discussion

In this study, a low-temperature (T < 130 °C) organic Rankine cycle (ORC) driven by an FPSC was integrated as a heat source. Three types of configurations, namely SORC, RORC, and DORC, were considered. The data related to solar radiation were taken from four different geographical sites in Colombia (Incoder, Granja-Paici, La Gran Via, and Las Flores) located in different areas of the country due to their high solar potential. Finally, a comparison was made regarding the performance of the configurations in terms of energy and exergy.

Table 3. Initial values for the modeling of the ORC configurations.

Configuration	Parameters	Value	Units
SORC/RORC/DORC	Turbine isentropic efficiency	80	%
SORC/RORC/DORC	Pump isentropic efficiency	80	%
SORC/RORC/DORC	Cooling water temperature	25	°C
SORC/RORC/DORC	Pinch Point condenser	10	°C
SORC/ROC	Pinch Point evaporator	10	°C
DORC	Pinch Point evaporators	20	°C
SORC	Condensation temperature	40	°C
RORC	Regenerator effectiveness	85	%
SORC/RORC/DORC	Pressure ratio (P1, P2)	2.5	-
SORC/RORC	Pressure ratio (P3)	6	-
DORC	Pressure ratio (P3)	2	-
DORC	Pressure ratio (P4)	1.5	-

presents the principal values used to simulate different ORC configurations; the assumption of isentropic efficiency for small turbines agrees with the postulate of Fontalvo et al. [47].

Table 4. Thermodynamic properties of RORC–Solar configuration.

State	T [K]	P [kPa]	H − h0 [kJ/kg]	s − s0 [kJ/kg-K]	$\dot{\mathbf{E}}$ [kJ/s]	$\dot{\mathbf{m}}$ [kg/s]
1	313.15	7.89	−132.35	−0.84	0.07	0.130
2	313.16	47.35	−132.30	−0.84	0.07	0.130
2r	318.29	47.35	−123.28	−0.84	0.14	0.130
2ls	358.95	47.30	−48.56	−0.60	1.30	0.130
2vs	358.95	39.03	320.65	0.45	8.77	0.130
3	358.98	39.03	327.99	0.45	9.58	0.130
4	321.94	7.89	282.28	0.48	2.67	0.130
4r	314.50	7.89	273.26	0.48	2.59	0.130
4vs	323.25	7.89	283.89	0.51	2.68	0.130
5	396.17	101.23	77.35	0.21	13.43	1.000
5a	396.23	202.46	77.47	0.21	13.45	1.000
5avs	396.17	202.46	77.35	0.21	13.19	1.000
5ls	368.98	199.68	28.46	0.08	4.36	1.000
6	363.58	196.93	18.96	0.05	2.95	1.000
7	298.15	101.30	104.92	0.00	0.00	2.510
7vs	303.15	99.11	125.82	0.07	0.44	2.510
8	303.17	96.89	125.91	0.07	0.44	2.510
9	408.09	101.23	99.44	0.27	17.48	1.000
9a	408.16	202.46	99.56	0.27	17.50	1.000
10	391.62	101.23	69.01	0.19	11.61	1.000

gives the main properties of each configuration which were obtained based on the data shown in Table 3.

The properties of the RORC and DORC systems are given in Tables S1 and S2, respectively.

Table 5. Results of the main parameters considered in the study.

Station	Parameters	SORC	RORC	DORC	Unit
Granja-Paicí	Net Power Output, ${\dot{\mathrm{W}}}_{\mathrm{n}\mathrm{e}\mathrm{t}}$	5.86	5.86	6.49	$\mathrm{k}\mathrm{W}$
	Thermal efficiency ORC, ${\mathsf{\eta }}_{\mathrm{I},\mathrm{O}\mathrm{R}\mathrm{C}}$	9.53	9.73	4.96	$\mathrm{\%}$
	Thermal Efficiency ORC–Solar, ${\mathsf{\eta }}_{\mathrm{I},\mathrm{O}\mathrm{R}\mathrm{C}-\mathrm{S}}$	15.77	15.77	17.46	$\mathrm{\%}$
	Exergetic efficiency ORC, ${\mathsf{\eta }}_{\mathrm{e}\mathrm{x}\mathrm{e}\mathrm{r},\mathrm{O}\mathrm{R}\mathrm{C}}$	44.5	45.4	28.45	$\mathrm{k}\mathrm{W}$
	Exergetic efficiency ORC–Solar, ${\mathsf{\eta }}_{\mathrm{e}\mathrm{x}\mathrm{e}\mathrm{r},\mathrm{O}\mathrm{R}\mathrm{C}-\mathrm{S}}$	7.49	7.49	8.30	$\mathrm{\%}$
	Heat useful gain, ${\dot{\mathrm{Q}}}_{\mathrm{c}\mathrm{o}\mathrm{l}}$	37.16	37.16	37.16	$\mathrm{\%}$
	Solar global radiation, ${\mathrm{I}}_0$	837.30	837.30	837.30	${\mathrm{W}/\mathrm{m}}^2$
Incoder	Net Power Output, ${\dot{\mathrm{W}}}_{\mathrm{n}\mathrm{e}\mathrm{t}}$	5.39	5.39	6.24	$\mathrm{k}\mathrm{W}$
	Thermal efficiency ORC, ${\mathsf{\eta }}_{\mathrm{I},\mathrm{O}\mathrm{R}\mathrm{C}}$	9.50	9.69	4.90	$\mathrm{\%}$
	Thermal Efficiency ORC–Solar, ${\mathsf{\eta }}_{\mathrm{I},\mathrm{O}\mathrm{R}\mathrm{C}-\mathrm{S}}$	29.69	29.69	34.38	$\mathrm{\%}$
	Exergetic efficiency ORC, ${\mathsf{\eta }}_{\mathrm{e}\mathrm{x}\mathrm{e}\mathrm{r},\mathrm{O}\mathrm{R}\mathrm{C}}$	44.9	45.7	28.52	$\mathrm{k}\mathrm{W}$
	Exergetic efficiency ORC–Solar, ${\mathsf{\eta }}_{\mathrm{e}\mathrm{x}\mathrm{e}\mathrm{r},\mathrm{O}\mathrm{R}\mathrm{C}-\mathrm{S}}$	10.20	10.20	18.81	$\mathrm{\%}$
	Heat useful gain, ${\dot{\mathrm{Q}}}_{\mathrm{c}\mathrm{o}\mathrm{l}}$	18.15	18.15	18.15	$\mathrm{\%}$
	Solar global radiation, ${\mathrm{I}}_0$	565.70	565.70	565.70	${\mathrm{W}/\mathrm{m}}^2$
La Gran Via	Net Power Output, ${\dot{\mathrm{W}}}_{\mathrm{n}\mathrm{e}\mathrm{t}}$	5.77	5.77	6.44	$\mathrm{k}\mathrm{W}$
	Thermal efficiency ORC, ${\mathsf{\eta }}_{\mathrm{I},\mathrm{O}\mathrm{R}\mathrm{C}}$	9.53	9.72	4.94	$\mathrm{\%}$
	Thermal Efficiency ORC–Solar, ${\mathsf{\eta }}_{\mathrm{I},\mathrm{O}\mathrm{R}\mathrm{C}-\mathrm{S}}$	17.18	17.18	19.18	$\mathrm{\%}$
	Exergetic efficiency ORC, ${\mathsf{\eta }}_{\mathrm{e}\mathrm{x}\mathrm{e}\mathrm{r},\mathrm{O}\mathrm{R}\mathrm{C}}$	44.7	45.5	28.46	$\mathrm{k}\mathrm{W}$
	Exergetic efficiency ORC–Solar, ${\mathsf{\eta }}_{\mathrm{e}\mathrm{x}\mathrm{e}\mathrm{r},\mathrm{O}\mathrm{R}\mathrm{C}-\mathrm{S}}$	7.85	7.85	8.77	$\mathrm{\%}$
	Heat useful gain, ${\dot{\mathrm{Q}}}_{\mathrm{c}\mathrm{o}\mathrm{l}}$	33.58	33.58	33.58	$\mathrm{\%}$
	Solar global radiation, ${\mathrm{I}}_0$	827.60	827.60	827.60	${\mathrm{W}/\mathrm{m}}^2$
Las Flores	Net Power Output, ${\dot{\mathrm{W}}}_{\mathrm{n}\mathrm{e}\mathrm{t}}$	6.07	6.07	6.61	$\mathrm{k}\mathrm{W}$
	Thermal efficiency ORC, ${\mathsf{\eta }}_{\mathrm{I},\mathrm{O}\mathrm{R}\mathrm{C}}$	9.54	9.73	4.98	$\mathrm{\%}$
	Thermal Efficiency ORC–Solar, ${\mathsf{\eta }}_{\mathrm{I},\mathrm{O}\mathrm{R}\mathrm{C}-\mathrm{S}}$	15.92	15.92	17.33	$\mathrm{\%}$
	Exergetic efficiency ORC, ${\mathsf{\eta }}_{\mathrm{e}\mathrm{x}\mathrm{e}\mathrm{r},\mathrm{O}\mathrm{R}\mathrm{C}}$	44.6	45.4	28.42	$\mathrm{k}\mathrm{W}$
	Exergetic efficiency ORC–Solar, ${\mathsf{\eta }}_{\mathrm{e}\mathrm{x}\mathrm{e}\mathrm{r},\mathrm{O}\mathrm{R}\mathrm{C}-\mathrm{S}}$	7.64	7.64	8.32	$\mathrm{\%}$
	Heat useful gain, ${\dot{\mathrm{Q}}}_{\mathrm{c}\mathrm{o}\mathrm{l}}$	38.13	38.13	38.13	$\mathrm{\%}$
	Solar global radiation, ${\mathrm{I}}_0$	893.60	893.60	893.60	${\mathrm{W}/\mathrm{m}}^2$

presents the main parameters considered in each system for the four stations obtained based on conditions reported in Table 3 at the time of highest radiation (12:00 p.m.). It can be seen that the Las Flores station had the highest value of total radiation, net power produced, and energy efficiency, followed by Granja-Paici, La Gran Via, and finally, Incoder.

Table 6. Exergy analysis of the systems based on SORC, RORC, or DORC.

Components	System	${\dot{\mathbf{A}}}_{}$ [m2]	${\dot{\mathbf{W}}}_{}$ [kW]	${\dot{\mathbf{E}}}_{\mathbf{D}}$ [kW]	IR [%]	FDR [%]
Collector Solar	SORC	100	-	77.5732	89.5434	92.9689
	RORC	100	-	77.5732	89.5434	92.9689
	DORC	100	-	77.6070	85.2296	92.9614
Pump 1 (P1)	SORC	-	0.1192	0.0956	0.1101	0.1146
	RORC	-	0.1192	0.0956	0.1103	0.1146
	DORC	-	0.1796	0.1434	0.1534	0.1718
Pump 2 (P2)	SORC	-	0.1183	0.0956	0.1101	0.1145
	RORC	-	0.1183	0.0956	0.1103	0.1145
	DORC	-	0.1874	0.1402	0.1540	0.1680
Pump 3 (P3)	SORC	-	0.0071	0.0010	0.0012	0.0012
	RORC	-	0.0071	0.0010	0.0012	0.0012
	DORC	-	0.0031	0.0004	0.0005	0.0005
Pump 4 (P4)	SORC	-	-	-	-	-
	RORC	-	-	-	-	-
	DORC	-	0.0014	0.0002	0.0002	0.0002
ITC1 (Evaporator)	SORC	2.6541	-	1.1895	1.3703	1.4255
	RORC	2.5768	-	1.0618	1.2256	1.2725
	DORC	1.9943	-	1.5864	1.7432	1.9013
ITC2 (Evaporator)	SORC	-	-	-	-	-
	RORC	-	-	-	-	-
	DORC	4.110		4.7470	5.2159	5.6891
ITC3 (Regenerator)	SORC	-	-	-	-	-
	RORC	38.83	-	0.0087	0.0100	0.0104
	DORC	-	-	-	-	-
ITC4 (Condenser)	SORC	1.2227	-	2.1393	2.4645	2.5639
	RORC	0.9079	-	2.0851	2.4068	2.4989
	DORC	7.1685	-	5.8639	6.4432	7.0277
T1 (Turbine)	SORC	-	4.7177	0.9802	1.1292	1.1748
	RORC	-	4.7177	0.9802	1.1315	1.1748
	DORC	-	2.7892	0.4278	0.4701	0.5127
T2 (Turbine)	SORC	-	-	-	-	-
	RORC	-	-	-	-	-
	DORC		3.6553	0.5332	0.5859	0.6390

gives the power, exergy destruction, irreversibility ratio (IR), and exergetic fuel depletion ratio (FDR). According to Table 6, in all systems, the collector had the highest exergy destruction, i.e., SORC (89.54%), RORC (89.54%), and DORC (85.22%) systems.

3.1. Daily Radiation Simulation

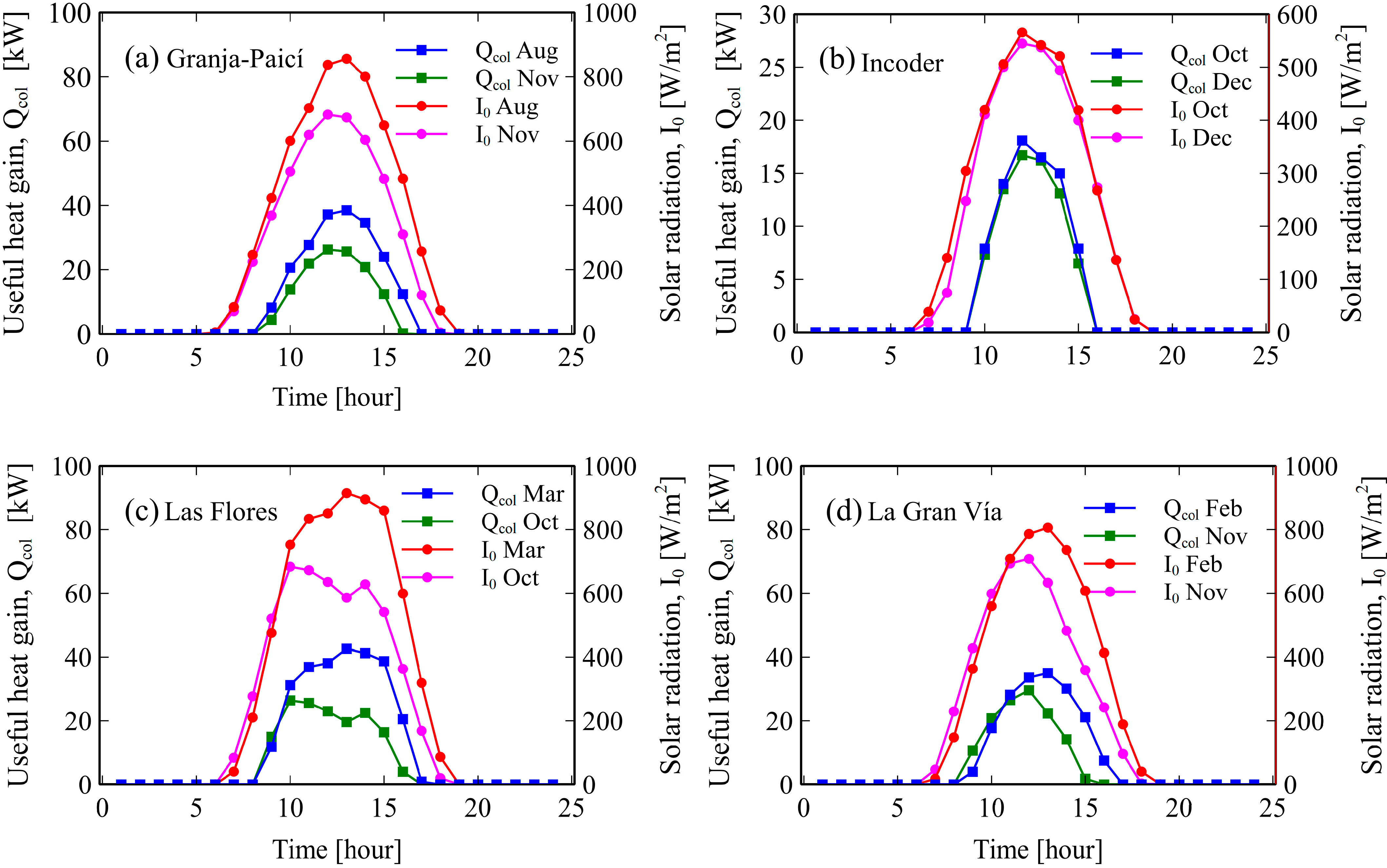
This section studies the behavior of daily radiation and the collector’s effective energy gain during the four seasons. For this purpose, the months with the highest and lowest accumulated daily radiation were considered (Figure 6).

Figure 6 shows each site’s heat profiles as a radiation function for maximum and minimum radiation months. The results show an increase in heat as the radiation increased, a peak at mid-day, and then a decrease as the radiation declined. It was also observed that Las Flores (Figure 6c) had the highest peak values of total solar radiation (914.4 W/m²) with a heat production of 38.5 kJ/kg, followed by the Paici station (856 W/m²), then La Gran Vía (805.9 W/m²), and finally Incoder (565 W/m²). Therefore, the Paici and Las Flores stations are the candidate sites with a greater potential for the exploitation of solar energy.

On the other hand, based on the maximum radiation values obtained in each zone, the temperature variation in the transitory state inside the tank was determined during the day. Figure 7 reveals that the temperature decreased during the first eight hours of the day. This decrease arises from the continuous load that the tank must supply to the ORC to ensure its performance. After 9:00 a.m., the temperature increased inside the dome when the solar irradiation began to heat the thermal oil.

This increase is associated with the fluid’s heat flow to the tank due to the heat gain of the collector. Finally, when the collection capacity of the system decreased due to a decrease in radiation, the tank temperature began to diminish. Despite these slight thermal variations, the ORC system had a minimum temperature input that allowed the working fluid to evaporate in the evaporator and thus obtain power in the hours when radiation was zero.

3.2. System Energy Analysis

This section determines the daily accumulated net power for each configuration of SORC, RORC, and DORC, and compares the energy performance at each of the four sites. It is pertinent to emphasize that the analysis is based on hourly radiation data for a representative day of each month to have a realistic estimation of the system’s behavior. The results are given in Figure 8.

Figure 8 shows that the accumulated daily power in each site for the SORC and RORC systems was not affected. For the SORC system, the average daily power for Granja-Paici, La Gran Vía, Incoder, and Las Flores was 137.98, 135.54, 126.57, and 142.37.45 kW/day, respectively. The same results were obtained for the RORC configuration, indicating that adding the regenerator to obtain greater heat and increase power is not reflected in power production. In other words, the accumulated power for the SORC system is the same for the RORC system in the four study areas.

One explanation for this behavior lies mainly in the low-temperature ranges. The effect of the storage tank is to maintain the minimum required temperature at the entrance of the evaporator in the face of fluctuations in hours of low radiation to preserve the system’s performance. In this sense, the turbine inlet temperature will be given by the minimum approach temperature of these systems, which was set at 40 °C (SORD and RORC). Therefore, the fluid expansion process inside the turbine for the daily temperature ranges will be kept almost constant, and consequently, the enthalpy difference will not increase. In addition, the power generation in kW will be the same for both systems. This behavior is reflected in Figure 8, where the bars with the lowest daily accumulated power correspond to the SORC and RORC systems, respectively.

On the other hand, the DORC system behaved much more favorably than the SORC and RORC systems in terms of power production. In the first instance, the results reveal a similar behavior to those obtained by the SORC and RORC systems regarding daily variation. However, the DORC system increased the net power output due to the double evaporation pressure. Unlike the values obtained in the simple and recovery cases, the DORC system yielded better values for Granja-Paici (160.89 kW/day, 14.24%), Gran Via (159.57 kW/day, 15.06%), Incoder (154.71 kW/day, 18.09%), and Las Flores (163.26 kW/day, 12.08%).

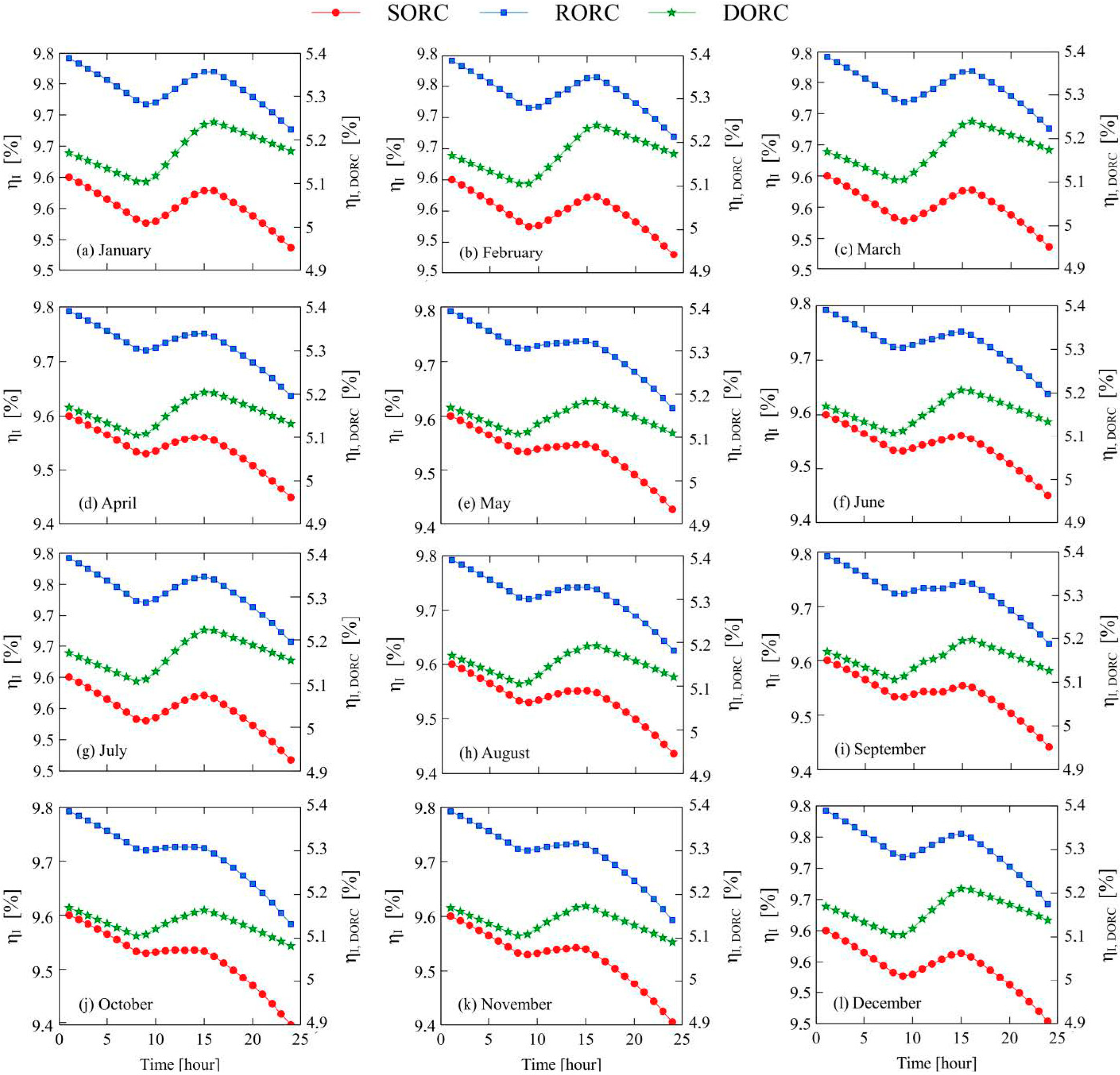
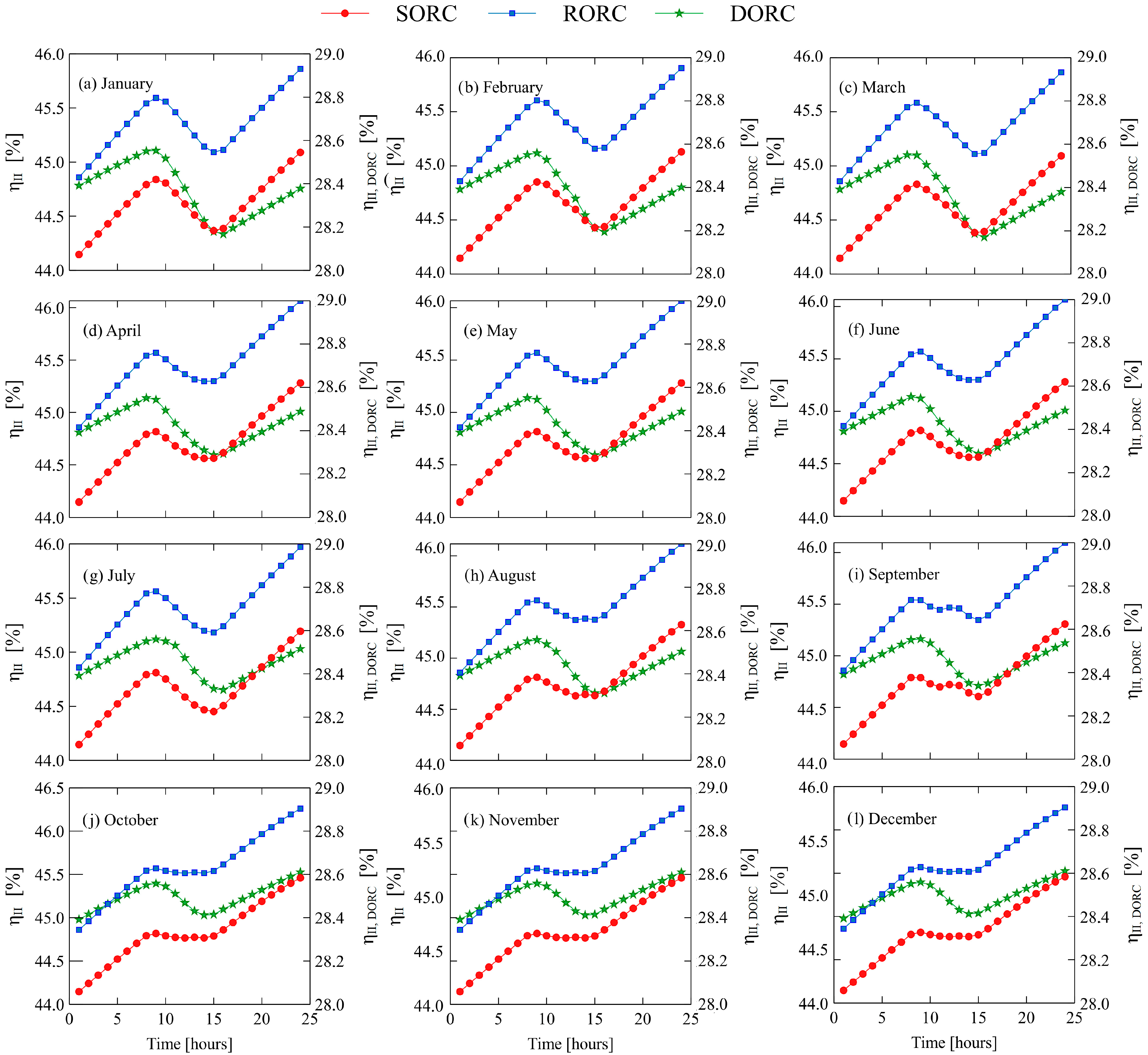
On the other hand, Figure 9 shows that efficiency tends to correspond with the time of day. In other words, the variation in energy efficiency tends to follow the temperature profile of the heat source (Figure 7). This behavior is similar to that found by Wang et al. [38] for RORC and the SORC systems. This same result was observed in each of the months of the Flores station, as shown in Figure 9. Therefore, the variations in efficiency remain practically within the same range each month. Therefore, one way to increase energy efficiency would be the incorporation of heat recovery equipment (e.g., a regenerator) or to increase the production of electrical energy through a greater area of the collector to increase the effective energy gain and, consequently, the heat transfer rate from the thermal oil to the working fluid. Nevertheless, this decision is framed toward a thermo–economic optimization that allows for reaching an optimal cost–benefit point in these systems.

3.3. Exergy Analysis

This section discusses the analysis performed on each proposed configuration, including the analysis of the exergy destruction for each component and exergy efficiency. These analyses considered the months with the highest radiation values, according to the results from Figure 6. The percentage of exergy destruction per component and the fuel depletion ratio (FDT) is calculated based on Table 4 and shown in Figure 10.

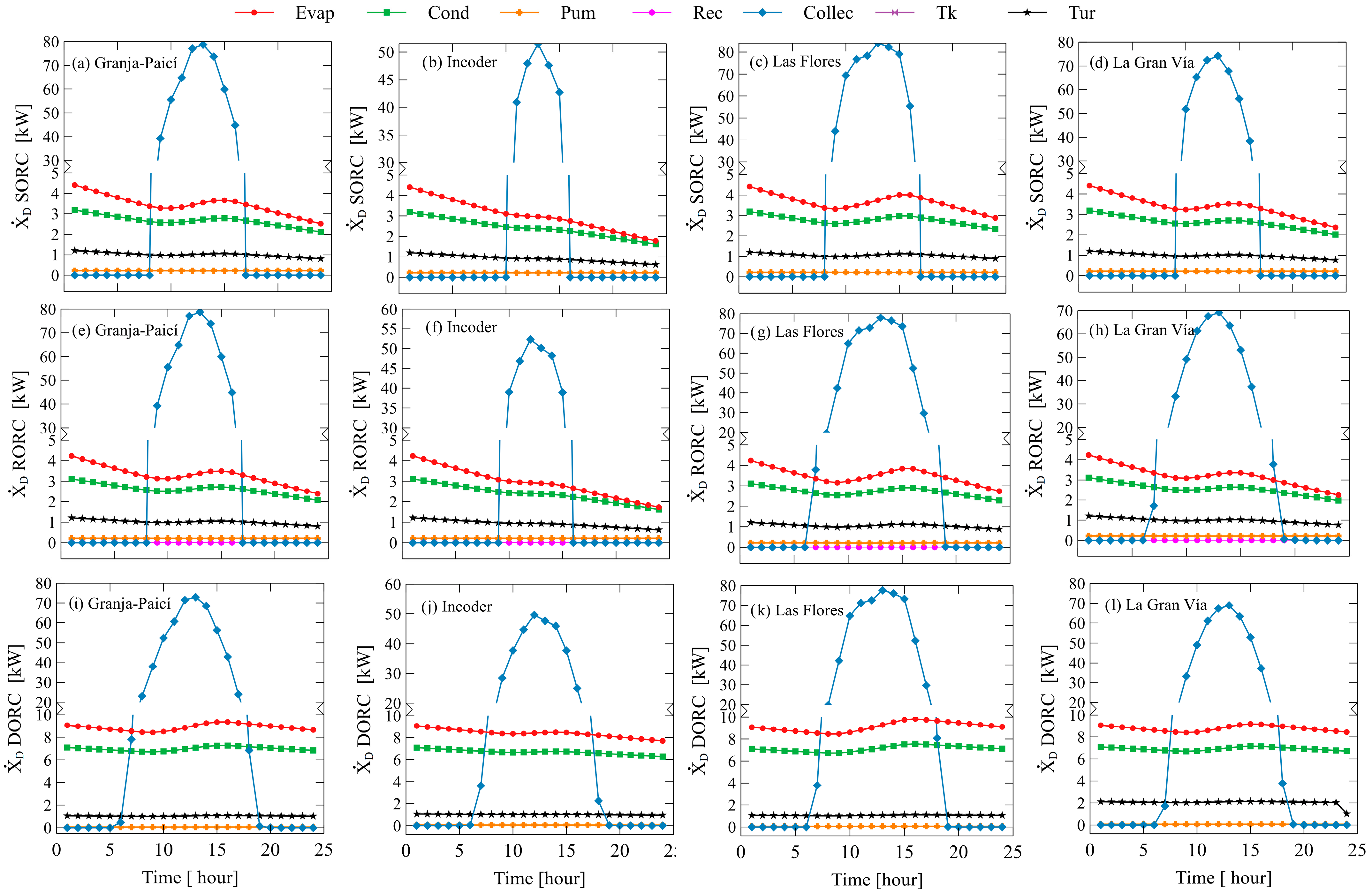
Figure 10 shows the variations in the exergy of each component. Figure 10a–d shows the hourly variation of exergy destruction of the SORC cycle for the four sites. In the first hours of the day, when there is no radiation on the collector, the exergy destruction was zero. However, as radiation began to be incident on the surface of he collector, irreversibility began to exist in this equipment. At mid-day, the maximum radiation was reached, and the highest exergy destruction rate in the ORC, RORC, and DORC were 77.57–89.54%, 77.57–89.54%, and 77.60–85.22%, respectively. This result is similar to those from Kerme et al. [35,39].

From the heat transfer point of view, the evaporator (Evap) had varying levels of exergy destruction in the range of 4.4 to 2.5 kW, while the condenser (Cond) ranged from 3.17 to 2.11 kW. These same trends were found for the RORC configuration. The exergy destruction rates of these equipment types are associated with the irreversibilities inside them due to heat transfer [40]. Furthermore, it was observed that exergy increases were associated with the change of seasons, which is closely related to the ability to supply heat from the heat source to the ORC circuit. Finally, Figure 10i shows the variation in exergy destruction for the DORC system. In this particular case, the collector was still the component with the highest exergy destruction rate, followed by the evaporators (ITC1 + ITC2) with values of 9 kW. The turbines and pumps had the lowest exergy destruction rate in this configuration.

Based on the results given in Figure 6 and Figure 7, the Las Flores station is the one that represents the best performance in terms of power compared with the other stations. The variations of exergy efficiency for the representative days of each month for the three configurations are shown in Figure 11.

Figure 11 reveals that the DORC system is the best configuration in terms of exergy. An important fact to highlight is that the efficiency behavior follows the thermal curve of the source. Therefore, the exergy efficiency will increase or decrease with the source temperature, whose maximum values coincide with the maximal radiation. This behavior is evident in the representative days of each month for the three configurations.

On the other hand, Figure 11 reveals that the DORC system has higher exergy efficiency than the SORC and RORC systems. According to Figure 7, in March at 12:00 p.m., the exergy efficiency of the DORC system was less than that of the SORC (53.0%) and RORC (52.0%) configurations. In addition, using two evaporators in the system makes it possible for the working fluid to follow the temperature profile of the thermal source (thermal oil) and, thus, reduce the exergy destruction and consequently increase the system efficiency [48], as shown in Figure 11.

It is important to mention that there are areas of uncertainty in the calculations. It should be noted that the mathematical model used to simulate the ORC cycle is based on certain assumptions and simplifications, such as the consideration of steady-state components and pressure loss depreciation. Therefore, the percentage of error in the energy gains could be in the range of 10% to 20%, which is within the range of acceptance for this type of study [22,38].

4. Conclusions

In this work, an energy and exergy study of different ORC configurations was carried out in four strategic sites in Colombia whose total radiation values for one year were determined from temperature and humidity data. Toluene was used as a working fluid for the ORC cycle and high-temperature thermal oil for the solar cycle.

Based on the total radiation data, it was found that the La Flores station represented the highest values. Consequently, an increase in the system temperature was obtained and yielded higher rates of effective energy gain in the collector. From the energy analysis, it was concluded that the SORC and RORC systems represented the same amounts of accumulated daily energy production for the four stations. However, the DORC system showed an increase of 12.08% for the spring season. However, there were differences in energy efficiency where the RORC system showed an increase of approximately 2% over the SORC system. The DORC configuration efficiency was lower than SORC (45.85%) and RORC (46.90%).

On the other hand, it was concluded that the solar collector was the main equipment for exergy destruction of the whole system resulting in 89% of the total exergy destruction. The storage tank was ranked 2nd (5.4%), and the evaporators were ranked 3rd (ITC1-1%, ITC2-2%). Pumps and turbines contributed the least to the loss of exergy. Finally, the DORC system represented a higher exergy efficiency.

There is a relevant limitation found in the system: it is not possible to generate additional energy, since it does not have an extra energy production system, or if a storm occurs that darkens the sky for several days, it could not compensate all the energy needed. Therefore, a possible future improvement is the incorporation of a line of ecological fuel that allows the supplying of thermal energy in these cases.

It can be concluded that adding a regenerator to the cycle (RORC) did not increase the net power production of the SORC. However, the energy and exergy efficiency of the RORC system was higher than the SORC system. Meanwhile, the DORC system presented greater energy production and the highest exergy efficiency rate for the SORC and DORC systems evaluated at the same base conditions. Therefore, the Las Flores station had the best performance due to its high accumulated radiation values.

Life cycle assessments to evaluate the potential environmental impact of RORC, DORC, and SORC technologies are suggested for future research. In addition, greenhouse gas emissions from different fluids should be calculated. Regarding technologies costs, an economic evaluation to determine the viability of the integrated power system is recommended.