Three Voltage Vector Duty Cycle Optimization Strategy of the Permanent Magnet Synchronous Motor Driving System for New Energy Electric Vehicles Based on Finite Set Model Predictive Control
Abstract
1. Introduction
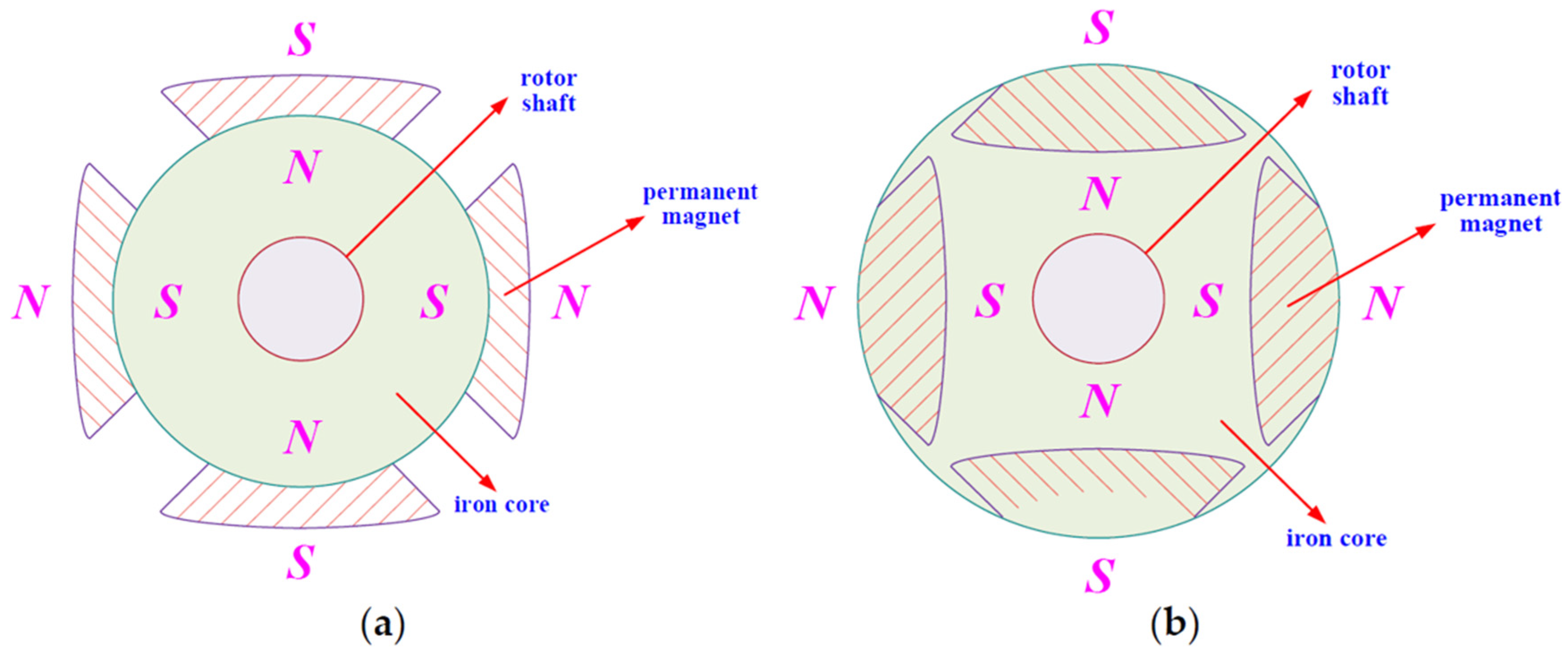
- A simple structure with a small volume that is lightweight and has low noise levels;
- A permanent magnet is used to provide excitation, with small excitation losses and high operational efficiency;
- Low rotating inertia, high starting electromagnetic torque, and excellent static and dynamic response performance.
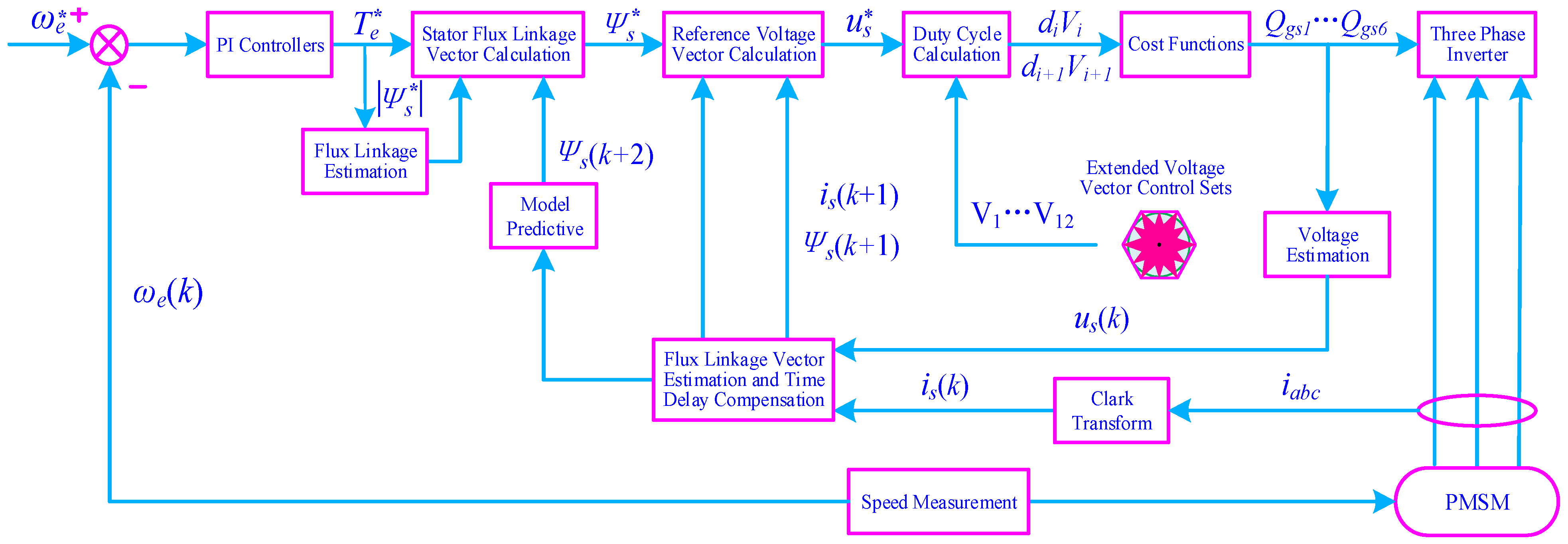
2. The Principles and Mathematical Description of Model Predictive Control for the PMSM
- Ignore the iron core magnetic resistance of stator and rotor, regardless of eddy current and hysteresis loss;
- Permanent magnet material conductivity is zero, and the internal permeability of the permanent magnet is the same as that of the air;
- The distributions of excitation and armature-reaction magnetic fields in air gaps are sinusoidal waves;
- The undamped winding of the rotor, armature resistance, and inductance of each phase winding in the stator are equal;
- In steady-state operation, the induced electromotive force waveforms generated in each phase winding are sinusoidal waves.
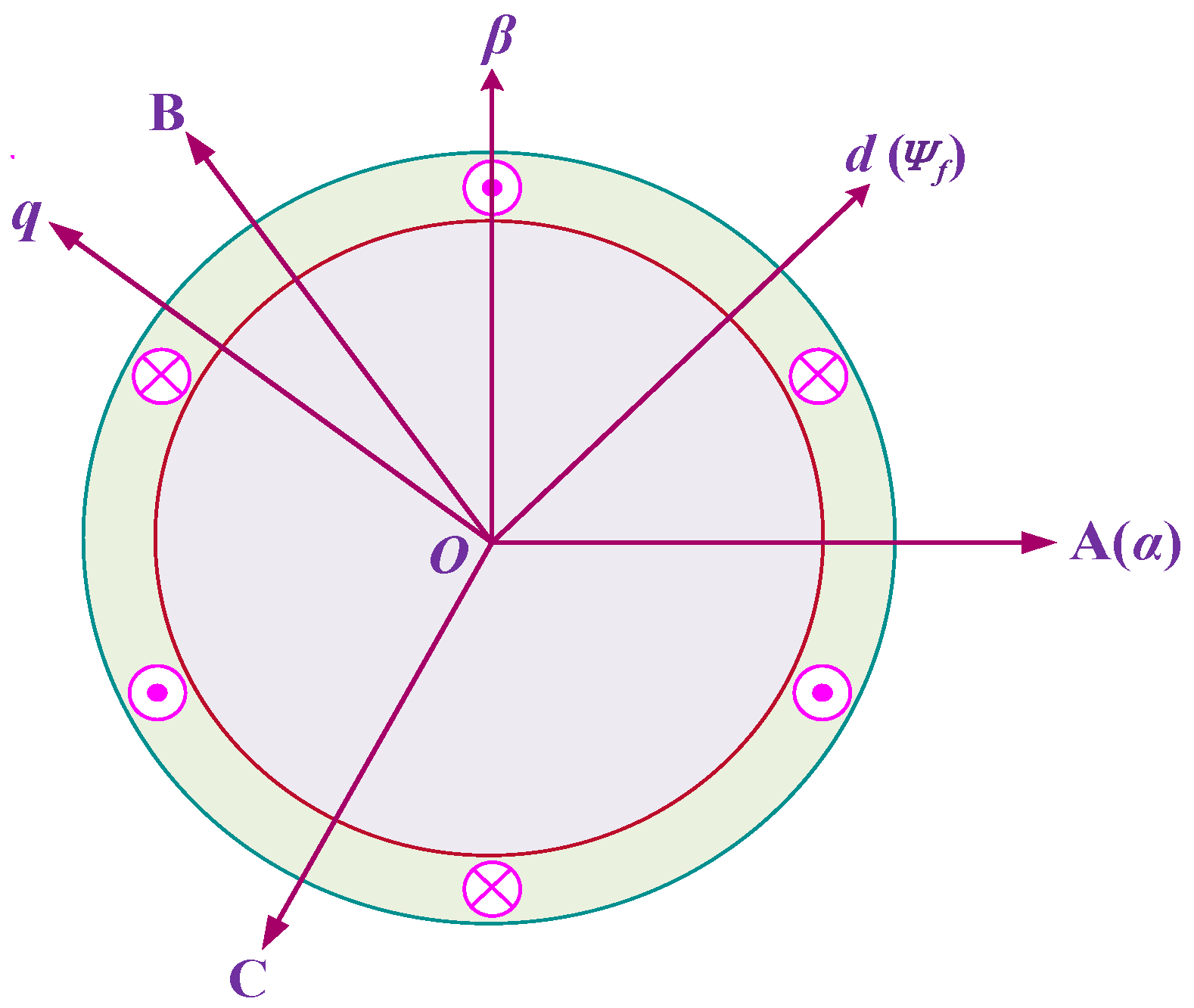
- A, B, and C represent a three-phase static coordinate system, which has three axes, A, B, and C, in the three-phase windings of the stator at angles of 120° to each other in space;
- and represent a static coordinate system, a two-phase static coordinate system, where the -axis is coincident with the A-axis in the three-phase static coordinate system, while the -axis advance counterclockwise electric angles are at 90° to the -axis;
- and represent a rotating coordinate system, which is a two-phase synchronous rotating coordinate system, in which the direction of the rotor flux linkage vector (the permanent magnet chain) is along the d-axis and rotates synchronously with the rotor, while the q-axis advances the d-axis electric angles 90° counterclockwise.
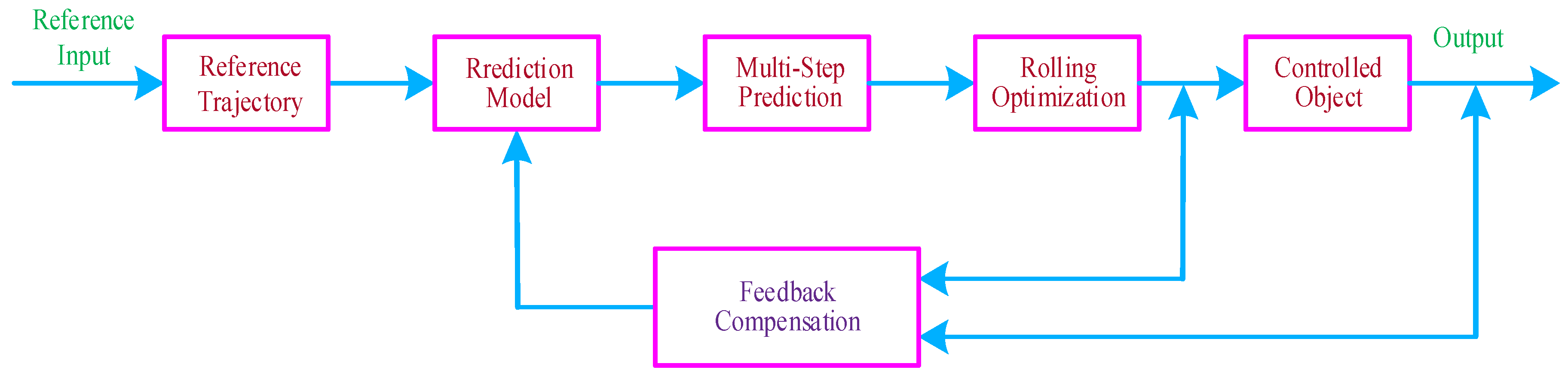
- It can be applied to a multi-variable control system;
- Constraints are used to optimize the controller, which is simple and easy to design;
- It has high flexibility to optimize solutions for specific application areas.
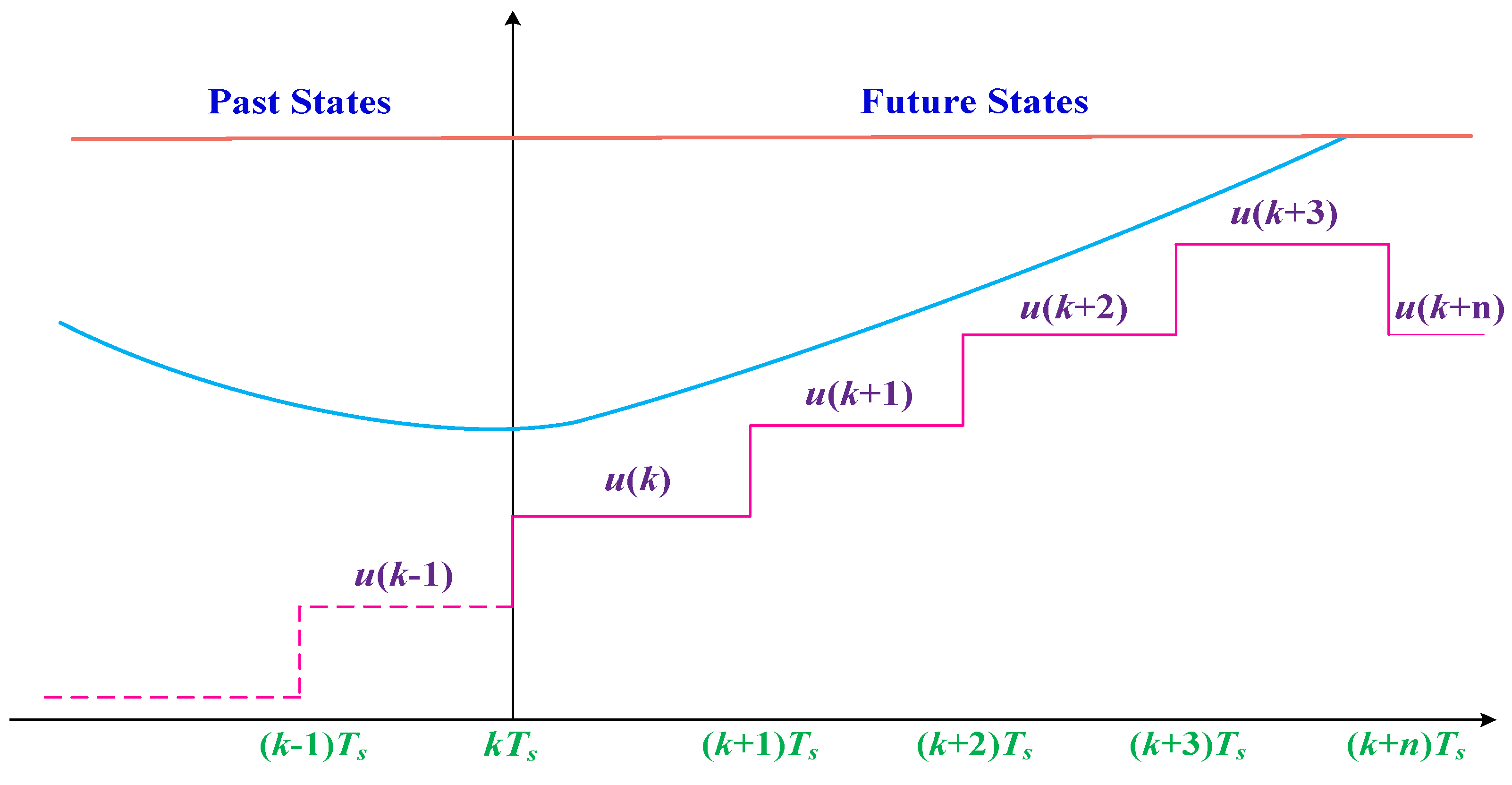
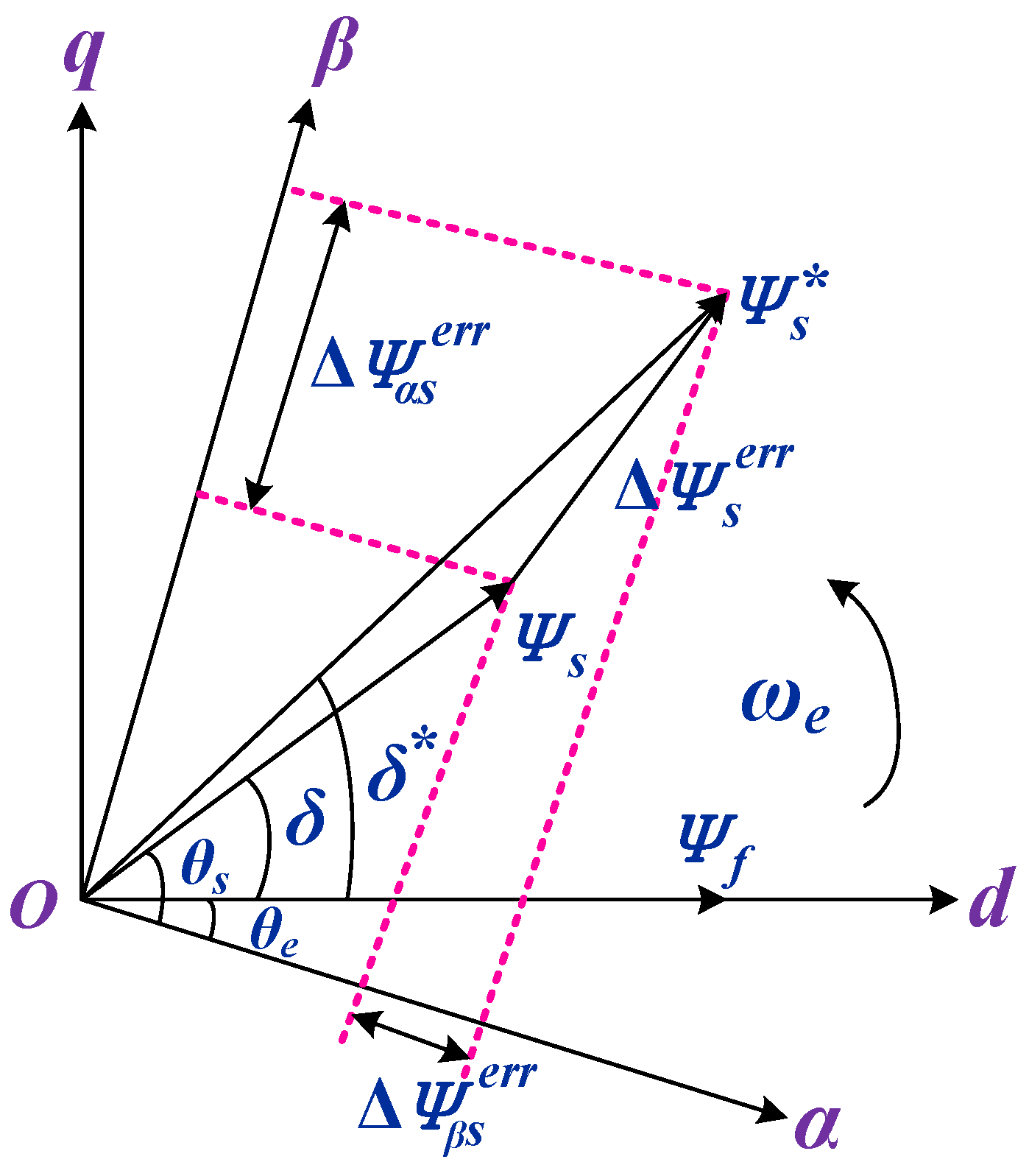
3. Reference Voltage Vector Calculation
4. Three Voltage Vector Duty Cycle Optimization
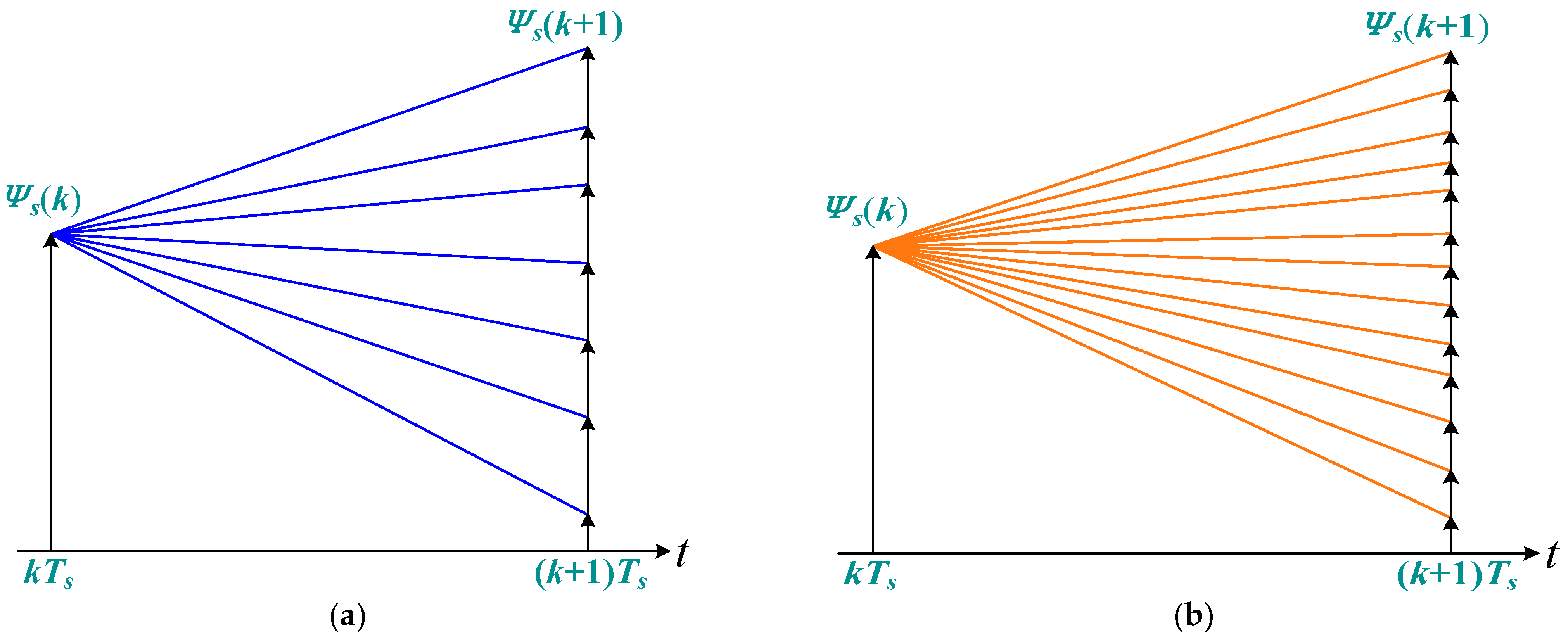
4.1. Alternative Voltage Vector Extension
4.2. Double Voltage Vector Duty Cycle Control
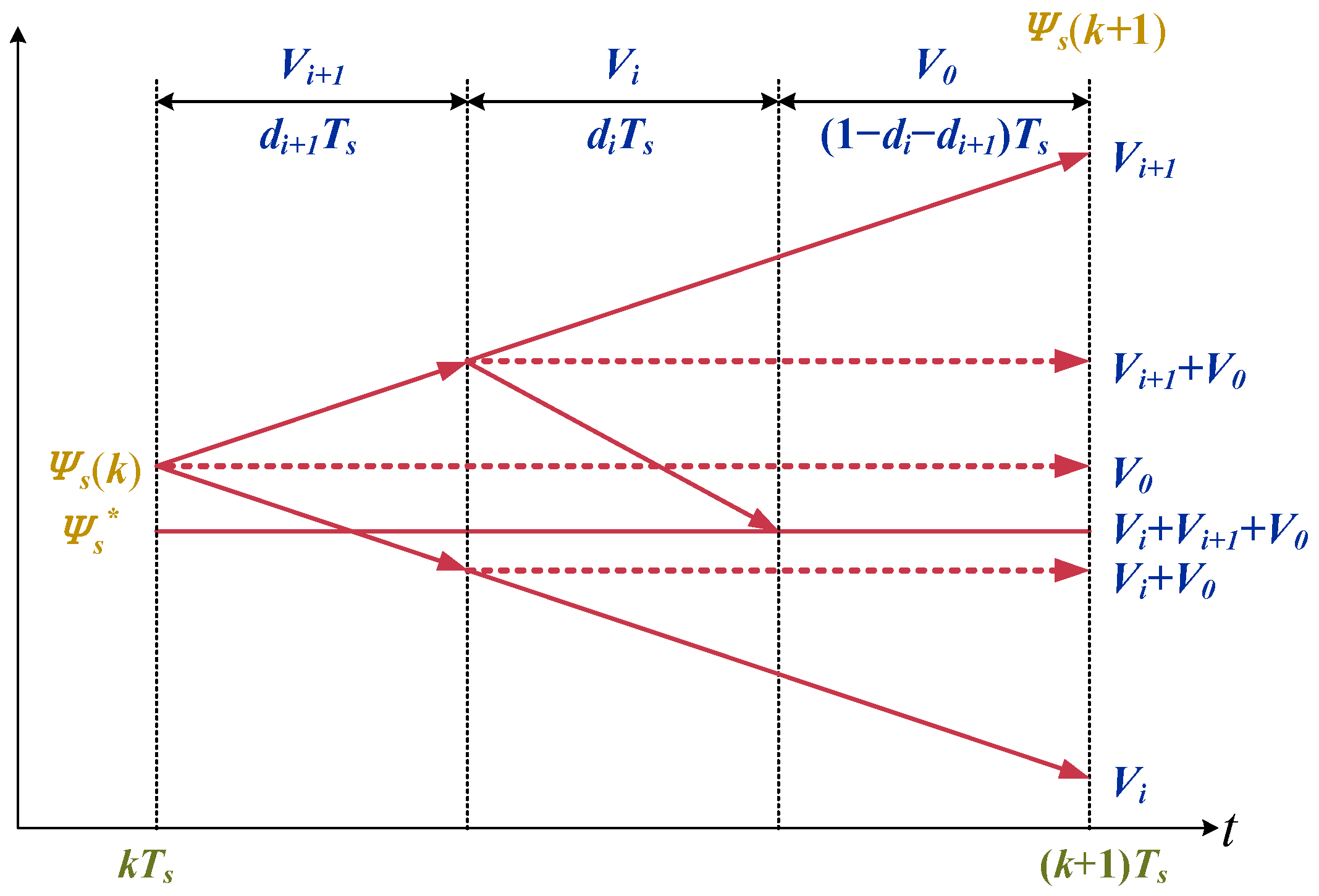
4.3. Three Voltage Vector Duty Cycle Control
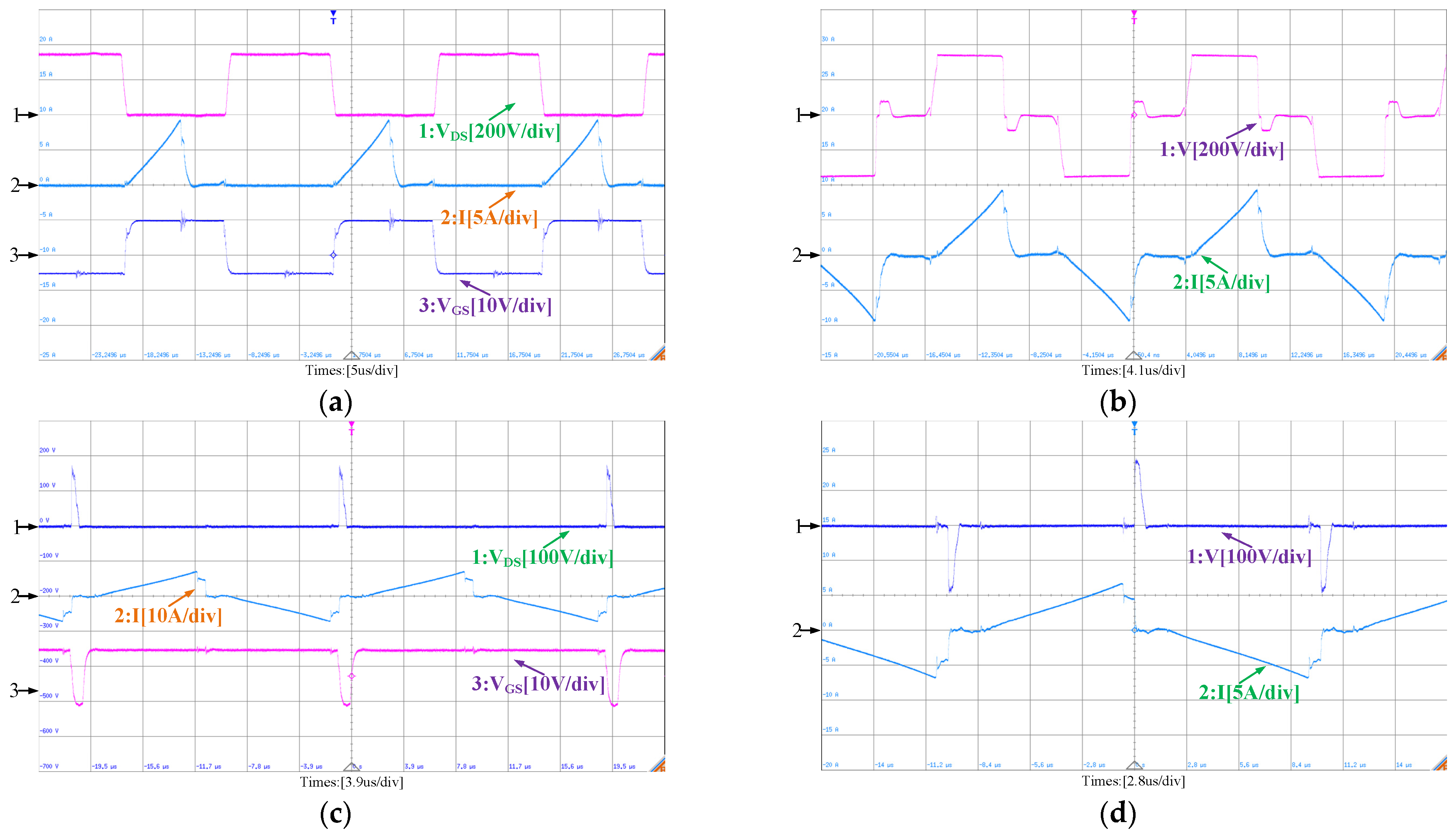
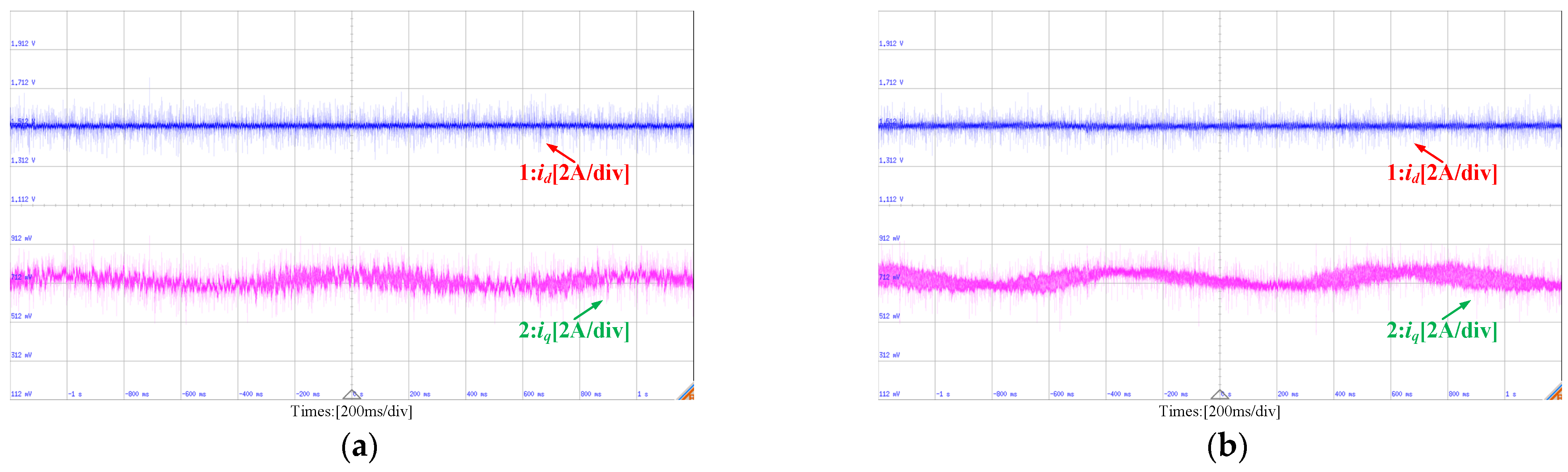
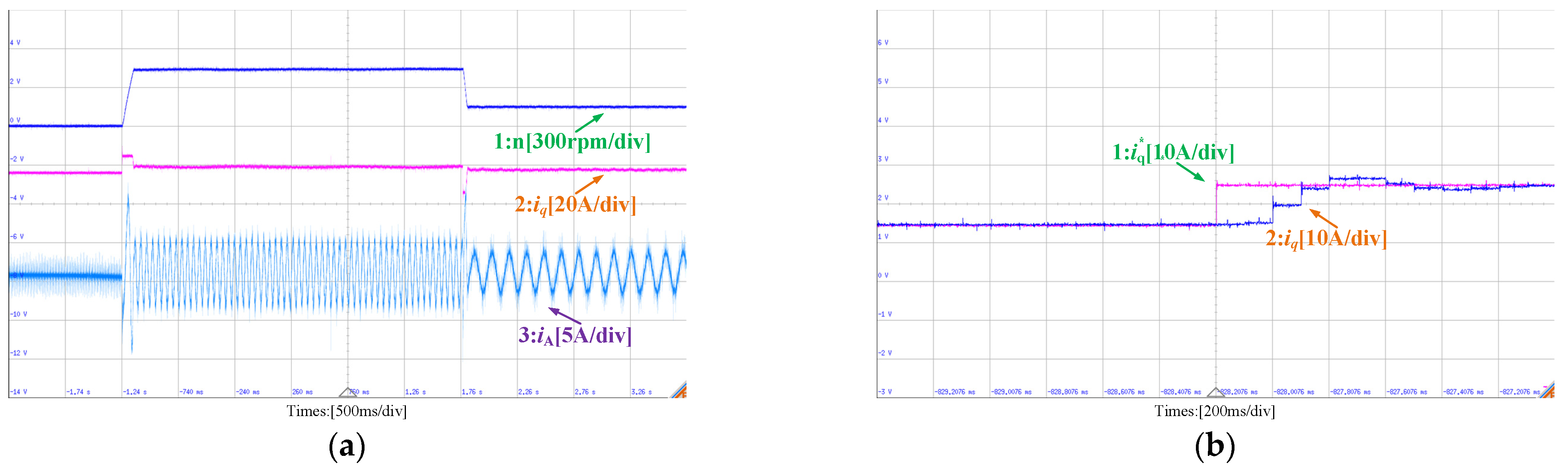
5. Experimental Results
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NEEVs | New energy electric vehicles |
| PMSM | Permanent magnet synchronous motor |
| DC | Direct current |
| AC | Alternating current |
| MPC | Model predictive control |
| FOC | Field-oriented control |
| DTC | Direct torque control |
| CCS-MPC | Continuous control set model predictive control |
| FCS-MPC | Finite control set model predictive control |
| FCS-MPTC | Finite control set model predictive torque control |
| FCS-MPCC | Finite control set model predictive current control |
| DSP | Digital signal processing |
| FPGA | Field-programmable gate array |
| SPMSM | Surface permanent magnet synchronous motor |
| IPMSM | Interior permanent magnet synchronous motor |
| Sample period | |
| At current time | |
| At next time | |
| Predictive value at next time | |
| Stator d-axis current of d and q rotating coordinate system | |
| Stator q-axis current of d and q rotating coordinate system | |
| Stator d-axis voltage of d and q rotating coordinate system | |
| Stator q-axis voltage of d and q rotating coordinate system | |
| Stator d-axis flux linkage of d and q rotating coordinate system | |
| Stator q-axis flux linkage of d and q rotating coordinate system | |
| Rotor electrical angular velocity | |
| d-axis inductance of d and q rotating coordinate system | |
| q-axis inductance of d and q rotating coordinate system | |
| Permanent magnet flux linkage magnitude | |
| Pole pair numbers | |
| Electromagnetic torque | |
| Stator resistance | |
| Stator flux linkage amplitude | |
| Load angle | |
| d-axis and q-axis inductance | |
| Reference electromagnetic torque | |
| Reference stator flux linkage amplitude | |
| Reference load angle | |
| Reference stator flux linkage vector | |
| Stator flux linkage vector | |
| Rotor flux vector linkage phase angle | |
| Stator flux vector linkage phase angle | |
| Error of stator flux linkage vector | |
| Projections of on the -axis | |
| Projections of on the -axis | |
| Reference stator flux vector linkage phase angle | |
| Stator voltage vector of the and static coordinate system | |
| Stator current vector of the and static coordinate system | |
| Reference stator voltage vector | |
| Action time | |
| Extended voltage vector | |
| Candidate stator voltage vector | |
| Duty cycle | |
| Zero-voltage vector | |
| New cost function of flux linkage error | |
| Included angle | |
| Duty cycle | |
| amplitude | |
| Reference stator voltage vector amplitude | |
| amplitude | |
| Reference rotor electrical angular velocity | |
| Rotor electrical angular velocity at current time | |
| Stator flux linkage vector at next time | |
| Stator flux linkage vector at the time after next | |
| Stator current vector at current time | |
| Stator voltage vector at current time | |
| Stator current vector at next time | |
| Extended voltage vector control sets | |
| Three-phase current | |
| Drive signal |
References
- Oliveira, H.; Moutinho, V. Renewable Energy, Economic Growth and Economic Development Nexus: A Bibliometric Analysis. Energies 2021, 14, 4578. [Google Scholar] [CrossRef]
- Kolosok, S.; Bilan, Y.; Vasylieva, T.; Wojciechowski, A.; Morawski, M. A Scoping Review of Renewable Energy, Sustainability and the Environment. Energies 2021, 14, 4490. [Google Scholar] [CrossRef]
- Zhang, J.; Cherian, J.; Parvez, A.M.; Samad, S.; Sial, M.S.; Ali, M.A.; Khan, M.A. Consequences of Sustainable Agricultural Productivity, Renewable Energy, and Environmental Decay: Recent Evidence from ASEAN Countries. Sustainability 2022, 14, 3556. [Google Scholar] [CrossRef]
- Shah, R.; Chen, R.; Woydt, M. The Effects of Energy Efficiency and Resource Consumption on Environmental Sustainability. Lubricants 2021, 9, 117. [Google Scholar] [CrossRef]
- Kucukvar, M.; Onat, N.C.; Kutty, A.A.; Abdella, G.M.; Bulak, M.E.; Ansari, F.; Kumbaroglu, G. Environmental Efficiency of Electric Vehicles in Europe Under Various Electricity Production Mix Scenarios. J. Clean. Prod. 2022, 335, 130291. [Google Scholar] [CrossRef]
- Guha, A.; Shom, S.; Rayyan, A.; Alahmad, M. Indices to Determine the Environmental and Economic Impact of Using an Electric Vehicle over Gasoline or Hybrid Vehicles on a Regional Basis. In Proceedings of the 2018 IEEE Transportation Electrification Conference and Expo (ITEC), Long Beach, CA, USA, 13–15 June 2018; pp. 731–7366. [Google Scholar] [CrossRef]
- Bicer, Y.; Dincer, I. Life Cycle Environmental Impact Assessments and Comparisons of Alternative Fuels for Clean Vehicles. Resour., Conserv. Recycl. 2018, 132, 141–157. [Google Scholar] [CrossRef]
- Wang, N.; Tang, G. A Review on Environmental Efficiency Evaluation of New Energy Vehicles Using Life Cycle Analysis. Sustainability 2022, 14, 3371. [Google Scholar] [CrossRef]
- Solarin, S.A.; Al-Mulali, U. Transportation fuel subsidies and CO2 emissions: The roles of economic complexity and uncertainty. Environ. Prog. Sustain. Energy 2022, 41, e13797. [Google Scholar] [CrossRef]
- Pielecha, J.; Skobiej, K.; Kurtyka, K. Exhaust Emissions and Energy Consumption Analysis of Conventional, Hybrid, and Electric Vehicles in Real Driving Cycles. Energies 2020, 13, 6423. [Google Scholar] [CrossRef]
- Chung, I.; Kang, H.; Park, J.; Lee, J. Fuel Economy Improvement Analysis of Hybrid Electric Vehicle. Int. J. Automot. Technol. 2019, 20, 531–537. [Google Scholar] [CrossRef]
- Chen, L.; Xu, H.; Sun, X.; Cai, Y. Three-vector-based model predictive torque control for a permanent magnet synchronous motor of EVs. IEEE Trans. Transp. Electrific. 2021, 7, 1454–1465. [Google Scholar] [CrossRef]
- Fang, X.; Lin, S.; Wang, X.; Yang, Z.; Lin, F.; Tian, Z. Model predictive current control of traction permanent magnet synchronous motors in six-step operation for railway application. IEEE Trans. Ind. Electron. 2022, 69, 8751–8759. [Google Scholar] [CrossRef]
- Zhou, D.; Ding, L.; Li, Y. Two-stage model predictive control of neutral-point-clamped inverter-fed permanent-magnet synchronous motor drives under balanced and unbalanced dc links. IEEE Trans. Ind. Electron. 2021, 68, 3750–3759. [Google Scholar] [CrossRef]
- Sun, C.; Sun, D.; Zheng, Z.; Nian, H. Simplified model predictive control for dual inverter-fed open-winding permanent magnet synchronous motor. IEEE Trans. Energy Convers. 2018, 33, 1846–1854. [Google Scholar] [CrossRef]
- Brosch, A.; Wallscheid, O.; Böcker, J. Torque and inductances estimation for finite model predictive control of highly utilized permanent magnet synchronous motors. IEEE Trans. Ind. Inform. 2021, 17, 8080–8091. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Y.; Wu, D.; Zhao, J.; Hu, Y. Model predictive current control with lower switching frequency for permanent magnet synchronous motor drives. IET Electr. Power Appl. 2022, 16, 267–276. [Google Scholar] [CrossRef]
- Yu, F.; Li, K.; Zhu, Z.; Liu, X. An over-modulated model predictive current control for permanent magnet synchronous motors. IEEE Access 2022, 10, 40391–40401. [Google Scholar] [CrossRef]
- Sun, X.; Li, T.; Tian, X.; Zhu, J. Fault-tolerant operation of a six-phase permanent magnet synchronous hub motor based on model predictive current control with virtual voltage vectors. IEEE Trans. Energy Convers. 2022, 37, 337–346. [Google Scholar] [CrossRef]
- Cao, B.; Grainger, B.; Wang, X.; Zou, Y.; Reed, G.; Mao, Z. Direct torque model predictive control of a five-phase permanent magnet synchronous motor. IEEE Trans. Power Electron. 2021, 36, 2346–2360. [Google Scholar] [CrossRef]
- Chen, W.; Zeng, S.; Zhang, G.; Shi, T.; Xia, C. A modified double vectors model predictive torque control of permanent magnet synchronous motor. IEEE Trans. Power Electron. 2019, 34, 11419–11428. [Google Scholar] [CrossRef]
- Hassan, M.; Ge, X.; Atif, R.; Woldegiorgis, A.; Mastoi, M.; Shahid, M. Computational efficient model predictive current control for interior permanent magnet synchronous motor drives. IET Power Electron. 2022, 15, 1111–1133. [Google Scholar] [CrossRef]
- Zhu, S.; Zhang, H. Simplified model predictive current control strategy for open-winding permanent magnet synchronous motor drives. J. Power Electron. 2021, 21, 911–920. [Google Scholar] [CrossRef]
- Su, D.; Zhang, C.; Dong, Y. Finite-state model predictive current control for surface-mounted permanent magnet synchronous motors based on current locus. IEEE Access 2017, 5, 27366–27375. [Google Scholar] [CrossRef]
- Chen, Z.; Qiu, J.; Jin, M. Prediction-error-driven position estimation method for finite-control-set model predictive control of interior permanent-magnet synchronous motors. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 282–295. [Google Scholar] [CrossRef]
- Agustin, C.A.; Yu, J.-t.; Lin, C.-K.; Fu, X.-Y. A Modulated Model Predictive Current Controller for Interior Permanent-Magnet Synchronous Motors. Energies 2019, 12, 2885. [Google Scholar] [CrossRef]
- Gong, Z.; Zhang, C.; Ba, X.; Guo, Y. Improved deadbeat predictive current control of permanent magnet synchronous motor using a novel stator current and disturbance observer. IEEE Access 2021, 9, 142815–142826. [Google Scholar] [CrossRef]
- Bai, C.; Yin, Z.; Zhang, Y.; Liu, J. Multiple-models adaptive disturbance observer-based predictive control for linear permanent-magnet synchronous motor vector drive. IEEE Trans. Power Electron. 2022, 37, 9596–9611. [Google Scholar] [CrossRef]
- Bai, C.; Yin, Z.; Zhang, Y.; Liu, J. Robust predictive control for linear permanent magnet synchronous motor drives based on an augmented internal model disturbance observer. IEEE Trans. Ind. Electron. 2022, 69, 9771–9782. [Google Scholar] [CrossRef]
- Fei, Q.; Deng, Y.; Li, H.; Liu, J.; Shao, M. Speed ripple minimization of permanent magnet synchronous motor based on model predictive and iterative learning controls. IEEE Access 2019, 7, 31791–31800. [Google Scholar] [CrossRef]
- Yang, T.; Kawaguchi, T.; Hashimoto, S.; Jiang, W. Switching Sequence Model Predictive Direct Torque Control of IPMSMs for EVs in Switch Open-Circuit Fault-Tolerant Mode. Energies 2020, 13, 5593. [Google Scholar] [CrossRef]
- Hou, L.; Ma, J.; Wang, W. Sliding mode predictive current control of permanent magnet synchronous motor with cascaded variable rate sliding mode speed controller. IEEE Access 2022, 10, 33992–34002. [Google Scholar] [CrossRef]
- Zheng, C.; Yang, J.; Gong, Z.; Xiao, Z.; Dong, X. Cascade-Free Modulated Predictive Direct Speed Control of PMSM Drives. Energies 2022, 15, 7200. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y. Dual-vector model predictive current control of permanent magnet synchronous motor drives with the segment golden search method. IEEE Access 2020, 8, 183826–183846. [Google Scholar] [CrossRef]
- Xu, L.; Chen, G.; Li, Q. Ultra-local model-free predictive current control based on nonlinear disturbance compensation for permanent magnet synchronous motor. IEEE Access 2020, 8, 127690–127699. [Google Scholar] [CrossRef]
- Brosch, A.; Hanke, S.; Wallscheid, O.; Böcker, J. Data-driven recursive least squares estimation for model predictive current control of permanent magnet synchronous motors. IEEE Trans. Power Electron. 2021, 36, 2179–2190. [Google Scholar] [CrossRef]
- Kiani, B.; Soleymani, S.; Mozafari, B.; Shourkaei, H. Model predictive based direct torque control for induction motor drives by sole-evaluation of two parameter independence duty ratios for each voltage vector. Electr. Power Compon. Syst. 2021, 48, 2019–2036. [Google Scholar] [CrossRef]
- Alsofyani, I.; Lee, K. Three-level inverter-fed model predictive torque control of a permanent magnet synchronous motor with discrete space vector modulation and simplified neutral point voltage balancing. J. Power Electron. 2022, 22, 22–30. [Google Scholar] [CrossRef]
- Infineon Technologies AG Silicon Intelligent Power Modules (IPM). Available online: https://www.infineon.com/cms/en/product/power/intelligent-power-modules-ipm/ (accessed on 9 October 2022).
- Infineon Technologies AG Motor Control ICs. Available online: https://www.infineon.com/cms/en/product/power/motor-control-ics/ (accessed on 9 October 2022).
- Infineon Technologies AG iMOTION™ Integrated Motor Control Solutions. Available online: https://www.infineon.com/cms/en/product/power/motor-control-ics/imotion-integrated/ (accessed on 9 October 2022).
- Infineon Technologies AG Microcontroller. Available online: https://www.infineon.com/cms/cn/product/microcontroller/ (accessed on 9 October 2022).


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Xu, B.; Jasni, J.; Radzi, M.A.M.; Azis, N.; Zhang, Q. Three Voltage Vector Duty Cycle Optimization Strategy of the Permanent Magnet Synchronous Motor Driving System for New Energy Electric Vehicles Based on Finite Set Model Predictive Control. Energies 2023, 16, 2684. https://doi.org/10.3390/en16062684
Zhang C, Xu B, Jasni J, Radzi MAM, Azis N, Zhang Q. Three Voltage Vector Duty Cycle Optimization Strategy of the Permanent Magnet Synchronous Motor Driving System for New Energy Electric Vehicles Based on Finite Set Model Predictive Control. Energies. 2023; 16(6):2684. https://doi.org/10.3390/en16062684
Chicago/Turabian StyleZhang, Chi, Binyue Xu, Jasronita Jasni, Mohd Amran Mohd Radzi, Norhafiz Azis, and Qi Zhang. 2023. "Three Voltage Vector Duty Cycle Optimization Strategy of the Permanent Magnet Synchronous Motor Driving System for New Energy Electric Vehicles Based on Finite Set Model Predictive Control" Energies 16, no. 6: 2684. https://doi.org/10.3390/en16062684
APA StyleZhang, C., Xu, B., Jasni, J., Radzi, M. A. M., Azis, N., & Zhang, Q. (2023). Three Voltage Vector Duty Cycle Optimization Strategy of the Permanent Magnet Synchronous Motor Driving System for New Energy Electric Vehicles Based on Finite Set Model Predictive Control. Energies, 16(6), 2684. https://doi.org/10.3390/en16062684






