Abstract
This paper presents the thermal calculations of an air-finned heat exchanger working at temperatures above zero degrees and their verification through testing on a real device. Then, on the basis of the calculations, the influence of evaporation temperature on the drying rate of the constant speed of air flowing through the exchanger was analysed. A quantitative analysis of the effect of the temperature difference between the air being dried and the evaporator on the acceleration of the process was performed. For the analysed case, the same water mass (condensate) can be obtained for an evaporation temperature of 0 °C almost four times faster than for 10 °C. To compare temperature cases, the SMER (specific moisture evaporation ratio) was calculated, which allowed the systems to be compared in terms of energy consumption. The theoretical analysis showed that by reducing the boiling point by 10 degrees, we could increase the SMER from 0.51 to 2.18 . After receiving the experimental results and including the efficiency of the system, these values were, respectively, 0.44 ± 0.01 and 1.91 ± 0.06 .
1. Introduction
Drying processes can consume from 5% to 25% of the total electricity consumed by various industrial enterprises that use dehumidification during production [1,2]. However, in the wood and textile industries, this value can reach 70% and 50%, respectively [3]. Due to such high participation and the desire to obtain products or provide services based on ecological and economical technologies and processes, clients are looking for solutions that, after appropriate analysis, can reduce energy consumption to varying degrees and thus simultaneously minimise operating costs. There are several types of drying devices, but the most popular are those based on electric heaters and exploiting the thermodynamic processes of heat pumps. Dryers based on refrigeration systems have lower energy consumption than traditional solutions, which is why they are becoming an increasingly popular choice, especially in devices in which the heat demand is up to several kW. As noted by Lee and Kim [4], the SMER coefficient for devices with a refrigeration system is three times higher than that for heater dryers. However, in the report of the US Department of Energy [5], it was determined that home clothes dryers with a heat pump are capable of using up to 50% less electricity but at a higher initial cost and longer drying time, which may also discourage potential buyers.
The drying process involves the removal of water from the material being dried. This is most often achieved by using hot and dry air. In the most commonly used drying devices, an electric heater is used to heat the external air, which in turn goes to the drying chamber, where water is evaporated from the material subjected to this process. The hot and humid air is then removed from the chamber, and another volume of the hot medium enters in its place. This system is called open-loop drying, which is characterised by low efficiency due to the loss of energy in the form of the waste heat contained in the hot air. The air circulation in a dehumidifier using a heat pump usually works as a closed system; the heated air on the condenser is directed to the drying chamber, and then it goes to the evaporator operating below the dew point temperature, where water vapour from the air condenses on its cold elements, the pipes and fins, intensifying the heat exchange process. The dehumidified air is directed back to the condenser, i.e., back to the starting point. Depending on the application, the heat pump can recover both latent and sensible heat from the working air, which has the potential for energy savings, especially for closed air circuits [6]. In addition, the dried air is capable of absorbing more water in the next cycle, which translates into the legitimacy of striving to obtain a drying medium of the highest possible temperature and low relative humidity. Due to the potential energy savings and the ability to control the parameters of the air at the outlet, the application of this technology in various industries has been described by researchers: agriculture [7,8,9,10], medicine [11,12], the chemical industry [2], the textile industry [13,14,15], the wood industry [16,17], and the paper industry [18]. Most scientists focus on researching innovation in the field of new drying methods and optimising the process and design to ensure lower energy consumption and improve overall efficiency [19]. In his work, Dean [20] built an analytical model simulating the dehumidification process in which he stated that the consumption of electricity was primarily influenced by the temperature and relative humidity of the air. Rezk and Forsberg in their work [21] analysed the process of designing an internal duct tumble dryer based on CFD software. They obtained a reduced pressure drop of up to 23% and an improved uniformity at the outflow boundary. The benefits of this approach include a more time effective design process and knowledge sharing with the CAD-engineer. Another publication [22] examined the influence of air temperature and flow velocity on the efficiency of the entire system. The validity of using an inverter compressor with variable rotational speed on the moisture extraction coefficient was also analysed [23]. There are many publications dedicated to the design and optimisation of heat exchangers [24,25,26,27,28,29]; there is also a mathematical model for a complete set of exchangers (evaporator and condenser) [30] in a finned air dryer. In a book, Zalewski and Niezgoda-Żelasko presented mathematical algorithms for calculating many types of single heat exchangers (i.e., finned heat exchangers) [24]. In article [25], the authors proposed an algorithm for the evaporation of melted water from a finned evaporator, which flowed into a container placed on the top of the compressor. In a publication [26], Zalewski presented a method of conducting thermal calculations of the surface area of a finned heat exchanger with known computational efficiency used for a ground heat pump. In another article [27], the same author presented a mathematical algorithm for thermal and hydraulic calculations that can be used for finned evaporators with a fan forcing the flow operating at different ambient temperatures. In the book [28], Shah and Sekulić reviewed the methodology of designing and calculating heat exchangers, presenting the basis of calculations for the ε-NTU method. The same relationships and calculation examples are also presented in one of the chapters of the publications [29].
As shown above, although the topic discussed in this article has been widely described by other authors, it has not been exhausted, especially in the context of optimising processes and construction. Due to the fact that heat pump-based dehumidifiers are an issue for the future, it is necessary to investigate the best possible efficiency of the refrigeration system as well as the optimal airflow in the zone where the dehumidified products are located. The influence of evaporation temperature on the efficiency of the process analysed in this work is an issue affecting the overall efficiency of the system. The connection of these two parameters would enable estimation of whether it is profitable to obtain lower evaporation temperatures that may result in a higher compressor pressure and increased electricity consumption in order to obtain a higher SMER index, which can be calculated by Equation (1) as the ratio of the mass of evaporated water () to the electricity consumption of the dryer ():
This article will enable the optimisation of the selection of refrigeration system components at the design stage, which will shorten the testing time of devices and speed up production. The analysis will be conducted for positive evaporation temperatures in order to ignore the effect of ice layer build-up on the evaporator elements.
2. Theoretical Model
The computational model of the finned air exchanger was presented by the authors in a publication based on the ε-NTU (number of transfer unit) method [30]. It enables the determination of both the air and the refrigerant heat transfer coefficients, the efficiency of condensers, as well as the parameters of the air behind the exchangers with known geometry, initial airflow conditions, and positive evaporation temperatures. As the model is applicable to an evaporator and condenser unit, the part that concerns refrigerant boiling is used, and the evaporating pressure corresponds to positive temperatures in order to prevent the occurrence of the exchanger frost phenomenon and the need to modify the algorithm. The model described in the publication mentioned above was extended by calculating the mass of condensate on the basis of the moisture content in the exhaust air from the heat exchanger.
The ε-NTU method is related to the efficiency of the exchanger, which can be defined as the ratio of the actual heat flux to the maximum heat flux:
On the basis of Equations (1)–(3) above, efficiency can be related to thermal performance, which can be described as Equation (4):
When we know the inlet and outlet temperatures of the exchanger, we are able to calculate its capacity, but this requires testing on a real device to measure air parameters. When the temperature behind the exchanger is unknown, this method requires an iterative procedure to determine the heat transfer coefficient . It should also be remembered that in the case of the evaporator, the phenomenon of water condensation on its cold elements may occur. Therefore, in addition to the sensible heat, the share level of the latent heat in the total heat capacity of the exchanger should be calculated, which is included in Equation (5) for the heat capacity of the air stream:
RCJ is the ratio of total heat to sensible heat. For air heating and cooling without dehumidification, its value is 1, so there is no latent heat transfer. In addition, as previously mentioned, the heat transfer coefficient should be determined on the basis of the heat transfer coefficient from the air and the medium, which should also be determined on the basis of the model described in the above-mentioned publication [30].
The calculations were conducted for the tested heat exchanger constructed of copper pipes and elbows and aluminium fins. The flow of air and refrigerant was counter-current with an in-line arrangement of the pipes. Refrigerant R290-propane was used. The geometry of the heat exchanger is shown in Figure 1 below and described in Table 1.
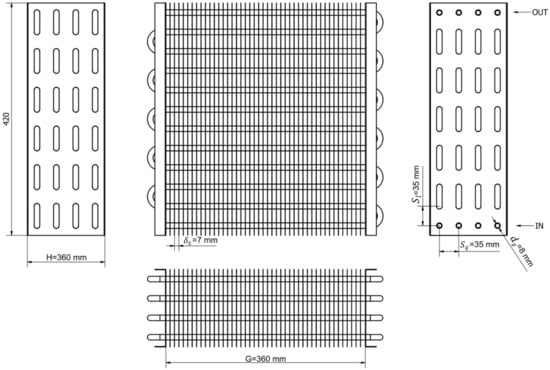
Figure 1.
Geometry of the analysed exchanger.

Table 1.
Technical data of the analysed exchanger.
The calculation was performed with the omission of thermal resistance (). The following values were assumed: gravity and atmospheric pressure .
Due to the fact that the tests were conducted for two different evaporation temperatures, the calculations were performed for two operating points of the heat pump: an evaporation temperature of 1.0 °C (refrigerant steam dryness fraction 0.3) and an evaporation temperature of 4.0 °C (refrigerant steam dryness fraction 0.3). The refrigeration system was based on the ecological thermodynamic refrigerant R290 (propane); Table 2 describes the thermodynamic properties used for calculations. The properties of the air for the initial temperature and relative humidity, which during the tests amounted to 24.7 °C and 59.9%, are also included in Table 2. Individual values were read from the Refrigeration Utilities program [31].

Table 2.
Thermodynamic properties for air and refrigerant.
The initial air parameters are the temperature and humidity in the climate chamber. Due to the need to perform several iterations of the calculations, the criterion that ends the calculations (Equation (6)) was used as the ratio of the difference in exchanger efficiency obtained from the current () and the previous iteration () and the exchanger efficiency obtained from the current iteration:
The results of the obtained air parameters at the exchanger outlet are presented below in Table 3. The table shows the calculations of the condensate mass increase () in one hour, which were calculated for the iteration that meets the criterion that ends the calculations.

Table 3.
Results of iterations of heat exchanger calculations: for an evaporation temperature of 1.0 °C, for an evaporation temperature of 4.0 °C.
The criterion from Formula (6) was achieved for the first set of data after four iterations, while for the heat exchanger calculations for the evaporation temperature of 4.0 °C, the criterion was achieved for the calculations of the fifth iteration. The results of these loops were taken into account in further analyses.
3. Experimental Test
To validate the model presented above, tests were conducted on a real device. The heat pump was tested at two operating points: I, for the evaporating temperature of 1.0 °C, and II, for the evaporating temperature of 4.0 °C. The measurement stand is shown in Figure 2. The dehumidifier consists of a drying part (a duct made from insulated sheet metal and an evaporator with fans) and a technical part (aggregate and electrical installation). The Embraco NEU6217U on/off piston compressor was used for the test.
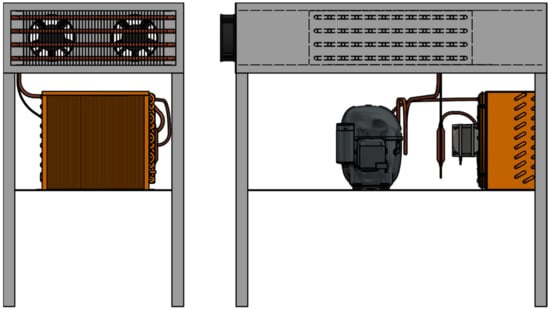
Figure 2.
Measurement stand.
The device was tested in a climatic chamber maintaining constant air parameters at 25 °C (±1 °C) and 60% relative humidity (±5%). The arrangement of the air-measuring probes is shown below in Figure 3.
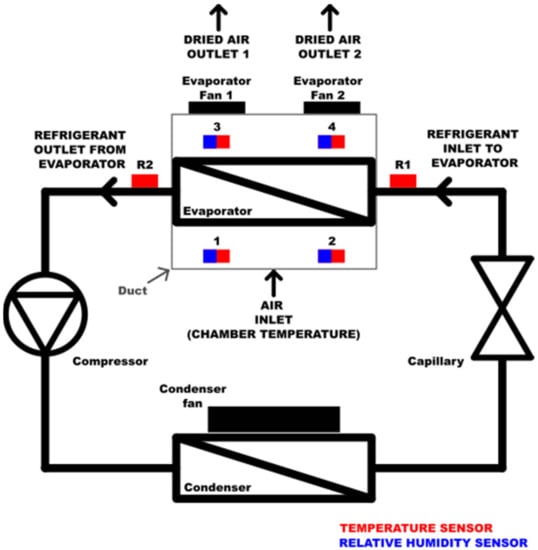
Figure 3.
Scheme of the tested device and the arrangement of the measuring probes.
The temperature and humidity were measured at four points: two in front of the evaporator (1 and 2) and two behind (3 and 4). The location of the points was selected in such a way as to reflect the real airflow as much as possible and in a manner that was not affected by random factors. Pt 100 temperature probes (range −100 °C to 450 °C and accuracy of 0.15 ± 0.002) and EE210 relative humidity probes (range 0% to 100% and accuracy of 1.3%) were used during the test. The surface temperature of the pipes before (R1) and after (R2) the evaporator was measured as required by the mathematical model, i.e., complete evaporation, and the determination of specific points of the refrigeration system. The probes attached to the pipes were insulated with a layer of Armaflex (rubber coating insulation) to minimise the impact of external conditions on the sensors. In the duct in front of the evaporator, the airflow velocity was measured at nine points where the lines crossed: three horizontal and three verticals. The average measurement result was 1.51 m/s. Air flow velocity was measured with a MeasureMe MT891 anemometer (range 0.4 to 30 m/s) with an accuracy of ± 3%. The operating pressure of the heat pump was measured in the aggregate area condensing pressure behind the condenser and evaporating pressure through the compressor service port. Then, the medium saturation temperature corresponding to the measured pressures was read [31]. To compensate for the influence of external conditions, the sheet metal duct in which the heat exchanger was located was insulated with a 20 mm layer of XPS (extruded polystyrene). The measurements started when the required air conditions behind the exchanger and in the climatic chamber were met. The duration was set at sixty minutes. The results of the measurements are shown in Figure 4 below and in Table 4. The points before the evaporator (1 and 2) and after (3 and 4) were averaged. Condensate from the evaporator was collected inside the tank under the heat exchanger duct, and the amount of mass of condensate was measured. Electricity consumption was measured using a meter Lumel N27P with an accuracy of ±0.5%
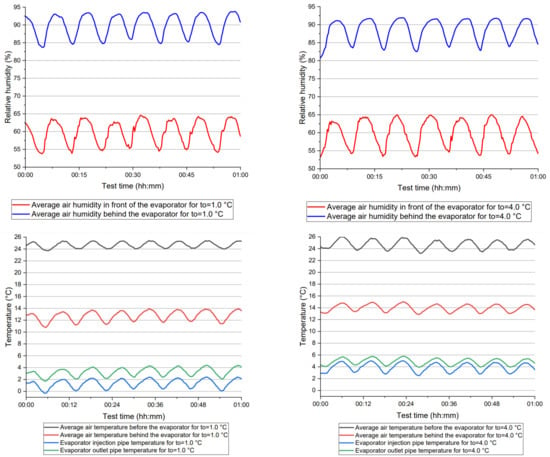
Figure 4.
Graphs of temperature and air humidity for two heat pump operating points.

Table 4.
Measurement results.
Figure 4 shows the periodic cycle of changes in temperature and humidity. As stated earlier, the test chamber (in which the analysed device is located) worked in the on/off mode with a temperature hysteresis of ±1 °C and a relative humidity of ±5%. Although its controller was set to the parameters of climate class III (25 °C and 60%), the measured air parameters before the evaporator at points 1 and 2 ranged from 24 °C to 26 °C and 55–65%, affecting the other measured values similarly, despite the continuous operation of the compressor and dryer fans throughout the test period. This required the test results to be averaged (see Table 4). The formulae for the mean standard deviation were used to determine the uncertainty of the measurements and calculation results. A composite uncertainty method based on the law of uncertainty propagation was used for the calculated results.
4. Verification of Results
For the above air parameters before and after the evaporator (Table 4), the enthalpies of these points were calculated in order to enable the calculation of the cooling capacity from the air side. By identifying the speed of the airflow, air density, and dimensions of the exchanger, the actual thermal efficiency of the exchanger could be calculated using Equation (8):
The individual data and results are presented below in Table 5.

Table 5.
Calculations of heat exchanger efficiency from the air side.
The power of the compressor was determined on the basis of the measurement of the total energy consumption, which was measured during the tests at 690 Wh. It is the power consumed by the compressor, the two fans on the evaporator, the fan on the condenser, and the controller. According to data from the manufacturers of these components, they consume 38 Wh [32,33], so the compressor itself consumes 652 Wh, which is more or less in line with the manufacturer’s stated power of 660 Wh. The experimental results and the catalogue data showed a small difference (5%) in the energy consumption of the compressor. The calculation and measurement results are presented below in Table 6.

Table 6.
Summary of calculations and tests.
The obtained evaporator performance results differed from the calculated values in Table 3 by more than 13% for the first and 10% for the second operating point of the system. The computational parameters of the air at the outlet of the evaporator, compared with those obtained experimentally, differed by approximately 2 °C and 5%. In addition to the heat gains from the environment and the measurement accuracy of the sensors used during the test, the results may have been affected by the assumptions of the zero-dimensional mathematical model, which does not consider changes in input parameters.
The graphs in Figure 4 show that the relative humidity periodically fluctuated by approximately 5%, and the temperature fluctuated by 3 °C. In addition, the mass of the condensate was lower than the calculated value by over 20%. This may also be influenced by the design of the duct in which the evaporator was located. Its lower part had only a slight slope, and a funnel was placed in the drip container from above, causing the incomplete flow of water into the container located under this part. A small amount of water remained on the cold elements of the evaporator because the mass of individual drops was too small to flow down the fins of the exchanger by gravity. In addition, the container was not sealed tightly, so a small amount of water evaporated.
The difference in the values of individual parameters presented in Table 6 may have resulted from not considering the actual efficiency of the heat pump components, which affected the results obtained. We are primarily talking about the compressor and the heat exchanger here. The algorithm on which the calculations are based takes into account the efficiency of the evaporator fins but does not take into account the unevenness of the airflow through the heat exchanger and does not gain the theoretical heat flux from the cold elements of the evaporator, causing a difference in air parameters at the outlet of the evaporator and a differing evaporator efficiency by 10% and 13% for the tested operating points of the refrigeration system. It can therefore be concluded that the efficiency of the dehumidifier system is only 85% to 90% of the theoretical efficiency calculation.
5. The Effect of Evaporation Temperature on Air-Drying Rate
The analysis was performed for the pressure range from 4.71 bar to 6.32 bar (boiling point 0 °C to 10 °C). The maximum value was defined by the operating envelope of the compressor used. The rest of the input parameters listed in the theoretical model section remained unchanged. Individual calculation results are presented in Table 7.

Table 7.
Summary of calculations for different evaporation temperature.
According to the calculations, the influence of the change in boiling point on the individual results was significant. The relative humidity at the outlet of the evaporator was practically unchanged, but it was defined as two variables depending on the mass of water vapour contained in the air and its temperature. The data provided by the manufacturer determined the electricity consumption of the compressor depending on the change in the evaporation temperature, which is also included in Table 7. Figure 5 presents a graph of the relationship between the boiling point and the calculated SMER coefficient, which takes into account the compressor’s electricity consumption plus the catalogue data of the fans and the controller. In addition, two points obtained during the described research are marked.
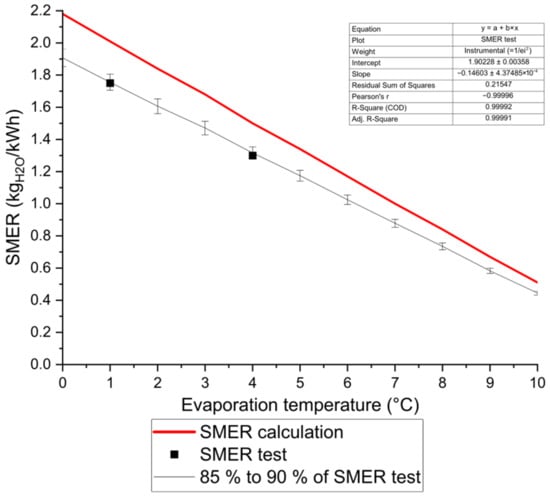
Figure 5.
Diagrams of changes in the theoretical SMER index depending on the evaporation temperature.
According to theoretical calculations with real efficiencies of elements, the equation of the black curve in Figure 5 is:
while maintaining the coefficient of determination, R-squared, at the level of 0.99991 and with the measurement uncertainty of 2.8% obtained for the tested operating points.
The given formula is generalized, although all the tests were performed for one type of construction. The methodology is similar for all types of air-cooled exchangers, so it can be expected that the formula will be similar for other geometries of exchangers; however, specific efficiencies of system elements have to be introduced for an individual case.
As shown above, calculations of the theoretical SMER coefficient are widely studied, but the efficiency in real devices is often neglected. The efficiency of the tested industrial dehumidifier system was approximately 85% of the theoretical efficiency calculations, so results may vary significantly in different cases.
The capacity of the exchanger, which is the total of the sensible and latent capacity, more than halved with the increase in the evaporation temperature. This is due to the lower absorption capacity of the water vapour contained in the air flows through the evaporator. For 0 °C and 10 °C, listed in Table 7, it can be seen that to dry the air to the same extent (to obtain the same mass of condensate), the drying time should be extended almost four times, which increases the energy consumption of the device. The most effective value of the theoretical SMER was obtained for the lowest evaporation temperature and amounted to 2.18 . Considering the efficiency of the dehumidifier determined by tests, the SMER value was 1.91 ± 0.06 . Therefore, from an economic point of view and for the efficiency of the drying process, it is necessary to strive to obtain the lowest above-zero temperatures of the surface of the evaporator on which the water condenses from the air. The air temperature at the outlet of the exchanger is lower by more than 5 °C in extreme cases, so depending on the purpose and the use of the heat pump (e.g., in the sphere of human comfort), it may be a problem, and an analysis should be performed to obtain the optimal air and technical parameters of the dehumidifier (e.g., electricity consumption).
6. Summary
The article showed the quantitative effect of the evaporation temperature on the energy efficiency of drying using the SMER parameter. A calculation example of a finned heat exchanger and values describing the efficiency and quality of drying were presented. The results obtained in the theoretical section were validated to check the correctness of the mathematical model. The obtained experimental results were consistent with the calculations, so the correctness of the applied algorithm was confirmed. In the next section, a theoretical analysis was performed on the influence of evaporation pressure on the speed of air drying.
The main conclusions that can be drawn from the results of the present study are listed below:
- Theoretical SMER calculations are widely studied, but the overall efficiency in real devices is often neglected, which can change the final results by several per cent, as shown in this article for the analysed case;
- Theoretical analysis of the influence of the evaporation temperature on the rate of air drying showed that it is reasonable to strive to design systems based on positive temperatures close to 0 °C;
- Actual efficiency values for equipment and heat exchangers were introduced on the basis of experimental studies. The SMER value for 0 °C after taking into account the efficiency was 1.91 ± 0.06 . By increasing the boiling point to 10 °C, the index decreased to less than 25% to 0.44 ± 0.01 , increasing the electricity consumption and the duration of dehumidifying the same volume of air;
- The dependence of the SMER on the cycle parameters makes it possible to optimise cycle control and dryer design.
The analysed case, although widely discussed in scientific research, may affect the correct selection of components and design assumptions for drying devices based on a refrigerant circuit. This applies not only to dehumidifiers based on a closed or open air-loop system but also to air conditioning and other related industries, where the air is cooled with evaporators operating at temperatures lower than the dew point temperature. It was shown that the temperature difference between the exchanger surface and the dried medium influenced the increase in the rate of air drying. Depending on the evaporation temperature, the power consumption of the compressor also changes, which, in extreme cases, can cause a significant increase in energy consumption when trying to maintain low evaporation temperatures. This analysis allows these two aspects to be related to each other and optimised according to the established design criteria.
Author Contributions
Conceptualisation, investigation, validation, resources, data curation, writing—original draft preparation, visualisation: T.M.; methodology, formal analysis, writing—review and editing, supervision P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available upon request from the corresponding authors.
Acknowledgments
Special thanks to company Juka sp. z o.o. sp. k. for the sharing of their device and the test chamber for the experimental tests described in this article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| surface area, | |
| specific heat capacity at constant pressure, | |
| diameter, | |
| energy consumption, Wh | |
| exchanger width, | |
| gravitational acceleration, | |
| exchanger height, | |
| enthalpy, | |
| Heat transfer coefficient related to surface A, | |
| molar mass, | |
| mass, | |
| mass flow, | |
| number of rows | |
| number of transfer units | |
| number of pipes | |
| number of injections | |
| atmospheric pressure, | |
| saturation pressure, | |
| critical pressure, | |
| partial pressure of water vapour molecules in the air, | |
| heat transfer coefficient of the exchanger, | |
| cooling capacity, | |
| thermal resistance of pollutants, | |
| heat of vaporisation, | |
| spacing longitudinal | |
| spacing transversal | |
| temperature, | |
| heat capacity of medium flux, | |
| moisture content in the air, | |
| Greek Symbols: | |
| heat transfer coefficient, | |
| thickness, | |
| efficiency | |
| thermal conductivity, | |
| dynamic viscosity, | |
| density, | |
| surface tension, | |
| relative air humidity, | |
| fin pitch, | |
| Subscripts: | |
| I | heat pump first operation point |
| II | heat pump second operation point |
| 1 | start/inlet value |
| end/outlet value | |
| c | refrigerant |
| cz | frontal area of exchanger |
| evap | condensate |
| o | evaporation |
| p | air |
| w | inner surface |
| outer surface | |
| fin | |
| liquid phase in a saturated state | |
| gas phase in a saturated state |
References
- Mujumdar, A.S.; Huang, L. Global R&D Needs in Drying. Dry Technol. 2007, 25, 647–658. [Google Scholar] [CrossRef]
- Colak, N.; Hepbasli, A. A review of heat-pump drying (HPD): Part 2—Applications and performance assessments. Energy Convers. Manag. 2009, 50, 2187–2199. [Google Scholar] [CrossRef]
- Minea, V. Drying heat pumps—Part I: System integration. Int. J. Refrig. 2013, 36, 643–658. [Google Scholar] [CrossRef]
- Lee, K.H.; Kim, O.J. Investigation on drying performance and energy savings of the batch-type heat pump dryer. Dry Technol. 2009, 27, 565–573. [Google Scholar] [CrossRef]
- U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Building Technologies Program. Energy Efficiency Program for Consumer Products and Commercial and Industrial Equipment; Technical Support Document; U.S. Department of Energy: Washington, DC, USA, 2021.
- Cao, X.; Zhang, J.; Li, Z.-Y.; Shao, L.-L.; Zhang, C.-L. Process simulation and analysis of a closed-loop heat pump clothes dryer. Appl. Therm. Eng. 2021, 199, 117545. [Google Scholar] [CrossRef]
- Rossi, S.J.; Neves, L.C.; Kieckbusch, T.G. Thermodynamic and energetic evaluation of heat pump applied to the drying of vegetable. In Proceedings of the 8th International Drying Symposium (IDS92), Montreal, Canada, 2–5 August 1992; pp. 1475–1484. [Google Scholar]
- Mellmann, J.; Fürll, C. Drying facilities for medicinal and aromatic plants–specific energy consumption and potential for optimization. J. Med. Spice Plants 2008, 13, 127–133. [Google Scholar]
- Clements, X.J.S.; Jolly, P. Study of Heat Pump Assisted Microwave Drying. Dry. Technol. 1993, 11, 1583–1616. [Google Scholar] [CrossRef]
- Patel, K.K.; Kar, A. Heat pump assisted drying of agricultural produce—An overview. J. Food Sci. Technol. Mysore 2011, 49, 142–160. [Google Scholar] [CrossRef]
- Ziegler, T.; Niebling, F.; Teodorov, T.; Mellmann, J. Heat pump drying of medicinal and spice plants—Possibilities of energy efficiency enhancement. J. Med. Spice Plants 2009, 14, 160–166. [Google Scholar]
- Ziegler, I.T.; Jubaer, H.; Mellmann, I.J. Simulation of a heat pump dryer for medicinal plants. Chem. Ing. Tech. 2012, 85, 353–363. [Google Scholar] [CrossRef]
- Schmidt, E.L.; Klocker, K.; Flacke, N.; Steimle, F. Applying the transcritical CO2 process to a drying heat pump. Int. J. Refrig. 1998, 21, 202–211. [Google Scholar] [CrossRef]
- Oktay, Z. Testing of a heat-pump-assisted mechanical opener dryer. Appl. Therm. Eng. 2003, 23, 153–162. [Google Scholar] [CrossRef]
- Graban, A.; Groll, E.; Braun, J.; Ziviani, D. Review of Heat Pump Tumble Clothes Dryer Energy Efficiency and Related Technologies. In Proceedings of the International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 24–28 May 2021. [Google Scholar]
- Fernandez-Golfin Seco, J.I.; Fernandez-Golfin Seco, J.J.; Hermoso, E.; Conde Garcia, M. Evaluation at industrial scale of electric-driven heat pump dryers (HPD). Holz Roh Werkst. 2004, 4, 261–267. [Google Scholar] [CrossRef]
- Prasertsan, S.; Saen-Saby, P. Heat pump dryers: Research and development needs and opportunities. Dry Technol. 1998, 16, 251–270. [Google Scholar] [CrossRef]
- Abrahamsson, K.; Stenstrom, S.; Aly, G.; Jernqvist, A. Application of heat pump systems for energy conservation in paper drying. Int. J. Energy Res. 1998, 21, 631–642. [Google Scholar] [CrossRef]
- Zhao, J.; Jian, Q.; Zhang, N.; Luo, L.; Huang, B.; Cao, S. The improvement on drying performance and energy efficiency of a tumbler clothes dryer with a novel electric heating element. Appl. Therm. Eng. 2018, 128, 531–538. [Google Scholar] [CrossRef]
- Deans, J. The modelling of a domestic tumbler dryer. Appl. Therm. Eng. 2001, 21, 977–990. [Google Scholar] [CrossRef]
- Rezk, K.; Forsberg, J. Geometry development of the internal duct system of a heat pump tumble dryer based on fluid mechanic parameters from a CFD software. Appl. Energy 2011, 88, 1596–1605. [Google Scholar] [CrossRef]
- Shengchun, L.; Xueqiang, L.; Mengjie, S.; Hailong, L.; Zhili, S. Experimental investigation on drying performance of an existed enclosed fixed frequency air source heat pump drying system. Appl. Therm. Eng. 2018, 130, 735–744. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Wang, J.; Wang, H.; Yu, X. Effect of compressor speeds on performance of a closed loop heat pump drying system. Appl. Therm. Eng. 2021, 195, 117220. [Google Scholar] [CrossRef]
- Niezgoda-Zelasko, B.; Zalewski, W. Chłodnicze I Klimatyzacyjne Wymienniki Ciepła. Obliczenia Cieplne, 1st ed.; Wydawnictwo Politechniki Krakowskiej: Cracow, Poland, 2013. [Google Scholar]
- Wongwises, S.; Anansauwapak, B. Prediction of evaporation of defrosted water in refrigerator water trays. Int. Commun. Heat Mass Transf. 2005, 32, 403–415. [Google Scholar] [CrossRef]
- Zalewski, W.; Kot, J. Obliczenia cieplne wymiennika stanowiącego ujęcie dolnego źródła ciepła powietrznej pompy ciepła. Czas. Inżynierii Lądowej Sr. I Archit. Politech. Rzesz. 2016, 63, 543–552. [Google Scholar] [CrossRef]
- Zalewski, W. Obliczenia cieplno-przepływowe wentylatorowych chłodnic powietrza (cz. 1). Chłodnictwo Organ Nacz. Organ. Tech. 2015, 50, 40–44. [Google Scholar] [CrossRef]
- Shah, R.K.; Sekulic, D.P. Fundamentals of Heat Exchanger Design; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Schmidt, K.G. Heat Transfer to Finned Tubes. In VDI Heat Atlas, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1273–1278. [Google Scholar] [CrossRef]
- Mołczan, T.; Cyklis, P. Mathematical Model of Air Dryer Heat Pump Exchangers. Energies 2022, 15, 7092. [Google Scholar] [CrossRef]
- Program Refrigeration Utilities version 2,84. Available online: www.et.dtu.dk/CoolPack (accessed on 17 November 2022).
- EBM Papst. Catalogue: Compact Fans for AC, DC and EC Version 2019-04. Available online: https://www.ebmpapst.fr/media/content/info-center/downloads/catalogs/Compact_fans_for_AC_and_DC_EN_04_2019.pdf (accessed on 19 February 2023).
- EBM Papst. Catalogue: Fans and Motors for Refrigerated Display Cases Version 2019-07. Available online: https://www.ebmpapst.com/content/dam/ebm-papst/media/catalogs/industries/Catalog_Axialfans_ESM-iQ_EN.pdf (accessed on 19 February 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).