Optimization of Electric Vehicles Charging Scheduling Based on Deep Reinforcement Learning: A Decentralized Approach

Abstract

The worldwide adoption of Electric Vehicles (EVs) has embraced promising advancements toward a sustainable transportation system. However, the effective charging scheduling of EVs is not a trivial task due to the increase in the load demand in the Charging Stations (CSs) and the fluctuation of electricity prices. Moreover, other issues that raise concern among EV drivers are the long waiting time and the inability to charge the battery to the desired State of Charge (SOC). In order to alleviate the range of anxiety of users, we perform a Deep Reinforcement Learning (DRL) approach that provides the optimal charging time slots for EV based on the Photovoltaic power prices, the current EV SOC, the charging connector type, and the history of load demand profiles collected in different locations. Our implemented approach maximizes the EV profit while giving a margin of liberty to the EV drivers to select the preferred CS and the best charging time (i.e., morning, afternoon, evening, or night). The results analysis proves the effectiveness of the DRL model in minimizing the charging costs of the EV up to 60%, providing a full charging experience to the EV with a lower waiting time of less than or equal to 30 min.

1. Introduction

The expansion of electric mobility has gained traction in recent years as an alternative to fossil-fueled cars. According to the International Energy Agency, the sales of Electric Vehicles (EVs) have tripled to reach 10 million by the end of 2022 [1].

Governments in Europe, specifically Germany, Norway, and France, are putting significant efforts into improving the electric mobility infrastructure and maintaining an environmentally friendly transportation network. However, the wide-scale adoption of the EV results in several challenges arising. The significant challenges for the car driver are the anxiety of running out of battery, facing long waiting hours for charging, or high charging costs [2]. According to a scientific report about the attitude of European car drivers toward EVs, it has been proved that the second most common cause that contributes to each individual’s reluctance to use EVs is the issues related to the battery recharging time. Therefore, it is mandatory to explore multiple scheduling strategies to limit potential charging inefficiency problems and guarantee a seamless charging experience for the EV driver [2].

Only a few studies have yielded the issue of the scheduling strategies in the last decade [3,4,5]. In [3], a comparative analysis was conducted and has proven difficult in solving the scheduling problems due to the complexity of the modelization of the charging environment using traditional optimization techniques (i.e., the Long Short-Term Memory (LSTM) and the Recurrent Neural Network (RNN)). A novel approach using Deep Reinforcement Learning (DRL) was introduced and has demonstrated its superiority in tackling the optimization of various EV charging problems. The authors in [4,5] showed the effectiveness of DRL in optimizing the charging duration and the cost. The authors suggested a model-free method that can handle charging problems like the uncertainty of arrival time and charging price fluctuation, which cannot be considered using traditional methods’ optimization approaches. The proposed approach [4] can potentially result in high demand during charging at lower prices. A smart scheduling solution based on DRL [6] developed a solution to plan long trips for EVs using generated scenarios. This approach depicted the scarcity of the real data that may lead to incorrect decisions, showcasing the importance of considering real-world data in the optimization scheduling problems.

A model-free reinforcement learning algorithm called Q-learning was proposed in [7] to optimize the charging cost for Vehicle-to-Grid (V2G) and Grid-to-Vehicle (G2V) charging behavior. Another use of Q-learning is the routing plan, presenting an energy-efficient solution for the EVs online. This approach assumed the model limitations in terms of handling a high-dimensional Q-table, which is addressed by employing Deep Q-Learning (DQL) methods. The authors in [8] propose a smart scheduling solution to coordinate the EV charging control of the voltage in the grid regarding the uncertainties of the charging process and load demand. Another model-free reinforcement learning is the Deep Deterministic Policy Gradient (DDPG), which has proven its prominence in solving the charging scheduling task specifically in continuous action–space environments. A real-time scheduling strategy was proposed based on the price signals to tackle the problem of a substantial number of EVs powered by the distribution network. In [9], the authors use Multi-Modal Approximate Dynamic Programming to optimize the scheduling of charging and discharging EVs while considering a single objective, which is the pricing schema [10]. The literature review indicated a remarkable focus on DRL techniques to address the charging scheduling problem. The authors in [6] proposed a DRL approach based on the Deep Q-Network (DQN) model that recommends the optimal charging station at the beginning of the trip based on the following features: State of Charge (SOC), trip distance, average speed, charging prices, and energy demand. However, this model presents some limitations, which are the long training time and the used dataset, which was not collected for real-world use cases. The challenge of the determination of the optimal charging scheduling-based model-free DRL model is tackled in previous research while considering the randomness of pricing and user preferences [11].

The majority of previous studies have used the DRL to solve different scheduling problems, and they achieved good results [8,9]. But the developed models present some shortcomings, such as the lack of findings evaluation and the use of simulated data that are far from the truth.

The overall goal of this work consists of the day-ahead prediction of the best EV charging time slots, with a focus on reducing the energy cost and the waiting time inside the Charging Station (CS), as well as guaranteeing a fast and full charging of EV batteries. Additionally, the EV’s driver preferences for the charging location, the charging connector type, and the desired charging part of the day are taken into consideration in the charging scheduling problem.

The main contributions of this paper are as follows:

• The prior study maintains a major focus on a single objective, especially reducing the energy cost [9], whereas our proposed method tackles two main objectives simultaneously: (1) the reduction in the charging cost and (2) the minimization of the waiting time, while giving a margin of flexibility to the EV to select a preferred location and a time of the day (i.e., morning, afternoon, evening, and night).
• Our model proposes a flexible choice regarding the number and the weight of constraints, cost, power, and load profiles.
• Some surveys used a multi-agent RL algorithm which does not imply a convergence toward the optimal policy, while our approach relies on one agent that is capable of resolving multiple objectives at the same time.
• We have developed a new algorithm to evaluate our proposed model.
• Our implemented model stands out by involving individual user preference in the charging process rather than previous work that significantly focuses on the CS profit.
• Our novel approach is based on real data rather than simulated scenarios which completely differ from real-world cases.

The remainder of this paper is organized as follows: Section 2 is devoted to introducing the system’s overall architecture, specifying the adopted variables and constraints, and detailing the mathematical formulation of the scheduling problem using the Markov Decision Process (MDP) framework. Section 3 describes the proposed solution based on the deep Q-Network (DQN) algorithm. Section 4 showcases the training phase and the simulation results. The last section is dedicated to conclusions and future works.

2. System Overall Architecture

2.1. System Overview

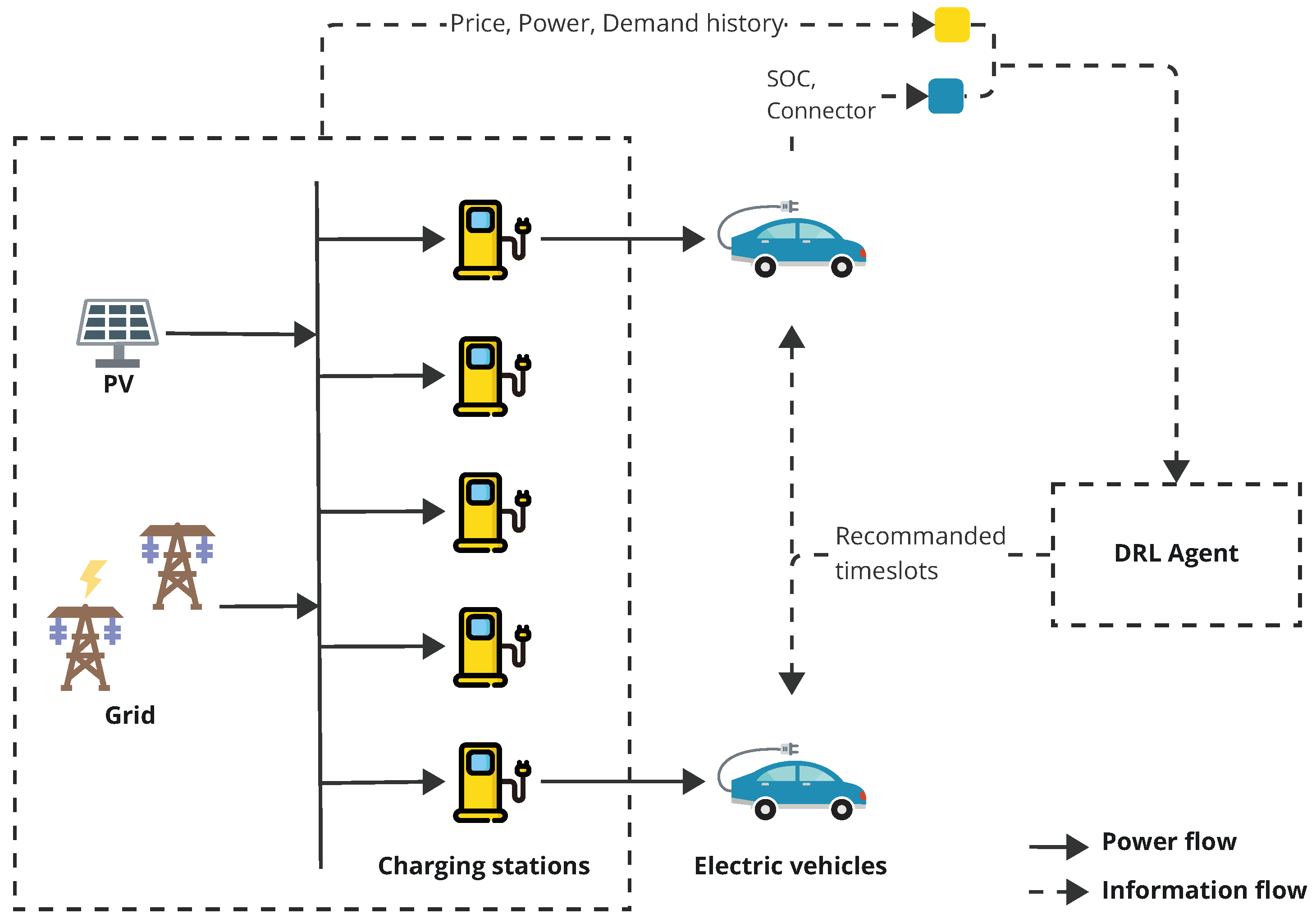
Our system is composed of multiple CSs located in different places, as depicted in Figure 1. Every CS contains multiple charging connectors (i.e., normal charging or fast charging) and a Hybrid Energy Storage System (HESS) made up of a Lithium battery and a Redox Flow Battery (RFB). Two sources of power are used to supply the HESS, i.e., the grid and the Photovoltaic powers [12,13]. Our main target is to determine the optimal time slots to charge the EV, based on a pre-selected location, and the initial EV SOC while considering the availability of the charging connector type at a specific part of the day. The EV in our proposed approach refers to any engine that is powered by electricity including automobiles, vans, bicycles, and even buses and trucks. There is no difference in dealing with Battery Electric Vehicles (BEVs) or Plug-in Hybrid Vehicles (PHEVs), since both can provide the SOC, which is the main variable in the decision process. Our system can be applied to many EVs at the same time; there is no scale restriction.

Our developed model deviates from being considered provisional distributed storage, and it explicitly focuses on the Grid-to-Vehicle (G2V) direction. We have made this decision since the dataset we use does not contain key features such as the EV battery size and SOC.

We implemented a DQN agent that makes optimal decisions on the basis of the observed charging environment that comprises the history of charging prices, the charging load demand, and the amount of power allocated to the EV battery. Additionally, we consider the amount of power delivered to the EV battery for an efficient charging experience as well as the specific charging connector type of the EV. Our proposed architecture is illustrated in Figure 1. We have opted for a decentralized optimized charging scheduling approach, i.e., the recommendation of the optimal charging time slots to all vehicles; hence, each decision is taken separately considering the individual preferences of each EV. We mean by the decentralized approach that the decision making regarding the optimum charging time slots for all vehicles is made separately, taking into consideration each EV driver’s preferences. In our system, the actor is the EV, i.e., if we implement the agent in an EV, it will make an individual decision based on the current SOC of each EV and the type of charging connector. The role of the CS is to provide data to train the DQN model. In our proposed architecture, we have decided on one agent able to solve multiple goals at the same time based on the designed reward function.

2.2. Variables and Constraints

To efficiently schedule the charging of EVs and enhance the charging experience of EV drivers, various variables are considered:

• Location: Considering different locations in the scheduling process can help the evaluation of the charging patterns and behavior in a specific area. Our system adopts the following locations: Highway, In the City, Countryside, Outside the City, and Near the Highway.
• Power availability: It is highly important to consider the amount of power that could be allocated to every EV at each location at a specific time slot.
• Connector type availability: It is vital that the charging schedule considers the availability of the required connector. This consideration avoids potential connector compatibility issues.
• Electric vehicle patterns: For refined charging planning, it is mandatory to incorporate the EV variables such as the SOC, the battery size, representing the amount of energy that can be stored in kiloWatt-hours (kWh), and the desired part of the day for charging, e.g., morning, afternoon, evening and night.

When optimizing the charging planning of an EV, various constraints namely, the  EV SOC, the charging time, and the power capacity, should be taken into account:

• EV SOC: It is designed to safeguard the battery life from damage and expressed as a percentage. It is necessary to limit the battery energy based on Equation (1):

  $$SO{C}_{min}\le SOC\le SO{C}_{max}$$

  (1)

  where $SO{C}_{min}$ is the minimum SOC and $SO{C}_{max}$ is the maximum SOC.
  We adopt an $SO{C}_{min}$ of 20%. Below this threshold, the damage could occur and the lifespan of the battery could be minimized. Moreover, stopping the charging at 80% ($SO{C}_{max}$) is recommended rather than achieving 100% of SOC, since full charging can result in high voltage and heat that may deteriorate the EV’s battery material.
• Charging time: It is the major constraint regarding the charging scheduling problem. It is important to take into account the preferences of an EV driver concerning the charging time. For instance, if the EV driver wants to charge in the morning, a restriction on available charging times is considered to ensure convenient charging in the preferred time slots.
• Power Capacity: It is an important factor that affects the charging planning. Given the user’s preference to fully charge the battery of his vehicle, it is imperative to meet the user’s expectations and ensure that the battery reaches its maximum. Based on the load demand, the availability of the charging station can provide an idea for the EV driver about the waiting time and help him improve his charging experience.

2.3. Mathematical Formulation: Markov Decision Process (MDP) Framework

The core challenge of the EV charging scheduling problem aligns with providing cost-efficient charging, giving precedence to fully charging the EV’s batteries, and minimizing the waiting time. Thus, considering the variation of the charging prices, the load demand during different parts of the day, and the EV patterns (e.g., the SOC and the charging time) is crucial to meet the system’s goals. To address these complexities, we have adopted the mathematical formulation of the EV charging scheduling problem based on an MDP with a 5-tuple (S, A, P, R, γ), where the following apply:

• S represents the set of states.
• A is a finite set of all possible actions.
• P is the state transition probability where P: $S\times A\times S\to [0,1]$.
• R denotes the reward signal for a given state and action.
• The discount factor $\gamma$ represents the importance of future rewards compared to immediate rewards.

2.3.1. State

The state is defined as a set of relevant information that the agent needs to make a decision. It is the environmental variables that affect directly the charging process of the EV. For each time step t, the state $s_t$ is given as follows:

$$s_t=(SO{C}_t,C_t,loc,t_{arr},p_{day},p{r}_k:p{r}_{k+6},p{o}_k:p{o}_{k+6},d_k:d_{k+6})$$

(2)

where the following apply:

• $SO{C}_t$ is the SOC of the EV at a time step t expressed as a percentage.
• $loc$ represents the location of the charging station.
• $t_{arr}$ is the arrival time of the EV to the CS in hours.
• $p_{day}$ indicates the part of the day, i.e., morning, afternoon, evening, and night.
• $p{r}_k$ is the charging price at a time slot k, where $t\in [k,k+6]$. Each part of the day is divided into six time slots in kWh/hour.
• $p{o}_k$ is the amount of power allocated at a time slot k in kWh.
• $d_k$ is the load demand at a time slot k. It represents the number of EVs for each time slot.

In addition, the state $s_t$ incorporates the history of the load demand for a specific time of day, the history of the power, and the associated prices. By including the history of past charging events, the agent can learn more of the charging requirement and gain more knowledge about power prices and load fluctuations which play a fundamental role in the selection of the optimal charging time slots.

2.3.2. Action

The action refers to the agent’s decision regarding a given state that the agent tries to optimize throughout the learning process. We have divided the day A into one-hour intervals ($\{T_1,T_2,\dots ,T_{24}\}$) as follows:

$$A=\{T_1,T_2,\dots ,T_{24}\}$$

(3)

2.3.3. Reward

In the environment simulation, at a time step t, a reward signal $r_t$ is sent to the agent after taking an action $a_t$ in a state $s_t$ to improve the evaluation of the agent decision process. In the charging scheduling environment, all the rewards are formulated as penalties. The design reward function involves multiple stakeholders from the points of view of the EV. The reward $r_t$ is the sum of the charging cost reward $r_{cost}$, the charging power reward $r_{power}$ and the reward of charging at high demand $r_{load}$ and is outlined by Equation (4).

$$r_t=r_{cost}+r_{power}+r_{load}$$

(4)

The various parts of the reward function are expressed in the following:

• The charging cost reward ${\mathit{r}}_{\mathit{cost}}$
  We design the charging cost reward in the form of a penalty multiplying the charging cost (kWh/€) by the charging price. $r_{cost}$ is given by the following Equation:

  $$r_{cost}=-\alpha ·p{r}_k^{a_t}·p{o}_k^{a_t}$$

  (5)

  where the following apply:
  • $\alpha$ is the charging cost coefficient.
  • $p{r}_k^{a_t}$ is the charging price of the selected time slot of the relevant action $a_t$ in €/kWh.
  • $p{o}_k^{a_t}$ is the charging power in kWh delivered at the selected time slot of the relevant action $a_t$.
• The EV charging level penalty ${\mathit{r}}_{\mathit{power}}$
  We penalize the agent for selecting a charging time slot that does not provide a maximum SOC.

  $$r_{power}=-\beta ·|SO{C}_{max}-SO{C}_t|$$

  (6)

  where the following apply:
  • $\beta$ is the charging level penalty coefficient.
  • $SO{C}_{max}$ is the maximum level of charge.
  • $SO{C}_t$ is the state of charge at the current state.
  The goal of the charging station is to provide a charging experience to the EV while maximizing the power delivered from the CS. To safeguard the battery life from damage, it is necessary to restrict the EV battery SOC from exceeding 80%. At each time step t, we calculated the new SOC level based on Equation (7):

  $$SO{C}_t=SO{C}_{t-1}+{\displaystyle \frac{p{o}^{a_t}}{C_a}}·100$$

  (7)

  where the following apply:
  • $p{o}^{a_t}$ is the power in kilowatt-hours (kWh) delivered after choosing a time slot t.
  • $C_a$ represents the battery capacity in kilowatt-hours (kWh).
• Charging penalty at high demand $r_{load}$
  Higher demand leads to a higher penalty, encouraging the agent to consider less congested time slots. The penalty term $r_{load}$ is defined as follows:

  $$r_{load}=-\lambda ·d^{a_t}$$

  (8)

  where the following apply:
  • $\lambda$ is the charging penalty at high demand.
  • $d^{a_t}$ is the load demand at the chosen time slot of the respective action $a_t$.

The coefficients $\alpha ,\beta$, and $\lambda$ are adjustable based on the EV driver’s preferences, whether to prioritize minimizing the charging cost for the EV, reducing the waiting time, or emphasizing a full battery charging experience where $\alpha +\beta +\lambda =1$.

3. DQN-Based Proposed Model

To address the day-ahead charging planning problem, we implement a model-free DRL model Deep Q-learning (DQL). DQL is an approach that combines the strengths of Q-learning with the representative power of Deep Learning (DL). In traditional Q-learning, when the state and action spaces are small, the Q-function can be represented using a table with each entry Q(s,a) that stores the expected cumulative reward of taking the action a in state s. However, representing real-world problems with high-dimensional state spaces with the Q-function as a table is infeasible due to the dimensionality constraint. Deep Q-learning overcomes this constraint by employing Neural Networks (NNs) to approximate the Q-function instead of a Q-table; a DQN is used to estimate the Q-values for each action given a state. We opted for the DQN algorithm for many reasons. First, DQN is intended to be a discrete action space precisely tailored to our scenario (i.e., each action represents a one-time slot). Second, the DQN algorithm converges faster compared to other algorithms; for example, the Soft Actor–Critic (SAC) algorithm, which is computationally much more expensive in training time and resources. Moreover, the DQN algorithm relies on the experience replay, which plays a major role in optimizing the decision process and hence leads to a faster convergence of the model. In essence, the combined advantages of the DQN including the fast convergence and the adaptability to discrete action spaces make it a compelling choice to solve our problem.

It overcomes the limitation of the state space dimensionality in Q-learning by incorporating Neural Networks (NNs) as a function approximation to calculate the optimal Q-value or the action-value function $Q^{\pi }(s,a)$, which refers to the expected return for performing an action $a_t$ in a state $s_t$ following a policy $\pi$. It represents how good it is to take an action in a particular state. The formula is presented in Equation (9):

$$Q_{\pi }(s,a)={\mathbb{E}}_{\pi }[G_t\mid s_t=s,a_t=a]={\mathbb{E}}_{\pi }\left[\sum _{k=0}^L{\gamma }^k{R}_{t+k+1}\mid s_t=s,a_t=a\right]$$

(9)

$Q^{\pi }(s,a)$ is equal to the sum of the discounted cumulative reward $G_t$ and L denotes the maximum of the time step. During the training of the DQN, the Q-value is updated according to the Bellman optimality equation expressed as:

$$Q_{\pi }(s,a)=\mathbb{E}[r_t+\gamma ·maxQ\pi (s_{t+1},a_{t+1})\mid s_t=s,a_t=a]$$

(10)

The Bellman equation updates the estimated action-value function based on the current estimates and the anticipated future rewards. During the learning process, the Q-value is refined progressively until reaching the optimal values $Q_{\pi }^{*}(s,a)$. To ensure a more stable and efficient training of the DQN, the technique of experience replay is introduced to store the past experiences of the agent–environment interactions. This method can help shift the action values from diverging due to the high correlation of transitions. Then, the experiences are sampled to train the DQN.

3.1. Deep Q-Agent

In the DQN algorithm [14], the agent employs a Deep Neural Network (DNN) to estimate the Q-values for each action. The state is fed to the NN to output at the end the predicted q-value for each action. The different layers of the DQN architecture are as follows:

• 24-neurons input layer representing the length of the state vector.
• The number of hidden layers is equal to two layers, which could be improved experimentally until reaching a stable performance of the training.
• The output layer denotes the Q-values for each action within the action space.

We referred to Adam optimizer, since it is known for its robustness and its ability to adjust dynamically the learning rate based on the network parameters.

3.2. Experience Replay

This phase takes place before starting the training of the DQN. Consequently, the agent A performs the $ϵ$-greedy strategy to choose an action. With a probability epsilon $ϵ$, the agent selects randomly an action which is choosing a random time slot for charging the EV otherwise. With a probability 1 − $ϵ$, it selects the action that matches the highest Q-value. This strategy facilitates the agent’s learning of the optimal policy and the selection of the most rewarding outcome based on the available information. A reasonable approach involved setting the memory length to 10,000. When we reach the limit of the memory, the new experience ($s_t$,$a_t$,$r_t$, $s_{t+1}$, $done$) is stored in a cyclic manner, enabling the new transitions to overwrite the older ones. This method provides an effective usage of memory while producing a diverse range of transitions for adequate training, as explained in [15].

3.3. Training Phase

In order to effectively train the DRL agent, we set the batch size to 32. Second, an epsilon decay rate of 0.001 was implemented to encourage the agent transition from exploration-heavy behavior to exploitation-driven decision making throughout the learning process. Initially set at 1, $ϵ$ gradually decreases to 0.1 during the learning process.

These settings help strike a balance between exploration and exploitation, enabling efficient and effective learning in the DRL agent. To respond to the scheduling objective of recommending the top two optimal charging time slots, a method has been developed that identifies and returns the actions with the highest Q-values. It enables the agent to prioritize the charging time slots; on the other hand, it accommodates the EV driver preferences and enhances the overall user experience by providing a range of options for the charging schedule. At the beginning of the training phase, we initialize the Q-Network Q, which predicts the Q-value of all the possible actions, and the target Q-network $Q^{\prime }$, which is a copy of the Q network that updates after a fixed number of iterations C. For a fixed number of episodes, the agent interacts with the environment to collect transitions that are stored in the replay buffer. The experiences are later sampled randomly to train the Q-network. Then, we compute the loss between the predicted Q-values and the target Q-values that we try to minimize during the training process. 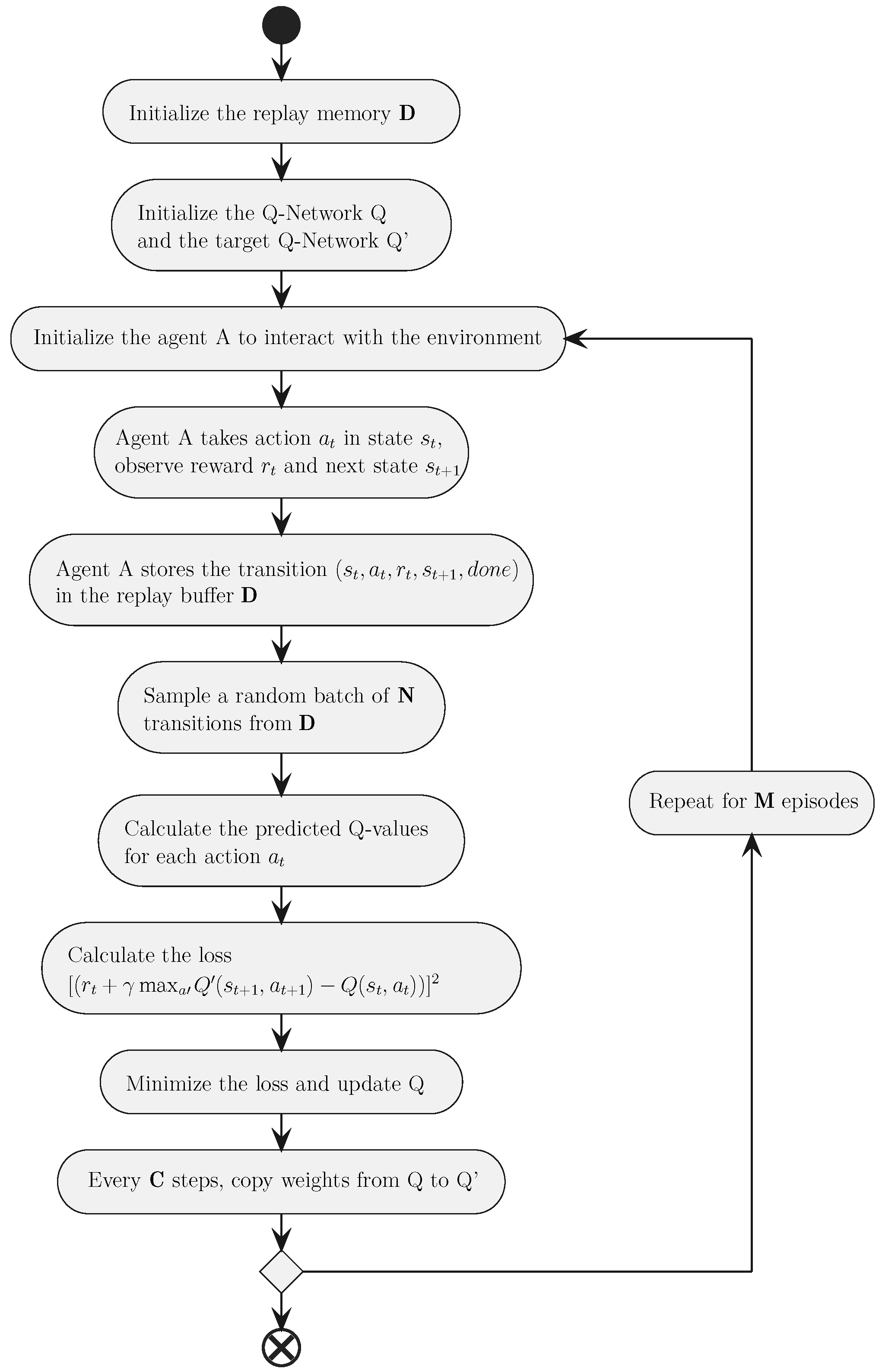The provided flowchart in Figure 2 outlines the sequential steps for the DQN algorithm.

4. Simulation Results and Discussion

4.1. Datasets

For training purposes, we have used two datasets: the first one is a load demand dataset, which consists of records of various charging events at different charging stations. The second one compromises the hourly simulated charging prices. The datasets underwent a set of preprocessing steps to align with the state space and the scheduling problem:

• Transform the 15-min charging prices data into hourly intervals and convert it to €/kWh unit.
• Aggregate the load demand per time slot, location, and connector type to extract the overall load demand.
• Extract additional information such as time of the day, part of the day, and weekday.

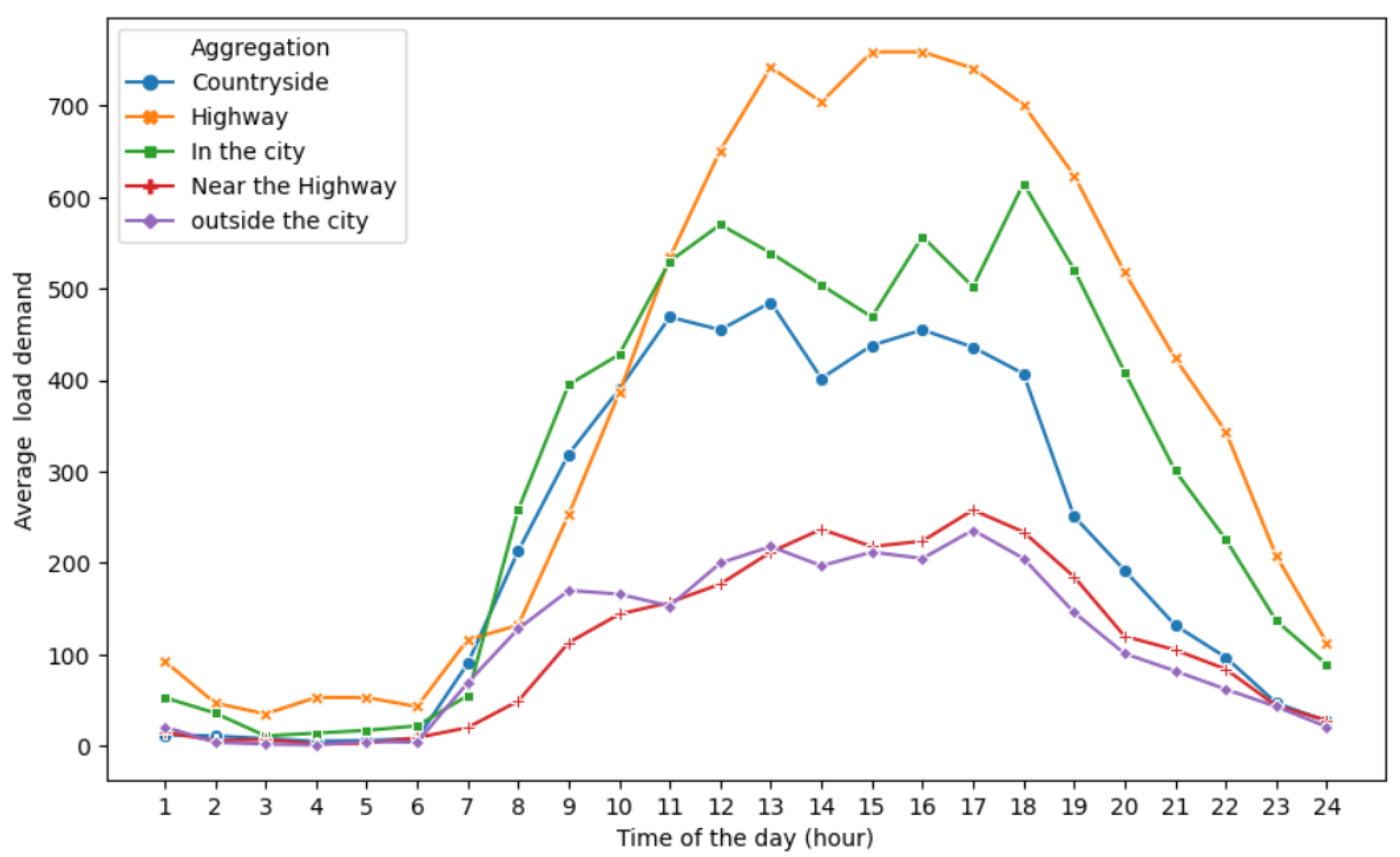
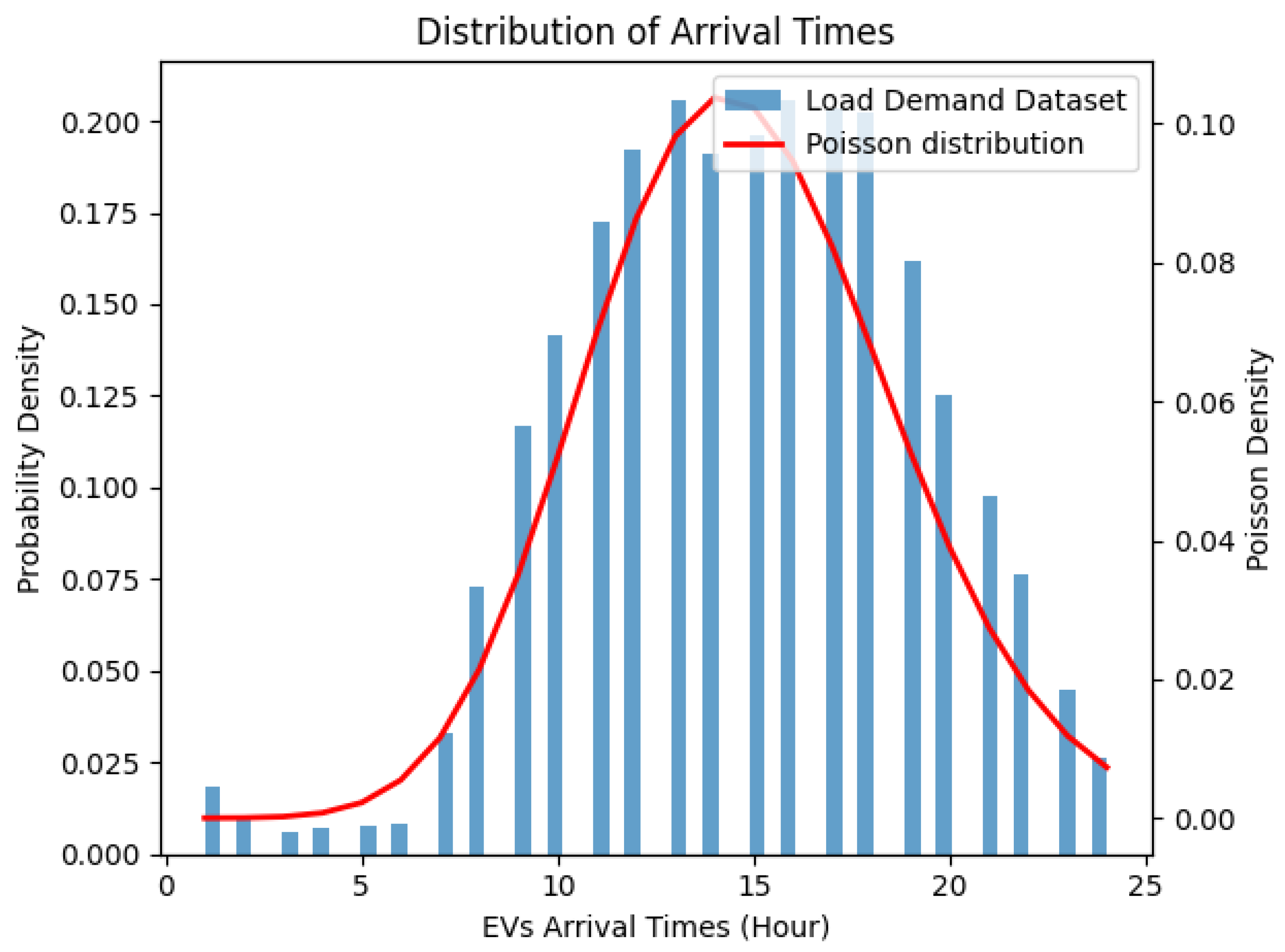
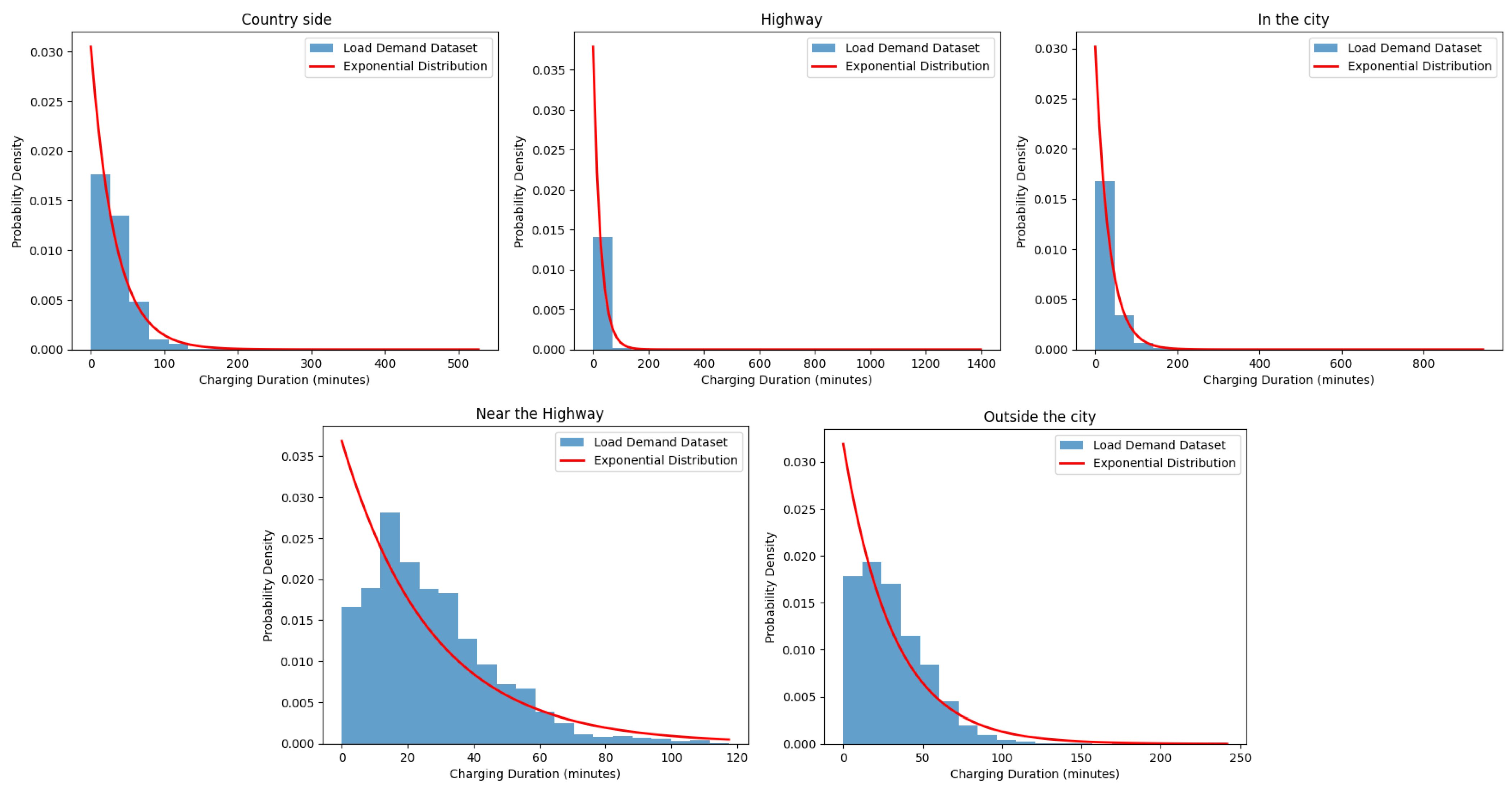
Figure 3 presents the distribution of the load demand for the different locations and Figure 4 illustrates the average prices for each time slot.

4.2. Environment Simulation Setup

The main goal of the simulation environment is to accurately capture the dynamics and complexities of the real-world charging scheduling problem based on the charging prices, the power allocated to the EV, and the load demand profile during the day. We consider the following assumptions:

Assumption 1.

The EV battery size is set to 30 kWh [16].

Assumption 2.

The initial SOC of the EV battery falls within one of the following ranges, i.e., Red [20–40%[, Orange [40–60%[, and Green [60–80%].

By categorizing the SOC within a range, we can accurately determine the vehicle’s charging level, enabling drivers to plan their range and optimize battery usage based on their preferences. Utilizing a range-based approach for SOC evaluation would provide more flexibility and accuracy compared to discrete values.

4.3. Testing Scenario

In general, the testing scenario is held to assess how well the agent has learned the optimal decisions within the given environment and ensure that the training has converged to the optimal policy. The testing is made up of three steps:

Step 1.

State specification

Within this step, we generated random states containing the SOC, part of the day, and the location. The charging prices, the charging power, and the load demand features are extracted from the dataset for a more realistic testing scenario.

Step 2.

Exploration disable

We have to turn off the exploration of the environment by setting the $ϵ$ to 0 to ensure that we test the learned policy and the agent no longer relies on choosing a random policy.

Step 3.

Action selection

The chosen optimal action is based on the highest Q-value of the learned policy.

4.4. Proposed Testing Algorithm

We propose an algorithm where we compare the agent’s decision to the ground truth. A comprehensive comparison is set between the learned decisions and the ideal case-testing scenario decision. The pseudo-code of the testing algorithm is depicted in Algorithm 1.

Algorithm 1 Agent’s performance testing algorithm

1: $correctDecisions\leftarrow 0$ 2: for each scenario in testScenarios do 3:   $randomEVpreferences\leftarrow \mathrm{GetRandom}(soc,location,day\_part,connector\_type)$ 4:   $prices\leftarrow$GetHistoryPrices 5:   $demand\leftarrow$GetHistoryDemand 6:   $powers\leftarrow$GetHistoryPower 7:   $GroundTruth\leftarrow$ GetOptimalTimeslots($powers,prices,demand$) 8:   $agentDecision\leftarrow \mathrm{RunAgent}(Random\_EV\_preferences,prices,demand,powers,)$ 9:   if $agentDecision$ is equal to $GroundTruth$ then ▹ $AgentDecision$ satisfies at least one objective 10:     $correctDecisions\leftarrow correctDecisions+1$ 11:   end if 12: end for 13: $percentageTrueDecision\leftarrow \mathrm{CalculatePercentage}(correctDecisions,TotalScenarios)$ 14: Output(“Agent’s decisions are true at least $percentageTrueDecision$ of the time.”)

We generated 2000 test scenarios where in each testing scenario, we compared the agent’s chosen time slots to the human decision based on the observed state. We made use of the success rate, which is calculated by dividing the number of times the agent correctly chooses the desired action in each scenario by the total number of testing use cases.

The result of the algorithm is a signification success rate percentage, which is about 80% of true decisions. The achieved success rate not only demonstrates the agent’s ability to generalize the learned policy but also a meaningful proficiency if applied to real-world scenarios, since the trained data (experiences) are based on the dataset.

To sum up, over 2000 test scenarios, we achieved that in 80% of cases, the agent successfully chooses the optimal time slots.

4.5. Training Analysis

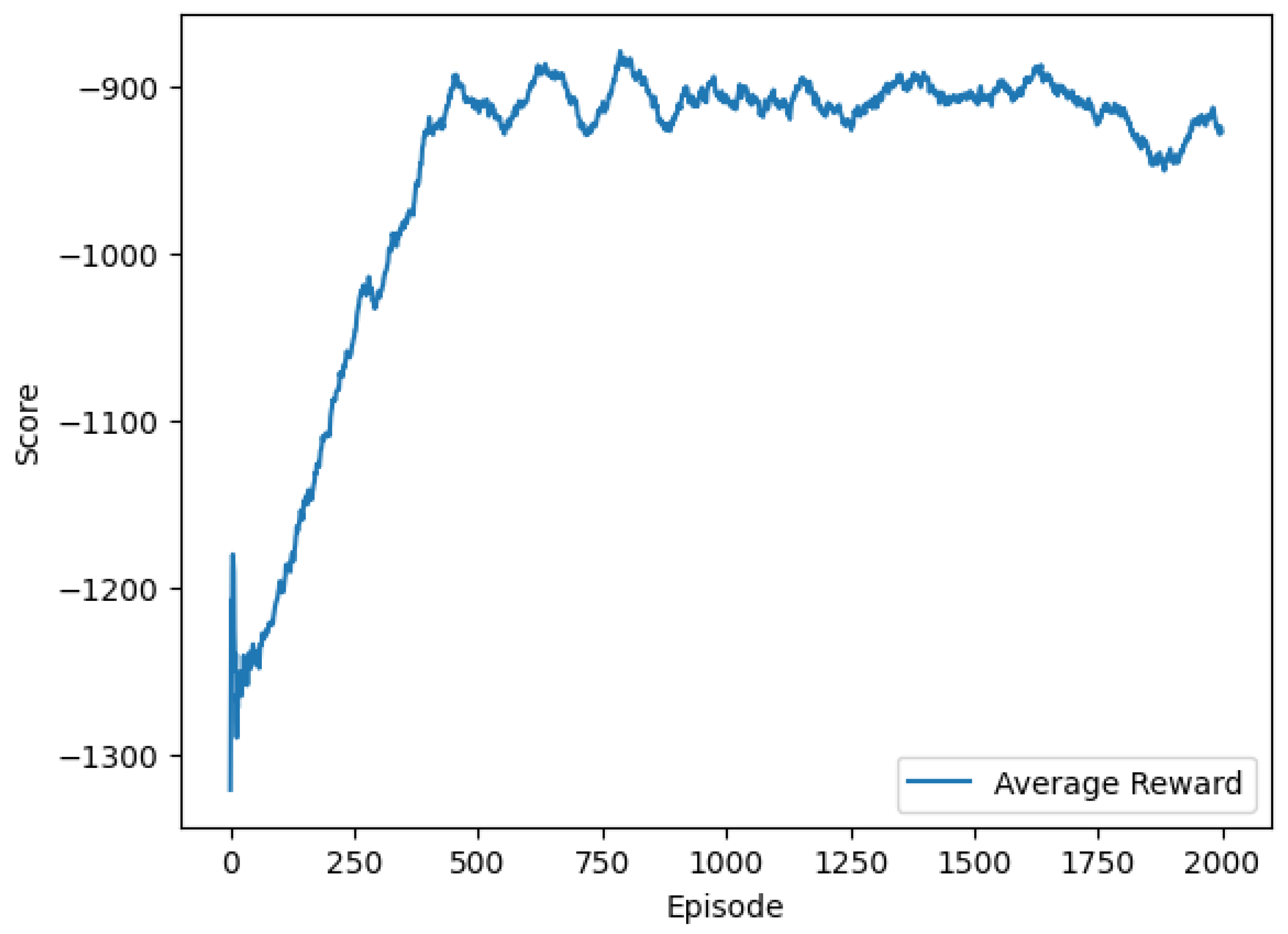
Figure 5 illustrates the training process of the DQN agent. We have run our model multiple times to ensure the reliability and robustness of the observed trends and outcomes. Figure 5 depicts the mean average reward graph and shows that the model converges into an optimal policy starting from episode number 500. This signifies that the agent is optimizing his actions over time. During the training phase, the discount factor was set to $\gamma =0.9$ over 2000 episodes.

The coefficients of the reward function were set to $\alpha =0.6, \beta =0.2$ and $\lambda =0.2$. The choice was based on prioritizing the optimization of the charging expenses. The training parameters are summarized in

Table 1. Daily average waiting time.

Symbol	Parameter	Value
$\gamma$	Discount factor	0.99
$ϵ$	Epsilon decay	0.001
M	Episodes	2000
N	Batch size	32
D	Replay buffer size	10.000
C	Update frequency	1000
$\alpha$	Cost coefficient	0.6
$\beta$	Power coefficient	0.2
$\lambda$	Load coefficient	0.2

. The training phase takes about 5 h, which is quite fast, since we work on a powerful machine. In some cases, the running time of a DRL algorithm is not a critical factor, which is our case, since we run on a powerful machine instance with a GPU of 200 GB.

4.6. Results

This section is depicted to evaluate the agent’s performance in providing the optimal time slots to charge the EV. The assessment turns around the main objective of the model: (1) minimize the waiting time, (2) deliver maximum power to the EV battery, and (3) optimize the charging expenses.

• Waiting time minimization

First, we calculated the average waiting time for each location based on the history of the load demand dataset.

We opted for the M/M/1 queue, which is a stochastic process based on two assumptions [17]: (1) Markovian Arrival Process and (2) Markovian Service Times.

• M: Markovian Arrival Process: In the EV scheduling context, M signifies that the arrival time of the EVs at the CS follows a Poisson process defined by:

  $$f\left(n\right)=e^{-\lambda }{\displaystyle \frac{{\lambda }^n}{n!}}$$

  (11)

  where $\lambda$ is the average arrival rate per hour and n is the occurrence of the charging event. Figure 6 depicts an example of the arrival time per hour. Based on this graph, we can conclude that the EV arrival times at the CS are independent.
• Markovian Service Times: There is an assumption here that the charging duration follows an exponential distribution, which is confirmed in our dataset for the five locations (see Figure 7).
  The waiting time calculation process based on the M/M/1 pursues the following steps:

  (a)

  First, we calculate the average charging duration of hourly charging events denoted $\mu$, which is defined as the average service rate.

  (b)

  Second, we calculate the EV arrival rate $\lambda$.

  (c)

  Then, we introduce the traffic intensity defined as $\rho =\frac{\lambda }{\mu }$.

  (d)

  Finally, we obtain the waiting time for each location and for each time of the day denoted q where $q=\frac{{\rho }^2}{1-\rho }·\frac{1}{\mu }$.

To assess the agent performance regarding the recommendation of the optimal time slots, we conducted a benchmark between the hourly waiting time calculated using the M/M/1 queuing model and the average waiting time of the recommended time slots by our DQN agent. The M/M/1 queuing model presents a reference theory to calculate the waiting time. We supposed that each location is an independent CS that considers the EVs arrival rate and traffic intensity for each time slot. Regarding the computation of the average waiting time, we calculated the agent’s performance over the average waiting time based on the load demand dataset for each location and for each specific time slot using the following formula:

$$\mathit{Waiting}\mathit{time}=\frac{\sum \mathit{Charging}\mathit{duration}}{\mathit{Number}\mathit{of}\mathit{EV}}$$

(12)

By considering this evaluation process, we gain valuable insights about the application and potential performance of our proposed method in real-world scenarios.

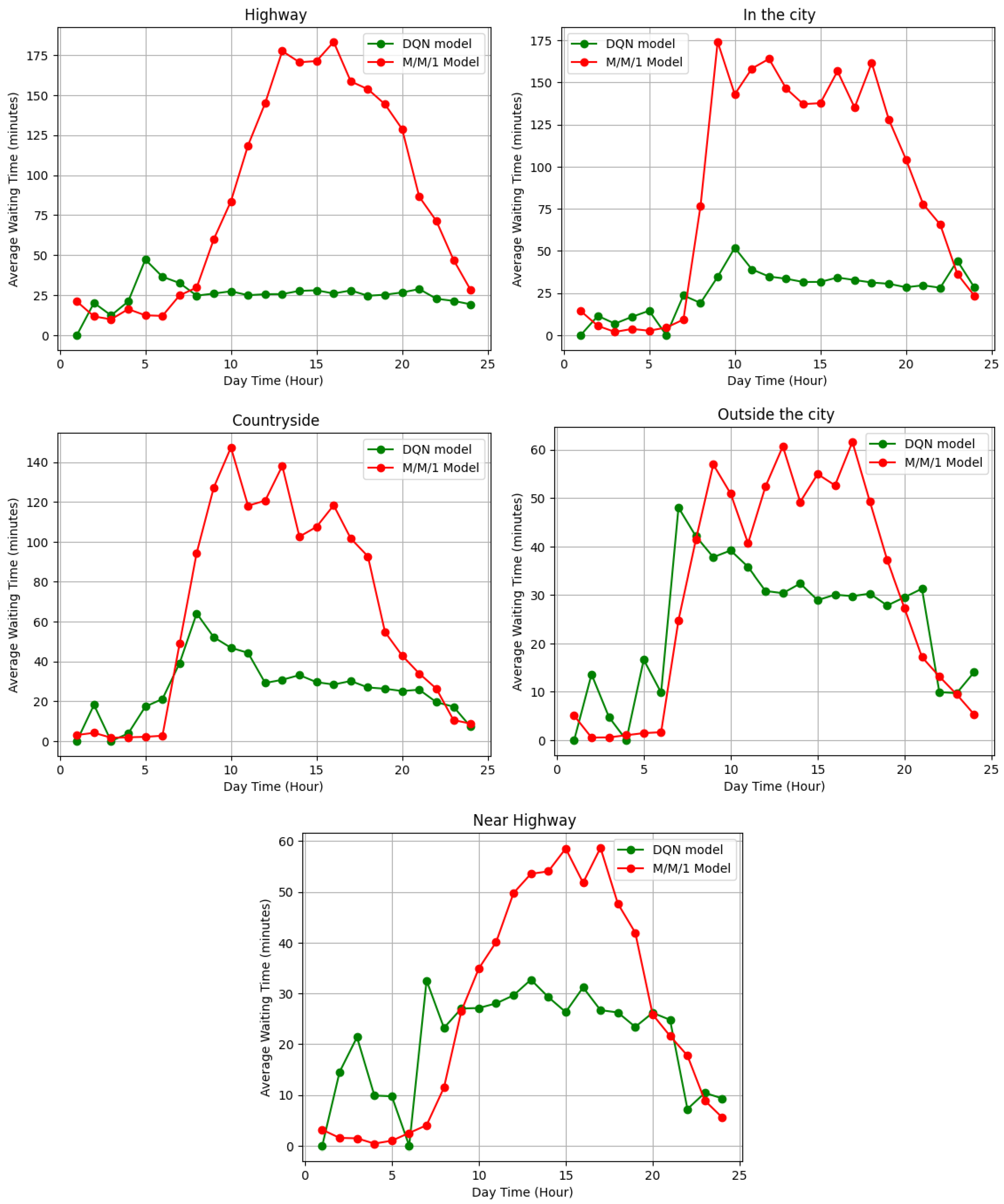
We conducted the described method on 10,000 scenarios to effectively evaluate the agent performance. The graphs in Figure 8 outline the agent’s recommended time slots demonstrating lower waiting time compared to the baseline model for the majority of the locations and during different times of the day. In the highway, city and countryside locations, a significant optimization in the waiting time is observed, especially at high demand hours between 10 a.m. and 8 p.m., compared to the baseline model M/M/1 queuing model. This disparity highlights the effectiveness of our proposed approach in bringing significant benefits to both rural and urban citizens as well as commuters. Further detailed analyses are summarized in

Table 2. Daily average waiting time.

Location	Waiting Time DQN Model (min)	Waiting Time M/M/1 Model (min)
Highway	31.03	86.08
In the City	26.01	86.11
Countryside	29.29	62.93
Outside the City	26.74	29.80
Near the Highway	19.77	29.80

.

We computed the average waiting time for the model-recommended time slots, and we benchmarked this with the average waiting time using the M/M/1 model. Notably, a significant reduction in the waiting time emerged along the highway with an average of 55 min and in the city with an average of 1 h of waiting time. Whereas outside the city and in the countryside, the waiting time is reduced by some minutes. These results showcase a significant reduction in the average waiting time, contributing to an enhanced charging experience for the EV driver.

• Charging cost optimization

To evaluate the effectiveness of the smart scheduling system in delivering a cost-efficient charging schedule, we tested our agent over multiple generated scenarios. We conclude that the agent succeeds in recommending the optimal charging slot for the EV. Through various scenarios, as detailed in

Table 3. Charging cost benchmark.

SOC Range	Location	Daily Average Charging Cost Profit (%)
Red	Highway	6.23
	In the City	48.4
	Countryside	56.8
	Outside the City	55
	Near the Highway	60
Yellow	Highway	47.9
	In the City	53.7
	Countryside	55.3
	Outside the City	56.8
	Near the Highway	41.1
Green	Highway	16.9
	In the City	37.4
	Countryside	39.1
	Outside the City	52.4
	Near the Highway	34.2

, we compare the average cost profit of our agent’s recommended time slots with the average charging cost of the whole day based on the datasets.

Based on the charging schedule results illustrating the average charging cost profit using the proposed charging scheduling method, we calculated the daily average cost profit presented in Table 3, while comparing the agent’s recommended time slot cost with the daily average charging cost data. We notice a significant reduction in the average charging time ranging from 60% in the Near the Highway location to 6% in the Highway location for the red initial EV SOC. This charging cost reduction is favorable for the EV driver if she/he follows the recommendation and opts for charging at lower prices. It is worth noting that the agent makes decisions based on the historical data of PV charging prices. To assess the performance of our proposed model, we have considered different key evaluation metrics. In contrast, most of the previous studies have assessed their work on the basis of one metric, which is cost minimization [18,19]. Our approach achieved a daily average cost profit of approximately 360 € annually. Previous research has resulted in 18.45% cost profit, while our approach has led to 60% of the profit [19].

• Prioritize full charging

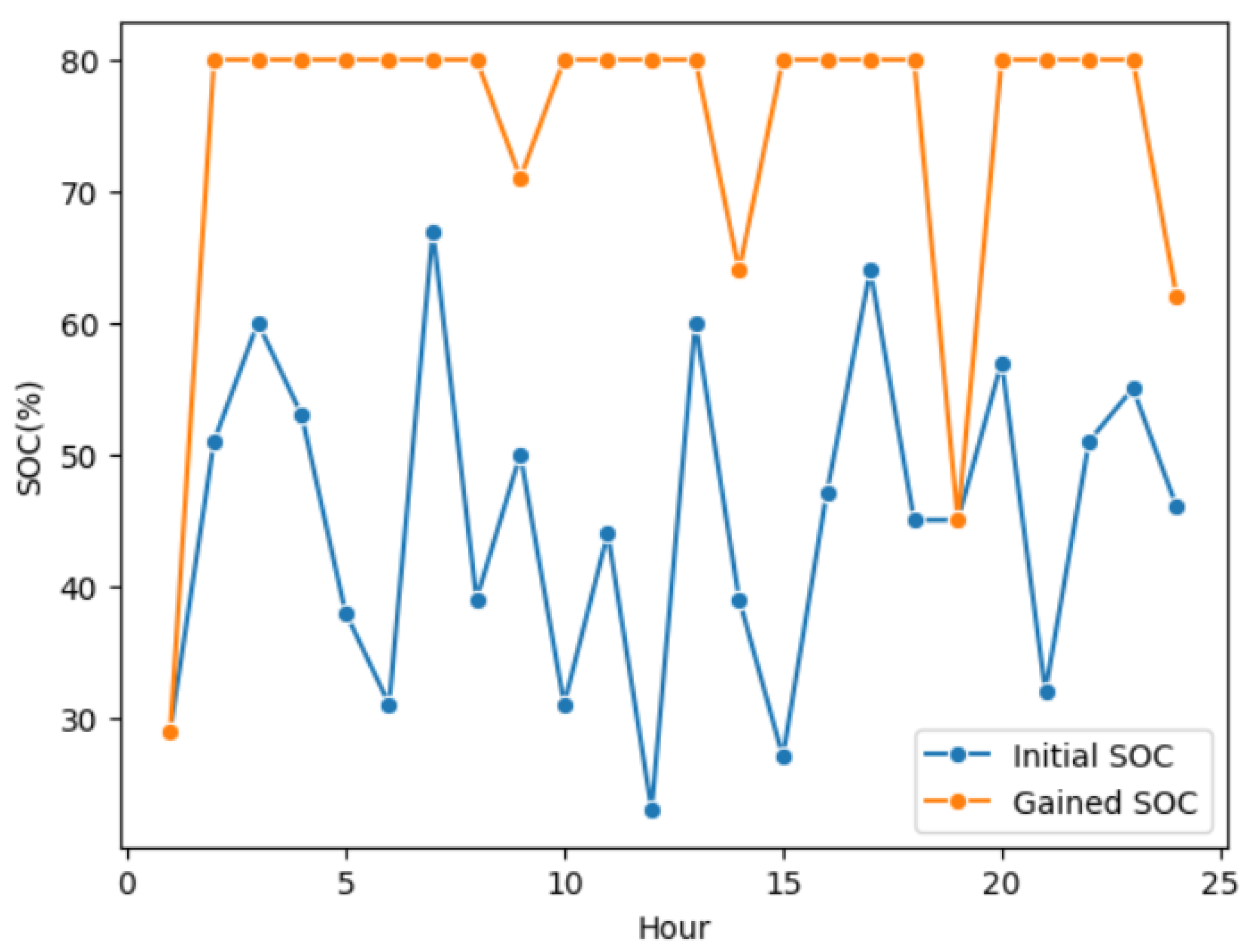
One of the primary targets of the scheduling problem is to provide the EV with a full charging experience. We set random initial values of the SOC and observed the agent’s behavior. We evaluate its performance to select the optimal time slot that guarantees full charging for the EV, as described in Figure 9.

According to Figure 9, we analyzed the agent performance for different SOC values during different hours of the day. The gained SOC refers to the SOC after testing the agent online (given a single state). The initial SOC is set randomly. We notice that the agent succeeds in selecting the optimal charging time slots that output a final SOC equal to 80% most of the time.However, the graph showcases some instances where the SOC did not reach its maximum and where the CS could not deliver power to the battery. Based on the load demand dataset, the server could have stopped, meaning that no current data are sent from the CS or the power provided to the EV is equal to 0.

5. Conclusions

As the industry endeavors to transition from fuel cars to electric ones, it is mandatory to include the vehicle driver’s preferences and habits in the charging process. In this context, we propose a model-free DRL solution that recommends the optimal time slots in the context of the day-ahead charging planning for the EV based on the preferred location and part of the day. We also consider the initial SOC and the connector type. To assess that the decision taken in the scheduling process is close enough to the real-word usage, we trained the model on real-world data that include the arrival times and the amount of power delivered to the EV for different locations. Furthermore, the testing algorithm showed that our model achieved a high level of success (80% of time) in recommending the optimal time slots. The experimental analysis proves the effectiveness of our novel approach in minimizing the charging costs up to 60%, reducing the waiting time in the charging station by an average of 30 min compared to a baseline queuing model (M/M/1). Finally, we validate the effectiveness of our method to provide a full charging experience to the EV.

Added to the cost and waiting time optimization, our proposed mechanism proved that we effectively recommend the optimal charging time slot for the EV owner that guarantees a full charging level to the EVB, which is set to 80%. In fact, our proposed model is capable of handling unseen use cases; for instance, if the initial SOC is less than 20%, it will still recommend the time slot that guarantees, as depicted in Figure 9, even if it is trained on an SOC which is between 20% and 80%, showing its ability to handle unseen charging states. Despite the tremendous results achieved by our novel approach, it presents a few limitations. The precise location of the CS is not specified in our model, as our proposed approach operates independently from any exact charging station location. Additionally, the battery capacity parameter is set at 30 kWh, and any deviation from this value would require retraining the model. These limitations, although present, do not decrease the effectiveness of our proposed method in recommending the optimal charging time slot for the EV.

We aim to consider the exact locations of the charging stations and the distance traveled to reach the charging point to boost the reliability and efficiency of our solution in real-world scenarios. Additionally, we aim to include an external factor that dynamically affects the charging process such as the weather and traffic conditions. These enhancements provide a more comprehensive insight into the charging process. Another future improvement could be the incorporation of the V2G direction, since only the case of G2V is treated in this proposed method.