Abstract
In this paper, a three-dimensional turbulent fluid dynamics numerical model of a 311 MVA full hydroelectric power plant unit is made, using the finite element method, to study and understand the ozone transport mechanisms inside the enclosured electric machine structure. In the real world, ozone is produced by partial discharges related to faults on stator bars. In order to analyse ozone transport from localised sources, a 3D fluid dynamic model of a complete hydrogenerator in operation is developed and presented for the first time. The model has a high level of geometric detail. Furthermore, a new proposal to simplify the modelling of radiators is implemented and validated. The modelled structure is based on a Campos Novos hydrogenerator electric machine and it consists of 378 coil-type stator bars made of copper covered by mica and, more externally, by a semiconductor coating layer. Other parts are also represented, including the stator core and air directors made of stainless steel, copper radiators, the rotor with its epoxy surface, and the concrete floor and concrete external walls. In the fluid dynamics model, a finite element mesh was designed to represent the air regions inside the hydrogenerator and the material surfaces that react with ozone (with their respective reaction rates), where the airflow and ozone transport are modelled using the Navier–Stokes equations and the mass conservation law. Partial discharge sources are represented by ozone sources with prismatic shapes, placed on surfaces of stator bars. Ozone concentrations have been calculated inside and around the generator machine. The rotor radius is 3.8075 m and its rotation frequency is 200 RPM. Radial air velocity due to interpole ventilation is also considered (2.2 m/s, as experimentally verified in loco. The radial velocity in the vicinity of the radiators is 3 m/s. It has been concluded that the ozone transport profile is influenced by the source positioning on the stator bars in such a way that source pinpointing is possible and it depends on determining the local and global maxima areas of ozone concentration at the radiators.
1. Introduction
Partial discharges (PDs) refer to small electrical discharges that occur in high-voltage electrical machines due to issues with the insulation materials or semiconductor coatings [1,2]. PD monitoring relies on techniques that enable the identification of issues in these machines, contributing to preventive and predictive maintenance. According to [3], there are four types of PDs that can occur in high-voltage electrical equipment: internal discharges, slot discharges, discharges in the end winding, and arcing and sparking.
Partial discharges generate ozone through electrochemical reactions involving electrons from the discharge and oxygen from the air [4]. The detection of ozone emanating from high-voltage equipment can serve as an indicator of the presence of partial discharges, which may be thus associated with insulation issues, and more frequently, surface PDs. The ozone produced during intense PD events may chemically deteriorate both the insulation and the core, contributing to the ageing of hydrogenerator components [5,6,7]. Consequently, ozone monitoring has emerged as a preventive procedure that has been extensively studied and developed, particularly over the last three decades.
Monitoring and detecting ozone in hydrogenerators are vital for protecting the equipment, ensuring operation safety, and enabling the development of predictive maintenance procedures. Several studies have been carried out in this knowledge field with significant advances in ozone detection [8,9,10,11,12,13,14,15,16].
In [8], practical procedures for measuring ozone concentrations and its generation rates in hydrogenerators’ stator bars are detailed. Additionally, in [9], various diagnostic methods for identifying PD in a heavily loaded motor generator are explored. The study revealed a correlation between ozone levels, voltage, and load, indicating potential dielectric defects.
In [10], online-obtained PRPD (phase-resolved partial discharge) maps and ozone measurements at BC Hydro’s Peace Canyon hydropower plant are presented. A graphical representation illustrates the ozone concentration around 360 degrees of a unit from the hydrogenerator, with sensors positioned at both the top and bottom sections of each cooler.
In [11,12], a laboratory experiment was conducted to investigate the distribution and behaviour of ozone in proximity to the stator winding and inside the generator core. Subsequently, ozone measurements were taken at the Shipsaw barrage, with sensors placed on the radiators of the generating units, and at the Isle-Maligne hydroelectric plant, with sensors positioned in openings on the outer shell. Ozone mapping around the generators was reported, and in one instance, it was possible to identify the source of localised PD activity.
In [13], a study was conducted to lower the elevated ozone concentration detected within hydrogenerators to a safe level for workers (less than 100 ppb). The research revealed that the ozone concentration in hydrogenerators is influenced by the adjustment of the louvres and the ventilation mode of the power plant.
In [14], a diagnostic software application for hydroelectric generators named MIDA version 1.984 is introduced. This application comprises modules that provide information such as PRPD measurements, Partial Discharge Analysis (PDA), and ozone concentration mapping around the generators, among other features.
In [15], the mechanisms responsible for triggering partial discharges (PDs) in hydrogenerators are identified. Various methods for PD detection are discussed, including ozone monitoring. It is noted that in the case of open ventilated machines, the ozone sensors are typically positioned on the radiators. However, for totally enclosed motors and generators, a hole is drilled in the machine housing at a location that facilitates proper airflow and sensor placement. The study reports that ozone concentrations exceeded 75 ppm in some instances.
In [16], the paper delves into the factors underlying surface partial discharges and provides detailed descriptions of detection methods. These methods encompass offline techniques, including local visual inspections and electrical assessments, as well as online procedures such as PRPD analysis and ozone measurements. Furthermore, in [16] it is also suggested that the ozone monitors measure overall ozone concentrations, serving as indicators of the collective PD levels resulting from winding faults.
Another knowledge field that plays a fundamental role in analysis of physics phenomena, and by consequence reducing costs of experimentation procedures and improving operation safety, is the realm of numerical modelling of hydrogenerators. Both two- and three-dimensional models have been developed in various areas of study [1,17,18,19,20,21,22]. Those models employ the finite element method and encompass electromagnetic analysis [17,19], thermal analysis [18,20,21], and mechanical analysis [22]. In [18], a two-dimensional computational fluid dynamics (CFDs) model is incorporated into their thermal model. To the best of our knowledge, there are currently no scientific papers that present a numerical model encompassing turbulent fluid dynamics for the entire 3D structure of a hydrogenerator.
In this paper, the authors develop an unprecedented 3D fluid dynamic model to simulate ozone transport from localised sources in a complete representation of an operational hydrogenerator. The model has a high level of geometric detailing and includes a new approach to reduce computational requirements for representing radiators. This level of detail allows observing the influence of the stator and the arrangement of the stator bars on the airflow and ozone transport from partial discharge sources. The influences from other components of the hydrogenerator (rotor, radiators, air directors, and walls) are also observed and analysed. The obtained ozone distribution profiles provide useful information to design adequate ozone sensing systems using, for instance, arrays of ozone sensors.
This study introduces a comprehensive numerical model of a complete generating unit at the Campos Novos Brazilian hydroelectric power plant. This model is designed to investigate and elucidate the gas flow within the enclosed structure and the ozone concentrations in and around the generator. In Section 2, we provide a theoretical review featuring the essential fluid dynamics equations. In Section 3, the description of the novel numerical model developed in this study is presented. Section 4 showcases the outcomes of our three-dimensional model, accompanied by a discussion on the findings. Finally, Section 5 presents our conclusions.
2. Theoretical Review
2.1. Partial Discharges in Hydrogenerators and Ozone Production
2.1.1. Partial Discharges
Partial discharge (PD) is a phenomenon characterised by dielectric breakdown within the insulation of electrical machines operating under high-voltage conditions. PDs can manifest in various forms, each with its own distinct characteristics and consequences [23,24].
Internal discharges arise due to imperfections in insulation, either present during manufacturing or developed over time due to continuous mechanical, thermal, or electrical stresses during machine operation [6,23]. These stresses lead to the formation of voids and delaminations inside the dielectric material. The presence of these faults further erodes and deteriorates insulation integrity, weakening it and making it more susceptible to breakdown. The formation of voids and delaminations within the dielectric material during the development of internal discharges introduces localised regions of reduced dielectric strength. This compromised insulation region becomes more susceptible to the rise of partial discharges when subjected to high electric fields. Consequently, internal discharges not only weaken the insulation system, but they also serve as precursors to more severe electrical breakdown events. It is usually not associated to ozone generation.
Slot discharges are known as the common failure mechanism of stator winding insutation [25] and manifest when the protective coating of the stator slots becomes compromised, typically as a result of vibrations, displacements, and friction associated with the movement of stator bars. This damage often initiates a gradual erosion process over time, leading to the deterioration of insulation integrity [3,10]. It is noteworthy that the time interval between the initiation of these discharges and the eventual breakdown of the insulation material tends to be relatively short. If there is sufficient air circulation in the slots and PD currents are present, ozone may be produced, which can produce nitric acid that can contribute to the failure process [25]. The occurrence probability of slot-damaging PDs is about 10% since it is linked to the frequency of occurrence of loosening of bars in their positions or in the overhang due to vibrations. This type of fault is less frequent than ageing-related PDs (32%) and PDs associated with contamination of the windings (25%) [26].
Surface discharges occur when the magnitude of the electric field surpasses the dielectric strength of the surrounding air. These discharges usually take place on the surface of the electrical insulation near the ends of the windings, normally started by a thermal effect or contamination of the winding end protective coating, which contribute to the degradation of insulation and can lead to insulation breakdown if left unaddressed. An electron avalanche can increase along the material surface if the voltage source remains on [27]. Since PDs occur in air, ozone is produced [16].
Discharges caused by contaminant particles occur when small conductive particles collect on the surface of the insulation. The different conductivity and electrical characteristics of the contaminant causes a change in the electric field, increasing the electric stress [28]. This electric stress creates localised regions of PD which produces ozone. These discharges gradually wear down the insulation material, leading to weak points and compromising the overall effectiveness of the insulation system. Contamination of the winding is the second more frequent cause of damaging PDs, with an occurrence probability of approximately 25% [26].
Figure 1 shows the main factors responsible for damaging the insulation systems of hydrogenerators [26]. Note that 60% of such events can be attributed to PDs. Approximately 40% of damaging discharges are related to ozone production (external discharges, in air).
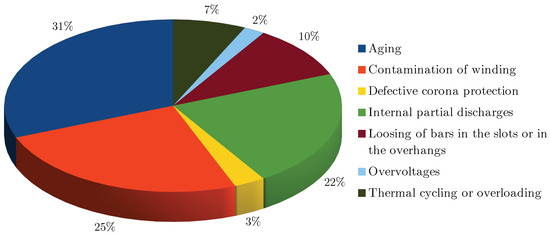
Figure 1.
Respective probabilities of factors leading to damages in insulation [26].
As evident, the occurrence of PDs, especially on the surface of electrical insulation, results in collisions between ions and electrons and the insulation material. These repeated collisions worsen the ongoing discharges and expedite the damaging processes. The integrity of the insulation material is crucial for the proper functioning and longevity of electrical machines. Therefore, it can be stated that the lifespan of these machines often relies on the health and reliability of the insulation. This deterioration can lead to significant economic losses due to compromised machine performance and increased maintenance and repair costs. Thus, ozone monitoring can be seen as a complementary tool for preventing the emergence of severe PD events. Due to its critical impact on the performance of hydrogenerators, standardised methods have been developed and implemented for the detection of PDs [29]. Ongoing research continues to explore new techniques for the precise detection and measurement of physical quantities associated with these faults. One noteworthy approach involves monitoring the byproducts generated as a result of PD phenomena, such as ozone.
2.1.2. Partial Discharges and Ozone Production
Depending on the location and materials involved, a partial discharge can result in various chemical byproducts within the hydrogenerator environment. When a PD occurs in an exposed area, where an ionised channel is in contact with the air, the detection of ozone serves as a valuable tool for detecting and identifying dielectric failures. This method relies on the principle that PD events generate electrical discharges with sufficient energy to initiate appreciable levels of electrochemical reactions in the surrounding air. In such cases, the chemical reactions
take place [1,4]. This ionization process leads to the formation of ozone molecules , which can be detected. Ozone concentrations in air are typically measured using electrochemical or ultraviolet ozone sensors.
2.2. Mass Conservation Law for Ozone
Given that ozone is the sole chemically diluted species under analysis in the air, the mass conservation law [30] is expressed by
where
In (2) and (3), is the diffusion flux vector field, given in mol/(ms), c is the molar concentration for the species, given in mol/m3, D is the diffusion coefficient (m/s), R is the molar rate of species production per unit volume, given in mol/(ms), and is the average mass velocity vector field (m/s).
In a steady-state, there is no change in the concentration c with respect to time t. Therefore, from (2), we can derive the steady-state equation
which is numerically solved in this work by using the finite element method [31].
2.3. Parameters of Ozone Fluid Dynamics
The ozone reaction rate R (mol/ms) can be calculated from the ozone yield , the power of discharges P, the ozone molar mass g/mol, and the volume of the region where ozone is generated (where the partial discharges occur). According to [32,33], it can be calculated by
The net flux of ozone deposition on surfaces [34] is given by
where is the mass accommodation coefficient of ozone to the deposition surface, C is the ozone concentration, l is the mean molecular free path (6.5 × 10 m, at 293 K and 1 atm), and is the Boltzmann velocity for ozone. Boltzmann velocity is given by
where JKmol is the universal gas constant and T is temperature (given in Kelvins). The ozone diffusion coefficient D in (3) is 1.82 × 10 m/s.
The mass accommodation coefficient depends on the surface material. The values of the parameter were measured in experiments conducted in the scientifc literature for different materials. The values used in this work are shown in Table 1. For epoxy paint, a typical value of was adopted for latex paint, since elastomeric latex is dispersed in the epoxy resin for the elasticization of epoxy binders that provides elevated crack resistance and viscosity of fracture [35].

Table 1.
Values of adopted for different materials in our numerical model.
3. The Novel Hydrogenerator Numerical Model
3.1. Geometry and Materials
The numerical model was developed using COMSOL Multiphysics software version 5.5. The hydrogenerator model is based on a generating unit of the Campos Novos brazilian hydroelectric power plant. Figure 2 shows the hydrogenerator structure and Table 2 lists its components, structural parts, materials, and figures with geometrical details.
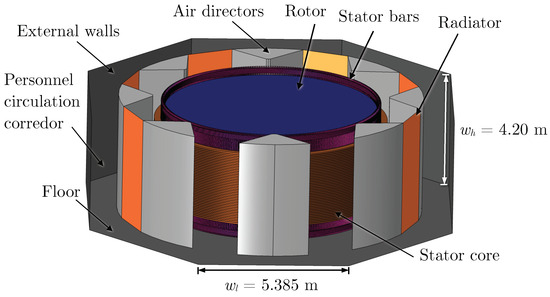
Figure 2.
Overview of the finite element model of the hydrogenerator: labeling of the structural parts. Wall height and width are provided.

Table 2.
The represented components and structural parts of the hydrogenerator, materials, and geometric details.
The external walls have an octagonal shape with edges measuring m and m (Figure 2). The stator bars measure m in height and mm in length. Representations of a bar and stator geometry, as defined in the numerical model, are illustrated in Figure 3. The stator core has a minor radius of m, a major radius of m, and comprises forty-two stages of magnetic steel laminations, each measuring mm in thickness and spaced at intervals of mm for ventilation. Each stage of the stator core features grooves measuring mm mm and teeth measuring mm mm (Figure 4).
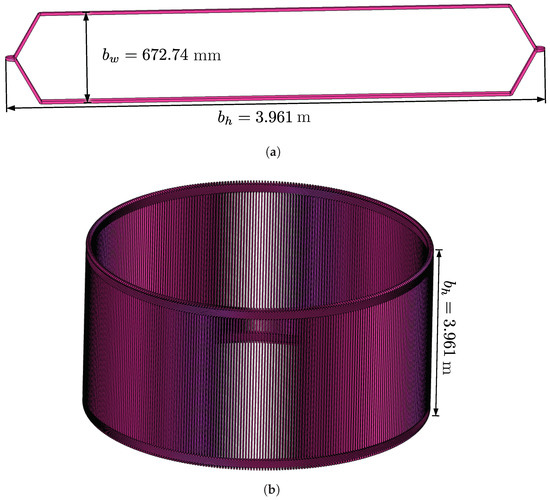
Figure 3.
Hydrogenerator stator bars and their dimensions: (a) the coil-type bar model and (b) all the 378 stator bars as arranged in the model of the hydrogenerator. Dimensions and are provided.
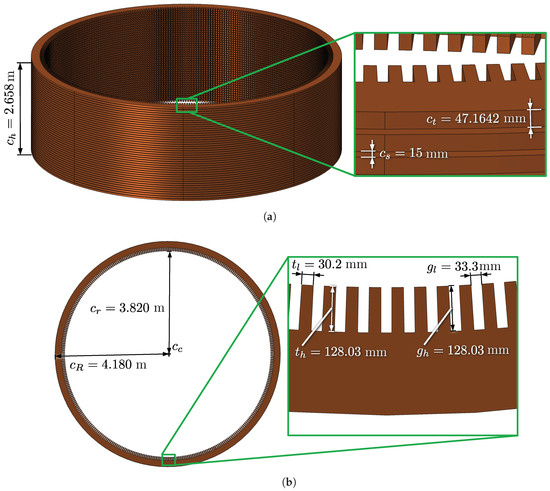
Figure 4.
Hydrogenerator stator core and its dimensions: (a) perspective view and (b) top view. Dimensions , and are given.
The air directors have a wedge-like shape, with eight units encircling the generator to guide air flow from the rotor to the radiators. These air directors possess lateral edges of m in length, external edges at radius m, and a height of m (Figure 5). Finally, the rotor is represented as a cylinder with height m and radius m. There are a total of eight radiators, each having a width m and height m (Figure 5). For the numerical model, the thickness of the radiator sheets is disregarded, with its contribution considered via boundary conditions.
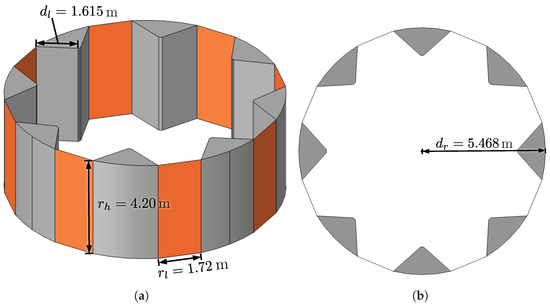
Figure 5.
Hydrogenerator air directors and radiator: (a) perspective view and (b) top view. The dimensions , , , and are given.
3.2. Boundary Conditions
At the lateral surface of the rotor, air velocity boundary conditions are applied to simulate the air angular and radial velocities at the lateral vicinity of the rotor, as detailed in [18]. Air angular velocity is, naturally, due the rotor revolutions. Radial velocity is due to the inter-pole ventilation. The rotor itself rotates at a constant speed of 200 RPM, resulting in an air angular velocity of 87.344 m/s at the lateral surface. Radial velocity data were obtained through experimental measurements within the radiator region of an actual machine, yielding an average speed of 3 m/s. Consequently, on the rotor’s lateral surface, the radial velocity is set to 2.2 m/s. The combined effect of this radial velocity and the gas transport contained by the air directors results in an average airflow speed of 3 m/s in the radiator regions.
The radiators are modelled by using a wire gauze screen model with the turbulent flow physics and flux discontinuity equivalent numerical model to transport diluted species through the surfaces that represent the radiators. The screen boundary condition is used when a fluid passes through a wire gauze. A resistance is created by gauze, which suppresses the tangential component of velocity of the gas that enters the screen [42]. This resistance depends on screen solidity (ratio of blocked area to the total area) and the Reynolds number, which in turn depends on the diameter d of the wires forming the screen. The expression used to represent this phenomenon via pressure drop is
where is the fluid density, u is the velocity of the fluid, and K is the resistance coefficient [43], which is commonly defined as
where
In (9) and (10), is the Reynolds number, d is the diameter of the wires, and v is the fluid kinematic viscosity.
The flux discontinuity boundary condition in transport of diluted species is defined by
where is the normal vector to the boundary surface (radiator), is the diffusion flux vector, is the average mass velocity vector, c is the molar concentration, and is the variation in total flux at the radiator surface as the gas moves from the upstream side (pre-radiator) to the downstream side (post-radiator).
A comparative test is conducted to determine the numeric values of the models’ parameters. Simulations are performed with a reduced numerical analysis region while maintaining the dimensions of the radiator. Two numerical scenarios are considered: one with the actual geometry of the radiator, representing the material stack, and another with an equivalent plane that incorporates the model’s screen and flux discontinuity. The configuration that presents a result similar to the realistic geometry is found to be and m for the screen in turbulent flow and mol/(ms) for the flux discontinuity in transport of diluted species. While requiring much less computational resources, the equivalent model agrees with the radiator full model. The obtained validation results are presented in Appendix A.
Surface reactions are modelled on the surfaces of all materials, where (6) is used. The parameter of each material in the model is given in Table 1.
The ozone sources are applied in typical regions of occurrence of partial discharges in hydrogenerator stator windings (Figure 6), representing surface contamination or coating degradation. In the numerical model, prisms are placed to represent PD regions associated with twelve ozone sources with different volumes.
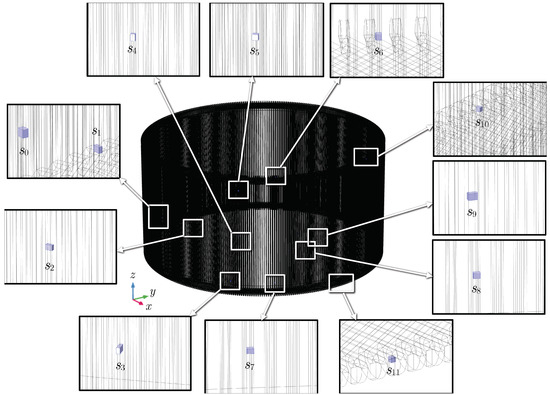
Figure 6.
Source positioning (and their labels) in hydrogenerator stator bars.
In this work, ozone sources on the stator bars are categorised into three height groups, according to their z-coordinates: bottom sources ( mm), intermediary sources ( mm and m), and top sources ( m). The height categorisation and sector in which each source is located are defined in Table 3. The molar rate of ozone production per unit volume mol/(ms) is applied to all sources. This way, the source regions with a volume of 9090 mm (source is used as reference) have an average volumetric concentration of 33,000 ppb, which is an ozone concentration found in the vicinity of hydrogenerators stator bars [11,12]. Table 4 presents the characteristics of each source (from to ): dimensions, volume, and ozone average volumetric concentration. Note that the average volumetric concentration in each prismatic source is proportional to the source volume.

Table 3.
Ozone source locations in simulations A to D: vertical and angular coordinates, height category, and sectors.

Table 4.
Volume and ozone average volumetric concentration for each source (simulations A to D).
3.3. Finite Element Mesh and Computational Resources
The computational mesh conceived for performing the simulations is shown in Figure 7. The mesh is designed in order to use nearly all the capacity of the available computers. This way, a predefined calibration method is used for fluid dynamics from COMSOL Multiphysics. With such a calibration procedure, the average element quality is 0.4107 and the number of tetrahedral elements that compose the mesh is 6,422,513 with 2,035,250 triangles, 695,575 edge elements, and 152,260 vertex elements. For the prisms that represent the sources, the maximum edge length of the mesh elements is 2 mm, so the mesh is very fine in the source regions (Figure 8).
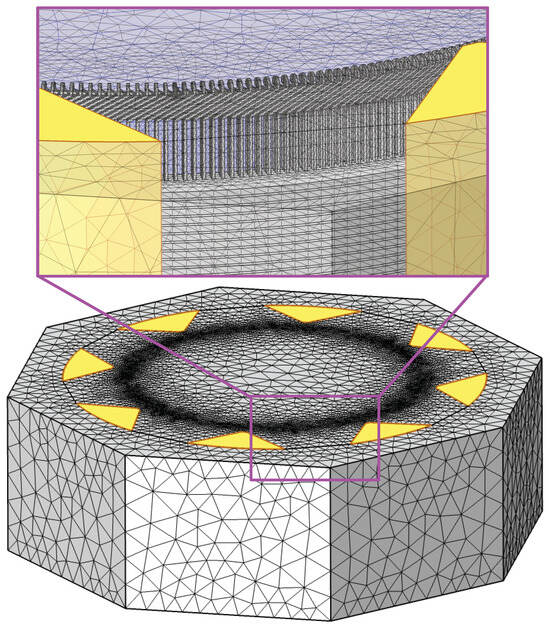
Figure 7.
Overview of the finite element mesh conceived for representing the hydrogenerator structure. Yellowish regions are air directors.
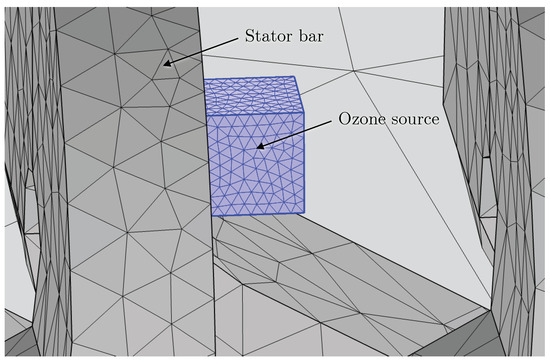
Figure 8.
Part of the conceived computational mesh for representing ozone sources (highlighted in blue) and stator bars.
Three workstations are employed to execute the simulations, each featuring an AMD Ryzen 9 5950X 16-Core Processor with 128 GB of RAM. All three computers operate in parallel for each simulation. The total runtime is 14 h 4 min and 14 s, with each simulation requiring approximately 123 GB of RAM per computer.
4. Results and Discussion
In this section, we present the numerical results. Each radiator is assigned with a specific label, from to , as illustrated in Figure 9, facilitating visualisation of respective ozone concentrations on the radiator surfaces. Understanding the results within the personnel circulation corridor is also particularly significant, as this area permits human traffic and offers feasible locations for the placement of ozone sensors for PD monitoring. It is worth noting that the maximum and average ozone concentrations in the corridor are calculated numerically in this work encompassing all the 360° around the hydrogenerator and spanning its entire height. Similarly, spatial average ozone concentration on a given radiator is obtained by averaging the gas concentration over the surface of that radiator.
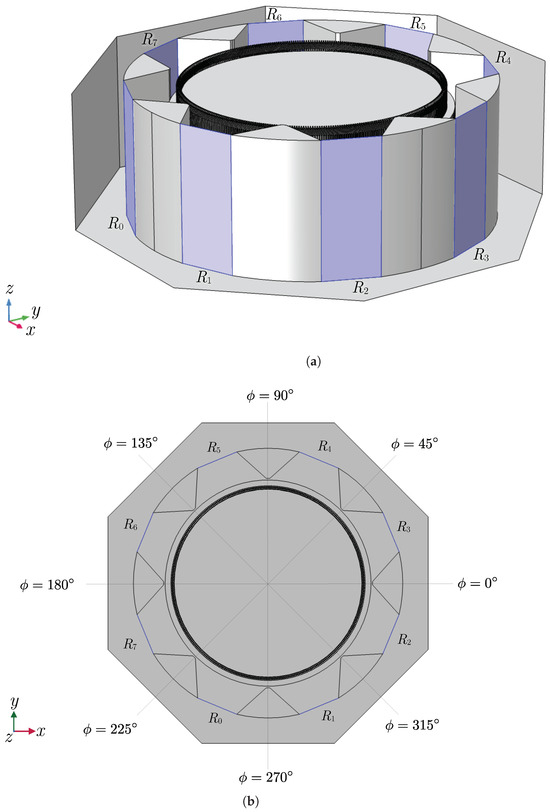
Figure 9.
Labels of each hydrogenerator radiator and angles of reference: (a) perspective view and (b) top view. Radiators are seen with shades of blue.
We conducted four simulations, labeled A, B, C, and D. In simulation A, nine ozone sources were activated (with sources , , and deactivated). For simulation B, ten sources were active (with sources and turned off). In simulation C, eleven sources were active (with source turned off), and simulation D had all sources activated (see source placement in Figure 6). The perspective views of ozone distribution for each simulation are presented in Figure 10 and Figure 11. Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 illustrate the velocity vector field and its impact on ozone flow within various regions of the hydrogenerator. Vector sizes are represented on a logarithmic scale. Subsequently, we present the ozone distributions on the radiator surfaces for each simulation, depicted in Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21.
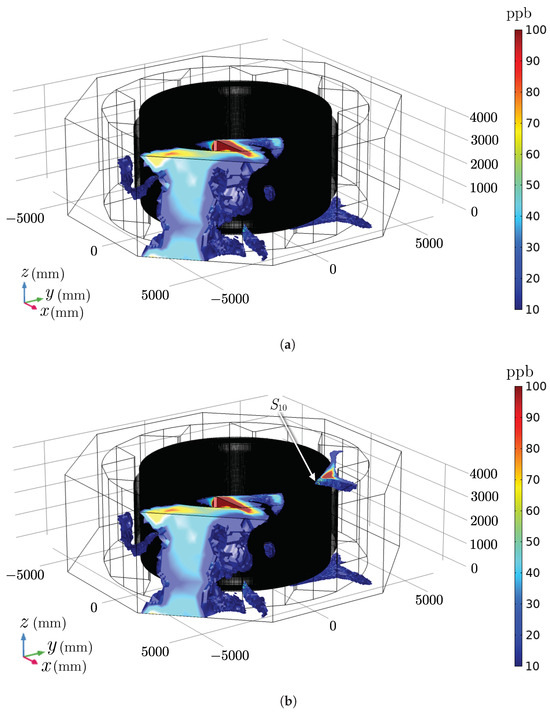
Figure 10.
Ozone concentration (ppb) overview in the numerical model of the hydrogenerator for simulations (a) A and (b) B (with source additionally activated).
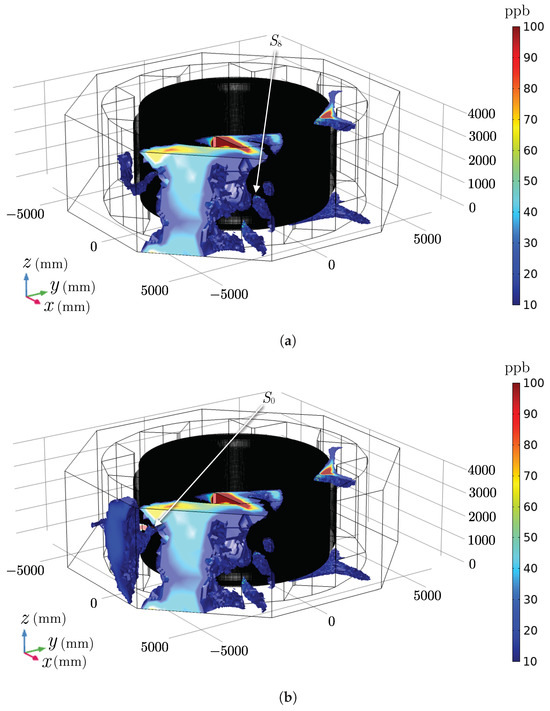
Figure 11.
Overview of ozone concentration (ppb) in numerical model of hydrogenerator in simulations: (a) C (source additionally activated) and (b) D (source additionally activated).
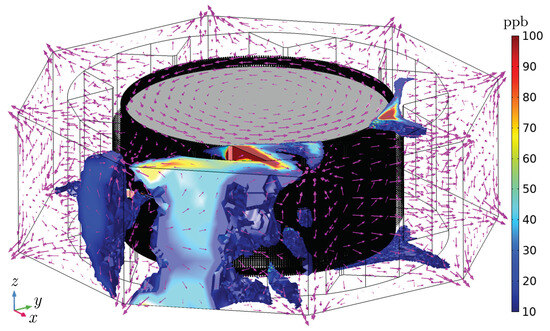
Figure 12.
Ozone concentration (ppb) overview in the numerical model of the hydrogenerator for simulation D (including vector velocity field with log-scale vector sizes).
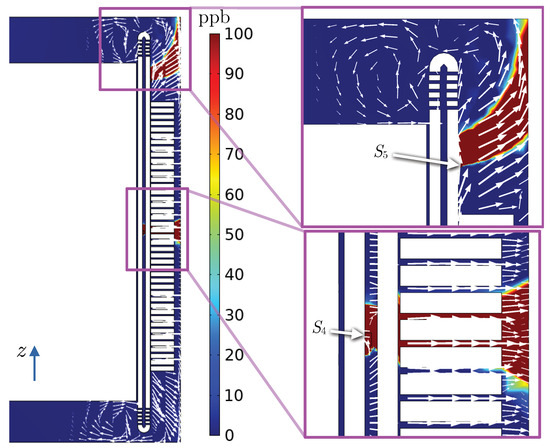
Figure 13.
Ozone distribution (ppb) and velocity field on the vertical plane perpendicular to sources and (simulation D, °).
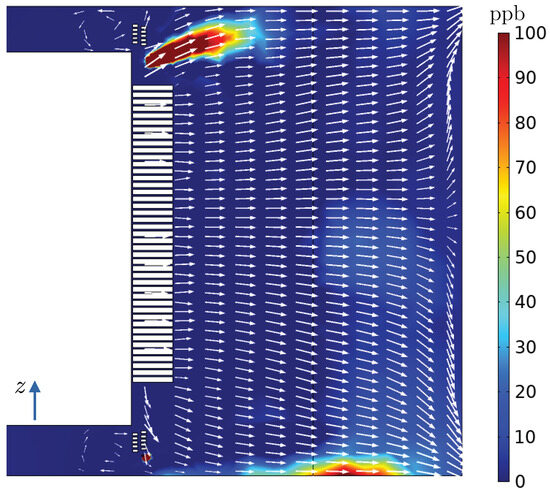
Figure 14.
Ozone distribution (ppb) and velocity field on the vertical plane perpendicular to radiator (simulation D, °).
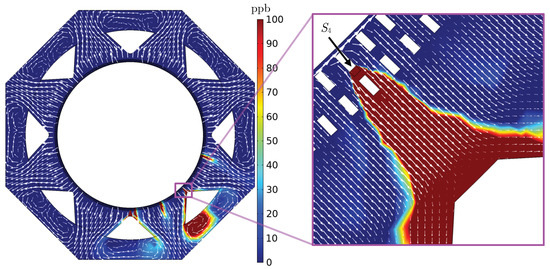
Figure 15.
Ozone distribution (ppb) and velocity field on the horizontal plane perpendicular to source (simulation D, m).
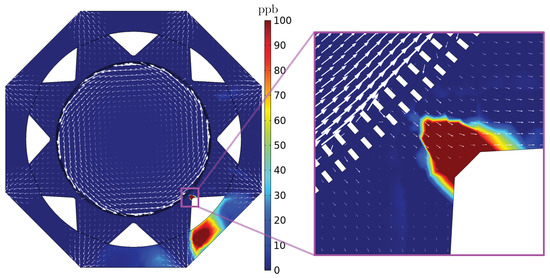
Figure 16.
Ozone distribution (ppb) and velocity field on a horizontal plane at the top region of the hydrogenerator (simulation D, m).
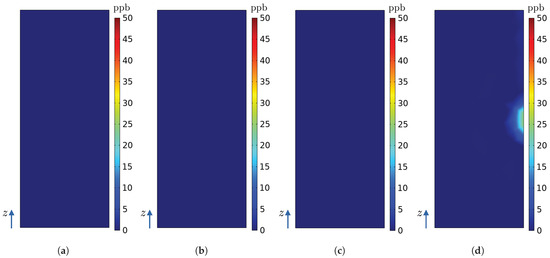
Figure 17.
Ozone concentrations (ppb) on the surface of radiator in the numerical model of the hydrogenerator for simulations (a) A, (b) B, (c) C and (d) D.
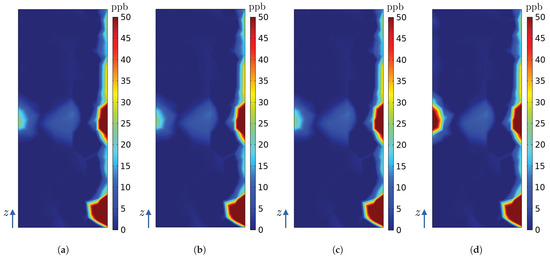
Figure 18.
Ozone concentrations (ppb) on the surface of radiator in numerical model of the hydrogenerator for simulations (a) A, (b) B, (c) C and (d) D.
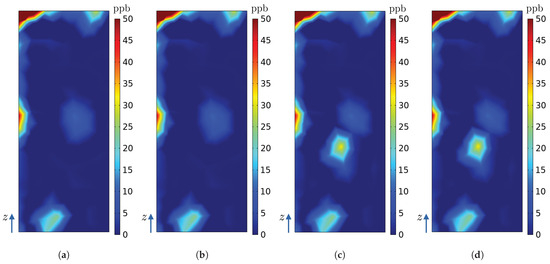
Figure 19.
Ozone concentrations (ppb) on the surface of radiator in the numerical model of the hydrogenerator for simulations (a) A, (b) B, (c) C, and (d) D.
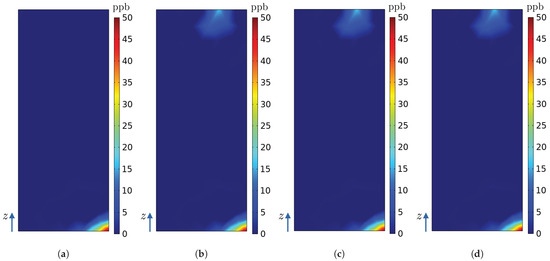
Figure 20.
Ozone concentrations (ppb) on the surface of the radiator in numerical model of the hydrogenerator for simulations (a) A, (b) B, (c) C, and (d) D.
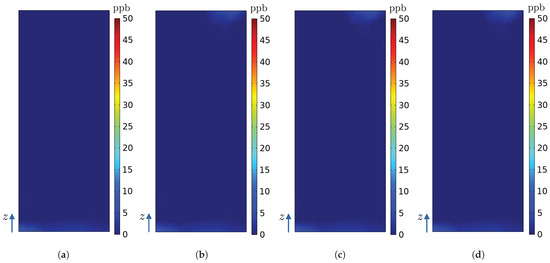
Figure 21.
Ozone concentrations (ppb) on the surface of the radiator in the numerical model of the hydrogenerator for simulations (a) A, (b) B, (c) C, and (d) D.
The results are presented in both 3D view and top view, displaying ozone concentrations starting from 10 ppb, which is the typical lower limit of detection for electrochemical ozone sensors. In Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, the colour map is set within the range of 10 to 100 ppb to enhance concentration visualization. However, it is important to note that the colour red represents values equal to or exceeding 100 ppb, as indicated in the respective figure captions. Similarly, in Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21, the colour map is configured for values in the range of 0 to 50 ppb, with the colour red indicating concentrations equal to or surpassing 50 ppb.
Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16 highlight the variation in the predominant component of the velocity field within the hydrogenerator, depending on the analysed height. In the central heights ( mm and mm), the velocity field is primarily radial, with minimal contributions from azimuthal and vertical components, as depicted in Figure 12, Figure 13, Figure 14 and Figure 15. Conversely, in the top and bottom regions ( mm or mm) of the hydrogenerator, azimuthal flow predominates, with notable influences from vertical components, as shown in Figure 12, Figure 13 and Figure 14 and Figure 16.
By analysing Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21, it is possible to observe the influence of the activation of each source. The effect of the first source activation (source ) is seen in Figure 10a,b, Figure 20a,b and Figure 21a,b. As is a source located at the upper region of the stator bar on sector , there is a great influence of the azimuthal component of the velocity (Figure 12, Figure 13 and Figure 14 and Figure 16), thus causing ozone to be carried to other sectors of the hydrogenerator, following the direction of rotation of the rotor (counterclockwise). Thus, it is possible to see contributions of this source in the ozone concentration of sectors and .
To verify the effect of activating the second source (source ), the following pairs of figures are analysed: Figure 10b, Figure 11a and Figure 19b,c. As source is a central source on sector , the ozone generated is mainly influenced by the radial velocity component (Figure 12, Figure 13, Figure 14 and Figure 15), which means that the greatest contribution of this source is in the sector at which it is located (sector ).
Finally, we assess the impact of the third and last source that is activated, , through the following pairs of figures: Figure 11a,b, Figure 17c,d and Figure 18c,d. Similar to , is positioned centrally and thus primarily influenced by the radial velocity component, as depicted in Figure 12, Figure 13, Figure 14 and Figure 15. However, being located between two sectors, its contribution to ozone concentration is evident in both of the respective sectorial radiators and . For a comprehensive overview of the maximum and average ozone concentration values across all simulations for each radiator and within the personnel circulation corridor, refer to Table 5.

Table 5.
Ozone concentrations (ppb) in personnel circulation corridor and on surface of radiators for each simulation (from A to B).
To compare the maximum and spatial average values of ozone concentration obtained in simulations A, B, C, and D, the equations
and
are used, where is the percentage difference between maximum ozone concentrations and obtained, respectively, in simulations i and j, and is the percentage difference between average ozone concentrations and obtained in simulations i and j, respectively. Table 6 and Table 7 show the percentage differences between ozone concentrations among the simulations.

Table 6.
Percentage differences between the maximum ozone concentrations among the simulations.

Table 7.
Percentage differences between the spatial average ozone concentrations among the simulations.
Table 6 and Table 7 provide a comprehensive understanding of how the placement of ozone sources within the hydrogenerator affects both maximum and average ozone concentrations. Analysis is performed across simulations A, B, C, and D.
Regarding maximum ozone concentration differences, the personnel circulation corridor demonstrates very small percentage differences between simulations A and B (0.0239%) and between simulations A and C (0.0095%). Simulation D, when compared to simulation B within the corridor, reveals an identical maximum ozone concentration. However, for radiator , simulation D exhibits a substantial 100% difference in maximum ozone concentration compared to simulation A for this specific radiator because concentration obtained from simulation A is zero and from simulation D it is 25 ppb. Radiators to show a maximum percentage difference of approximately 1.17% across all simulations due to ozone source activation.
Turning to spatial average ozone concentration differences, the personnel circulation corridor again shows minimal discrepancies between simulations A and B (0.07%) and between simulations A and C (0.29%). However, simulation D, when compared to simulations A and B within the corridor, displays significant 9.88% and 11.04% differences in average ozone concentrations. Radiators to now show important percentage differences for average concentrations, from 9.98% to 88.15%. Percentage differences under 1% are also seen.
These findings emphasise the critical influence of ozone source placement within the hydrogenerator, particularly in areas like the personnel circulation corridor and especially on radiators. Average concentrations show more important percentage differences since high concentration spots are seen on radiators as sources are activated, indicating that multiple ozone sensors per radiator might be necessary to properly monitor the gas concentrations over time.
Using the knowledge gained from the previous four simulations, we conduct two additional simulations, denoted as E and F, to explore the impact of ozone sources distributed throughout all sectors of the hydrogenerator. Simulation E involves the activation of 101 sources evenly distributed over the entire 360-degree span of the hydrogenerator stator bars. In simulation F, we introduce an additional nine sources that are simultaneously activated, resulting in a total of 110 sources. This setup allows us to investigate the effects of activating multiple sources concurrently. The nine sources introduced in simulation F are depicted in Figure 22, Figure 23 and Figure 24, and detailed information regarding their positions, dimensions, and ozone concentration values is provided in Table 8 and Table 9.
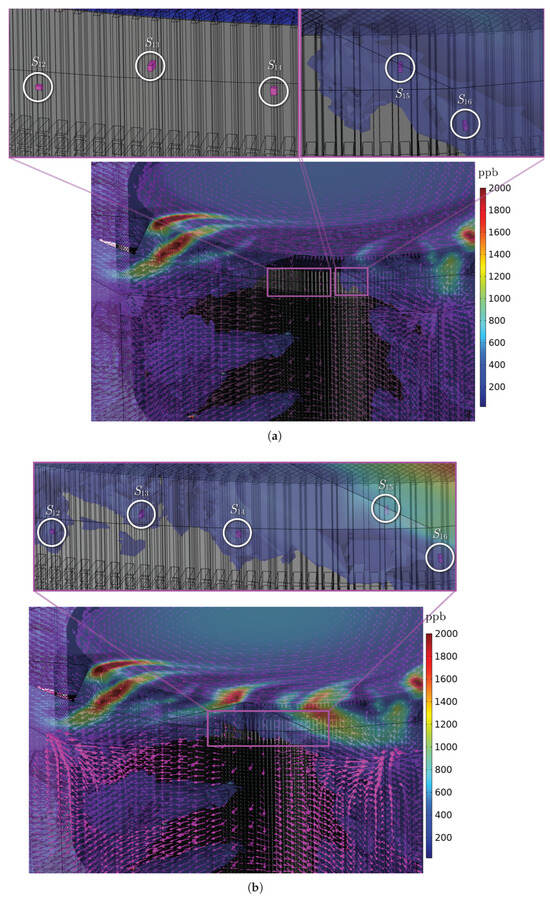
Figure 22.
Influence of sources (°) to (°) in simulations (a) E and (b) F.

Figure 23.
Localized influence in the region of sources (°) and (°) in simulations (a) E and (b) F.
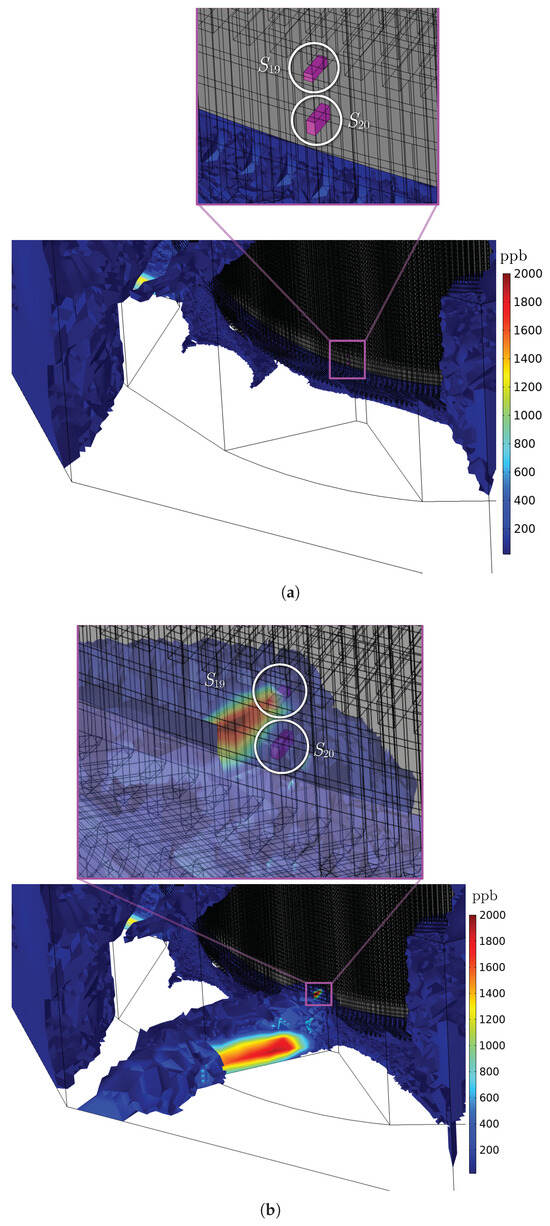
Figure 24.
Localized influence in the region of sources (°) and (°) in simulations (a) E and (b) F.

Table 8.
Location of each ozone source in simulations E and F, their height class, and sector.

Table 9.
Volume and ozone average volumetric concentration for each source in simulations E and F.
To make the simulations feasible on the available computing hardware, we had to make adjustments to the mesh resolution in the region of the sources. We allowed COMSOL automatic mesh generation to work across the entire geometry, resulting in a computational mesh consisting of 6,042,019 elements. This approach made it possible to run the simulations using 118 GB of RAM.
The results of simulations E and F are presented in Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28 and Figure 29. Figure 22, Figure 23 and Figure 24 delve into the localised influence of the activated sources, Figure 25 provides an overview of the ozone distribution, and Figure 26, Figure 27, Figure 28 and Figure 29 present the ozone distributions on the radiator surfaces. In Figure 22, Figure 23, Figure 24 and Figure 25, the colour scale ranges from 20 to 2000 ppb to enhance the visibility of concentration variations. Consequently, the red colour represents values equal to or exceeding 2000 ppb. Similarly, in Figure 26, Figure 27, Figure 28 and Figure 29, the colour scale spans from 0 to 300 ppb.
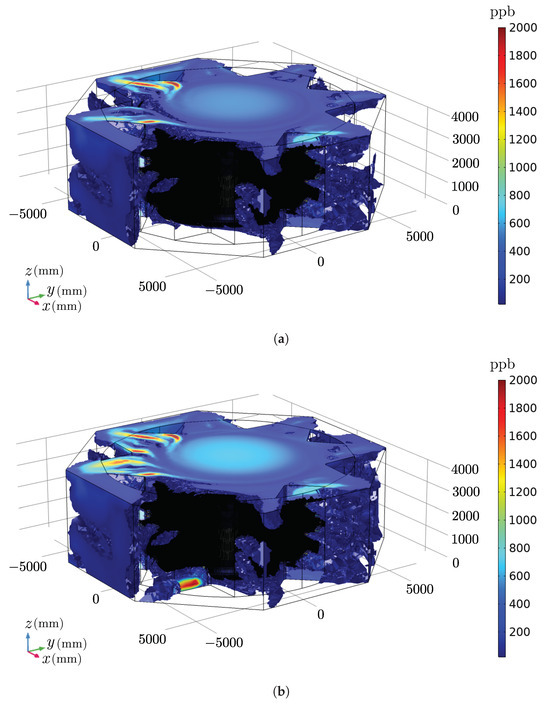
Figure 25.
Perspective view of ozone concentration (ppb) in numerical model of hydrogenerator in simulations (a) E and (b) F.
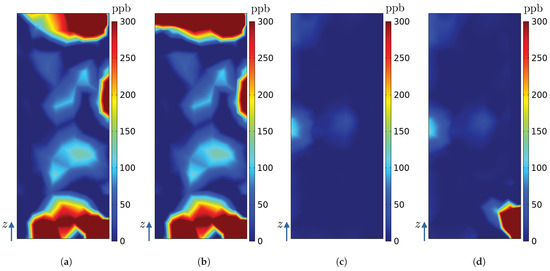
Figure 26.
Ozone concentration (ppb) on the surfaces of the radiators and in the numerical model of the hydrogenerator: (a) (simulation E), (b) (simulation F), (c) (simulation E), and (d) (simulation F).
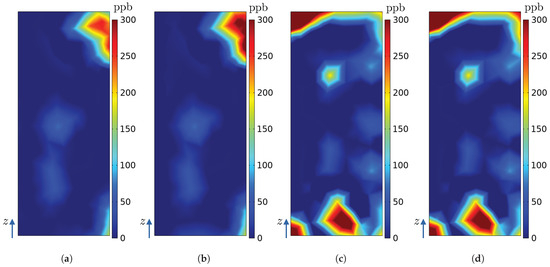
Figure 27.
Ozone concentration (ppb) on the surfaces of the radiators and in the numerical model of the hydrogenerator: (a) (simulation E), (b) (simulation F), (c) (simulation E), and (d) (simulation F).
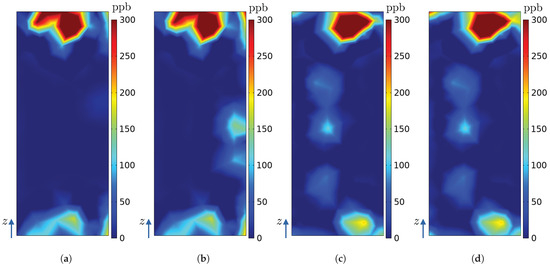
Figure 28.
Ozone concentration (ppb) on the surfaces of the radiators and in the numerical model of the hydrogenerator: (a) (simulation E), (b) (simulation F), (c) (simulation E), and (d) (simulation F).
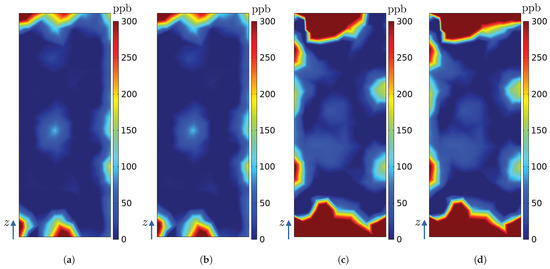
Figure 29.
Ozone concentration (ppb) on the surfaces of the radiators and in the numerical model of the hydrogenerator: (a) (simulation E), (b) (simulation F), (c) (simulation E), and (d) (simulation F).
Even with several ozone sources activated at the same time, by analysing the results, the same pattern obtained in simulations A to D can be seen, i.e, even if there are new sources of ozone, the ozone advection will adapt to an established general flow pattern, which is the same in all simulations, as the rotor geometry and operating conditions are not changed. This can be explained because in all simulations (A to F) the velocity field is the same because the geometry of the problem remained unchanged. Sources to are positioned at the top region of the hydrogenerator, so they are greatly influenced by azimuthal velocity and vertical components (Figure 22 and Figure 25). In addition, source is close to the intermediate region between R0 and R7, which contributes to the ozone generated by it being transported through trajectories that reach the surface of more than one radiator.
Sources and are positioned at half height of the hydrogenerator, so the ozone generated by them is mainly influenced by the radial component of velocity, having its greatest relevance in the sector in which they are positioned (Figure 23 and Figure 25). In such cases, high ozone concentration spots are seen in radiators’ surfaces, as previously discussed, which tend to be radially aligned to the sources producing the concentration spots on the radiator. This fact suggests that various ozone sensors might be needed per radiator if proper monitoring of PDs is intended, specially when PD pinpointing is of interest.
Finally, the sources and are located at the bottom of the stator bars, which means that there is also a great influence of the vertical and azimuthal velocity components, so their contribution of ozone concentration is seen in more than one radiator (see Figure 24 and Figure 25).
With the ozone concentrations on the surface of the radiators obtained in the simulations and shown in Figure 26, Figure 27, Figure 28 and Figure 29, Table 10 shows the maximum ozone concentration obtained on each radiator surface. Furthermore, a polar graph showing maximum ozone concentration on each radiator is given by Figure 30. The polar graph in Figure 30 is comparable to experimental ozone polar profiles published in [10,11,12], which indicates the ozone of the highest concentrations measured on each radiator of their real-world generating machine.

Table 10.
Maximum ozone concentration on each radiator.
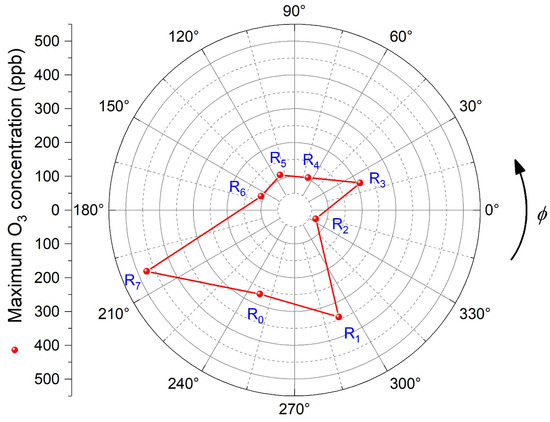
Figure 30.
Maximum concentrations of ozone on the radiators as a function of (numerical model).
5. Conclusions
In this work, fluid dynamic simulations were performed using a computational model developed in this paper based on a complete generating machine of the Campos Novos Brazilian hydroelectric power plant. In order to understand and analyse the fluid dynamics of the gases inside the structure and verify the calculated ozone concentration levels inside and outside the machine, a CFD model representing a unit of the hydroelectric power plant was developed using a finite-element-based software. The analysis of the results was carried out both qualitatively and quantitatively from the rotor, with a radius of 3.8075 m and rotation frequency of 200 RPM, and ozone sources placed over the structure of the stator bars. The average volumetric concentration of 33,000 ppb was used as a basis for sources of 9090 mm. Sources with larger volumes have higher concentrations and sources with smaller volumes have lower concentrations.
The influence of the position of an ozone source on the stator bar of a hydrogenerator was assessed. It was found that sources located at the upper and lower ends of the stator bar are more influenced by the azimuthal component of the velocity field, while those located in the central region are more influenced by the radial component. This means that when analysing the distribution of ozone concentration on the surface of the radiators, detecting ozone in the central regions of the radiator is indicative of the presence of ozone sources radially aligned with the detection site. Ozone detected on the right and left edges of the radiator is influenced by the air directors, which makes the location of the source more complicated. Ozone detected near the upper and lower edges of the radiator can be carried to several other sectors by the azimuthal velocity component. In conclusion, the occurrence of PD (ozone) sources at intermediate heights within the hydrogenerator leads to ozone concentrations primarily influenced by the radial component of velocity. This means that multiple ozone sensors per radiator may be necessary to accurately pinpoint PD occurrences at intermediate heights. However, caution must be taken if there are PD sources at the bottom or top of stator bars or between two radiators, as ozone transport is governed by the azimuthal component of velocity in these cases.
In future works, it is planned to position electrochemical ozone sensors on the radiators of the Brazilian hydroelectric plant Campos Novos for comparison with numerical results and monitoring, mapping, and localising partial discharges.
Author Contributions
Conceptualization, R.M.S.d.O., V.D. and L.D.S.d.A.; methodology, L.D.S.d.A., R.M.S.d.O. and V.D.; software, L.D.S.d.A., G.G.G. and N.M.L.; validation, R.M.S.d.O., L.D.S.d.A. and V. D.; formal analysis, R.M.S.d.O., L.D.S.d.A. and V.D.; investigation, R.M.S.d.O., L.D.S.d.A., V.D., G.G.G. and N.M.L.; resources, V.D.; data curation, G.G.G. and L.D.S.d.A.; writing—original draft preparation, G.G.G. and R.M.S.d.O.; writing—review and editing, R.M.S.d.O., V.D., L.D.S.d.A. and G.G.G.; visualization, G.G.G.; supervision, R.M.S.d.O. and V.D.; project administration, V.D.; funding acquisition, V.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research and the APC were funded by CPFL, ENERCAN, and BAESA via the R&D project 475 with contract number 00642-2905/2019, which is regulated by the ANEEL R&D program. The APC invoice has been paid via FADESP (Fundação de Amparo e Desenvolvimento da Pesquisa).
Data Availability Statement
Data are contained within the manuscript.
Acknowledgments
Authors are grateful to CPFL, ENERCAN, BAESA, and the Federal University of Pará (UFPA) for their support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this appendix, we present benchmark tests of the equivalent screen model of the radiator. The representation of radiators using the screen model is also an unprecedented contribution of this work that made it possible to match the hydrogenerator simulation’s required resources to the available computational capacity and it was based on the theoretical background given in [42,43] as a starting point. The simulations comparing the adjusted parameters of the equivalent screen model with the realistic radiator model (copper sheets representation) results are shown in Figure A1, Figure A2, Figure A3, Figure A4 and Figure A5. Figure A1 shows ozone transmission, for screen and copper sheet models, through the radiator as functions of air velocity.
In Figure A2, Figure A3, Figure A4 and Figure A5, the ventilation velocity is set to 3 m/s, which is the average radial air velocity experimentally measured in the real generator. Figure A2 shows the ozone distributions’ perspective views for the cases where the radiator is represented with the screen model and realistic copper radiator simulations. Figure A3 shows the air velocity field on the -plane crossing the domain in its half. Figure A4 shows the distributions of ozone on the same -plane and cases of Figure A3. Finally, Figure A5 shows the distribution of ozone on the -plane separated by 10 mm from the radiator plane (at the radiator gas output side).
The results shown in this appendix indicate that the equivalent screen model of the radiator is suitable to replace the realistic model and, therefore, it is suitable to represent radiators in the hydrogenerator model. Note that the realistic copper-sheets-based-model would significantly increase the computational resources required to carry out the CFD simulations of the hydrogenerator.
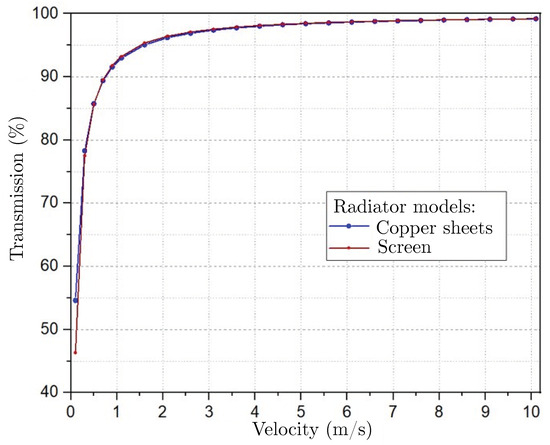
Figure A1.
Ozone transmissions through numerical models of radiators as functions of air velocity: copper sheets and screen models.
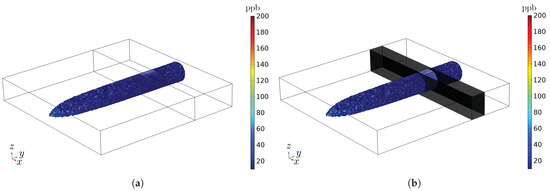
Figure A2.
Perspective views of ozone concentration distributions (ppb) in benchmark simulations obtained with (a) the radiator screen model and (b) the realistic copper representation of the radiator.
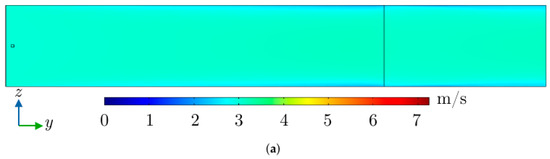
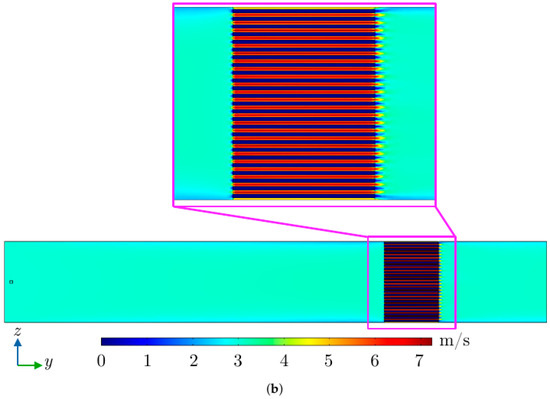
Figure A3.
Magnitude of velocity field (m/s) on -plane in benchmark simulations: (a) radiator screen model and (b) realistic copper representation of the radiator and the source region indicated by the small square at the left side.
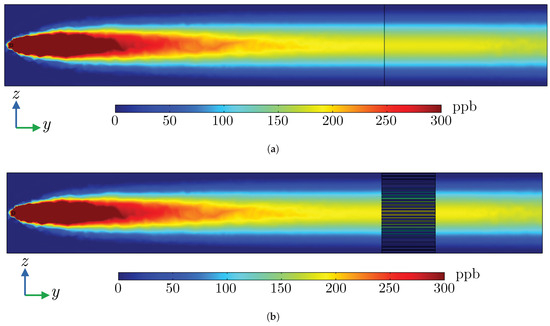
Figure A4.
Ozone concentrations (ppb) on -plane in benchmark simulations: (a) radiator screen model and (b) realistic copper representation of the radiator.
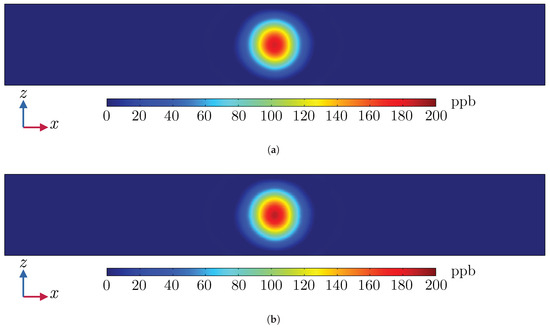
Figure A5.
Ozone concentrations (ppb) on -plane in benchmark simulations: (a) radiator screen model and (b) realistic copper representation of the radiator.
References
- Ehya, H.; Faiz, J. Electromagnetic Analysis and Condition Monitoring of Synchronous Generators; John Wiley & Sons: Piscataway, NJ, USA, 2023. [Google Scholar]
- Hudon, C.; Belec, M.; Levesque, M. Study of slot partial discharges in air-cooled generators. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1675–1690. [Google Scholar] [CrossRef]
- Stone, G.; Maughan, C. Vibration Sparking and Slot Discharge in Stator Windings. In Proceedings of the Conference Record of the 2008 IEEE International Symposium on Electrical Insulation, Vancouver, BC, Canada, 9–12 June 2008; pp. 148–152. [Google Scholar]
- Chen, J.; Davidson, J.H. Ozone Production in the Positive DC Corona Discharge: Model and Comparison to Experiments. Plasma Chem. Plasma Process. 2002, 22, 495–522. [Google Scholar] [CrossRef]
- Hudon, C.; Belec, M. Partial discharge signal interpretation for generator diagnostics. IEEE Trans. Dielectr. Electr. Insul. 2005, 12, 297–319. [Google Scholar] [CrossRef]
- Stone, G.; Wu, R. Examples of stator winding insulation deterioration in new generators. In Proceedings of the 2009 IEEE 9th International Conference on the Properties and Applications of Dielectric Materials, Harbin, China, 19–23 July 2009; pp. 180–185. [Google Scholar]
- Istad, M.; Runde, M.; Nysveen, A. A Review of Results From Thermal Cycling Tests of Hydrogenerator Stator Windings. IEEE Trans. Energy Convers. 2011, 26, 890–903. [Google Scholar] [CrossRef]
- Rodriguez, R.; Rux, L. Ozone Abatement in Air-Cooled Hydroelectric Generators; Technical Report; United States Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1997. [Google Scholar]
- Binder, E.; Draxler, A.; Egger, H.; Hummer, A.; Fuchs, H.R.; Koglek, H.; Müller, F.; Drpic, M.; Hoof, M.; Käfer, R.; et al. Entwicklungen und Nachweisuntersuchungen von Diagnosemethoden für Wasserkraftgeneratoren. E&I Elektrotech. Informationstech. 2000, 117, 794–805. [Google Scholar]
- Belec, M.; Li, S.; Nguyen, D.; Lepine, L.; Guddemi, C.; Lessard-Deziel, D.; Schwartz, T.; Lamarre, L. Investigation and diagnosis of a 184-MVA air-cooled generator heavily affected by slot partial discharge activity. In Proceedings of the 2007 Electrical Insulation Conference and Electrical Manufacturing Expo, Nashville, TN, USA, 22–24 October 2007; pp. 85–90. [Google Scholar]
- Lépine, L.; Lessard-Deziel, D.; Belec, M.; Guddemi, C.; Nguyen, D.N. Understanding ozone distribution inside stator core and measurements inside air-cooled generators to assess partial discharges problems. In Proceedings of the Iris Rotating Machine Conference 2007, San Antonio, TX, USA, 4–7 June 2007; pp. 1–10. [Google Scholar]
- Hudon, C.; Belec, M.; Levesque, M. Using Ozone Measurements to Diagnose Partial Discharge in Generators. Renew. Energy World 2008, 27, 1–7. [Google Scholar]
- Millet, C.; Nguyen, D.N.; Lepine, L.; Belec, M.; Lessard-Deziel, D.; Guddemi, C. Case study-high ozone concentration in hydro generators. In Proceedings of the 2009 IEEE Electrical Insulation Conference, Montreal, QC, Canada, 31 May–3 June 2009; pp. 178–182. [Google Scholar]
- Vouligny, L.; Hudon, C.; Nguyen, D.N. Design of MIDA, a Web-Based Diagnostic Application for Hydroelectric Generators. In Proceedings of the 2009 33rd Annual IEEE International Computer Software and Applications Conference, Seattle, WA, USA, 20–24 July 2009; Volume 2, pp. 166–171. [Google Scholar]
- Stone, G.; Sedding, H. Detection of stator winding stress relief coating deterioration in conventional and inverter fed motors and generators. In Proceedings of the 2016 International Conference on Condition Monitoring and Diagnosis (CMD), Xi’an, China, 25–28 September 2016; pp. 270–273. [Google Scholar]
- Dehlinger, N.; Stone, G. Surface partial discharge in hydrogenerator stator windings: Causes, symptoms, and remedies. IEEE Electr. Insul. Mag. 2020, 36, 7–18. [Google Scholar] [CrossRef]
- Fratila, M.; Benabou, A.; Tounzi, A.; Dessoude, M. Iron Loss Calculation in a Synchronous Generator Using Finite Element Analysis. IEEE Trans. Energy Convers. 2017, 32, 640–648. [Google Scholar] [CrossRef]
- Syaeful Alam, H.; Djunaedi, I.; Soetraprawata, D. Thermal Study for Power Uprating of 400 MW Generator Using Numerical Simulation. Int. J. Mater. Mech. Manuf. 2017, 5, 191–195. [Google Scholar] [CrossRef][Green Version]
- Deaconu, S.; Topor, M.; Tutelea, L.; Nuca, I.; Burduniuc, M. Wind or Hydro Homo-Heteropolar Synchronous Generators: Equivalent Magnetic Circuit and FEM Analysis. MATEC Web Conf. 2018, 210, 1–7. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Y.; Xu, X. Comparisons of Concentrated and Distributed Winding PMSM in MV Power Generation. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 2437–2443. [Google Scholar] [CrossRef]
- Carounagarane, C.; Chelliah, T.R.; Khare, D. Analysis on Thermal Behavior of Large Hydrogenerators Operating with Continuous Overloads. IEEE Trans. Ind. Appl. 2020, 56, 1293–1305. [Google Scholar] [CrossRef]
- de Barros, A.; Galai, A.; Ebrahimi, A.; Schwarz, B. Practical Modal Analysis of a Prototyped Hydrogenerator. Vibration 2021, 4, 853–864. [Google Scholar] [CrossRef]
- Stone, G.C.; Culbert, I.; Boulter, E.A.; Dhirani, H. Electrical Insulation for Rotating Machines, 2nd ed.; IEEE Press Series on Power Engineering; Wiley-Blackwell: Hoboken, NJ, USA, 2012. [Google Scholar]
- Stone, G.C.; Cavallini, A.; Behrmann, G.; Serafino, C.A. Practical Partial Discharge Measurement on Electrical Equipment; Wiley-IEEE Press: New York, NY, USA, 2023. [Google Scholar]
- Stone, G.C.; Maughan, C.V.; Nelson, D.; Schultz, R.P. Impact of Slot Discharges and Vibration Sparking on Stator Winding Life in Large Generators. IEEE Electr. Insul. Mag. 2008, 24, 14–21. [Google Scholar] [CrossRef]
- Sumereder, C. Statistical lifetime of hydro generators and failure analysis. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 678–685. [Google Scholar] [CrossRef]
- Illias, H.; Yuan, T.S.; Bakar, A.H.A.; Mokhlis, H.; Chen, G.; Lewin, P.L. Partial discharge patterns in high voltage insulation. In Proceedings of the 2012 IEEE International Conference on Power and Energy (PECon), Kota Kinabalu, Malaysia, 2–5 December 2012; pp. 750–755. [Google Scholar]
- Dymond, J.; Stranges, N.; Younsi, K.; Hayward, J. Stator winding failures: Contamination, surface discharge, tracking. IEEE Trans. Ind. Appl. 2002, 38, 577–583. [Google Scholar] [CrossRef]
- McDermid, W. IEEE guide for the measurement of partial discharges in AC electric machinery. In Proceedings of the 2012 IEEE International Symposium on Electrical Insulation, San Juan, PR, USA, 10–13 June 2012; pp. 659–660. [Google Scholar]
- Chung, T.J. Computional Fluid Dynamics; Press Syndicate of the University of Cambridge: Cambridge, UK, 2002. [Google Scholar]
- Zienkiewicz, O.; Taylor, R.; Zhu, J. Introduction to the Equations of Fluid Dynamics and the Finite Element Approximation; Elsevier Butterworth-Heinemann: Burlington, MA, USA, 2005; pp. 1–27. [Google Scholar] [CrossRef]
- Buntat, Z. Ozone Generation Using Electrical Discharges: A Comparative Study between Pulsed Streamer Discharge and Atmospheric Pressure Glow Discharge. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2005. [Google Scholar]
- de Oliveira, R.M.S.; Zampolo, R.F.; Alcantara, L.D.S.; Girotto, G.G.; Lopes, F.H.R.; Lopes, N.M.; Brasil, F.S.; Nascimento, J.A.S.; Dmitriev, V. Analysis of Ozone Production Reaction Rate and Partial Discharge Power in a Dielectric-Barrier Acrylic Chamber with 60 Hz High-Voltage Electrodes: CFD and Experimental Investigations. Energies 2023, 16, 6947. [Google Scholar] [CrossRef]
- Cano-Ruiz, J.A.; Kong, D.; Balas, R.B.; Nazaroff, W.W. Removal of reactive gases at indoor surfaces: Combining mass transport and surface kinetics. Atmos. Environ. 1993, 27, 2039–2050. [Google Scholar] [CrossRef]
- Shalin, R.E. Polymer Matrix Composites; Chapman & Hall: Cambridge, UK, 1995. [Google Scholar]
- Mueller, F.X.; Loeb, L.; Mapes, W.H. Decomposition rates of ozone in living areas. Environ. Sci. Technol. 1973, 7, 342–346. [Google Scholar] [CrossRef]
- Simmons, A.; Colbeck, I. Resistance of various building materials to ozone deposition. Environ. Technol. 1990, 11, 973–978. [Google Scholar] [CrossRef]
- Cataldo, F.; Ursini, O. The Role of Carbon Nanostructures in the Ozonization of Different Carbon Black Grades, Together with Graphite and Rubber Crumb in an IR Gas Cell. Fullerenes Nanotub. Carbon Nanostructures 2007, 15, 1–20. [Google Scholar] [CrossRef]
- Reiss, R.; Ryan, P.B.; Koutrakis, P.; Tibbetts, S.J. Ozone reactive chemistry on interior latex paint. Environ. Sci. Technol. 1995, 29, 1906–1912. [Google Scholar] [CrossRef] [PubMed]
- Morrison, G.C. Ozone-Surface Interactions: Investigations of Mechanisms, Kinetics, MassTransport, and Implications for Indoor Air Quality. Ph.D. Thesis, University of California, Santa Barbara, CA, USA, 1999. [Google Scholar]
- Gusakov, A.G.; Voropayev, A.G.; Zheludkevich, M.L.; Vecher, A.A.; Raspopov, S.A. Studies of the interaction of copper with atomic and molecular oxygen. Phys. Chem. Chem. Phys. 1999, 1, 5311–5314. [Google Scholar] [CrossRef]
- Schubauer, G.B.; Spangenberg, W.G.; Klebanoff, P.S. Aerodynamic Characteristics of Damping Screens; Technical Report; National Advisory Committee for Aeronautics: Boston, MA, USA, 1950. [Google Scholar]
- Roach, P. The generation of nearly isotropic turbulence by means of grids. Int. J. Heat Fluid Flow 1987, 8, 82–92. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).