Empirical Degradation Models of the Different Indexes of the Proton Exchange Membrane Fuel Cell Based on the Component Degradation
Abstract
:1. Introduction
2. Simulation of PEMFC Degradation
2.1. Simulation Process and Assumptions
- (a)
- Assuming that each component of the PEMFC undergoes synchronous degradation, i.e., PEM, CL, GDL, and BP are degraded at the same percentage when the PEMFC is operating.
- (b)
- Assuming synchronous degradation of each component parameter, the PEMFC exhibits the most severe degradation.
- (c)
- Assuming that the PEMFC operates at a constant current, all auxiliary subsystems can operate stably. The flow rate, pressure, and temperature of reactants (hydrogen and air), coolant flow rate, and DC/DC load current can remain unchanged.
2.2. Parameters of Each Component under Different Degradation Levels
3. Results and Discussion
3.1. Empirical Degradation Models of the Performance Indexes
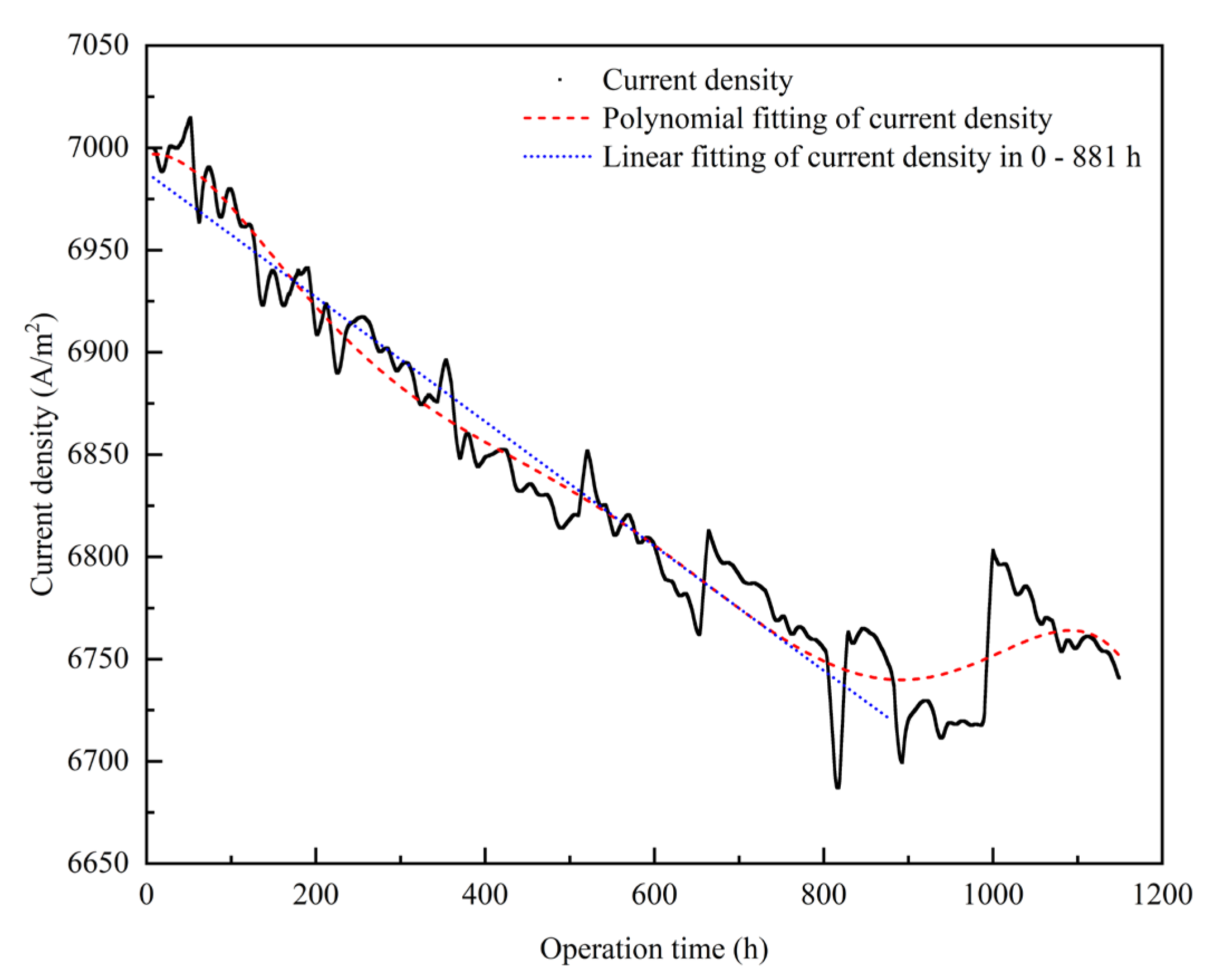
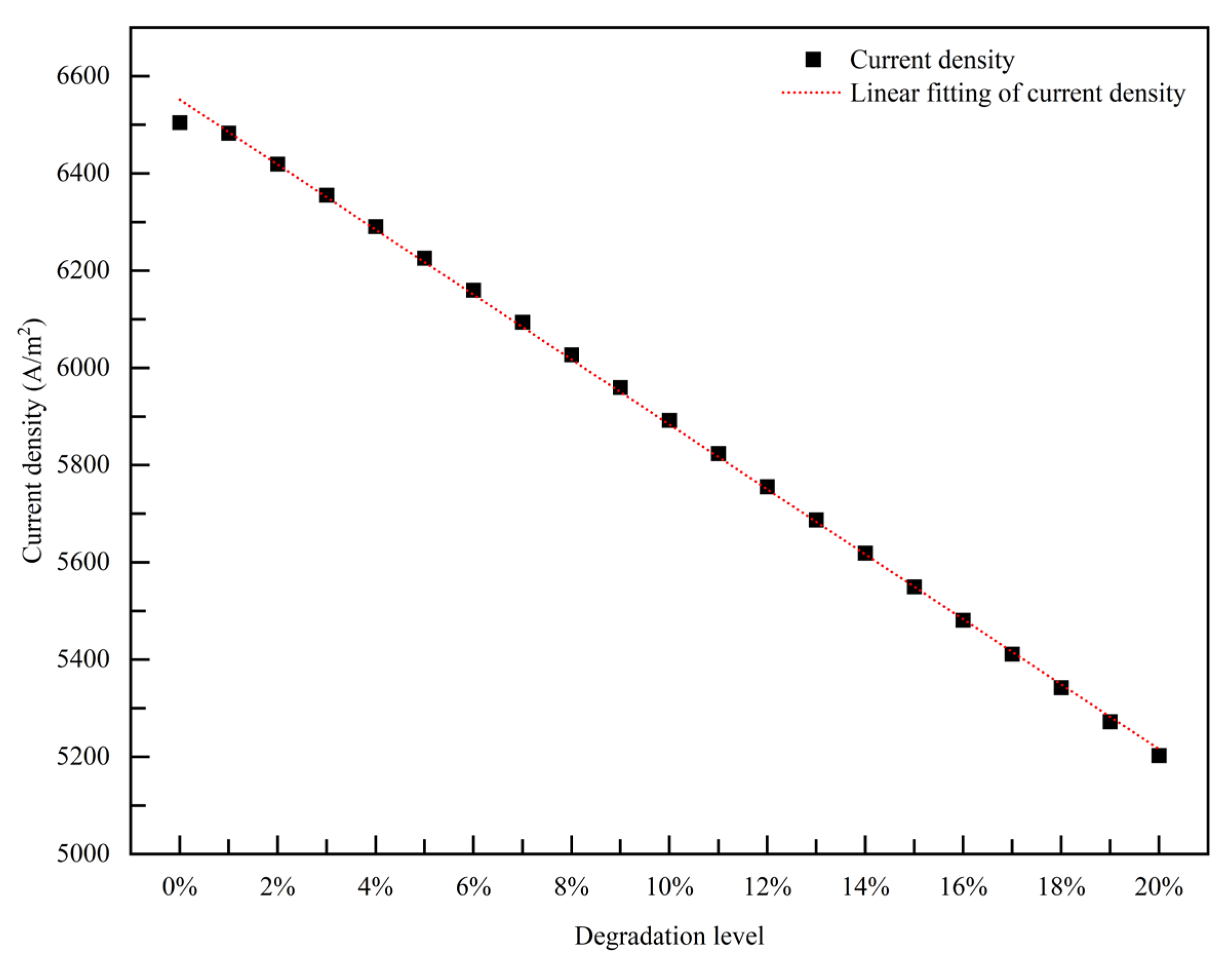
3.1.1. Empirical Degradation Model of Current Density
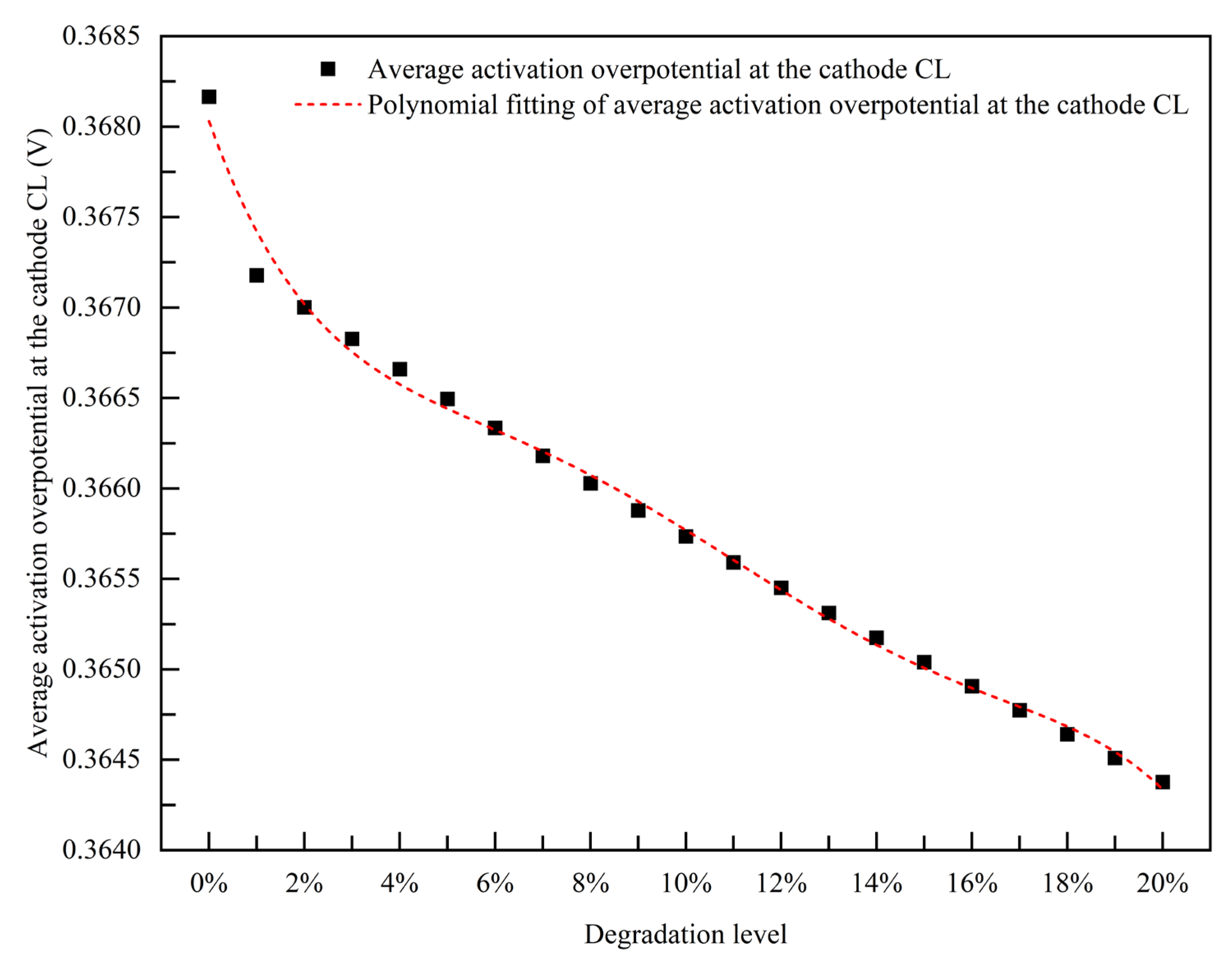
3.1.2. Empirical Degradation Model of Average Activation Overpotential at the Cathode CL
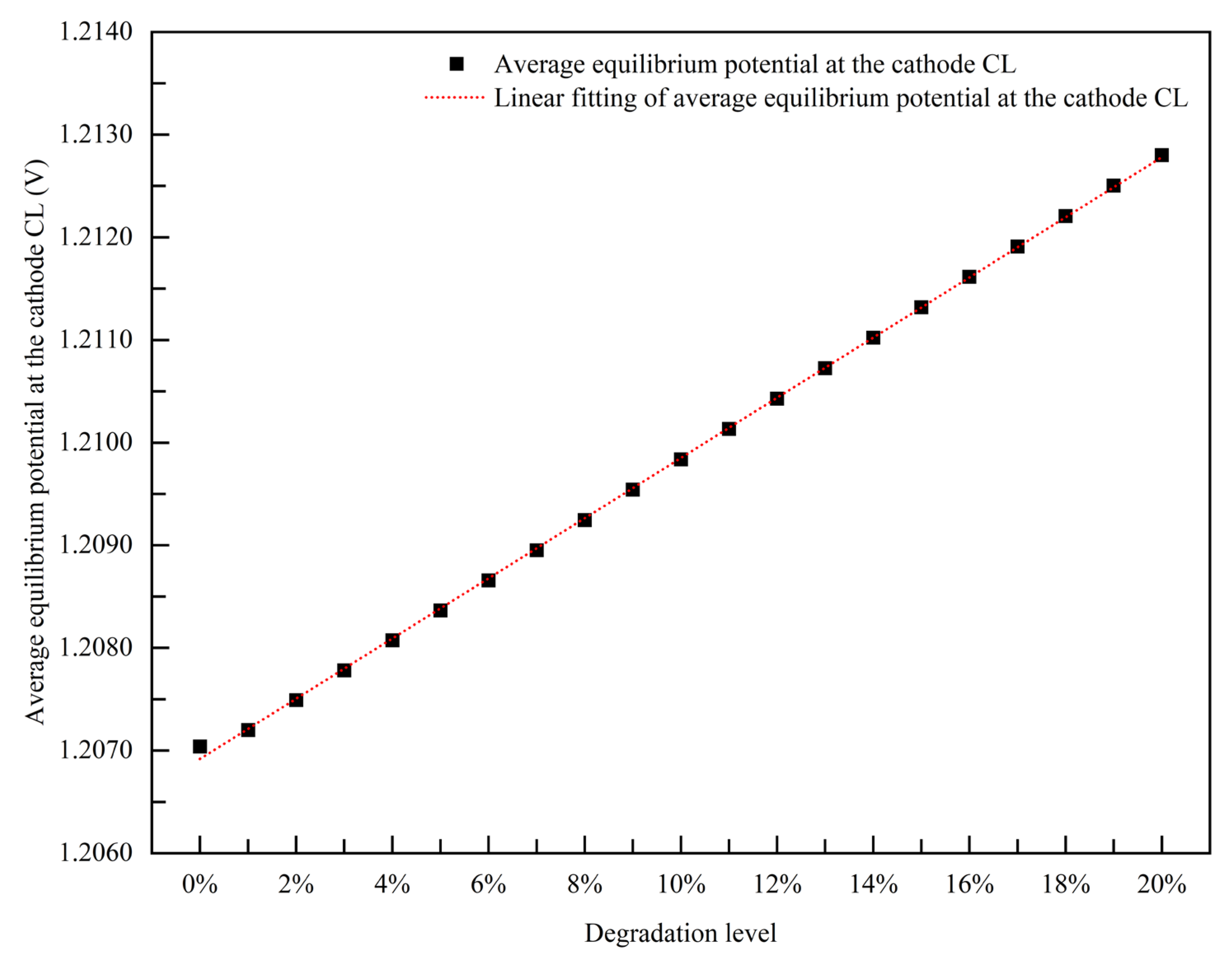
3.1.3. Empirical Degradation Model of Average Equilibrium Potential at the Cathode CL
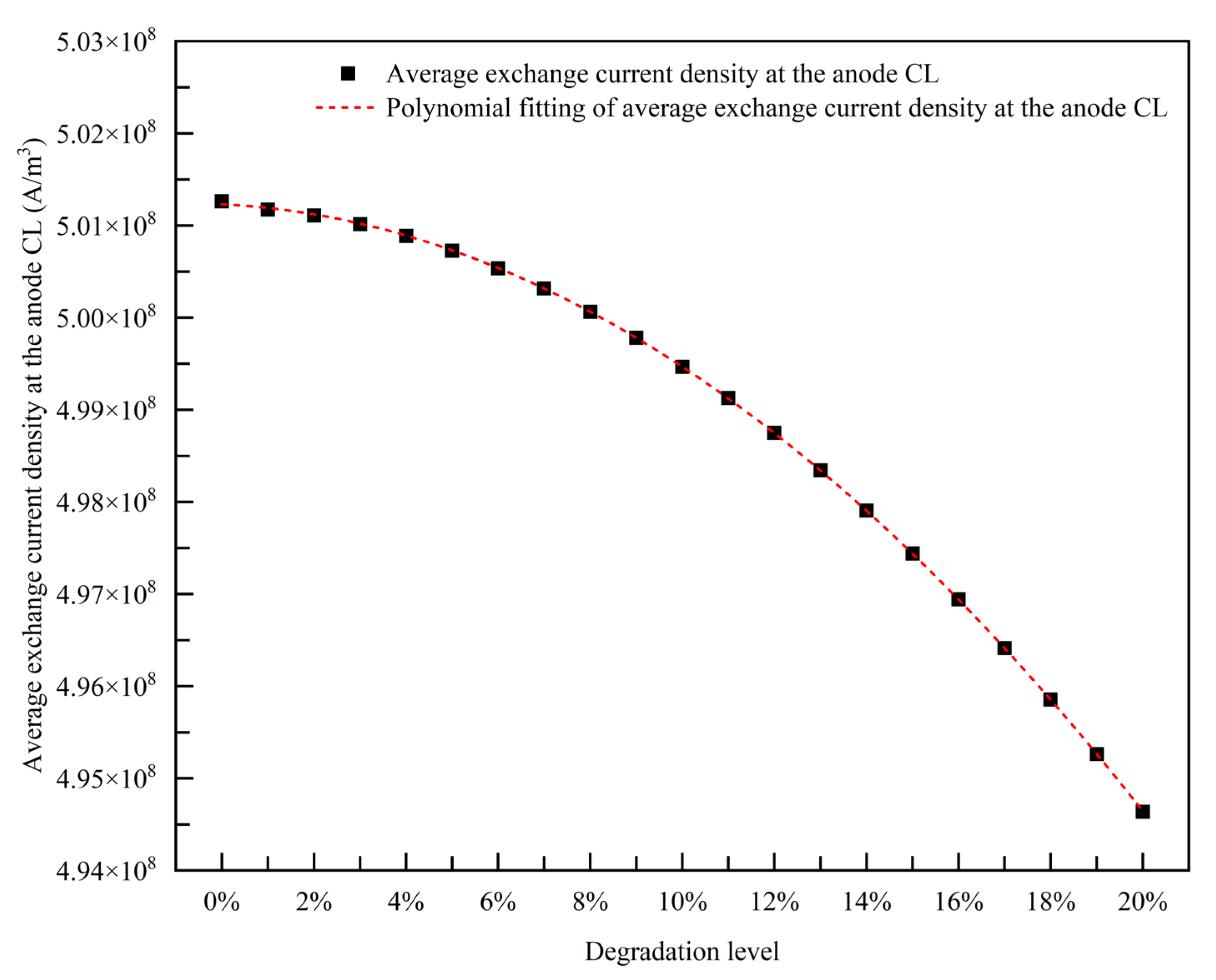
3.1.4. Empirical Degradation Model of Average Exchange Current Density at the Anode CL
3.2. Empirical Degradation Models of the Distribution Indexes
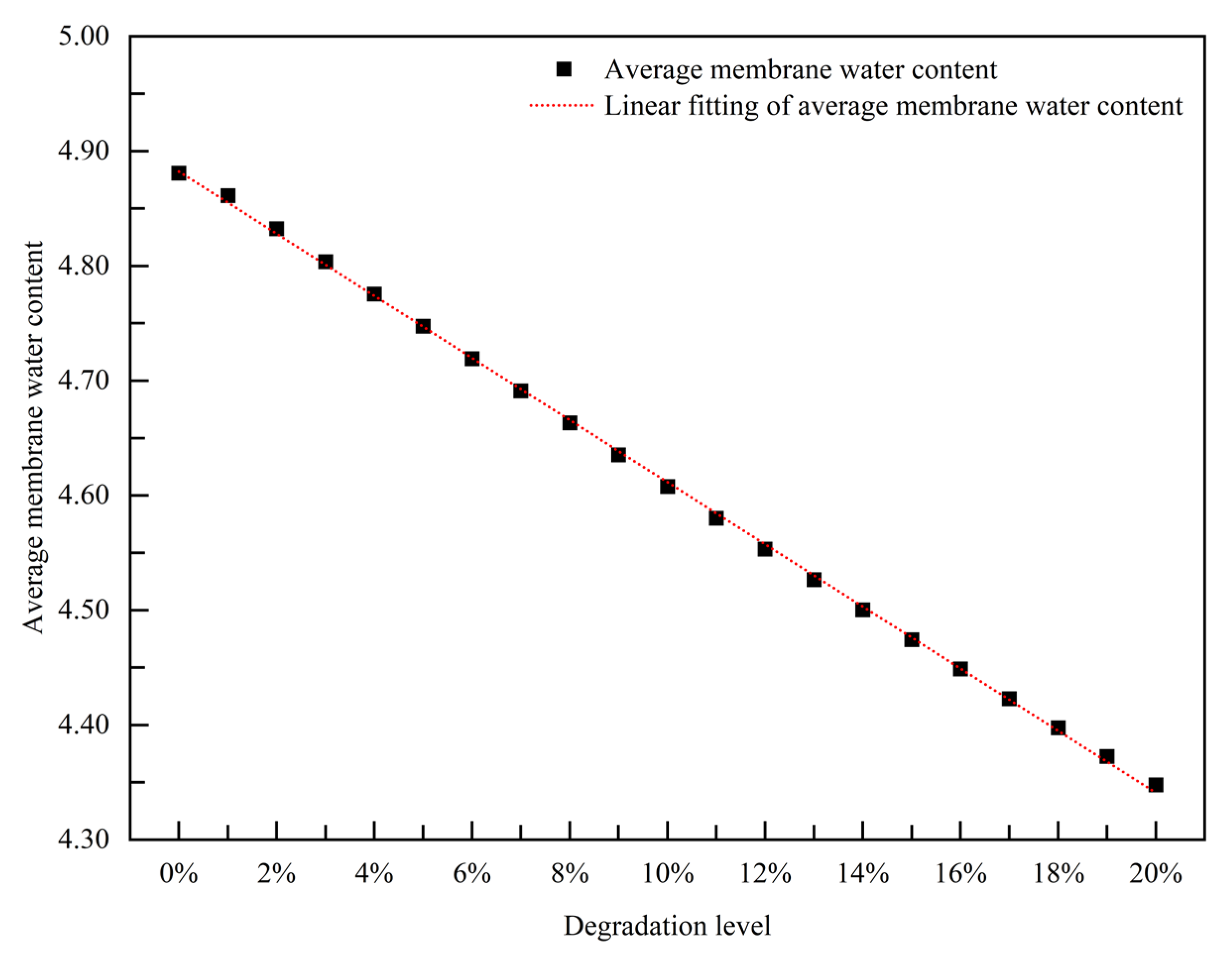
3.2.1. Empirical Degradation Model of Average Membrane Water Content
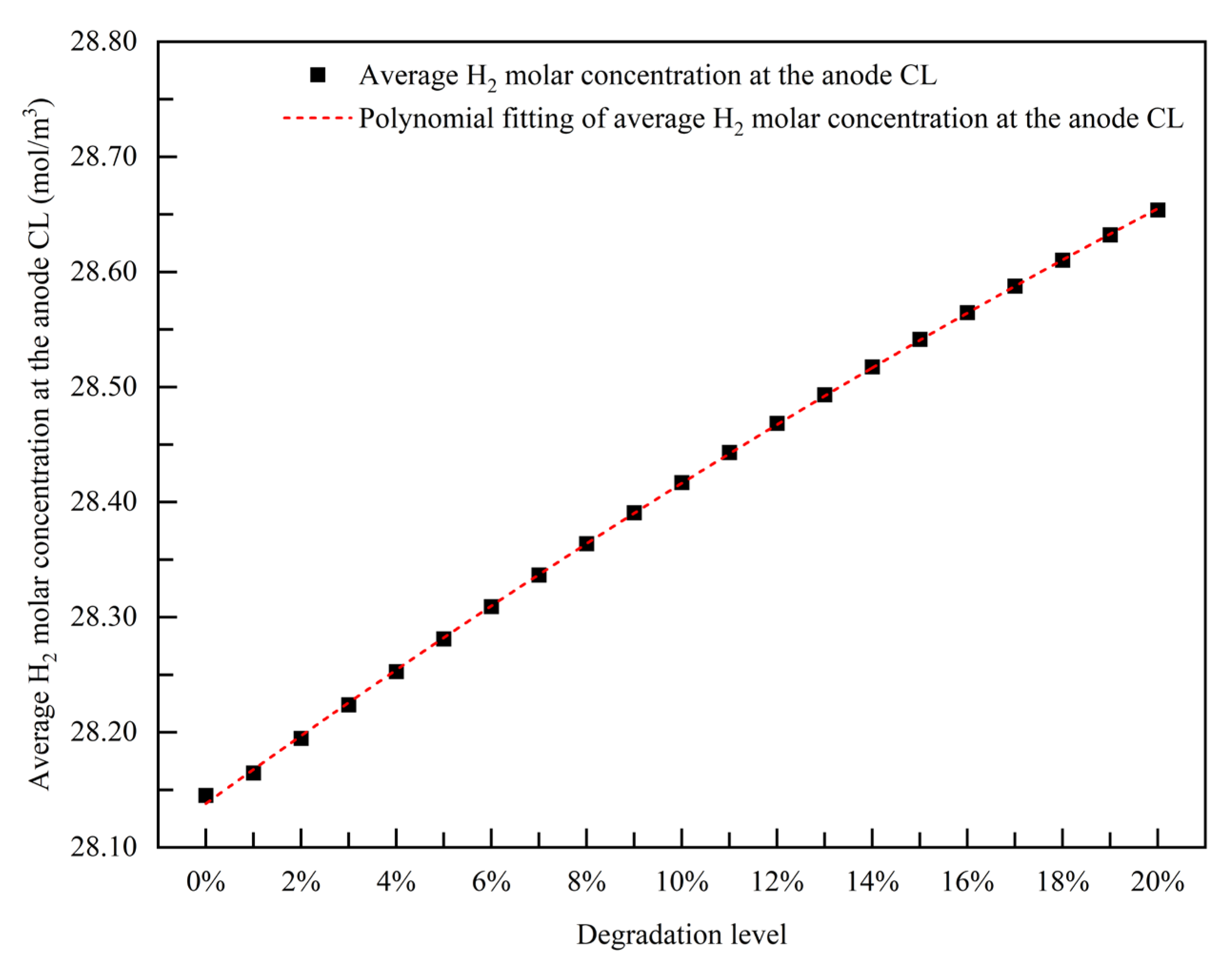
3.2.2. Empirical Degradation Model of Average H2 Molar Concentration at the Anode CL
3.2.3. Empirical Degradation Model of Average O2 Molar Concentration at the Cathode CL
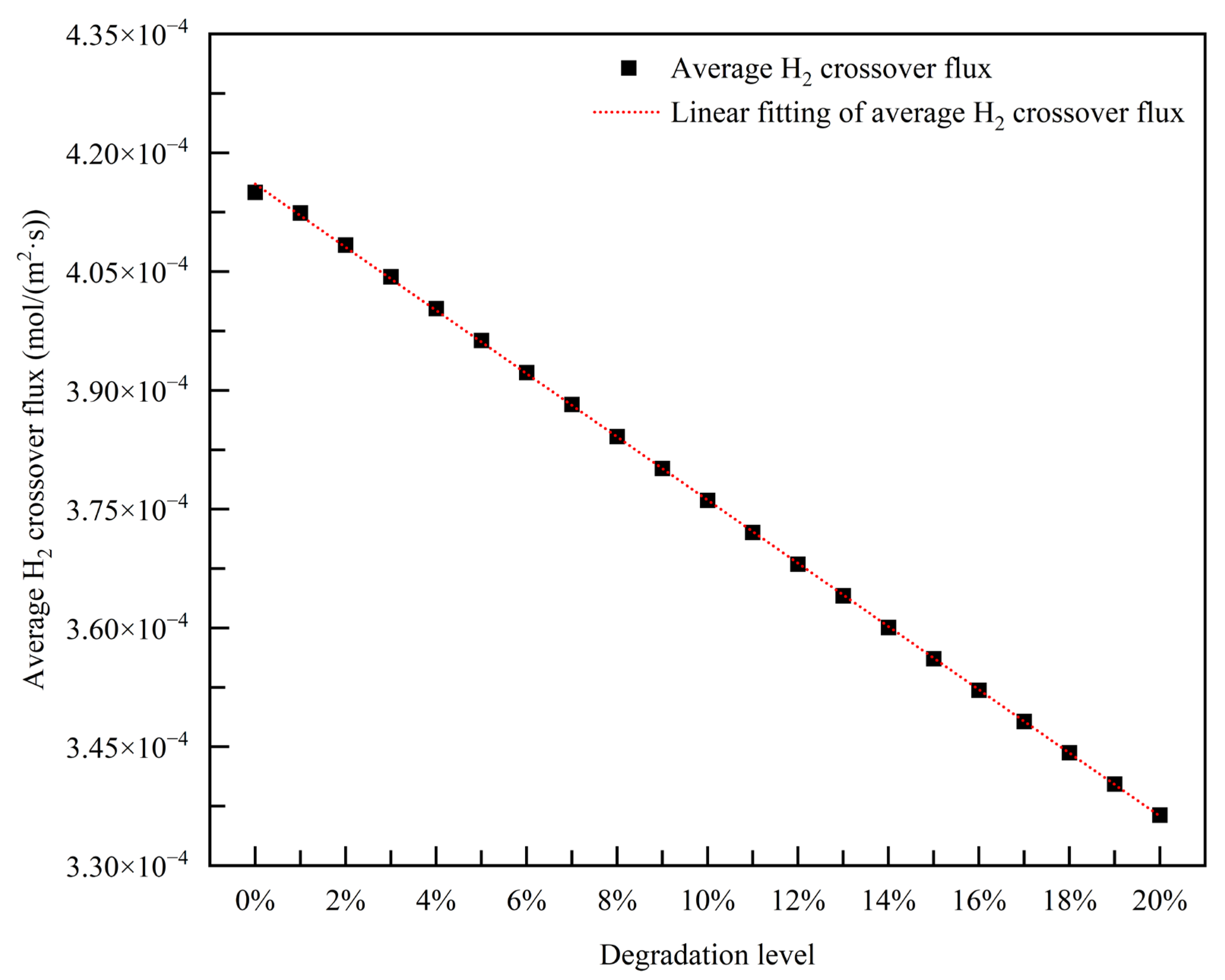
3.2.4. Empirical Degradation Model of Average H2 Crossover Flux
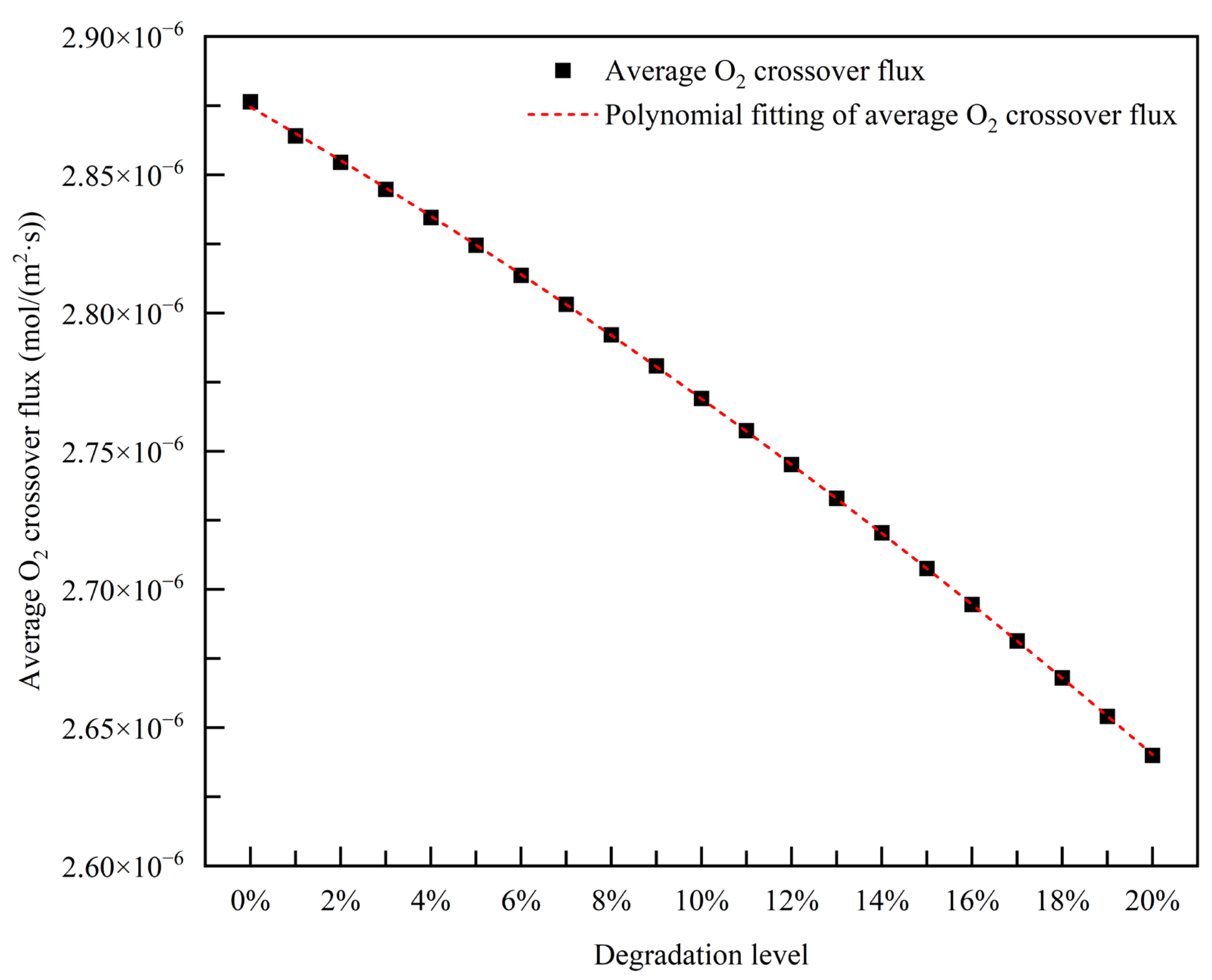
3.2.5. Empirical Degradation Model of Average O2 Crossover Flux
4. Conclusions
- (a)
- The parameters specific values of the PEM, CL, GDL, and BP of PEMFCs under different degradation levels are clarified, with degradation percentages of 0, 1%, …, 20%, respectively. The PEM parameters include the electro-osmotic drag coefficient, ionic conductivity, thermal conductivity, and water diffusion coefficient. The CL parameters include the agglomerate radius, electrical conductivity, average pore diameter, porosity, thermal conductivity, ionomer film thickness, and electrolyte volume fraction. The GDL parameters include the average pore diameter, porosity, and thermal conductivity. The BP parameter includes the electrical conductivity.
- (b)
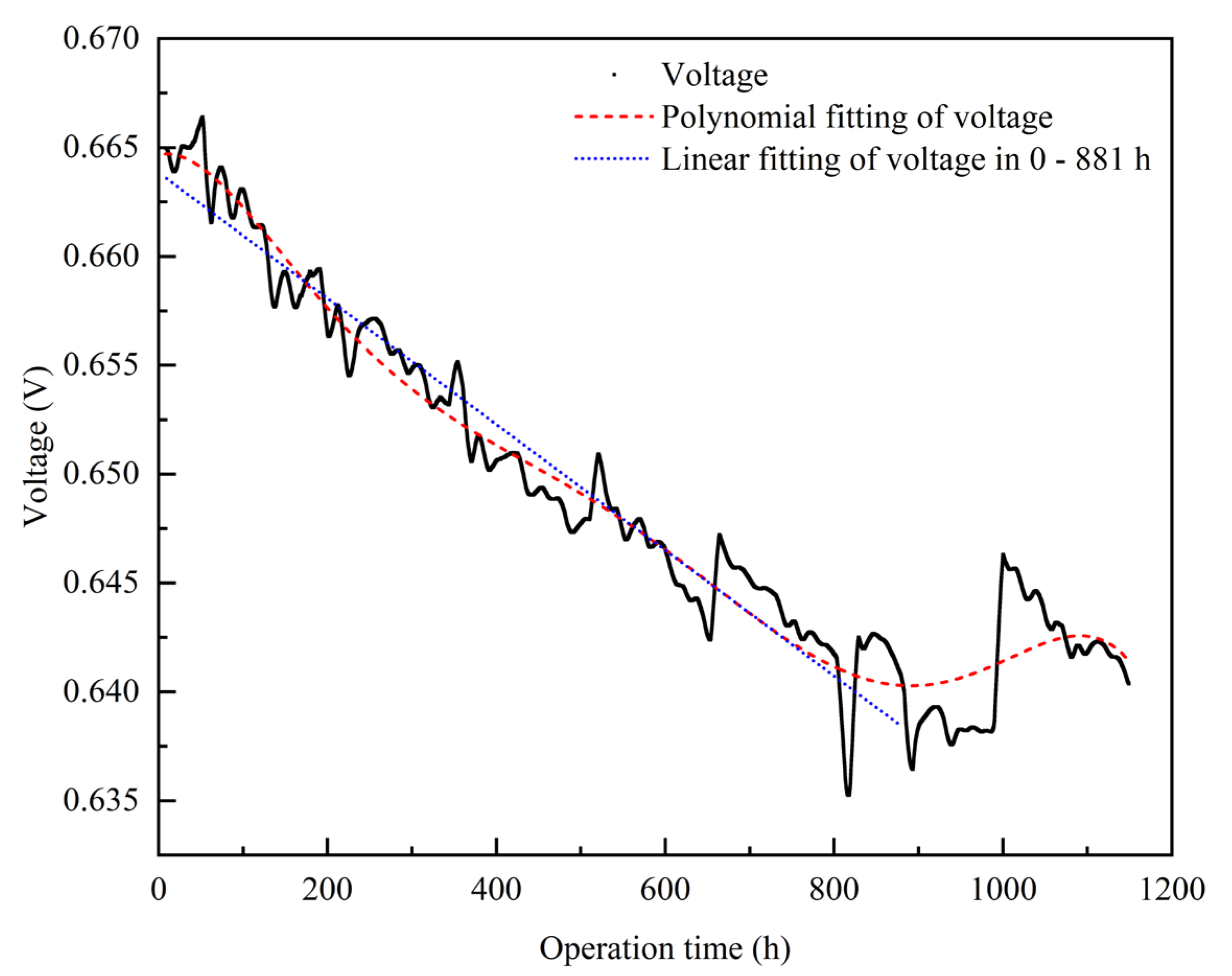
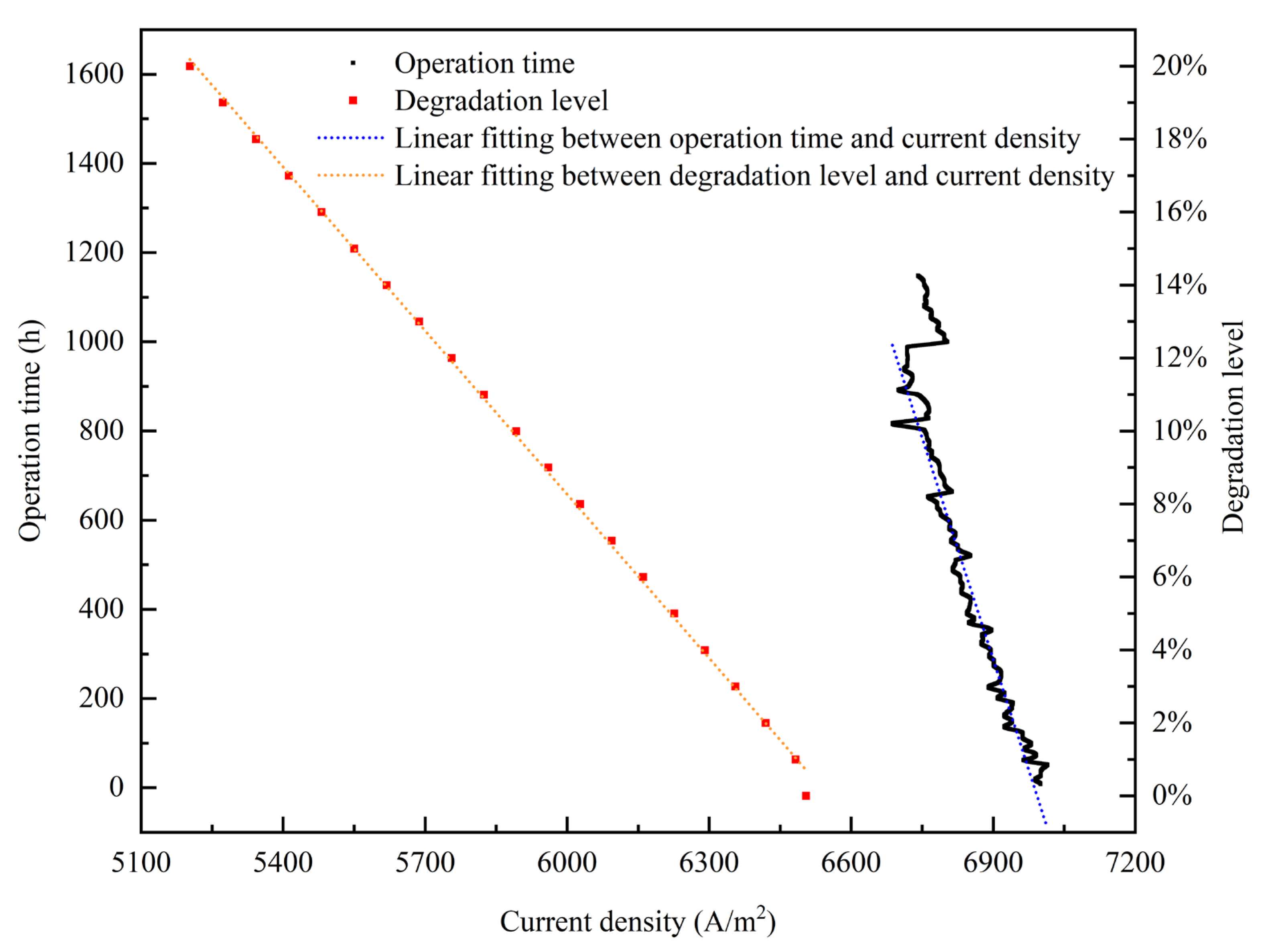
- The relationship between the experimental and simulation results is established by the index of current density, and the relationship between the operation time and degradation level of the PEMFC is obtained. The empirical degradation models of the different indexes of the PEMFC are established. Among them, the empirical degradation models of current density, average equilibrium potential on the cathode CL, average membrane water content, average oxygen molar concentration on the cathode CL, and average hydrogen crossover flux can be represented by the linear function. The empirical degradation models of the average exchange current density on the anode CL, average hydrogen molar concentration on the anode CL, and average oxygen crossover flux can be represented by the quadratic function. The empirical degradation model of average activation overpotential on the cathode CL can be represented by the quintic function.
- (c)
- The above models enrich the macroscopic and microscopic characterization of PEMFC degradation, and the established models can be used for PEMFC control system design and PEMFC degradation analysis, providing new ideas for PEMFC degradation description.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mostafa, M.M. Post-materialism, religiosity, political orientation, locus of control and concern for global warming: A multilevel analysis across 40 nations. Soc. Indic. Res. 2015, 128, 1273–1298. [Google Scholar] [CrossRef]
- Santos-Alamillos, F.J.; Archer, C.L.; Noel, L.; Budischak, C.; Facciolo, W. Assessing the economic feasibility of the gradual decarbonization of a large electric power system. J. Clean. Prod. 2017, 147, 130–141. [Google Scholar] [CrossRef]
- Ren, F.; Long, D. Carbon emission forecasting and scenario analysis in Guangdong Province based on optimized Fast Learning Network. J. Clean. Prod. 2021, 317, 128408–128424. [Google Scholar] [CrossRef]
- Xu, L.; Fan, M.; Yang, L.; Shao, S. Heterogeneous green innovations and carbon emission performance: Evidence at China’s city level. Energy Econ. 2021, 99, 105269–105285. [Google Scholar] [CrossRef]
- Huang, J.; Li, X.; Wang, Y.; Lei, H. The effect of energy patents on China’s carbon emissions: Evidence from the STIRPAT model. Technol. Forecast. Soc. Chang. 2021, 173, 121110–121121. [Google Scholar] [CrossRef]
- Zhou, S.; Fan, L.; Zhang, G.; Gao, J.; Lu, Y.; Zhao, P.; Wen, C.; Shi, L.; Hu, Z. A review on proton exchange membrane multi-stack fuel cell systems: Architecture, performance, and power management. Appl. Energy 2022, 310, 118555. [Google Scholar] [CrossRef]
- Chen, X.; Lin, B. Towards carbon neutrality by implementing carbon emissions trading scheme: Policy evaluation in China. Energy Policy 2021, 157, 112510–112522. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Vezzù, K.; Pagot, G.; Cavinato, G.; Nale, A.; Herve Bang, Y.; Di Noto, V. Hybrid inorganic-organic proton-conducting membranes based on SPEEK doped with WO3 nanoparticles for application in vanadium redox flow batteries. Electrochim. Acta 2019, 309, 311–325. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, L.; Pei, P.; Yao, S.; Wang, F. Asymptotic analysis for the inlet relative humidity effects on the performance of proton exchange membrane fuel cell. Appl. Energy 2018, 213, 573–584. [Google Scholar] [CrossRef]
- Li, Y.; Yang, F.; Chen, D.; Hu, S.; Xu, X. Thermal-physical modeling and parameter identification method for dynamic model with unmeasurable state in 10-kW scale proton exchange membrane fuel cell system. Energy Convers. Manag. 2023, 276, 116580. [Google Scholar] [CrossRef]
- Fukuhara, S.; Marx, N.; Ettihir, K.; Boulon, L.; Ait-Amirat, Y.; Becherif, M. A lumped fluidic model of an anode chamber for fault tolerant strategy design. Int. J. Hydrogen Energy 2016, 41, 5037–5047. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Salama, R.S.; El-Hakam, S.A.; Khder, A.S.; Ahmed, A.I. Synthesis of sulfated zirconium supported MCM-41 composite with high-rate adsorption of methylene blue and excellent heterogeneous catalyst. Colloids Surf. A Physicochem. Eng. Asp. 2021, 616, 126361–126371. [Google Scholar] [CrossRef]
- Salama, R.S.; Mannaa, M.A.; Altass, H.M.; Ibrahim, A.A.; Khder, A.E.-R.S. Palladium supported on mixed-metal–organic framework (Co–Mn-MOF-74) for efficient catalytic oxidation of CO. RSC Adv. 2021, 11, 4318–4326. [Google Scholar] [CrossRef] [PubMed]
- Karpenko-Jereb, L.; Sternig, C.; Fink, C.; Tatschl, R. Membrane degradation model for 3D CFD analysis of fuel cell performance as a function of time. Int. J. Hydrogen Energy 2016, 41, 13644–13656. [Google Scholar] [CrossRef]
- Chandesris, M.; Vincent, R.; Guetaz, L.; Roch, J.S.; Thoby, D.; Quinaud, M. Membrane degradation in PEM fuel cells: From experimental results to semi-empirical degradation laws. Int. J. Hydrogen Energy 2017, 42, 8139–8149. [Google Scholar] [CrossRef]
- Robin, C.; Gérard, M.; Quinaud, M.; d’Arbigny, J.; Bultel, Y. Proton exchange membrane fuel cell model for aging predictions: Simulated equivalent active surface area loss and comparisons with durability tests. J. Power Source 2016, 326, 417–427. [Google Scholar] [CrossRef]
- Moein-Jahromi, M.; Kermani, M.J.; Movahed, S. Degradation forecast for PEMFC cathode-catalysts under cyclic loads. J. Power Source 2017, 359, 611–625. [Google Scholar] [CrossRef]
- Fan, L.; Gao, J.; Lu, Y.; Shen, W.; Zhou, S. Analysis of the Influence of Component Degradation on Different Degradation Indexes of PEMFC. Energies 2023, 16, 7806. [Google Scholar] [CrossRef]
- Fan, L.; Zhou, S.; Zhao, P.; Gao, J. A Novel Hybrid Method Based on the Sliding Window Method for the Estimation of the State of Health of the Proton Exchange Membrane Fuel Cell; SAE Technical Paper Series; SAE: Shanghai, China, 2023. [Google Scholar]
- Yan, S.; Yang, M.; Sun, C.; Xu, S. Liquid Water Characteristics in the Compressed Gradient Porosity Gas Diffusion Layer of Proton Exchange Membrane Fuel Cells Using the Lattice Boltzmann Method. Energies 2023, 16, 6010. [Google Scholar] [CrossRef]


| Degradation Level | Electro-Osmotic Drag Coefficient (-) | Ionic Conductivity (S/m) | Thermal Conductivity (W/(m·K)) | Water Diffusion Coefficient (m2/s) |
|---|---|---|---|---|
| 0 | 0.113600 | 0.187900 | 0.200 | 2.1600 × 10−11 |
| 1% | 0.112464 | 0.186021 | 0.202 | 2.1384 × 10−11 |
| 2% | 0.111328 | 0.184142 | 0.204 | 2.1168 × 10−11 |
| 3% | 0.110192 | 0.182263 | 0.206 | 2.0952 × 10−11 |
| 4% | 0.109056 | 0.180384 | 0.208 | 2.0736 × 10−11 |
| 5% | 0.107920 | 0.178505 | 0.210 | 2.0520 × 10−11 |
| 6% | 0.106784 | 0.176626 | 0.212 | 2.0304 × 10−11 |
| 7% | 0.105648 | 0.174747 | 0.214 | 2.0088 × 10−11 |
| 8% | 0.104512 | 0.172868 | 0.216 | 1.9872 × 10−11 |
| 9% | 0.103376 | 0.170989 | 0.218 | 1.9656 × 10−11 |
| 10% | 0.102240 | 0.169110 | 0.220 | 1.9440 × 10−11 |
| 11% | 0.101104 | 0.167231 | 0.222 | 1.9224 × 10−11 |
| 12% | 0.099968 | 0.165352 | 0.224 | 1.9008 × 10−11 |
| 13% | 0.098832 | 0.163473 | 0.226 | 1.8792 × 10−11 |
| 14% | 0.097696 | 0.161594 | 0.228 | 1.8576 × 10−11 |
| 15% | 0.096560 | 0.159715 | 0.230 | 1.8360 × 10−11 |
| 16% | 0.095424 | 0.157836 | 0.232 | 1.8144 × 10−11 |
| 17% | 0.094288 | 0.155957 | 0.234 | 1.7928 × 10−11 |
| 18% | 0.093152 | 0.154078 | 0.236 | 1.7712 × 10−11 |
| 19% | 0.092016 | 0.152199 | 0.238 | 1.7496 × 10−11 |
| 20% | 0.090880 | 0.150320 | 0.240 | 1.7280 × 10−11 |
| Degradation Level | Agglomerate Radius (m) | Electrical Conductivity (S/m) | Average Pore Diameter (m) | Porosity (-) | Thermal Conductivity (W/(m·K)) | Ionomer film Thickness (m) | Electrolyte Volume Fraction (-) |
|---|---|---|---|---|---|---|---|
| 0 | 5.00 × 10−7 | 13,514.00 | 5.00 × 10−8 | 0.400 | 2.7400 | 5.00 × 10−8 | 0.2500 |
| 1% | 5.05 × 10−7 | 13,378.86 | 5.05 × 10−8 | 0.404 | 2.7674 | 4.95 × 10−8 | 0.2475 |
| 2% | 5.10 × 10−7 | 13,243.72 | 5.10 × 10−8 | 0.408 | 2.7948 | 4.90 × 10−8 | 0.2450 |
| 3% | 5.15 × 10−7 | 13,108.58 | 5.15 × 10−8 | 0.412 | 2.8222 | 4.85 × 10−8 | 0.2425 |
| 4% | 5.20 × 10−7 | 12,973.44 | 5.20 × 10−8 | 0.416 | 2.8496 | 4.80 × 10−8 | 0.2400 |
| 5% | 5.25 × 10−7 | 12,838.30 | 5.25 × 10−8 | 0.420 | 2.8770 | 4.75 × 10−8 | 0.2375 |
| 6% | 5.30 × 10−7 | 12,703.16 | 5.30 × 10−8 | 0.424 | 2.9044 | 4.70 × 10−8 | 0.2350 |
| 7% | 5.35 × 10−7 | 12,568.02 | 5.35 × 10−8 | 0.428 | 2.9318 | 4.65 × 10−8 | 0.2325 |
| 8% | 5.40 × 10−7 | 12,432.88 | 5.40 × 10−8 | 0.432 | 2.9592 | 4.60 × 10−8 | 0.2300 |
| 9% | 5.45 × 10−7 | 12,297.74 | 5.45 × 10−8 | 0.436 | 2.9866 | 4.55 × 10−8 | 0.2275 |
| 10% | 5.50 × 10−7 | 12,162.60 | 5.50 × 10−8 | 0.440 | 3.0140 | 4.50 × 10−8 | 0.2250 |
| 11% | 5.55 × 10−7 | 12,027.46 | 5.55 × 10−8 | 0.444 | 3.0414 | 4.45 × 10−8 | 0.2225 |
| 12% | 5.60 × 10−7 | 11,892.32 | 5.60 × 10−8 | 0.448 | 3.0688 | 4.40 × 10−8 | 0.2200 |
| 13% | 5.65 × 10−7 | 11,757.18 | 5.65 × 10−8 | 0.452 | 3.0962 | 4.35 × 10−8 | 0.2175 |
| 14% | 5.70 × 10−7 | 11,622.04 | 5.70 × 10−8 | 0.456 | 3.1236 | 4.30 × 10−8 | 0.2150 |
| 15% | 5.75 × 10−7 | 11,486.90 | 5.75 × 10−8 | 0.460 | 3.1510 | 4.25 × 10−8 | 0.2125 |
| 16% | 5.80 × 10−7 | 11,351.76 | 5.80 × 10−8 | 0.464 | 3.1784 | 4.20 × 10−8 | 0.2100 |
| 17% | 5.85 × 10−7 | 11,216.62 | 5.85 × 10−8 | 0.468 | 3.2058 | 4.15 × 10−8 | 0.2075 |
| 18% | 5.90 × 10−7 | 11,081.48 | 5.90 × 10−8 | 0.472 | 3.2332 | 4.10 × 10−8 | 0.2050 |
| 19% | 5.95 × 10−7 | 10,946.34 | 5.95 × 10−8 | 0.476 | 3.2606 | 4.05 × 10−8 | 0.2025 |
| 20% | 6.00 × 10−7 | 10,811.20 | 6.00 × 10−8 | 0.480 | 3.2880 | 4.00 × 10−8 | 0.2000 |
| Degradation Level | Average Pore Diameter (m) | Porosity (-) | Thermal Conductivity (W/(m·K)) |
|---|---|---|---|
| 0 | 1.500 × 10−6 | 0.400 | 5.00 |
| 1% | 1.515 × 10−6 | 0.404 | 5.05 |
| 2% | 1.530 × 10−6 | 0.408 | 5.10 |
| 3% | 1.545 × 10−6 | 0.412 | 5.15 |
| 4% | 1.560 × 10−6 | 0.416 | 5.20 |
| 5% | 1.575 × 10−6 | 0.420 | 5.25 |
| 6% | 1.590 × 10−6 | 0.424 | 5.30 |
| 7% | 1.605 × 10−6 | 0.428 | 5.35 |
| 8% | 1.620 × 10−6 | 0.432 | 5.40 |
| 9% | 1.635 × 10−6 | 0.436 | 5.45 |
| 10% | 1.650 × 10−6 | 0.440 | 5.50 |
| 11% | 1.665 × 10−6 | 0.444 | 5.55 |
| 12% | 1.680 × 10−6 | 0.448 | 5.60 |
| 13% | 1.695 × 10−6 | 0.452 | 5.65 |
| 14% | 1.710 × 10−6 | 0.456 | 5.70 |
| 15% | 1.725 × 10−6 | 0.460 | 5.75 |
| 16% | 1.740 × 10−6 | 0.464 | 5.80 |
| 17% | 1.755 × 10−6 | 0.468 | 5.85 |
| 18% | 1.770 × 10−6 | 0.472 | 5.90 |
| 19% | 1.785 × 10−6 | 0.476 | 5.95 |
| 20% | 1.800 × 10−6 | 0.480 | 6.00 |
| Degradation Level | Electrical Conductivity (S/m) |
|---|---|
| 0 | 1.4500 × 106 |
| 1% | 1.4355 × 106 |
| 2% | 1.4210 × 106 |
| 3% | 1.4065 × 106 |
| 4% | 1.3920 × 106 |
| 5% | 1.3775 × 106 |
| 6% | 1.3630 × 106 |
| 7% | 1.3485 × 106 |
| 8% | 1.3340 × 106 |
| 9% | 1.3195 × 106 |
| 10% | 1.3050 × 106 |
| 11% | 1.2905 × 106 |
| 12% | 1.2760 × 106 |
| 13% | 1.2615 × 106 |
| 14% | 1.2470 × 106 |
| 15% | 1.2325 × 106 |
| 16% | 1.2180 × 106 |
| 17% | 1.2035 × 106 |
| 18% | 1.1890 × 106 |
| 19% | 1.1745 × 106 |
| 20% | 1.1600 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, L.; Gao, J.; Lu, Y.; Shen, W.; Zhou, S. Empirical Degradation Models of the Different Indexes of the Proton Exchange Membrane Fuel Cell Based on the Component Degradation. Energies 2023, 16, 8012. https://doi.org/10.3390/en16248012
Fan L, Gao J, Lu Y, Shen W, Zhou S. Empirical Degradation Models of the Different Indexes of the Proton Exchange Membrane Fuel Cell Based on the Component Degradation. Energies. 2023; 16(24):8012. https://doi.org/10.3390/en16248012
Chicago/Turabian StyleFan, Lei, Jianhua Gao, Yanda Lu, Wei Shen, and Su Zhou. 2023. "Empirical Degradation Models of the Different Indexes of the Proton Exchange Membrane Fuel Cell Based on the Component Degradation" Energies 16, no. 24: 8012. https://doi.org/10.3390/en16248012
APA StyleFan, L., Gao, J., Lu, Y., Shen, W., & Zhou, S. (2023). Empirical Degradation Models of the Different Indexes of the Proton Exchange Membrane Fuel Cell Based on the Component Degradation. Energies, 16(24), 8012. https://doi.org/10.3390/en16248012






