A Data-Driven Prediction Method for Proton Exchange Membrane Fuel Cell Degradation
Abstract
1. Introduction
2. Fuel Cell Aging Experimental Implementation
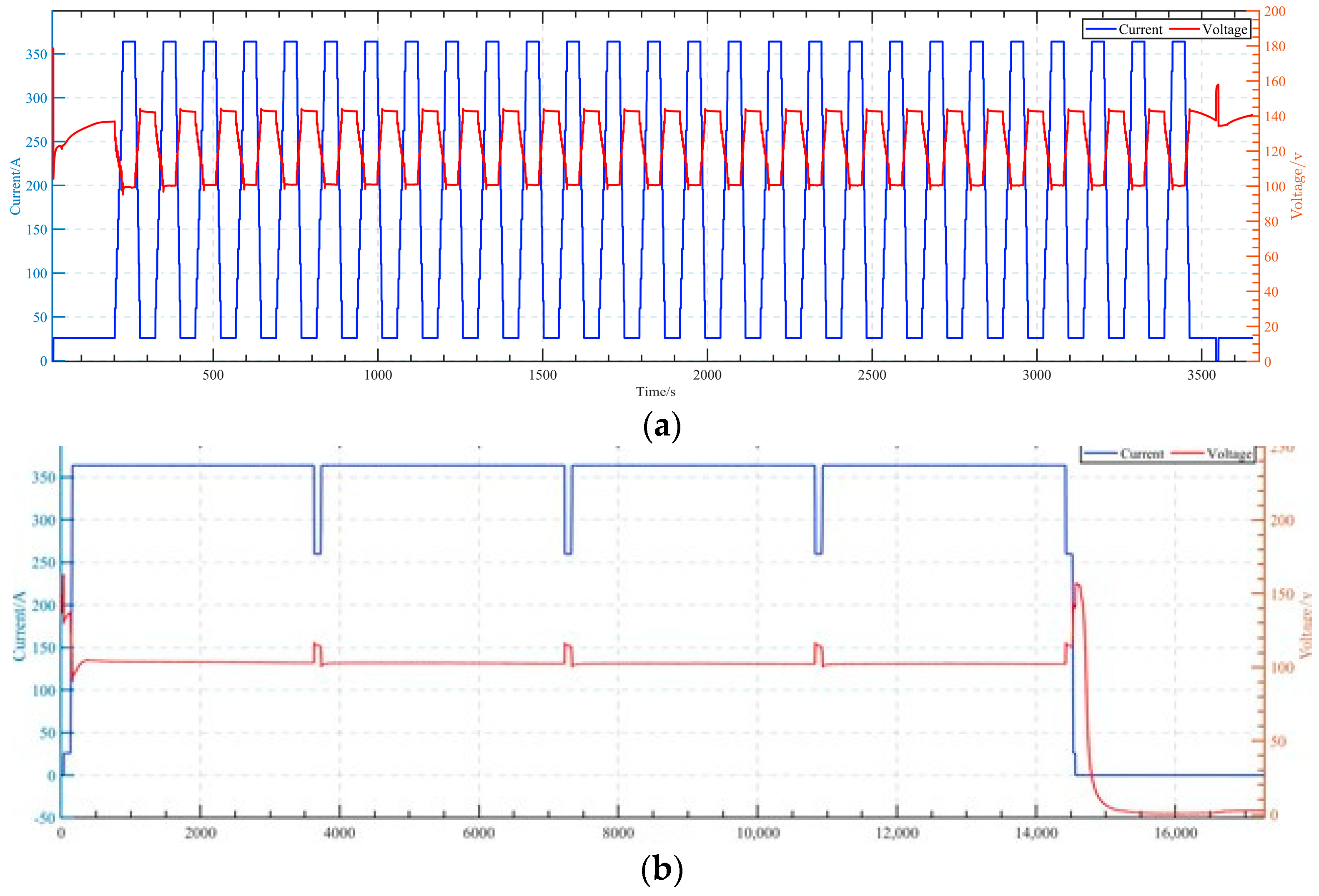
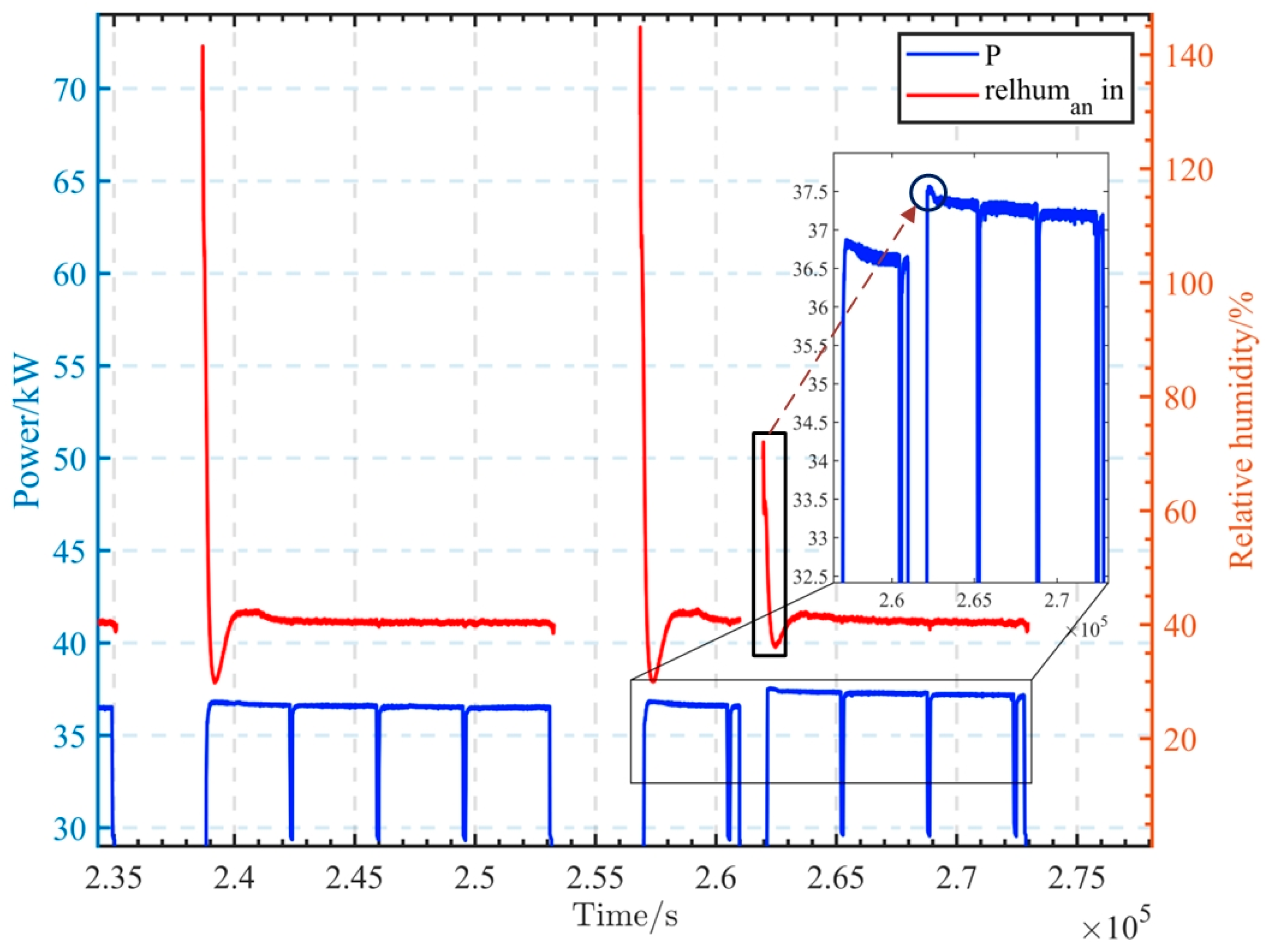
2.1. Fuel Cell Degradation Phenomena
2.2. Aging Experiments for the Fuel Cell
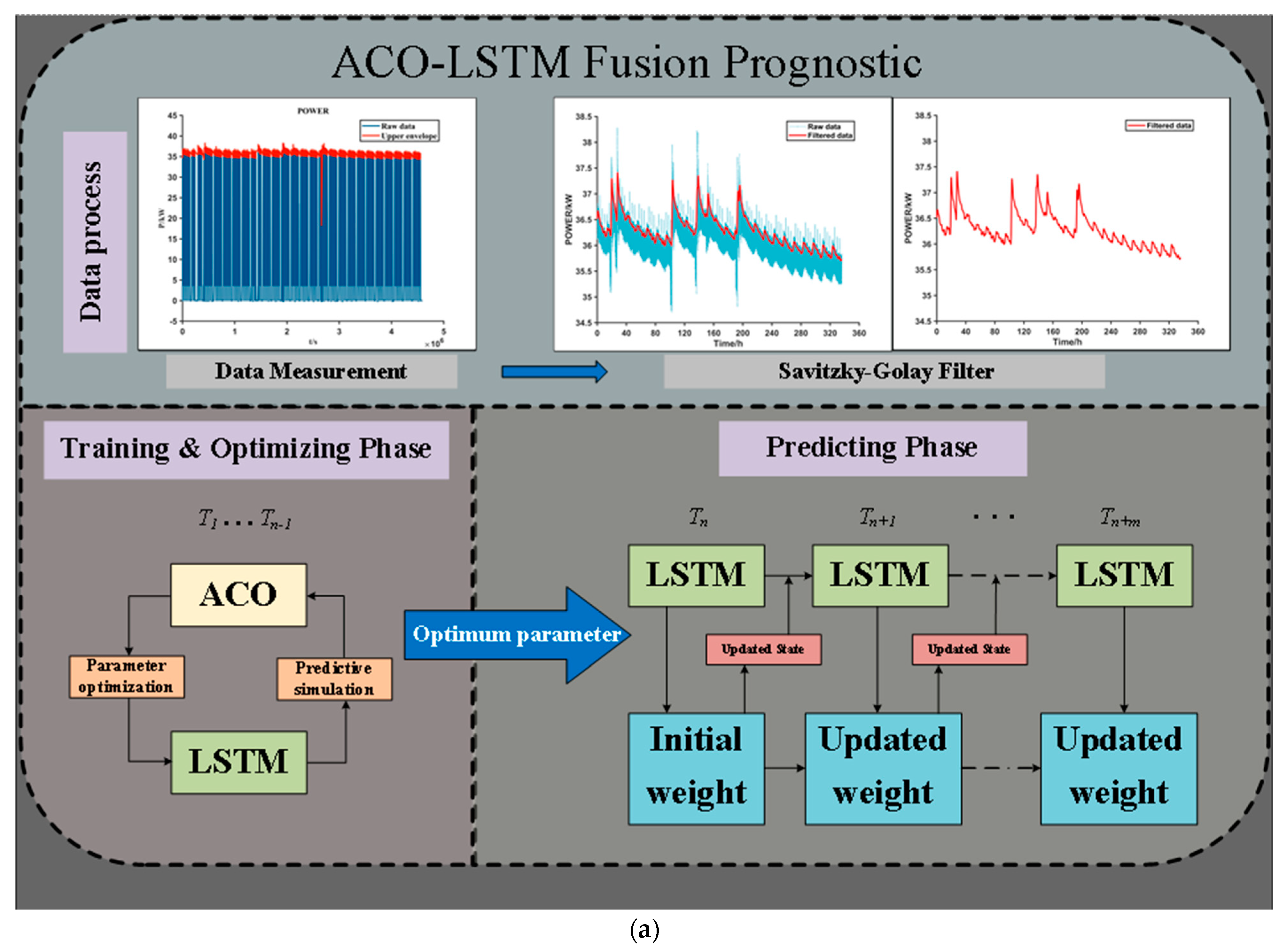
3. Degradation Model with an ACO-LSTM Architecture
3.1. Data Acquisition and Processing
3.2. LSTM Architecture
- (1)
- Forget gate: the first step of the LSTM algorithm is to selectively discard part of the information with the forget gate. It receives the inputs of and , then outputs a number between 0 and 1 to the internal state , where 1 represents the fully reserved state and 0 indicates complete discarding.
- (2)
- Input gate and input node: the second step is to decide which information to store in the internal state. This step needs to be completed in two small steps. First, the input gate (t) determines which values to update; then, a candidate state is created by the input node :Thus, Equations (3)–(5) can update the old internal state to .
- (3)
- Output gate: the output gate determines what information to output.
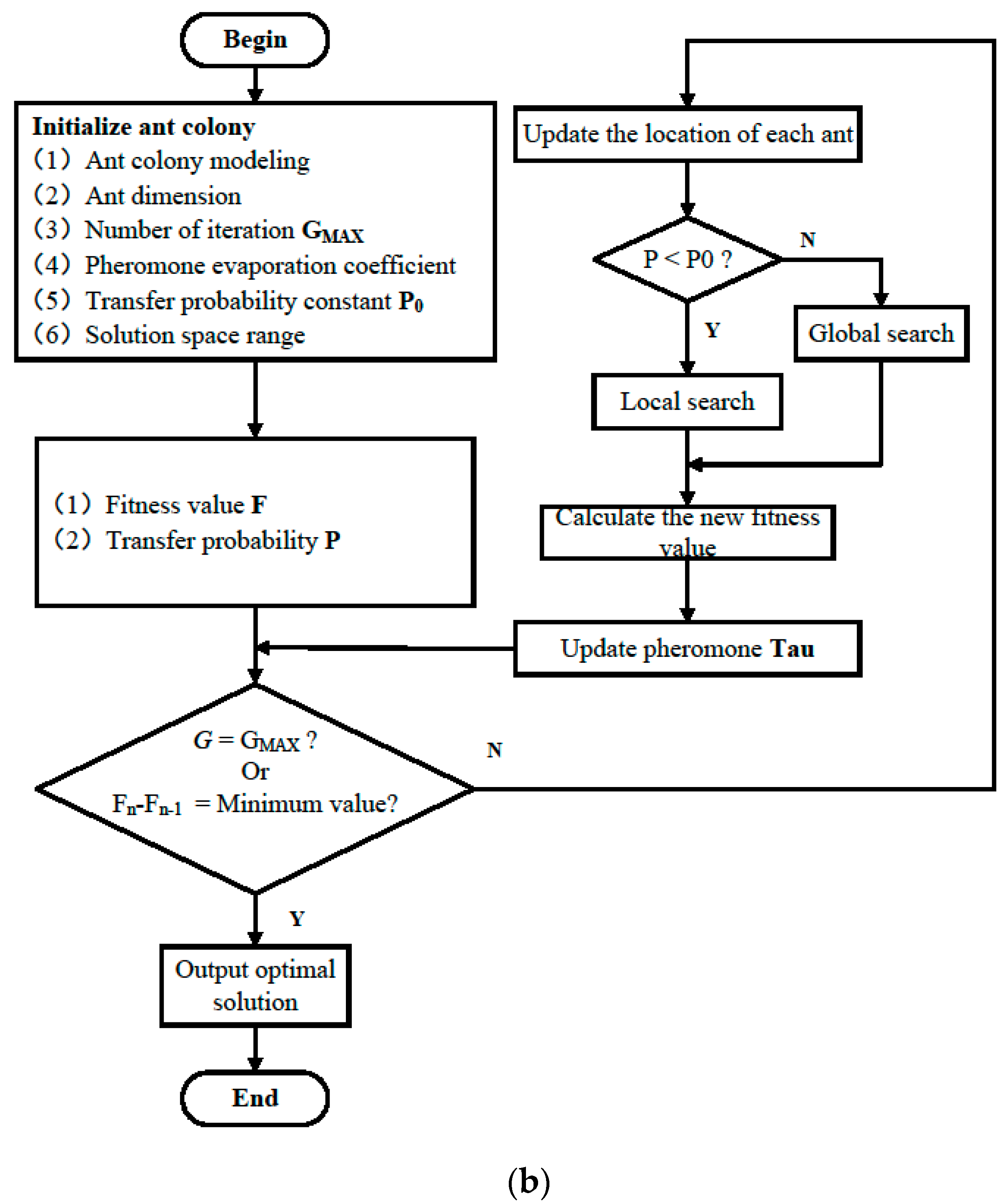
3.3. Structure and Implementation of ACO
3.4. Dropout
3.5. ACO-LSTM Approach
- (1)
- After the dataset is initially divided into a training set and a prediction set, the training set is subdivided into an LSTM simulation training set and an ACO optimization set.
- (2)
- The ACO algorithm is initialized, and a two-dimensional (initial learning rate, dropout probability) ant population is randomly generated.
- (3)
- The LSTM simulation training set is used as the training set, and the ACO optimization set is used as the test set to simulate the LSTM prediction process and let the ant with the smallest prediction error (defined as the RMSE in this paper) produce the densest pheromone in each iteration.
- (4)
- When the end condition is satisfied, the ant with the smallest historical error is selected as the optimal solution. Then, the optimal initial learning rate and dropout probability are obtained from this solution and are used to obtain the prediction results.
4. Degradation Prediction Results
4.1. Criteria of Predictive Performance
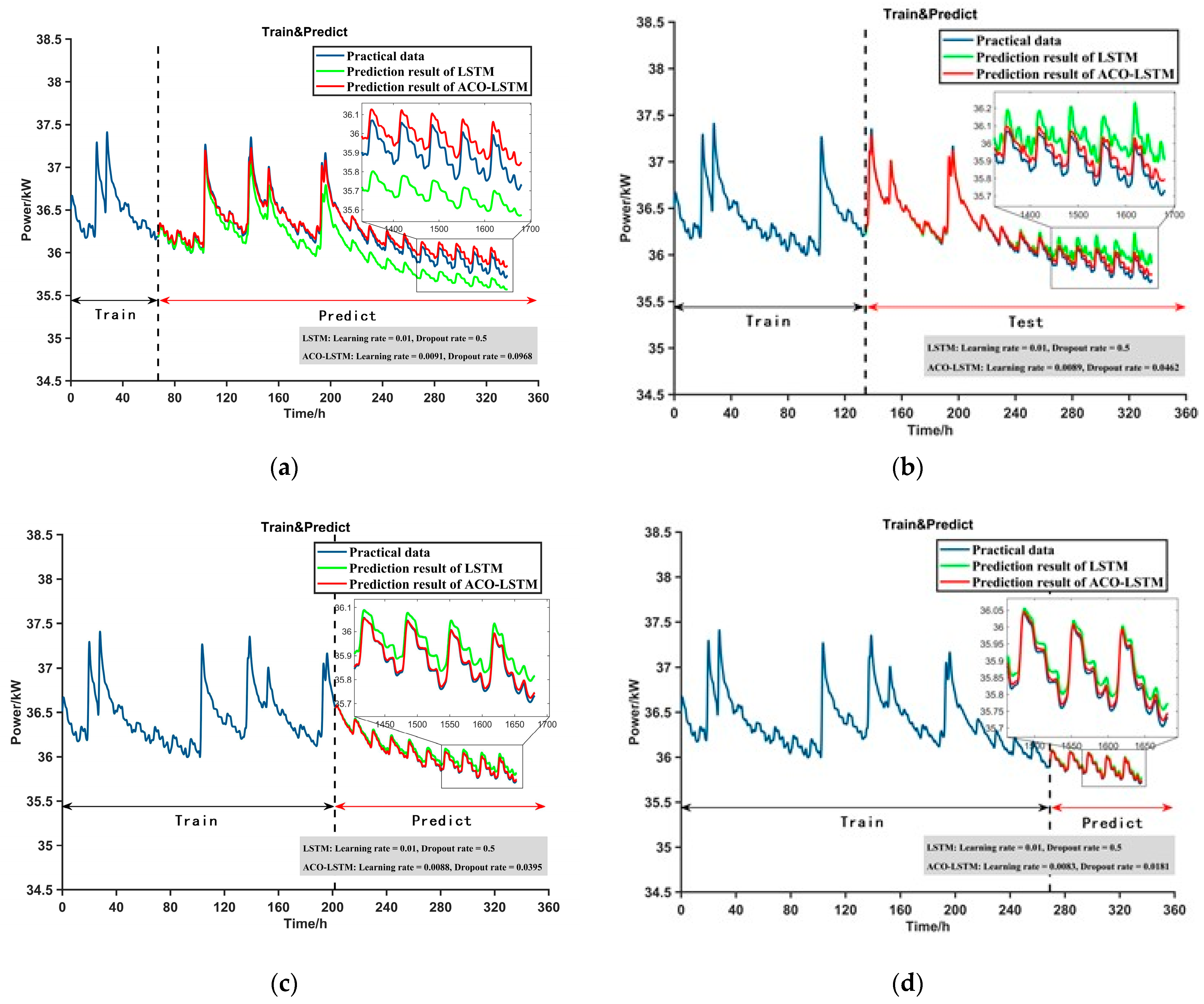
4.2. Degradation Prediction Model Based on ACO-LSTM
4.3. Verification of the Degradation Prediction Model
4.4. Conclusions
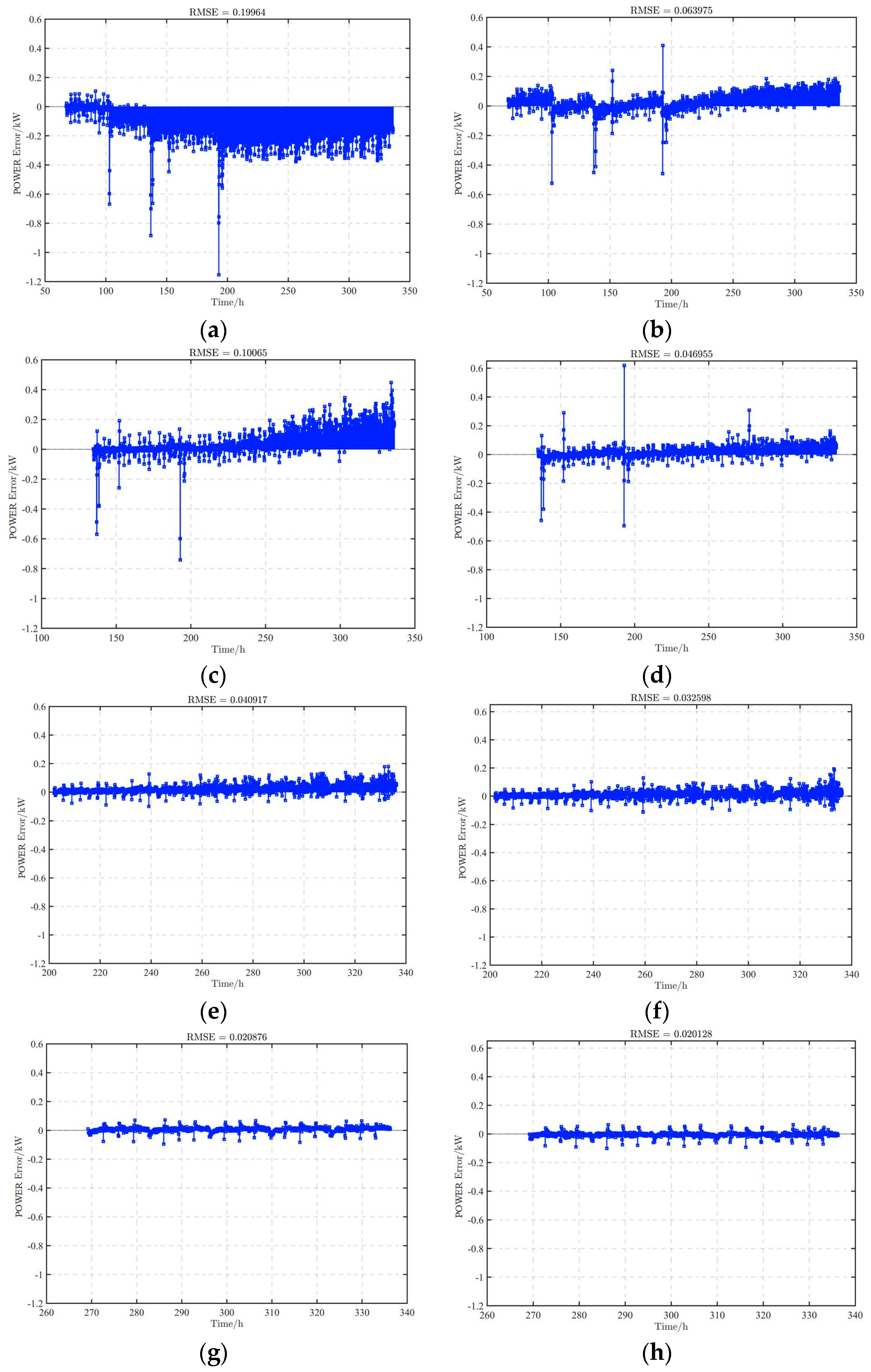
- The results show that ACO-LSTM can efficaciously train the high-precision degradation prediction model under different training data ratios and has a significant improvement compared with the traditional LSTM, especially in the case of a low data ratio.
- The proposed model shows good prediction performance in working conditions that are completely different from the training conditions, which proves its excellent generalizability.
- However, when there is a large instantaneous change in the prediction data, the prediction model loses part of its tracking ability, although its performance is still better than that of the traditional LSTM.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Lin, R.; Feng, B.; Yang, Z. Investigation of the effect of cathode stoichiometry of proton exchange membrane fuel cell using localized electrochemical impedance spectroscopy based on print circuit board. Int. J. Hydrogen Energy 2019, 44, 7564–7573. [Google Scholar] [CrossRef]
- Silva, R.E.; Gouriveau, R.; Jemeï, S.; Hissel, D.; Boulon, L.; Agbossou, K.; Steiner, N.Y. Proton exchange membrane fuel cell degradation prediction based on adaptive neuro-fuzzy inference systems. Int. J. Hydrogen Energy 2014, 39, 11128–11144. [Google Scholar] [CrossRef]
- Yuan, H.; Dai, H.; Wei, X.; Ming, P. Model-based observers for internal states estimation and control of proton exchange membrane fuel cell system: A review. J. Power Sources 2020, 468, 228376. [Google Scholar] [CrossRef]
- Yan, S.; Yang, M.; Sun, C.; Xu, S. Liquid Water Characteristics in the Compressed Gradient Porosity Gas Diffusion Layer of Proton Exchange Membrane Fuel Cells Using the Lattice Boltzmann Method. Energies 2023, 16, 6010. [Google Scholar] [CrossRef]
- Zhong, D.; Lin, R.; Jiang, Z.; Zhu, Y.; Liu, D.; Cai, X.; Chen, L. Low temperature durability and consistency analysis of proton exchange membrane fuel cell stack based on comprehensive characterizations. Appl. Energy 2020, 264, 114626. [Google Scholar] [CrossRef]
- Lin, R.; Che, L.; Shen, D.; Cai, X. High durability of pt-ni-ir/c ternary catalyst of pemfc by stepwise reduction synthesis. Electrochim. Acta 2020, 330, 135251. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, Y.; Zang, P.-F.; Wang, Y. Energy management strategy of fuel cell bus based on pontryagin’s minimum principle. J. Jilin Univ. Eng. Technol. Ed. 2020, 50, 36–43. [Google Scholar]
- Lin, R.-H.; Xi, X.-N.; Wang, P.-N.; Wu, B.-D.; Tian, S.-M. Review on hydrogen fuel cell condition monitoring and prediction methods. Int. J. Hydrogen Energy 2019, 44, 5488–5498. [Google Scholar] [CrossRef]
- Keller, R.; Ding, S.X.; Müller, M.; Stolten, D. Fault-tolerant model predictive control of a direct methanol-fuel cell system with actuator faults. Control. Eng. Pract. 2017, 66, 99–115. [Google Scholar] [CrossRef]
- Tang, W.; Lin, R.; Weng, Y.; Zhang, J.; Ma, J. The effects of operating temperature on current density distribution and impedance spectroscopy by segmented fuel cell. Int. J. Hydrogen Energy 2013, 38, 10985–10991. [Google Scholar] [CrossRef]
- Vasilyev, A.; Andrews, J.; Jackson, L.; Dunnett, S.; Davies, B. Component-based modelling of pem fuel cells with bond graphs. Int. J. Hydrogen Energy 2017, 42, 29406–29421. [Google Scholar] [CrossRef]
- Park, J.; Oh, H.; Ha, T.; Lee, Y.I.; Min, K. A review of the gas diffusion layer in proton exchange membrane fuel cells: Durability and degradation. Appl. Energy 2015, 155, 866–880. [Google Scholar] [CrossRef]
- Chen, H.; Pei, P.; Song, M. Lifetime prediction and the economic lifetime of proton exchange membrane fuel cells. Appl. Energy 2015, 142, 154–163. [Google Scholar] [CrossRef]
- Zhang, X.; Pisu, P. Prognostic-oriented fuel cell catalyst aging modeling and its application to health-monitoring and prognostics of a pem fuel cell. Int. J. Progn. Health Manag. 2020, 5. [Google Scholar] [CrossRef]
- Li, Y.; Yang, F.; Chen, D.; Hu, S.; Xu, X. Thermal-physical modeling and parameter identification method for dynamic model with unmeasurable state in 10-kW scale proton exchange membrane fuel cell system. Energy Convers. Manag. 2023, 276, 116580. [Google Scholar] [CrossRef]
- Hu, Z.; Xu, L.; Li, J.; Ouyang, M.; Song, Z.; Huang, H. A reconstructedfuel cell life-prediction model for a fuel cell hybrid city bus. Energy Convers. Manag. 2018, 156, 723–732. [Google Scholar] [CrossRef]
- Lu, L.; Ouyang, M.; Huang, H.; Pei, P.; Yang, F. A semi-empirical voltage degradation model for a low-pressure proton exchange membrane fuel cell stack under bus city driving cycles. J. Power Sources 2007, 164, 306–314. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D.; Pera, M.C.; Zerhouni, N. Degradations analysis and aging modeling for health assessment and prognostics of PEMFC. Reliab. Eng. Syst. Saf. 2016, 148, 78–95. [Google Scholar] [CrossRef]
- Ou, M.; Zhang, R.; Shao, Z.; Li, B.; Yang, D.; Ming, P.; Zhang, C. A novel approach based on semi-empirical model for degradation prediction of fuel cells. J. Power Sources 2021, 488, 229435. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Q.; Zhang, L.; Zhou, K.; Zong, Y.; Liu, H.; Li, J.; Ma, L. Degradation prediction of pemfcs using stacked echo state network based on genetic algorithm optimization. IEEE Trans. Transp. Electrif. 2021, 8, 1454–1466. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, S.; Zhao, H.; Wang, Y. Durability estimation and short- term voltage degradation forecasting of vehicle pemfc system: Development and evaluation of machine learning models. Appl. Energy 2022, 326, 119975. [Google Scholar] [CrossRef]
- He, K.; Mao, L.; Yu, J.; Huang, W.; He, Q.; Jackson, L. Long-term performance prediction of pemfc based on lasso-esn. IEEE Trans. Instrum. Meas. 2021, 70, 3511611. [Google Scholar] [CrossRef]
- Zhu, W.; Guo, B.; Li, Y.; Yang, Y.; Xie, C.; Jin, J.; Gooi, H.B. Uncertainty quantification of proton-exchange-membrane fuel cells degradation prediction based on bayesian-gated recurrent unit. eTransportation 2023, 16, 100230. [Google Scholar] [CrossRef]
- Hua, Z.; Zheng, Z.; Pahon, E.; Pera, M.-C.; Gao, F. Multi-timescale lifespan prediction for pemfc systems under dynamic operating conditions. IEEE Trans. Transp. Electrif. 2022, 8, 345–355. [Google Scholar] [CrossRef]
- Morando, S.; Jemei, S.; Hissel, D.; Gouriveau, R.; Zerhouni, N. Proton exchange membrane fuel cell ageing forecasting algorithm based on echo state network. Int. J. Hydrogen Energy 2016, 42, 1472–1480. [Google Scholar] [CrossRef]
- Wu, Y.; Breaz, E.; Gao, F.; Paire, D.; Miraoui, A. Nonlinear performance degradation prediction of proton exchange membrane fuel cells using relevance vector machine. IEEE Trans. Energy Convers. 2016, 31, 1570–1582. [Google Scholar] [CrossRef]
- Ma, R.; Yang, T.; Breaz, E.; Li, Z.; Briois, P.; Gao, F. Data-driven proton exchange membrane fuel cell degradation predication through deep learning method. Appl. Energy 2018, 231, 102–115. [Google Scholar] [CrossRef]
- Zuo, B.; Cheng, J.; Zhang, Z. Degradation prediction model for proton exchange membrane fuel cells based on long short-term memory neural network and savitzky-golay filter. Int. J. Hydrogen Energy 2021, 46, 15928–15937. [Google Scholar] [CrossRef]
- Gouriveau, M.H.R.; Hissel, D. IEEE phm 2014 Data Challenge: Outline, Experiments, Scoring of Results, Winners. Tech. Rep. 2014. [Google Scholar]
- Pukrushpan, J.T. Modeling and Control of Fuel Cell Systems and Fuel Processors. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2003. [Google Scholar]
- Dong, S.; Luo, T. Bearing degradation process prediction based on the pca and optimized ls-svm model. Meas. J. Int. Meas. Confed. 2013, 46, 3143–3152. [Google Scholar] [CrossRef]
- Chen, J.; Jing, H.; Chang, Y.; Liu, Q. Gated recurrent unit based recurrent neural network for remaining useful life prediction of nonlinear deterioration process. Reliab. Eng. Syst. Saf. 2019, 185, 372–382. [Google Scholar] [CrossRef]
- Mao, L.; Jackson, L.; Davies, B. Effectiveness of a novel sensor selection algorithm in pem fuel cell online diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 7301–7310. [Google Scholar] [CrossRef]
- Pei, P.; Chen, D.; Wu, Z.; Ren, P. Nonlinear methods for evaluating and online predicting the lifetime of fuel cells. Appl. Energy 2019, 254, 113730. [Google Scholar] [CrossRef]
- Revankar, S.T.; Majumdar, P. Fuel Cells: Principles, Design, and Analysis, Fuel Cells Principles, Design, and Analysis; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Huang, S.Y.; Ganesan, P.; Jung, H.Y.; Popov, B.N. Development of supported bifunctional oxygen electrocatalysts and corrosion- resistant gas diffusion layer for unitized regenerative fuel cell applications. J. Power Sources 2012, 198, 23–29. [Google Scholar] [CrossRef]
- Xing, L.; Hossain, M.A.; Tian, M.; Beauchemin, D.; Adjemian, K.T.; Jerkiewicz, G. Platinum electro-dissolution in acidic media upon potential cycling. Electrocatalysis 2014, 5, 96–112. [Google Scholar] [CrossRef]
- Zhang, S.; Yuan, X.Z.; Hin, J.; Wang, H.; Friedrich, K.A.; Schulze, M. A review of platinum-based catalyst layer degradation in proton exchange membrane fuel cells. J. Power Sources 2009, 194, 588–600. [Google Scholar] [CrossRef]
- Lim, C.; Ghassemzadeh, L.; Van Hove, F.; Lauritzen, M.; Kolodziej, J.; Wang, G.G.; Holdcroft, S.; Kjeang, E. Membrane degradation during combined chemical and mechanical accelerated stress testing of polymer electrolyte fuel cells. J. Power Sources 2004, 257, 102–110. [Google Scholar] [CrossRef]
- Curtin, D.E.; Lousenberg, R.D.; Henry, T.J.; Tangeman, P.C.; Tisack, M.E. Advanced materials for improved pemfc performance and life. J. Power Sources 2004, 131, 41–48. [Google Scholar] [CrossRef]
- Yuan, X.Z.; Hui, L.; Zhang, S.; Martin, J.; Wang, H. A review of polymer electrolyte membrane fuel cell durability test protocols. J. Power Sources 2011, 196, 9107–9116. [Google Scholar] [CrossRef]
- Schettino, B.M.; Duque, C.A.; Silveira, P.M. Current-transformer saturation detection using savitzky-golay filter. IEEE Trans. Power Deliv. 2016, 31, 1400–1401. [Google Scholar] [CrossRef]
- Wu, M.T.; Tsai, M.H.; Huang, Y.Z.; Islam, S.H.; Hassan, M.M.; Alelaiwi, A.; Fortino, G. Applying an ensemble convolutional neural network with savitzky golay filter to construct a phonocardiogram prediction model. Appl. Soft Comput. 2019, 78, 29–40. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]



| LSTM | ACO-LSTM | |
|---|---|---|
| Hidden units | 100 | 100 |
| Solver | Adam | Adam |
| Iteration number | 100 | 100 |
| Learning rate decay algebra | 50 | 50 |
| Learning rate decay rate | 0.2 | 0.2 |
| Learning rate | 0.01 | Adaptive optimization |
| Dropout probability | 0.5 | Adaptive optimization |
| ACO-LSTM | 20% | 40% | 60% | 80% |
|---|---|---|---|---|
| Learning rate | 0.0091 | 0.0089 | 0.0088 | 0.0083 |
| Dropout probability | 0.0968 | 0.0462 | 0.0395 | 0.0181 |
| LSTM | 20% | 40% | 60% | 80% |
|---|---|---|---|---|
| MAPE | 0.0049 | 0.0019 | 0.0008 | 0.0004 |
| RMSE | 0.1996 | 0.1007 | 0.0409 | 0.0209 |
| R2 | 0.6328 | 0.9135 | 0.9604 | 0.9573 |
| ACO-LSTM | 20% | 40% | 60% | 80% |
| MAPE | 0.0014 | 0.0009 | 0.0007 | 0.0003 |
| RMSE | 0.0640 | 0.0470 | 0.0326 | 0.0201 |
| R2 | 0.9623 | 0.9812 | 0.9774 | 0.9603 |
| LSTM | FC1 (Stability) | FC2 (Rated) |
|---|---|---|
| MAPE | 0.0006 | 0.0012 |
| RMSE | 0.0406 | 0.0564 |
| R2 | 0.9857 | 0.9584 |
| ACO-LSTM | FC1 (Stability) | FC2 (Rated) |
| MAPE | 0.0005 | 0.0008 |
| RMSE | 0.0330 | 0.0463 |
| R2 | 0.9905 | 0.9711 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Min, H.; Zhao, H.; Sun, W.; Zeng, B.; Ma, Q. A Data-Driven Prediction Method for Proton Exchange Membrane Fuel Cell Degradation. Energies 2024, 17, 968. https://doi.org/10.3390/en17040968
Wang D, Min H, Zhao H, Sun W, Zeng B, Ma Q. A Data-Driven Prediction Method for Proton Exchange Membrane Fuel Cell Degradation. Energies. 2024; 17(4):968. https://doi.org/10.3390/en17040968
Chicago/Turabian StyleWang, Dan, Haitao Min, Honghui Zhao, Weiyi Sun, Bin Zeng, and Qun Ma. 2024. "A Data-Driven Prediction Method for Proton Exchange Membrane Fuel Cell Degradation" Energies 17, no. 4: 968. https://doi.org/10.3390/en17040968
APA StyleWang, D., Min, H., Zhao, H., Sun, W., Zeng, B., & Ma, Q. (2024). A Data-Driven Prediction Method for Proton Exchange Membrane Fuel Cell Degradation. Energies, 17(4), 968. https://doi.org/10.3390/en17040968





