Abstract
The competitiveness of large-scale offshore wind parks is influenced by the intermittent power generation of wind turbines, which impacts network service costs such as reserve requirements, capacity credit, and system inertia. Buffer power plants smooth the peaks in power generation, distribute electric power when the wind is absent or insufficient, and improve the capacity factor of wind parks and their profitability. By substituting the variable pressure storage with an underwater variable volume air reservoir and reducing the wastage of compression heat using liquid Thermal Energy Storage (TES), which eliminates the combustor, the plant design allows overcoming the most common drawbacks of CAES plants. Underwater Compressed Air Energy Storage (UW-CAES) plants are investigated with a thermodynamic model to drive the power plant design toward efficiency maximization. Functional maps, constrained on the plant pressure ratio and the number of compressor/turbine phases with inter-refrigerated/inter-heating phases, are drawn by solving the model iteratively for the heat exchangers’ effectiveness to meet the target turbine discharge temperature, selected in advance to avoid unfeasible mathematical solutions.
1. Introduction
Nowadays, wind parks play a pivotal role in the efforts to transition towards a more sustainable and environmentally responsible future. Large-scale wind parks symbolize a strategical shift from fossil fuel dependency towards cleaner, greener energy sources. Offshore installations capitalize on the consistent wind resource in open water, offering higher energy production and enhancing the grid integration with renewable energy sources. However, the wind pattern fluctuations pose challenges to the electrical grid management. The intermittency necessitates technological solutions integrating the grid to balance supply and demand, with the disadvantage of increasing operational costs and complexity. Wind power energy intermittency causes low-capacity credit, which means that renewable fleets of a given nominal power can replace only a fraction of that power on the electrical system [1].
In principle, an energy storage coupled with a power generation system mitigates the intermittency, improving the capacity credit, and allowing the electrical system to meet peak demands. Among recent solutions like batteries, superconductors, regenerative fuel cells, and Pumped Hydroelectric Storage, Compressed Air Energy Storage (CAES) is an affordable technology to store and utilize intermittent renewable energy when needed [2]. Traditional CAES systems use methane gas burners to preheat the air sampled from the compressed air storage reservoir. Recently, CAES systems store the heat produced during compression in Thermal Energy Storage (TES) and release it during expansion, increasing the plant’s efficiency and cutting polluting emissions by reducing methane consumption.
Kim et al. [3] examined the advantaged of CAES plants, highlighting their high reliability, economic feasibility, and minimal environmental impact, thereby positioning them as a viable option for large-scale energy storage. The authors also addressed associated disadvantages, such as compression-dissipated heat, dependence on fossil fuels, and dependence on geological formations. Lund and Salgi [4] criticized the investment in conventional CAES as the feasibility would depend on the regulating power market. Limited capacity would benefit from the monthly payment from the market, which is also likely to change in price during the plant’s lifetime. However, if coupled with wind power systems, an abundant storage volume placed in underground caverns would be available to deal with intermittency and daily energy output of modern wind parks with a minor environmental impact. Guo et al. [5] explained the coupling of CAES systems with wind, solar, and biomass renewable energy sources, employing series, parallel, and integrated couplings. They investigated the advantages and disadvantages of each system, emphasizing that wind-CAES installations facilitate the comprehensive exploitation of wind energy, thereby amplifying the CAES output. Bouman et al. [6] performed the life cycle assessment of conventional natural gas combustion CAES and Thermal Energy Storage CAES based on an adiabatic process (A-CAES), showing that both configurations have a lower environmental impact per kWh of electricity than that of the average electricity mix, except mineral resource depletion. Ochmann et al. [7] resumed the advantages of A-CAES in a lower environmental impact than conventional CAES, due to the elimination of the auxiliary fuel combustion during the discharge process and in higher energy efficiency by exploiting a large amount of heat stored during the compression instead of losing it irreversibly. Thermal energy is stored in the TES during compression and is released during the expansion, approximating an isothermal process for maximizing the cycle efficiency. CAES layout improvements were depicted by Cardenas and Garvey [8] with a recent TES + HX unit based on packed-bed thermal storage, air-to-air heat exchangers, and an ambient air blower. This system showed a low levelized cost of storage compared to conventional heat storage subsystems and an efficiency improvement.
Different CAES solutions adopt constant-volume storage, with compressed air accumulated in pressurized tanks, caverns, depleted oil or gas fields, or abandoned mines. A disadvantage is that the electrical power output produced by the turbines decreases with the drop in air pressure as it is discharged from the storage. Diversely, a variable-volume tank maintains a constant pressure during air depletion. This solution can be adapted to underwater variable-volume tanks at depths up to 600 m, thus achieving constant-pressure storage in the range of 40–60 bar. A new Pumped Hydro Storage (PHS) is investigated, such as the famous StenSea project [9], pumping seawater in and out of submerged hollow spheres of polyester or fiberglass fabric with coatings with reversible pumps.
Rabi et al. [10] conducted a comprehensive review of CAES facilities, delineating their strengths and weaknesses. The study further provided a valuable reference for the strategic planning and integration of diverse CAES into energy systems. The authors elucidated primary limitations inherent in CAES technologies, notably encompassing prolonged response times, low depth of discharge, and suboptimal round-trip efficiency. The attainment of high cycle efficiency necessitates the adoption of a specific compressor and expansion process design [11]. It is crucial to opt for adiabatic compression departing from the conventional isothermal compression, typically accomplished through inter-refrigeration. The combination of high pressure and temperature in the last phases and the demand for high efficiency and fast start-up times is not achieved by conventional compressors. Compression ratios of about 50 are critical for compressors, as the air temperature increase in about 700 °C is challenging for materials. Cooled compression by injecting water into the air stream was proposed, but the solution is still under investigation. An expansion ratio of 50 is not actually a problem for turbines as it is obtained in a few turbine phases with isentropic efficiencies above 90%. Heat has to be added before air expansion to avoid extremely low temperatures at the turbine discharge, possibly leading to ice formation.
Compared to existent and operational CAES system schemes (Alabama [1], Huntorf [12,13,14]), the system is designed with Thermal Energy Storage to accumulate the heat removed from the compressed air and an extensive concrete expansion vessel as an underwater reservoir [15]. The thermal energy stored during the compression phase is transferred to the air extracted from the reservoir to keep the turbine inlet temperature constant during the expansion. The pressure of the reservoir is kept constant by the hydrostatic pressure, and so is the inlet pressure at the first inter-heater. During the discharge process, the vessel is filled with water as the air is released to the turbine. Alternatively, energy bags can be used as reservoirs [16]. Wang et al. conducted numerical modeling of the pressurized accumulator for UW-CAES applications, considering various flow conditions [17]. Through modular analyses, they determined that the natural frequency of the accumulator significantly exceeded the vortex-shedding frequency behind the pressurized reservoir, indicating a low risk of fatigue damage attributable to vortex-induced vibration.
The hot TES constitutes a separate insulated tank [18] receiving the thermal energy from the inter-refrigerated heat exchangers, to be released to the inter-heated heat exchangers upstream of the expanders. Such a UW-CAES power plant is suitable for grid-connected and isolated power grids. Floating offshore wind parks in deep waters [19] are preferred layouts for this solution (Figure 1) because the proximity of the storage to the turbines minimizes the pressure losses of the system.
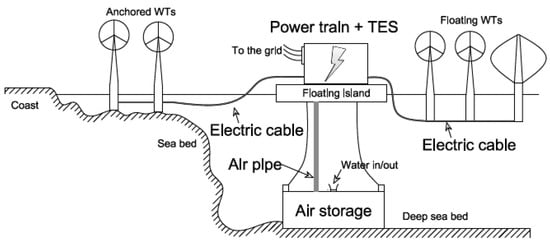
Figure 1.
Floating offshore wind farm with a UW-CAES plant.
The performance analysis of a UW-CAES system was conducted by Wang et al. [20]. The findings from energy and exergy assessments indicate that the round-trip efficiency is responsive to the isentropic efficiency of expanders and compressors, as well as the efficiencies of electric motors and generators. The effects of heat exchangers, the self-discharge rate of the reservoir, the inner diameter of pneumatic pipelines, and the insulation of the hot-oil tank on the round-trip exergy efficiency were found to exhibit highly nonlinear behavior.
The optimization between the minimum compression specific work and the maximum specific expansion work is idealized as an isothermal process. However, massive heat exchange through turbo-machinery is not technically feasible, while it is practicable only partially for reciprocating machines [21]. Currently, para-isothermal processes like inter-refrigerated compression and inter-heated expansion are realized to approach ideal isothermal processes (Figure 2), and the whole compression/expansion process is subdivided into elementary pressure ratio phases. A limiting number of compression and expansion phases of 5–6 may be economically feasible by balancing the additional investment cost and marginal work-efficiency gain.
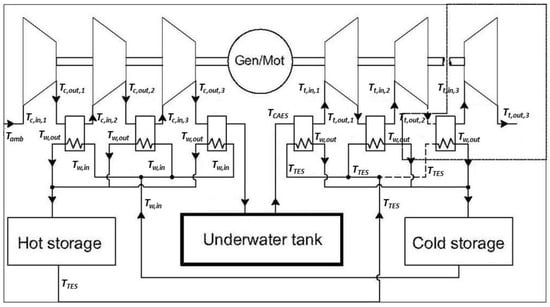
Figure 2.
Detailed CAES system layout power train + TES.
The maximum air temperature rise during compression is lowered. It leads to low-pressure water used as a cooling medium and lower TES temperatures, driving a reduction in thermal losses during heat exchange. Hence, a combination of para-isothermal compression/expansion processes and TES represents a technological solution to improving the efficiency of CAES systems. For such a system, Hunt et al. [22] estimated an investment cost from 1500 to 3000 USD/kW for installed capacity and from 1 to 10 USD/kWh for energy storage, additionally indicating that the greater the sea depth, the lesser the cost of the project.
Different works are based on A-CAES modeling, even though just a few treat UW plants. A model was developed by Zhou et al. [23] to illustrate variable conditions and the feasibility of an A-CAES system. The treatment of heat exchangers is similar to what is shown in this work in Section 2.4 and Section 2.5, with outlet temperatures developed as a function of the heat exchanger’s effectiveness. Tola et al. [24] modeled two configurations of an A-CAES plant with air and thermal oil. Since the tanks in the oil plant operate at an increasing pressure, structural issues occur, showing the need for design and maintenance of the tanks. Sciacovelli et al. [25] presented a dynamic model for an A-CAES plant featuring packed bed TES, encompassing full and off-design performance. Their model incorporated algebraic and differential sub-models, elucidating the transient characteristics of the thermal storage, cavern dynamics, and compression/expansion phases. The model demonstrated round-trip efficiency outputs surpassing 70%, with TES efficiency exceeding 90%.
A preliminary design of a UW-CAES operating at constant hydrostatic pressure and variable volume was investigated by Astolfi et al. [26]. The system included modular multi-stage compressors, partial intercoolers, an expansion turbine incorporating pre-heaters, TES with distinct temperature levels, and an underwater modular CAES. Their assessment indicated that a round-trip efficiency in the range 75–80% is achieved contingent upon the configuration of the compressor section. Notably, an adequate turbine inlet temperature was allowed through the utilization of the TES, facilitating the recovery of heat generated during compression.
The turbine discharge temperature must be bounded inferiorly to prevent ice formation and superiorly due to technological limitations in heat exchange. While CAES plant performance is affected by the turbine discharge temperature, the impact of variations in discharge temperature has not been extensively studied in the existing literature. The limitations on the turbine discharge temperature, as explained in Section 2.8, suggest an iterative approach accomplished by specifying a target discharge temperature. With some simplifying assumptions, the specific work of the compression and expansion phases is determined by iterating the heat exchangers’ effectiveness. Hence, a numerical model of a modern UW-CAES plant is developed with a thermodynamic cycle maximizing the round-trip efficiency as a function of the turbine discharge temperature. The optimization of efficiency is accomplished through the minimization of compressor specific work and the maximization of turbine specific work. In addition, the model optimizes the number of para-isothermal compression/inter-refrigeration phases and the number of para-isothermal expansion/inter-heating phases.
Predictions of CAES efficiency, TES temperature, and turbine specific work are developed as a function of the plant pressure ratio and the number of compression/inter-refrigeration and expansion/inter-heating phases.
A simple routine in Matlab developed through the literature equations of turbogas systems and heat exchangers enabled the development of the presented UW-CAES plant efficiency prediction method. The following approximations provide easy access to this method:
- -
- The temperature of the pressurized air TCAES in the underwater tank is defined in a steady state at the end of its natural cooling process to simulate plant operating conditions when the wind power is insufficient.
- -
- The heating storage is approximated as adiabatic. However, the hot water temperature in the thermal storage TTES is determined mathematically by the heat recovery calculation from the compression cycle.
- -
- Pressure losses in the exchangers are approximated with a sub-model. In contrast, continuous pressure drops in the air and water piping are not considered because they depend on the type of plant layout.
- -
- The mathematical solutions in the domain are investigated for equal heat capacities and air and water flows, implying that Cmin/Cmax = 1 is desirable to reduce entropy in counter-current heat exchangers [27,28].
- -
- A unitary air mass flow rate is assumed, allowing the problem to be treated by specific magnitude or a unit power for general validity.
2. Physical Model
2.1. Gas Model
The air pressure to develop in the UW-CAES system must be equal to or higher than that of water at the reservoir depth. The working temperature in the cycle is at least twice the reduced temperature of the plant (TCAES/Tc). Therefore, the approximation of the thermodynamic cycle with the Ideal Gas Law is generally feasible.
Since the air critical pressure pc is 37.36 bar, the condition for the reduced pressure of the plant (pCAES/pc) << 1 is limited to a few bars, beyond which the air behaves as a Real Gas. However, for the purposes of this work, the error committed by applying the ideal gas law on specific heat Cp and polytropic index k is limited and thus considered acceptable.
2.2. UW-CAES
Assuming that the air is drawn by the compressor from the environment at standard pressure patm, the CAES plant pressure ratio β is introduced by Equation (1), with the barometric pressure at the plant water depth denoted by pCAES.
β = pCAES/patm
The CAES temperature TCAES is determined at the discharge of the last compressor phase. However, its significance arises only when the expanders are immediately operating, a scenario rarely encountered. Generally, the compressor operates during periods of surplus electricity from the wind park, which does not align with the shutdown intervals of wind turbines. After several hours of downtime, the pressurized reservoir experiences abundant heat loss. A steady thermal equilibrium is established between the pressurized reservoir and the external environment. The temperature is, thus, approximated with a permanent thermocline as a function of depth [29].
The pressure ratio β is correlated to the depth d in [m] according to Stevin’s law, i.e., d = (pCAES − patm) × (ρw × g)−1, with the average water density in kg/m3 denoted by ρw, and the gravity acceleration denoted by g. Reasonably, ρw is assumed to be 1025 kg/m3. By disregarding its actual temperature and assuming a complete cooling of the reservoir, the UW-CAES temperature TCAES is determined according to the permanent thermocline. Consequently, the air is pre-heated from this temperature in the expander section. Note that the CAES volume, and thus the energy buffer over a time period, is not investigated in this work and is left for future assessment.
2.3. TES
The hot TES temperature is determined as the cooling water mass flow mixes at the exit of all heat exchangers. Regardless of the number of devices, as the water mass flow rates are equal, the mixing temperature is achieved from the mean value (2). The temperature at the outlet of each heat exchanger is denoted by Tw,out,i, and the compressor/inter-refrigerated phases are denoted by Nc. The hot TES temperature is then equal to TTES. The thermal storage and all pipes are considered adiabatic, so no heat flow is allowed in steady-state from the TES and surroundings. In turn, TTES denotes the inlet temperature of the water heating the airflow upstream of the turbine phases. Diversely, the cold water feeding each inter-refrigerator past each compressor phase is always at 288.15 K, irrespective of the upstream water flow mixing, while no pressure data are investigated for the water circuit.
TTES = Σi Tw,out,i/Nc
The water flows mixing downstream the pre-heaters would determine a new cold TES temperature. Although not discussed further, the maximum temperature for TES for water is limited by the critical point of saturated water, while typical plants operate at a maximum temperature of 250 °C [18].
2.4. Inter-Refrigeration
Counter-flow inter-refrigeration heat exchangers are modeled using Equation (3), in which ε denotes the heat exchangers’ effectiveness, Ta,in and Ta,out denote the inlet and outlet air flow temperatures, respectively, and Tw,in denotes the cold water inlet temperature. Air and water heat capacities are denoted by Ca and Cw, with Cmin = min (Ca, Cw).
ε = (Ca/Cmin) × (Ta,in − Ta,out)/(Ta,in − Tw,in)
The inlet air temperature at the first inter-refrigerator equals the ambient temperature, Ta,in = Tamb, while for the following exchangers, Ta,in = Tc,out, with the outlet temperature of the i-th compressor phase defined by Tc,out. The cold water inlet temperature is assigned Tw,in = 288.15 K. Equation (3) solved for Ta,out yields Equation (4), with the air temperature variation denoted by ΔTa (5).
Ta,out = ε × (Cmin/Ca) × Tw,in + Ta,in × (1 − ε × (Cmin/Ca))
Δ
Ta = (Ta,in − Ta,out)
Since the heat transferred from air to water is the same, the water outlet temperature Tw,out is determined from Equation (6), with its temperature variation ΔTw (7) and the air to water heat capacity ratio Cr defined as Ca/Cw.
Tw,out = Tw,in + Cr × ΔTa
ΔTw = (Tw,out − Tw,in)
The pressure drop Δphe through the heat exchanger is formulated with Equation (8) with Δpu equal to the 3% of the inlet pressure pa,in. Hence, the outlet pressure pa,out is determined from Equation (9).
Δphe = pa,in × Δpu
pa,out = pa,in − Δphe = pa,in × (1 − Δpu)
2.5. Inter-Heating
The model of counter-flow inter-heating heat exchangers is developed according to Equation (10), with the known water inlet temperature Tw,in = TTES. In this case, the unknown term is represented by the water outlet temperature Tw,out.
ε = (Cw/Cmin) × (Tw,in − Tw,out)/(Tw,in − Ta,in)
Solving this mathematical statement for Tw,out yields Equation (11), so that the water temperature variation ΔTw is determined from Equation (12).
Tw,out = ε × (Cmin/Ca) × Ta,in + Tw,in × (1 − ε × (Cmin/Ca))
ΔTw = (Tw,in − Tw,out)
On the air side, the unknown Ta,out is determined from Equation (13) by introducing the heat capacity ratio, and thus, the airflow temperature variation ΔTa (14), i.e.,
Ta,out = Ta,in + ΔTw/Cr
ΔTa = (Ta,out − Ta,in)
The equations to determine the pressure drop of the heat exchanger are equal to (8,9).
2.6. Compressor Phases
The CAES pressure in the variable-volume underwater reservoir is developed using multiple compression phases succeeded by heat exchangers recovering thermal energy.
To overcome the pressure losses of exchangers and piping, the maximum pressure developed in the cycle pc,out must be > pCAES.
If the inlet pressure of the heat exchanger pa,in is equal to the compressor outlet pressure, pc,out can be written as pc,out = pa,out/(1 − Δpu). For a single-phase compressor and a single inter-refrigeration phase, pc,in = patm, and pa,out = pCAES, so that the pressure ratio, defined as βc = (pc,out/pc,in), becomes a function of β, i.e., βc = β/(1 − Δpu). The algebraic development for Nc phases of equal βc,i yields Equation (15) for a generic i-th phase. The compression ratio ensures achieving the phase outlet pressure pc,out (16).
βc,i = β 1/Nc/(1 − Δpu)
pc,out = pc,in × βc
The outlet temperature Tc,out is now determined from the mathematical statement (17) as a function of the polytropic efficiency ηp,c of the process [30], the polytropic index k, the pressure ratio βc, and the compressor phase inlet temperature Tc,in. The polytropic efficiencies selected for the compressor and the turbine are ηp,c = 0.892, ηp,t = 0.925, respectively. The first phase inlet temperature Tc,in equals the environment air temperature, while the last phase discharge temperature and pressure are those supplied to the CAES system. However, the temperature is allowed to drop to a constant value for its later use in the expanders.
Tc,out = Tc,in × βc,i (k−1)/(k×ηp,c)
Finally, the specific work of the compressor phase is achieved by the product of the specific heat to the temperature variation in the thermodynamic process (18). The sum of each partial specific work yields the specific work of the compressor (19).
Wi,c = Cp × ΔTc,i
Wc = Σi Wi,c
2.7. Turbine Phases
The pre-heaters increase the air temperature before its expansion in the gas turbine. Each phase develops a different pressure ratio βt,i from that achieved in the previous section. Equation (20) shows the result for the i-th turbine phase, valid for Nt turbine phases, and includes the heat exchangers’ pressure drop. The equation ensures that the air pressure discharging from the turbine is equal to or higher than patm. The outlet pressure is thus given by Equation (21).
βt,i = β 1/Nt × (1 − Δpu)
pt,out = pt,in/βt
Equivalent to the compressor treatment, the phase outlet temperature Tt,out is given by Equation (22) as a function of polytropic efficiency ηp,t, polytropic index k, pressure ratio βt, and inlet temperature Tt,in.
Tt,out = Tt,in/βt,i ηp,t×(k−1)/k
The specific work of the expansion phase is defined as the product of the specific heat to the temperature variation in the thermodynamic process (23). The sum of each partial specific work yields the specific work of the gas turbine (24).
Wi,t = Cp × ΔTt,i
Wt = Σi Wi,t
2.8. Numerical Method
The inter-refrigerated compression and inter-heated expansion sections are modeled at equal mass flow rates, similar to the work of Tola et al. [24]. In addition, a constant effectiveness ε is assumed in all heat exchange processes.
The discharge temperature may vary depending on the processed airflow and its thermodynamic conditions in the cycle. A low air temperature may determine ice formation at the turbine outlet, even with an ambient air temperature above 0 °C. If the moist air temperature approaches freezing point, antifreeze systems are needed to protect the devices from damage that could cause fast-moving ice particles. Although the effect of humidity is neglected, it is sufficient to demonstrate that the air discharged from the cycle is kept beyond a safety margin.
The round-trip efficiency η is investigated from the hypothesis η = η(Cr, ε, β, N, Tamb, Tw,in, TCAES). Currently, the ambient air temperature Tamb and cold water inlet temperature Tw,in are treated as constants for a steady problem, i.e., 25 °C and 15 °C, respectively. The temperature achieved by the CAES reservoir TCAES after its asymptotic cooling varies slightly as a function of depth based on the permanent thermocline. Since TCAES can be written algebraically as a function of the pressure ratio β, it is no longer considered independent.
Intending to maintain the heat capacity of the TES medium Cw equal to that of the air Ca, as in the work of Zhou et al. [23], the heat capacity ratio yields Cr = 1, irrespective of the pressure ratio and the number of phases. Since the plant capacity is not investigated, a unitary air mass flow rate is assumed.
By increasing the number of phases N, a given plant efficiency is achieved by lowering ε, thus reducing the “cost” in performing the heat exchange, i.e., resulting in a lower enthalpy exchange from air to water in inter-refrigerators and from water to air in inter-heaters. The peak in η reduces at high N, but η becomes more evenly distributed over the domain of ε. The dependency of the round-trip efficiency from the independent variable Cr is discarded, resulting in η = η(ε, β, N).
Analytical solutions do not allow distinguishing between technically acceptable and unacceptable solutions. A control of the air temperature released by the turbine is the focus of the present optimization, implying that η = η(ε, β, N, Tt,out). Since a mathematical solution avoiding a discharge temperature near the freezing temperature is desirable, a convenient safety margin of 10 °C is chosen for Tt,out,des. A high ΔTt improves the round-trip efficiency of the plant η, which, in turn, is defined as the turbine-to-compressor specific work ratio (25). ΔTt also depends on the turbine inlet temperature, which is influenced by the heat exchanged from the TES and the number of turbine phases Nt.
η = Wt/Wc
The plant efficiency is calculated with a simple routine in Matlab developed according to the scheme illustrated in Figure 3. From a first guess of ε, compressor and turbine phases are solved sequentially, thus achieving the turbine outlet temperature Tt,out at the last turbine phase. The heat exchangers’ effectiveness ε is updated with Equation (27), reducing the deviation |Tt,out − Tt,out,des| at each iteration. At convergence, the error falls within tolerance, i.e., |Tt,out − Tt,out,des| < tol, and the target discharge temperature Tt,out.des is obtained at the outlet of the thermodynamic cycle. The boundary conditions for η and ε are introduced as 0 < η < 1 and 0 < ε < 1. The formula to update ε is derived from the last inter-heater heat exchange, assuming the ratio of heat capacities for the heat exchanger Ca/Cmin = 1. Replacing Tt,out,des = Tt,out into the expander Equation (22) and solving for Tt,in, it gives:
Tt,in = Tt,out × βt,end ηp,t×(k−1)/k
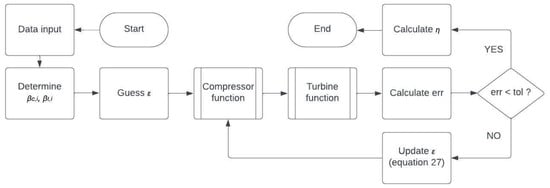
Figure 3.
Iterative scheme for the CAES thermodynamic cycle.
The actual effectiveness ε(j) is developed from Equations (10) and (26) yielding Equation (27), which is solved to update the thermodynamic cycle and the last heat exchanger inlet temperature Ta,in,end(j) up to convergence of the variable Tt,out.
ε(j) = (Tt,out,des × βt,end ηp,t×(k−1)/k − Ta,in,end(j))/(TTES − Ta,in,end(j))
3. Results and Discussion
The method yields several outputs, encompassing CAES efficiency, TES water temperature, and specific work of compressor and turbine phases. Initially, simulations are performed with varying CAES pressure ratios. The resulting trends of efficiency, specific work, and water storage temperature are illustrated for plants with reservoirs at different depths, once the number of phases is defined. Next, simulations are performed with a constant CAES pressure ratio while modifying the number of phases. This test facilitates the optimization of the para-isothermal phases in a CAES plant for a chosen turbine discharge temperature. The optimization with varying Tt,out is illustrated in charts corresponding to each pressure ratio.
Contour plots of efficiency η as a function of the turbine discharge temperature Tt,out and the pressure ratio β are presented in Figure 4 for a constant number of phases N. The increase in the discharge temperature shows a substantial improvement in the CAES plant η at a constant β due to a drop in the compressor specific work and a rise in the turbine specific work, as shown later on. Diversely, an increase in β at a constant Tt,out results in a decline in the round-trip efficiency driven by a sharper increase in the compressor specific work than that of the turbine specific work, despite the availability of a higher storage temperature in the TES.
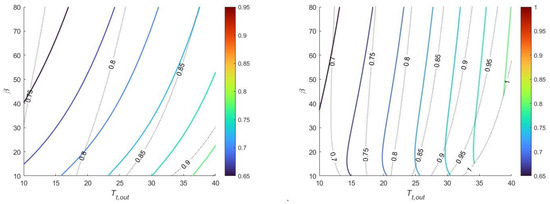
Figure 4.
Contour plots of the round-trip efficiency η as a function of the turbine discharge temperature Tt,out, pressure ratio β for dual-phase plants N = 2 (left) and multi-phase plants N = 4. (right). The dotted lines represent the heat exchangers’ effectiveness ε solving the mathematical problem.
In other words, an identical target efficiency is not feasible at the same Tt,out in plants at different β. A rise in Tt,out is imperative to achieve the same η in plants with increasing β. In this example, the trend of the round trip efficiency becomes almost vertical at N = 4, indicating that η is just slightly dependent on β at high N. Furthermore, equal η is achieved at a lower Tt,out in plants with more phases. The interrupted curves in the charts represent inadmissible solutions beyond the boundary conditions.
The TTES is unconstrained in this work. As illustrated in Figure 5, the turbine discharge temperature TTES increases with β and, thus, with depth. The variation in TTES depends on the setpoint of Tt,out, which alters the exchangers’ effectiveness. For example, the storage temperature is higher in dual-phase plants (N = 2) compared to four-phase plants (N = 4) due to the higher enthalpy available at the inter-refrigerators. Furthermore, with a turbine discharge temperature Tt,out of 10 °C in a dual-phase plant, a TTES between 140–305 °C on the domain of β is expected, whereas it drops to 75–145 °C in a four-phase plant.
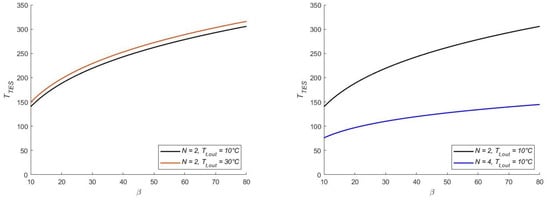
Figure 5.
Plots of the TES temperature TTES as a function of the pressure ratio β, for dual-phase plants N = 2 and different turbine discharge temperatures Tt,out (left), and for dual or four-phase plants N = 2–4 and a single value of Tt,out (right).
Figure 6 illustrates the increment in the turbine specific work Wt and compressor specific work Wc vs. the pressure ratio at a constant Tt,out. The left chart illustrates N = 2, while the right chart shows N = 2 to 4. For a given number of phases N, if the turbine discharge temperature is raised from 10 °C to 30 °C at a constant β, Wt slightly decreases, and Wc marginally increases. This observation indicates that a higher discharge temperature is beneficial for improving efficiency.
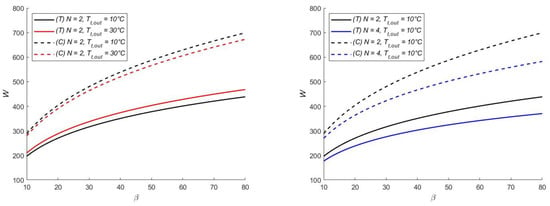
Figure 6.
Plots of the turbine specific work Wt (continuous lines) and compressor specific work Wc (dashed lines) as a function of the pressure ratio β, for different turbine discharge temperatures Tt,out (left), and for pressure ratios β = 25 or β = 50 and a single value of Tt,out (right).
Maintaining a constant turbine discharge temperature, the increase in the compressor specific work is higher than that of the turbine at a low N with an increasing β. Therefore, an increase in the number of phases N is beneficial for the plant only at high β, as depicted in the right chart.
The numerical solution of the mathematical problem is investigated for variable discharge temperature Tt,out, and a reasonable number of phases (N = 2 to 8) in Figure 7. The left and right charts represent pressure ratios of 25 and 50, respectively. The intersection of the desired cost iso-curve (i.e., effectiveness ε) with the target efficiency η determines the number of phases needed to achieve the design round-trip efficiency. For instance, at β = 25, five-turbine and compressor phases are required to achieve η = 0.725 at a discharge temperature of 25.3 °C. This design solution implies a substantial cost for the technology with high enthalpy exchange between the fluids (ε = 0.853). However, the same η is achieved with four phases at a Tt,out = 25.8 °C and a moderately lower effectiveness ε = 0.845, resulting in a drop in the investment cost. The same rationale applies to the chart at higher β, with the distinction that a different ε is required to enable the plant to reach the target η. The inflection point of the target η iso-curve at a constant β represents a point at a minimum “technical cost” considering the number of phases and effectiveness generating that efficiency.
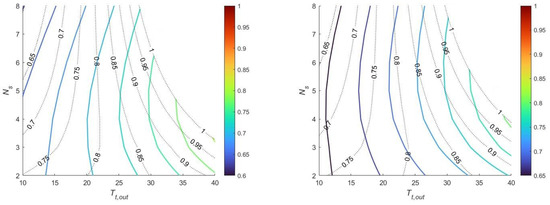
Figure 7.
Contour plots of the round-trip efficiency η as a function of the turbine discharge temperature Tt,out and number of phases N for pressure ratio β = 25 (left) and β = 50 (right). The dotted lines represent the heat exchangers’ effectiveness ε solving the mathematical problem.
The decreasing trend of TTES as a function of the number of phases N is shown in Figure 8. This phenomenon is explained by the lower enthalpy of water as the number of compression phases increases, indicating a reduced heat transfer to the compressed air at the turbine section. With air discharge temperatures between 10 and 30 °C, a TTES range of approximately 59–205 °C is expected at β = 25 (left chart), while it varies to 67–262 °C at β = 50 (right chart).
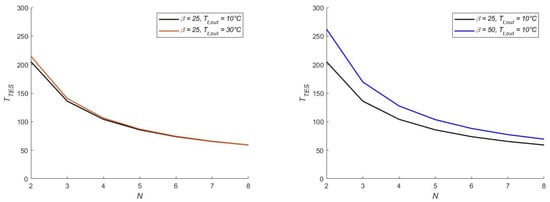
Figure 8.
Plots of the TES temperature TTES as a function of the number of phases N, for CAES pressure ratio β = 25 and different turbine discharge temperatures Tt,out (left), and for pressure ratios β = 25 or β = 50 and a single value of Tt,out (right). The dotted lines represent the heat exchangers’ effectiveness ε solving the mathematical problem.
The compressor specific work Wc and the expander specific work Wt decrease with an increase of N, as shown in Figure 9. However, both exhibit a broad increase if the turbine discharge temperature is raised from 10 °C to 30 °C at a constant N. As will be clarified shortly, it is not possible to increase much the discharge temperature because unacceptable solutions arise due to the boundary condition of the maximum heat exchangers’ effectiveness. Furthermore, at a given N, the compressor specific work Wc may increase faster or slower than the turbine specific work Wt, depending on Tt,out, and β. It demonstrates that a number of phases optimizing the plant efficiency exist. According to the numerical data, we found that the number of phases optimizing the plant efficiency at a high β is higher than the number of phases optimizing the plant efficiency at a low β while maintaining constant Tt,out.
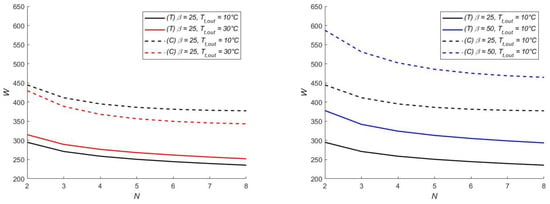
Figure 9.
Plots of the turbine specific work Wt (continuous lines) and compressor specific work Wc (dashed lines) as a function of the number of phases N, for pressure ratio β = 25 and different turbine discharge temperatures Tt,out (left), and for pressure ratios β = 25 or β = 50 and a single value of Tt,out (right).
The optimum number of phases is clearly indicated in Figure 10 over the N-η plane, with efficiency curves drawn for different Tt,out, excluding those for Tt,out > 30 °C due to a lack of feasible solutions determined by the boundary condition on ε. The N maximizing η corresponds to the optimum sought at each plant pressure ratio. The optimum N at a given turbine discharge temperature generally increases with the CAES β, while by fixing β, it increases with Tt,out. The turbine enthalpy variation decreases with an increase in N. However, as the reduction in the compressor enthalpy variation is more significant, an optimum efficiency is found at a given β and Tt,out. Moreover, these charts show that the optimized round-trip efficiency is compliant with the outputs shown by Astolfi et al. [26].
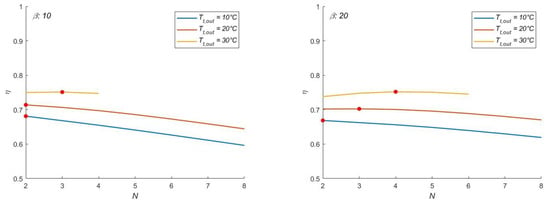
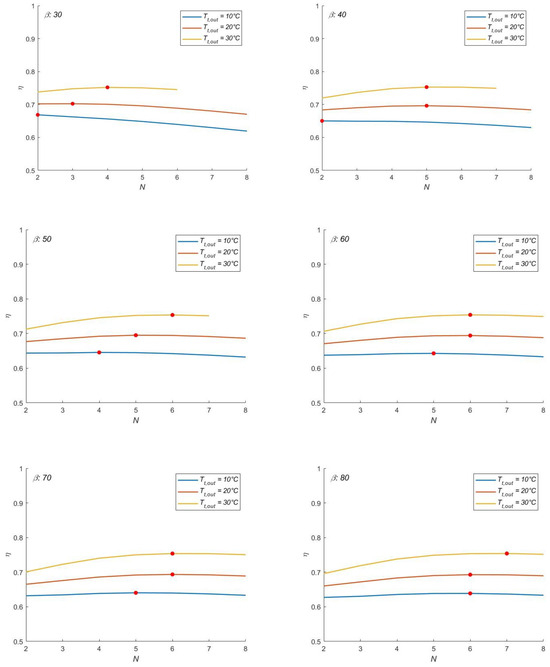
Figure 10.
Optimum round-trip efficiency η as a function of the number of phases N, for different turbine discharge temperatures Tt,out.
4. Conclusions
A model iterating the heat exchangers’ effectiveness is developed to ensure an outline modeling for constant pressure UW-CAES systems. The maximum efficiency expected from the CAES plant is quickly computed once that pressure ratio, ambient air temperature, thermal storage temperature, and CAES temperature are defined. Hence, considering approximations such as the adiabaticity of the TES, the constant temperature of the pressurized reservoir, the simplified model of the exchangers’ pressure drop, and the equality between the heat capacities of the two fluids, the proposed method facilitates the estimate of the plant performance and allows to integrate the producibility of the wind farm with that of the CAES plant, thus limiting the drawback of the wind intermittency.
A high turbine discharge temperature always boosts the plant’s round-trip efficiency, increasing the turbine specific work. However, the turbine discharge temperature is constrained to ensure proper operation between a minimum safety temperature, chosen to avoid ice formation, and a maximum threshold, bounded by the maximum heat exchangers’ effectiveness, beyond which no acceptable solution is depicted.
Optimizing high-pressure ratio plants offers the advantage of enhancing efficiency while maintaining a constant discharge temperature. However, it necessitates consideration of additional technical and material limitations, such as increasing the temperature of Thermal Energy Storage (TES) and the need for reservoirs operating at extremely high pressures. Furthermore, improving the efficiency in high-pressure ratio plants entails a substantial investment to maximize the number of phases, resulting in higher costs. In contrast, optimizing efficiency in low-pressure ratio plants is more feasible as it requires only a few phases. The drawback is that low-pressure ratio plants may exhibit lower efficiency at a low turbine discharge temperature.
The given iterative approach can be used to calculate the optimal number of phases for maximizing round-trip efficiency, considering the selected turbine discharge temperature and plant pressure ratio. If the selected number of phases is less than the optimum, the round-trip efficiency decreases due to a more significant increase in compressor specific work than that of the turbine. Likewise, if the chosen number of phases exceeds the optimum, the plant efficiency diminishes due to a more substantial reduction in the turbine specific work than that in the compressor.
Possible improvements to the model may include the following:
- -
- The pressure drop in ducts and pipes can be calculated based on the actual layout of the system.
- -
- The pressure drop in the exchangers can be determined using the manufacturer’s exchanger data sheets. In addition, the size of the exchangers can be derived from the NTU method.
- -
- When the wind farm has an intermittent operation, and the CAES plant is activated, the expected temperature reached by the pressurized air can be determined with a transient model.
Author Contributions
Conceptualization, L.C., L.B. and D.O.; methodology, L.C.; software, L.C.; validation, L.C.; formal analysis, L.C. and L.B.; investigation, L.C. and D.O.; resources, L.B.; data curation, L.C.; writing—original draft preparation, L.C.; writing—review and editing, L.C. and L.B; visualization, L.C.; supervision, L.B.; project administration, L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
UW-CAES—Underwater Compressed Air Energy Storage; A-CAES—Adiabatic compressed air energy storage; TES—Thermal Energy Storage.
Nomenclature
| Ca | Air heat capacity [kJ K−1 s−1] |
| Cw | Water heat capacity [kJ K−1 s−1] |
| Cmin | Minimum heat capacity [kJ K−1 s−1] |
| Cp | Air specific heat [kJ kg−1 K−1] |
| Cp,w | Water specific heat [kJ kg−1 K−1] |
| Cr | Heat capacity ratio [-] |
| d | Depth [m] |
| g | Gravity acceleration [m s−2] |
| Nc | Compressor phases # |
| N | phases # |
| Nt | Turbine phases # |
| patm | Ambient pressure [bar] |
| pa,in | Air inlet pressure [bar] |
| pa,out | Air outlet pressure [bar] |
| pc | Air critical pressure [bar] |
| pCAES | CAES pressure [bar] |
| Tatm | Ambient temperature [K] |
| Ta,in | Air inlet temperature [K] |
| Ta,out | Air outlet temperature [K] |
| Tc | Air critical temperature [K] |
| TCAES | CAES temperature [K] |
| Tc,in | Compressor phase inlet temperature [K] |
| Tc,out | Compressor phase outlet temperature [K] |
| TTES | TES temperature [K] |
| Tt,in | Turbine phase inlet temperature [K] |
| Tt,out | Turbine phase outlet temperature [K] |
| Tt,out,des | Design discharge temperature [K] |
| Tw,in | Water inlet temperature [K] |
| Tw,out | Water outlet temperature [K] |
| Wc | Compressor specific work [kJ kg−1] |
| Wt | Turbine specific work [kJ kg−1] |
| β | CAES pressure ratio [-] |
| βc,i | Compressor phase pressure ratio [-] |
| βt,i | Turbine phase pressure ratio [-] |
| Δphe | Heat exchangers’ pressure drop [bar] |
| Δpc | Compressor phase pressure drop [bar] |
| Δpu | Per unit pressure drop [-] |
| Δpt | Turbine phase pressure drop [bar] |
| ΔTa | Air temperature variation [K] |
| ΔTc | Compressor temperature variation [K] |
| ΔTt | Turbine temperature variation [K] |
| ΔTw | Water temperature variation [K] |
| ε | Heat exchangers’ effectiveness [-] |
| η | CAES plant round-trip efficiency [-] |
| ηp,c | Compressor polytropic efficiency [-] |
| ηt,c | Turbine polytropic efficiency [-] |
| k | Polytropic index [-] |
| ρw | Sea water density [kg m−3] |
References
- De Biasi, V. 110 MW McIntosh CAES Plant Over 90% Availability and 95% Reliability. Gas Turbine World 1998, 28, 26–28. [Google Scholar]
- Cavallo, A.J. Controllable and Affordable Utility-Scale Electricity from Intermittent Wind Resources and Compressed Air Energy Storage (CAES). Energy 2007, 32, 120–127. [Google Scholar] [CrossRef]
- Kim, Y.M.; Lee, J.H.; Kim, S.J.; Favrat, D. Potential and Evolution of Compressed Air Energy Storage: Energy and Exergy Analyses. Entropy 2012, 14, 1501–1521. [Google Scholar] [CrossRef]
- Lund, H.; Salgi, G. The Role of Compressed Air Storage Energy Storage (CAES) in Future Sustainable Energy Systems. Energy Convers. Manag. 2009, 50, 1172–1179. [Google Scholar] [CrossRef]
- Guo, H.; Kang, H.; Xu, Y.; Zhao, M.; Zhu, Y.; Zhang, H.; Chen, H. Review of Coupling Methods of Compressed Air Energy Storage Systems and Renewable Energy Resources. Energies 2023, 16, 4667. [Google Scholar] [CrossRef]
- Bouman, E.A.; Øberg, M.M.; Hertwich, E.G. Environmental Impact of Balancing Offshore Wind Power with Compressed Air Energy Storage (CAES). Energy 2016, 95, 91–98. [Google Scholar] [CrossRef]
- Ochmann, J.; Rusin, K.; Rulik, S.; Waniczek, S.; Bartela, L. Experimental and Computational Analysis of Packed-Bed Thermal Energy Storage Tank Designed for Adiabatic Compressed Air Energy Storage System. Appl. Therm. Eng. 2022, 213, 118750. [Google Scholar] [CrossRef]
- Cardenas, B.; Garvey, S. A Directly Charged Thermal Store for Compressed Air Energy Storage Systems. J. Energy Storage 2023, 71, 108183. [Google Scholar] [CrossRef]
- Lay, C.; Garg, A.; Bard, J.; Puchta, M. StenSea—Stored Energy in the Sea. In Proceedings of the 7th International Renewable Energy Storage Conference and Exhibition, IRES 2012, Berlin, Germany, 12–14 November 2012; Volume 7. [Google Scholar]
- Rabi, A.M.; Radulovic, J.; Buick, J.M. Comprehensive Review of Compressed Air Energy Storage (CAES) Technologies. Thermo 2023, 3, 104–126. [Google Scholar] [CrossRef]
- Bullough, C.; Gatzen, C.; Jakiel, C.; Koller, M.; Nowi, A.; Zunft, S. Advanced Adiabatic Compressed Air energy Storage for the Integration of Wind Energy. In Proceedings of the European Wind Energy Conference, EWEC 2004, London, UK, 22–25 November 2004; Volume 22, p. 25. [Google Scholar]
- Hoffeins, H. Huntorf Air Storage Gas Turbine Power Plant. Energy Supply 1990, 90, 202. [Google Scholar]
- Crotogino, F.; Mohmeyer, K.U.; Scharf, R. Huntorf CAES: More than 20 Years of Successful Operation. In Proceedings of theConference: Solution Mining Research Institute (SMRI) Spring Meeting 2001, Orlando, FL, USA, 15–18 April 2001. [Google Scholar]
- Raju, M.; Khaitan, S.K. Modeling and Simulation of Compressed Air Storage in Caverns: A Case Study of the Huntorf Plant. Appl. Energy 2012, 89, 474–481. [Google Scholar] [CrossRef]
- Available online: https://www.iee.fraunhofer.de/en/topics/stensea.html (accessed on 25 October 2023).
- Pimm, A.J.; Garvey, S.D.; De Jong, M. Design and Testing of Energy Bags for Underwater Compressed Air Energy Storage. Energy 2014, 66, 496–508. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Cen, H.; Ting, D.S.K.; Carriveau, R.; Xiong, W. Large-Eddy Simulation of a Full-Scale Underwater Energy Storage Accumulator. Ocean Eng. 2021, 234, 109184. [Google Scholar] [CrossRef]
- Bauer, T.; Zunft, S.; Linder, M.; Bauer, D.; Dietrich, R.U.; Seitz, A. Opportunities of High Temperature Thermal Energy Storage Technologies in the Process Industry. Heat Process. 2016, 4, 65–72. [Google Scholar]
- Battisti, L.; Benini, E.; Brighenti, A.; Raciti Castelli, M.; Dell’Anna, S.; Dossena, V.; Persico, G.; Schmit Paulsen, U.; Pedersen, T.F. Wind tunnel Testing of the DeepWind Demonstrator in Design and Tilted Operating Conditions. Energy 2016, 111, 484–497. [Google Scholar] [CrossRef]
- Wang, Z.; Xiong, W.; Carriveau, R.; Ting, D.S.K.; Wang, Z. Energy, Exergy, and Sensitivity Analyses of Underwater Compressed Air Energy Storage in an Island Energy System. Int. J. Energy Res. 2019, 43, 2241–2260. [Google Scholar] [CrossRef]
- Grazzini, G.; Milazzo, A. A Thermodynamic Analysis of Multistage Adiabatic CAES. Proc. IEEE 2012, 100, 461–472. [Google Scholar] [CrossRef]
- Hunt, J.D.; Zakeri, B.; Nascimento, A.; De Jesus Pacheco, D.A.; Patro, E.R.; Đurin, B.; Pereira, M.G.; Filho, W.L.; Wada, Y. Isothermal Deep Ocean Compressed Air Energy Storage: An Affordable Solution for Seasonal Energy Storage. Energies 2023, 16, 3118. [Google Scholar] [CrossRef]
- Zhou, Q.; Du, D.; Lu, C.; He, Q.; Liu, W. A Review of Thermal Energy Storage in Compressed Air Energy Storage System. Energy 2019, 188, 115993. [Google Scholar] [CrossRef]
- Tola, V.; Marcello, F.C.; Cocco, D.; Cau, G. Performance Assessment of Low-Temperature A-CAES (Adiabatic Compressed Air Energy Storage) Plants. J. Therm. Sci. 2022, 31, 1279–1292. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Li, Y.; Chen, H.; Wu, Y.; Wang, J.; Garvey, S.; Ding, Y. Dynamic Simulation of Adiabatic Compressed Air Energy Storage (A-CAES) Plant with Integrated Thermal Storage—Link Between Components Performance and Plant Performance. Appl. Energy 2017, 185, 16–28. [Google Scholar] [CrossRef]
- Astolfi, M.; Guandalini, G.; Belloli, M.; Hirn, A.; Silva, P.; Campanari, S. Preliminary Design and Performance Assessment of an Underwater CAES System (UW-CAES) for Wind Power Balancing. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019; Volume 3: Coal, Biomass, Hydrogen, and Alternative Fuels; Cycle Innovations; Electric Power; Industrial and Cogeneration; Organic Rankine Cycle Power Systems, V003T06A009. ASME: New York, NY, USA, 2019. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons US: Hoboken, NJ, USA, 2011. [Google Scholar]
- Kays, W.M.; London, A.L. Compact Heat Exchangers, 2nd ed.; National Press: Washington, DC, USA, 1955. [Google Scholar]
- Available online: https://en.wikipedia.org/wiki/Thermocline#/media/File:ThermoclineSeasonDepth.png (accessed on 25 October 2023).
- Dixon, S.L.; Hall, C.A. Fluid Mechanics and Thermodynamics of Turbomachinery, 7th ed.; Butterworth-Heinemann: Oxford, UK; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).