Multi-Objective Assessment and Optimization of a High-Temperature Proton Exchange Membrane Fuel Cell: Steady-State Analysis
Abstract
:1. Introduction
2. Principle and Methodology
2.1. Principle of the HT-PEMFC
2.2. Electrochemical Modeling
2.3. Energy and Exergy Analysis
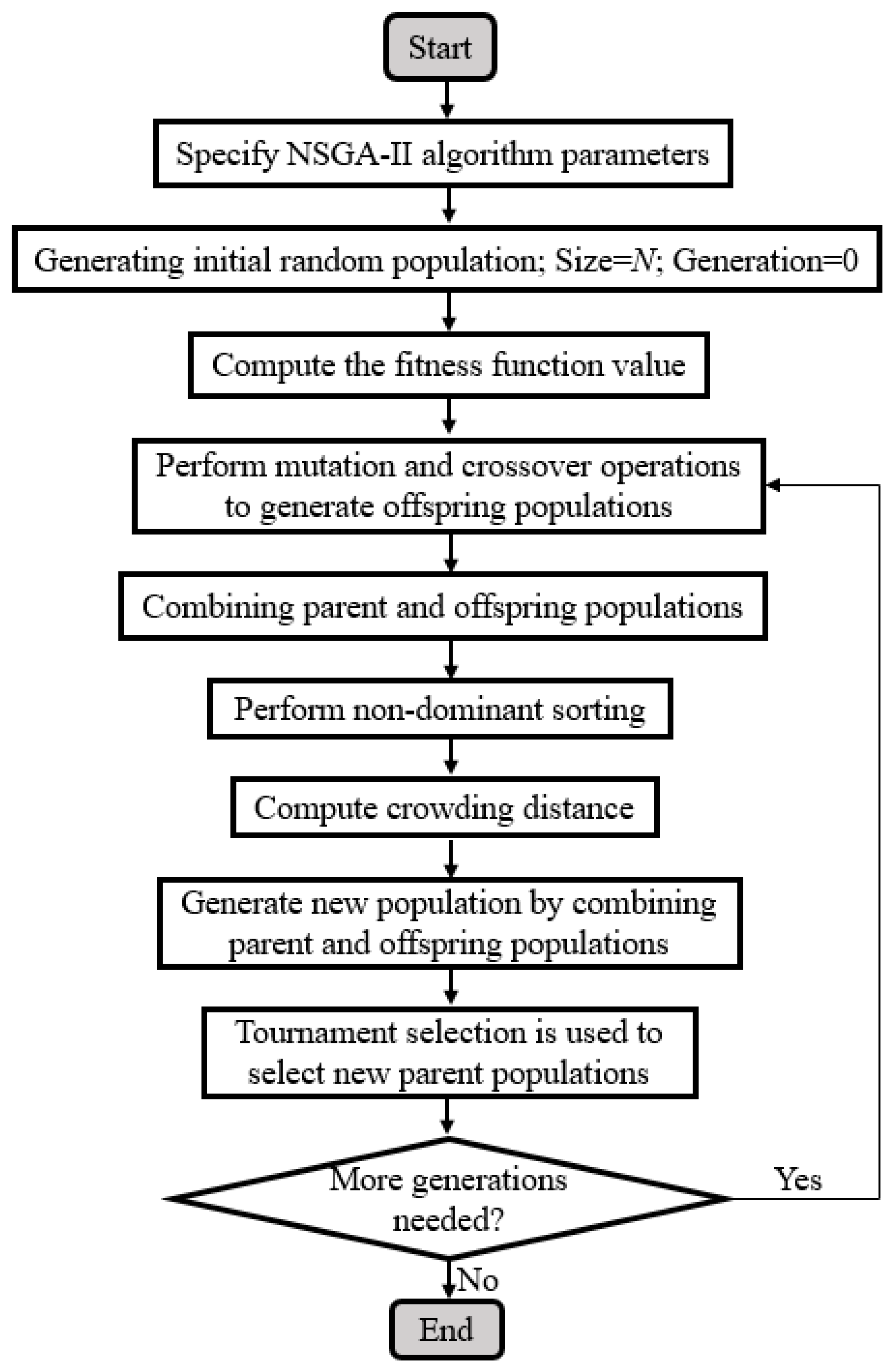
2.4. Optimization
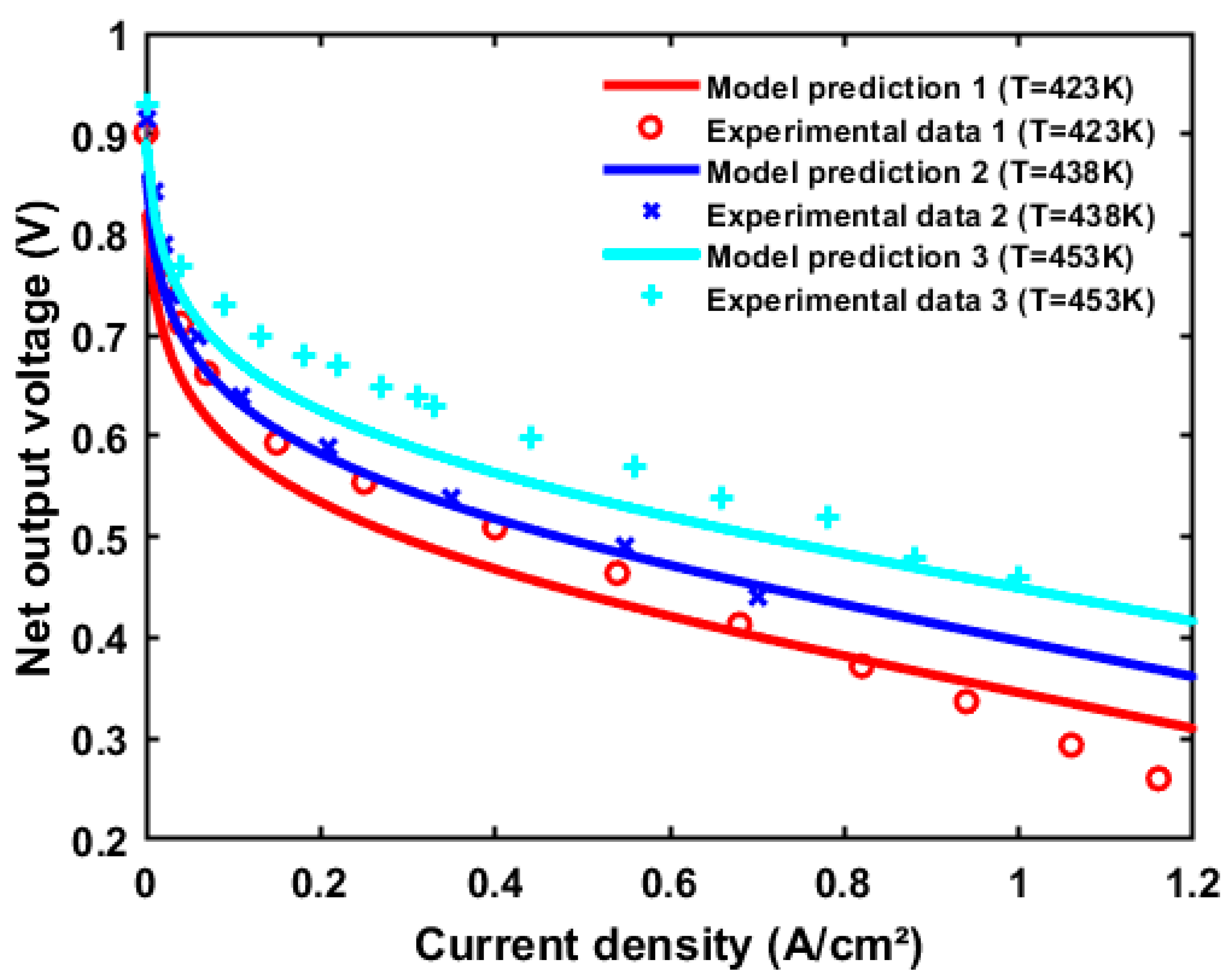
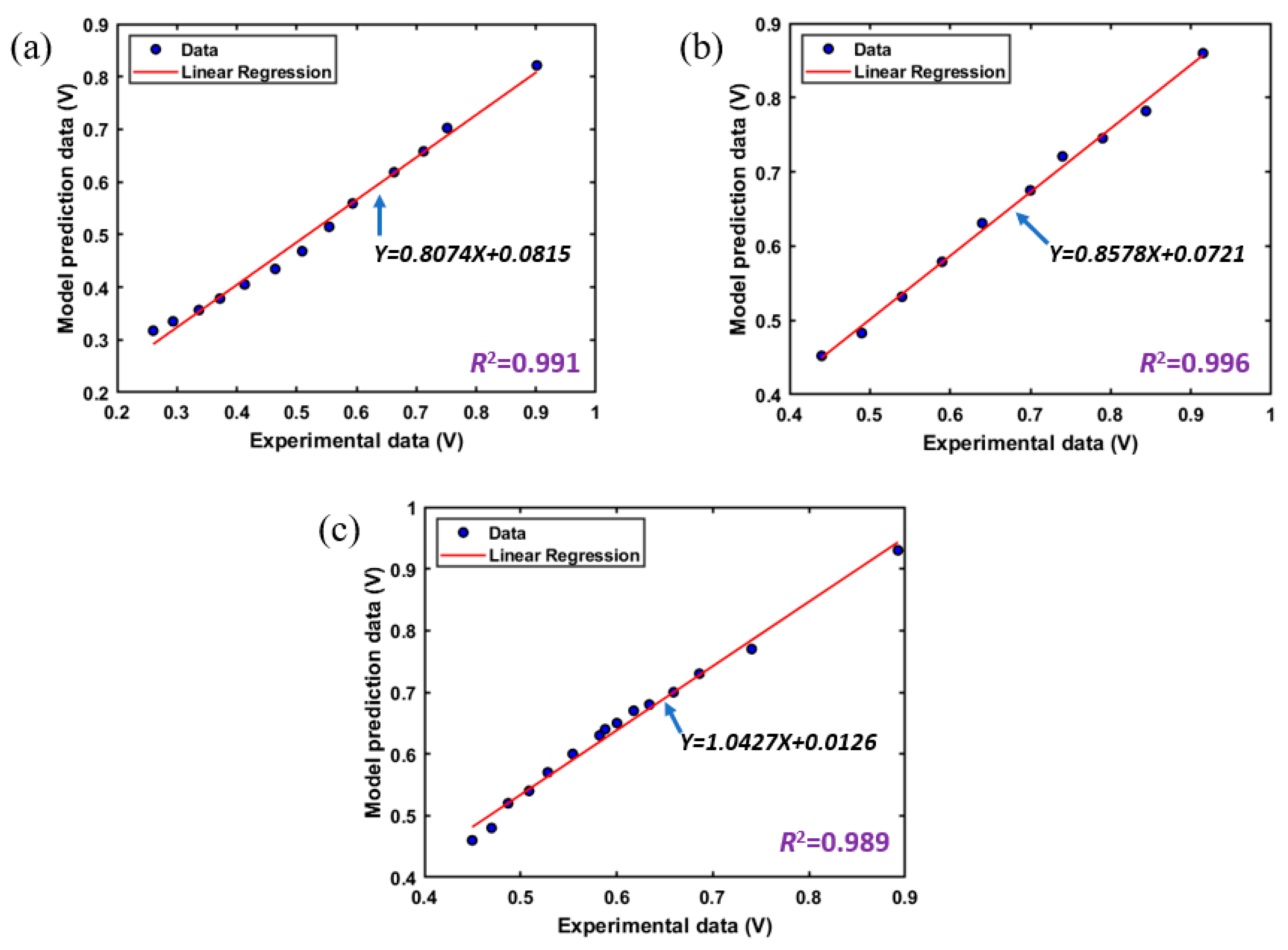
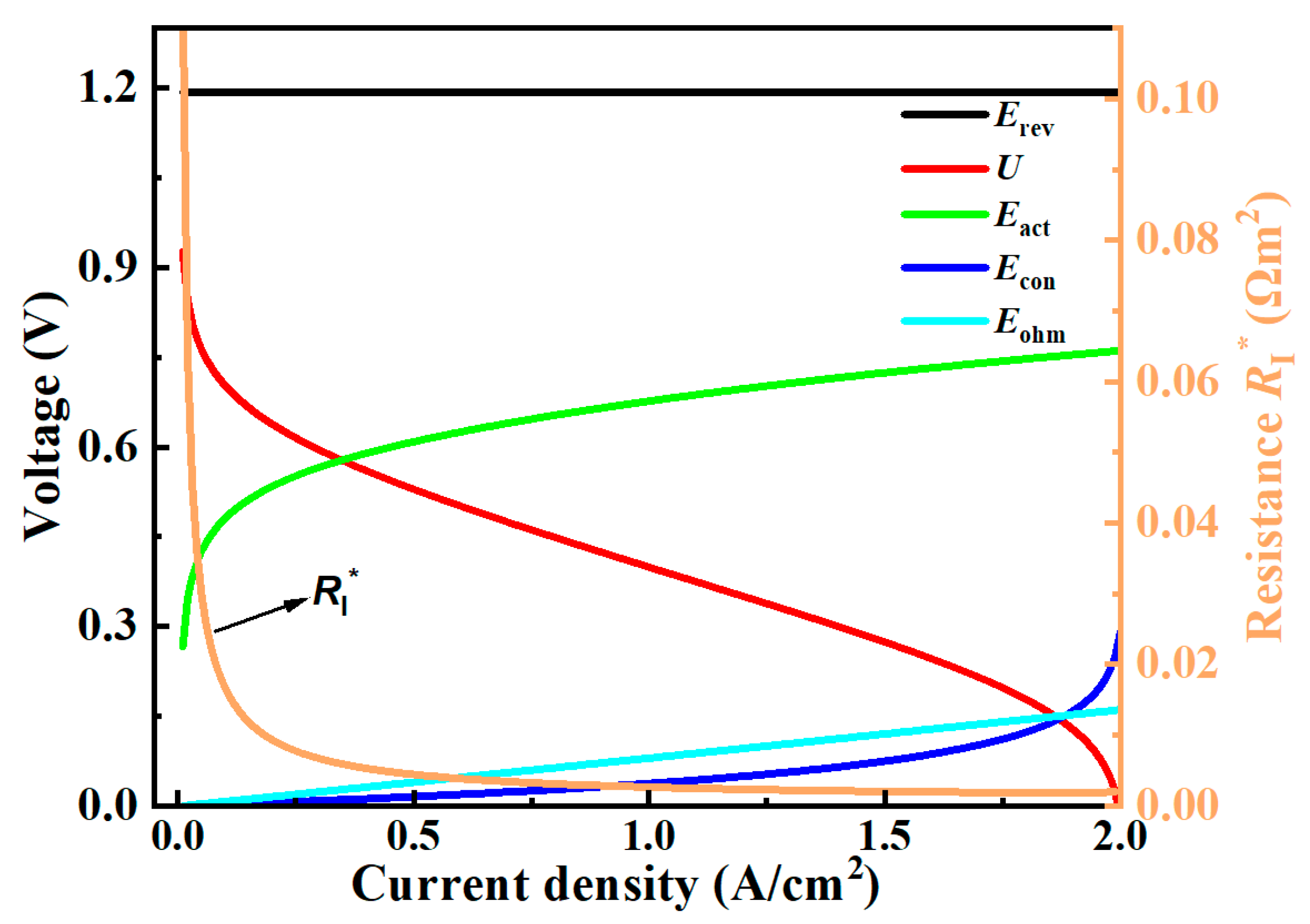
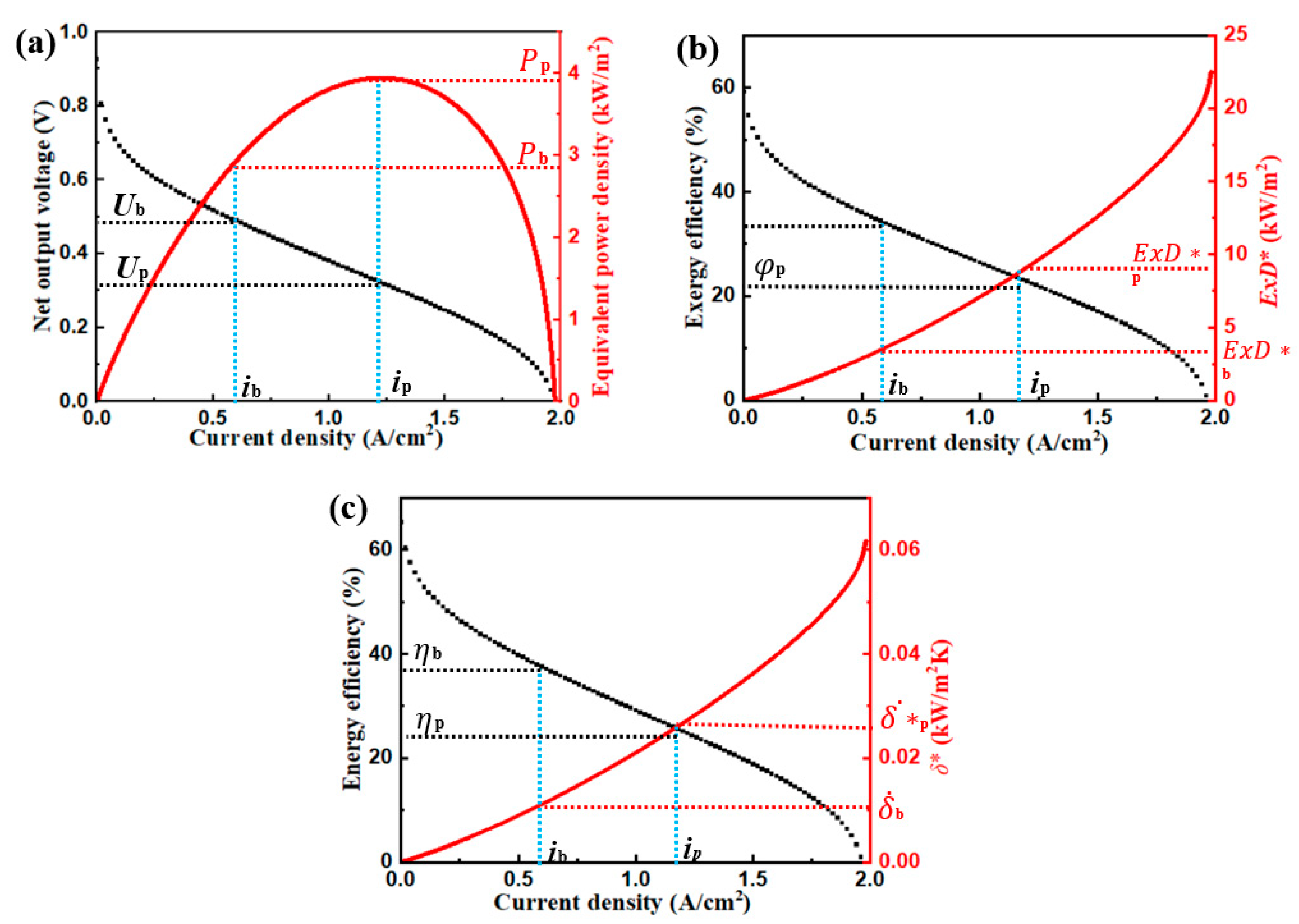
3. Generic Performance Characteristics
4. Parametric Studies
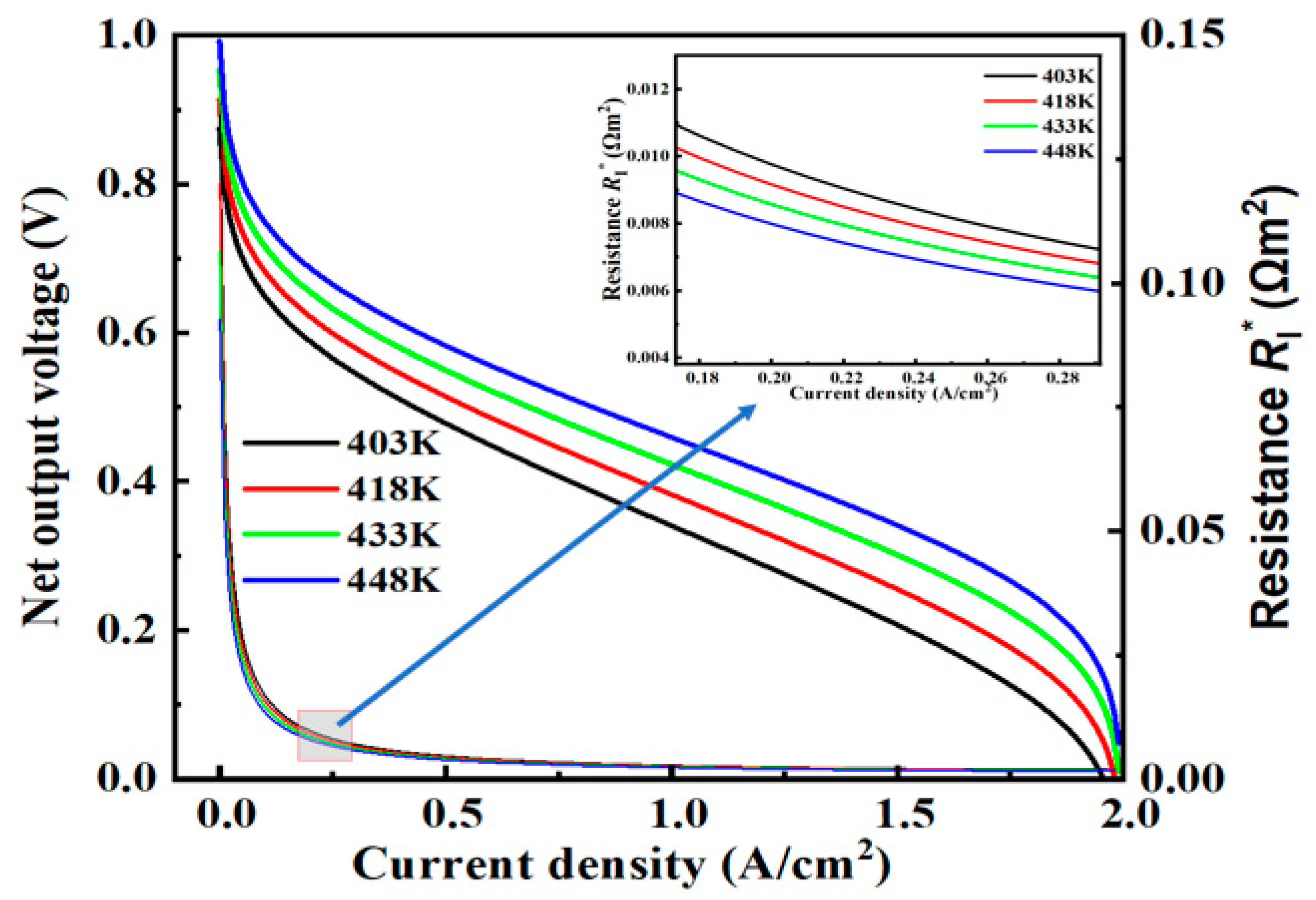
4.1. Operating Temperature
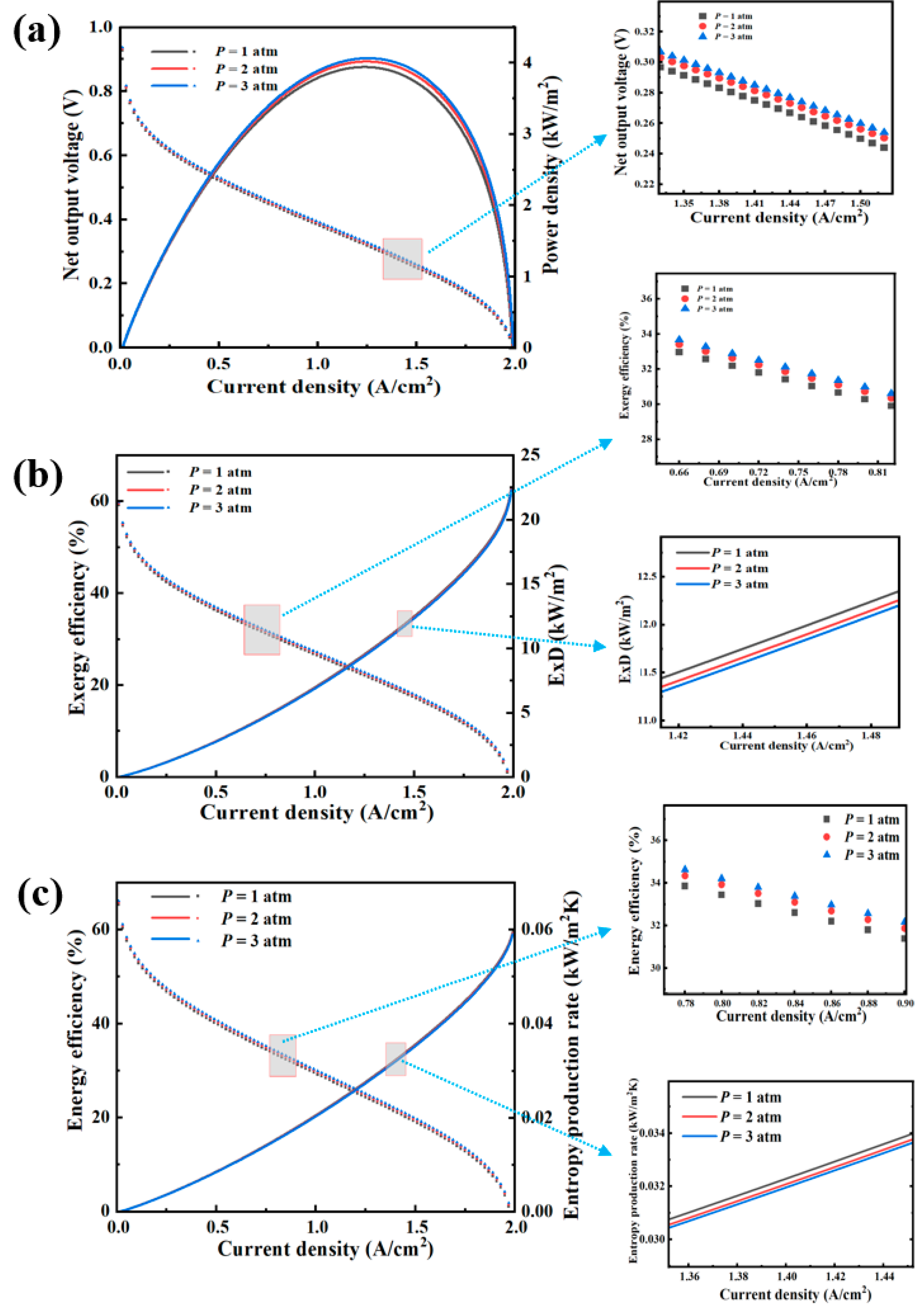
4.2. Operating Pressure
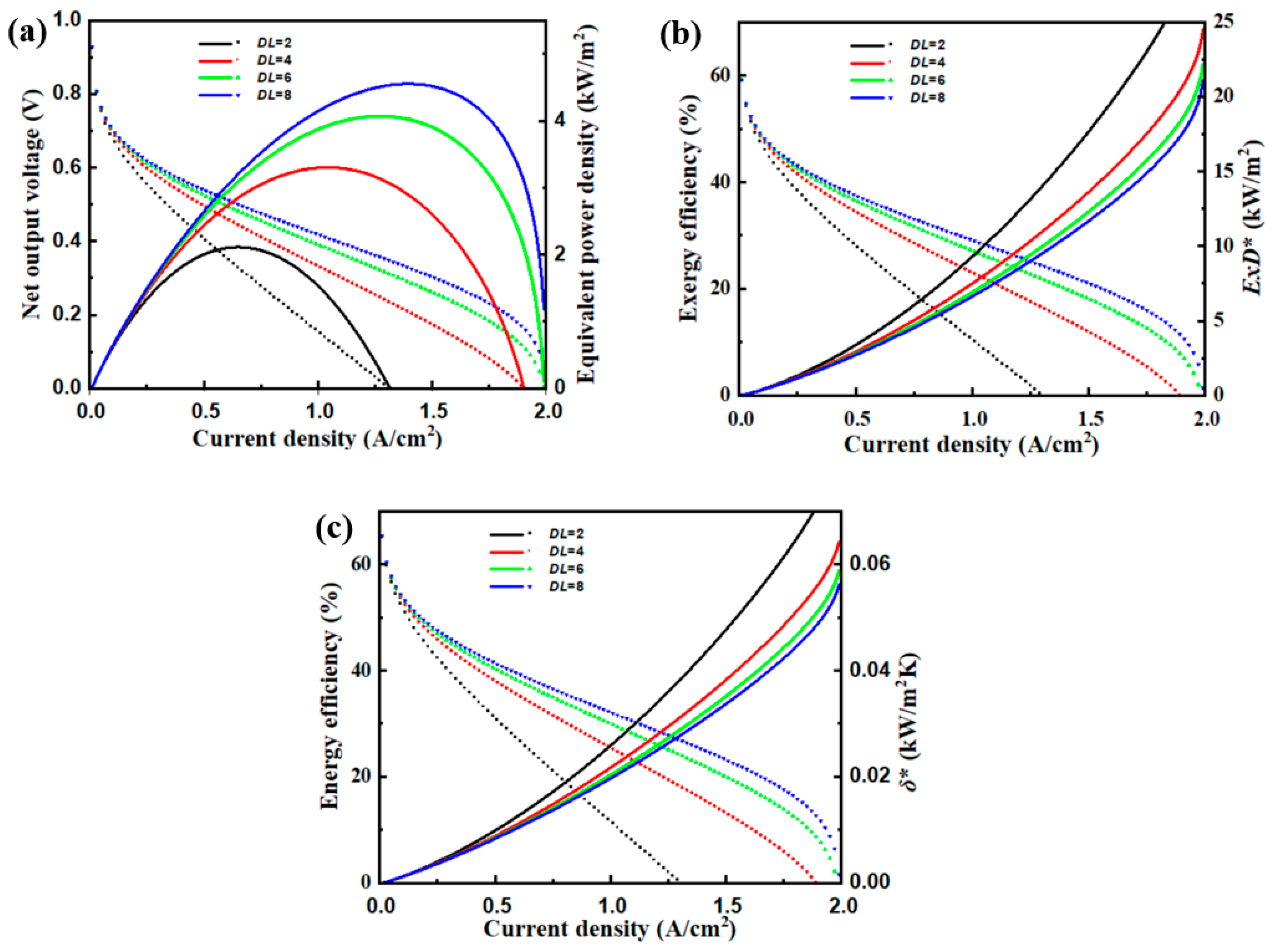
4.3. Doping Level
4.4. Membrane Thickness
5. Optimization Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| root-mean-square error | |
| R2 | R-squared |
| reversible potential (V) | |
| net output voltage (V) | |
| molar entropy change (J mol−1K−1) | |
| p | partial pressure (atm) |
| molar fraction | |
| T | operating temperature (K) |
| operating current density (A cm−2) | |
| membrane thickness (cm) | |
| A0 | pre-exponential coefficient |
| activation energy (J mol−1) | |
| A | effective working area (m2) |
| limiting current density (A cm−2) | |
| power output (kW m−2) | |
| molar enthalpy change (J mol−1) | |
| standard molar enthalpy (J mol−1) | |
| equivalent internal resistant (Ω) | |
| standard molar entropy ((J mol−1 K−1) | |
| Greek symbols | |
| δ | entropy production (kJ K−1) |
| charge transfer coefficient | |
| proton conductivity of the membrane (S m−1) | |
| Subscripts and superscripts | |
| rev | reversible |
| act | activation |
| ohm | ohmic |
| con | concentration |
| * | unit area |
| · | unit time |
| an | anode |
| cat | cathode |
| e | electron |
| I | internal resistance |
| 0 | environmental condition |
References
- Al-Tememy, M.G.H.; Devrim, Y. Development of effective bimetallic catalyst for high-temperature PEM fuel cell to improve CO tolerance. Int. J. Energy Res. 2021, 45, 3343–3357. [Google Scholar] [CrossRef]
- Alegre, C.; Alvarez-Manuel, L.; Mustata, R.; Valiño, L.; Lozano, A.; Barreras, F. Assessment of the durability of low-cost Al bipolar plates for High Temperature PEM fuel cells. Int. J. Hydrogen Energy 2019, 44, 12748–12759. [Google Scholar] [CrossRef]
- Nalbant, Y.; Colpan, C.O.; Devrim, Y. Energy and exergy performance assessments of a high temperature-proton exchange membrane fuel cell based integrated cogeneration system. Int. J. Hydrogen Energy 2020, 45, 3584–3594. [Google Scholar] [CrossRef]
- Saeedan, M.; Afshari, E.; Ziaei-Rad, M. Modeling and optimization of turbulent flow through PEM fuel cell cooling channels filled with metal foam-a comparison of water and air cooling systems. Energy Convers. Manag. 2022, 258, 115486. [Google Scholar] [CrossRef]
- Wu, W.; Zhai, C.; Sui, Y.; Zhang, H. A novel distributed energy system using high-temperature proton exchange membrane fuel cell integrated with hybrid-energy heat pump. Energy Convers. Manag. 2021, 235, 113990. [Google Scholar] [CrossRef]
- Guo, H.; Li, Z.; Sun, P.; Pei, H.; Zhang, L.; Cui, W.; Yin, X.; Hui, H. Enhancing proton conductivity and durability of crosslinked PBI-Based high-temperature PEM: Effectively doping a novel cerium triphosphonic-isocyanurate. J. Electrochem. Soc. 2021, 168, 024510. [Google Scholar] [CrossRef]
- Lv, B.; Geng, K.; Yin, H.; Yang, C.; Hao, J.; Luan, Z.; Huang, Z.; Qin, X.; Song, W.; Li, N. Polybenzimidazole/cerium dioxide/graphitic carbon nitride nanosheets for high performance and durable high temperature proton exchange membranes. J. Membr. Sci. 2021, 639, 119760. [Google Scholar] [CrossRef]
- Bai, H.; Peng, H.; Xiang, Y.; Zhang, J.; Wang, H.; Lu, S.; Zhuang, L. Poly (arylene piperidine) s with phosphoric acid doping as high temperature polymer electrolyte membrane for durable, high-performance fuel cells. J. Power Sources 2019, 443, 227219. [Google Scholar] [CrossRef]
- Nikiforov, A.; Petrushina, I.; Christensen, E.; Tomás-García, A.; Bjerrum, N. Corrosion behaviour of construction materials for high temperature steam electrolysers. Int. J. Hydrogen Energy 2011, 36, 111–119. [Google Scholar] [CrossRef]
- Kannan, A.; Kabza, A.; Scholta, J. Long term testing of start–stop cycles on high temperature PEM fuel cell stack. J. Power Sources 2015, 277, 312–316. [Google Scholar] [CrossRef]
- Yan, W.-M.; Chen, C.-Y.; Liang, C.-H. Comparison of performance degradation of high temperature PEM fuel cells with different bipolar plates. Energy 2019, 186, 115836. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, W.; Ehteshami, M.M.; Wang, Y.; Chan, S.H. Determination of the optimal operating temperature range for high temperature PEM fuel cell considering its performance, CO tolerance and degradation. Energy Convers. Manag. 2015, 105, 433–441. [Google Scholar] [CrossRef]
- Kerr, R.; García, H.; Rastedt, M.; Wagner, P.; Alfaro, S.; Romero, M.; Terkelsen, C.; Steenberg, T.; Hjuler, H. Lifetime and degradation of high temperature PEM membrane electrode assemblies. Int. J. Hydrogen Energy 2015, 40, 16860–16866. [Google Scholar] [CrossRef]
- Barati, S.; Mehdipourghazi, M.; Abdollahi, M.; Hooshyari, K.; Khoshandam, B. Preparation, characterization and proton transport of new porous nanocomposite membranes based on polybenzimidazole, lignin and TiO2 nanoparticles for high temperature PEM fuel cells. Int. J. Energy Res. 2021, 45, 20057–20072. [Google Scholar] [CrossRef]
- Subianto, S. Recent advances in polybenzimidazole/phosphoric acid membranes for high-temperature fuel cells. Polym. Int. 2014, 63, 1134–1144. [Google Scholar] [CrossRef]
- Chandan, A.; Hattenberger, M.; El-Kharouf, A.; Du, S.; Dhir, A.; Self, V.; Pollet, B.G.; Ingram, A.; Bujalski, W. High temperature (HT) polymer electrolyte membrane fuel cells (PEMFC)–A review. J. Power Sources 2013, 231, 264–278. [Google Scholar] [CrossRef]
- Du, B.; Guo, Q.; Pollard, R.; Rodriguez, D.; Smith, C.; Elter, J. PEM fuel cells: Status and challenges for commercial stationary power applications. JOM 2006, 58, 45–49. [Google Scholar] [CrossRef]
- Dimitrova, Z.; Nader, W.B. PEM fuel cell as an auxiliary power unit for range extended hybrid electric vehicles. Energy 2022, 239, 121933. [Google Scholar] [CrossRef]
- Li, Y.; Li, D.; Ma, Z.; Zheng, M.; Lu, Z.; Song, H.; Guo, X.; Shao, W. Performance analysis and optimization of a novel vehicular power system based on HT-PEMFC integrated methanol steam reforming and ORC. Energy 2022, 257, 124729. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, H.; Yan, P.; Jermsittiparsert, K. Multi-objective optimization for efficient modeling and improvement of the high temperature PEM fuel cell based Micro-CHP system. Int. J. Hydrogen Energy 2020, 45, 6970–6981. [Google Scholar] [CrossRef]
- Mamaghani, A.H.; Najafi, B.; Casalegno, A.; Rinaldi, F. Optimization of an HT-PEM fuel cell based residential micro combined heat and power system: A multi-objective approach. J. Clean. Prod. 2018, 180, 126–138. [Google Scholar] [CrossRef]
- Sarabchi, N.; Mahmoudi, S.S.; Yari, M.; Farzi, A. Exergoeconomic analysis and optimization of a novel hybrid cogeneration system: High-temperature proton exchange membrane fuel cell/Kalina cycle, driven by solar energy. Energy Convers. Manag. 2019, 190, 14–33. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H.; Yuan, J.; Wang, J.; Zhao, J.; Wang, F.; Miao, H.; Hou, S. Energetic and exergetic analyses of a combined system consisting of a high-temperature polymer electrolyte membrane fuel cell and a thermoelectric generator with Thomson effect. Int. J. Hydrogen Energy 2019, 44, 16918–16932. [Google Scholar] [CrossRef]
- Ye, L.; Jiao, K.; Du, Q.; Yin, Y. Exergy analysis of high-temperature proton exchange membrane fuel cell systems. Int. J. Green Energy 2015, 12, 917–929. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H. Performance analyses of a combined system consisting of high-temperature polymer electrolyte membrane fuel cells and thermally regenerative electrochemical cycles. Energy 2020, 193, 116720. [Google Scholar] [CrossRef]
- Araya, S.S.; Zhou, F.; Liso, V.; Sahlin, S.L.; Vang, J.R.; Thomas, S.; Gao, X.; Jeppesen, C.; Kær, S.K. A comprehensive review of PBI-based high temperature PEM fuel cells. Int. J. Hydrogen Energy 2016, 41, 21310–21344. [Google Scholar] [CrossRef]
- Li, D.; Li, S.; Ma, Z.; Xu, B.; Lu, Z.; Li, Y.; Zheng, M. Ecological performance optimization of a high temperature proton exchange membrane fuel cell. Mathematics 2021, 9, 1332. [Google Scholar] [CrossRef]
- Li, D.; Li, Y.; Ma, Z.; Zheng, M.; Lu, Z. Exergetic performance coefficient analysis and optimization of a high-temperature proton exchange membrane fuel cell. Membranes 2022, 12, 70. [Google Scholar] [CrossRef]
- Bayat, M.; Özalp, M.; Gürbüz, H. Comprehensive performance analysis of a high-temperature PEM fuel cell under different operating and design conditions. Sustain. Energy Technol. Assess. 2022, 52, 102232. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, X.; Zhang, H.; Hou, S. Energetic, exergetic and ecological analyses of a high-temperature proton exchange membrane fuel cell based on a phosphoric-acid-doped polybenzimidazole membrane. Sustain. Energy Technol. Assess. 2020, 38, 100671. [Google Scholar] [CrossRef]
- Xia, L.; Zhang, C.; Hu, M.; Jiang, S.; Chin, C.S.; Gao, Z.; Liao, Q. Investigation of parameter effects on the performance of high-temperature PEM fuel cell. Int. J. Hydrogen Energy 2018, 43, 23441–23449. [Google Scholar] [CrossRef]
- Nalbant, Y.; Colpan, C.O.; Devrim, Y. Development of a one-dimensional and semi-empirical model for a high temperature proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2018, 43, 5939–5950. [Google Scholar] [CrossRef]
- Haghighi, M.; Sharifhassan, F. Exergy analysis and optimization of a high temperature proton exchange membrane fuel cell using genetic algorithm. Case Stud. Therm. Eng. 2016, 8, 207–217. [Google Scholar] [CrossRef]
- Li, H.; Xu, B.; Lu, G.; Du, C.; Huang, N. Multi-objective optimization of PEM fuel cell by coupled significant variables recognition, surrogate models and a multi-objective genetic algorithm. Energy Convers. Manag. 2021, 236, 114063. [Google Scholar] [CrossRef]
- Zamora, H.; Plaza, J.; Cañizares, P.; Lobato, J.; Rodrigo, M.A. Improved electrodes for high temperature proton exchange membrane fuel cells using carbon nanospheres. ChemSusChem 2016, 9, 1187–1193. [Google Scholar] [CrossRef] [PubMed]
- Jiao, K.; Li, X. A Three-Dimensional Non-isothermal Model of High Temperature Proton Exchange Membrane Fuel Cells with Phosphoric Acid Doped Polybenzimidazole Membranes. Fuel Cells 2010, 10, 351–362. [Google Scholar] [CrossRef]
- Li, Q.; Aili, D.; Hjuler, H.A.; Jensen, J.O. High Temperature Polymer Electrolyte Membrane Fuel Cells; Springer: Cham/Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2016; Volume 545. [Google Scholar]
- Yuan, H.; Dai, Y.; Li, H.; Wang, Y. Modeling of high-temperature polymer electrolyte membrane fuel cell for reaction spatial variation. Int. J. Heat Mass Transf. 2022, 195, 123209. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H.; Zhao, J.; Wang, F.; Wang, J.; Miao, H.; Yuan, J. Performance evaluation of an integrated high-temperature proton exchange membrane fuel cell and absorption cycle system for power and heating/cooling cogeneration. Energy Convers. Manag. 2019, 181, 292–301. [Google Scholar] [CrossRef]
- Olapade, P.O.; Meyers, J.P.; Borup, R.L.; Mukundan, R. Parametric study of the morphological proprieties of HT-PEMFC components for effective membrane hydration. J. Electrochem. Soc. 2011, 158, B639. [Google Scholar] [CrossRef]
- Najafi, B.; Mamaghani, A.H.; Baricci, A.; Rinaldi, F.; Casalegno, A. Mathematical modelling and parametric study on a 30 kWel high temperature PEM fuel cell based residential micro cogeneration plant. Int. J. Hydrogen Energy 2015, 40, 1569–1583. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, G.; Chen, J. Multi-objective optimisation analysis and load matching of a phosphoric acid fuel cell system. Int. J. Hydrogen Energy 2012, 37, 3438–3446. [Google Scholar] [CrossRef]
- Arshad, A.; Ali, H.M.; Habib, A.; Bashir, M.A.; Jabbal, M.; Yan, Y. Energy and exergy analysis of fuel cells: A review. Therm. Sci. Eng. Prog. 2019, 9, 308–321. [Google Scholar] [CrossRef]
- Szargut, J. Exergy Method: Technical and Ecological Applications; WIT Press: Southampton, UK, 2005. [Google Scholar]
- Zhang, X.; Chen, X.; Lin, B.; Chen, J. Maximum equivalent efficiency and power output of a PEM fuel cell/refrigeration cycle hybrid system. Int. J. Hydrogen Energy 2011, 36, 2190–2196. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, L.; Liao, T.; Zhou, Y.; Zhao, Y.; Chen, J. Exploiting the waste heat from an alkaline fuel cell via electrochemical cycles. Energy 2018, 142, 983–990. [Google Scholar] [CrossRef]
- Wu, Z.; Zhu, P.; Yao, J.; Tan, P.; Xu, H.; Chen, B.; Yang, F.; Zhang, Z.; Ni, M. Thermo-economic modeling and analysis of an NG-fueled SOFC-WGS-TSA-PEMFC hybrid energy conversion system for stationary electricity power generation. Energy 2020, 192, 116613. [Google Scholar] [CrossRef]
- Nguyen, H.Q.; Aris, A.M.; Shabani, B. PEM fuel cell heat recovery for preheating inlet air in standalone solar-hydrogen systems for telecommunication applications: An exergy analysis. Int. J. Hydrogen Energy 2016, 41, 2987–3003. [Google Scholar] [CrossRef]
- Seifert, U. Entropy production along a stochastic trajectory and an integral fluctuation theorem. Phys. Rev. Lett. 2005, 95, 040602. [Google Scholar] [CrossRef]
- Cohce, M.; Dincer, I.; Rosen, M. Energy and exergy analyses of a biomass-based hydrogen production system. Bioresour. Technol. 2011, 102, 8466–8474. [Google Scholar] [CrossRef]
- Chen, Z.; Zuo, W.; Zhou, K.; Li, Q.; Huang, Y.; Jiaqiang, E. Multi-objective optimization of proton exchange membrane fuel cells by RSM and NSGA-II. Energy Convers. Manag. 2023, 277, 116691. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, S.; Huang, X.; Luo, X.; Tu, Z. 4E analysis and multiobjective optimization of a PEMFC-based CCHP system with dehumidification. Energy Convers. Manag. 2021, 248, 114789. [Google Scholar] [CrossRef]
- Sousa, T.; Mamlouk, M.; Scott, K. An isothermal model of a laboratory intermediate temperature fuel cell using PBI doped phosphoric acid membranes. Chem. Eng. Sci. 2010, 65, 2513–2530. [Google Scholar] [CrossRef]
- Üregen, N.; Pehlivanoğlu, K.; Özdemir, Y.; Devrim, Y. Development of polybenzimidazole/graphene oxide composite membranes for high temperature PEM fuel cells. Int. J. Hydrogen Energy 2017, 42, 2636–2647. [Google Scholar] [CrossRef]
- Ubong, E.; Shi, Z.; Wang, X. Three-dimensional modeling and experimental study of a high temperature PBI-based PEM fuel cell. J. Electrochem. Soc. 2009, 156, B1276. [Google Scholar] [CrossRef]
- Barnston, A. Correspondence among the Correlation [root mean square error] and Heidke Verifcation Measures; Refinement Heidke Score. Cover. Weather. Forecast. Weather. Forecast. 1992, 7, 699–709. [Google Scholar] [CrossRef]
- Han, I.-S.; Chung, C.-B. Performance prediction and analysis of a PEM fuel cell operating on pure oxygen using data-driven models: A comparison of artificial neural network and support vector machine. Int. J. Hydrogen Energy 2016, 41, 10202–10211. [Google Scholar] [CrossRef]
- Leader, J.; Yue, Y.; Walluk, M.; Trabold, T. Voltage degradation of high-temperature PEM fuel cells operating at 200° C under constant load and start-stop conditions. Int. J. Hydrogen Energy 2022, 47, 18820–18830. [Google Scholar] [CrossRef]
- Thomas, S.; Jeppesen, C.; Steenberg, T.; Araya, S.S.; Vang, J.R.; Kær, S.K. New load cycling strategy for enhanced durability of high temperature proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2017, 42, 27230–27240. [Google Scholar] [CrossRef]
- Hwa, S. Energy-and exergy-based working fluid selection and performance analysis of a high-temperature PEMFC-based micro-CCHP system. Appl. Energy 2017, 204, 446–458. [Google Scholar]
- Tseng, C.-J.; Heush, Y.-J.; Chiang, C.-J.; Lee, Y.-H.; Lee, K.-R. Application of metal foams to high temperature PEM fuel cells. Int. J. Hydrogen Energy 2016, 41, 16196–16204. [Google Scholar] [CrossRef]
- Rosli, R.; Sulong, A.; Daud, W.; Zulkifley, M.; Husaini, T.; Rosli, M.; Majlan, E.; Haque, M. A review of high-temperature proton exchange membrane fuel cell (HT-PEMFC) system. Int. J. Hydrogen Energy 2017, 42, 9293–9314. [Google Scholar] [CrossRef]
- Saidi, H.; Uthman, H. Phosphoric acid doped polymer electrolyte membrane based on radiation grafted poly (1-vinylimidazole-co-1-vinyl-2-pyrrolidone)-g-poly (ethylene/tetrafluoroethylene) copolymer and investigation of grafting kinetics. Int. J. Hydrogen Energy 2017, 42, 9315–9332. [Google Scholar] [CrossRef]
- Han, S.; Jeong, Y.H.; Jung, J.H.; Begley, A.; Choi, E.; Yoo, S.J.; Jang, J.H.; Kim, H.-J.; Nam, S.W.; Kim, J.Y. Spectrophotometric analysis of phosphoric acid leakage in high-temperature phosphoric acid-doped polybenzimidazole membrane fuel cell application. J. Sens. 2016, 2016, 5290510. [Google Scholar] [CrossRef]
- Ribeirinha, P.; Abdollahzadeh, M.; Pereira, A.; Relvas, F.; Boaventura, M.; Mendes, A. High temperature PEM fuel cell integrated with a cellular membrane methanol steam reformer: Experimental and modelling. Appl. Energy 2018, 215, 659–669. [Google Scholar] [CrossRef]



| Parameters | Value | Units |
|---|---|---|
| Electrons numbers, ne | 2 | / |
| Doping level, DL | 5.6 | / |
| Operating temperature, T | 423 | K |
| Faraday constant, F | 96,485 | C/mol |
| Membrane thickness, tmem | 0.01 | cm |
| Limiting current density, jL | 2 | A/cm2 |
| Charge transfer coefficient, α | 0.5 | / |
| Anode gas compositions | 100% H2 | / |
| Cathode gas compositions | 21% O2/79% N2 | / |
| Composite constant | 500 | J/(m2 K s) |
| Anode pressure, | 1 | atm |
| Cathode pressure, | 1 | atm |
| Relative humidity, RH | 3.8 | % |
| Universal gas constant, R | 8.314 | J/(mol·K) |
| Temperature of environment, T0 | 298.15 | K |
| Pressure of environment, P0 | 1 | atm |
| Parameters | Equations | |
|---|---|---|
| Thermodynamic equilibrium potential [5,23,29] | (4) | |
| (5) | ||
| (6) | ||
| (7) | ||
| (8) | ||
| Activation overpotential [5,32] | (9) | |
| (10) | ||
| (11) | ||
| (12) | ||
| (13) | ||
| Ohmic overpotential [39] | (14) | |
| (15) | ||
| (16) | ||
| B0 = | (17) | |
| (18) | ||
| Concentration overpotential [40] | (19) | |
| Net output voltage [41] | (20) | |
| Internal resistance [42] | (21) | |
| Parameters | Equations | |
|---|---|---|
| Energy analysis | ||
| Net power output [46] | (22) | |
| Heat dissipation (convective and/or conductive) [25] | (23) | |
| Waste heat [47] | (24) | |
| where | ||
| Energy efficiency [47] | , where | (25) |
| Exergy analysis | ||
| Total exergy [24] | (26) | |
| Physical exergy [24] | (27) | |
| Chemical exergy [44] | (28) | |
| Total input exergy rate [48] | (29) | |
| Output exergy rate [48] | (30) | |
| Exergy destruction rate [48] | (31) | |
| Entropy production rate [49] | (32) | |
| Exergy efficiency [50] | (33) | |
| Parameters | Value | Units |
|---|---|---|
| Electrons numbers, ne | 2 | / |
| Doping level, DL | 5.6 | / |
| Operating temperature, T | 423/438/453 | K |
| Faraday constant, F | 96,485 | C/mol |
| Membrane thickness, tmem | 0.005/0.0055/0.01 | cm |
| Limiting current density, jL | 2 | A/cm2 |
| Charge transfer coefficient, α | 0.5 | / |
| Anode gas compositions | 100% H2 | / |
| Cathode gas compositions | 21% O2/ 79% N2 | / |
| Composite constant | 500 | J/(m2 K s) |
| Anode pressure, | 1 | atm |
| Cathode pressure, | 1 | atm |
| Relative humidity, RH | 3.8 | % |
| Universal gas constant, R | 8.314 | J/(mol·K) |
| Temperature of environment, T0 | 298.15 | K |
| Pressure of environment, P0 | 1 | atm |
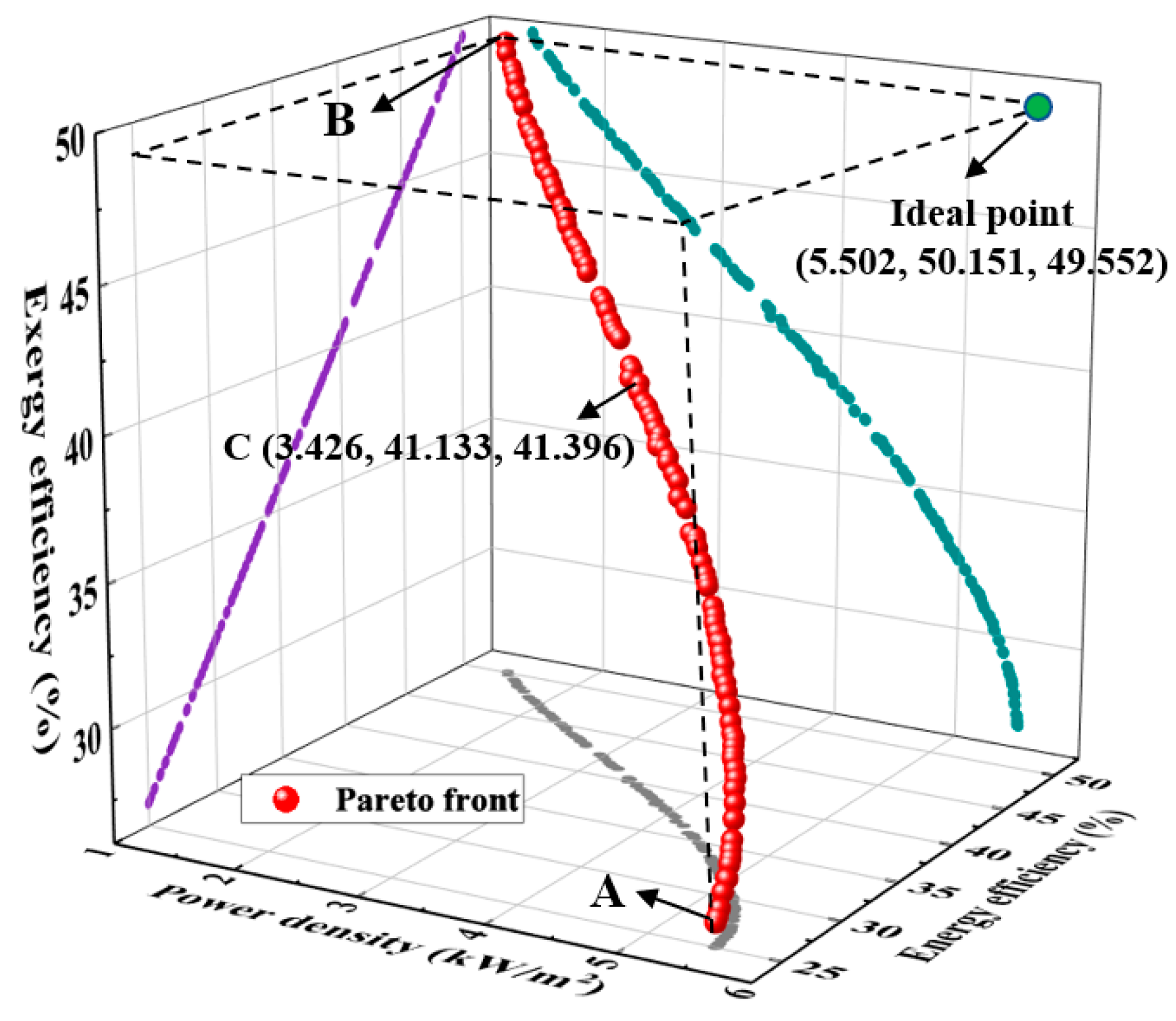
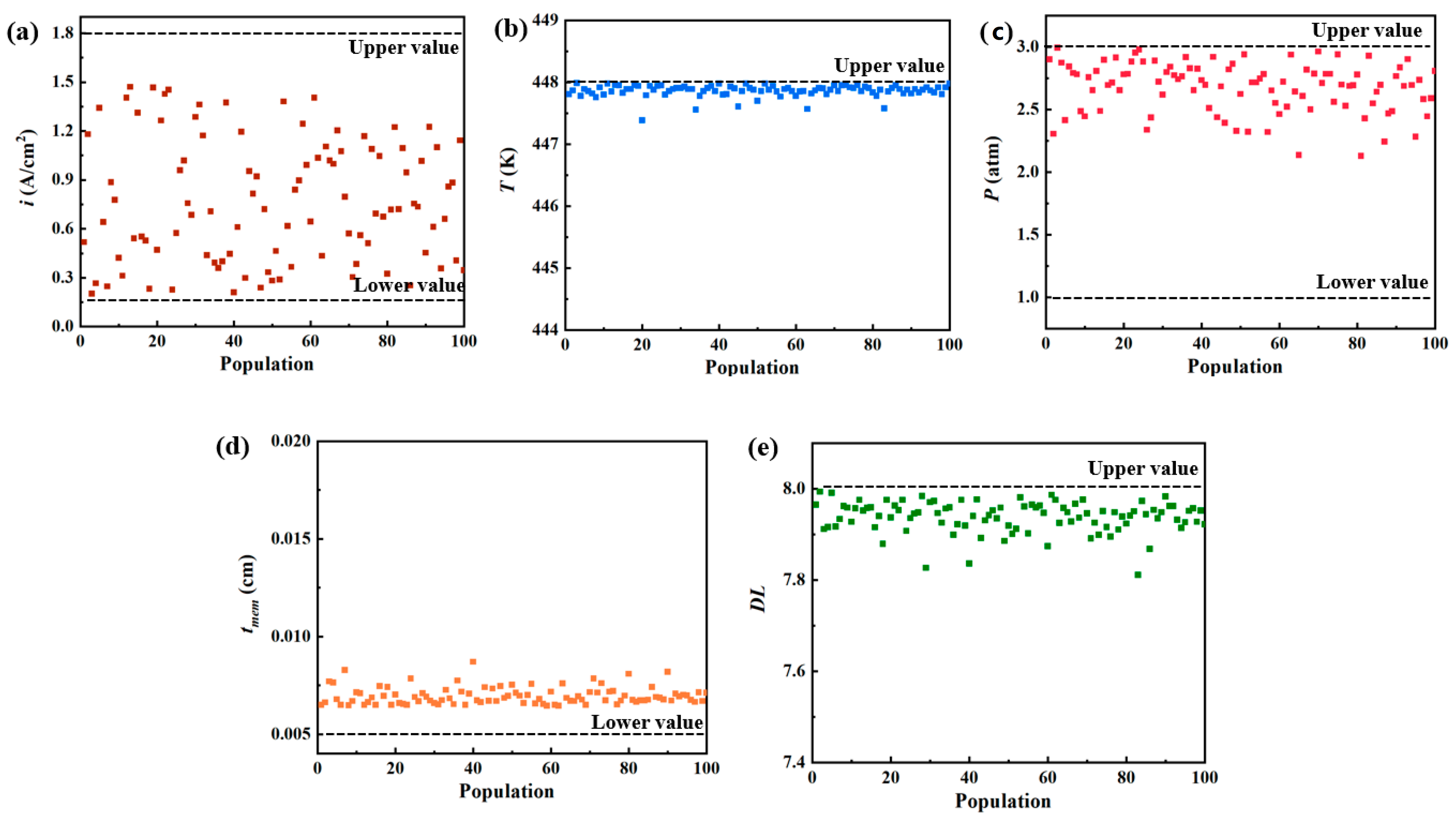
| Parameters | BC-1 | BC-2 | A | B | C |
|---|---|---|---|---|---|
| i (A/cm2) | 0.60 | 1.23 | 1.47 | 0.20 | 0.57 |
| T (K) | 423.00 | 423.00 | 447.96 | 447.99 | 447.95 |
| p (atm) | 1.00 | 1.00 | 1.01 | 2.99 | 2.88 |
| DL | 5.60 | 5.60 | 7.95 | 7.91 | 7.94 |
| tmem (cm) | 0.0100 | 0.0100 | 0.0066 | 0.0077 | 0.0069 |
| P* (kW/m2) | 2.93 | 3.94 | 5.50 | 1.38 | 3.43 |
| (%) | 33.96 | 24.54 | 25.03 | 50.15 | 41.13 |
| (%) | 37.50 | 22.22 | 26.83 | 49.55 | 41.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Z.; Araya, S.S.; Liso, V.; Zhu, J. Multi-Objective Assessment and Optimization of a High-Temperature Proton Exchange Membrane Fuel Cell: Steady-State Analysis. Energies 2023, 16, 7991. https://doi.org/10.3390/en16247991
Zhong Z, Araya SS, Liso V, Zhu J. Multi-Objective Assessment and Optimization of a High-Temperature Proton Exchange Membrane Fuel Cell: Steady-State Analysis. Energies. 2023; 16(24):7991. https://doi.org/10.3390/en16247991
Chicago/Turabian StyleZhong, Zhaoda, Samuel Simon Araya, Vincenzo Liso, and Jimin Zhu. 2023. "Multi-Objective Assessment and Optimization of a High-Temperature Proton Exchange Membrane Fuel Cell: Steady-State Analysis" Energies 16, no. 24: 7991. https://doi.org/10.3390/en16247991
APA StyleZhong, Z., Araya, S. S., Liso, V., & Zhu, J. (2023). Multi-Objective Assessment and Optimization of a High-Temperature Proton Exchange Membrane Fuel Cell: Steady-State Analysis. Energies, 16(24), 7991. https://doi.org/10.3390/en16247991








