Abstract
The effect of watertightness criteria on structural assessment was investigated in this study through the design of a semi-submersible floater for a 10 MW wind turbine. A structural assessment was carried out for the ultimate, fatigue, and serviceability limit states, where six cases of combinations of the loading conditions and structural requirements were assumed for the assessment of watertightness. The different assessment conditions for watertightness resulted in different designs of prestressing tension, which also caused differences in the design margins for the ultimate limit states as well as the SN diagram used for the assessment of the fatigue limit states. The maximum stress acting on the member of the floating wind turbine differed by about 7.6 to 16.2% for the 50-year and 1-year environmental conditions. The small difference between the stresses for the two return periods can be attributed to the large component of the wind turbine thrust in the variable loads. When the partial load factor of 1.0 was used, the structural requirement in the prestressing design caused larger differences compared to the return period of the loading conditions in the watertightness assessment. The use of the partial load factor of 0.5 for the prestressing design also caused a large difference in the results of the structural assessment, indicating the necessity of further investigation of the determination of the partial load factor for floating offshore wind turbines.
1. Introduction
Cost reduction is an essential task for floating offshore wind turbines, and using concrete instead of steel for the supporting floating structures can become one of the solutions. For practical application of concrete in floating offshore wind turbines, clarification of the design criteria is required. Existing knowledge about concrete has been mostly accumulated in the field of civil engineering, where assessment methods are summarized in design guidelines such as the EuroCode [1] and the guideline “Standard Specifications for Concrete Structures” [2] issued by the Japan Society of Civil Engineers (referred to as the JSCE guideline in the discussions below). For the application of concrete for offshore structures, a design guideline is provided by DNV [3] (referred to as the DNV guideline in the discussions below) based mainly on the experiences in the field of oil and gas. While these guidelines provide fundamental assessment methodologies for concrete structures, some technical concerns remain for application to floating offshore wind turbines.
One of the technical concerns related to using concrete for the substructure of floating offshore wind turbines is the watertightness. Unlike steel, which has been widely used for the floating substructures, concrete members are subject to cracking. Cracking in concrete will increase the permeability, which needs to be limited since the change in the total weight of the floater can affect the overall dynamic responses of the system. For the assessment of watertightness related to cracks, criteria are provided in existing guidelines. In the JSCE guideline, an informative reference is given that concrete with crack widths smaller than 0.1 mm yields extremely low permeability under water pressure below 0.9 N/mm2. However, the corresponding loading condition to assess the crack width is not defined. In the DNV guideline, the loading condition for the assessment of the watertightness is defined as the same as the ultimate limit states (ULS), except that the partial factor for the environmental loads is set to 0.5 instead of 1.3 used for the ULS. For the structural requirement, a permanent compression zone is required to ensure tightness against leakages of fluids. The requirements in the DNV guideline are mainly based on the experiences from the oil and gas industry, while the applicability for floating wind turbines remains unclear, as the loading characteristics can be different because of the large fluctuating loadings from the operating wind turbine. Determination of adequate criteria for watertightness for concrete offshore floating wind turbines is required. For the determination of the criteria, insights into the concrete structural response when it is used in floating wind turbines are required.
The concept of concrete floating offshore wind turbines has been examined in previous studies. Viselli et al. (2016) [4] and Pegalajar-Jurado et al. (2018) [5] proposed concrete semi-submersible floaters, Campos et al. (2016) [6] designed a spar-type floater, and Walia et al. (2017) [7] studied TLP-type concrete floaters. In these studies, aspects of concrete floaters such as the floater motions, the cost leverages, and construction methods were studied, while few discussions were conducted regarding the structural behavior of the concrete members.
The aim of this study is to investigate the influence of the criteria of watertight assessment on the limit states of the concrete substructures through the design of a concrete floating offshore wind turbine to contribute to the determination of the design criteria. First, a semi-submersible concrete floater and the accompanying structural cross-sections are designed using currently available guidelines. In the design process, several cases of loading conditions and structural requirements for the assessment of watertightness are assumed for the design of the prestressing of the concrete substructures. The ultimate states of the substructure are evaluated using the commonly used structural assessment methods, and the effect of the watertightness criteria on the ultimate states is examined by comparing the structural assessment results of different prestressing designs. The concrete structural models designed in the process are also intended to contribute to further detailed studies on the determination of the design criteria for concrete substructures for floating offshore wind turbines.
It is noted that the expression “watertightness” used in this study is referring to the permeability related to the cracking, although intact concrete structures also have a certain amount of permeability depending on the material properties, surface conditions, and construction status. It is also noted that the limitation of cracking is related to the corrosion protection for steel bars as well. Considering that the criteria for crack widths for corrosion protection are more relaxed than those for watertightness in both the JSCE guideline and the DNV guideline, only the watertightness criteria are targeted in this study. The crack limitation criteria for corrosion protection may need further investigation.
2. Design Basis for the Concrete Floater
2.1. Design Philosophy and Guidelines
The design of the concrete floater in this study was conducted using the JSCE guideline, which has been widely used in the design of civil engineering structures such as road bridges and dams. The JSCE guideline adopts a performance-based design format, which allows the design to have greater flexibility by defining the performance requirements for safety, serviceability, durability, and recoverability. The assessment method is equivalent to the load and resistance factor method. The safety performance corresponds to the assessment of the ultimate limit states (ULS) and the fatigue limit states (FLS), and the serviceability and durability performance is related to the serviceability limit state (SLS). Although the definition of “limit states” is not directly used in the JSCE guideline, it is used in the discussion for this study to clarify the specific load cases under discussion. In this study, the design of the floater was performed for the major load cases of ULS, FLS, and SLS, and the recoverability and the accidental load cases were not considered. The definitions of the loading conditions for each limit state were based on IEC61400-3-1 [8], which is the international standard for floating offshore wind turbines. This standard is referred to as the IEC standard in the discussions below.
2.2. Metocean Data and the Design Load Case
The target site for the design of the concrete floater was chosen to be the same as the Fukushima FORWARD project [9], which is about 20 km from the coast of Fukushima, Japan. Although the water depth at the site of the project is about 120 m, it was changed to 200 m for the present design to simplify the hydrodynamic modeling and the mooring design. The metocean conditions used for the design of the floater are summarized in Table 1. The wind and wave conditions at a 50-year return period that were used for the first phase of the construction [9] were used in the present design. For the investigation of suitable load conditions to assess the SLS, which will be discussed in detail in Section 2.5.3, wave conditions for a 1-year return period were used in this study. As the information for the wave conditions for a 1-year return period for the target site is not publicly available, data for another site [10] that has a similar significant wave height for a 50-year return period with the target site is used. For the evaluation of fatigue, data of the annual mean wind speed, the wind shear at normal conditions, and the Weibull parameters for the yearly wind distribution are obtained from the database “NeoWinds”, [11] in which the statistics are provided based on the results from the Advanced Research WRF (Weather Research and Forecasting Model) for user-specified sites.

Table 1.
Summary of the metocean condition used for the floater.
2.3. Mounted Wind Turbine
For the wind turbine mounted on the floating substructure, a reference model known as the DTU10MW wind turbine, which was proposed by the Technical University of Denmark, was used. Details of the wind turbine model including the aerodynamic and structural properties of the turbine can be found in [12]. The reference model originally included the models for both the wind turbine and the steel tower to be installed onshore. In this study, the steel tower was newly designed for the present floater to withstand the ultimate strength of the floater and to avoid the resonance of the tower with the 3P and 9P frequencies of the blade rotation. The basic properties of the wind turbine and the newly designed steel tower are summarized in Table 2, and the properties of the cross-sections of the tower are shown in Table 3.

Table 2.
Basic properties of the mounted wind turbine and the steel tower.

Table 3.
Properties of the cross-sections of the steel tower.
A baseline controller was originally provided for the reference 10 MW wind turbine [13]. However, as the reference wind turbine model was designed for a bottom-fixed tower installed onshore, it may cause unfavorable effects such as negative damping when mounted on a floater, especially for wind speeds above the rated wind speed where the blade pitch controller is activated. For the present floating wind turbine, a set of coefficients for the PI controller of the blade pitch was designed in [14] to mitigate these effects. The amount of change introduced by the controller to the blade pitch angle is shown in Equation (1).
where is the gear ratio, is the proportional gain defined as the function of the blade pitch angle , is the integration time, is the rotation speed of the rotor, and φ is the rotor azimuth angle calculated with φ = ∫Ω dt. In this study, is determined considering the motion characteristics of the floater using the method presented in Lemmer et al. (2020) [15]. The obtained values for the proportional gain are shown in Figure 1, and an example of the performance of the controller when the wind turbine is mounted on the floater is shown in Figure 2 for the rotational speed and the blade pitch angle at the mean wind speed of 12 m/s, which is just above the rated wind speed of 11.4 m/s. It is seen from Figure 2 that the newly designed controller resulted in a smaller variance in the blade pitch angle and the rotational speed compared to the original baseline controller. Details of the design of the controller and its effect on the dynamic response of the floating wind turbine can be found in Oh et al. (2021) [14].
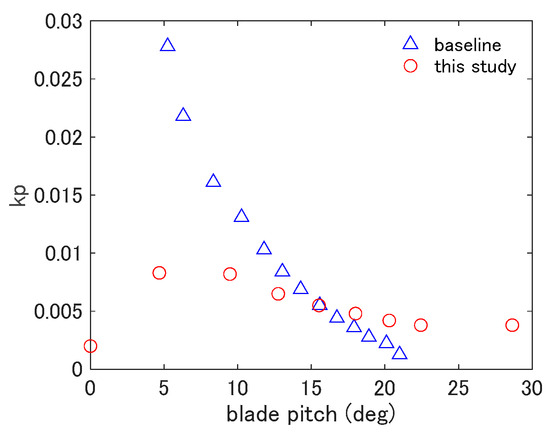
Figure 1.
Comparison of the proportional gains for the baseline controller for DTU reference wind turbine and the controller used in this study.
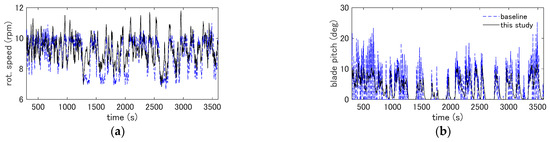
Figure 2.
Comparison of the performance of the baseline controller for the DTU reference wind turbine and the controller used in this study for (a) the rotational speed and (b) the blade pitch angle.
2.4. Material and Safety Factors
The structural assessment for the concrete members of the floating substructure is conducted using a load and resistance factor design format based on the JSCE guideline as shown in Equation (2).
where S is the design load effect, is the design resistance, is the characteristic load, and is the characteristic resistance. is the partial load factor that accounts for the uncertainty of the loads, is the material factor that accounts for the uncertainty of the material strength, and is the member factor that accounts for the uncertainty of the geometry of the member. For the present floater, concrete that has the characteristic compressive strength of concrete of 60 N/mm2 is used. The design compressive strength of concrete , the design tensile strength of concrete , and Young’s modulus of concrete are evaluated as shown in Equations (3), (4), and (5) respectively.
where is the material factor for concrete. Although the performance-based design format in the JSCE guideline allows the designer to use user-defined values for the safety factors based on the desired failure probability, reference values for the safety factors are provided based on experiences in the field of civil engineering. While the failure probabilities and safety factors suitable for concrete offshore wind turbines may need further investigation, this study uses the proposed values shown in the JSCE guideline, which are 1.3 for the material factor of concrete , 1.0 for the material factor of steel , and 1.3 for the member factor . The partial load factor used in the assessment of each limit state is discussed in the following section.
2.5. Design Load Cases
2.5.1. Ultimate Limit States
Among the various design load cases (DLCs) defined in the IEC standard for the evaluation of the ULS, the two representative cases, DLC 1.6 and DLC 6.1, were evaluated for the design of the present floater. DLC1.6 is the case where the turbine is operating under normal stochastic wind and severe sea state. Two representative mean wind speeds that can result in the ultimate loads were considered. One is 11.4 m/s, which is the rated wind speed, and the other is 14.0 m/s, which is above the rated wind speed and is likely to be affected by the negative damping phenomena. The significant wave height with a 50-year return period was used for both mean wind speeds, and three cases of significant wave periods around the significant wave period of the 50-year return period were considered. DLC6.1 is the case where the turbine is parked under extreme wind and wave conditions. Both the wind and the wave of the 50-year return period were used, and a range of wave periods were also considered. Environmental conditions for each load case for the ULS are summarized in Table 4. For each combination of the wind condition and the wave condition, a simulation was run for six cases of random seeds, and the run that gave the maximum loads was used for the structural design.

Table 4.
Load cases used for the assessment of the ULS.
For the partial load factor , different values are suggested for different types of loads in the JSCE guideline. For the permanent loads, which are defined as the loads where fluctuations are rare or extremely small relative to the mean value such as the dead weight, the hydrostatic pressure, and the prestressing forces, values of 1.0 to 1.2 are suggested. For fluctuating loads, which are defined as the frequently fluctuating loads such as the live loads, the wind loads, and the loads related to temperature change, values of 1.1 to 1.2 are suggested. Meanwhile, the IEC standard suggests a partial load factor of 1.35 for the assessment of the ULS. In this study, for the compensation of the two guidelines, a partial load factor of 1.35 is applied to the fluctuating loads obtained from the dynamic analysis, and 1.0 is applied to the prestressing tension for the evaluation of the ULS.
2.5.2. Fatigue Limit States
For the evaluation of the FLS, the design load case DLC 1.2 in the IEC standard was considered. DLC1.2 is the case to evaluate the loads during the wind turbine operation under normal wind and wave conditions throughout its lifetime. In this study, mean wind speeds from 5 m/s to 25 m/s, which are the wind speeds of the cut-in to the cut-out of the wind turbine, respectively, are considered in 2 m/s bins. The significant wave height and wave period that correspond to each wind speed are estimated using the SMB prediction method as shown in Equations (6) and (7).
where is the mean wind speed at 10 m height, and g is the gravity acceleration. F is the fetch parameter, which was set to 23,500 according to the estimation for the target site. The partial load factor of 1.0, which is recommended in both the JSCE guideline and the IEC standard, was used in this study for the evaluation of the FLS.
2.5.3. Serviceability Limit States
The SLS is the design case to consider the state of the structure during normal use, including the watertightness. When prestressed concrete is used, the assessment of the watertightness is mainly related to the design of the prestressing steel for crack control. This limit state is not considered in the IEC standard, which has been mainly targeted at steel floaters. The definition of the loading conditions and the structural requirements for the assessment of watertightness for floating offshore wind turbines are also not available in the existing concrete guidelines, as discussed in the introduction. For the investigation of the influence of watertightness criteria on the ultimate states of concrete substructures in ULS and FLS, three cases of loading conditions and two cases of structural requirements were assumed for the design of the prestressing steel in this study. Case 1 of the loading conditions is the same as the ULS that is shown in Table 4, where the environmental conditions correspond to the 50-year return period, and the partial load factor is set to 1.0. Case 2 of the loading conditions is the same as the DNV guideline, where the loading conditions for the ULS are used with . As a new load case of the loading condition for the assessment of the SLS, Case 3 was defined in this study as shown in Table 5. This is the case where the wave is at the condition of a 1-year return period, the wind is at normal condition, and the wind turbine is operating. The purpose of setting up this load case is to investigate the characteristics of the loading of floating wind turbines by showing the difference between the responses to the loading conditions of 50-year and 1-year return periods and to simulate an example case wherein a certain amount of permeability is tolerated when the ballast water can be controlled over a period of, for example, one year. The load factor is set to 1.0 in this case. For the structural requirements, fully compressed conditions and partially compressed conditions were considered. The former refers to the state where only compression stress is acting on the cross-section, and the latter refers to the state where tensile stress is allowed on the cross-section, but cracks are not allowed. The structural requirement by the DNV guideline is somewhere between the fully and partially compressed conditions, and the requirement in the JSCE guideline can be regarded as a more relaxed requirement than the partially compressed conditions. The combination of the loading conditions and the structural requirements considered in the assessment of the SLS is summarized in Section 4.3. The prestressing tension is designed for each case shown in the table.

Table 5.
Additional load case used for the assessment of SLS.
3. Analysis Methods
3.1. Dynamic Analysis of the Floating Wind Turbine
For the evaluation of the dynamic responses of the floating wind turbine, an in-house code for the aero-hydro-servo-elastic coupled analysis “NK-UTWind” [16] is used. The tower and the floater of the floating wind turbine are modeled with a three-dimensional beam model in the N degree of freedom of which the equation of motion shown in Equation (8) is solved in the time domain.
where is the displacement, is the mass matrix, is the stiffness matrix, and is the Rayleigh damping matrix. is the hydrodynamic force that can be modeled with both Morison’s equation and potential flow theory. is the restoring force, and is the force from the mooring lines. The aerodynamic and inertia forces from the wind turbine are calculated with OpenFAST [17] and passed to NK-UTWind as at the tower-top node. From NK-UTWind, the displacement and velocity of the tower-top node are passed to OpenFAST at each time step. For the present calculation, Morison’s equation shown in Equation (9) is used for the estimation of .
where is the water density, is the diameter of the member, is the velocity of the water particle, is the added mass coefficient, and is the drag coefficient. Added mass coefficients and drag coefficients were all set at 1.0. The wave was modeled using first-order linear wave theory. is calculated with the quasi-static catenary model. The time step was set to 0.02 s, and Rayleigh damping was set to 0.02% for the purpose of numerical stabilization.
3.2. Structural Assessment
3.2.1. Ultimate Limit States
The structural assessment was conducted by comparing the design load S and the design resistance R, as shown in Equation (2). For cross-sections subjected to both axial force and bending moment, the design resistance was estimated using the following procedure shown in Chapter 8 of the JSCE guideline for the design of the prestressed concrete. First, the cylindrical cross-sections of the floater members were divided into 96 segments. Then a temporal value for the neutral axis position was assumed, and the strain distribution was obtained using the Bernoulli–Euler theory. Strain at each segment was calculated assuming that the concrete strain at the compression edge has reached the ultimate compressive strain , which was estimated using Equation (10).
The stress-strain diagrams shown in Figure 3 were then used to obtain the stress at each segment of the cross-section, and the obtained stress values were summed to obtain the combined compressive stress of the concrete , the combined tensile stress of the reinforcing steel , and the combined tensile stress of the prestressing steel . The equilibrium condition of the forces in the cross-section gives Equation (11).
where is the axial force acting on the cross-section. Solving Equation (11) yields the value of the neutral axis position x. The obtained value for the neutral axis position was then used to estimate the position of the action of the combined compressive stress of the concrete, , using Equation (12).
where is the stress of concrete, b is the wall thickness, and y is the coordinate of the segment. Using the obtained results, the design bending resistance was obtained as shown in Equation (13).
where is the coordinate of the acting point of the axial force, is the coordinate of the acting point of the reinforcing steel, and is the coordinate of the acting point of the prestressing steel.
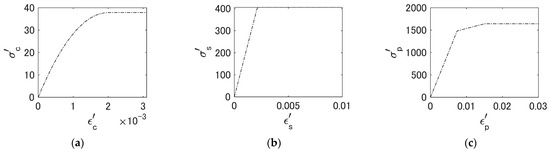
Figure 3.
Stress-strain diagrams used for bending and axial capacity estimation for (a) concrete, (b) reinforcing steel, and (c) prestressing steel.
The estimation of the shear resistance of structural members subjected to axial forces is recommended to be calculated using non-linear finite element analysis or a similar method. Meanwhile, for structural members where axial compressive stress is small relative to the compressive strength, a simplified formula for the estimation of the design shear resistance is proposed in the JSCE guideline as shown in Equation (14).
where d is the effective height, which is the distance from the compression edge to the centroid of the reinforcing steel, is the wall thickness, and is estimated using 0.2∛(). , , and are the correction factors to account for the effect of the effective height, the ratio of the steel in the cross-section in the axial direction, and the bending moment, respectively, which are estimated using Equations (15)–(17).
where is the bending moment required to counteract the stresses generated by the axial forces at the tensile edge for the design bending moment. The shear resistance of the shear reinforcement was estimated using Equation (18).
where is the area of the shear reinforcing steel in the cross-section in the range of , is the design yield strength of the reinforcing steel, is the angle of the reinforcing steel with the member axis, and is the spacing between the shear reinforcement. The total shear resistance of the cross-section was obtained by the sum of and .
3.2.2. Fatigue Limit States
The fatigue limit state was assessed using the cumulative linear damage theory, where the accumulated damage D is estimated using Equation (19).
where n is the number of cycles, and N is the number of cycles to failure. The number of cycles to failure was estimated using the SN diagram represented by Equation (20).
where is the ratio of the maximum stress to the compression strength, and is the ratio of the minimum stress to the compression strength. is the coefficient set to 0.85 for the stress variation in the compression-compression range and 1.0 for the stress variation in the tensile-tensile range. For concrete frequently filled with water, the coefficient K is set to 10 in the JSCE guideline. The time series of the cross-sectional loads obtained with NK-UTWind were broken down into hysteresis cycles by matching the local minima with the local maxima of the random loads using rainflow counting. Each cycle is characterized by the mean and amplitude of the load. Then the number of cycles was counted and accumulated for all the load cases in a 20-year lifetime.
3.2.3. Serviceability Limit States and the Design of the Prestressing Steel
In this study, tensile stress on concrete is controlled using prestressing steel. The amount of tension required to be installed in the prestressing steel is estimated using Equation (21).
where and are the axial stress due to the axial force and the bending moment, respectively. The maximum tensile stress is estimated by taking the maximum value of all the time series of the tensile stress that was estimated from the cross-sectional forces using the Bernoulli-Euler theory for the load cases discussed above. is the axial stress due to the prestressing tension and is estimated using , where is the effective prestressing force and is the area of concrete in the cross-section. is the stress acting on concrete. For the fully compressed condition, , while for the partially compressed condition. It is noted that the effective prestressing force is the actual force introduced in the structure. The initially loaded prestressing tension will decrease to the effective prestressing tension due to causes such as friction between the tension material and the sheath, relaxation of the prestressing steel, and the shrinkage of concrete.
4. Design of the Concrete Floater
4.1. Floater Geometries
The semi-submersible concrete floater was designed with one main column (MC), three side columns (SC), three lower hulls (LH), and braces. The increase in the diameter of the SC and the length of the LH leads to increased restoring forces, increased wave excitation forces, and decreased pitch natural frequency, and therefore the increase of the wave excited pitch and the decrease of the wind excited pitch of the floater. Larger wall thickness is related to a higher center of gravity of the floater and therefore larger dynamic motions, which need to be compensated for by the larger side column width and longer hull length. The effect of the geometries of the structural members on the motion responses for semi-submersible floaters for a 10 MW wind turbine has been studied in Oh (2021) [18] using a simplified hydrodynamic model. The semi-submersible floater used for the sensitivity study consisted of one main column, three side columns, three lower hulls, and three upper hulls that were all made of concrete. Results showed that the geometry that gave the minimum floater pitch was approximately 12 to 14 m for the diameter of the side column and 35 to 45 m for the length of the lower hull. These results were used as the initial design point for the concrete floater in this study. The final design of the floater is determined using the results of the dynamic analysis using NKUTWind so that the maximum floater pitch for the ULS conditions is below 10 degree. Optimization of the geometries related to the floater motion was not conducted.
The designed concrete floater is named “NKCSemi.” The outline of the floater and the global coordinate used in this study are shown in Figure 4, and the geometries of the floater members are shown in Table 6. The three SC members are named SC1, SC2, and SC3, and the three LH members are named LH1, LH2, and LH3. The origin of the global coordinate is set at the crossing point of the centerline of the MC and the still water line as shown in Figure 4b. The diameter is 14 m for MC and 12 m for SC, and the length of LH is 46 m. MC, SC, and LH are made of concrete. The side columns and the lower hulls are connected to the main column with braces made of steel, which is different from the floater used for the sensitivity analysis in Oh (2021) [18], in which the side columns were connected to the main column using a concrete upper deck. The purpose of the use of the steel braces in the present floater is to lower the height of the center of gravity of the floater, thus reducing the maximum pitch angle. The draft of the floater is 20 m, and the upper braces are located at 10 m height from the still water line. The displacement of the floater is 18,748.7 m3. Water ballast is used, where 1.54E + 06 kg of water is added inside the LH members. Three mooring lines are connected to the three side columns as shown in Figure 4. The properties of the mooring lines are shown in Table 7. The natural frequencies of the total system including the wind turbine, tower, and floater are 147 s, 20.0 s, and 16.1 s for surge, heave, and pitch motion, respectively.
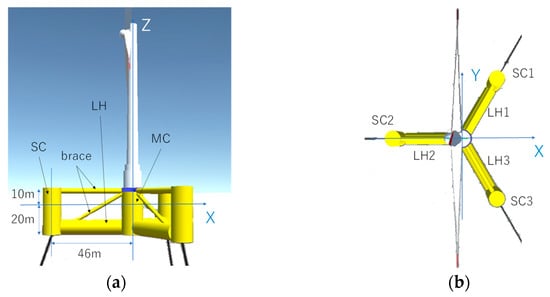
Figure 4.
The (a) outline and the (b) global coordinate of the concrete floater.

Table 6.
Properties of the cross-sections of the floater.

Table 7.
Properties of the mooring system.
4.2. Dynamic Response
The dynamic response of NKCSemi for the load cases defined in Section 2.5 was estimated using NK-UTWind. The floater members MC, SC, and LH were each modeled using six nodes in the three-dimensional beam model, and the internal forces were investigated for five cross-sections for each structural member. Considering the symmetric property of the floater geometry, the results for MC, SC1, SC2, LH1, and LH2 were assessed. Figure 5 shows the power spectra of the floater motions in the heave and pitch for the DLC 1.6, the DLC 6.1 for the ULS assessment, and the additional case DLC X for the SLS assessment. It is seen from the figure that the floater motion was mainly excited at the natural frequencies of the rigid floater motion and the frequencies of the input waves. Heave and pitch motions were similar for DLC 1.6 and DLC 6.1, as the wave conditions were the same for the two load cases. Differences between DLC 1.6 and DLC 6.1 are mainly seen in the lower frequencies of the pitch motion, which was excited by the thrust loads from the wind turbine. Pitch motion in the lower frequencies for DLC 1.6 and DLC X were similar, as the wind conditions were the same for the two load cases. The dynamic motion of DLC X in higher frequencies was small compared to DLC 1.6 and DLC 6.1, which can be attributed to the frequencies of the input wave in DLC X is further away from the pitch natural frequency compared to those in DLC 1.6 and DLC 6.1.
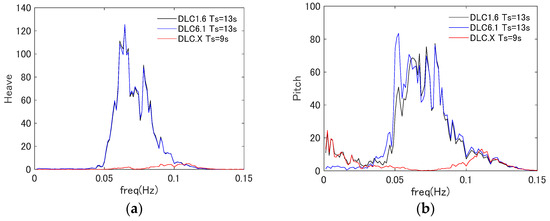
Figure 5.
Power spectrum density of the (a) heave and (b) pitch motion of the floater.
For the cross-sectional forces, z = 10 m for MC, z = −15 m for SC1, and x = −7 m for LH1 were the cross-sections that were subjected to the largest von Mises stress for the load cases of the ULS. Examples of the power spectra of the shear force in the x direction () and the bending moments in the y direction () at these cross-sections are shown in Figure 6 and Figure 7, respectively, for DLC 1.6, DLC 6.1, and DLC X. It is seen from the figures that the dynamic components of the cross-sectional forces are mainly seen for the frequencies related to the input wave and floater motion (0.05 to 0.15 Hz), the frequency of tower first mode (0.41 Hz), and the lower frequencies below 0.03 Hz that are related to the thrust loads from the wind turbine. Dynamic components for DLC 1.6 and DLC 6.1, which have the same wave conditions but different wind conditions, were similar, while the differences were mainly seen in the frequencies around the tower first mode and the lower frequencies below 0.05 Hz that are caused by the operational loads from the wind turbine. Dynamic components for DLC 1.6 and DLC X, which have the same wind conditions but different wave conditions, were also similar for most frequencies, while differences were mainly seen in the frequencies around 0.05 Hz, which corresponds to the pitch natural frequency. This result corresponds to the smaller floater pitch motion observed for DLC X, as shown in Figure 5.
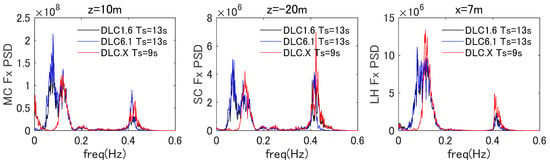
Figure 6.
Power spectrum density of the shear force Fx in the representative cross-sections of MC, SC, and LH.
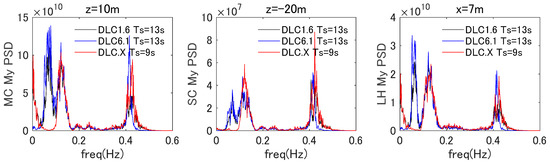
Figure 7.
Power spectrum density of the bending moment My in the representative cross-sections of MC, SC, and LH.
4.3. Structural Design of the Floater Members
Using the cross-sectional forces obtained with NK-UTWind, the structural design of the cross-sections was conducted. The minimum design requirements for the concrete structure were set as 30 mm for the distance between the sheaths of the prestressing steel, 20 mm for the distance between the reinforcing steel and the sheaths, and 100 mm for the distance between the reinforcing steel bars. The required minimum cover depths for the reinforcing steel and the prestressing steel were set at 75 mm and 90 mm, respectively. These values were determined according to the JSCE guideline. The details of the designed cross-sections of MC, SC, and LH are shown in Figure 8 and Table 8. For all three members, reinforcing steel was installed in 1.875 degrees pitch, and the prestressing steel was installed in 3.75 degrees pitch using sheaths of 88 mm diameter. The distances between the sheath and the steel and the cover depths in the designed cross-sections were all above the criteria.
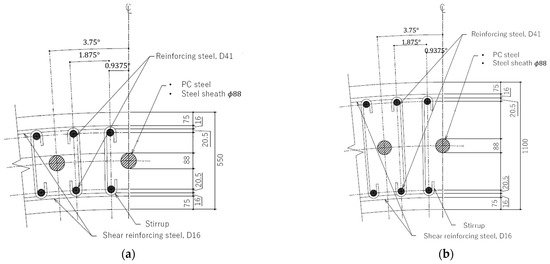
Figure 8.
Outline of the cross-sections of the prestressing concrete structure for (a) MC and SC and (b) LH.

Table 8.
Properties of the cross-sections of the concrete members.
As discussed in Section 2.5.3, the amount of tension introduced in the prestressing steel needs to be estimated through the assessment of watertightness in the SLS, while a solid definition for the loading conditions and the structural requirement for floating wind turbines are missing in the current design guidelines. In the present study, the tension in the prestressing steel was estimated for the combinations of three cases of loading conditions, a 50-year return period with = 1.0, a 50-year return period with = 0.5, and a 1-year return period with = 1.0. For the structural requirement, the fully compressed condition and the partially compressed condition were considered. Table 9 shows the results of maximum tensile stress from all the loading conditions and the amount of tension required in the prestressing steel for different combinations of the loading conditions and the structural requirements. It is seen from the table that the difference between the maximum tensile stress for the 50-year return period and the 1-year return period was only 7.6 to 16.2% for the three cross-sections when = 1.0 was used. When the partial load factor of 0.5 was used for the load of the 50-year return period, which is the load condition for the SLS defined in the DNV guideline, the tensile stress became 40 to 46% smaller compared to the loads of the 1-year return period. The small difference between the maximum tensile stress for the loading conditions of 50-year and 1-year return periods can be attributed to the large contribution of the loadings from the operating wind turbine to the cross-sectional forces in the targeted cross-sections. As discussed in the previous section, the difference between DLC 1.6 and DLC X was only observed around the frequencies of the floater pitch natural frequency, and other components were similar. Present results indicate that for the dynamic responses with these characteristics, the application of the load factor of 0.5 can underestimate the loadings. Table 9 shows that differences were also seen in the required tension in the prestressing steel for the fully compressed and partially compressed conditions. The differences in the required tension for PC1 and PC2 were 37%, 69%, and 30% for MC, SC, and LH, respectively, and the differences in the required prestressing tension for PC5 and PC6 were 42%, 82%, and 32% for MC, SC, and LH, respectively, which are similar to the results for PC1 and PC2. Even for the same loading conditions, the difference in the structural requirements can result in more than 30% difference in the prestressing tension. The present results of the designed prestressing tension using the three cases of loading conditions and two cases of structural requirements indicate that further investigations into both the adequate load conditions and structural criteria are required for the rational design of concrete offshore wind turbines. The structural integrity for the ULS and FLS of the designed cross-sections is investigated in the following section together with the effect of the amount of the installed tension in the prestressing steel on the results of the structural assessment.

Table 9.
Tension in the prestressing steel for each cross-section of the floater member.
5. Effect of Prestressing Design on Structural Assessment Results
5.1. Ultimate Limit States
Structural assessment for the ULS was conducted for the cross-sections with the six cases of the prestressing tension shown in Table 9 to demonstrate the structural integrity of the designed cross-sections as well as to investigate the effect of the prestressing tension on the assessed results. Figure 9 shows the results of the design load effect S and the bending resistance R for the axial force and the bending moment for the cross-sections of the concrete members MC, SC, and LH. The different colors of the lines in the figure correspond to different loading conditions used for the design of the prestressing tension, while the solid lines and the dashed lines represent the fully compressed and partially compressed conditions for the structural requirements, respectively. It is seen from the figure that the bending resistance of the cross-section varied with the change of the installed tension in prestressing steel, and the difference in the installed prestressing tension resulted in different design load effects in the axial direction. As a result, the ratio of the design load effect and the design resistance , which indicates the design margin, differed between the six cases of the prestressing design for each structural member. The differences due to the prestressing tension were small in SC because of the relatively relaxed design of the cross-section, and results for MC and LH are discussed for the investigation of the effect of the prestressing tension. Comparing the cases with prestressing tension designed with the loading conditions of 50-year and 1-year return periods using = 1, the difference in was about 8% in MC and 0% in LH for the fully compressed condition (PC1 and PC5) and 2% in MC and 5% in LH for partially compressed conditions (PC2 and PC6). Comparing the cases of the prestressing tension designed for the same loading conditions but different structural requirements, the difference in was about 18% in MC and 16% in LH (PC1 and PC2), and 11% in MC and 20% in LH (PC5 and PC6). The differences due to the structural requirement in the prestressing design were larger compared to the differences due to the return period used in the loading conditions when = 1 is used. When = 0.5 was used for the 50-year return period for the design of the prestressing tension, the design margin became 12% and 25% larger for MC and LH, respectively, compared to the case of = 1 used with the 1-year return period for the fully compressed condition (PC3 and PC5). These differences are reduced to 4% and 8% for MC and LH, respectively, for the partially compressed condition (PC4 and PC6). The use of the load factor 0.5 will increase the design margin more greatly compared to the difference caused by the use of different return periods, and the difference is more pronounced for the fully compressed conditions where the prestressing tension is higher compared to the partially compressed conditions. The present floater was designed to endure the design of PC1, which is the case that showed the least design margin. As both the loading conditions and the structural requirements used for the design of the prestressing steel had a considerable impact on the assessed results for the ULS, further detailed studies on the definitions for the SLS can lead to a more rational design with reduced diameters and concrete thickness compared to the present design.
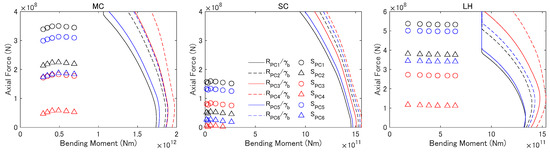
Figure 9.
Design load effect and design resistances for the axial force and the bending moment for MC, SC, and LH.
The assessment results for the shear forces are shown in Figure 10. It is seen from the figure that the design resistance R varied depending on the design of the prestress. The shear resistance increased with the increase in the prestressing tension, which is the result of the correction for bending moments, as shown in Equation (18). The maximum differences in the design margin for the shear forces between the six cases of the prestressing design were approximately 9% for MC and 14% for LH, indicating that the design of the prestressing steel can also affect the design margin for shear forces. As the estimation of shear resistance was conducted using the simplified equations, the results shown in Figure 10 are not enough for quantitative discussions of the effect of prestressing tension on the ULS assessment for shear forces. Although the feasibility of the design of the cross-section for shear forces was confirmed with the present assessment, more accurate shear resistances need to be evaluated using a method such as the non-linear finite element analysis for the quantitative estimation of the effect of the prestressing tension.
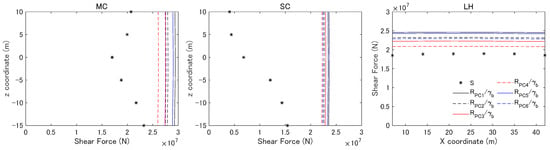
Figure 10.
Design load effect and design resistances for the shear force for MC, SC, and LH.
5.2. Fatigue Limit States
Assessment for the FLS was conducted for the cross-sections with the six cases of the design of the prestressing tension to demonstrate the structural integrity of the designed cross-sections as well as to investigate the effect of the prestressing tension on the assessed results. Figure 11 shows the results of the 20-year rainflow count for bending moment , which is the main contributor to the fluctuating axial stress, for the cross-section that showed the largest cumulative fatigue damage in MC, SC, and LH. It is seen from the figure that the maximum amplitude of the bending moment was up to approximately 1.5 × 105 kNm for MC, 4 × 104 kNm for SC, and 1.5 × 105 kNm for LH. The SN diagram for concrete shown in Equation (20) is plotted in Figure 12 for each case of prestressing tension. It is seen from the figure that a difference in the prestressing tension causes a difference in the SN diagram, where larger stress amplitudes are more greatly affected by the prestressing design. The maximum axial stress amplitudes corresponding to the cross-sectional forces are approximately 2.0 N/mm2 for MC, 0.8 N/mm2 for SC, and 2.7 N/mm2 for LH. These amplitudes of the axial stress correspond to the number of cycles to failure of 108 to 109, according to Figure 12. The JSCE guideline recommends the use of Equation (20) up to the number of cycles to failure of 108. Although the guideline suggests that Equation (20) gives safer results when the number of cycles to failure exceeds 108, future research may be required on a more accurate estimation of fatigue design for this stress range. It is noted that the cross-sections for the present floater were designed to withstand the ULS for the prestressing design of PC1, which is the most severe case and which can have a large design margin when the requirements for the SLS are weakened. If the prestressing tension is designed with more relaxed regulations, the cross-sections may have smaller diameters and thinner wall thickness, which can result in much larger stress amplitudes and thus a larger effect from the prestressing design for fatigue loadings.
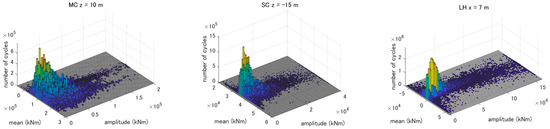
Figure 11.
Number of cycles in each bin of the mean and amplitude of the bending moment for 20 years for MC, SC, and LH.
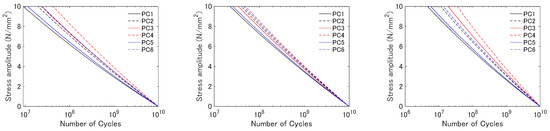
Figure 12.
Comparison of the SN diagram between different prestressing design for MC, SC, and LH.
Using the results of the rainflow count shown in Figure 11 and the SN diagrams shown in Figure 12, the cumulative damage ratio for 20 years was calculated and is shown in Figure 13. In the JSCE guideline, which is mostly applied to onshore civil engineering structures, the limit for the cumulative damage ratio is defined as 1.0. In the DNV guideline, the limit is defined as 0.33 for members with limited access for inspection and repair, 0.5 for members below or in the splash zone, and 1.0 for members above the splash zone. Results in Figure 13 show that the cumulative damage ratio was below the requirement for both guidelines for all the cross-sections. The figure also shows that the cross-sections z = 10 m in MC, z = −15 m in SC, and x = 7 m in LH showed the highest fatigue damage, which corresponds to the cross-sections that showed the largest design values for the ULS. The effect of the prestressing tension was larger in these cross-sections compared to the rest since the effect of prestressing tension becomes larger for larger stress amplitude, as shown in Figure 12. Taking the cross-section x = 7m in LH as an example, which showed the largest effect from the prestressing tension, the difference of the cumulative damage ratios between PC1 and PC5, which have the same structural requirements but different return periods for the loading conditions for the prestress design, was 2%. The difference between PC1 and PC2, which has the same loading condition but different structural requirements, was 8%. The effect of structural requirement had a larger effect on the fatigue damage compared to the return period of the loadings for the design of the prestressing steel when the load factor of 1.0 is used. Comparing the results between PC1 and PC3, which have the same structural requirements and return periods for the loading conditions but different partial load factors, the difference in the cumulative damage ratio is 10%, indicating that the load factor can also have a large impact on the fatigue damage and needs to be chosen carefully. The obtained results also indicate that appropriate settings of both the load conditions and the structural requirement for the design of prestressing steel can lead to a more rational design of the cross-sections against fatigue damage.
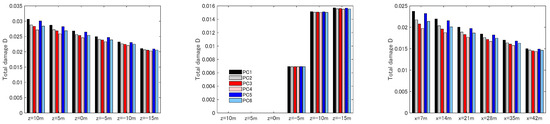
Figure 13.
Comparison of the cumulative fatigue damage for different prestressing designs.
6. Conclusions
Through the design of a concrete semi-submersible floater and the associated cross-sections for the concrete members, the effect of watertightness criteria on the structural limit states of ULS and FLS was investigated. The following conclusions were obtained.
- The different assessment conditions for watertightness resulted in different designs of prestressing tension, which also caused differences in the design margins for the ultimate limit states as well as the SN diagram used for the assessment of the fatigue limit states.
- The maximum stress acting on the member of the floating wind turbine differed by about 7.6 to 16.2% for the 50-year and 1-year environmental conditions. The small difference between the stress for the two return periods can be attributed to the large component of the wind turbine thrust in the variable loads.
- When the partial load factor of 1.0 is used, the structural requirement in the prestressing design caused larger differences compared to the return period of the loading conditions in the watertightness assessment. The use of the partial load factor of 0.5 for the prestressing design also caused a large difference in the results of the structural assessment, indicating the necessity of further investigation of the determination of the partial load factor for floating offshore wind turbines.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available in FigShare at https://doi.org/10.6084/m9.figshare.24780297.
Conflicts of Interest
The author declares no conflict of interest.
References
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Ruels and Rules for Buildings. British Standards Institution: London, UK, 2005.
- Japan Society of Civil Engineers. Standard Specifications for Concrete Structures [Design]; Japan Society of Civil Engineers: Tokyo, Japan, 2017. [Google Scholar]
- DNVGL-ST-C502; Offshore Concrete Structures. DNV GL: Calgary, Canada, 2018.
- Viselli, A.M.; Goupee, A.J.; Dagher, H.J.; Allen, C.K. Design and model confirmation of the intermediate scale VolturnUS floating wind turbine subjected to its extreme design conditions offshore. Wind Energy 2016, 19, 1161–1177. [Google Scholar] [CrossRef]
- Pegalajar-Jurado, A.; Bredmose, H.; Borg, M.; Straume, J.G.; Landbø, T.; Andersen, H.S.; Yu, W.; Müller, K.; Lemmer, F. State-of-the-art model for the LIFES50+ OO-Star Wind Floater Semi 10MW floating wind turbine. J. Phys. Conf. Ser. 2018, 1104, 012024. [Google Scholar] [CrossRef]
- Campos, A.; Molins, C.; Gironella, X.; Trubat, P. Spar concrete monolithic design for offshore wind turbines. Marit. Eng. 2016, 169, 49–63. [Google Scholar] [CrossRef]
- Walia, D.; Schunemann, P.; Kuhl, M.; Adam, F.; Hartmann, H.; Großmann, J.; Ritschel, U. Prestressed ultra high performance concrete members for a TLP substructure for floating wind turbines. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- IEC61400-3-1; Design Requirements for Fixed Offshore Wind Turbines. International Electrotechnical Commission: Geneva, Switzerland, 2019.
- Ishihara, T.; Shimada, K.; Imakita, A. Metocean design condition for “Fukushima FORWARD” project. In Proceedings of the Grand Renewable Energy 2014, Tokyo, Japan, 30 July–1 August 2014. [Google Scholar]
- New Energy and Industrial Technology Development Organization. Accomplishment Report/Next Generation Floating Offshore Wind Power Generation System Demonstration Study (Semi-Sub Type); New Energy and Industrial Technology Development Organization: Tokyo, Japan, 2016. [Google Scholar]
- NeoWinds. Available online: https://appwdc1.infoc.nedo.go.jp/Nedo_Webgis/top.html (accessed on 23 October 2023).
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Natarajan, A.; Hansen, M.H. Description of the DTU 10MW Reference Wind Turbine; DTU Wind Energy Report I-0092; Technical University of Denmark: Roskilde, Denmark, 2013. [Google Scholar]
- Hansen, M.H.; Henriksen, L.C. Basic DTU Wind Energy Controller; DTU Wind Energy Report; Technical University of Denmark: Roskilde, Denmark, 2013. [Google Scholar]
- Oh, S.; Lemmer, F.; Raach, S. A study on the effect of wind turbine controller on the sectional forces of a semi-sub floater. In Proceedings of the 43th Wind Energy Symposium, Tokyo, Japan, 18–19 November 2021. [Google Scholar]
- Lemmer, F.; Yu, W.; Schlipf, D.; Cheng, P.W. Robust gain scheduling baseline controller for floating offshore wind turbines. Wind Energy 2020, 23, 17–30. [Google Scholar] [CrossRef]
- Oh, S.; Ishii, K.; Iijima, K.; Suzuki, H. Implementation of potential flow hydrodynamics to time-domain analysis of flexible platforms of floating offshore wind turbines. J. Phys. Conf. Ser. 2019, 1356, 012041. [Google Scholar] [CrossRef]
- Jonkman, J.M. The New Modularization Framework for the FAST Wind Turbine CAE Tool. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Dallas, TX, USA, 7–10 January 2013. [Google Scholar]
- Oh, S. Comparison of concrete and steel semi-submersible floaters for 10MW wind turbines. J. Phys. Conf. Ser. 2021, 2018, 012029. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).