A Review on the Effect of Electrical Steel Manufacturing Processes on the Performance of Electric Machines
Abstract
:1. Introduction
2. Electrical Machines Core Losses
3. Cutting Process
3.1. Modeling of the Degradation Effect by Cutting
3.2. Implement the Developed B-H Curves into FEM
4. Stacking Process
4.1. Back-Lack
- Allowing complete design freedom because manufacturing aspects such as interlocking or welding seam positions are not required.
- Because the laminations have no way of expanding, full-face adhesive bonding allows for the tightest tolerances and excellent shape stability.
- Bonding has no effect on the magnetic flux lines of the ESLs as shown in Figure 10c.
- Lamination stacks with the tightest manufacturing tolerances improve heat dissipation by improving heat transfer between the laminations and the housing.
- Back lack effectively dampens vibrations in laminations [83].
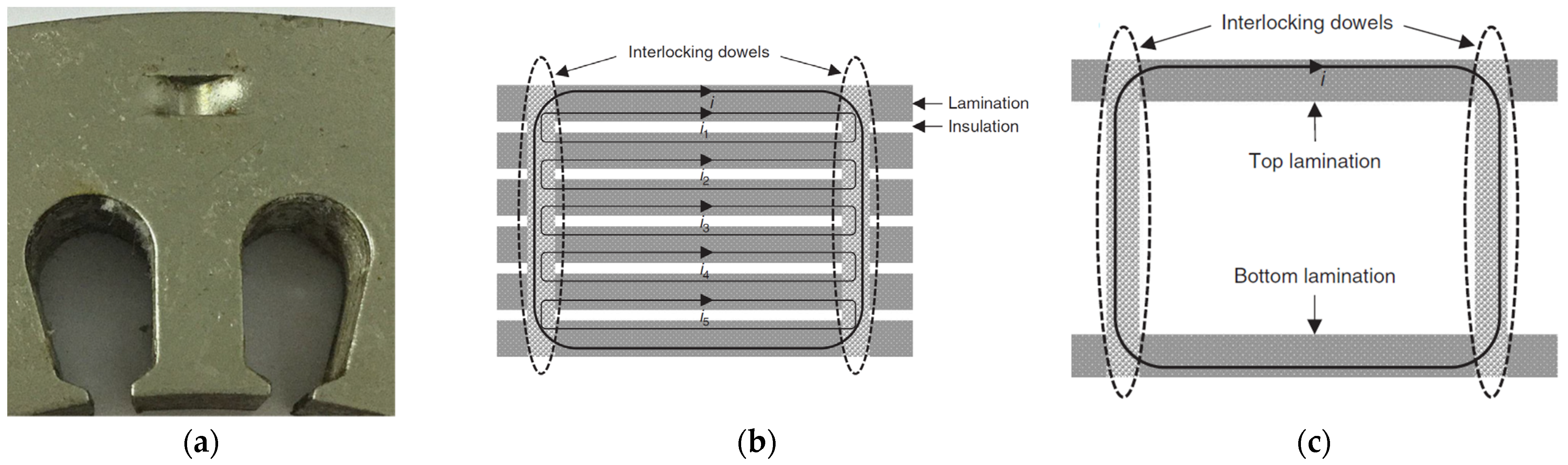
4.2. Interlocking Process
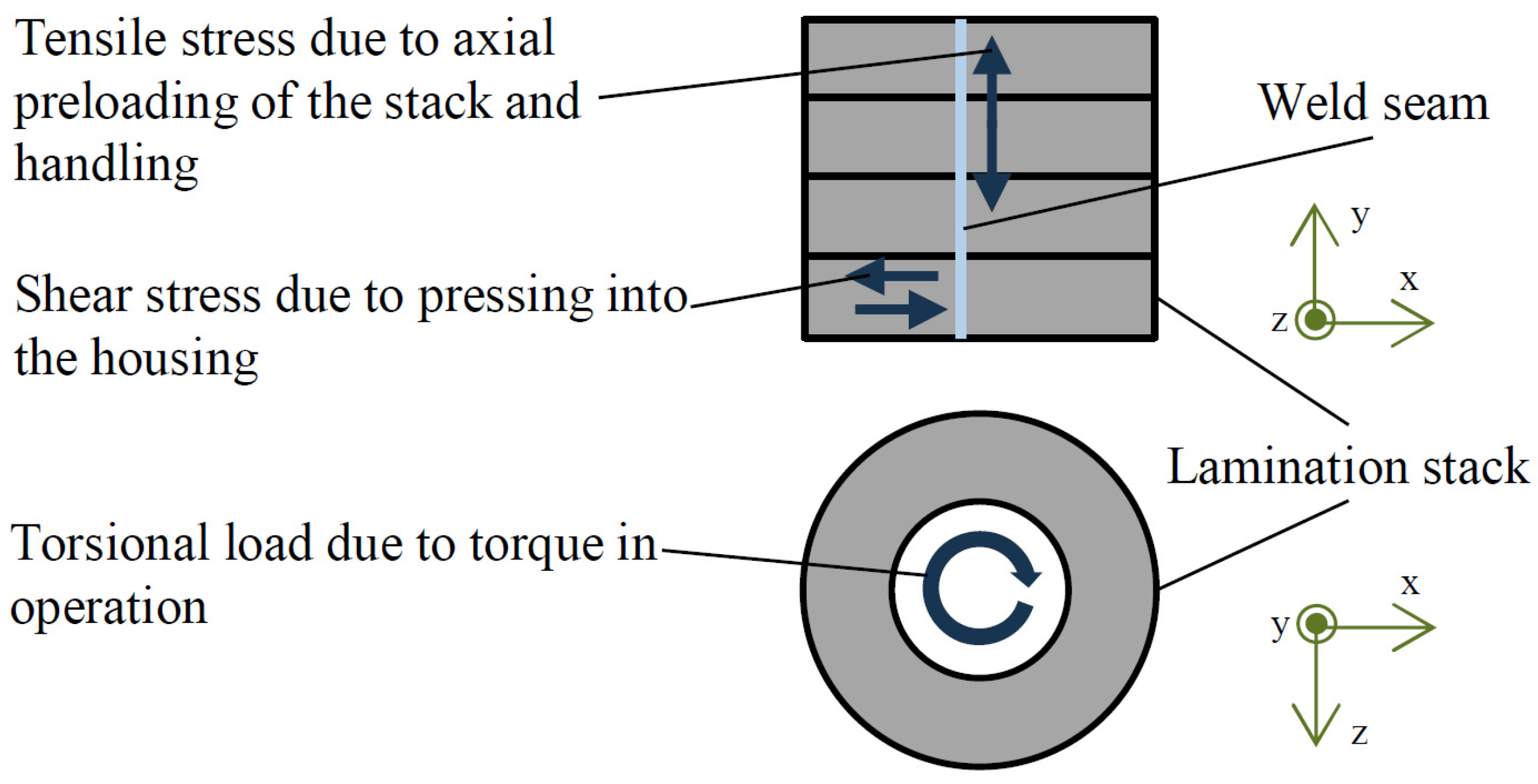
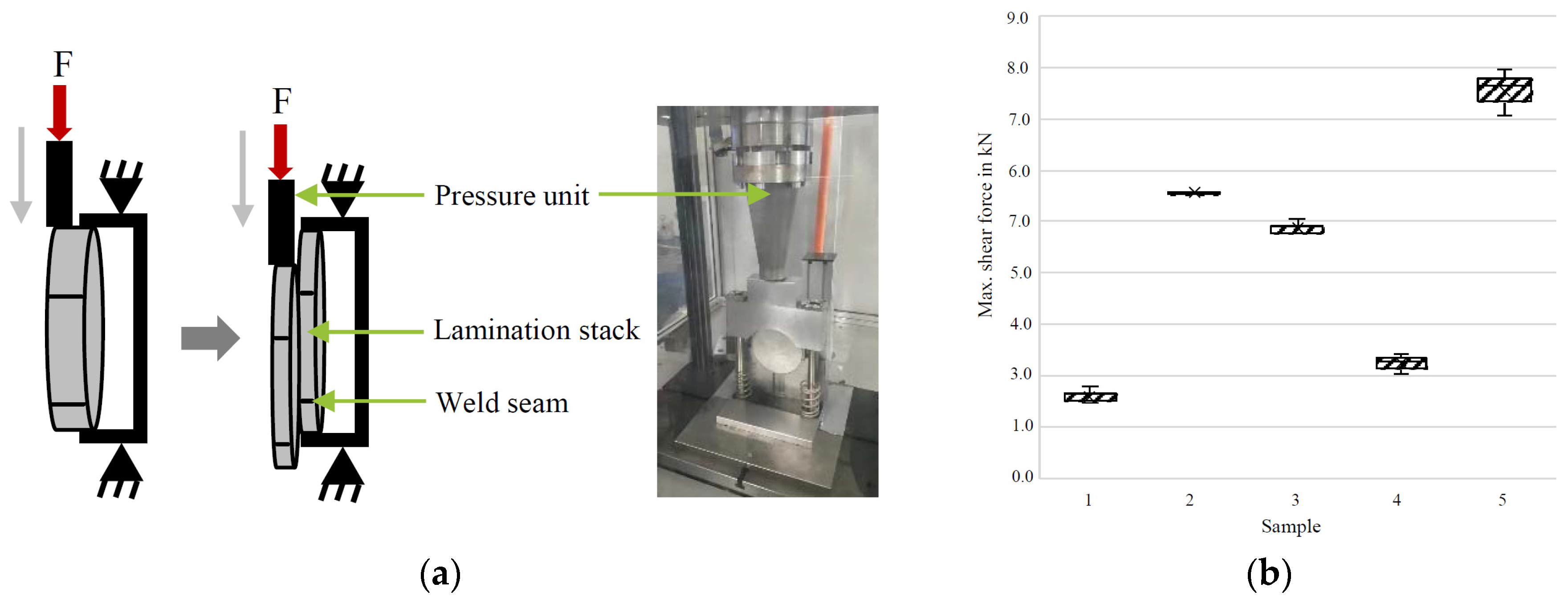
4.3. Welding Process
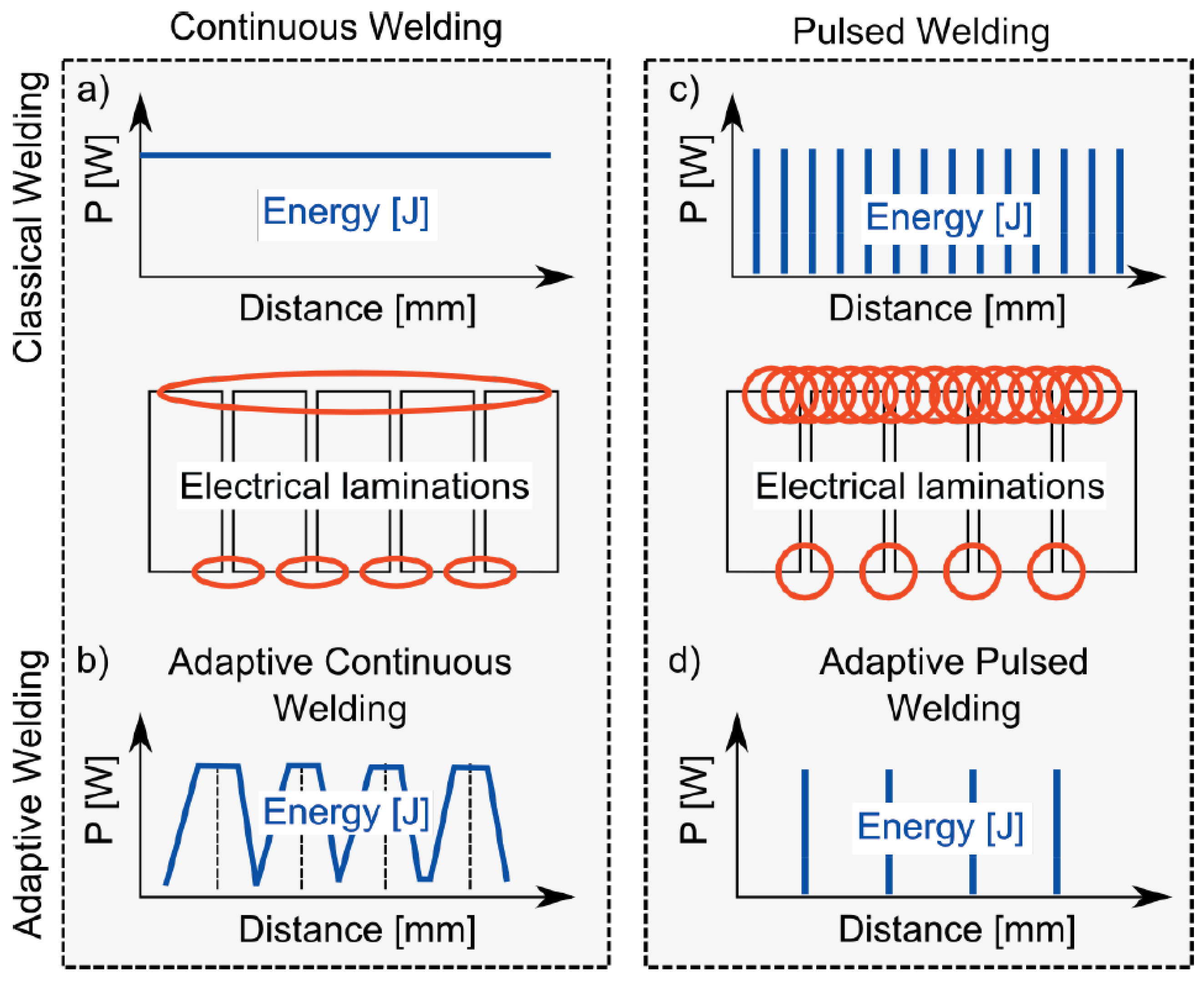
4.3.1. Different Types of Welding
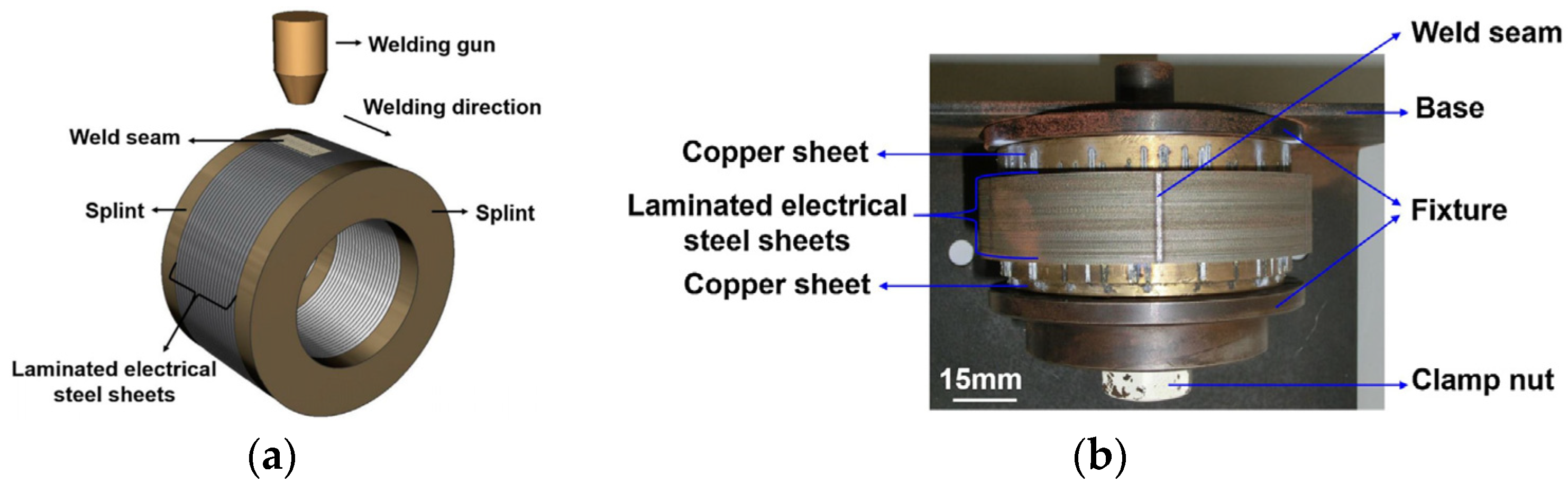
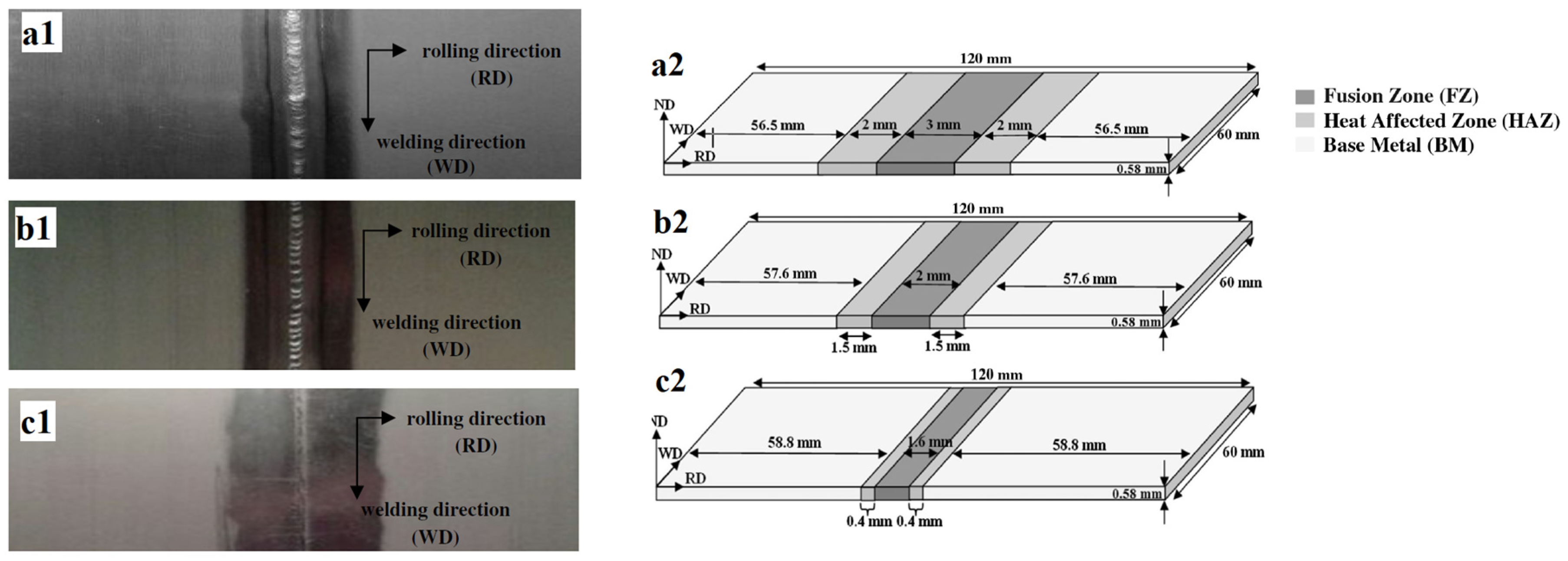
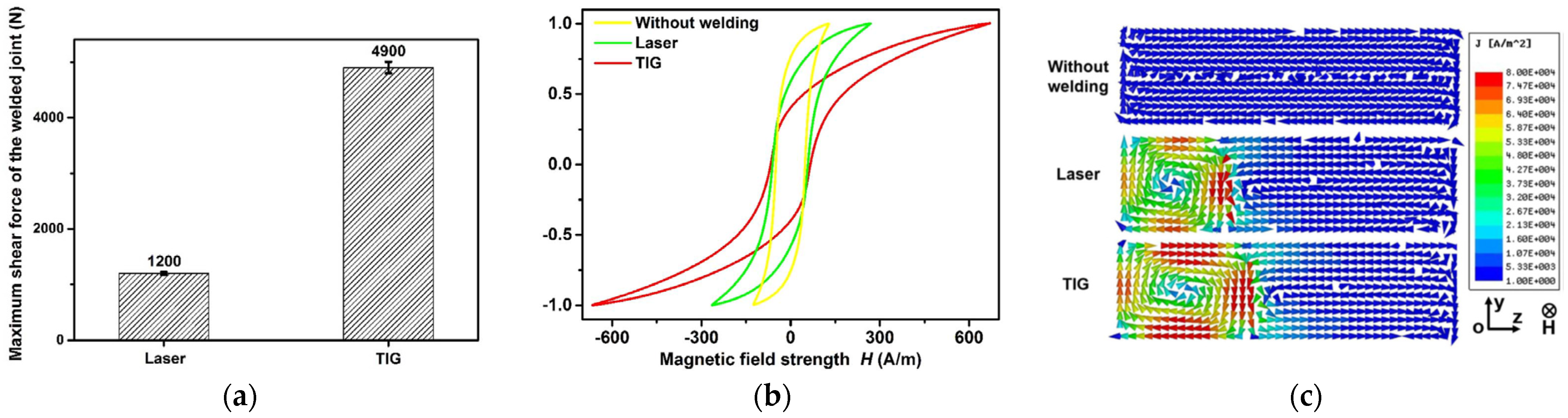
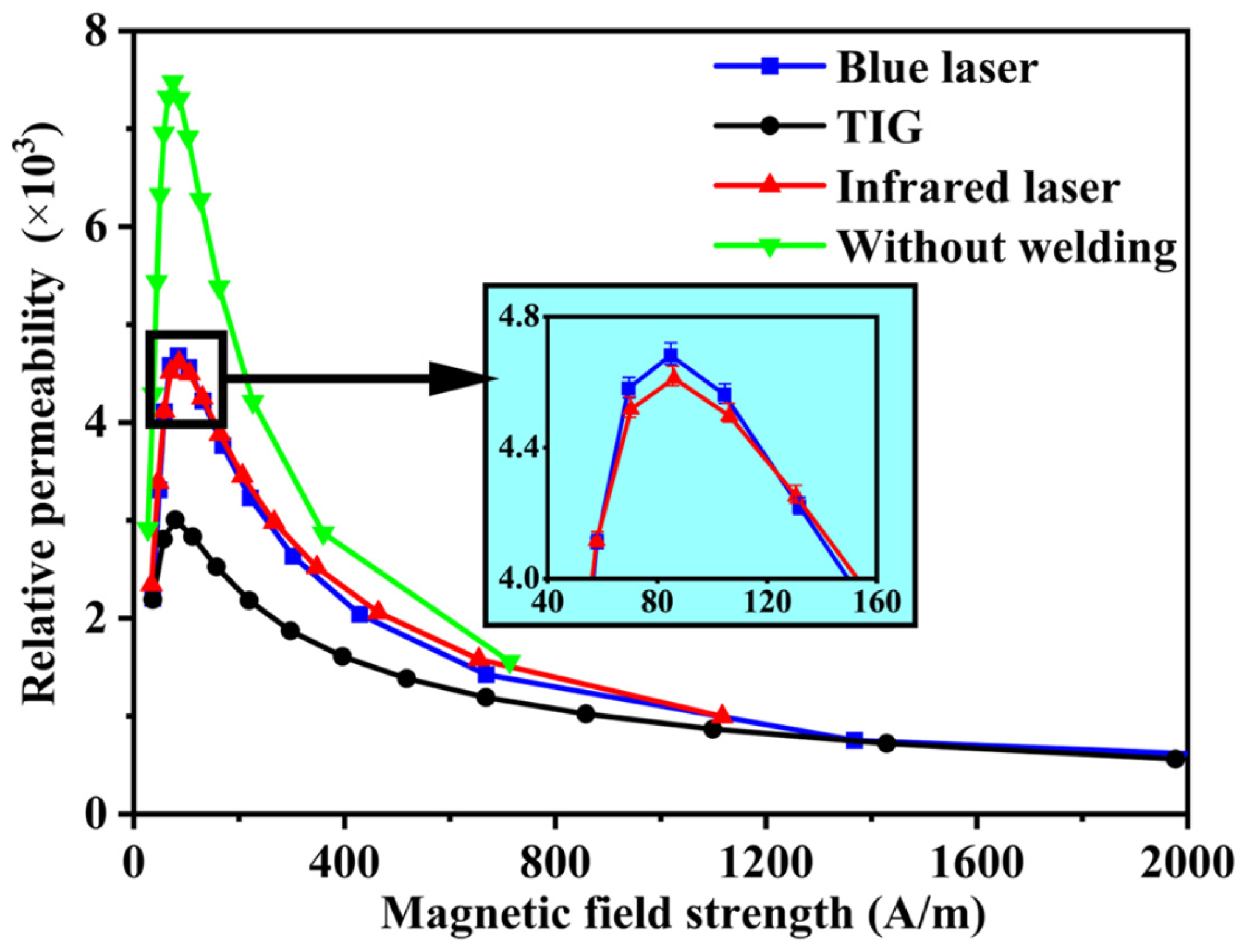
4.3.2. Laser Welding Types
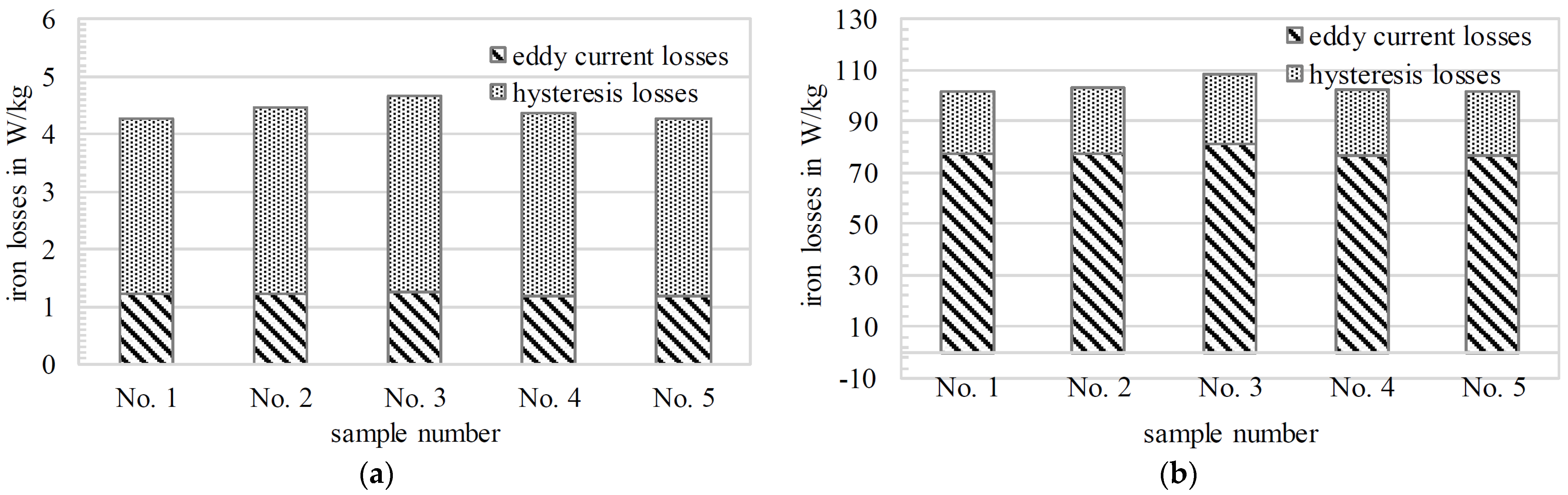
- The linear welded samples have the lowest total losses of 4.26 W/kg.
- The laser power parameters gave the most significant impact on the total losses.
- The losses are decreased by increasing the width of the wobble area because the microstructure is less damaged, and the energy input is more evenly distributed. Consequently, Hysteresis losses decrease.
4.3.3. Analytical Analysis
4.4. Performance Comparison of Different Joining Techniques
5. Stress Relief Annealing
- Punched then welded only.
- Punched, annealed for stress relief, and then welded.
- Punched, welded, and then annealed for stress relief.
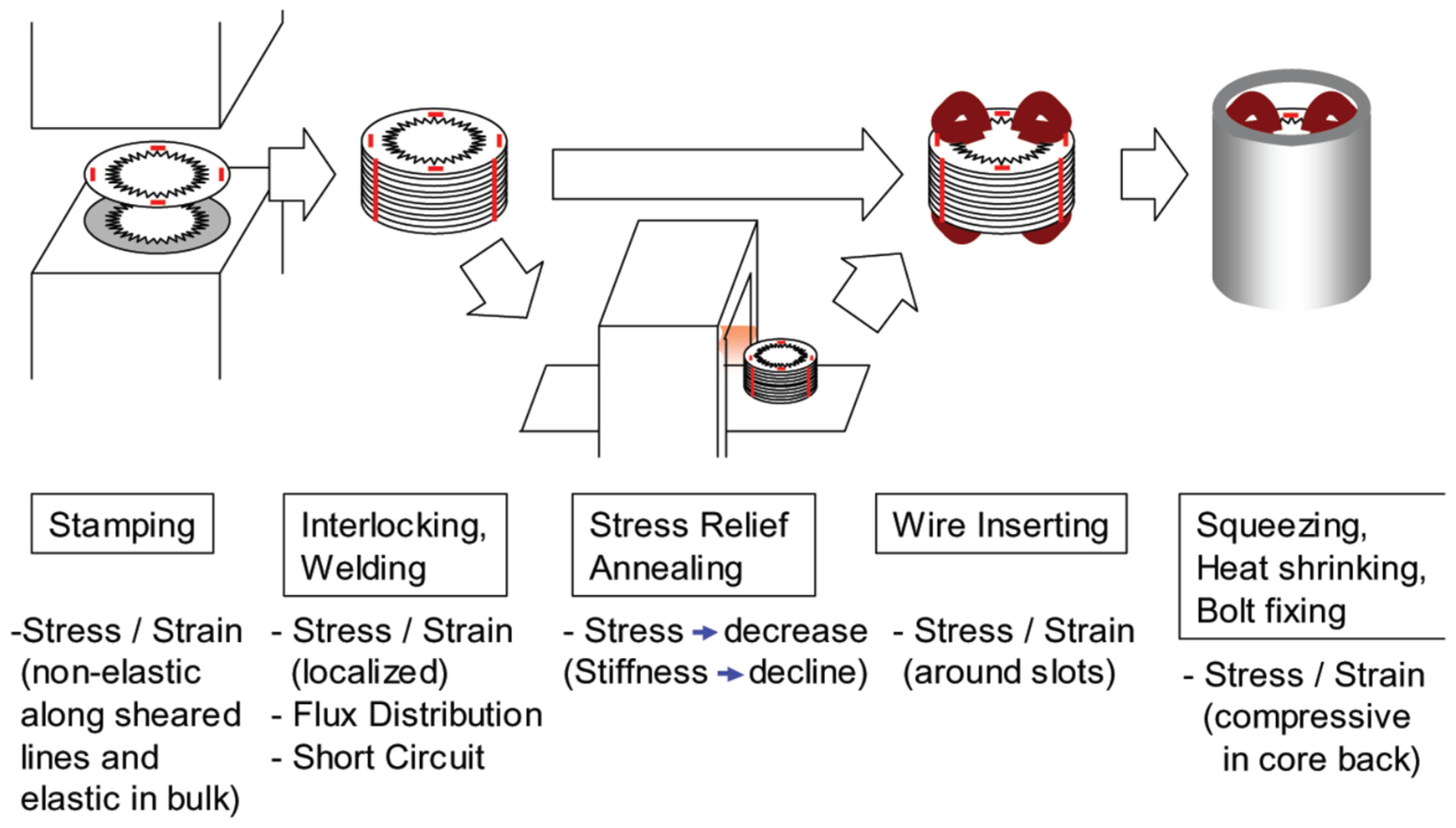
6. Shrink Fitting/Housing
7. Suggestion
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mahmouditabar, F.; Vahedi, A.; Takorabet, N. Design and Analysis of Interior Permanent Magnet Motor for Electric Vehicle Application Considering Irreversible Demagnetization. IEEE Trans. Ind. Appl. 2022, 58, 284–293. [Google Scholar] [CrossRef]
- Nobahari, A.; Vahedi, A.; Nasiri-Zarandi, R. A Modified Permanent Magnet-Assisted Synchronous Reluctance Motor Design for Torque Characteristics Improvement. IEEE Trans. Energy Convers. 2022, 37, 989–998. [Google Scholar] [CrossRef]
- Rafiee, V.; Faiz, J. Robust Design of an Outer Rotor Permanent Magnet Motor through Six-Sigma Methodology Using Response Surface Surrogate Model. IEEE Trans. Magn. 2019, 55, 8107110. [Google Scholar] [CrossRef]
- Nasiri-Zarandi, R.; Ghaheri, A.; Abbaszadeh, K. Thermal Modeling and Analysis of a Novel Transverse Flux HAPM Generator for Small-Scale Wind Turbine Application. IEEE Trans. Energy Convers. 2020, 35, 445–453. [Google Scholar] [CrossRef]
- Baker, N.J.; Jordan, S. Comparison of Two Transverse Flux Machines for an Aerospace Application. IEEE Trans. Ind. Appl. 2018, 54, 5783–5790. [Google Scholar] [CrossRef]
- Baker, N.J.; Raihan, M.A.H.; Almoraya, A.A. A Cylindrical Linear Permanent Magnet Vernier Hybrid Machine for Wave Energy. IEEE Trans. Energy Convers. 2019, 34, 691–700. [Google Scholar] [CrossRef]
- Bali, M.; Muetze, A. Modeling the Effect of Cutting on the Magnetic Properties of Electrical Steel Sheets. IEEE Trans. Ind. Electron. 2017, 64, 2547–2556. [Google Scholar] [CrossRef]
- Clerc, A.J.; Muetze, A. Measurement of stator core magnetic degradation during the manufacturing process. IEEE Trans. Ind. Appl. 2012, 48, 1344–1352. [Google Scholar] [CrossRef]
- Mohammadi, A.A.; Zhang, S.; Pop, A.C.; Gyselinck, J.J.C. Effect of Electrical Steel Punching on the Performance of Fractional-kW Electrical Machines. IEEE Trans. Energy Convers. 2022, 37, 1854–1863. [Google Scholar] [CrossRef]
- Poskovic, E.; Ferraris, L.; Bramerdorfer, G.; Cossale, M. A Thermographic Method to Evaluate Different Processes and Assembly Effects on Magnetic Steels. IEEE Trans. Ind. Appl. 2022, 58, 3405–3413. [Google Scholar] [CrossRef]
- Vaschetto, S.; Gmyrek, Z.; Dobler, C.; Bramerdorfer, G.; Cavagnino, A. Experimental Assessment and Modeling of Losses in Interlocked Magnetic Cores. IEEE Trans. Ind. Appl. 2022, 58, 4450–4460. [Google Scholar] [CrossRef]
- Electrical Steel Sheet for Traction Motor of Hybrid/Electric Vehicles. Available online: https://www.researchgate.net/publication/289668081_Electrical_steel_sheet_for_traction_motor_of_hybridelectric_vehicles (accessed on 12 June 2023).
- Goldbeck, G.; Cossale, M.; Kitzberger, M.; Bramerdorfer, G.; Andessner, D.; Amrhein, W. Incorporating the Soft Magnetic Material Degradation to Numerical Simulations. IEEE Trans. Ind. Appl. 2020, 56, 3584–3593. [Google Scholar] [CrossRef]
- Cossale, M.; Kitzberger, M.; Goldbeck, G.; Bramerdorfer, G.; Andessner, D.; Amrhein, W. Local Degradation in Soft Magnetic Materials: A Simplified Modeling Approach. IEEE Trans. Ind. Appl. 2019, 55, 5897–5905. [Google Scholar] [CrossRef]
- Bali, M.; De Gersem, H.; Muetze, A. Finite-element modeling of magnetic material degradation due to punching. IEEE Trans. Magn. 2014, 50, 745–748. [Google Scholar] [CrossRef]
- M’Zali, N.; Martin, F.; Sundaria, R.; Henneron, T.; Benabou, A.; Belahcen, A. Finite-Element Modeling of Magnetic Properties Degradation Due to Plastic Deformation. IEEE Trans. Magn. 2020, 56, 7506704. [Google Scholar] [CrossRef]
- Xia, C.; Wang, H.; Wu, Y.; Wang, H. Joining of the Laminated Electrical Steels in Motor Manufacturing: A Review. Materials 2020, 13, 4583. [Google Scholar] [CrossRef]
- Dems, M.; Gmyrek, Z.; Komeza, K. The Influence of Cutting Technology on Magnetic Properties of Non-Oriented Electrical Steel—Review State of the Art. Energies 2023, 16, 4299. [Google Scholar] [CrossRef]
- Bali, M.; Muetze, A. The degradation depth of non-grain oriented electrical steel sheets of electric machines due to mechanical and laser cutting: A state-of-the-art review. IEEE Trans. Ind. Appl. 2019, 55, 366–375. [Google Scholar] [CrossRef]
- IEC 60404-2:1996/AMD1:2008/COR1:2018; Corrigendum 1—Amendment 1—Magnetic Materials—Part 2: Methods of Measurement of Magnetic Properties of Electrical Steel Strip and Sheet by Means of an Epstein Frame. International Electrotechnical Commission: Geneva, Switzerland, 2018. Available online: https://webstore.iec.ch/publication/62746 (accessed on 19 May 2023).
- IEC 60404-10:2016; Magnetic Materials—Part 10: Methods of Measurement of Magnetic Properties of Electrical Steel Strip and Sheet at Medium Frequencies. International Electrotechnical Commission: Geneva, Switzerland, 2016. Available online: https://webstore.iec.ch/publication/26102 (accessed on 19 May 2023).
- IEC 60404-3:2022; Magnetic Materials—Part 3: Methods of Measurement of the Magnetic Properties of Electrical Steel Strip and Sheet by Means of a Single Sheet Tester. International Electrotechnical Commission: Geneva, Switzerland, 2022. Available online: https://webstore.iec.ch/publication/66641 (accessed on 19 May 2023).
- IEC 60404-6:2018; Magnetic Materials—Part 6: Methods of Measurement of the Magnetic Properties of Magnetically Soft Metallic and Powder Materials at Frequencies in the Range 20 Hz to 100 kHz by the Use of Ring Specimens. International Electrotechnical Commission: Geneva, Switzerland, 2018. Available online: https://webstore.iec.ch/publication/27825 (accessed on 20 May 2023).
- Wang, H.; Zhang, Y.; Li, S. Laser welding of laminated electrical steels. J. Mater. Process. Technol. 2016, 230, 99–108. [Google Scholar] [CrossRef]
- Fiorillo, F. Characterization and Measurement of Magnetic Materials; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Krings, A.; Nategh, S.; Wallmark, O.; Soulard, J. Influence of the welding process on the performance of slotless pm motors with sife and nife stator laminations. IEEE Trans. Ind. Appl. 2014, 50, 296–306. [Google Scholar] [CrossRef]
- Schlegel, J.P.; Batistela, N.J.; Sadowski, N.; Kuo-Peng, P.; Bastos, J.; Rigoni, M.; de Etspíndola, A.A.; Dokonal, L. Testing strategies to evaluate non-oriented electrical steels losses. J. Microw. Optoelectron. Electromagn. Appl. 2012, 11, 304–315. [Google Scholar] [CrossRef]
- Colombo, L.; Soltanipour, S.; Tokat, A.; Reinap, A.; Thiringer, T.; Fernandez, F.M.; Lindström, J.; Alaküla, M. Statistical Assessment of Core Loss Measurement Techniques for Laminated Steel. In Proceedings of the [2023] IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Newcastle upon Tyne, UK, 13–14 April 2023. [Google Scholar] [CrossRef]
- Schoppa, A.P. Einfluss der Be- und Verarbeitung auf die Magnetischen Eigenschaften von Schlussgeglühtem, Nichtkornorientiertem Elektroband. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2001. [Google Scholar]
- Arshad, W.M.; Ryckebush, T.; Magnussen, F.; Lendenmann, H.; Soulard, J.; Etriksson, B.; Malmros, B. Incorporating lamination processing and component manufacturing in electrical machine design tools. In Proceedings of the 2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 23–27 September 2007; pp. 94–102. [Google Scholar] [CrossRef]
- Schoppa, A.; Louis, H.; Pude, F.; Von Rad, C. Influence of abrasive waterjet cutting on the magnetic properties of non-oriented electrical steels. J. Magn. Magn. Mater. 2003, 254–255, 370–372. [Google Scholar] [CrossRef]
- Emura, M.; Landgraf, F.J.G.; Ross, W.; Barreta, J.R. The influence of cutting technique on the magnetic properties of electrical steels. J. Magn. Magn. Mater. 2003, 254–255, 358–360. [Google Scholar] [CrossRef]
- Belhadj, A.; Baudouin, P.; Breaban, F.; Deffontaine, A.; Dewulf, M.; Houbaert, Y. Effect of laser cutting on microstructure and on magnetic properties of grain non-oriented electrical steels. J. Magn. Magn. Mater. 2003, 256, 20–31. [Google Scholar] [CrossRef]
- Gaworska-Koniarek, D.; Szubzda, B.; Wilczyński, W.; Drosik, J.; Karaś, K. The influence of assist gas on magnetic properties of electrotechnical steel sheets cut with laser. J. Phys. Conf. Ser. 2011, 303, 012091. [Google Scholar] [CrossRef]
- Bayraktar, Ş.; Turgut, Y. Experimental and statistical analysis of the effects of punching and laser cutting methods on induction motor efficiency and total magnetic losses in silicon lamination sheets. J. Magn. Magn. Mater. 2023, 572, 170599. [Google Scholar] [CrossRef]
- Loisos, G.; Moses, A.J. Effect of mechanical and Nd:YAG laser cutting on magnetic flux distribution near the cut edge of non-oriented steels. J. Mater. Process. Technol. 2005, 161, 151–155. [Google Scholar] [CrossRef]
- Peksoz, A.; Erdem, S.; Derebasi, N. Mathematical model for cutting effect on magnetic flux distribution near the cut edge of non-oriented electrical steels. Comput. Mater. Sci. 2008, 43, 1066–1068. [Google Scholar] [CrossRef]
- Bali, M.; Muetze, A. Influence of Different Cutting Techniques on the Magnetic Characteristics of Electrical Steels Determined by a Permeameter. IEEE Trans. Ind. Appl. 2017, 53, 971–981. [Google Scholar] [CrossRef]
- Xiang, Q.; Cheng, L.; Wu, K. Effects of Laser Cutting Parameters on the Magnetic Properties of 50W350 High-Grade Non-Oriented Electrical Steel. Materials 2023, 16, 1642. [Google Scholar] [CrossRef]
- Bali, M. Magnetic Material Degradation due to Different Cutting Techniques and Its Modeling for Electric Machine Design. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2016. Available online: https://diglib.tugraz.at/magnetic-material-degradation-due-to-different-cutting-techniques-and-its-modeling-for-electric-machine-design-2016 (accessed on 1 July 2023).
- Kurosaki, Y.; Mogi, H.; Fujii, H.; Kubota, T.; Shiozaki, M. Importance of punching and workability in non-oriented electrical steel sheets. J. Magn. Magn. Mater. 2008, 320, 2474–2480. [Google Scholar] [CrossRef]
- Winter, K.; Liao, Z.; Ramanathan, R.; Axinte, D.; Vakil, G.; Gerada, C. How non-conventional machining affects the surface integrity and magnetic properties of non-oriented electrical steel. Mater. Des. 2021, 210, 110051. [Google Scholar] [CrossRef]
- Reinlein, M.; Verlag, S. Simulation der Eisenverluste und des Magnetisierungsbedarfs unter Berücksichtigung von Fertigungseinflüssen in Induktionsmaschinen. Shaker: Düren and Maastricht, Germany. 1986. Available online: https://www.amazon.de/Magnetisierungsbedarfs-Ber%C3%BCcksichtigung-Fertigungseinfl%C3%BCssen-Induktionsmaschinen-Kaiserslauterer/dp/3844063579 (accessed on 1 July 2023).
- Pulnikov, A.; Melkebeek, J.; Dupré, L. Modification of Magnetic Properties of Non Oriented Electrical Steels by the Production of Electromagnetic Devices/Alexandre Pulnikov. 2004. Available online: http://hdl.handle.net/1854/LU-8597986 (accessed on 8 June 2023).
- Demir, Y.; Ocak, O.; Ulu, Y.; Aydin, M. Impact of lamination processing methods on performance of permanent magnet synchronous motors. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1218–1223. [Google Scholar] [CrossRef]
- Robert, F.; Prince A, A.; Fredo A R, J. Influence of wire electrical discharge machine cutting parameters on the magnetization characteristics of electrical steel laminations. Mater. Today Proc. 2022, 52, 746–750. [Google Scholar] [CrossRef]
- Lautre, N.K.; Dharmik, B.Y. Surface Integrity and Core Loss in Lamination Coated Thin Sheets of M-43 Grade Cold Rolled Non-grain-Oriented Electrical Steel. J. Mater. Eng. Perform. 2022, 31, 9001–9018. [Google Scholar] [CrossRef]
- Dems, M.; Komeza, K.; Gmyrek, Z.; Szulakowski, J. The Effect of Sample’s Dimension and Cutting Technology on Magnetization and Specific Iron Losses of FeSi Laminations. Energies 2022, 15, 2086. [Google Scholar] [CrossRef]
- Manescu, V.; Paltanea, G.; Ferrara, E.; Nemoianu, I.V.; Fiorillo, F.; Gavrila, H. Influence of mechanical and water-jet cutting on the dynamic magnetic properties of NO Fe-Si steels. J. Magn. Magn. Mater. 2020, 499, 166257. [Google Scholar] [CrossRef]
- Manescu-Paltanea, V.; Paltanea, G.; Nemoianu, I.V. Degradation of Static and Dynamic Magnetic Properties of Non-Oriented Steel Sheets by Cutting. IEEE Trans. Magn. 2018, 54, 2001705. [Google Scholar] [CrossRef]
- Bali, M.; De Gersem, H.; Muetze, A. Determination of Original Nondegraded and Fully Degraded Magnetic Properties of Material Subjected to Mechanical Cutting. IEEE Trans. Ind. Appl. 2016, 52, 2297–2305. [Google Scholar] [CrossRef]
- Bali, M.; De Gersem, H.; Muetze, A. Determination of Original Nondegraded and Fully Degraded Magnetic Characteristics of Material Subjected to Laser Cutting. IEEE Trans. Ind. Appl. 2017, 53, 4242–4251. [Google Scholar] [CrossRef]
- Vandenbossche, L.; Jacobs, S.; Henrotte, F.; Hameyer, K. Impact of cut edges on magnetization curves and iron losses in e-machines for automotive traction. World Electr. Veh. J. 2010, 4, 587–596. [Google Scholar] [CrossRef]
- Kedous-Lebouc, A.; Cornut, B.; Perrier, J.C.; Manfé, P.; Chevalier, T. Punching influence on magnetic properties of the stator teeth of an induction motor. J. Magn. Magn. Mater. 2003, 254–255, 124–126. [Google Scholar] [CrossRef]
- Kedous-Lebouc, A.; Messal, O.; Youmssi, A. Joint punching and frequency effects on practical magnetic characteristics of electrical steels for high-speed machines. J. Magn. Magn. Mater. 2017, 426, 658–665. [Google Scholar] [CrossRef]
- Goldbeck, G.; Cossale, M.; Kitzberger, M.; Bramerdorfer, G.; Andessner, D.; Amrhein, W. Numerical Implementation of Local Degradation Profiles in Soft Magnetic Materials. In Proceedings of the 2018 23rd International Conference on Electrical Machines, ICEM 2018, Alexandroupoli, Greece, 3–6 September 2018; pp. 1037–1043. [Google Scholar] [CrossRef]
- Sundaria, R.; Lehikoinen, A.; Arkkio, A.; Belahcen, A. Effects of Manufacturing Processes on Core Losses of Electrical Machines. IEEE Trans. Energy Convers. 2021, 36, 197–206. [Google Scholar] [CrossRef]
- Sundaria, R.; Nair, D.G.; Lehikoinen, A.; Arkkio, A.; Belahcen, A. Effect of Laser Cutting on Core Losses in Electrical Machines—Measurements and Modeling. IEEE Trans. Ind. Electron. 2020, 67, 7354–7363. [Google Scholar] [CrossRef]
- Sundaria, R.; Nair, D.G.; Lehikoinen, A.; Arkkio, A.; Belahcen, A. Loss Model for the Effects of Steel Cutting in Electrical Machines. In Proceedings of the 2018 23rd International Conference on Electrical Machines, ICEM 2018, Alexandroupoli, Greece, 3–6 September 2018; pp. 1260–1266. [Google Scholar] [CrossRef]
- Gurbuz, I.T.; Martin, F.; Billah, M.M.; Belahcen, A.; Rasilo, P. Effective Implementation of the Effect of Electrical Steel Sheet Cutting into Finite-Element Simulation. In Proceedings of the 2022 IEEE 20th Biennial Conference on Electromagnetic Field Computation (CEFC), Denver, CO, USA, 24–26 October 2022. [Google Scholar] [CrossRef]
- Martin, F.; Aydin, U.; Sundaria, R.; Rasilo, P.; Belahcen, A.; Arkkio, A. Effect of Punching the Electrical Sheets on Optimal Design of a Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2018, 54, 8102004. [Google Scholar] [CrossRef]
- Gmyrek, Z.; Cavagnino, A.; Ferraris, L. Estimation of the magnetic properties of the damaged area resulting from the punching process: Experimental research and FEM modeling. IEEE Trans. Ind. Appl. 2013, 49, 2069–2077. [Google Scholar] [CrossRef]
- Gmyrek, Z.; Cavagnino, A. Analytical method for determining the damaged area width in magnetic materials due to punching process. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Fort Collins, CO, USA, 7–10 November 2011; pp. 1764–1769. [Google Scholar] [CrossRef]
- Dems, M.; Gmyrek, Z.; Komeza, K. Analytical Model of an Induction Motor Taking into Account the Punching Process Influence on the Material Properties’ Change of Lamination. Energies 2021, 14, 2459. [Google Scholar] [CrossRef]
- Alatawneh, N.; Saleem, A.; Rahman, T.; Lowther, D.A.; Chromik, R. Modelling and analysis of the effects of cutting of core laminations in electric machines. IET Electr. Power Appl. 2020, 14, 2355–2361. [Google Scholar] [CrossRef]
- Rasilo, P.; Aydin, U.; Holopainen, T.P.; Arkkio, A. Analysis of iron losses on the cutting edges of induction motor core laminations. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 1312–1317. [Google Scholar] [CrossRef]
- Colombo, L.; Tokat, A.; Bitsi, K.; Márquez-Fernández, F.J.; Alakula, M. Performance Degradation due to Cut Edge Effect for an Axial-Flux Induction Machine. In Proceedings of the 2022 International Conference on Electrical Machines, ICEM 2022, Valencia, Spain, 5–8 September 2022; pp. 1253–1259. [Google Scholar] [CrossRef]
- Bourchas, K.; Stening, A.; Soulard, J.; Broddefalk, A.; Lindenmo, M.; Dahlen, M.; Gyllensten, F. Quantifying Effects of Cutting and Welding on Magnetic Properties of Electrical Steels. IEEE Trans. Ind. Appl. 2017, 53, 4269–4278. [Google Scholar] [CrossRef]
- Mach, M.; Hajek, V. Model of a small induction machine with effects of manufacturing. In Proceedings of the 2015 International Conference on Electrical Drives and Power Electronics (EDPE), Tatranska Lomnica, Slovakia, 21–23 September 2015; pp. 319–323. [Google Scholar] [CrossRef]
- Soltanipour, S.; Thiringer, T.; Lindström, J. Battery Electric Vehicle Performance Evaluation by Considering Punching Effect on PMSM Iron Cores. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 2162–2168. [Google Scholar] [CrossRef]
- Sano, H.; Narita, K.; Zeze, E.; Yamada, T.; Kazuki, U.; Akatsu, K. A practical approach for electromagnetic analysis with the effect of the residual strain due to manufacturing processes. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar] [CrossRef]
- Credo, A.; Petrov, I.; Pyrhonen, J.; Villani, M. Impact of manufacturing stresses on multiple-rib Synchronous Reluctance Motor performance. IEEE Trans. Ind. Appl. 2022, 59, 1253–1262. [Google Scholar] [CrossRef]
- Vandenbossche, L.; Jacobs, S.; Jannot, X.; McClelland, M.; Saint-Michel, J.; Attrazic, E. Iron loss modelling which includes the impact of punching, applied to high-efficiency induction machines. In Proceedings of the 2013 3rd International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 29–30 October 2013. [Google Scholar] [CrossRef]
- Hofmann, M.; Naumoski, H.; Herr, U.; Herzog, H.G. Magnetic Properties of Electrical Steel Sheets in Respect of Cutting: Micromagnetic Analysis and Macromagnetic Modeling. IEEE Trans. Magn. 2016, 52, 2000114. [Google Scholar] [CrossRef]
- Bramerdorfer, G. Effect of the Manufacturing Impact on the Optimal Electric Machine Design and Performance. IEEE Trans. Energy Convers. 2020, 35, 1935–1943. [Google Scholar] [CrossRef]
- Elfgen, S.; Steentjes, S.; Bohmer, S.; Franck, D.; Hameyer, K. Influences of Material Degradation Due to Laser Cutting on the Operating Behavior of PMSM Using a Continuous Local Material Model. IEEE Trans. Ind. Appl. 2017, 53, 1978–1984. [Google Scholar] [CrossRef]
- Weiss, H.A.; Trober, P.; Golle, R.; Steentjes, S.; Leuning, N.; Elfgen, S.; Hameyer, K.; Volk, W. Impact of Punching Parameter Variations on Magnetic Properties of Nongrain-Oriented Electrical Steel. IEEE Trans. Ind. Appl. 2018, 54, 5869–5878. [Google Scholar] [CrossRef]
- Goldbeck, G.; Bramerdorfer, G.; Amrhein, W. Impact of local degradation in soft magnetic materials on performance of permanent magnet synchronous machines. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 3081–3087. [Google Scholar] [CrossRef]
- Mohammadi, A.A.; Zhang, S.; Gyselinck, J.; Pop, A.C.; Zhang, W. Manufacturing-induced Cogging Torque in Segmented Stator Permanent-magnet Machines with respect to Steel Punching. IEEE Trans. Magn. 2022, 58, 1–8. [Google Scholar] [CrossRef]
- Elfgen, S.; Steentjes, S.; Böhmer, S.; Franck, D.; Hameyer, K. Continuous Local Material Model for Cut Edge Effects in Soft Magnetic Materials. IEEE Trans. Magn. 2016, 52, 2001304. [Google Scholar] [CrossRef]
- Sundaria, R.; Lehikoinen, A.; Hannukainen, A.; Arkkio, A.; Belahcen, A. Mixed-Order Finite-Element Modeling of Magnetic Material Degradation Due to Cutting. IEEE Trans. Magn. 2018, 54, 7402008. [Google Scholar] [CrossRef]
- Crevecoeur, G.; Sergeant, P.; Dupré, L.; Vandenbossche, L.; Van De Walle, R. Analysis of the local material degradation near cutting edges of electrical steel sheets. IEEE Trans. Magn. 2008, 44, 3173–3176. [Google Scholar] [CrossRef]
- Advantages of Full-Face Bonding. Available online: https://www.voestalpine.com/isovac/en/Product-overview/Backlack/Advantages-of-full-face-bonding (accessed on 9 June 2023).
- Schneider, M.; Urban, N.; Franke, J. Relation of joining parameters of stator core production and iron loss. In Proceedings of the 2017 7th International Electric Drives Production Conference (EDPC), Würzburg, Germany, 5–6 December 2017. [Google Scholar] [CrossRef]
- Brochures. Available online: https://www.waelzholz.com/en/downloads/brochures.html (accessed on 9 June 2023).
- Imamori, S.; Steentjes, S.; Hameyer, K. Influence of Interlocking on Magnetic Properties of Electrical Steel Laminations. IEEE Trans. Magn. 2017, 53, 8108704. [Google Scholar] [CrossRef]
- Zhou, G.Y.; Hao, H.; Jin, M.J.; Shen, J.X. Influence of interlocking dowels on motor core loss. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 808–820. [Google Scholar] [CrossRef]
- Shen, J.X.; Zhou, G.Y.; Jin, S.L.; Hao, H. Analysis of iron loss in interlocked lamination core. In Proceedings of the 2015 International Conference on Sustainable Mobility Applications, Renewables and Technology (SMART), Kuwait, Kuwait, 23–25 November 2015. [Google Scholar] [CrossRef]
- Mahmouditabar, F.; Vahedi, A.; Takorabet, N. Robust Design of BLDC Motor Considering Driving Cycle. IEEE Trans. Transp. Electrif. 2023, in press. [CrossRef]
- Harrington, D.B. Turbine Generators. In Encyclopedia of Physical Science and Technology; Academic Press: Cambridge, MA, USA, 2003; pp. 193–215. [Google Scholar] [CrossRef]
- Gmyrek, Z.; Cavagnino, A. Influence of Punching, Welding, and Clamping on Magnetic Cores of Fractional KiloWatt Motors. IEEE Trans. Ind. Appl. 2018, 54, 4123–4132. [Google Scholar] [CrossRef]
- Gmyrek, Z.; Cavagnino, A.; Vaschetto, S.; Bramerdorfer, G. Loss Modeling for Interlocked Magnetic Cores. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 1060–1066. [Google Scholar] [CrossRef]
- Ziegler, M.; Brandl, F.; Kuehl, A.; Franke, J. Evaluation of Laser-welded Electrical Steel Laminations for Electric Motors. In Proceedings of the 12th International Symposium on Advanced Topics in Electrical Engineering, ATEE 2021, Bucharest, Romania, 25–27 March 2021. [Google Scholar] [CrossRef]
- Brachthäuser, N.; De Paoli, A.; Schäfer, P.; Senn, G. Laserstrahlschweissen von Paketierten Elektroblechen. ATZproduktion 2011, 4, 38–43. [Google Scholar] [CrossRef]
- Bali, M.; Muetze, A. Influences of CO2 Laser, FKL Laser, and Mechanical Cutting on the Magnetic Properties of Electrical Steel Sheets. IEEE Trans. Ind. Appl. 2015, 51, 4446–4454. [Google Scholar] [CrossRef]
- Katayama, S. Defect formation mechanisms and preventive procedures in laser welding. In Handbook of Laser Welding Technologies; Woodhead Publishing: Sawston, UK, 2013; pp. 332–373. [Google Scholar] [CrossRef]
- Cui, R.; Li, S. Pulsed laser welding of laminated electrical steels. J. Mater. Process. Technol. 2020, 285, 116778. [Google Scholar] [CrossRef]
- Vegelj, D.; Zajec, B.; Gregorčič, P.; Možina, J. Adaptive pulsed-laser welding of electrical laminations. Stroj. Vestn. J. Mech. Eng. 2014, 60, 106–114. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Chen, K.; Li, S. Comparison of laser and TIG welding of laminated electrical steels. J. Mater. Process. Technol. 2017, 247, 55–63. [Google Scholar] [CrossRef]
- Schade, T.; Ramsayer, R.M.; Bergmann, J.P. Laser welding of electrical steel stacks investigation of the weldability. In Proceedings of the 2014 4th International Electric Drives Production Conference, EDPC 2014, Nuremberg, Germany, 30 September–1 October 2014. [Google Scholar] [CrossRef]
- Mahrle, A.; Beyer, E. Modeling and simulation of the energy deposition in laser beam welding with oscillatory beam deflection. In Proceedings of the 26th International Congress on Applications of Lasers and Electro-Optics, ICALEO 2007, Cincinnati, OH, USA, 29 October–1 November 2007. [Google Scholar]
- Ziegler, M.; Mayr, A.; Seefried, J.; Kuehl, A.; Franke, J. Potentials of process monitoring during laser welding of electrical steel laminations. In Proceedings of the 2019 9th International Electric Drives Production Conference, EDPC 2019, Esslingen, Germany, 3–4 December 2019. [Google Scholar] [CrossRef]
- Ziegler, M.; Brandl, F.; Franke, J.; Kuhl, A. Numerical Simulation of the Laser Welding Process for Electrical Steel Laminations. In Proceedings of the 2022 12th International Electric Drives Production Conference, EDPC 2022, Regensburg, Germany, 29–30 November 2022. [Google Scholar] [CrossRef]
- Leuning, N.; Steentjes, S.; Hameyer, K.; Gerhards, B.; Reisgen, U. Analysis of a novel laser welding strategy for electrical steel laminations. In Proceedings of the 2017 7th International Electric Drives Production Conference, EDPC 2017, Würzburg, Germany, 5–6 December 2017. [Google Scholar] [CrossRef]
- Tang, Z.; Zhang, X.; Wan, L.; Ouyang, Y.; Gao, Z.; Wei, Q.; Wang, A.; Yang, H.; Wu, Y.; Zhang, Y.; et al. Bluelaser welding of laminated electrical steels: Dynamic process, weld bead characteristics, mechanical and magnetic properties. J. Mater. Process. Technol. 2023, 312, 117859. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y. Modeling of Eddy-Current Losses of Welded Laminated Electrical Steels. IEEE Trans. Ind. Electron. 2017, 64, 2992–3000. [Google Scholar] [CrossRef]
- Vourna, P. Characterization of Electron Beam Welded Non-Oriented Electrical Steel with Magnetic Barkhausen Noise. Key Eng. Mater. 2014, 605, 39–42. [Google Scholar] [CrossRef]
- Vourna, P.; Ktena, A. Metallurgical, Mechanical and Magnetic Properties of Electrical Steel Sheets in TIG and PLASMA Welding. Key Eng. Mater. 2013, 543, 479–482. [Google Scholar] [CrossRef]
- Dharmik, B.Y.; Lautre, N.K. Performance assessment of CMT over GTA welding on stacked thin sheets of CRNGO electrical steel. Mater. Lett. 2020, 272, 127901. [Google Scholar] [CrossRef]
- Dharmik, B.Y.; Lautre, N.K. CMT and GTA welding on microstructural characteristics and magnetic performance of thin CRNO electrical steel sheets. Mater. Chem. Phys. 2023, 295, 127128. [Google Scholar] [CrossRef]
- Vourna, P.; Ktena, A.; Tsakiridis, P.E.; Hristoforou, E. An accurate evaluation of the residual stress of welded electrical steels with magnetic Barkhausen noise. Measurement 2015, 71, 31–45. [Google Scholar] [CrossRef]
- EN 10106:2015; Cold Rolled Non-Oriented Electrical Steel Strip and Sheet Delivered in the Fully Processed State. iTeh, Inc.: Newark, DE, USA, 2015. Available online: https://standards.iteh.ai/catalog/standards/cen/abe948e0-1bf5-4929-896b-a351503f658b/en-10106-2015 (accessed on 18 May 2023).
- Ukwungwu, D.; Krichel, T.; Schauerte, B.; Leuning, N.; Olschok, S.; Reisgen, U.; Hameyer, K. Electromagnetic assessment of welding processes for packaging of electrical sheets. In Proceedings of the 2020 10th International Electric Drives Production Conference, EDPC 2020, Ludwigsburg, Germany, 8–9 December 2020. [Google Scholar] [CrossRef]
- Daem, A.; Ibrahim, M.N.; Sergeant, P.; Dupré, L. Stress-Dependent Magnetic Equivalent Circuit for Modeling Welding Effects in Electrical Steel Laminations. Machines 2022, 10, 1153. [Google Scholar] [CrossRef]
- Leitner, S.; Gruebler, H.; Muetze, A. Effect of Manufacturing Influences on Magnetic Performance Parameters of Sub-Fractional Horsepower Motors. IEEE Trans. Magn. 2021, 57, 8205209. [Google Scholar] [CrossRef]
- Hilinski, E.J.; Johnston, G.H. Annealing of electrical steel. In Proceedings of the 2014 4th International Electric Drives Production Conference, EDPC 2014, Nuremberg, Germany, 30 September–1 October 2014. [Google Scholar] [CrossRef]
- Chiang, C.C.; Knight, A.M.; Hsieh, M.-F.; Tsai, M.-G.; Liu, B.H.; Chen, I.-G.; Gaing, Z.-L.; Tsai, M.-C. Effects of annealing on magnetic properties of electrical steel and performances of SRM after punching. IEEE Trans. Magn. 2014, 50, 8203904. [Google Scholar] [CrossRef]
- Rodrigues, D.L.; Nishikawa, T.S.P.; Almeida, A.A.; Landgraf, F.J.G.; Martin, R.V. The Effect of Recovery Annealing on the Magnetic and Mechanical Properties of Nonoriented Electrical Steels. IEEE Trans. Magn. 2014, 50, 2002204. [Google Scholar] [CrossRef]
- Zhang, H.; Zeng, L.; An, D.; Pei, R. Magnetic Performance Improvement Caused by Tensile Stress in Equivalent Iron Core Fabricated by High-Strength Non-Oriented Electrical Steel. IEEE Trans. Magn. 2022, 58, 8600105. [Google Scholar] [CrossRef]
- Abbaschian, R.; Abbaschian, L.; Reed-Hill, R.E. Physical Metallurgy Principles; Cengage Learning: London, UK, 2009; 750p. [Google Scholar]
- Mierczak, L.; Denke, P.; Klimczyk, P.; Siebert, S. Advanced measurement technologies for magnetic materials used in automotive applications. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems, ICEMS 2019, Harbin, China, 11–14 August 2019. [Google Scholar] [CrossRef]
- Camilleri, R.; Howey, D.A.; McCulloch, M.D. Experimental investigation of the thermal contact resistance in shrink fit assemblies with relevance to electrical machines. In Proceedings of the 7th IET International Conference on Power Electronics, Machines and Drives (PEMD 2014), Manchester, UK, 8–10 April 2014. [Google Scholar] [CrossRef]
- Reinlein, M.; Regnet, M.; Hubert, T.; Kremser, A.; Werner, U.; Bonig, J. Influence of Villari Effect on the magnetizing current of Induction Machines by shrink fitting of rotor cores. In Proceedings of the 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM 2016, Capri, Italy, 22–24 June 2016; pp. 1316–1323. [Google Scholar] [CrossRef]
- Takahashi, N.; Morimoto, H.; Yunoki, Y.; Miyagi, D. Effect of shrink fitting and cutting on iron loss of permanent magnet motor. J. Magn. Magn. Mater. 2008, 320, e925–e928. [Google Scholar] [CrossRef]
- Zhu, L.; Fan, B.; Han, X.; Tang, R. Effects of shrink fitting on iron losses of a permanent magnet synchronous motor with an amorphous core. IET Electr. Power Appl. 2022, 16, 996–1003. [Google Scholar] [CrossRef]
- Fujisaki, K.; Hirayama, R.; Kawachi, T.; Satou, S.; Kaidou, C.; Yabumoto, M.; Kubota, T. Motor core iron loss analysis evaluating shrink fitting and stamping by finite-element method. IEEE Trans. Magn. 2007, 43, 1950–1954. [Google Scholar] [CrossRef]
- Fujisaki, K.; Satoh, S. Numerical calculations of electromagnetic fields in silicon steel under mechanical stress. IEEE Trans. Magn. 2004, 40, 1820–1825. [Google Scholar] [CrossRef]
- Diao, K.; Sun, X.; Yao, M. Robust-Oriented Optimization of Switched Reluctance Motors Considering Manufacturing Fluctuation. IEEE Trans. Transp. Electrif. 2022, 8, 2853–2861. [Google Scholar] [CrossRef]
- DIN 4760:1982; Form Deviations; Concepts; Classification System. German Institute for Standardisation: Berlin, Germany, 1982. Available online: https://webstore.ansi.org/standards/din/din47601982 (accessed on 25 August 2023).
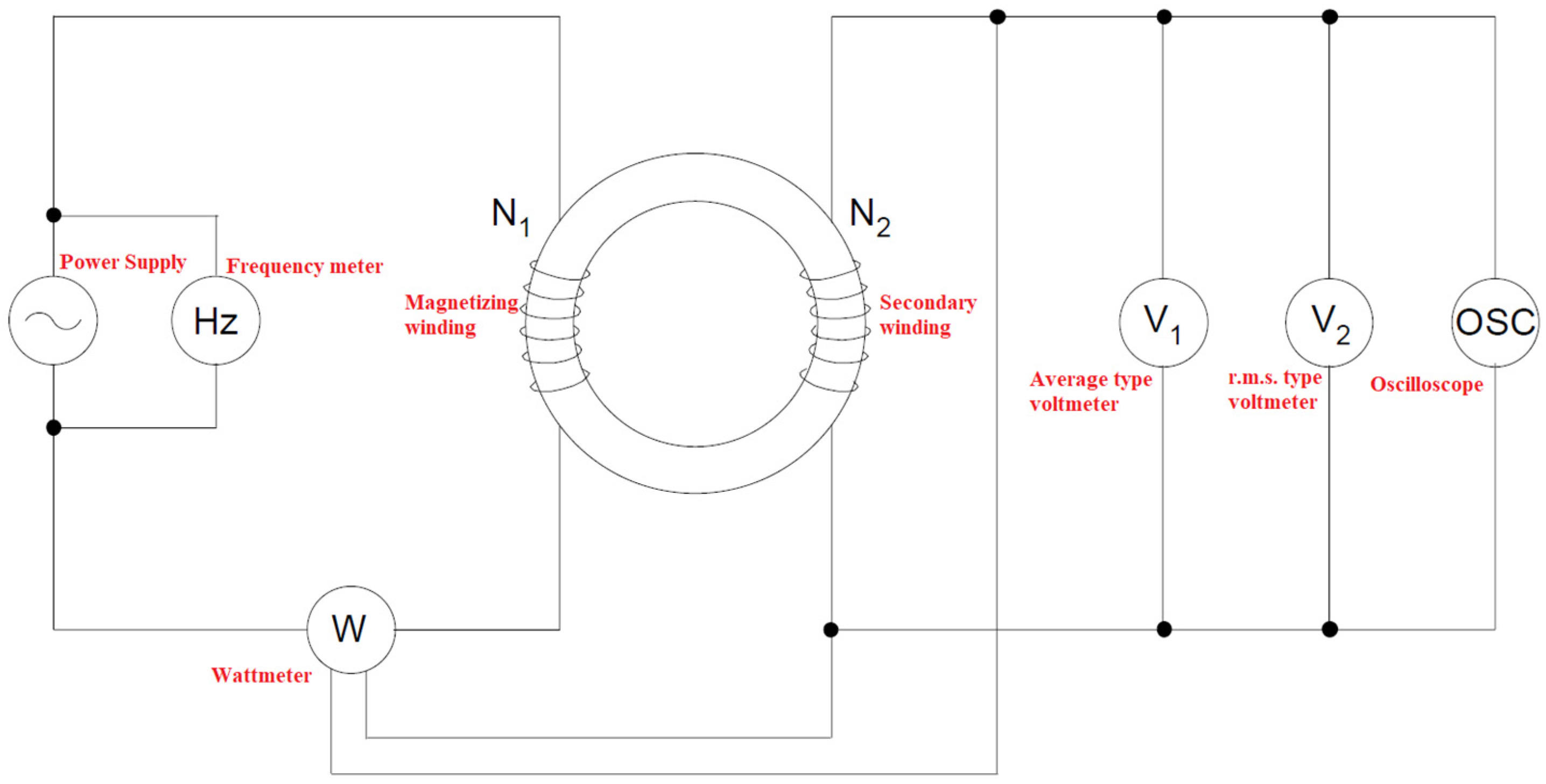
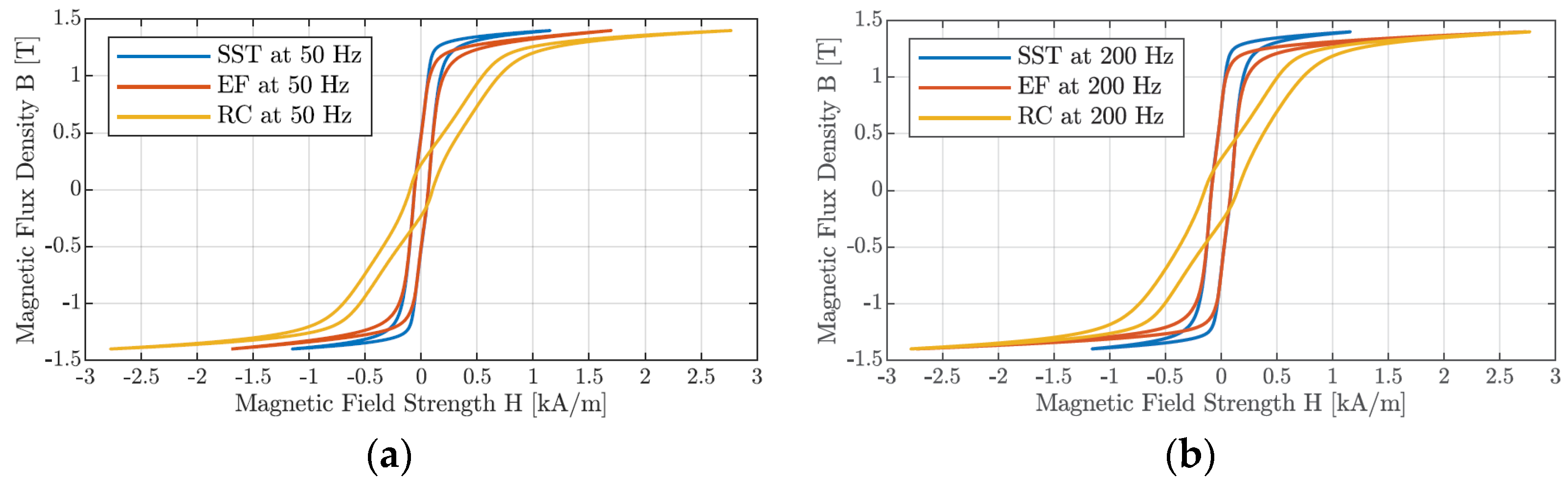








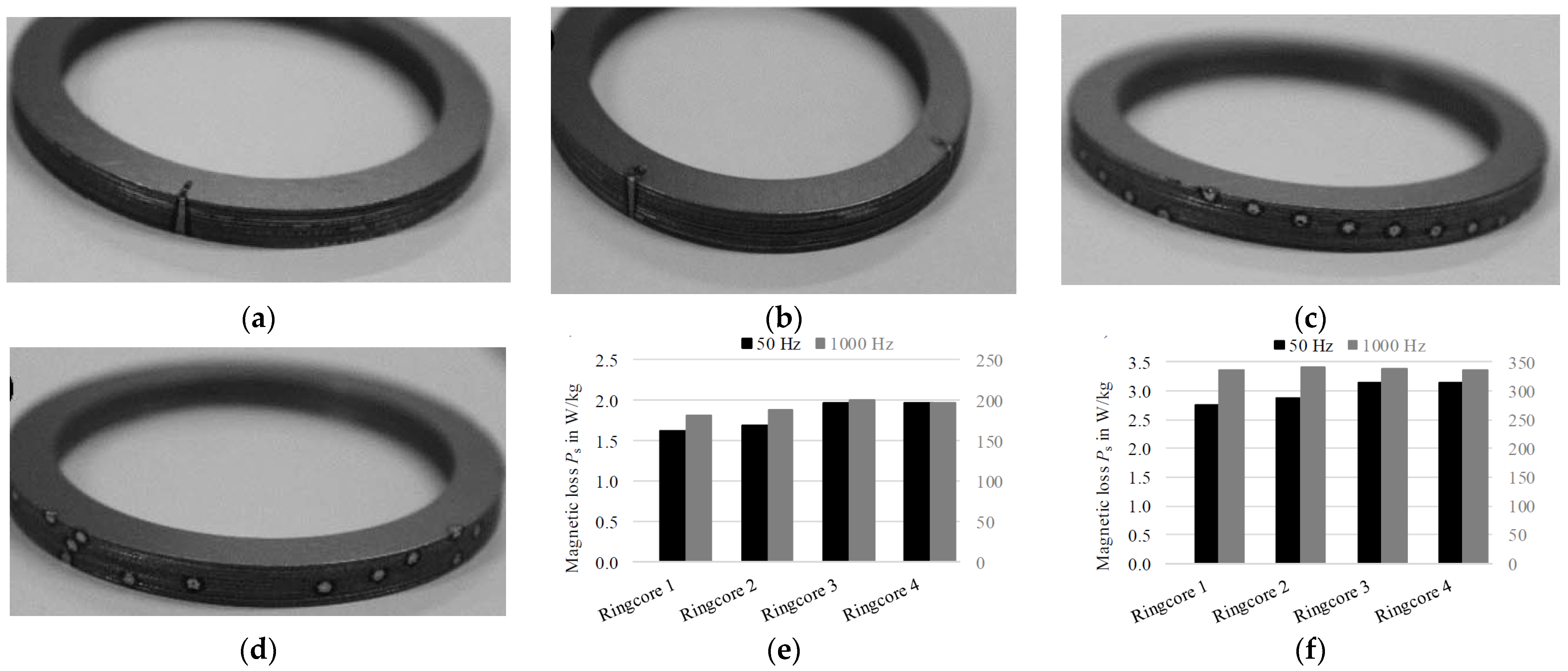




| Measuring Device | 50 Hz | 100 Hz | 200 Hz | 400 Hz |
|---|---|---|---|---|
| RC | 2.98 [W/kg] | 6.98 [W/kg] | 17.3 [W/kg] | 45.6 [W/kg] |
| EF | 2.19 [W/kg] | 5.09 [W/kg] | 13.2 [W/kg] | 34.2 [W/kg] |
| SST | 2.23 [W/kg] | 5.16 [W/kg] | 12.6 [W/kg] | [W/kg] |
| REF | B-H Curve Formula | Core Losses Formula | Description |
|---|---|---|---|
| [49,50] | The authors assume that hysteresis losses are impacted by degradation. Similar assumptions were made about anomalous losses, whereas eddy current losses were thought to be unrelated to the cutting effect. | ||
| [51,52] | Data points (H, ), and (H, ) are calculated from the measured data of two samples with identical material and cutting technique but different widths, denoted by (H, ) and (H, ), where , , , and all correspond to the same magnetic field strength H. | ||
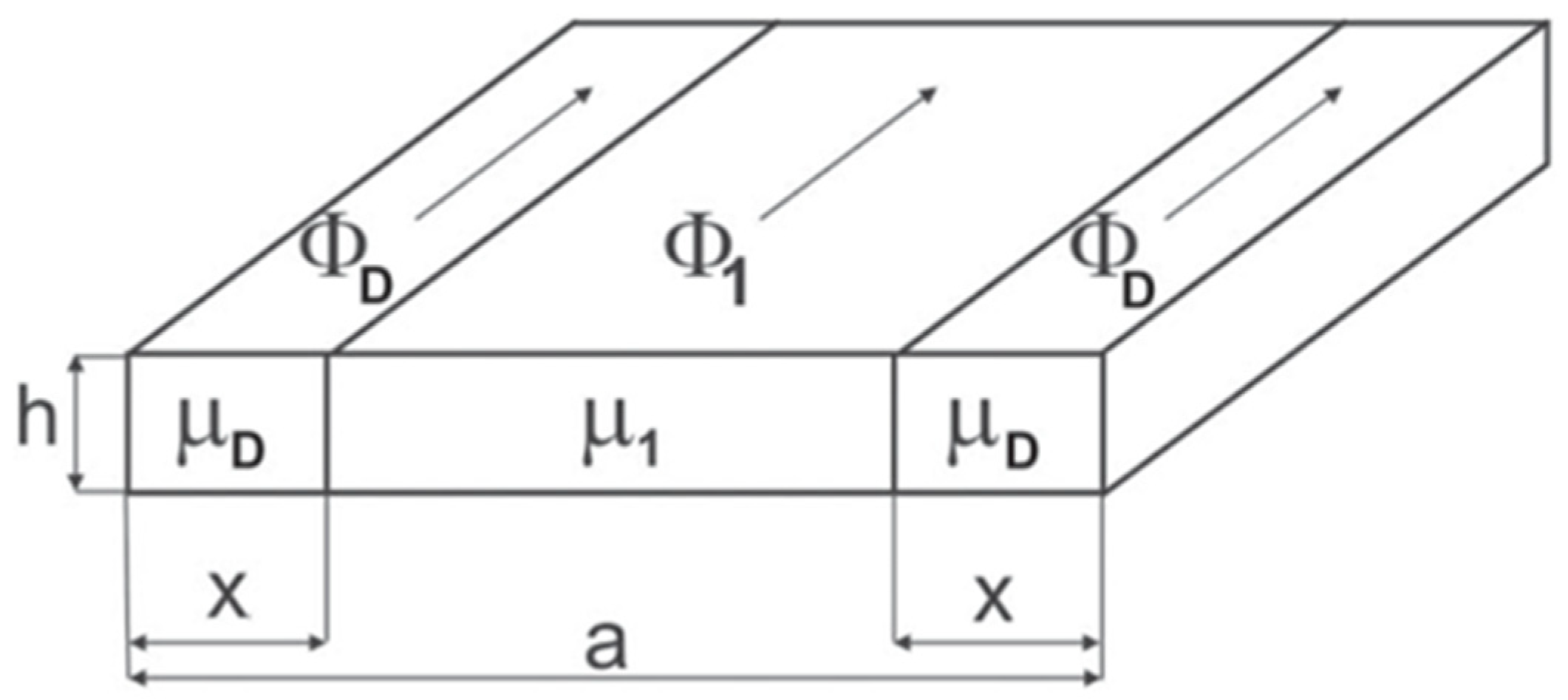
| [29] | The magnetic field strength, chemical composition, and grain size are all described by the parameters , and A. is half the width of the sample. | ||
| [53] | is degradation depth and it depends on the on the distance from the cut edge . The experimental data are used to determine the values of Both and . | ||
| [37] | - | The material parameters vary depending on the silicon content, grain size, magnetic flux density, and frequency. | |
| [15] | (Bi, Hi) is scaled to (Bi, Hi/γ(s)) | Degradation factor at the cut edge (, distance from the cut edge (s), and the depth where the effect of degradation was reduced to one third ( are depended on the experimental data.” | |
| [54] | An exponential change in permeability is assumed in the adapted model which its value decrease from the center of tooth toward the cutting line. | ||
| [55] | ---- | The degradation parameter ( must be determined through experimental data. Also, and denote the sample width and the sheet thickness, respectively. | |
| [13,14,56] | and are the distance from the cut edge and the width of the damaged zone, respectively. | ||
| [57,58,59] | and are determined by experimental data. | ||
| [9] | The term “exponential” is used to consider the physical principle that as the distance from the cut edge increases, the cutting effect should also decrease. The term with field intensity refers to limiting the punching effect to the area beneath and around the knee of the BH curve. | ||
| [60] | An exponential profile is used to describe the loss density in the compromised core. In contrast to other works, it assumes that both hysteresis and eddy current losses are impacted. | ||
| [61] | Magnetization saturation is assumed to exist regardless of cutting stress. is a material parameter that is affected by the initial susceptibility. The deteriorated susceptibility is represented by a cumulative Gumbel distribution that varies with distance to the cut edge d. With different cumulative Gumbel distributions, the loss coefficients , , , and depend on the distance to the cutting edge. |
| No. | Power | Speed | The width of Seam | Method |
|---|---|---|---|---|
| 1 | 200 (W) | 10 (mm/s) | - | Linear |
| 2 | 350 (W) | 8 (mm/s) | 0.5 (mm) | Wobbling 50 Hz |
| 3 | 750 (W) | 8 (mm/s) | 0.5 (mm) | Wobbling 50 Hz |
| 4 | 350 (W) | 8 (mm/s) | 1.5 (mm) | Wobbling 50 Hz |
| 5 | 350 (W) | 20 (mm/s) | 1.5 (mm) | Wobbling 50 Hz |
| Sample | Welding Strategy | Number of Seams | Power (W) | Speed (mm/s) | Contact Torque (N.m) |
|---|---|---|---|---|---|
| 1 | Linear | 8 | 600 | 50 | 40 |
| 2 | Wobbling | 8 | 600 | 12 | 120 |
| 3 | Wobbling | 8 | 600 | 12 | 40 |
| 4 | Wobbling | 4 | 600 | 12 | 40 |
| 5 | Wobbling | 8 | 650 | 10 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmouditabar, F.; Baker, N. A Review on the Effect of Electrical Steel Manufacturing Processes on the Performance of Electric Machines. Energies 2023, 16, 7954. https://doi.org/10.3390/en16247954
Mahmouditabar F, Baker N. A Review on the Effect of Electrical Steel Manufacturing Processes on the Performance of Electric Machines. Energies. 2023; 16(24):7954. https://doi.org/10.3390/en16247954
Chicago/Turabian StyleMahmouditabar, Farshid, and Nick Baker. 2023. "A Review on the Effect of Electrical Steel Manufacturing Processes on the Performance of Electric Machines" Energies 16, no. 24: 7954. https://doi.org/10.3390/en16247954
APA StyleMahmouditabar, F., & Baker, N. (2023). A Review on the Effect of Electrical Steel Manufacturing Processes on the Performance of Electric Machines. Energies, 16(24), 7954. https://doi.org/10.3390/en16247954








