Abstract
The cylinder liner and piston ring form the most crucial friction pair in the diesel engine, contributing 35–40% of its overall friction losses. Recent research indicates that transient heat transfer significantly affects piston ring lubrication. However, the impact of such a transfer on varying surface textures and lubrication traits remains unclear. This paper takes the piston ring–cylinder liner of a certain diesel engine as the research object, which is based on a two-dimensional averaged Reynolds function and Greenwood–Tripp micro convex body contact model; establishes a numerical calculation model of the transient heat fluid lubrication characteristics of a vertical piston ring–cylinder liner assembly by combining the oil film thickness equation, energy equation, lubricating oil viscosity–temperature, and viscosity pressure characteristics; avoids large errors associated with assuming different temperature values for lubricants; and also uses the cylinder liner surface texturing technique to examine the effects of surface texturing on lubrication properties in the presence of transient thermal fluids. The findings indicate that employing transient thermal fluid for determining the mean value of the oil film temperature in isothermal lubrication calculations yields comparable values for minimum oil film thickness and frictional power consumption, while the friction power consumption calculated by the transient thermal fluid is slightly lower. The depth of the recesses on the surface of the cylinder liner should be minimized, while the radius of the texture should be maximized, taking into consideration the current circumstances. Compared with a cylindrical texture, a spherical texture achieves lower friction with good lubrication indexes.
1. Introduction
The cylinder liner and piston ring form the most crucial friction pair in the engine, contributing 35–40% of its overall friction losses [1]. Therefore, in order to save energy, reduce emissions, and improve engine efficiency, it is important to reduce friction between the piston ring and the cylinder liner. The movement of the piston rings in the cylinder liners significantly affects the decrease in friction, lubricant consumption, and wear [2,3,4]. To enhance the tribological performance of the piston ring–cylinder liner assembly during operation, there has been considerable discussion on the surface micro-texturing technique; however, because the tribology of the working process between the piston rings and cylinder liner involves numerous variables, to increase the calculation rate, many studies ignore the variation of lubricating oil temperature between friction pairs or treat it as a thermostatic thermal fluid [5,6,7], which improves the computational efficiency but is far from the actual working process. Therefore, it is crucial to take into account the immediate fluctuation in temperature of the lubricating oil between the frictional regions of the piston ring and cylinder liner and its impact on the lubricating friction properties [8,9,10,11].
For the study of lubrication within the piston ring texture, by taking into account the impact of temperature, Rosalind Takata et al. studied the impact of various structural parameters of the cylinder liner surface texture and the type of lubricating oil on the flow coefficient, pressure coefficient, and friction power consumption in the average Reynolds equation, which showed that the effective friction power consumption can be reduced by 30% through the surface texture [12]. The comparison of the lubrication characteristics of isothermal fluids on contact surfaces at different constant temperatures was also investigated in the paper, and the findings illustrate the need to consider the fluctuation in oil film temperature when examining piston ring–cylinder liner units. Guo et al. demonstrated that two important factors that affect the oil film temperature are the speed of the piston ring and the applied load [13]. Significant temperature increases occur at the oil film exit and in the textured area. In this region, the energy equation does not account for the effect of frictional heat resulting from micro convex body contact. Gu et al. used an averaged Reynolds equation that takes into account cavity corrections and a two-dimensional energy equation that takes into account viscous dissipative heat and contact frictional heat; the structural surface temperature equation was established, and a study of mixed piston ring–cylinder liner lubrication with coating and texture was carried out [14]. The results show that low thermal inertia coating has significantly lower frictional power consumption than high thermal inertia coating, and localized high temperature may occur in the fluid within the texture. Liu et al. have demonstrated that the rise in temperature resulting from frictional heat is considerable and holds an immense impact on the tribological properties of piston rings [15]. A properly designed surface texture reduces both friction and wear.
In recent years, more parameters and influence factors in piston ring lubrication studies have been taken into account in calculation models; however, there are relatively few studies considering the effects of transient heat transfer on the pressure of oil film and the distribution of thickness and friction. Also, the impact of various surface textures on piston ring lubrication properties while considering the impact of heat transfer remains inconclusive. In this paper, we present a computational model of the transient thermal fluid mixing lubrication that occurs between the piston ring and cylinder liner. The model measures the oil film pressure and temperature between the friction surfaces of the piston ring and cylinder liner. It also examines the real-time effect of oil film temperature on lubrication performance; evaluates the effects of spherical textures on the surface of the cylinder liner with varying areal densities, pit depths, and radii on the lubrication characteristics based on transient thermal fluid models; and compares the differences in lubrication characteristics between spherical and cylindrical textures.
2. Basic Theories and Formulas
2.1. Lubrication Equation
We use the average Reynolds control equation as follows [16]:
where h represents the thickness of the oil film, denotes the average pressure of oil film, represents the average clearance, , represent the pressure flow coefficient, represents the shear force coefficient, represents the lubricating oil density, U represents the sliding speed of the piston ring relative to the cylinder liner, and is the combined roughness of the two contact faces.
where represents the combined standard variance of the rough cylinder liner height and represents the combined standard variance of the rough height of the piston rings.
represents the contact factor, which can be calculated from the following formula:
The specific formula of the pressure flow coefficient is shown as follows:
where C and r are constants and H represents the film thickness ratio, which has the following definition:
The shear flow coefficient formula is as follows:
The formula is as follows:
where A1, A2, a, b, c are constants.
Once the oil film thickness is determined, the pressure of the oil film on the contact surface between the piston ring and cylinder liner can be obtained by utilizing an over-relaxation iteration method to resolve Equation (1). By integrating the given formula as follows, the pressure of the oil film on the entire surface of the piston ring can be determined:
The model assumes oil-rich lubrication. The piston ring’s upper position on the cylinder liner indicates the start of the oil film, while its segment away from the top marks the end of the film. Consequently, gas pressure on both sides of the piston ring equals the oil film pressure at the inlet and outlet.
The constraints are the following:
where represents the pressure of gas at the inlet of the piston ring; at moment indicate the pressure entering and leaving the oil film, respectively. The initial inlet pressure of the first ring equals the engine's burst pressure, and the outlet pressure equals the gas pressure positioned between the first and second rings.
2.2. Micro-Convex Body Contact Model
In a state of mixed lubrication, when the two parts are moving relative to each other, the concave peaks will also provide load-bearing force due to micro-convex body contact in addition to the oil film that provides load-bearing force; thus, the theoretical analysis of piston ring–cylinder lubrication theory should consider the impact of micro-convex body contact. We use Greenwood and Tripp’s micro-convex body contact model as a basis [17] and assume that the relative sliding surface roughness follows a Gaussian distribution to establish the contact model between micro-convex bodies present on the surface of the piston cylinder liner. The equation for determining the bearing capacity of the micro-convex body is as follows:
where is the pressure of the apparent contact surface, is the micro-convex body density, represents the radius of curvature of the rough peak, and E represents the equivalent elastic modulus of the material.
The force exerted on micro-convex bodies via body contact can be calculated by measuring the pressure on their apparent contact surfaces, expressed as follows:
The expression for friction caused by micro-convex body contact is:
where represents the constant of the shear stress and represents the coefficient of the boundary friction.
2.3. Oil Film Temperature Control Equation
The calculations of viscosity and density for the oil film require calculations of its temperature, which is influenced by several factors. When defining the temperature control equation for the oil film, the energy equation for the oil film without considering factors such as radiation and heat transfer in the x-direction uses the following equation:
In addition, as the piston ring–cylinder liner assembly is regularly lubricated by a mixture while operating, the heat generated by micro-convex body contact must also be factored into the energy equation; thus, Equation (14) needs to be modified by adding the following correction Equation [18]:
where is the friction arising from the contact between micro-convex bodies, represents the pressure caused by contact with the micro-convex body, and is the micro-convex body friction coefficient.
Therefore, after considering the effect of micro-convex body contact on oil film temperature, the energy equation is presented below [14]:
The piston ring can be in direct contact with the film of oil, which facilitates the transfer of heat from both the piston and the hot gas in the cylinder to the film of the oil. Subsequently, the efficient heat transfer between the piston and cylinder liner can be carried out by the oil film transferring the heat to the cylinder liner. The temperature control equation for the piston rings is determined by a Laplace transform, as follows:
where represents the piston ring's density, represents the piston ring's specific heat capacity, and represents the piston ring's thermal conductivity.
Using a specific diesel engine type as the subject of the study, this research aims to examine the impact of elements such as cylinder liner thermal deflection and surface texture on the lubrication of the piston ring–cylinder liner assembly in steady-state conditions. Table 1 displays the fundamental structural parameters.

Table 1.
Texture surface structure parameters.
The cylinder liner wall surface is stationary relative to the piston ring; the piston ring along the cylinder liner wall reciprocates movement, and such a friction mode of movement obviously belongs to the sliding friction. This paper discusses the process of heat generation by sliding friction.
In the finite element analysis of the temperature field of the friction heat generation process, there are two modeling methods: the first one is to take the heat generated by friction as the volume heat generation of the friction material; and the second one is to take the heat generated by friction as the surface heat flux input, that is, to take the heat generated by friction as the boundary heat flux rate in the differential equation of heat conduction. Because the piston reciprocates on the inner surface of the cylinder liner, the process of heat generation by friction between the outer surface of the piston ring and the inner surface of the cylinder liner is very complicated, and the whole process is related to the contact nonlinearity and thermal boundary nonlinearity; therefore, it is more difficult to solve the convergence. In order to make the calculation easier to converge, the heat energy generated by friction is generally treated as the surface heat flow input so that the heat energy generated by friction becomes the boundary conditions of the temperature field control equations, and in this way, the degree of model nonlinearity can be reduced. Therefore, the second temperature field modeling method is used in this paper.
Figure 1 displays the lubrication properties of the initial compression ring, including its structural parameters and profile. The remaining structural and material parameters can be found in Table 2.
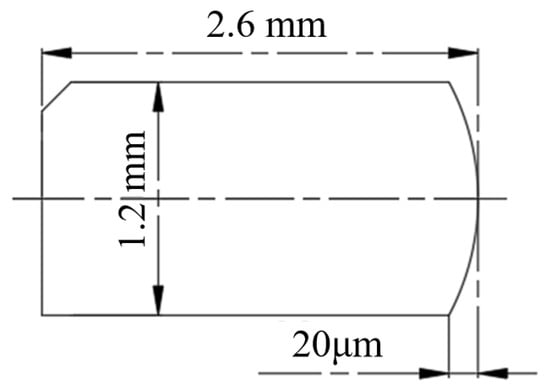
Figure 1.
First compression ring profile and parameters.

Table 2.
Basic calculation parameters.
2.4. Cylinder Liner Surface Texture Parameters
This paper establishes a lubrication calculation model on the basis of both the textured cylinder liner and the first compression ring, using them as examples. Meanwhile, the surface parameters related to the micro-morphology and the cylinder liner data related to the piston ring can be found in Table 1.
To aid the theoretical analysis and numerical computation, the non-uniform factors that affect the piston ring’s back-and-forth movement, such as lubrication conditions, load, and circumferential wear, are simplified. Because the oil film that existed in the contact surface between the piston ring and cylinder liner assembly is much thinner than the diameter of the cylinder liner, the theoretical investigation hardly takes into account the curvature of the oil film, and the cylinder liner can be unfolded into a flat surface along the axial direction, as shown in Figure 2.
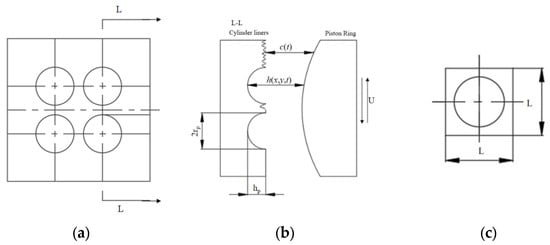
Figure 2.
Piston ring–cylinder liner surface micro-structure schematic. (a) Woven liner surface. (b) Cylinder liner–piston. (c) Control unit ring sectional view.
As shown in Figure 2c, the control unit for the pit is a square with length L, and the density of the pit is defined as .
3. Validation and Results
3.1. Validation of the Numerical Calculation Model
Friction and wear tests were conducted on the piston ring–cylinder liner test specimens using the UMT-2 multifunctional friction and wear test machine. The test bench is shown in Figure 3, which is mainly composed of a reciprocating motion mechanism, load loading mechanism, fixture, and other parts; under the reciprocating driving mode of the test machine, the relative sliding speed of the cylinder liner–piston ring is zero at the two stop positions, and the relative sliding speed of the cylinder liner–piston ring is the maximum at the middle position of the stroke. In the experiment, the piston ring is pressed on the surface of the cylinder liner sample by the normal loading force, simulating the reciprocating motion of the piston ring in the cylinder liner between the upper and lower stops of the actual engine.

Figure 3.
Friction and wear test bench.
The piston ring selected in the experiment is shown in Figure 4, and the sample of the cylinder liner with a different weave was processed by laser micromachining technology. The cylinder liner with three different weaves was placed into anhydrous ethanol and cleaned by an ultrasonic cleaner; then, the liner was used to carry out the friction and wear test under the fluid lubrication after the completion of the test.

Figure 4.
Test piston rings.
Measurements were taken to obtain the friction force of the test specimen, and the average friction coefficient of the test, i.e., the test value, was obtained from the applied loading force and the equivalent host speed; furthermore, simulation calculations were performed to obtain the calculated average friction coefficient, also known as the calculation value, based on the fundamental theory and formulas discussed in Section 2. The specific validation scheme is detailed in Table 3. A comparison between the experimental results and the simulated results, along with the corresponding errors, is presented in Table 4.

Table 3.
The model validates the different schemes.

Table 4.
Model validation comparison table.
The errors between the test value and the calculation value primarily stem from the collection error in the average friction coefficient during the experimental process and the iterative error in the numerical calculations. The overall error does not exceed 12%, indicating that the established model is reliable.
Due to the minimal difference between the test value and the calculation value for experimental Scheme 1 in Table 4, it is considered as the benchmark for subsequent simulation calculations involving different cavity structures.
3.2. Transient Thermal Fluid Compared with Isothermal Fluid Lubrication Solution Results
The changes in both the pressure distribution of the oil film and the minimum thickness of the oil film with respect to the angle of the crankshaft is depicted in Figure 5a. The data indicate that the pressure of the oil film curve rises considerably in areas with adequate lubrication, while the pressure effect of the fluid increases during the stroke. As illustrated in Figure 5b, the temperature of the lubricant film and the speed of the piston ring vary with the angle of the crankshaft, with the highest oil layer temperature being encountered at the midpoint of the power stroke. This is influenced by the speed at which the piston ring is moving and the thermal energy exchanged with the high-pressure gas when it exerts power, transferring heat to the oil film. The hydrodynamic effect is less pronounced at the top and bottom dead center, the amount of work consumed by the viscous resistance of the lubricating oil is reduced, and minimal values of oil film temperature occur. Figure 5c displays the fluctuations in lubricant film temperature and pressure as a function of the crankshaft angle. It is noteworthy that the angle of the crankshaft corresponding to the time when the oil film temperature is at its highest point experiences a delay in response to the angle of the crankshaft corresponding to the time when the oil film pressure is at its highest point. The pressure of the oil film reaches its maximum at a crankshaft angle of 370°, while the highest oil film temperature is reached at a crankshaft angle of 450°. The primary reason for this is that the highest pressure of oil film coincides with the upper stop of the cylinder liner, and it takes some time for the piston rings to travel from the top dead center to the middle of the cylinder liner. The minimal difference between the temperature’s minimum value of the lubricant film and its corresponding pressure can be attributed to the lubricant film temperature’s minimum value point coinciding with the position where the piston ring rotation speed is 0; at the same time, the hydrodynamic pressure effect of the lubricant film is at its weakest, leading to the minimum oil film pressure value. The lubricant film temperature attains its minimum value at speed 0.
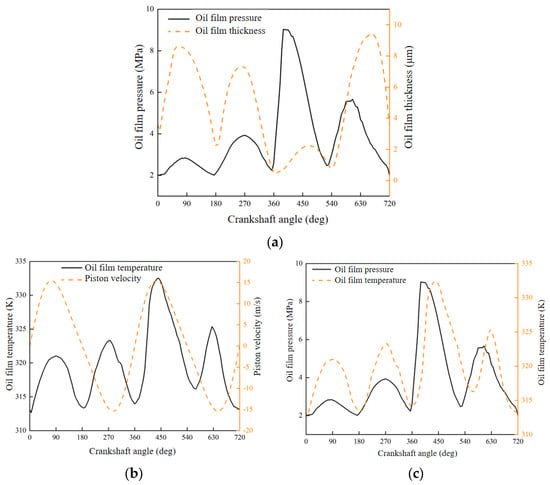
Figure 5.
Transient thermal fluid lubrication results. (a) Oil film pressure distribution and minimum oil film thickness vary according to the angle of the crankshaft. (b) Oil film temperature and piston ring speed vary with the crankshaft angle. (c) Oil film temperature and pressure vary with the crankshaft angle.
A comparison of results for isothermal and transient thermal fluids is shown in Figure 4, solving for isothermal thermal fluids only by evaluating the mean Renault equation as well as the micro-convex contact model; when solving for transient thermal fluids, in addition to solving the mean Renault equation and the micro-convex contact model, the variation in temperature of the lubricant lube throughout the whole engine operation is taken into consideration by solving the energy equation, which consequently affects the viscosity of the lube.
Figure 6a shows the minimum lube film thickness varying with the crankshaft rotation angle under different thermal lube models. The general trend of the minimum lube film thickness curve is basically consistent with the results, but it is obvious that the minimum lube film thickness estimated when using transient hot fluid is much smaller than when using isothermal fluid. The difference in the value exists primarily in the mid-piston stage between the top and bottom terminals of the cylinder liner. The main reason is that the piston rings run much faster than the rest of the region, the higher relative slip speed increases the hydrodynamic action, and the increased viscous resistance creates a large amount of friction heat; furthermore, there is a large gap among the piston rings and cylinder liners, which leads to an extremely difficult transfer of heat from the lube to the inner wall surface of the cylinder liner.
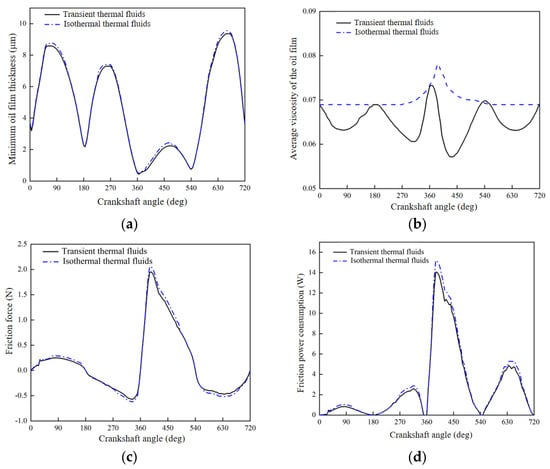
Figure 6.
Comparison results of the lubrication characteristics of isothermal and transient thermal fluid models. (a) Oil film thickness change curve. (b) Average viscosity change curve. (c) Friction force change curve. (d) Friction work change curve.
Figure 6b shows the average viscosity curve of the lube with the angle of the crankshaft during the operation of the lubrication system. The average viscosity is estimated by adding the viscosity of each control unit and then dividing by the sum of the control unit. The change in average viscosity reflects the degree of influence of temperature and pressure on the lube viscosity in the lubrication system of the piston ring lining assembly. When the isothermal fluid is used as the calculation model, the change in lube viscosity mainly occurs in the power stroke. At this point, the lube pressure reaches its maximum value, causing the lube to gradually increase its average viscosity. However, when using transient thermal fluids as the calculation model, the mean viscosity is constantly changing with the crankshaft rotation angle, and the maximum of the average viscosity is taken from the corresponding position of the top dead center of the piston because the viscosity of the lube at this time is affected by the temperature and pressure distribution of the lube film.
Figure 6c shows the trend of friction force with crankshaft rotation under different thermal fluid models when the lubrication system works. The trends in friction forces generated by different thermal fluid models are generally consistent; however, there are some differences between the intermediate phase of the compression stroke and the beginning phase of the power stroke, and the friction generated by using the transient hot fluid model is generally lower than that generated by using the isothermal hot fluid model. This is because of the temperature of the lube film rising in the intermediate of the stroke, which corresponds to a slight decrease in viscosity, also reduces the viscous resistance of the lube, as shown in Figure 6a,b.
Figure 6d shows the trend of friction power consumption with the crankshaft angle under different thermal fluid models when the lubrication system is operating. The curve distribution of the friction power consumption has a similar trend to Figure 6c; the friction power consumption curves are distributed consistently overall, but transient thermal fluid models that are in the intermediate of the travel produce less friction power consumption than isothermal thermos fluid models. This is mainly because the reduction of friction forces is facilitated by the reduction of frictional power consumption when the travel distance and speed are the same. Just like Figure 6 shows, different calculation models have a certain effect on the lubrication characteristics; using transient thermal fluids as the calculation model allows for more accurate calculations and better matches the actual operation of the engine.
3.3. Effect of Various Pit Structural Characteristics on the Piston Ring–Cylinder Liner Assembly Lubrication Characteristics
3.3.1. Impact of Pit Surface Density on Lubrication Properties
In this section, under the validation scheme labeled as Scheme 1 in Table 4, characterized by a cavity diameter of 50 μm, depth of 5 μm, axial spacing of 600 μm, and radial spacing of 400 μm, three distinct cavity densities with different structural configurations are selected to investigate their influence on the lubrication characteristics within a transient thermal fluid model.
Figure 7a portrays the trend of change in lube film pressure with different pit surface densities. At a 600° crankshaft angle, the pressure of the lube film decreases gradually with increasing pit surface density, but the values are not that different, and in the case of transient thermal fluid models, the pit surface density produces a weak impact on the distribution of the lube film pressure. For example, the trend of changing the minimum lube film thickness under different pit surface densities is indicated in Figure 7b. With the increase in pit surface density, the minimum lube film thickness also increases. At the minimum point, due to the harsh working environment, the piston running speed is relatively low, and the minimum lube film thickness has almost nothing to do with the size of the surface density.
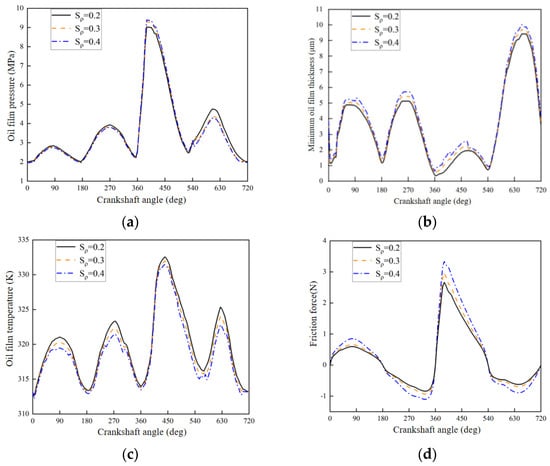
Figure 7.
The different pit surface densities affect piston ring lubrication. (a) Lube film pressure. (b) Minimum lube film thickness. (c) Temperature of lube film. (d) Friction force.
Figure 7c shows the alteration of the temperature of lube film due to different pit surface densities. Overall, the temperature change curve of the lube film is consistent. Accompanied by the ascendance in the density of the pit surface, the temperature of the lube film decreases gradually, and changes, especially in the intermediate of the stroke, are particularly noticeable. This is mainly due to the increased density of the concave surface, which increases the lube film–cylinder liner contact area, further leading to an increase in the heat dissipated toward the cylinder sleeve from the lube film. As a consequence, the heat during piston ring operation that is generated by the viscous resistance of the lube film is less than the heat emitted by the lube film. For example, Figure 7d shows the trend of friction with crankshaft angle over different pit surface densities. There is a 10–15% difference between the values at the maximum and minimum friction, and the growth of pit surface density is accompanied by an increase in friction. This is mainly because the amount of friction is mainly influenced by the combination of lubricant viscosity and lube film thickness, which decrease and increase, respectively, for different pit surface densities, resulting in increased friction. The above analysis shows that only from the angle of reducing friction and improving lubrication performance, when under certain conditions, 20% pit surface density is more beneficial to reducing friction and improving lubrication performance.
3.3.2. Transient Thermal Fluid Compared with Isothermal Fluid Lubrication Solution Results
In this section, under the validation scheme labeled as Scheme 1 in Table 4, characterized by a cavity diameter of 50 μm, axial spacing of 600 μm, and radial spacing of 400 μm, three distinct textured cavity depths (5 μm, 8 μm, 10 μm) are selected to investigate their influence on the lubrication characteristics within a transient thermal fluid model.
The trend of lube film pressure with crankshaft angle for different pit depths in transient thermal fluid models is depicted in Figure 8a. At different pit depths, the variation trend of the lube pressure distribution is basically the same. Near the crankshaft angles of 360° and 630°, the maximum lube pressure will surge with the increase in pit depth. As shown in Figure 8b, under the transient hot fluid model, the variation trend of the minimum lube film thickness is related to different pit depths and crankshaft angles. The trend of change in the minimum film thickness distribution is generally consistent at the different pit depths, and the alteration in the lube film thickness gradually increases with increasing pit depth in areas where lubrication is sufficient; however, in areas where lubrication is insufficient, the variation of the lube film thickness gradually decreases with increasing pit depth. This is mainly due to the dominant hydrodynamic action in areas where lubrication is sufficient, and the increased pit depth facilitates lube film storage and flow, increasing lube film thickness; however, in regions where lubrication is insufficient, the compression effect of the piston rings dominates, and the excessive pit depth is insufficient for the distribution of lubricant, leading to a reduction in lube film thickness. From the angle of lube film thickness alone, the texture pit depth should be selected at a smaller value to maintain that there is the lube film is not too thick in areas where lubrication is sufficient and not too small in areas where lubrication is insufficient.
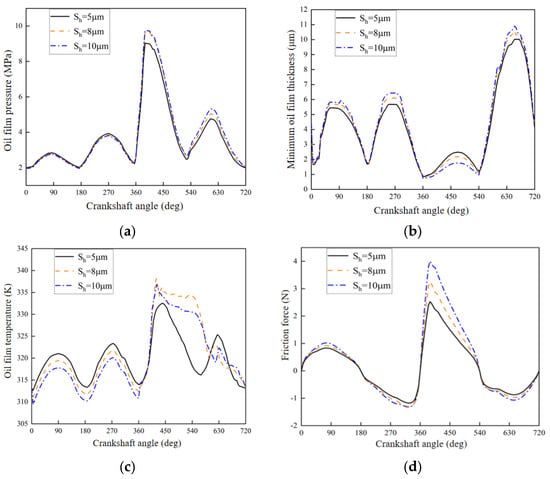
Figure 8.
Different pit depths affect piston ring lubrication. (a) Lube film pressure. (b) Minimum lube film thickness. (c) Temperature of lube film. (d) Friction force.
As shown in Figure 8c, under the transient hot fluid model, the temperature of the lube film distribution at different pit depths changes with the crankshaft angle. The instantaneous temperature of the lube film varies considerably at different pit depths. When the pit depth is 5 μm in a well-lubricated area, the temperature of lube film is low; when the pit depth is 8 μm and 10 μm, in the area of insufficient lubrication, the temperature of lube film can reach 60 °C, while the high temperature duration can reach a 140° crankshaft angle. At this time, the thickness of lube film decreases with the increase in the pit depth. In comparison, the increase in temperature of the lube film is greater when the same amount of heat is absorbed. Figure 8d shows the changes of the friction curve corresponding to different crater depths with the crankshaft rotation angle under the transient thermal fluid model. In addition to the power stroke, the impact of different pit depths on friction during the rest of the work process is relatively small. In areas with sufficient lubrication, the texture pit depth is 8 μm and 10 μm, and the corresponding friction values are almost the same but are all greater than the 5 μm corresponding friction force at 2.7 N. The increase in the depth of the pit is followed by a moderate increase in friction force. and the friction force increases by 50–80% in areas where lubrication is insufficient, mainly due to the thin lube film, which increases the boundary lubrication ratio; the micro-convex friction increases significantly. This results in increased friction.
3.3.3. Impact of Pit Radius on Lubrication Characteristics
In this section, under the validation scheme labeled as Scheme 1 in Table 4, characterized by a cavity depth of 5 μm, axial spacing of 600 μm, and radial spacing of 400 μm, three distinct textured cavity radii (25 μm, 30 μm, 35 μm) are selected to investigate their influence on the lubrication characteristics within a transient thermal fluid model.
It could be observed that the distribution of lubricant film pressure is associated with the engine crankshaft angle for different pit radii under the transient thermal fluid model in Figure 9a. The distribution of lubricant film pressure generally changes in a consistent trend, and values do not change much except for the 360° crankshaft angle at different pit radii. From the results of the experiment, we can conclude that the oil film pressure is less affected by the radius of the weave pits. The minimum oil film thickness curve attributed to different pit radii under the transient thermal fluid models is also related to the crankshaft angle in Figure 9b. The minimal oil film thickness associated at the individual crankshaft angles varies significantly in different pit radii. In well-lubricated areas, an increase in the radius of the pit leads to an enlarged oil film thickness, whereas in poorly lubricated areas, the result is the opposite, which is primarily attributed to the predominance of hydrodynamic pressure effects in the well-lubricated region. In areas where lubrication is insufficient, the hydrodynamic action decreases with the piston ring speed; conversely, the increased pit radius does not facilitate the flow of the lubricating oil.
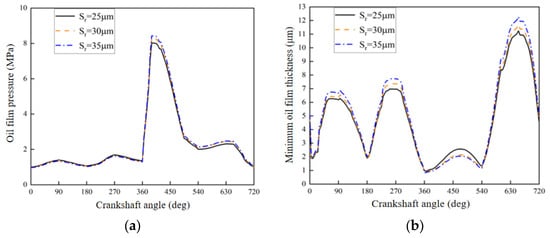
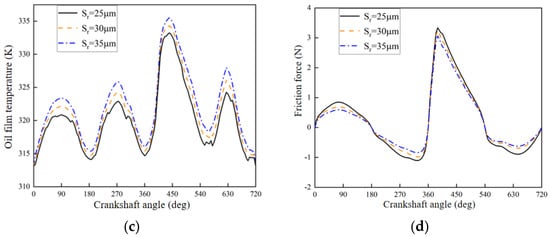
Figure 9.
Different pit radii affect piston ring lubrication. (a) Lubrication oil film pressure. (b) Minimum oil film thickness. (c) Lubrication oil film temperature. (d) Friction force.
Under the transient thermal fluid model, the oil film temperature corresponding to different crater radii versus the crankshaft rotation angle is illustrated in Figure 9c. The temperature changes significantly at the halfway point of the stroke. As the radius of the weave pit increases, the oil film thickness increases gradually, and then the oil film temperature increases. In comparison, the lubricant film temperature rises in the region of the power stroke, mainly due to the lubricant film thickness decreasing gradually in this area, which produces little difference in heat and heat dissipation; thus, the oil film temperature rises gently. The trend of friction corresponding to the different pit radii with the angle of the crankshaft under the transient thermal fluid model is illustrated in Figure 9d. Overall, the friction obtained using the transient thermal fluid calculation model decreases as the pit radius increases, but the maximum friction decreases as the pit radius increases. From the angle of reducing friction and improving the lubricating characteristics, the pit radius should be chosen as far as possible from a larger one. Although the larger pit radius can reduce friction, it is not sensible to increase the pit radius; this is attributed to the fact that the lubricant film thickness increases as the pit radius increases. In turn, too thick of an oil film thickness affects lubrication adversely.
3.3.4. Impact of Different Texture Shapes on Lubricating Characteristics
Friction coefficient changes with the crankshaft angle being in the range of 350–370° can be seen in Figure 10. When the engine transitions from compression stroke to power stroke, the texture system contributes well to the reduction of the friction coefficient, mainly because the texture system enhances the hydrodynamic action, thereby increasing the oil film load-bearing capacity. It is capable of carrying more radial loads. This conclusion is also reflected in articles [19,20].
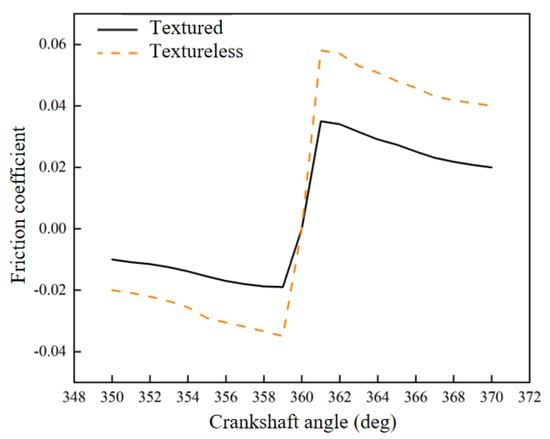
Figure 10.
Impact of surface texture on lubrication characteristics.
The main analysis in this subsection is on spherical and cylindrical pits. Under transient thermal fluid models, the relationship between the lubricant film pressure distribution for different types of pits and the crankshaft angle is illustrated in Figure 9a. The pressure distribution curve for the two types of pits is generally not very different, simply because the values for the first half of the power stroke differ by a certain amount and because the variation is less than 5%; as a result, variations in the type of pit has almost little influence on the distribution of the lubricant film pressure.
In Figure 9b, the variations in the minimal oil film thickness corresponding to different types of pits under transient thermal fluid models with the crankshaft angle is illustrated. It can be observed that the two types of pits have a quite distinct effect on the lubricant film thickness under the transient thermal fluid model. At the middle of each stroke, with sufficient lubrication, the lubricant film thickness under the cylindrical pit is greater than the one under the spherical pit. The films of cylindrical pits are 5% thicker than the lubricant film thickness associated with spherical pits; on the contrary, at the upper dead center of the cylinder sleeve where lubrication is insufficient, there is no apparent difference in the film thickness between the two types of pits. This proves that cylindrical pits have a more fluid dynamic pressure effect than spherical pits in well-lubricated areas. Nevertheless, the impact of both on oil film thickness is not significant in areas where lubrication is insufficient and operating conditions are harsh.
Under the transient thermal fluid model, the oil film temperature varies for different pit types, and the distribution of the lubricant film temperature for different crankshaft angles is demonstrated in Figure 11c. The oil film temperature curve for two different pits can be observed to be distributed the same overall, and in different regions, the trend of the lubricant film temperature changes slightly differently. In well-lubricated areas, the lubricant film temperature for the cylindrical pit is lower than the temperature for the spherical pit; in areas where lubrication is insufficient, the oil film temperature for the spherical pit is lower than the cylindrical pit, but the maximum temperature for the two is not significantly different. This also proves that cylindrical and spherical pits have a higher oil film heat transfer coefficient than spherical pits in well-lubricated areas. Meanwhile, in areas of harsh lubrication, the combined effect of high-temperature gas as well as high load makes both types of pits have little effect on oil film temperature.
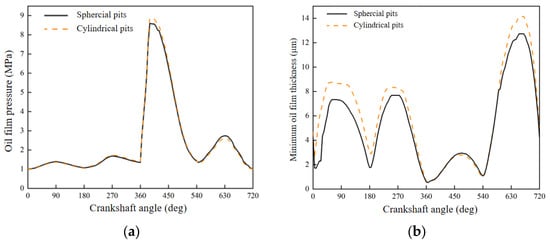
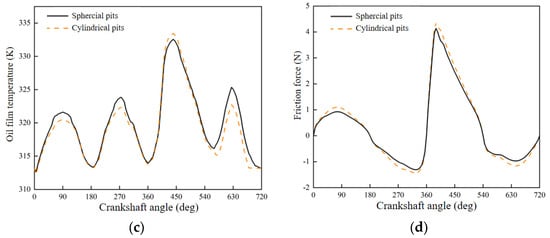
Figure 11.
Spherical and cylindrical pits affect piston ring lubrication. (a) Lubrication film pressure. (b) Minimum oil film thickness. (c) Lubrication film temperature. (d) Friction force.
Figure 11d shows that the friction force corresponding to different crater types changes accordingly with the increasing crankshaft angle under transient thermal fluid models. The friction distribution curve for two different pits can be observed to be the same overall, while the trend of friction change varies slightly in different areas. In well-lubricated mid-stroke areas, the cylindrical pits correspond to more friction than the spherical pits; meanwhile, in areas where lubrication is insufficient, the spherical pits correspond to nearly the same friction as the cylindrical shapes. This phenomenon could be explained primarily by the reason that the oil film temperature corresponding to the spherical pits in well-lubricated areas is slightly higher than the cylindrical pits and the viscosity decreases mainly with increasing oil film temperature in the case of a moderate difference in the oil film pressure. Likewise, when the reduction in friction caused by a decrease in viscosity is more dominant than the increase in shear due to increased oil film thickness, the friction is therefore reduced. In areas where the lubrication is insufficient, there is little change in lubricant film pressure, thickness, and temperature. Thus, the friction change is not noticeable. From the perspective of reducing friction and improving lubrication characteristics only, spherical pits should be selected for the surface texture, which ensures that the friction decreases while lubricating indicators such as oil film temperature perform well.
4. Conclusions
- (1)
- Transient thermal fluid calculations can resolve the large error of the lubrication oil assumptions for different temperature values when calculating iso-temperature lubrication. The minimum oil film thickness and friction power loss for isothermal and transient thermal fluid is approximate when the lubricant temperature is calculated using the transient thermal fluid for the average value of the oil film temperature. The transient thermal fluid-calculated friction power consumption is slightly lower.
- (2)
- In transient thermal fluids, lubrication characteristics are subject to a diverse range of structural parameters, and the radius, surface density, and depth of micro-concave pits have a more significant effect on lubrication. Using the current calculation model, the pit surface density is 20% and the depth is 5 μm from the perspective of reducing friction and improving lubrication performance; a radius of 35 μm for the ball pit combination ensures low friction force and friction power consumption as far as possible in advance to ensure that sufficient oil film thickness can be achieved to minimize the negative impact on the stability of the friction pair lubrication.
- (3)
- In well-lubricated areas, the oil film temperature for the cylindrical pit is lower than the temperature for the spherical pit; in areas where lubrication is insufficient, the oil film temperature for the spherical pit is lower than the cylindrical pit. From the perspective of reducing friction and improving lubrication characteristics, spherical pits should be selected for surface texturing, which ensures that the friction decreases while lubricating indicators such as the oil film temperature perform well.
Author Contributions
Conceptualization, H.Z.; methodology, H.Z.; writing—original draft preparation, H.Z.; formal analysis, H.Z.; project administration, H.Z.; investigation, H.Z. and X.L.; validation, K.S. and J.G.; formal analysis, H.J.; software, J.G.; funding acquisition, X.L. and S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grant number 52005149 and the Natural Science Foundation of Hebei Province under grant number E2022202026 and the Weifang Science and Technology Development Program Projects under grant number 2022ZJ1231.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
Author Junzhen Gong was employed by the company Weichai Power Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships and there was no potential conflict of interest.
Nomenclature
| Oil film thickness | |
| Average oil film pressure | |
| Average clearance | |
| Pressure flow coefficient | |
| Shear force coefficient | |
| Density of lubricant | |
| Sliding velocity of piston rings relative to the cylinder liner | |
| Overall roughness of the two contacting surfaces | |
| Comprehensive standard deviation of the roughness height of the cylinder liner | |
| Comprehensive standard deviation of the roughness height of the piston rings | |
| Contact factor | |
| Film thickness ratio | |
| Oil film pressure at the contact surface | |
| Gas pressure at the inlet of the piston rings | |
| Pressure at the oil film inlet and outlet at time t | |
| Pressure on the apparent contact surface | |
| Density of asperities | |
| Radius of curvature of rough peaks | |
| Equivalent modulus of elasticity | |
| Shear stress constant | |
| Boundary friction coefficient | |
| Friction force caused by asperity contacts | |
| Pressure caused by asperity contacts | |
| Friction coefficient of asperities | |
| Density of piston rings | |
| Specific heat capacity of piston rings | |
| Thermal conductivity of piston rings |
References
- Atulkar, A.; Pandey, R.K.; Subbarao, P.M.V. Role of textured piston rings/liners in improving the performance behaviors of IC engines: A review with vital findings. Surf. Topogr. Metrol. Prop. 2021, 9, 023002. [Google Scholar] [CrossRef]
- Delprete, C.; Razavykia, A. Piston ring-liner lubrication and tribological performance evaluation, A review. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2018, 232, 193–209. [Google Scholar] [CrossRef]
- Forero, J.D.; Ochoa, G.V.; Alvarado, W.P. Study of the piston Secondary movement on the tribological performance of a single Cylinder low-displacement diesel engine. Lubricants 2020, 8, 97. [Google Scholar] [CrossRef]
- Zimmer, M.; Vlădescu, S.C.; Mattsson, L.; Fowell, M.; Reddyhoff, T. Shear-area variation, A mechanism that reduces hydrodynamic friction in macro-textured piston ring liner contacts. Tribol. Int. 2021, 161, 107067. [Google Scholar] [CrossRef]
- Xiu, Y.L.; Jiao, B.; Lu, X.; Zou, D.; Ma, X.; Neville, A. A statistical piston ring lubrication model considering the tribofilm and its effect of two-stroke Marine engines. Tribol. Int. 2023, 177, 107996. [Google Scholar] [CrossRef]
- Zavos, A.; Nikolakopoulos, P.G. Modelling of transient flow of piston ring-liner contact using synthetic lubricants. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 2042–2056. [Google Scholar] [CrossRef]
- Zavos, A. Effect of Coating and Low Viscosity oils on Piston Ring Friction under Mixed Regime of Lubrication through Analytical Modelling. Lubricants 2021, 9, 124. [Google Scholar] [CrossRef]
- Jiao, B.; Li, T.; Ma, X.; Wang, C.; Xu, H.; Lu, X.; Liu, Z. Lubrication analysis of the piston ring of a two-stroke marine diesel engine considering thermal effects. Eng. Fail. Anal. 2021, 129, 105659. [Google Scholar] [CrossRef]
- Zhou, L.; Bai, M.L.; Sun, G.H. 3D heat transfer, lubrication and friction coupled study for piston ring-liner on diesel engines. J. Mech. Sci. Technol. 2019, 33, 939–953. [Google Scholar] [CrossRef]
- Mishra, P.C. Thermal Modeling of Thin Lubricant Film Within Piston Compression Ring and Rough Cyliner Conjuction. Front. Mech. Eng. 2020, 5, 68. [Google Scholar] [CrossRef]
- Zhou, L.; Sun, G.H.; Guo, Y.Y.; Bai, M.L. Effects of ring pack friction heat on temperature fields of piston set-liner. Int. J. Automot. Technol. 2020, 21, 1569–1578. [Google Scholar] [CrossRef]
- Takata, R.K. Effects of Lubricant Viscosity and Surface Texturing on Ring-Pack Performance in Internal Combustion Engines; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006. [Google Scholar]
- Guo, S.G.; Wang, B.; Chang, Q.Y. Transient Thermal Hydrodynamic Lubrication Analysis of Textured Piston Ring/Cylinder Liner. Solid State Phenom. 2018, 279, 172–178. [Google Scholar] [CrossRef]
- Gu, C.X.; Meng, X.H.; Zhang, D. Analysis of the coated and textured ring/liner conjunction based on a thermal mixed lubrication model. Frication 2018, 6, 420–431. [Google Scholar] [CrossRef]
- Liu, Z.; Ning, X.; Meng, X.; Liao, Q.; Wang, J. Starved lubrication analysis for the top ring and cylinder liner of a Two-stroke marine diesel engine considering the thermal effect of friction. Int. J. Engine Res. 2023, 24, 336–359. [Google Scholar] [CrossRef]
- Patio, N.; Cheng, H. Application of average flow model to lubrication between rough sliding surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar]
- Greenwood, J.A.; Tripp, J. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M. Theoretical and experimental investigation of traction coefficient in line-contact EHL of rough surfaces. Tribol. Int. 2014, 70, 179–189. [Google Scholar] [CrossRef]
- Morris, N.; Leighton, M.; De la Cruz, M.; Rahmani, R.; Rahnejat, H.; Howell-Smith, S. Combined numerical and experimental investigation of the micro-hydrodynamics of chevron-based textured patterns influencing junctional friction of sliding contacts. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 316–335. [Google Scholar] [CrossRef]
- Morris, N.; Rahmani, R.; Rahnejat, H.; King, P.D.; Howell-Smith, S. A numerical model to study the role of surface textures at top dead center Reverse in the pistol ring to cylinder liner contact. J. Tribol. 2016, 138, 021703. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).