Improved Two-Fluid Model for Segregated Flow and Integrated Multiphase Flow Modeling for Downhole Pressure Predictions
Abstract
:1. Introduction
2. Model Development
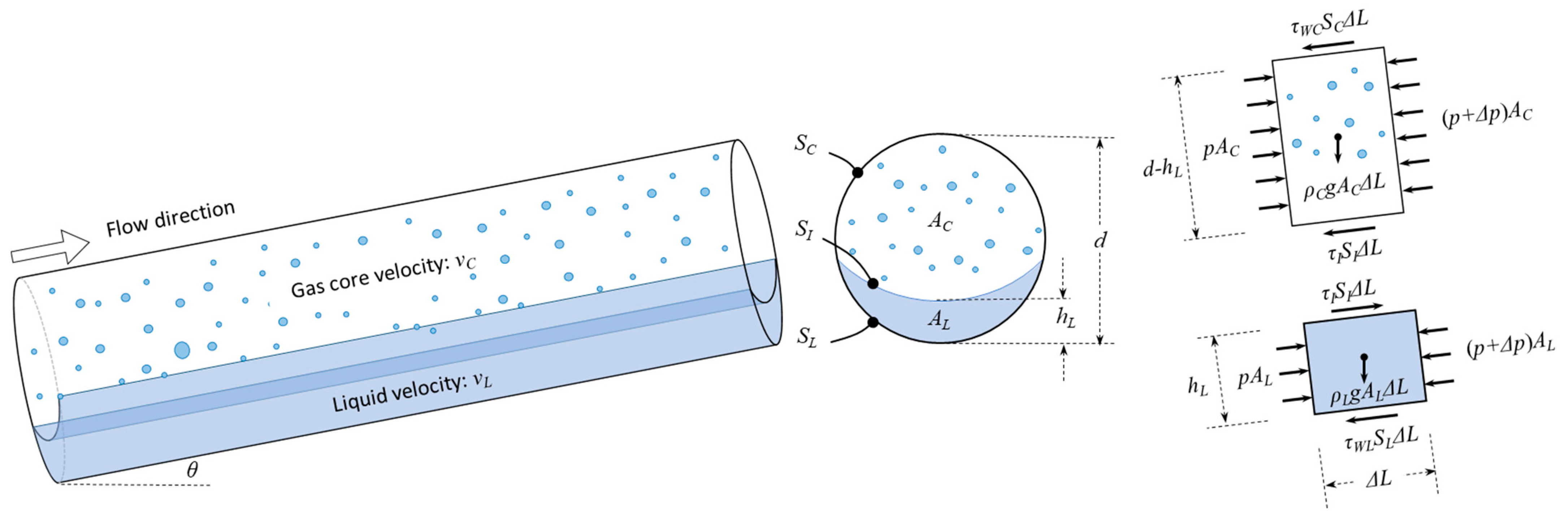
2.1. Improved Two-Fluid Model for Segregated Flow
2.1.1. Improved Correlation for Wetted Perimeters
2.1.2. Improved Model for Pressure Gradient Predictions
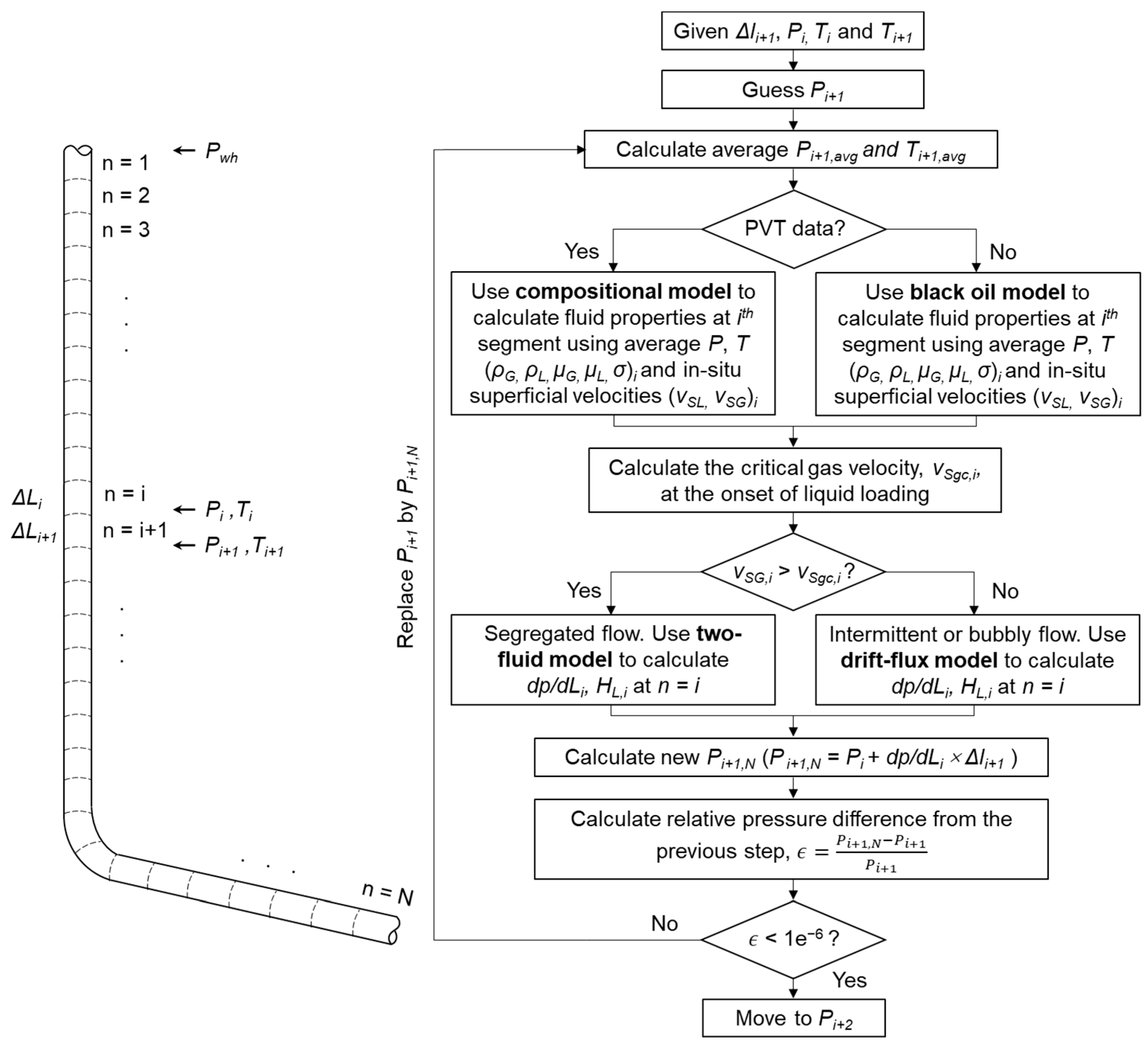
2.2. Integrated Model Development
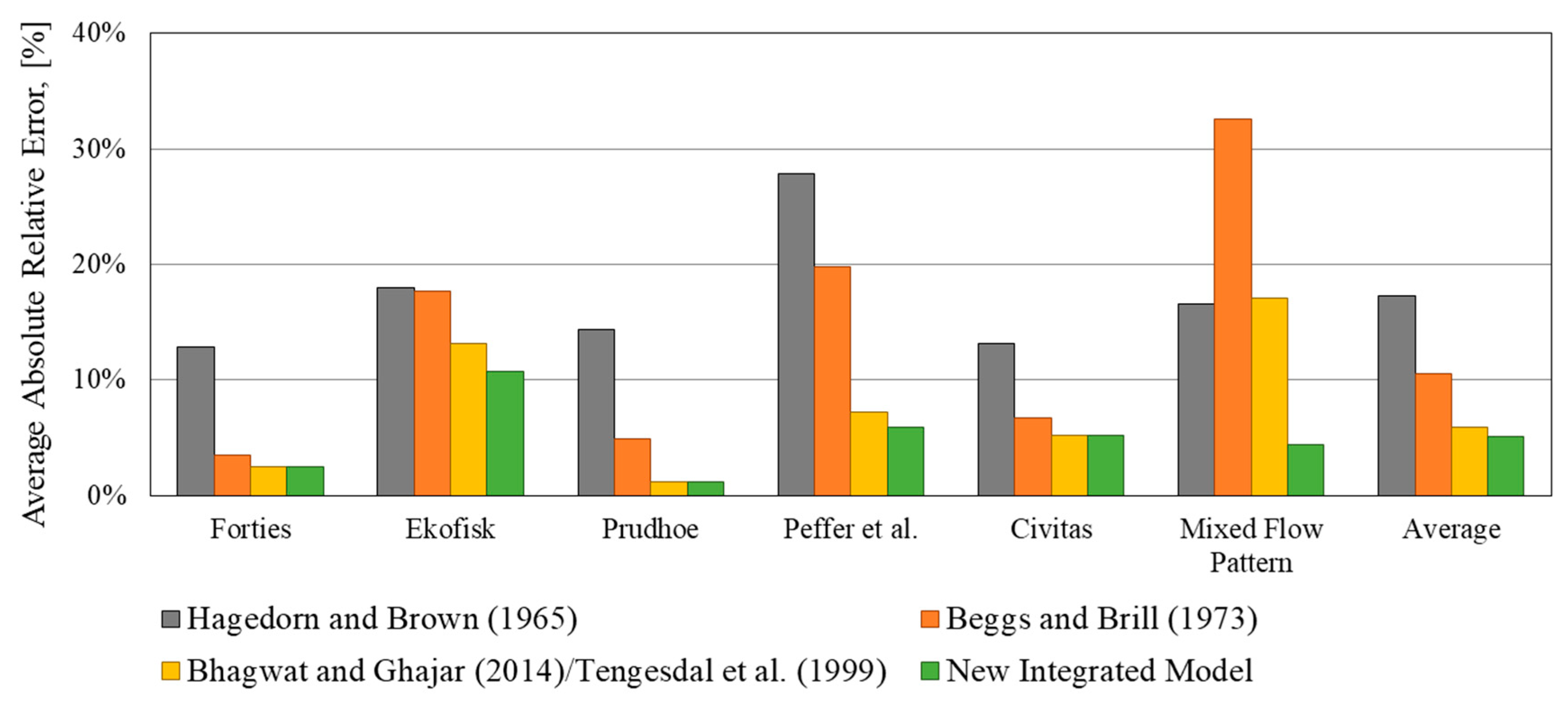
3. Model Evaluation
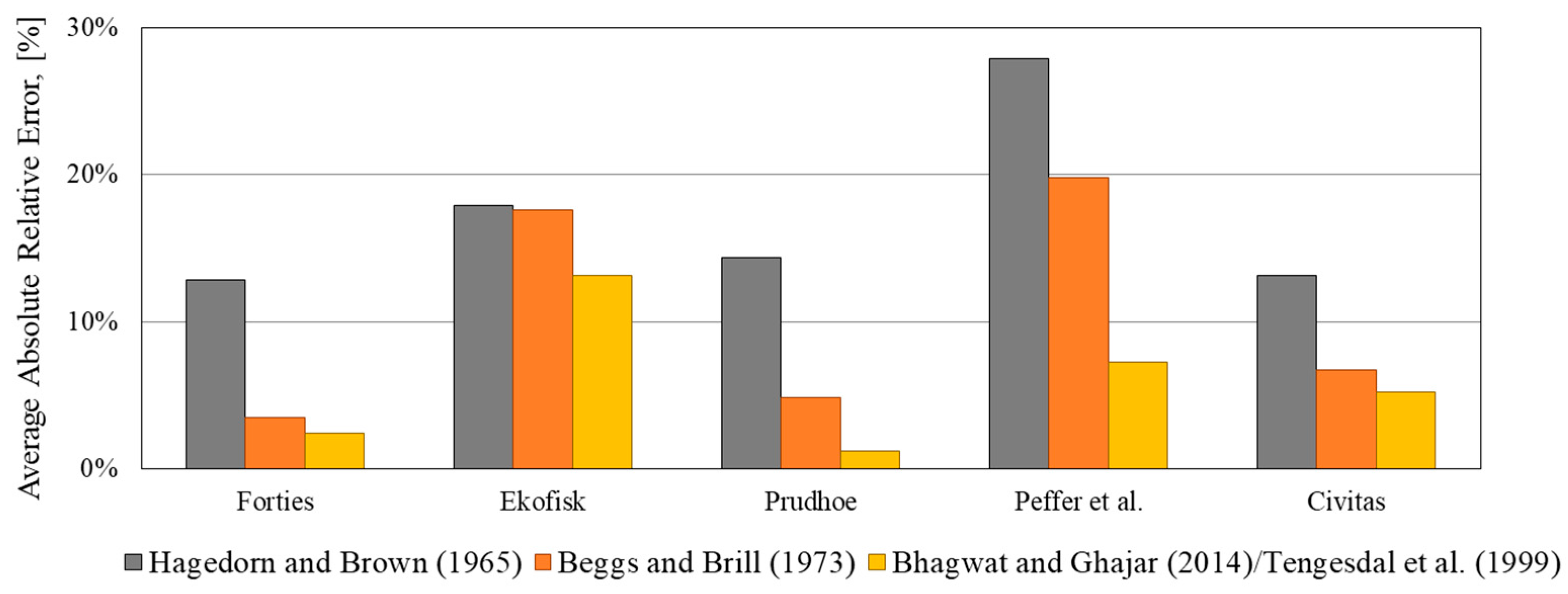
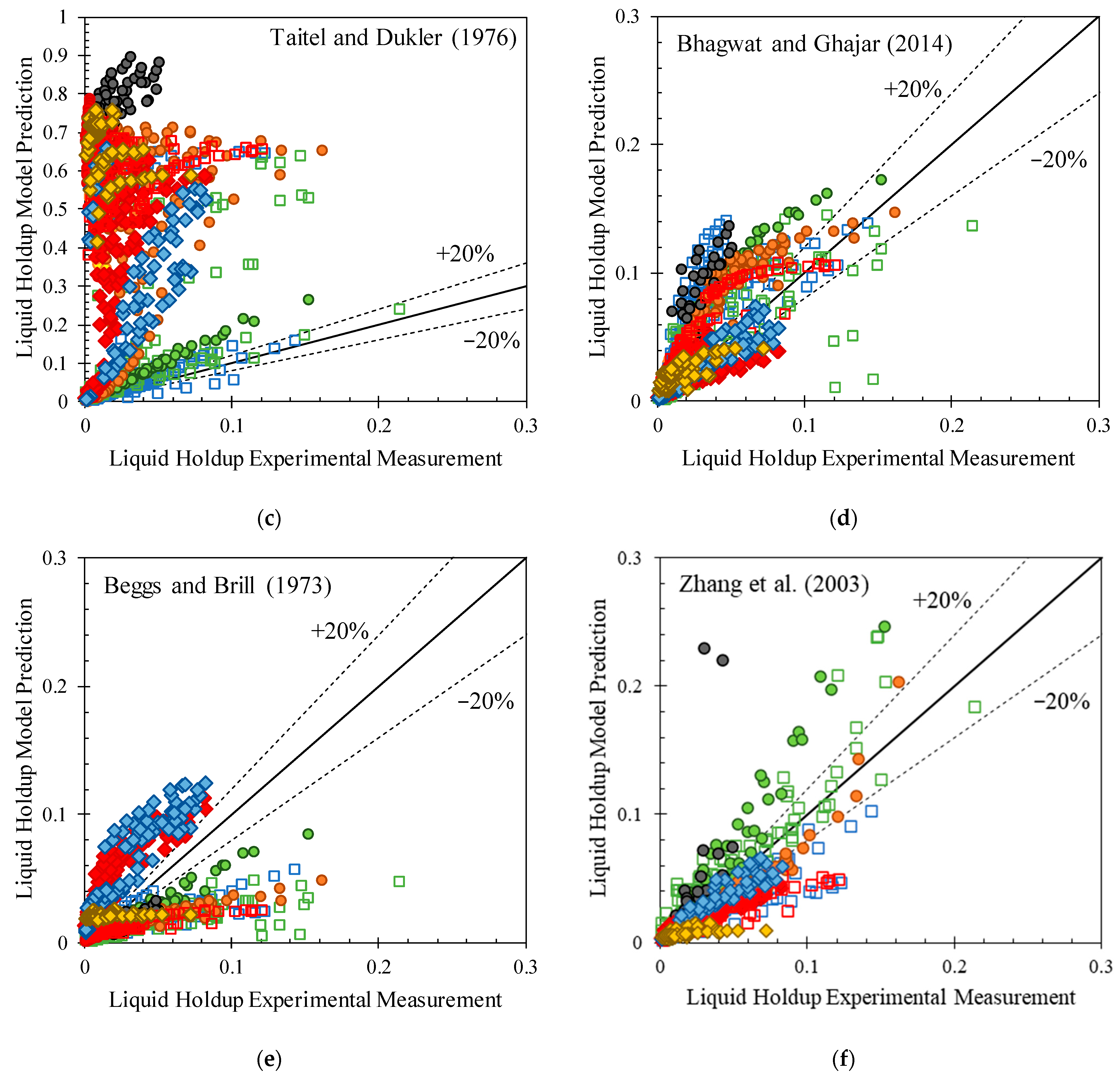
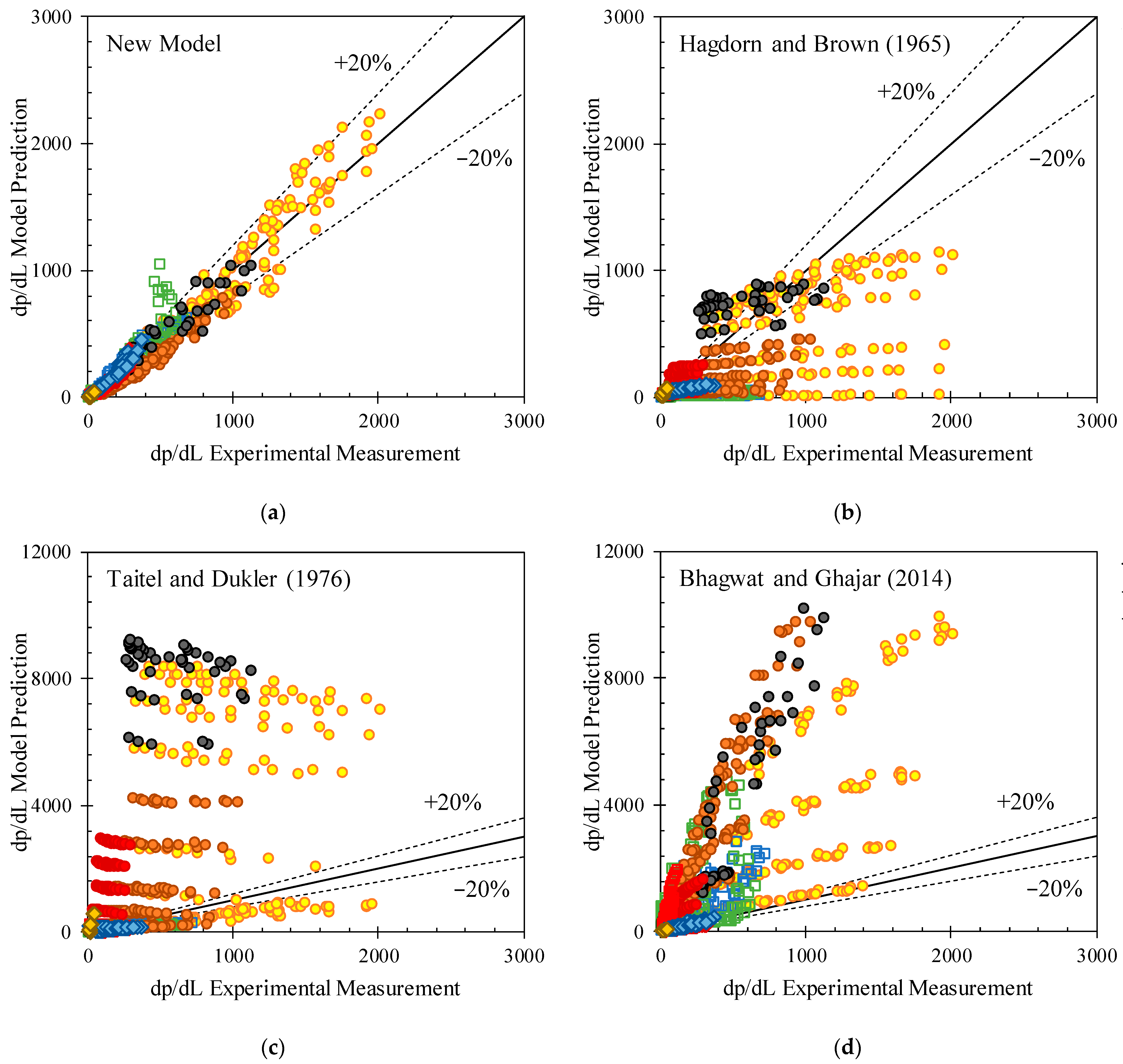
3.1. Two-Fluid Model Evaluation
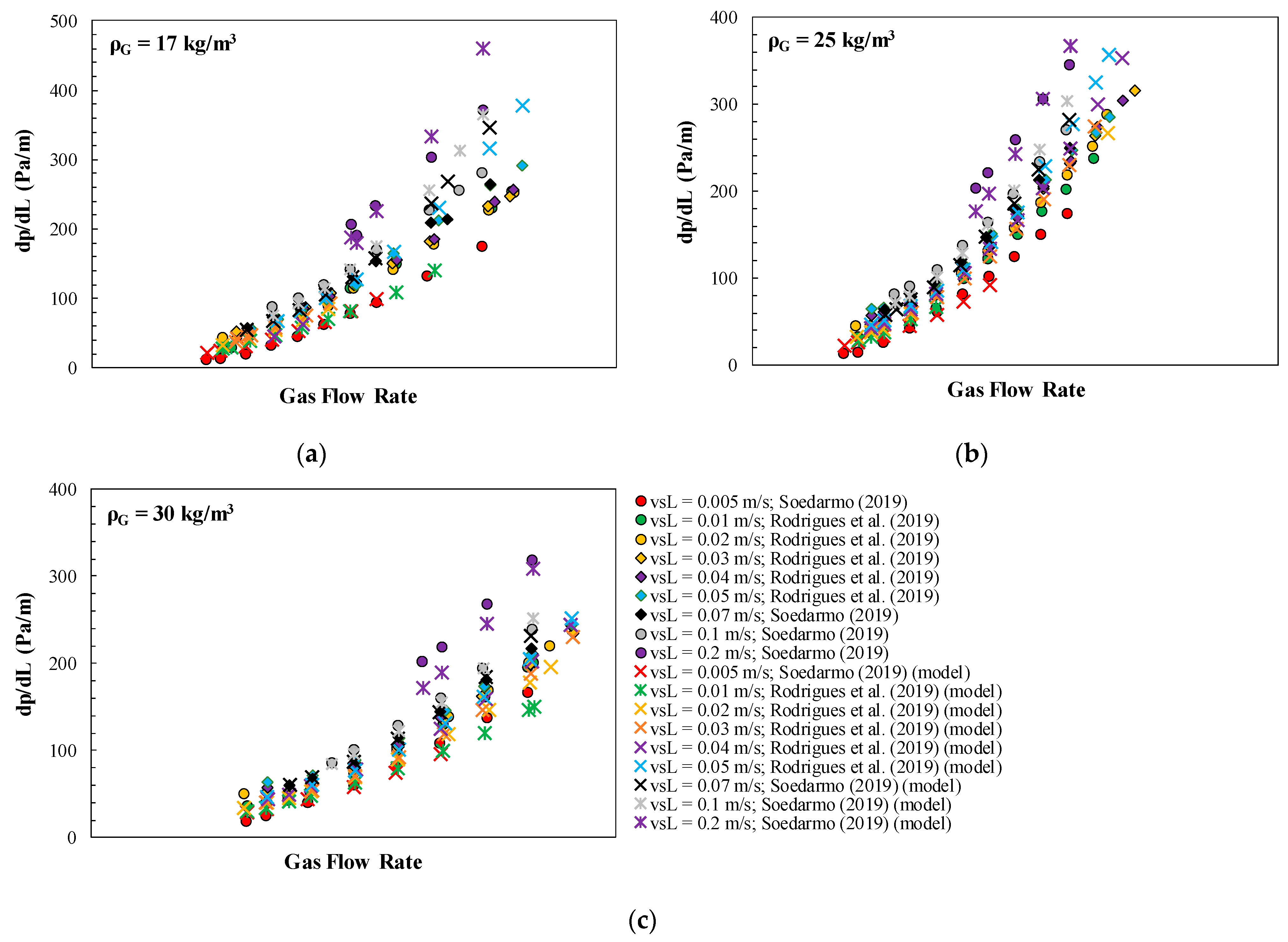
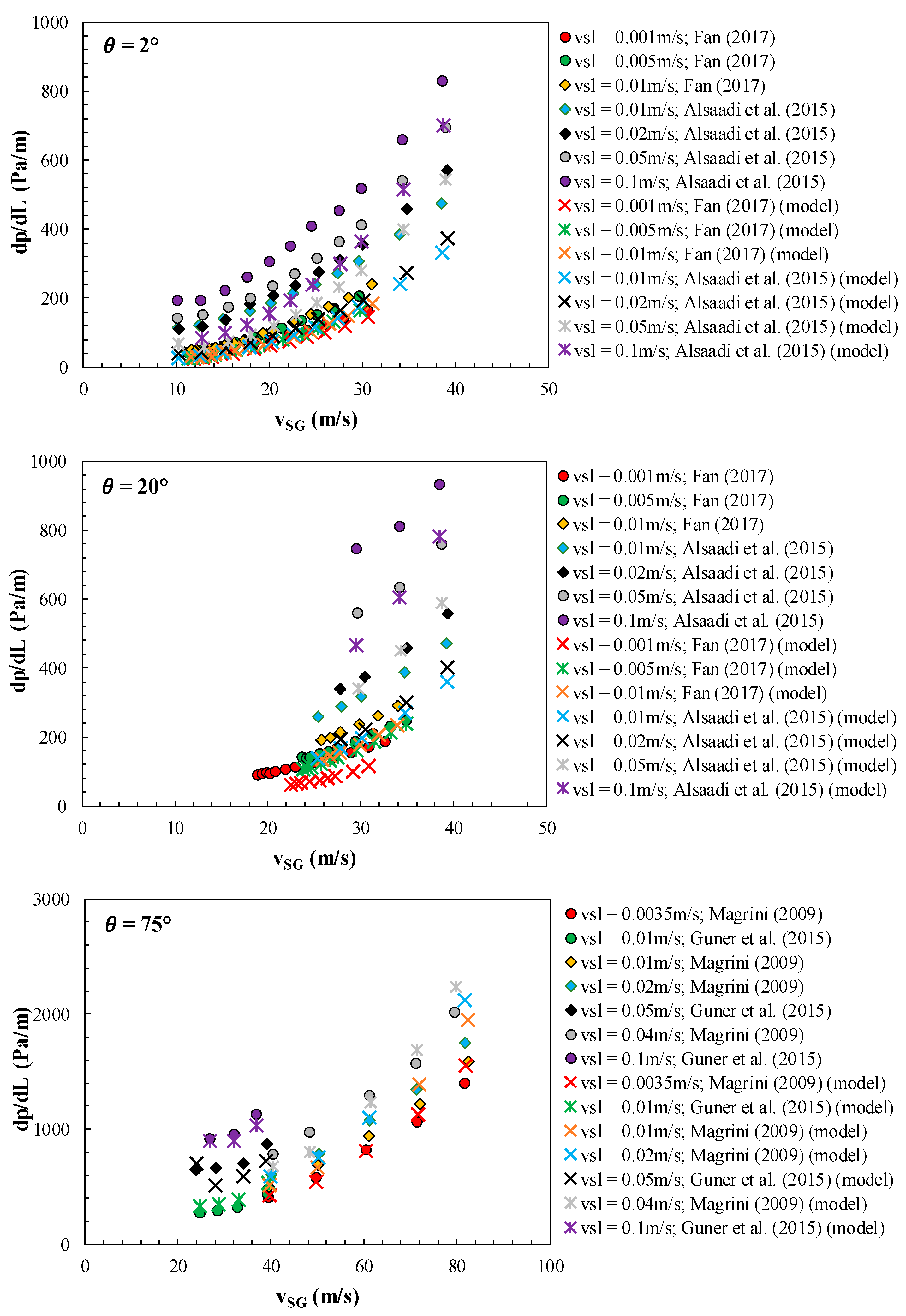
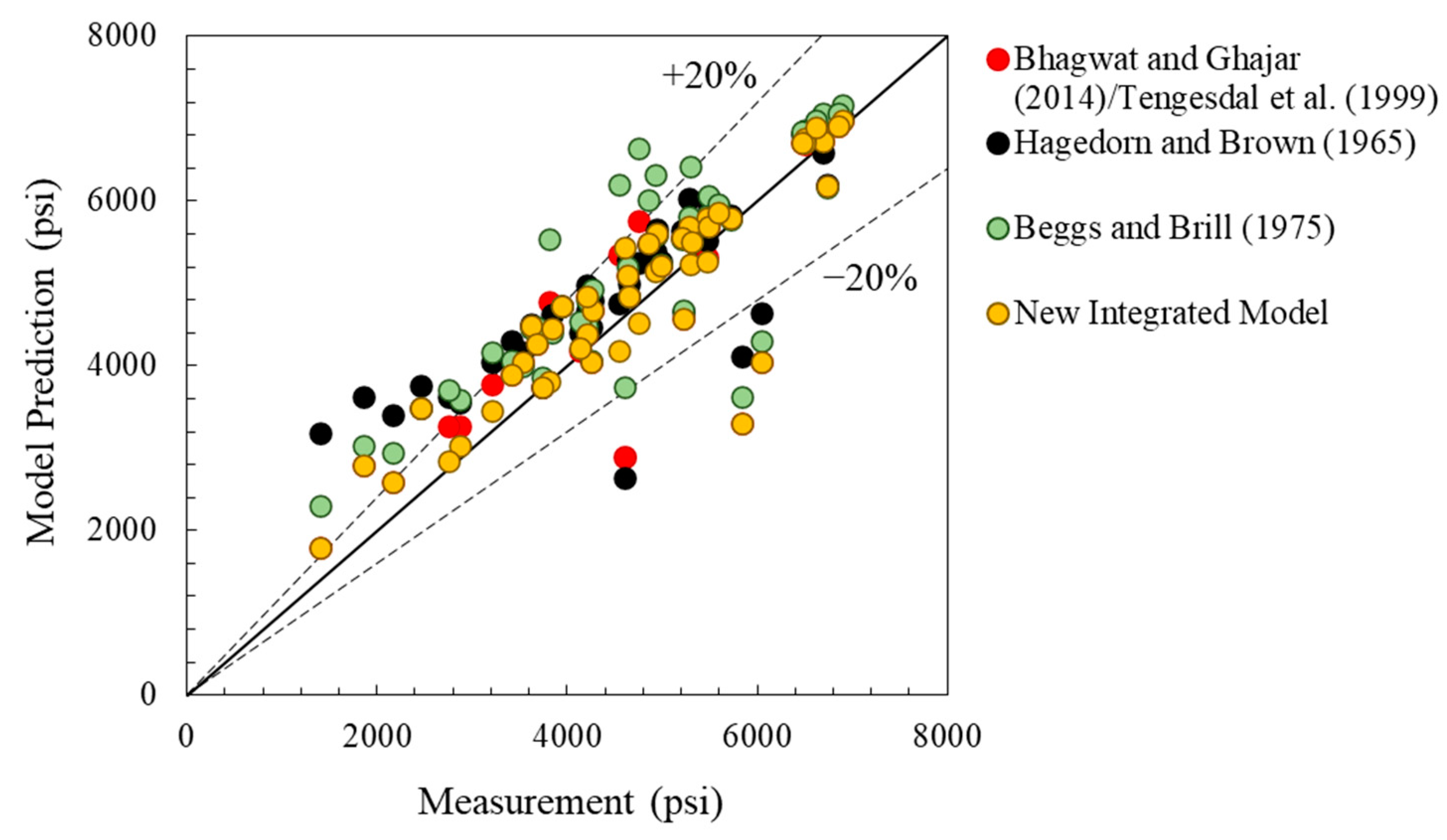
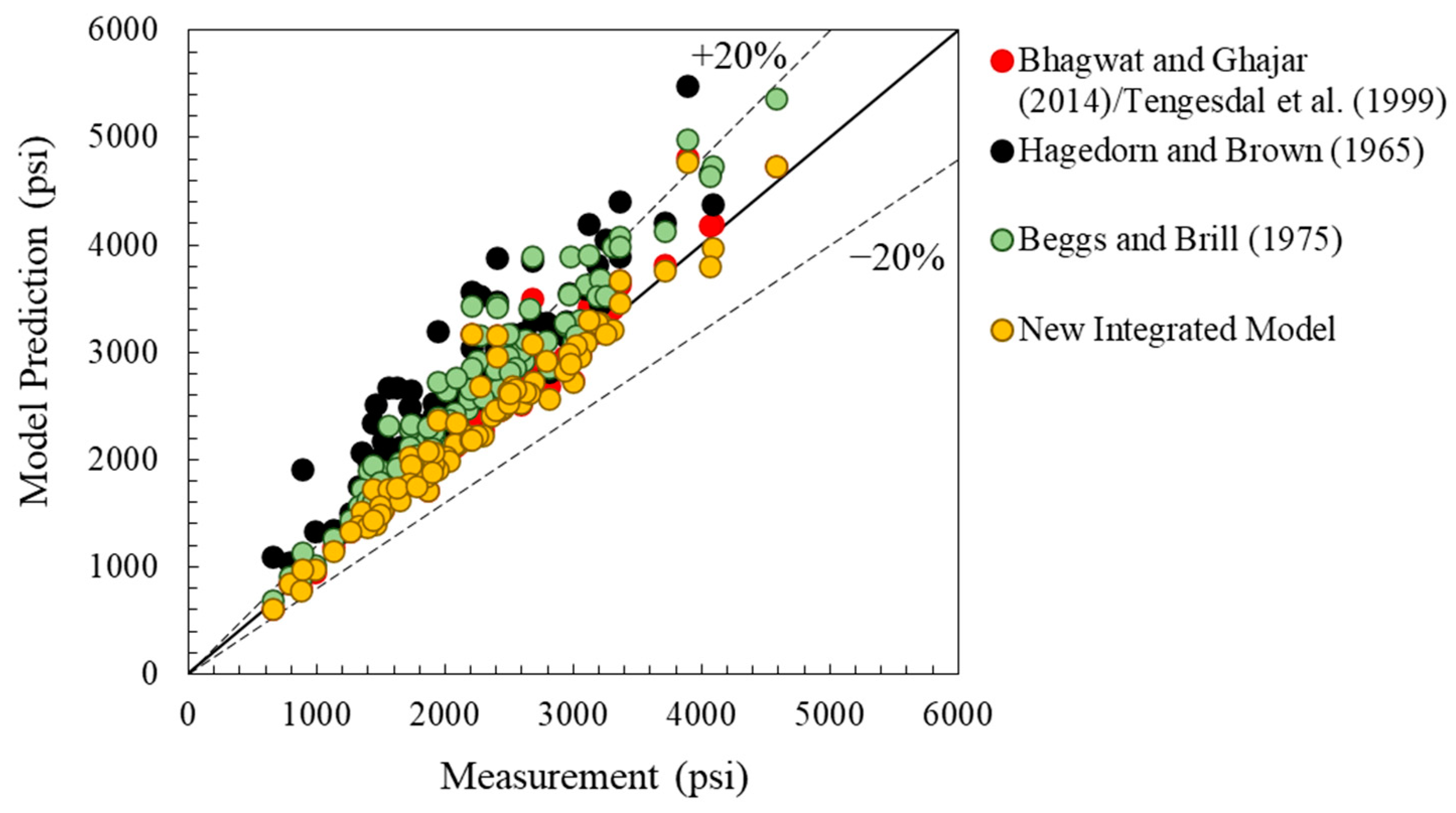
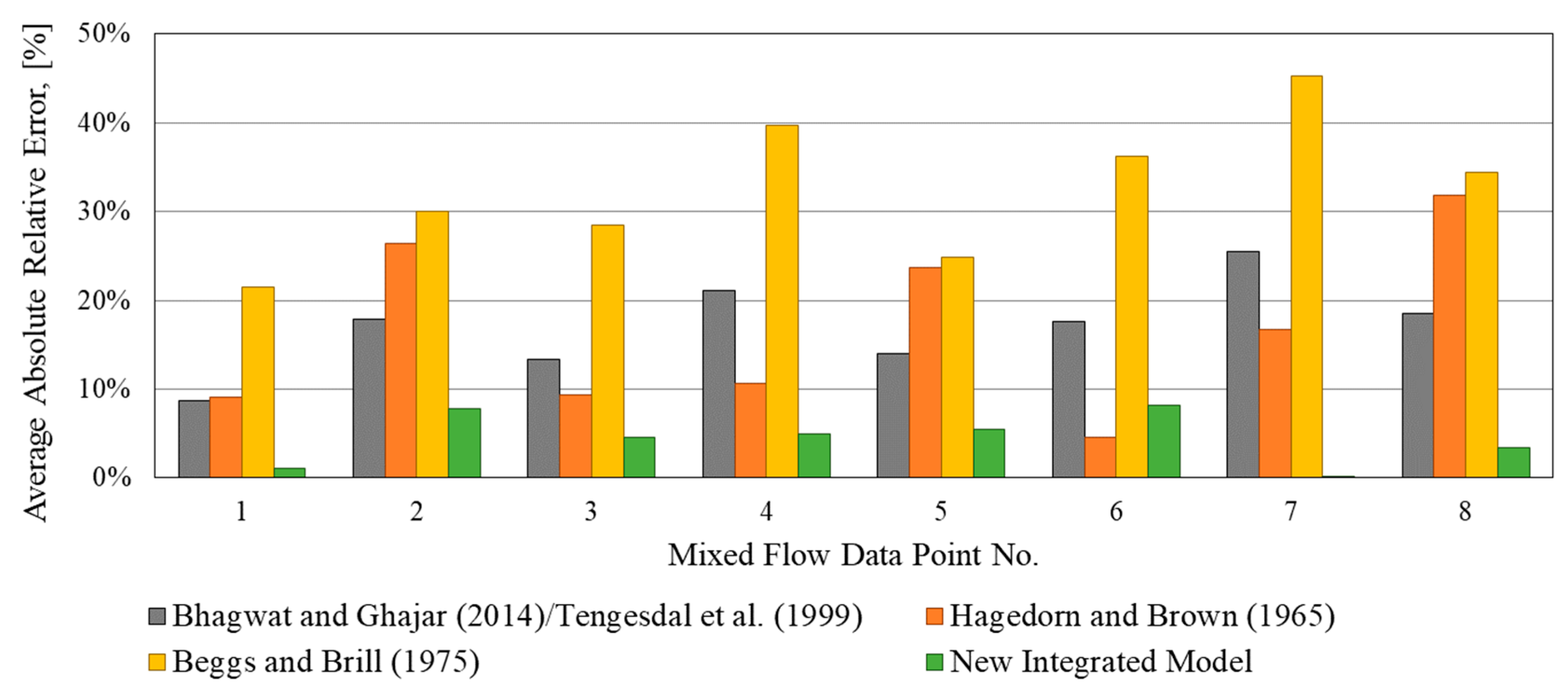
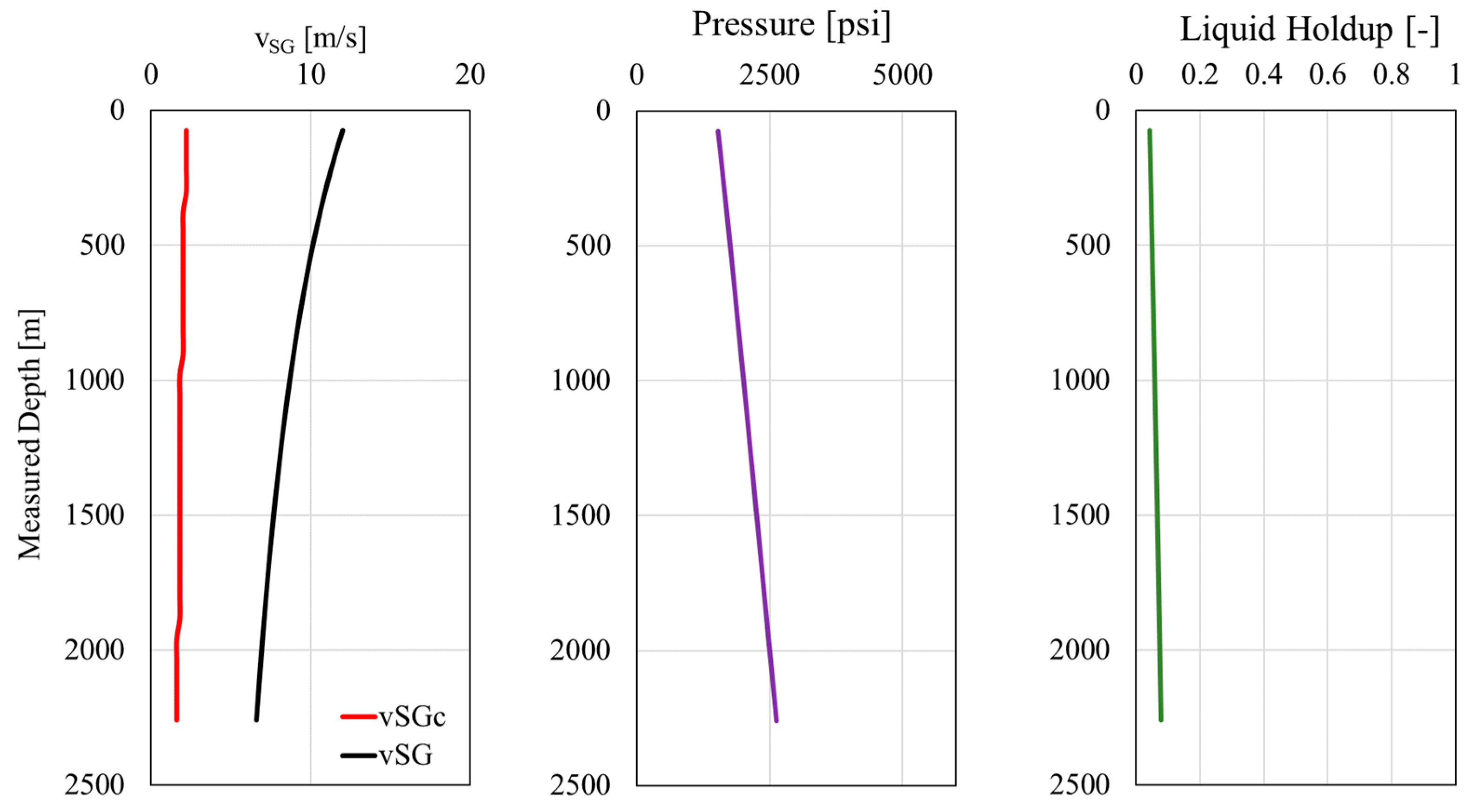
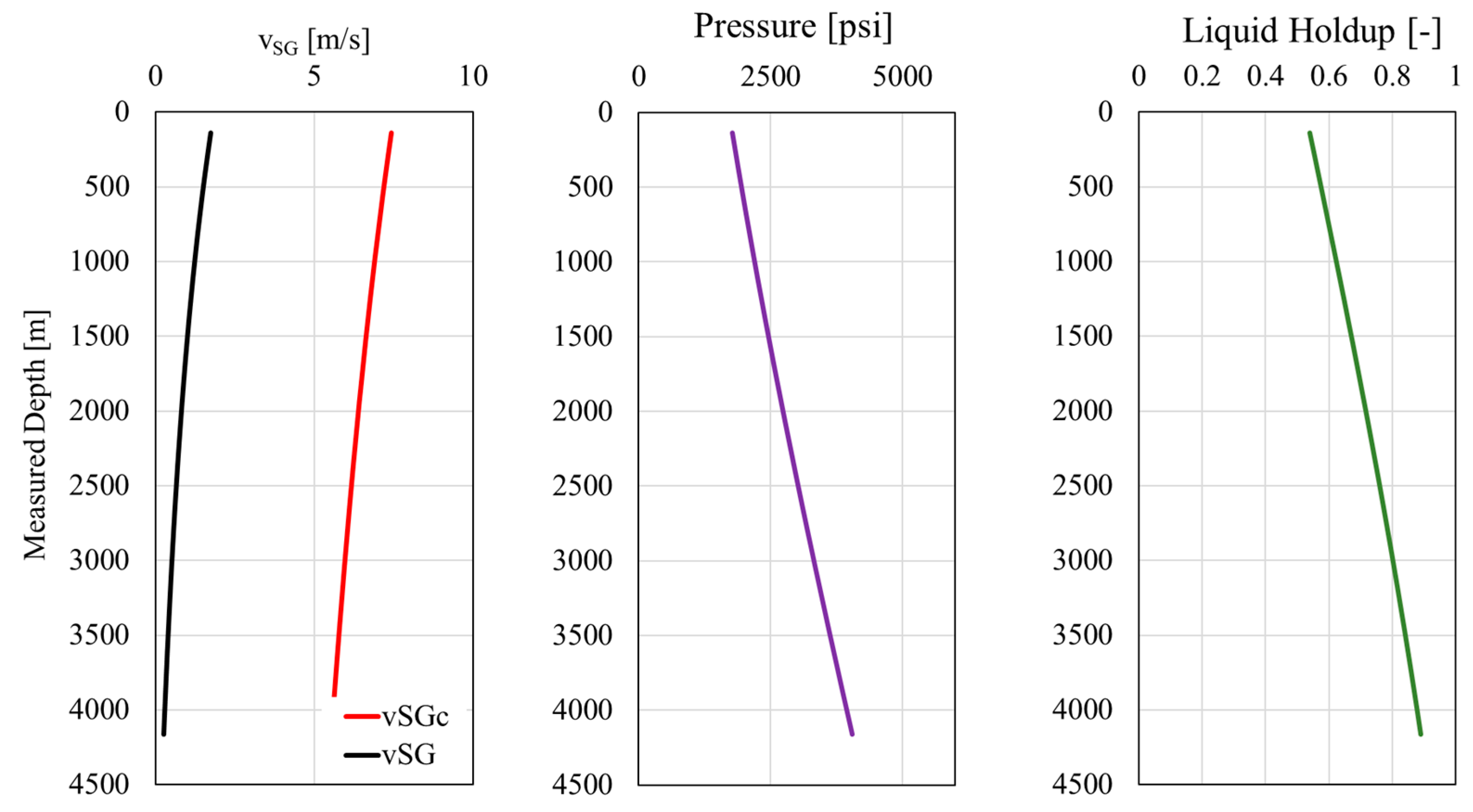
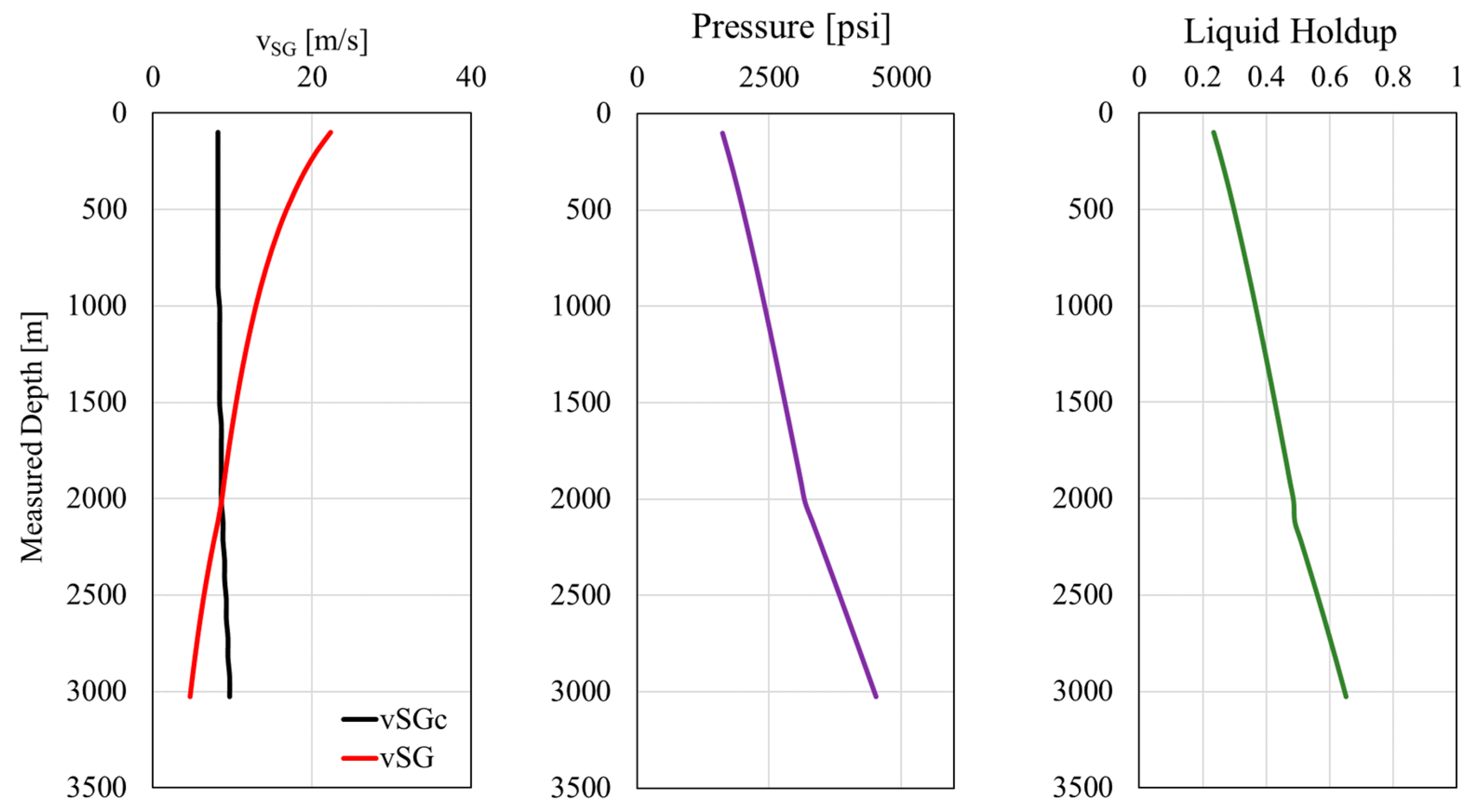
3.2. Integrated Model Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beggs, H.D. Production Optimization Using NODAL Analysis; Society of Petroleum Engineers: Richardson, TX, USA, 2003. [Google Scholar]
- Ishinbaev, N.A.; Krasnov, A.N.; Yu Prakhova, M.; Novikova, Y.V. Analysis of the Downhole Measurement System’s Pressure and Temperature Measuring Channel Calibration Errors. J. Phys. Conf. Ser. 2021, 2096, 012066. [Google Scholar] [CrossRef]
- Shoham, O. Mechanistic Modeling of Gas-Liquid Two-Phase Flow in Pipes; Society of Petroleum Engineers: Richardson, TX, USA, 2006. [Google Scholar]
- PIPESIM 2019—Steady-State Multiphase Flow Simulator. Available online: https://www.software.slb.com/-/media/software-media-items/software/documents/external/product-sheets/20-is-000057_pipesim_2019_technical_description.pdf (accessed on 1 November 2023).
- Taitel, Y.; Dukler, A.E. A model for predicting flow regime transitions in horizontal and near horizontal gas-liquid flow. AIChE J. 1976, 22, 47–55. [Google Scholar] [CrossRef]
- Zhang, H.-Q.; Wang, Q.; Sarica, C.; Brill, J.P. Unified Model for Gas-Liquid Pipe Flow via Slug Dynamics—Part 1: Model Development. J. Energy Res. Technol. 2003, 125, 266–273. [Google Scholar] [CrossRef]
- Xiao, J.J.; Shonham, O.; Brill, J.P. A Comprehensive Mechanistic Model for Two-Phase Flow in Pipelines. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 23–26 September 1990. SPE-20631-MS. [Google Scholar]
- Rastogi, A.; Fan, Y. Machine learning augmented two-fluid model for segregated flow. Fluids 2022, 7, 12. [Google Scholar] [CrossRef]
- Magrini, K.L. Liquid Entrainment in Annular Gas-liquid Flow in Inclined Pipes. Master’s Thesis, The University of Tulsa, Tulsa, OK, USA, 2009. [Google Scholar]
- Fan, Y. An Investigation of Low Liquid Loading Gas-Liquid Stratified Flow in Near-horizontal Pipes. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 2005. [Google Scholar]
- Meng, W. Low Liquid Loading Gas-Liquid Two-Phase Flow in Near-Horizontal Pipes. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 1999. [Google Scholar]
- Brill, J.P.; Chen, X.T.; Flores, J.G.; Marcano, R. Transportation of Liquids in Multiphase Pipelines under Low Liquid Loading Conditions; Final Report; The Pennsylvania State University: Pennsylvania, PA, USA, 1995. [Google Scholar]
- Alsaadi, Y.; Pereyra, E.; Torres, C.; Sarica, C. Liquid Loading of Highly Deviated Gas Wells from 60° to 88°. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015. [Google Scholar]
- Guner, M.; Pereyra, E.; Sarica, C.; Torres, C. An Experimental Study of Low Liquid Loading in Inclined Pipes from 90° to 45°. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, OK, USA, 1–5 March 2015. [Google Scholar] [CrossRef]
- Fan, Y. A Study of the Onset of Liquid Accumulation and Pseudo-slug Flow Characterization. Ph.D. Thesis, University of Tulsa, Tulsa, OK, USA, 2017. [Google Scholar]
- Rodrigues, H.T.; Pereyra, E.; Sarica, C. Pressure effects on low-liquid-loading oil/gas flow in slightly upward inclined pipes: Flow pattern, pressure gradient, and liquid holdup. SPE J. 2019, 24, 2221–2238. [Google Scholar] [CrossRef]
- Alsaadi, Y. Low Liquid Loading Two-Phase and Three-Phase Flows in Slightly Upward Inclined Pipes. Ph.D. Thesis, University of Tulsa, Tulsa, OK, USA, 2019. [Google Scholar]
- Soedarmo, A.A. Gas-Oil Flow in Upward-Inclined Pipes: Pseudo-Slug Flow Modeling and Upscaling Studies. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 2019. [Google Scholar]
- Langsholt, M.; Holm, H. Liquid Accumulation in Gas-Condensate Pipelines—An Experimental Study. In Proceedings of the 13th International Conference on Multiphase Production Technology, Edinburgh, UK, 13–15 June 2007. [Google Scholar]
- Zhang, H.-Q.; Sarica, C. A model for wetted-wall fraction and gravity center of liquid film in gas/liquid pipe flow. SPE J. 2011, 16, 692–697. [Google Scholar] [CrossRef]
- Fan, Y.; Pereyra, E.; Sarica, C.; Schleicher, E.; Hampel, U. Analysis of flow pattern transition from segregated to slug flow in upward inclined pipes. Int. J. Multiph. Flow 2019, 115, 19–39. [Google Scholar] [CrossRef]
- Rastogi, A.; Fan, Y. Experimental and modeling study of onset of liquid accumulation. J. Nat. Gas. Sci. Eng. 2020, 73, 103064. [Google Scholar] [CrossRef]
- Turner, R.G.; Hubbard, M.G.; Dukler, A.E. Analysis and prediction of minimum flow rate for the continuous removal of liquids from gas wells. J. Pet. Technol. 1969, 21, 1475–1482. [Google Scholar] [CrossRef]
- Coleman, S.B.; Clay, H.B.; McCurdy, D.G.; Norris, L.H. A new look at predicting gas-well load-up. J. Pet. Technol. 1991, 43, 329–333. [Google Scholar] [CrossRef]
- Li, M.; Lei, S.; Li, S. New View on Continuous-Removal Liquids from Gas Wells. SPE Prod. Fac. 2002, 17, 42–46. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Liu, Q.W. A New Method to Calculate the Minimum Critical Liquid Carrying Flow Rate for Gas Wells. Pet. Geol. Oilfield Dev. Daqing 2007, 6, 82–85. [Google Scholar]
- Barnea, D. Transition from annular flow and from dispersed bubble flow—Unified models for the whole range of pipe inclinations. Int. J. Multiph. Flow 1986, 12, 733–744. [Google Scholar] [CrossRef]
- Luo, S.; Kelkar, M.; Pereyra, E.; Sarica, C. A new comprehensive model for predicting liquid loading in gas wells. SPE Prod. Oper. 2014, 29, 337–349. [Google Scholar] [CrossRef]
- Biberg, D.; Hoyer, N.; Holm, H. Accounting for flow model uncertainties in gas-condensate field design using the OLGA High Definition Stratified Flow Model. In Proceedings of the 17th International Conference on Multiphase Production Technology, Cannes, France, 10–12 June 2015. BHR-2015-G5. [Google Scholar]
- Shekhar, S.; Kelkar, M.; Hearn, W.J.; Hain, L.L. Improved prediction of liquid loading in gas wells. SPE Prod. Oper. 2017, 32, 539–550. [Google Scholar] [CrossRef]
- Fan, Y.; Pereyra, E.; Sarica, C. Onset of liquid-film reversal in upward-inclined pipes. SPE J. 2018, 23, 1630–1647. [Google Scholar] [CrossRef]
- Bhagwat, S.M.; Ghajar, A.J. A flow pattern independent drift flux model based void fraction correlation for a wide range of gas–liquid two phase flow. Int. J. Multiph. Flow 2014, 59, 186–205. [Google Scholar] [CrossRef]
- Tengesdal, J.Ø.; Kaya, A.S.; Sarica, C. Flow-pattern transition and hydrodynamic modeling of churn flow. SPE J. 1999, 4, 342–348. [Google Scholar] [CrossRef]
- Hagedorn, A.R.; Brown, K.E. Experimental study of pressure gradients occurring during continuous two-phase flow in small-diameter vertical conduits. J. Pet. Technol. 1965, 17, 475–484. [Google Scholar] [CrossRef]
- Beggs, D.H.; Brill, J.P. A study of two-phase flow in inclined pipes. J. Pet. Technol. 1973, 25, 607–617. [Google Scholar] [CrossRef]
- Peffer, J.W.; Miller, M.A.; Hill, A.D. An improved method for calculating bottomhole pressures in flowing gas wells with liquid present. SPE Prod. Eng. 1988, 3, 643–655. [Google Scholar] [CrossRef]
- Asheim, H. MONA, an accurate two-phase well flow model based on phase slippage. SPE Prod. Eng. 1986, 1, 221–230. [Google Scholar] [CrossRef]
- Andritsos, N.; Hanratty, T.J. Interfacial instabilities for horizontal gas-liquid flows in pipelines. Int. J. Multiph. Flow 1987, 13, 583–603. [Google Scholar] [CrossRef]





| Dataset | d [m] | θ [°] | vSL [m/s] | vSG [m/s] | ρG [kg/m3] | ρL [kg/m3] | μL [Pa s] |
|---|---|---|---|---|---|---|---|
| Magrini (2009) [9] | 0.0762 | 0–90 | 0.0035–0.04 | 36–82 | 1.6 | 1000 | 0.001 |
| Fan (2005) [10] | 0.0508 | –2–2 | 0.0002–0.05 | 5–25 | 1.6 | 1000 | 0.001 |
| Meng (1999) [11] | 0.1496 | 0 | 0.001–0.055 | 5–28 | 1.8 | 886 | 0.0054 |
| Brill et al. (1995) [12] | 0.0508 | –2–2 | 0.004–0.046 | 4–13 | 1.13 | 815 | 0.0018 |
| Al-Saadi et al. (2015) [13] | 0.0508 | 2–30 | 0.01–0.1 | 10–40 | 1.6 | 1000 | 0.001 |
| Guner et al. (2015) [14] | 0.0762 | 45–90 | 0.01–0.1 | 12–40 | 1.6 | 1000 | 0.001 |
| Fan (2017) [15] | 0.0762 | 2–20 | 0.001–0.01 | 10–30 | 1.6 | 1000 | 0.001 |
| Rodrigues et al. (2019) [16] | 0.0762 | 2 | 0.01–0.05 | 4–16 | 17, 25, 30 | 760 | 0.0013 |
| Alsaadi (2019) [17] | 0.1524 | 2 | 0.005–0.05 | 15–30 | 1.23 | 760, 1000 | 0.001, 0.0016 |
| Soedarmo (2019) [18] | 0.1524 | 2 | 0.005–0.2 | 4–16 | 17, 25, 30 | 760 | 0.0018 |
| Langsholt and Holm (2007) [19] | 0.1524 | 0.5–5 | 0.001 | 1.8–4 | 22.6 | 812 | 0.0018 |
| Source | Well Name | Data Points | Properties Range | |
|---|---|---|---|---|
| Field Data | Civitas Resources | - | 104 | ; ID 2″–4″ ; ; GOR |
| Literature | Peffer et al. (1988) [36] | - | 93 | ; ID ; ; GOR ; |
| Forties | 37 | ; ID = ; ; GOR ; | ||
| Asheim (1986) [37] | Ekofisk | 50 | ; ID = ; ; GOR | |
| Prudhoe Bay | 29 | ; ID ; GOR | ||
| Dataset\Models | Average Absolute Relative Error | |||||
|---|---|---|---|---|---|---|
| Zhang et al. (2003) [6] | Bhagwhat and Ghajar (2014) [32] | Beggs and Brill (1973) [35] | Hagedorn and Brown (1965) [34] | Taitel and Dukler (1976) [5] | Improved Model | |
| Magrini (2009) [9] | 20.3% | 93.4% | 30.8% | 1635.2% | 76.6% | 25.6% |
| Fan (2005) [10] | 23.8% | 101.6% | 44.5% | 484.6% | 44.2% | 24.3% |
| Meng (1999) [11] | 72.6% | 63.5% | 63.0% | 727.9% | 221.6% | 73.1% |
| Brill et al. (1995) [12] | 40.3% | 98.9% | 39.2% | 149.6% | 93.9% | 38.8% |
| Al-Saadi et al. (2015) [3] | 34.3% | 94.3% | 53.5% | 244.3% | 267.3% | 34.4% |
| Guner et al. (2015) [14] | 393.0% | 173.1% | 39.9% | 344.4% | - | 44.5% |
| Fan (2017) [15] | 32.2% | 66.9% | 37.1% | 1348.2% | 162.7% | 33.1% |
| Rodrigues et al. (2019) [16] | 53.1% | 42.7% | 283.9% | 1013.9% | 653.4% | 53.1% |
| Alsaadi et al. (2019) [17] | 38.3% | 96.3% | 48.4% | 365.8% | 285.8% | 38.3% |
| Soedarmo (2019) [18] | 32.0% | 25.3% | 214.5% | 769.1% | 476.3% | 32.0% |
| Langsholt and Holm (2007) [19] | 48.6% | 123.7% | 198.0% | 834.3% | - | 48.6% |
| Total | 48.3% | 84.7% | 86.1% | 765.8% | 179.7% | 37.6% |
| Dataset\Models | Average Absolute Relative Error | |||||
|---|---|---|---|---|---|---|
| Zhang et al. (2003) [6] | Bhagwhat and Ghajar (2014) [32] | Beggs and Brill (1973) [35] | Hagedorn and Brown (1965) [34] | Taitel and Dukler (1976) [5] | Improved Model | |
| Magrini (2009) [9] | 256.6% | 252.4% | 40.5% | 49.7% | 43.1% | 12.9% |
| Fan (2005) [10] | 56.2% | 401.1% | 78.9% | 105.6% | 31.1% | 15.4% |
| Meng (1999) [11] | 83.1% | 883.3% | 67.0% | 112.3% | 45.3% | 33.0% |
| Brill et al. (1995) [12] | 50.2% | 1087.3% | 21.9% | 95.6% | 62.4% | 64.1% |
| Al-Saadi et al. (2015) [3] | 31.9% | 724.6% | 10.8% | 67.8% | 57.5% | 41.3% |
| Guner et al. (2015) [14] | 384.0% | 635.8% | 16.6% | 64.3% | - | 13.8% |
| Fan (2017) [15] | 14.6% | 415.3% | 44.0% | 47.6% | 31.1% | 25.6% |
| Rodrigues et al. (2019) [16] | 56.3% | 19.5% | 10.1% | 50.7% | 38.1% | 12.2% |
| Alsaadi et al. (2019) [17] | 16.7% | 1050.4% | 51.3% | 48.9% | 33.5% | 28.2% |
| Soedarmo (2019) [18] | 86.0% | 26.1% | 27.7% | 57.2% | 30.1% | 13.3% |
| Langsholt and Holm (2007) [19] | 9.9% | 39.3% | 27.1% | 33.5% | - | 7.1% |
| Total | 83.8% | 483.9% | 40.3% | 69.1% | 40.1% | 24.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkhezzi, A.; Fan, Y. Improved Two-Fluid Model for Segregated Flow and Integrated Multiphase Flow Modeling for Downhole Pressure Predictions. Energies 2023, 16, 7923. https://doi.org/10.3390/en16247923
Alkhezzi A, Fan Y. Improved Two-Fluid Model for Segregated Flow and Integrated Multiphase Flow Modeling for Downhole Pressure Predictions. Energies. 2023; 16(24):7923. https://doi.org/10.3390/en16247923
Chicago/Turabian StyleAlkhezzi, Abdullah, and Yilin Fan. 2023. "Improved Two-Fluid Model for Segregated Flow and Integrated Multiphase Flow Modeling for Downhole Pressure Predictions" Energies 16, no. 24: 7923. https://doi.org/10.3390/en16247923
APA StyleAlkhezzi, A., & Fan, Y. (2023). Improved Two-Fluid Model for Segregated Flow and Integrated Multiphase Flow Modeling for Downhole Pressure Predictions. Energies, 16(24), 7923. https://doi.org/10.3390/en16247923