Stick–Slip Vibration Characteristics Study of the Drill String Based on PID Controller

Abstract

In order to address the issue of drill string stick–slip vibration, which leads to drill bit wear and reduces the drilling velocity, we conducted a study on the characteristics of stick–slip vibration using a proportional-integral-derivative (PID) controller. By applying the principles of rigid body mechanics, we established a two-degree-of-freedom torsional dynamics equation and derived the first-order differential dynamics equation for the drill string. Subsequently, we designed a PID controller and obtained an equation for the control of stick–slip vibration. The research findings indicate that variations in the difference between the static and dynamic friction coefficients directly impact the nature of the limit cycles in the phase plane. As this difference decreases, the limit cycle narrows and the stick–slip vibrations weaken progressively. When the static and dynamic friction coefficients are equalized, no stick–slip vibrations occur within the drill string. The implementation of PID control effectively manages stick–slip vibrations in the drill string, with greater efficiency observed in controlling the turntable velocity compared to the drill bit velocity. This research provides valuable insights for the development of control strategies aimed at mitigating stick–slip vibrations in drilling engineering applications, thereby facilitating the efficient and safe extraction of oil and gas resources.

1. Introduction

With sustainable economic development, conventional oil and gas resources are gradually becoming unable to meet the energy demand, which is leading to an intensified divide between supply and demand. Oil and gas exploration and development trends show a transition from shallow to deep and land to ocean, with the exploitation of unconventional oil and gas resources beginning late in the development period [1,2]. However, the development conditions of new oil and gas resources, such as the formation pressure, rock drill ability, geological environment, and other factors, are complex and diverse, bringing more challenges for drilling engineering [3,4]. Especially challenging is the drilling process of deep or ultra-deep wells, because, as the well depth increases, the geological formations alternate between soft and hard, while the hardness of the rock is greater and the size of the wellbore gradually decreases, which results in the low transmission efficiency of the weight on bit (WOB) and torque, and the drill string system becomes prone to stick–slip vibration [5,6,7]. When stick–slip vibration occurs, the drill bit is prone to viscous slippage, which generates stress and strain fluctuations that accelerate the wear and failure of the drill bit and affect the drilling velocity. It also easily causes surface equipment failure and underground safety accidents, which are not conducive to efficient and safe production [8,9]. Therefore, a generation mechanism study of the stick–slip vibration of the drill string system has an important role in formulating a stick–slip vibration suppression strategy to reduce the wear failure of the drill bit and improve the drilling efficiency.

For the stick–slip vibration of the drill string system, Wang Ruihe et al. assumed the system as a single-degree-of-freedom torsional pendulum model and used a nonlinear mathematical model to describe the stick–slip phenomenon. They calculated the torsional response frequency of the drill string and discussed the parameters of the stick–slip vibration [10]. In order to reduce the stick–slip phenomenon, Tian Jialin proposed an innovative coupling tool based on longitudinal torsion and studied the dynamics model of a BHA connected by the tool based on Lagrange theory [11]. DeJun Ba verified the stick–slip vibration of oil drilling through simulation and semi-physical experiments [12]. Yevhen Kovalyshen used a mathematical method to couple axial and torsional vibration and analyzed the influence factors of stick–slip vibration during deep well drilling [13]. Lin Yao-Qun assumed that the rotation velocity of the turntable was constant and the friction was considered as a function expression of the rotation velocity. A simplified torsional pendulum model of the bottom hole assembly (BHA) established that the stick–slip vibration could be reduced by changing the static friction [14]. Steven Paul Barton et al. studied the vibration of the drill string with or without a drilling oscillator and showed that the drilling oscillator could be used to reduce the stick–slip vibration and the friction of the drill string, which could increase the drilling velocity [15]. The study of the stick–slip vibration of the drill string provides a theoretical basis for stick–slip vibration control, which has a promotional effect in terms of optimizing drilling engineering. However, the effective control of drill string stick-slip vibration still needs further study, and a controller can be used to control the drilling parameters so as to reduce or eliminate the stick-slip vibration of the drill string.

In order to mitigate or eliminate the stick-slip vibration of the drill string, J. D. Jansen established a torsion pendulum model and suggested that the ground drive should be an active damping control system, which could eliminate the stick-slip vibration of the drill bit. The results were identified through the experimental data [16]. Abdelbaset Laib proposed an optimal mixed interval type 2 fuzzy PID + I logic controller (OH-IT2FPID + I) for a multi-degree-of-freedom drill string system using a practical group optimization algorithm [17]. Eva M. Navarro-López et al. simplified the drill string system into an equivalent mass, and, based on the synovial motion characteristics and balance characteristics, linear state feedback control was used to analyze the bifurcation and transition phases of the drill string system, and then the parameter design of the controller was completed [18]. James D.J. MacLean utilized improved integrated resonance control (MIRC) tracking to achieve the required drilling speed. The low-dimensional two-degree-of-freedom drill string model incorporated the drill bit’s interaction with the rock in open-loop control and clearly showed that there was an unnecessary stick–slip response [17]. B. Besselink et al. proposed a stick–slip control system; the effect of velocity reduction on WOB was analyzed and the formation of stick–slip torsional vibration was explained by using the singular perturbation and average method [19,20]. With the combination of a mathematical model, a stick–slip vibration controller for the drill string can be established, which can control the drilling parameters to reduce or control the stick–slip vibration and eliminate its adverse effects. However, the vibration characteristics of the drill string system by the controller need further discussion.

In order to investigate a control strategy for stick–slip vibration, an analysis of the drill string characteristics is conducted based on PID control. By applying rigid body mechanics principles, the two-degree-of-freedom torsional dynamic equation of the drill string is established and its first-order differential equation is derived. The stick–slip response process of the drill string is analyzed, and a PID controller is employed to regulate the input torque. Following the selection principle for integral and differential coefficients, the PID control equation for stick–slip vibration is determined. Furthermore, an analysis of the stick–slip vibration characteristics of the drill bit is performed. These results provide a valuable reference for the alleviation of stick–slip vibration in drilling operations and provide guidance for the efficient production of oil and gas.

2. Drill String Coupled Dynamic Models

The stick–slip vibration of the drill string is studied. Due to the complex movement of the drill string in the drilling process of a hard formation, the drill string is simplified and the following assumptions are made. The turntable and BHA are regarded as an equivalent mass and the drill string mass is superimposed onto the BHA. The effect of the drilling fluid on the drill string system is equivalent to viscous damping. The axial vibration of the drill bit is ignored. The frictional effect of the drill bit and rock or drill string and wellbore wall is comprehensively addressed, in which the friction torque is considered as a nonlinear function of the rotation velocity.

The stick–slip vibration model of the drill string is established as shown in Figure 1, where $J_r$ and $J_b$ represent the equivalent rotational inertia of the turntable and the BHA, respectively. ${\theta }_r$ and ${\theta }_b$ are the rotational angular displacement of the turntable and the BHA, respectively. $k$ is the equivalent torsional stiffness, $c$ is the equivalent damping coefficient, and $T_m$, $T_{ar}$, $T_{ab}$, $T_{fb}$ are the input torque, the fluid viscous torque of the turntable, the viscous damping torque of the drill bit, and the friction torque of the drill bit, respectively. $c_r$ is the viscous damping coefficient of the drilling fluid at the turntable. $c_b$ is the viscous damping coefficient of the drilling fluid at the BHA. $W_{ob}$ is the WOB that is suffered by the bit.

Based on rigid body mechanics, the torsional dynamic equation of the drill string is established as

$$\left\{\begin{array}{l}{J}_r{\ddot{\theta }}_r+c({\dot{\theta }}_r-{\dot{\theta }}_b)+k({\theta }_r-{\theta }_b)+c_r{\dot{\theta }}_r=T_m\\ J_b{\ddot{\theta }}_b+c({\dot{\theta }}_b-{\dot{\theta }}_r)+k({\theta }_b-{\theta }_r)+c_b{\dot{\theta }}_b=-T_{fb}(x)-T_{ab}\end{array}\right.$$

(1)

The input torque and the viscous damping torque of the bit are expressed as follows.

$$\left\{\begin{array}{l}{T}_m=Jr\ddot{\theta }r+T_t+T_{ar}\hfill \\ T_{ab}=c_b{\omega }_b\hfill \end{array}\right.$$

(2)

in which $T_t$ is the coupling torque between the turntable and the BHA.

The expression of the friction torque of the drill bit is defined as

$$T_{fb}=\left\{\begin{array}{l}c({\dot{\theta }}_r-{\dot{\theta }}_b)+k({\theta }_r-{\theta }_b)-c_b{\omega }_b, {\omega }_b<D_v \mathrm{and} \left|T_{eb}\right|<T_{sb}\\ {\mu }_{sb}{W}_{ob}{R}_b\mathrm{sgn}(c({\dot{\theta }}_r-{\dot{\theta }}_b)+k({\theta }_r-{\theta }_b)-c_b{\omega }_b), {\omega }_b<D_v \mathrm{and} \left|T_{eb}\right|\ge T_{sb}\\ R_b{W}_{ob}\left[{\mu }_{cb}+({\mu }_{sb}-{\mu }_{cb})e^{-\gamma |{\omega }_b|/v_f}\right]\mathrm{sgn}({\omega }_b), {\omega }_b\ge D_v\end{array}\right.$$

(3)

in which $D_v$ is the defined boundary layer thickness, ${\omega }_b$ is the angular velocity of the BHA, ${\mu }_{sb}$ is the static friction coefficient, ${\mu }_{cb}$ is the Coulomb friction coefficient, $v_f$ is the constant in the Karnopp friction model [21], $R_b$ is the radius of the drill bit, and $T_{eb}$ is the driving torque of the drill bit.

The rotational inertia of the BHA is composed of the rotational inertia of the drill bit, drill collar, and drill pipe, which can be written as

$$\left\{\begin{array}{l}{J}_{bit}=J_{tool}+\rho \frac{L_p}{3}\frac{\pi }{32}(D_p{}^4-d_p)\\ J_c=\rho \frac{\pi L_c}{32}(D_c{}^4-d_c)\\ J_p=\rho \frac{\pi L_p}{32}(D_p{}^4-d_p)\end{array}\right.$$

(4)

where $J_{bit}$ represents the total moment inertia of the drill bit side, $J_{tool}$ is the moment inertia of the drill bit, and $J_c$ and $J_p$ are the moment inertia of the drill collar and the drill rod, respectively. $D_p$ and $d_p$ are the inner and outer diameters of the drill pipe, respectively; $L_p$ and $L_c$ are the length of the drill pipe and drill collar, respectively. $D_c$ and $d_c$ are the inner and outer diameters of the drill collar, respectively.

Then, the rotational inertia of the BHA can be obtained.

$$J_b=J_{tool}+\frac{\pi }{32}[\frac{4L_p}{3}(D_p{}^4-d_p{}^4)+L_c(D_c{}^4-d_c{}^4)]$$

(5)

In Equation (1), the calculation expressions of the equivalent viscosity coefficient and the equivalent rigidity coefficient of the drill pipe are as follows.

$$\left\{\begin{array}{l}k=\frac{G}{L_p}\frac{\pi }{32}\left(D_p{}^4-d_p{}^4\right)\\ c=c_l\frac{L_p}{3}\end{array}\right.$$

(6)

in which $G$ is the shear modulus and $c_l$ is the damping coefficient of the per unit length of the drill pipe.

The vibration frequency of the turntable and the BHA can be expressed as

$$\left\{\begin{array}{l}{\Omega }_r=\frac{1}{2\pi }\sqrt{\frac{k}{J_r}}\\ {\Omega }_b=\frac{1}{2\pi }\sqrt{\frac{k}{J_b}}\\ {\Omega }_0=\sqrt{{\Omega }_r^2+{\Omega }_b^2}=\frac{1}{2\pi }\left(\sqrt{\frac{k}{J_r}+\frac{k}{J_b}}\right)\end{array}\right.$$

(7)

where ${\Omega }_r$, ${\Omega }_b$, and ${\Omega }_o$ are the natural vibration frequency of the turntable, BHA, and drill string, respectively.

To facilitate the solution, the dynamic equation of the drill string is simplified as

$$\left\{\begin{array}{l}\frac{d^2{\theta }_r}{d{t}^2}=-\frac{c}{J_r}\left(\frac{d{\theta }_r}{dt}-\frac{d{\theta }_b}{dt}\right)-\frac{k}{J_r}\left({\theta }_r-{\theta }_b\right)-\frac{c_r}{J_r}\frac{d{\theta }_r}{dt}+\frac{1}{J_r}{T}_m\\ \frac{d^2{\theta }_b}{d{t}^2}=-\frac{c}{J_b}\left(\frac{d{\theta }_b}{dt}-\frac{d{\theta }_r}{dt}\right)-\frac{k}{J_b}\left({\theta }_b-{\theta }_r\right)-\frac{c_b}{J_b}\frac{d{\theta }_b}{dt}-\frac{1}{J_b}{T}_{fb}\end{array}\right.$$

(8)

We assume that the system state vector can be written as

$$x={\left({\theta }_r,\frac{d{\theta }_r}{dt},{\theta }_b,\frac{d{\theta }_b}{dt}\right)}^T=(x_1,x_2,x_3,x_4)$$

(9)

Then, the dynamic equations of the drill string can be expressed by a first-order differential equation.

$$\left\{\begin{array}{l}{\dot{x}}_1=\frac{d{\theta }_r}{dt}\hfill \\ {\dot{x}}_2=-\frac{c}{J_r}\left(x_2-x_4\right)-\frac{k}{J_r}\left(x_1-x_3\right)-\frac{c_r}{J_r}{x}_2+\frac{1}{J_r}{T}_m\hfill \\ {\dot{x}}_3=\frac{d{\theta }_b}{dt}\hfill \\ {\dot{x}}_4=-\frac{c}{J_b}\left(x_4-x_2\right)-\frac{k}{J_b}\left(x_3-x_1\right)-\frac{c_b}{J_b}{x}_4-\frac{1}{J_b}{T}_{fb}(x)\hfill \end{array}\right.$$

(10)

The stick–slip response process of the drill string is analyzed, and the time-history response of the angular displacement and angular velocity of the turntable are determined by

$$\left\{\begin{array}{l}{\theta }_r(t)=x_1(t)\\ {\dot{\theta }}_r(t)={\omega }_r=x_2(t)\end{array}\right.$$

(11)

The time-history response of the angular displacement and angular velocity of the drill bit can be expressed by the following equation:

$$\left\{\begin{array}{l}{\theta }_b(t)=x_3(t)\\ {\dot{\theta }}_b(t)={\omega }_b=x_4(t)\end{array}\right.$$

(12)

Thus, the time-history response expression of the angular acceleration of the drill bit can be obtained.

$${\ddot{\theta }}_b(t)=-\frac{c}{J_b}[x_4(t)-x_2(t)]-\frac{k}{J_b}[x_3(t)-x_1(t)]-\frac{c_b}{J_b}{x}_4(t)-\frac{T_{fb}}{J_b}$$

(13)

The time-history response of the angular displacement and angular velocity of the drill bit relative to the turntable is as follows:

$$\left\{\begin{array}{l}{\theta }_{br}(t)={\theta }_b-{\theta }_r=x_3(t)-x_1(t)\\ {\dot{\theta }}_{br}(t)={\omega }_b-{\omega }_r=x_4(t)-x_2(t)\end{array}\right.$$

(14)

The driving torque of the drill bit is expressed as

$$c[x_2(t)-x_4(t)]+k[x_1(t)-x_3(t)]-c_b{x}_4(t)=T_{eb}$$

(15)

The expression of the friction torque of the drill bit is written as

$$T_{fb}=\left\{\begin{array}{l}c[x_2(t)-x_4(t)]+k[x_1(t)-x_3(t)]-c_b{x}_4(t),\hspace{0.17em} x_4(t)<D_v \mathrm{and} \left|T_{eb}\right|<T_{sb}\\ {\mu }_{sb}{W}_{ob}{R}_b\mathrm{sgn}(c[x_2(t)-x_4(t)]+k[x_1(t)-x_3(t)]-c_b{x}_4(t)), x_4(t)<D_v \mathrm{and} \left|T_{eb}\right|\ge T_{sb}\\ R_b{W}_{ob}\left[{\mu }_{cb}+({\mu }_{sb}-{\mu }_{cb})e^{-\gamma |{\omega }_b|/v_f}\right]\mathrm{sgn}(x_4(t)), x_4(t)\ge D_v\end{array}\right.$$

(16)

Assuming that the drill bit is separated from the bottom of the hole, there is no friction torque when the drill bit rotates and T_fb= 0; thus, Equation (8) is written as

$$\left\{\begin{array}{l}\frac{d^2{\theta }_r}{d{t}^2}=-\frac{c}{J_r}\left(\frac{d{\theta }_r}{dt}-\frac{d{\theta }_b}{dt}\right)-\frac{k}{J_r}\left({\theta }_r-{\theta }_b\right)-\frac{c_r}{J_r}\frac{d{\theta }_r}{dt}+\frac{1}{J_r}{T}_m\\ \frac{d^2{\theta }_b}{d{t}^2}=-\frac{c}{J_b}\left(\frac{d{\theta }_b}{dt}-\frac{d{\theta }_r}{dt}\right)-\frac{k}{J_b}\left({\theta }_b-{\theta }_r\right)-\frac{c_b}{J_b}\frac{d{\theta }_b}{dt}\end{array}\right.$$

(17)

The value is set as 0.5 when the static friction coefficient is equal to the dynamic friction coefficient, and the expression of the friction torque of the drill bit is obtained.

$$T_{fb}=\left\{\begin{array}{l}c[x_2(t)-x_4(t)]+k[x_1(t)-x_3(t)]-c_b{x}_4(t),\hspace{0.17em} x_4(t)<D_v \mathrm{and} \left|T_{eb}\right|<T_{sb}\\ {\mu }_{sb}{W}_{ob}{R}_b\mathrm{sgn}(c[x_2(t)-x_4(t)]+k[x_1(t)-x_3(t)]-c_b{x}_4(t)), x_4(t)<D_v \mathrm{and} \left|T_{eb}\right|\ge T_{sb}\\ R_b{W}_{ob}{\mu }_{cb}\mathrm{sgn}(x_4(t)), \hspace{0.17em}{\omega }_b\ge D_v\end{array}\right.$$

(18)

3. Case Studies and Results Analyses

The numerical calculation of the established mathematical model is completed when the input torque of the turntable is set as 10 kN, and examples of the calculation parameters are shown in

Table 1. Example parameters.

Name of Parameter	Value
Static WOB, Wob (N)	97,347
Radius of drill bit, Rb (m)	0.155
Moment of inertia of turntable, Jr (kg × m2)	2122
Rotary inertia of BHA Jb (kg × m2)	581
Equivalent stiffness coefficient of drill string, k (N·m/rad)	654
Equivalent damping coefficient of drill string, c (N·ms/rad)	23..2
Coefficient of viscous damping of turntable, cr (N·ms/rad)	325
Static friction coefficient, μsb	0.8
Dynamic friction coefficient, μcb	0.5
Boundary layer coefficient, Dv	10−6

.

Figure 2 shows the results of the angular displacement of the rotating platform and the drill, with an initial condition of zero, where a, b, and c represent, respectively, the response, sliding, and viscosity phases. The angular displacement of the rotary table increases continuously and almost linearly under the action of the input moment. The angular displacement of the bit starts at 0 and increases continuously for about 5 s. This is the response phase of the drill column. The input torque is transmitted downwards, and, when the drive torque in the bit position is sufficient to exceed the maximum static friction torque, the bit begins to spin. The angular displacement of the bit increases continuously, and its angular displacement increases faster than the rotary table, marking the sliding phase. When the angular displacement of the bit remains constant, it enters the viscous phase. After this, the bit continues to repeat the sliding phase—it becomes sticky. The cycle is the total duration of the glue phase and the slip phase, approximately 6 s. Therefore, the vibration frequency of slip stick is approximately 0.167 hz. The self-vibrating frequency on the bit side is about 0.169 hz. The glue slip vibrations are essentially consistent with the results of the self-vibrating frequency. This means that the accuracy of the numerical results is guaranteed.

For the time−history response of the angular acceleration of the drill bit, the calculation result is shown in Figure 3. The maximum positive angular acceleration is 13.7 rad/s² and the maximum negative angular acceleration is 20.8 rad/s². According to the calculation result, the drill bit first accelerates and rotates and then decelerates to zero, and the drill bit accelerates again to rotate after a period of time, reflecting a periodic motion law.

The angular displacement and angular velocity of the rotary table with the bit without a moment of friction are shown in Figure 4. When there is no moment of friction in the drill, the angular displacement of the drill increases uniformly and essentially coincides with the angular displacement of the rotary table. In the initial phase, the angular speed of the rotary table and drill has increased steadily. When the speed increases to its maximum value, the rotation speed of the rotary table stabilizes around 27.5 rad/s and the bit speed fluctuates in the range of 27 to 28 rad/s. As shown in Figure 4, the bit always rotates with the rotary table. Compared to the rotating platform, the drill has no angular displacements in the front or back. Because the angular velocity of the drill is not 0, there is no slip in the position of the drill. Therefore, the presence of a moment of friction in the drill is a necessary prerequisite for the drilling column to produce viscous vibrations.

The static friction coefficient is adjusted to 0.5, while keeping other parameters unchanged. Figure 5 presents the results of the angular velocity and angular displacement when the static and dynamic friction coefficients are equal. Within the time interval of 0~4 s, the drill bit exhibits zero angular displacement, followed by a steady increase in angular displacement without any occurrence of the stick–slip phenomenon. Once stabilized, the relative angular displacement between the drill bit and turntable remains constant. The turntable’s angular velocity gradually increases from zero until reaching stability, whereas the drill bit’s angular velocity starts increasing after 4 s with subsequent significant fluctuations observed. These findings indicate that when there is no disparity between the static and dynamic friction coefficients, stick–slip vibration does not occur in the drill string system.

In order to obtain the influence of the friction coefficient, the input angular velocity of the turntable is set to a certain value of 5 rad/s. The values of the static and the dynamic friction coefficients are changed and the numerical combinations of different static and dynamic friction coefficients are shown in

Table 2. Different combinations of static and dynamic friction coefficients.

	Combination 1	Combination 2	Combination 3	Combination 4	Combination 5
μsb	0.8	0.7	0.6	0.7	0.6
μcb	0.5	0.4	0.3	0.5	0.5

.

For different combinations of friction coefficients, the maximum static friction torque and dynamic friction torque of the drill bit can be determined by T_sb = μ_sbR_bW_ob and T_cb = μ_cbR_bW_ob. The specific values are shown in

Table 3. Different combinations of maximum static and dynamic friction torque.

	Combination 1	Combination 2	Combination 3	Combination 4	Combination 5
Tsb	12,071 N·m	10,562 N·m	9053 N·m	10,562 N·m	9053 N·m
Tcb	7544 N·m	6036 N·m	4527 N·m	7544 N·m	7544 N·m

.

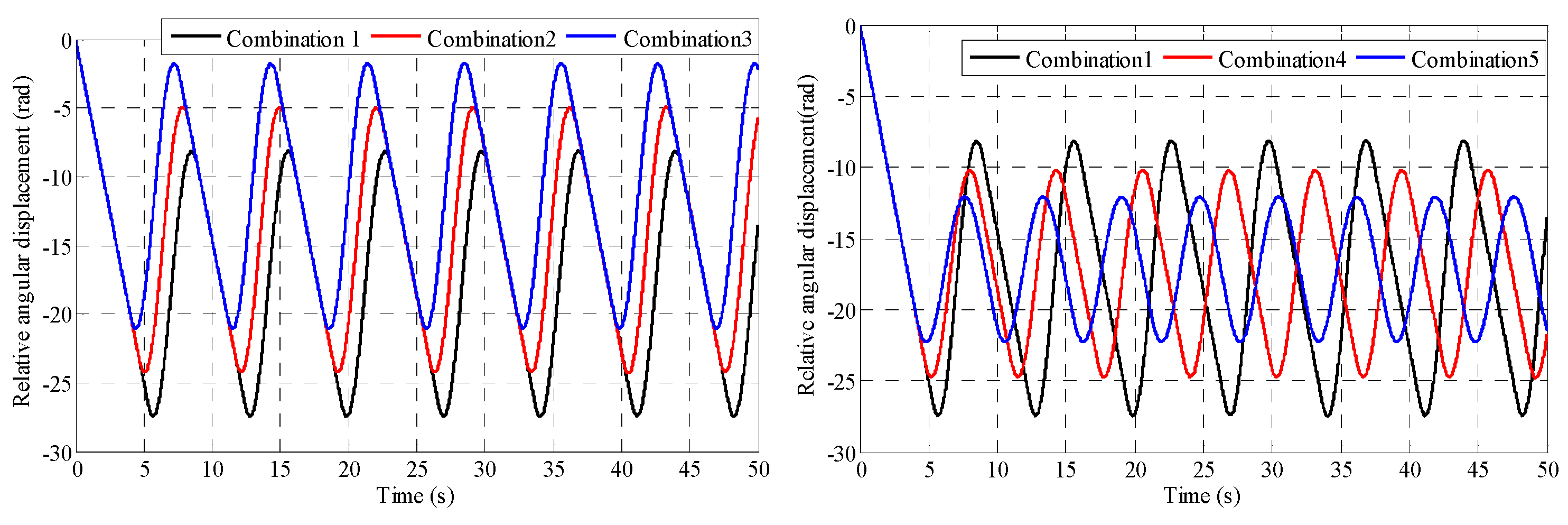
Figure 6 illustrates the results of the relative angular displacement for different combinations of the static and dynamic friction coefficients. As both coefficients decrease simultaneously, there is a reduction in the maximum static friction torque exerted on the drill bit. Consequently, under smaller friction coefficients, earlier rotation initiation occurs for the drill bit at an equivalent turntable velocity, along with the reduced magnitude of its corresponding angular displacement, implying the earlier onset of the stick–slip vibration phenomenon as well. However, regardless of the combination applied, the fluctuation amplitude remains consistent for each case examined herein. It can be concluded that distinct combinations of static and dynamic friction coefficients contribute to varying degrees of stick–slip vibration within the drill bit system; specifically, combination 1 exhibits the highest response amplitude, followed by combination 4 and then combination 5, regarding the duration.

Figure 7 illustrates the relative angular velocity of the drill bit under different combinations of the static and dynamic friction coefficients. When the difference between the static and dynamic friction coefficients remains constant, the shape and pattern of the curves for the three combinations are mostly identical. However, when the difference varies, the stick–slip vibration and the corresponding viscous and slippage phases exhibit periodic characteristics. As the static friction coefficient decreases, the amplitude of the angular velocity fluctuation of the drill bit also decreases. Additionally, the maximum rotational velocity of the relative turntable sequentially decreases during the slippage phase, leading to a corresponding reduction in the duration of the stick–slip cycle.

The variation in the friction torque of the drill bit under different combinations of static and dynamic friction coefficients is illustrated in Figure 8. During the slip phase, the friction torque corresponds to the dynamic friction torque, while, during the viscous phase, it corresponds to the static friction torque. In systems exhibiting stick–slip vibration, segmentation occurs in the drill bit’s friction torque due to disparities between the static and dynamic friction coefficients. When transitioning from the slip phase to the viscous phase, there is a sudden decrease in the friction torque. Subsequently, during the viscous phase, a balanced state is reached and the friction torque gradually increases until it reaches its maximum static value for the drill bit. Both the amplitude and period of stick–slip vibration decrease with a decreasing difference between the static and dynamic friction coefficients.

The relative phase plane of the drill bit has been analyzed under various combinations of static and dynamic friction coefficients, as depicted in Figure 9. The initial angular displacement of the drill bit varies with changes in the static friction coefficient. A decrease in the static friction coefficient results in a rightward shift in the overall relative phase plane of the drill bit. For a given set of friction coefficients, the motion of the drill bit relative to the turntable forms a limit cycle within the phase plane. When there is a constant difference between the static and dynamic friction coefficients, the size of this limit cycle remains unchanged. As this difference decreases, however, the limit cycle progressively contracts inwardly while simultaneously reducing both the amplitude and angular velocity of the drill bit’s angular displacement. The position of the equilibrium at which this limit cycle centers is determined by the dynamic friction coefficient alone; thus, it remains consistent across all combinations tested due to the identical dynamic friction coefficients employed therein.

4. Design of Stick–Slip Vibration PID Controller

In order to control the stick–slip vibration of the drill string, a PID controller is introduced and its general expression is defined as

$$U_{PID}=K_{p}e\left(t\right)+K_i\frac{1}{T_i}{\displaystyle {\int }_0^{t}e\left(t\right)dt+K_d\frac{de\left(t\right)}{dt}}=Kp\left[e\left(t\right)+\frac{1}{T_i}{\displaystyle {\int }_0^{t}e\left(t\right)dt+T_d\frac{de\left(t\right)}{dt}}\right]$$

(19)

According to Equation (10), the following expressions can be obtained.

$$\left\{\begin{array}{l}\begin{array}{l}{\dot{x}}_1=\frac{d{\theta }_r}{dt}\\ {\dot{x}}_2=-\frac{c}{J_r}\left(x_2-x_4\right)-\frac{k}{J_r}\left(x_1-x_3\right)-\frac{c_r}{J_r}{x}_2+\frac{1}{J_r}\mathrm{U}\end{array}\hfill \\ \begin{array}{l}{\dot{x}}_3=\frac{d{\theta }_b}{dt}\\ {\dot{x}}_4=-\frac{c}{J_b}\left(x_4-x_2\right)-\frac{k}{J_b}\left(x_3-x_1\right)-\frac{c_b}{J_b}{x}_4-\frac{1}{J_b}{T}_{fb}(x)\end{array}\hfill \end{array}\right.$$

(20)

The main purpose of the control is to eliminate the stick–slip vibration phenomenon at the drill bit position and cause the drill bit to rotate at a constant angular velocity. According to Equation (19), the control equation for the input torque U is given by

$$\mathrm{U}=K_p(\Omega -{\dot{x}}_4)+K_i{\displaystyle {\int }_0^t(\Omega -{\dot{x}}_1)d\tau +}{K}_d({\dot{x}}_1-{\dot{x}}_4)$$

(21)

where Ω is the ideal velocity of the drill bit, and $K_i,K_d$, and K_p are the integral coefficient, differential coefficient, and proportional coefficient of the PID controller, respectively.

The optimal parameter ranges of K_p, K_i, and K_d need to be determined. According to the parameter selection principle of the PID controller, the value of the proportional coefficient is determined to be 15. For the integral coefficient, a larger value is set and then the value decreases in turn. The ideal velocity of the drill bit is set to 12 rad/s and the time-history responses of the angular velocity of the turntable and the drill bit with different integral coefficients are shown in Figure 10.

When the integral coefficient decreases gradually from 60, the response time of the drill string increases gradually. In the range of $K_i$ = 30~60, stick–slip vibrations occur briefly before reaching a stable state, where the turntable and drill bit achieve synchronous rotation. However, when $K_i$ is between 10 and 20, the velocity of the turntable and drill bit oscillates, and the drill string fails to reach a stable state within the given calculation time. As a result, the optimal value for the integral coefficient K_i is determined to be 35.

For the differential coefficient, a smaller value is set and then the differential coefficient increases in turn and the ideal velocity of the drill bit remains unchanged. The angular velocity of the turntable and the drill bit with different differential coefficients is shown in Figure 11. As the differential coefficient gradually increases from 10 to 40, the oscillation amplitude of the angular velocity at the drill bit increases. When the differential coefficient is 40, there is stick–slip vibration in the drill string. According to the parameter selection principle of the PID controller, the value of the differential coefficient is determined to be 40 × 30% = 12.

According to the selection results of the integral coefficient and differential coefficient, the PID control equation of the stick–slip vibration can be written as

$$\mathrm{U}=15(\Omega -{\dot{x}}_4)+35{\displaystyle {\int }_0^t(\Omega -{\dot{x}}_1)d\tau +}12({\dot{x}}_1-{\dot{x}}_4)$$

(22)

The response of the drill string with the action of the PID controller has been analyzed, and the angular velocity results of the turntable and the drill bit are presented in Figure 12. During the first 32 s, the drill bit is in a viscous phase, and its angular velocity remains at zero. Subsequently, stick–slip vibrations occur, causing the angular velocity to increase continuously. After about 90 s, the angular velocity of the drill bit reaches the desired value and fluctuates within a certain range. Similarly, the angular velocity of the turntable reaches 12 rad/s after about 90 s, and it no longer oscillates. The PID controller effectively controls the stick–slip vibration of the drill string, and it has a better control effect on the rotation velocity of the turntable.

The time-history response of the driving torque and friction torque of the drill bit with the action of the PID controller is depicted in Figure 13. During the initial 32 s, both the friction torque and driving torque increase simultaneously. From 32 to 42 s, the friction torque of the drill bit oscillates, corresponding to the stick–slip vibration observed in Figure 13. Subsequently, the friction torque stabilizes at a constant value equal to the dynamic friction torque. The driving torque of the drill bit exhibits significant fluctuations between 32 and 90 s. However, in the range of 75.80 to 76.60 s, the driving torque displays a simple harmonic dynamic characteristic.

Based on the analysis conducted on the relative angular displacement and velocity data obtained from the PID controller’s action on the drill bit, we can derive its corresponding relative phase plane, as illustrated in Figure 14. Upon the initiation of rotation for drilling purposes, it becomes evident that the angular velocity consistently lags behind the angular displacement for our observed drill bit. Initially increasing before subsequently decreasing again, this lagging displacement gradually approaches convergence towards an equilibrium point along a spiral trajectory within its respective phase plot curve. It is worth noting that there are no indications or formations in these observations related to stable stick–slip vibrations occurring at or near the monitoring location of the drilling tool.

When the rotational inertia of turntable J_r and the equivalent damping coefficient of drill string c exist in perturbation, with the action of the PID controller, the angular velocity time–history response of the turntable and drill bit can be obtained, as shown in Figure 15 and Figure 16. When J_r exists in perturbation, it does not have a significant impact on the movement of the drill string system. The drill string system also reaches a stable state at 90 s and does not produce stick–slip vibration. Compared with the result shown in Figure 13, the angular velocity of the turntable and the drill bit are greater when the drill string system is stable, which results from the change in the rotational inertia of the turntable. According to Figure 15 and Figure 16, with the action of the PID controller, the angular velocity of the turntable and the drill bit are essentially the same. The results show that the established PID controller has strong robustness. When the drill string system parameters J_r and c exist in perturbation, the stick–slip vibration of the drill string system can be suppressed by the PID controller and it enables the drill string system to gradually become stable, which can improve the drilling efficiency.

5. Conclusions

Based on the principles of rigid body mechanics, we establish a two-degree-of-freedom torsional dynamics equation for the drill string and obtain the first-order dynamics differential equation. We analyze the stick–slip response of the drill string under specific parameter conditions, which is a necessary condition for its vibration.

The nature of the limit cycle in the phase plane of the drill bit remains unchanged when determining the difference between the static and dynamic friction coefficients. As this difference decreases, both the limit cycle and stick–slip vibration gradually weaken. When there is no difference between the static and dynamic friction coefficients, stick–slip vibration cannot occur in the drill string.

According to the drill string dynamics model, we design a PID controller to effectively control the input torque. By determining appropriate integral and differential coefficients, we derive a PID control equation for stick–slip vibration. With this PID controller in action, effective control over stick–slip vibration is achieved while demonstrating a better control effect on the turntable rotation velocity compared to that on the drill bit.