Cooling Strategy Optimization of Cylindrical Lithium-Ion Battery Pack via Multi-Counter Cooling Channels
Abstract
:1. Introduction
1.1. Research Background
1.2. Literature Review
1.3. Motivation and Novelty
2. Computational Models and Verification
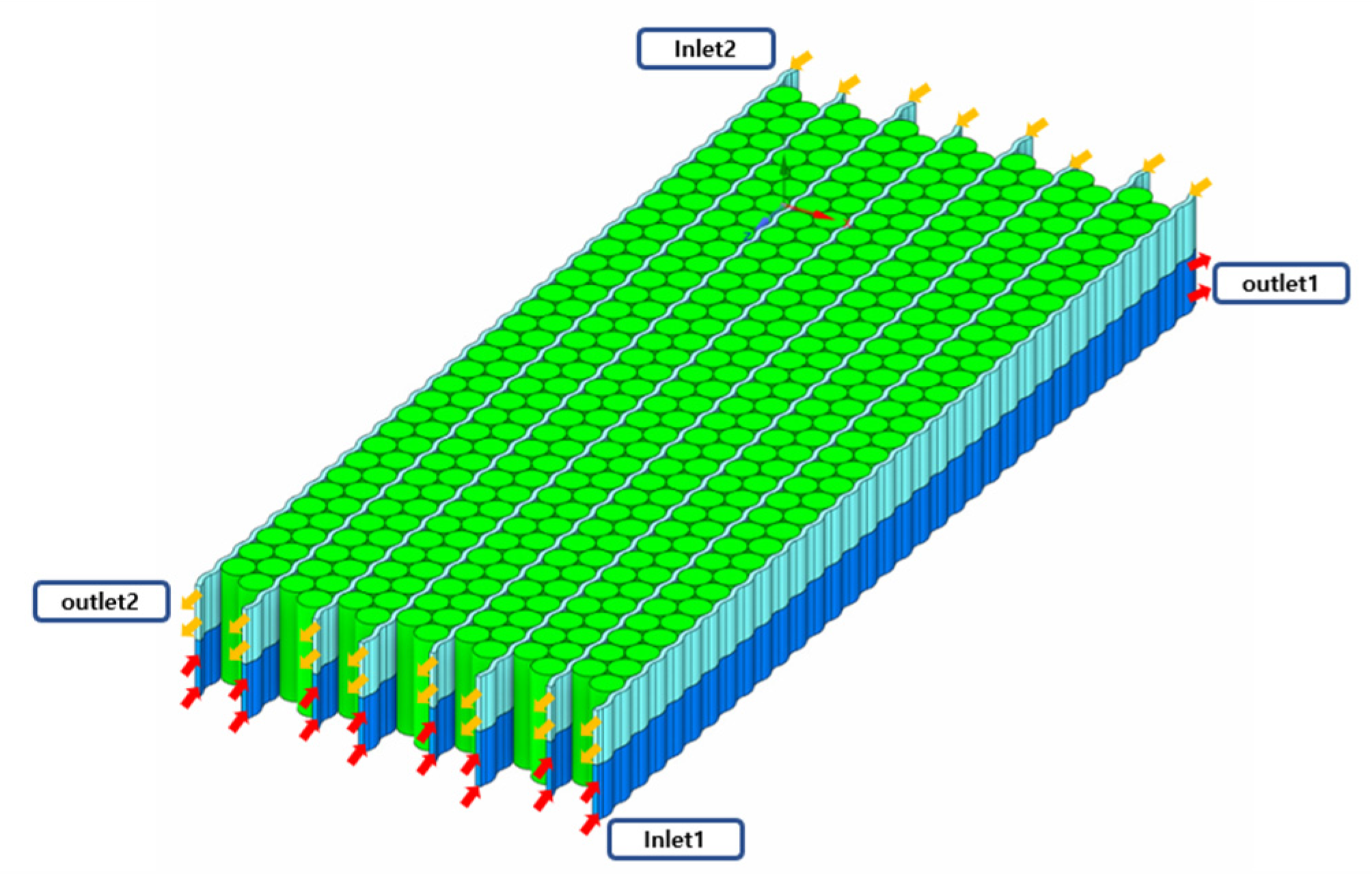
2.1. Geometry and Boundary Conditions
2.2. Governing Equations
- The physical properties of the battery material are uniform, and the heat generated by the battery is constant and uniform.
- The current density is uniform throughout the battery during the charge–discharge cycle.
- Thermal radiation is neglected.
2.3. Grid Independence Verification
3. Results and Discussion
3.1. Reliability Verification of the Model
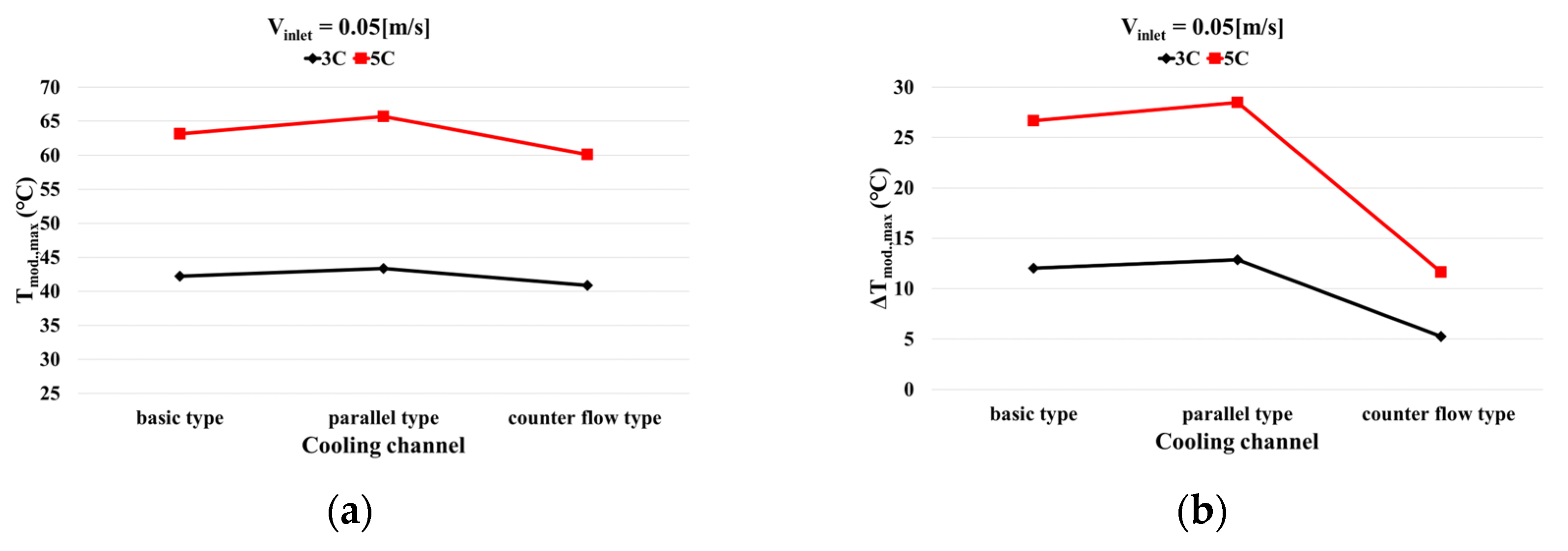
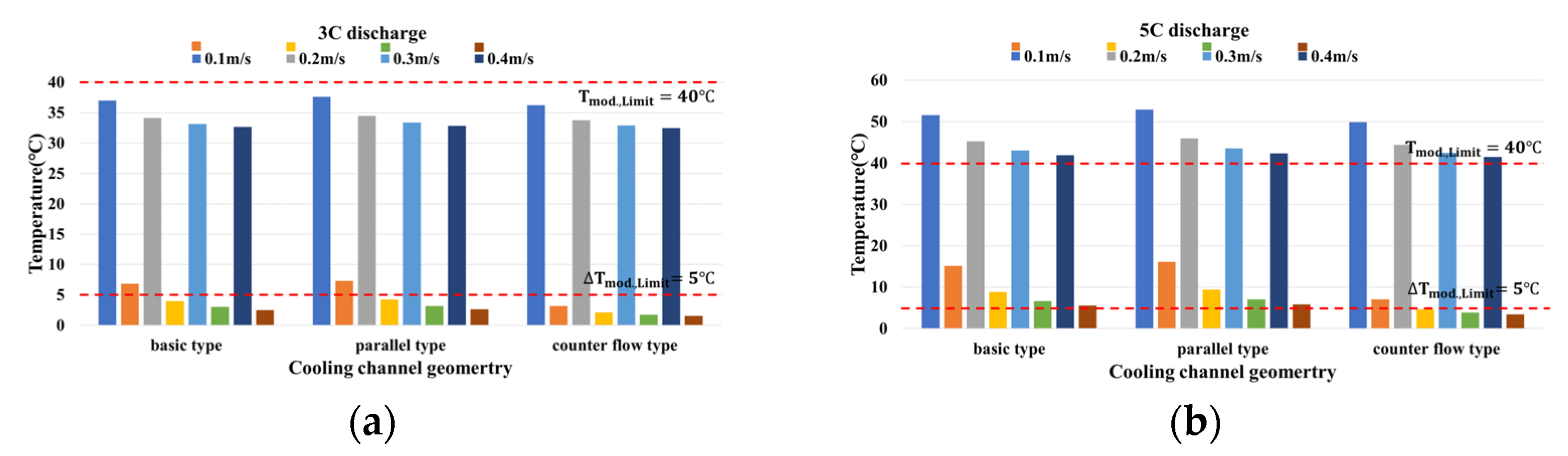
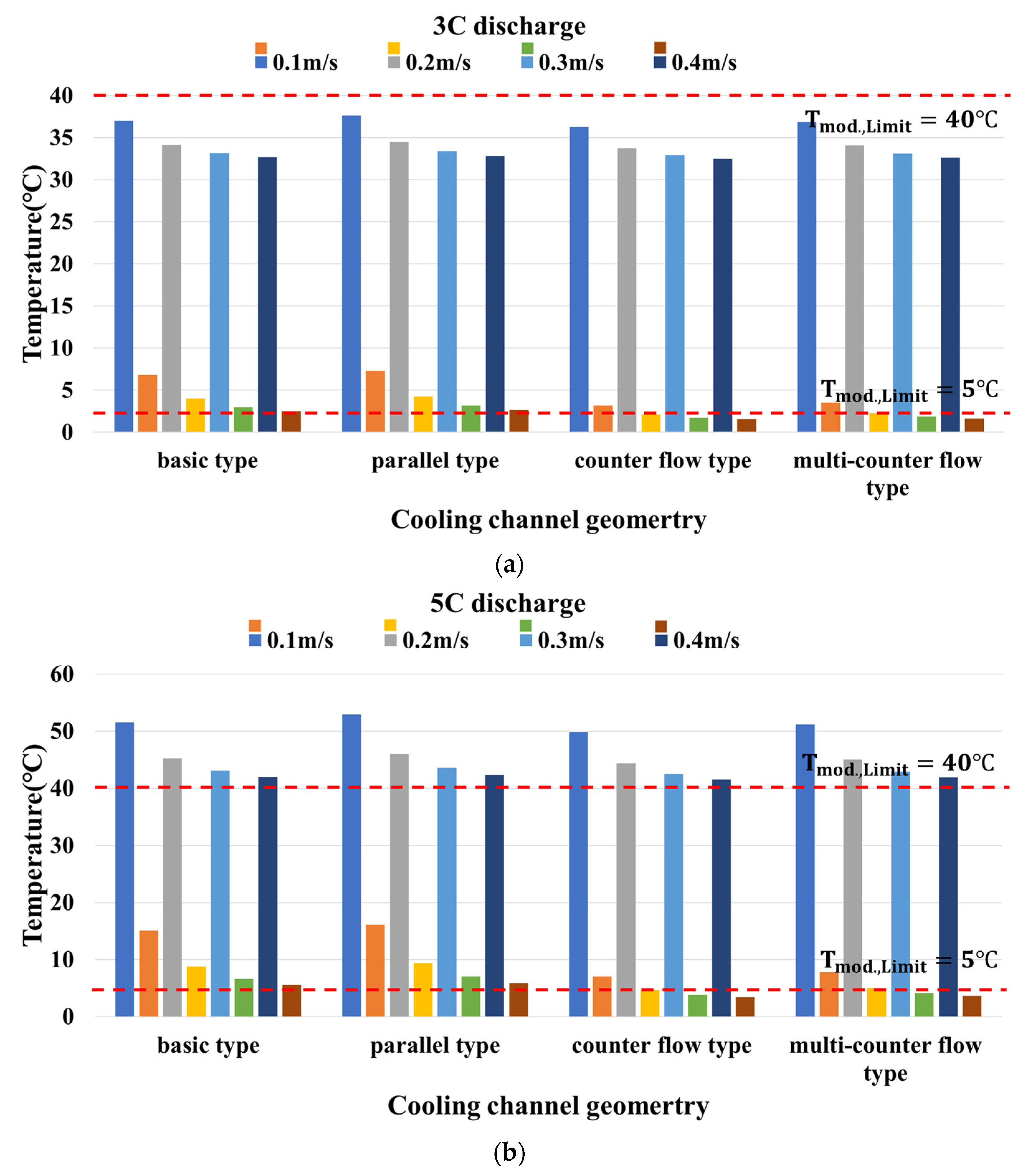
3.2. Effect of Cooling Channel Geometry on BTM
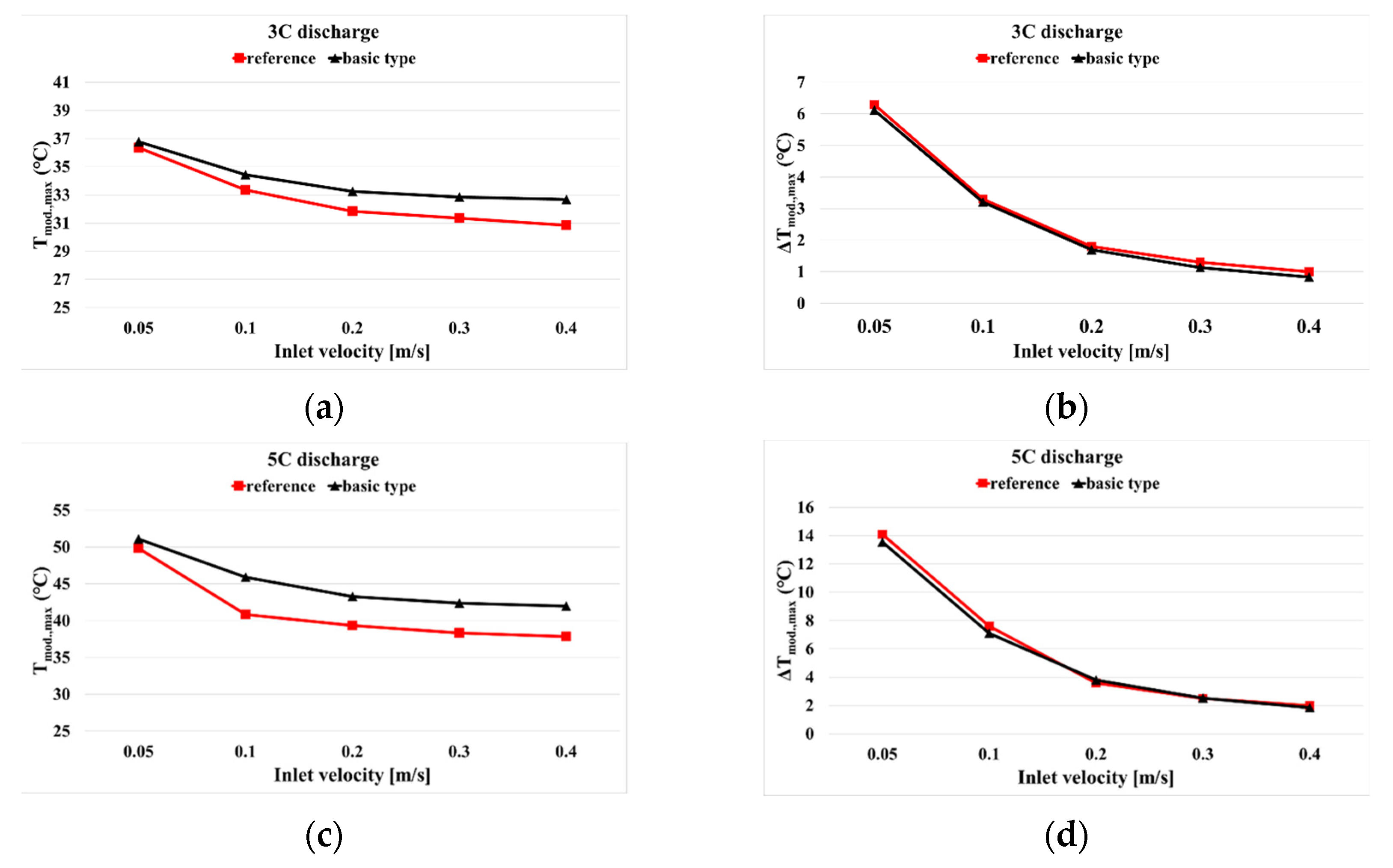
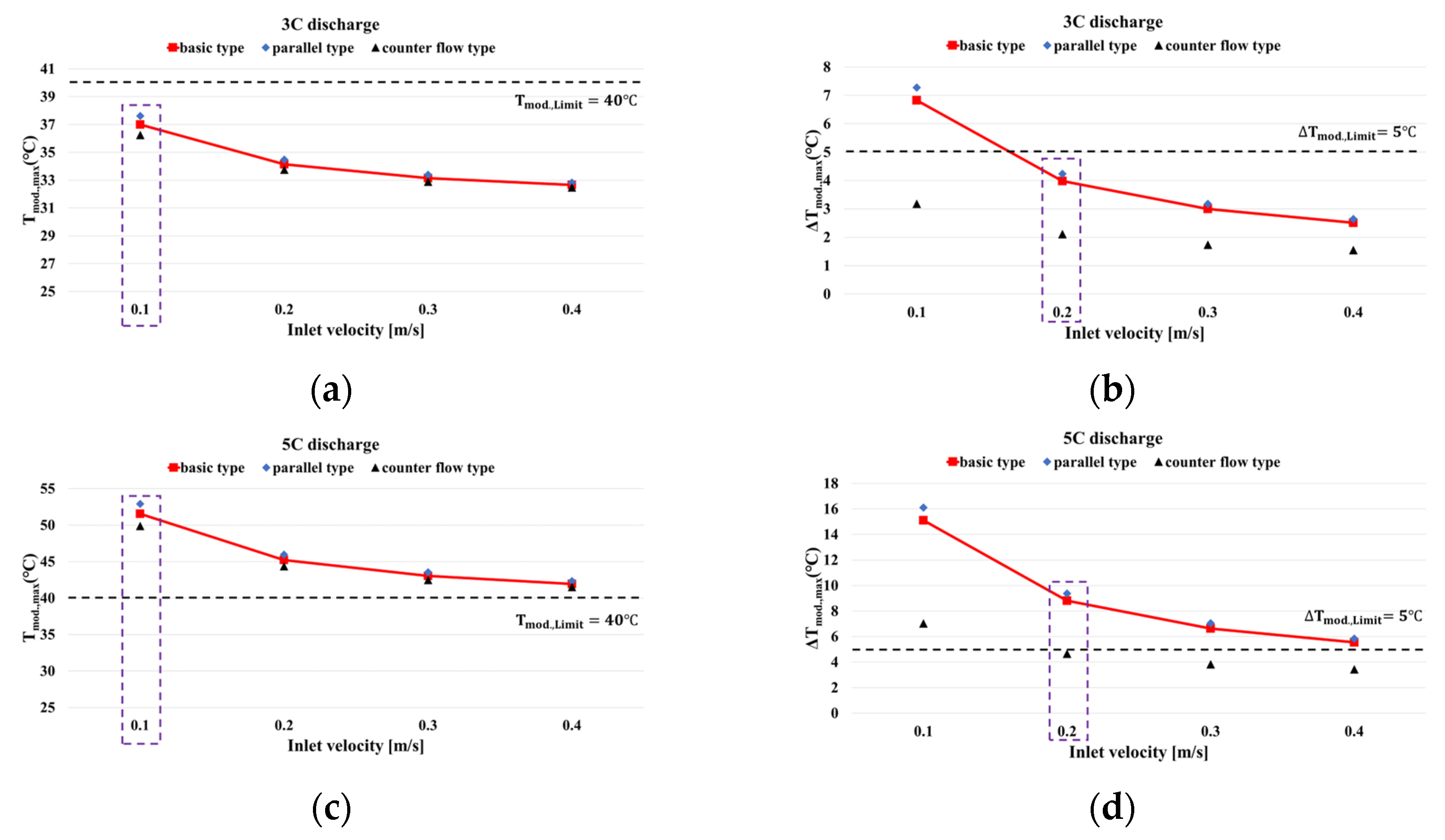
3.3. Effect of Coolant Inlet Velocity on BTM
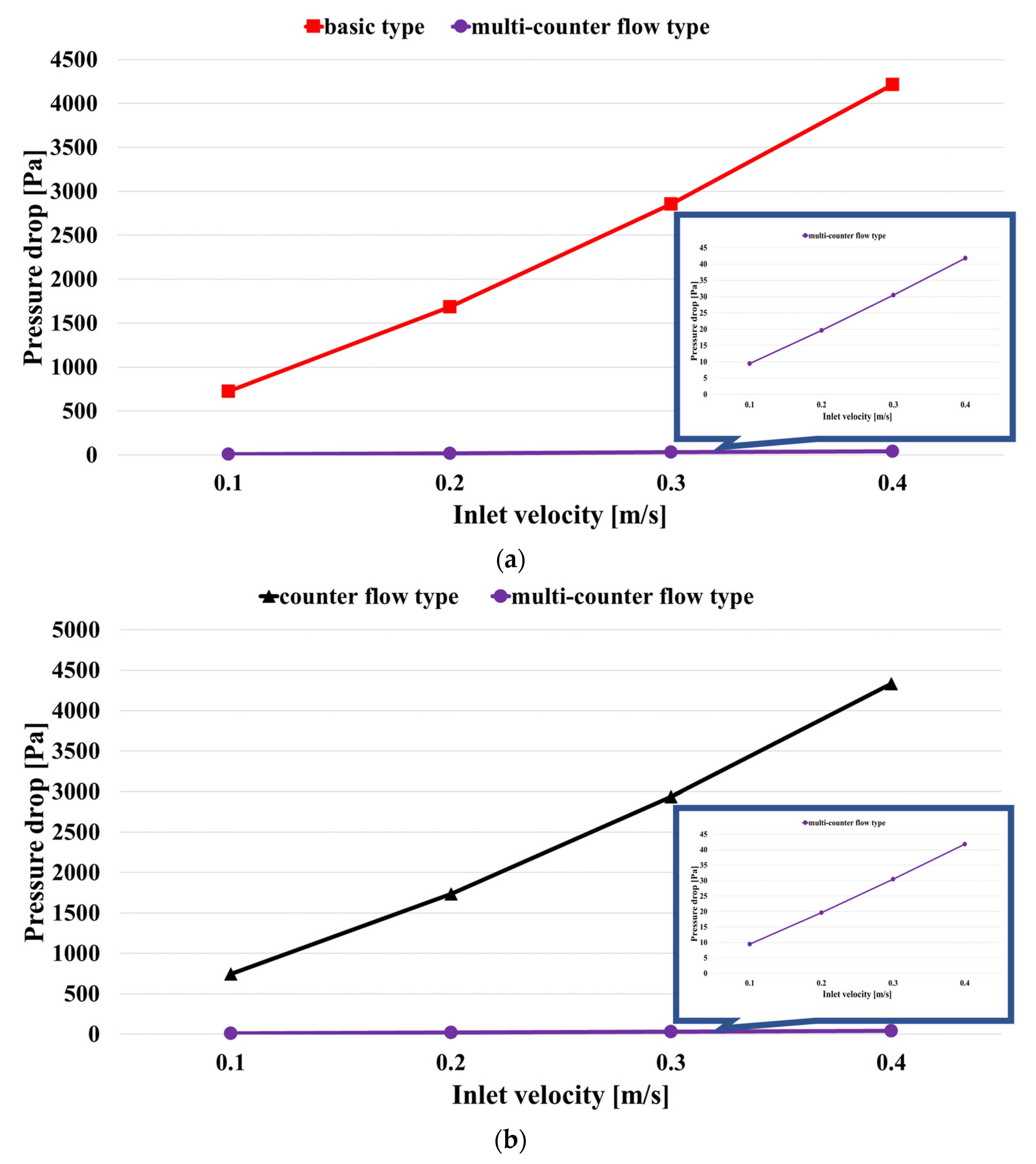
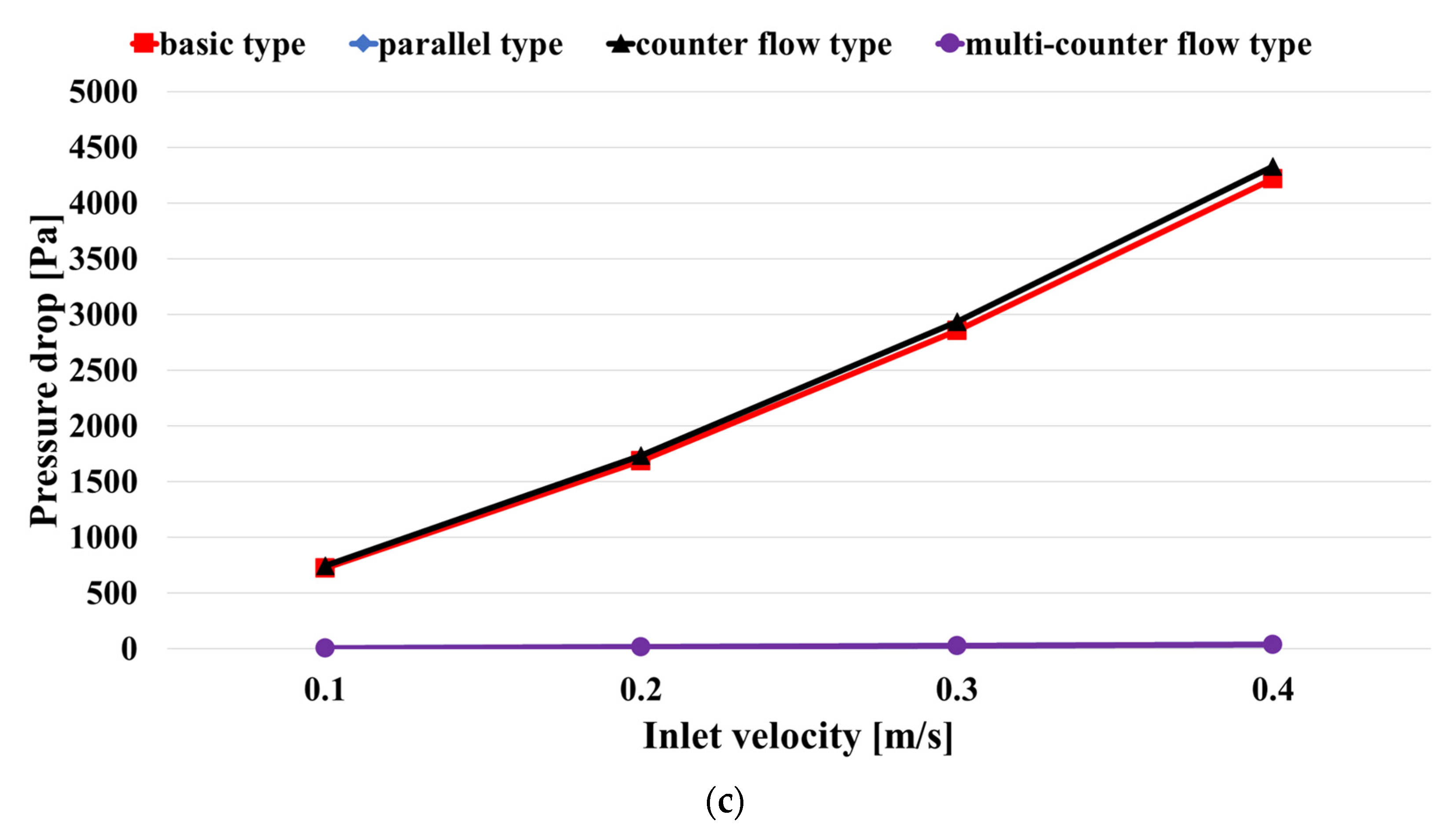
3.4. Effect of Pressure Drop on BTM
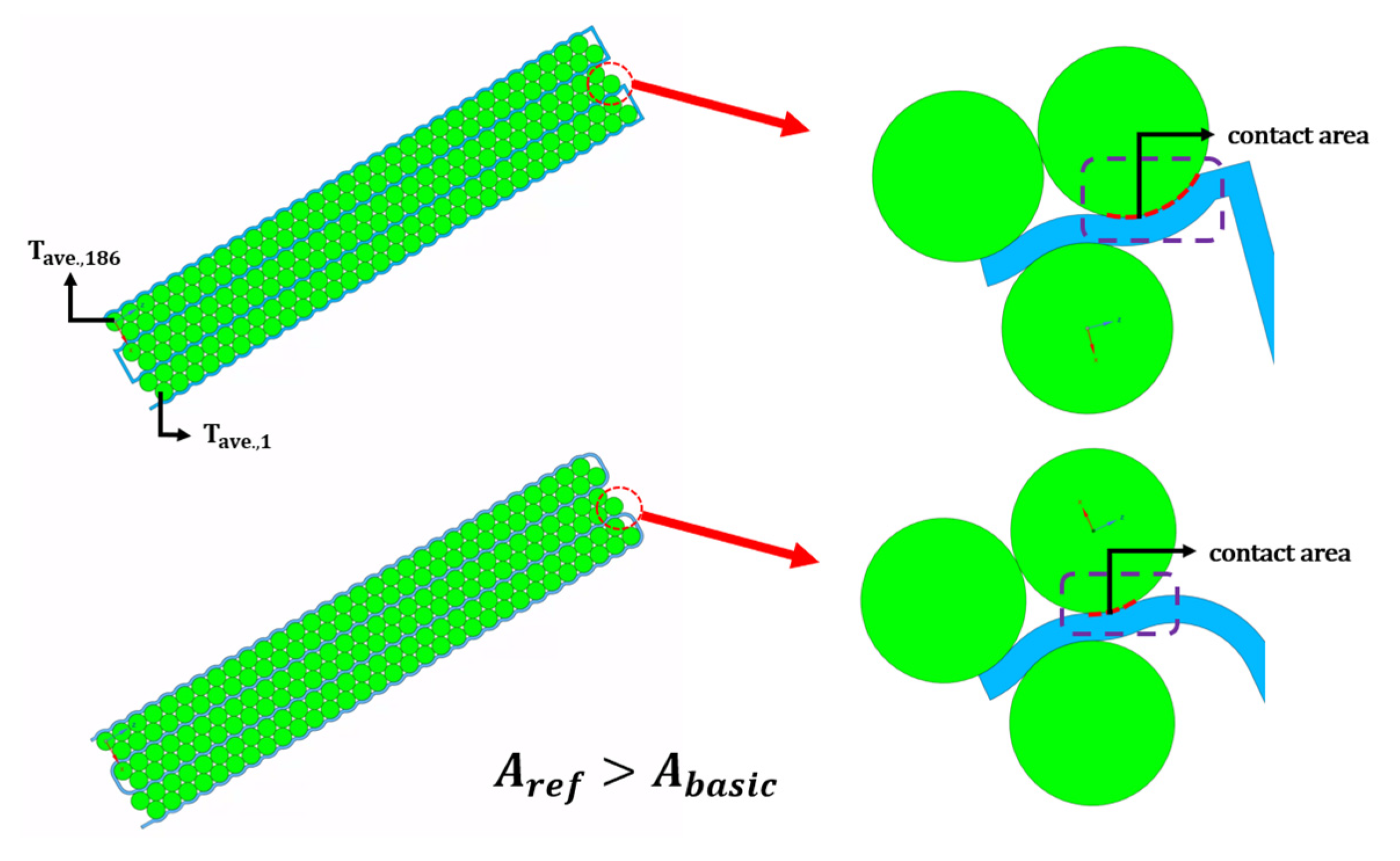
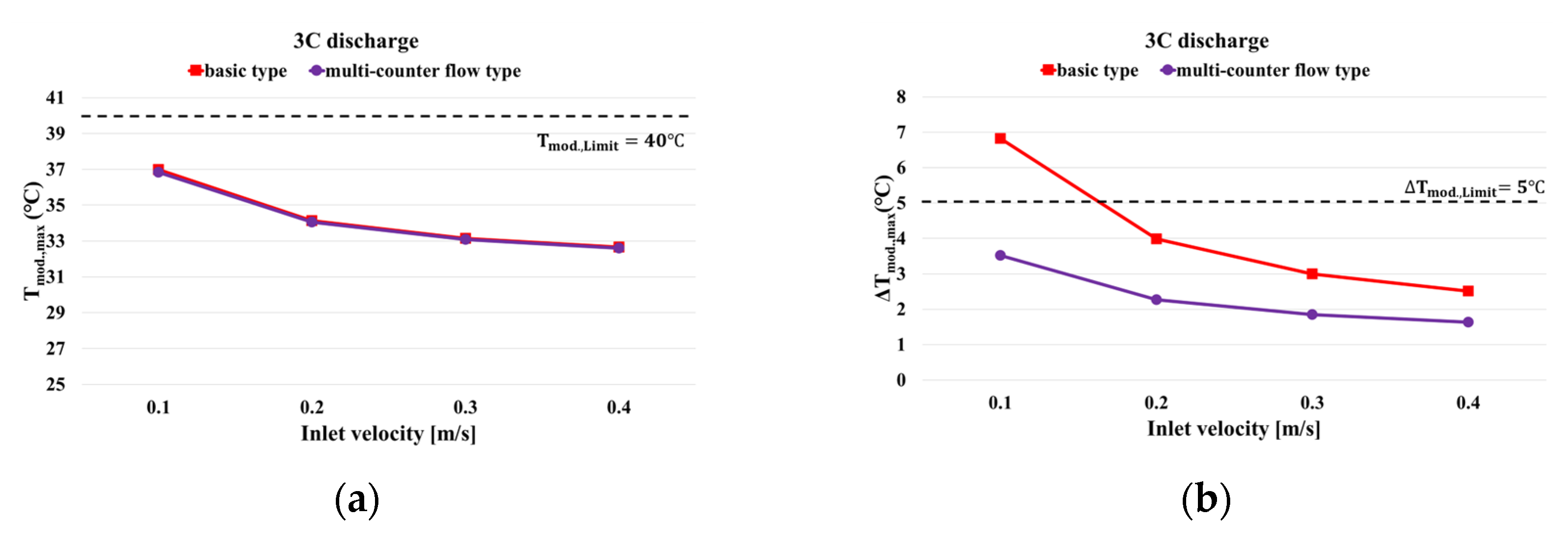
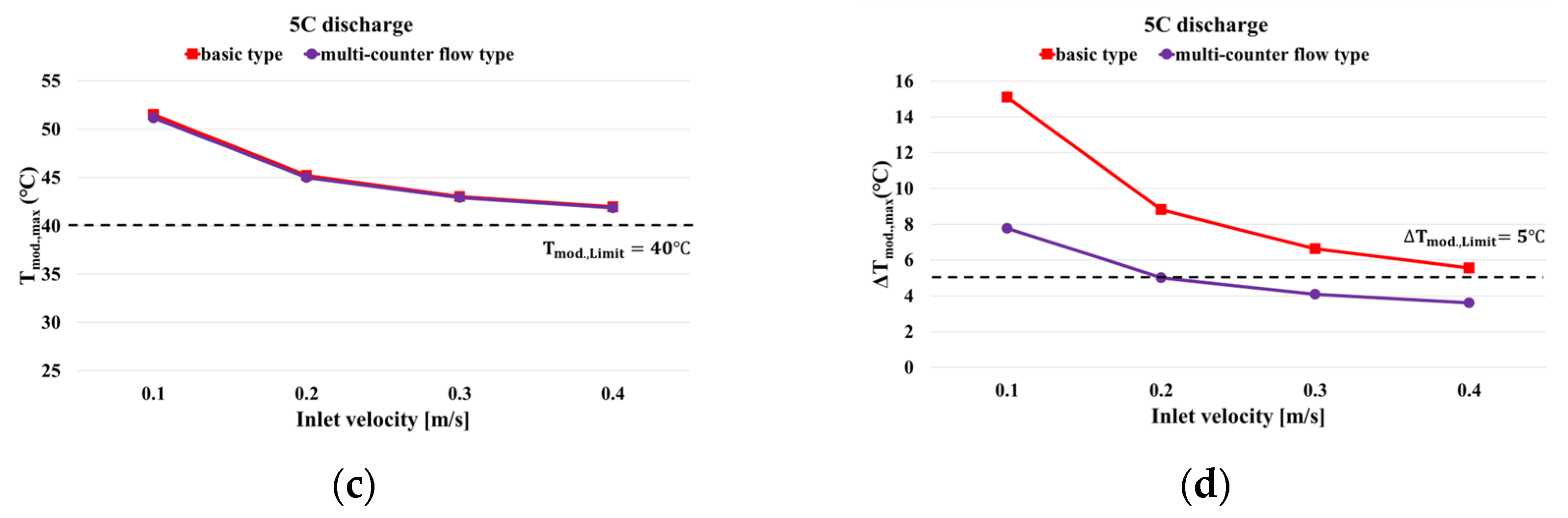
3.5. Effect of Optimized Cooling Channel
4. Conclusions
- The superior cooling performance of the counter flow type compared to the basic type was confirmed, as evidenced by the reduced maximum temperature and temperature difference within the battery module. However, the counter flow type exhibited a higher pressure drop and power consumption than the basic type.
- The parallel type had a small pressure drop but did not properly remove the heat generated from the battery; meanwhile, the counter flow type had a high pressure drop but effectively removed the battery heat. Therefore, this study proposed the use of a multi-counter flow type cooling channel, which combined the advantages of both channels to reduce the pressure drop and maintain the battery module temperature appropriately.
- The multi-counter flow type channel achieved both efficient cooling and low power consumption. Further, it was confirmed that the maximum temperature and temperature difference in the module were relatively small compared with those of the counter flow type.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Niu, J.; Yang, J.; Liu, T.; Bao, F.; Wang, Q. In-situ explosion limit analysis and hazards research of vent gas from lithium-ion battery thermal runaway. J. Energy Storage 2022, 56, 106146. [Google Scholar] [CrossRef]
- Qiu, Y.; Jiang, F. A review on passive and active strategies of enhancing the safety of lithium-ion batteries. Int. J. Heat Mass Transf. 2022, 184, 122288. [Google Scholar] [CrossRef]
- Xin-Gang, Z.; Wenjie, L.; Wei, W.; Shuran, H. The impact of carbon emission trading on green innovation of China’s power industry. Environ. Impact Assess. Rev. 2023, 99, 107040. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Negnevitsky, M.; Zhang, H. A review of air-cooling battery thermal management systems for electric and hybrid electric vehicles. J. Power Sources 2021, 501, 230001. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, F.; Xu, L.; Kong, J.; Yang, Q. Thermal performance of cylindrical Lithium-ion battery thermal management system based on air distribution pipe. Int. J. Heat Mass Trans. 2019, 131, 984–998. [Google Scholar] [CrossRef]
- Saechan, P.; Dhuchakallaya, I. Numerical study on the air-cooled thermal management of Lithium-ion battery pack for electrical vehicles. Energy Rep. 2022, 8, 1264–1270. [Google Scholar] [CrossRef]
- Sheng, L.; Su, L.; Zhang, H.; Li, K.; Fang, Y.; Ye, W.; Fang, Y. Numerical investigation on a lithium ion battery thermal management utilizing a serpentine-channel liquid cooling plate exchanger. Int. J. Heat Mass Transf. 2019, 141, 658–668. [Google Scholar] [CrossRef]
- Xu, C.; Steubing, B.; Hu, M.; Harpprecht, C.; van der Meide, M.; Tukker, A. Future greenhouse gas emissions of automotive lithium-ion battery cell production. Resour. Conserv. Recycl. 2022, 187, 106606. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, H.; Peng, C.; Liu, X. Exploring the role of environmental regulations in the production and diffusion of electric vehicles. Comput. Ind. Eng. 2022, 173, 108675. [Google Scholar] [CrossRef]
- Zeng, W.; Niu, Y.; Li, S.; Hu, S.; Mao, B.; Zhang, Y. Cooling performance and optimization of a new hybrid thermal management system of cylindrical battery. Appl. Therm. Eng. 2022, 217, 119171. [Google Scholar] [CrossRef]
- Held, M.; Tuchschmid, M.; Zennegg, M.; Figi, R.; Schreiner, C.; Mellert, L.D.; Welte, U.; Kompatscher, M.; Hermann, M.; Nachef, L. Thermal runaway and fire of electric vehicle lithium-ion battery and contamination of infrastructure facility. Renew. Sustain. Energy Rev. 2022, 165, 112474. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Mathieu, R.; Briat, O.; Gyan, P.; Vinassa, J.-M. Comparison of the impact of fast charging on the cycle life of three lithium-ion cells under several parameters of charge protocol and temperatures. Appl. Energy 2021, 283, 116344. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, W.; Li, H.; Wan, W.; Zhang, W.; Zhuo, W.; Liu, Q. Heat transfer characteristics and low-temperature performance of a lithium-ion battery with an inner cooling/heating structure. Appl. Therm. Eng. 2023, 219, 119352. [Google Scholar] [CrossRef]
- Esho, I.; Shah, K.; Jain, A. Measurements and modeling to determine the critical temperature for preventing thermal runaway in Li-ion cells. Appl. Therm. Eng. 2018, 145, 287–294. [Google Scholar] [CrossRef]
- Appleberry, M.C.; Kowalski, J.A.; Africk, S.A.; Mitchell, J.; Ferree, T.C.; Chang, V.; Parekh, V.; Xu, Z.; Ye, Z.; Whitacre, J.F.; et al. Avoiding thermal runaway in lithium-ion batteries using ultrasound detection of early failure mechanisms. J. Power Sources 2022, 535, 231423. [Google Scholar] [CrossRef]
- Parekh, M.H.; Li, B.; Palanisamy, M.; Adams, T.E.; Tomar, V.; Pol, V.G. In Situ Thermal Runaway Detection in Lithium-Ion Batteries with an Integrated Internal Sensor. ACS Appl. Energy Mater. 2020, 3, 7997–8008. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, F.; Zhou, H.; Wang, Q.; Kong, J. Thermal performance of cylindrical lithium-ion battery thermal management system integrated with mini-channel liquid cooling and air cooling. Appl. Therm. Eng. 2020, 175, 115331. [Google Scholar] [CrossRef]
- Wang, H.; Tao, T.; Xu, J.; Mei, X.; Liu, X.; Gou, P. Cooling capacity of a novel modular liquid-cooled battery thermal man-agement system for cylindrical lithium ion batteries. Appl. Therm. Eng. 2020, 178, 115591. [Google Scholar] [CrossRef]
- Mahamud, R.; Park, C. Reciprocating air flow for Li-ion battery thermal management to improve temperature uniformity. J. Power Sources 2011, 196, 5685–5696. [Google Scholar] [CrossRef]
- Yu, K.; Yang, X.; Cheng, Y.; Li, C. Thermal analysis and two-directional air flow thermal management for lithium-ion battery pack. J. Power Sources 2014, 270, 193–200. [Google Scholar] [CrossRef]
- Huo, Y.; Rao, Z.; Liu, X.; Zhao, J. Investigation of power battery thermal management by using mini-channel cold plate. Energy Convers. Manag. 2015, 89, 387–395. [Google Scholar] [CrossRef]
- Chen, D.; Jiang, J.; Kim, G.-H.; Yang, C.; Pesaran, A. Comparison of different cooling methods for lithium ion battery cells. Appl. Therm. Eng. 2016, 94, 846–854. [Google Scholar] [CrossRef]
- Zhao, R.; Gu, J.; Liu, J. An experimental study of heat pipe thermal management system with wet cooling method for lithium ion batteries. J. Power Sources 2015, 273, 1089–1097. [Google Scholar] [CrossRef]
- Greco, A.; Cao, D.; Jiang, X.; Yang, H. A theoretical and computational study of lithium-ion battery thermal management for electric vehicles using heat pipes. J. Power Sources 2014, 257, 344–355. [Google Scholar] [CrossRef]
- Rao, Z.; Huo, Y.; Liu, X.; Zhang, G. Experimental investigation of battery thermal management system for electric vehicle based on paraffin/copper foam. J. Energy Inst. 2015, 88, 241–246. [Google Scholar] [CrossRef]
- Coleman, B.; Ostanek, J.; Heinzel, J. Reducing cell-to-cell spacing for large-format lithium ion battery modules with aluminum or PCM heat sinks under failure conditions. Appl. Energy 2016, 180, 14–26. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, S. A review of power battery thermal energy management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Panchal, S.; Khasow, R.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Thermal design and simulation of mini-channel cold plate for water cooled large sized prismatic lithium-ion battery. Appl. Therm. Eng. 2017, 122, 80–90. [Google Scholar] [CrossRef]
- Shan, S.; Li, L.; Xu, Q.; Ling, L.; Xie, Y.; Wang, H.; Zheng, K.; Zhang, L.; Bei, S. Numerical investigation of a compact and lightweight thermal management system with axially mounted cooling tubes for cylindrical lithium-ion battery module. Energy 2023, 274, 127410. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, C.; Gao, Q.; Wang, G.; Liu, M.; Guo, Y.; Xiao, C.; Yan, Y. Status and development of electric vehicle integrated thermal management from BTM to HVAC. Appl. Therm. Eng. 2015, 88, 398–409. [Google Scholar] [CrossRef]
- Xie, J.; Wang, Y.; He, S.; Zhang, G.; Liu, X.; Yang, X. A simple cooling structure with precisely-tailored liquid cooling plate for thermal management of large battery module. Appl. Therm. Eng. 2022, 212, 118575. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, S.; Lu, Y.; Huang, R.; Yu, X. Study on a liquid cooled battery thermal management system pertaining to the transient regime. Appl. Therm. Eng. 2020, 180, 115793. [Google Scholar] [CrossRef]
- Zhao, C.; Sousa, A.C.; Jiang, F. Minimization of thermal non-uniformity in lithium-ion battery pack cooled by channeled liquid flow. Int. J. Heat Mass Transf. 2019, 129, 660–670. [Google Scholar] [CrossRef]
- Zhao, C.; Cao, W.; Dong, T.; Jiang, F. Thermal behavior study of discharging/charging cylindrical lithium-ion battery module cooled by channeled liquid flow. Int. J. Heat Mass Transf. 2018, 120, 751–762. [Google Scholar] [CrossRef]
- Xie, L.; Huang, Y.; Lai, H. Coupled prediction model of liquid-cooling based thermal management system for cylindrical lithium-ion module. Appl. Therm. Eng. 2020, 178, 115599. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, F.; Zhang, Q.; Wang, Q.; Song, Z. Thermal management of cylindrical lithium-ion battery based on a liquid cooling method with half-helical duct. Appl. Therm. Eng. 2019, 162, 114257. [Google Scholar] [CrossRef]
- Sheng, L.; Zhang, H.; Su, L.; Zhang, Z.; Zhang, H.; Li, K.; Fang, Y.; Ye, W. Effect analysis on thermal profile management of a cylindrical lithium-ion battery utilizing a cellular liquid cooling jacket. Energy 2021, 220, 119725. [Google Scholar] [CrossRef]
- Zhuang, Y.; Chen, T.; Chen, J.; Li, J.; Guan, M.; Chen, Y. Thermal uniformity performance of a hybrid battery thermal management system using phase change material and cooling plates arrayed in the manner of honeycomb. Therm. Sci. Eng. Prog. 2021, 26, 101094. [Google Scholar] [CrossRef]
- Liang, G.; Li, J.; He, J.; Tian, J.; Chen, X.; Chen, L. Numerical investigation on a unitization-based thermal management for cylindrical lithium-ion batteries. Energy Rep. 2022, 8, 4608–4621. [Google Scholar] [CrossRef]
- Pakrouh, R.; Hosseini, M.; Bahrampoury, R.; Ranjbar, A.; Borhani, S. Cylindrical battery thermal management based on microencapsulated phase change slurry. J. Energy Storage 2021, 40, 102602. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.; Wu, W.; Chen, K.; Hong, S.; Lai, Y. A critical review of battery thermal performance and liquid based battery thermal management. Energy Convers. Manag. 2019, 182, 262–281. [Google Scholar] [CrossRef]
- Qin, J.; Pan, H.; Rahman, M.; Tian, X.; Zhu, Z. Introducing compressibility with SIMPLE algorithm. Math. Comput. Simul. 2021, 180, 328–353. [Google Scholar] [CrossRef]
- Min, J.K.; Lee, C.-H. Numerical study on the thermal management system of a molten sodium-sulfur battery module. J. Power Sources 2012, 210, 101–109. [Google Scholar] [CrossRef]
- An, Z.; Chen, X.; Zhao, L.; Gao, Z. Numerical investigation on integrated thermal management for a lithium-ion battery module with a composite phase change material and liquid cooling. Appl. Therm. Eng. 2019, 163, 114345. [Google Scholar] [CrossRef]
- Saw, L.; Ye, Y.; Tay, A. Electrochemical–thermal analysis of 18650 Lithium Iron Phosphate cell. Energy Convers. Manag. 2013, 75, 162–174. [Google Scholar] [CrossRef]
- Chen, S.; Wan, C.; Wang, Y. Thermal analysis of lithium-ion batteries. J. Power Sources 2005, 140, 111–124. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef]
- Basu, S.; Patil, R.S.; Ramachandran, S.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Oh, D.; Yeo, T.; Doo, S. Non-isothermal electrochemical model for lithium-ion cells with composite cathodes. J. Power Sources 2015, 283, 132–150. [Google Scholar] [CrossRef]
- Williford, R.E.; Viswanathan, V.V.; Zhang, J.-G. Effects of entropy changes in anodes and cathodes on the thermal behavior of lithium ion batteries. J. Power Sources 2009, 189, 101–107. [Google Scholar] [CrossRef]
- Reynier, Y.F.; Yazami, R.; Fultz, B. Thermodynamics of Lithium Intercalation into Graphites and Disordered Carbons. J. Electrochem. Soc. 2004, 151, A422–A426. [Google Scholar] [CrossRef]

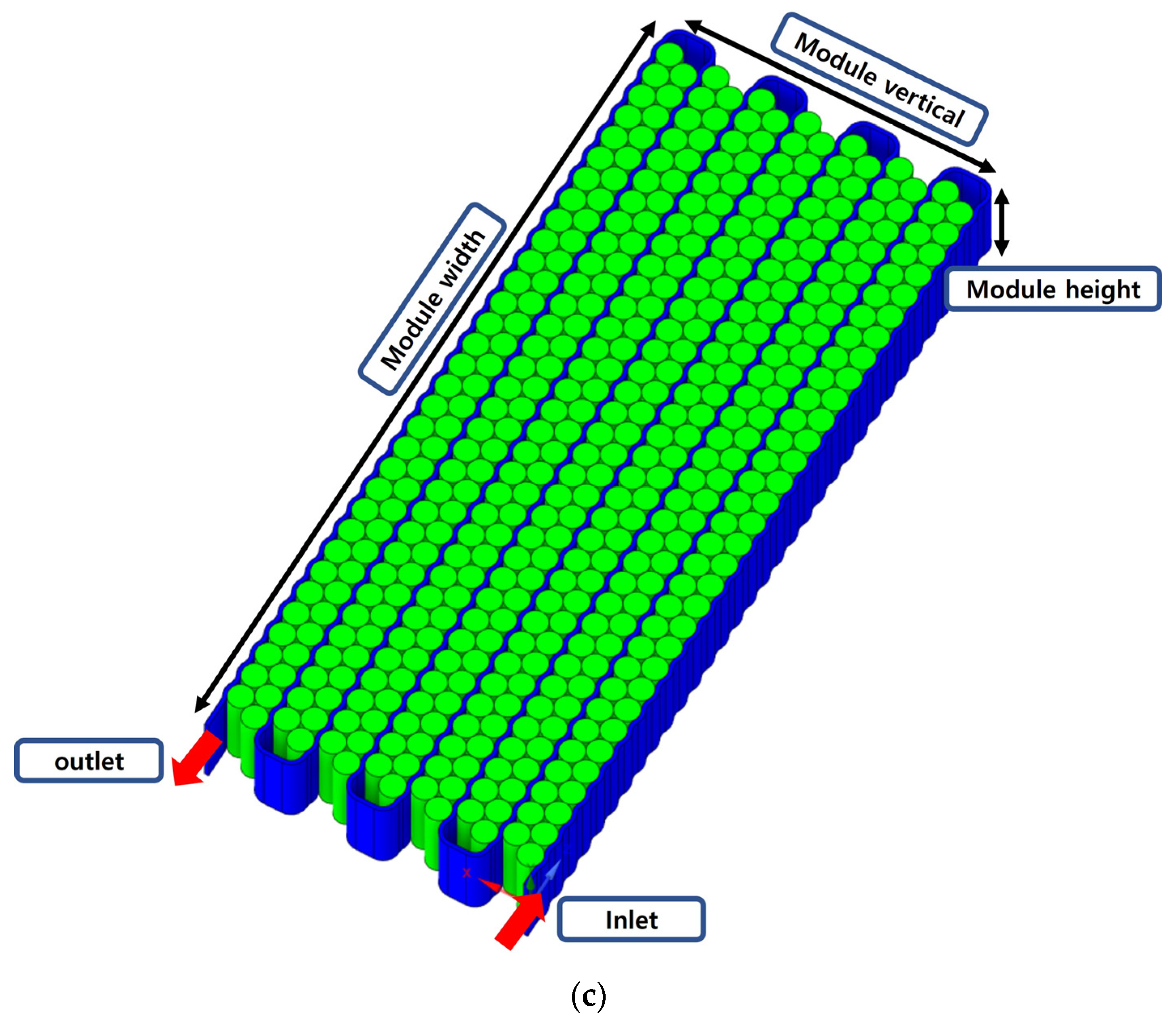


| Basic Type | Parallel Type | Counter Flow Type | Unit | |
|---|---|---|---|---|
| Battery diameter | 18 | 18 | 18 | mm |
| Battery height | 65 | 65 | 65 | mm |
| Cooling channel width | 3 | 3 | 3 | mm |
| Cooling channel height | 65 | 65 | 32.5 | mm |
| Heat transfer region | 50.75 | 50.75 | 50.75 | Angle |
| Number of cells | 448 | 448 | 448 | EA. |
| Condition | Value | Unit | |
|---|---|---|---|
| Battery | Convective heat transfer coefficient | 5 | |
| Ambient air temperature | 25 | °C | |
| Coolant | Inlet velocity | 0.05, 0.1, 0.2, 0.3, 0.4 | m/s |
| Inlet temperature | 25 | °C | |
| Outlet pressure | Ambient pressure | Pa | |
| Walls | All walls, except inlets and outlets | Insulated | - |
| Initialization | Initial temperature | 25 | °C |
| Material | Density | Heat Capacity | Thermal Conductivity | Viscosity |
|---|---|---|---|---|
| Battery cells [45] | 2720 | 300 | 3 | - |
| Coolant water | 998.2 | 4182 | 0.6 | 0.001003 |
| Grid Size | 1.6 mm | 1.4 mm | 1.2 mm | 1.0 mm |
|---|---|---|---|---|
| Theoretical coolant outlet temperature (°C) | 38.6 | 38.6 | 38.6 | 38.6 |
| Simulation coolant outlet temperature (°C) | 36.62 | 36.64 | 36.73 | 36.74 |
| Error rate | 5.13% | 5.1% | 4.84% | 4.82% |
| Inlet Velocity [m/s] | [Pa] | [Pa] | [Pa] | [Pa] | [Pa] |
|---|---|---|---|---|---|
| 0.1 | 723.29 | 9.14 | 714.15 | 747.02 | 23.72 |
| 0.2 | 1686.92 | 19.03 | 1667.89 | 1737.25 | 50.32 |
| 0.3 | 2856.43 | 29.50 | 2826.92 | 2937.94 | 81.51 |
| 0.4 | 4217.28 | 40.48 | 4331.96 | 4331.96 | 114.67 |
| Inlet Velocity [m/s] | Basic Type | Parallel Type | Counter Flow Type | |||
|---|---|---|---|---|---|---|
| 0.1 | o | x | o | x | o | o |
| 0.2 | o | o | o | o | o | o |
| 0.3 | o | o | o | o | o | o |
| 0.4 | o | o | o | o | o | o |
| Inlet Velocity [m/s] | Basic Type | Parallel Type | Counter Flow Type | |||
|---|---|---|---|---|---|---|
| 0.1 | x | x | x | x | x | x |
| 0.2 | x | x | x | x | x | o |
| 0.3 | x | x | x | x | x | o |
| 0.4 | x | x | x | x | x | o |
| Inlet Velocity [m/s] | [Pa] | [Pa] | [Pa] | [Pa] | [Pa] |
|---|---|---|---|---|---|
| 0.1 | 723.29 | 9.42 | 713.87 | 747.02 | 737.6 |
| 0.2 | 1686.92 | 19.64 | 1667.28 | 1737.25 | 1717.61 |
| 0.3 | 2856.43 | 30.47 | 2825.96 | 2937.94 | 2907.47 |
| 0.4 | 4217.28 | 41.80 | 4175.48 | 4331.96 | 4290.16 |
| Inlet Velocity [m/s] | Basic Type | Parallel Type | Counter Flow Type | Multi-Counter Flow Type | ||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | o | x | o | x | o | o | o | o |
| 0.2 | o | o | o | o | o | o | o | o |
| 0.3 | o | o | o | o | o | o | o | o |
| 0.4 | o | o | o | o | o | o | o | o |
| Inlet Velocity [m/s] | Basic Type | Parallel Type | Counter Flow Type | Multi-Counter Flow Type | ||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | x | x | x | x | x | x | x | x |
| 0.2 | x | x | x | x | x | o | x | x |
| 0.3 | x | x | x | x | x | o | x | o |
| 0.4 | x | x | x | x | x | o | x | o |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, H.; Hong, S.; Yun, J.; Han, J. Cooling Strategy Optimization of Cylindrical Lithium-Ion Battery Pack via Multi-Counter Cooling Channels. Energies 2023, 16, 7860. https://doi.org/10.3390/en16237860
Jeon H, Hong S, Yun J, Han J. Cooling Strategy Optimization of Cylindrical Lithium-Ion Battery Pack via Multi-Counter Cooling Channels. Energies. 2023; 16(23):7860. https://doi.org/10.3390/en16237860
Chicago/Turabian StyleJeon, Hyeonchang, Seokmoo Hong, Jinwon Yun, and Jaeyoung Han. 2023. "Cooling Strategy Optimization of Cylindrical Lithium-Ion Battery Pack via Multi-Counter Cooling Channels" Energies 16, no. 23: 7860. https://doi.org/10.3390/en16237860
APA StyleJeon, H., Hong, S., Yun, J., & Han, J. (2023). Cooling Strategy Optimization of Cylindrical Lithium-Ion Battery Pack via Multi-Counter Cooling Channels. Energies, 16(23), 7860. https://doi.org/10.3390/en16237860






