Advances in Computational Fluid Dynamics Modeling for Biomass Pyrolysis: A Review

Abstract

Pyrolysis, a process for extracting valuable chemicals from waste materials, leverages computational fluid dynamics (CFD) to optimize reactor parameters, thereby enhancing product quality and process efficiency. This review aims to understand the application of CFD in pyrolysis. Initially, the need for pyrolysis and its role in biomass valorization are discussed, and this is followed by an elaboration of the fundamentals of CFD studies in terms of their application to the pyrolysis process. The various CFD simulations and models used to understand product formation are also explained. Pyrolysis is conducted using both conventional and microwave-assisted pyrolysis platforms. Hence, the reaction kinetics, governing model equations, and laws are discussed in the conventional pyrolysis section. In the microwave-assisted pyrolysis section, the importance of wavelength, penetration depth, and microwave conversion efficiencies on the CFD are discussed. This review provides valuable insights to academic researchers on the application of CFD in pyrolysis systems. The modeling of pyrolysis by computational fluid dynamics (CFD) is a complex process due to the implementation of multiple reaction kinetics and physics, high computational cost, and reactor design. These challenges in the modeling of the pyrolysis process are discussed in this paper. Significant solutions that have been used to overcome the challenges are also provided with potential areas of research and development in the future of CFD in pyrolysis.

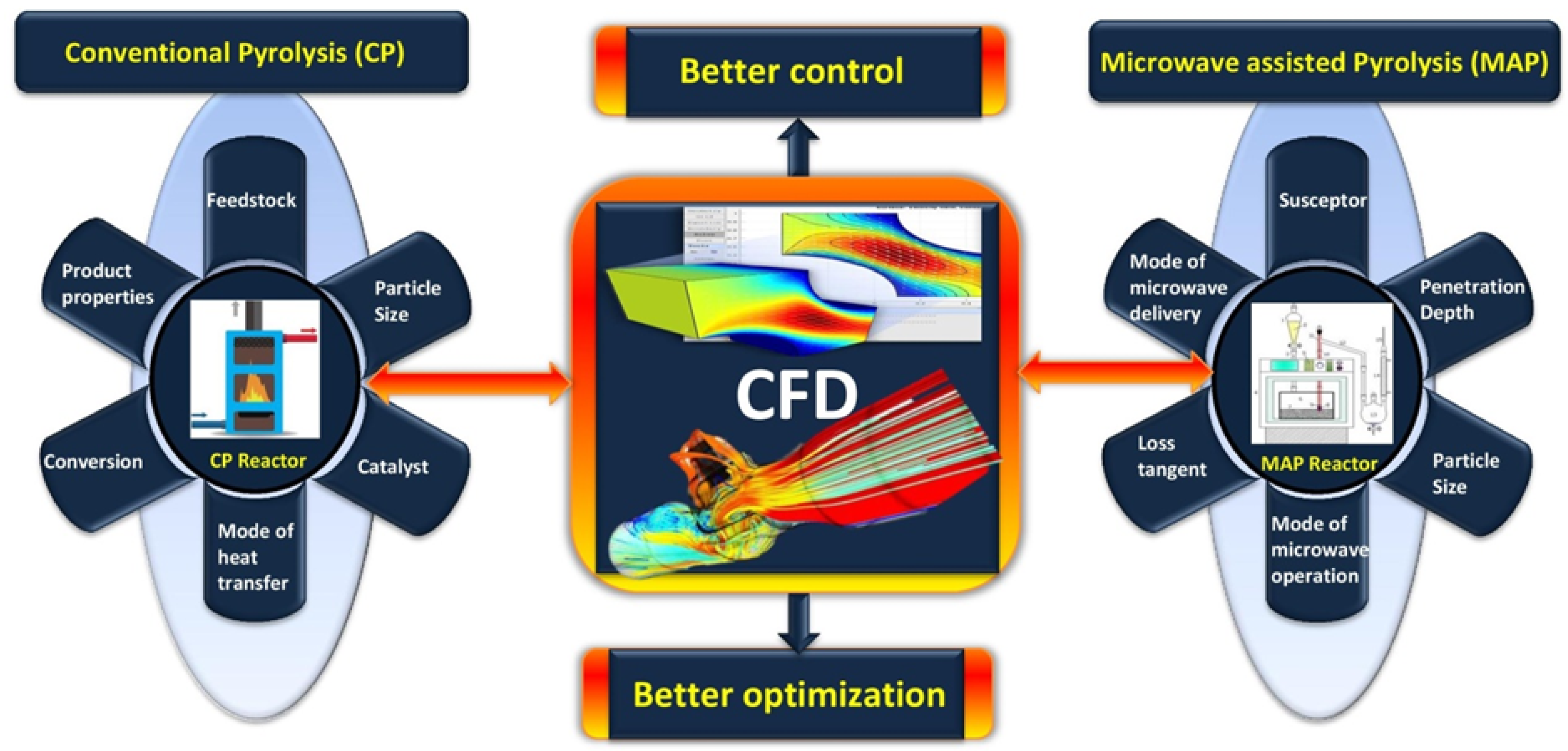
1. Introduction

1.1. Pyrolysis of Biomass and Waste Plastics

The rapid growth of the global population and depletion of fossil fuel resources have driven the research community to explore the recovery of essential chemicals from alternative and waste feedstocks [1]. The technologies involved in waste valorization include liquefaction, gasification, pyrolysis, and direct combustion [2]. Pyrolysis is an efficient thermo-chemical approach for recovering valuable products, which include liquid hydrocarbons, liquid oxygenates, gaseous hydrocarbons, and carbonaceous char. The term “pyrolysis” is derived from Greek, wherein “pyro” and “lysis” refer to fire and decomposition, respectively [3]. Since pyrolysis is an endothermic process, an energy input is required to heat the feedstock to the required reaction temperature. The heat of the reaction plays a significant role in the pyrolysis process [4]. The temperature-dependent reaction rate of pyrolysis is often governed by the Arrhenius equation. To date, pyrolysis technology remains one of the more significant research topics due to its capability of producing multi-products that have wide applications [5,6].

Catalytic pyrolysis processes [7] have gained the most significant attention in producing aromatics from biomass wastes. Pyrolysis can also enhance the properties of the hydro-char that is obtained by the hydrothermal carbonization of biomass waste [6]. Waste biomass can also be used to produce biochar for the removal of heavy metals from aqueous solutions during the pyrolysis process [8]. Recently, research has focused on co-pyrolysis, which involves the thermal co-processing of biomass and plastic mixtures [9]. The interactions between biomass and plastic waste during the co-pyrolysis process play an important role in the quality of the products (i.e., bio-oil, char, and bio-gas) derived from the process [10]. In addition, the heat transfer mechanisms also modulate the product specifications. Uniform heat distribution within the feedstock is essential for enhancing the required product selectivity. The generation of pyrolysis vapors and their flow pattern need to be controlled to enhance the efficiency of the process. The conduction mode of heat transfer is dominant in the solid phase of feedstocks, whereas, in the molten phase, the convection mode of heat flow occurs. Hence, understanding convection heat transfer is essential. Convection heat transfer facilitates overall heat transfer, uniform heating, high feedstock conversion rates, and enhanced energy efficiency. The modeling of such a process is important, and simulation results would be useful for experimental operation and equipment design.

1.2. The Role of Modeling in Pyrolysis

The role of modeling in pyrolysis is to develop a better understanding of the physical and chemical factors that affect the process. This includes the mechanism of heat transfer, the flow profiles within the reactor setup, phase change processes, and the reaction kinetics for waste material conversion. However, the complexity of the pyrolysis reaction makes conventional computational fluid dynamics (CFD) modeling difficult. Modeling when using model compounds is not accurate for actual feedstocks due to the influence of inorganic compounds on pyrolysis reactions, and due to the neglect of the potential relationships between various feedstock components. To accurately analyze biomass pyrolysis mechanisms, multi-scale modeling and experimental studies are necessary, and this is achieved by taking into consideration the interactions between biomass components and the in situ catalytic effect of biochar on product yields. Developing CFD models for biomass pyrolysis with better accuracy and optimized algorithms is also a significant challenge [11,12,13].

2. The Fundamentals of CFD

The fundamentals of CFD involve using a cost-effective and efficient simulation method for studying the process of pyrolysis, thereby allowing for both the design and optimization of process units. By simulating the features of chemical reactions and transport laws in reactors, CFD can help to understand the effect of hydrodynamics on the effectiveness of chemical kinetics and to the overall process in a reactor. It is a useful tool for predicting the essential parameters needed for controlling and optimizing installations. CFD simulations provide numerical solutions to the non-linear differential equations that govern the transport laws for mass, momentum, and energy through a system, and discretization techniques such as the finite difference model (FDM), finite volume method (FVM), and finite element method (FEM) have been used. CFD simulations are cost-effective and provide comprehensive information on the nature of flow and reaction processes through exhaustive data on velocity, temperature, and concentration profiles, which can be difficult to obtain through experimental research. CFD is flexible in adapting to new reaction conditions and settings, and it is aided by commercial packages that enhance the user experience and simplify the modeling of complex reactions or process setups. The three components of a CFD study are the pre-processor, solver, and post-processor [14,15,16,17].

2.1. Role of CFD in Pyrolysis

The pyrolysis process involves the devolatilization step, and various models have been developed to describe this step accurately. These models can predict the output patterns of flow, temperature, and product quality specifications at various parametric conditions. CFD has become a crucial simulation tool, and it is used in addressing various research and commercial aspects of the pyrolysis process. With the fast expansion of computational resources and software, CFD models for pyrolysis with better accuracy and optimized algorithms are now possible. CFD modeling can provide essential transport features at a lower cost compared to experimental methods. However, experiments are still required to test the applicability and efficiency of numerical models to predict the performance of real pyrolysis reactor setups. Therefore, significant research has been conducted recently on the CFD simulation of pyrolysis to improve our knowledge and utilization of the process [18].

To simulate the pyrolysis of different feedstocks, CFD models use sub-models of the reactor at the molecule, particle, and cell levels [19]. Temperature variation, flow rate, and output distribution during pyrolysis have been investigated using CFD simulation. Various studies have used CFD models to simulate different scenarios for various pyrolysis operating parameters, particle sizes, average heating rates, and the reaction mechanisms of the pyrolysis of different feedstocks. Three-phase product yields and the effect of temperature on the yields have also shown good correlation with experimentally obtained results, thereby showing the accuracy and viability of CFD simulations [20].

In their review paper, Luo et al. [19] provided a comprehensive overview of computational fluid dynamics (CFD) simulations of biomass pyrolysis in fluidized bed reactors, with a particular focus on particle-scale models. The authors examined various aspects of CFD simulations, including the mathematical formulation of fluidization, heat and mass transfer, reaction kinetics, and multi-phase flow modeling. They also discussed different types of particle-scale models, such as the Eulerian–Eulerian and Eulerian–Lagrangian approaches, as well as their respective advantages and limitations. The authors highlighted recent advances in modeling techniques, including the use of the discrete element method (DEM) for studying granular flow behavior and the incorporation of sub-grid-scale models to capture fine-scale phenomena. The paper concluded with an outlook on the future development of CFD simulations in biomass pyrolysis, thereby emphasizing the need for improved numerical techniques, multi-scale modeling, and experimental validation. Further, Lu et al. [21] discussed the application of MFiX (Multi-phase Flow with Interphase eXchanges) software for multi-scale CFD simulations of biomass fast pyrolysis. The authors provided an overview of the MFiX code and its capabilities, including its support for a range of multi-phase flow models, such as the Eulerian–Eulerian and Eulerian–Lagrangian approaches. They explored various aspects of biomass pyrolysis modeling when using MFiX, including reaction kinetics, heat and mass transfer, and fluid–particle interactions. The paper also reviewed recent studies that had employed MFiX-based simulations to investigate different aspects of biomass fast pyrolysis, such as reactor design, process optimization, and scaling up. The authors highlighted the benefits and challenges of using MFiX for pyrolysis simulations, and they suggested future research directions, including the integration of advanced sub-grid-scale models, improved numerical techniques, and experimental validations through which to enhance the accuracy and reliability of MFiX-based simulations in biomass pyrolysis applications.

CFD models have also been used to model fluidized pyrolysis bed reactors through the approach of computational particle fluid dynamics. To be acceptable for particle-scale computational fluid dynamics, exhaustive pyrolysis kinetic schemes and predictions should be reduced to simple statistical models. Numerous experiments and molecular simulations have been used to thoroughly analyze the chemical compositions and reactions that occur in biomass pyrolysis. Lumped global apparent kinetics is a useful technique for CFD simulations at the reactor scale. The pyrolysis products can be divided into biochar, bio-oil, and bio-gas by a simplified model of the kinetics [22,23,24,25,26]. Figure 1 illustrates the detailed application of CFD in pyrolysis.

Several studies have utilized computational fluid dynamics (CFD) to model pyrolysis processes, including both conventional and microwave-assisted pyrolysis. For example, Jayathilake and Rudra [27] investigated the use of CFD in modeling the pyrolysis of biomass and waste plastics, and they found that CFD simulations could effectively predict the behavior of key parameters such as producer gas yield and syngas composition. However, the accuracy of CFD simulations depends on several factors, including the availability of accurate reaction kinetics and the ability to model heat and mass transfer in the reactor. Ortner et al. [28] developed a computationally inexpensive modeling approach for the combustion of pulverized sewage sludge in entrained flow furnaces. Their study aimed to provide a CFD model that could rapidly and accurately provide solutions for efficient applications in research and development. The authors used a surrogate approach to implement the addition of limestone additive into the SFM model under the assumption of a complete calcination of the material. The models developed in this study can serve as a basis for more detailed particle kinetic models in the near future.

Another example of the use of CFD modeling in the context of biomass upgrading was demonstrated by Mendecka et al. [29]. Their work focused on the use of hydrothermal carbonization to upgrade olive pomace, and they employed CFD modeling to simulate the thermo-fluid dynamic performance of the process in a batch reactor. The authors used a parametric analysis to evaluate the temperature fields inside the reactor, and the output mass yields were understood as a function of the power input required by the process. The numerical results were validated with the experimental measurements that were conducted previously on a similar batch reactor. While the paper focused on hydrothermal carbonization rather than conventional pyrolysis, it provided an example of how CFD modeling can be used to understand the complex fluid dynamics, heat transfer, and reaction kinetics phenomena occurring under high-temperature and high-pressure conditions. This can be relevant to the discussion of the role of CFD in pyrolysis, as well as for the potential in using CFD modeling to optimize pyrolysis reactor design and to improve the efficiency of the process.

2.1.1. A Brief Overview of CFD Modeling Techniques for Pyrolysis

Pyrolysis is a complex phenomenon that involves the thermal decomposition of solid materials at elevated temperatures in the absence of oxygen. The pyrolysis process can be described by various physical and chemical mechanisms, and mathematical models on this process require accurately understanding and predicting the behavior of pyrolysis systems. CFD simulations can be used to model the pyrolysis process, but these simulations require a detailed understanding of the governing equations and the physical mechanisms involved in pyrolysis. There are various pyrolysis models that have been used in CFD simulations, including lumped models, distributed models, and detailed kinetic models. The choice of model depends on the level of detail required and the available computational resources. Lumped models, which assume that the solid material undergoes a one-step reaction to produce volatile gases and char, are the simplest type of pyrolysis model. The governing equations for a lumped model include a mass balance equation, an energy balance equation, and a chemical reaction rate equation. Distributed models are more complex than lumped models, and they account for the spatial variation of the pyrolysis reaction rate within the solid material. The governing equations for distributed models include a mass balance equation, an energy balance equation, and a diffusion equation. The mass balance equation and energy balance equation are similar to those in lumped models [30,31,32].

Detailed kinetic models, which account for the detailed chemical kinetics of a pyrolysis reaction, are the most complex pyrolysis models. These models require a detailed understanding of the chemical reactions involved, and they are computationally expensive. The governing equations for detailed kinetic models include a set of chemical kinetic rate equations, which describe the rates of the various chemical reactions involved in the pyrolysis process. These models also include mass and energy balance equations, which are similar to those in lumped and distributed models.

The most commonly used pyrolysis models in CFD are based on the assumption of two competing processes: devolatilization and char combustion. Devolatilization is the process by which volatile gases are released from the solid fuel, while char combustion is the process by which the remaining solid fuel is converted to ash. The rate of devolatilization and char combustion is typically governed by kinetic models that describe the reaction rates of the pyrolysis process. The most widely used kinetic models in CFD are the Arrhenius and global reaction model [33,34,35,36]. The Arrhenius model is based on the assumption that the rate reaction is proportional to the exponential function of temperature. The global reaction model assumes that the rate of devolatilization and char combustion is governed by a single reaction step. Recently, more advanced pyrolysis models have been developed to consider the complex interactions between the solid fuel, volatile gases, and char. These models include the discrete particle model, the multi-scale model, and the detailed chemistry model [37,38,39,40,41]. The discrete particle model (DPM) is a Lagrangian approach that tracks the individual particles of solid fuel, volatile gases, and char. The DPM model allows for a detailed characterization of the pyrolysis process, as well as for predictions of the size and shape of the particles produced during pyrolysis. The governing equations for the DPM model include the conservation of mass, momentum, and energy equations for each particle. The multi-scale model (MSM) is a hierarchical approach that considers the pyrolysis process at multiple scales, from the molecular level to the macroscopic level. The MSM model includes detailed chemistry models that describe the pyrolysis process at the molecular level, and the continuum models describe the transport phenomena at the macroscopic level. The governing equations for the MSM model include the transport equations for mass, momentum, and energy at each scale. The detailed chemistry model is a comprehensive approach that considers the detailed chemical reactions involved in the pyrolysis process. The detailed chemistry model includes a large number of chemical reactions and species, and it requires a high level of computational resources. The governing equations for the detailed chemistry model include the conservation equations for each chemical species, as well as the transport equations for mass, momentum, and energy.

In recent years, there has been growing interest in the use of CFD modeling to study the pyrolysis of biomass and waste plastics. One notable example is the integrated CFD-DEM (Discrete Element Method) and multi-step pyrolysis model [42], which combines fluid dynamics, heat and mass transfer, particle collisions, and the detailed thermo-chemical conversion of biomass. This model represents a significant advancement in the field of CFD modeling for pyrolysis as it allows for the accurate prediction of pyrolysis product yields and the evolution of syngas and tar species. Furthermore, this model can be used to study more complex issues such as tar removal and pollutant formation. Further, Luo et al. [43] proposed a CFD-DEM simulation of particle fluidization behavior and glycerol gasification in a supercritical water fluidized bed. The study was aimed at investigating the effect of particle size and fluidization velocity on the fluidization behavior of particles and the glycerol gasification process. The authors used the CFD-DEM method to simulate the fluidization behavior of particles and the glycerol gasification process in a supercritical water fluidized bed. The results showed that the fluidization behavior of particles and the glycerol gasification process were significantly affected by the particle size and fluidization velocity. The study provided valuable insights into the fluidization behavior of particles and the glycerol gasification process in a supercritical water fluidized bed, which can be useful for optimizing the design and operation of supercritical water gasification reactors. Chen et al. [44] discussed the use of CFD-DEM simulation in terms of modeling spouted bed dynamics in pyrolysis reactors, with a focus on the fluidized bed–chemical vapor deposition (FB-CVD) particle coating process. The study compared two different models for simulating spouted bed dynamics—CFD-DEM and CFD-LBM—and it found that the CFD-DEM model is more accurate for particle coating simulation. The study also investigated the impact of particle adhesion on spouted bed dynamics, and it found that the adhesion model leads to higher spouted heights.

Table 1. Different microwave modeling techniques and the solver used in the literature.

Models	Advantages	Disadvantages
Discrete Particle Model	It is preferred for granular or particulate systems, as well as for granular flow. It is suitable for investigating individual particle interactions. It finds application in blending and inter particle interactions	It is not suitable for large-scale or a large number of particle systems, and it has limitations in chemical reaction systems and modeling fluid flow
Multi-scale Model	It is suitable for the investigation of hierarchical and complex systems that are to be captured with significant information at the molecular, meso, and macro scales	Implementation is computationally expensive and complicated since the comprehensive understanding of the multiple scales and models are necessary
Detailed Chemistry Models	It is suitable for the investigation of complex chemical reaction systems, such as pyrolysis and combustion	A large number of chemical species involved in the systems are computationally expensive. Also, it is not suitable for systems where chemical kinetics are less dominant

shows a comparison of the models with the advantages and disadvantages of the discrete particle model, multiscale model, and of detailed chemistry models.

2.1.2. Sub Models for the Complex Physical and Chemical Processes during Biomass Pyrolysis

(A)

Reaction kinetics of pyrolysis

The pyrolysis of biomass is a thermo-chemical means for the conversion of biomass in the absence of oxygen so as to obtain a range of products such as bio oil, bio gas, and char. As of now, understanding the kinetics of the pyrolysis process has been a key area of interest for more than four decades. Reaction kinetic studies assist in predicting the yield of products, as well as aid in the optimization of reaction conditions for the maximum yield of desired products. The kinetics of biomass pyrolysis has been largely examined using thermal analysis methods. Thermo-gravimetric analysis experiments were conducted in coordination with ICTAC guidelines [45,46] to obtain reliable decomposition data for kinetic analysis. Comprehensive reviews have been provided by the ICTAC on the sample characterization, selection of appropriate heating rate, modeling isothermal/non-isothermal kinetic data, the verification of kinetic models, and for the significance of the kinetic parameters obtained [45,46,47,48].

The kinetic models for biomass pyrolysis can be divided into two broad categories, i.e., model fitting methods and model-free methods. Model fitting methods are conventional methods that are based on identifying a reaction network for the conversion of biomass to its products, and they are utilized by using the reaction network to evaluate the activation energy and pre-exponential factor for the set of reactions. This has led to the formulation of many global models (single-step and multi-step methods) regarding the conversion of biomass to char, bio-oil, volatiles, etc. Some of the global models that are widely used are shown in Table 2. Owing to the simplistic nature of these models and the ease of making kinetic predictions, the global models were explored widely by the researchers [49,50,51,52]. However, the reliability of the kinetic triplet obtained from these models was questionable. The activation energy and the pre-exponential factor obtained from these methods was largely influenced by the choice of the reaction mechanism (nth order reaction, diffusion reaction models, core-shrinking models, etc.). As the kinetic parameters were estimated by a forcible statistical fitting of the decomposition data to the chosen reaction mechanism, the ambiguity of the kinetic interpretations was a significant challenge to the widespread applicability of global kinetic models.

Model-free kinetic methods [46,51,52] evaluate the activation energy for the pyrolysis process without making any modelistic assumptions. Hence, they provide trustworthy kinetic predictions. The isoconversional methods of the Friedman, Kissinger, Kissinger Akahira Sunose, Flynn Wall Ozawa, and Vyazovkin methods are some of the more popular methods used extensively in the literature. The kinetic compensation effect is then used for an estimation of the pre-exponential factor [51,52]. Distributed activation energy models have also been used extensively recently to model the decomposition of biomass. They work by assuming the complex reaction proceeds through a series of independent reactions, which can be represented by activation energy distributions (symmetric/non-symmetric) [53].

Wide variability in the kinetic data for the biomass samples that decompose under similar pyrolysis conditions can be observed in the scientific literature. This drawback stems from the fact that no kinetic model to date has demonstrated the potential for efficiently modeling the intrinsic reaction mechanism and multi-step kinetic behaviour. Also, the applicability of kinetic predictions from small-scale TGA studies to large-scale pyrolysis reactor setups is uncertain. To predict the decomposition behavior in real pyrolysis reactors, the CFD models have to be coupled with single-particle reaction models. The parametric effects for single-particle reaction models have not yet been studied in the literature, and they should be addressed in the future.

Table 2. Reaction kinetics applied in the CFD modeling of biomass pyrolysis.

Types of Kinetics	Reaction Kinetic Steps		Reference
ine   Single-component single-step reaction kinetics	Competitive	Wood → gas Wood → tar Wood → char	[54,55,56,57]
	Non-competitive	Wood → gas + tar + char
Single-component multi-step reaction kinetics	Wood virgin→ Wood activated→ Gas + Tar + Char Wood → Tar; Tar → Gas		[58,59]
Multi-component single-step reaction kinetics	Cellulose → Gas + Tar + Char Hemicellulose → Gas + Tar + Char Lignin → Gas + Tar + Char		[60,61]
ine   Multi-component multi-step reaction kinetics	Cellulose	1. Biomass Activation	[62]
	Hemicellulose	2. Biomass decomposition to tar
	Lignin	3. Biomass decomposition to char and gas

Table 2. Reaction kinetics applied in the CFD modeling of biomass pyrolysis.

Types of Kinetics	Reaction Kinetic Steps		Reference
ine   Single-component single-step reaction kinetics	Competitive	Wood → gas Wood → tar Wood → char	[54,55,56,57]
	Non-competitive	Wood → gas + tar + char
Single-component multi-step reaction kinetics	Wood virgin→ Wood activated→ Gas + Tar + Char Wood → Tar; Tar → Gas		[58,59]
Multi-component single-step reaction kinetics	Cellulose → Gas + Tar + Char Hemicellulose → Gas + Tar + Char Lignin → Gas + Tar + Char		[60,61]
ine   Multi-component multi-step reaction kinetics	Cellulose	1. Biomass Activation	[62]
	Hemicellulose	2. Biomass decomposition to tar
	Lignin	3. Biomass decomposition to char and gas

(B)

Conservation equations for the biomass components

As the kinetics and the reaction mechanism for the pyrolysis process are incorporated in the numerical model, the conservative equations for each component of biomass are integrated into the model equations. The thermal decomposition of biomass is a combined effect of the decomposition of the individual biomass components i.e., lignin, cellulose, and hemicellulose. However, it is difficult to write conservation equations based on the three constituents as their synergistic effects are still not completely understood as of now. Hence, pyrolysis products are lumped into two fractions, i.e., solid or char and gaseous fraction [11,32]. The mass and momentum balance equation for solids and volatile gases is coupled with the energy equation to assist in evaluating the yield of the volatile gases and char. The macroscopic kinetic equations for each component are derived from the kinetic model. Due to the conversion process, the source terms of the appearance/disappearance of the components (positive/negative sign) are added in the mass conservation equations for each term as follows:

$$\frac{\partial \rho }{\partial t}+div\left(\rho \overrightarrow{v}\right)=S_m$$

(1)

$$S_{m,\mathrm{gas}}=\frac{k_2·m_{\mathrm{biomass}}}{V}$$

(2)

$$S_{m,\mathrm{char}}=\frac{k_3·m_{\mathrm{biomass}}}{V},$$

(3)

where $k_2$, $k_3$, and $k_4$ are the kinetic rate constants for the reactions obtained by the reaction kinetic studies [49,63]. The liquid fraction of condensable gases has also been considered in some models as an additional model component. The energy conservation for solids is expressed by the following equation:

$${\rho }_s{C}_{ps}\frac{\partial T_s}{\partial t}+\nabla q_s=Q_s$$

(4)

where $Q_s$ is the energy source term due to the pyrolysis reaction, and it is expressed in terms of the specific heat of the pyrolysis reaction.

For the fluid (volatile gas/condensed liquid) domain, the energy equation is as follows [32,49]:

$${\rho }_f{C}_{p,f}\frac{\partial T_f}{\partial t}+{\rho }_f{C}_{p,f}{u}_f·\nabla ·T_f+\nabla ·q_f=Q_f$$

(5)

(C)

Moisture evaporation

The evaporation of moisture has also been considered by several researchers in their mathematical model for pyrolysis process. Moisture evaporation can be modeled as an additional mass transfer phenomena in the energy balance equation. The volumetric source terms for evaporation is added into the model equations. Different equations for the source terms have been given in the literature depending upon the approach taken to model moisture evaporation. Lee et al. [64], Hobbs et al. [65], and Di Blasi [66] considered the phenomena as a diffusion controlled evaporation process, and they defined the heat source term as follows:

$$S_{m,\mathrm{evap}.\mathrm{water}}={\nu }_p{A}_p{D}_m\left({\rho }_v-{\rho }_{{\mathrm{H}}_2\mathrm{O}}\right)$$

(6)

where: $v_p$—particle density number; $A_p$—particle surface area; $D_m$—mass transfer coefficient; ${\rho }_v$—moisture concentration in the particle; and ${\rho }_{{\mathrm{H}}_2{\mathrm{O}}^{-}}$ moisture concentration in the particle surroundings (mass/gas volume).

The above expression considers that the temperature remains constant in the drying phase. A constant rate of evaporation is independent of temperature, and the moisture content can be assumed for such cases.

Some researchers have modeled the moisture evaporation as a mass transfer step, and they have considered the temperature dependency of the biomass sample while defining the mass source term. The following expression given by Wickramaarachchi and Narayana [67] has been widely explored by researchers:

$$S_{m,\mathrm{evap}.\mathrm{water}}=\frac{\left(T_S-T_i\right)·m_{\mathrm{moisture}}·c_{p,H_{2}O}}{V·\mathsf{\Delta }h·\mathsf{\Delta }t}$$

(7)

where $T_S$—feedstock temperature; $T_i$—initial temperature of the feedstock; $c_{p,{\mathrm{H}}_2{\mathrm{O}}^{-}}$—specific heat capacity of water; $\mathsf{\Delta }h$—water evaporation heat; and $\mathsf{\Delta }t$—calculation time step size.

A high moisture content in the biomass results in a low calorific value; hence, many researchers have considered a pre-treatment of the sample to remove moisture before the pyrolysis process. In such cases, the modeling of moisture removal can be avoided.

(D)

Variation in physical properties

As the pyrolysis reaction progresses, the sample mass decreases and the porous biomass undergoes particle shrinkage or swelling depending upon the internal structure, orientation, and the source of the biomass [68]. This further complicates the interplay between heat and mass transfer both on the surface and inside the biomass sample. Under these conditions, the assumption of constant physical properties in the model equations needs to be relaxed as the physical properties are now a function of temperature [49]. The thermal conductivity of the sample decreases drastically (reduction by 70–80%) as the biomass sample is converted to char [69,70]. The density also shows a similar behavior and is modeled as a linear function of temperature. The specific heat capacity shows a feeble dependence on temperature [70].

The physical properties of the biomass sample are also taken as a function of conversion (X(t)) of the biomass to volatiles and char [63,71,72,73]. Effective properties are defined as a function of conversion by the expression given by Equation (8), where $\varphi$ is any physical property (density, thermal conductivity, or specific heat).

$$\varphi \left(\mathrm{t}\right)=\mathrm{X}\left(\mathrm{t}\right){\varphi }_{\mathrm{biomass}}\left(\mathrm{t}\right)+[1-\mathrm{X}\left(\mathrm{t}\right)]{\varphi }_{\mathrm{char}}$$

(8)

Some researchers have considered the contribution of radiative heat transfer during the biomass pyrolysis process on thermal conductivity. Radiant conductivity has been shown to have additional dependence on the porosity and the pore diameter for single, large-particle pyrolysis. Several models for radiant conductivities have been given in the literature. Some of the commonly employed models used were developed by Chan et al. [72] and Panton and Rittmann [73].

(E)

The heat of pyrolysis

The thermal effects in biomass pyrolysis greatly influence the intra-particle temperature distribution, and they also adversely affect the optimal operation of the decomposition process at the desired temperature. The heat of pyrolysis acts as a heat source for influencing the temperatures on the surface and the interior of the heated pyrolysis products. This varies with the progress of the decomposition reaction, thereby giving rise to variable temperature gradients and hotspots within the particle. The temperature distribution within the particle is essential in the design of the pyrolysis reactor. Several thermal models have been developed to model this effect in the CFD studies for the decomposition of biomass [69,74,75,76,77,78]. The heat transfer in porous media modeled using Darcy’s law have been used in the literature to numerically analyze the thermal effects in a pyrolysis process [69,76,77,78]. The strong coupling in the velocity, the temperature fields, and the complex physics of the process pose significant challenges for the researchers in this field. The numerical predictions from CFD studies need sufficient experimental studies to validate the numerical results for the distribution of velocity and temperature fields. The paucity in the experimental results for the prediction of the intra-particle velocity and temperature fields is also a major research barrier. A recent study by Wijayanti et al. [69] compared the experimental and numerical results of the average temperature distribution within a biomass packed bed during a pyrolysis process. The two predictions only matched during the initial phase of the pyrolysis process. As the thermal effects set in, large deviations in the two profiles could be observed. The heat of reaction strongly influenced the heat transfer rates in the packed bed. Hence, more research efforts need to be expended both experimentally and numerically on understanding the effect of heat of reaction during a pyrolysis process.

2.2. Research Gap and Objectives

The existing literature indicates a significant research gap in the in-depth analysis of CFD modeling for both the reactor system as a whole and various particle domains [63]. The temperature distribution within the biomass feedstock and the pyrolysis reactor is a critical factor in the development of the pyrolysis process, and it is influenced by particle geometry, heating conditions, and its surroundings. A detailed CFD model can enable real-time process observation and the measurement of various parameters that define the process and reactor functioning, which would be physically or economically impractical under experimental studies. To the best of our knowledge, no prior reviews or relevant studies have been conducted on this specific topic.

The extensive use of CFD for modeling biomass pyrolysis in reactors at the particle scale exists in the literature, and there also exists a systematic discussion and comparison of model creation for the modeling of intra-particle transport–reaction processes during biomass pyrolysis [19]. A CFD model of the pyrolysis of slag granules in an oven was studied with a focus on resource use and thermal energy storage efficiency [79]. The development of the pyrolysis of waste plastic polymer species from both analytical and modeling considerations was examined with an improvement in product yields and characteristics from both analytical and modeling considerations [80]. There was a presentation of quantitative and qualitative findings, as well as an explanation of the main mathematical equations used to analyze advanced pyrolysis processes through CFD.

This paper aims to comprehensively study the pyrolysis of feedstocks in advanced pyrolysis systems such as microwave-assisted pyrolysis and solar pyrolysis through CFD modeling. There are no prior reviews regarding the CFD simulation of microwave-assisted pyrolysis and solar pyrolysis, and the use of CFD modeling to research advanced pyrolysis is still in its developmental stage. This paper presents both quantitative and qualitative findings, along with an explanation of the main mathematical equations used to analyze advanced pyrolysis processes through CFD.

3. CFD in Conventional Pyrolysis

3.1. Analysis of CFD Studies

With the rise in interest in biomass pyrolysis, numerical modeling studies have been conducted to investigate the process at different scales. These scales range from the molecular level and reaction kinetics to the reactor level for estimating product compositions [81,82,83]. Although multi-scale investigations are crucial, the input parameters from the molecular and particle scales are elementary and require integration with reactor levels for designing, scaling up, and optimizing industrial applications. Biomass pyrolysis is complex due to its multi-phase flow, as well as due to the several chemical reactions that occur during the process. Furthermore, the dynamics of the process become more complicated due to the formation and interaction of different phases. As a result, the system becomes multiscale, and the inter and intra-particle mass, momentum, and heat transfer are coupled with the production of bio-gas during pyrolysis. While experimental investigations are possible, numerical simulations have become more attractive due to the rise in computational power. Researchers have been modeling the reactor to examine reactor design, scale up, and optimization studies so as to obtain the best operating conditions [12,84,85,86].

Researchers are primarily interested in the complex kinetics of the pyrolysis that is followed by reactor design and particle modeling. To develop an economic and efficient reactor for pyrolysis, a comprehensive understanding of the transport phenomenon, along with reaction kinetics, is essential. Computational fluid dynamics (CFD) is a well-recognized numerical modeling field for solving complex multi-phase flow problems, and it is also suitable for modeling and simulating the biomass pyrolysis system.

Biomass pyrolysis occurs in multiple stages, including water evaporation; the emissions of volatile matter, gases, and tar; and the production of fixed carbon or char. The secondary decomposition of the products occurs within the feedstock particle and gas phase. Intra-particle heat transfer and chemical conversion processes, coupled with external flow control, regulate the formation of product gas, char, and carbon. Syngas formation in the reactor is primarily driven by heat transfer, as well as by the movement of the gas products and particle collisions. The heat and mass transfer of biomass particles with reaction kinetics play a significant role during pyrolysis. During microwave pyrolysis, the heat produced can cause the reactor walls to deform.

Solar pyrolysis is a promising technology for converting biomass into valuable products when using solar energy. This technique involves the use of concentrated solar radiation to heat the biomass to high temperatures in the absence of oxygen, thus causing it to decompose into different compounds. Solar pyrolysis offers several advantages over traditional methods that rely on fossil fuels, including reduced carbon emissions and increased energy efficiency. Several studies have been conducted to investigate the feasibility and potential of solar pyrolysis, including experiments with different types of biomass and solar reactors. For instance, Kumar et al. [87] demonstrated the production of bio-oil from sawdust that had a high yield and energy efficiency, while Mujumdar et al. [88] produced biochar from wood chips with a high carbon content and low ash content (thus making it suitable for soil amendment). Additionally, Zhao et al. [89] investigated the use of solar pyrolysis to produce biochar from a corn stover with low heavy metal content. These studies suggest that solar pyrolysis could become a promising technology for sustainable biomass conversion.

3.2. Reaction Kinetics for CFD Simulation

As discussed in the literature, biomass constitutes three major components: cellulose; hemicellulose, which is a type of polysaccharide; and lignin, which is a polymer of cyclic organic material. The yield of the products formed in the pyrolysis is strongly dependent on the reaction temperature, heating rate, and time. In comparison with conventional techniques, pyrolysis operates at low temperatures. The low temperatures with long residence times produce char, and high temperatures with long residence times produce significant amounts of gas. Average temperatures and small residence are required to produce oils with high heat rates. Fast pyrolysis takes place within few seconds; therefore, the reaction kinetics, phase change, heat, and species balance play major roles. In these cases, maintaining an optimum temperature is a big challenge when trying to avoid undesirable products. The reaction kinetics of biomass pyrolysis are very complex due to the presence of multiple diverse chemical species and unknown kinetics. Biomass kinetics depend on the biomass characteristics, de-volatilization, secondary gas phase reactions, and char formation. Long-chain hydrocarbons, in general, go through two stages of decomposition, i.e., primary and secondary reactions. The primary reactions are classified as (a) the decomposition of aldehydes, carbonyl, acids, and alcohols, (b) the depolymerization of the sugars, and (c) the dehydration of the char gases. The secondary reactions are mainly the cracking and water gas shift reactions, which occur at high temperatures. Thermal degradation of the cellulose takes place in two steps: those with a low temperature range and high activation energy, and those with a high temperature range and low activation energy. Therefore, the combination of these multiple reaction steps makes biomass pyrolysis a complicated process [90]. Implementing biomass pyrolysis in CFD simulations without the fundamental steps in the reaction kinetics of the conversion process is very difficult. Essential biomass pyrolysis reactions, such as devolatilization and the cracking of tar, must be considered in CFD modeling [91]. However, implementing all of the reaction kinetics may predict accurate reactor performance, but that would simultaneously consume a great deal of computational power. To optimize both cases, researchers have applied lumped global kinetics, which involves the consideration of a finite number of reactants and reactions. In the past few decades, several studies have reported detailed kinetics for overall biomass pyrolysis. Single-component single-step reaction kinetics have been applied to investigate the reaction kinetics in CFD simulations.

The reaction kinetics of wood decomposition were studied using single-component and single-step reaction kinetics. Competitive reaction types [54,55] are generally defined as parallel reactions, wherein each product is formed by feedstock, and the non-competitive reaction types [56] are defined as series reactions (where all of the products obtained from feedstock are obtained in a single reaction, as shown in Table 2). Single-component multi-step reaction kinetics that are followed by secondary decomposition for the decomposition of wood-based biomass into simpler, smaller molecules have been employed in CFD studies [58,59]. To study the primary components’ effect in biomass, such as cellulose, hemicellulose, and lignin, multi-component single-step reaction kinetics have been used. In this scheme, each component’s conversion to products such as gas, tar, and char is considered as one single-step reaction [60]. Following numerous kinetic investigations, a multi-component, multi-stage reaction kinetics model was suggested, which was derived by integrating all of the proposed schemes [62]. This scheme was the most accurate among all due to the implementation of biomass activation, biomass decomposition to tar, and biomass decomposition into char, as well as then further into gas for all of the components such as cellulose, hemicellulose, and lignin [92,93]. The reactor performance and accuracy mainly depend on the kinetics considered in the CFD calculations, which are uncertain in lumped kinetic models. To overcome this challenge, Mellin et al. developed a complex reaction kinetics by integrating the chemistry of each component’s decomposition kinetics comprehensively, as well as by modeling it in 3D CFD simulations [94]. Various reaction kinetics were applied using CFD, and they are shown in

Table 3. Transport equations and kinetics applied on Biomass system in the literature (F: Fluid; P: Particle).

System	Model Type	Mass Conservation		Momentum Conservation		Heat Conservation		Kinetics	Remarks	References
		F	P	F	P	F	P
Biomass bubbling fluidized bed	Multi-phase particle in cell framework	A	NA	A	A	A	A	Semi global kinetics	Model successfully captured the product yield at various operating conditions, and it found that the velocity and temperature of reaction were the most impacted parameters	[97]
Spouted bed reactor	Multi-phase particle in cell framework	A	A	A	A	A	A	Semi global kinetics	CPFD model with MSB-TGA results were not accurate due to the insignificant secondary tar decomposition kinetics	[97]
Imbert downdraft gasifier	Species transport along with k-$\epsilon$ for turbulence and the discrete phase model for particles	A	NA	A	A	A	A	Finite-rate reaction kinetics	CFD model applied to obtain producer gas composition to optimize the operating conditions and design parameters	[98]
Fluidized bed reactor	Eulerian–Eulerian CFD model	A	A	A	A	A	A	Lumped, multi-component, multi-stage kinetic mode	Fast pyrolysis major parameters predicted by CFD model with defined cellulose, hemicellulose and lignin	[99]
Fluidized bed reactor	Eulerian multi-phase flow model	A	A	A	A	A	A	Simple, global, and advanced kinetic scheme	Hydrodynamics predicted the mixing behaviors, and the advanced kinetic scheme improved the prediction	[93]
Fluidized bed reactor	Eulerian–Eulerian multi-fluid CFD model	A	A	A	A	A	A	Competitive reaction kinetics	Implementation of the particle shrinkage effects during pyrolysis improved the model prediction	[100]
Spouted bed reactor	Eulerian–Eulerian multi-phase CFD model	A	A	A	A	A	A	Competitive single-component single-step kinetics	The addition of kinetic theory granular flow to the CFD model enables one to predict pyrolysis yields better	[101]
Spouted bed reactor	Eulerian–Lagrangian particles in cell model	A	A	A	A	A	A	Two-step kinetic mechanism	The physical and thermo- chemical properties of biomass pyrolysis in spouted reactors are explored	[102]

A—applied; NA—not applied; F—fluid; and P—particle.

. The chemical percolation devolatilization (CPD) model was initially applied to study the devolatilization phenomenon in coal combustion. Later, it was developed into the Bio-CPD model to study biomass pyrolysis in the gas release during volatilization, as well as in the coke formation of cellulose, hemicellulose, and lignin [95,96]. It is a simplified and computationally feasible approach for modeling the complex pyrolysis reactions.

3.3. Development of Numerical Models

To model biomass pyrolysis, a comprehensive understanding of mass, momentum, and heat transport is essential. The pyrolysis process has been simulated using various reactor setups, including fixed-bed reactors, fluidized bed reactors, and ablative reactors. In a fixed-bed setup, the biomass feedstock is packed into the bed, and the gas flows through the voids of the packed bed. Heat is supplied from the bed walls, and it flows through the external feedstock particles toward the center of the bed. Once this energy reaches the surface of the feedstock, intra-particle heat transfer occurs in the radial direction. The pressure difference created in the packed bed drives the produced gas to merge with the inlet gas stream. Porous media characteristics are used to simulate the behavior of the biomass feedstock during the conversion process, and these are based on the properties of the packed bed and the gas flow through the voids.

During computations, a packed bed is typically divided into two zones: a fluid flow regime and the porous media. In general, a pseudo-thermal equilibrium assumption is made to simplify the numerical simulations, whereby the porous media is considered a homogeneous medium [49]. The biomass pyrolysis system is a multi-phase and multi-component porous medium.

The mass conservation equation is shown in Equation (9)

$$\epsilon \frac{\partial }{\partial t}{s}_l{\rho }_l+\nabla ·\left(s_l{\rho }_{l}v\right)=s_m,$$

(9)

where $\epsilon$ is the porosity of the medium, $s_l$ is the local volume fraction of the phase 1, $v_l$ is the superficial velocity vector (which can be obtained from the Darcy law for phase 1), and $s_m$ denotes the interfacial mass transfer rate from all of the phases to phase 1. If there is no source or sink in the system, then $s_m=0$.

Momentum transfer equation in phase 1 in the form obtained from Darcy’s law Equation (10) or Equation (11).

$$v_l=-\mathrm{K}\frac{k_{rl}}{{\mu }_l}\left(\nabla P_l-{\rho }_{l}g\right)$$

(10)

$$\frac{\partial s_l{\rho }_{l}v}{\partial t}+\nabla ·s_l{\rho }_{l}v·v=-\nabla ·\left(s_l{T}_l\right)-s_l\nabla P_l-\frac{v{\mu }_l}{\mathrm{K}}+R_l+s_l{\rho }_{l}g$$

(11)

In Equation (10), the gravitational force effects are considered. $\mathrm{K}$ is the absolute permeability of the feedstock material, $k_r$ denotes the relative permeability of the feedstock, ${\mu }_l$ denotes the viscosity of phase $1,\nabla P_l$ is the pressure drop in phase $1,{\rho }_l$ is the density, $R_l$ is the momentum source term, $T_l$ is the shear stress, and $\mathrm{g}$ is the acceleration of gravity.

The species balance or mass transfer equation is shown in Equation (12).

$$\frac{\partial \epsilon {\rho }_l{s}_l{C}_l^{\propto }}{\partial t}+\nabla ·{\rho }_l{v}_l{C}_l^{\alpha }=-\nabla ·\left(\epsilon {\rho }_l{s}_l{D}_l^{\alpha }\nabla C_l^{\alpha }\right)+S_m$$

(12)

Equation (12) denotes the mass balance equation, where $C_l^{\propto }$ is the species, the $\alpha$ concentration in phase 1, and the right hand side first term is the diffusive flux of species ∝ in phase 1 due to the diffusion of molecules. The external reactions or component generation are denoted by the second term, $s_m$, in Equation (12). The energy conservation equation is shown in Equation (13).

$$C_{pg}\frac{\partial }{\partial t}T\left(\epsilon h_l{s}_l{\rho }_l\right)+\nabla ·\left({\rho }_l{u}_l{h}_l\right)=\nabla ·\left(s_l{k}_1\nabla T\right)+q_l$$

(13)

Equation (13) denotes the heat balance equation, where $C_{pg}$ indicates the specific heat capacity of the gas, and $k_1$ and $q_1$ are the thermal conductivity of phase 1 and the heat flux related to phase 1, respectively. Local thermal equilibrium is the assumption widely applied in CFD simulations to simplify multi-phase equations into one, and this is achieved by considering the negligible thermal gradient in the system (i.e., $\frac{\partial }{\partial r}T=0,T_l=T$).

In general, the heat flux of the several phases written in summation of the individual phases is shown in Equation (14).

$$\sum _l{q}_l=q$$

(14)

The term enthalpy, $h_1$, can be written as is shown in Equation (15).

$$h_k=h_k^0+{\int }_0^T{c}_{\mathrm{Psff}}dT,$$

(15)

where $c_{\mathrm{peff}}$ is the effective specific heat capacity, and $h_k^0$ denotes the standard enthalpy at the reference temperature of $298\mathrm{K}$.

Wang and Chen et al. developed a finite difference one-dimensional heat and mass transfer model to study the hygroscopic effect in the freeze drying of skim milk [103]. The simulation results showed that the drying time was 33.3% shorter with the presence of the dielectric material. Rattanadecho developed a two-dimensional finite difference model to investigate the microwave heating of wood when using a rectangular guide [104]. The sample size, irradiation time, and temperature dependency on wood dielectric properties were accurately predicted by this model. Finite element modeling is the another widely used approach after the finite difference method in the modeling of pyrolysis. Romano et al. developed a three-dimensional finite element model, which includes electromagnetic field distributions by solving the Maxwell and Lambert laws. FEMLAB was the commercial software package applied to simulate the heat distribution during microwave heating of the food [105]. Geedipalli et al. investigated the role of a carousel in the improvement of heat distributions in microwave ovens with the finite element model coupled with the Maxwell equation. ANSYS computational software was used to simulate the microwave environment, in which it was predicted that the application of the carousel would increase the temperature uniformity by 40% [106]. The finite element model in combination with Maxwell equations has also been applied to investigate the heating process, and this was achieved by microwaves in the catalytic bed for the purpose of methanol steam reformation [107].

3.4. CFD in Conventional Pyrolysis Reactors

Computational fluid dynamics (CFD) has been extensively used to study conventional pyrolysis reactors, including fluidized and packed bed reactors. It has been used to understand the mass, momentum, and energy balance equations used in multiple phases, as shown in

Table 4. Different microwave modeling techniques and the solver used in the literature.

Solver	Application or System	Law	Dimension	Variable	Reference
Finite Difference	Microwave furnace	Maxwell	Two	Temperature and electric field	[108]
Finite Difference	Freeze drying	-	One	Temperature	[103]
Finite Difference	Microwave heating	Maxwell	Three	Temperature and electric field	[104]
Finite Difference	Microwave-assisted pyrolysis of wood block	Maxwell	Two	Temperature and electric field	[109]
Calorimetric Technique	Microwave drying	Lambert	Zero	Power	[110]
Finite Element	Microwave drying	Lambert	Three	Moisture and temperature	[111]
Finite Element	Microwave drying	Lambert and Maxwell	Three	Temperature and absorbed power	[105]
Finite Element	Microwave heating with stationary and rotating objects	Maxwell	Three	Temperature and absorbed power	[106]
Finite Element	Steam methanol reforming by microwave heating	Maxwell	Three	Temperature, conversion, and yield	[107]
Finite Element	Convective or microwave-assisted drying	Maxwell	Two	Temperature and moisture	[112]

. For example, biomass fast pyrolysis was investigated in a bubble fluidized bed using a 3D reactive gas–solid CFD simulation. Semi-global chemical kinetics were incorporated for the pyrolysis reaction in the solid and fluid flow. A CFD multi-phase particle-in-cell approach showed a perfect match with experimental studies [97]. However, there was a significant difference in the product yield when compared to other experimental studies due to the application of different chemical kinetics on the secondary decomposition reaction of the tar when using computational particle fluid dynamics (CPFD), whereby the semi-global kinetics obtained from a spouted bed thermo-gravimetric analyzer (MSB-TGA) were used to predict the product yield. The inaccuracy could be reduced if the actual spouted bed reactor kinetics were incorporated with the CFD model [98].

CFD is a useful tool for modeling complex processes such as biomass pyrolysis due to the excellent heat, momentum, and mass profile predictions, which are coupled with the reaction kinetics. For instance, an Eulerian–Eulerian multi-phase CFD model successfully predicted the key features in a fast pyrolysis that was conducted in a biomass fluidized bed reactor by providing known amounts of cellulose, hemicellulose, and lignin [93]. An Eulerian–Eulerian CFD model predicted the experimental results better by relating the particle size, mixing behavior, and multi-phase flow hydrodynamics. Advanced kinetic schemes with more exhaustive network combinations improved these predictions [100]. During pyrolysis, the biomass particle size gradually decreases, which must be incorporated into the CFD model for accurate predictions. A Eulerian–Eulerian multi-phase fluid model was developed to study this behavior by incorporating competitive reactive kinetics with the particle shrinkage effect. The model forecast that, with an increase in the char content, the particle size would shrink and the density would increase [101]. The Eulerian–Eulerian method follows the interpenetrating continua. This approach is mostly applicable in the thermo-chemical conversions in fluidized beds due to the simplification in interparticle collisions, which reduces the computational speed. However this approach is not suitable for obtaining intra-particle physics estimations of a solid-phase process. The Eulerian–Langragian method is well suited for the estimation of gas- and solid-phase physics, as well as for thermo-chemical properties at a smaller scale. A two-dimensional CFD model that was incorporated with the kinetic granular flow model showed a good match with the experimental studies conducted regarding hydrodynamics and yield predictions in a spouted bed reactor [102]. The physical and thermo-chemical properties of biomass pyrolysis in a spouted reactor were estimated using the multi-phase particle-in-cell approach with the Eulerian–Lagrangian method [113]. The simulation results showed that the accumulation of the biomass particles at the annulus affected the thermo-chemical behavior of the system. Increases in the gas inlet velocities improved the vertical flux and turbulence of the gas phase. According to a literature survey, a CFD model with the implementation of particle shrinkage effects, advanced kinetic schemes of secondary decomposition reactions, and particle hydrodynamics can predict complex biomass pyrolysis.

In addition to fluidized beds, a CFD Eulerian packed bed model was applied to grate biomass furnaces in order to study bed morphology, fouling, slagging, and corrosion during combustion. The CFD tool was widely used to design the packed bed based on hydrodynamics, as well as on mass and heat transfer characteristics [114,115]. A comprehensive understanding of biomass pyrolysis is required to predict the thermo-chemical and physical characteristics of the process. Therefore, novel multi-scale models were developed for the couple reaction kinetics, intra-particle, and inter-particle interactions in a packed bed. Multi-scale estimations of pyrolysis are possible by combining pyrolysis kinetics, particle-scale models, and superquadric discrete element method-computational fluid dynamics (super DEM-CFD) in the open-source code of MFix [116]. This model solves the particle, in one dimension, inside the particle, and it also simultaneously solves the packed bed in the axial direction. The packed bed results showed significant non-uniformities in temperature and mass fraction. The Eulerian and Lagrangian approaches in multi-scale and multi-phase CFD methods have been widely used in biomass pyrolysis [32]. Figure 2 illustrates the application of CFD in conventional pyrolysis reactors.

4. CFD Models for Microwave-Assisted Pyrolysis

The applications of CFD in microwave-assisted pyrolysis are of a significantly lesser number compared to biomass pyrolysis or gasification studies. The major difference observed between microwave-assisted pyrolysis and other conventional studies was in the definition of the energy source term. An additional energy source term would be added for the solid phase in a porous media. The biomass absorbing power produces the internal heat generation that occurs during the microwave-assisted pyrolysis caused by the microwaves. The famous Lambert law is generally applied to define this source term. Increases in the temperature of the biomass depends on the total microwave energy absorbed by the biomass material. The microwave absorption power per volume can be expressed as an exponential decay, which is proportional to the penetration depth and surface absorption [117]. The absorption power can be expressed as in Equation (16).

$$P=P_0{e}^{-y/D_y}$$

(16)

In the above equation, y is the distance from the biomass surface, $D_p$ denotes the penetration depth, and $P_0$ is the microwave surface power absorption. The penetration depth (shown in Equation (17)) can be represented as function of the dielectric constant and loss factors.

$$D_p=\frac{{\lambda }_{\mathrm{freespace}}/\left(2\pi \sqrt{{28}_r^{dc}}\right)}{\sqrt{1+{\left(\frac{l_r^{lf}}{0_r^{dc}}\right)}^2}}$$

(17)

The ${\lambda }_{\mathrm{freespace}}$ denotes the microwave wave length in the free space, ${\epsilon }_r^{dt}\mathrm{I}$ is the dielectric constant, and ${\epsilon }_r^{lf}$ is the dielectric loss factor. The microwave power (MWP) is derived as is shown in Equation (18).

$$MWP=S{P}_0{\int }_0^L{e}^{-y/D_p}dy$$

(18)

The microwave surface power absorption can be obtained by solving Equation (19).

$$P_0=\left(\frac{Mp}{s}\right)\left(1-e^{\left(\frac{\mathrm{r}}{D_p}\right)}\right)D_p$$

(19)

s is the cross sectional area in ${\mathrm{m}}^2$, and t is the sample thickness in $\mathrm{m}$. Solving the given equations of the microwave absorption power is obtained using Equation (20).

$$P=\left[\frac{\frac{MP}{S}}{1-e^{-\frac{t}{D_p}}{D}_p}\right]e^{\left(-\frac{y}{D_p}\right)}$$

(20)

The microwave absorbed power per volume (MAP) is used in the heat conservation equation of the porous media, which is represented by Equation (21).

$$MAP=\frac{p}{\mathrm{volume}\mathrm{of}\mathrm{the}\mathrm{biomass}\mathrm{particles}}$$

(21)

The energy balance equation of the porous media can be written as Equation (22) [118].

$$C_{pg}\frac{\partial }{\partial t}T\left(\epsilon h_l{s}_l{p}_l\right)+\nabla ·\left(p_l{u}_l{h}_l\right)=\nabla ·\left(s_l{k}_1\nabla T\right)+q_l+MAP$$

(22)

Microwave-assisted heating generally contains several electromagnetic equations, which represent the motion of microwaves in the free space. To incorporate the microwave irradiation term in the heat conservation, Maxwell equations are applied. The microwave radiation modeling for biomass gasification can be improved with the addition of external effects such as the phase change and boundary movement in the system. The electric and magnetic fields are given through Equations (23) and (24) [119,120].

$$\epsilon \frac{\partial E}{\partial t}=\nabla \times H-{\sigma }_{e}E$$

(23)

$$\mu \frac{\partial H}{\partial t}=-\nabla \times E$$

(24)

where ${\sigma }_{\theta }$ is the electric conductivity, $\mu$ is the magnetic permeability, and $\epsilon$ is the electrical permittivity.

In addition to the energy balance equations and electromagnetic wave equations described in the previous sections, the velocity equations play a crucial role in predicting the fluid flow, heat transfer, and chemical reactions during microwave-assisted pyrolysis since the species, momentum, and energy balance equations are coupled. The Navier–Stokes equations, which consist of the continuity equation and the momentum equation, are the primary equations used to describe the fluid flow in the process [121,122]. The continuity equation accounts for the conservation of mass in the fluid domain, and it is given by Equation (25).

$$\nabla ·\left(\rho u\right)=0$$

(25)

The momentum equation represents the conservation of momentum, and it is given by Equation (26).

$$\frac{\partial \left(\rho u\right)}{\partial t}+\nabla ·(\rho u\otimes u)=-\nabla p+\nabla ·\left(\mu (\nabla u+{(\nabla u)}^T)\right)+F$$

(26)

where $\rho$ is the fluid density, u is the fluid velocity vector, p is the pressure, $\mu$ is the dynamic viscosity, and F is the body force vector (which includes gravity and the electromagnetic forces that are due to microwaves) [121,122].

Furthermore, the discrete phase model (DPM) is often used to simulate the behavior of solid biomass particles during microwave-assisted pyrolysis [123]. The DPM calculates the particle trajectory using the Lagrangian approach, and it considers the forces acting on the particles such as the drag, lift, and virtual mass forces. In combination with the energy balance and electromagnetic wave equations, the velocity equations provide a comprehensive framework for modeling and analyzing the complex multi-phase flow and heating phenomena in microwave-assisted pyrolysis systems.

Compared to the normal conventional and microwave-assisted pyrolysis, the major difference for the accurate predictions is found in the additional source term $q_e$. The energy conservation equation can be written as Equation (27), which is the simplified version of the Equations (13) and (22).

$$\rho C_p\frac{\partial }{\partial t}T=\nabla ·(k\nabla T)+q_e$$

(27)

Here, $\rho$ is the density, $C_p$ is the specific heat capacity, and k is the thermal conductivity. $q_e$ is the major term that represents the microwave heating in the system. The heat generation term can be written as is expressed in Equation (28).

$$q_e=2\pi f{\epsilon }_0{\epsilon }_r(tan\delta )E^2$$

(28)

Here, E is the electric field, $\epsilon$ is the dielectric constant, and f is the frequency. In general, microwave irradiation not only effects the microwave properties of the material, but also dielectric properties such as the permittivity and dielectric constant [124,125]. Heating effects of the microwave can be written as is expressed in Equations (8)–(10), and this is achieved by combining them with the microwave absorption power.

Temperature and moisture profiles can be obtained by solving Equations (29) and (30) during the process of microwave heating [126].

$$\frac{\partial W}{\partial t}=\frac{\partial \left[D_{eff}(T,W)\frac{\partial W}{\partial z}\right]}{\partial z}+\frac{\partial \left[D_{eff}(T,W)\frac{\partial W}{\partial r}\right]}{\partial r}$$

(29)

$${\rho }_2\left(C_{pg}+W{C}_{PW}\right)\frac{\partial }{\partial t}T=k\frac{\partial \left[\frac{\partial T}{\partial z}\right]}{\partial z}+k\frac{\partial \left[\frac{\partial T}{\partial r}\right]}{\partial r}+Q$$

(30)

Here, W is the moisture present in the biomass, $D_{eff}$ is the effective diffusivity, and r and z are the radial and axial coordinates, respectively. The materials change their volume by shrinking during the microwave irradiation, which can be defined by Equations (31) and (32) [111].

$$\frac{\partial Y}{\partial t}=D_m{\nabla }^{2}Y$$

(31)

$${\rho }_m{C}_{pm}\frac{\partial T}{\partial t}=\nabla \left(K_n\nabla T\right)+Q,$$

(32)

where Q is the microwave source term, and m represents the multiple layers on which the material can form. D is written as a function of the temperature (T), E is the activation energy and moisture content, and X is shown in Equations (33) and (34).

$$D=\frac{1}{1+X}\left[D_0{e}^{-\left[\frac{E_0}{R}\left(\frac{1}{T}-\frac{1}{T_T}\right)\right]}+D_i{e}^{-\left[\frac{b_i}{R}\left(\frac{1}{T}\frac{1}{T_T}\right)\right]}\right]$$

(33)

$$Q=2\beta \left(\frac{R}{r}\right)Q_{0r}{e}^{[-2\beta (R-r\left)\right]}+2\beta \left(\frac{R}{r}\right)Q_{0z}{e}^{\left[-2\beta \left(\frac{H}{2}-z\right)\right]}$$

(34)

In the context of solar pyrolysis, CFD modeling plays an essential role in predicting the heat transfer, temperature distribution, and chemical reactions during the process. One of the key aspects of solar pyrolysis is the radiative heat transfer, which involves the absorption and scattering of concentrated solar radiation by the biomass particles. The radiative transfer equation (RTE) can be used to describe this phenomenon:

$$\frac{dI(\mathit{r},\mathsf{\Omega })}{ds}=-\kappa \left(\mathit{r}\right)I(\mathit{r},\mathsf{\Omega })+\sigma \left(\mathit{r}\right){\int }_{4\pi }I(\mathit{r},{\mathsf{\Omega }}^{\prime })\mathsf{\Phi }({\mathsf{\Omega }}^{\prime },\mathsf{\Omega })d{\mathsf{\Omega }}^{\prime }+q\left(\mathit{r}\right),$$

(35)

where $I(\mathit{r},\mathsf{\Omega })$ is the radiative intensity at position $\mathit{r}$ in direction $\mathsf{\Omega }$, $\kappa \left(\mathit{r}\right)$ is the absorption coefficient, and $\sigma \left(\mathit{r}\right)$ is the scattering coefficient, $\mathsf{\Phi }({\mathsf{\Omega }}^{\prime },\mathsf{\Omega })$ is the scattering phase function, and $q\left(\mathit{r}\right)$ is the internal source term [127].

The energy balance equation for the solid biomass phase in solar pyrolysis can be written as follows:

$${\rho }_s{C}_{p,s}\frac{\partial T_s}{\partial t}=\nabla ·(k_s\nabla T_s)+S_{abs},$$

(36)

where ${\rho }_s$ is the solid biomass density, $C_{p,s}$ is the specific heat capacity of the solid biomass, $T_s$ is the solid biomass temperature, $k_s$ is the thermal conductivity of the solid biomass, and $S_{abs}$ is the absorbed solar radiation [128]. This equation takes into account the conduction heat transfer within the biomass particles, as well as the energy input from the absorbed solar radiation.

These governing equations, along with the previously mentioned Navier–Stokes equations and the discrete phase model (DPM), provide a comprehensive framework for the CFD modeling of solar pyrolysis processes.

Microwave source terms can be solved by either Maxwell’s equations or Lambert’s law. Although Lambert’s law simplifies the equation, it does not study the impact of the electromagnetic field. However, Maxwell equations are well suited for studying the dielectric properties of biomass materials. Various models have been developed based on the two basic laws, as shown in Table 3.

A finite difference scheme was applied in the earlier stages to study the influence of microwaves in the furnace, and this was studied by unsteady-state Maxwell equations, which were coupled with energy equations [108]. Maxwell equations were implemented with the transport equations to investigate the electromagnetic field effect on the process. The coupled electromagnetic thermal model simulation aided in understanding the effect of the working frequency and feed size, and the dielectric properties were investigated by the finite difference model. Thermal modeling of the food drying in the microwaves were studied by calonimetric techniques, and the microwave power absorption was also defined as shown in Equation (20). The finite difference time domain technique was used to model the freeze drying process, as well as to investigate the adsorption and desorption in the porous media. Silicon carbide was applied as the dielectric material, and milk was applied as the aqueous media. The heat and mass transfer profiles predicted by the model were in good agreement with other experiments [103]. The model simulation results predicted that the vapor movement in the porous medium was the dry rate that was being controlled in the first stage, and the heat transfer was the drying rate control in the later stage. A wave guide is generally used in microwave heating and drying. Moreover, to detect the temperature and power distribution, finite difference time domain models were applied. Simulation results were used to identify the fundamental parameters and to guide the microwaves [104]. A generalized mathematical model for microwave heating was used to describe the heat distribution in the wood samples accurately. Most of the heating was predicted at the center of the samples, which is where the electric field was at the maximum. A detailed two-dimensional mathematical model coupled with electromagnetic effects predicted the experimental results of microwave-assisted pyrolysis characteristics for wood-based biomass samples. The term for volumetric heating as a source term in the energy balance was assisted in a uniform heating from the internal region to the external region during pyrolysis [109]. The simulated results predicted the volumetric heating with a reaction zone that increased continuously from the center to the surface of the material. A comparison of microwave pyrolysis with the conventional heating conducted in this study showed significant differences in the spatial distributions of the temperature, feed conversion, and species densities. The finite element method is the discretization technique that is most widely used in CFD simulations. Transient heat and mass conservation equations can be easily computed using the FEM method for non-homogeneous reaction media such as carrots. Microwave effects have been incorporated in the CFD code by the Maxwell and Lambert laws, and the shrinking-core model has been employed to introduce non-homogeneity in the reaction system [111]. CFD simulations for microwave-assisted pyrolysis can also simulate the microwave heating of the food. The finite element package FEMLAB has been used extensively to estimate temperature and absorbed power distribution [105]. The power supplied by microwaves to cylindrical geometry was implemented with the Lambert law in this study. The simulation results predicted that the cylinders with smaller radii have high absorption power, which reduces with increases in the radius. The radius of the cylinder was more than the critical radius once the radial temperature profile coincided with the axial temperature profiles.

CFD has multiple applications, such as modeling food that are in stationary and angular rotating positions when on a rotating turntable in a microwave oven. The simulation results showed that there was an improvement of 37–43% in the uniform temperature distribution in the food that was on a carousel [106]. CFD models applied with Maxwell equations efficiently predicted the hydrogen yields during the steam methanol reformation (SMR) that took place with the methanol decomposition in the catalyst bed. The numerical model suggested an increase in operating power improved the hydrogen yield and ${\mathrm{CO}}_2$ selectivity [107]. The microwave drying process has been applied in several applications in the pharmaceutical, paper, wood, and polymer industries. The multi-physics approach when combined with Maxwell equations that include various transport equations for heat and mass transfer is the best choice when applied to designing a convective/microwave-assisted drying system [112]. Liquid water and water vapor mass balance equations have been coupled with heat transfer and Maxwell equations for electromagnetic field implementation. This convective microwave-assisted model predicted the thermal maps of the microwave drying of food. The simulation results confirmed that the impact of the dielectric properties in the process were significant. The application of CFD in microwave-assisted pyrolysis can be seen in Figure 2.

5. Challenges in CFD for Modeling Pyrolysis

Computational fluid dynamics (CFD) is a powerful tool for studying and optimizing pyrolysis processes. However, there are several challenges associated with using CFD for pyrolysis modeling. In this section, we will discuss some of the major challenges associated with the CFD modeling of pyrolysis.

• Complex chemical kinetics: Pyrolysis is characterized by a multifaceted array of chemical reactions, which encompass primary and secondary cracking, gasification, and char combustion. The intricacies of these reactions stem from their highly nonlinear nature and their strong dependency on variables such as temperature, pressure, and material composition. While CFD provides a robust framework for simulating fluid flow and heat transfer processes, it often struggles to accurately replicate the full complexity of pyrolysis reaction kinetics. This shortcoming is primarily due to the approximate nature of reaction models and the challenges in fully integrating detailed chemical kinetics within the CFD simulations. As highlighted in several studies [11,34,48,49,53], the inherent limitations of CFD in capturing the nuanced dynamics of these chemical processes underscore the need for the continual refinement of reaction models and computational strategies.
• High computational cost: One of the limitations of conventional CFD in modeling biomass pyrolysis is its high computational cost. The pyrolysis process occurs over a wide range of spatial and temporal scales, from the molecular scale of cellulose microfibrils to the meter scale of industrial reactors. This wide range of scales makes it challenging to accurately resolve all of the relevant physical processes using CFD. Additionally, the high temperatures and pressures involved in pyrolysis can result in highly transient and turbulent flow fields, thus further increasing the computational cost of the simulation. Therefore, conventional CFD models may not be able to capture all the relevant physical processes in biomass pyrolysis, and multi-scale CFD models are necessary to simulate the process accurately and efficiently [18,21].
• Uncertainty in input parameters: The complexity and variability in pyrolysis reactions are notably influenced by the characteristics of the biomass feedstock, such as particle size, composition, and moisture content. Vikram et al. [32] emphasized that reaction kinetics are significantly affected by factors like the heating rate and the initial temperature of the feedstock. Accurately capturing and integrating these parameters into CFD simulations is a critical challenge, thereby leading to uncertainty in modeling predictions. This is particularly pronounced in biomass pyrolysis due to the heterogeneity of the biomass material and the intricate nature of its thermal decomposition. The selection of the modeling approach, which includes kinetic, network, or mechanistic models, also impacts the input requirements and the ease of coupling with CFD simulations. For instance, network models, including the CPD model highlighted by Hameed et al. [11], often necessitate fewer input parameters, and they are more easily aligned with CFD, thus potentially reducing uncertainties. Nonetheless, despite these modeling advancements and their integration with CFD, the accurate prediction of pyrolysis product yields—like char, tar, and volatile matter—remains a complex task. This complexity is further heightened by the influence of inorganic species in the biomass and the dynamic interactions among its primary components (i.e., cellulose, hemicellulose, and lignin).
• Lack of experimental data: Despite significant advances in pyrolysis research, a notable gap persists in the availability of comprehensive experimental data for validating CFD models. References in key studies have highlighted specific shortcomings, such as insufficient data on biomass properties and the impacts of these properties on the pyrolysis process. Challenges in experimental setups, the scarcity of reference materials, and uncertainties in kinetic modeling further exacerbate the difficulty in accurately aligning CFD models with real-world phenomena. This deficiency in robust experimental validation not only underscores the complexities inherent in pyrolysis modeling, but it also poses a persistent hurdle in enhancing the precision and reliability of these models [49,129].
• Modeling of multi-physics phenomena: Pyrolysis presents a sophisticated amalgamation of heat transfer, mass transfer, and chemical reactions, each of which are governed by intricate physical and chemical principles. Successfully modeling these multi-physics phenomena demands the application of advanced numerical techniques, as well as precise, reliable models for each constituent process. The complexity is escalated by the necessity to accurately represent the transport phenomena of both the volatile and solid products that are generated during pyrolysis. This includes not only the accurate portrayal of the thermal degradation of biomass, but also the subsequent dynamics of evolved gases and residual solids within the reactor environment. Further, the modeling must account for the transient nature of these processes and their interdependence, i.e., how the evolution of gases influences the heat and mass transfer, as well as, in turn, the chemical reaction rates. The interaction of these variables creates a challenging scenario for CFD simulations, wherein the fidelity of the model to real-world phenomena is critical [13,19].
• Modeling of particle behavior: Pyrolysis predominantly revolves around the thermal decomposition of solid biomass particles. These particles, during the pyrolysis process, can exhibit intricate behaviors, which include agglomeration, fragmentation, and attrition. Such behaviors are influenced by the inherent heterogeneity of the biomass material and the dynamic interactions among its primary components [32]. Additionally, the hydrodynamic reactions of these particles in the turbulent flow, when coupled with the release of volatiles and the formation of char, contribute to the complexity. Accurately capturing these multi-faceted behaviors within the framework of CFD modeling is a daunting challenge. The integration of kinetic and network models [11] can provide insights into particle behavior. However, the precise simulation of particles in a turbulent reactor environment, when there are evolving physical and chemical properties, remains a pivotal challenge in ensuring the fidelity of CFD simulations of biomass pyrolysis.
• Optimization of reactor design: CFD plays a pivotal role in optimizing the design of pyrolysis reactors, thereby enabling the precise simulation and analysis of various operational scenarios [130]. The optimization process, however, is complicated by the extensive range of design parameters that must be considered. These parameters include the properties of the feedstock, the rate of heating, the specific geometry of the reactor, and the flow rates of gases and liquids within the system. Each of these factors can significantly influence the efficiency and effectiveness of the pyrolysis process, thereby presenting a considerable challenge in leveraging CFD to achieve an optimal reactor design [131]. The complexity arises from not only the sheer number of variables, but also their interdependencies and the impact they have on the reactor’s thermal and flow dynamics.

6. Potential Areas of Research and Development in the Future of CFD in Pyrolysis

Computational fluid dynamics modeling in biomass pyrolysis has a significant role in process optimization, cost reduction, and environment sustainability. CFD modeling can be applied in several ways to solve the following real world problems:

• The design of the reactor is one of major outputs from the modeling, and it can be used to enhance the process efficiency and desired product yield.
• The operating conditions such as temperature, pressure, and the feedstock and susceptor characteristics can be investigated at multiple probabilities so as to optimize the product yield.
• It simplifies the design of scaled-up experiments for biomass pyrolysis from lab to pilot, as well as from the industrial scale transitions by the mitigation of energy consumption.
• Computational experiments such as multi-stage processes with parametric and sensitivity analysis implementation is easily conducted by the application of CFD modeling.
• Emission prediction and separation of the exhaust gases from the products to improve the product quality and to mitigate carbon emissions.

Some potential areas of research and development in the future of CFD in pyrolysis may include the following:

• The development of accurate and validated models: CFD models for pyrolysis need to be validated against experimental data to ensure their accuracy and reliability. Future research could focus on developing more accurate and validated models for the purpose of predicting the behavior of pyrolysis reactors.
• Multi-scale modeling: Pyrolysis is a multi-scale phenomenon that occurs at different spatial and temporal scales. Future research could focus on developing multi-scale CFD models that can capture the behavior of pyrolysis at different scales.
• Integration of CFD with other techniques: CFD can be combined with other techniques such as experimental measurements, optimization algorithms, and machine learning to improve the accuracy and efficiency of pyrolysis simulations.

7. Conclusions

In this review, we have discussed the application of computational fluid dynamics (CFD) in the modeling of pyrolysis processes, specifically with a focus on conventional pyrolysis, microwave-assisted pyrolysis, and solar pyrolysis. Pyrolysis is a complex thermal decomposition process that involves a variety of chemical reactions, heat and mass transfer, and multi-phase flow phenomena. The use of CFD allows for researchers and engineers to gain a deeper understanding of these processes, to optimize reactor designs, and to improve the efficiency of pyrolysis systems. CFD is a very useful application tool for understanding the pyrolysis process. The operating parameters including pressure, temperature, velocity, catalyst quantity, and vapor residence time, and these can be optimized and controlled via numerical simulations at the reactor scale. The data obtained from pyrolysis experiments can be used to develop the numerical models that are applicable to a wide range of conditions, and crucial assessments and predictions can be made with the use of such simulations. For a pyrolysis process, the reaction kinetics can be understood by knowing the product formation and the corresponding operating parameters. The rate governing steps and temperatures can be predicted by using CFD simulations. The effect of the type of reactor used in pyrolysis process on the product formation and overall process efficiency can also be envisaged using CFD simulations. However, as the complexity of pyrolysis processes increases with the introduction of microwave and solar energy sources, CFD modeling becomes more challenging due to the need to incorporate additional physical phenomena such as electromagnetic field interactions and radiation effects. Microwave-assisted pyrolysis introduces the challenge of modeling microwave energy absorption and its interaction with the dielectric properties of biomass materials. Solar pyrolysis, on the other hand, requires the incorporation of solar radiation models and the effect of concentrating solar power in the pyrolysis process. Despite these challenges, CFD has proven to be a valuable tool in understanding and optimizing these advanced pyrolysis processes. The existing literature provides a solid foundation for the CFD modeling of pyrolysis, but there is still much room for improvement, particularly in addressing the challenges associated with microwave-assisted and solar pyrolysis. Future research should focus on the development of more accurate and validated models for these advanced pyrolysis processes, as well as the integration of CFD with other techniques such as experimental measurements, optimization algorithms, and machine learning so as to further enhance the accuracy and efficiency of pyrolysis simulations. Additionally, multi-scale modeling that can capture the behavior of pyrolysis at different scales may be another promising area of research that could to help overcome the challenges posed by the complexity of these processes. Overall, this review highlights the importance of CFD in advancing our understanding of pyrolysis, as well as the potential for further developments in this field.