State of Charge Estimation of Lithium-Ion Battery Based on Back Propagation Neural Network and AdaBoost Algorithm

Abstract

The accurate estimation of the state of charge (SOC) of lithium-ion batteries is critical in battery energy storage systems. This paper introduces a novel approach, the AdaBoost–BPNN model, to overcome the limitations of traditional data-driven estimation methods, such as a low estimation accuracy and poor generalization ability. The proposed model employs a back propagation neural network (BPNN) for the preliminary estimation. Subsequently, an AdaBoost–BPNN model is developed as a strong learner using the AdaBoost integration algorithm. Each BPNN sub-model serves as a weak learner within the AdaBoost framework. The final output of the strong learner is obtained by combining the individual outputs from the weak learners using weighting factors. This adaptive adjustment of weighting factors enhances the accuracy of SOC estimation. The proposed SOC estimation algorithm is evaluated and validated through experimental analysis. Throughout the paper, theoretical analysis is conducted, and the proposed AdaBoost–BPNN model is validated and verified using experimental results. The results demonstrate that the AdaBoost–BPNN model outperforms traditional methods in accurately estimating SOC under various conditions, including constant current-constant voltage (CCCV) charging, dynamical stress testing (DST), US06, a federal urban driving schedule (FUDS), and pulse discharge conditions.

1. Introduction

With the rapid expansion of the automobile industry and the increasing pace of urbanization, environment-related concerns and energy issues have emerged as significant global priorities [1,2,3]. In response to these challenges, the development of electric vehicles has gained widespread attention due to their eco-friendly characteristics and the abundant availability of electricity as an energy source [4,5,6]. Among the different types of batteries, lithium-ion batteries are widely utilized for energy storage in electric vehicles. This preference is primarily attributed to their advantages, including high power density, fast charging capabilities, a long lifespan, and low self-discharge rates [7,8,9,10].

In a battery system, the state of charge (SOC) is a critical indicator to reflect the status of a battery. It is defined as the ratio of available capacity to the total capacity of the battery [11]. Accurately estimating the SOC is of utmost important for enhancing battery system performance, preventing overcharging or over-discharging, and extending the service life of the battery [12]. However, directly measuring the SOC value is not feasible, and it can only be estimated or calculated through the parameters that can be measured directly, such as current, voltage, and temperature. As a result, accurately determining the SOC is a challenging task [13].

Various approaches for SOC estimation have been proposed, including the traditional method, circuit model method, data-driven method, and the artificial intelligence method, among others. Coulomb counting (CC) [14] and open circuit voltage (OCV) [15] are the most common traditional methods. The CC method involves integrating the current over time to estimate the SOC [14]. However, the accuracy of this method heavily relies on the precision of the initial SOC estimation and the current measurements. Otherwise, errors can accumulate over time and impact estimation accuracy. On the other hand, the OCV method establishes a lookup table, to correlate measured voltage values with corresponding SOC values. Nevertheless, this method yields accurate results only when the battery remains idle for extended periods. During charging or discharging operations, the varying current makes it challenging to measure or calculate the OCV value accurately [15].

The circuit model-based method is another candidate to estimate SOC. Typically, this method is combined with Kalman filter [15,16,17] and unscented Kalman filter [18] to determine the model parameters. The accuracy of this method relies heavily on the precision of the established equivalent circuit model. However, the reactions taking place within the battery and the associated calculations are intricate. Additionally, extending the equivalent circuit model to accommodate different battery types with varying materials or dynamic behaviors presents significant challenges. Consequently, establishing an accurate and universally applicable battery model continues to be a difficult task.

Given the limitations associated with conventional methods, such as low accuracy and insufficient real-time performance, there is an increasing recognition of the necessity of exploring alternative approaches for SOC estimation. In response to these constraints, the data-driven approach has emerged as a prominent and transformative alternative, capable of revolutionizing the field of SOC estimation. This shift towards data-driven methodologies marks a significant turning point in the pursuit of more precise and real-time SOC estimations. It offers a promising avenue to overcome the challenges that have traditionally hindered progress in this field [19].

In data-driven models, the knowledge of the internal structure or chemical reactions within the battery is not necessarily required [20]. Common data-driven methods include the support vector machine (SVM) method [21], neural network (NN) method [22], and the deep learning (DL) method [23], among others. The selection of model structure and parameter settings greatly influence the estimation accuracy in these methods. Wang et al. [21] proposed a joint estimation model based on the neural network and support vector machine models, which successfully estimated the SOC and the electric quantity within a maximum mean square error of 0.85%. However, this approach did not consider the impact of temperature on the SOC, nor did it discuss the testing data under actual electric vehicle conditions. Feng et al. [24] proposed a gated recurrent neural network. In this network, current, voltage, and temperature are inputs, and it can achieve a less than 3.5% estimation error under different temperature test conditions. However, this method does not condition the optimization of model parameters, and the initial parameter setting is not discussed. To address the issue of model parameter setting, a particle swarm optimization was discussed by Mao et al. [25], based on Levy flight, to optimize the SOC estimation model of BPNN. The results demonstrated a higher estimation accuracy under various test conditions, compared to the traditional BPNN model without optimized model parameters.

In addition to improving the accuracy of network estimation results, utilizing algorithms to enhance network data is another potential solution. Wang et al. [26] introduced a fusion model that combines the stacking method, support sector regression, AdaBoost algorithm, and the random forest algorithm to predict battery SOC. However, this approach significantly increased the computational costs. In fact, the AdaBoost algorithm can meet the requirements at a low cost by combining various weak learners into a strong learner. Li et al. [27] presented an AdaBoost–Rt-RNN model and validated its performance using data from battery pulse discharge experiments. The results indicated that the ensemble model was improved by the AdaBoost–Rt algorithm, which demonstrated better predictive accuracy than a single RNN model. However, RNN’s complex structure makes it susceptible to the vanishing gradient problem, particularly when using non-saturating activation functions, resulting in a reduced estimation accuracy. Xie et al. [28] proposed an AdaBoost–Elman algorithm for lithium-ion battery SOC estimation. The proposed algorithm combined the dynamic properties of Elman neural networks with the accuracy-improving capability of the AdaBoost algorithm. This combination resulted in a strong learner with a higher estimation accuracy and dynamic properties, enabling accurate state of charge (SOC) estimations in the short term. Despite the strong dynamic performance and memory capabilities of Elman neural networks, they have disadvantages, such as high complexity and a tendency to overfit. When faced with complex problems or large datasets, they require more computational resources and have very long training times. BPNN, on the other hand, is less affected by the vanishing gradient problem and offers a simpler structure, leading to higher modeling efficiency.

In light of the constraints posed by conventional methodologies, and with a conscious effort to circumvent the inherent intricacies of complex model architectures and the protracted computational demands they entail, this research paper introduces a novel neural network model that is meticulously engineered to address the formidable challenge of SOC estimation within battery systems. This innovative approach ingeniously incorporates the AdaBoost algorithm, orchestrating the sequential assembly of numerous weak learners and judiciously assigning weighted importance to their input and output data. Consequently, this method culminates in a profound enhancement of the accuracy achieved in SOC estimation, marking a significant leap forward in this domain. The substantial contributions of this paper, encompassing advancements in model optimization, algorithmic integration, and SOC estimation precision, are encapsulated in the following summary:

(a)

This paper introduces an BPNN model as a weak learner for SOC estimation. BPNN can continuously update internal weights and thresholds to achieve result error reduction.

(b)

The AdaBoost algorithm is employed to combine multiple weak learners. It calculates the relative error rate of input data and assigns weights to the output data of each weak learner.

(c)

The proposed SOC estimation model is evaluated and validated under various working conditions, including US06, FUDS, and pulse discharge scenarios. The performance of the model is assessed to ensure its effectiveness and applicability.

The subsequent structure is organized as follows. Section 2 describes the optimization steps of the weak learner and the composition of the strong learner and shows the specific structure of the AdaBoost–BPNN model, as well as how to use this model to estimate SOC. Section 3 uses the dataset to conduct experiments and validates the performance of the presented model. Section 4 gives the conclusion.

2. Theoretical Analysis

In the proposed modeling approach, multiple BPNNs are employed as the weak learners within the AdaBoost algorithm. The relative error of the output results from each weak learner is compared to a predefined threshold φ. Based on this comparison, the error rate and output weight a_i for the subsequent weak learner are calculated. By cascading multiple weak learners, a strong learner is generated. The output of each BPNN is then multiplied by weighting factors a₁ through a_n to enhance the prediction accuracy of the SOC. The following sections provide a detailed description and analysis of the design process of the presented AdaBoost–BPNN model.

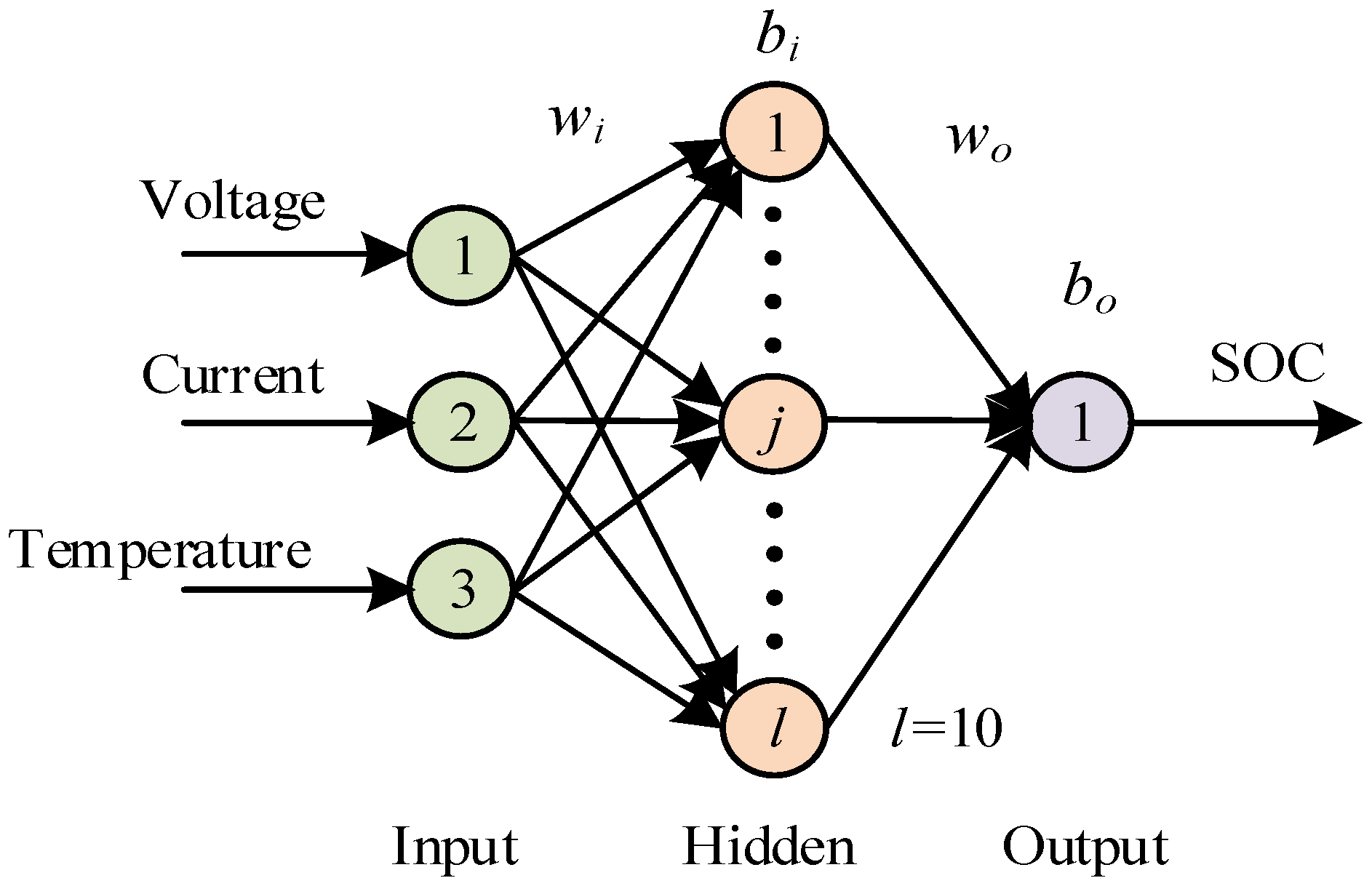
A BPNN is a type of artificial neural network designed for supervised learning tasks. It consists of an input layer, one or more hidden layers, and an output layer of interconnected neurons. The key principle of BPNN is to iteratively adjust the weights and biases of these connections to minimize the error between the network’s predictions and the actual target values. This optimization process is performed through gradient descent, where the network computes the gradient of the error with respect to its weights and updates them in the opposite direction of the gradient, gradually reducing the prediction error over multiple training iterations. BPNN leverages the chain rule to propagate error gradients backward through the layers, hence the name backpropagation, and this iterative learning process allows it to learn complex relationships and make accurate predictions in various domains, including pattern recognition, classification, and regression tasks. In this paper, the structure of BPNN, serving as the weak learner, is illustrated in Figure 1. Voltage, current, and temperature are utilized as the input of this model, while SOC is the output. w_i and b_i are the weighting factor and threshold from input layer to hidden layer, respectively. w_o and b_o are the weighting factor and threshold from the hidden layer to the output layer.

From Figure 1, the chain derivative rule for BPNN is as follows:

$$E=\frac{1}{2}{\displaystyle \sum _{k=1}^m{(SO{C}_k-SO{C}_k^{*})}^2}=\frac{1}{2}{\displaystyle \sum _{k=1}^m{(e_k)}^2}$$

(1)

$$\Delta w_i=-\eta \frac{\partial E}{\partial w_i}=\eta {\displaystyle \sum _{k=1}^m{e}_k{w}_{o}f({\displaystyle \sum _{i=1}^n{w}_i{x}_i+b_i})x_i}$$

(2)

$$\Delta w_o=-\eta \frac{\partial E}{\partial w_o}=\eta e_{k}ne{t}_j$$

(3)

$$\Delta b_i=-\eta \frac{\partial E}{\partial b_i}=\eta {\displaystyle \sum _{k=1}^m{e}_k{w}_{o}f({\displaystyle \sum _{i=1}^n{w}_i{x}_i+b_i})}$$

(4)

$$\Delta b_o=-\eta \frac{\partial E}{\partial b_o}=\eta e_k$$

(5)

where η is the learning rate, net_j represents the output of hidden layer, and f(x) is the activation function. In this paper, tansig is used as the activation function of BPNN.

The AdaBoost algorithm is an ensemble learning technique that combines multiple weak learners to create a strong learner. Initially, all training samples are equally weighted, and weak learners are trained. In each iteration, high error samples are given higher importance, encouraging the next weak learner to focus on the previously challenging instances. The final ensemble bestows more influence upon learners with superior performance, and their collective decisions are amalgamated to yield precise predictions. AdaBoost is renowned for its effectiveness in handling intricate datasets, as it emphasizes difficult examples and culminates in a formidable and accurate prediction model.

After establishing each individual BPNN model as a weak learner, multiple weak learners are cascaded, using the AdaBoost algorithm, to create a strong learner. The complete schematic diagram of the AdaBoost–BPNN model is illustrated in Figure 2. The iterative calculation process of the AdaBoost algorithm is discussed below.

(1)

Model Input:

We assume that the training set consists of n sample pairs (x₁, y₁), …, (x_j, y_j), …, (x_n, y_n). The number of weak learners is determined as k, and the threshold φ is set to evaluate the acceptability of the weak learners’ predictions. In this paper, the threshold of relative error, φ, is defined as the average value of the error rates across all weak learner.

(2)

Parameter Initialization:

The initial weak learner is assigned a serial number i = 1. The error weight for each sample in the input parameters of the initial weak learner is denoted as D₁ = 1/n. Additionally, the initial error rate of each weak learner is set as ε_i = 0.

(3)

Iterative Calculations:

The training set is utilized as the input data of the weak learner as shown in Figure A1 of Appendix A. The relative error, denoted as ARE_i(j), for each sample is calculated, based on the corresponding output f_i(x_j), as given by (6):

$$AR{E}_i(j)=\left|\frac{f_i(x_j)-y_j}{y_j}\right|$$

(6)

If ARE_i(j) > φ, the error rate is updated as ε_i = ∑D_i(j). Subsequently, the error weight for each sample in the training set of the next weak learner is calculated based on the error rate, as given by (7):

$$D_{i+1}(j)=\frac{D_i(j)}{D_{sum}}\times \left\{\begin{array}{l}{\epsilon }_i^2,AR{E}_i(j)\le \phi \\ 1,AR{E}_i(j)>\phi \end{array}\right.$$

(7)

where D_sum represents the normalization factor, which can make the sum of the updated weights equal to one.

The output weight a_i of the current weak learner is calculated, as given by (8):

$$a_i=\frac{1}{2\exp (\left|{\epsilon }_i\right|)}$$

(8)

After each iteration, the sequence number i of weak learners increases by one. The estimated value of SOC is estimated, as given by (9):

$$\mathrm{SOC}={\displaystyle \sum _{i=1}^k{a}_i{f}_i(x)}$$

(9)

where f_i(x) indicates the output data of the ith weak learner.

3. Results

In this section, the experimental results, using both open-source battery data and laboratory hardware, are presented and discussed, to validate the performance of the proposed AdaBoost–BPNN model. During the data acquisition process, the sliding filter algorithm and low-pass filter are utilized, to filter and reduce noise in the data.

3.1. Model Evaluation Index

To mitigate slow convergence and lengthy training times, the input data are normalized to the range of [−1,1] using the normalization formula given by (10):

$$x_i=\frac{2(x-x^{*})}{x_{\max }-x_{\min }}$$

(10)

where x is the original input data and x_i is the normalized value of x, x_max and x_min are the maximum and minimum input values, respectively, and x^* is the average of x_max and x_min.

The root mean square error (RMSE) and maximum error (MAX) are utilized as evaluation indicators. The calculation equations are given by (11) and (12):

$$\mathrm{RMSE}=\sqrt{\frac{1}{m}{\displaystyle \sum _{i=1}^m{(Y_i-Y_i^{*})}^2}}$$

(11)

$$\mathrm{MAX}=\max (|Y_i-Y_i^{*}|)$$

(12)

where m represents the number of samples, Y_i and Y_i^* are the real value and estimated output value, respectively.

3.2. Experimental Results and Discussion

In order to conduct a comprehensive and rigorous assessment of the performance of the proposed AdaBoost–BPNN model, we have meticulously curated a dataset that encompasses a diverse range of critical parameters and variables. This dataset incorporates vital information such as terminal voltage, load current, charge and discharge capacity, battery temperature, and sampling frequency. Notably, these data points have been meticulously collected from a lithium-ion battery subjected to the demanding conditions of the DST, US06, and the FUDS cycles. By encompassing such a rich and multifaceted dataset, our evaluation endeavors are poised to provide a thorough and holistic analysis of the AdaBoost–BPNN model’s performance under a spectrum of challenging and real-world operating scenarios. This dataset is sourced from the CALCE battery research group of the University of Maryland [29] and the parameters of the battery are shown in

Table 1. Parameters of battery.

Parameters	Value
Capacity rating	1100 mAh
Cell chemistry	LiFePO4
Voltage rating	3.3 V
Diameter	18 mm
Length	65 mm

. In the dataset, the battery undergoes an initial charging process from 0% SOC to 100% SOC using the CCCV method, which is followed by a complete discharge under each working/driving condition. The DST data are utilized as the training dataset, while the US06 and FUDS data are employed as the test dataset.

In this test, the current, voltage, and temperature data of the lithium-ion battery during CCCV charging operation are collected. Based on the dataset, the estimation results and errors of the BPNN model, Particle Swarm Optimization (PSO) – BPNN model, and the presented AdaBoost–BPNN model are shown in Figure 3 and

Table 2. SOC estimation results under CCCV charging.

Model	RMSE (%)	MAX (%)
BPNN	0.77	3.6
PSO–BPNN	0.60	4.1
AdaBoost–BPNN	0.21	1.4

. It can be observed that the presented AdaBoost–BPNN model has the best performance with 0.21% RMSE and 0.14% MAE. In Figure 3a, from 200 s to 300 s duration time, the other three models have an obvious estimation error within ±3%, while the presented model reduces this value to within ±1%. Furthermore, as can be seen in Figure 3b, AdaBoost–BPNN exhibits smaller errors, compared to BPNN and PSO–BPNN. The maximum error for BPNN and PSO–BPNN is close to 4%, while AdaBoost–BPNN only has a 1.4% error. This indicates that not only does the AdaBoost–BPNN model have a high accuracy, but it also has minimal error fluctuations, avoiding sudden changes in error.

Figure 4 and Figure 5 illustrate the SOC estimation results under US06 and FUDS test conditions. Observing the results, it is evident that the standard BPNN exhibits significant fluctuations. This is because the BPNN model has random initial parameters, which can lead to underfitting and result in high disturbances in its estimation. After optimizing the initial parameters of BPNN using the PSO algorithm, the PSO–BPNN model demonstrates reduced fluctuations, while the AdaBoost–BPNN model achieves the smoothest estimation, that closer aligns with the reference values. Unlike the principles of the PSO algorithm, the AdaBoost algorithm does not directly optimize the initial parameters of BPNN. Instead, it assigns different weights to the relationship between the output results of BPNN and the input variables. This way, it reduces the impact of error data on the results, making the results more accurate. Figure 6 provides a comparison of errors among the three models under both driving cycles at a temperature of 20 °C. It is apparent that the AdaBoost–BPNN model exhibits smaller errors compared to the other models. Among them, BPNN even reaches a maximum error of over 25%, while the error range of PSO–BPNN lies between ±5% and ±10%. On the other hand, AdaBoost–BPNN demonstrates remarkably smooth error performance, with a maximum error not exceeding 3%.

It is evidently clear from the comprehensive analysis of the results that the AdaBoost–BPNN model stands out prominently by consistently demonstrating notably smaller errors, in comparison with the other competing models under examination. This conspicuous superiority in error minimization underscores the robustness and effectiveness of the AdaBoost–BPNN model, affirming its superior performance and highlighting its capability to substantially outperform its counterparts in this evaluative context.

Table 3. SOC estimation results for US06 at various temperatures.

US06	RMSE (%)			MAX (%)
	BPNN	PSO–BPNN	AdaBoost–BPNN	BPNN	PSO–BPNN	AdaBoost–BPNN
0 °C	5.76	1.55	0.58	33.19	8.63	2.13
20 °C	4.64	1.32	0.56	24.19	6.30	2.45
30 °C	3.48	1.23	0.42	14.39	4.79	1.89
50 °C	3.65	1.16	0.49	9.74	5.58	2.00

and

Table 4. SOC estimation results for FUDS at various temperatures.

FUDS	RMSE (%)			MAX (%)
	BPNN	PSO–BPNN	AdaBoost–BPNN	BPNN	PSO–BPNN	AdaBoost–BPNN
0 °C	7.17	1.50	0.67	38.44	7.89	2.90
20 °C	5.94	1.49	0.63	27.36	8.74	2.61
30 °C	4.52	1.44	0.62	27.47	7.61	2.29
50 °C	3.91	1.73	0.75	17.64	8.36	3.67

present the RMSE and MAX values for BPNN, PSO–BPNN, and AdaBoost–BPNN models at different temperatures during US06 and FUDS driving cycles. The results clearly demonstrate that the standard BPNN model yields an imprecise SOC estimation, with a RMSE ranging from 3% to 6%. Moreover, the MAX value reaches 33.19% under the US06 driving cycle at 0 °C, which is deemed unacceptable. However, with the standard BPNN employing the AdaBoost algorithm for cascading, significantly improved estimation results are achieved. The RMSE is reduced to around 0.5%, and the MAX value is lowered to below 2.5%, indicating the enhanced accuracy of the proposed model.

3.3. Hardware Setup Test and Discussion

In order to validate the proposed AdaBoost–BPNN model, a hardware test bench platform is constructed, as depicted in Figure 7. The test bench comprises a Smacq USB-3223 data collector, two DC power sources, an electric load, an 18,650 lithium-ion battery, a temperature sensor, and a computer. This setup is used to conduct pulse discharge experiments with the 18,650 lithium-ion battery. The 18,650 lithium-ion battery used in the experiments has a 2.6 Ah capacity and 3.7 V nominal voltage. The data collector plays a crucial role in gathering voltage and temperature measurements from the battery at a sampling frequency of 100 kHz. The temperature sensor measures the voltage across the thermistor using a voltage divider circuit, and then the voltage data are converted into temperature data using a lookup table. In addition, a calibration algorithm is also conducted to reduce the temperature sensing error. The experimental setup involves discharging the battery with a pulse load current of 2.6 A for a duration of 360 s, followed by a resting period of 720 s. This discharge process is repeated 10 times.

The estimation results and corresponding error curves with the BPNN model, PSO–BPNN model and the proposed AdaBoost–BPNN model are shown in Figure 8 and summarized in

Table 5. SOC estimation results under the sectional pulse discharge condition.

Model	RMSE (%)	MAX (%)
BPNN	1.26	12.32
PSO–BPNN	1.07	12.21
AdaBoost–BPNN	0.63	3.62

. We utilize 60% of the data as a training data set, and the remaining 40% of the data are treated as a test dataset.

From the experimental results, it is shown that we can achieve a lower error rate with the proposed AdaBoost–BPNN model throughout the entire discharging process, whereas both the BPNN and PSO–BPNN models exhibit increased estimation errors during the transient stage of load current changes. The MAX error of both the BPNN and PSO–BPNN models exceeds 12% and is concentrated at the points where the current changes occur. On the other hand, the MAX error of the AdaBoost–BPNN model is 3.62%.

In addition, as can be seen from Figure 8, under pulse discharge conditions, SOC exhibits both a steady state and a declining state. When the discharge current is 0 A, the SOC value remains constant, and at this time, the predicted values of both BPNN and PSO–BPNN fluctuate near the actual value, while the AdaBoost–BPNN model’s predicted values are very close to the actual value. When the discharge current is 2.6 A, the SOC value linearly decreases, and at this point, the results of all three models can closely approximate the actual value. However, during the transition of SOC between the steady state and declining state, all three models show noticeable errors in their predictions. Particularly, when SOC is at 30%, the prediction errors for BPNN and PSO–BPNN models exceed 10%, whereas the AdaBoost–BPNN model’s error is below 2% at this point. This indicates that the proposed model exhibits excellent predictive performance in both static and dynamic scenarios.

In summary, the AdaBoost–BPNN model, as introduced and thoroughly examined within the confines of this research paper, emerges as the unequivocal champion in the realm of SOC estimation accuracy, when juxtaposed with the conventional and widely utilized BPNN and PSO–BPNN models. The comprehensive battery of experiments and meticulous data analyses conducted herein serve as incontrovertible evidence of the AdaBoost–BPNN model’s exceptional prowess in delivering a top-tier performance. Across a spectrum of performance metrics, the empirical results emphatically underscore the AdaBoost–BPNN model’s superiority, establishing it as the undisputed leader in the domain of SOC estimation for battery systems, thereby ushering in a new era of precision and reliability in this critical field of study.

4. Additional Discussion

4.1. Comparison of Different Models

In order to evaluate the estimation performance of the proposed model, it is compared with some advanced existing methods, including long short-term memory (LSTM), convolutional neural network (CNN), gated recurrent unit (GRU), fully convolutional network (FCN), and recurrent neural network (RNN), and some improved methods [30,31,32,33]. In addition, there have been some hybrid models, such as LSTM–centralized Kalman filter (CKF), and LSTM–adaptive centralized Kalman filter (ACKF), recently proposed for SOC estimation, and they have also achieved good results [31].

Table 6. SOC estimation results of different methods for FUDS at 20 °C.

Methods	FUDS
	RMSE (%)	MAX (%)
LSTM [31,32]	3.30	19.3
RNN [30]	2.73	/
Base on search algorithm (BSA)–GRNN [30]	2.17	/
Business intelligence (BI)–GRU [30]	1.30	/
LSTM–Attention [33]	1.18	/
PSO–BPNN	1.49	8.74
LSTM–CKF [31]	2.80	14.3
LSTM–ACKF [31]	0.90	2.70
Proposed model	0.63	2.61

shows the RMSE and MAX of various models under the FUDS driving cycle at 20 °C.

It can be observed that the proposed model exhibits a high estimation accuracy. Among the showcased models, the LSTM model, improved with attention technique, demonstrates good performance in the FUDS condition, ranking just below the hybrid model LSTM–ACKF and the proposed model. The LSTM–Attention and Bi–GRU models perform similarly in terms of accuracy. The remaining models exhibit slightly lower accuracies. Overall, at 20 °C, under FUDS conditions, the proposed model outperforms existing advanced deep learning methods and hybrid models in SOC estimation accuracy.

4.2. Discussion for Computational Burden

While the proposed model can significantly enhance SOC estimation accuracy, it is essential to avoid incurring an excessive computational burden in the process. To evaluate the computational load of the proposed model, it is compared with the BPNN and PSO–BPNN models.

Table 7. Computation burden results for FUDS at 20 °C.

Method	RMSE (%)	MAX (%)	Computation Time (s)
BPNN	5.94	27.36	0.49
PSO–BPNN	1.49	8.74	0.77
Proposed model	0.63	2.61	0.97

presents the results and computation time for SOC estimation under FUDS at 20 °C. Compared to the BPNN, the proposed model exhibits a superior performance with highly accurate results, although it requires a longer computation time. The BPNN yields estimation results that exhibit significant fluctuations, as evidenced by its RMSE and MAX values of 5.94% and 27.36%, respectively. In contrast, the proposed hybrid model delivers highly accurate and smooth results, with RMSE and MAX values of only 0.63% and 2.61%. Although the proposed model takes less than twice the computation time of the BPNN, it produces errors that are 9–10 times smaller. Overall, the proposed model demonstrates better performance than both the BPNN and PSO–BPNN models, in terms of RMSE and MAX, while still maintaining an acceptable computation time.

5. Conclusions

This paper introduces a novel AdaBoost–BPNN model for the accurate and generalizable estimation of battery SOC. The model is thoroughly evaluated through extensive simulations and hardware experiments. Its performance is systematically compared against conventional BPNN and PSO–BPNN models. The results demonstrate that the proposed model consistently outperforms the others in terms of SOC estimation accuracy, especially during discharge scenarios that represent common driving cycles and pulse current discharges. Impressively, when subjected to the demanding US06 driving cycle, the proposed model achieves an RMSE of only 0.42% and a maximum error (MAX) of just 1.89%. Similarly, under the FUDS driving cycle, the RMSE and MAX are further reduced to impressive values of 0.60% and 2.29%, respectively. Notably, even when exposed to the challenging conditions of pulse current discharges, the proposed model maintains a high level of accuracy in SOC estimation. These comprehensive results unequivocally highlight the profound effectiveness and robustness of the AdaBoost–BPNN model, establishing it as an exceptionally reliable tool for achieving highly precise battery SOC estimations across a wide range of operating scenarios.

Our future research endeavors will continue to focus on advancing the field of SOC estimation, with a specific emphasis on lithium-ion batteries. We plan to delve deeper into this domain, aiming to unravel the intricate relationships between different model structures and various battery parameters that inherently impact the performance of SOC estimation techniques. Furthermore, we are dedicated to continuously refining the algorithm, driven by an unwavering pursuit of excellence, to achieve the formidable goals of real-time control and precise correction of battery SOC values. This multifaceted approach will further solidify our commitment to enhancing the accuracy and applicability of SOC estimation methodologies in the realm of lithium-ion batteries.