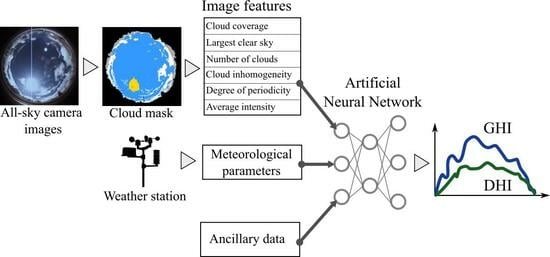
Estimation of Solar Irradiance Using a Neural Network Based on the Combination of Sky Camera Images and Meteorological Data
Abstract
1. Introduction
- An ANN-based hybrid model is presented to estimate solar irradition parameters, using data sources of different modalities as an input, in particular all-sky imagery and meteorological data;
- Six features characterizing sky conditions are introduced based on meteorological expertise. The features are obtained by means of traditional image processing from all-sky images. The advantages of this approach are two-fold: it incorporates crucial information about the condition of the sky, while it significantly decreases the amount of data used compared to image-based neural networks;
- The impact of the different meteorological parameters on the estimation accuracy is investigated by comparing the performance of the model when different combinations of parameters are used as input.
1.1. Related Works
1.2. The Impact of Clouds on Irradiance
2. Methodology
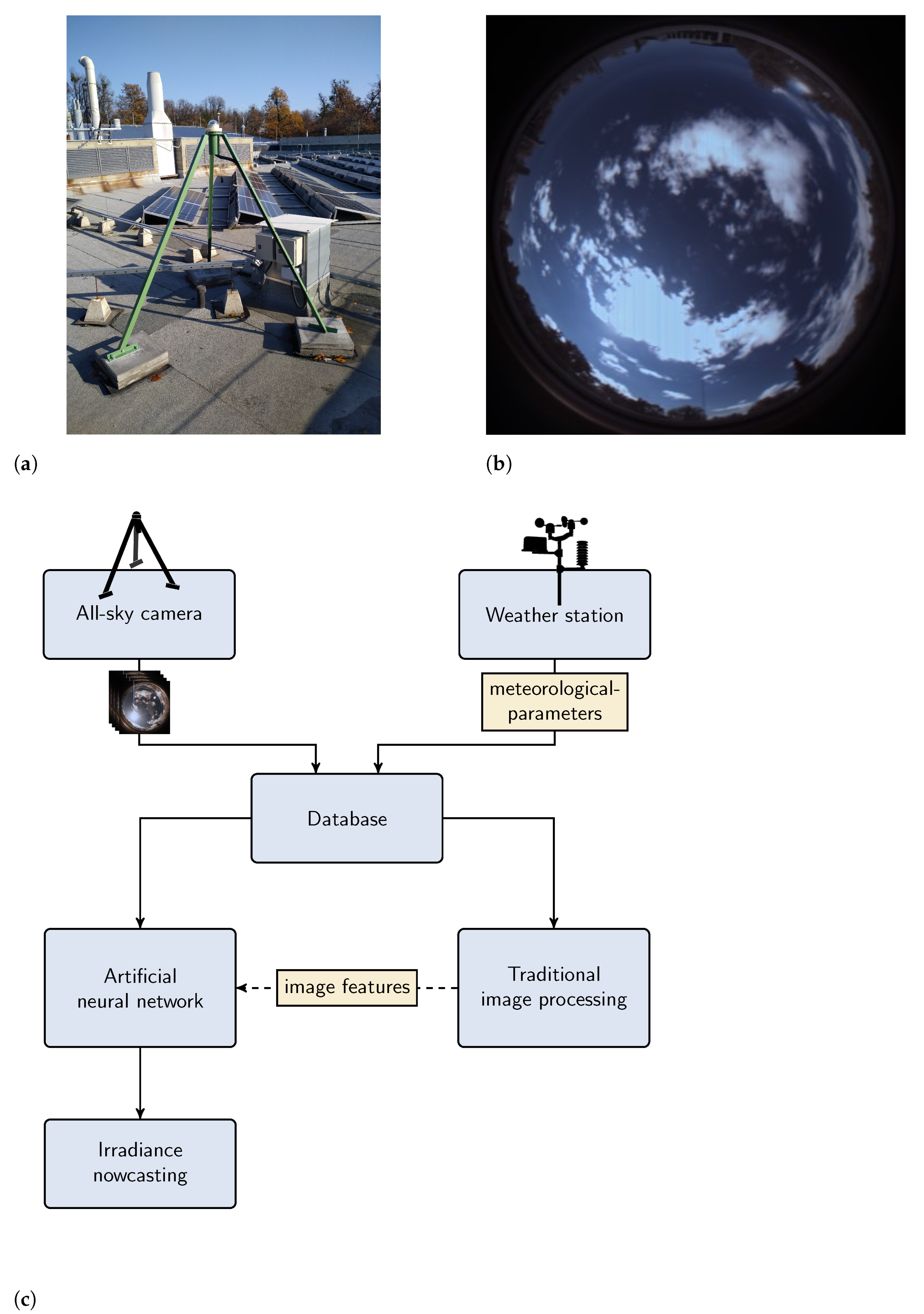
2.1. Instrumentation and Measurement
2.2. Traditional Image Processing
2.2.1. Camera Calibration and Image Preprocessing
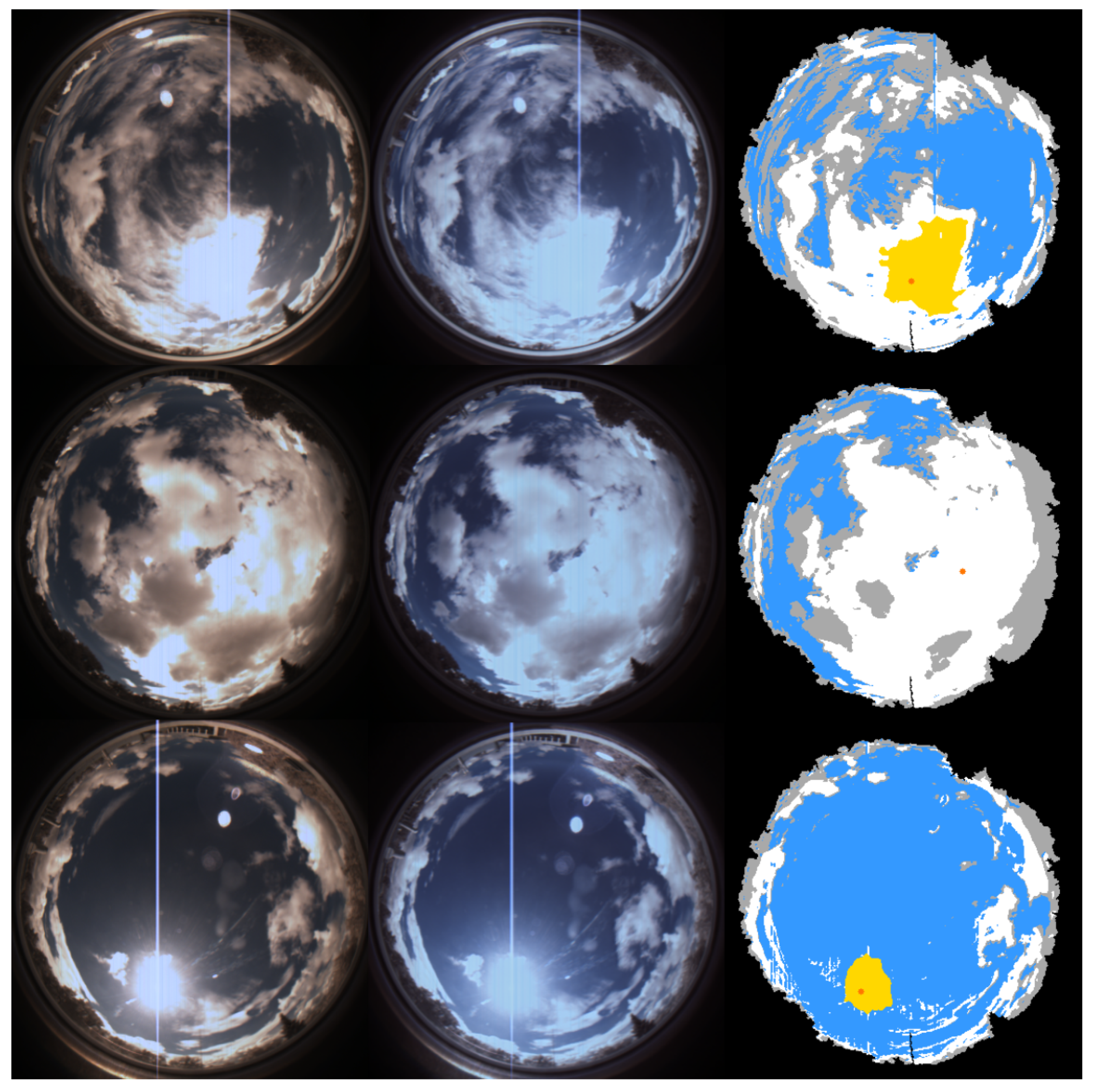
2.2.2. All-Sky Image Segmentation
2.2.3. Image Features
- Cloud coverage: The ratio of pixels covered by clouds to the total pixels in the image. GHI has a strong relationship with this parameter, but is not fully characterized by it. This parameter is the extension of the traditional octa-based cloud cover metric [3];
- Largest clear sky area: The ratio of pixels of the largest contiguous clear sky area to the total pixels in the image. The time trend of the size of the clear sky could provide information about cloud drift;
- Number of individual clouds: The number of contiguous cloud regions in the segmented image is a crucial factor in cloud type classification. It is also an important indicator of the temporal variability of radiation;
- Cloud inhomogeneity: Proportion of thick cloud regions to the total cloud region. This parameter is extracted using Otsu’s method as described in Ref. [40], separating thick, dark clouds from thinner, white clouds. This parameter is characteristic of certain cloud types;
- Degree of cloud periodicity: High periodicity is a characteristic feature of altocumulus clouds. This cloud genus exerts a substantial modifying impact on solar radiation, as detailed in Ref. [41], where it is noted that the most significant cloud radiative effect occurs when altocumulus clouds partially obscure the solar disk. The assessment of periodicity entails extracting an indicator through a 2D Fourier transform applied over the image domain. First, a frequency range is determined empirically, containing harmonic components typically seen in highly periodic cloud images. Then, the energy encoded by the components in the range relative to the total energy of the image is calculated. This feature discriminates against periodic altocumulus clouds (a typical sky condition characterized by altocumulus clouds is shown in Figure 4);
- Average intensity: Average intensity of image pixels calculated across all three channels. This metric quantifies the overall radiance of the image, a parameter strongly correlated with GHI. However, this feature can be misleading thanks to the HDR merging performed on the images.
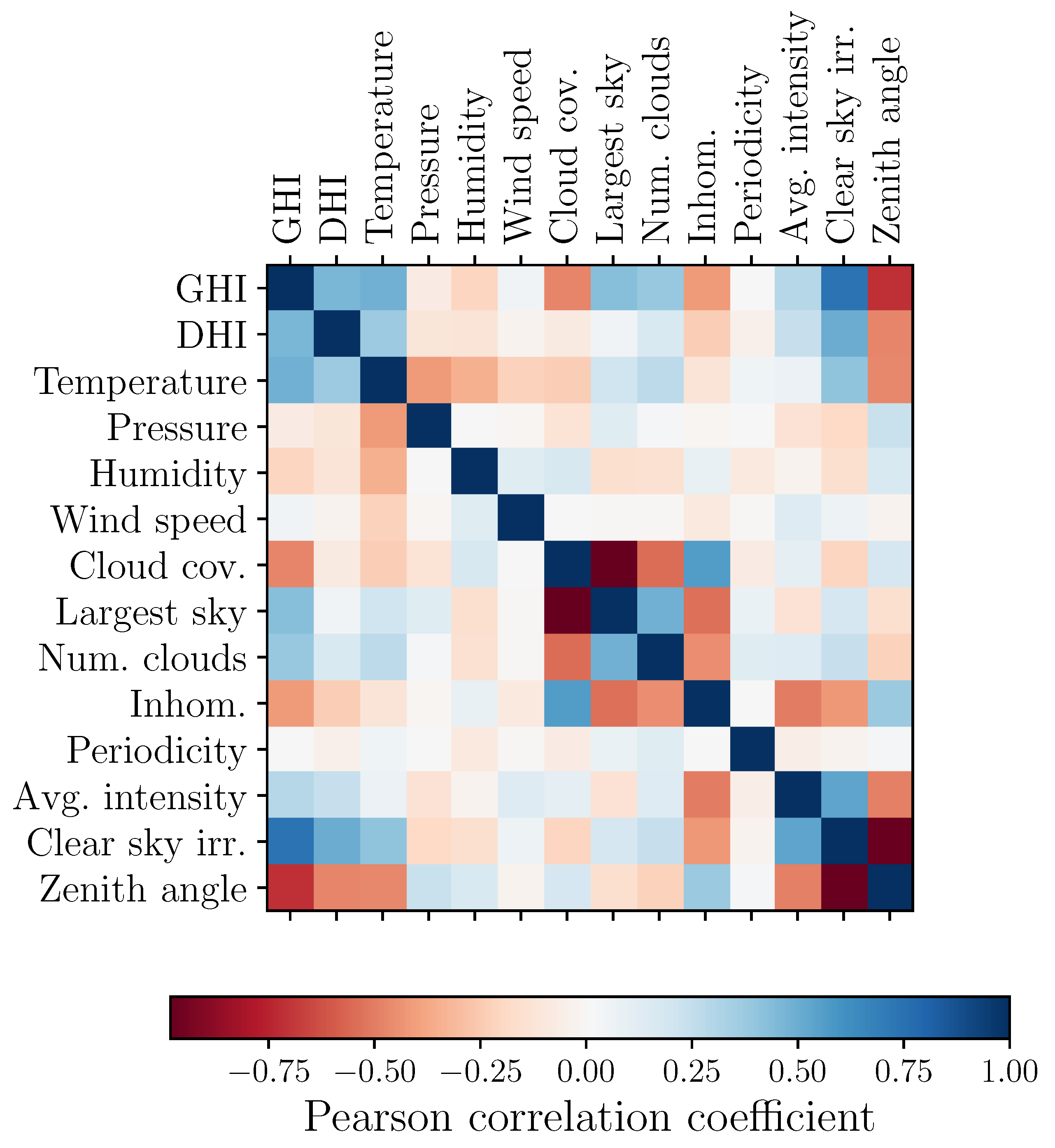
2.3. Meteorological Scenarios
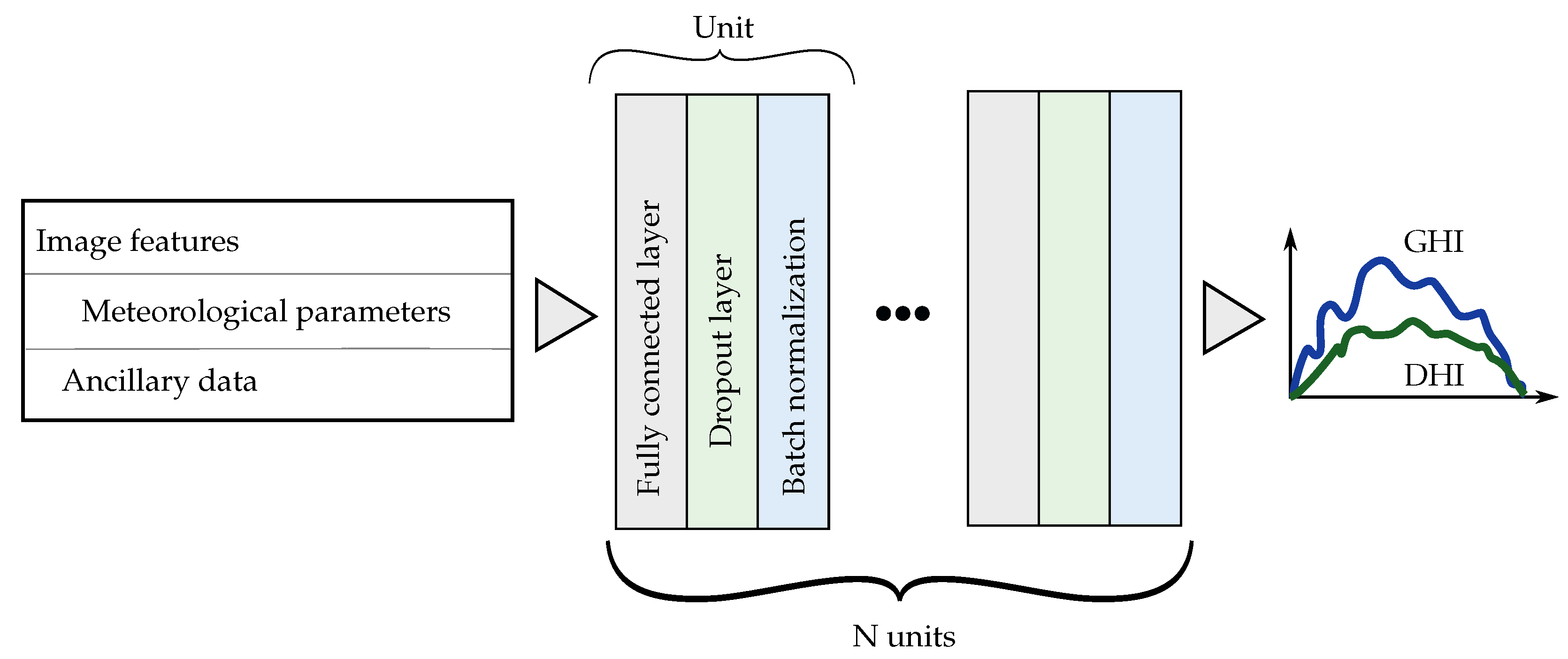
2.4. Deep Neural Network
2.4.1. Data Processing
2.4.2. Network Architecture
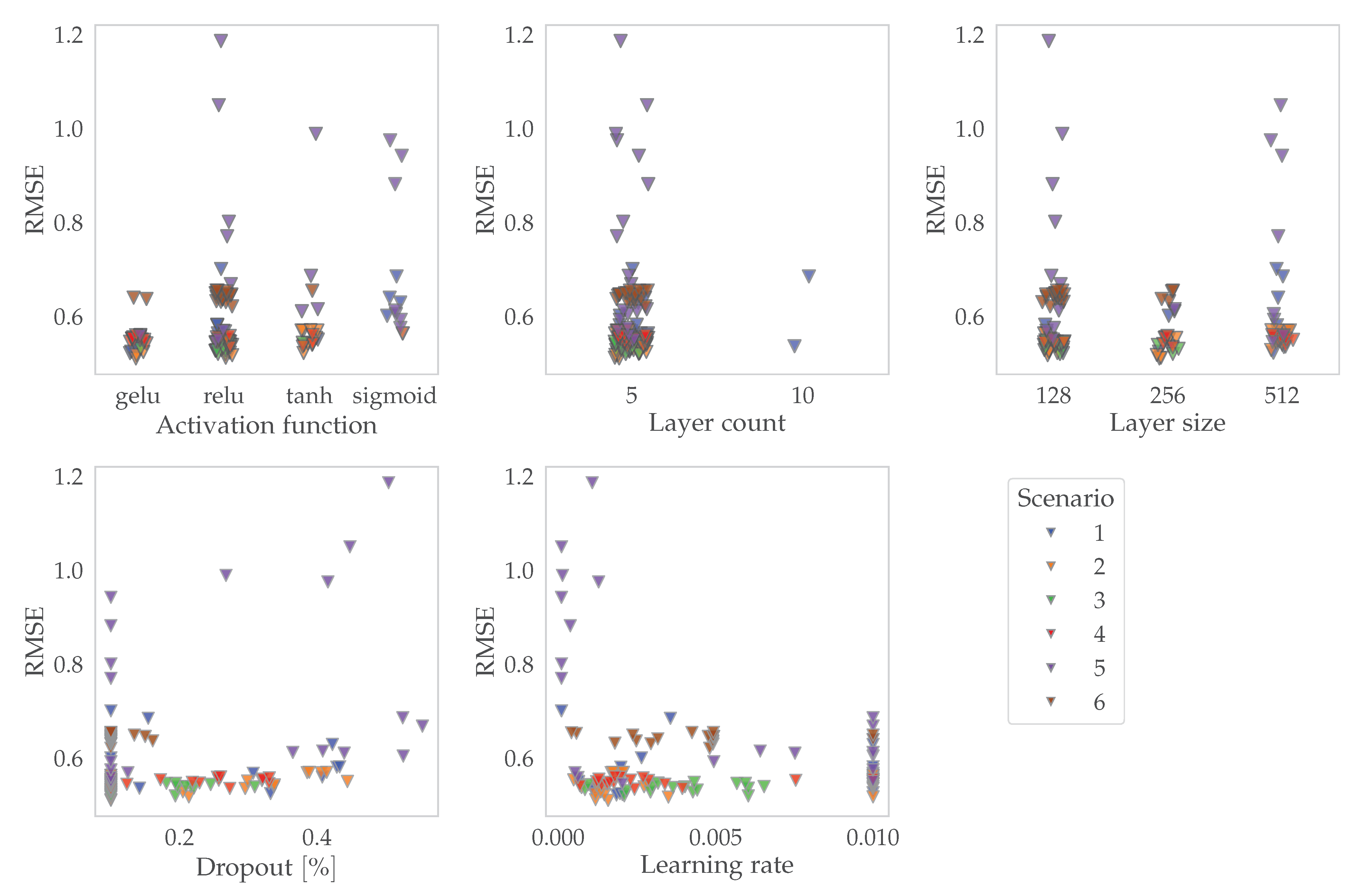
2.4.3. Hyperparameter-Optimization
2.5. Evaluation Metrics
- Root Mean Square Error:
- Mean Bias Error:
- Mean Absolute Percentage Error:
- The coefficient of determination:where is the inferred value (GHI or DHI) and denotes the measured value at time step i. and denotes the mean of estimates and measurements across all time steps and N denotes the number of samples the error is calculated for.
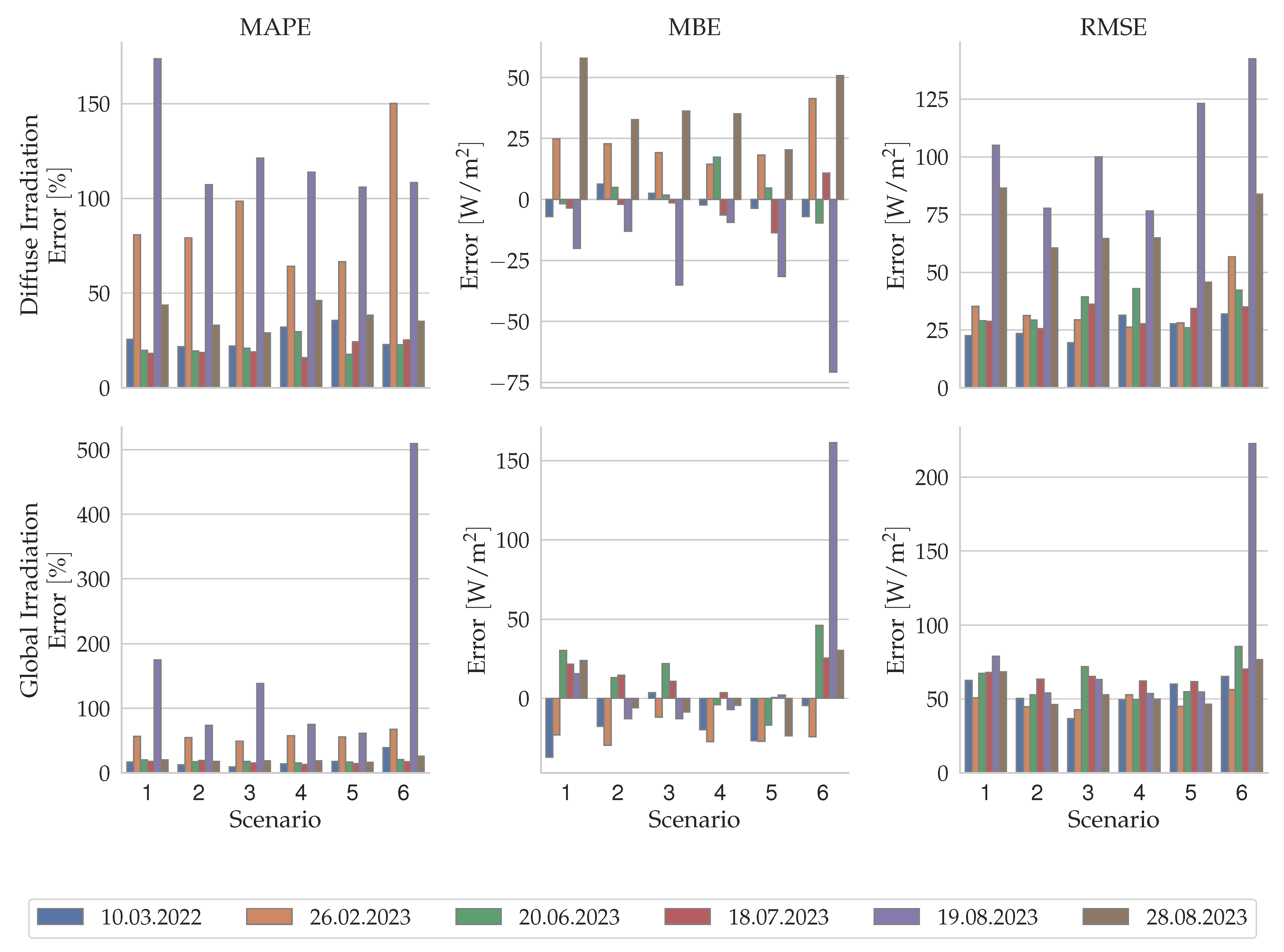
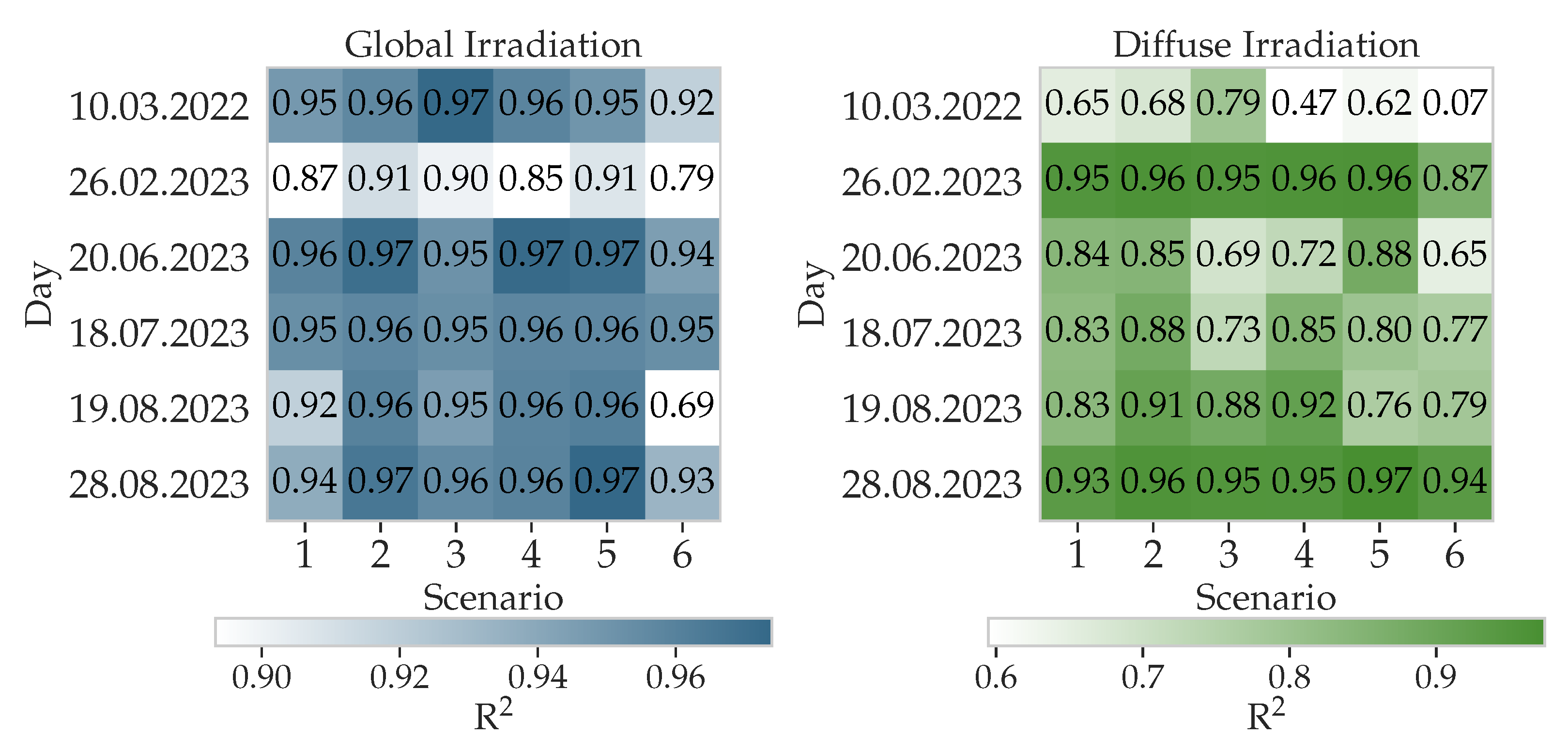
3. Results
4. Discussion
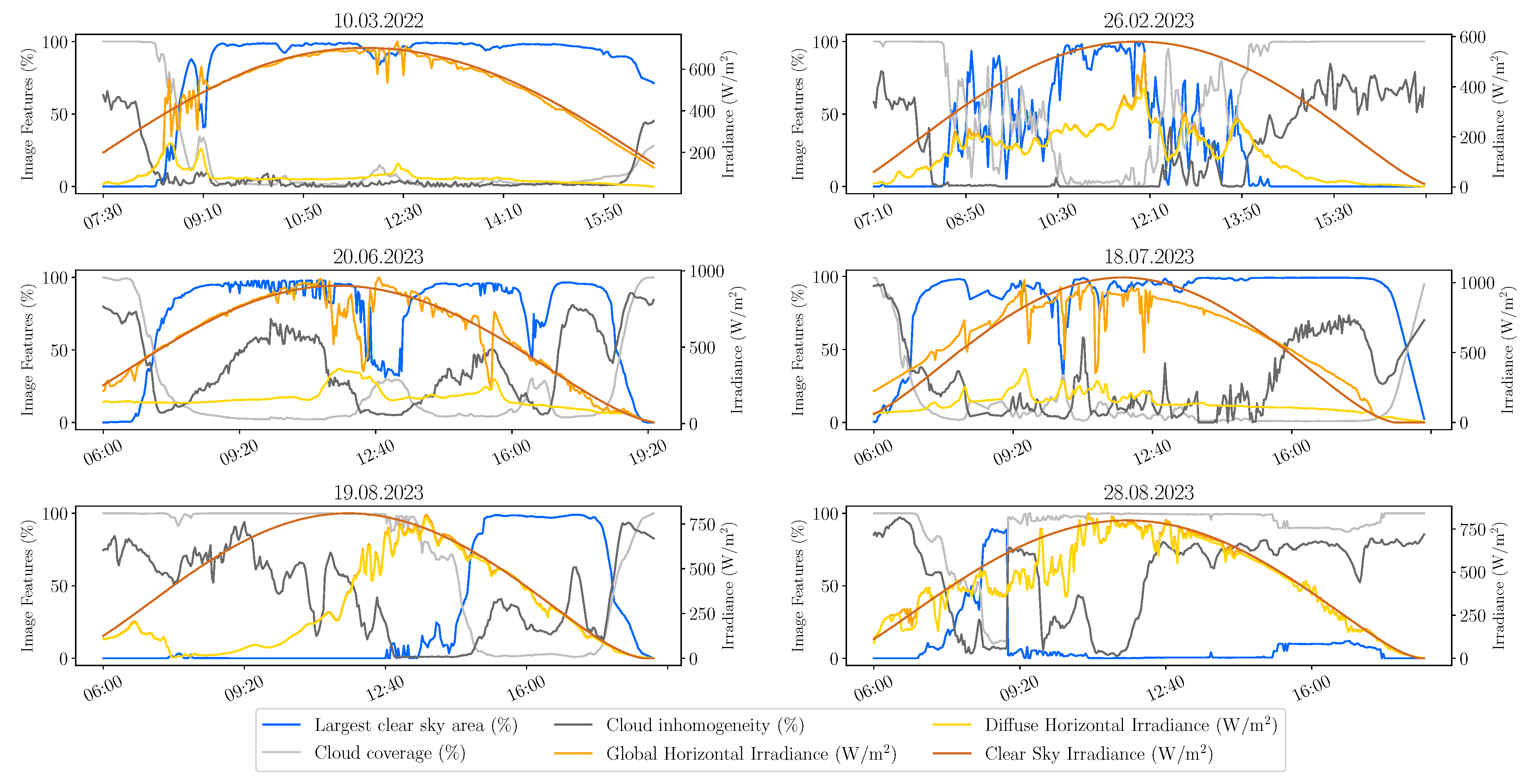
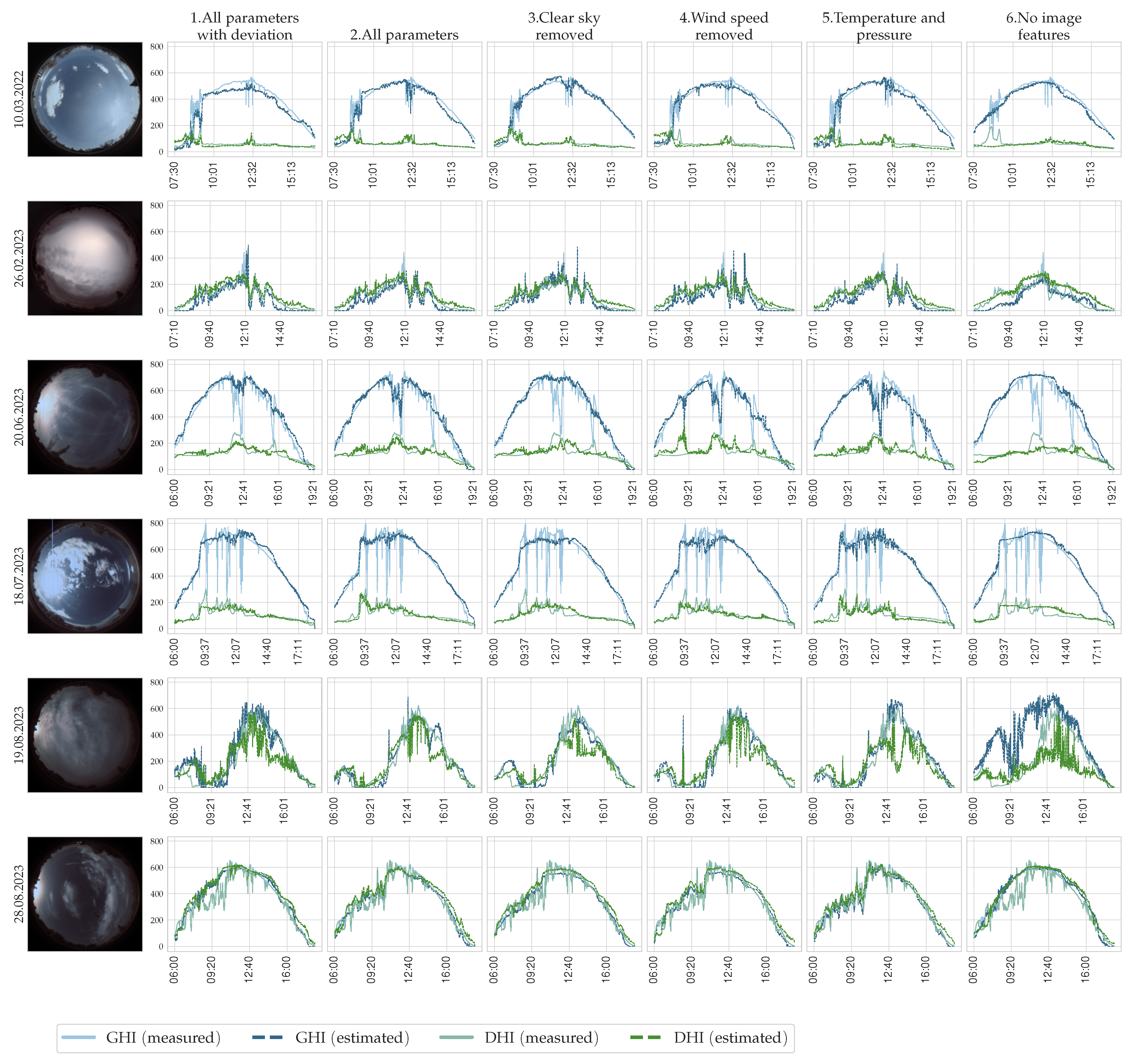
4.1. Accuracy for Selected Days
4.2. Comparative Analysis: Benchmarking against Existing Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
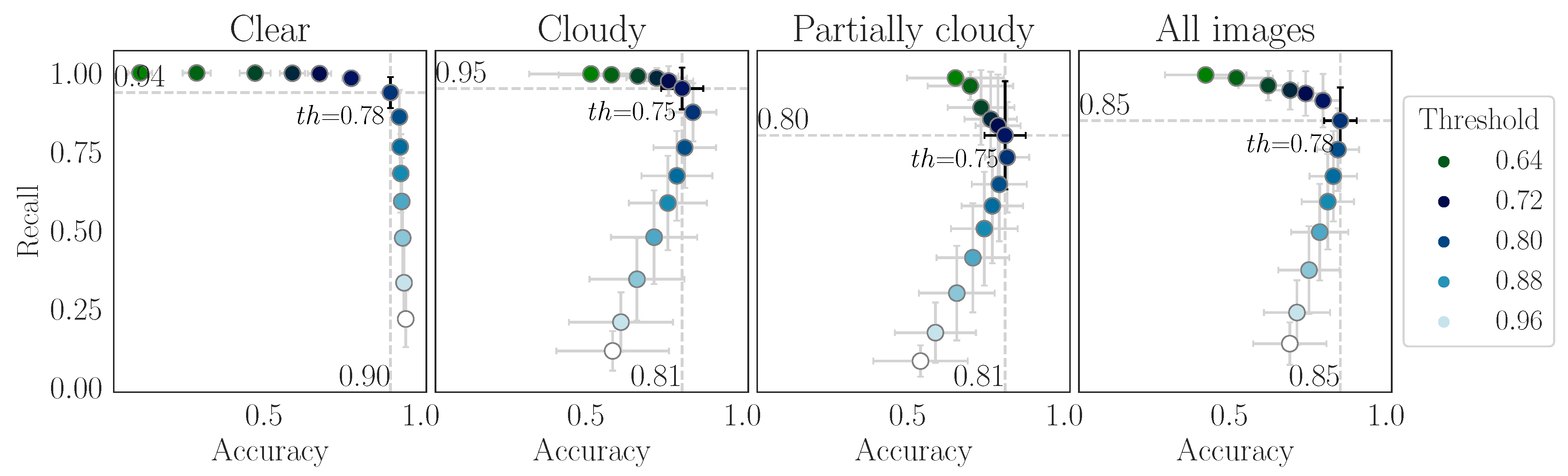
Appendix B
References
- Snapshot of Global PV Markets 2023. 2023. Available online: https://iea-pvps.org/snapshot-reports/snapshot-2023/ (accessed on 12 November 2023).
- Werner, M.; Ehrhard, R. Incident Solar Radiation over Europe Estimated from METEOSAT Data. J. Appl. Meteorol. Climatol. 1984, 23, 166–170. [Google Scholar] [CrossRef]
- Matuszko, D. Influence of the extent and genera of cloud cover on solar radiation intensity. Int. J. Climatol. 2012, 32, 2403–2414. [Google Scholar] [CrossRef]
- Jewell, W.; Ramakumar, R. The Effects of Moving Clouds on Electric Utilities with Dispersed Photovoltaic Generation. IEEE Trans. Energy Convers. 1987, EC-2, 570–576. [Google Scholar] [CrossRef]
- Barbieri, F.; Rajakaruna, S.; Ghosh, A. Very short-term photovoltaic power forecasting with cloud modeling: A review. Renew. Sustain. Energy Rev. 2017, 75, 242–263. [Google Scholar] [CrossRef]
- Samu, R.; Calais, M.; Shafiullah, G.; Moghbel, M.; Shoeb, M.A.; Nouri, B.; Blum, N. Applications for solar irradiance nowcasting in the control of microgrids: A review. Renew. Sustain. Energy Rev. 2021, 147, 111–187. [Google Scholar] [CrossRef]
- Mellit, A.; Massi Pavan, A.; Ogliari, E.; Leva, S.; Lughi, V. Advanced methods for photovoltaic output power forecasting: A review. Appl. Sci. 2020, 10, 487. [Google Scholar] [CrossRef]
- Li, Z.; Wang, K.; Li, C.; Zhao, M.; Cao, J. Multimodal Deep Learning for Solar Irradiance Prediction. In Proceedings of the 2019 International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Atlanta, GA, USA, 14–17 July 2019; pp. 784–792. [Google Scholar] [CrossRef]
- Hu, K.; Wang, L.; Li, W.; Cao, S.; Shen, Y. Forecasting of solar radiation in photovoltaic power station based on ground-based cloud images and BP neural network. IET Gener. Transm. Distrib. 2022, 16, 333–350. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, J.; Zhang, W.; Hodge, B.M. Convolutional neural networks for intra-hour solar forecasting based on sky image sequences. Appl. Energy 2022, 310, 118438. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Balafas, C.; Athanassopoulou, M.; Argyropoulos, T.; Skafidas, P.; Dervos, C. Effect of the diffuse solar radiation on photovoltaic inverter output. In Proceedings of the Melecon 2010—2010 15th IEEE Mediterranean Electrotechnical Conference, Valletta, Malta, 26–28 April 2010; pp. 58–63. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Ahmed, A.; Khalid, M. A review on the selected applications of forecasting models in renewable power systems. Renew. Sustain. Energy Rev. 2019, 100, 9–21. [Google Scholar] [CrossRef]
- Chu, Y.; Pedro, H.T.; Li, M.; Coimbra, C.F. Real-time forecasting of solar irradiance ramps with smart image processing. Sol. Energy 2015, 114, 91–104. [Google Scholar] [CrossRef]
- Saleh, M.; Meek, L.; Masoum, M.A.; Abshar, M. Battery-less short-term smoothing of photovoltaic generation using sky camera. IEEE Trans. Ind. Inform. 2017, 14, 403–414. [Google Scholar] [CrossRef]
- Wen, H.; Du, Y.; Chen, X.; Lim, E.; Wen, H.; Jiang, L.; Xiang, W. Deep learning based multistep solar forecasting for PV ramp-rate control using sky images. IEEE Trans. Ind. Inform. 2020, 17, 1397–1406. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F. Intra-hour DNI forecasting based on cloud tracking image analysis. Sol. Energy 2013, 91, 327–336. [Google Scholar] [CrossRef]
- Caldas, M.; Alonso-Suárez, R. Very short-term solar irradiance forecast using all-sky imaging and real-time irradiance measurements. Renew. Energy 2019, 143, 1643–1658. [Google Scholar] [CrossRef]
- Rajagukguk, R.A.; Ramadhan, R.A.A.; Lee, H.J. A Review on Deep Learning Models for Forecasting Time Series Data of Solar Irradiance and Photovoltaic Power. Energies 2020, 13, 6623. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Deep learning models for solar irradiance forecasting: A comprehensive review. J. Clean. Prod. 2021, 318, 128566. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, P.; Zhang, F.; Song, Q. CloudNet: Ground-based cloud classification with deep convolutional neural network. Geophys. Res. Lett. 2018, 45, 8665–8672. [Google Scholar] [CrossRef]
- Lin, Y.; Duan, D.; Hong, X.; Han, X.; Cheng, X.; Yang, L.; Cui, S. Transfer learning on the feature extractions of sky images for solar power production. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Chu, Y.; Coimbra, C.F. Short-term probabilistic forecasts for direct normal irradiance. Renew. Energy 2017, 101, 526–536. [Google Scholar] [CrossRef]
- Hosseini, M.; Katragadda, S.; Wojtkiewicz, J.; Gottumukkala, R.; Maida, A.; Chambers, T.L. Direct Normal Irradiance Forecasting Using Multivariate Gated Recurrent Units. Energies 2020, 13, 3914. [Google Scholar] [CrossRef]
- Terrén-Serrano, G.; Martínez-Ramón, M. Kernel learning for intra-hour solar forecasting with infrared sky images and cloud dynamic feature extraction. Renew. Sustain. Energy Rev. 2023, 175, 113125. [Google Scholar] [CrossRef]
- Tsai, W.C.; Tu, C.S.; Hong, C.M.; Lin, W.M. A Review of State-of-the-Art and Short-Term Forecasting Models for Solar PV Power Generation. Energies 2023, 16, 5436. [Google Scholar] [CrossRef]
- Wang, F.; Li, J.; Zhen, Z.; Wang, C.; Ren, H.; Ma, H.; Zhang, W.; Huang, L. Cloud Feature Extraction and Fluctuation Pattern Recognition Based Ultrashort-Term Regional PV Power Forecasting. IEEE Trans. Ind. Appl. 2022, 58, 6752–6767. [Google Scholar] [CrossRef]
- Almeida, M.P.; Muñoz, M.; de la Parra, I.; Perpiñán, O. Comparative study of PV power forecast using parametric and nonparametric PV models. Sol. Energy 2017, 155, 854–866. [Google Scholar] [CrossRef]
- Nouri, B.; Wilbert, S.; Segura, L.; Kuhn, P.; Hanrieder, N.; Kazantzidis, A.; Schmidt, T.; Zarzalejo, L.; Blanc, P.; Pitz-Paal, R. Determination of cloud transmittance for all sky imager based solar nowcasting. Sol. Energy 2019, 181, 251–263. [Google Scholar] [CrossRef]
- Sánchez, G.; Serrano, A.; Cancillo, M. Effect of cloudiness on solar global, solar diffuse and terrestrial downward radiation at Badajoz (Southwestern Spain). Opt. Pura Apl. 2012, 45, 33–38. [Google Scholar] [CrossRef]
- C. Valdelomar, P.; Gómez-Amo, J.L.; Peris-Ferrús, C.; Scarlatti, F.; Utrillas, M.P. Feasibility of ground-based sky-camera HDR imagery to determine solar irradiance and sky radiance over different geometries and sky conditions. Remote Sens. 2021, 13, 5157. [Google Scholar] [CrossRef]
- Mertens, T.; Kautz, J.; Van Reeth, F. Exposure Fusion. In Proceedings of the 15th Pacific Conference on Computer Graphics and Applications (PG’07), Maui, HI, USA, 29 October–2 November 2007; pp. 382–390. [Google Scholar] [CrossRef]
- Juncklaus Martins, B.; Cerentini, A.; Mantelli, S.L.; Loureiro Chaves, T.Z.; Moreira Branco, N.; von Wangenheim, A.; Rüther, R.; Marian Arrais, J. Systematic review of nowcasting approaches for solar energy production based upon ground-based cloud imaging. Sol. Energy Adv. 2022, 2, 100019. [Google Scholar] [CrossRef]
- Chow, C.W.; Urquhart, B.; Lave, M.; Dominguez, A.; Kleissl, J.; Shields, J.; Washom, B. Intra-hour forecasting with a total sky imager at the UC San Diego solar energy testbed. Sol. Energy 2011, 85, 2881–2893. [Google Scholar] [CrossRef]
- Bradski, G. The OpenCV Library. Dr. Dobb’S J. Softw. Tools Prof. Program. 2000, 25, 120–123. [Google Scholar]
- Tzoumanikas, P.; Nikitidou, E.; Bais, A.; Kazantzidis, A. The effect of clouds on surface solar irradiance, based on data from an all-sky imaging system. Renew. Energy 2016, 95, 314–322. [Google Scholar] [CrossRef]
- Heinle, A.; Macke, A.; Srivastav, A. Automatic cloud classification of whole sky images. Atmos. Meas. Tech. 2010, 3, 557–567. [Google Scholar] [CrossRef]
- Kazantzidis, A.; Tzoumanikas, P.; Blanc, P.; Massip, P.; Wilbert, S.; Ramirez-Santigosa, L. Short-term forecasting based on all-sky cameras. In Renewable Energy Forecasting; Elsevier: Amsterdam, The Netherlands, 2017; pp. 153–178. [Google Scholar]
- Tang, J.; Lv, Z.; Zhang, Y.; Yu, M.; Wei, W. An improved cloud recognition and classification method for photovoltaic power prediction based on total-sky-images. J. Eng. 2019, 2019, 4922–4926. [Google Scholar] [CrossRef]
- Schade, N.H.; Macke, A.; Sandmann, H.; Stick, C. Enhanced solar global irradiance during cloudy sky conditions. Meteorol. Z. 2007, 16, 295–303. [Google Scholar] [CrossRef]
- Lefevre, M.; Oumbe, A.; Blanc, P.; Espinar, B.; Gschwind, B.; Qu, Z.; Wald, L.; Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Arola, A.; et al. McClear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. {TensorFlow}: A system for {Large-Scale} machine learning. In Proceedings of the 12th USENIX symposium on operating systems design and implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Wu, J.; Chen, X.Y.; Zhang, H.; Xiong, L.D.; Lei, H.; Deng, S.H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Zhang, J.; Zhao, L.; Deng, S.; Xu, W.; Zhang, Y. A critical review of the models used to estimate solar radiation. Renew. Sustain. Energy Rev. 2017, 70, 314–329. [Google Scholar] [CrossRef]
- AlSkaif, T.; Dev, S.; Visser, L.; Hossari, M.; van Sark, W. A systematic analysis of meteorological variables for PV output power estimation. Renew. Energy 2020, 153, 12–22. [Google Scholar] [CrossRef]
- Berrizbeitia, S.E.; Jadraque Gago, E.; Muneer, T. Empirical models for the estimation of solar sky-diffuse radiation. A review and experimental analysis. Energies 2020, 13, 701. [Google Scholar] [CrossRef]
- Vijayakumar, G.; Kummert, M.; Klein, S.A.; Beckman, W.A. Analysis of short-term solar radiation data. Sol. Energy 2005, 79, 495–504. [Google Scholar] [CrossRef]
- Papatheofanous, E.A.; Kalekis, V.; Venitourakis, G.; Tziolos, F.; Reisis, D. Deep Learning-Based Image Regression for Short-Term Solar Irradiance Forecasting on the Edge. Electronics 2022, 11, 3794. [Google Scholar] [CrossRef]
- Sansine, V.; Ortega, P.; Hissel, D.; Ferrucci, F. Hybrid Deep Learning Model for Mean Hourly Irradiance Probabilistic Forecasting. Atmosphere 2023, 14, 1192. [Google Scholar] [CrossRef]




| Data Type | Notation | Unit | Source | Preprocessing | Utilization | |
|---|---|---|---|---|---|---|
| Measured quantities | Temperature | T | Weather station | Standardization | Input | |
| Pressure | P | |||||
| Relative Humidity | RH | % | ||||
| Wind Speed | WS | |||||
| Global Horizontal Irradiance | GHI | Backpropagated | ||||
| Diffuse Horizontal Irradiance | DHI | |||||
| Twilight Sensor Measurement | Determining valid data ranges | |||||
| Ancillary data | Clear Sky Irradiance | CSI | Clear Sky dataset | Standardization | Input | |
| Soral Zenith Angle | SZA | |||||
| Datetime | DT | Weather station and camera timestamps aligned | Conversion to circular representation Standardization | Input, alignment of image features and weather data | ||
| Image Features | IF | Image processing | Standardization | Input |
| Scenario | Temperature | Pressure | Relative Humidity | Wind Speed | Clear Sky Index | Solar Zenit Angle | Datetime | Image Feature | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| avg | std | avg | std | avg | std | avg | std | |||||
| 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| 2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| 3 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| 4 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| 5 | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| 6 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| Hyperparameter | Values |
|---|---|
| Number of layers | 1, 3, 5, 10 |
| Layer size | 128, 256, 512 |
| Activation | tanh, sigmoid, relu, gelu |
| Dropout rate | 0.1–0.8 |
| Learning rate of the Adam algorithm | 0.0001–0.01 |
| Scenario | Activation | Layer Count | Units | Dropout | Learning Rate | No. of Parameters | MFLOPS |
|---|---|---|---|---|---|---|---|
| 1 | gelu | 5 | 128 | 0.1 | 0.01 | 70,914 | 8.9 |
| 2 | gelu | 5 | 256 | 0.23 | 0.0045 | 274,434 | 35 |
| 3 | relu | 5 | 128 | 0.1 | 0.01 | 71,554 | 8.87 |
| 4 | relu | 5 | 256 | 0.16 | 0.0012 | 273,922 | 34.5 |
| 5 | relu | 5 | 512 | 0.55 | 0.01 | 1,071,618 | 136 |
| 6 | relu | 5 | 128 | 0.58 | 0.0017 | 72,194 | 9 |
| Scenario | Quantity | RMSE () | MBE () | MAPE (%) | |
|---|---|---|---|---|---|
| 1 | GHI | 108.23 | −23.20 | 56.51 | 0.87 |
| DHI | 57.10 | −7.01 | 52.74 | 0.87 | |
| 2 | GHI | 107.38 | −31.52 | 55.03 | 0.88 |
| DHI | 55.62 | −9.78 | 52.00 | 0.88 | |
| 3 | GHI | 107.20 | −25.25 | 54.96 | 0.88 |
| DHI | 57.75 | −7.10 | 52.23 | 0.87 | |
| 4 | GHI | 108.79 | −36.98 | 53.00 | 0.88 |
| DHI | 54.75 | −8.50 | 51.83 | 0.88 | |
| 5 | GHI | 111.62 | −40.52 | 53.27 | 0.88 |
| DHI | 56.77 | −10.37 | 52.05 | 0.88 | |
| 6 | GHI | 126.84 | −2.11 | 75.12 | 0.82 |
| DHI | 76.59 | −9.28 | 73.42 | 0.76 |
| Scenario | Quantity | RMSE () | MAPE (%) | MBE () | |
|---|---|---|---|---|---|
| 1 | GHI | 79.35 | 30.96 | −0.87 | 0.94 |
| DHI | 36.28 | 24.55 | −0.84 | 0.96 | |
| 2 | GHI | 71.58 | 30.07 | 0.91 | 0.95 |
| DHI | 31.25 | 23.19 | −0.84 | 0.97 | |
| 3 | GHI | 89.33 | 43.77 | 2.00 | 0.92 |
| DHI | 41.93 | 28.53 | −3.15 | 0.95 | |
| 4 | GHI | 70.52 | 23.93 | −0.97 | 0.95 |
| DHI | 30.23 | 19.25 | −2.74 | 0.97 | |
| 5 | GHI | 66.48 | 21.59 | −3.62 | 0.96 |
| DHI | 27.54 | 17.14 | −3.42 | 0.98 | |
| 6 | GHI | 83.19 | 30.68 | 2.69 | 0.93 |
| DHI | 38.56 | 25.87 | 2.37 | 0.95 |
| Source | Scenario | Quantity | RMSE () | rRMSE | rMAE | MBE () | rMBE | |
|---|---|---|---|---|---|---|---|---|
| Present study | 1 | GHI | 79.35 | 0.21 | 0.13 | −0.87 | 0.00 | 0.94 |
| DHI | 36.28 | 0.21 | 0.14 | −0.84 | 0.00 | 0.96 | ||
| 2 | GHI | 71.58 | 0.19 | 0.11 | 0.91 | 0.00 | 0.95 | |
| DHI | 31.25 | 0.18 | 0.12 | −0.84 | 0.00 | 0.97 | ||
| 3 | GHI | 89.33 | 0.23 | 0.15 | 2 | 0.01 | 0.92 | |
| DHI | 41.93 | 0.25 | 0.17 | −3.15 | −0.02 | 0.95 | ||
| 4 | GHI | 70.52 | 0.18 | 0.11 | −0.97 | 0.00 | 0.95 | |
| DHI | 30.23 | 0.18 | 0.11 | −2.74 | −0.02 | 0.97 | ||
| 5 | GHI | 66.48 | 0.17 | 0.1 | −3.62 | −0.01 | 0.96 | |
| DHI | 27.54 | 0.16 | 0.1 | −3.42 | −0.02 | 0.98 | ||
| 6 | GHI | 83.19 | 0.22 | 0.13 | 2.69 | 0.01 | 0.93 | |
| DHI | 38.56 | 0.23 | 0.15 | 2.37 | 0.01 | 0.95 | ||
| [46] | GHI | 88.33–142.22 | 0.11–0.32 | 24.66 | ||||
| [47] | GHI | 0.12–0.16 | 0.068–0.12 | 0.01–0.02 | ||||
| [48] | DHI | 0.8–0.87 |
| Source | Model | Forecast Horizon | Input Dataset | RMSE | MAE | Training | Trainable Parameters (×106) | MOPS |
|---|---|---|---|---|---|---|---|---|
| [50] | ResNet50 with sun mask | nowcasting | 763,264 samples 3 years sky images | 66.79 | 36.02 | 23.51 | 1330 | |
| ResNet50 quantized | 67.01 | 39.18 | ||||||
| SqueezeNet with sun mask | 62.93 | 38.56 | 0.74 | 2300 | ||||
| SqueezeNet quantized | 72.27 | 45.84 | ||||||
| [51] | MLP | 1 h | 1
year 243,011 samples weather data, sky images | 118.04 | 85.89 | 11 | 0.109 | |
| CNN | 109.47 | 74.53 | 340 | 4.19 | ||||
| CNN-LSTM | 100.58 | 66.09 | 1600 | 7 | ||||
| Present study | ANN (Scenario 5) | nowcasting | 300,000 samples 2 years weather data, sky images | 66.48 | 37.38 | 240 1 | 0.27 | 136 |
| ANN (Scenario 2) | 71.58 | 41.54 | 240 1 | 1 | 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barancsuk, L.; Groma, V.; Günter, D.; Osán, J.; Hartmann, B. Estimation of Solar Irradiance Using a Neural Network Based on the Combination of Sky Camera Images and Meteorological Data. Energies 2024, 17, 438. https://doi.org/10.3390/en17020438
Barancsuk L, Groma V, Günter D, Osán J, Hartmann B. Estimation of Solar Irradiance Using a Neural Network Based on the Combination of Sky Camera Images and Meteorological Data. Energies. 2024; 17(2):438. https://doi.org/10.3390/en17020438
Chicago/Turabian StyleBarancsuk, Lilla, Veronika Groma, Dalma Günter, János Osán, and Bálint Hartmann. 2024. "Estimation of Solar Irradiance Using a Neural Network Based on the Combination of Sky Camera Images and Meteorological Data" Energies 17, no. 2: 438. https://doi.org/10.3390/en17020438
APA StyleBarancsuk, L., Groma, V., Günter, D., Osán, J., & Hartmann, B. (2024). Estimation of Solar Irradiance Using a Neural Network Based on the Combination of Sky Camera Images and Meteorological Data. Energies, 17(2), 438. https://doi.org/10.3390/en17020438