Optimized Dispatch of Regional Integrated Energy System Considering Wind Power Consumption in Low-Temperature Environment
Abstract
:1. Introduction
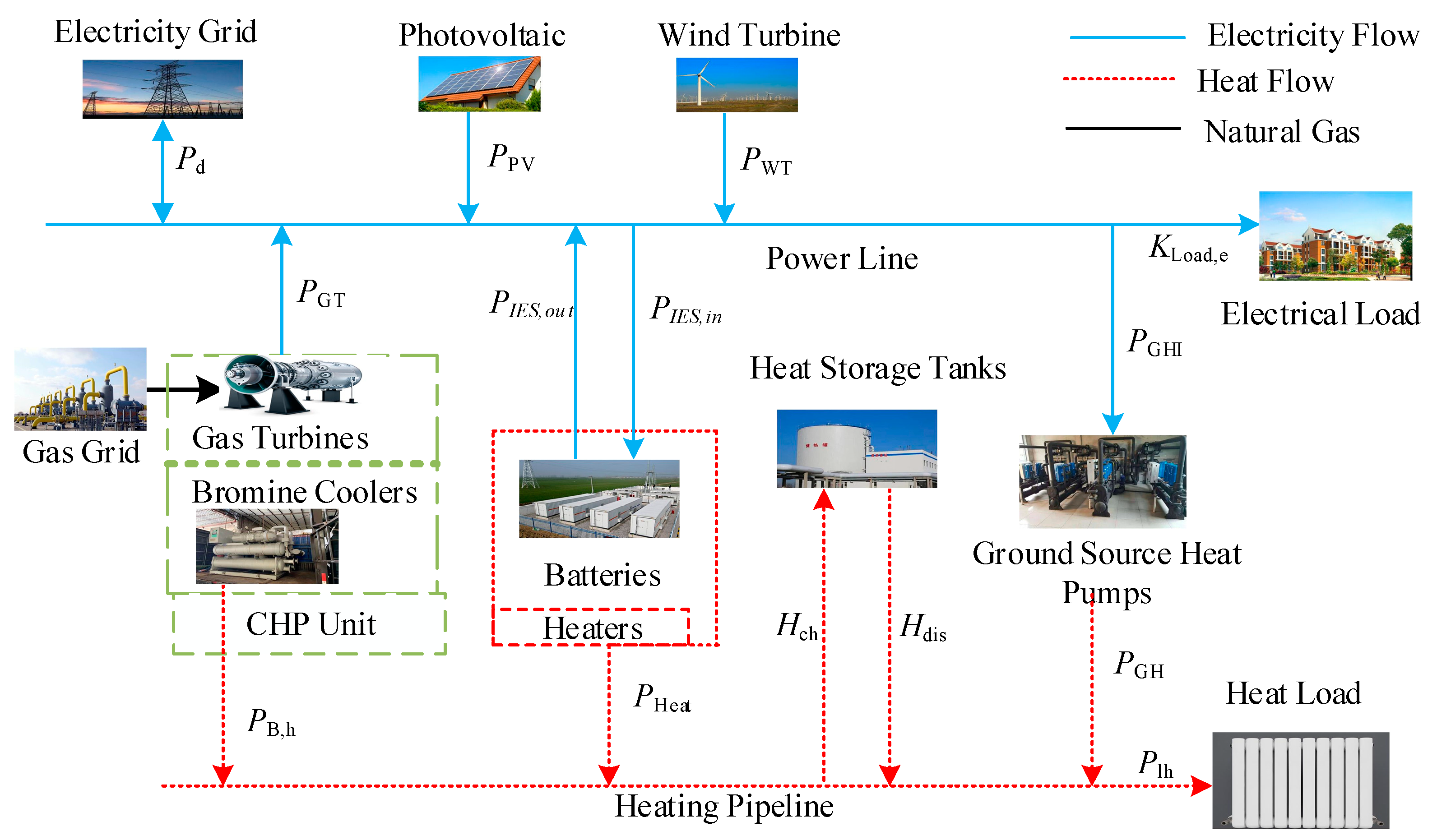
2. Integrated Energy System Architecture
2.1. CHP System
2.2. Ground Source Heat Pump
2.3. Fine Energy Storage Equipment
2.3.1. Battery Storage Model
2.3.2. Model of Heat Storage Tank
3. Combined Heat and Power Demand Response Mechanism
3.1. Electric Load Demand Response
3.2. Heat Load Demand Response
4. Scenario Selection and CVaR Theory
4.1. Uncertain Scenario Selection
4.2. CVaR Overview
5. RIES Coordinated Optimization Model Considering CVaR
5.1. Objective Function
- O&M costs
- Electricity Interaction Costs
- Environmental costs
- Wind abandonment costs
- Cost of gas purchases
5.2. Restrictive Condition
- Electrical and thermal power balance constraints:
- Controllable unit operating constraints:
- Interactive power constraints with the higher grid:
- Wind power output constraints:
- Energy storage device constraints
- Electric load demand response constraints
6. Calculus Analysis
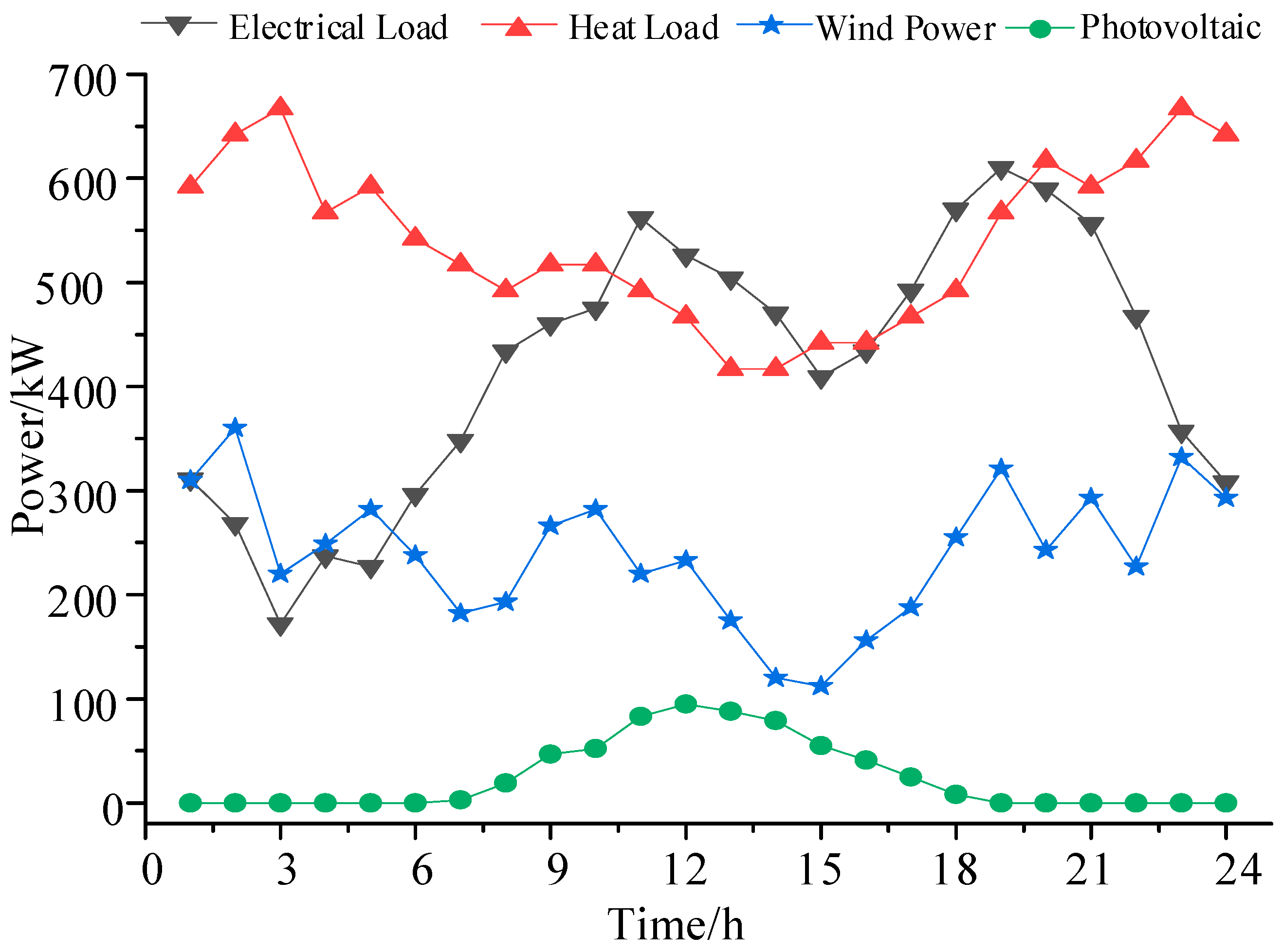
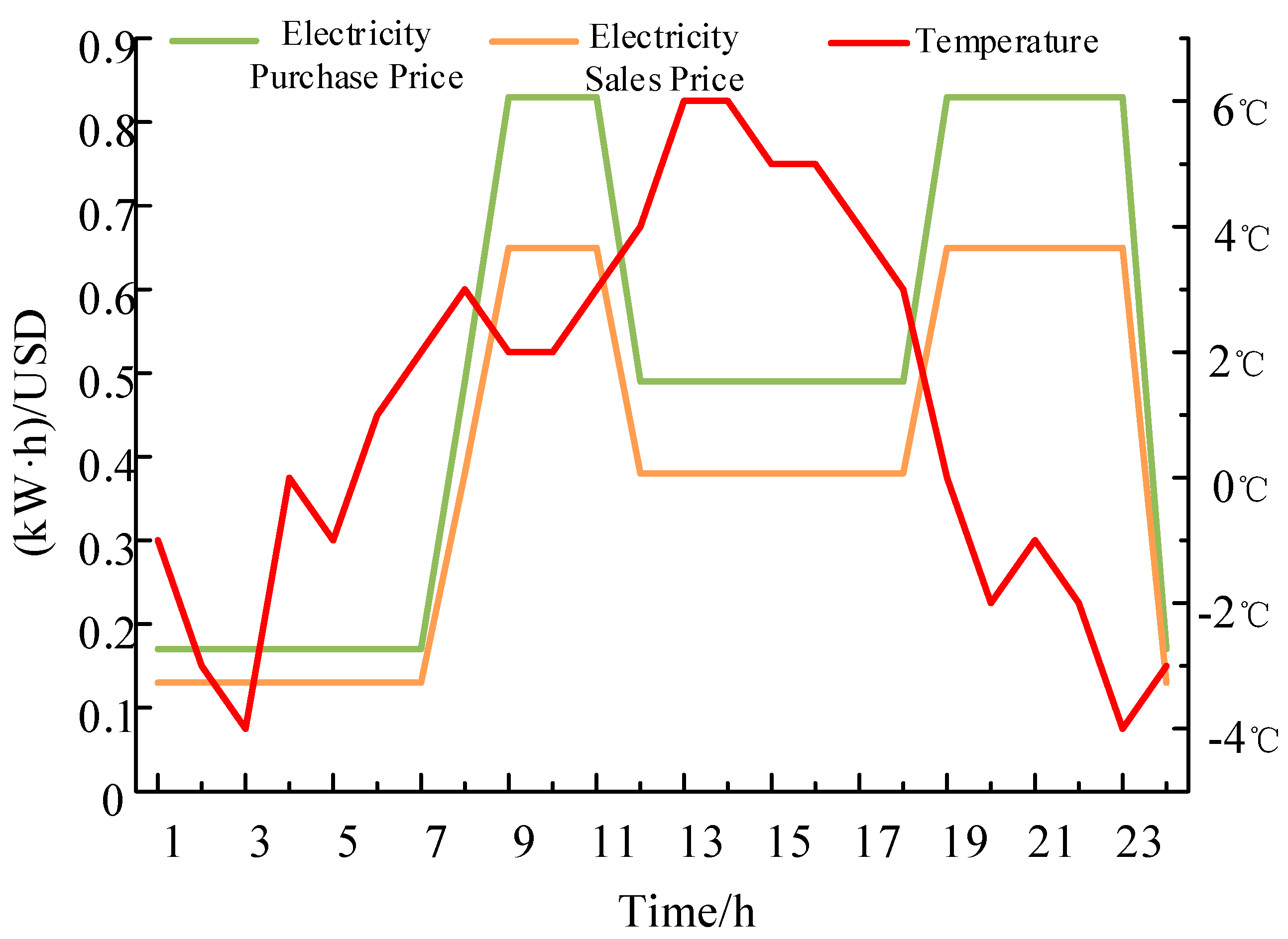
6.1. Parameterization
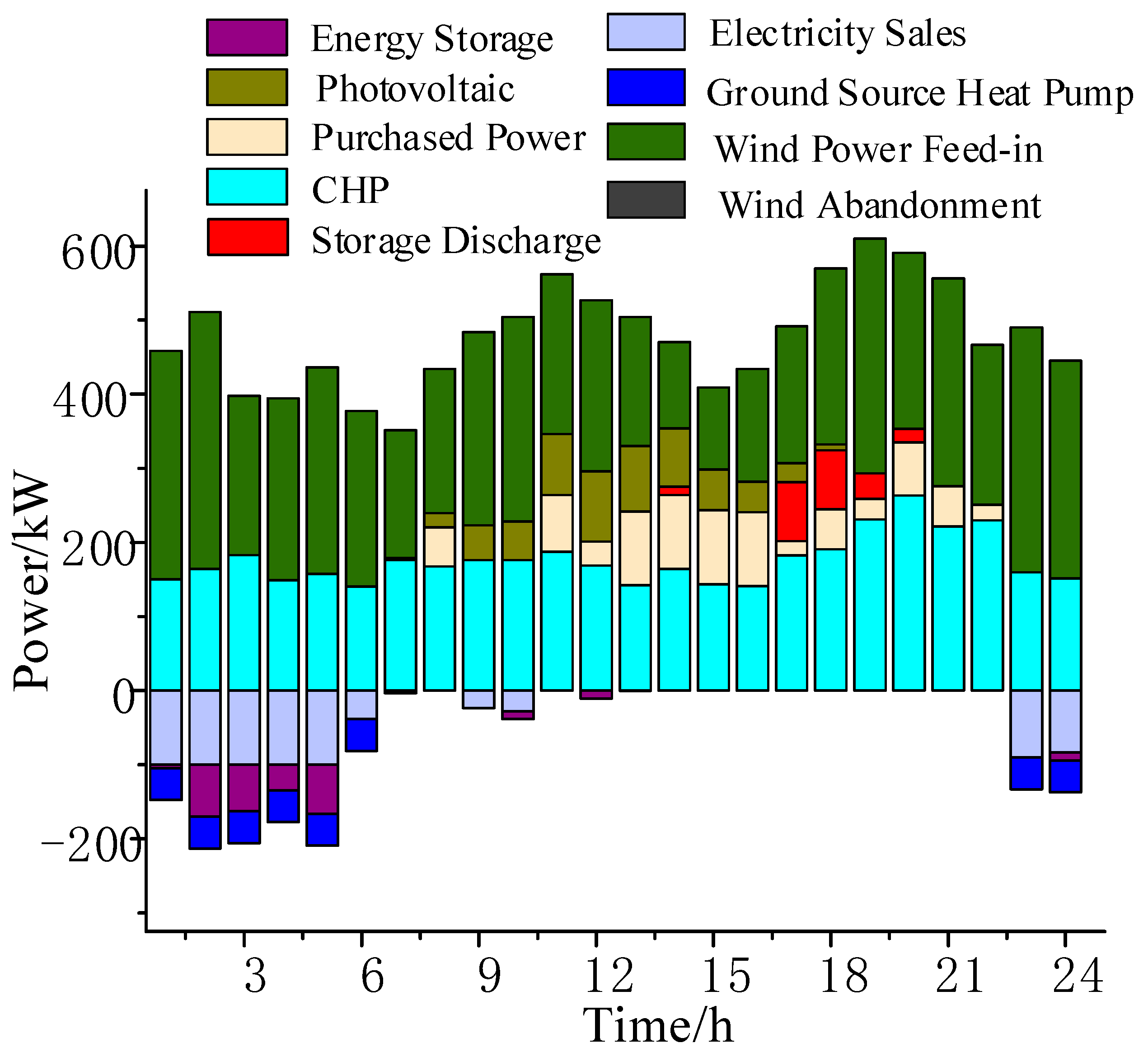
6.2. Optimized Operation Results and Analysis
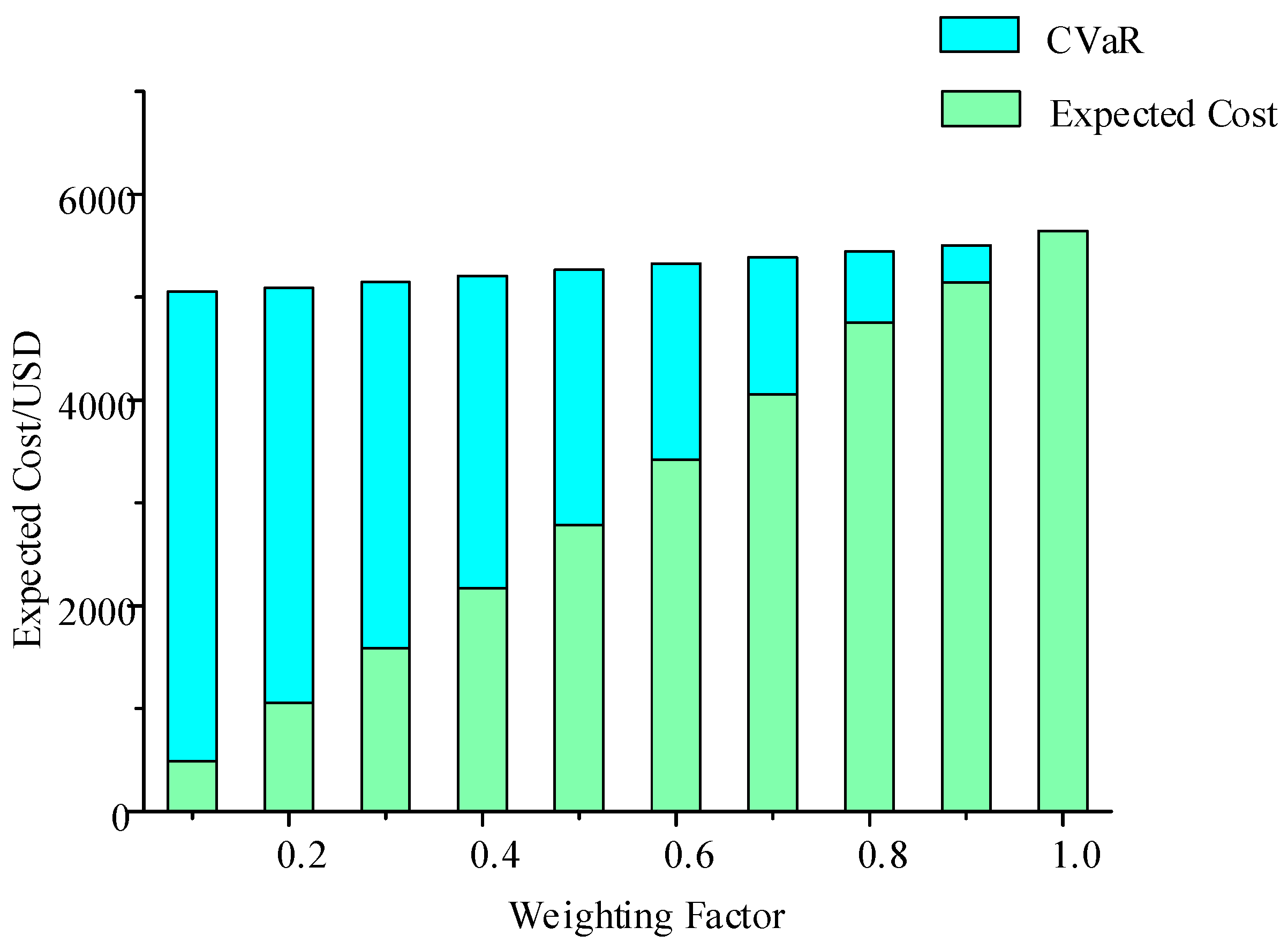
6.3. Analysis of the Effect of Weighting Coefficients on the Results of RIES Scheduling
7. Conclusions
- (1)
- The fine energy storage model takes into account the influence of ambient temperature, capacity, and other constraints, the equipment output is more in line with the actual situation than the traditional energy storage model, and the reliability of the system optimization and scheduling is higher.
- (2)
- Comprehensive consideration of electricity and heat flexible load demand response can effectively reduce the peak and valley difference in the user load while taking into account the wind power consumption capacity and economic benefits.
- (3)
- Compared to traditional deterministic models, it is more reasonable to utilize the CVaR theory to describe the risk of returns from wind power uncertainty.
- (4)
- The adjustment of the weight coefficients in the CVaR theory according to the historical operation information and the actual situation during the actual scheduling process can further improve the comprehensive efficiency of the system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RIES | Regional Integrated Energy Systems |
| CvaR | Conditional Value-at-Risk |
| CHP | Combined, Heating and Power |
| IDR | Integrated Demand Response |
| IES | Integrated Energy Storage |
| WT | Wind Turbines |
| PV | Photovoltaic |
| GSHP | Ground Source Heat Pumps |
| HST | Heat Storage Tank |
| BC | Bromine Chiller |
| GT | Gas Turbine |
| PBDR | Price-Based Demand Response |
| PMV | Predicted Mean Vote |
| VaR | Value at Risk |
| O&M | Operation and Maintenance |
References
- Wang, Y.; Wang, Y.; Huang, Y.; Li, F.; Zeng, M.; Li, J.; Wang, X.; Zhang, F. Planning and operation method of the regional integrated energy system considering economy and environment. Energy 2019, 171, 731–750. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Y.; Ju, L.; Wang, T.; Tan, Q.; Wang, J.; Tan, Z. A multi-objective scheduling optimization model for hybrid energy system connected with wind-photovoltaic-conventional gas turbines, CHP considering heating storage mechanism. Energies 2019, 12, 425. [Google Scholar] [CrossRef]
- Wang, J.; Deng, H.; Qi, X. Cost-based site and capacity optimization of multi-energy storage system in the regional integrated energy networks. Energy 2022, 261, 125240. [Google Scholar] [CrossRef]
- Xu, J.; Wang, X.; Gu, Y.; Ma, S. A data-based day-ahead scheduling optimization approach for regional integrated energy systems with varying operating conditions. Energy 2023, 283, 128534. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, R.; Wang, L.; Zeng, S.; Li, Y. Optimal operation of regional integrated energy system considering demand response. Appl. Therm. Eng. 2021, 191, 116860. [Google Scholar] [CrossRef]
- Zhang, S.; Miao, S.; Li, Y.; Yin, B.; Li, C. Regional integrated energy system dispatch strategy considering advanced adiabatic compressed air energy storage device. Int. J. Electr. Power Energy Syst. 2021, 125, 106519. [Google Scholar] [CrossRef]
- Zhu, H.; Li, H.; Liu, G.; Ge, Y.; Shi, J.; Li, H.; Zhang, N. Energy storage in high renewable penetration power systems: Technologies, applications, supporting policies and suggestions. CSEE J. Power Energy Syst. 2020, 1–9. [Google Scholar] [CrossRef]
- Zheng, W.; Lu, H.; Zhang, M.; Wu, Q.; Hou, Y.; Zhu, J. Distributed energy management of multi-entity integrated electricity and heat systems: A review of architectures, optimization algorithms, and prospects. IEEE Trans. Smart Grid 2023. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Z.; Zheng, F.; Zhou, R.; Le, J.; An, X. Cooperative optimization scheduling of the electricity-gas coupled system considering wind power uncertainty via a decomposition-coordination framework. Energy 2020, 194, 116827. [Google Scholar] [CrossRef]
- Sun, G.; Li, Y.; Chen, S.; Wei, Z.; Chen, S.; Zang, H. Dynamic stochastic optimal power flow of wind power and the electric vehicle integrated power system considering temporal-spatial characteristics. J. Renew. Sustain. Energy 2016, 8, 053309. [Google Scholar] [CrossRef]
- Ju, L.; Li, H.; Zhao, J.; Chen, K.; Tan, Q.; Tan, Z. Multi-objective stochastic scheduling optimization model for connecting a virtual power plant to wind-photovoltaic-electric vehicles considering uncertainties and demand response. Energy Convers. Manag. 2016, 128, 160–177. [Google Scholar] [CrossRef]
- Li, P.; Yu, D.; Yang, M.; Wang, J. Flexible look-ahead dispatch realized by robust optimization considering CVaR of wind power. IEEE Trans. Power Syst. 2018, 33, 5330–5340. [Google Scholar] [CrossRef]
- Levy, D.; Carmon, Y.; Duchi, J.C.; Sidford, A. Large-scale methods for distributionally robust optimization. Adv. Neural Inf. Process. Syst. 2020, 33, 8847–8860. [Google Scholar]
- Wang, Y.; Li, F.; Yang, J.; Zhou, M.; Song, F.; Zhang, D.; Xue, L.; Zhu, J. Demand response evaluation of RIES based on improved matter-element extension model. Energy 2020, 212, 118121. [Google Scholar] [CrossRef]
- Zhao, D.; Xia, X.; Tao, R. Optimal configuration of electric-gas-thermal multi-energy storage system for regional integrated energy system. Energies 2019, 12, 2586. [Google Scholar] [CrossRef]
- Yang, L.; Han, Q.; Li, X. Economic Dispatch of Multi Region Electric and Heat Energy System Using Two Stage Demand Response for Better Integration of Wind Power. J. Electr. Eng. Technol. 2022, 17, 2553–2563. [Google Scholar] [CrossRef]
- Wang, J.; Zong, Y.; You, S.; Træholt, C. A review of Danish integrated multi-energy system flexibility options for high wind power penetration. Clean Energy 2017, 1, 23–35. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, L.; Nie, J.; Li, Y. Techno-economic analysis of air source heat pump applied for space heating in northern China. Appl. Energy 2017, 207, 533–542. [Google Scholar] [CrossRef]
- Cai, B.; Li, H.; Hu, Y.; Liu, L.; Huang, J.; Lazzaretto, A.; Zhang, G. Theoretical and experimental study of combined heat and power (CHP) system integrated with ground source heat pump (GSHP). Appl. Therm. Eng. 2017, 127, 16–27. [Google Scholar] [CrossRef]
- Matjanov, E. Gas turbine efficiency enhancement using absorption chiller. Case study for Tashkent CHP. Energy 2020, 192, 116625. [Google Scholar] [CrossRef]
- Fatullah, M.A.; Rahardjo, A.; Husnayain, F. Analysis of discharge rate and ambient temperature effects on lead acid battery capacity. In Proceedings of the 2019 IEEE International Conference on Innovative Research and Development (ICIRD), Jakarta, Indonesia, 28–30 June 2019; pp. 1–5. [Google Scholar]
- Low, W.Y.; Abdul Aziz, M.J.; Idris, N.R.N. Modelling of lithium-titanate battery with ambient temperature effect for charger design. IET Power Electron. 2016, 9, 1204–1212. [Google Scholar] [CrossRef]
- Ruetschi, P. Aging mechanisms and service life of lead–acid batteries. J. Power Sources 2004, 127, 33–44. [Google Scholar] [CrossRef]
- Arslan, M.; Igci, A.A. Thermal performance of a vertical solar hot water storage tank with a mantle heat exchanger depending on the discharging operation parameters. Sol. Energy 2015, 116, 184–204. [Google Scholar] [CrossRef]
- Cabeza, L.F. Advances in thermal energy storage systems: Methods and applications. In Advances in Thermal Energy Storage Systems; Elsevier: Amsterdam, The Netherlands, 2021; pp. 37–54. [Google Scholar]
- Yang, C.; Meng, C.; Zhou, K. Residential electricity pricing in China: The context of price-based demand response. Renew. Sustain. Energy Rev. 2018, 81, 2870–2878. [Google Scholar] [CrossRef]
- Shewale, A.; Mokhade, A.; Funde, N.; Bokde, N.D. An overview of demand response in smart grid and optimization techniques for efficient residential appliance scheduling problem. Energies 2020, 13, 4266. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.; Wang, Y.; Zeng, M.; Yu, H.; Li, F.; Zhang, F. Optimal scheduling of the RIES considering time-based demand response programs with energy price. Energy 2018, 164, 773–793. [Google Scholar] [CrossRef]
- Yau, Y.; Chew, B. A review on predicted mean vote and adaptive thermal comfort models. Build. Serv. Eng. Res. Technol. 2014, 35, 23–35. [Google Scholar] [CrossRef]
- Gao, B.; Pan, Y.; Chen, Z.; Wu, F.; Ren, X.; Hu, M. A spatial conditioned Latin hypercube sampling method for mapping using ancillary data. Trans. GIS 2016, 20, 735–754. [Google Scholar] [CrossRef]
- Stoyanov, S.V.; Rachev, S.T.; Fabozzi, F.J. Sensitivity of portfolio VaR and CVaR to portfolio return characteristics. Ann. Oper. Res. 2013, 205, 169–187. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–42. [Google Scholar] [CrossRef]
- Dong, L.; Li, M.; Hu, J.; Chen, S.; Zhang, T.; Wang, X.; Pu, T. A hierarchical game approach for optimization of regional integrated energy system clusters considering bounded rationality. CSEE J. Power Energy Syst. 2023, 1–11. [Google Scholar] [CrossRef]
- Li, P.; Yang, M.; Wu, Q. Confidence interval based distributionally robust real-time economic dispatch approach considering wind power accommodation risk. IEEE Trans. Sustain. Energy 2020, 12, 58–69. [Google Scholar] [CrossRef]
- Ju, L.; Tan, Q.; Lu, Y.; Tan, Z.; Zhang, Y.; Tan, Q. A CVaR-robust-based multi-objective optimization model and three-stage solution algorithm for a virtual power plant considering uncertainties and carbon emission allowances. Int. J. Electr. Power Energy Syst. 2019, 107, 628–643. [Google Scholar] [CrossRef]
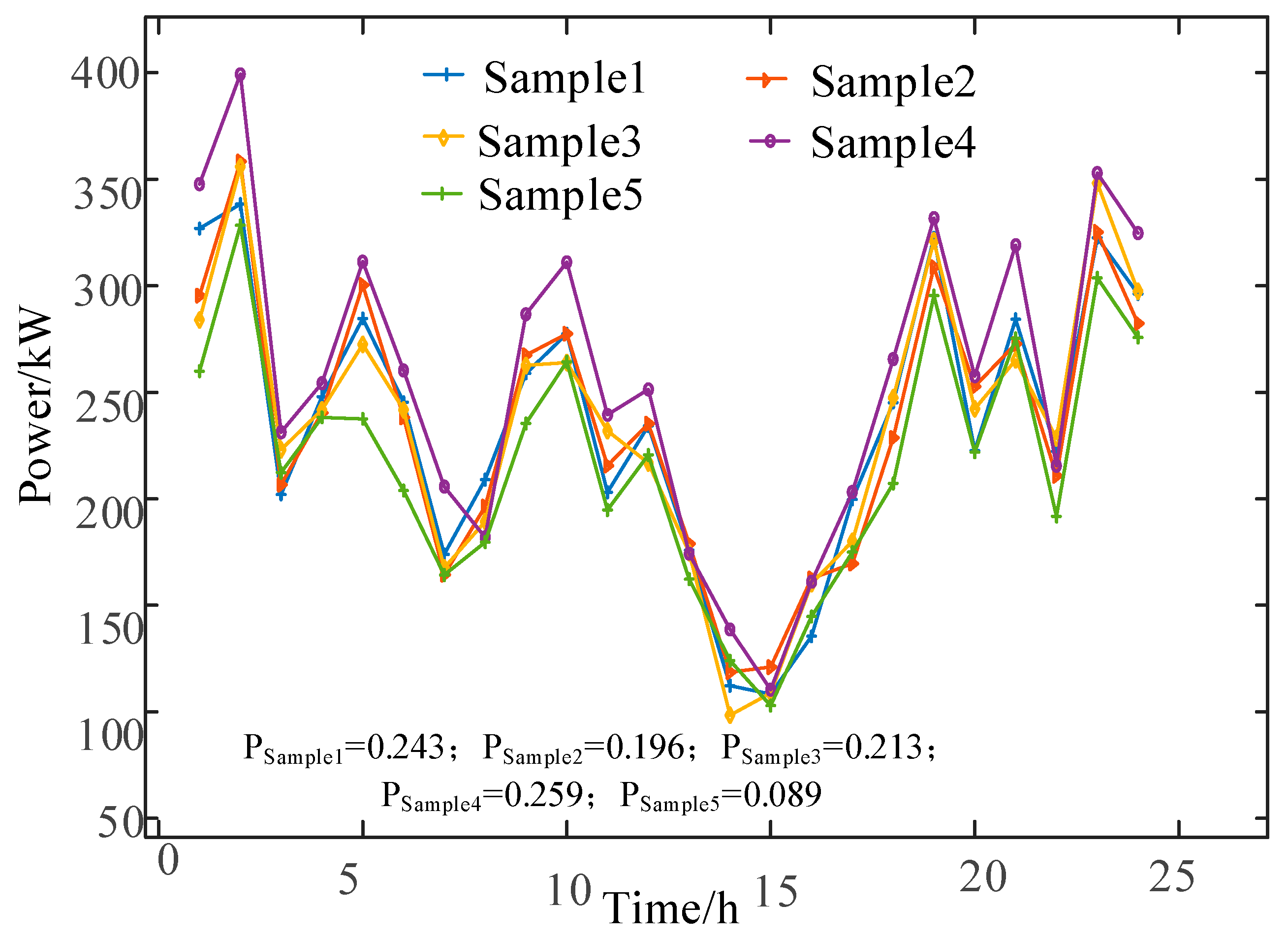
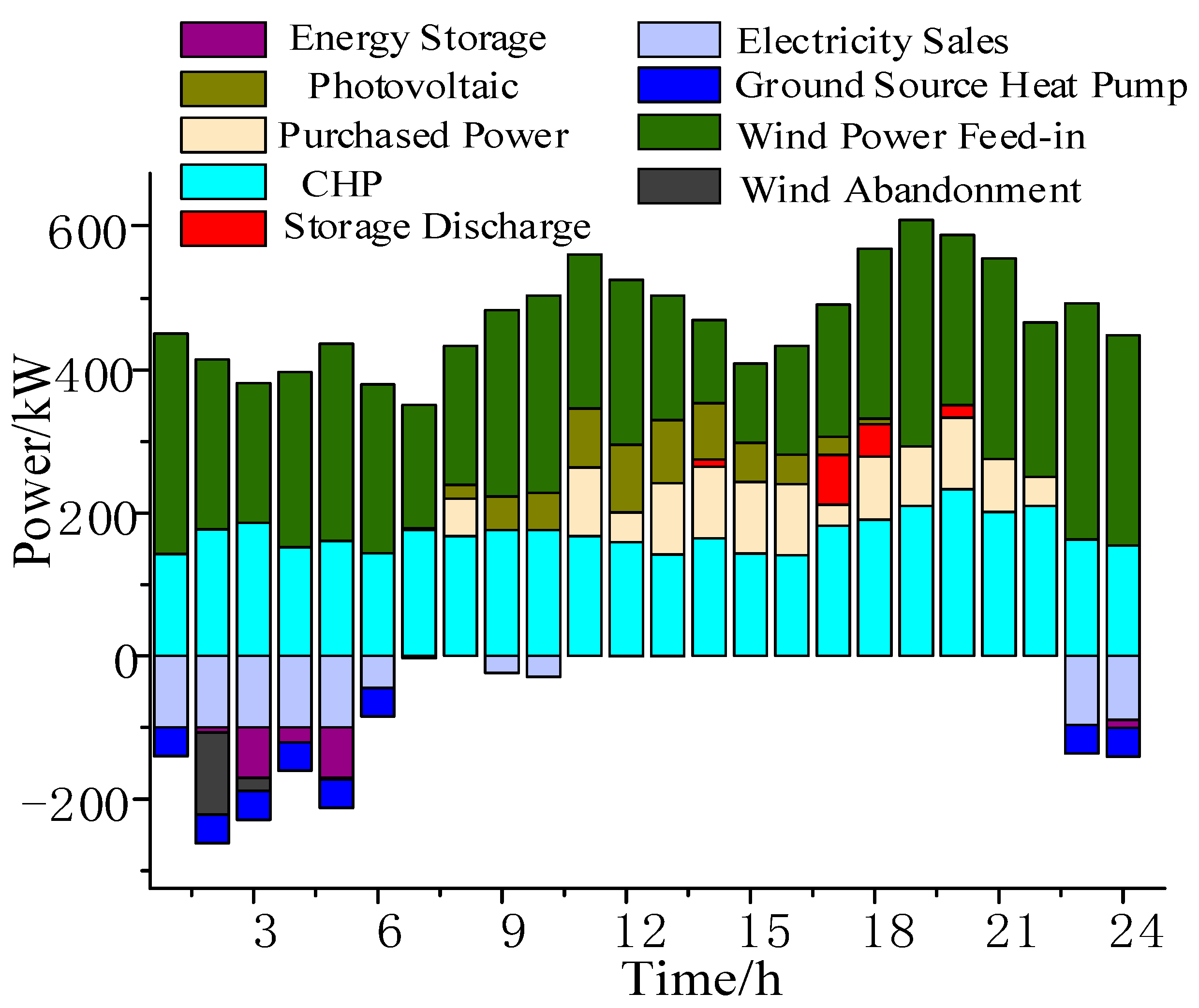
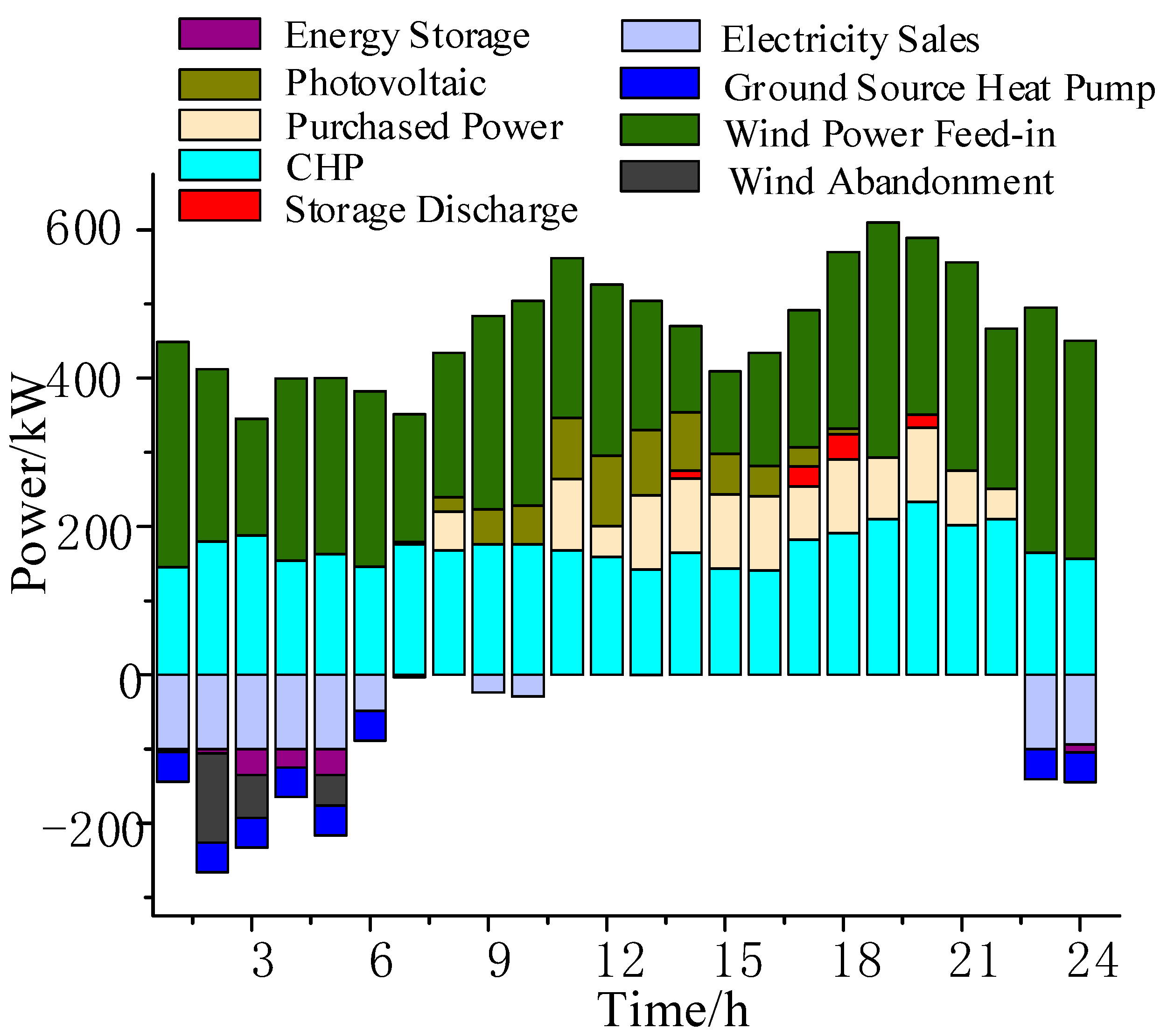
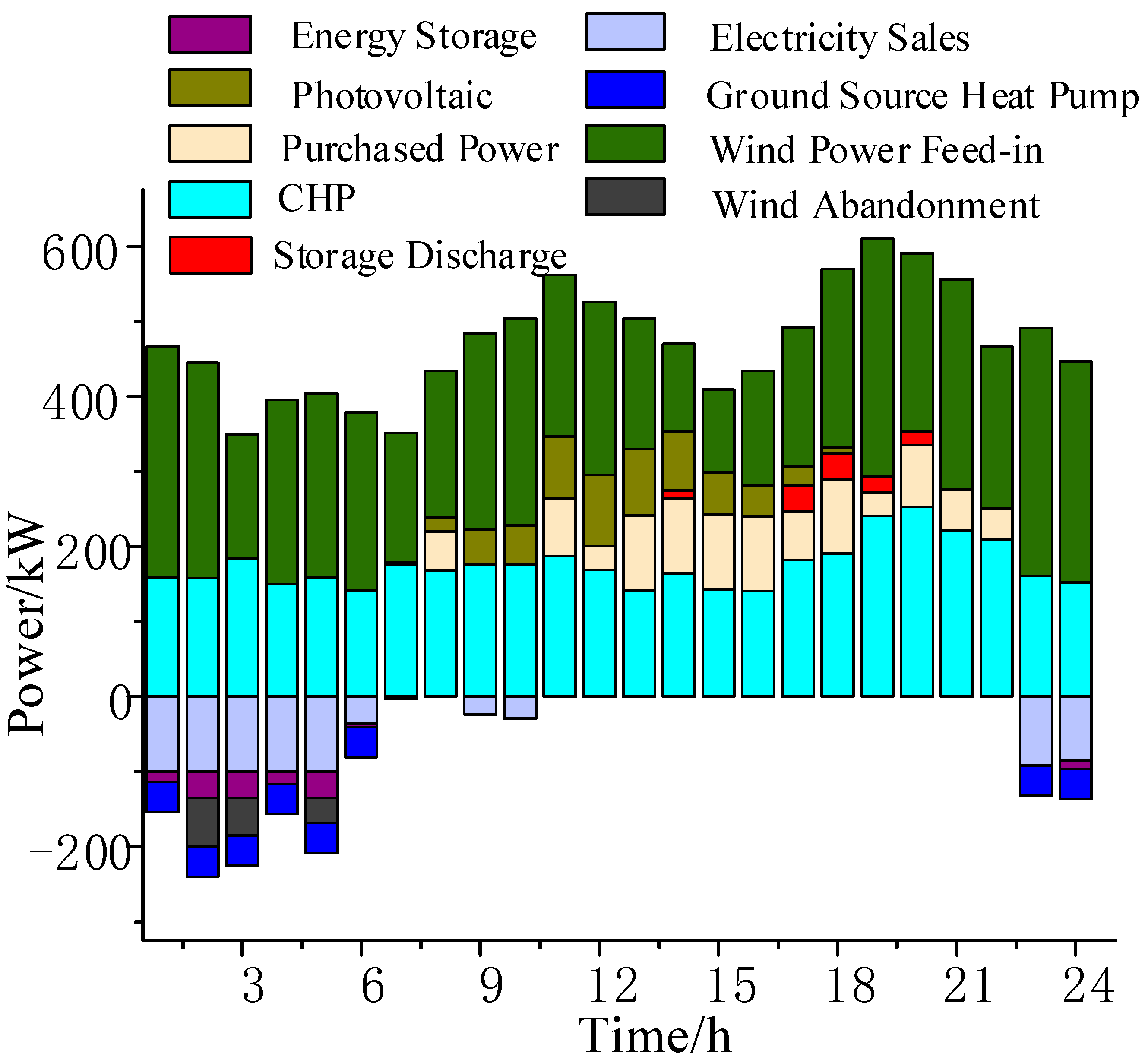

| Parameter | Batteries | Heat Storage Tanks | Parameter | Heat Storage Tanks | Batteries |
|---|---|---|---|---|---|
| Capacity/(kW·h) | 200 | 300 | Initial energy storage state | 0.2 | 0.2 |
| Charging and discharging rate | 0.9 | 0.88 | Maximum energy storage state | 0.9 | 0.9 |
| Attrition rate | 0.001 | 0.01 | Minimum energy storage state | 0 | 0.2 |
| O&M unit price (USD/kW·h) | 0.051 | 0.045 | Maximum charge and discharge power/kW | 50 | 50 |
| Type | SO2 | NOX | CO2 |
|---|---|---|---|
| Gas turbine emission standard (g/kWh) | 0.023 | 4.795 | 170.16 |
| Emission standard of purchased power (g/kWh) | 6.4 | 2.32 | 696 |
| Treatment cost of each pollutant (USD/t) | 1000 | 1950 | 9.75 |
| Parameter | GT | GSHP | PW | PV | Grid |
|---|---|---|---|---|---|
| Power upper limit/kW | 500 | 30 | 400 | 100 | 100 |
| Lower power limit/kW | 50 | 0 | 0 | 0 | 0 |
| Climbing rate upper limit/(kW/min) | 6 | 4 | — | — | — |
| Climbing rate lower limit/(kW/min) | 5 | 3 | — | — | — |
| Efficiency | 0.24 | 3 | — | — | — |
| O&M unit price (USD/kW·h) | 0.053 | 0.026 | 0.029 | 0.025 | — |
| Cost Category (USD/Day) | Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 |
|---|---|---|---|---|
| Total Cost | 5620.5 | 5706.2 | 5646.7 | 5502.5 |
| Expected Cost | 5558.8 | 5648.5 | 5548.3 | 5442.4 |
| CVaR | 6175.8 | 6234.4 | 6208.2 | 6043.5 |
| Fuel Cost | 4292.3 | 4319.3 | 4275 | 4266.9 |
| Maintenance Cost | 446.7 | 441.1 | 443.7 | 455.3 |
| Environmental Costs | 56.57 | 58.67 | 56.64 | 54.41 |
| Purchase and Sale Costs | 766.5 | 833.8 | 812.5 | 665.8 |
| Wind Abandonment Cost | 3.96 | 6.35 | 3.15 | 0 |
| Wind Power Consumption Rate | 95.54% | 91.42% | 97.37% | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Huang, J.; Li, Z.; Qi, H. Optimized Dispatch of Regional Integrated Energy System Considering Wind Power Consumption in Low-Temperature Environment. Energies 2023, 16, 7791. https://doi.org/10.3390/en16237791
Li L, Huang J, Li Z, Qi H. Optimized Dispatch of Regional Integrated Energy System Considering Wind Power Consumption in Low-Temperature Environment. Energies. 2023; 16(23):7791. https://doi.org/10.3390/en16237791
Chicago/Turabian StyleLi, Liangkai, Jingguang Huang, Zhenxing Li, and Hao Qi. 2023. "Optimized Dispatch of Regional Integrated Energy System Considering Wind Power Consumption in Low-Temperature Environment" Energies 16, no. 23: 7791. https://doi.org/10.3390/en16237791
APA StyleLi, L., Huang, J., Li, Z., & Qi, H. (2023). Optimized Dispatch of Regional Integrated Energy System Considering Wind Power Consumption in Low-Temperature Environment. Energies, 16(23), 7791. https://doi.org/10.3390/en16237791





