Power Distribution Systems’ Vulnerability by Regions Caused by Electrical Discharges
Abstract
:1. Introduction
1.1. Literature Review
1.2. Contributions
- (1)
- Incorporation of a geographic space to estimate regions vulnerable to failures in a PDS. Previous estimations of areas vulnerable to faults are essential information to aid decision-making and guide preventive actions by the power utilities. Such actions can avoid all inconveniences and additional costs after faults occur in a PDS.
- (2)
- GWEA by regions is accomplished from local variables associated with faults and electrical discharges. GWEA allows for separate exploratory analyses of electrical discharge and faults and the search for local associations between these variables in each region of the city.
1.3. Paper Structure
2. Energy Supply Interruptions: Electrical Discharges
3. Spatial Data Analysis
3.1. Exploratory Spatial Data Analysis
3.1.1. Spearman’s Correlation Coefficient
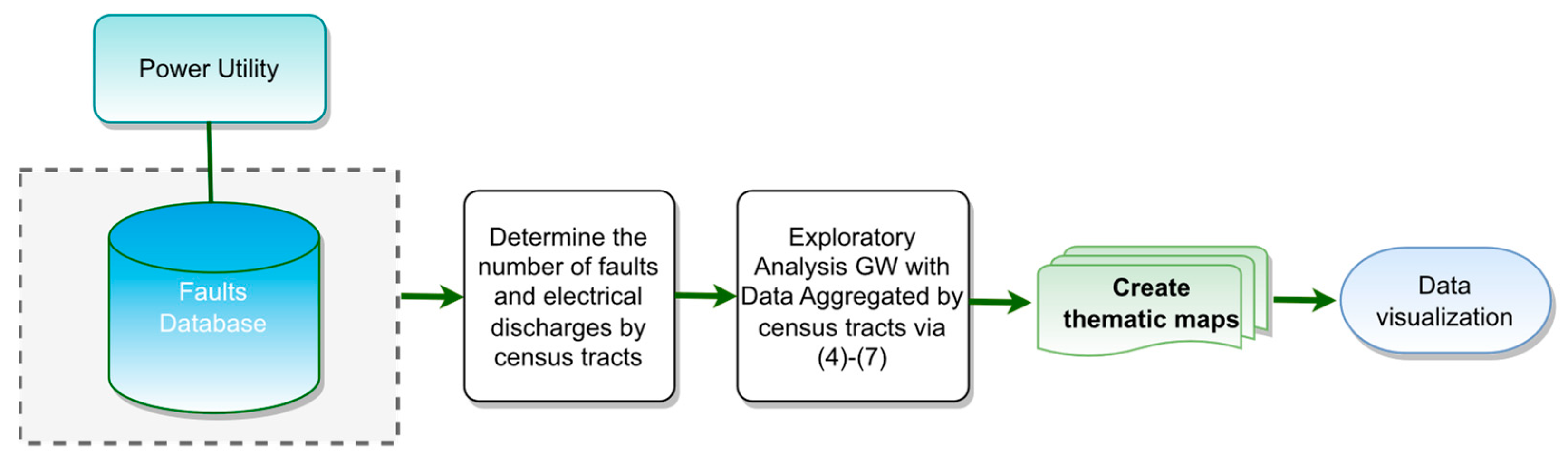
3.2. Spatial Analysis with Data Aggregated by Regions
3.2.1. Weighting Matrix
3.2.2. Geographically Weighted Statistics Metrics
4. Results and Discussion
4.1. Case Study in A Brazilian City
4.2. Database Description
4.3. Exploratory Spatial Data Analysis
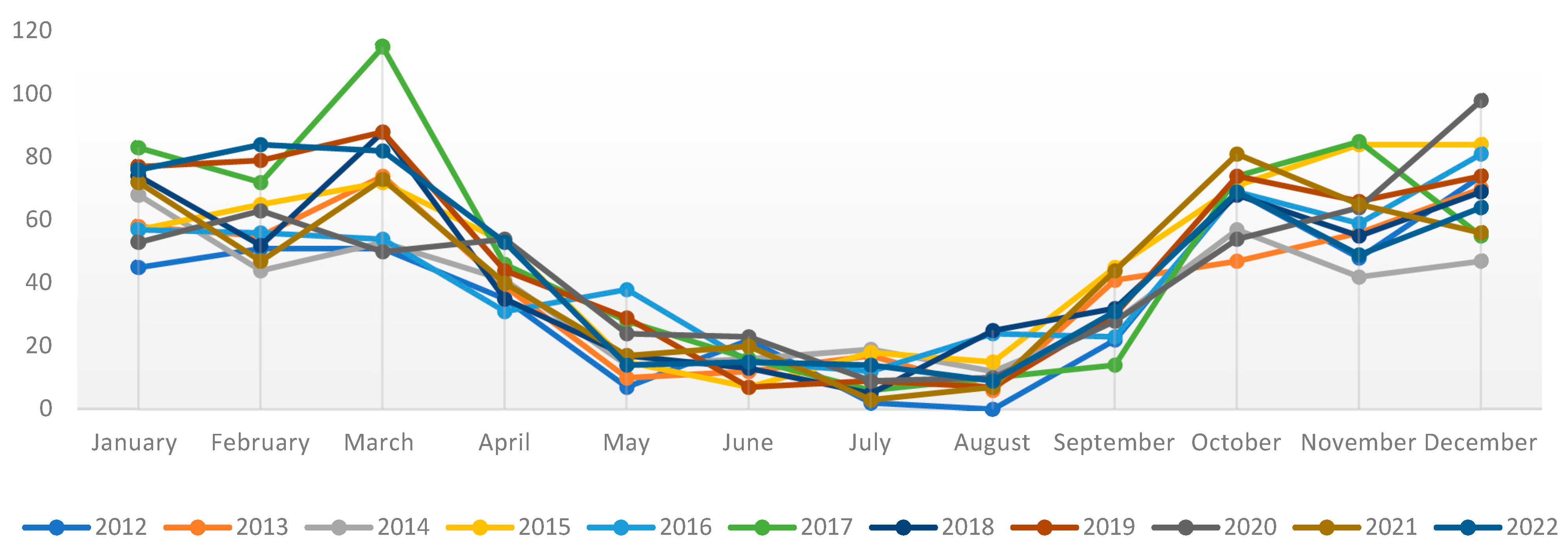
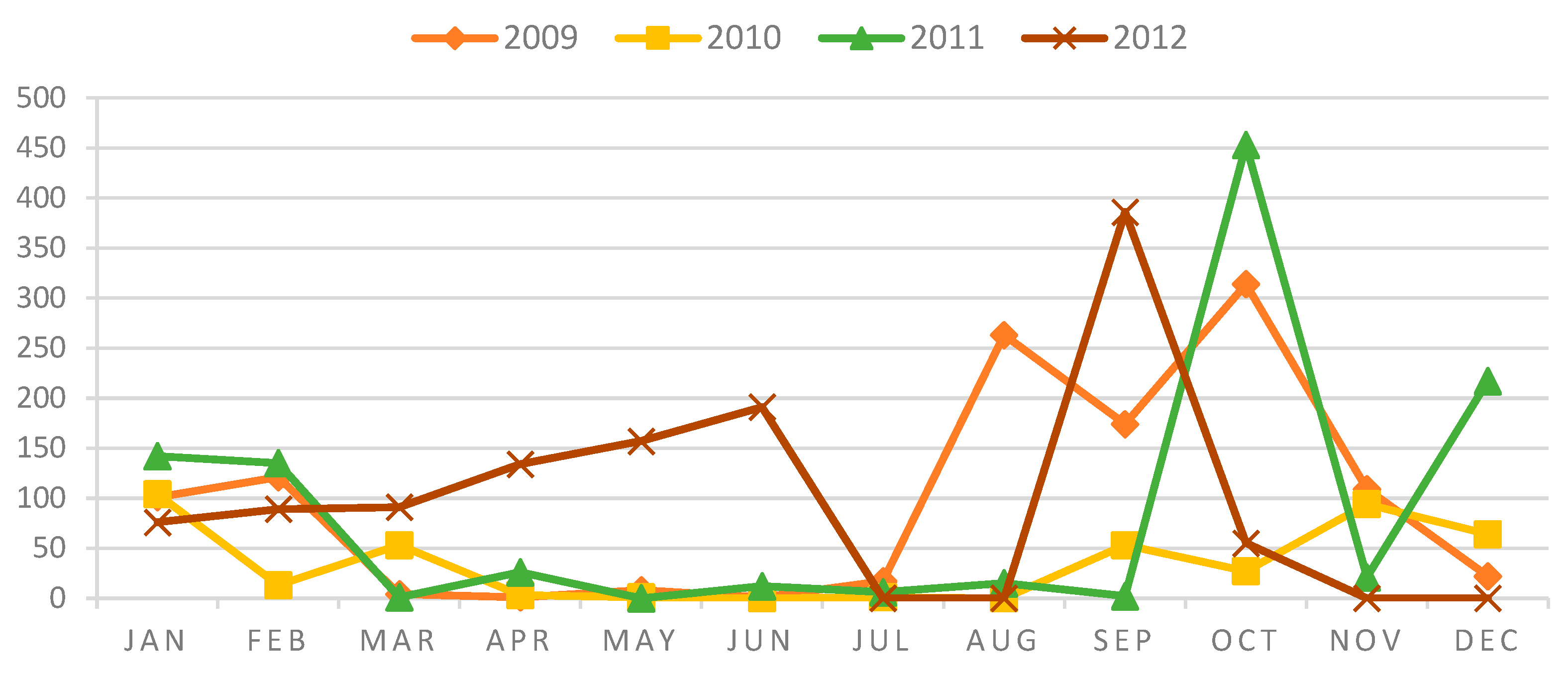
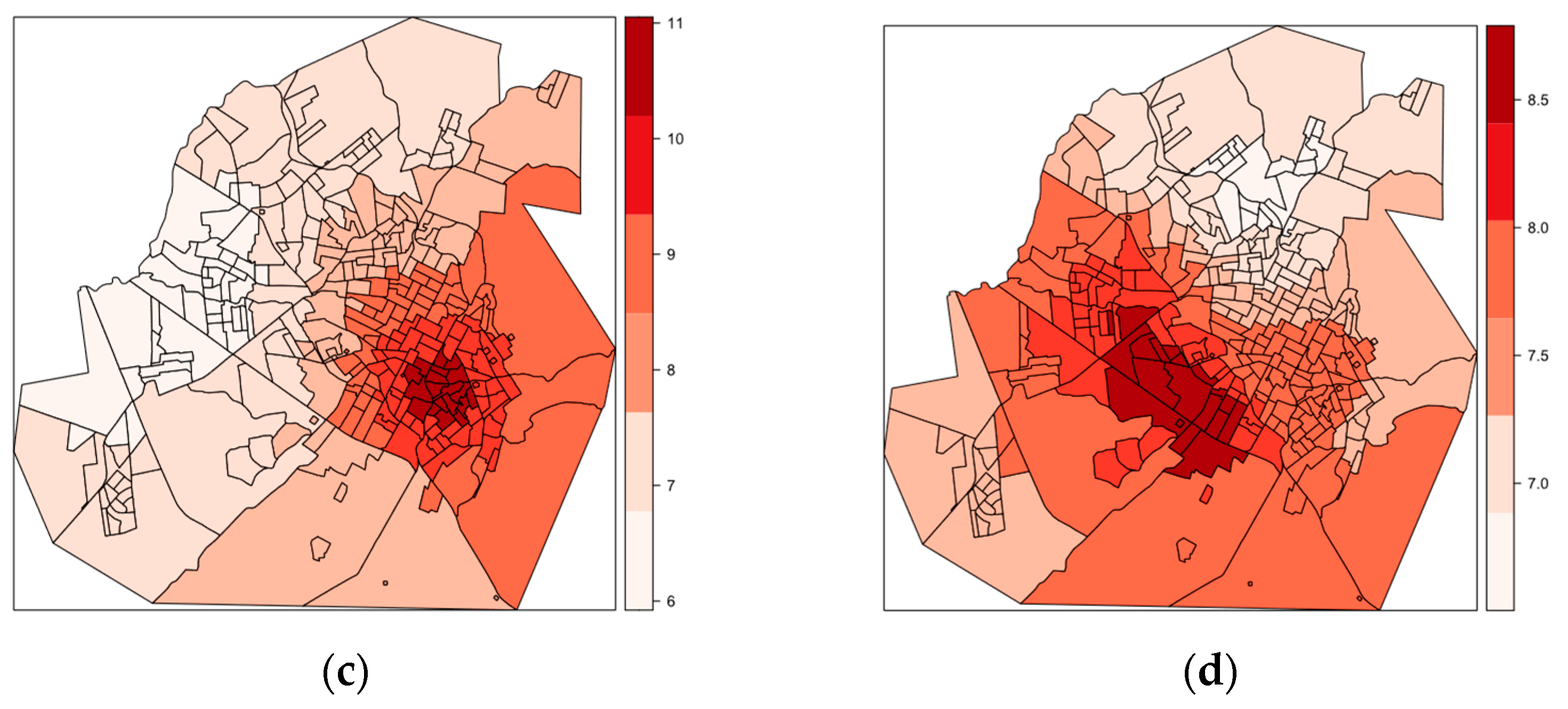
4.3.1. Electrical Discharges
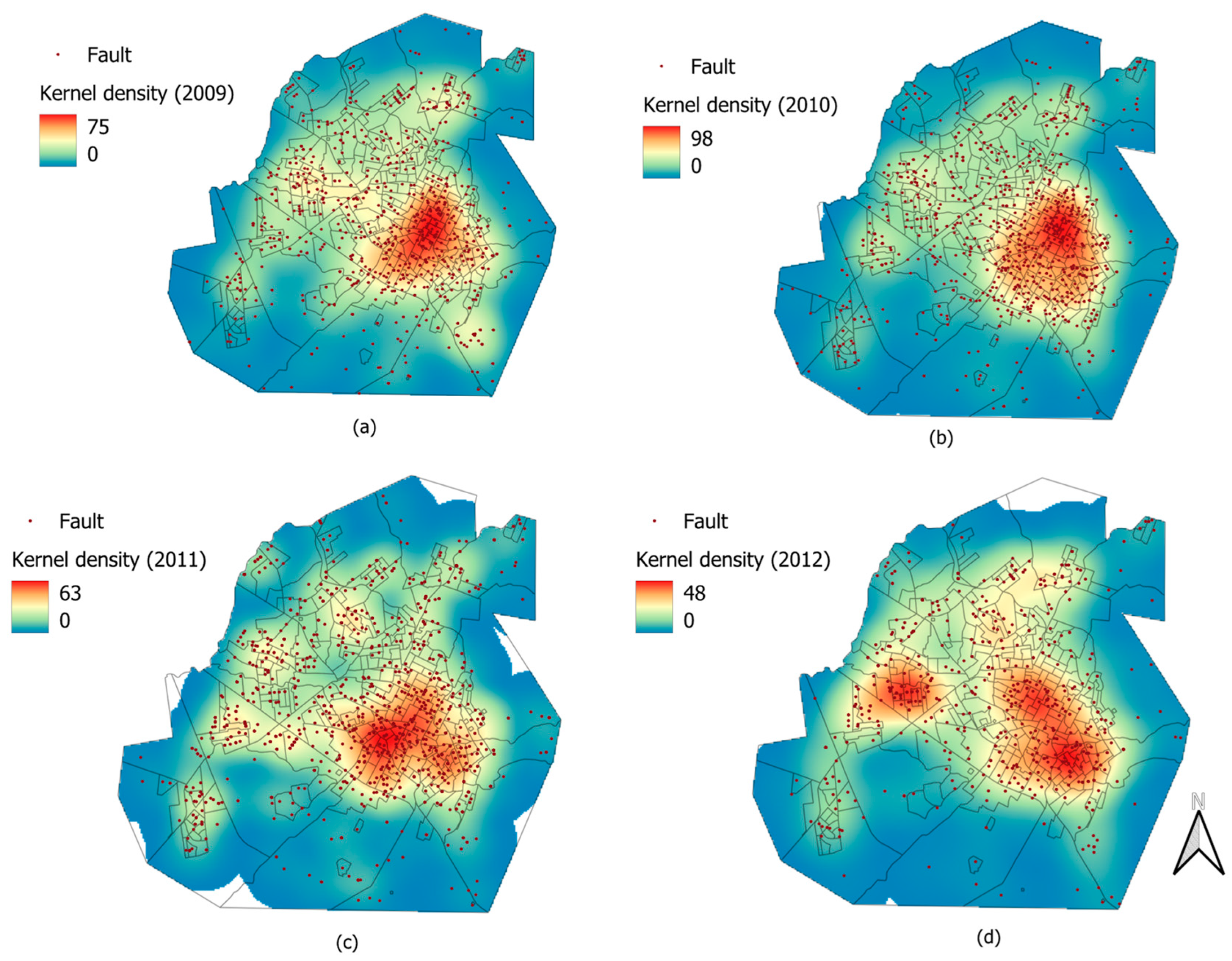
4.3.2. Number of Faults in Transformers by Regions
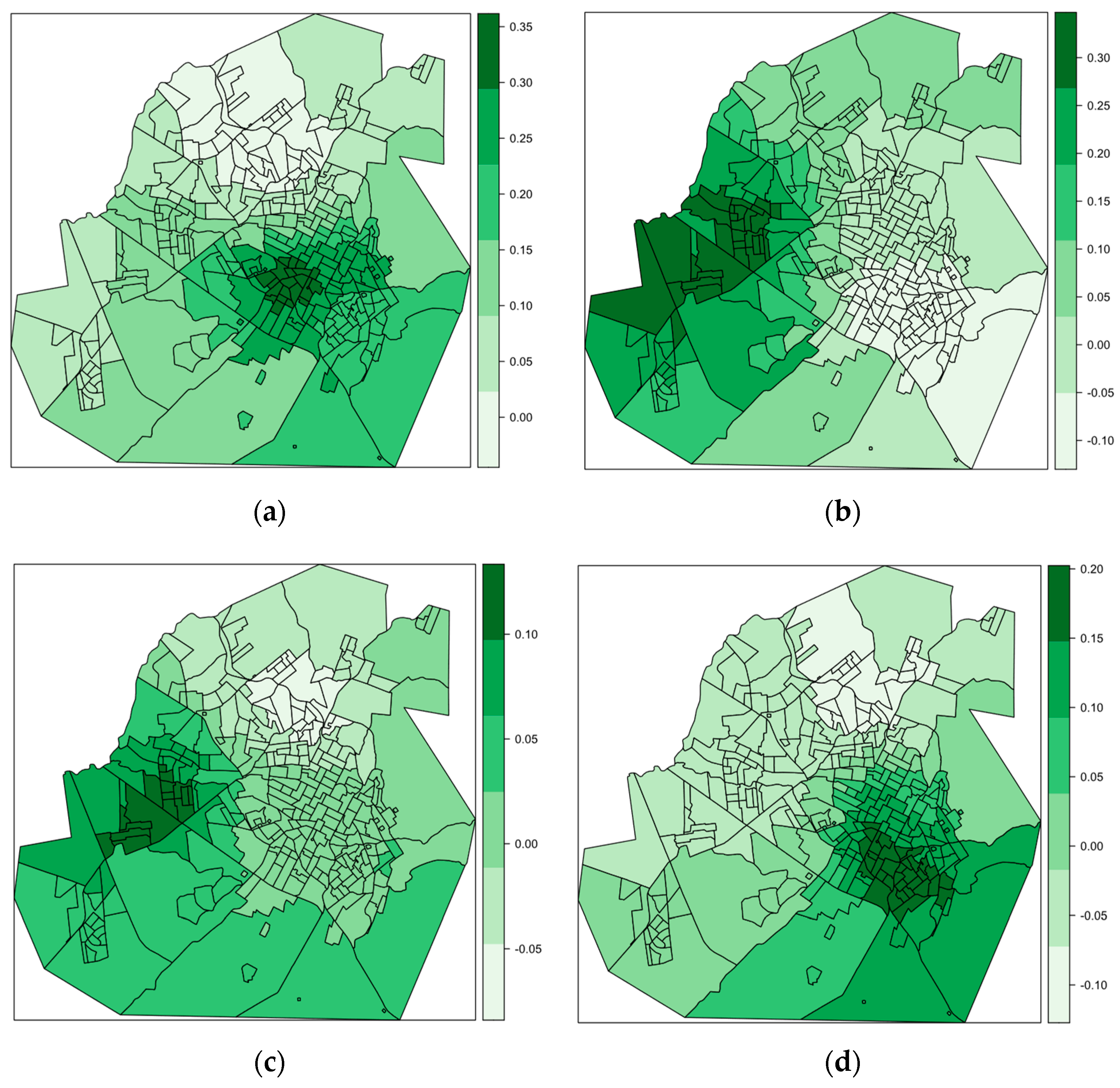
4.3.3. Geographically Weighted Summary Statistics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Q.; Li, X.; Liao, J.; Xiong, T. Power failure risk assessment and management based on stochastic line failures in distribution network including distributed generation. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 1303–1312. [Google Scholar] [CrossRef]
- Gururajapathy, S.S.; Mokhlis, H.; Illias, H.A. Fault location and detection techniques in power distribution systems with distributed generation: A review. Renew. Sustain. Energy Rev. 2017, 74, 949–958. [Google Scholar] [CrossRef]
- Mikropoulos, P.N.; Tsovilis, T.E. Statistical Method for the Evaluation of the Lightning Performance of Overhead Distribution Lines. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 202–211. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, T.; Luo, F.; Li, P.; Yao, L. Fault incidence matrix based reliability evaluation method for complex distribution system. IEEE Trans. Power Syst. 2018, 33, 6736–6745. [Google Scholar] [CrossRef]
- Leite, J.B.; Mantovan, J.R.S.; Dokic, T.; Chen, Q.Y.; Kezunovic, M. Failure Probability Metric by Machine Learning for Online Risk Assessment in Distribution Networks. In Proceedings of the 2017 IEEE PES Innovative Smart Grid Technologies Conference-Latin America (ISGT Latin America), Quito, Ecuador, 20–22 September 2017; pp. 1–6. [Google Scholar]
- Souza, F.A.; Castoldi, M.F.; Goedtel, A. A cascade perceptron and Kohonen network approach to fault location in rural distribution feeders. Appl. Soft Comput. 2020, 96, 106627. [Google Scholar] [CrossRef]
- National Electric System Operator, “Supply Quality”, ONS. Available online: https://www.ons.org.br/ (accessed on 1 July 2023). (In Portuguese).
- da Silva Santos, A.; Faria, L.T.; Lopes, M.L.M.; Lotufo, A.D.P.; Minussi, C.R. Efficient Methodology for Detection and Classification of Short-Circuit Faults in Distribution Systems with Distributed Generation. Sensors 2022, 22, 9418. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Wang, J.; Huang, J.; Cao, P. Detection and classification of short-circuit faults in distribution networks based on fortescue approach and softmax regression. Int. J. Electr. Power Energy Syst. 2020, 118, 105812. [Google Scholar] [CrossRef]
- Chaitanya, B.K.; Yadav, A. An intelligent fault detection and classification scheme for distribution lines integrated with distributed generators. Comput. Electr. Eng. 2018, 69, 28–40. [Google Scholar] [CrossRef]
- Elnozahy, M.S.; El-Shatshat, R.A.; Salama, M.M.A. Single-phasing detection and classification in distribution systems with a high penetration of distributed generation. Electr. Power Syst. Res. 2016, 131, 41–48. [Google Scholar] [CrossRef]
- Dehghani, M.; Khooban, M.H.; Niknam, T. Fast fault detection and classification based on a combination of wavelet singular entropy theory and fuzzy logic in distribution lines in the presence of distributed generations. Int. J. Electr. Power Energy Syst. 2016, 78, 455–462. [Google Scholar] [CrossRef]
- Yuan, J.; Jiao, Z. Faulty feeder detection based on image recognition of current waveform superposition in distribution networks. Appl. Soft Comput. 2022, 130, 109663. [Google Scholar] [CrossRef]
- AL-Sakkaf, A.-S.A.; AL-Ramadan, B.M. Applications of GIS in Electrical Power System; King Fahd University of Petroleum and Minerals: Dhahran, Saudi Arabia, 2013; pp. 1–6. [Google Scholar]
- Shafiullah, M.; Rahman, S.M.; Mortoja, M.G.; Al-Ramadan, B. Role of spatial analysis technology in power system industry: An overview. Renew. Sustain. Energy Rev. 2016, 66, 584–595. [Google Scholar] [CrossRef]
- Câmara, G.; Carvalho, M.S.; Cruz, O.G.; Correa, V. Spatial Analysis of Areas; Editora EMBRAPA: Brasília, Brazil, 2004. (In Portuguese) [Google Scholar]
- Abdulrahman, I.; Radman, G. Power system spatial analysis and visualization using geographic information system (GIS). Spat. Inf. Res. 2019, 28, 101–112. [Google Scholar] [CrossRef]
- Chen, C.; Kezunovic, M. Fuzzy Logic Approach to Predictive Risk Analysis in Distribution Outage Management. IEEE Trans. Smart Grid 2016, 7, 2827–2836. [Google Scholar] [CrossRef]
- Goerdin, S.A.V.; Smit, J.J.; Mehairjan, R.P.Y. Monte Carlo simulation applied to support risk-based decision making in electricity distribution networks. In Proceedings of the 2015 IEEE Eindhoven PowerTech, PowerTech 2015, Eindhoven, The Netherlands, 29 June–2 July 2015; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Muñoz, D.S.; Garcia, J.L.D. GIS-based tool development for flooding impact assessment on electrical sector. J. Clean. Prod. 2021, 320, 128793. [Google Scholar] [CrossRef]
- Bernstein, A.; Bienstock, D.; Hay, D.; Uzunoglu, M.; Zussman, G. Power Grid Vulnerability to Geographically Correlated Failures–Analysis and Control Implications. In Proceedings of the IEEE INFOCOM 2014-IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2634–2642. [Google Scholar]
- Handayani, K.; Filatova, T.; Krozer, Y. The vulnerability of the power sector to climate variability and change: Evidence from Indonesia. Energies 2019, 12, 3640. [Google Scholar] [CrossRef]
- Mortensen, L.K.; Shaker, H.R.; Veje, C.T. Relative fault vulnerability prediction for energy distribution networks. Appl. Energy 2022, 322, 119449. [Google Scholar] [CrossRef]
- Albasri, F.A.; Zaki, A.Z.; Al Nainoon, E.; Alawi, H.; Ayyad, R. A Fault Location System Using GIS and Smart Meters for the LV Distribution System. In Proceedings of the 2019 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies, Sakhier, Bahrain, 22–23 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Su, X. Engineering fault intelligent monitoring system based on Internet of Things and GIS. Nonlinear Eng. 2023, 12, 20220322. [Google Scholar] [CrossRef]
- Chen, P.-C.; Dokic, T.; Stokes, N.; Goldberg, D.W.; Kezunovic, M. Predicting weather-associated impacts in outage management utilizing the GIS framework. In Proceedings of the 2015 IEEE PES Innovative Smart Grid Technologies Latin America (ISGT LATAM), Montevideo, Uruguay, 5–7 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 417–422. [Google Scholar]
- Xu, Y.; Tong, C.; Xiang, M.; Wang, T.; Xu, J.; Zheng, J. Lightning risk estimation and preventive control method for power distribution networks referring to the indeterminacy of wind power and photovoltaic. Electr. Power Syst. Res. 2023, 214, 108896. [Google Scholar] [CrossRef]
- Sestasombut, P.; Ngaopitakkul, A. Evaluation of a direct lightning strike to the 24 kV distribution lines in Thailand. Energies 2019, 12, 3193. [Google Scholar] [CrossRef]
- Mestriner, D.; de Moura, R.A.R.; Procopio, R.; de Oliveira Schroeder, M.A. Impact of grounding modeling on lightning-induced voltages evaluation in distribution lines. Appl. Sci. 2021, 11, 2931. [Google Scholar] [CrossRef]
- Miyazaki, T.; Okabe, S. Field analysis of the occurrence of distribution-line faults caused by lightning effects. IEEE Trans. Electromagn. Compat. 2011, 53, 114–121. [Google Scholar] [CrossRef]
- Druck, S.; Carvalho, M.S.; Câmara, G.; Monteiro, A.M.V. Spatial Analysis of Geographic Data; Editora EMBRAPA: Brasília, Brazil, 2004. (In Portuguese) [Google Scholar]
- Le Gallo, J.; Ertur, C. Exploratory spatial data analysis of the distribution of regional per capita GDP in Europe, 1980–1995. Pap. Reg. Sci. 2003, 82, 175–202. [Google Scholar] [CrossRef]
- Haining, R. Spatial Data Analysis: Theory and Practice; Cambrigdge University Press: Cambrigdge, UK, 2003; Volume 1. [Google Scholar]
- Faria, L.T.; Melo, J.D.; Padilha-Feltrin, A. Spatial-Temporal Estimation for Nontechnical Losses. IEEE Trans. Power Deliv. 2016, 31, 362–369. [Google Scholar] [CrossRef]
- Ventura, L.; Feliz, G.; Vargas, R.; Faria, L.T.; Melo, J.D. Estimation of Non-Technical Loss Rates by Regions. Electr. Power Syst. Res. 2023, 223, 109685. [Google Scholar] [CrossRef]
- Tobler, W.R. Cellular geography. In Philosophy in Geography; Springer: Berlin/Heidelberg, Germany, 1979; pp. 379–386. [Google Scholar]
- Bivand, R.S.; Pebesma, E.; Gómez-Rubio, V. Applied Spatial Data Analysis with R; Springer: Berlin/Heidelberg, Germany, 2013; Volume 10. [Google Scholar]
- Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. JSS J. Stat. Softw. 2015, 63, 1–52. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression a method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Dykes, J.; Brunsdon, C. Geographically weighted visualization: Interactive graphics for scale-varying exploratory analysis. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1161–1168. [Google Scholar] [CrossRef]
- Kuster, K.K.; Santos, S.L.F.; Piantini, A.; Lazzaretti, A.E.; Mello, L.G.; Pinto, C.L.S. An Improved Methodology for Evaluation of Lightning Effects on Distribution Networks. In Proceedings of the 2017 International Symposium on Lightning Protection (XIV SIPDA), Natal, Brazil, 2–6 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 261–267. [Google Scholar]








| Fault Reasons | Number of Annual Faults | |||||
|---|---|---|---|---|---|---|
| 2020 | % | 2021 | % | 2022 | % | |
| Adverse Weather Conditions | 708 | 29.75% | 704 | 29.82% | 743 | 35.01% |
| Fires | 587 | 24.66% | 633 | 26.81% | 250 | 11.80% |
| Equipment Failures | 144 | 6.05% | 167 | 7.10% | 127 | 6.00% |
| Tree Vegetation | 135 | 5.67% | 87 | 3.70% | 97 | 4.60% |
| Human Failures | 109 | 4.58% | 141 | 6.00% | 136 | 6.41% |
| Parameters | Evaluated Years | |||
|---|---|---|---|---|
| 2009 | 2010 | 2011 | 2012 | |
| Maximum | 39 | 26 | 40 | 39 |
| Minimum | 0 | 0 | 0 | 0 |
| Average | 2.35 | 0.79 | 1.82 | 1.80 |
| Standard deviation | 5.78 | 2.52 | 4.55 | 5.03 |
| Total number | 707 | 239 | 548 | 542 |
| Parameters | Evaluated Years | |||
|---|---|---|---|---|
| 2009 | 2010 | 2011 | 2012 | |
| Maximum | 42 | 21 | 27 | 13 |
| Minimum | 0 | 0 | 0 | 0 |
| Average | 3.14 | 3.55 | 3.83 | 2.08 |
| Standard deviation | 4.08 | 3.63 | 4.28 | 2.35 |
| Total number | 946 | 1069 | 1153 | 626 |
| Evaluated Years | |||
|---|---|---|---|
| 2009 | 2010 | 2011 | 2012 |
| 0.4407 | 0.6553 | 0.5073 | 0.5432 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, A.S.; Faria, L.T.; Lopes, M.L.M.; Minussi, C.R. Power Distribution Systems’ Vulnerability by Regions Caused by Electrical Discharges. Energies 2023, 16, 7790. https://doi.org/10.3390/en16237790
Santos AS, Faria LT, Lopes MLM, Minussi CR. Power Distribution Systems’ Vulnerability by Regions Caused by Electrical Discharges. Energies. 2023; 16(23):7790. https://doi.org/10.3390/en16237790
Chicago/Turabian StyleSantos, Andréia S., Lucas Teles Faria, Mara Lúcia M. Lopes, and Carlos R. Minussi. 2023. "Power Distribution Systems’ Vulnerability by Regions Caused by Electrical Discharges" Energies 16, no. 23: 7790. https://doi.org/10.3390/en16237790
APA StyleSantos, A. S., Faria, L. T., Lopes, M. L. M., & Minussi, C. R. (2023). Power Distribution Systems’ Vulnerability by Regions Caused by Electrical Discharges. Energies, 16(23), 7790. https://doi.org/10.3390/en16237790






