Accuracy Assessment of Charge-Mode Accelerometers Using Multivariate Regression of the Upper Bound of the Dynamic Error
Abstract
1. Introduction
2. Materials and Methods
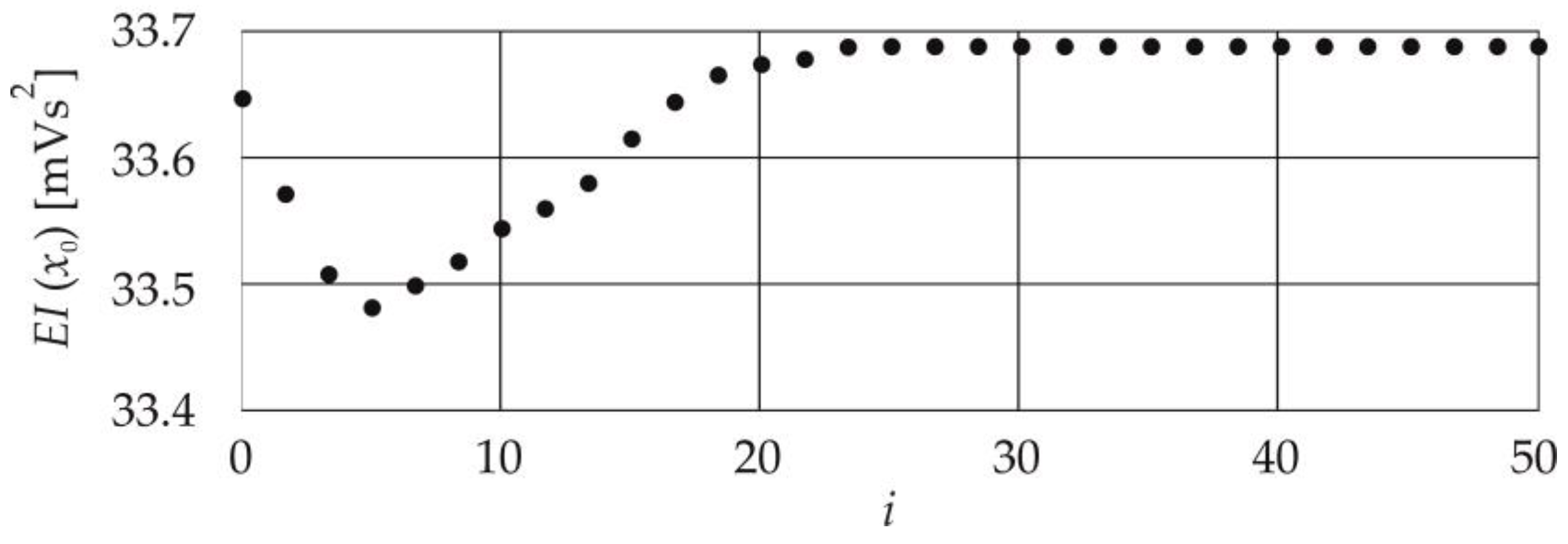
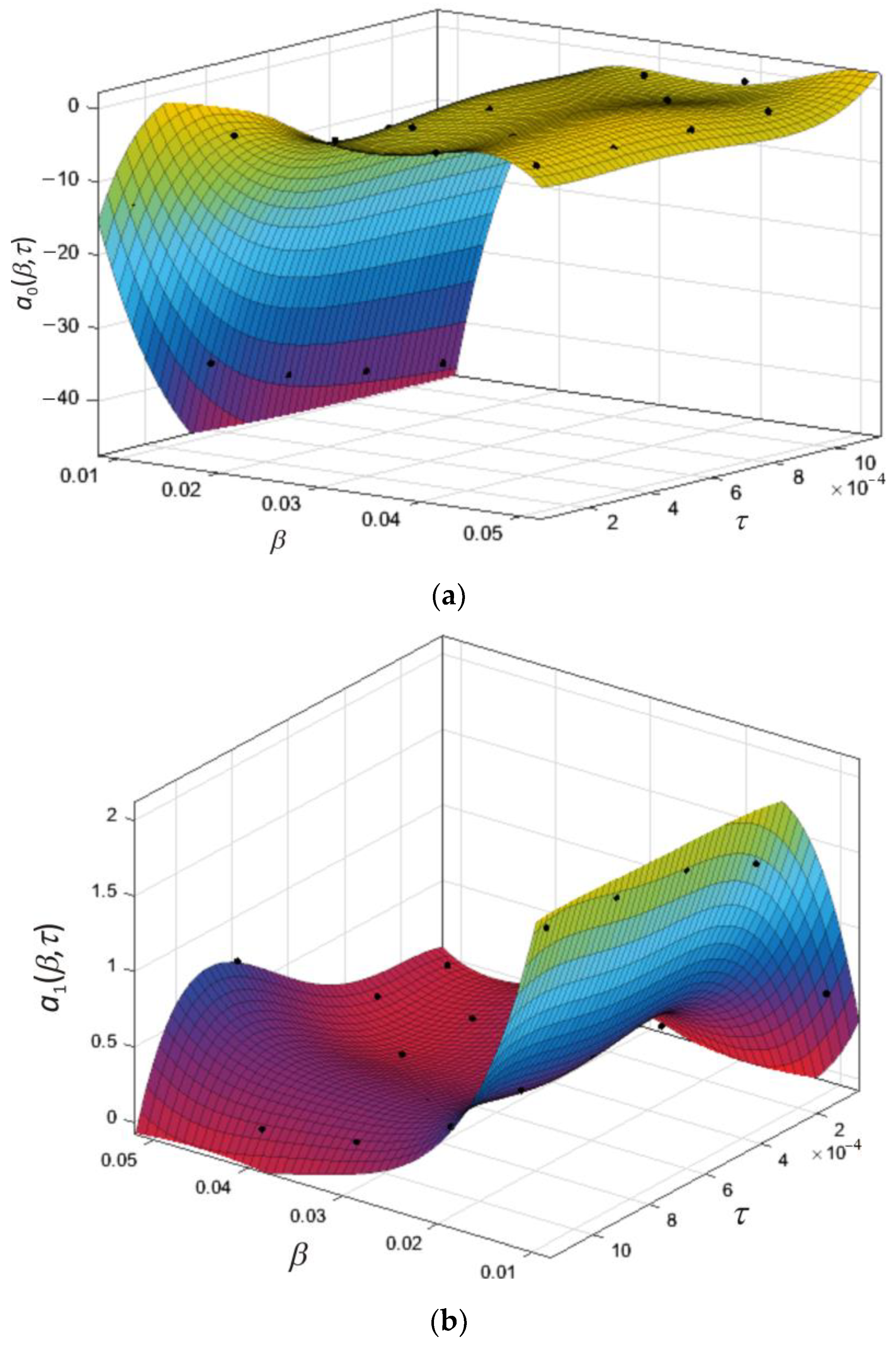
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morelle, C.; Théron, D.; Roch-Jeune, I.; Tilmant, P.; Okada, E.; Vaurette, F.; Grimbert, B.; Derluyn, J.; Degroote, S.; Germain, M.; et al. A micro-electro-mechanical accelerometer based on gallium nitride on silicon. Appl. Phys. Lett. 2023, 122, 033502. [Google Scholar] [CrossRef]
- Sanjuan, J.; Sinyukov, A.; Warrayat, M.F.; Guzman, F. Gyro-free inertial navigation systems based on linear opto-mechanical accelerometers. Sensors 2023, 23, 4093. [Google Scholar] [CrossRef]
- Goyal, D.; Pabla, B.S. Development of non-contact structural health monitoring system for machine tools. J. Appl. Res. Technol. 2016, 14, 245–258. [Google Scholar] [CrossRef]
- Wei, H.; Wu, M.; Cao, J. New matching method for accelerometers in gravity gradiometer. Sensors 2017, 17, 1710. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Jiang, S.; Liu, Y.; Wang, Y.; Qi, P. Design and optimization of a triangular shear piezoelectric acceleration sensor for microseismic monitoring. Geofluids 2022, 964502, 3964502. [Google Scholar] [CrossRef]
- Zhai, Z.; Xiong, X.; Ma, L.; Wang, Z.; Wang, K.; Wang, B.; Zhang, M.; Zou, X. A scale factor calibration method for MEMS resonant accelerometers based on virtual accelerations. Micromachines 2023, 14, 1408. [Google Scholar] [CrossRef]
- Juliani, F.; de Barros, E.; Mathias, M.H. A tool for controlling accelerometers. Secondary calibration data. Comptes Rendus Méc. 2013, 341, 687–696. [Google Scholar] [CrossRef]
- Scott, J.J.; Rowlands, A.V.; Cliff, D.P.; Morgan, P.J.; Plotnikoff, R.C.; Lubans, D.R. Comparability and feasibility of wrist- and hip-worn accelerometers in free-living adolescents. J. Sci. Med. Sport 2017, 2, 1101–1106. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Zhang, X.; Shan, X.; Hu, L.; Zhang, X.; Hou, C.; Xie, T. A novel bird-shape broadband piezoelectric energy harvester for low frequency vibrations. Micromachines 2023, 14, 421. [Google Scholar] [CrossRef]
- Schilling, L.; Dalhoff, P. Piezoelectric patch transducers: Can alternative sensors enhance bearing failure prediction? J. Phys. Conf. Ser. 2019, 1356, 012015. [Google Scholar] [CrossRef]
- JCGM 100:2008; BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, and OIML, Guide to the Expression of Uncertainty in Measurement. JCGM: Sèvres, France, 1995.
- Bertuletti, S.; Cereatti, A.; Comotti, D.; Caldara, M.; Croce, U.D. Static and dynamic accuracy of an innovative miniaturized wearable platform for short range distance measurements for human movement applications. Sensors 2017, 17, 1492. [Google Scholar] [CrossRef]
- Layer, E. Modelling of Simplified Dynamical Systems; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2002; ISBN 9783642628566. [Google Scholar]
- Rutland, N.K. The principle of matching: Practical conditions for systems with inputs restricted in magnitude and rate of change. IEEE Trans. Autom. Control 1994, 39, 550–553. [Google Scholar] [CrossRef]
- Layer, E.; Tomczyk, K. Measurements: Modelling and Simulation of Dynamic Systems; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 3642045871/9783642045875. [Google Scholar]
- Yu, J.C.; Lan, C.B. System modeling of microaccelerometer using piezoelectric thin films. Sens. Actuator A Phys. 2001, 88, 178–186. [Google Scholar] [CrossRef]
- Sun, X.T.; Jing, X.J.; Xu, J.; Cheng, L. A quasi-zero-stiffness-based sensor system in vibration measurement. IEEE Trans. Ind. Electron. 2014, 61, 5606–6114. [Google Scholar] [CrossRef]
- Link, A.; Täbner, A.; Wabinski, W.; Bruns, T.; Elster, C. Modelling accelerometers for transient signals using calibration measurement upon sinusoidal excitation. Measurement 2007, 40, 928–935. [Google Scholar] [CrossRef]
- JCGM 101:2008; BIPM, IEC, IFCC, ILAC, ISO, IUPAC, IUPAP, and OIML. Evaluation of Measurement Data: Supplement 1 to the Guide to the Expression of Uncertainty in Measurement—Propagation of Distributions Using a Monte Carlo Method. JCGM: Sèvres, France, 2008.
- Tomczyk, K. Impact of uncertainties in accelerometer modeling on the maximum values of absolute dynamic error. Measurement 2016, 80, 71–78. [Google Scholar] [CrossRef]
- Honig, M.L.; Steiglitz, K. Maximizing the output energy of a linear channel with a time and amplitude limited input. IEEE Trans. Inf. Theory 1992, 38, 1041–1052. [Google Scholar] [CrossRef][Green Version]
- Elia, M.; Taricco, G.; Viterbo, E. Optimal energy transfer in bandlimited communication channels. IEEE Trans. Inf. Theory 1999, 45, 2020–2029. [Google Scholar] [CrossRef][Green Version]
- Gu, S.; Luo, Z.; Chu, Y.; Xu, Y.; Jiang, Y.; Guo, J. Trace Alignment Preprocessing in Side-Channel Analysis Using the Adaptive Filter. IEEE Trans. Inf. Forensics Secur. 2023, 18, 5580–5591. [Google Scholar] [CrossRef]
- Guo, J.; Liu, Y.; Lin, L.; Li, S.; Cai, J.; Chen, J.; Huang, W.; Lin, Y.; Xu, J. Chromatic Plasmonic Polarizer-Based Synapse for All-Optical Convolutional Neural Network. Nano Lett. 2023, 23, 9651–9656. [Google Scholar] [CrossRef]
- Krebs, R.; Rothstein, B.; Roelle, J. Rubrics Enhance Accuracy and Reduce Cognitive Load in Self-Assessment. Metacogn. Learn. 2022, 17, 627–650. [Google Scholar] [CrossRef]
- Peiyuan, Z.; Guorui, X.; Lan, D. Initial performance assessment of Galileo High Accuracy Service with software-defined receiver. GPS Solut. 2023, 28, 2. [Google Scholar] [CrossRef]
- Egert, J.; Kreutz, C. Rcall: An R interface for MATLAB. SoftwareX 2023, 21, 101276. [Google Scholar] [CrossRef]
- Roman, C.; Morales, M.G. On the integration of Mathcad capabilities into a mass transfer operations course in chemical engineering studies. Comput. Appl. Eng. Educ. 2022, 31, 938–951. [Google Scholar] [CrossRef]
- Tomczyk, K. Assessment of convergence of the algorithm for determining the upper bound of dynamic error on the example of acceleration sensors. In Proceedings of the 20th International Conference on Research and Education in Mechatronics (REM), Wels, Austria, 23–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Sinha, P. Multivariate polynomial regression in data mining: Methodology, problems and solutions. Int. J. Sci. Eng. Res. 2013, 4, 962–965. [Google Scholar]
- Rady, E.-H.A.; Ziedan, D. Estimation of population total using local polynomial regression with two auxiliary variables. J. Stat. Appl. Probab. 2014, 2, 129–136. [Google Scholar] [CrossRef]
- Tomczyk, K. Polynomial approximation of the maximum dynamic error generated by measurement systems. Prz. Elektrotechniczny 2019, 95, 124–127. [Google Scholar] [CrossRef]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar] [CrossRef]
- Bargues, À.S.; Sanz, J.-L.P.; Martín, R.M. Optimal experimental design for parametric identification of the electrical behaviour of bioelectrodes and biological tissues. Mathematics 2022, 10, 837. [Google Scholar] [CrossRef]
- Tomczyk, K. Problems in modelling charge output accelerometers. Metrol. Meas. Syst. 2016, 23, 645–659. [Google Scholar] [CrossRef]

| Parameter | Unit of Measure | Description |
|---|---|---|
| Piezoelectric constant | ||
| Total resistance of accelerometer, cable and voltage Amplifier | ||
| F | Total capacitance of accelerometer, cable and voltage amplifier | |
| V/N | Charge sensitivity | |
| Voltage sensitivity | ||
| kg | Mechanical sensitivity | |
| s | Time constant | |
| Damping ratio | ||
| rad/s | Pulsation of undamped natural vibrations | |
| Hz | Frequency of undamped natural vibrations | |
| State matrix | ||
| Input matrix | ||
| Output matrix |
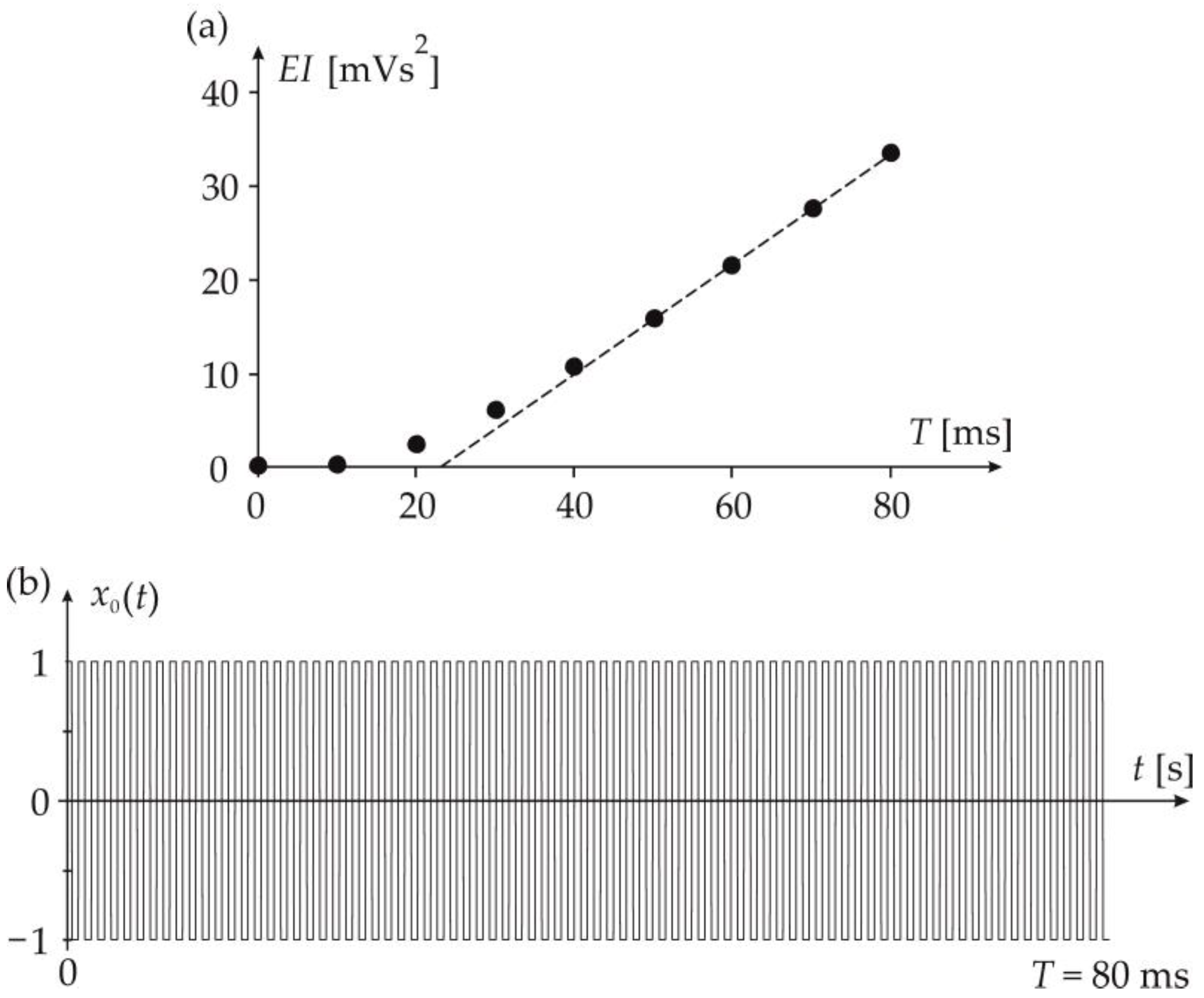
| 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | |
| 0 | 0.49 | 2.64 | 6.29 | 10.90 | 16.02 | 21.53 | 27.74 | 33.65 |
| [ms] | ||||||
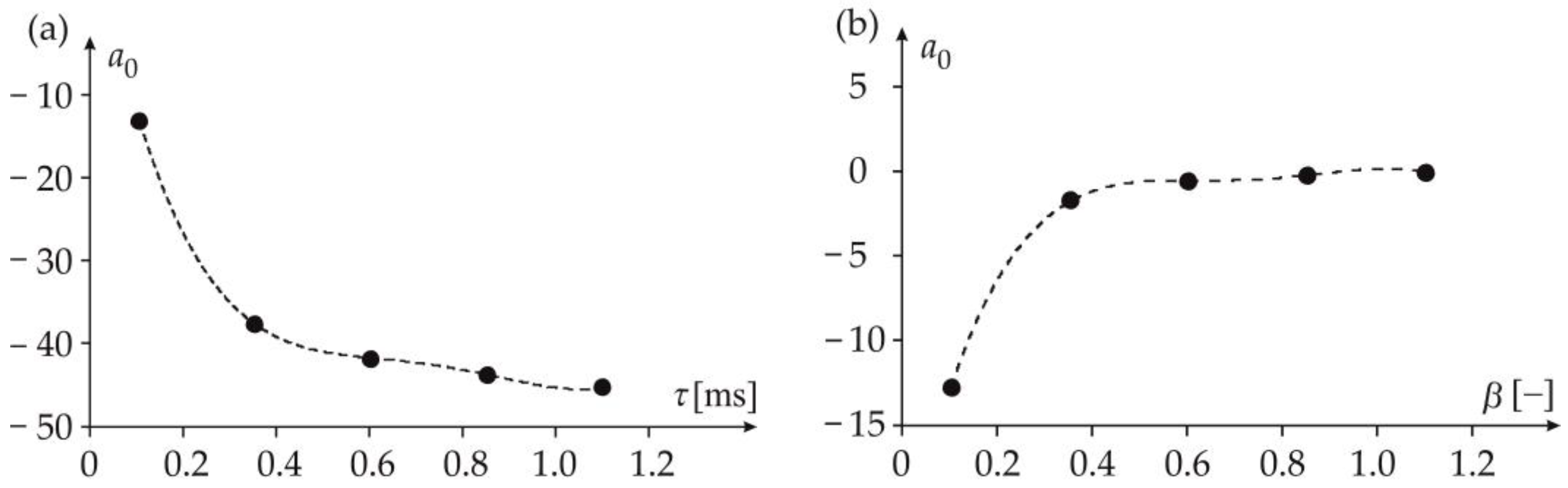
| 0.100 | 0.350 | 0.600 | 0.850 | 1.10 | ||
| 0.01 | −12.8 | −37.5 | −41.6 | −43.6 | −45.2 | |
| 0.02 | −1.80 | −4.90 | −5.90 | −5.90 | −6.20 | |
| 0.03 | −0.530 | −1.30 | −1.50 | −3.30 | −1.90 | |
| 0.04 | −0.230 | −0.650 | −0.730 | −0.740 | −0.770 | |
| 0.05 | −0.0500 | −0.330 | −0.320 | −0.320 | −0.310 | |
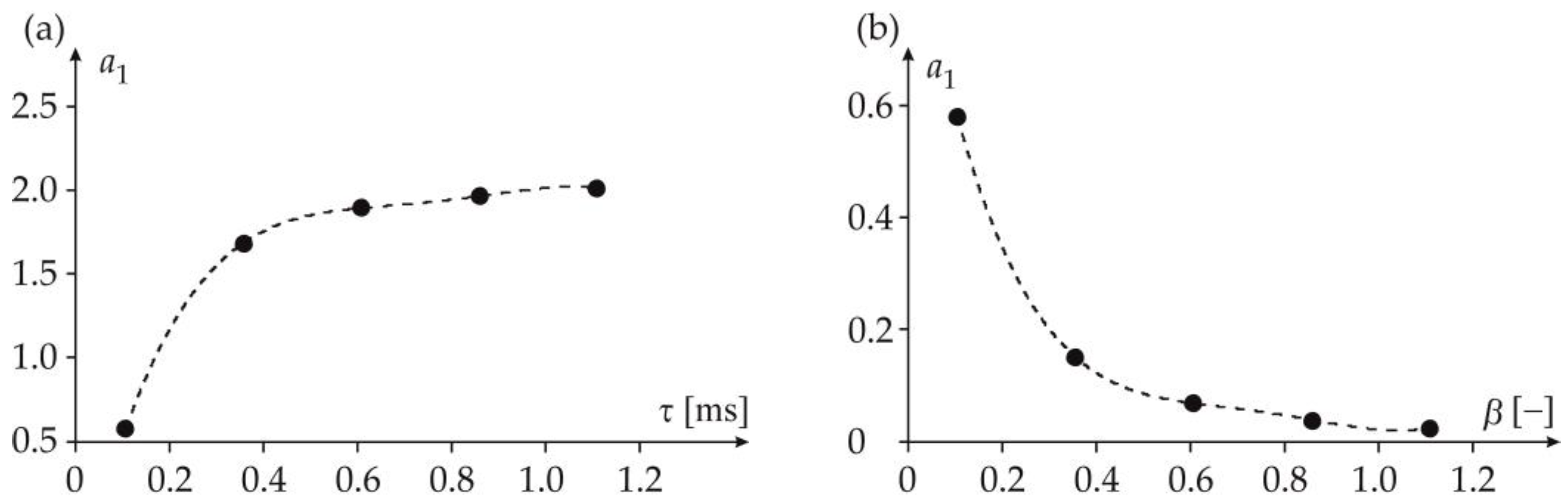
| [ms] | ||||||
| 0.100 | 0.350 | 0.600 | 0.850 | 1.10 | ||
| 0.01 | 0.580 | 1.69 | 1.90 | 1.97 | 2.02 | |
| 0.02 | 0.150 | 0.430 | 0.490 | 0.505 | 0.515 | |
| 0.03 | 0.0670 | 0.190 | 0.215 | 0.245 | 0.230 | |
| 0.04 | 0.0380 | 0.109 | 0.123 | 0.127 | 0.129 | |
| 0.05 | 0.0235 | 0.0700 | 0.0780 | 0.0805 | 0.0815 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomczyk, K.; Kowalczyk, M. Accuracy Assessment of Charge-Mode Accelerometers Using Multivariate Regression of the Upper Bound of the Dynamic Error. Energies 2023, 16, 7784. https://doi.org/10.3390/en16237784
Tomczyk K, Kowalczyk M. Accuracy Assessment of Charge-Mode Accelerometers Using Multivariate Regression of the Upper Bound of the Dynamic Error. Energies. 2023; 16(23):7784. https://doi.org/10.3390/en16237784
Chicago/Turabian StyleTomczyk, Krzysztof, and Małgorzata Kowalczyk. 2023. "Accuracy Assessment of Charge-Mode Accelerometers Using Multivariate Regression of the Upper Bound of the Dynamic Error" Energies 16, no. 23: 7784. https://doi.org/10.3390/en16237784
APA StyleTomczyk, K., & Kowalczyk, M. (2023). Accuracy Assessment of Charge-Mode Accelerometers Using Multivariate Regression of the Upper Bound of the Dynamic Error. Energies, 16(23), 7784. https://doi.org/10.3390/en16237784







