Experimental Investigation of Thermal Properties of Frozen Tap, Demineralized, and Sea Water
Abstract
:1. Introduction
2. Experimental Approach
2.1. Measurement Technique
2.2. Measurement Uncertainty
2.3. Sample Preparation and Examination Procedure
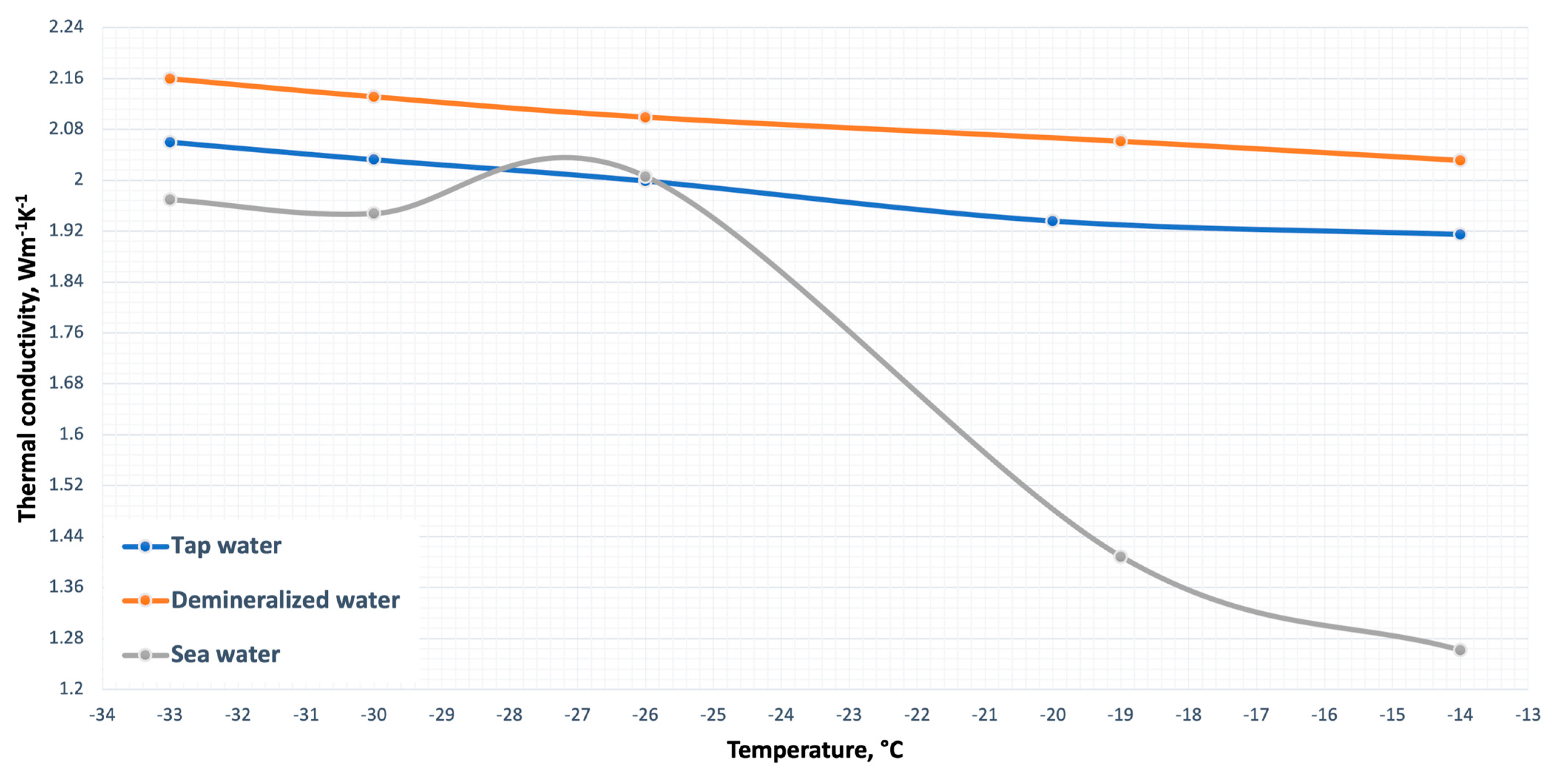
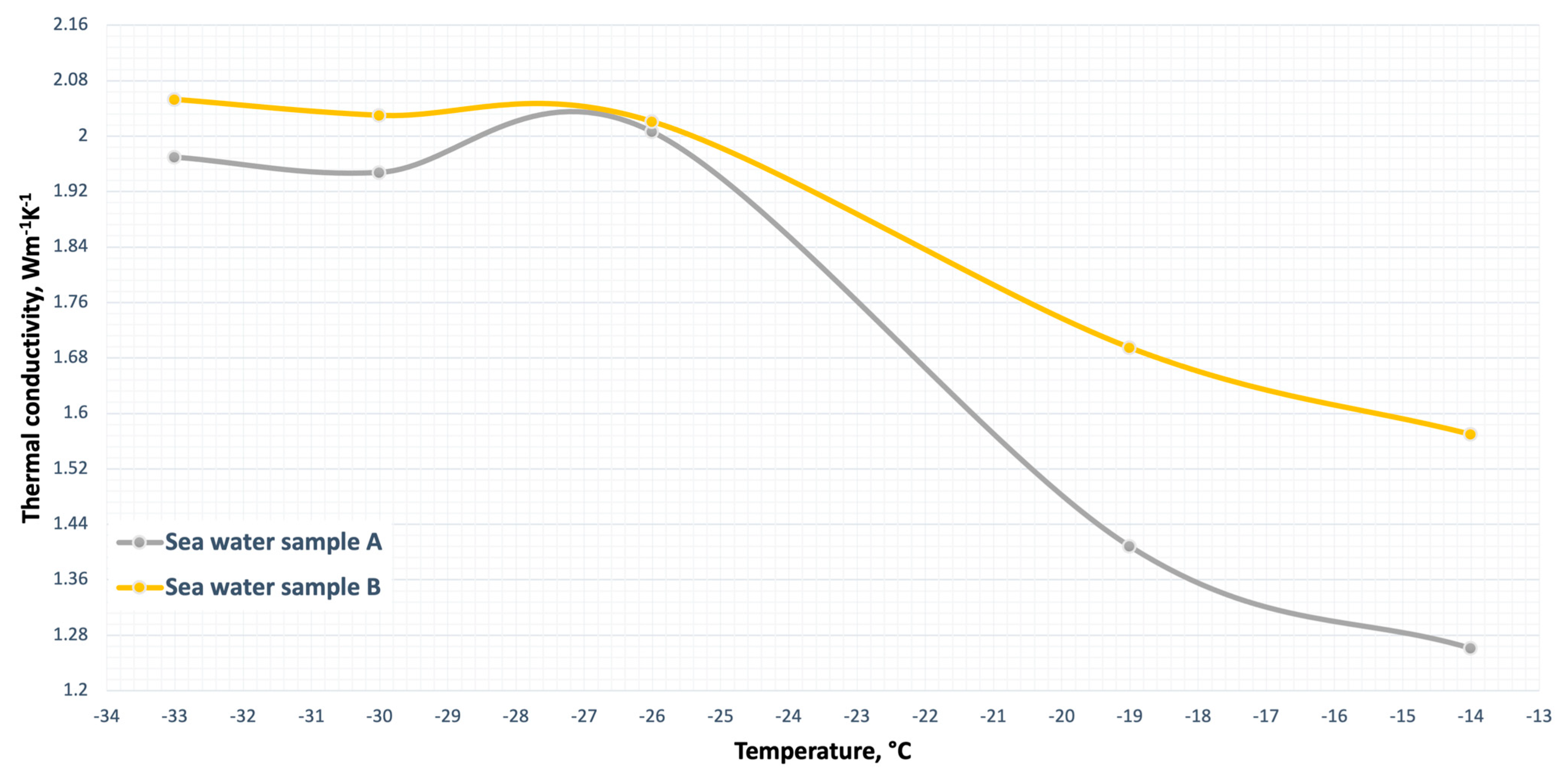
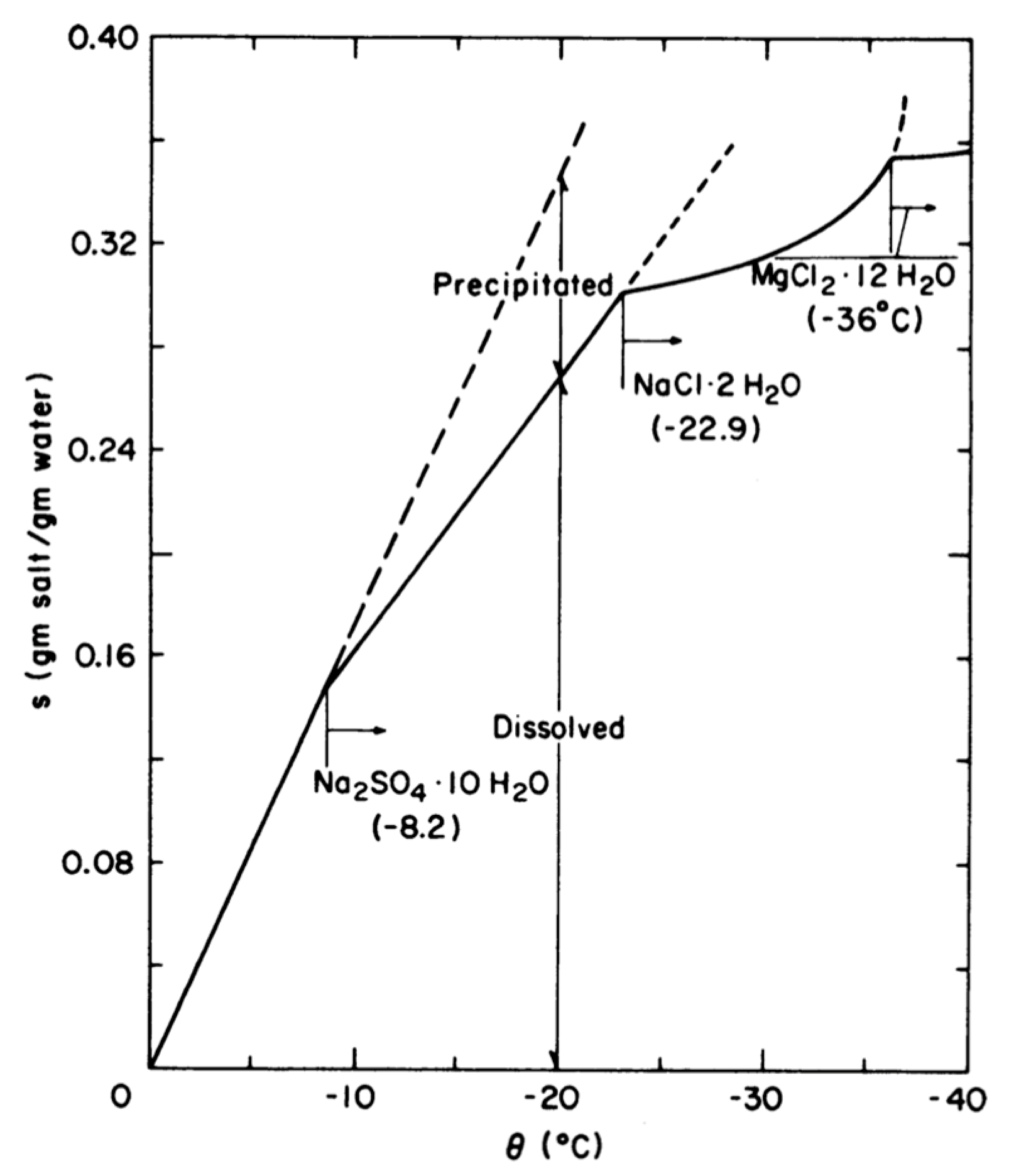
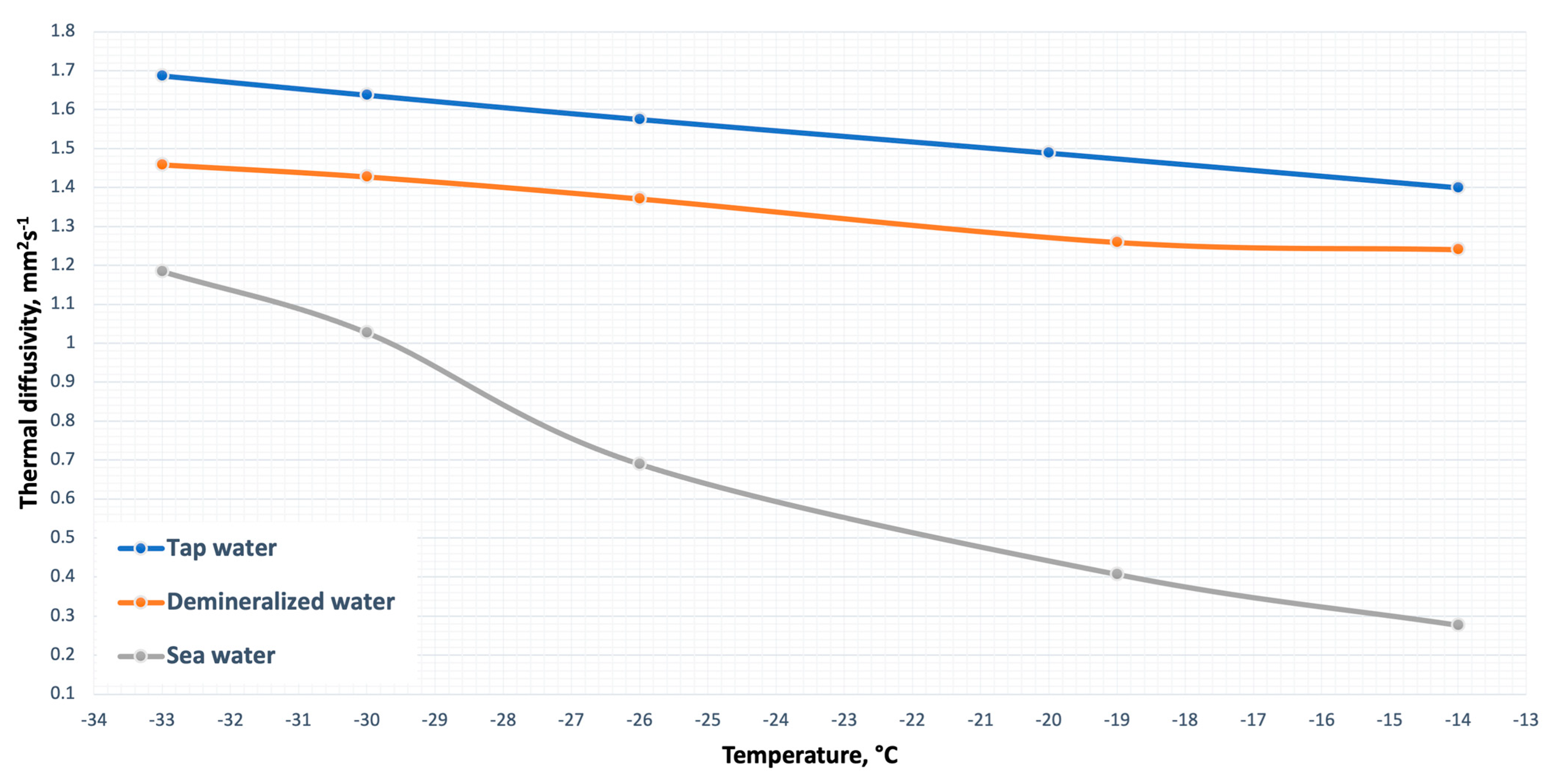
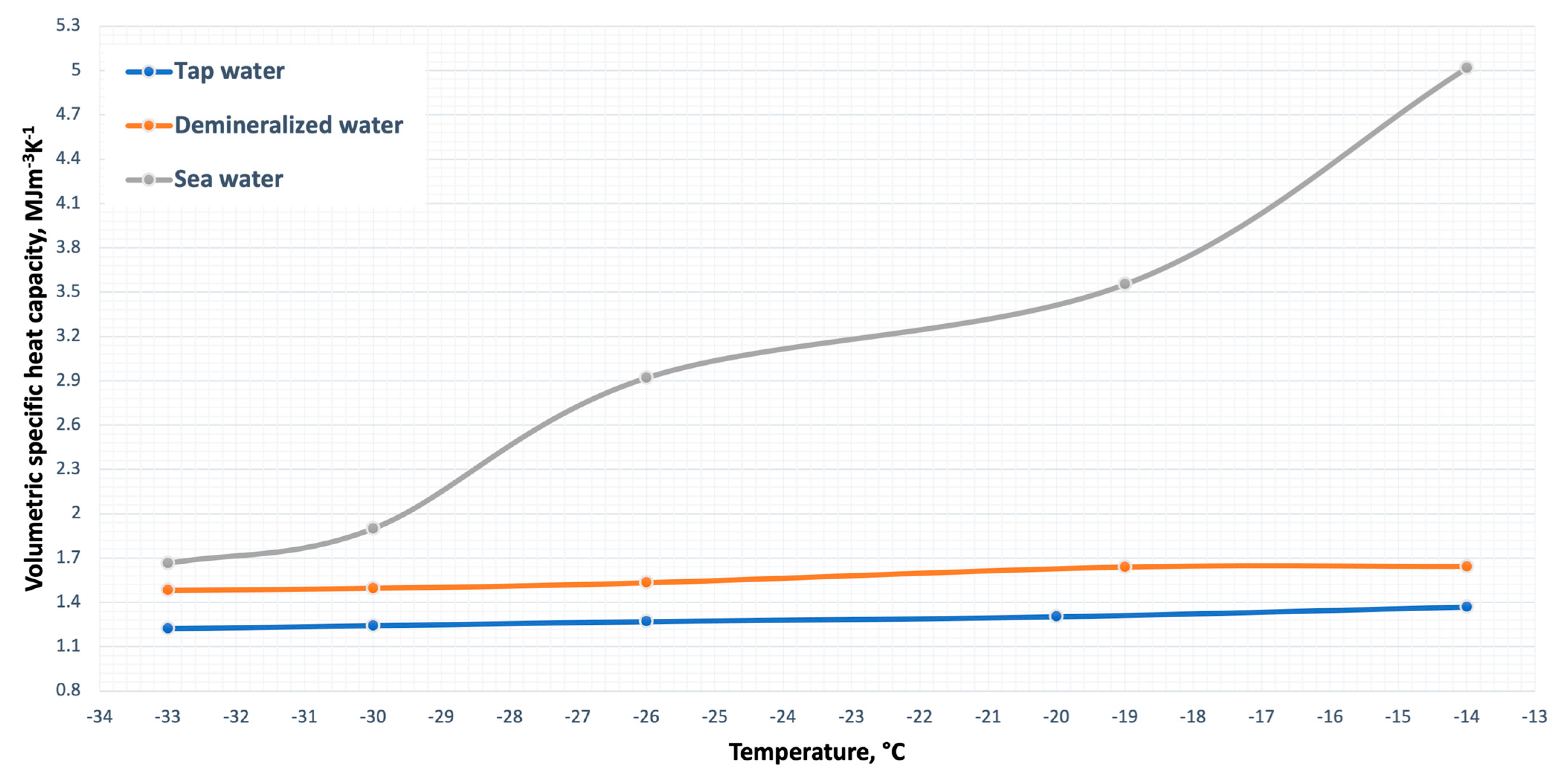
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, Y.; Ning, Y.; Wu, C.; Xu, M.; Akhtar, S.; Mujumdar, A.S.; Sasmito, A.P. Experimental investigation of producing ice slurry with water using opposed-nozzle impinging jet method. Appl. Therm. Eng. 2023, 219, 119568. [Google Scholar] [CrossRef]
- Rezaei, M.; Pakravan, H.A. Thermo-fluidic characteristics of ice slurry flows in U-bend pipes for cold thermal energy storage. J. Energy Storage 2023, 57, 106224. [Google Scholar] [CrossRef]
- Hu, R.; Liu, X.; Zhang, X. Experimental study on supercooled water release supercooled state for generating ice crystals. J. Mol. Liq. 2023, 375, 121277. [Google Scholar] [CrossRef]
- Ahn, J.H.; Kim, H.; Kim, J.H.; Kim, J.Y. Evaporative cooling performance characteristics in ice thermal energy storage with direct contact discharging for food cold storage. Appl. Energy 2023, 330, 120334. [Google Scholar] [CrossRef]
- Xie, M.; Chen, L.; Wu, K.; Liu, Z.; Lin, J.; Jiang, C.; Xie, S.; Zhao, Y. A novel peak shaving approach to improving load flexibility of the Allam cycle by integrating cold energy storage. J. Clean. Prod. 2023, 386, 135769. [Google Scholar] [CrossRef]
- Ghaith, F.A.; Dag, R.O. Performance and feasibility of utilizing solar powered ice storage system for space cooling applications. Energy Convers. Manag. X 2022, 16, 100319. [Google Scholar] [CrossRef]
- Liu, Z.; Quan, Z.; Zhang, N.; Wang, Y.; Yang, M.; Zhao, Y. Energy and exergy analysis of a novel direct-expansion ice thermal storage system based on three-fluid heat exchanger module. Appl. Energy 2023, 330, 120371. [Google Scholar] [CrossRef]
- Xing, M.; Jing, D.; Chen, H.; Zhang, H.; Wang, R. Ice thermal energy storage enhancement using aligned carbon nanotubes under external magnetic field. J. Energy Storage 2022, 56, 105931. [Google Scholar] [CrossRef]
- Zhang, C.; Chai, D.; Fan, Y.; Zhang, W.; Yu, M.; Wang, Z.; Jiang, L. Numerical Analysis of Heat Transfer Behaviours of Melting Process for Ice Thermal Storage Based on Various Heat Source Configurations. Sustainability 2023, 15, 365. [Google Scholar] [CrossRef]
- Abhishek, A.; Kumar, B.; Kim, M.H.; Lee, Y.T.; Chung, J.D.; Kim, S.T.; Kim, T.; Lee, C.; Lee, K. Comparison of the performance of ice-on-coil LTES tanks with horizontal and vertical tubes. Energy Build. 2019, 183, 45–53. [Google Scholar] [CrossRef]
- Powel, R.W. Thermal conductivities and expansion coefficients of water and ice. Adv. Phys. 1958, 7, 276–297. [Google Scholar] [CrossRef]
- Lees, C.H. Effects of temperature and pressure on the thermal conductivities of solids. Part I. The effect of temperature on the thermal conductivities of some electrical insulators. Philos. Trans. R. Soc. Lond. Ser. A 1905, 204, 433–466. [Google Scholar]
- Jakob, M.; Erk, S. The thermal conductivity of ice between 0 °C and −125 °C. Z. Ges Kalte-Ind. 1929, 36, 229–234. [Google Scholar]
- Schofield, F.H.; Hall, J.A. Thermal insulating materials for moderate and low temperatures. In International Critical Tables; McGraw: New York, NY, USA, 1927; Volume 2, p. 312. [Google Scholar]
- Van Dusen, M.S.; Washburn, E.W. Thermal conductivity of non-metallic solids. In International Critical Tables of Numerical Data, Physics, Chemistry and Technology; McGraw: New York, NY, USA, 1929; Volume 5, pp. 216–217. [Google Scholar]
- Ratcliffe, E.H. The thermal conductivity of ice new data on the temperature coefficient. Philos. Mag. 1962, 7, 1197–1203. [Google Scholar] [CrossRef]
- Yen, Y. Review of Thermal Properties of Snow, Ice, and Sea Ice; CRREL Technical Report 81-10; United States Army Corps of Engineers, Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1981. [Google Scholar]
- Fukusako, S. Thermophysical properties of ice, snow, and sea ice. Int. J. Thermophys. 1990, 11, 353–372. [Google Scholar] [CrossRef]
- Bonales, L.J.; Rodriguez, A.C.; Sanz, P.D. Thermal conductivity of ice prepared under different conditions. Int. J. Food Prop. 2017, 20, 610–619. [Google Scholar] [CrossRef]
- Trodahl, H.J.; Wilkinson, S.O.F.; McGuinness, M.J.; Haskell, T.G. Thermal conductivity of sea ice; dependence on temperature and depth. Geophys. Res. Lett. 2001, 28, 1279–1282. [Google Scholar] [CrossRef]
- Zeng, D.; Li, Y.; Liu, H.; Yang, Y.; Peng, L.; Zhu, C.; Zhao, N. Superhydrophobic coating induced anti-icing and deicing characteristics of an airfoil. Colloids Surf. A Physicochem. Eng. Asp. 2023, 660, 130824. [Google Scholar] [CrossRef]
- Chen, J.; Sun, C.; Sun, X.; Dan, H.; Huang, X. Finite difference model for predicting road surface ice formation based on heat transfer and phase transition theory. Cold Reg. Sci. Technol. 2023, 207, 103772. [Google Scholar] [CrossRef]
- Kreutz, M.; Ait Alla, A.; Lütjen, M.; Ohlendorf, J.-H.; Freitag, M.; Thoben, K.-D.; Zimnol, F.; Greulich, A. Ice prediction for wind turbine rotor blades with time series data and a deep learning approach. Cold Reg. Sci. Technol. 2023, 206, 103741. [Google Scholar] [CrossRef]
- Davalos, D.; Chowdhury, J.; Hangan, H. Joint wind and ice hazard for transmission lines in mountainous terrain. J. Wind Eng. Ind. 2023, 232, 105276. [Google Scholar] [CrossRef]
- Gao, Y.; Ding, Z. Investigation of water freezing in gas diffusion layer of PEMFC using lattice Boltzmann method. Ionics 2022, 29, 285–298. [Google Scholar] [CrossRef]
- Jurčević, M.; Penga, Ž.; Klarin, B.; Nižetić, S. Numerical analysis and experimental validation of heat transfer during solidification of phase change material in a large domain. J. Energy Storage 2020, 30, 101543. [Google Scholar] [CrossRef]
- Jurčević, M.; Nižetić, S.; Arıcı, M.; Ocłoń, P. Comprehensive analysis of preparation strategies for phase change nanocomposites and nanofluids with brief overview of safety equipment. J. Clean. Prod. 2020, 274, 122963. [Google Scholar] [CrossRef]
- Shojaeefard, M.H.; Jourabian, M.; Darzi, A.A.R. Rectangular heat sink filled with PCM/hybrid nanoparticles composites and cooled by intruded T-shaped cavity: Numerical investigation of thermal performance. Int. Commun. Heat Mass Transf. 2021, 127, 105527. [Google Scholar] [CrossRef]
- Hot Disk®. Available online: https://www.hotdiskinstruments.com/products-services/instruments/tps-500/ (accessed on 21 October 2022).
- Gustafsson, S.E. Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials. Rev. Sci. Instrum. 1991, 62, 797–804. [Google Scholar] [CrossRef]
- Bohač, V.; Gustavsson, M.K.; Kubičar, L.; Gustafsson, S.E. Parameter estimations for measurements of thermal transport properties with the hot disk thermal constants analyser. Rev. Sci. Instrum. 2000, 71, 15–19. [Google Scholar] [CrossRef]
- ISO 22007-2:2022; Plastics—Determination of Thermal Conductivity and Thermal Diffusivity—Part 2: Transient Plane Heat Source (Hot Disc) Method. International Organization for Standardization: Geneva, Switzerland, 2022.
- Jurčević, M.; Nižetić, S.; Čoko, D.; Hoang, A.T.; Papadopoulos, A.M. Experimental investigation of novel hybrid phase change materials. Clean Technol. Environ. Policy 2022, 24, 201–212. [Google Scholar] [CrossRef]
- Kapton Polyimide Characteristics. Available online: https://www.dielectricmfg.com/knowledge-base/kapton/ (accessed on 22 November 2022).
- RS PRO. Available online: https://www.docs.rs-online.com/9b34/A700000007350702.pdf (accessed on 4 December 2022).
- Pico Technology. Available online: https://www.picotech.com/data-logger/tc-08/usb-tc-08-specifications (accessed on 4 December 2022).
- Water Supply and Sewerage Split. Available online: https://www.vik-split.hr/o-nama/djelatnost/vodoopskrba (accessed on 20 November 2023).
- Mihanović, H.; Vilibić, I.; Šepić, J.; Matić, F.; Ljubešić, Z.; Mauri, E.; Gerin, R.; Notarstefano, G.; Poulain, P.-M. Observation, preconditioning and recurrence of exceptionally high salinities in the Adriatic sea. Front. Mar. Sci. 2021, 8, 672210. [Google Scholar] [CrossRef]





| Heating power | 450 mW |
| Measurement time | 40 s |
| Available probing depth | 15 mm |
| Sample temperature | from −14 °C to −33 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bošnjak, J.; Jurčević, M.; Bodrožić Ćoko, N.; Nižetić, S. Experimental Investigation of Thermal Properties of Frozen Tap, Demineralized, and Sea Water. Energies 2023, 16, 7745. https://doi.org/10.3390/en16237745
Bošnjak J, Jurčević M, Bodrožić Ćoko N, Nižetić S. Experimental Investigation of Thermal Properties of Frozen Tap, Demineralized, and Sea Water. Energies. 2023; 16(23):7745. https://doi.org/10.3390/en16237745
Chicago/Turabian StyleBošnjak, Jelena, Mišo Jurčević, Natalia Bodrožić Ćoko, and Sandro Nižetić. 2023. "Experimental Investigation of Thermal Properties of Frozen Tap, Demineralized, and Sea Water" Energies 16, no. 23: 7745. https://doi.org/10.3390/en16237745
APA StyleBošnjak, J., Jurčević, M., Bodrožić Ćoko, N., & Nižetić, S. (2023). Experimental Investigation of Thermal Properties of Frozen Tap, Demineralized, and Sea Water. Energies, 16(23), 7745. https://doi.org/10.3390/en16237745







