Short-Term Prediction for Indoor Temperature Control Using Artificial Neural Network
Abstract
:1. Introduction
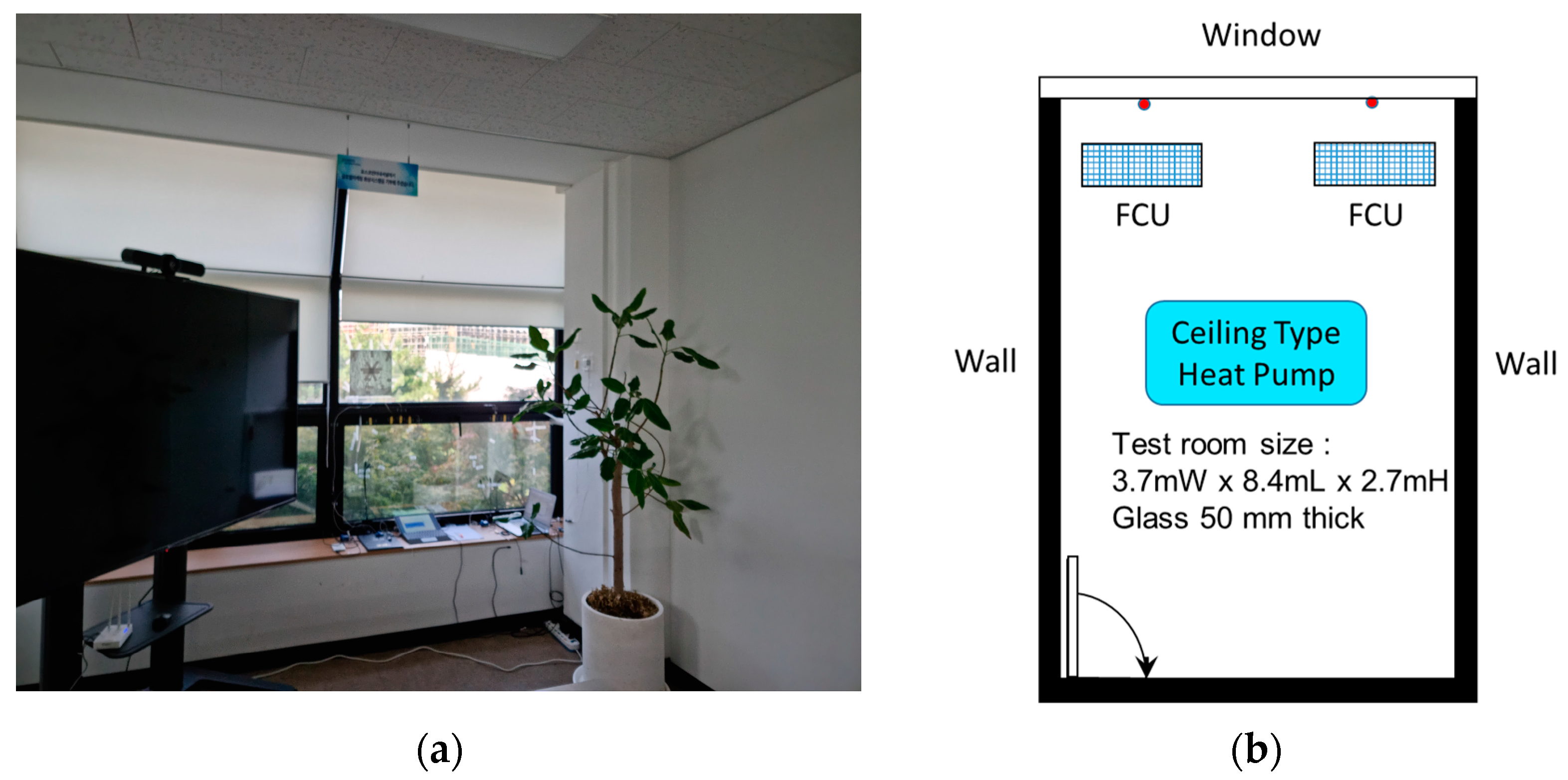
2. Data Preparation and Methods
2.1. Data Preparation
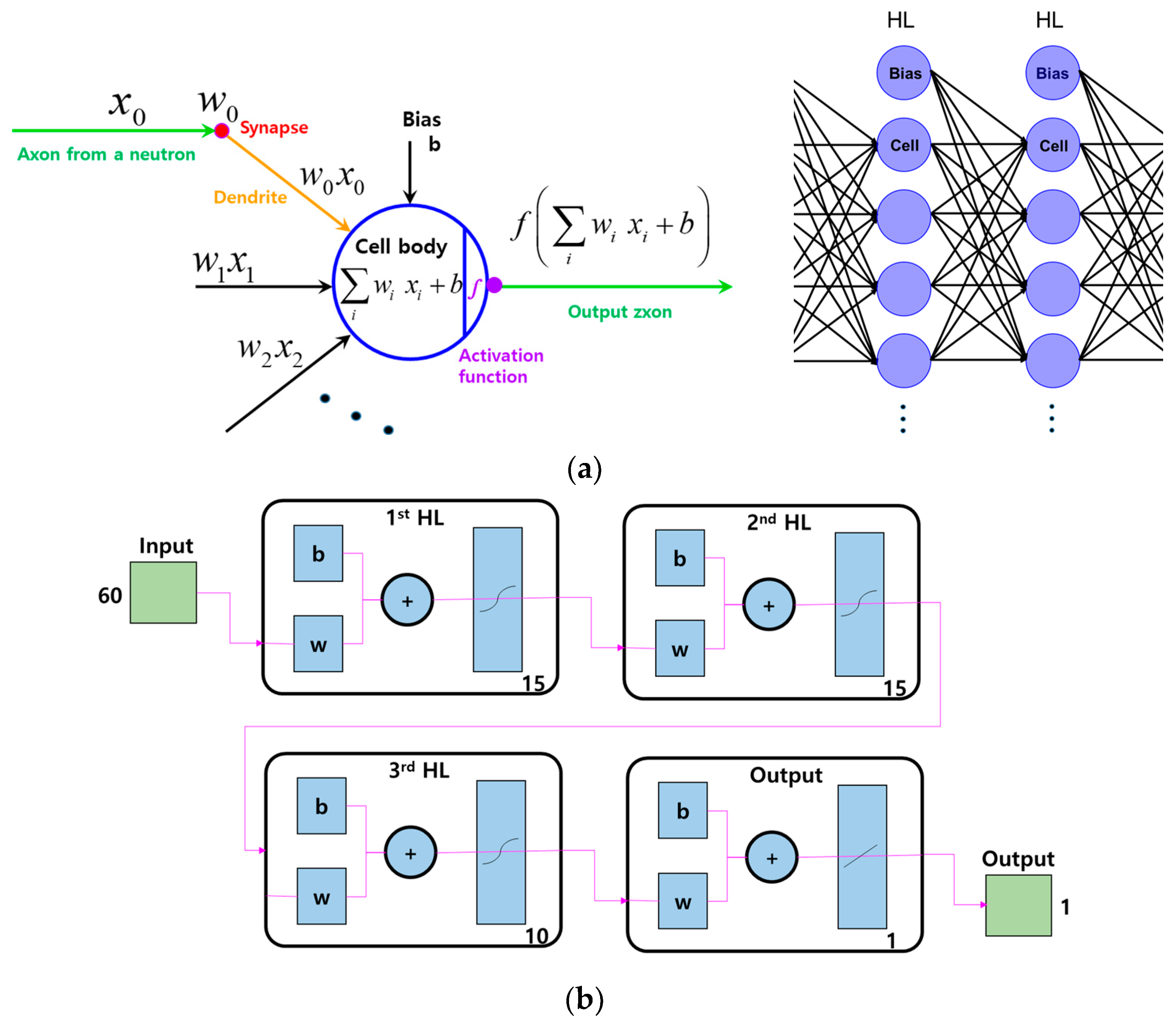
2.2. Multilayer Perceptron
3. Results and Discussion
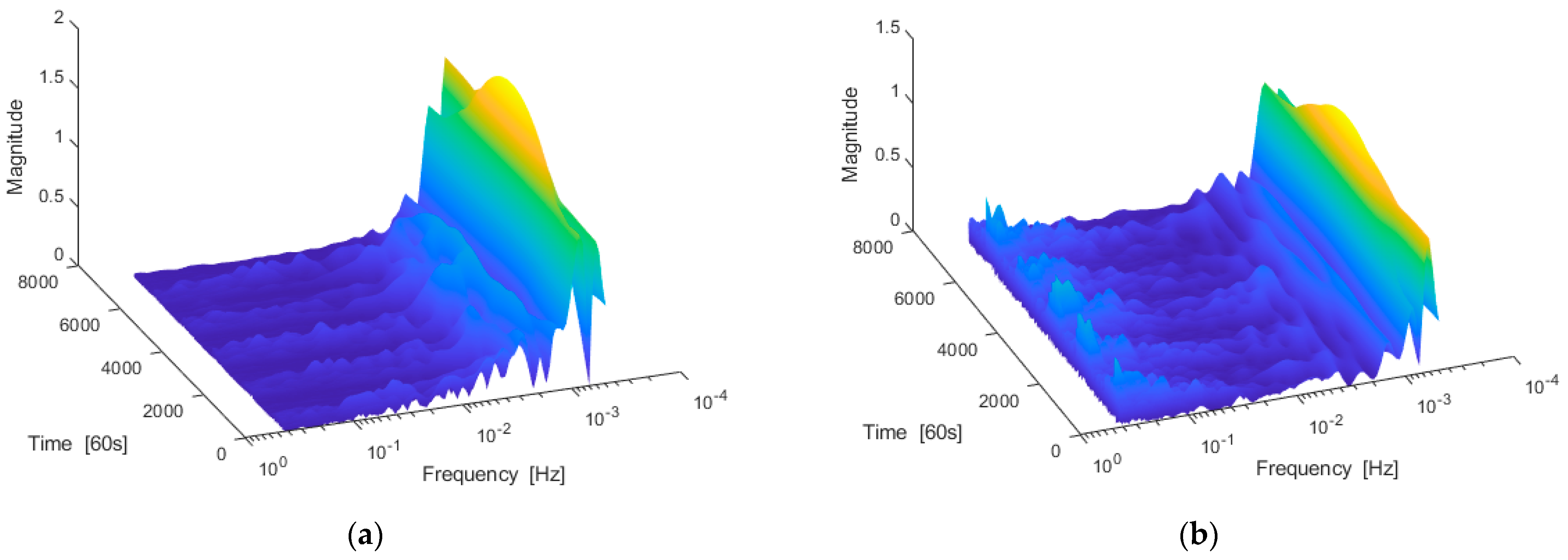
3.1. Data Analysis
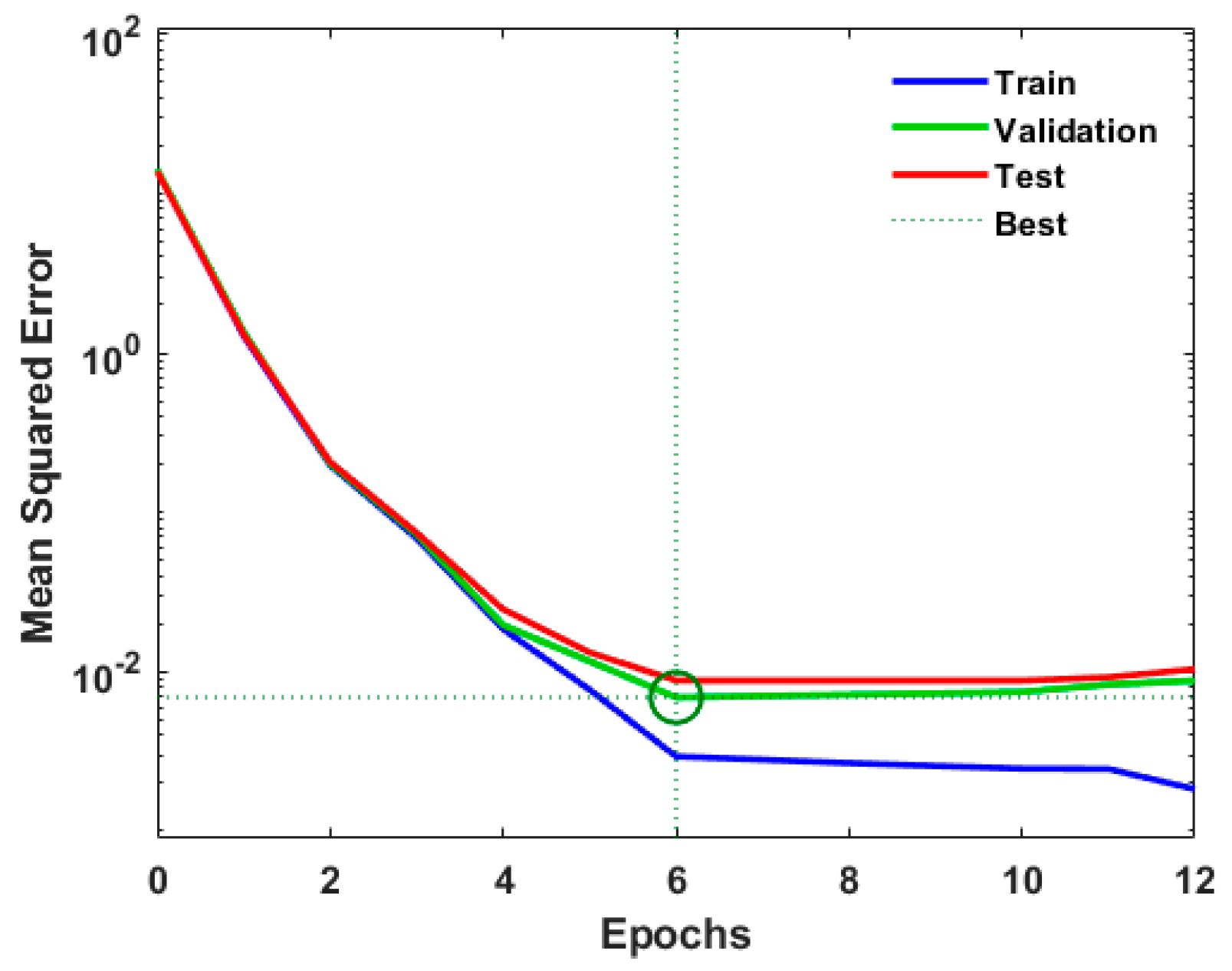
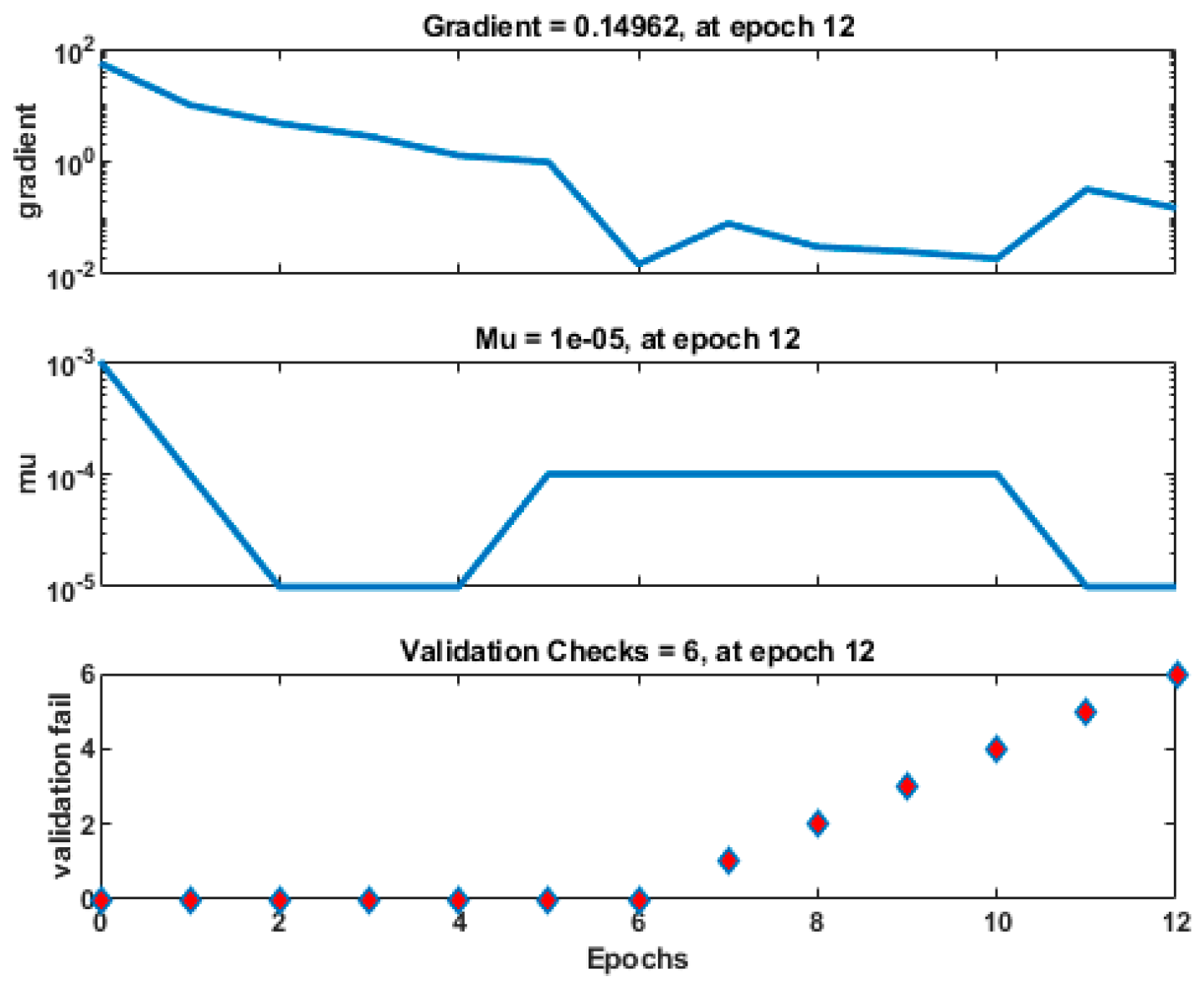
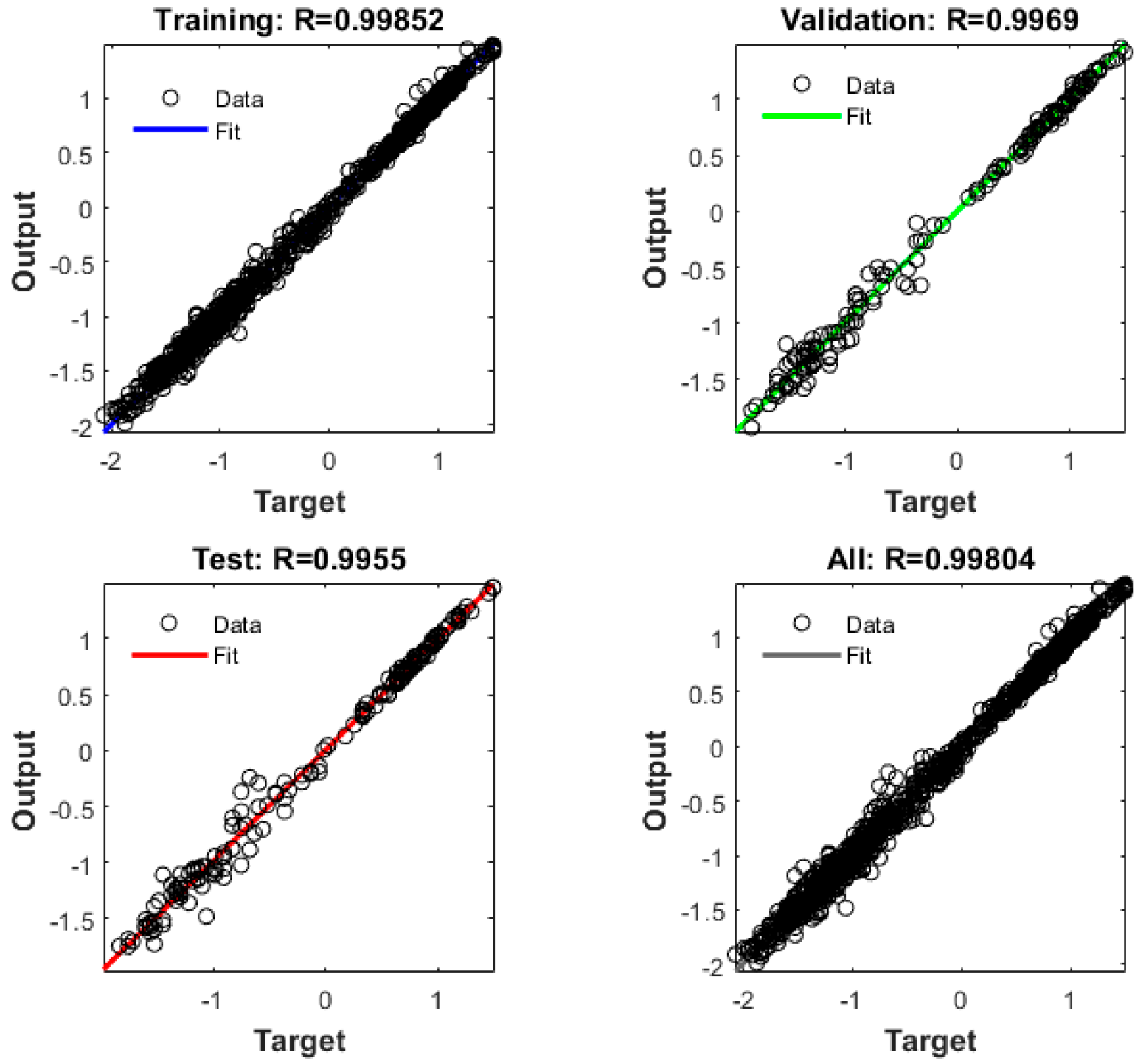
3.2. Artificial Neural Network
3.3. Multivariate MLP Neural Network Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial intelligence |
| ANN | Artificial neural networks |
| CNN | Convolutional neural network |
| CVRMSE | Coefficient of variation of RMSE |
| FCU | Fan coil unit |
| LSTM | Long short-term memory |
| MLP | Multilayer perceptron |
| MPC | Model predictive controller |
| MAE | Mean absolute error |
| MAPE | Maximum absolute percent error |
| MBE | Mean bias error |
| MRE | Mean relative error |
| MSE | Mean squared error |
| NMBE | Normalized MBE |
| NRMSE | Normalized RMSE |
| RMSE | Root mean square error |
| RMSPE | Root mean square percentage error |
| SSE | Sum squared error |
References
- International Energy Agency. Energy Systems, Buildings. Available online: https://www.iea.org/energy-system/buildings (accessed on 19 September 2023).
- Tafakkori, R.; Fattahi, A. Introducing novel configurations for double-glazed windows with lower energy loss. Sustain. Energy Technol. Assess. 2021, 43, 100919. [Google Scholar] [CrossRef]
- ASHRAE. Handbook Fundamentals, SI, International Edition, 1997; ASHRAE Handbook—HVAC Applications; ASHRAE Parsons: Peachtree Corners, GA, USA, 2007.
- Lu, C.; Li, S.; Lu, Z. Building energy prediction using artificial neural networks: A literature survey. Energy Build. 2021, 262, 111718. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y. Data-driven modeling of building thermal dynamics: Methodology and state of the art. Energy Build. 2019, 203, 109405. [Google Scholar] [CrossRef]
- Bourdeau, M.; Zhai, X.Q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Kirubakaran, V.; Sahu, C.; Radhakrishnan, T.; Sivakumaran, N. Energy efficient model based algorithm for control of building HVAC systems. Ecotoxicol. Environ. Saf. 2015, 121, 236–243. [Google Scholar] [CrossRef] [PubMed]
- Ming, W.; Sun, P.; Zhang, Z.; Qiu, W.; Du, J.; Li, X.; Zhang, Y.; Zhang, G.; Liu, K.; Wang, Y.; et al. A systematic review of machine learning methods applied to fuel cells in performance evaluation, durability prediction, and application monitoring. Int. J. Hydrogen Energy 2023, 48, 5197–5228. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering—Machine Learning, Dynamical Systems, and Control, 2nd ed.; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Park, B.K.; Cho, D.W.; Shin, H.J. Energy Analysis for Variable Air Volume System. Mag. Soc. Air-Cond. Refrig. Eng. Korea 1988, 17, 575–582. [Google Scholar]
- Roman, N.D.; Bre, F.; Fachinotti, V.D.; Lamberts, R. Application and characterization of metamodels based on artificial neural networks for building performance simulation: A systematic review. Energy Build. 2020, 217, 109972. [Google Scholar] [CrossRef]
- Tien, P.W.; Wei, S.; Darkwa, J.; Wood, C.; Calautit, J.K. Machine Learning and Deep Learning Methods for Enhancing Building Energy Efficiency and Indoor Environmental Quality—A Review. Energy AI 2022, 10, 100198. [Google Scholar] [CrossRef]
- Chen, Z.; Xiao, F.; Guo, F.; Yan, J. Interpretable machine learning for building energy management: A state-of-the-art review. Adv. Appl. Energy 2023, 9, 100123. [Google Scholar] [CrossRef]
- Noye, S.; Martinez, R.M.; Carnieletto, L.; DeCarli, M.; Aguirre, A.C. A review of advanced ground source heat pump control: Artificial intelligence for autonomous and adaptive control. Renew. Sustain. Energy Rev. 2022, 153, 111685. [Google Scholar] [CrossRef]
- Bellagarda, A.; Cesari, S.; Aliberti, A.; Ugliotti, F.; Bottaccioli, L.; Macii, E.; Patti, E. Effectiveness of neural networks and transfer learning for indoor air-temperature forecasting. Autom. Constr. 2022, 140, 104314. [Google Scholar] [CrossRef]
- Attoue, N.; Shahrour, I.; Younes, R. Smart Building; Use of the Artificial Neural Network Approach for Indoor Temperature Forecasting. Energies 2018, 11, 395. [Google Scholar] [CrossRef]
- Kreuzer, D.; Munz, M.; Schlüter, S. Short-term temperature forecasts using a convolutional neural network—An application to different weather stations in Germany. Mach. Learn. Appl. 2020, 2, 100007. [Google Scholar] [CrossRef]
- Xu, C.; Chen, H.; Wang, J.; Guo, Y.; Yuan, Y. Improving prediction performance for indoor temperature in public buildings based on a novel deep learning method. Build. Environ. 2019, 148, 128–135. [Google Scholar] [CrossRef]
- Kamel, E.; Javan-Khoshkholgh, A.; Abumahfouz, N.; Huang, S.; Huang, X.; Farajidavar, A.; Qiu, Y. A case study of using multi-functional sensors to predict the indoor air temperature in classrooms. ASHRAE Trans. 2020, 26, 3–11. [Google Scholar]
- Aliberti, A.; Bottaccioli, L.; Macii, E.; Cataldo, S.D.; Acquaviva, A.; Patti, E. A non-linear autoregressive model for indoor air-temperature predictions in smart buildings. Electronics 2019, 8, 979. [Google Scholar] [CrossRef]
- Cifuentes, J.; Marulanda, G.; Bello, A.; Reneses, J. Air temperature forecasting using machine learning techniques: A review. Energies 2020, 13, 4215. [Google Scholar] [CrossRef]
- Park, B.K.; Kim, C.-J. Unsteady Heat Flux Measurement and Predictions Using Long Short-Term Memory Networks. Buildings 2023, 13, 707. [Google Scholar] [CrossRef]
- Pawar, P.; Kumar, M.T.; Vittal, K.P. An IoT based Intelligent Smart Energy Management System with accurate forecasting and load strategy for renewable generation. Measurement 2020, 152, 107187. [Google Scholar] [CrossRef]
- Schwenzer, M.; Ay, M.; Bergs, T.; Dirk Abel, D. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Mathlab. Deep Learning Toolbox; Mathoworks: Natick, MA, USA, 2022. [Google Scholar]
- Chapra, S.C.; Canale, R.P. Numerical Method for Engineers, 4th ed.; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Brownlee, J. Deep Learning for Time Series Forecasting—Predict the Future with MLPs, CNNs, and LSTMs in Python; Machine Learning Mastery: San Juan, PR, USA, 2020. [Google Scholar]
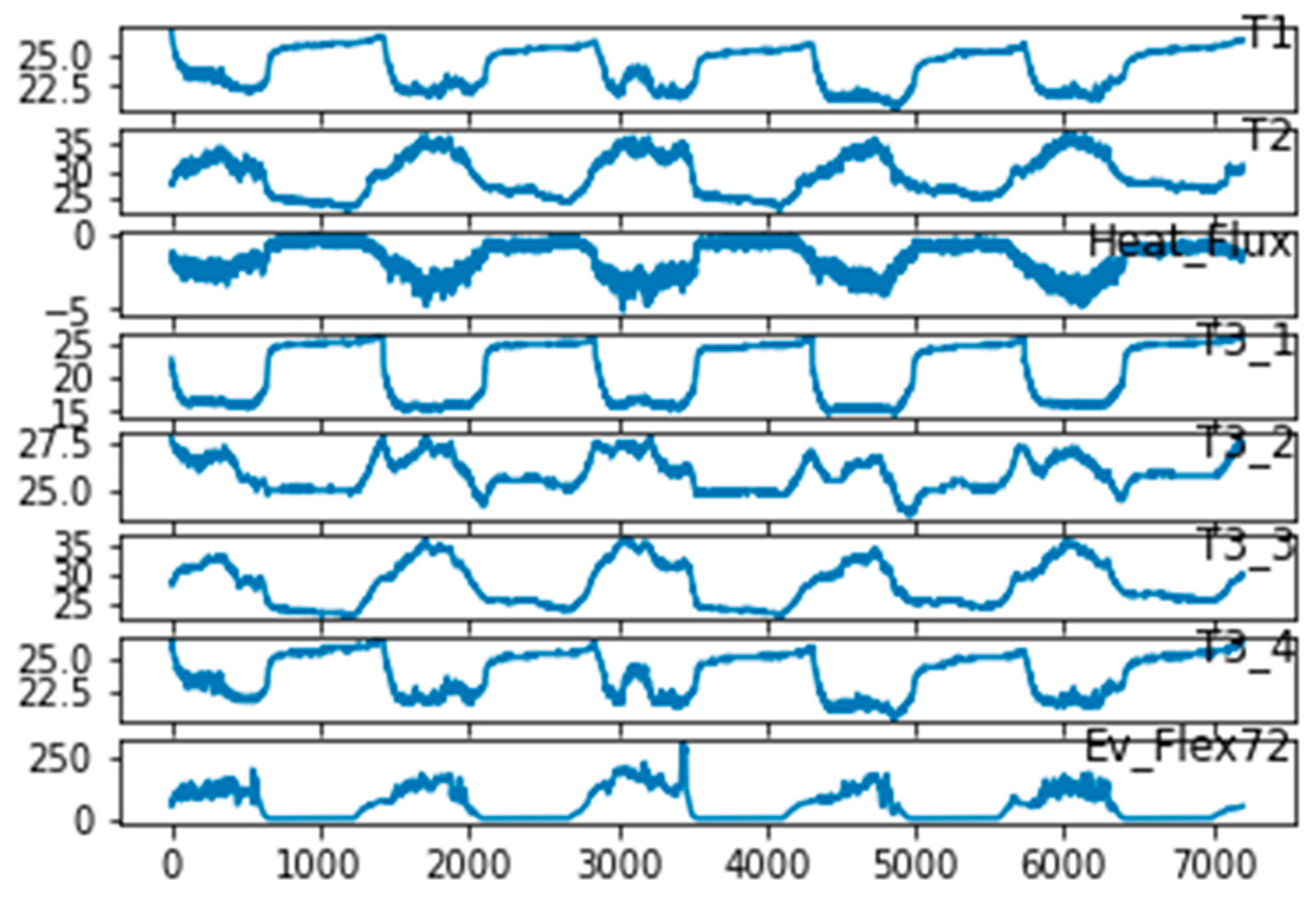



| Minimum | Maximum | Mean | Standard Dev. | |
|---|---|---|---|---|
| T1 (Indoor temp.) | 20.75 | 27.06 | 24.09 | 1.61 |
| T2 (Outdoor temp.) | 22.94 | 37 | 29.02 | 3.58 |
| Heat_Flux (Heat flux) | −5.12 | −0.04 | −1.64 | 1.04 |
| T3_1 (FCU outlet temp.) | 14.75 | 26.25 | 20.96 | 4.31 |
| T3_2 (Pane inside temp.) | 23.75 | 27.75 | 25.84 | 0.85 |
| T3_3 (Pane outside temp.) | 23 | 36 | 28.22 | 3.67 |
| T3_4 (Indoor temp. 2) | 20.5 | 26.25 | 23.81 | 1.59 |
| Ev_Flex72 (Illuminance) | 0.13 | 316.8 | 57.81 | 62.37 |
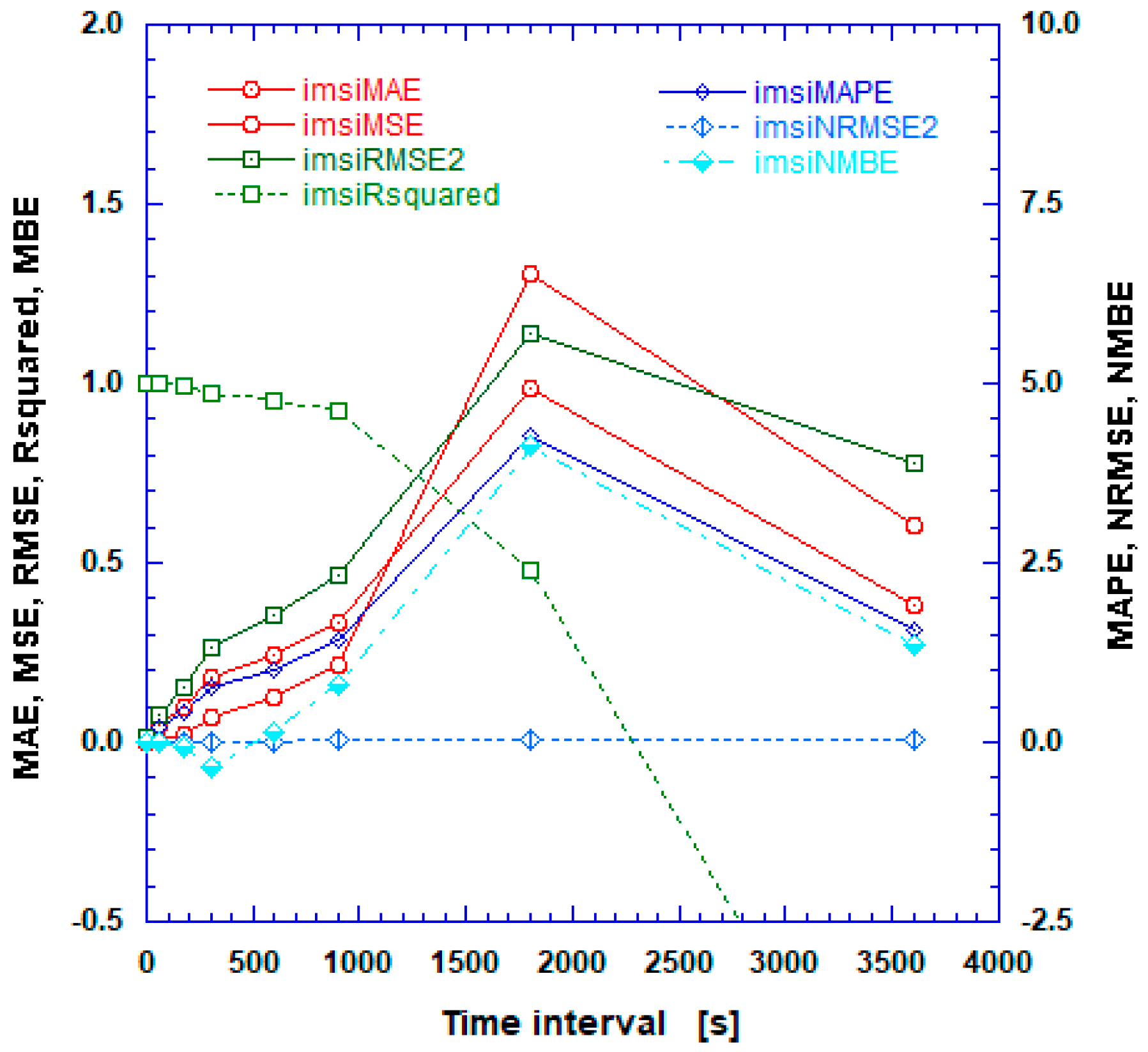
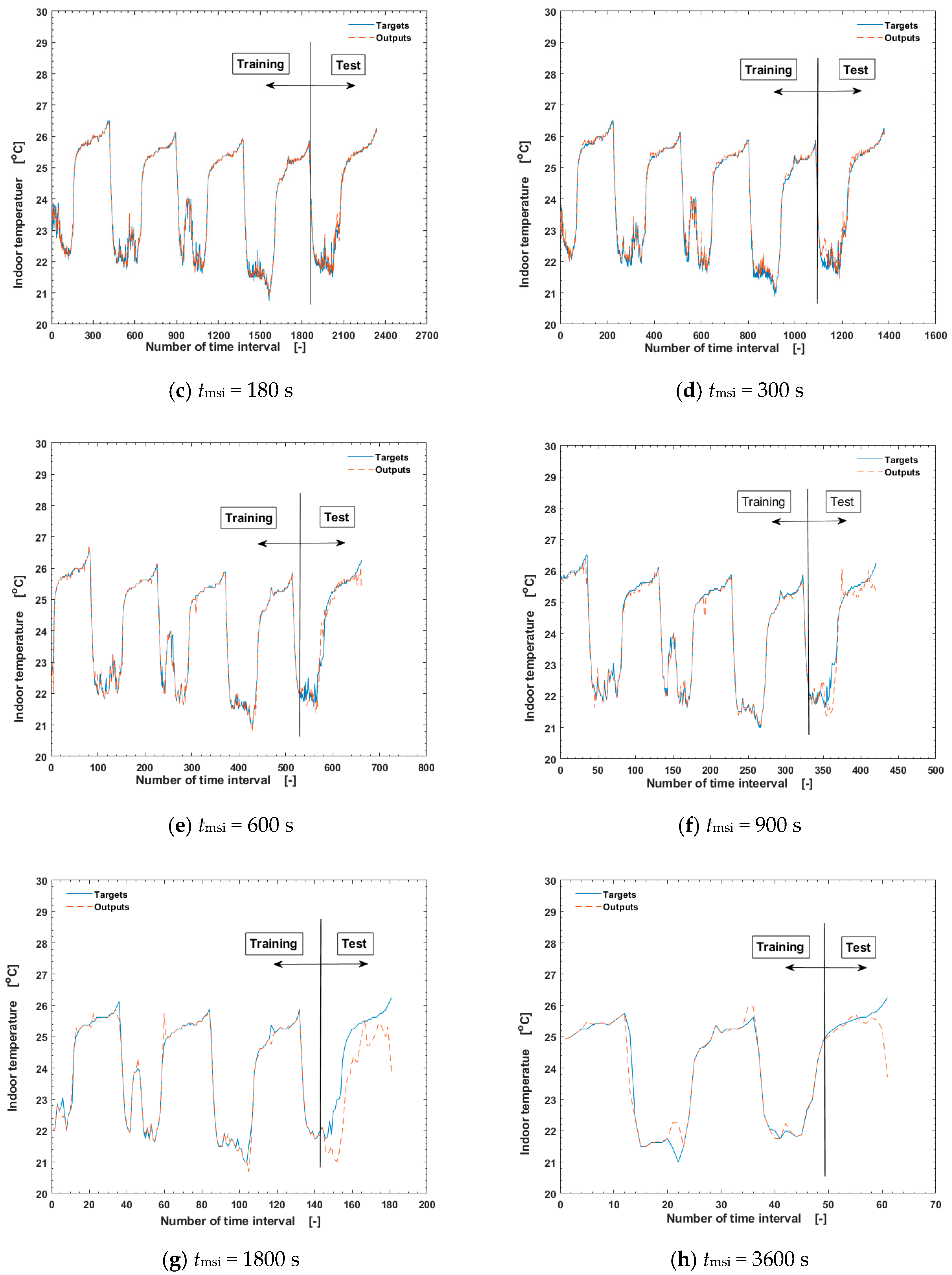
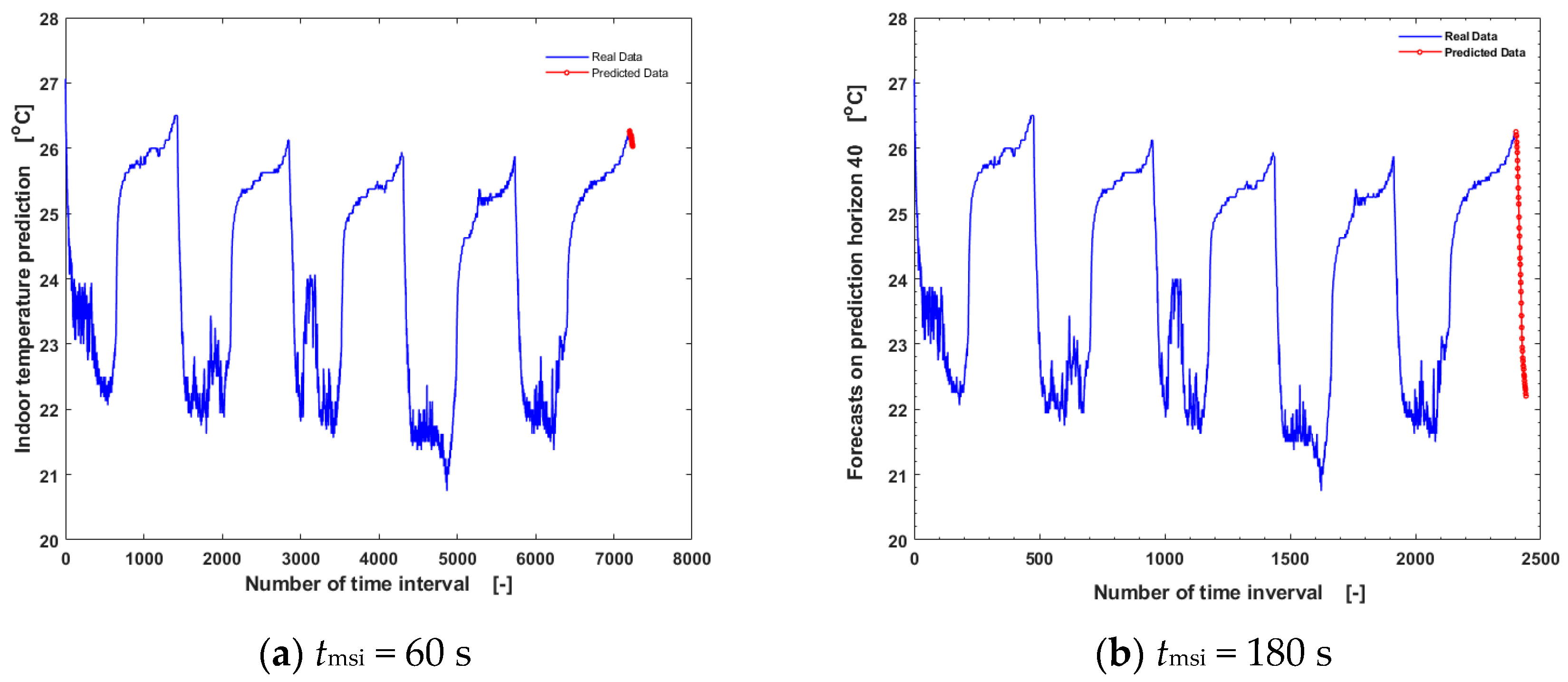
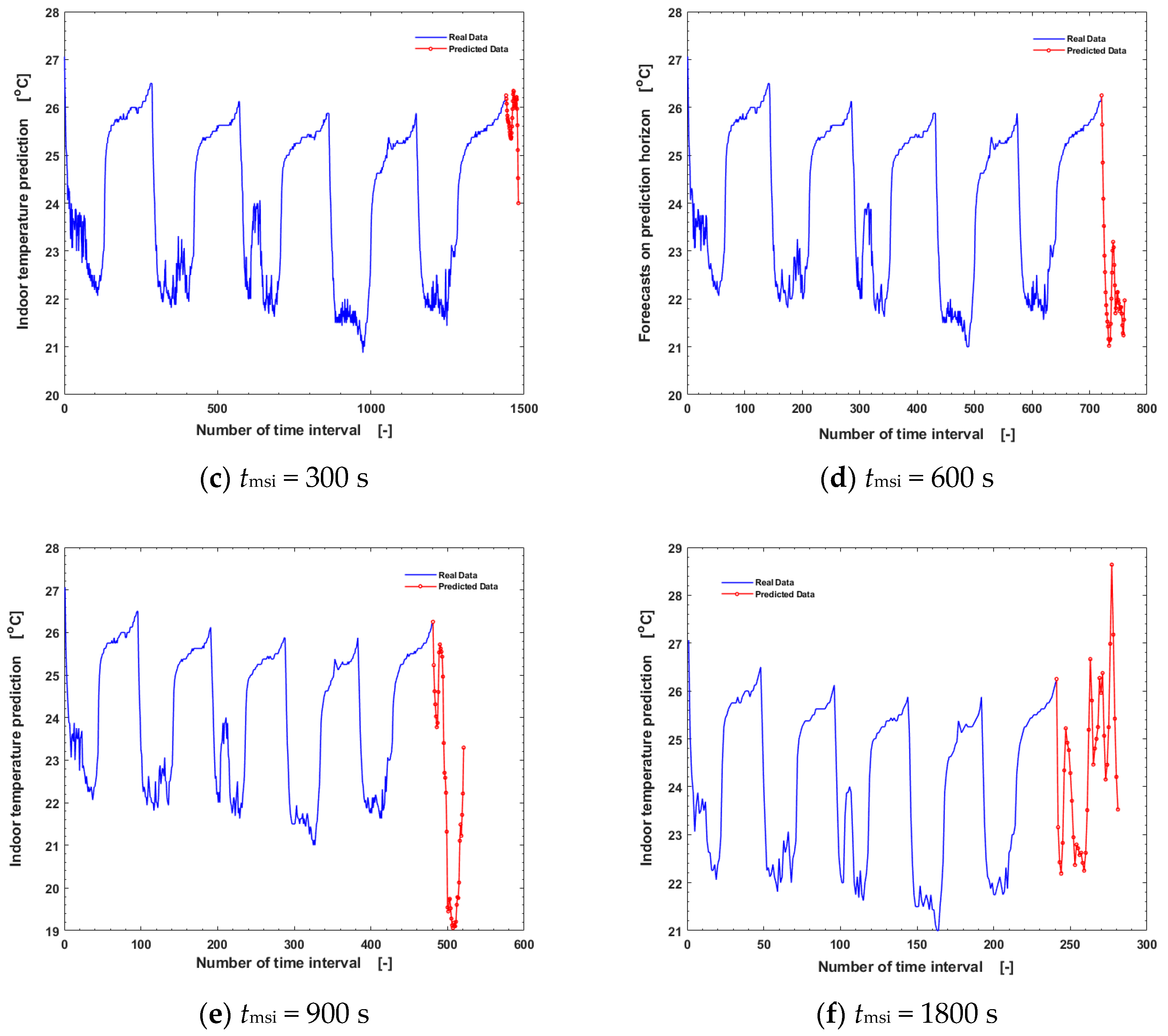
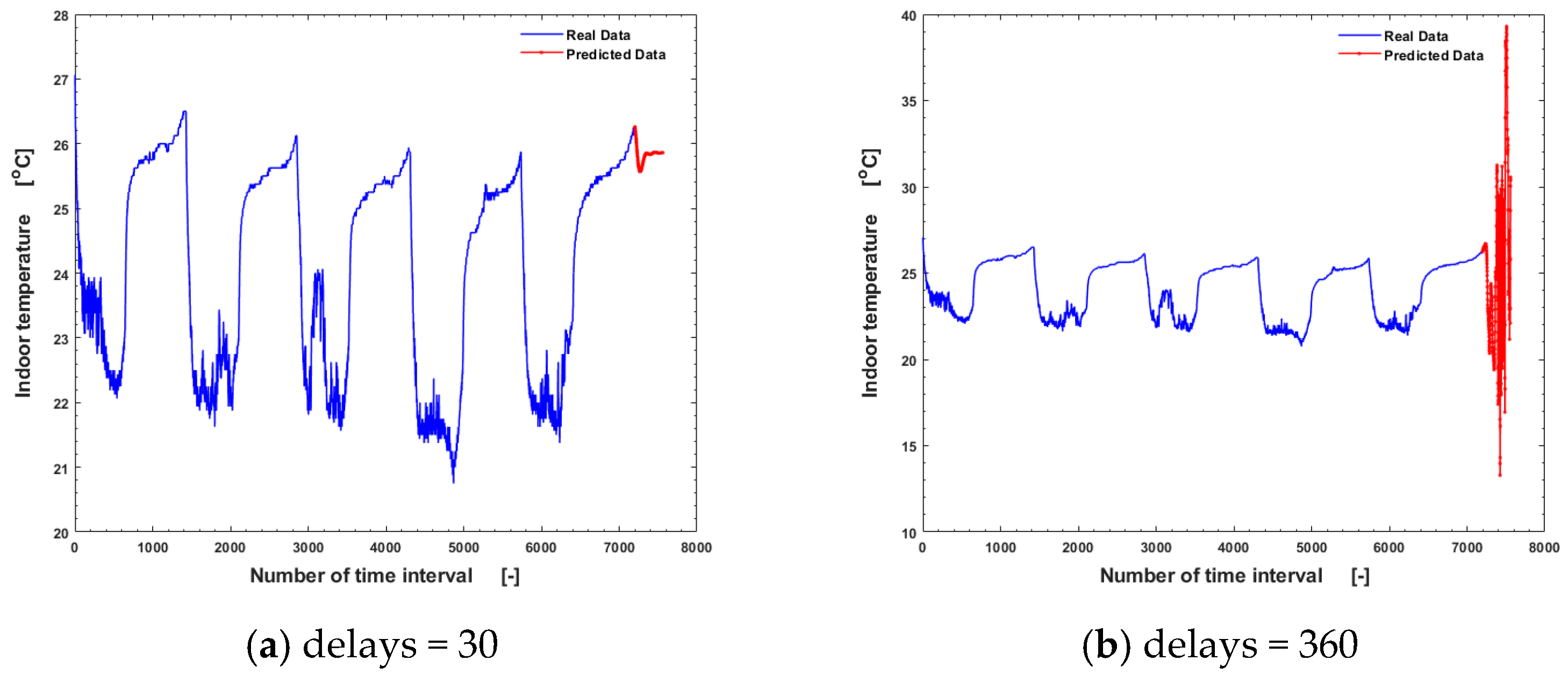
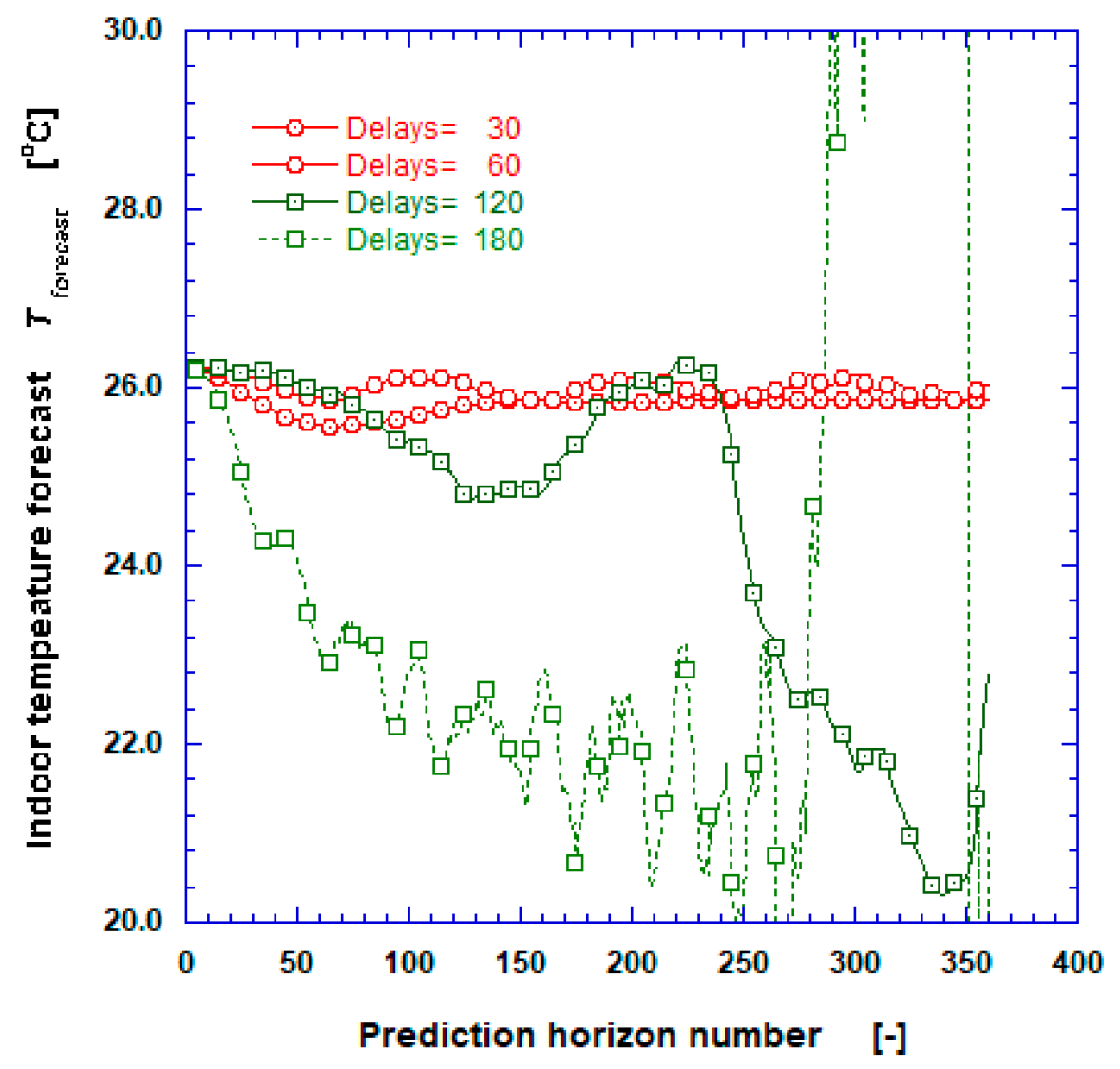
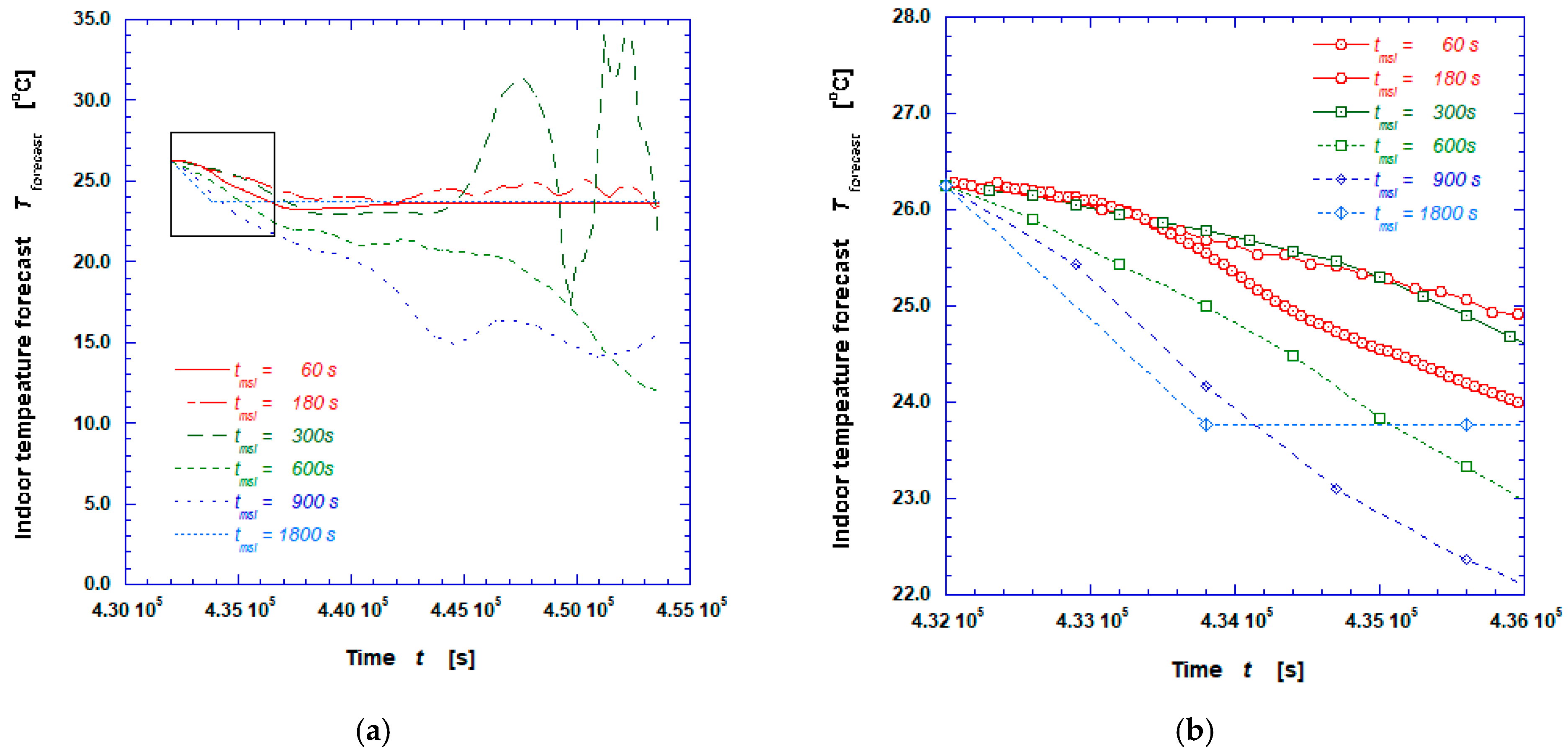
| tmsi [s] | R2 | RMSE | MAE | MAPE | MSE | NRMSE | CVRMSE | SSE | MBE | NMBE |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.999907 | 0.015853 | 0.006926 | 0.028927 | 0.000251 | 0.000660 | 0.323356 | 21.709646 | −0.000289 | −0.001201 |
| 60 | 0.997692 | 0.079449 | 0.049032 | 0.215387 | 0.006312 | 0.003306 | 1.620667 | 9.013649 | 0.002019 | 0.008402 |
| 180 | 0.991236 | 0.155063 | 0.094141 | 0.409750 | 0.024044 | 0.006448 | 3.160925 | 11.252788 | −0.017319 | −0.071967 |
| 300 | 0.973576 | 0.261109 | 0.178304 | 0.768951 | 0.068178 | 0.010847 | 5.312462 | 18.817129 | −0.085975 | −0.355893 |
| 600 | 0.953170 | 0.353070 | 0.240478 | 1.021933 | 0.124658 | 0.014607 | 7.186175 | 16.454886 | 0.032537 | 0.134789 |
| 900 | 0.921878 | 0.463206 | 0.330218 | 1.414434 | 0.214560 | 0.019075 | 9.436804 | 18.023009 | 0.190081 | 0.788933 |
| 1800 | 0.479917 | 1.142341 | 0.987249 | 4.263700 | 1.304944 | 0.046210 | 23.447295 | 46.977975 | 0.984554 | 4.147949 |
| 3600 | −1.312062 | 0.777090 | 0.384812 | 1.575031 | 0.603868 | 0.030344 | 15.458737 | 7.246419 | 0.340019 | 1.345580 |
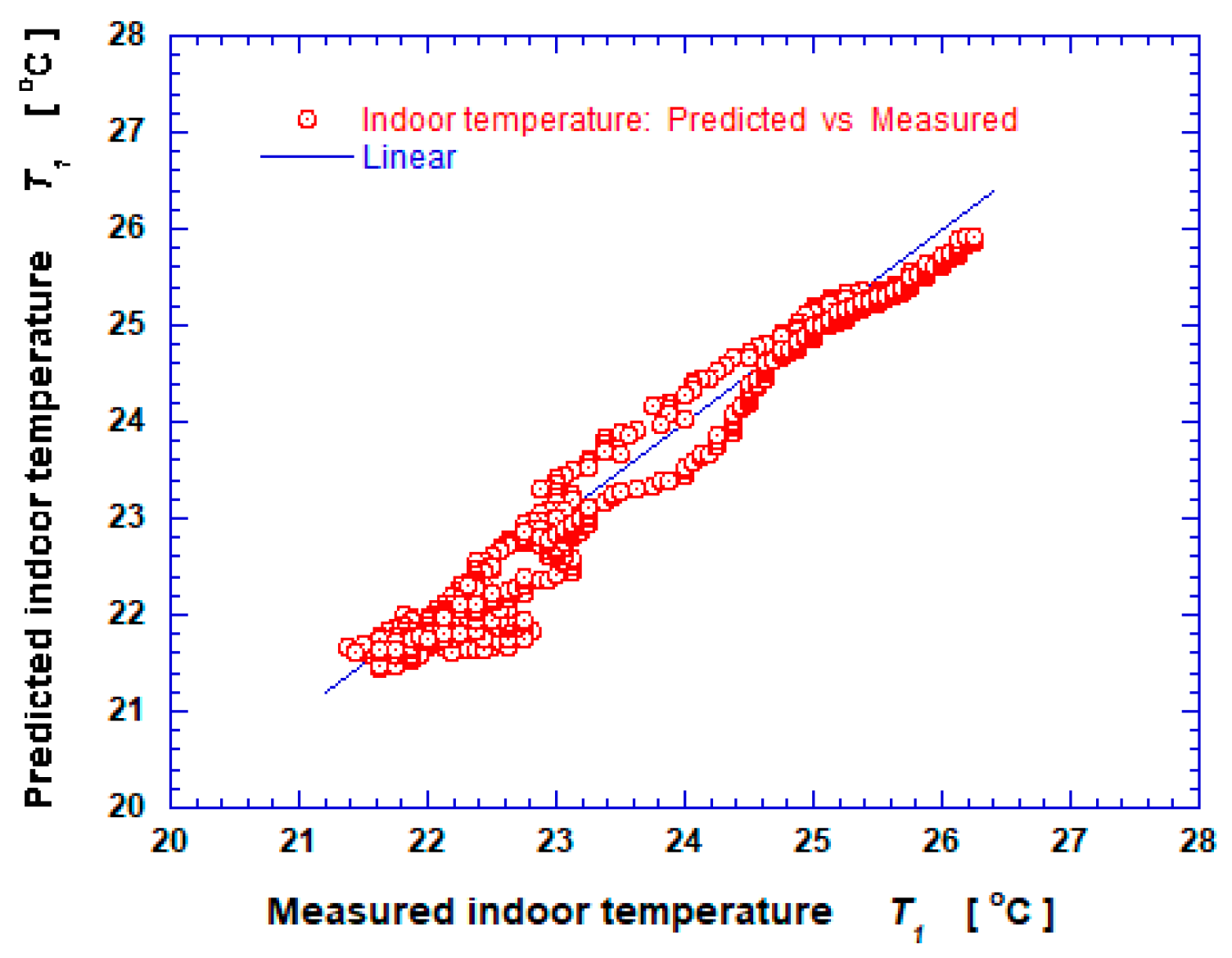
| R2 | RMSE | MAE | MAPE | MSE | CVRMSE | SSE | MBE | NMBE | MRE | |
|---|---|---|---|---|---|---|---|---|---|---|
| MLP (univariate) | 0.998 | 0.079 | 0.049 | 0.215 | 0.006 | 1.620 | 9.013 | 0.002 | 0.008 | 8.4 × 10−5 |
| MLP (multivariate) | 0.974 | 0.264 | 0.224 | 0.933 | 0.069 | 5.359 | 102.03 | −0.197 | −0.817 | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, B.K.; Kim, C.-J. Short-Term Prediction for Indoor Temperature Control Using Artificial Neural Network. Energies 2023, 16, 7724. https://doi.org/10.3390/en16237724
Park BK, Kim C-J. Short-Term Prediction for Indoor Temperature Control Using Artificial Neural Network. Energies. 2023; 16(23):7724. https://doi.org/10.3390/en16237724
Chicago/Turabian StylePark, Byung Kyu, and Charn-Jung Kim. 2023. "Short-Term Prediction for Indoor Temperature Control Using Artificial Neural Network" Energies 16, no. 23: 7724. https://doi.org/10.3390/en16237724
APA StylePark, B. K., & Kim, C.-J. (2023). Short-Term Prediction for Indoor Temperature Control Using Artificial Neural Network. Energies, 16(23), 7724. https://doi.org/10.3390/en16237724






