Evaluation of Landweber Coupled Least Square Support Vector Regression Algorithm for Electrical Capacitance Tomography for LN2–VN2 Flow
Abstract
:1. Introduction
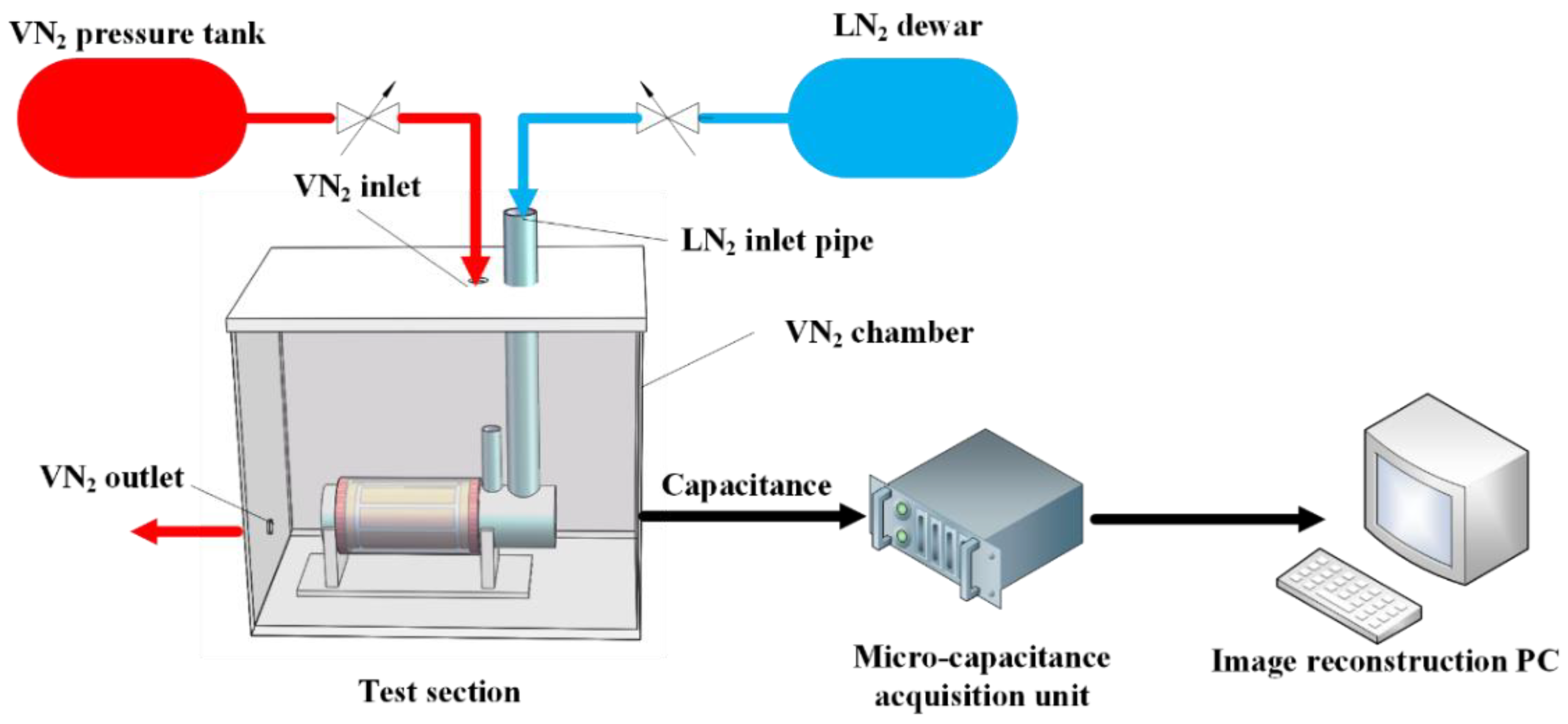
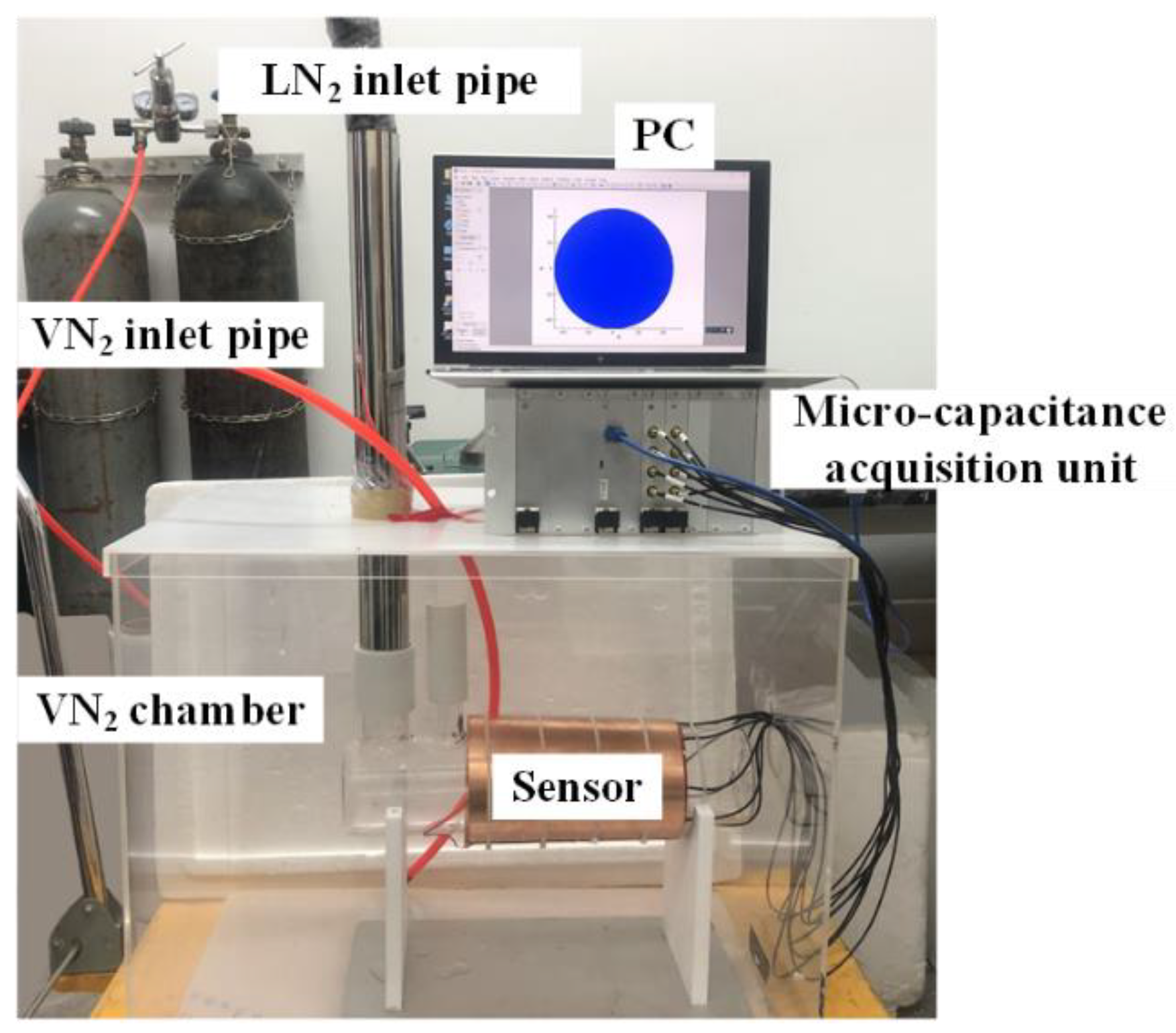
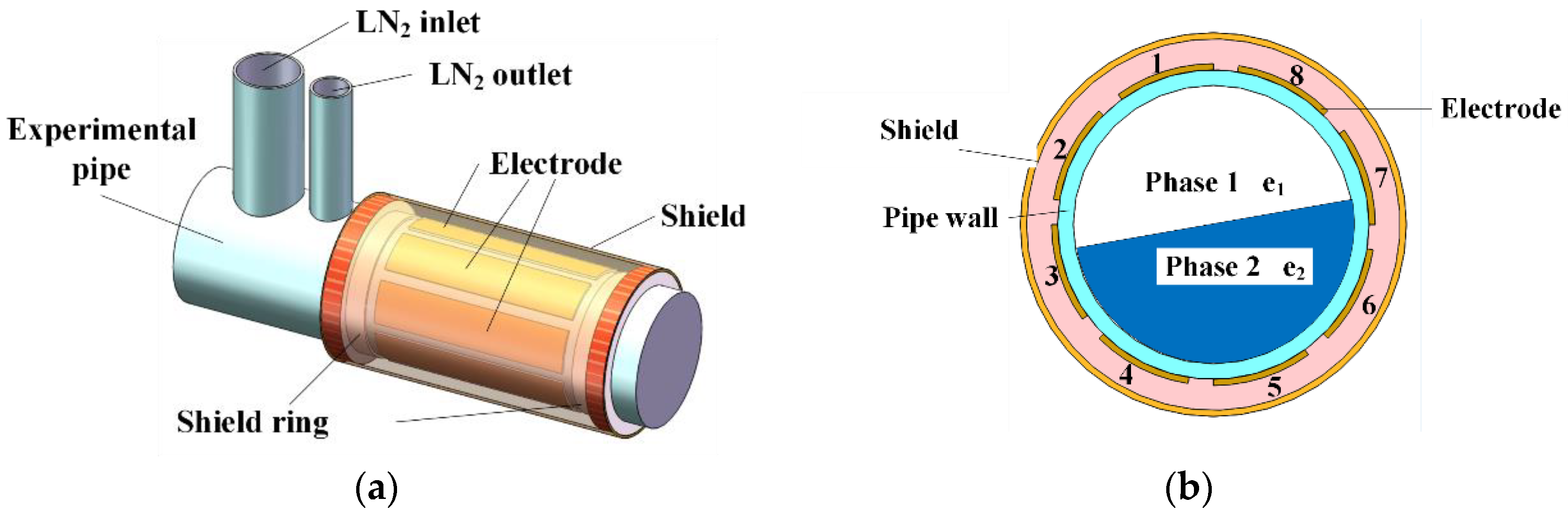
2. ECT Cryogenic Experimental System
3. Image Reconstruction Approach
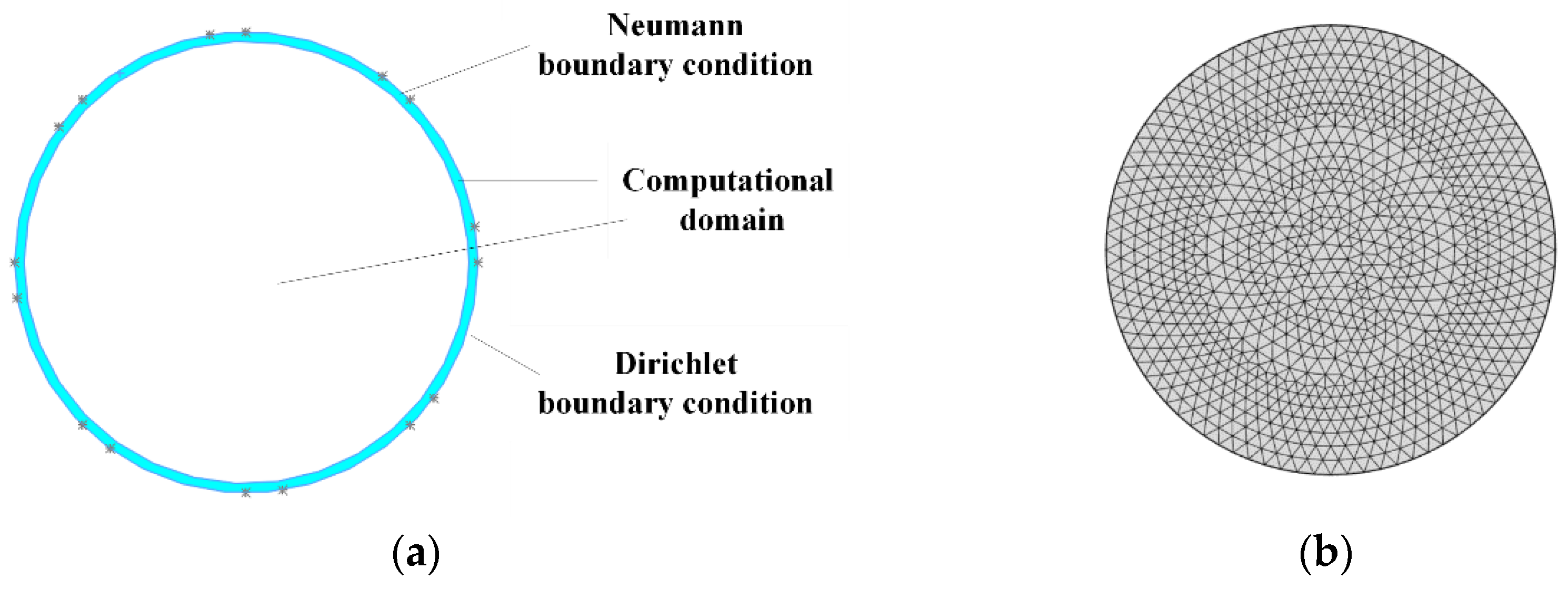
3.1. Forward Problem of ECT
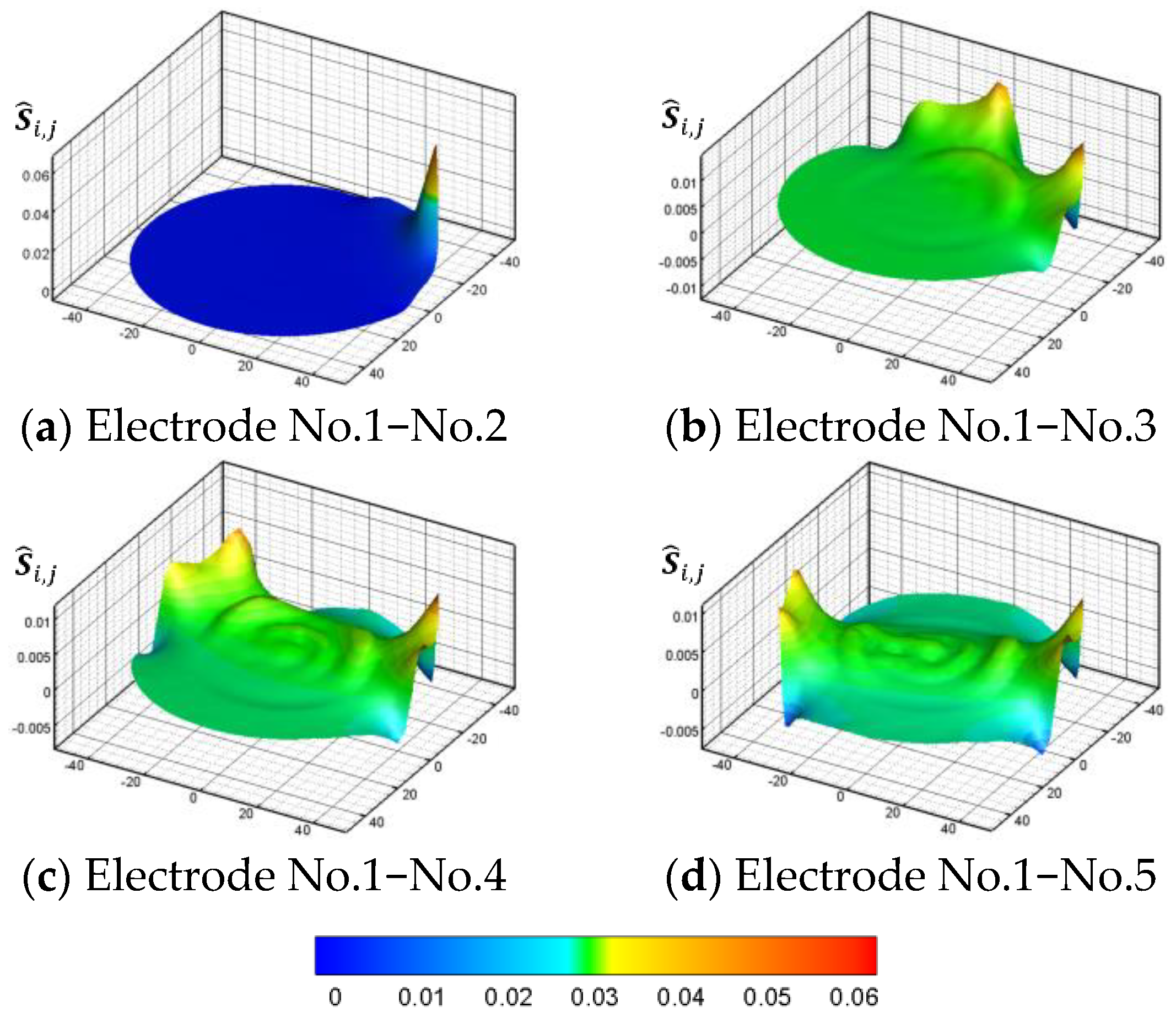
3.2. Calculation of Sensitivity Field
3.3. The Inverse Problem of ECT
3.3.1. Linear Back-Projection (LBP) Algorithm
3.3.2. Landweber Iterative Algorithm
3.3.3. Landweber Coupled LSSVR Algorithm
4. Experiment and Analysis
4.1. The Tentative Experiments
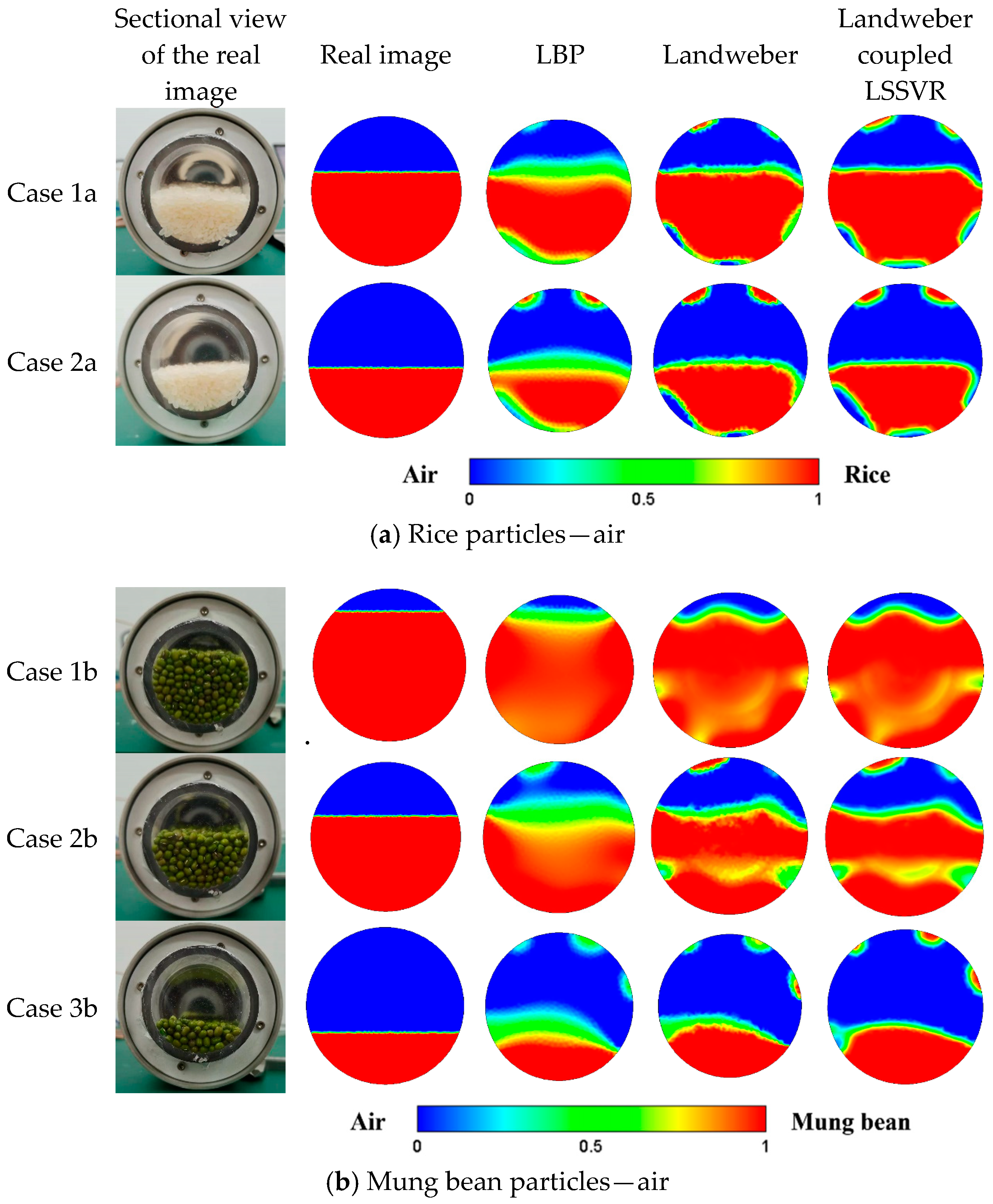
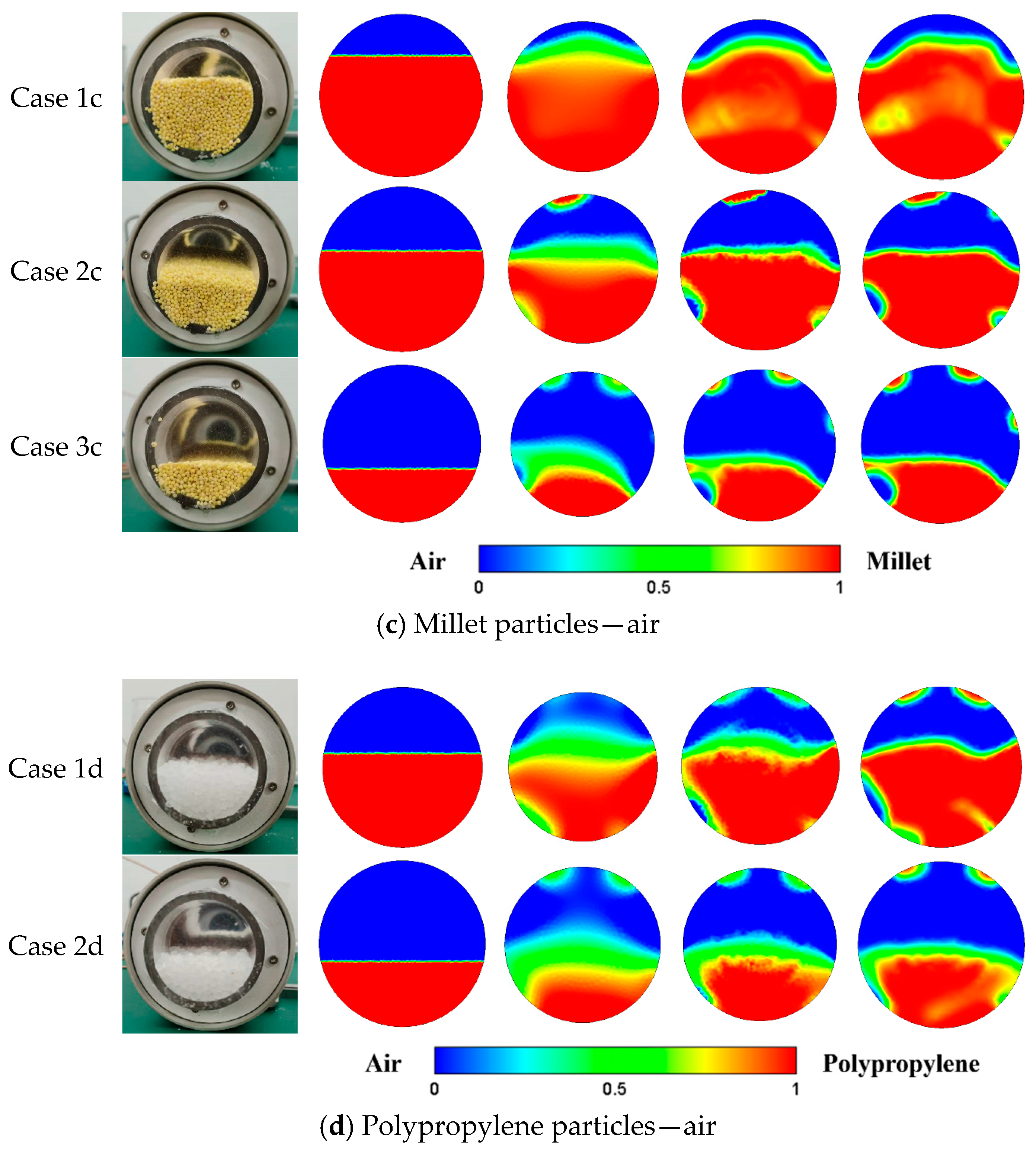
4.2. Cryogenic Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Linear offset vector of LSSVR | Normalized sensitive field matrix | |
| b | Coefficient vector of LSSVR | Normalized sensitive field between the measuring electrode i and j | |
| C | Capacitance value | Excitation voltage | |
| Normalized vector of dielectric permittivity distribution | Residual error of normalized capacitance | ||
| Kernal function | Greek symbol | ||
| M | Total number of effective capacitance values | ||
| N | Total number of grid cells | Iteration step size | |
| Unit normal vector at the wall | Electrode position | ||
| Electric potential distribution | Dielectric permittivity distribution | ||
| P(.) | Projection operation | Normalized measured capacitance vector | |
| Q | Quantity of electric charge | Computational domain | |
| Sensitive field between the measuring electrode i and j | Boundary of the computational domain which is not covered by the electrode area | ||
References
- Sakamoto, Y.; Kobayashi, H.; Naruo, Y.; Takesaki, Y.; Nakajima, Y.; Furuichi, A.; Tsujimura, H.; Kabayama, K.; Sato, T. Investigation of the Void Fraction–quality Correlations for Two-phase Hydrogen Flow Based on the Capacitive Void Fraction Measurement. Int. J. Hydrogen Energy 2019, 44, 18483–18495. [Google Scholar] [CrossRef]
- Yang, Z.Q.; Chen, G.F.; Zhuang, X.R.; Song, Q.L.; Deng, Z.; Shen, J.; Gong, M.Q. A New Flow Pattern Map for Flow Boiling of R1234ze(E) in a Horizontal Tube. Int. J. Multiph. Flow 2018, 98, 24–35. [Google Scholar] [CrossRef]
- Forte, G.; Clark, P.; Yan, Z.; Stitt, E.H.; Marigo, M. Using a Freeman Ft4 Rheometer and Electrical Capacitance Tomography to Assess Powder Blending. Powder Technol. 2018, 337, 25–35. [Google Scholar] [CrossRef]
- Chen, J.Y.; Wang, Y.C.; Zhang, W.; Qiu, L.M.; Zhang, X.B. Capacitance-based Liquid Holdup Measurement of Cryogenic Two-phase Flow in a Nearly-horizontal Tube. Cryogenics 2017, 84, 69–75. [Google Scholar] [CrossRef]
- Khalil, A.; Mcintosh, G.; Boom, R. Experimental Measurement of Void Fraction in Cryogenic Two Phase Upward Flow. Cryogenics 1981, 21, 411–414. [Google Scholar] [CrossRef]
- Filippov, Y.P.; Kovrizhnykh, A.M.; Miklayev, V.M.; Sukhanova, A.K. Metrological Systems for Monitoring Two-phase Cryogenic Flows. Cryogenics 2000, 40, 279–285. [Google Scholar] [CrossRef]
- Filippov, Y.P. How to Measure Void Fraction of Two-phase Cryogenic Flows. Cryogenics 2001, 41, 327–334. [Google Scholar] [CrossRef]
- Filippov, Y.P.; Kakorin, I.; Kovrizhnykh, A.M. New Solutions to Produce a Cryogenic Void Fraction Sensor of Round Cross-section and Its Applications. Cryogenics 2013, 57, 55–62. [Google Scholar] [CrossRef]
- Harada, K.; Murakami, M.; Ishii, T. PIV Measurements for Flow Pattern Void Fraction in Cavitating Flows of He II and He I. Cryogenics 2006, 46, 648–657. [Google Scholar] [CrossRef]
- Che, H.Q.; Ye, J.M.; Tu, Q.Y.; Yang, W.Q.; Wang, H.G. Investigation of Coating Process in Wurster Fluidised Bed Using Electrical Capacitance Tomography. Chem. Eng. Res. Des. 2018, 132, 1180–1192. [Google Scholar] [CrossRef]
- Guo, Q.; Ye, M.; Yang, W.Q.; Liu, Z. A Machine Learning Approach for Electrical Capacitance Tomography Measurement of Gas–solid Fluidized Beds. Aiche J. 2019, 65, e16583. [Google Scholar] [CrossRef]
- Mohamad, E.J.; Rahim, R.A.; Rahiman, M.H.F.; Ameran, H.L.M.; Muji, S.Z.M.; Marwah, O.M.F. Measurement and Analysis of Water/oil Multiphase Flow Using Electrical Capacitance Tomography Sensor. Flow Meas. Instrum. 2016, 47, 62–70. [Google Scholar] [CrossRef]
- Yang, W.Q.; Stott, A.L.; Beck, M.S.; Xie, C.G. Development of Capacitance Tomographic Imaging Systems for Oil Pipeline Measurements. Rev. Sci. Instrum. 1995, 66, 4326–4332. [Google Scholar] [CrossRef]
- Ortiz-alemán, C.; Martin, R. Inversion of Electrical Capacitance Tomography Data By Simulated Annealing: Application to Real Two-phase Gas–oil Flow Imaging. Flow Meas. Instrum. 2005, 16, 157–162. [Google Scholar] [CrossRef]
- Ismail, I.; Gamio, J.; Bukhari, S.; Yang, W.Q. Tomography for Multi-phase Flow Measurement in the Oil Industry. Flow Meas. Instrum. 2005, 16, 145–155. [Google Scholar] [CrossRef]
- Dyakowski, T.; Edwards, R.B.; Xie, C.G.; Williams, R.A. Application of Capacitance Tomography to Gas-solid Flows. Chem. Eng. Sci. 1997, 52, 2099–2110. [Google Scholar] [CrossRef]
- Cui, Z.Q.; Yang, C.Y.; Sun, B.Y.; Wang, H.X. Liquid Film Thickness Estimation Using Electrical Capacitance Tomography. Meas. Sci. Rev. 2014, 14, 8–15. [Google Scholar] [CrossRef]
- Román, A.; Cronin, J.; Ervin, J.; Byrd, L. Measurement of the Void Fraction and Maximum Dry Angle Using Electrical Capacitance Tomography Applied to a 7 mm Tube with R-134a. Int. J. Refrig. 2018, 95, 122–132. [Google Scholar] [CrossRef]
- Xie, H.J.; Chen, H.; Gao, X.; Zheng, X.D.; Zhi, X.Q.; Zhang, X.B. Theoretical Analysis of Fuzzy Least Squares Support Vector Regression Method for Void Fraction Measurement of Two-phase Flow by Multi-electrode Capacitance Sensor. Cryogenics 2019, 103, 102969. [Google Scholar] [CrossRef]
- Xie, H.J.; Xia, T.; Tian, Z.N.; Zheng, X.D.; Zhang, X.B. A Least Squares Support Vector Regression Coupled Linear Reconstruction Algorithm for ECT. Flow Meas. Instrum. 2021, 77, 101874. [Google Scholar] [CrossRef]
- Xia, T.; Xie, H.J.; Wei, A.B.; Zhou, R.; Qiu, L.M.; Zhang, X.B. Preliminary Study on Three-dimensional Imaging of Cryogenic Two-phase Flow Based on Electrical Capacitance Volume Tomography. Cryogenics 2020, 110, 103127. [Google Scholar] [CrossRef]
- Hunt, A.; Rusli, I.; Schakel, M.; Kenbar, A. High-speed Density Measurement for Lng and Other Cryogenic Fluids Using Electrical Capacitance Tomography. Cryogenics 2021, 113, 103207. [Google Scholar] [CrossRef]
- Sun, S.J.; Zhang, W.B.; Sun, J.T.; Cao, Z.; Xu, L.J.; Yan, Y. Real-Time Imaging and Holdup Measurement of Carbon Dioxide Under CCS Conditions Using Electrical Capacitance Tomography. IEEE Sens. J. 2018, 18, 7551–7559. [Google Scholar] [CrossRef]
- Tian, Z.; Gao, X.; Qiu, L.; Zhang, X. Experimental imaging and algorithm optimization based on deep neural network for electrical capacitance tomography for LN2-VN2 flow. Cryogenics 2022, 127, 103568. [Google Scholar] [CrossRef]
- Gao, X.; Tian, Z.; Qiu, L.; Zhang, X. A hybrid deep learning model for ECT image reconstruction of cryogenic fluids. Flow Meas. Instrum. 2022, 87, 102228. [Google Scholar]
- Xie, C.G.; Huang, S.M.; Hoyle, B.S.; Thorn, R.; Lenn, C.; Snowden, D.; Beck, M.S. Electrical capacitance tomography for flow imaging system model for development of image reconstruction algorithms and design of primary sensors. Proc. G Circuits Devices Syst. 1992, 139, 89–98. [Google Scholar] [CrossRef]
- Yang, W.Q.; Spink, D.M.; York, T.A.; McCann, H. An Image-reconstruction Algorithm Based on Landweber’s Iteration Method for Electrical-capacitance Tomography. Meas. Sci. Technol. 1999, 10, 1065–1069. [Google Scholar] [CrossRef]
- Soleimani, M.; Lionheart, W.R.B. Nonlinear Image Reconstruction for Electrical Capacitance Tomography Using Experimental Data. Meas. Sci. Technol. 2005, 16, 1987–1996. [Google Scholar] [CrossRef]
- Liu, S.; Fu, L.; Yang, W.Q. Optimization of an Iterative Image Reconstruction Algorithm for Electrical Capacitance Tomography. Meas. Technol. 1999, 10, 1970–1980. [Google Scholar] [CrossRef]
- Wang, H.X.; Tang, L.; Cao, Z. An Image Reconstruction Algorithm Based on Total Variation with Adaptive Mesh Refinement for ECT. Flow Meas. Instrum. 2007, 18, 262–267. [Google Scholar] [CrossRef]
- Li, Y.; Yang, W.Q. Image Reconstruction by Nonlinear Landweber Iteration for Complicated Distributions. Meas. Sci. Technol. 2008, 19, 94014. [Google Scholar] [CrossRef]
- Yang, W.Q.; Liu, S. Electrical Capacitance Tomography with Square Sensor. Electron. Lett. 1999, 35, 295–296. [Google Scholar] [CrossRef]
- Xie, H.J.; Yu, L.; Zhou, R.; Qiu, L.M.; Zhang, X.B. Preliminary Evaluation of Cryogenic Two-phase Flow Imaging Using Electrical Capacitance Tomography. Cryogenics 2017, 86, 97–105. [Google Scholar] [CrossRef]
- Cui, Z.Q.; Wang, Q.; Xue, Q.; Fan, W.R.; Zhang, L.L.; Cao, Z.; Sun, B.Y.; Wang, H.X.; Yang, W.Q. A Review on Image Reconstruction Algorithms for Electrical Capacitance/resistance Tomography. Sens. Rev. 2016, 36, 429–445. [Google Scholar] [CrossRef]
- Isaksen, Ø. A Review of Reconstruction Techniques for Capacitance Tomography. Meas. Sci. Technol. 1996, 7, 325–337. [Google Scholar] [CrossRef]
- Liao, A.M.; Zhou, Q.Y. Application of ECT and Relative Change Ratio of Capacitances in Probing Anomalous Objects in Water. Flow Meas. Instrum. 2015, 45, 7–17. [Google Scholar] [CrossRef]
- Yang, W.Q.; Peng, L.H. Image Reconstruction Algorithms for Electrical Capacitance Tomography. Meas. Sci. Technol. 2003, 14, R1–R13. [Google Scholar] [CrossRef]
- Peng, L.H.; Merkus, H.; Scarlett, B. Using Regularization Methods for Image Reconstruction of Electrical Capacitance Tomography. Part. Part. Syst. Charact. 2000, 17, 96–104. [Google Scholar] [CrossRef]
- Yang, Y.J.; Peng, L.H. Data Pattern with ECT Sensor and Its Impact on Image Reconstruction. IEEE Sens. J. 2013, 13, 1582–1593. [Google Scholar] [CrossRef]
- Smits, G.F.; Jordaan, E.M. Improved SVM regression using mixtures of kernels. In Proceedings of the International Joint Conference on Neural Networks, IEEE Xplore, Honolulu, HI, USA, 12–17 May 2002; pp. 2785–2790. [Google Scholar]


| Fluid Pair | Relative Dielectric Permittivity |
|---|---|
| Water/Air (at 300 K) | 77.747/1.0005 |
| Liquid/Vapor nitrogen (at 78 K) | 1.4337/1.0021 |
| Liquid/Vapor oxygen (at 90 K) | 1.4877/1.0016 |
| Liquid/Vapor methane (at 112 K) | 1.6299/1.0020 |
| Parameter | Value | |
|---|---|---|
| Landweber | Iteration number | 5 |
| Landweber coupled LSSVR | Iteration number | 5 |
| 0.9 | ||
| 0.1 | ||
| 2 |
| Fluid Pair | Relative Dielectric Permittivity |
|---|---|
| Polypropylene/Air | 1.6201/1.0005 |
| Mung bean/Air | 5.5728/1.0005 |
| Millet/Air | 5.2995/1.0005 |
| Rice/Air | 6.035/1.0005 |
| VF Error (%) | |||
|---|---|---|---|
| LBP | Landweber | Landweber Coupled LSSVR | |
| Case 1a | 4.815 | 11.278 | 10.885 |
| Case 2a | 3.576 | 2.821 | 0.485 |
| Case 1b | 15.459 | 4.703 | 8.078 |
| Case 2b | 11.509 | 8.652 | 8.961 |
| Case 3b | 0.013 | 4.442 | 3.635 |
| Case 1c | 35.277 | 32.297 | 13.843 |
| Case 2c | 3.272 | 4.127 | 1.506 |
| Case 3c | 1.891 | 5.464 | 0.695 |
| Case 1d | 11.746 | 8.868 | 8.571 |
| Case 2d | 4.802 | 8.570 | 5.822 |
| CC | |||
|---|---|---|---|
| LBP | Landweber | Landweber Coupled LSSVR | |
| Case 1a | 0.898 | 0.895 | 0.901 |
| Case 2a | 0.803 | 0.759 | 0.835 |
| Case 1b | 0.768 | 0.724 | 0.873 |
| Case 2b | 0.917 | 0.904 | 0.888 |
| Case 3b | 0.884 | 0.835 | 0.872 |
| Case 1c | 0.901 | 0.890 | 0.808 |
| Case 2c | 0.914 | 0.883 | 0.896 |
| Case 3c | 0.868 | 0.772 | 0.827 |
| Case 1d | 0.902 | 0.887 | 0.893 |
| Case 2d | 0.882 | 0.879 | 0.895 |
| IE (%) | |||
|---|---|---|---|
| LBP | Landweber | Landweber Coupled LSSVR | |
| Case 1a | 26.681 | 26.813 | 24.225 |
| Case 2a | 50.139 | 56.888 | 42.269 |
| Case 1b | 25.406 | 28.744 | 14.998 |
| Case 2b | 23.552 | 24.839 | 26.365 |
| Case 3b | 35.202 | 42.097 | 42.785 |
| Case 1c | 14.219 | 14.436 | 22.205 |
| Case 2c | 24.774 | 26.699 | 26.810 |
| Case 3c | 42.244 | 55.445 | 46.828 |
| Case 1d | 34.418 | 35.540 | 28.145 |
| Case 2d | 60.383 | 57.993 | 34.736 |
| LBP | Landweber | Landweber Coupled LSSVR | ||
|---|---|---|---|---|
| VF error (%) | Case 1 | 12.831 | 9.979 | 8.478 |
| Case 2 | 26.047 | 15.215 | 14.883 | |
| Case 3 | 22.967 | 21.447 | 21.549 | |
| CC | Case 1 | 0.940 | 0.963 | 0.975 |
| Case 2 | 0.793 | 0.929 | 0.935 | |
| Case 3 | 0.874 | 0.889 | 0.889 | |
| IE (%) | Case 1 | 12.831 | 9.979 | 8.478 |
| Case 2 | 26.047 | 15.215 | 14.883 | |
| Case 3 | 22.967 | 21.447 | 21.549 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Z.-N.; Gao, X.-X.; Xia, T.; Zhang, X.-B. Evaluation of Landweber Coupled Least Square Support Vector Regression Algorithm for Electrical Capacitance Tomography for LN2–VN2 Flow. Energies 2023, 16, 7661. https://doi.org/10.3390/en16227661
Tian Z-N, Gao X-X, Xia T, Zhang X-B. Evaluation of Landweber Coupled Least Square Support Vector Regression Algorithm for Electrical Capacitance Tomography for LN2–VN2 Flow. Energies. 2023; 16(22):7661. https://doi.org/10.3390/en16227661
Chicago/Turabian StyleTian, Ze-Nan, Xin-Xin Gao, Tao Xia, and Xiao-Bin Zhang. 2023. "Evaluation of Landweber Coupled Least Square Support Vector Regression Algorithm for Electrical Capacitance Tomography for LN2–VN2 Flow" Energies 16, no. 22: 7661. https://doi.org/10.3390/en16227661
APA StyleTian, Z.-N., Gao, X.-X., Xia, T., & Zhang, X.-B. (2023). Evaluation of Landweber Coupled Least Square Support Vector Regression Algorithm for Electrical Capacitance Tomography for LN2–VN2 Flow. Energies, 16(22), 7661. https://doi.org/10.3390/en16227661






