Design and Analysis of an Adaptive Dual-Drive Lift–Drag Composite Vertical-Axis Wind Turbine Generator
Abstract
:1. Introduction
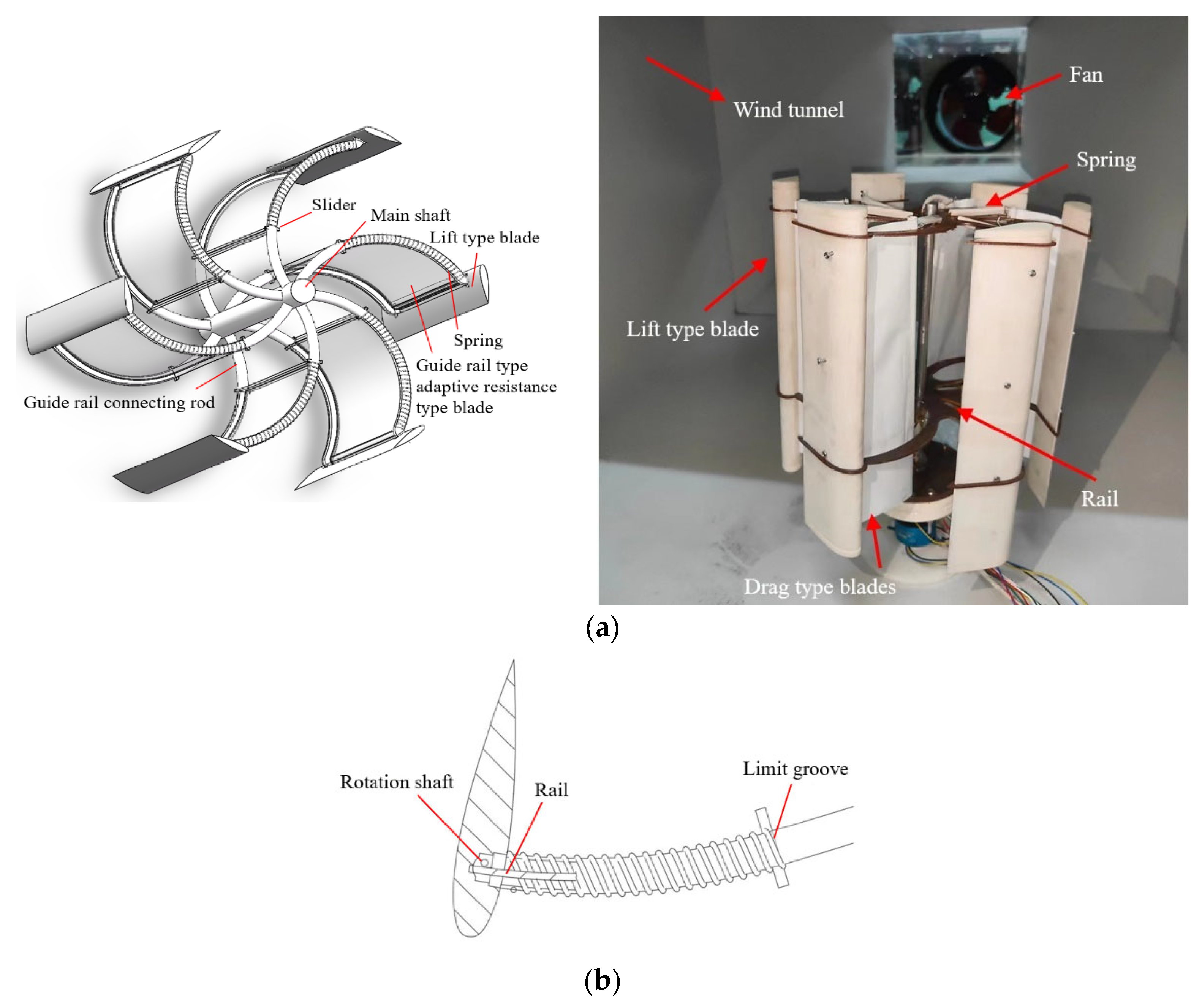
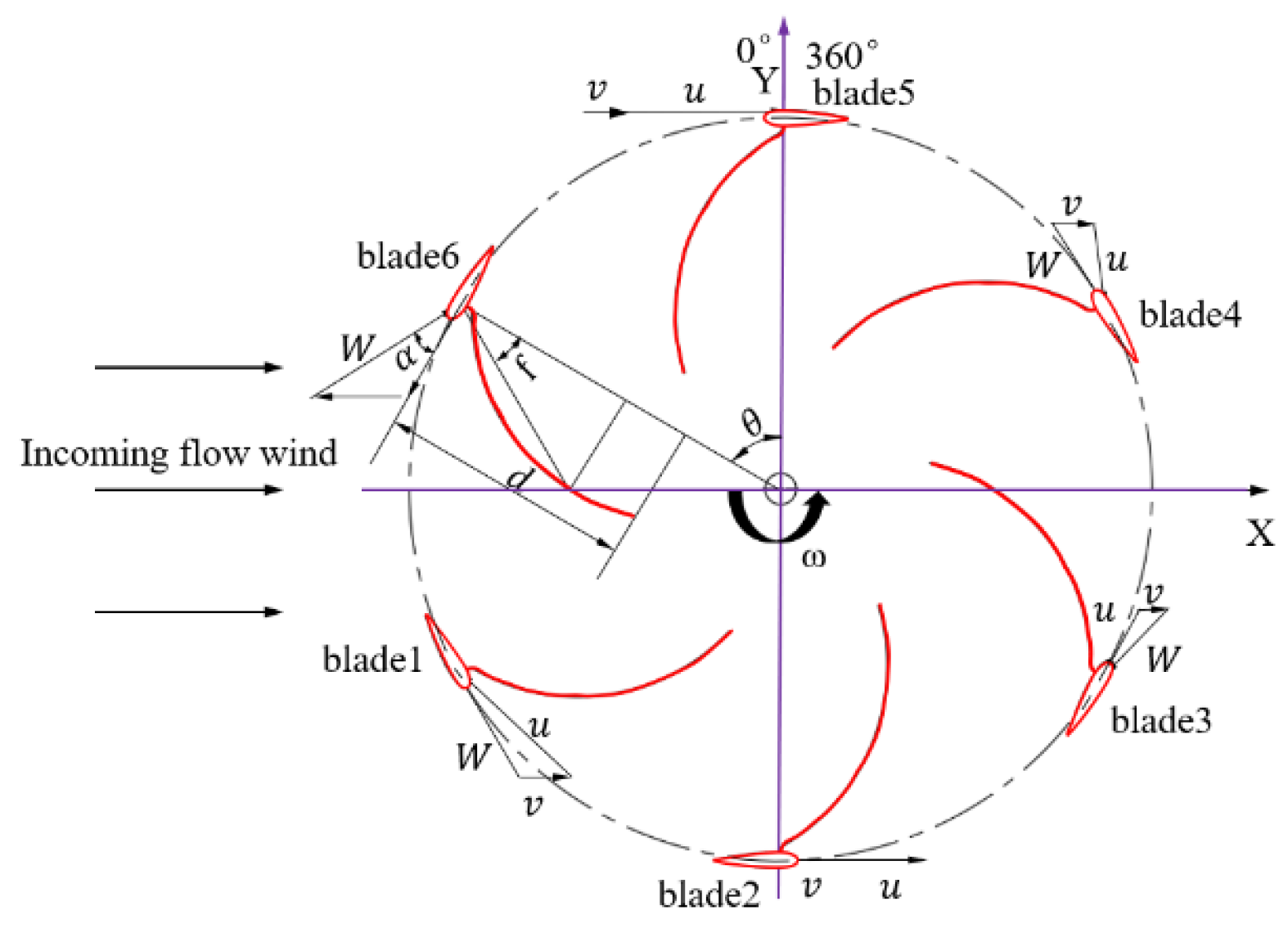
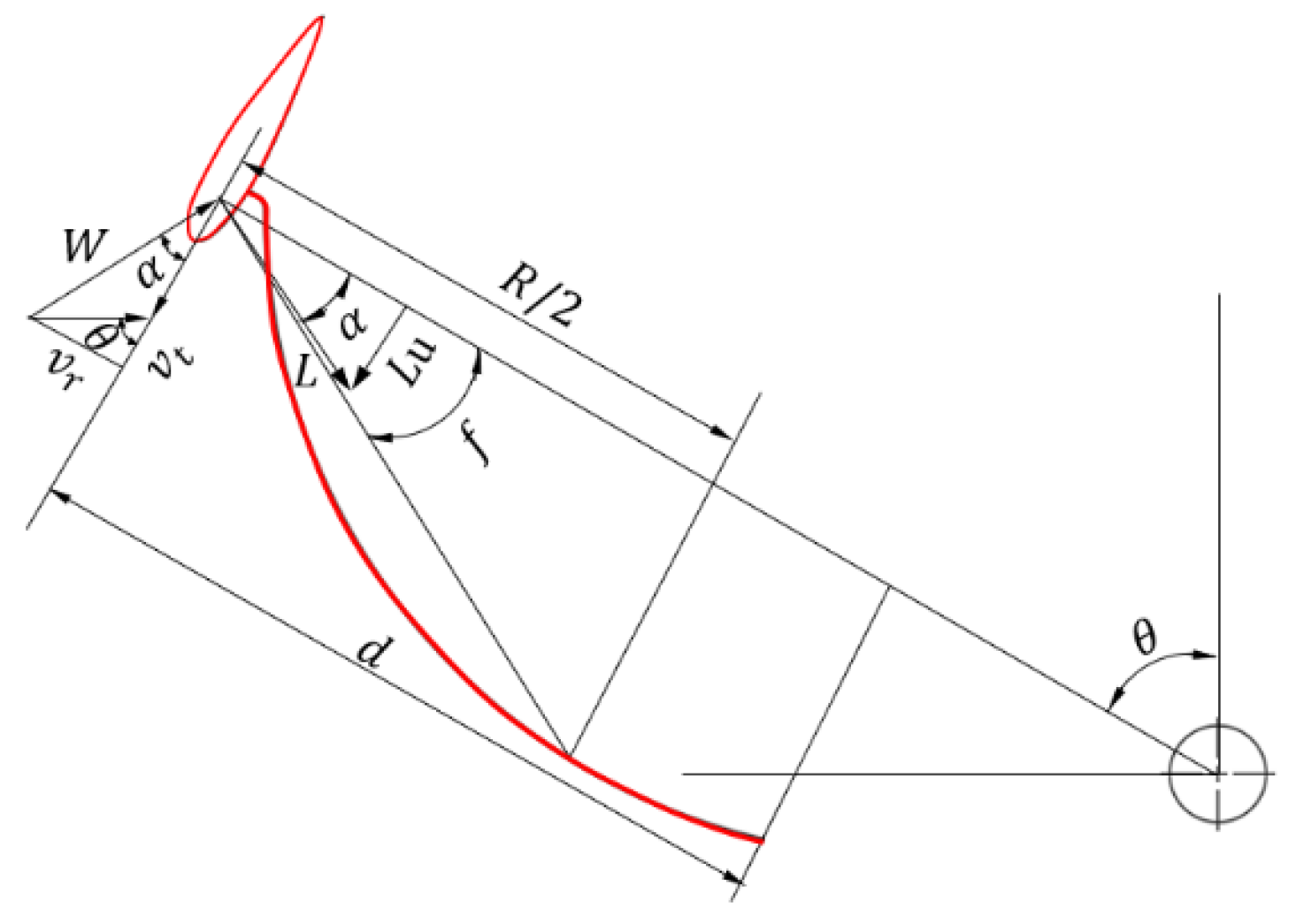
2. Model and Parameter Definitions
3. Numerical Approach
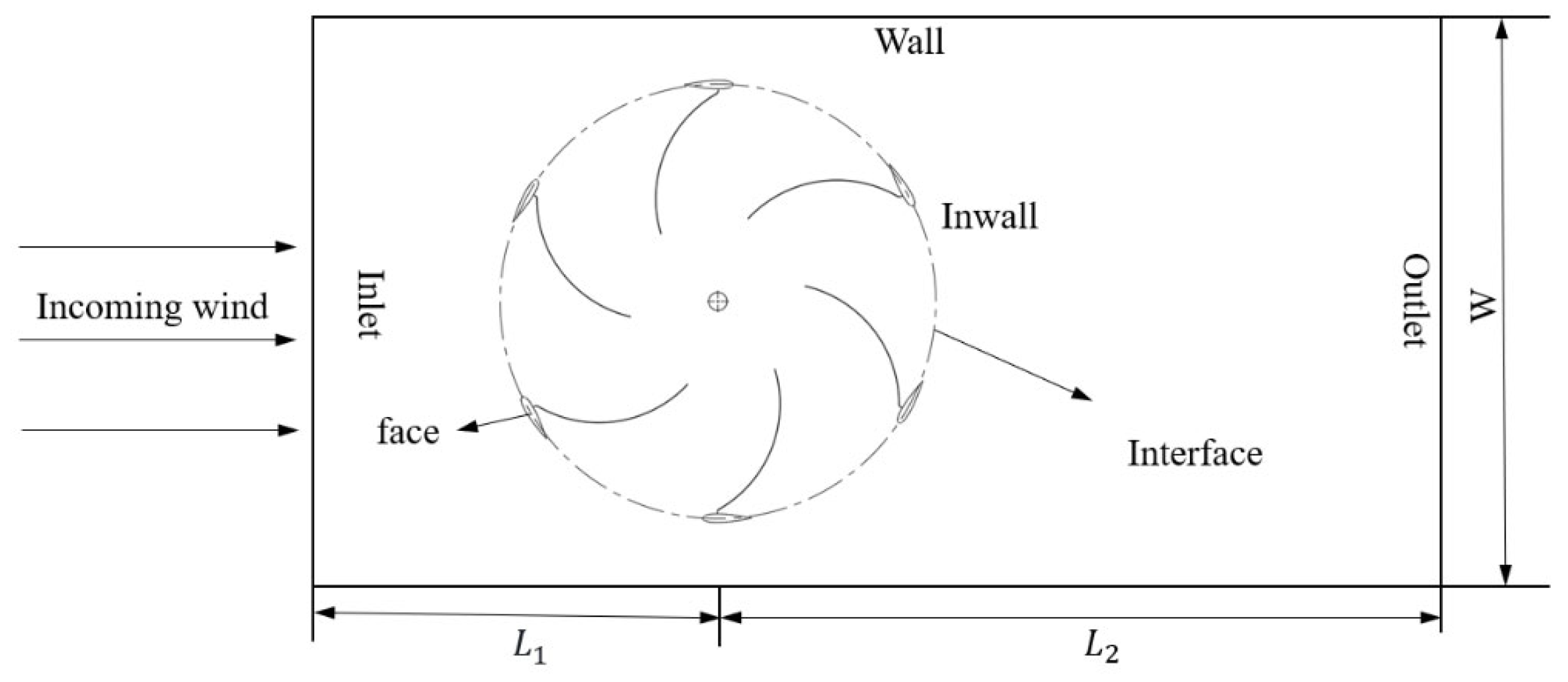
3.1. Mesh
3.2. Boundary Conditions
3.3. Turbulence Model
3.4. Simulation Parameters
4. Results and Discussion
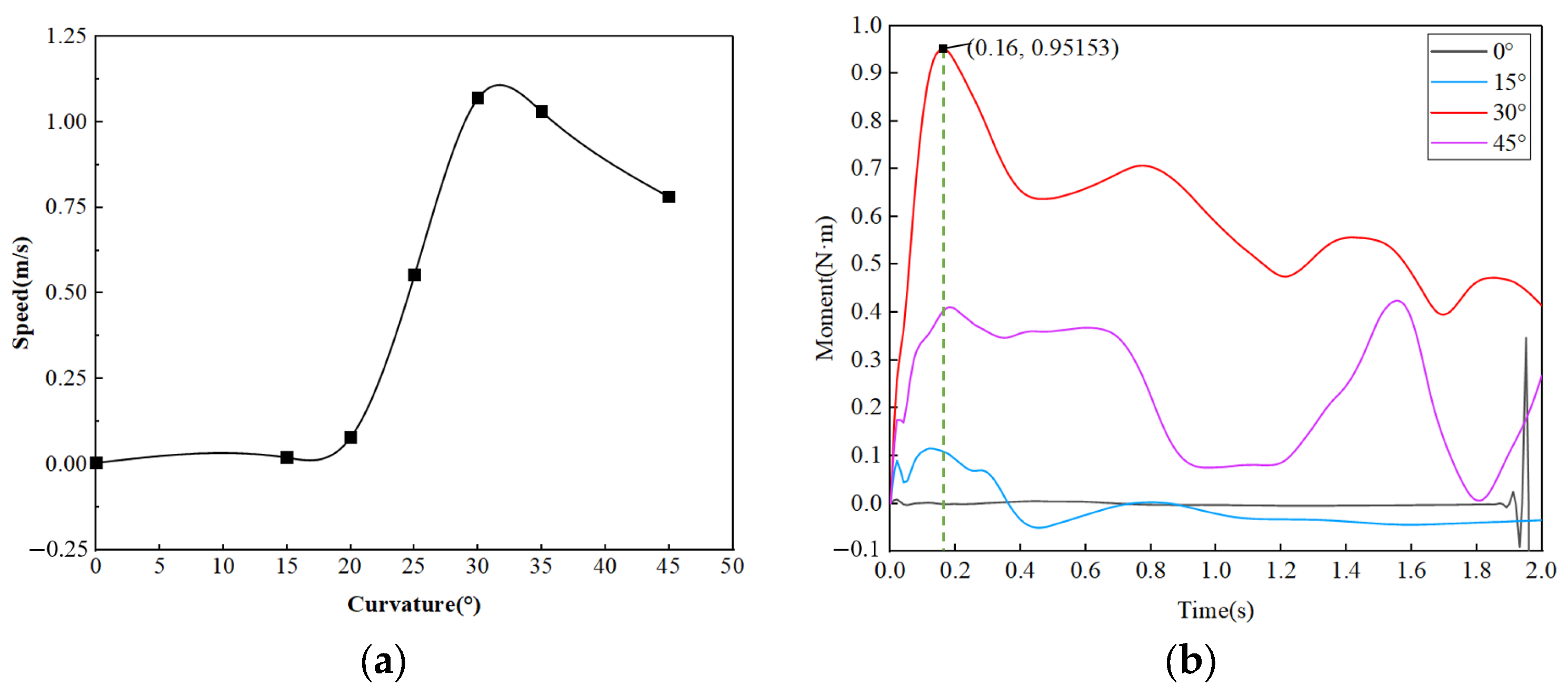
4.1. Exploration of Blade Curvature
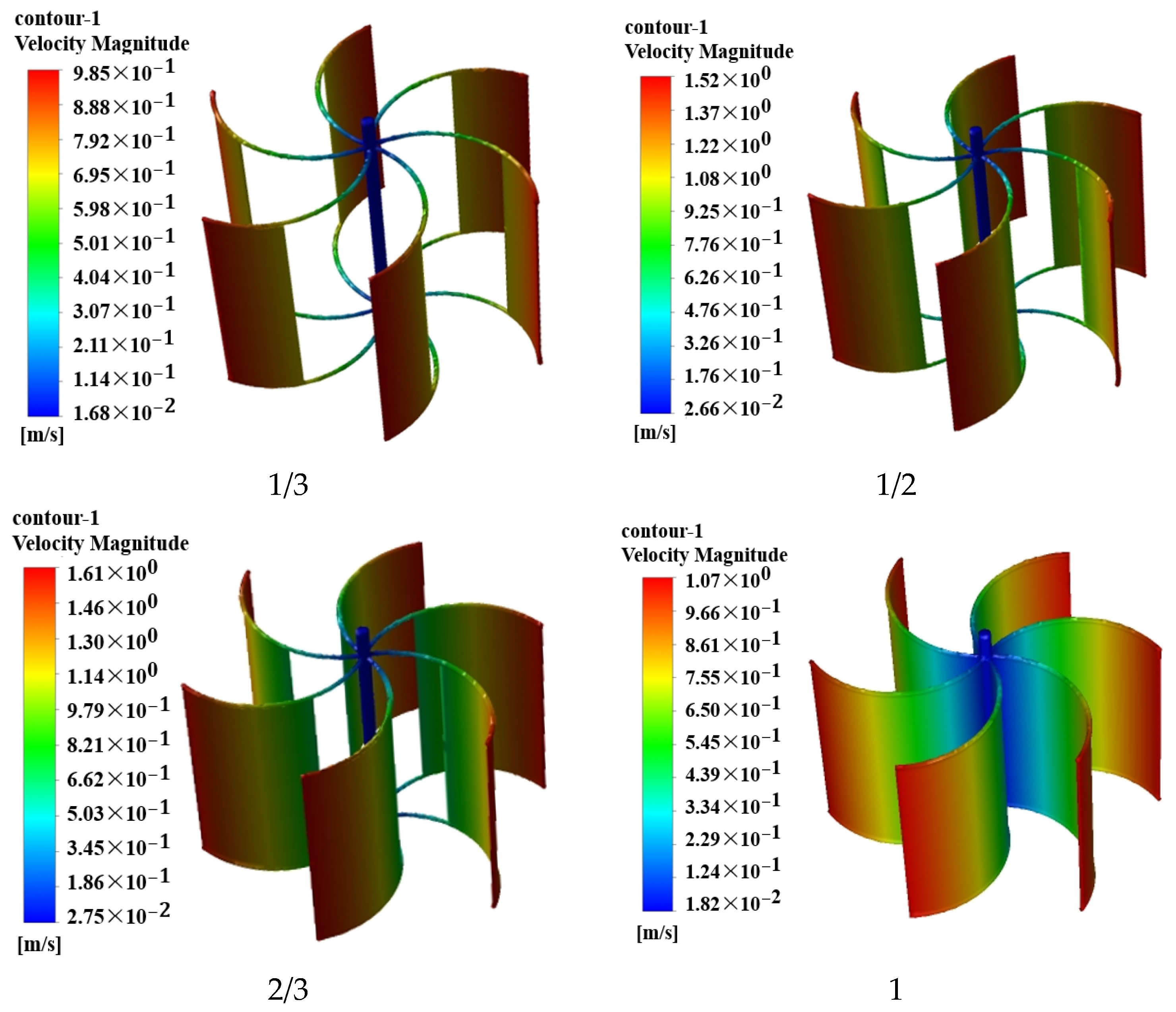
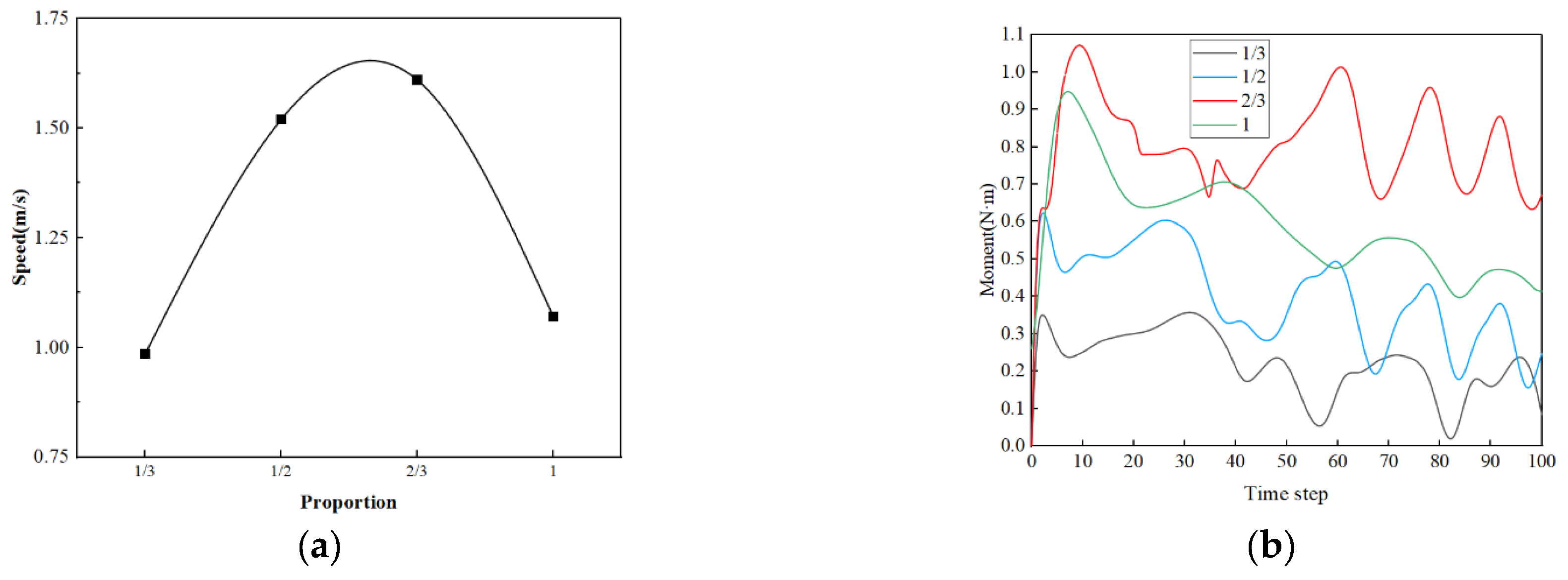
4.2. Exploration of Blade Width
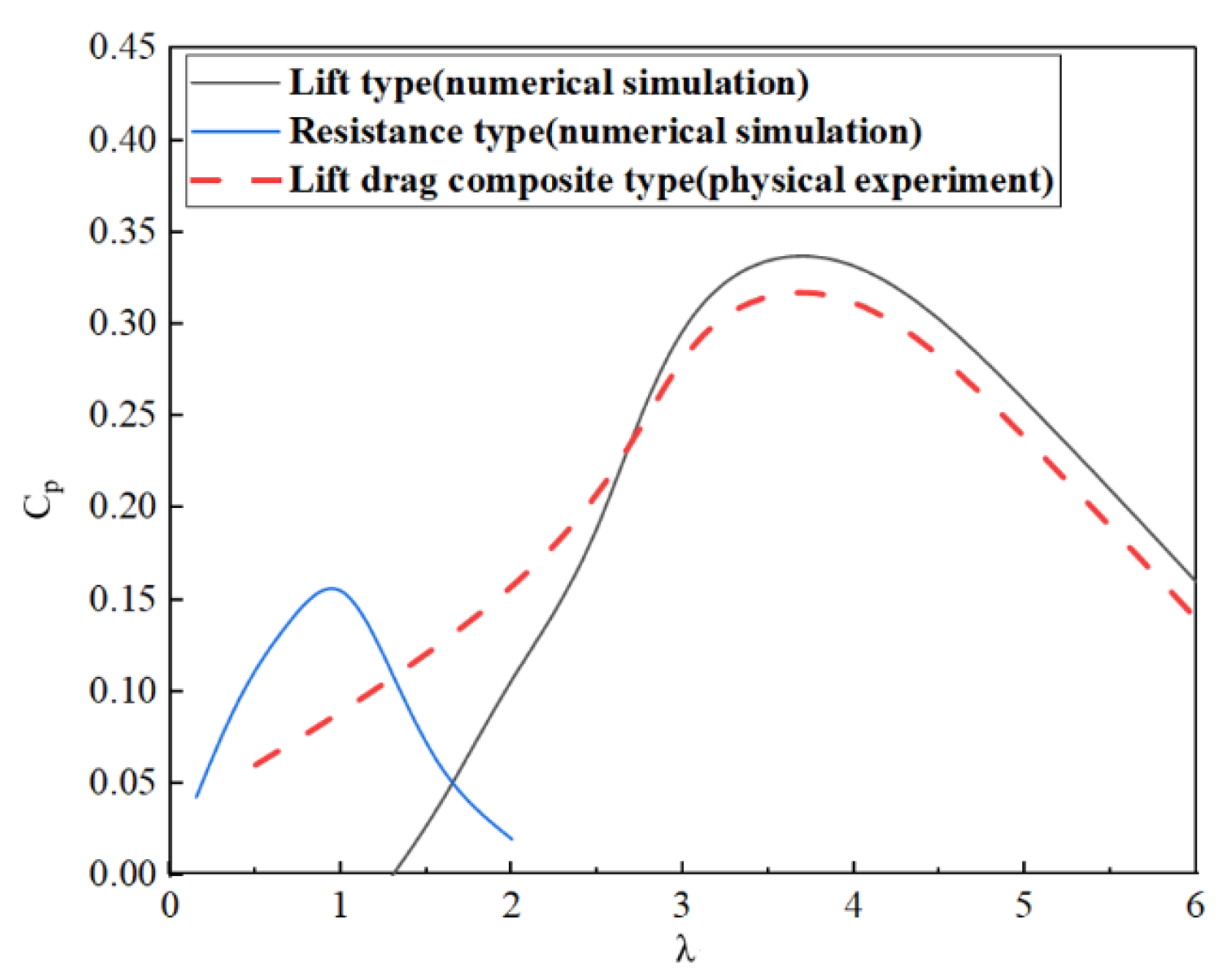
5. Experimental Details
6. Conclusions
- An adaptive double-drive lift–drag composite vertical-axis wind turbine is designed, which mainly includes lift-type and drag-type blades so that the vertical-axis wind turbine can make full use of wind energy, and a design method for the double drive is proposed. In this method, the guide rail adaptive drag-type blade occupies two-thirds of the area between the main axis and the lift-type blade, and the airflow can pass through the hollow part smoothly. It can effectively improve the self-starting ability. The theoretical equation of the lift–drag composite wind turbine is constructed, and the theoretical inference and the design of the adaptive system are completed.
- The finite element model of the lift–drag composite wind turbine is established. The aerodynamic performance analysis of the lift–drag composite wind turbine in Fluent shows that the aerodynamic performance of the lift–drag composite wind turbine is the best when the curvature of the drag blade is 30° and the ratio of the blade width is 2/3.
- The simulation analysis and experimental test showed that the wind turbine can start when the incoming wind is 1.6 m/s, which is 23.8% lower than the existing lift-type wind turbine’s starting wind speed of 2.1 m/s. The comprehensive wind energy utilization of the adaptive double-drive lift–drag composite vertical-axis wind turbine was 5.98% higher than that of the ordinary lift-type wind turbine. At the same time, when the wind speed reaches 8.8 m/s, the drag-type blade completely shrinks and turns into a lift-type wind turbine, which can be applied to wind power generation in high-wind-speed wind farms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahela, O.P.; Gupta, N.; Khosravy, M.; Patel, N. Comprehensive Overview of Low Voltage Ride Through Methods of Grid Integrated Wind Generator. IEEE Access 2019, 7, 99299–99326. [Google Scholar] [CrossRef]
- Valipour, M.; Singh, V.P. Global Experiences on Wastewater Irrigation: Challenges and Prospects. Balanc. Urban Dev. Options Strateg. Liveable Cities 2016, 72, 289–327. [Google Scholar] [CrossRef]
- Sharma, V.; Sharma, G. Recent development in the field of wind turbine. Mater. Today Proc. 2022, 64, 1512–1520. [Google Scholar] [CrossRef]
- Yuyi, Z.; Decai, Z.; Liang, L.; Wenbin, T.; Jun, L. The Design of Vertical Axis Wind Turbine Rotor for Antarctic. Inf. Technol. J. 2013, 12, 604–613. [Google Scholar] [CrossRef]
- Dhote, A.; Bankar, V. Design, analysis and fabrication of savonius vertical axis wind turbine. Int. Res. J. Eng. Technol. 2015, 2, 2048–2054. [Google Scholar]
- Salyers, T.E. Experimental and Numerical Investigation of Aerodynamic Performance for Vertical-Axis Wind Turbine Models with Various Blade Designs. Master’s Thesis, Georgia Southern University, Statesboro, GA, USA, 2016. [Google Scholar]
- Wang, B.; Geoffroy, S.; Bonhomme, M. Urban form study for wind potential development. Environ. Plan. B Urban Anal. City Sci. 2022, 49, 76–91. [Google Scholar] [CrossRef]
- Kumar, R.; Raahemifar, K.; Fung, A.S. A critical review of vertical axis wind turbines for urban applications. Renew. Sustain. Energy Rev. 2018, 89, 281–291. [Google Scholar] [CrossRef]
- Bedon, G.; Antonini, E.G.; De Betta, S.; Castelli, M.R.; Benini, E. Evaluation of the different aerodynamic databases for vertical axis wind turbine simulations(Review). Renew. Sustain. Energy Rev. 2014, 40, 386–399. [Google Scholar] [CrossRef]
- Thakur, N.; Biswas, A.; Kumar, Y.; Basumatary, M. CFD analysis of performance improvement of the Savonius water turbine by using an impinging jet duct design. Chin. J. Chem. Eng. 2019, 27, 794–801. [Google Scholar] [CrossRef]
- Al-Ghriybah, M.; Zulkafli, M.F.; Didane, D.H.; Mohd, S. Review of the recent power augmentation techniques for the savonius wind turbines. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 60, 71–84. [Google Scholar]
- El-Askary, W.A.; Nasef, M.H.; AbdEL-hamid, A.A.; Gad, H.E. Harvesting wind energy for improving performance of Savonius rotor. Wind Eng. Ind. Aerodyn. 2015, 139, 8–15. [Google Scholar] [CrossRef]
- Mosbahi, M.; Ayadi, A.; Chouaibi, Y.; Driss, Z.; Tucciarelli, T. Performance study of a Helical Savonius hydrokinetic turbine with a new deflector system design. Energy Convers. Manag. 2019, 194, 55–74. [Google Scholar] [CrossRef]
- Bhayo, B.A.; Al-Kayiem, H.H. Experimental characterization and comparison of performance parameters of S-rotors for standalone wind power system. Energy 2017, 138, 752–763. [Google Scholar] [CrossRef]
- Gharaati, M.; Xiao, S.; Wei, N.J.; Martínez-Tossas, L.A.; Dabiri, J.O.; Yang, D. Large Eddy Simulation of Helical- and Straight-Bladed Vertical Axis Wind Turbines in Boundary Layer Turbulence. J. Renew. Sustain. Energy 2022, 14, 053301. [Google Scholar] [CrossRef]
- Zamani, M.; Nazari, S.; Moshizi, S.A.; Maghrebi, M.J. Three dimensional simulation of J-shaped Darrieus vertical axis wind turbine. Energy 2016, 116, 1243–1255. [Google Scholar] [CrossRef]
- Mahdi, Z.; Mohammad Javad, M.; Seyed Rasoul, V. Starting torque improvement using J-shaped straight-bladed Darrieus vertical axis wind turbine by means of numerical simulation. Renew. Energy 2016, 95, 109–126. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, X.; Dong, X.; Zhu, B.; Huang, D.; Zheng, Z. Numerical investigation on aerodynamic performance of a novel vertical axis wind turbine with adaptive blades. Energy Convers. Manag. 2016, 108, 275–286. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.; Yang, M.; Xu, H. The effect of the opening ratio and location on the performance of a novel vertical axis Darrieus turbine. Energy 2015, 89, 819–834. [Google Scholar] [CrossRef]
- Sengupta, A.R.; Biswas, A.; Gupta, R. Comparison of low wind speed aerodynamics of unsymmetrical blade H-Darrieus rotors-blade camber and curvature signatures for performance improvement. Renew. Energy Int. J. 2019, 139, 1412–1427. [Google Scholar] [CrossRef]
- Sun, X.; Chen, Y.; Cao, Y.; Wu, G.; Zheng, Z.; Huang, D. Research on the aerodynamic characteristics of a lift drag hybrid vertical axis wind turbine. Adv. Mech. Eng. (Sage Publ. Inc.) 2016, 8, 1. [Google Scholar] [CrossRef]
- Hosseini, A.; Goudarzi, N. Design and CFD study of a hybrid vertical-axis wind turbine by employing a combined Bach-type and H-Darrieus rotor systems. Energy Convers. Manag. 2019, 189, 49–59. [Google Scholar] [CrossRef]
- Feng, F.; Tong, G.; Ma, Y.; Li, Y. Numerical Simulation and Wind Tunnel Investigation on Static Characteristics of VAWT Rotor Starter with Lift-Drag Combined Structure. Energies 2021, 14, 6167. [Google Scholar] [CrossRef]
- Islam, M.; Ting, D.S.-K.; Fartaj, A. Aerodynamic models for Darrieus-type straight-bladed vertical axis wind turbines. Renew. Sustain. Energy Rev. 2008, 12, 1087–1109. [Google Scholar] [CrossRef]
- Aihara, A.; Mendoza, V.; Goude, A.; Bernhoff, H. A numerical study of strut and tower influence on the performance of vertical axis wind turbines using computational fluid dynamics simulation. Wind Energy 2022, 25, 897–913. [Google Scholar] [CrossRef]
- Ge, M.; Ke, W.; Chen, H. Pitch control strategy before the rated power for variable speed wind turbines at high altitudes. J. Hydrodyn. 2019, 31, 379–388. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, Y.; Zhang, A.; Hu, C.; Liu, S.; Li, Z. Hydrodynamic performance of vertical axis hydrokinetic turbine based on Taguchi method. Renewable Energy 2022, 186, 573–584. [Google Scholar] [CrossRef]
- Celik, Y.; Ingham, D.; Ma, L.; Pourkashanian, M. Design and aerodynamic performance analyses of the self-starting H-type VAWT having J-shaped aerofoils considering various design parameters using CFD. Energy 2022, 251, 123881. [Google Scholar] [CrossRef]
- Tian, W.; Mao, Z.; Zhang, B.; Li, Y. Shape optimization of a Savonius wind rotor with different convex and concave sides. Renew. Energy: Int. J. 2018, 117, 287–299. [Google Scholar] [CrossRef]
- Pope, K.; Naterer, G.F.; Dincer, I.; Tsang, E. Power correlation for vertical axis wind turbines with varying geometries. Int. J. Energy Res. 2011, 35, 423–435. [Google Scholar] [CrossRef]
- Xu, Y.L.; Peng, Y.X.; Zhan, S. Optimal blade pitch function and control device for high-solidity straight-bladed vertical axis wind turbines. Appl. Energy 2019, 242, 1613–1625. [Google Scholar] [CrossRef]
- Zhu, H.T.; Hao, W.X.; Li, C.; Ding, Q.W. Numerical study of effect of solidity on vertical axis wind turbine with Gurney flap. J. Wind Eng. Ind. Aerodyn. 2019, 186, 17–31. [Google Scholar] [CrossRef]
- Sagharichi, A.; Zamani, M.; Ghasemi, A. Effect of solidity on the performance of variable_pitch vertical axis wind turbine. Energy 2018, 161, 753–775. [Google Scholar] [CrossRef]
- Xiang, B.; Miao, W.; Li, C.; Ni, L. Effect of Blade Solidity on Wind Field Aerodynamic Characteristics in Vertical Axis Wind Turbine Group. Therm. Power Eng. 2020, 11, 135–142. [Google Scholar] [CrossRef]
- Qu, J.; Liu, R.; Qu, P.; Yin, W.; Zhao, Y. Effects of combination of blade number and chord length on performance of vertical axis wind turbine. Renew. Energy 2017, 5, 734–739. [Google Scholar] [CrossRef]
- Li, Y.; Tong, G.; Qu, C.; Feng, F. Numerical simulation of aerodynamic characteristics of straight-bladed vertical axis wind turbine with large solidities. J. Drain. Irrig. Mach. Eng. 2022, 7, 701–706. [Google Scholar]
- Chen, Y.; Fu, X.; Zhang, J.; Star, O.; Wu, C.; Zhao, R. Effect of Solidity on the Performance of a Vertical Axis Wind Turbine byNumerical Simulation Analysis. New Energy Prog. 2017, 6, 409–416. [Google Scholar] [CrossRef]


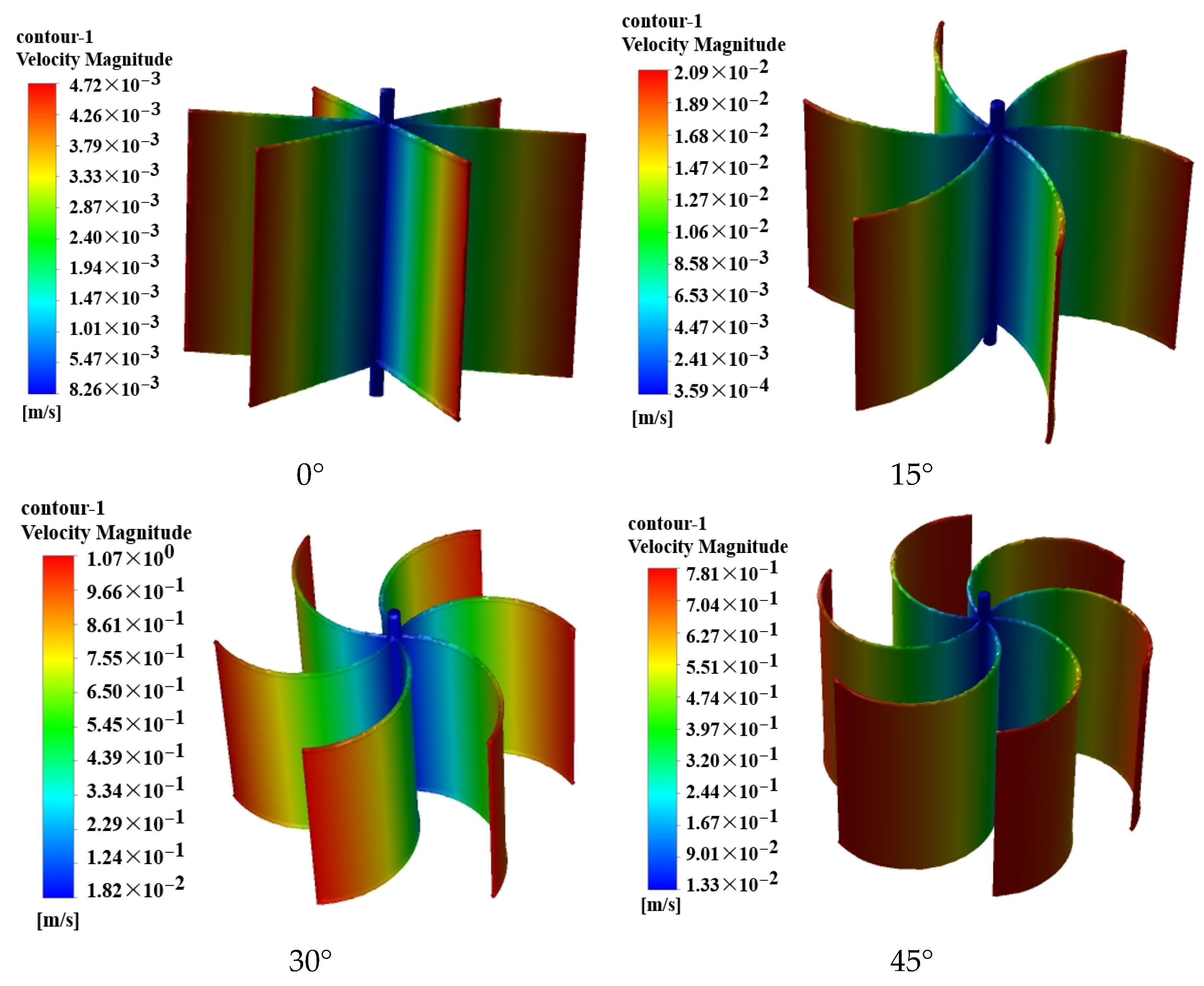




| Parameter | Numerical Value |
|---|---|
| Chord length c/mm | 40 |
| Radius R/mm | 340 |
| Height H/mm | 580 |
| Number of blades/pieces | 6 |
| Curvature parameter/° | 0°, 15°, 30°, 45° |
| Name | Diameter | Length | Square-Mouth Edge Length | |
|---|---|---|---|---|
| Soft connection | 420 | 350 | - | |
| Round to square | - | 400 | 350 | |
| Test section | - | 600 | 350 | |
| Gradual expansion section | Small end | - | 500 | 350 |
| Big end | 900 | |||
| Settling chamber | - | 900 | 900 | |
| Name | Parameter | Name | Parameter |
|---|---|---|---|
| Generator model | NE-50 WS | Rated voltage/V | 12 |
| Rated power/W | 50 | Rated speed/rpm | 750 |
| Starting torque/N·m | >0.15 | Weight/kg | 1.5 |
| Working temperature rise/°C | <70 | Insulation level | H |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, P.; Li, Y.; Gao, Q.; Lian, S.; Wu, Q. Design and Analysis of an Adaptive Dual-Drive Lift–Drag Composite Vertical-Axis Wind Turbine Generator. Energies 2023, 16, 7529. https://doi.org/10.3390/en16227529
Yan P, Li Y, Gao Q, Lian S, Wu Q. Design and Analysis of an Adaptive Dual-Drive Lift–Drag Composite Vertical-Axis Wind Turbine Generator. Energies. 2023; 16(22):7529. https://doi.org/10.3390/en16227529
Chicago/Turabian StyleYan, Pengfei, Yaning Li, Qiang Gao, Shuai Lian, and Qihui Wu. 2023. "Design and Analysis of an Adaptive Dual-Drive Lift–Drag Composite Vertical-Axis Wind Turbine Generator" Energies 16, no. 22: 7529. https://doi.org/10.3390/en16227529
APA StyleYan, P., Li, Y., Gao, Q., Lian, S., & Wu, Q. (2023). Design and Analysis of an Adaptive Dual-Drive Lift–Drag Composite Vertical-Axis Wind Turbine Generator. Energies, 16(22), 7529. https://doi.org/10.3390/en16227529








