Heat and Mass Transfer Processes and Evaporation of a Liquid Droplet on a Structured Surface
Abstract
:1. Introduction
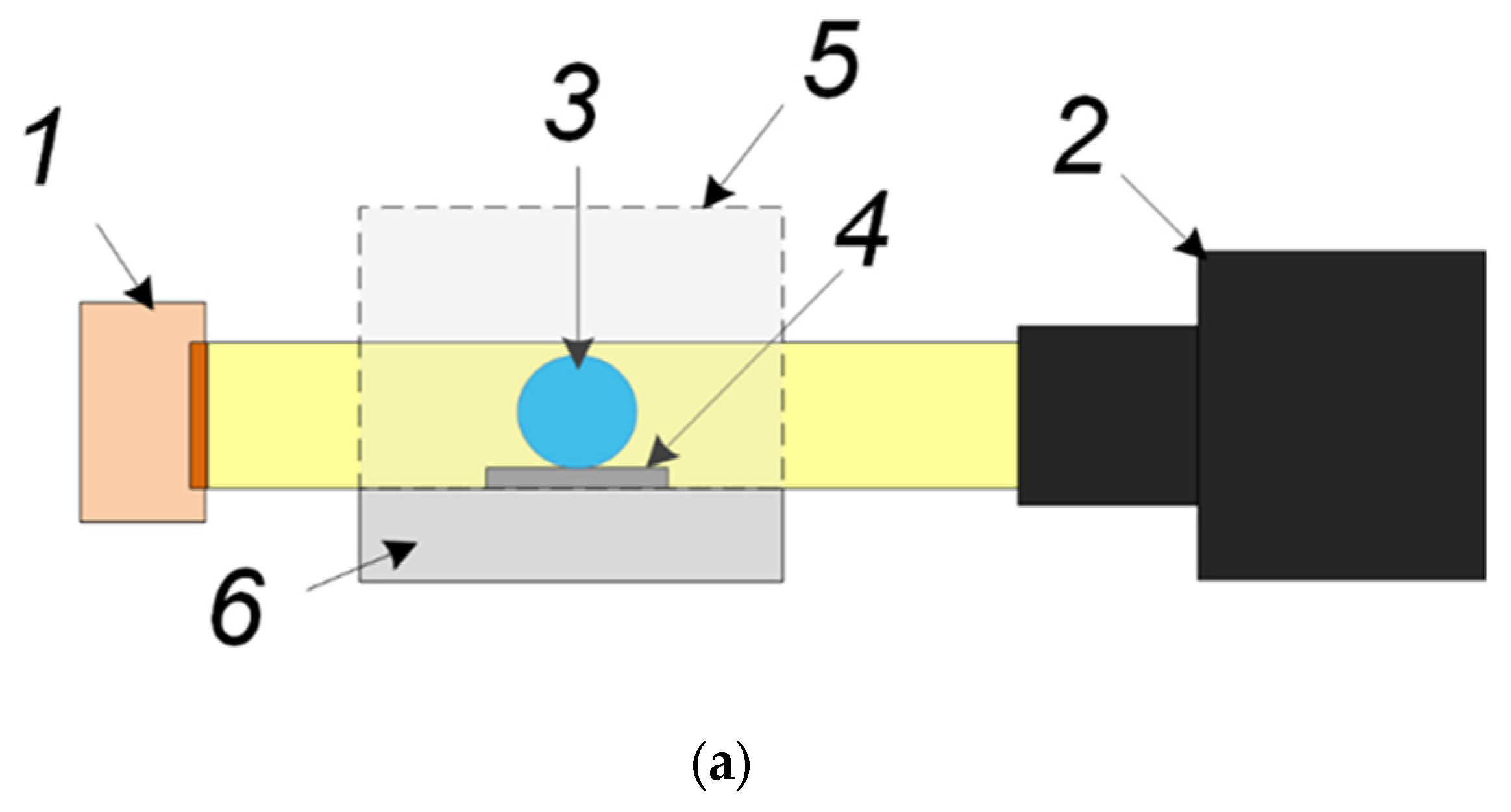
2. Experimental Research
2.1. Materials
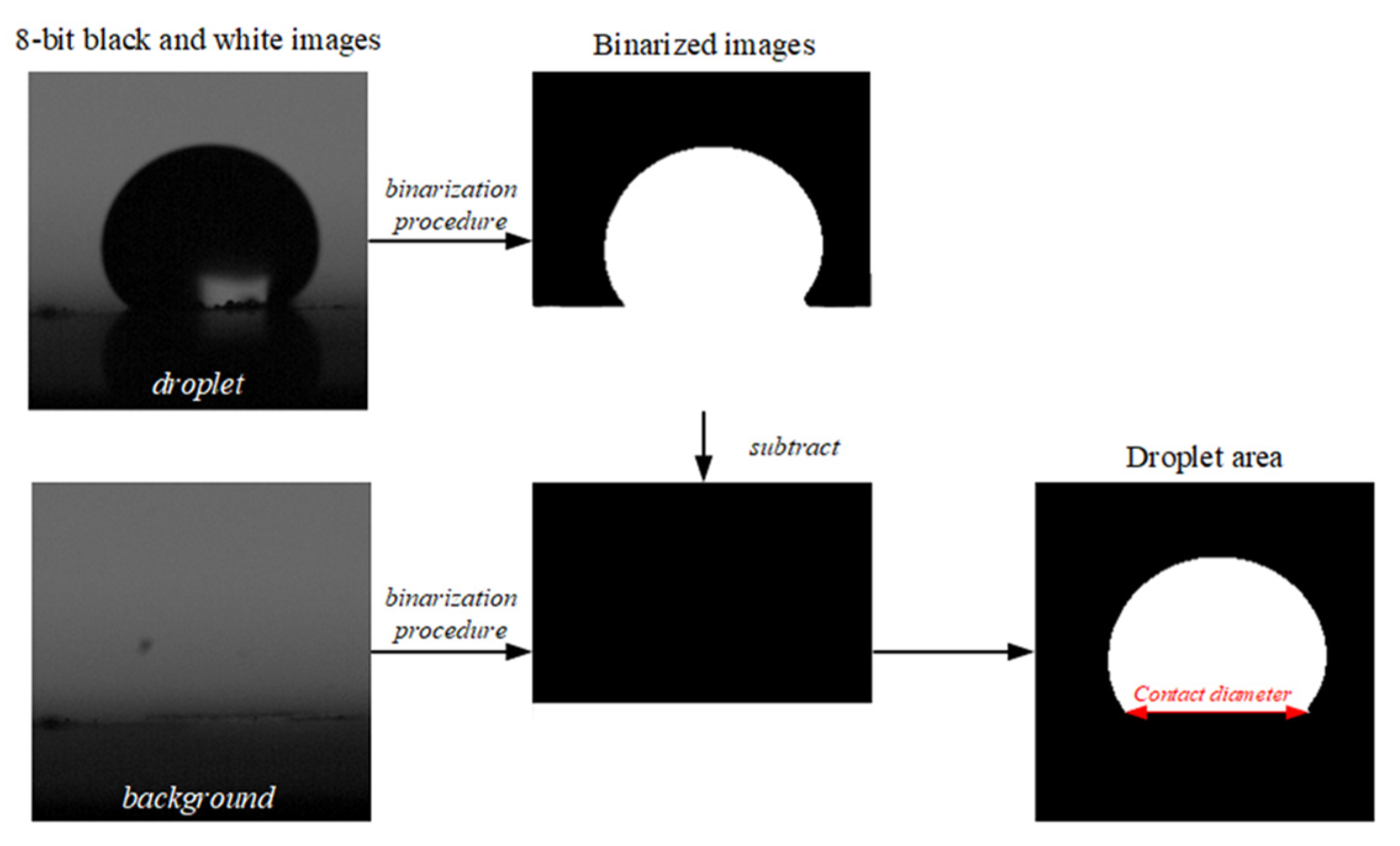
2.2. Experimental Technique
3. Physical and Mathematical Model
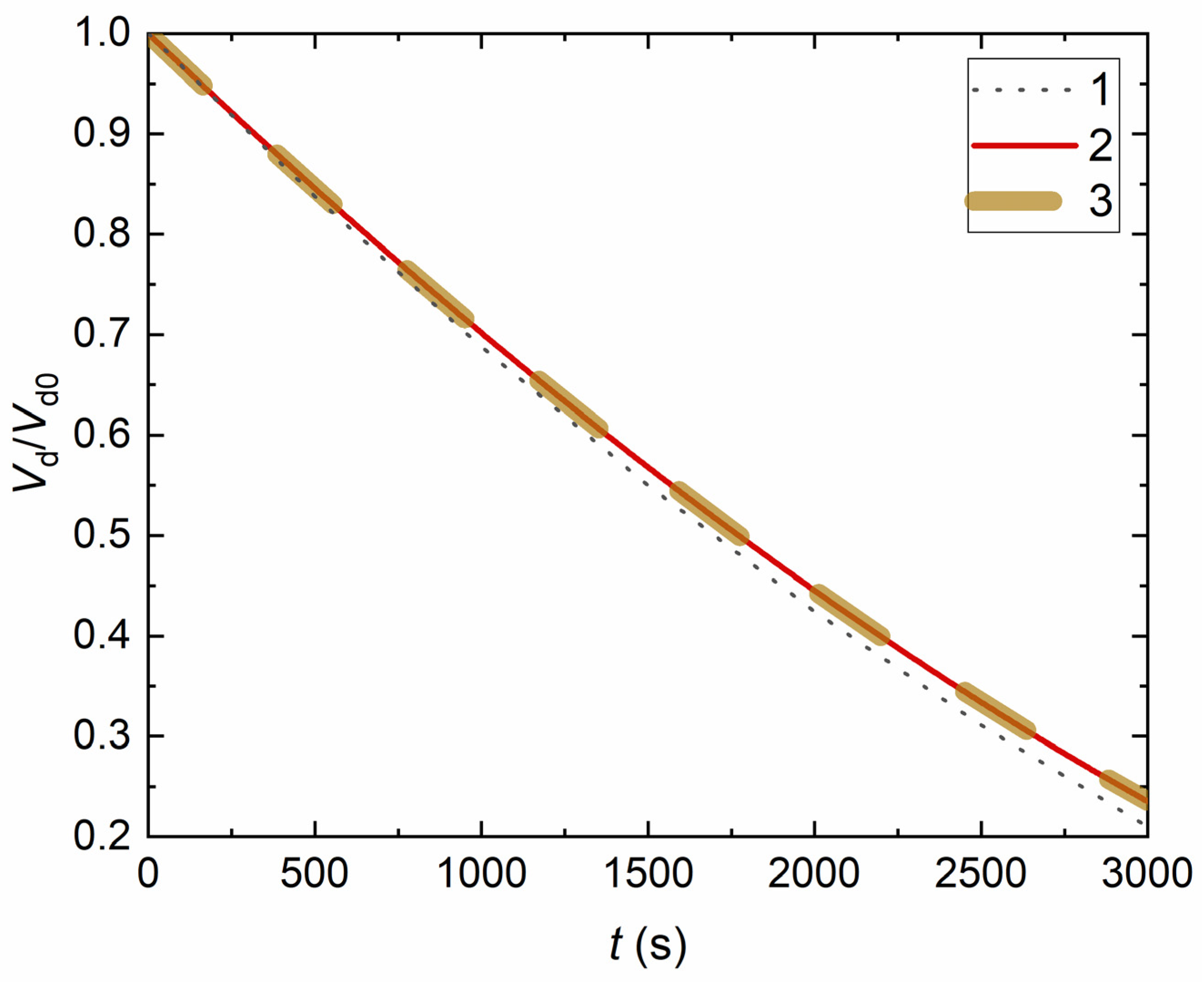
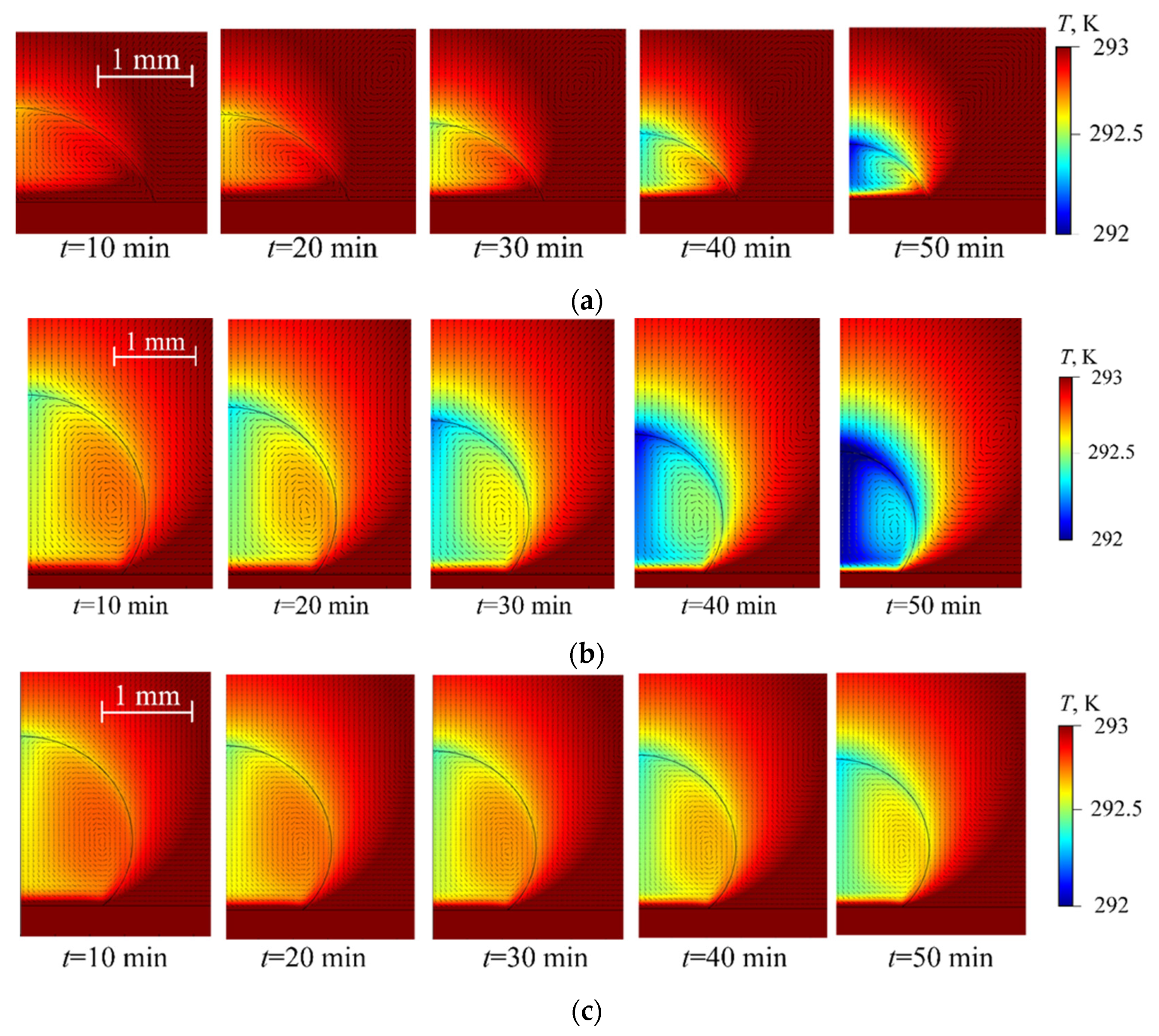
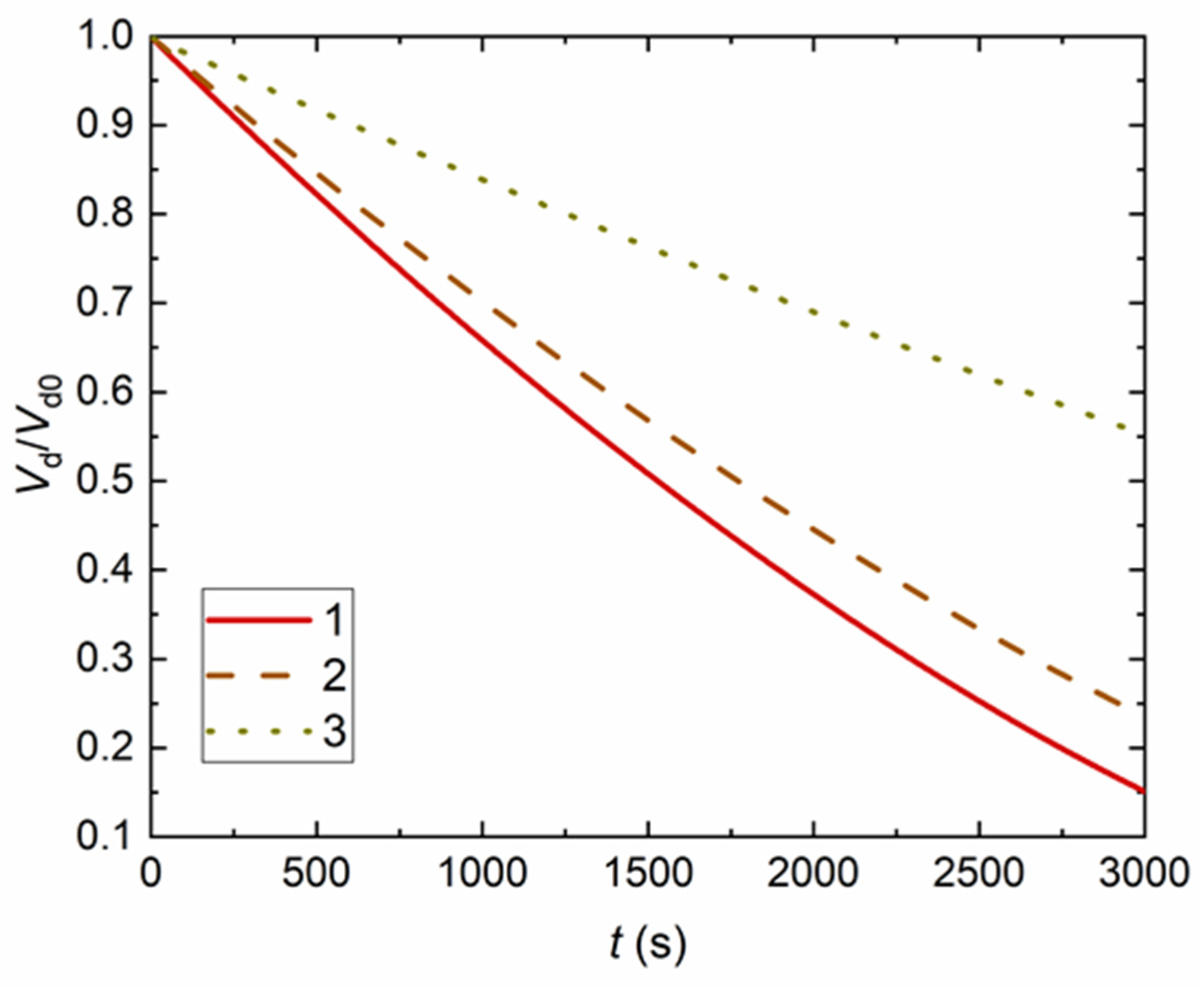
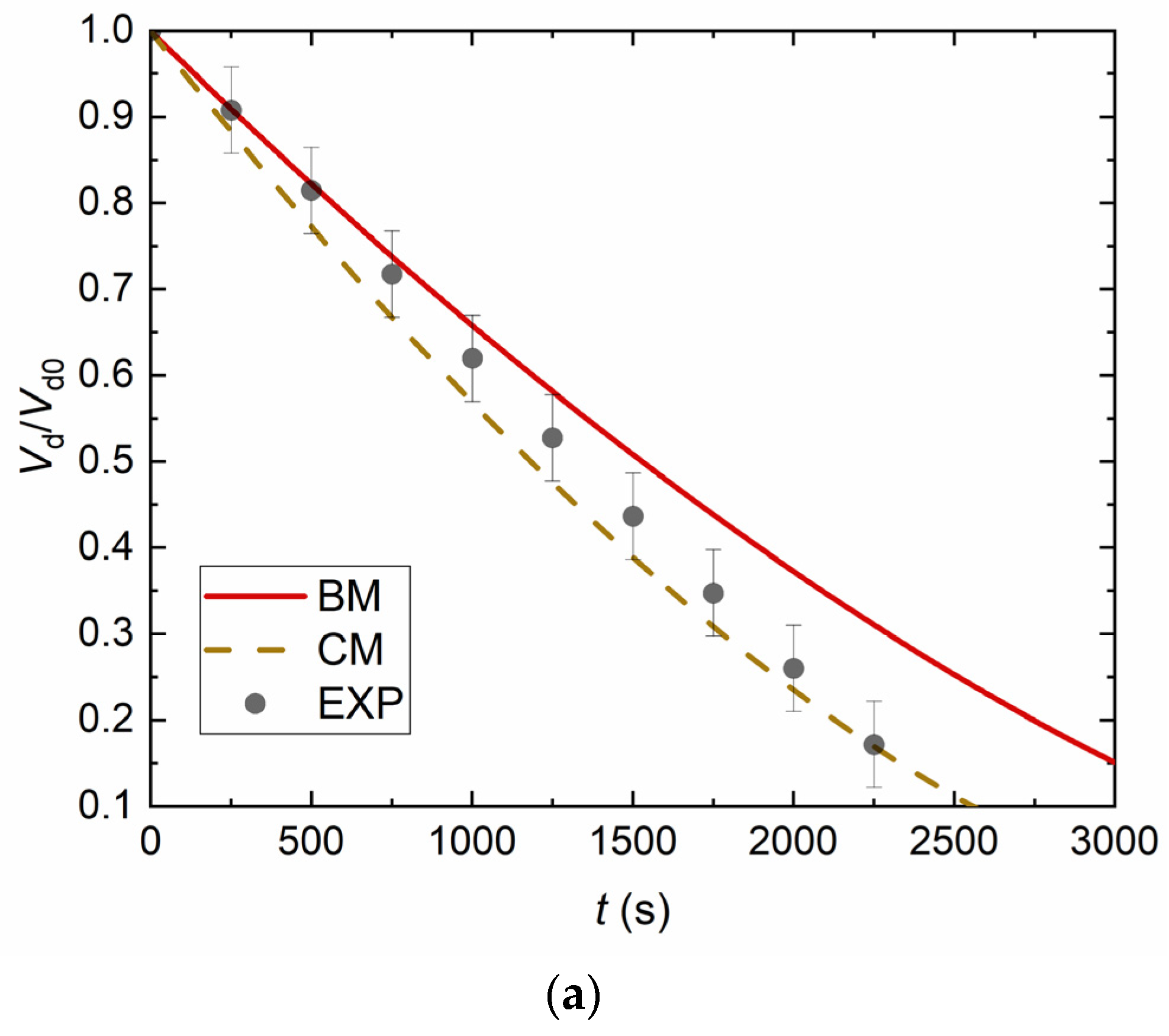
4. Experimental Data vs. Modeling and Discussion
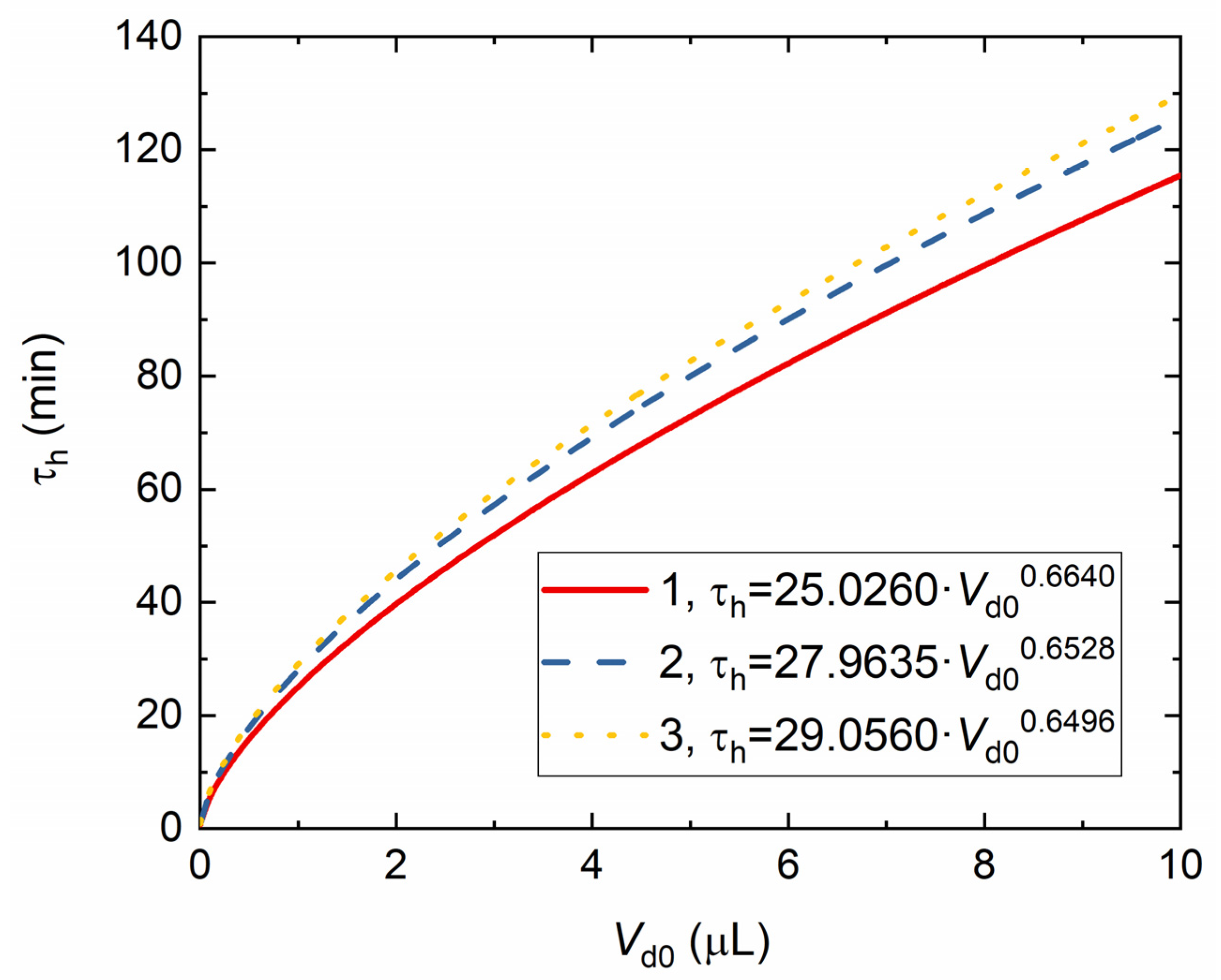
5. Practical Importance and Applications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| C | Heat capacity, J/(kg·K) |
| c | Molar volume concentration of water vapor, mole/m3 |
| W | Water vapor diffusion coefficient, m2/s |
| Fst | Surface tension force, N |
| g | Gravitational constant, m/s2 |
| h | Heat transfer coefficient, W/(m2·K) |
| Mass evaporation rate, kg/(m2·s) | |
| k | Thermal conductivity, W/(m·K) |
| Ld | Vaporization heat of water, J/kg |
| M | Molar mass of water, kg/mol |
| n | Normal vector to the droplet surface |
| Saturation vapor pressure, Pa | |
| p | Pressure, Pa |
| Evaporation rate, m/s | |
| r, z | Labels of axes, m |
| S | Root squared deviation |
| T | Temperature, K |
| u, w | Velocity projections along the r and z axes, m/s |
| Y | Mass concentration |
| Ysat | Mass concentration of water vapors under saturation conditions |
| Greek | |
| κ | Thermal diffusivity, m2/s |
| µ | Dynamic viscosity, Pa·s |
| ρ | Fluid density in the cell, kg/m3 |
| σ | Surface tension of water, N/m |
| Φ | Dissipative function, 1/s2 |
| Index | |
| 0 | Initial conditions |
| 1 | Water |
| 2 | Air |
| d | Droplet |
| eff | Effective |
| g | Gas |
| i | Number of material |
| l | Liquid |
| ref | Reference value |
| v | Vapor |
References
- de Lara, L.R.; Jagdheesh, R.; Ocaña, J.L. Corrosion Resistance of Laser Patterned Ultrahydrophobic Aluminium Surface. Mater. Lett. 2016, 184, 100–103. [Google Scholar] [CrossRef]
- Blanken, N.; Saleem, M.S.; Thoraval, M.J.; Antonini, C. Impact of Compound Drops: A Perspective. Curr. Opin. Colloid Interface Sci. 2021, 51, 101389. [Google Scholar] [CrossRef]
- Kumar, S.S.; Hiremath, S.S. Effect of Surface Roughness and Surface Topography on Wettability of Machined Biomaterials Using Flexible Viscoelastic Polymer Abrasive Media. Surf. Topogr. Metrol. Prop. 2019, 7, 015004. [Google Scholar] [CrossRef]
- Shahidzadeh, N.; Schut, M.F.L.; Desarnaud, J.; Prat, M.; Bonn, D. Salt Stains from Evaporating Droplets. Sci. Rep. 2015, 5, 10335. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Xu, E.; Wu, G.; Li, H.Z. Drop Impact on Superhydrophobic Surface with Protrusions. Chem. Eng. Sci. 2020, 212, 115351. [Google Scholar] [CrossRef]
- Guo, C.; Sun, Y.; Zhao, D. Experimental Study of Droplet Impact on Superheated Cylindrical Surfaces. Exp. Therm. Fluid Sci. 2021, 121, 110263. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, W.; Wang, J.; Liu, C.; Yuan, M. Numerical Investigation on Heat Transfer Enhancement and Surface Temperature Non-Uniformity Improvement of Spray Cooling. Int. J. Therm. Sci. 2022, 173, 107374. [Google Scholar] [CrossRef]
- Kleinhans, U.; Wieland, C.; Frandsen, F.J.; Spliethoff, H. Ash Formation and Deposition in Coal and Biomass Fired Combustion Systems: Progress and Challenges in the Field of Ash Particle Sticking and Rebound Behavior. Prog. Energy Combust. Sci. 2018, 68, 65–168. [Google Scholar] [CrossRef]
- Charpentier, T.V.J.; Neville, A.; Millner, P.; Hewson, R.W.; Morina, A. Development of Anti-Icing Materials by Chemical Tailoring of Hydrophobic Textured Metallic Surfaces. J. Colloid Interface Sci. 2013, 394, 539–544. [Google Scholar] [CrossRef]
- Cheng, W.L.; Zhang, W.W.; Chen, H.; Hu, L. Spray Cooling and Flash Evaporation Cooling: The Current Development and Application. Renew. Sustain. Energy Rev. 2016, 55, 614–628. [Google Scholar] [CrossRef]
- Khodaei, M.; Shadmani, S. Superhydrophobicity on Aluminum through Reactive-Etching and TEOS/GPTMS/Nano-Al2O3 Silane-Based Nanocomposite Coating. Surf. Coat. Technol. 2019, 374, 1078–1090. [Google Scholar] [CrossRef]
- Jain, A.; Kumari, N.; Jagadevan, S.; Bajpai, V. Surface Properties and Bacterial Behavior of Micro Conical Dimple Textured Ti6Al4V Surface through Micro-Milling. Surf. Interfaces 2020, 21, 100714. [Google Scholar] [CrossRef]
- Zaferani, S.H.; Peikari, M.; Zaarei, D.; Danaee, I.; Fakhraei, J.M.; Mohammadi, M. Using Silane Films to Produce an Alternative for Chromate Conversion Coatings. Corrosion 2013, 69, 372–387. [Google Scholar] [CrossRef]
- Liu, H.; Tang, Y.; Xie, Y.; Lu, L.; Wan, Z.; Tang, W.; Yang, L.; Yang, D. Effect of Pulsed Nd: YAG Laser Processing Parameters on Surface Properties of Polyimide Films. Surf. Coat. Technol. 2019, 361, 102–111. [Google Scholar] [CrossRef]
- Yarin, A.L. Drop Impact Dynamics: Splashing, Spreading, Receding, Bouncing… Annu. Rev. Fluid Mech. 2005, 38, 159–192. [Google Scholar] [CrossRef]
- Josserand, C.; Thoroddsen, S.T. Drop Impact on a Solid Surface. Annu. Rev. Fluid Mech. 2016, 48, 365–391. [Google Scholar] [CrossRef]
- Xu, R.N.; Cao, L.; Wang, G.Y.; Chen, J.N.; Jiang, P.X. Experimental Investigation of Closed Loop Spray Cooling with Micro- and Hybrid Micro-/Nano-Engineered Surfaces. Appl. Therm. Eng. 2020, 180, 115697. [Google Scholar] [CrossRef]
- Chen, J.N.; Zhang, Z.; Ouyang, X.L.; Jiang, P.X. Dropwise Evaporative Cooling of Heated Surfaces with Various Wettability Characteristics Obtained by Nanostructure Modifications. Nanoscale Res. Lett. 2016, 11, 158. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, S.S.; Chang, W.C. Microspray Quenching on Nanotextured Surfaces via a Piezoelectric Atomizer with Multiple Arrays of Micronozzles. Int. J. Heat Mass Transf. 2018, 121, 832–844. [Google Scholar] [CrossRef]
- Tang, Y.; Tang, B.; Li, Q.; Qing, J.; Lu, L.; Chen, K. Pool-Boiling Enhancement by Novel Metallic Nanoporous Surface. Exp. Therm. Fluid Sci. 2013, 44, 194–198. [Google Scholar] [CrossRef]
- Dong, L.; Quan, X.; Cheng, P. An Experimental Investigation of Enhanced Pool Boiling Heat Transfer from Surfaces with Micro/Nano-Structures. Int. J. Heat Mass Transf. 2014, 71, 189–196. [Google Scholar] [CrossRef]
- Betz, A.R.; Xu, J.; Qiu, H.; Attinger, D. Do Surfaces with Mixed Hydrophilic and Hydrophobic Areas Enhance Pool Boiling? Appl. Phys. Lett. 2010, 97, 141909. [Google Scholar] [CrossRef]
- Voglar, J.; Gregorčič, P.; Zupančič, M.; Golobič, I. Boiling Performance on Surfaces with Capillary-Length-Spaced One- and Two-Dimensional Laser-Textured Patterns. Int. J. Heat Mass Transf. 2018, 127, 1188–1196. [Google Scholar] [CrossRef]
- Kruse, C.M.; Anderson, T.; Wilson, C.; Zuhlke, C.; Alexander, D.; Gogos, G.; Ndao, S. Enhanced Pool-Boiling Heat Transfer and Critical Heat Flux on Femtosecond Laser Processed Stainless Steel Surfaces. Int. J. Heat Mass Transf. 2015, 82, 109–116. [Google Scholar] [CrossRef]
- Grabas, B. Vibration-Assisted Laser Surface Texturing of Metals as a Passive Method for Heat Transfer Enhancement. Exp. Therm. Fluid Sci. 2015, 68, 499–508. [Google Scholar] [CrossRef]
- Surtaev, A.; Kuznetsov, D.; Serdyukov, V.; Pavlenko, A.; Kalita, V.; Komlev, D.; Ivannikov, A.; Radyuk, A. Structured Capillary-Porous Coatings for Enhancement of Heat Transfer at Pool Boiling. Appl. Therm. Eng. 2018, 133, 532–542. [Google Scholar] [CrossRef]
- Dash, S.; Garimella, S.V. Droplet Evaporation Dynamics on a Superhydrophobic Surface with Negligible Hysteresis. Langmuir 2013, 29, 10785–10795. [Google Scholar] [CrossRef] [PubMed]
- Samanta, A.; Wang, Q.; Shaw, S.K.; Ding, H. Roles of Chemistry Modification for Laser Textured Metal Alloys to Achieve Extreme Surface Wetting Behaviors. Mater. Des. 2020, 192, 108744. [Google Scholar] [CrossRef]
- Gurrala, P.; Balusamya, S.; Banerjeea, S.; Sahu, K.S. Evaporation of Pure and Binary Droplets on Curved Substrates. Int. J. Heat Mass Transf. 2022, 196, 123212. [Google Scholar] [CrossRef]
- Dash, S.; Garimella, S.V. Droplet Evaporation on Heated Hydrophobic and Superhydrophobic Surfaces. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2014, 89, 042402. [Google Scholar] [CrossRef]
- Hu, D.; Wu, H.; Liu, Z. Effect of Liquid-Vapor Interface Area on the Evaporation Rate of Small Sessile Droplets. Int. J. Therm. Sci. 2014, 84, 300–308. [Google Scholar] [CrossRef]
- Lyu, N.; He, H.; Wang, F.; Liang, C.; Zhang, X. Droplet Evaporation Characteristics on Heated Superhydrophobic Surface Subjected to Airflow. Int. J. Heat Mass Transf. 2021, 181, 121874. [Google Scholar] [CrossRef]
- Yao, J.; Wang, J.; Dong, Q.; Wang, D.; Zhang, W.; Xu, H.; Zuo, L. Lattice Boltzmann Study of Droplet Evaporation on a Heated Substrate under a Uniform Electric Field. Appl. Therm. Eng. 2022, 211, 118517. [Google Scholar] [CrossRef]
- Lalanne, C.; Magdelaine, Q.; Lequien, F.; Fullana, J.M. Numerical Model Using a Volume-Of-Fluid Method for the Study of Evaporating Sessile Droplets in Both Unpinned and Pinned Modes. Eur. J. Mech. B/Fluids 2021, 89, 267–273. [Google Scholar] [CrossRef]
- Huang, W.; He, X.; Liu, C.; Li, X.; Liu, Y.; Collier, C.P.; Srijanto, B.R.; Liu, J.; Cheng, J. Droplet Evaporation on Hot Micro-Structured Superhydrophobic Surfaces: Analysis of Evaporation from Droplet Cap and Base Surfaces. Int. J. Heat Mass Transf. 2022, 185, 122314. [Google Scholar] [CrossRef]
- Lee, H.J.; Choi, C.K.; Lee, S.H. Local Heating Effect on Thermal Marangoni Flow and Heat Transfer Characteristics of an Evaporating Drople. Int. J. Heat Mass Transf. 2022, 195, 123206. [Google Scholar] [CrossRef]
- Shang, X.; Zhang, X.; Nguyen, T.B.; Tran, T. Direct Numerical Simulation of Evaporating Droplets Based on a Sharp-Interface Algebraic VOF Approach. Int. J. Heat Mass Transf. 2022, 184, 122282. [Google Scholar] [CrossRef]
- Diddens, C.; Li, Y.; Lohse, D. Competing Marangoni and Rayleigh Convection in Evaporating Binary Droplets. J. Fluid Mech. 2021, 914, A23. [Google Scholar] [CrossRef]
- Guo, Q.; Cheng, P. Direct Numerical Simulations of Sessile Droplet Evaporation on a Heated Horizontal Surface Surrounded by Moist Air. Int. J. Heat Mass Transf. 2019, 134, 828–841. [Google Scholar] [CrossRef]
- Kazemian, B.B.; Cheng, P. Simulations of Contact Angle Hysteresis Effects in Droplet Sliding on Inclined Isothermal Surfaces and Droplet Evaporating on Heated Horizontal Surfaces by a Lattice Boltzmann Method with a Variable Solid-Fluid Interaction Strength Scheme. Int. J. Heat Mass Transf. 2022, 186, 122454. [Google Scholar] [CrossRef]
- Fernandes, H.C.M.; Vainstein, M.H.; Brito, C. Modeling of Droplet Evaporation on Superhydrophobic Surfaces. Langmuir 2015, 31, 7652–7659. [Google Scholar] [CrossRef] [PubMed]
- Tam, D.; von Arnim, V.; McKinley, G.H.; Hosoi, A.E. Marangoni Convection in Droplets on Superhydrophobic Surfaces. J. Fluid Mech. 2009, 624, 101–123. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Islamova, A.G.; Orlova, E.G.; Ivashutenko, A.S.; Shanenkov, I.I.; Zykov, I.Y.; Feoktistov, D.V. Influence of Roughness on Polar and Dispersed Components of Surface Free Energy and Wettability Properties of Copper and Steel Surfaces. Surf. Coatings Technol. 2021, 422, 127518. [Google Scholar] [CrossRef]
- Boinovich, L.B.; Emelyanenko, A.M.; Emelyanenko, K.A.; Domantovsky, A.G.; Shiryaev, A.A. Comment on “Nanosecond Laser Textured Superhydrophobic Metallic Surfaces and Their Chemical Sensing Applications” by Duong V. Ta, Andrew Dunn, Thomas J. Wasley, Robert W. Kay, Jonathan Stringer, Patrick J. Smith, Colm Connaughton, Jonathan D. Shephard. Appl. Surf. Sci. 2016, 379, 111–113. [Google Scholar] [CrossRef]
- Liu, W.; Cai, M.; Luo, X.; Chen, C.; Pan, R.; Zhang, H.; Zhong, M. Wettability Transition Modes of Aluminum Surfaces with Various Micro/Nanostructures Produced by a Femtosecond Laser. J. Laser Appl. 2019, 31, 22503. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Feoktistov, D.V.; Orlova, E.G.; Zykov, I.Y.; Islamova, A.G. Droplet State and Mechanism of Contact Line Movement on Laser-Textured Aluminum Alloy Surfaces. J. Colloid Interface Sci. 2019, 553, 557–566. [Google Scholar] [CrossRef]
- Islamova, A.; Orlova, E. Wettability Inversion of Aluminum-Magnesium Alloy Surfaces. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1019, 012085. [Google Scholar] [CrossRef]
- Feoktistov, D.V.; Glushkov, D.O.; Kuznetsov, G.V.; Orlova, E.G. Gel Fuels Based on Oil-Filled Cryogels: Corrosion of Tank Material and Spontaneous Ignition. Chem. Eng. J. 2020, 421, 127765. [Google Scholar] [CrossRef]
- Darem Ahmad Inge van den Boogaert, J.M.R.P.; Jouhara, H. Hydrophilic and Hydrophobic Materials and Their Applications. Energy Sources Part A Recover. Util. Environ. Eff. 2018, 40, 2686–2725. [Google Scholar] [CrossRef]
- Cao, L.; Hu, H.A.; Gao, D. Design and Fabrication of Micro-Textures for Inducing a Superhydrophobic Behavior on Hydrophilic Materials. Langmuir 2007, 23, 4310–4314. [Google Scholar] [CrossRef]
- Roberts, C.C.; Rao, R.R.; Loewenberg, M.; Brooks, C.F.; Galambos, P.; Grillet, A.M.; Nemer, M.B. Comparison of Monodisperse Droplet Generation in Flow-Focusing Devices with Hydrophilic and Hydrophobic Surfaces. Lab Chip 2012, 12, 1540–1547. [Google Scholar] [CrossRef] [PubMed]
- Butt, H.J.; Liu, J.; Koynov, K.; Straub, B.; Hinduja, C.; Roismann, I.; Berger, R.; Li, X.; Vollmer, D.; Steffen, W.; et al. Contact Angle Hysteresis. Curr. Opin. Colloid Interface Sci. 2022, 59, 101574. [Google Scholar] [CrossRef]
- Huhtamäki, T.; Tian, X.; Korhonen, J.T.; Ras, R.H.A.A. Surface-Wetting Characterization Using Contact-Angle Measurements. Nat. Protoc. 2018, 13, 1521–1538. [Google Scholar] [CrossRef]
- Kuznetsov, G.V.; Feoktistov, D.V.; Orlova, E.G.; Misyura, S.Y.; Morozov, V.S.; Islamova, A.G. Evaporation Modes of LiBr, CaCl2, LiCl, NaCl Aqueous Salt Solution Droplets on Aluminum Surface. Int. J. Heat Mass Transf. 2018, 126, 161–168. [Google Scholar] [CrossRef]
- Gelderblom, H.; Marín, Á.G.; Nair, H.; Van Houselt, A.; Lefferts, L.; Snoeijer, J.H.; Lohse, D. How Water Droplets Evaporate on a Superhydrophobic Substrate. Phys. Rev. E—Stat. Nonlinear Soft Matter. Phys. 2011, 83, 026306. [Google Scholar] [CrossRef]
- Popov, Y.O. Evaporative Deposition Patterns: Spatial Dimensions of the Deposit. Phys. Rev. E 2005, 71, 36313. [Google Scholar] [CrossRef]
- Nguyen, T.A.H.; Nguyen, A.V.; Hampton, M.A.; Xu, Z.P.; Huang, L.; Rudolph, V. Theoretical and Experimental Analysis of Droplet Evaporation on Solid Surfaces. Chem. Eng. Sci. 2012, 69, 522–529. [Google Scholar] [CrossRef]
- Gleason, K.; Putnam, S.A. Microdroplet Evaporation with a Forced Pinned Contact Line. Langmuir 2014, 30, 10548–10555. [Google Scholar] [CrossRef]
- Deegan, R.D.; Bakajin, O.; Dupont, T.F.; Huber, G.; Nagel, S.R.; Witten, T.A. Contact Line Deposits in an Evaporating Drop. Phys. Rev. E 2000, 62, 756–765. [Google Scholar] [CrossRef]
- Castanet, G.; Antonov, D.V.; Strizhak, P.A.; Sazhin, S.S. Effects of Water Subdroplet Location on the Start of Puffing/Micro-Explosion in Composite Fuel-Water Droplets. Int. J. Heat Mass Transf. 2022, 186, 122466. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. Reference Manual. Available online: https://doc.comsol.com/ (accessed on 8 June 2023).
- Bozorgmehr, B.; Murray, B.T. Numerical Simulation of Evaporation of Ethanol−Water Mixture Droplets on Isothermal and Heated Substrates. ACS Omega 2021, 6, 12577–12590. [Google Scholar] [CrossRef]
- Antonov, D.V.; Fedorenko, R.M.; Strizhak, P.A.; Sazhin, S.S. A Simple Model of Heating and Evaporation of Droplets on a Superhydrophobic Surface. Int. J. Heat Mass Transf. 2023, 201, 123568. [Google Scholar] [CrossRef]
- Yaws, L.C. Yaws’ Handbook of Thermodynamic and Physical Properties of Chemical Compounds; Knovel: New York, NY, USA, 2003. [Google Scholar]
- Bernardin, J.D.; Stebbins, C.J.; Mudawar, I. Effects of Surface Roughness on Water Droplet Impact History and Heat Transfer Regimes. Int. J. Heat Mass Transf. 1996, 40, 73–88. [Google Scholar] [CrossRef]
- Gumulya, M.; Utikar, R.P.; Pareek, V.; Mead-Hunter, R.; Mitra, S.; Evans, G.M. Evaporation of a Droplet on a Heated Spherical Particle. Chem. Eng. J. 2015, 278, 309–319. [Google Scholar] [CrossRef]
- Sen, U.; Roy, T.; Ganguly, R.; Angeloni, L.A.; Schroeder, W.A.; Megaridis, C.M. Explosive Behavior during Binary-Droplet Impact on Superheated Substrates. Int. J. Heat Mass Transf. 2020, 154, 119658. [Google Scholar] [CrossRef]
- Mura, E.; Calabria, R.; Califano, V.; Massoli, P.; Bellettre, J. Emulsion Droplet Micro-Explosion: Analysis of Two Experimental Approaches. Exp. Therm. Fluid Sci. 2014, 56, 69–74. [Google Scholar] [CrossRef]
- Yahaya Khan, M.; Abdul Karim, Z.A.; Aziz, A.R.A.; Heikal, M.R.; Crua, C. Puffing and Microexplosion Behavior of Water in Pure Diesel Emulsion Droplets During Leidenfrost Effect. Combust. Sci. Technol. 2017, 189, 1186–1197. [Google Scholar] [CrossRef]
- Glushkov, D.O.; Kuznetsov, G.V.; Strizhak, P.A. Simultaneous Ignition of Several Droplets of Coal–Water Slurry Containing Petrochemicals in Oxidizer Flow. Fuel Process. Technol. 2016, 152, 22–33. [Google Scholar] [CrossRef]
- Lee, D.; Kim, H.Y.; Yoon, S.S.; Cho, C.P. Group Combustion of Staggeringly Arranged Heptane Droplets at Various Reynolds Numbers, Oxygen Mole-Fractions, and Separation Distances. Fuel 2010, 89, 1447–1460. [Google Scholar] [CrossRef]
- Antonov, D.V.; Fedorenko, R.M.; Strizhak, P.A. Micro-Explosion and Puffing of a Group of Two-Component Droplets. Appl. Therm. Eng. 2020, 181, 116023. [Google Scholar] [CrossRef]
- Sheng, H.Z.; Chen, L.; Zhang, Z.P.; Wu, C.K.; An, C.; Cheng, C.Q. The Droplet Group Microexplosions in Water-in-Oil Emulsion Sprays and Their Effects on Diesel Engine Combustion. Symp. Combust. 1994, 25, 175–181. [Google Scholar] [CrossRef]
- Dai, M.; Perot, J.B.; Schmidt, D.P. Heat Transfer within Deforming Droplets. In Proceedings of the American Society of Mechanical Engineers, Internal Combustion Engine Division (Publication) ICE, New Orleans, LA, USA, 8–11 September 2002; Volume 39. [Google Scholar]
- Zubkov, V.S.; Cossali, G.E.; Tonini, S.; Rybdylova, O.; Crua, C.; Heikal, M.; Sazhin, S.S. Mathematical Modelling of Heating and Evaporation of a Spheroidal Droplet. Int. J. Heat Mass Transf. 2017, 108, 2181–2190. [Google Scholar] [CrossRef]
- Tonini, S.; Cossali, G.E. An Exact Solution of the Mass Transport Equations for Spheroidal Evaporating Drops. Int. J. Heat Mass Transf. 2013, 60, 236–240. [Google Scholar] [CrossRef]
- Tonini, S.; Cossali, G.E. An Analytical Model of Liquid Drop Evaporation in Gaseous Environment. Int. J. Therm. Sci. 2012, 57, 45–53. [Google Scholar] [CrossRef]
- Antonov, D.V.; Kuznetsov, G.V.; Misyura, S.Y.; Strizhak, P.A. Temperature and Convection Velocities in Two-Component Liquid Droplet until Micro-Explosion. Exp. Therm. Fluid Sci. 2019, 109, 109862. [Google Scholar] [CrossRef]
- Volkov, R.S.; Kuznetsov, G.V.; Strizhak, P.A. Temperature and Velocity Fields of the Gas-Vapor Flow near Evaporating Water Droplets. Int. J. Therm. Sci. 2018, 134, 337–354. [Google Scholar] [CrossRef]
- Abram, C.; Fond, B.; Heyes, A.L.; Beyrau, F. High-Speed Planar Thermometry and Velocimetry Using Thermographic Phosphor Particles. Appl. Phys. B Lasers Opt. 2013, 111, 155–160. [Google Scholar] [CrossRef]






| Material | Physical Properties |
|---|---|
| Water | ; |
| Air |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antonov, D.V.; Islamova, A.G.; Orlova, E.G. Heat and Mass Transfer Processes and Evaporation of a Liquid Droplet on a Structured Surface. Energies 2023, 16, 7505. https://doi.org/10.3390/en16227505
Antonov DV, Islamova AG, Orlova EG. Heat and Mass Transfer Processes and Evaporation of a Liquid Droplet on a Structured Surface. Energies. 2023; 16(22):7505. https://doi.org/10.3390/en16227505
Chicago/Turabian StyleAntonov, Dmitrii V., Anastasia G. Islamova, and Evgeniya G. Orlova. 2023. "Heat and Mass Transfer Processes and Evaporation of a Liquid Droplet on a Structured Surface" Energies 16, no. 22: 7505. https://doi.org/10.3390/en16227505
APA StyleAntonov, D. V., Islamova, A. G., & Orlova, E. G. (2023). Heat and Mass Transfer Processes and Evaporation of a Liquid Droplet on a Structured Surface. Energies, 16(22), 7505. https://doi.org/10.3390/en16227505










