Research on the Control Method of the PV Grid-Connected Inverter under an Asymmetrical Power Grid Fault
Abstract
:1. Introduction
- (1)
- Most of the studies on resonance problems of grid-connected inverters are still based on the fact that grid-connected inverters themselves are prone to resonance problems. There is a lack of studies that consider the influence of external factors on the normal operation of grid-connected inverters.
- (2)
- In previous studies, there are fewer studies on grid-connected inverters when the asymmetrical faults occur in the grid. However, with regard to the grid-connected inverter, as an important connecting link between new energy power generation and the power grid, it is of great practical significance to carry out research on the grid-connected inverter for PV power generation under the asymmetrical fault of the power grid.
- (1)
- The PI-DR current controller proposed in this paper integrates double-resonant (DR) controllers on the basis of traditional PI controllers, which can realize the achieve accurate and effective control of the negative-sequence current component and harmonic component, and realize the normal grid-connected operation of the PV grid-connected inverter in the case of asymmetrical faults in the power grid.
- (2)
- When the asymmetrical faults occur in the grid, the PI-DR mention controller does not need to separate the positive and negative sequences of the current, and can directly control the output current in the forward synchronous rotating coordinate system without difference, and the dynamic response to the current control is faster.
- (3)
- Grid asymmetrical faults are frequent in power systems. The effectiveness of the PI-DR current controller proposed in this paper is verified in simulation experiments. The simulation experiments prove that the PI-DR current controller can improve the dynamic performance of the grid-connected inverter and the grid-connected power quality, and the simulation experiment results also show that the method has a certain reference value in practical engineering applications.
2. Structure and Mathematical Model of PV Power Generation System under Asymmetrical Power Grid Fault
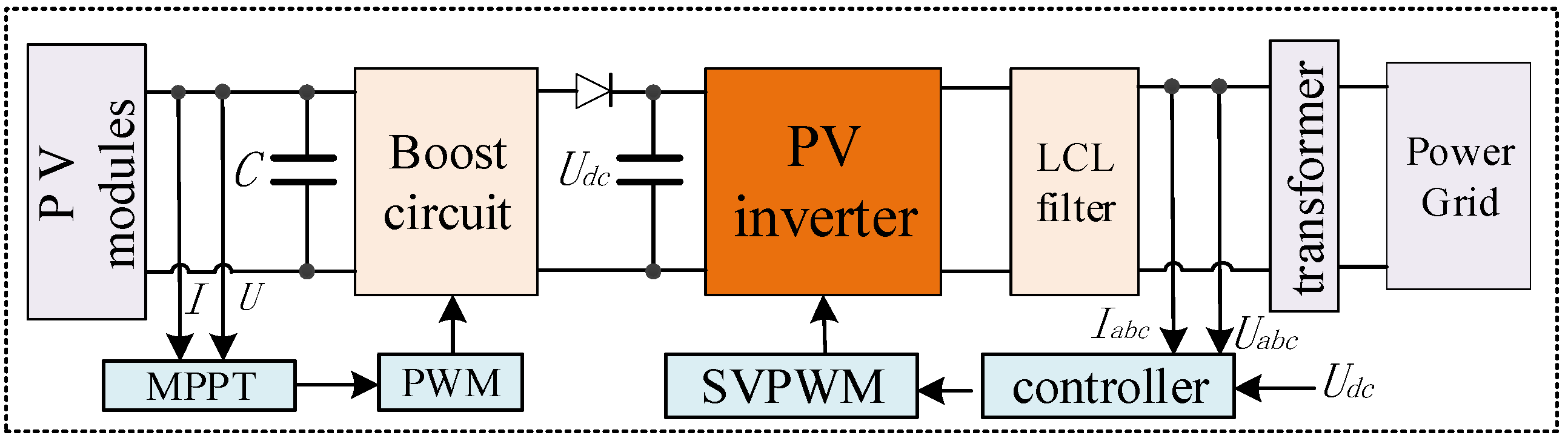
2.1. Structure of PV Generation System
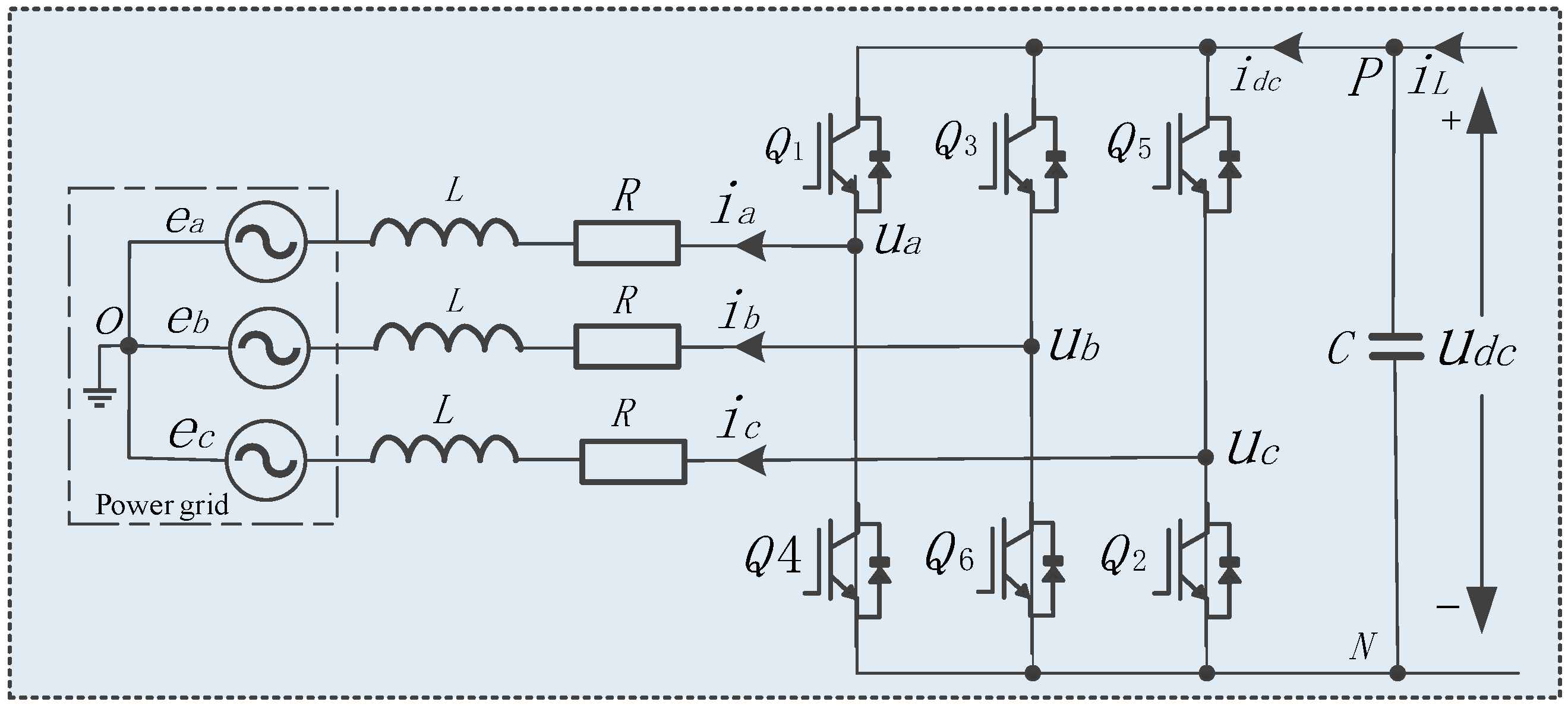
2.2. Mathematical Model of PV Grid-Connected Inverter under Asymmetrical Power Grid Fault
3. Control Method of the PV Power Generation Grid-Connected Inverter under Asymmetrical Grid Fault
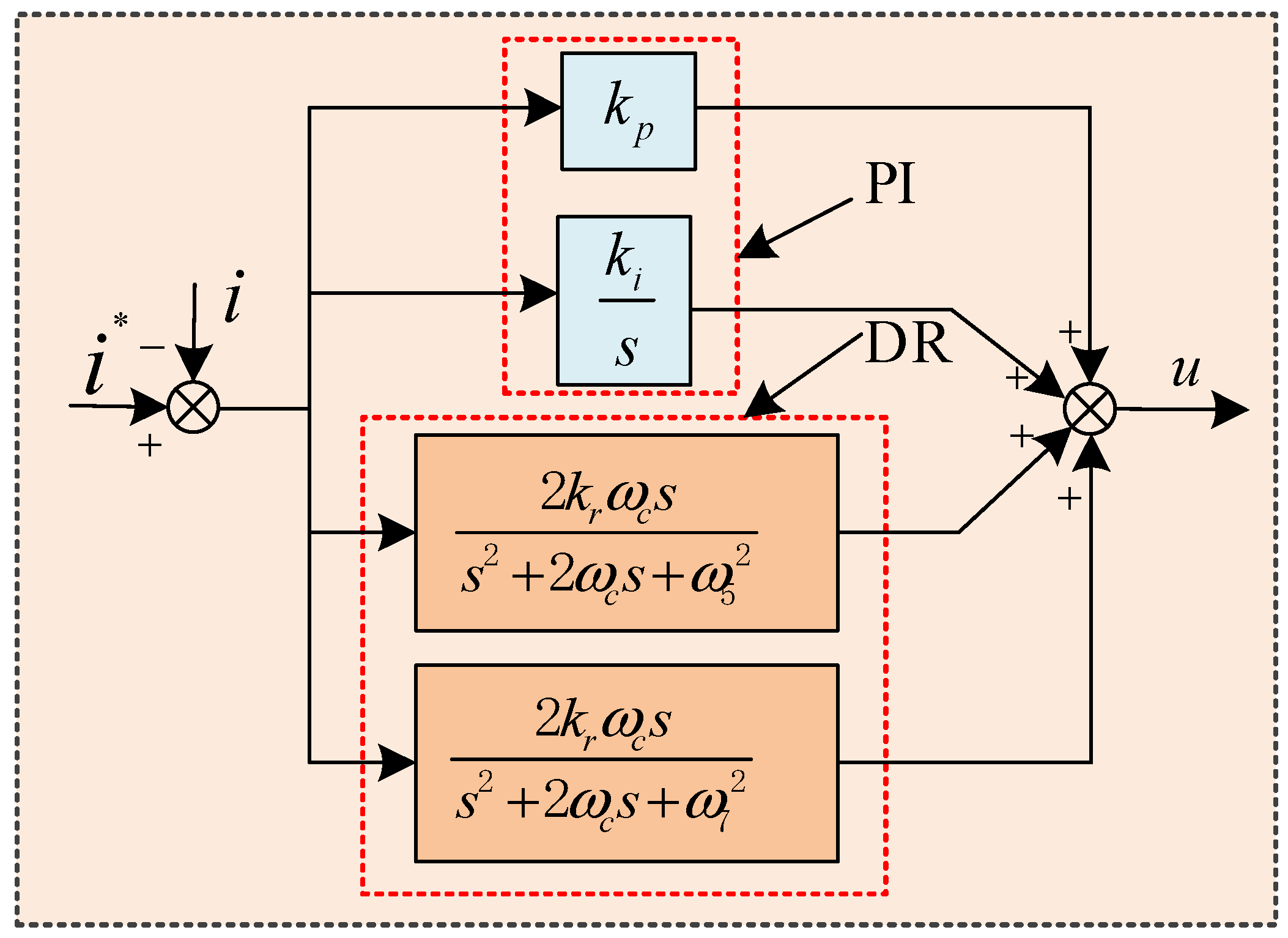
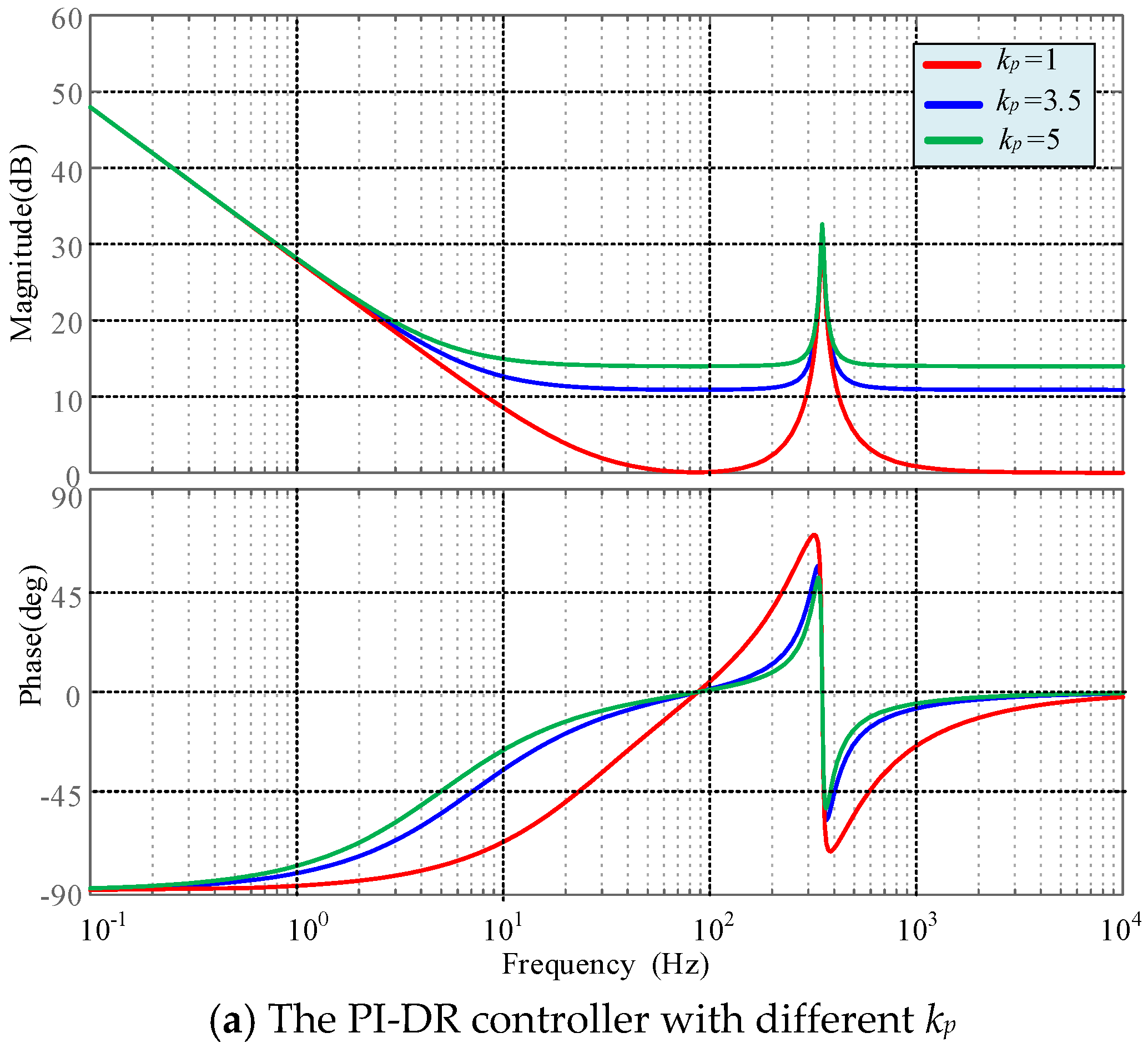
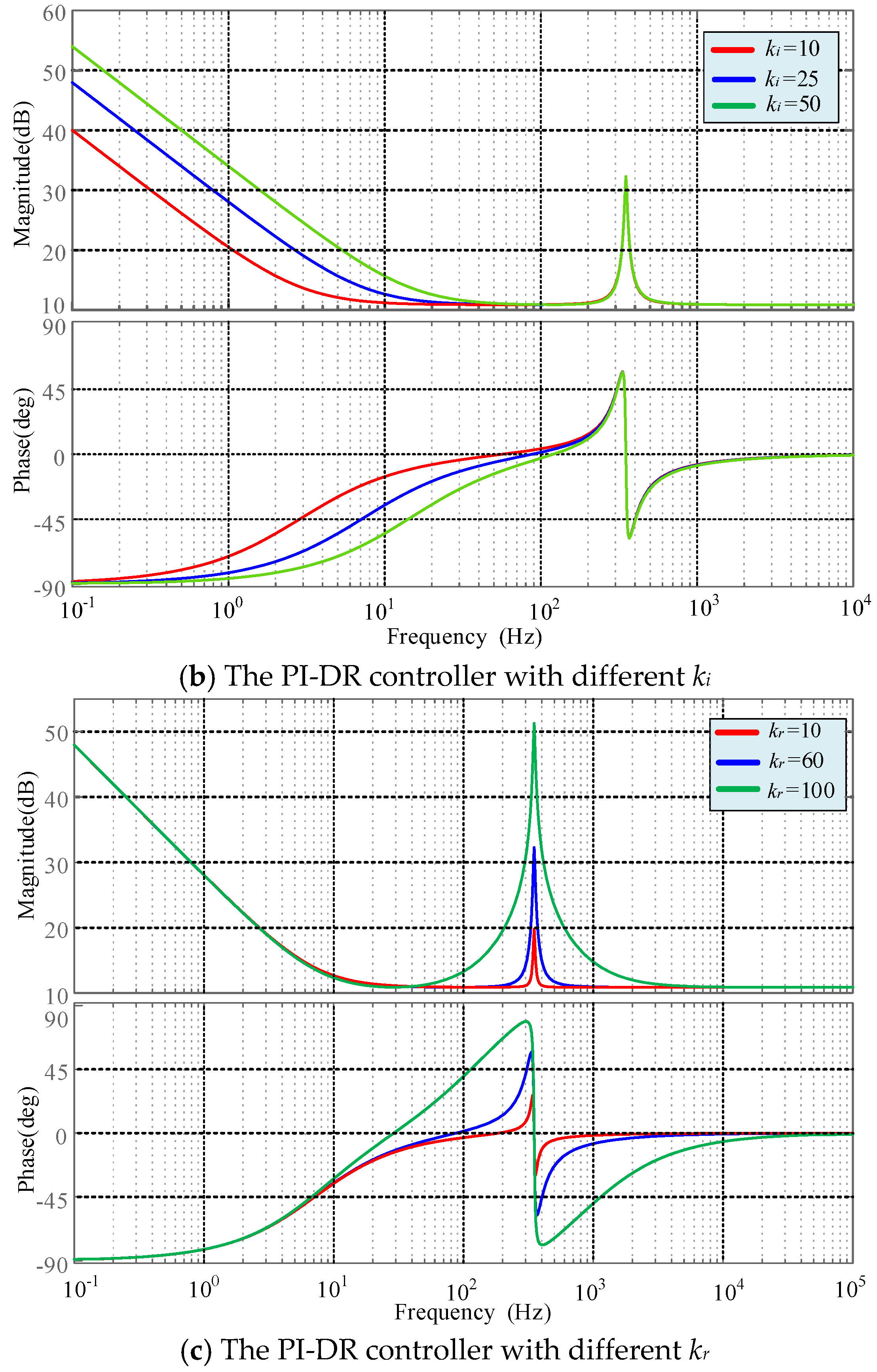
3.1. Principle of the PI-DR Controller
3.2. The Positive and Negative Sequence Current Command Calculation
- Objective I: Control the negative-sequence component of the grid-side current and achieve control of the fifth and seventh harmonic components, that is, , which can be obtained from Equations (8) and (9):
- Objective II: Control the second fluctuations of the grid-side active power, that is, , which can be obtained from Equations (8) and (9):
- Objective III: Control the second fluctuations of the grid-side reactive power, that is, , which can be obtained from Equations (8) and (9):
3.3. The PV Grid-Connected Inverter Control System Design
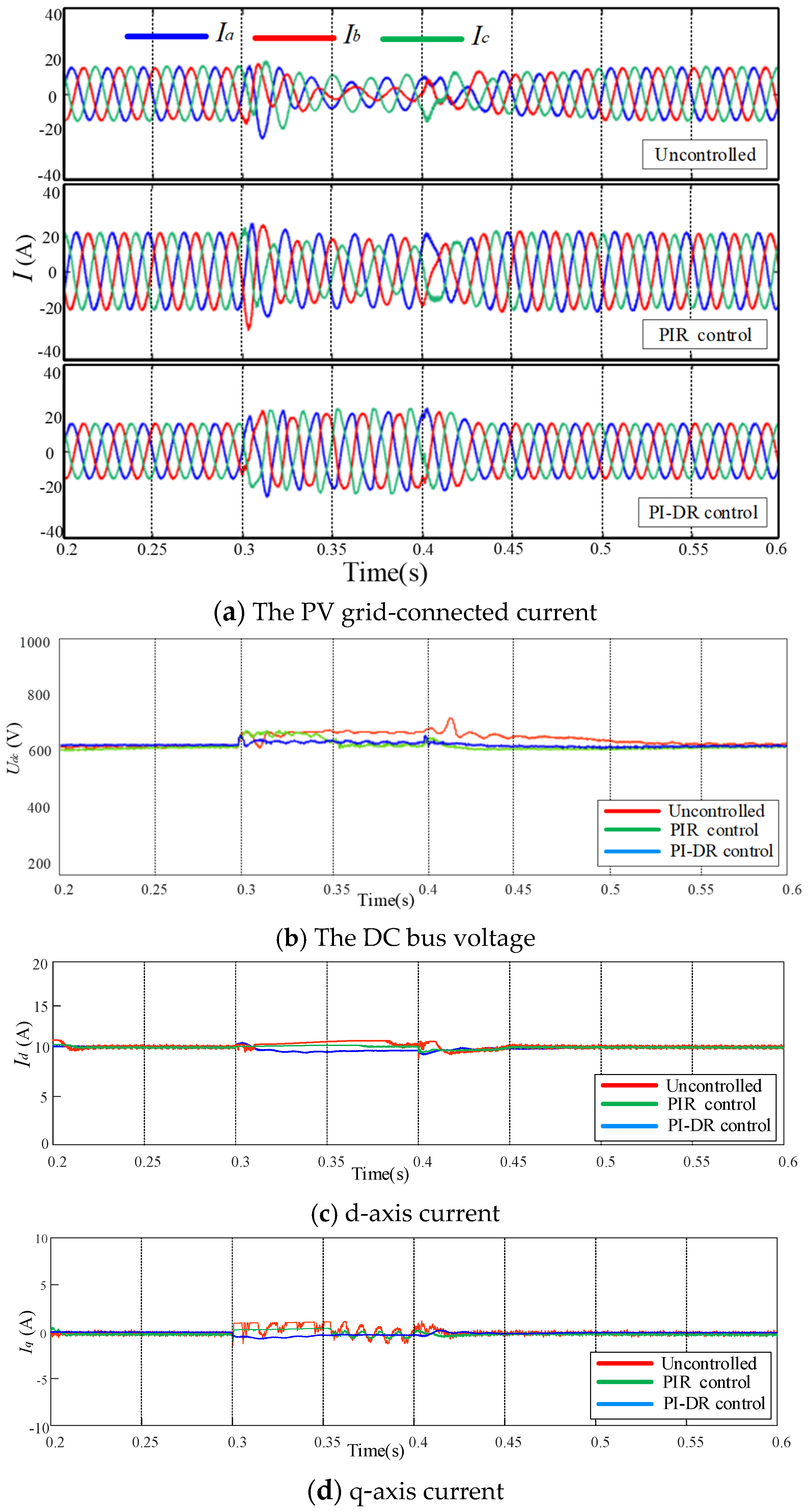
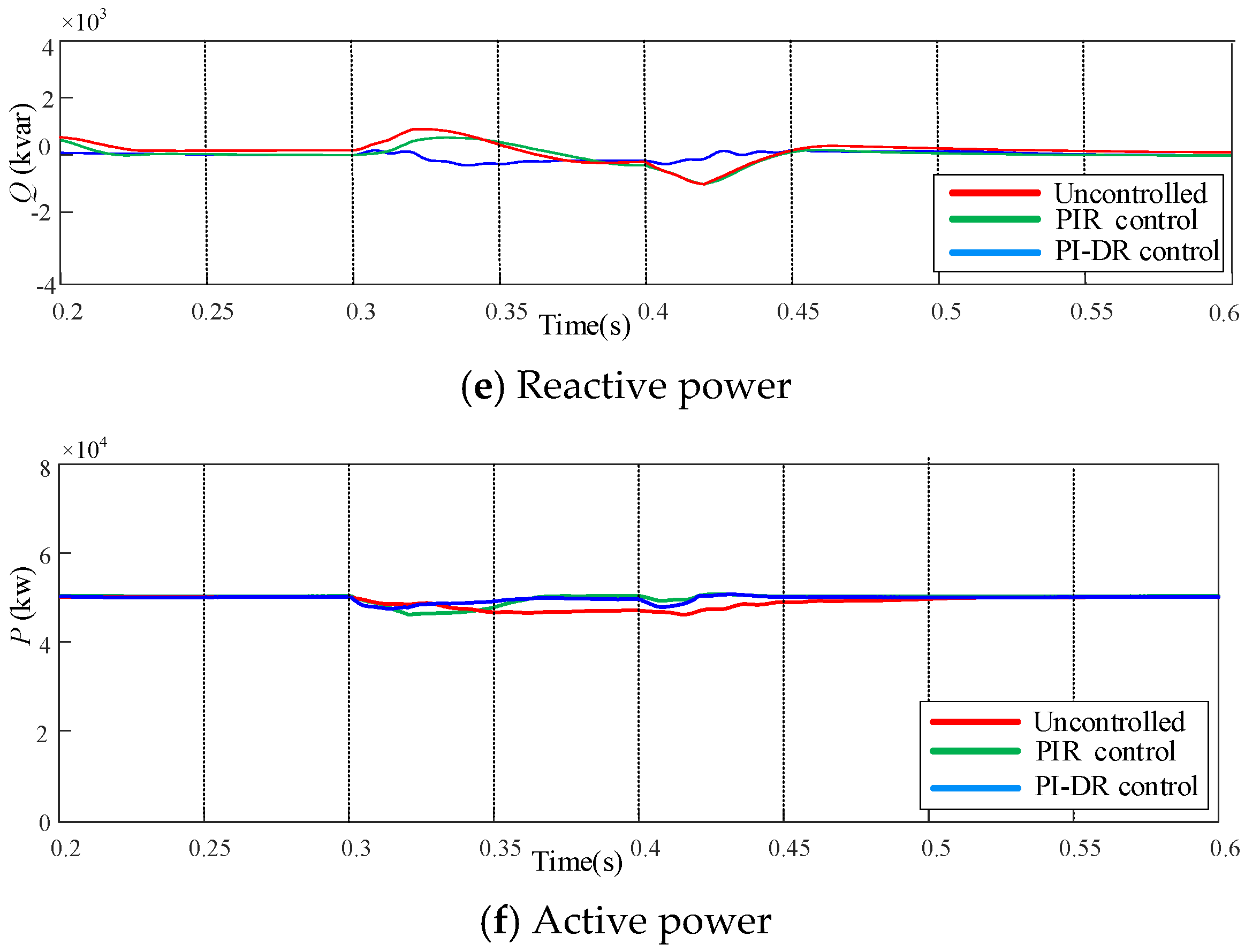
4. Simulation and Results
5. Conclusions
- The PI-DR controller is based on the traditional PI control and incorporates DR controllers; when an asymmetrical fault occurs in the grid, the PI and the DR controllers work together. Therefore, when an asymmetrical fault occurs in the grid, the PI-DR controller can guarantee the normal grid-connected operation of the PV inverter.
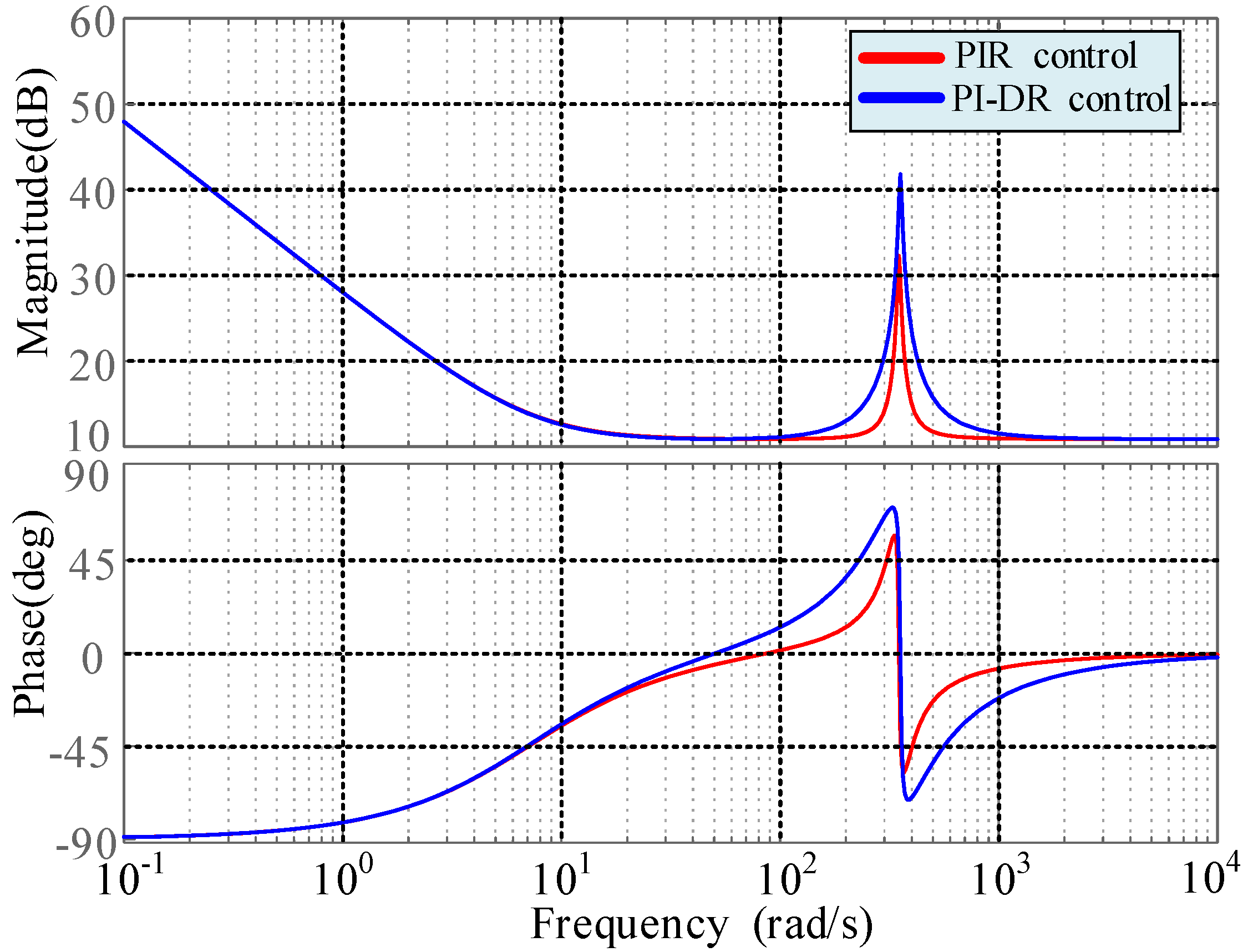
- The PI-DR controller can provide infinite gain to the signal at the point of resonance frequency; therefore, it can achieve accurate and effective control of the negative-sequence current component of the double-frequency fluctuation and the fifth and seventh harmonic components in the forward synchronous rotating coordinate system.
- The PI-DR controller has a faster dynamic response to current control because it does not require positive- and negative-sequence decomposition.
- The PI-DR current controller can improve the grid-connected power quality, and the results of the simulation experiments show that the PI-DR controller has some reference value in practical engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Chao, Q.; Wu, C.Y.; Xu, L.J. Researching Review of Photovoltaic Grid-Connected Inverter. Electr. Energy Manag. Technol. 2016, 17, 12–16. [Google Scholar]
- Zhang, M.; Wang, J.; Zhang, S.; Gao, L.; Guo, X.; Chen, L.; Xu, Y. Harmonic Resonance Analysis and Impedance Remodeling Method of Multi-Inverter Grid-Connected System. Electronics 2023, 12, 3684. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, L.; Molinas, M. Damping region extension for digitally controlled LCL-type grid-connected inverter with capacitor-current feedback. IET Power Electron. 2018, 11, 1974–1982. [Google Scholar] [CrossRef]
- Pan, D.; Ruan, X.; Bao, C.; Li, W.; Wang, X. Capacitor-current-feedback active damping with reduced computation delay for improving robustness of LCL-type grid-connected inverter. IEEE Trans. Power Electron. 2014, 29, 3414–3427. [Google Scholar] [CrossRef]
- Yang, D.; Ruan, X.; Wu, H. A Real-time computation method with dual sampling mode to improve the current control performance of the LCL type grid-connected inverter. IEEE Trans. Ind. Electron. 2015, 62, 4563–4572. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, H.G. LCL grid connected inverter control strategy based on two-degree-of-freedom internal model control. Mod. Electr. Power 2018, 6, 86–91. [Google Scholar]
- Zhong, P.; Sun, J.; Tian, Z.; Huang, M.; Yu, P.; Zha, X. An Improved Impedance Measurement Method for Grid-Connected Inverter Systems Considering the Background Harmonics and Frequency Deviation. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4236–4247. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Adaptive control of grid-connected inverters based on online grid impedance measurements. IEEE Trans. Sustain. Energy 2014, 5, 516–523. [Google Scholar] [CrossRef]
- Cui, X.; Wu, J.; Liu, X.; Chen, Y.; Xie, Z.; Xue, F.; Liu, Y.; Luo, C. Large-Signal Impedance Modeling and Stability Analysis of a Grid-Connected Inverter Considering the Influence of a Limiter in Different Control Links. Energies 2023, 16, 6227. [Google Scholar] [CrossRef]
- Chen, J.; Yan, Z.Y.; Zhao, B. On the impedance Modelling and Grid-connected Characteristics of the Three-phase Droop Controlled Inverter. Proc. CSEE 2019, 16, 4846–4856. [Google Scholar]
- Tong, X.; Zhong, M.; Zhang, X.; Deng, J.; Zhang, Z. Voltage regulation strategy of AC distribution network based on distributed PV grid-connected inverter. J. Eng. 2019, 16, 2525–2528. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.-M.; Zhu, P.; Yao, J.; Yang, G.-H. Research on control strategy of three phase photovoltaic grid-connected inverter based on virtual flux. Electr. Meas. Instrum. 2015, 52, 41–45. [Google Scholar]
- Jiang, R.; Jiang, T.; Xu, L. Research on Inverter Control Strategy of PV Integrated into Distribution Network. Electr. Eng. 2017, 12, 96–100. [Google Scholar]
- Alathamneh, M.; Ghanayem, H.; Yang, X.; Nelms, R.M. Three-Phase Grid-Connected Inverter Power Control under Unbalanced Grid Conditions Using a Time-Domain Symmetrical Components Extraction Method. Energies 2022, 15, 6936. [Google Scholar] [CrossRef]
- Gada, S.; Fekik, A.; Mahdal, M.; Vaidyanathan, S.; Maidi, A.; Bouhedda, A. Improving Power Quality in Grid-Connected Photovoltaic Systems: A Comparative Analysis of Model Predictive Control in Three-Level and Two-Level Inverters. Sensors 2023, 23, 7901. [Google Scholar] [CrossRef]
- Cupertino, A.F.; Xavier, L.S.; Brito, E.M.; Mendes, V.F.; Pereira, H.A. Benchmarking of power control strategies for photovoltaic systems under unbalanced conditions. Int. J. Power Energy Syst. 2018, 106, 335–345. [Google Scholar] [CrossRef]
- Ouyang, S.; Ma, W.J. Control strategy for PV inverter under unbalanced grid voltage. Appl. Electron. Technol. 2018, 44, 147–150. [Google Scholar] [CrossRef]
- Xu, H.C.; Teng, Y.F.; Wang, X.R. A control strategy combining repetitive control and quasi-PR control for PMSG grid-side converter. Power Syst. Prot. Control 2018, 5, 153–156. [Google Scholar]
- Peng, C.; Heng, N. Torque Ripple Restraint Strategy of DFIG Under Unbalanced Grid Voltage Conditions Based on Resonant Control Loop. Proc. CSEE 2015, 35, 1756–1767. [Google Scholar]
- Jiang, Y.; Li, Y.; Tian, Y.; Wang, L. Phase-Locked Loop Research of Grid-Connected Inverter Based on Impedance Analysis. Energies 2018, 11, 3077. [Google Scholar] [CrossRef]
- Tiwari, R.; Babu, N.R.; Arunkrishna, R.; Sanjeevikumar, P. Comparison Between PI Controller and Fuzzy Logic-Based Control Strategies for Harmonic Reduction in Grid-Integrated Wind Energy Conversion System. In Advances in Smart Grid and Renewable Energy, Proceedings of the ETAEERE-2016, Majhitar, Sikkim, 17–18 December 2016; Springer: Singapore, 2018; pp. 978–981. [Google Scholar]
- Arulkumar, K.; Vijayakumar, D.; Palanisamy, K. Modeling and control strategy of three phase neutral point clamped multilevel PV inverter connected to the grid. J. Build. Eng. 2015, 3, 195–202. [Google Scholar] [CrossRef]
- Abbassi, R.; Marrouchi, S.; Saidi, S.; Abbassi, A.; Chebbi, S. Optimal Energy Management Strategy and Novel Control Approach for DPGSs Under Unbalanced Grid Faults. J. Circuits Syst. Comput. 2019, 28, 1950057. [Google Scholar] [CrossRef]
- Alepuz, S.; Calle, A.; Busquets-Monge, S.; Kouro, S.; Wu, B. Use of Stored Energy in PMSG Rotor Inertia for Low-Voltage Ride-Through in Back-to-Back NPC Converter-Based Wind Power Systems. IEEE Trans. Ind. Electron. 2013, 60, 1787–1796. [Google Scholar] [CrossRef]
- Femat, R.; Vázquez, N.; Vazquez, E. Current Control Based on Limit Cycle Stability for Photovoltaic Arrays. IET Renew. Power Gener. 2020, 14, 725–733. [Google Scholar]
- Cao, N.; Cao, Y.; Liu, J. Modeling and Analysis of Grid-Connected Inverter for PV Generation. Adv. Mater. Res. 2013, 760–762, 451–456. [Google Scholar] [CrossRef]
- Haddadi, A.; Kocar, I.; Mahseredjian, J.; Karaagac, U.; Farantatos, E. Negative sequence quantities-based protection under inverter-based resources—Challenges and impact of the German grid code. Electr. Power Syst. Res. 2020, 188, 106573. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Xu, P.; Li, D.; Liu, B. A Current Control Method for Grid-Connected Inverters. Energies 2023, 16, 6558. [Google Scholar] [CrossRef]
- Lu, D.D.; Fang, M. Simulation Study of Software Phase-Locked Loop Based on the Synchronous Reference Frame for Three-phase Grid. J. Huaiyin Inst. Technol. 2015, 24, 26–30. [Google Scholar]
- Zhuang, Y.; Xu, W.M.; Li, S.Q. Research on the Control System of the Inverter about Distributed Photovoltaic Generation. Electric Switchgear. 2019, 4, 60–62, 68. [Google Scholar]
- Le, K.A.; Ai, X.; Dang, N.H. Hierarchical control strategy for voltage unbalance compensation in micro-grid. J. Harbin Inst. Technol. 2016, 48, 46–52. [Google Scholar]
- Lin, C.W.; Liu, T.J.; Gui, J. Double Closed-Loop Control of the Three-Level Rectifier Based on Synchronous PI Current Decoupling. Appl. Mech. Mater. 2013, 385–386, 1179–1183. [Google Scholar] [CrossRef]
- Yang, X.; Wang, T.; Xu, Y. Voltage feedforward control of LCL grid-connected inverter based on virtual inductor. Acta Energiae Solaris Sin. 2020, 41, 56–63. [Google Scholar]
- Subramanian, S.B.; Varma, R.K.; Vanderheide, T. Impact of grid voltage feed-forward filters on coupling between DC link voltage and AC Voltage controllers in smart PV solar systems. IEEE Trans. Sustain. Energy 2020, 11, 381–390. [Google Scholar] [CrossRef]
- Zhao, Q.L.; Song, W.L.; Yuan, J. Research on grid-connected inverter stability based on current error signal compensation in weak grid. Acta Energiae Solaris Sin. 2019, 40, 2833–2841. [Google Scholar]
- Zhang, X.; Zhang, G.; Qian, J.L. Design of PIR Controller with the Ability of Low Harmonic Damping. Trans. China Electrotech. Soc. 2016, 31, 19–27. [Google Scholar]
- El Karkri, Y.; Rey-Boué, A.B.; El Moussaoui, H.; Stöckl, J.; Strasser, T.I. Improved Control of Grid-connected DFIG-based Wind Turbine using Proportional-Resonant Regulators during Unbalanced Grid. Energies 2019, 12, 4041. [Google Scholar] [CrossRef]
- Liu, B.; Zie, J.J.; Li, J.; Wu, J.J. Novel Grid-Connected Current Control Strategies Based on Self-Adaptive Proportional-Resonant. Trans. China Electrotech. Soc. 2013, 28, 186–195. [Google Scholar]
- Dai, Z.W.; Shu, J.; Wu, C.H.; Wang, H.; Song, X.R.; Zhang, W. Study on control strategy of photovoltaic grid-connected inverter based on LC filter. Adv. New Renew. Energy 2014, 2, 453–499. [Google Scholar]
- Pan, J.J.; Liu, Y.X.; Sun, H.N.; Zhang, Q.J.; Liu, M.Y. Control Strategy of LCL-Filtered Grid-Connected Inverter Based on Quasi-Proportional Resonant and Grid Voltage Feed-Forward. Electr. Mach. Control Appl. 2016, 43, 23–27. [Google Scholar]

| Parameter | Value |
|---|---|
| Grid-side voltage Un/V | 380 |
| DC side voltage Udc/V | 600 |
| Grid-side filtering inductance L/mH | 6 |
| DC-side support capacitor C/mF | 1.5 |
| Switching frequency fs/kHz | 6 |
| Control Strategy | I (%) | Id (%) | Iq (%) | Udc (%) | Q | P |
|---|---|---|---|---|---|---|
| Uncontrolled | 3.96 | 4.75 | 4.83 | 3.63 | 2.76 | 2.85 |
| PI-R control | 1.53 | 1.89 | 1.91 | 1.32 | 1.25 | 1.14 |
| PI-DR control | 0.28 | 0.63 | 0.81 | 0.54 | 0.18 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, S.; Lu, M.; Wang, R.; Liu, D. Research on the Control Method of the PV Grid-Connected Inverter under an Asymmetrical Power Grid Fault. Energies 2023, 16, 7504. https://doi.org/10.3390/en16227504
Tian S, Lu M, Wang R, Liu D. Research on the Control Method of the PV Grid-Connected Inverter under an Asymmetrical Power Grid Fault. Energies. 2023; 16(22):7504. https://doi.org/10.3390/en16227504
Chicago/Turabian StyleTian, Shiji, Min Lu, Ruikang Wang, and Di’an Liu. 2023. "Research on the Control Method of the PV Grid-Connected Inverter under an Asymmetrical Power Grid Fault" Energies 16, no. 22: 7504. https://doi.org/10.3390/en16227504
APA StyleTian, S., Lu, M., Wang, R., & Liu, D. (2023). Research on the Control Method of the PV Grid-Connected Inverter under an Asymmetrical Power Grid Fault. Energies, 16(22), 7504. https://doi.org/10.3390/en16227504






