Abstract
The article presents the solution of a power rectifier system dedicated to cooperating with an electric generator based on a special synchronous generator, which can be used in wind or water energy systems. In this generator, a pair of three-phase windings in a stator is utilized. One of the windings is connected in a star, and the second one is connected in a delta configuration. Two six-pulse uncontrolled (diode) rectifiers are included at the outputs of the windings. The rectifiers are coupled by a pulse transformer. The primary windings of this transformer are supplied by a power-electronics current source called a current modulator. With the help of this current modulator, the quasi-sinusoidal magnetomotive force (mmf) in the stator of the machine can be obtained. Additionally, to improve the efficiency of the described system, the low-power transistor rectifier, which is connected to the DC bus of the current modulator, has been used. With the help of this converter, it is possible to control and stabilize the voltage level in a DC circuit. It works, in this case, in inverter mode. The principle of working and elaborated control methods of the current modulator and the additional rectifier are presented. Selected results of simulation and experimental tests are also presented.
1. Introduction
Wind and water power systems have emerged as two of the dominant renewable sources of energy with immense growth potential across the globe, including in Poland [,,]. In particular, the use of wind energy has become a very popular solution in recent years. According to the Global Wind Energy Council [], in 2015, the wind turbine industry reached the milestone of 60 GW in new installations per year. Moreover, the previous annual record was set at the level of over 51 GW of new capacity. In total, by the end of 2015, the wind power capacity was 432 GW—17% of the growth in a market. Eight years later, on 15 June 2023, the global wind industry reached the 1 TW milestone. Recently completed wind power projects in China, the USA, Morocco, and Europe have pushed the capacity across that level threshold as the industry has delivered on the ever-growing ambitions of governments around the world [].
The main types of generators used in renewable sources of energy (RESs) that cooperate with wind or water turbines are AC poly-phase machines. There are two main major types: induction and synchronous. In this article, a special type of synchronous generator with permanent magnets (PMSG) is analyzed. These machines are known for being the most efficient choice amidst the current generator designs on the market [,,,]. Furthermore, their great performance and low cost of conservation during their long lifespan make them the best choice in the cost-efficiency sense.
An unconventional type of synchronous generator, named the PMSG generator with magnetic flux modulation (PMSGFM), was used in the presented energy conversion system. Its main structure and principle of working are described in the next chapter. A dedicated special power electronics circuit, which is used to convert the electric energy produced by a generator, had to be applied.
Additionally, to improve the efficiency, it was proposed to use a low-power transistor rectifier (LPTR). With the help of this converter, it became possible to transfer electric energy to the AC grid. In this way, the voltage stabilization in the DC bus of the current modulator was also achieved. The elaborated control algorithms of this active rectifier are also discussed.
The last part of this article describes chosen simulation and experimental results of this research.
2. The Unconventional PMSG Generator with Magnetic Flux Modulation
The essential part of the power conversion system is the generator (G). It is especially useful when cooperating with wind or water turbines. It is possible, thanks to the dedicated power electronics converter, to return the produced energy to the grid (on-grid mode) or to use it locally (off-grid mode). In addition, cooperation with chemical energy stores can be also considered.
The high efficiency of the whole system is the main goal to be achieved. The effectiveness of the conversion of mechanical energy into electrical energy must be achieved via the simple means of the electrical structure. As a consequence of this, agenerator, with notably designed stator windings and a distinctive power electronics converter, is proposed. It is able to enforce a sinusoidal magnetomotive force (mmf). A consequence of this is that the resultant magnetic flux is relatively similar to a sine wave. Hence, it limits the power loss in “iron”, which, in addition to the loss in “copper”, is one of the dominant power losses in the generator.
The power electronics converter connects the generator to the load (L). It has a simplified design, which mostly uses the uncontrolled rectifiers. The reason for this is that it provides a high energy conversion efficiency. The main spheres of application are medium and large power systems, where the advantages are notably evident.
The simplified block diagram of the main part of the system is shown in Figure 1. The source of the electrical energy is a synchronous generator with an unconventional construction when it comes to the stator windings. It consists of a pair of three-phase windings in the stator. The first of the windings is connected in the star and the second one in the delta connection. The voltages at the power terminals of the generator (windings) should be the same in terms of the values, but the voltages are shifted relative to each other by an angle of π/6.
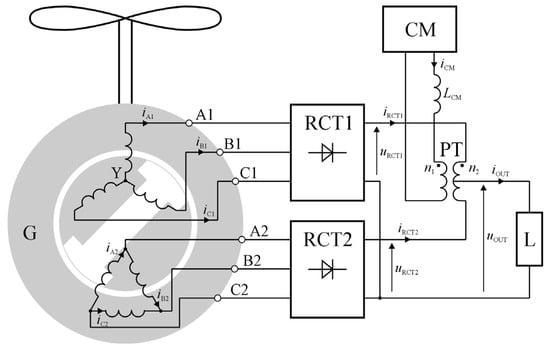
Figure 1.
Block scheme of the power conversion system based on synchronous generator with magnetic flux modulation, where iA1, iB1, iC1—phase currents for star windings; iA2, iB2, iC2—phase currents for delta windings; iRCT1, iRCT2—output currents of diode rectifiers; uRCT1, uRCT2—output voltages of diode rectifiers; iCM—current of modulator; and iout—load current [].
Both windings feed two independent six-pulse diode rectifiers (RCT1, RCT2). The power electronics-controlled current source—in other words, the current modulator (CM)—is located at the outputs of both rectifiers, shaping their output currents (, ). The CM generates the output current (). The current runs through the primary winding of the pulse transformer (PT). This transformer has divided the secondary winding. It interconnects the outputs of both rectifiers, which means that influencing the shapes of the rectifiers’ output currents is possible by applying the flowing through the pulse transformer (PT) [,,]. The interrelation between the rectifier’s output currents, the modulator’s current, and the system’s output () is presented in Formulas (1)–(3):
where , are PT winding turns and .
The main goal of the current modulator with the pulse transformer is to provide the suitable shape of each phase current of the generator (G). Thus, as a result, the mmf associated with a given pair of windings (star–delta) is a sine wave. This reduces power loss in its magnetic circuit to a minimum value. This phenomenon has been called “the modulation of the magnetic flux”. It refers directly to the principles of the CM operation. So, the generator can be named, in this case, as a synchronous generator with a permanent magnet with magnetic flux modulation (PMSGMF). In order to ensure the sine shape of the mmf, the MFM output current must comply with Equation (4) []:
where is the frequency of the generators’ output voltage.
However, if the modulator generates the signal, which is described by this equation, it should be noted that the sine wave of the resultant mmf associated with only one given pair of windings (star–delta) will be obtained. In the remaining given pair of windings, the resultant mmf will be additionally deformed. This is not a preferred solution. For this reason, the current modulator should generate a signal characterized by the same phase shift in relation to each of the individual resultant mmf values of the presented generator. As a consequence, the modulator should generate a signal described by Equation (5).
The current given by (5) has a triangular shape, and its fundamental frequency is six times higher than the current value of . Taking into account (5), the expected shapes of the phase currents of the generator will look like those shown in Figure 2.
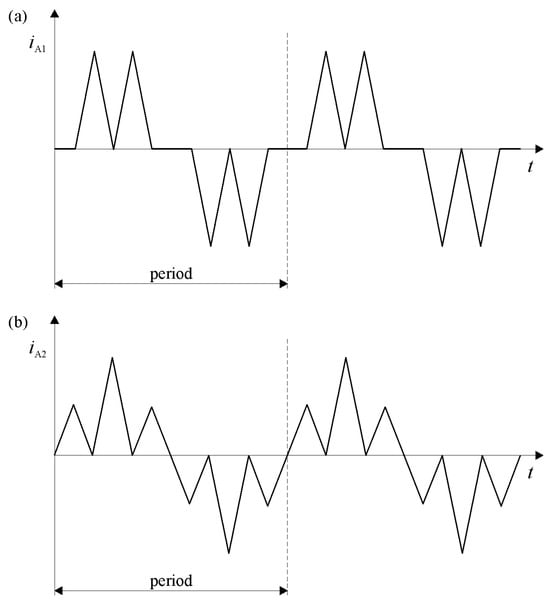
Figure 2.
Theoretical shape of the phase current of the PMSGFM generator for a group of connections: (a) star (iA1) and (b) delta (iA2) [].
As a consequence, the mmf associated with each pair of stator windings is quasi-sinusoidal (Figure 3).
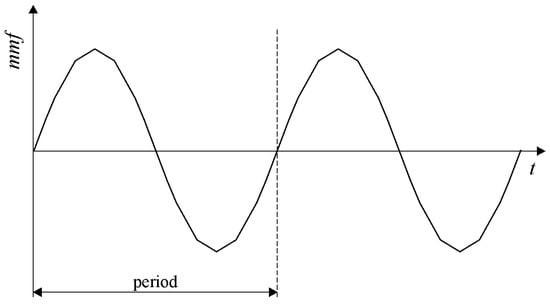
Figure 3.
Resultant mmf associated with a pair of windings—the first one is connected in the star, while the second in the delta configuration [].
By shaping the phase currents of the star–delta windings (Figure 2), it is possible to influence the resultant mmf associated with given pairs of windings.
From the perspective of the intricacy of the system’s construction, a very important detail is that the power of the current modulator with the pulse transformer is really low, theoretically about 2.35% [], in comparison to the system’s nominal output power.
3. The Power Electronic Current Modulator (CM)
3.1. The Power and Control Circuit of the Current Modulator
The power structure, with a simplified control system of the current modulator, is presented in Figure 4 (this scheme does not include a coupling pulse transformer).
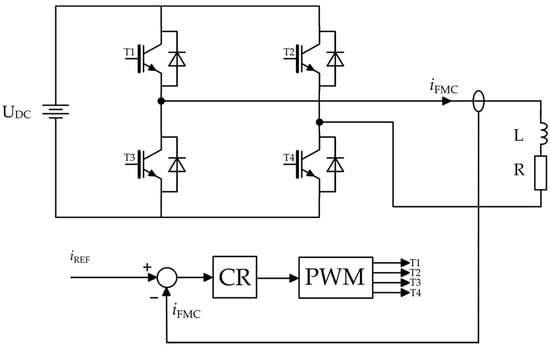
Figure 4.
Scheme of the current modulator based on the H-bridge structure with the output filter.
The main circuit was built on the basis ofa power electronics-controlled current source, which took the form of a transistor H-bridge with an inductive element at the output. It was given that a closed-loop control system was utilized with the negative feedback from the modulator current (iFMC) signal generated by the modulator. This signal indirectly influenced the shaping of the resultant flux in the stator of the generator.
In order to achieve the most accurate representation of the reference signal in the output signal, an unconventional current regulator (CR) was used in the control path. Its structure and the method of selecting parameters are described in the next subsection.
The PWM block (pulse-width modulator) was implemented in a simulation model, which was elaborated during the research, by using a comparator, comparing the output signal of the regulator (CR) with a triangular carrier signal. Additionally, a sampling and hold system was used. It worked with a frequency that was two times higher than the switching frequency of the transistors. In this way, the double-update operating mode of the PWM generator implemented in the ADSP-21369 type signal processor, which was used in the experimental model, was mapped []. As a consequence, the delay introduced into the control path was reduced to half of the period of the carrier waveform.
The linear model of the current modulator developed on the basis of the theory of signals is shown in Figure 5. It was developed on the basis of the synthesis of the power circuit and control circuit of the system described above. This model was used in the selection of the structure and parameters of the current regulator used in the control circuit.
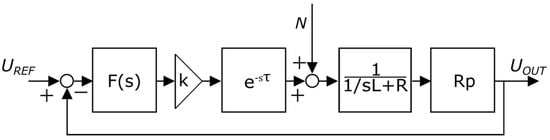
Figure 5.
The linear model of the current modulator [].
Immediately after the current regulator in the form of a low-pass filter (F(s)) is the 0-order amplifier block (k). It represents the resultant amplification of the control system and the power part of the current modulator, which is expressed by Equation (6).
Here, kf is the gain of the low-pass filter F(S), UDC is the voltage value in the DC circuit of the MFM modulator, and UAmpPWM is the amplitude of the carrier signal of the PWM block
The block corresponds to the resultant delay contributed by the PWM block and the inverter. The delays resulting from the implementation of the control algorithm by the real processor system in the considered case are omitted. The R and L values represent, respectively, the short-circuit resistance and inductance of generator windings with star–delta connections and pulse transformer, i.e., the resistance and inductance of the output current modulator filter. The resistance RP corresponds to the conversion constant of the current measuring transducer located in the output circuit of the current modulator. The signal represents the voltage induced in the secondary windings of a pulse transformer, but it is omitted in further considerations.
3.2. The Structure and Parameters of Current Regulator Implemented in Control System of CM
During the simulation tests, criteria for the selection of parameters and the structure of the current regulator (CR) in the power electronic control path of the current modulator were formulated []. On their basis, the target solution was selected, and this was then verified at the stage of simulation and also through experimental research.
The first of the analyzed criteria was the limitation of the rate of change of the modulating signal of the PWM block. This condition was necessary in order to achieve the correct switching frequency of the transistors—that is, equal to the frequency of the carrier signal. This condition is expressed by Formula (7):
where F(s) is the transmittance of the current regulator (CR) and uPWM is the carrier signal.
Another important criterion for the optimal selection of the regulator structure was to establish the stability of the closed control system, with the most faithful representation of the reference signal in the output signal possible. The Bode criterion was used to analyze the stability, enabling, among others, us to take into account the influence of the delay term. An important condition resulting from this criterion was the need to ensure the highest possible value of the open system transmittance modulus in the useful frequency band in order to faithfully reproduce the reference signal. On the other hand, the value of this modulus had to be less than 1 (0 dB) for a phase shift equal to −180° and greater in order to ensure stability. The transmittance of an open system is described by Relation (8):
The last of the analyzed criteria for the selection of the structure and parameters of the current regulator was the criterion related to the aliasing effect occurring in the feedback signal [,]. This effect takes place in discrete signal processing systems and is a consequence of such systems not satisfying the Kotelnikov–Shanonn theorem, which defines the maximum value of the sampled signal bandwidth in relation to the sampling frequency. The limitation of the frequency band of the output signal, and, consequently, also of the differential signal, was ensured by the use of a low-pass structure, which performed the function of a current regulator, and the output filter in the current modulator.
On the basis of the elaborated criteria, the responses of the system to various parameters of the current regulator with the structure of a low-pass filter were examined. Assuming the switching frequency of the semiconductors to be at the level of 12 kHz, the cutoff frequency of the filter F(s) was 6 kHz. In this way, the requirements specified by the Kotelnikov–Shanonn theorem on the minimum sampling frequency of continuous signals were referred to (the PWM block should be treated, in this case, as a sampling and holding system).
Based on the research results, the current regulator was modified with an additional structure, which is described by Relation (9) [].
This additional structure is based on a differentiator term (high-pass filter), which is characterized by a positive phase shift. In principle, this structure is designed to minimize the phase delay effects introduced in the control path. The time constant of the differentiating part TR was determined using Formula (10):
The delay was equal to half of the transistor impulse period, which resulted from the fact that the modulation depth factor was determined twice during the PWM period (double-update mode).
The use of a modified regulator (with an additional high-pass filter) made it possible to increase the resultant transmittance gain of the open system while maintaining the stability of the closed system. This was confirmed by the frequency characteristics of the system, represented in the form of Equations (11) and (12):
The frequency, amplitude, and phase characteristics of an open circuit for a regulator with the structure of only a low-pass filter and an elaborated regulator consisting of a combination of high- and low-pass filters for the same gain value are presented in Figure 6. The obtained values of phase margins and gain have higher values in the second case.
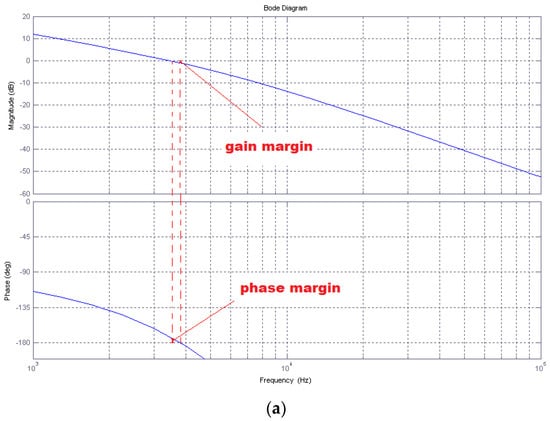
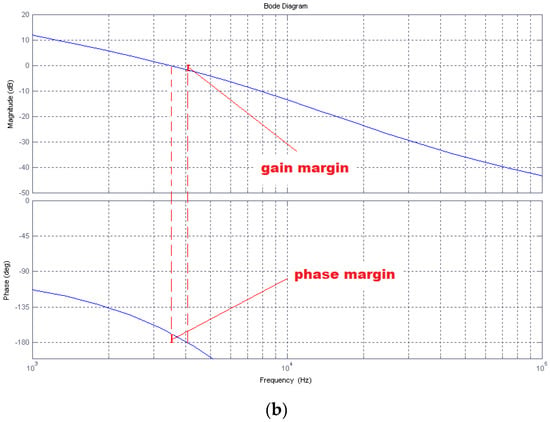
Figure 6.
Amplitude and phase characteristics of an open circuit for (a) a current regulator with a low-pass filter structure and (b) a current regulator consisting of a combination of high- and low-pass filters.
Figure 7 shows selected test results of the signal simulation model of the system for the current regulator in the form of only a low-pass filter and with an additional high-pass structure. The values of the resultant gain in both cases were the same. A rectangular waveform was used as a reference signal, which allowed us to reliably compare the dynamic parameters of both solutions. Both the higher level of oscillations around the reference signal and their longer decay time in the case of the control system without an additional high-pass filter indicate a smaller margin of stability compared to the solution with the regulator being a series connection of both filters.
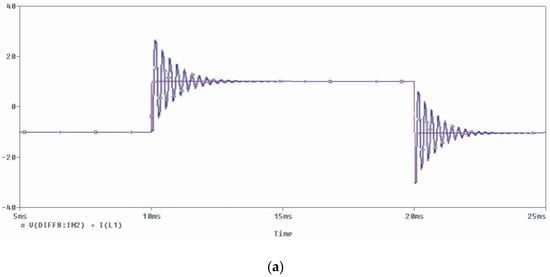
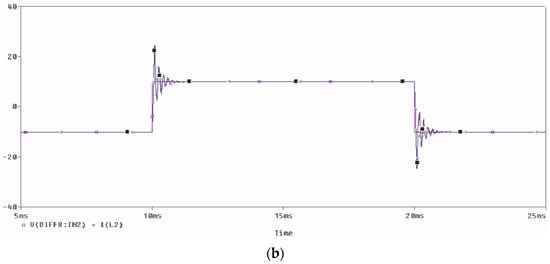
Figure 7.
Reference and output signals of the current modulator for low-pass filters (a) and additional high-pass filters (b) implemented in the control system.
The development of an unconventional regulator with a phase corrector (high-pass filter) made it possible to increase the gain in relation to the solution based on a single low-pass filter by approx. 30%. This was confirmed by the results of experimental research on the built current modulator, which are discussed in Section 5.
As a consequence, the quality of mapping the reference signal in the high-current output signal of the current modulator was improved.
4. The Additional Low-Power Transistor Rectifier in the DC Circuit of the Current Modulator
4.1. The Principle of Working and Main Circuit of the Additional Transistor Rectifier
Additionally, to improve the efficiency of the presented system, the low-power transistor rectifier (LPTR), connected to the DC circuit of the current modulator, was used. With help of this converter, it is possible, among others, to control and stabilize the voltage in the DC bus of the modulator. It works, in this case, in inverter mode. Figure 8 explains how to solve the problem of connecting to the power-electronic current modulator. In this way, control of the voltage in the DC bus of the modulator by returning energy to the AC voltage grid is assured.
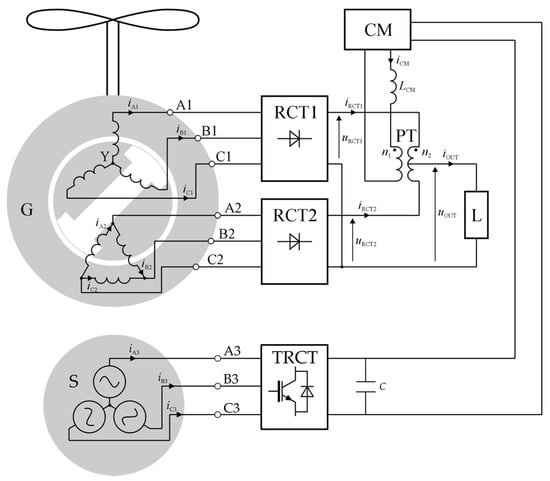
Figure 8.
The ideal model of a generator with flux modulation (PMSGFM) and additional transistor rectifier.
It should be emphasized that the power of this active rectifier is only about 2.35% of the power of the whole system, similar to the current modulator with a pulse transformer. This is a very big advantage of the described solution. For this reason, it is possible to use an additional transistor rectifier in both single- and three-phase variants. In the further part of this article, the use of a single-phase version of this system is considered. The use of a transformer coupling the transistor rectifier with the AC voltage grid is not always necessary. This element must be used in cases where the voltage in the DC bus of the modulator is lower than the amplitude of the AC voltage. The fulfillment of this condition is necessary in order to enable the proper operation of the described subsystem.
4.2. The Control Algorithm of the Additional Transostor Rectifier
As mentioned, the additional low-power rectifier works in this application in inverter mode, thus enabling the return of energy to the AC voltage grid. This energy is transferred from the output circuit of the diode rectifiers through the pulse transformer and current modulator to the DC intermediate circuit. This DC bus, which is common to both the transistor rectifier (LPTR) and the current modulator (CM), is indirectly responsible for shaping the resultant flux in the generator stator.
The value of the transferred energy depends on the amplitude of the modulating current signal and the voltage induced on the pulse transformer. The energy flow in this part of the system is presented in Figure 9.
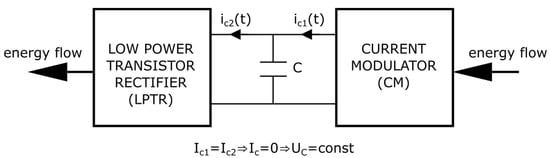
Figure 9.
The idea scheme of energy flow between the current modulator and additional low-power transistor rectifier.
The reference phase grid current for this additional rectifier is determined from Equation (13) for a three-phase system and (14) for a single-phase system.
Here, PDC is the power transferred by the current modulator to the intermediate circuit (DC bus), uL(t) is the grid voltage, and UL is the RMS value of the grid voltage.
Figure 10 shows a basic idea of an elaborated control system for a transistor rectifier operating in inverter mode.
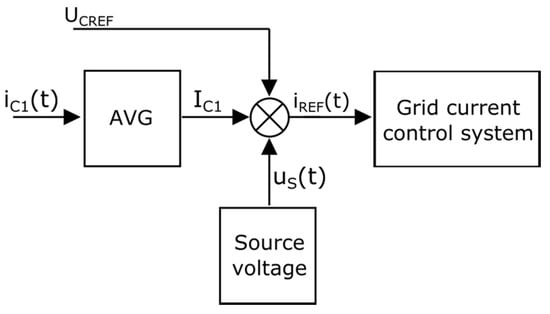
Figure 10.
The basic block diagram of a control system for an additional transistor rectifier.
This allows to obtain the AC grid current resembling a sinusoidal shape for a wide range of changes in both the reference voltage on the capacitor UCREF in the DC bus and the current generated by the current modulator (the amplitude of the signal generated by the modulator depends on the average value of the output current iout).This is achieved by directly determining the active power PDC transferred to the DC circuit by the modulator. This PDC power is equal to the product of the reference voltage on the capacitor in the DC circuit of the modulator and the average value of the current ic1(t), which is described by Relation (15):
where IC1 is the average value of the current in the intermediate circuit of the current modulator.
The voltage uS(t) is expressed by Formula (16). In order to ensure an inverter mode in the transistor rectifier, it is shifted by 180 electrical degrees in relation to the AC grid voltage:
where uL2(t) is the voltage of the secondary side of the matching transformer and UL2 is the RMS value of this voltage.
At the output of the multiplier block, the reference active current is obtained, and this must be generated by the transistor rectifier to achieve a voltage in the DC circuit equal to the reference voltage UCREF. The last element of the control path is the block of the current follow-up control system, consisting of the current regulator and the PWM block (similarly as in the case of the current modulator, which was described previously).
It should be indicated that for the correct functioning of the described system, it is compulsory to ensure that the voltage on the intermediate circuit capacitors is higher than the amplitude of the phase AC voltage (for a single-phase system) or the amplitude of the phase-to-phase voltage (for a three-phase system) of the secondary side of the coupling transformer.
In the control algorithm, which was presented above, power losses in the circuits were not included in the energy balance. Now, taking into account these losses, in order to determine the correct reference active current and, consequently, also the amount of energy returned to the AC grid, an additional voltage regulator was implemented. This regulator compared the reference voltage UCREF with the real voltage uC(t) on the capacitor of the DC bus (Figure 11).
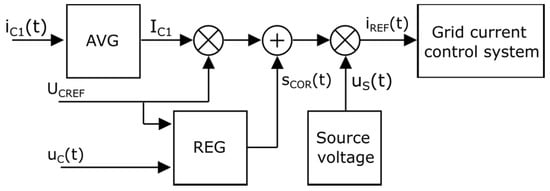
Figure 11.
The modified block diagram of the control system with an additional voltage regulator.
Instead of the voltage regulator, it is also possible to use a current regulator comparing the average values of the output current iC1(t) of the current modulator and the input current iC2(t) of the transistor rectifier in the intermediate DC circuit between these converters. If the equality condition IC1 = IC2 is fulfilled, the average value of the capacitor current IC is equal to zero, so its voltage does not change. The block diagram of the control system with the additional current regulator is shown in Figure 12.
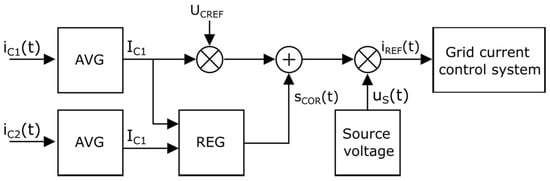
Figure 12.
The modified block diagram of the control system with an additional current regulator.
Both control systems, with additional voltage or current regulators, yield similar results. The applied regulators are responsible only for the correction of errors in determining the active reference current resulting from power losses in the circuits. In their case, the output signals determined by these correcting regulators take relatively small values, thus minimizing the distortion of the reference current for the low-power transistor rectifier. Thus, it is possible to obtain the grid current generated by this converter in a manner very similar to the sinusoidal signal.
However, for this control algorithm concept, it is necessary to charge the DC bus capacitors at the start to a voltage level that is close to the reference voltage UCREF. For this purpose, during the system start-up procedure, while the current modulator is running, the transistor rectifier should be temporarily deactivated (until the DC bus voltage level is close to the reference voltage UCREF). The rectifier current reference signal can be suitably expressed by Expression (17).
The signal named sCOR (t) means, in this case, the output correction signal of the additional voltage or current regulator.
5. Selected Results of Simulation and Experimental Research
The results presented in this chapter were obtained via both simulation and experimentation. The flux modulation concept for the generator was verified on the basis of simulation tests. At this stage of research, the construction of a new physical model of the generator was still in progress. The power electronic system was built physically. For this purpose, instead of the generator, a transformer with appropriate connection groups was used (Figure 13).
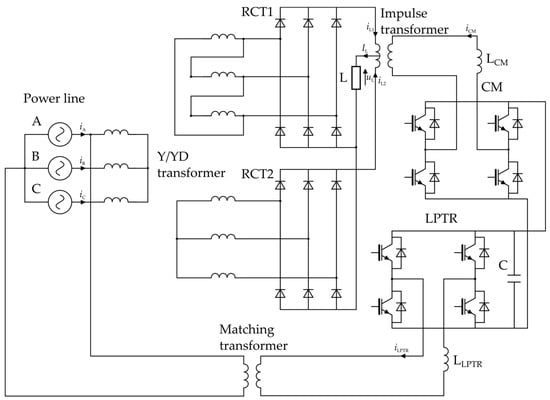
Figure 13.
The scheme of the power circuit of the elaborated system that was used during the research.
In order to check the effectiveness of the proposed unconventional PMSGFM with star–delta winding, a comparative analysis of the finite element method (FEM) was carried out. The torque constant and core losses were compared with a standard designed PMSG. The Ansys Maxwell environment was used, and in this, two FEM PMSG models were developed. The geometries of the magnetic circuits of both models were identical. The only difference was related to the design of the stator windings []. The individual coils were placed in the same slots, and the numbers of turns in the star and delta coils were set to produce the same value of electromotive force between the lines. For comparison purposes, the simulation parameters, including mesh density, time step size, and Newton Raphson procedure tolerance, were retained during model testing []. Due to the different numbers of turns in the star and delta winding coils, the slot current eq i was determined. The value of this equivalent signal was referenced to the total mmf in the slot generated by particular phase windings according to the equation below:
The results of the finite element analysis provide the conclusion that if a machine with star–delta winding is compared to a machine with a standard-designed magnetic circuit, there is practically no observable decrease in performance. Both of the machines present the same torque vs. current characteristics. Moreover, the calculated core losses are the same (Figure 14).
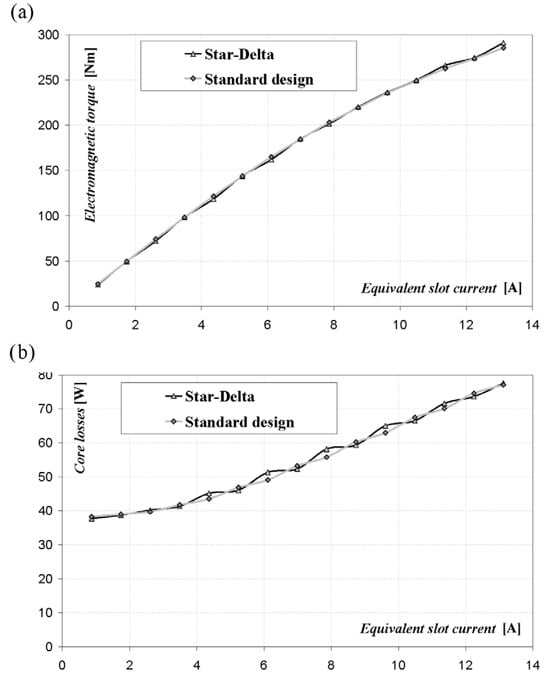
Figure 14.
Average electromagnetic torque (a) and core losses (b) as functions of the equivalent current for machines with a standard design and a generator with star–delta winding [].
The determined back emf waveforms from line to line () for the star winding, and also the phase () for the delta winding, are presented in Figure 15a, while the line-to-line signals of a model with a classic design are shown in Figure 15b.
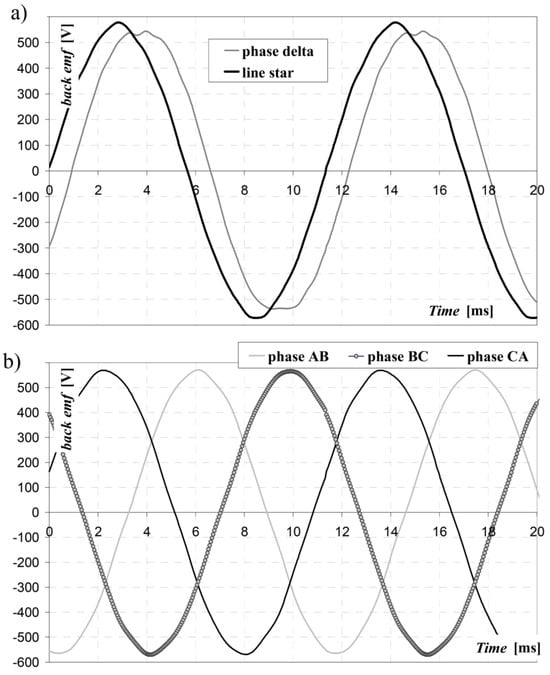
Figure 15.
Back emf waveforms: (a) phase delta winding and line-to-line star winding; (b) waveforms of , , and in a standard machine [].
Since the core losses in the cases of both described generators (standard and with star–delta winding groups) were at the same level, it may seem that the proposed generator solution is not justified. However, it should be remembered that the efficiency of the entire system is also greatly influenced by the converters cooperating with the generator. Therefore, in the following part, a comparative analysis of the efficiency of the power electronic circuit is conducted. Two structures are considered, namely:
- -
- The described structure based on diode rectifiers with a current modulator, which is dedicated to PMSGFM with star–delta windings;
- -
- A fully controlled classical transistor rectifier, which is supplied by a standard PMSG generator.
For the evaluation of the loss in the power-electronic circuits of the elaborated systems, simulation models of these sections were built in the OrCAD environment []. Models of IGBT IPMs were based on components produced by MITSUBISHI ELECTRIC. For calculations of power losses in the used modules, this company provides its own software, which is called Melcosim ver. 5.4.2.
In the first case, for the system based on current modulation, a replacement model of the generator was used. This structure consisted of the three-winding transformer with a secondary side winding connected in star and delta. The primary side was connected to a three-phase voltage source with an output signal that varied in the range of 80 ÷ 400 V. The output frequency varied in the range of 10 ÷ 50 Hz. The model of the proposed power electronics circiuit consists of the following blocks:
The diode rectifiers—this model is based on twothree-phase bridge diode rectifier modulesof type 26MT120 (25 A/1200 V), produced by VISHAY [];
The current modulator—the main utilized elements were the IGBT-based H-bridge, output inductive low-pass filter, and pulse transformer; the used model of the semiconductor device was based on the IPM/IGBT module type PM25CL1A120 (25 A/1200 V); the models of the coil and impulsive transformer were based on physical devices []; the additional transistor rectifier was build in the same way as the current modulator.
Other basic parameters of this system were as follows:
- -
- Nominal output values for generator: fGN = 50 Hz, UGoutN = 535 V, IGoutN = 10 A;
- -
- Nominal output values for current modulator: LCM = 350 ÷ 450 μH (the coil inductance value depended on the value of the coil current), frequency of carrier signal: 10 kHz.
The schematic diagram of the power circuit of the elaborated system that was used during the tests is presented in Figure 13.
In the second case, for the system without current modulation, the generator was replaced by a three-phase energetic transformer, which wasutilized in the star configuration. The active transistor rectifier also used PM25CL1A120. The rated output voltage was equal to 600 V and the rated current was 9 A. The schematic diagram of the power circuit of the used model is shown in Figure 16.
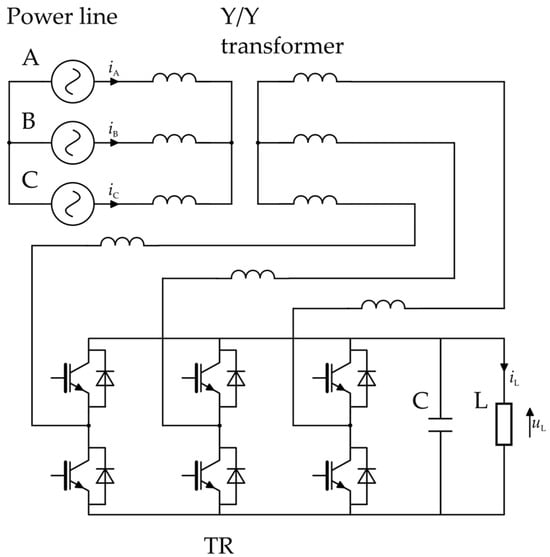
Figure 16.
The scheme of the power circuit based on an active transistor rectifier that was used during the research.
Figure 17 presents the curves of the simulation model efficiency (ηE) for both the MSS (Model of the Standard System) and the MNS (Model of the Novelty System based on current modulation) vs. the relative output power of a power electronics system.
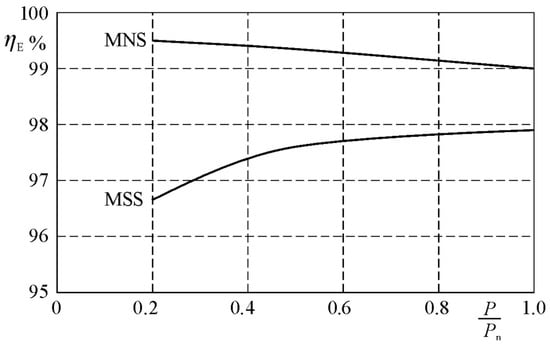
Figure 17.
Efficiency curves of MNS and MSS vs. relative output power [,].
The efficiency of the elaborated system was higher than in the case of a classic model by 1.1 ÷ 2.9% depending on the output power.
During the works, the construction and preliminary tests of the power-electronic part of the described system were carried out (the generator with the star–delta winding group is currently under construction). The main circuits of the current modulator (CM) and the additional low-power transistor rectifier (LPTR) were built on the basis of two modules (PM50RSA120 from Mitsubishi) []. Current- and voltage-measuring transducers were implemented using LA 55-P/SP1 and LV 25-P elements from LEM [,]. These converters are also equipped with an optoelectronic galvanic isolation system enabling the separation of the power circuits from the control part.
The control system of the power-electronic current modulator and the transistor rectifier was built with the help of the ALS-G3-1369 system. It is based on a floating-point signal processor of the SHARC 3 family—the ADSP-21369 generation from Analog Devices. As a result of using an efficient signal processor equipped with an extensive, 16-channel PWM generator module, it is possible to implement complex control algorithms for power-electronic converters [].
The analog-to-digital interface based on AD7656BST chips is responsible for processing analog signals []. It is equipped with two 16-bit 6-channel analog-to-digital converters with simultaneous sampling. During the experimental tests, the impulse frequency (PWM frequency) was assumed to be 12 kHz and the signal sampling frequency to be 240 kHz.
In the source code, a control system based on unconventional structures of elaborated current regulators was implemented. For this purpose, digital filters with infinite impulse response (IIR) were used. This allowed to increase the gain of the regulators while maintaining a stable closed-loop system. In Figure 18 are shown the output signals for both variants of the current regulator (with only a low-pass filter structure and with an additional high-pass filter), which were utilized in the control path of the current modulator. In this case, it works as a controlled power-electronics current source. As a reference signal, the square waveform was used.
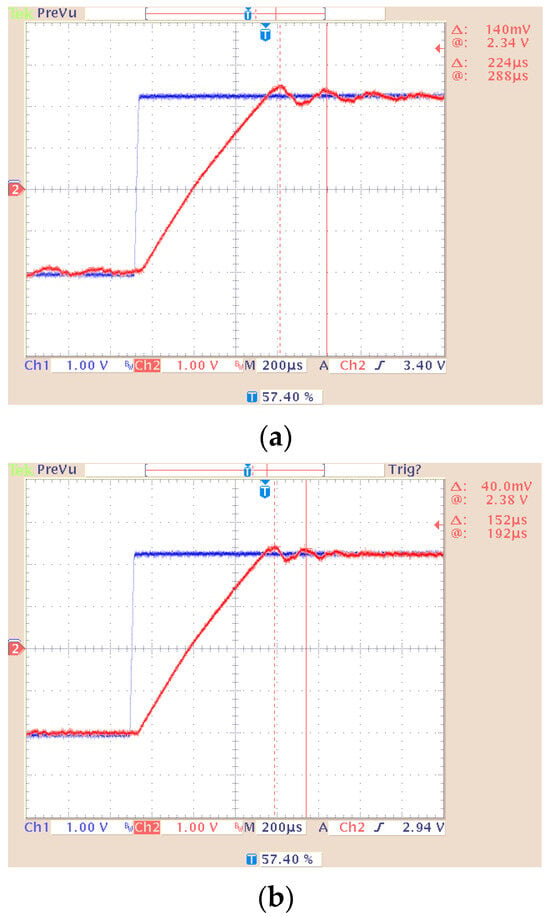
Figure 18.
Output and reference signal of the current modulator for: (a) regulator with a low-pass filter structure; (b) a regulator based on a high- and low-pass filter.
The amplification k values were chosen in such a way as to enable the excitation of the system. The values of k for both variants of the regulator differed by 30%. Based on the obtained results, it was found that the oscillation frequency of the output signal was higher in the case of the implemented additional high-pass structure. This proves a wider usable frequency response and, consequently, the better dynamics of the entire system. As a consequence, the quality of mapping the reference signals for the current modulator and the low-power transistor rectifier was improved.
The elaborated-during-research algorithm for controlling the additional rectifier, which works in inverter mode, was also implemented. In this case, the structure of the current regulator was the same as in the case of the control path of the current modulator.
Figure 19 presents the output signals of diode rectifiers and the signal generated by the current modulator for the physical model. The resultant grid current for the selected phase is shown in Figure 20. However, based on the earlier results, it can be concluded that this current corresponds to the resultant magnetomotive force (mmf) of the synchronous generator PMSGFM associated with a given pair of windings with a star–delta connection group.
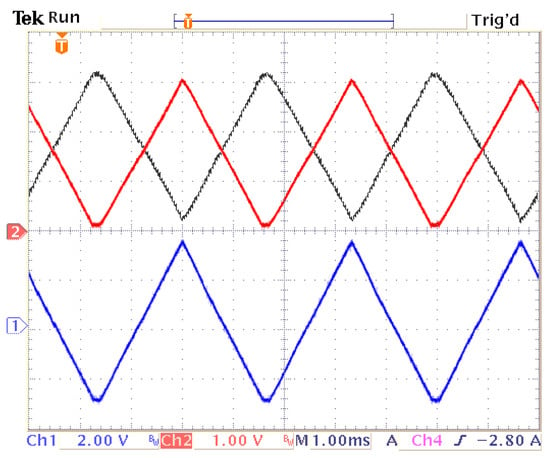
Figure 19.
Waveforms of the output currents of the diode bridges (black and red colors) and the output current of the current modulator (blue color).
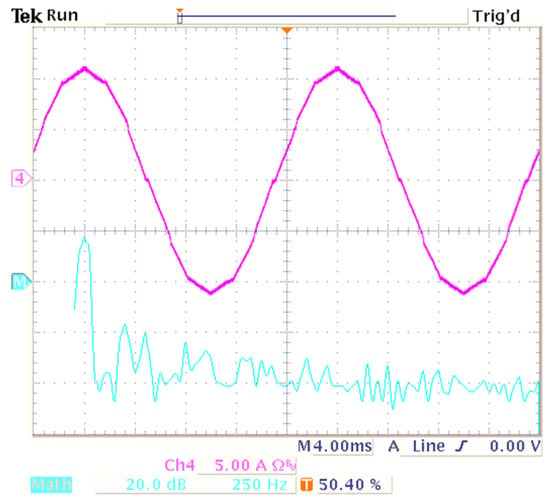
Figure 20.
Waveform and spectral analysis of the grid current.
The voltage waveform on the primary side of the transformer coupling the transistor rectifier (LPTR) with the AC grid and the current generated by this subsystem are presented in Figure 21.
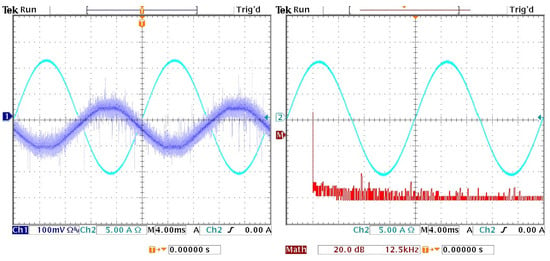
Figure 21.
Waveforms of current (azure) and voltage (dark blue) on the primary side of the matching transformer of the transistor rectifier and spectral analysis of the current (red).
It can be observed that these signals are shifted by 180 electrical degrees. This is due to the work of the transistor rectifier in the inverter mode. It is estimated that the use of this additional converter will increase the efficiency of the whole system by about 2%, which is not without significance at high power. The signal of the DC bus of the LPTR and CM is shown in Figure 22.
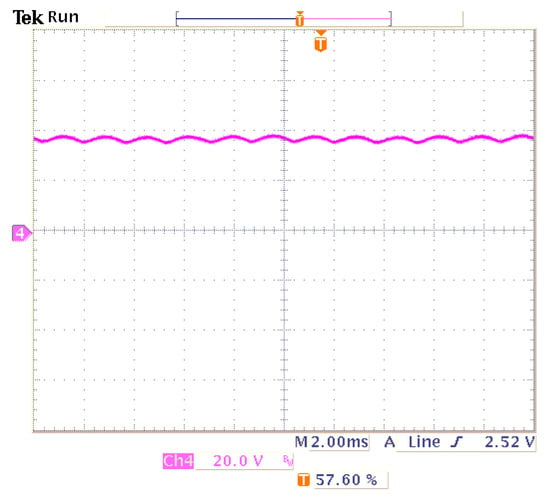
Figure 22.
The waveform of voltage in the DC bus of the transistor rectifier and current modulator.
The described experimental results confirm the correct functioning of the implemented control algorithm for the additional transistor rectifier. The stabilization of the voltage on the DC bus was ensured, with the return of energy to the AC grid. Visible pulsations in the DC bus (Figure 22) resulted from the twelve-pulse nature of the diode rectifier, which was used in the main power circuit.
6. Conclusions
The presented system based on asynchronous generator with flux modulation (PMSGFM) is characterized by the relatively simple structure of the power section (classic diode rectifiers are used). Such a solution allows one to achieve high reliability and high efficiency with regards to the power electronics part. In order to minimize the losses in the generator, an unconventional design of the stator windings and a current modulator coupled with diode rectifiers through a broadband pulse transformer are used. In addition, the low-power transistor rectifier is used to increase the efficiency of the whole system. This also makes it possible to stabilize the voltage in the intermediate circuit of the current modulator.
It should be highlighted that the described solution is very beneficial, especially for medium- and high-power systems. The power of the current modulator and the additional transistor rectifier is only 2.35% of the power of the whole system, which significantly reduces costs and simplifies the construction of the high-current part. Furthermore, it is characterized by very high reliability. Even if the current modulator fails, it is still possible to transfer energy from the generator to the load.
Funding
This research received no external funding.
Data Availability Statement
The data is available at the link: https://sin.put.poznan.pl/people/details/michal.krystkowiak.
Conflicts of Interest
The author declares no conflict of interest.
References
- Strielkowski, W.; Civín, L.; Tarkhanova, E.; Tvaronavičienė, M.; Petrenko, Y. Renewable Energy in the Sustainable Development of Electrical Power Sector: A Review. Energies 2021, 14, 8240. [Google Scholar] [CrossRef]
- Zbroński, D.; Otwinowski, H.; Górecka-Zbrońska, A.; Urbaniak, D.; Wyleciał, T. Analysis of Changes in Electricity Generation from Renewable Energy Sources after Poland’s Accession to Structures of the European Union. Energies 2023, 16, 4794. [Google Scholar] [CrossRef]
- Brodny, J.; Tutak, M.; Saki, S.A. Forecasting the Structure of Energy Production from Renewable Energy Sources and Biofuels in Poland. Energies 2020, 13, 2539. [Google Scholar] [CrossRef]
- Available online: https://www.gwec.net/wp-content/uploads/vip/GWEC-Global-Wind-2015-Report_April-2016_19_04.pdf (accessed on 21 July 2023).
- Available online: https://gwec.net/1twcelebration/ (accessed on 21 July 2023).
- Heng, T.Y.; Ding, T.; Chang, C.W.J.; Ping, T.; Yian, H.C.; Dahari, M. Permanent Magnet Synchronous Generator design optimization for wind energy conversion system: A review. Energy Rep. 2022, 8, 277–282. [Google Scholar] [CrossRef]
- Polinder, H. Overview of and trends in wind turbine generator systems. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar] [CrossRef]
- Fang, H.-w.; Song, R.-n.; Xiao, Z.-x. Optimal Design of Permanent Magnet Linear Generator and Its Application in a Wave Energy Conversion System. Energies 2018, 11, 3109. [Google Scholar] [CrossRef]
- Nityanand; Pandey, A.K. Electrical Engineering Aspects and Future Trends for PMSG Turbines and Power Converters: A Present Market Survey. In Proceedings of the 2018 International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 13–14 April 2018; pp. 683–688. [Google Scholar] [CrossRef]
- Gwóźdź, M.; Krystkowiak, M.; Jędryczka, C.; Gulczyński, A.; Matecki, D. Generator with modulated magnetic flux for wind turbines. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 469–478. [Google Scholar] [CrossRef]
- Supronowicz, H.; Strzelecki, R. Power Factor in AC Power Systems and Methods of Its Improvement; OWPW: Warsaw, Poland, 2000. (In Polish) [Google Scholar]
- Rolek, J. Analysis of Systems with a Parallel Connection of Diode Converters with Modulation in the DC Circuit. Ph.D. Dissertation, Kielce University of Technology, Kielce, Poland, 2011. [Google Scholar]
- Krystkowiak, M. Power Rectifier System with Improved Indicators with Power Electronic Current Modulator. Ph.D. Dissertation, Poznan Univesity of Technology, Poznan, Poland, 2009. [Google Scholar]
- Gwóźdź, M.; Krystkowiak, M.; Ciepliński, Ł.; Strzelecki, R. A Wind Energy Conversion System Based on a Generator with Modulated Magnetic Flux. Energies 2020, 13, 3285. [Google Scholar] [CrossRef]
- Brogan, W.L. Modern Control Theory; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Datasheetspdf. Available online: https://docs.rs-online.com/eae0/A700000006404577.pdf (accessed on 21 July 2023).
- Datasheetspdf. Available online: https://www.allelco.com/pdf-95/PM150CL1A120.pdf (accessed on 21 July 2023).
- Datasheetspdf. Available online: https://datasheetspdf.com/datasheet/PM50RSA120.html (accessed on 21 July 2023).
- LEM. Available online: https://www.lem.com/en/product-list/la-55psp1 (accessed on 21 July 2023).
- LEM. Available online: https://www.lem.com/en/product-list/lv-25p (accessed on 21 July 2023).
- Analog Devices. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/ADSP-21369.pdf (accessed on 9 March 2021).
- Analog Devices. Available online: https://www.analog.com/media/en/technical-documentation/data-sheets/AD7656_7657_7658.pdf (accessed on 21 July 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).