Investigating the Performance of Efficient and Stable Planer Perovskite Solar Cell with an Effective Inorganic Carrier Transport Layer Using SCAPS-1D Simulation
Abstract
:1. Introduction
2. SCAPS Simulation
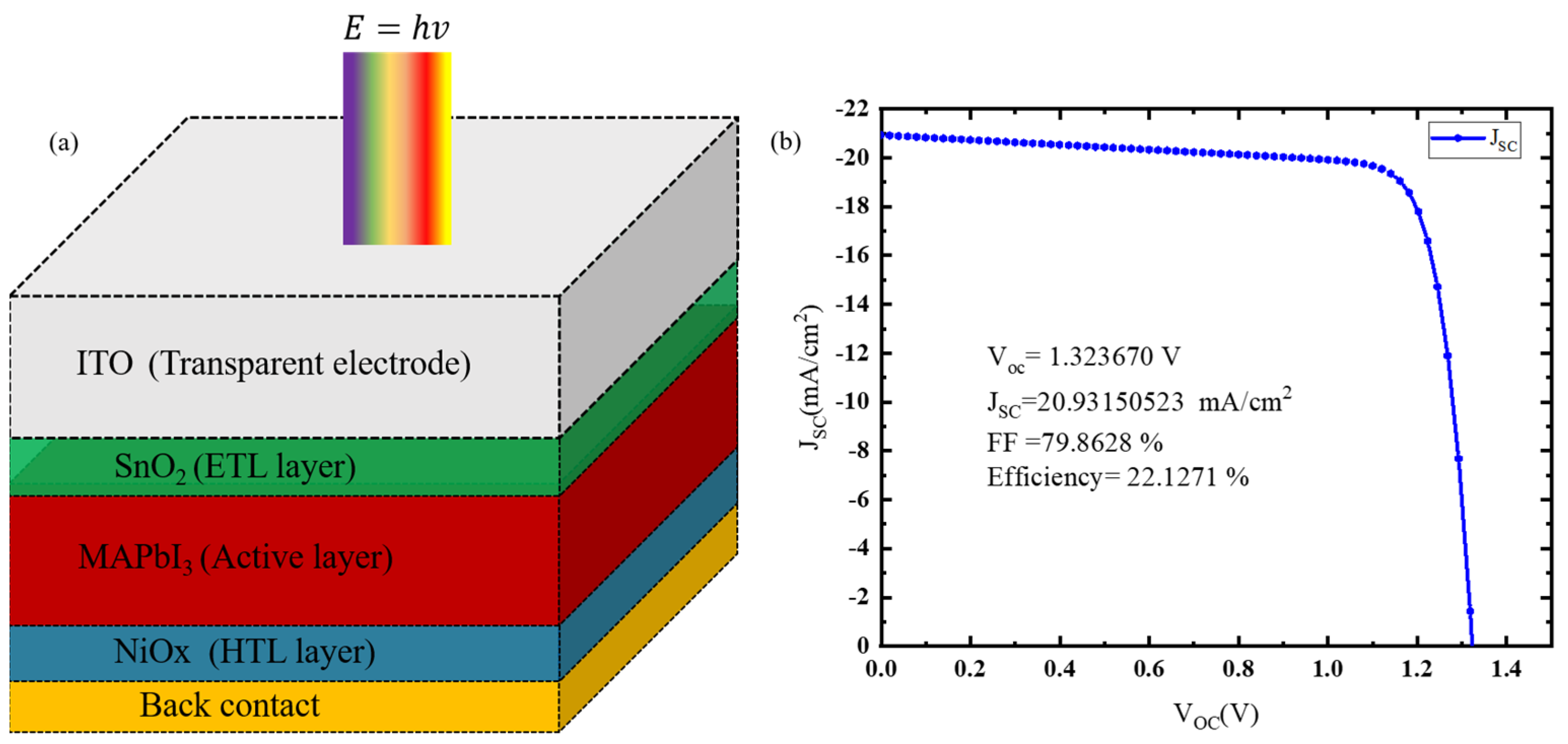
3. Proposed Device Model
| Parameters | Materials | |||
|---|---|---|---|---|
| ITO [34] | NiOX | CH3NH3PbI3 | SnO2 | |
| Thickness (nm) | 300 | 50–200 | 100–1600 | 50–200 |
| Dielectric constant | 9.00 | 10.7 [35] | 10.0 [35] | 8.00 [35] |
| Electron affinity (, χ (eV)) | 4.00 | 2.1 [36] | 4.1 [37] | 3.93 [38] |
| Bandgap, Eg (eV) | 3.5 | 3.7 [39] | 1.6 [40,41] | 3.6 [38] |
| Effective conduction band density, Nc (cm−3) | 2.2 × 1018 | 2.8 × 1019 [42] | 2 × 1018 | 3.1 × 1018 [43] |
| Effective valence band density, Nv (cm−3) | 1.8 × 1019 | 1.8 × 1019 [42] | 1 × 1018 | 2.5 × 1019 [43] |
| Mobility of electron, μn (cm2/(V s)) | 20 | 12.0 [44] | 100 | 15 [45] |
| Mobility of hole, μp (cm2/(V s)) | 10 | 25.0 [44] | 100 | 0.1 [45] |
| Donor concentration ND (cm−3) | 1.0 × 1021 | 0.0 | 1 × 109 | 1019 |
| Acceptor concentration NA (cm−3) | 0 | 1 × 1015 | 1 × 109 | 0.0 |
| Defect density (1/cm3) | 1 × 1015 | 1 × 1014 | 1 × 1014 | 1 × 1014 |
| Absorption coefficients (α) | [46] | [47] | [47] | [47] |
| Parameters | ETL/MAPbI3 | HTL/MAPbI3 |
|---|---|---|
| Defect type | Neutral | Neutral |
| Capture cross section of electrons (cm−2) | 1 × 1019 | 1 × 1019 |
| Capture cross section of holes (cm−2) | 1 × 10−19 | 1 × 1019 |
| Energetic distribution | Single | Single |
| Reference for defect energy level Et | Above the highest EV | Above the highest EV |
| Reference energy (eV) | 0.6 | 0.6 |
| Total density (1/cm2) | 1 × 1010–1 × 1020 | 1 × 1010–1 × 1020 |
4. Result and Discussion
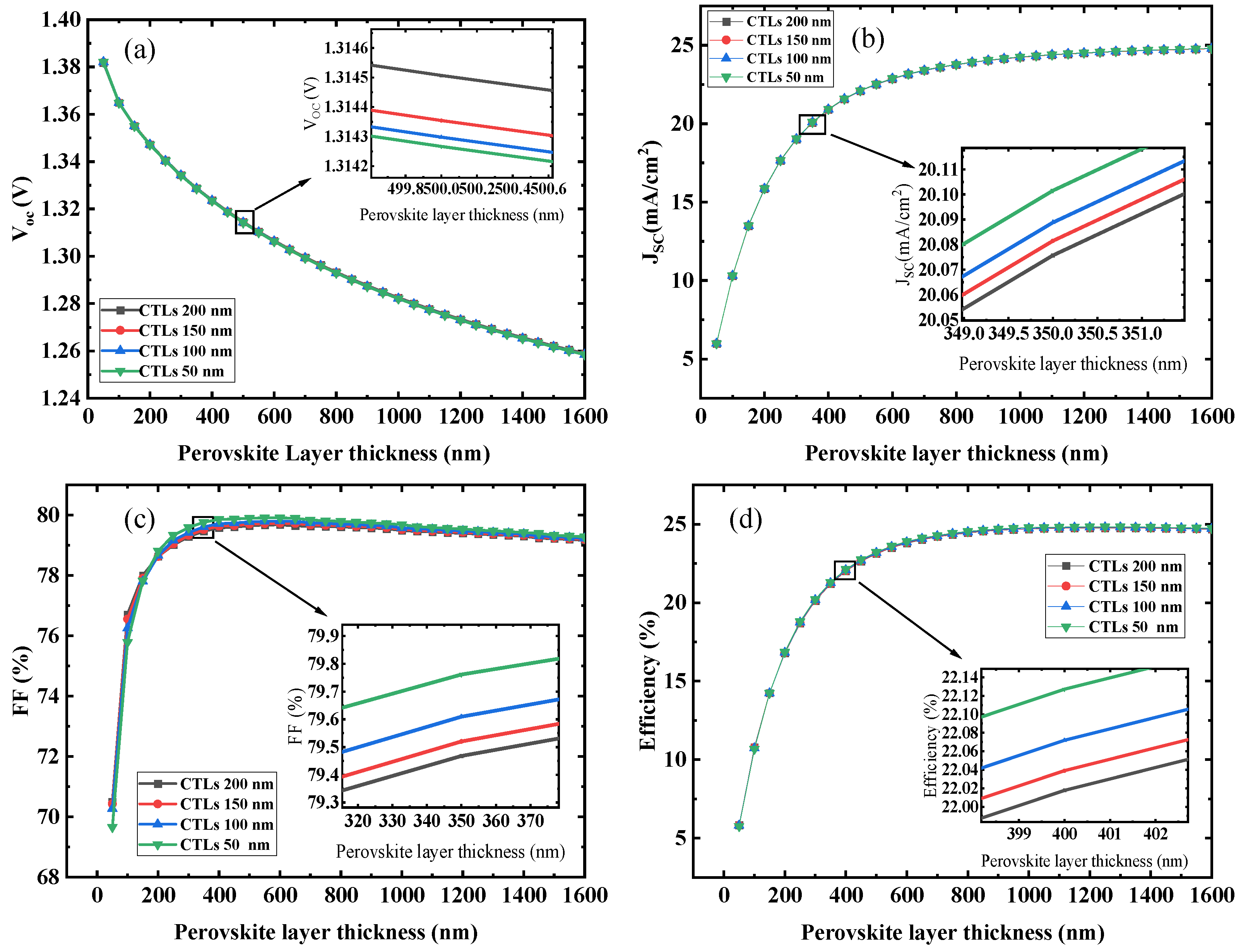
4.1. Effects of Layer Thickness
4.2. Effects of Light Intensity and Quantum Efficiency
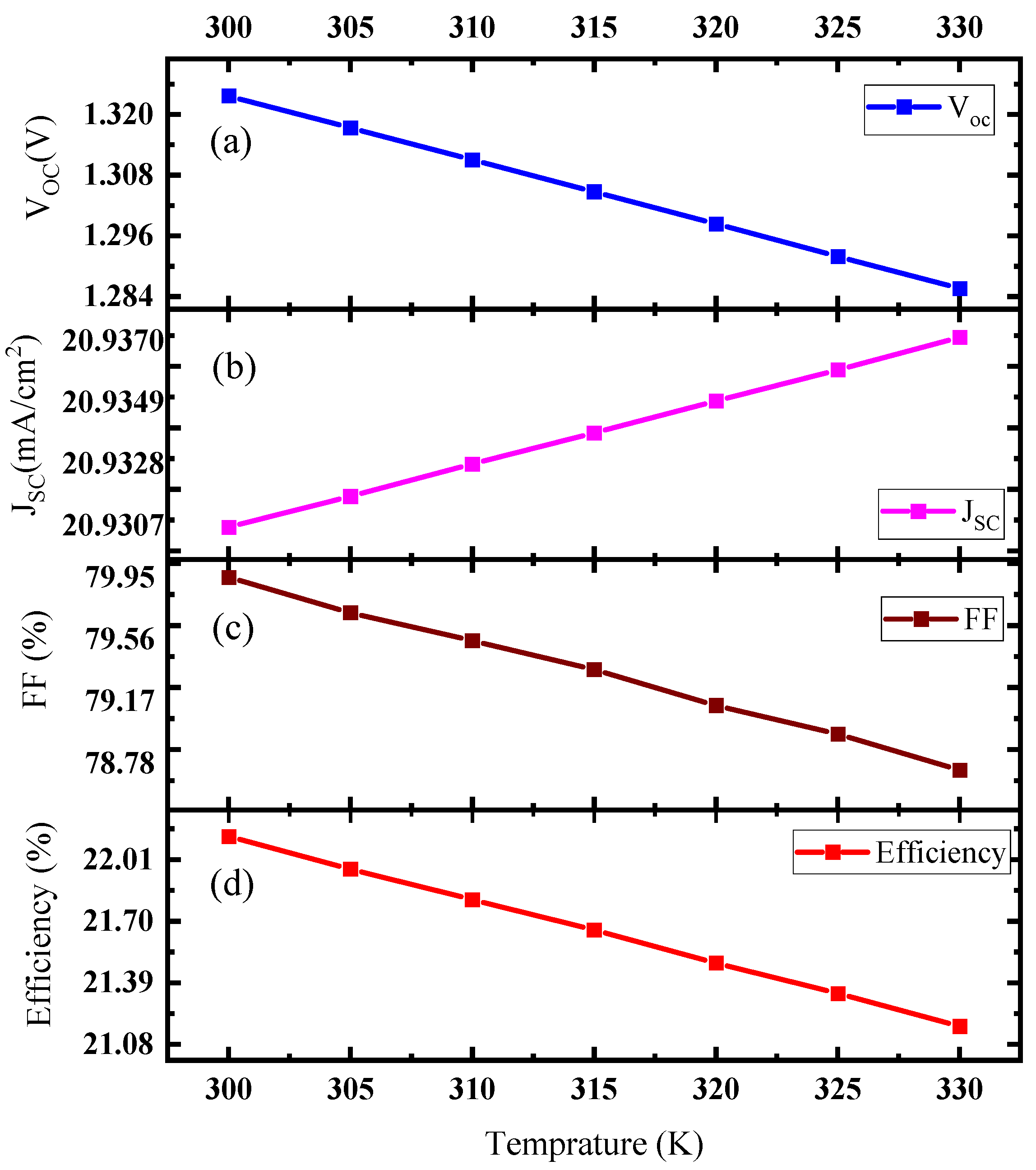
4.3. Effects of Temperature
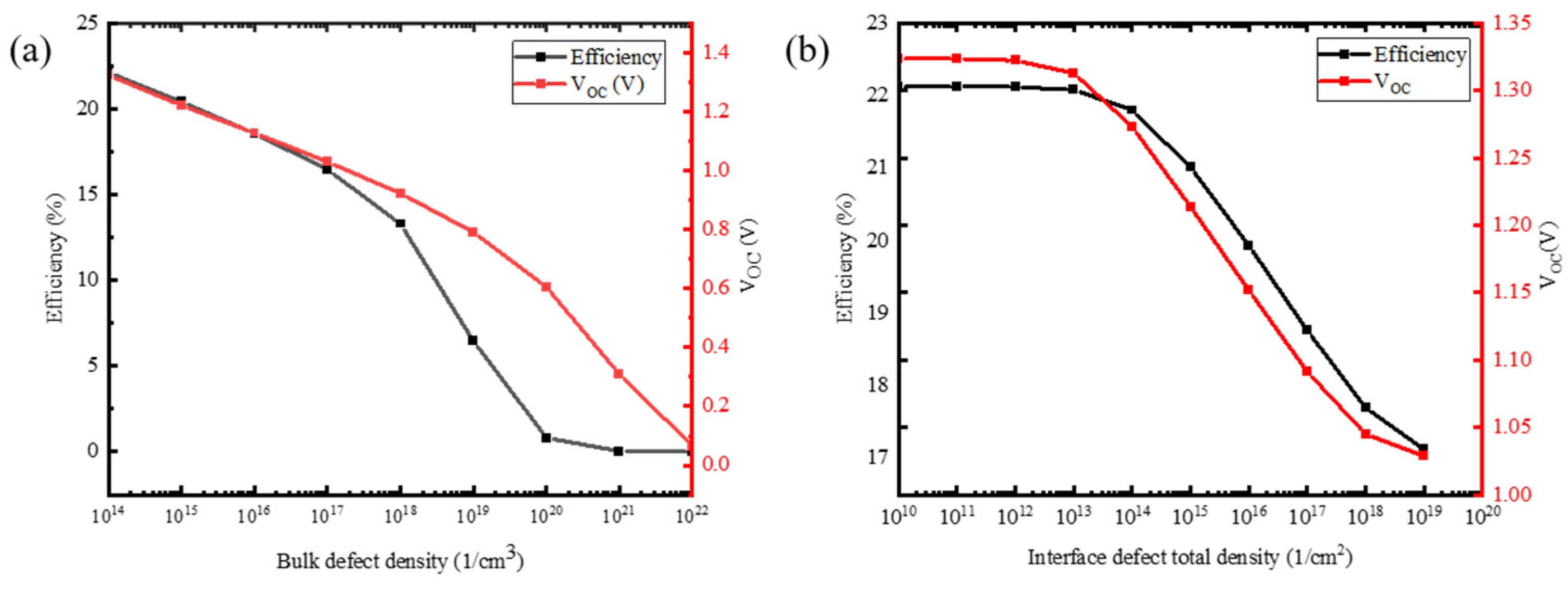
4.4. Effects of Bulk Defects and Interface Defects Density
4.5. Effects of Parasitic Resistance and Work Function of Back Contact
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gagliardi, A.; Abate, A. Mesoporous Electron-Selective Contacts Enhance the Tolerance to Interfacial Ion Accumulation in Perovskite Solar Cells. Am. Chem. Soc. 2018, 3, 163–169. [Google Scholar] [CrossRef]
- Seo, S.; Jeong, S.; Park, H.; Shin, H.; Park, N.G. Atomic layer deposition for efficient and stable perovskite solar cells. Chem. Commun. 2019, 55, 2403–2416. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.; Song, Q.; Tadaki, D.; Niwano, M.; Hirano-Iwata, A. Unveil the Full Potential of Integrated-Back-Contact Perovskite Solar Cells Using Numerical Simulation. ACS Appl. Energy Mater. 2018, 1, 970–975. [Google Scholar] [CrossRef]
- Zhao, P.; Lin, Z.; Wang, J.; Yue, M.; Hao, Y. Numerical simulation of planar heterojunction perovskite solar cells based on SnO2 electron transport layer. ACS Appl. Energy Mater. 2019, 2, 4504–4512. [Google Scholar] [CrossRef]
- Bisquert, J.; Qi, Y.; Ma, T.; Yan, Y. Advances and Obstacles on Perovskite Solar Cell Research from Material Properties to Photovoltaic Function. ACS Energy Lett. 2017, 2, 520–523. [Google Scholar] [CrossRef]
- Cameron, J.; Skabara, P.J. The damaging effects of the acidity in PEDOT:PSS on semiconductor device performance and solutions based on non-acidic alternatives. Mater. Horiz. 2020, 7, 1759–1772. [Google Scholar] [CrossRef]
- Kim, H.S.; Seo, J.Y.; Park, N.G. ChemInform Abstract: Material and Device Stability in Perovskite Solar Cells. ChemInform 2016, 9, 2528–2540. [Google Scholar] [CrossRef]
- Lee, S.W.; Kim, S.; Bae, S.; Cho, K.; Chung, T.; Mundt, L.E.; Lee, S.; Park, S.; Park, H.; Schubert, M.C. UV Degradation and Recovery of Perovskite Solar Cells. Sci. Rep. 2016, 6, 38150. [Google Scholar] [CrossRef]
- Hossain, M.A.; Khoo, K.T.; Cui, X.; Poduval, G.K.; Zhang, T.; Li, X.; Li, W.M.; Hoex, B. Atomic layer deposition enabling higher efficiency solar cells: A review. Nano Mater. Sci. 2020, 2, 204–226. [Google Scholar] [CrossRef]
- Lee, Y.; Jeon, N.; Kim, B.; Shim, H.; Yang, T.Y.; Seok, S.I.; Seo, J.; Im, S.G. A Low-Temperature Thin-Film Encapsulation for Enhanced Stability of a Highly Efficient Perovskite Solar Cell. Adv. Energy Mater. 2018, 8, 1701928. [Google Scholar] [CrossRef]
- Lübke, D.; Hartnagel, P.; Hülsbeck, M.; Kirchartz, T. Understanding the Thickness and Light-Intensity Dependent Performance of Green-Solvent Processed Organic Solar Cells. ACS Mater. Au 2023, 3, 215–230. [Google Scholar] [CrossRef]
- Saikrishna, G.; Parida, S.; Behera, R. Effect of parasitic resistance in solar photovoltaic panel under partial shaded condition. In Proceedings of the 2015 International Conference on Energy Systems and Applications, Pune, India, 30 October–1 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 396–401. [Google Scholar]
- Van Dyk, E.; Meyer, E.L. Analysis of the effect of parasitic resistances on the performance of photovoltaic modules. Renew. Energy 2004, 29, 333–344. [Google Scholar] [CrossRef]
- Wen, L.; Zhou, M.; Wang, C.; Mi, Y.; Lei, Y. Energy Storage: Nanoengineering Energy Conversion and Storage Devices via Atomic Layer Deposition. Adv. Energy Mater. 2016, 6, 1600468. [Google Scholar] [CrossRef]
- Hossain, M.K.; Ishraque Toki, G.; Samajdar, D.; Rubel, M.; Mushtaq, M.; Islam, M.R.; Rahman, M.F.; Bhattarai, S.; Bencherif, H.; Mohammed, M.K. Photovoltaic performance investigation of Cs3Bi2I9-based perovskite solar cells with various charge transport channels using DFT and SCAPS-1D frameworks. Energy Fuels 2023, 37, 7380–7400. [Google Scholar] [CrossRef]
- Saha, N.; Brunetti, G.; Armenise, M.N.; Carlo, A.D.; Ciminelli, C. Modeling Highly Efficient Homojunction Perovskite Solar Cells With Graphene-TiO2 Nanocomposite as the Electron Transport Layer. IEEE J. Photovolt. 2023, 13, 705–710. [Google Scholar] [CrossRef]
- Mushtaq, S.; Tahir, S.; Ashfaq, A.; Sebastian Bonilla, R.; Haneef, M.; Saeed, R.; Ahmad, W.; Amin, N. Performance optimization of lead-free MASnBr3 based perovskite solar cells by SCAPS-1D device simulation. Sol. Energy 2023, 249, 401–413. [Google Scholar] [CrossRef]
- Hussain, C.; Hassan, Y.; Abed, F. Optimization of Organic-Inorganic Perovskite Solar Cell Layers. In Research Square. 2022. Available online: https://www.researchsquare.com/article/rs-2084341/v1 (accessed on 23 September 2023).
- Sunny, A.; Rahman, S.; Khatun, M.M.; Ahmed, S.R.A. Numerical study of high performance HTL-free CH3NH3SnI3-based perovskite solar cell by SCAPS-1D. AIP Adv. 2021, 11, 065102. [Google Scholar] [CrossRef]
- Ibrahim, H.K.; Sabaawi, A.M.A.; Algwari, Q.T. Study of defects in CH3NH3PbI3-based perovskite solar cells. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1152, 012032. [Google Scholar] [CrossRef]
- Samiul Islam, M.; Sobayel, K.; Al-Kahtani, A.; Islam, M.A.; Muhammad, G.; Amin, N.; Shahiduzzaman, M.; Akhtaruzzaman, M. Defect Study and Modelling of SnX3-Based Perovskite Solar Cells with SCAPS-1D. Nanomaterials 2021, 11, 1218. [Google Scholar] [CrossRef]
- Basyoni, M.S.S.; Salah, M.M.; Mousa, M.; Shaker, A.; Zekry, A.; Abouelatta, M.A.; Alshammari, M.T.; Al-Dhlan, K.A.; Gontrand, C. On the Investigation of Interface Defects of Solar Cells: Lead-Based vs Lead-Free Perovskite. IEEE Access 2021, 9, 130221–130232. [Google Scholar] [CrossRef]
- Mehmood, S.; Kaleem, M.; Nazir, S.; Israr, A.; Mirza, H.T. Numerical Analysis of Stable and Low Cost Perovskite Solar Cell with an Enhanced Inorganic Electron and Hole Transport Layers. J. Nanoelectron. Optoelectron. 2020, 15, 725–733. [Google Scholar] [CrossRef]
- Islam, M.B.; Yanagida, M.; Shirai, Y.; Nabetani, Y.; Miyano, K. NiOx Hole Transport Layerfor Perovskite Solar Cells with Improved Stability and Reproducibility. ACS Omega 2017, 2, 2291–2299. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.-C.; Yu, S.-M.; Lee, K.-M.; Lin, C.-J.; Liou, B.-Y.; Chen, F.-R. Oxidized nickel to prepare an inorganic hole transport layer for high-efficiency and stability of CH3NH3PbI3 perovskite solar Cells. Energies 2022, 15, 919. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J.; Huang, Y.; Liu, F.; Lv, M.; Chen, S.; Hu, L.; Tang, J.; Yao, J.; Dai, S. Mesoporous SnO2 nanoparticle films as electron-transporting material in perovskite solar cells. RSC Adv. 2015, 5, 28424–28429. [Google Scholar] [CrossRef]
- Ke, W.; Fang, G.; Liu, Q.; Xiong, L.; Qin, P.; Tao, H.; Wang, J.; Lei, H.; Li, B.; Wan, J. Low-temperature solution-processed tin oxide as an alternative electron transporting layer for efficient perovskite solar cells. J. Am. Chem. Soc. 2015, 137, 6730–6733. [Google Scholar] [CrossRef] [PubMed]
- Kavan, L.; Steier, L.; Grätzel, M. Ultrathin buffer layers of SnO2 by atomic layer deposition: Perfect blocking function and thermal stability. J. Phys. Chem. C 2017, 121, 342–350. [Google Scholar] [CrossRef]
- Ke, W.; Zhao, D.; Cimaroli, A.J.; Grice, C.R.; Qin, P.; Liu, Q.; Xiong, L.; Yan, Y.; Fang, G. Effects of annealing temperature of tin oxide electron selective layers on the performance of perovskite solar cells. J. Mater. Chem. A 2015, 3, 24163–24168. [Google Scholar] [CrossRef]
- Qin, X.; Zhao, Z.; Wang, Y.; Wu, J.; Jiang, Q.; You, J. Recent progress in stability of perovskite solar cells. J. Semicond. 2017, 38, 011002. [Google Scholar] [CrossRef]
- Lin, S.; Yang, B.; Qiu, X.; Yan, J.; Shi, J.; Yuan, Y.; Tan, W.; Liu, X.; Huang, H.; Gao, Y. Efficient and stable planar hole-transport-material-free perovskite solar cells using low temperature processed SnO2 as electron transport material. Org. Electron. 2018, 53, 235–241. [Google Scholar] [CrossRef]
- Wu, P.; Wang, S.; Li, X.; Zhang, F. Advances in SnO2-based perovskite solar cells: From preparation to photovoltaic applications. J. Mater. Chem. A 2021, 9, 19554. [Google Scholar] [CrossRef]
- Burgelman, M.; Decock, K.; Khelifi, S.; Abass, A. Advanced electrical simulation of thin film solar cells. Thin Solid Film. 2013, 535, 296–301. [Google Scholar] [CrossRef]
- Abdelaziz, S.; Zekry, A.; Shaker, A.; Abouelatta, M. Investigating the performance of formamidinium tin-based perovskite solar cell by SCAPS device simulation. Opt. Mater. 2020, 101, 109738. [Google Scholar] [CrossRef]
- Rahman, M.S.; Miah, S.; Marma, M.S.W.; Sabrina, T. Simulation based investigation of inverted planar perovskite solar cell with all metal oxide inorganic transport layers. In Proceedings of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Chittagong, Bangladesh, 7–9 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Ratcliff, E.L.; Meyer, J.; Steirer, K.X.; Armstrong, N.R.; Olson, D.; Kahn, A. Energy level alignment in PCDTBT: PC70BM solar cells: Solution processed NiOx for improved hole collection and efficiency. Org. Electron. 2012, 13, 744–749. [Google Scholar] [CrossRef]
- Goje, A.; Ludin, N.; Teridi, M.M.; Syafiq, U.; Ibrahim, M.; Nawab, F.; Syakirin, A. Design and Simulation of Lead-Free Flexible Perovskite Solar cell Using SCAPS-1D. In Proceedings of the International Conference on Sustainable, Renewable & Energy Efficiency, Bangi, Malaysia, 7–8 November 2022; IOP Conference Series: Materials Science and Engineering. IOP Publishing: Bristol, England, 2023; p. 012004. [Google Scholar]
- Baena, J.P.C.; Steier, L.; Tress, W.; Saliba, M.; Neutzner, S.; Matsui, T.; Giordano, F.; Jacobsson, T.J.; Kandada, A.R.S.; Zakeeruddin, S.M. Highly efficient planar perovskite solar cells through band alignment engineering. Energy Environ. Sci. 2015, 8, 2928–2934. [Google Scholar] [CrossRef]
- Tian, H.; Fan, H.; Dong, G.; Ma, L.; Ma, J. NiO/ZnOp–n heterostructures and their gas sensing properties for reduced operating temperature. RSC Adv. 2016, 6, 109091–109098. [Google Scholar] [CrossRef]
- Eom, K.; Kwon, U.; Kalanur, S.S.; Park, H.J.; Seo, H. Depth-resolved band alignments of perovskite solar cells with significant interfacial effects. J. Mater. Chem. A 2017, 5, 2563–2571. [Google Scholar] [CrossRef]
- Castro, E.; Cerón, M.R.; Garcia, A.H.; Kim, Q.; Etcheverry-Berríos, A.; Morel, M.J.; Díaz-Torres, R.; Qian, W.; Martinez, Z.; Mendez, L. A new family of fullerene derivatives: Fullerene-curcumin conjugates for biological and photovoltaic applications. RSC Adv. 2018, 8, 41692–41698. [Google Scholar] [CrossRef] [PubMed]
- Rödl, C.; Schleife, A. Photoemission spectra and effective masses of n-and p-type oxide semiconductors from first principles: ZnO, CdO, SnO2, MnO, and NiO. Phys. Status Solidi A 2014, 211, 74–81. [Google Scholar] [CrossRef]
- Olson, D.C.; Ginley, D.S. Nanostructured TCOs (ZnO, TiO2, and Beyond). In Handbook of Transparent Conductors; Springer: Berlin/Heidelberg, Germany, 2011; pp. 425–457. [Google Scholar]
- Shan, F.; Liu, A.; Zhu, H.; Kong, W.; Liu, J.; Shin, B.; Fortunato, E.; Martins, R.; Liu, G. High-mobility p-type NiOx thin-film transistors processed at low temperatures with Al2O3 high-k dielectric. J. Mater. Chem. C 2016, 4, 9438–9444. [Google Scholar] [CrossRef]
- Farahani, S.V.; Veal, T.D.; Mudd, J.J.; Scanlon, D.O.; Watson, G.; Bierwagen, O.; White, M.; Speck, J.S.; McConville, C.F. Valence-band density of states and surface electron accumulation in epitaxial SnO2 films. Phys. Rev. B 2014, 90, 155413. [Google Scholar] [CrossRef]
- Holman, Z.C.; Filipič, M.; Descoeudres, A.; De Wolf, S.; Smole, F.; Topič, M.; Ballif, C. Infrared light management in high-efficiency silicon heterojunction and rear-passivated solar cells. J. Appl. Phys. 2013, 113, 013107. [Google Scholar] [CrossRef]
- Manzoor, S.; Häusele, J.; Bush, K.A.; Palmstrom, A.F.; Carpenter, J.; Zhengshan, J.Y.; Bent, S.F.; Mcgehee, M.D.; Holman, Z.C. Optical modeling of wide-bandgap perovskite and perovskite/silicon tandem solar cells using complex refractive indices for arbitrary-bandgap perovskite absorbers. Opt. Express 2018, 26, 27441–27460. [Google Scholar] [CrossRef] [PubMed]
- Jimoh, O.M.; Florence, I.N.; Akinbolati, A.; Nnachi, C.; Ajani, C.; Gyuk, P.M.; Magaji, S.; Danladi, E. Investigating the Performance of Perovskite Solar Cells Using Nickel Oxide and Copper Iodide as P-type Inorganic layers by SCAPS-1D Simulation. Phys. Access 2022, 37–50. [Google Scholar] [CrossRef]
- Sajid, S.; Elseman, A.M.; Ji, J.; Dou, S.; Wei, D.; Huang, H.; Cui, P.; Xi, W.; Chu, L.; Li, Y. Computational study of ternary devices: Stable, low-cost, and efficient planar perovskite solar cells. Nano-Micro Lett. 2018, 10, 51. [Google Scholar] [CrossRef]
- Yasodharan, R.; Senthilkumar, A.; Ajayan, J.; Mohankumar, P. Effects of layer thickness on Power Conversion Efficiency in Perovskite solar cell: A numerical simulation approach. In Proceedings of the 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, 15–16 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1132–1135. [Google Scholar]
- Stockhausen, V.; Andrade, L.; Ivanou, D.; Stannowski, B.; Mendes, A. Incident angle and light intensity variation: A comparative impact study on perovskite, Dye-sensitized and silicon heterojunction solar cells towards building-integrated applications. Sol. Energy Mater. Sol. Cells 2019, 191, 451–458. [Google Scholar] [CrossRef]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A comprehensive review of maximum power point tracking (mppt) techniques used in solar pv systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Gholami-Milani, A.; Ahmadi-Kandjani, S.; Olyaeefar, B.; Kermani, M.H. Performance analyses of highly efficient inverted all-perovskite bilayer solar cell. Sci. Rep. 2023, 13, 8274. [Google Scholar] [CrossRef]
- Schwenzer, J.A.; Rakocevic, L.; Gehlhaar, R.; Abzieher, T.; Gharibzadeh, S.; Moghadamzadeh, S.; Quintilla, A.; Richards, B.S.; Lemmer, U.; Paetzold, U.W. Temperature variation-induced performance decline of perovskite solar cells. ACS Appl. Mater. Interfaces 2018, 10, 16390–16399. [Google Scholar] [CrossRef]
- Varshni, Y.P. Temperature dependence of the energy gap in semiconductors. Physica 1967, 34, 149–154. [Google Scholar] [CrossRef]
- Pauwels, H.J.; Vanhoutte, G. The influence of interface state and energy barriers on the efficiency of heterojunction solar cells. J. Phys. D Appl. Phys. 1978, 11, 649–667. [Google Scholar] [CrossRef]
- Haider, S.Z.; Anwar, H.; Wang, M. A comprehensive device modelling of perovskite solar cell with inorganic copper iodide as hole transport material. Semicond. Sci. Technol. 2018, 33, 035001. [Google Scholar] [CrossRef]
- Tress, W. Perovskite Solar Cells on the Way to Their Radiative Efficiency Limit—Insights Into a Success Story of High Open-Circuit Voltage and Low Recombination. Adv. Energy Mater. 2017, 7, 1602358. [Google Scholar] [CrossRef]
- Jamal, M.; Shahahmadi, S.; Wadi, M.A.A.; Chelvanathan, P.; Asim, N.; Misran, H.; Hossain, M.; Amin, N.; Sopian, K.; Akhtaruzzaman, M. Effect of defect density and energy level mismatch on the performance of perovskite solar cells by numerical simulation. Optik 2019, 182, 1204–1210. [Google Scholar] [CrossRef]
- Chouhan, A.S.; Jasti, N.P.; Avasthi, S. Effect of interface defect density on performance of perovskite solar cell: Correlation of simulation and experiment. Mater. Lett. 2018, 221, 150–153. [Google Scholar] [CrossRef]
- Jan, S.T.; Noman, M. Influence of layer thickness, defect density, doping concentration, interface defects, work function, working temperature and reflecting coating on lead-free perovskite solar cell. Sol. Energy 2022, 237, 29–43. [Google Scholar]
- Lakhdar, N.; Hima, A. Electron transport material effect on performance of perovskite solar cells based on CH3NH3GeI3. Opt. Mater. 2020, 99, 109517. [Google Scholar] [CrossRef]
- Ngoupo, A.T.; Ouédraogo, S.; Zougmoré, F.; Ndjaka, J. Numerical analysis of ultrathin Sb2Se3-based solar cells by SCAPS-1D numerical simulator device. Chin. J. Phys. 2021, 70, 1–13. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehmood, S.; Xia, Y.; Qu, F.; He, M. Investigating the Performance of Efficient and Stable Planer Perovskite Solar Cell with an Effective Inorganic Carrier Transport Layer Using SCAPS-1D Simulation. Energies 2023, 16, 7438. https://doi.org/10.3390/en16217438
Mehmood S, Xia Y, Qu F, He M. Investigating the Performance of Efficient and Stable Planer Perovskite Solar Cell with an Effective Inorganic Carrier Transport Layer Using SCAPS-1D Simulation. Energies. 2023; 16(21):7438. https://doi.org/10.3390/en16217438
Chicago/Turabian StyleMehmood, Safdar, Yang Xia, Furong Qu, and Meng He. 2023. "Investigating the Performance of Efficient and Stable Planer Perovskite Solar Cell with an Effective Inorganic Carrier Transport Layer Using SCAPS-1D Simulation" Energies 16, no. 21: 7438. https://doi.org/10.3390/en16217438
APA StyleMehmood, S., Xia, Y., Qu, F., & He, M. (2023). Investigating the Performance of Efficient and Stable Planer Perovskite Solar Cell with an Effective Inorganic Carrier Transport Layer Using SCAPS-1D Simulation. Energies, 16(21), 7438. https://doi.org/10.3390/en16217438





