Multiple-Relaxation-Time Lattice Boltzmann Simulation of Soret and Dufour Effects on the Thermosolutal Natural Convection of a Nanofluid in a U-Shaped Porous Enclosure
Abstract
:1. Introduction
2. Theoretical Formulation
2.1. Problem Statement
2.2. Properties of Nanofluids
2.3. Macroscale Dimensional Governing Equations
2.4. Non-Dimensional Equation
2.5. Numerical Methods
2.6. Wall Boundary Conditions
2.7. Heat and Mass Transfer Rate
2.8. Formulation of Entropy Production
3. Grid Independent Test
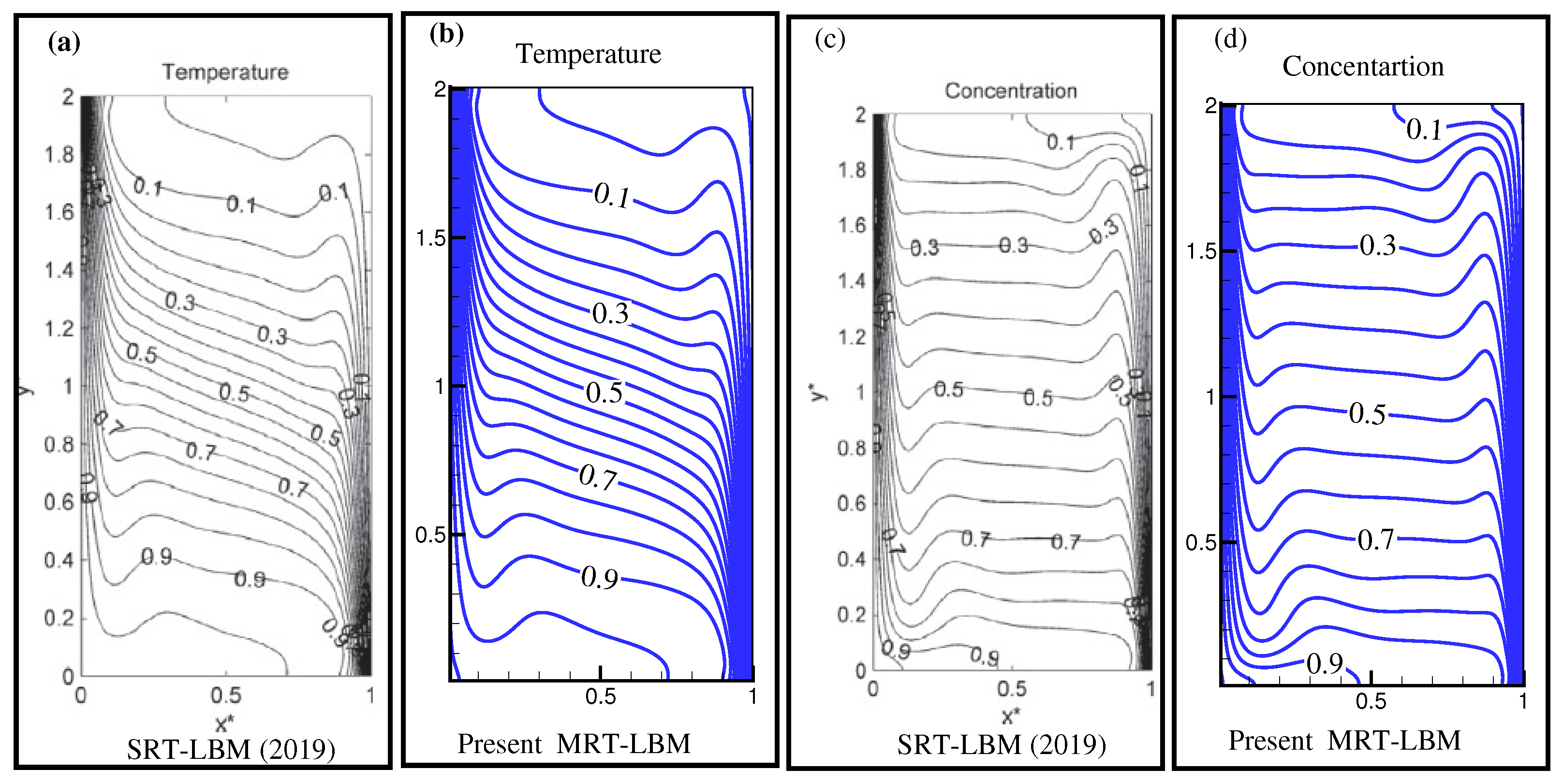
4. Code Validation
4.1. Code Validation for the Porous Media
4.2. Code Validation for the Soret and Dufour Effects
5. Results and Discussion
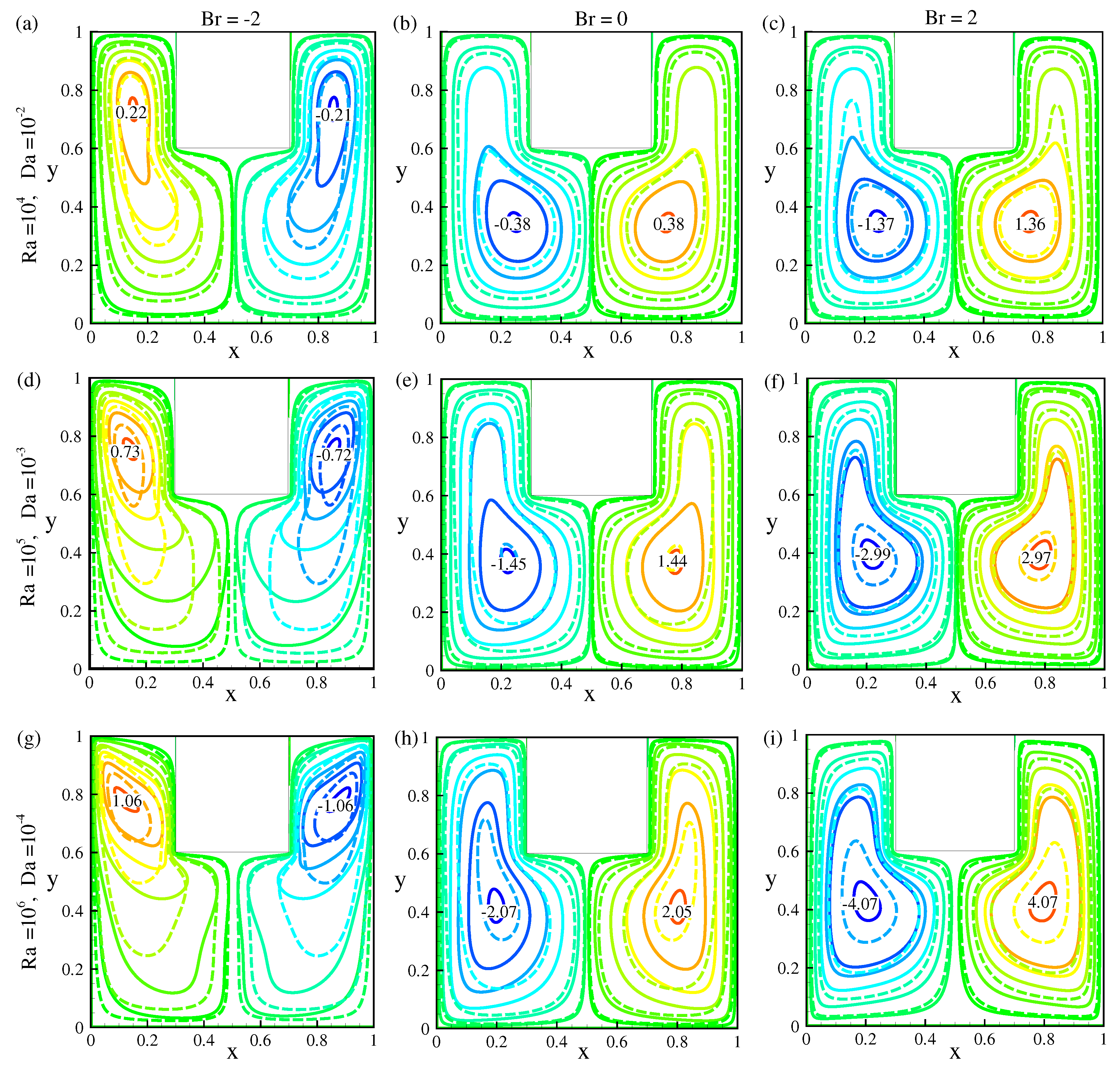
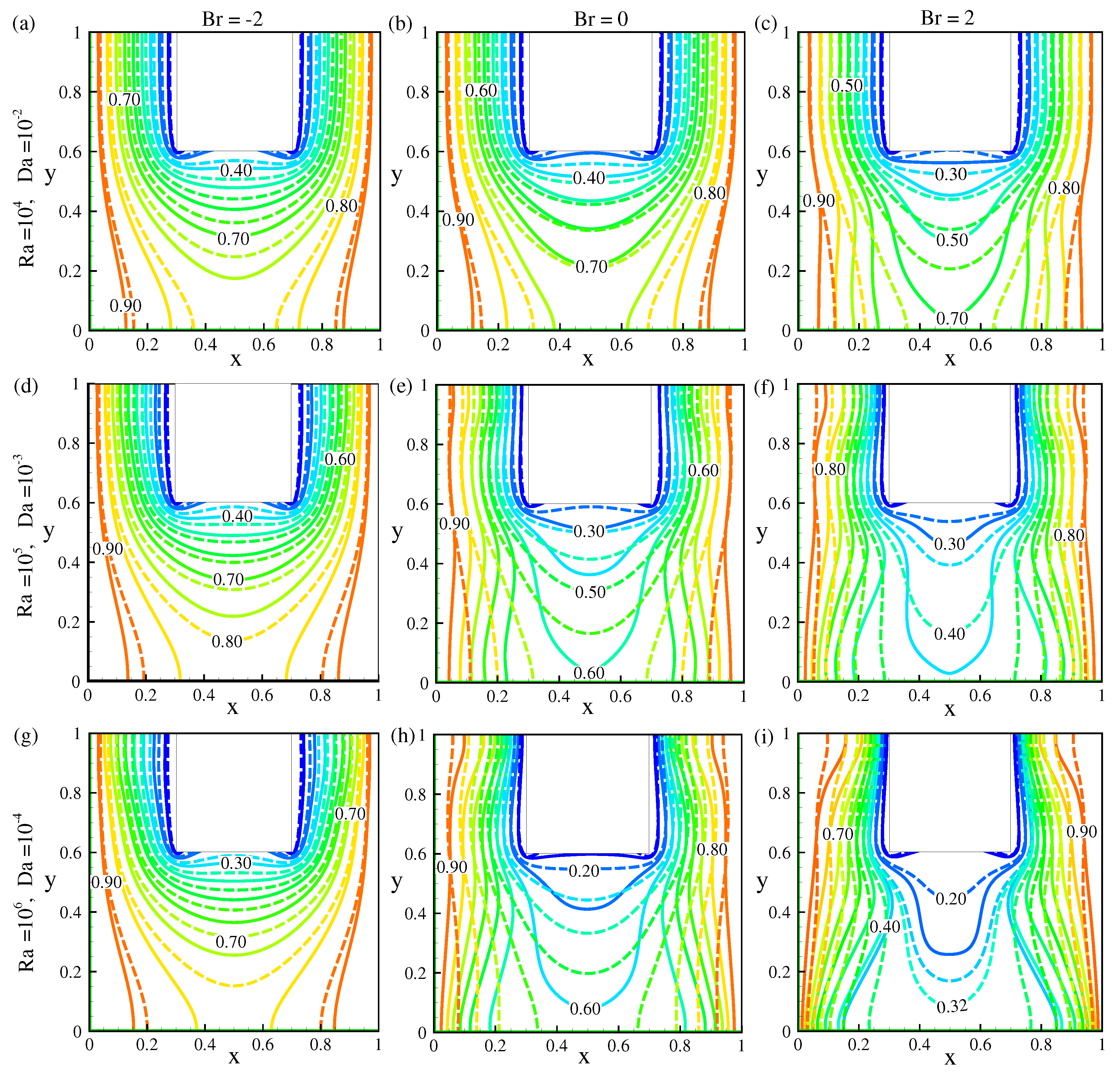
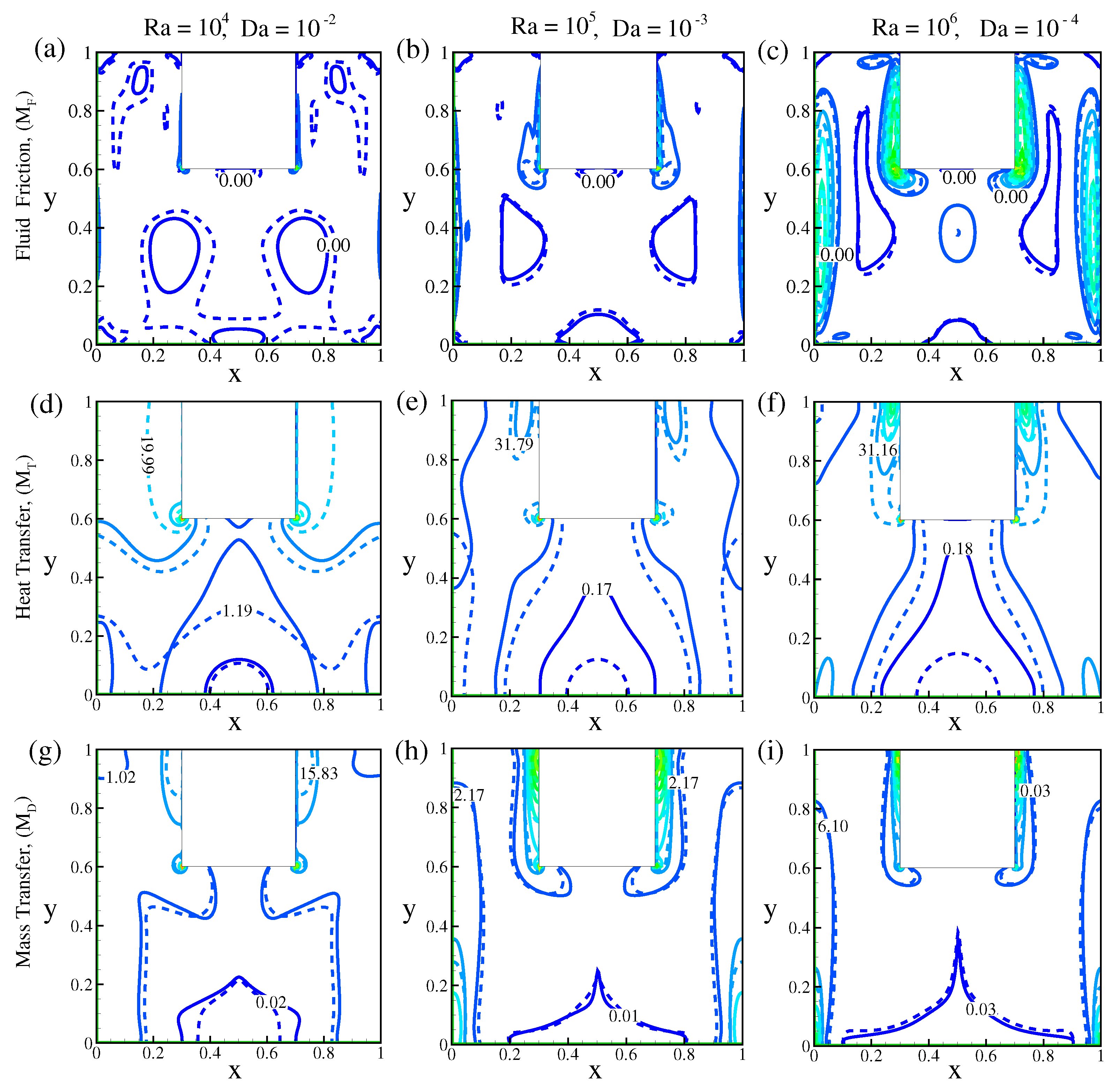
5.1. Observation of Streamlines, Isotherms and Isoconcentrations
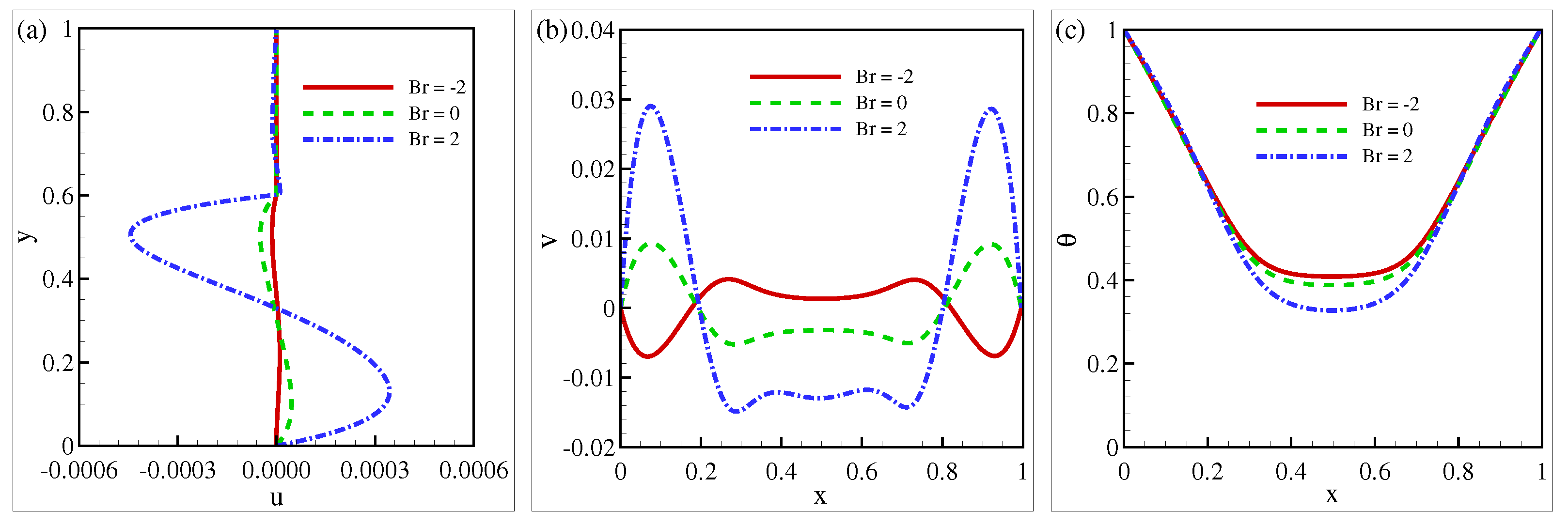
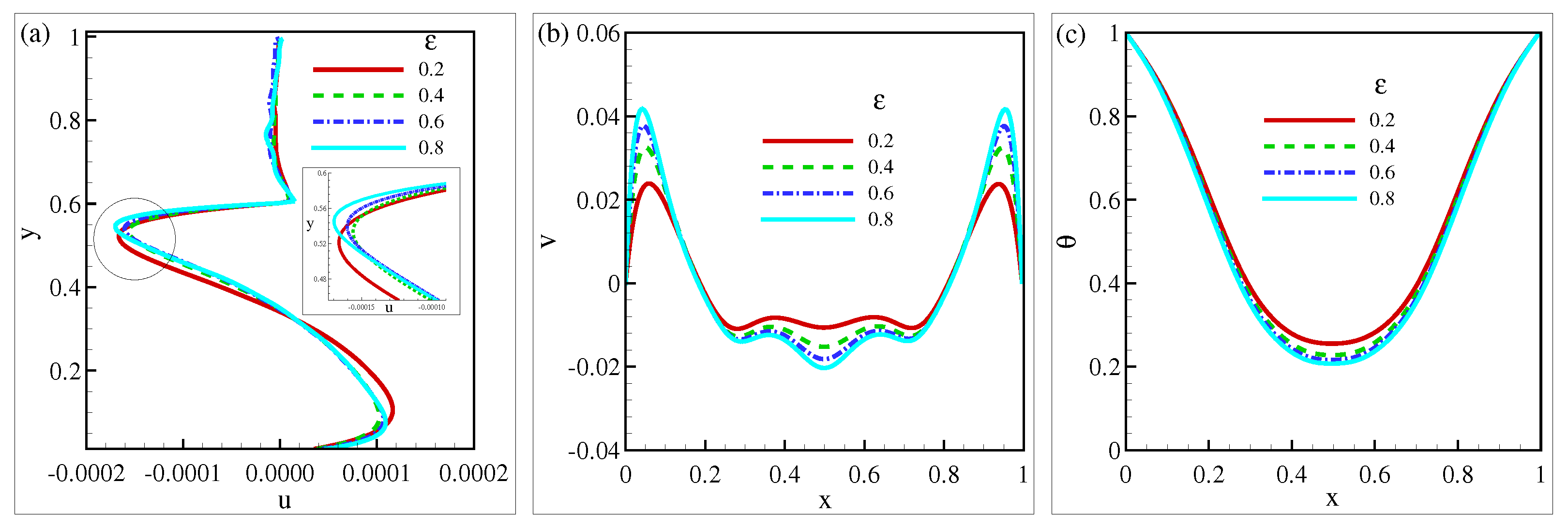
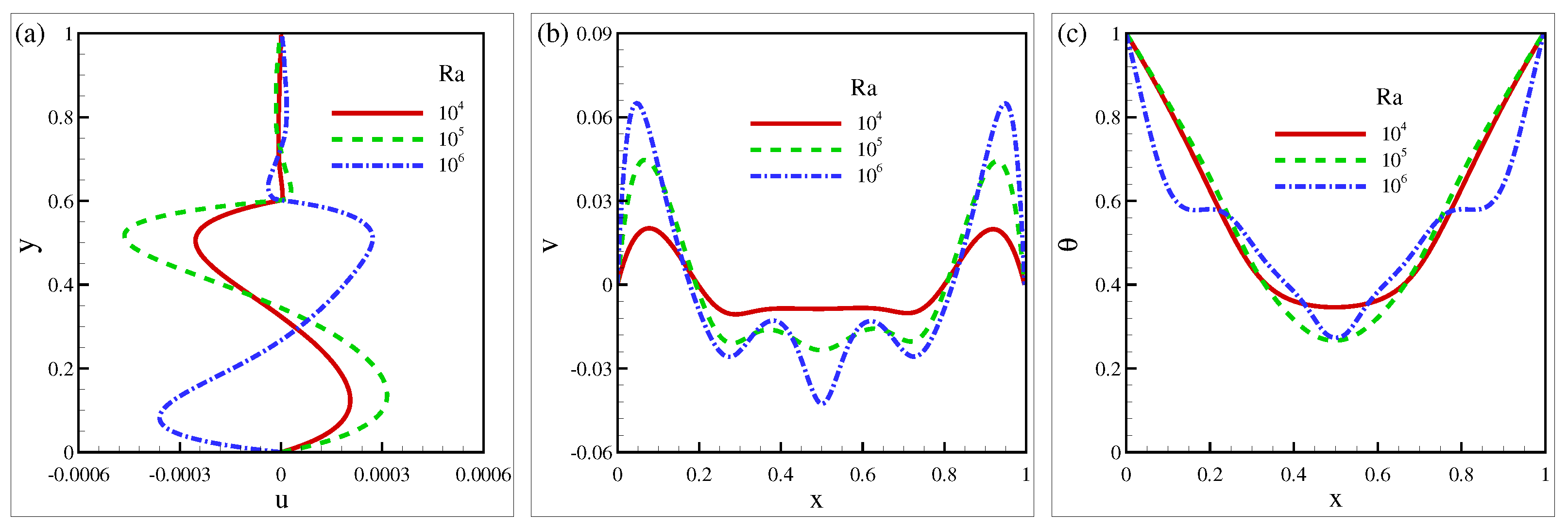
5.2. Velocity and Temperature Effects
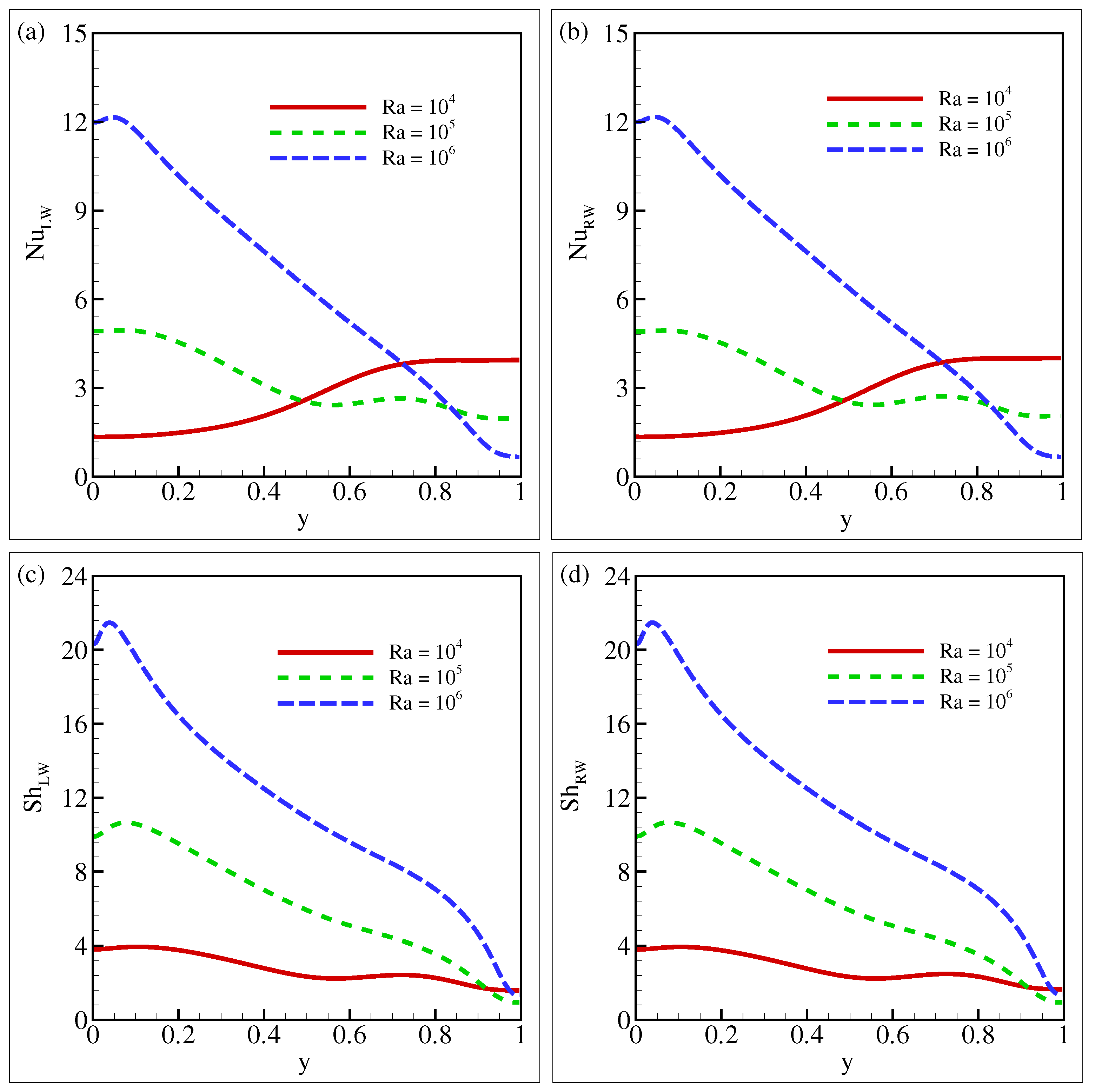
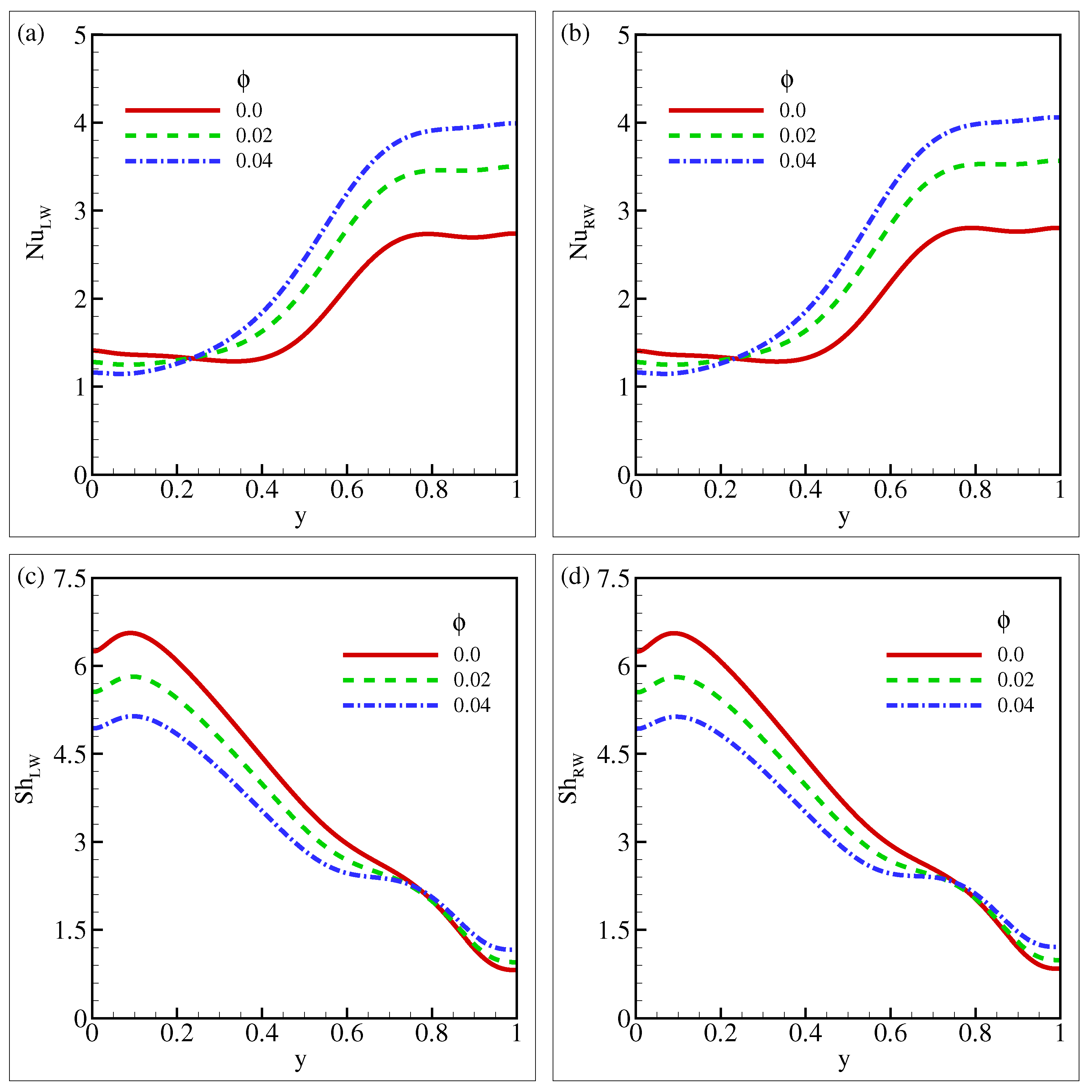
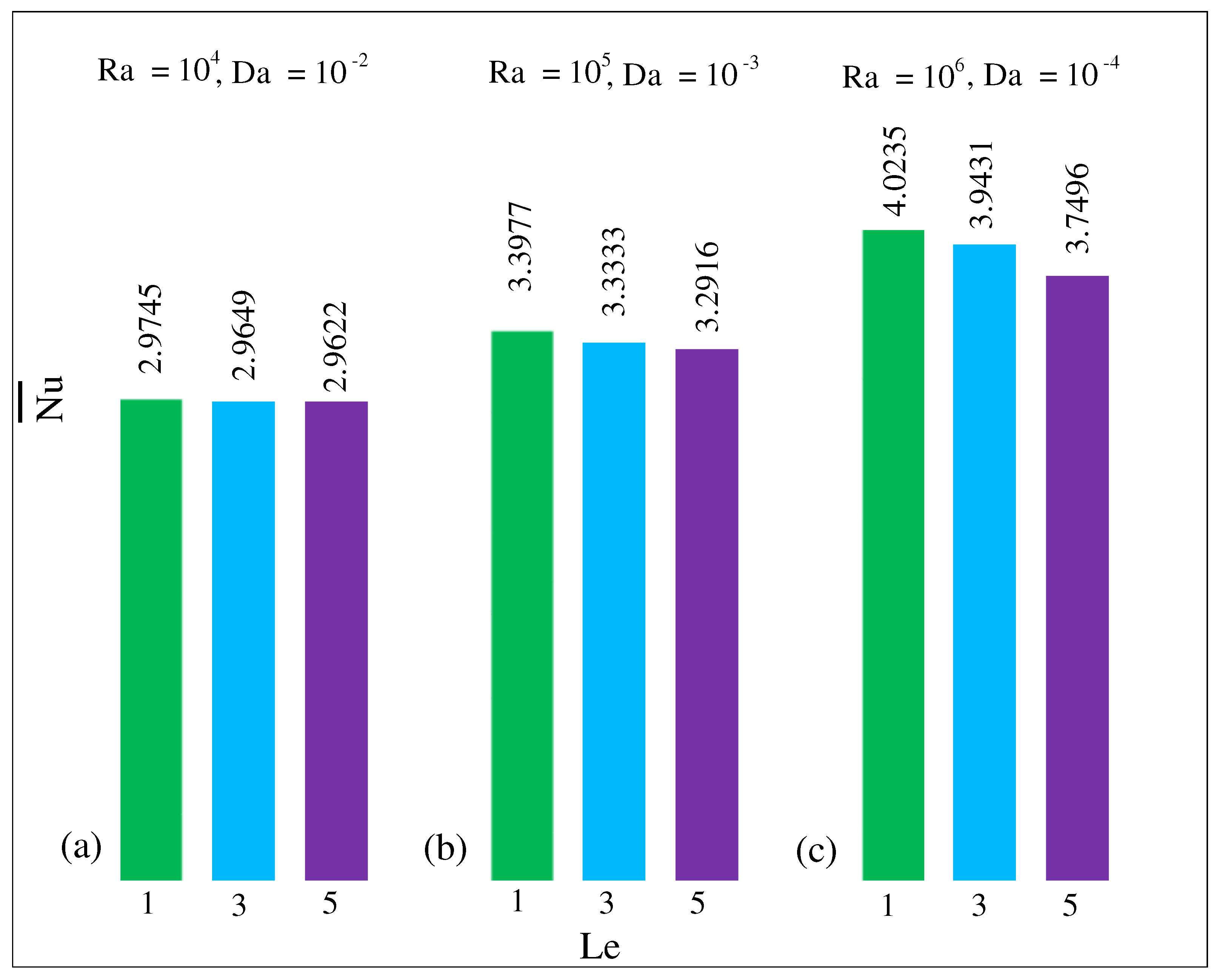
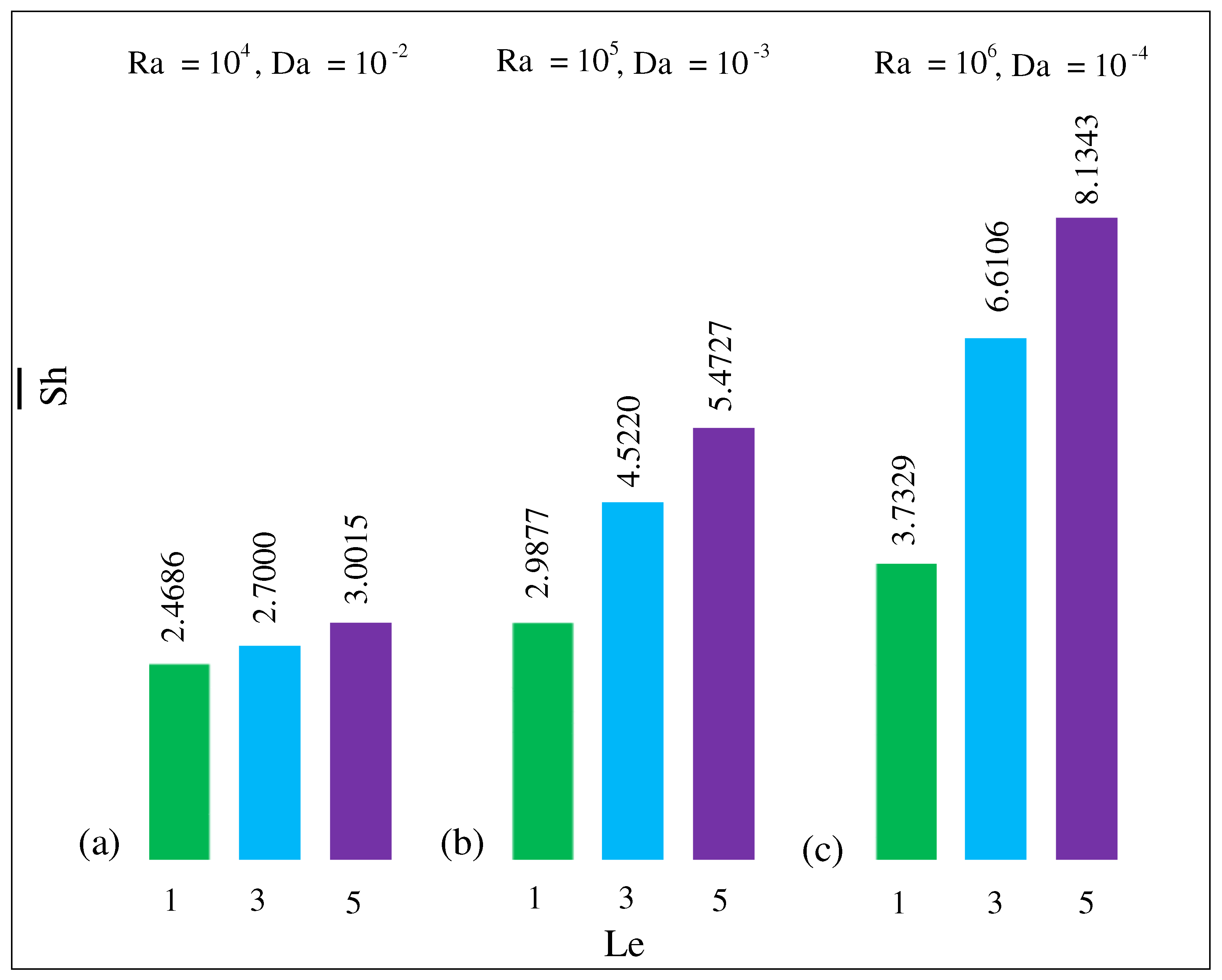
5.3. Mean Nusselt Number and Mean Sherwood Number for Different Parameters
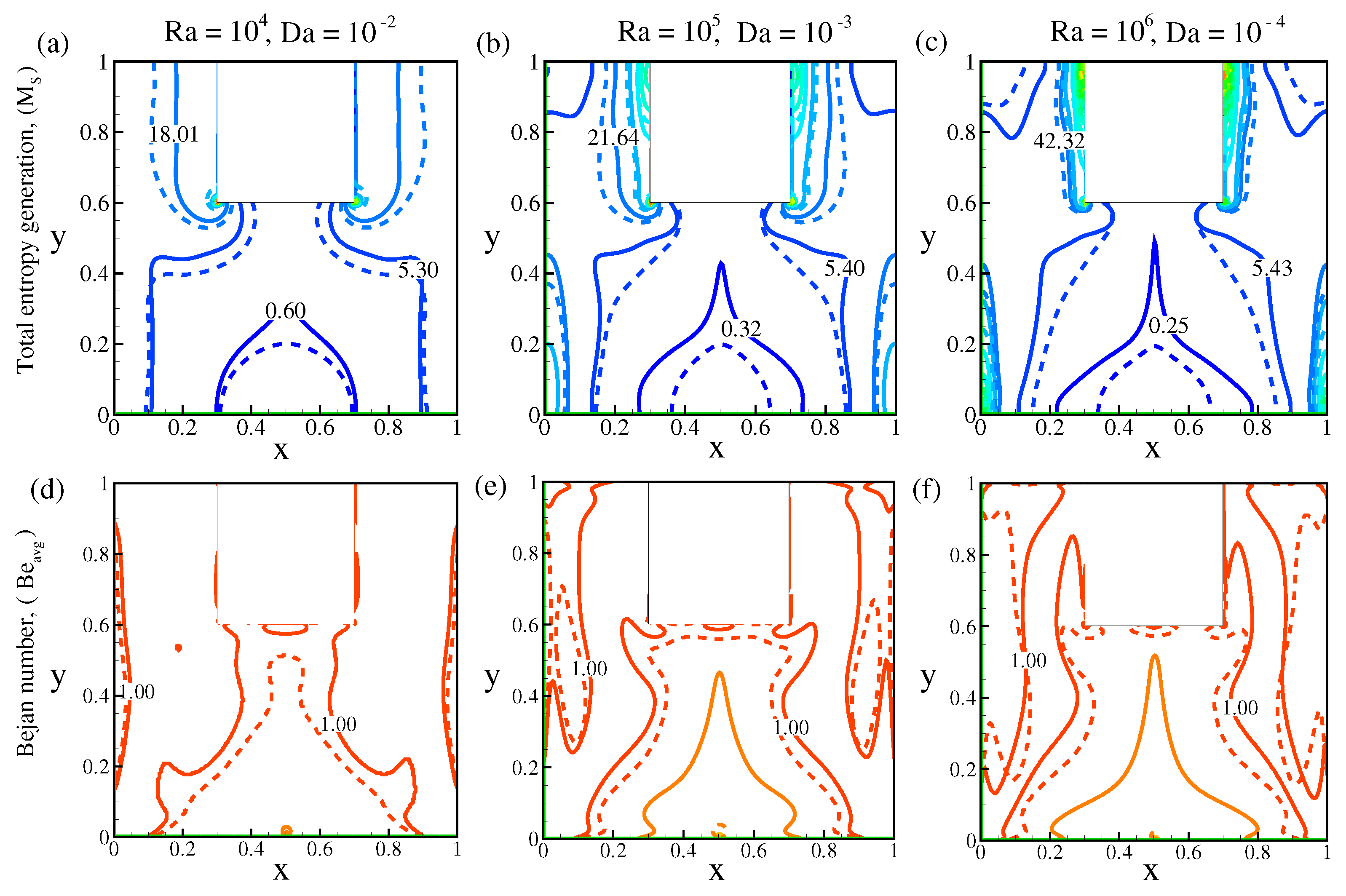
5.4. Entropy Generation
6. Response Surface Methodology
Response Surface Analysis
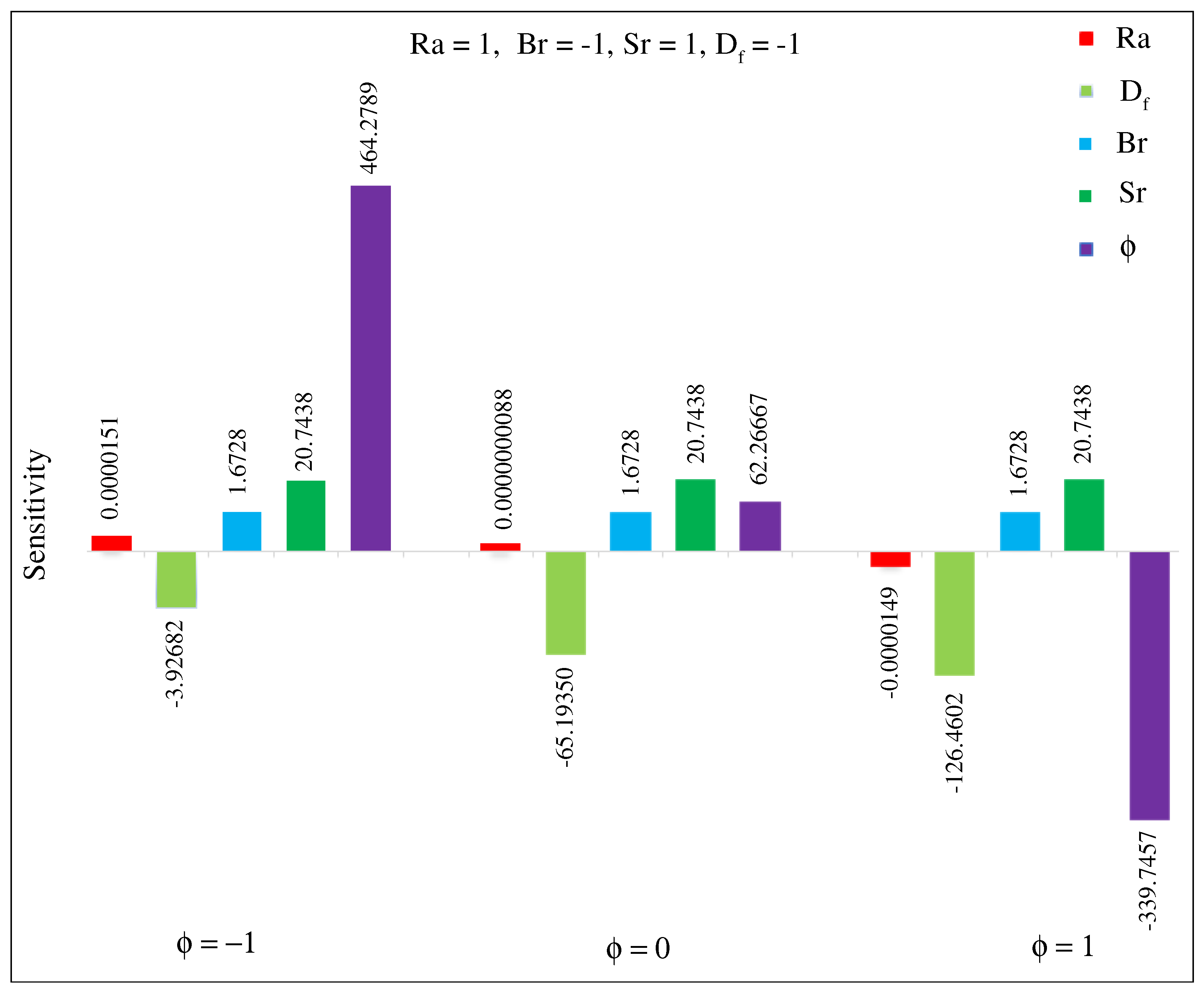
7. Sensitivity Analysis
8. Conclusions
- The fluid flow is enhanced as the Rayleigh number and buoyancy force increase. The isotherm and isoconcentration densities close to the hot wall grow when the buoyancy force shifts from a negative to a positive value.
- The u-velocity at mid-x rises between but decreases between by growing the . The v-velocity at mid-y enhances close to the walls and reduces in the middle of the cavity for rising and . The temperature distribution also decreases by increasing and .
- The v-velocity at mid-y decreases near the walls but enhances at the down-indented part of the U-shape with increasing . The temperature distribution rises as the rises.
- The temperature distribution at the down-indented portion of the U-shape and the v-velocity at mid-y decrease as the number rises. But they increase close to the walls as the number rises.
- The local and the local increase as the number rises but reduce as the volume fraction increases.
- The and decrease as the Darcy number falls, but both rise as the number increases. The and the rise as the buoyancy ratio shifts from a negative to a positive value.
- As the number reduces, the reduces, but the rises.
- The fluid friction rises as the number rises, but reduces as the volume fraction rises. The heat transfer increases for = and , but decreases for = as the volume fraction rises.
- The is always more than , which indicates the irreversibility becomes heat transfer dominant.
- The generated correlation equation from the RSM approach demonstrates the correlation between the output and the input parameters.
- The and have a positive sensitivity, but and have a negative sensitivity only for higher values of .
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | ||
| ANOVA | Analysis of variance | |
| BFEDM | Brinkman–Forchheimer extended Darcy model | |
| FEM | Finite element method | |
| FVM | Finite volume method | |
| LBM | Lattice Boltzmann method | |
| MHD | Magnetohydrodynamics | |
| MRT | Multiple-relaxation-time | |
| RSM | Response surface methodology | |
| Nomenclature | ||
| English symbols | ||
| Local Bejan number | ||
| Mean Bejan number | ||
| Buoyancy ratio | ||
| C | Concentration of the fluid | kg m |
| Specific heat | J kg K | |
| D | Mass diffusivity | m s |
| Darcy number | ||
| Dufour number | ||
| g | Gravitational acceleration | m s |
| H | Height of the cavity | m |
| L | Length of the cavity | |
| Lewis number | ||
| k | Thermal conductivity | J m s K |
| Local Nusselt number | ||
| Mean Nusselt number | ||
| Dimensional pressure | ||
| P | Dimensionless pressure | |
| Prandtl number | ||
| Rayleigh number | ||
| M | Entropy generation | J m s K |
| Entropy due to fluid friction | ||
| Entropy due to heat transfer | ||
| Entropy due to mass transfer | ||
| Total entropy | ||
| Soret number | ||
| Sherwood number | ||
| Mean Sherwood number | ||
| T | Temperature | K |
| Temperature of the cold wall | (K) | |
| Temperature of the heated wall | ||
| t | Dimensional time | s |
| Dimensionless time | ||
| , | Dimensional velocity components along horizontal and | m s |
| vertical directions | ||
| Dimensionless velocity components | ||
| Dimensional Cartesian coordinates | m | |
| Dimensionless Cartesian coordinates | ||
| Greek letters | ||
| Thermal diffusivity | m s | |
| Thermal expansion coefficient | K | |
| Dimensionless temperature function | ||
| Dynamic viscosity | kg m s | |
| Kinematic viscosity | m s | |
| Fluid density | kg m | |
| Volume fraction | ||
| Porosity | ||
References
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Anee, M.J.; Siddiqa, S.; Hasan, M.F.; Molla, M.M. Lattice Boltzmann simulation of natural convection of ethylene glycol-alumina nanofluid in a C-shaped enclosure with MFD viscosity through a parallel computing platform and quantitative parametric assessment. Phys. Scr. 2023, 98, 095203. [Google Scholar] [CrossRef]
- Wang, X.; Song, Y.; Li, C.; Zhang, Y.; Ali, H.M.; Sharma, S.; Li, R.; Yang, M.; Gao, T.; Liu, M.; et al. Nanofluids application in machining: A comprehensive review. Int. J. Adv. Manuf. Technol. 2023. [Google Scholar] [CrossRef]
- Can, A.; Selimefendigil, F.; Öztop, H.F. A review on soft computing and nanofluid applications for battery thermal management. J. Energy Storage 2022, 53, 105214. [Google Scholar] [CrossRef]
- Kulkarni, S.; Chavali, S.; Dikshit, S. A review on analysis of Vapour Compression Refrigeration System (VCRS) for its performance using different ecofriendly refrigerants and nanofluids. Mater. Today Proceed. 2023, 72, 878–883. [Google Scholar] [CrossRef]
- Rahmani, M.; Nejad, A.S.; Barzoki, M.F.; Kasaeian, A.; Sameti, M. Simulation of solar absorption refrigeration cycle with CuO nanofluid for summer cooling of a residential building. Therm. Sci. Eng. Prog. 2022, 34, 101419. [Google Scholar] [CrossRef]
- Gürdal, M.; Arslan, K.; Gedik, E.; Minea, A.A. Effects of using nanofluid, applying a magnetic field, and placing turbulators in channels on the convective heat transfer: A comprehensive review. Renew. Sustain. Energy Rev. 2022, 162, 112453. [Google Scholar] [CrossRef]
- Mehta, B.; Subhedar, D.; Panchal, H.; Said, Z. Synthesis, stability, thermophysical properties and heat transfer applications of nanofluid–A review. J. Mol. Liq. 2022, 364, 120034. [Google Scholar] [CrossRef]
- Malika, M.; Ashokkumar, M.; Sonawane, S.S. Mathematical and numerical investigations of nanofluid applications in the industrial heat exchangers. In Applications of Nanofluids in Chemical and Bio-medical Process Industry; Elsevier: Amsterdam, The Netherlands, 2022; pp. 53–78. [Google Scholar]
- Liu, Q.; Feng, X.B.; Xu, X.T.; He, Y.L. Multiple-relaxation-time lattice Boltzmann model for double-diffusive convection with Dufour and Soret effects. Int. J. Heat Mass Transf. 2019, 139, 713–719. [Google Scholar] [CrossRef]
- Xu, H.; Luo, Z.; Lou, Q.; Zhang, S.; Wang, J. Lattice Boltzmann simulations of the double-diffusive natural convection and oscillation characteristics in an enclosure with Soret and Dufour effects. Int. J. Therm. Sci. 2019, 136, 159–171. [Google Scholar] [CrossRef]
- Magyari, E.; Postelnicu, A. Double-diffusive natural convection flows with thermosolutal symmetry in porous media in the presence of the Soret–Dufour effects. Transp. Porous Media 2011, 88, 149–167. [Google Scholar] [CrossRef]
- Ghachem, K.; Kolsi, L.; Khan, S.U.; Abbas, T.; Maatki, C.; Saeed, M. Soret and Dufour aspect of viscoelastic fluid due to moving cylinder with viscous dissipation and convective boundary conditions. J. Indian Chem. Soc. 2023, 100, 100913. [Google Scholar] [CrossRef]
- Islam, M.M.; Molla, M.M.; Siddiqa, S.; Sheremet, M.A. MRT-LB simulation and response surface analysis of natural convection of non-Newtonian ferrofluid in an enclosure with non-uniformly heated radiator through GPU computing. Eng. Anal. Bound. Elem. 2023, 157, 92–118. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, S.; Xiong, W.; Ye, L.; Liu, H.; Zhu, W.; Mu, Y.; Niu, W. Physical and Numerical Simulation of Tight Gas Flow at the Microscale. Energies 2023, 16, 5937. [Google Scholar] [CrossRef]
- Wanner, J.; Birke, K.P. Investigation of the Influence of Electrode Surface Structures on Wettability after Electrolyte Filling Based on Experiments and a Lattice Boltzmann Simulation. Energies 2023, 16, 5640. [Google Scholar] [CrossRef]
- Islam, M.M.; Hasan, M.F.; Molla, M.M. Analysis of Heat Transfer Characteristics of MHD Ferrofluid by the Implicit Finite Difference Method at Temperature-Dependent Viscosity Along a Vertical Thin Cylinder. Iran. J. Sci. Technol. Trans. Mech. Eng. 2023. [Google Scholar] [CrossRef]
- Amiri, I.; Rashed, A.N.Z. Power enhancement of the U-shape cavity microring resonator through gap and material characterizations. J. Opt. Commun. 2019, 1–5. [Google Scholar] [CrossRef]
- Wu, H.; Kulatilake, P.H.; Zhao, G.; Liang, W.; Wang, E. A comprehensive study of fracture evolution of brittle rock containing an inverted U-shaped cavity under uniaxial compression. Comput. Geotech. 2019, 116, 103219. [Google Scholar] [CrossRef]
- Ali, F.H.; Hamzah, H.K.; Egab, K.; Arıcı, M.; Shahsavar, A. Non-Newtonian nanofluid natural convection in a U-shaped cavity under magnetic field. Int. J. Mech. Sci. 2020, 186, 105887. [Google Scholar] [CrossRef]
- Ma, Y.; Mohebbi, R.; Rashidi, M.; Yang, Z. Simulation of nanofluid natural convection in a U-shaped cavity equipped by a heating obstacle: Effect of cavity’s aspect ratio. J. Taiwan Inst. Chem. Eng. 2018, 93, 263–276. [Google Scholar] [CrossRef]
- Nabwey, H.A.; Rashad, A.; Khan, W.A.; Alshber, S.I. Effectiveness of magnetize flow on nanofluid via unsteady natural convection inside an inclined U-shaped cavity with discrete heating. Alex. Eng. J. 2022, 61, 8653–8666. [Google Scholar] [CrossRef]
- Esfe, M.H.; Rostamian, H.; Toghraie, D.; Hekmatifar, M.; Abad, A.T.K. Numerical study of heat transfer of U-shaped enclosure containing nanofluids in a porous medium using two-phase mixture method. Case Stud. Therm. Eng. 2022, 38, 102150. [Google Scholar] [CrossRef]
- Sajjadi, H.; Delouei, A.A.; Izadi, M.; Mohebbi, R. Investigation of MHD natural convection in a porous media by double MRT lattice Boltzmann method utilizing MWCNT–Fe3O4/water hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 132, 1087–1104. [Google Scholar] [CrossRef]
- Saha, B.C.; Mahapatra, T.; Pal, D. Heat and mass flow in lid-driven magnetohydrodynamic double diffusive mixed convection of nanofluid within a trapezoidal enclosure. J. Nanofluids 2019, 8, 817–829. [Google Scholar] [CrossRef]
- Nithyadevi, N.; Yang, R.J. Double diffusive natural convection in a partially heated enclosure with Soret and Dufour effects. Int. J. Heat Fluid Flow 2009, 30, 902–910. [Google Scholar] [CrossRef]
- He, B.; Lu, S.; Gao, D.; Chen, W.; Li, X. Lattice Boltzmann simulation of double diffusive natural convection of nanofluids in an enclosure with heat conducting partitions and sinusoidal boundary conditions. Int. J. Mech. Sci. 2019, 161, 105003. [Google Scholar] [CrossRef]
- El-Shorbagy, M.; Eslami, F.; Ibrahim, M.; Barnoon, P.; Xia, W.F.; Toghraie, D. Numerical investigation of mixed convection of nanofluid flow in a trapezoidal channel with different aspect ratios in the presence of porous medium. Case Stud. Therm. Eng. 2021, 25, 100977. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Rostami, S. Optimization of heating-cooling generators with porous components/cryogenic conductors on natural convection in a porous enclosure: Using different two-phase models and single-phase model and using different designs. Int. Commun. Heat Mass Transf. 2020, 111, 104472. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Heatline visualization of natural convection in a thick walled open cavity filled with a nanofluid. Int. J. Heat Mass Transf. 2017, 109, 175–186. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Miroshnichenko, I.V.; Sheremet, M.A. Numerical analysis of unsteady conjugate natural convection of hybrid water-based nanofluid in a semicircular cavity. J. Therm. Sci. Eng. Appl. 2017, 9, 041004. [Google Scholar] [CrossRef]
- Bondarenko, D.S.; Sheremet, M.A.; Oztop, H.F.; Ali, M.E. Natural convection of Al2O3/H2O nanofluid in a cavity with a heat-generating element. Heatline visualization. Int. J. Heat Mass Transf. 2019, 130, 564–574. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Cianfrini, M.; Corcione, M.; Quintino, A. Natural convection in square enclosures differentially heated at sides using alumina-water nanofluids with temperature-dependent physical properties. Therm. Sci. 2015, 19, 591–608. [Google Scholar] [CrossRef]
- Corcione, M.; Cianfrini, M.; Quintino, A. Two-phase mixture modeling of natural convection of nanofluids with temperature-dependent properties. Int. J. Therm. Sci. 2013, 71, 182–195. [Google Scholar] [CrossRef]
- Chen, X.; Yu, P.; Winoto, S.; Low, H. Free convection in a porous wavy cavity based on the Darcy-Brinkman-Forchheimer extended model. Numer. Heat Transf. Part A Appl. 2007, 52, 377–397. [Google Scholar] [CrossRef]
- Ren, Q.; Chan, C.L. Numerical study of double-diffusive convection in a vertical cavity with Soret and Dufour effects by lattice Boltzmann method on GPU. Int. J. Heat Mass Transf. 2016, 93, 538–553. [Google Scholar] [CrossRef]
- Rahman, A.; Nag, P.; Molla, M.M. Non-Newtonian effects on MHD thermosolutal free convection and entropy production of nanofluids in a rectangular enclosure using the GPU-based mesoscopic simulation. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Liu, Q.; He, Y.L.; Li, Q.; Tao, W.Q. A multiple-relaxation-time lattice Boltzmann model for convection heat transfer in porous media. Int. J. Heat Mass Transf. 2014, 73, 761–775. [Google Scholar] [CrossRef]
- Trouette, B. Lattice Boltzmann simulations of a time-dependent natural convection problem. Comput. Math. Appl. 2013, 66, 1360–1371. [Google Scholar] [CrossRef]
- Molla, M.M.; Haque, M.J.; Khan, M.A.I.; Saha, S.C. Gpu accelerated multiple-relaxation-time lattice boltzmann simulation of convective flows in a porous media. Front. Mech. Eng. 2018, 4, 15. [Google Scholar] [CrossRef]
- Wang, J.; Wang, D.; Lallemand, P.; Luo, L.S. Lattice Boltzmann simulations of thermal convective flows in two dimensions. Comput. Math. Appl. 2013, 65, 262–286. [Google Scholar] [CrossRef]
- Mezrhab, A.; Moussaoui, M.A.; Jami, M.; Naji, H.; Bouzidi, M. Double MRT thermal lattice Boltzmann method for simulating convective flows. Phys. Lett. A 2010, 374, 3499–3507. [Google Scholar] [CrossRef]
- Ilis, G.G.; Mobedi, M.; Sunden, B. Effect of aspect ratio on entropy generation in a rectangular cavity with differentially heated vertical walls. Int. Commun. Heat Mass Transf. 2008, 35, 696–703. [Google Scholar] [CrossRef]
- Magherbi, M.; Abbassi, H.; Brahim, A.B. Entropy generation at the onset of natural convection. Int. J. Heat Mass Transf. 2003, 46, 3441–3450. [Google Scholar] [CrossRef]
- Nithiarasu, P.; Seetharamu, K.N.; Sundararajan, T. Natural convective heat transfer in a fluid saturated variable porosity medium. Int. J. Heat Mass Transf. 1997, 40, 3955–3967. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, T.S. A lattice Boltzmann model for convection heat transfer in porous media. Num. Heat. Transf. Part B 2005, 47, 157–177. [Google Scholar] [CrossRef]
- Ali, L.; Kumar, P.; Iqbal, Z.; Alhazmi, S.E.; Areekara, S.; Alqarni, M.; Mathew, A.; Apsari, R. The optimization of heat transfer in thermally convective micropolar-based nanofluid flow by the influence of nanoparticle’s diameter and nanolayer via stretching sheet: Sensitivity analysis approach. J. Non-Equilib. Thermodyn. 2023. [Google Scholar] [CrossRef]




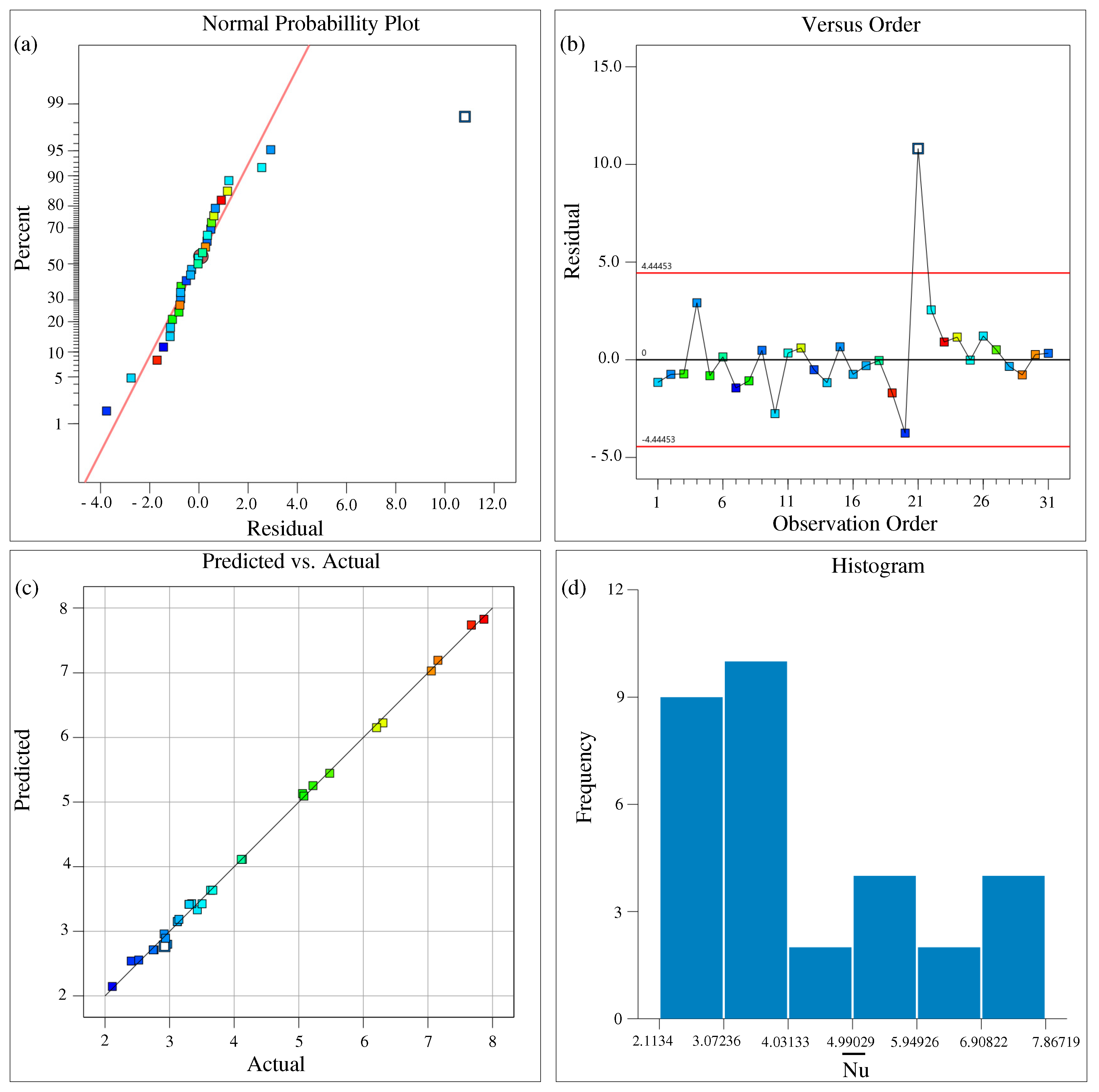
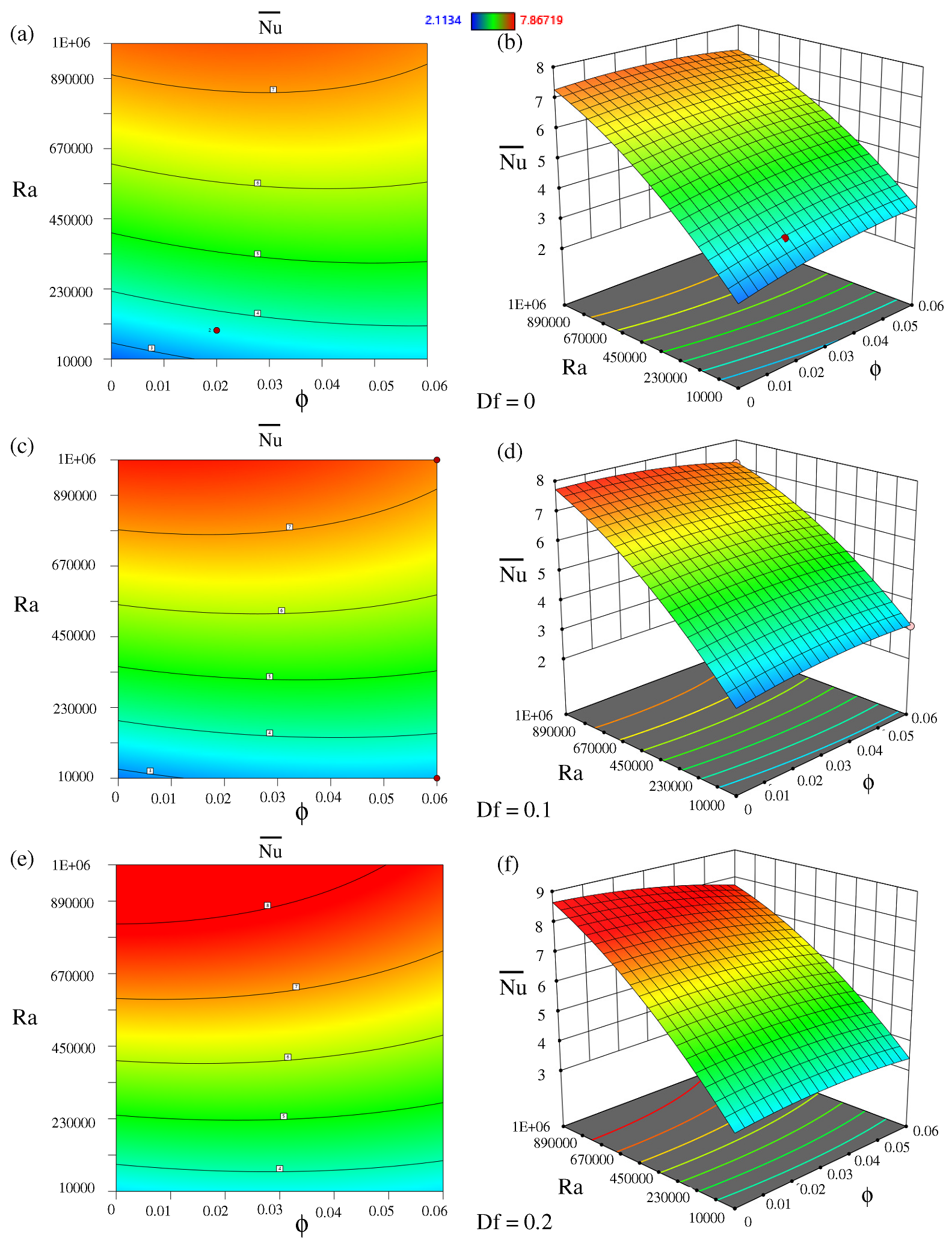
| Ref. | Numerical Methods | Flow Domain | Study Method | Parameters and Ranges | Grid Size |
|---|---|---|---|---|---|
| Esfe et al. [23] | FVM, | U-shaped | Free | , | 2100 cells |
| Ansys | enclosure | convection, | , | ||
| Fluent, | porous media, | ||||
| laminar | |||||
| nanofluid | |||||
| Ali et al. [20] | FEM | U-shaped | Natural | , | |
| cavity | convection | , | |||
| , | |||||
| , | |||||
| nanofluid | |||||
| Liu et al. [10] | LBM | Rectangular | Double- | , | |
| enclosure | diffusive | , | |||
| convection, | , | ||||
| laminar | |||||
| Sajjadi et al. [24] | LBM | Square | MHD natural | , | |
| cavity | convection, | , | |||
| porous media | , | ||||
| , | |||||
| , | |||||
| MWCNT- | |||||
| , | |||||
| Hybrid nanofluid | |||||
| Xu et al. [11] | LBM | Square | Double-diffusive | , | |
| enclosure | natural convection | , | |||
| , | |||||
| , | |||||
| Saha et al. [25] | Second | Trapezoidal | MHD double- | , | |
| order | enclosure | diffusive mixed | , | ||
| FDM | convection | , , | |||
| . | |||||
| Nithyadevi [26] | Control | Square | Double-diffusive | , | |
| volume | enclosure | natural convection | , | ||
| method | , | ||||
| , | |||||
| , | |||||
| He et al. [27] | LBM | Square | Natural | , | |
| cavity | convection | , | |||
| , | |||||
| Physical Properties | Base Fluid () | |
|---|---|---|
| [J kg K | 4179 | 765 |
| [kg m | 997.1 | 3970 |
| k [W m k | 0.613 | 40 |
| [K | 21 | 0.85 |
| [kg m | - |
| Mean Nusselt Number () | Mean Sherwood Number () | |||||
|---|---|---|---|---|---|---|
| Lattice Size | ||||||
| 4.1052 | 3.9712 | 3.9689 | 7.9802 | 8.1335 | 8.4913 | |
| 3.9041 | 3.8843 | 3.9689 | 7.7580 | 7.9398 | 8.3437 | |
| 3.8729 | 3.8336 | 3.9689 | 7.6921 | 7.8811 | 8.2904 | |
| Nithiarasu et al. [46] | Guo and Zhao [47] | Present | ||
|---|---|---|---|---|
| 1.067 | 1.066 | 1.0579 | ||
| 2.550 | 2.603 | 2.6263 |
| Mean Nusselt Number () | Mean Sherwood Number () | |||||
|---|---|---|---|---|---|---|
| Xu et al. [11] | Ren et al. [37] | Present | Xu et al. [11] | Ren et al. [37] | Present | |
| 1.2027 | 1.2020 | 1.2055 | 1.4654 | 1.4683 | 1.4879 | |
| 1.7443 | 1.7407 | 1.7179 | 2.5766 | 2.5943 | 2.5374 | |
| 2.8976 | 2.9153 | 2.9238 | 4.6108 | 4.6993 | 4.7109 | |
| 5.0852 | 5.1808 | 5.1688 | 8.3294 | 8.5134 | 8.4593 | |
| Mean Nusselt Number () | Mean Sherwood Number () | ||||||
|---|---|---|---|---|---|---|---|
| 3.1901 | 3.1754 | 3.1754 | 2.8634 | 3.1279 | 3.4280 | ||
| 3.1735 | 3.1720 | 3.1658 | 2.7396 | 3.0246 | 3.2989 | ||
| 3.1533 | 3.1515 | 3.1544 | 2.2806 | 2.5394 | 2.6936 | ||
| 3.1499 | 3.1512 | 3.1520 | 2.1979 | 2.4648 | 2.7470 | ||
| 4.2372 | 4.2656 | 4.2710 | 6.3332 | 6.5770 | 6.9152 | ||
| 4.0901 | 4.1275 | 4.1257 | 6.1286 | 6.3911 | 6.7514 | ||
| 3.3910 | 3.3860 | 3.4887 | 5.0495 | 5.3723 | 5.7572 | ||
| 3.1482 | 3.1456 | 3.1498 | 2.4609 | 2.7390 | 3.0472 | ||
| 8.3345 | 8.3160 | 8.3493 | 11.6521 | 12.2481 | 12.8763 | ||
| 8.1715 | 8.1556 | 8.1821 | 11.5961 | 12.1203 | 12.7423 | ||
| 7.1137 | 7.1243 | 7.1427 | 10.8865 | 11.3945 | 11.9208 | ||
| 3.9041 | 3.8843 | 3.9689 | 7.7580 | 7.9398 | 8.3437 | ||
| Mean Nusselt Number () | Mean Sherwood Number () | ||||||
|---|---|---|---|---|---|---|---|
| 2.2550 | 2.6084 | 2.8082 | 4.8906 | 4.8280 | 4.6701 | ||
| 0 | 0 | 3.0187 | 3.0996 | 3.0270 | 7.3294 | 6.8599 | 5.5523 |
| 2 | 4.1048 | 4.0648 | 3.8840 | 11.0281 | 10.4693 | 9.6477 | |
| 2.4319 | 2.7955 | 2.9959 | 4.9429 | 4.87796 | 4.6419 | ||
| 0 | 3.2595 | 3.3191 | 3.2530 | 7.2247 | 6.9384 | 6.1021 | |
| 2 | 4.4107 | 4.2971 | 4.0623 | 11.0223 | 10.4048 | 9.5648 | |
| 2.6068 | 2.9882 | 3.2209 | 5.0754 | 5.3167 | 5.5715 | ||
| 0 | 3.4705 | 3.4584 | 3.3663 | 7.2541 | 6.8339 | 5.5646 | |
| 2 | 4.7076 | 4.5443 | 4.2937 | 11.0216 | 10.3454 | 9.5161 | |
| 0.0 | 0.000024 | 4.639946 | 3.769352 | 8.409322 | 0.999997 | ||
| 0.04 | 0.000017 | 5.638370 | 3.157865 | 8.796251 | 0.999998 | ||
| 0.0 | 0.000068 | 6.265106 | 6.671517 | 12.936691 | 0.999995 | ||
| 0.04 | 0.000059 | 6.659704 | 5.614256 | 12.274019 | 0.999995 | ||
| 0.0 | 0.000131 | 8.444187 | 10.408137 | 18.852455 | 0.999993 | ||
| 0.04 | 0.000114 | 8.048875 | 8.899719 | 16.948708 | 0.999993 | ||
| 0.0 | 0.000024 | 4.548592 | 3.797055 | 8.345671 | 0.999997 | ||
| 0.04 | 0.000017 | 5.585220 | 3.170225 | 8.755461 | 0.999998 | ||
| 0.0 | 0.000070 | 6.067520 | 6.733653 | 12.801243 | 0.999995 | ||
| 0.04 | 0.000061 | 6.507360 | 5.601581 | 12.109002 | 0.999995 | ||
| 0.0 | 0.000136 | 8.102488 | 10.455931 | 18.558554 | 0.999993 | ||
| 0.04 | 0.000117 | 7.812779 | 8.935463 | 16.748359 | 0.999993 | ||
| 0.0 | 0.000024 | 4.514655 | 3.811956 | 8.326635 | 0.999997 | ||
| 0.04 | 0.000017 | 5.560058 | 3.182364 | 8.742438 | 0.999998 | ||
| 0.0 | 0.000073 | 6.024801 | 6.794440 | 12.819314 | 0.999994 | ||
| 0.04 | 0.000062 | 6.447220 | 5.640145 | 12.087426 | 0.999995 | ||
| 0.0 | 0.000141 | 8.059910 | 10.534990 | 18.595040 | 0.999992 | ||
| 0.04 | 0.000119 | 7.715879 | 8.984502 | 16.700500 | 0.999993 |
| Source | Totality of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 83.28 | 20 | 4.16 | 261.81 | < | Significant |
| 42.77 | 1 | 42.77 | 2689.02 | < | ||
| 2.550 | 1 | 2.55 | 160.34 | < | ||
| 4.380 | 1 | 4.38 | 275.46 | < | ||
| 0.0002 | 1 | 0.0002 | 0.0134 | 0.9102 | ||
| 0.0066 | 1 | 0.0066 | 0.4141 | 0.5344 | ||
| 0.2062 | 1 | 0.2062 | 12.97 | 0.0048 | ||
| 3.090 | 1 | 3.09 | 194.17 | < | ||
| 0.1365 | 1 | 0.1365 | 8.58 | 0.0151 | ||
| 0.5344 | 1 | 0.5344 | 33.6 | 0.0002 | ||
| 0.0282 | 1 | 0.0282 | 1.77 | 0.2125 | ||
| 0.2643 | 1 | 0.2643 | 16.62 | 0.0022 | ||
| 0.1650 | 1 | 0.165 | 10.38 | 0.0092 | ||
| 0.1207 | 1 | 0.1207 | 7.59 | 0.0203 | ||
| 0.0731 | 1 | 0.0731 | 4.6 | 0.0577 | ||
| 0.0042 | 1 | 0.0042 | 0.2645 | 0.6183 | ||
| 0.1342 | 1 | 0.1342 | 8.44 | 0.0157 | ||
| 0.2387 | 1 | 0.2387 | 15.01 | 0.0031 | ||
| 0.2370 | 1 | 0.237 | 14.9 | 0.0032 | ||
| 0.0302 | 1 | 0.0302 | 1.9 | 0.1981 | ||
| 0.1164 | 1 | 0.1164 | 7.32 | 0.0221 | ||
| Residual | 0.1590 | 10 | 0.0159 | |||
| Lack of Fit | 0.1582 | 5 | 0.0316 | 180.98 | < | Significant |
| Pure Error | 0.0009 | 5 | 0.0002 | |||
| Cor Total | 83.440 | 30 |
| 1 | −1 | −1 | 0 | −1 | 17.83454 | 0.6553 | 20.7438 | 464.2789 | |
| 0 | −43.43214 | 0.6553 | 20.7438 | 62.26667 | |||||
| 1 | − | −104.6988 | 0.6553 | 20.7438 | −339.7457 | ||||
| 1 | −1 | −1 | 1 | −1 | −3.92682 | 1.6728 | 20.7438 | 464.2789 | |
| 0 | −65.19350 | 1.6728 | 20.7438 | 62.26667 | |||||
| 1 | − | −126.4602 | 1.6728 | 20.7438 | −339.7457 | ||||
| 1 | −1 | 0 | 0 | −1 | 17.83454 | 0.0445 | 21.7614 | 464.2789 | |
| 0 | −43.43214 | 0.0445 | 21.7614 | 62.26667 | |||||
| 1 | − | −104.6988 | 0.0445 | 21.7614 | −339.7457 | ||||
| 1 | −1 | 0 | 1 | −1 | −3.92682 | 1.0620 | 21.7614 | 464.2789 | |
| 0 | −65.19350 | 1.0620 | 21.7614 | 62.26667 | |||||
| 1 | − | −126.4602 | 1.0620 | 21.7614 | −339.7457 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islam, M.M.; Hasan, M.F.; Molla, M.M. Multiple-Relaxation-Time Lattice Boltzmann Simulation of Soret and Dufour Effects on the Thermosolutal Natural Convection of a Nanofluid in a U-Shaped Porous Enclosure. Energies 2023, 16, 7229. https://doi.org/10.3390/en16217229
Islam MM, Hasan MF, Molla MM. Multiple-Relaxation-Time Lattice Boltzmann Simulation of Soret and Dufour Effects on the Thermosolutal Natural Convection of a Nanofluid in a U-Shaped Porous Enclosure. Energies. 2023; 16(21):7229. https://doi.org/10.3390/en16217229
Chicago/Turabian StyleIslam, Md. Mahadul, Md Farhad Hasan, and Md. Mamun Molla. 2023. "Multiple-Relaxation-Time Lattice Boltzmann Simulation of Soret and Dufour Effects on the Thermosolutal Natural Convection of a Nanofluid in a U-Shaped Porous Enclosure" Energies 16, no. 21: 7229. https://doi.org/10.3390/en16217229
APA StyleIslam, M. M., Hasan, M. F., & Molla, M. M. (2023). Multiple-Relaxation-Time Lattice Boltzmann Simulation of Soret and Dufour Effects on the Thermosolutal Natural Convection of a Nanofluid in a U-Shaped Porous Enclosure. Energies, 16(21), 7229. https://doi.org/10.3390/en16217229









