Study on Thermal Performance of Electric Heating System with Salt Hydrate-PCM Storage
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Methods and Procedures
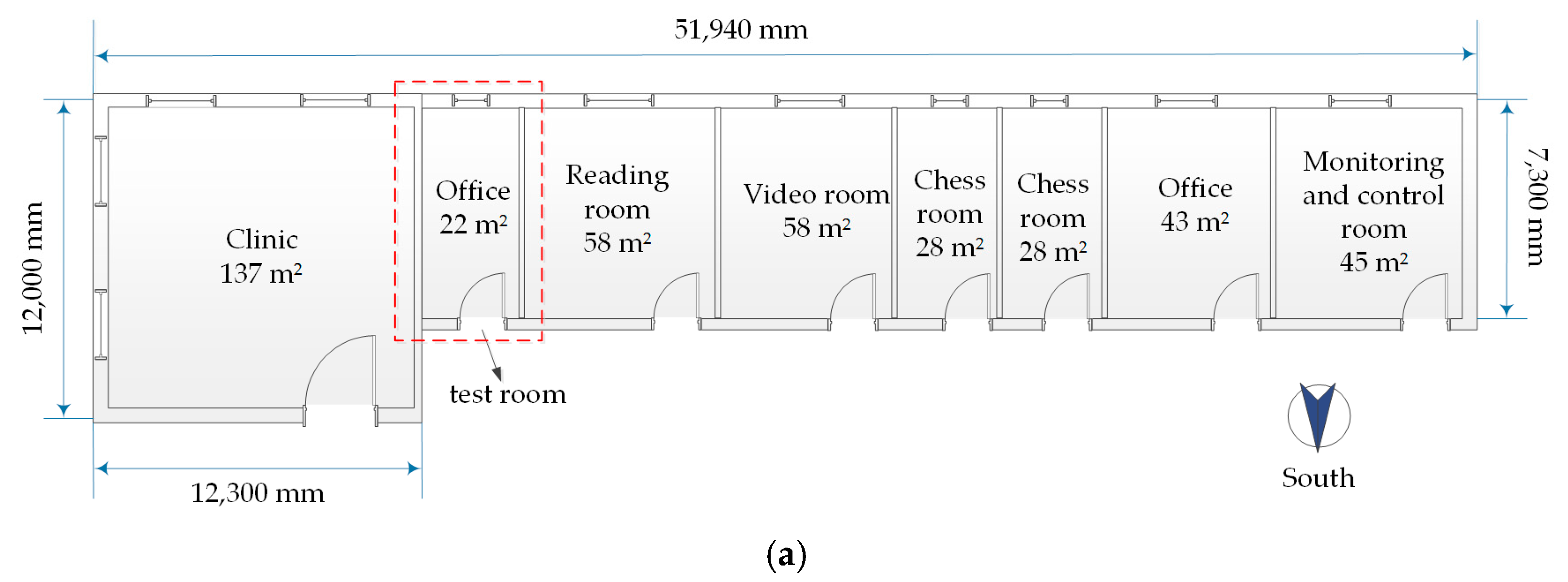
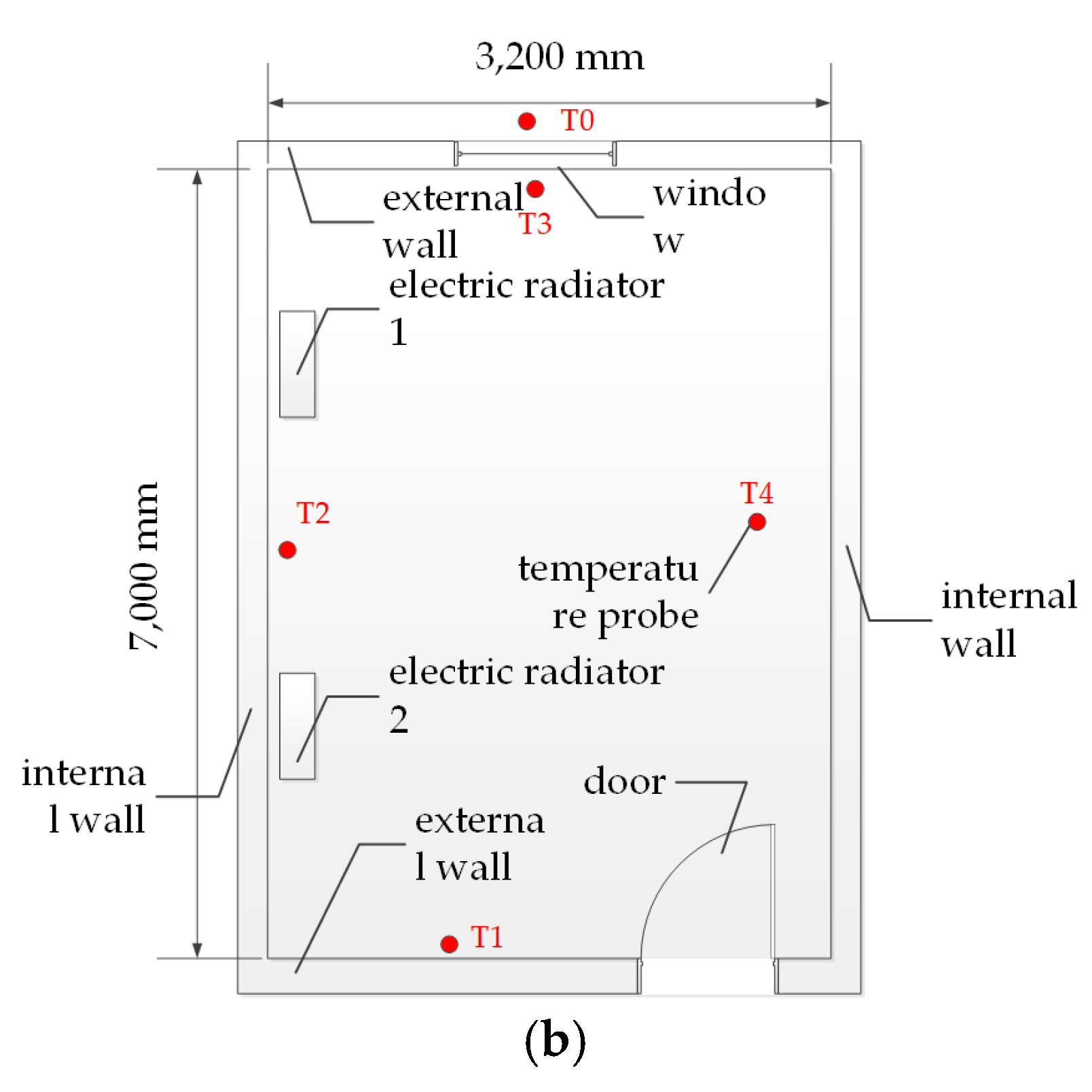
2.1.1. Room Test
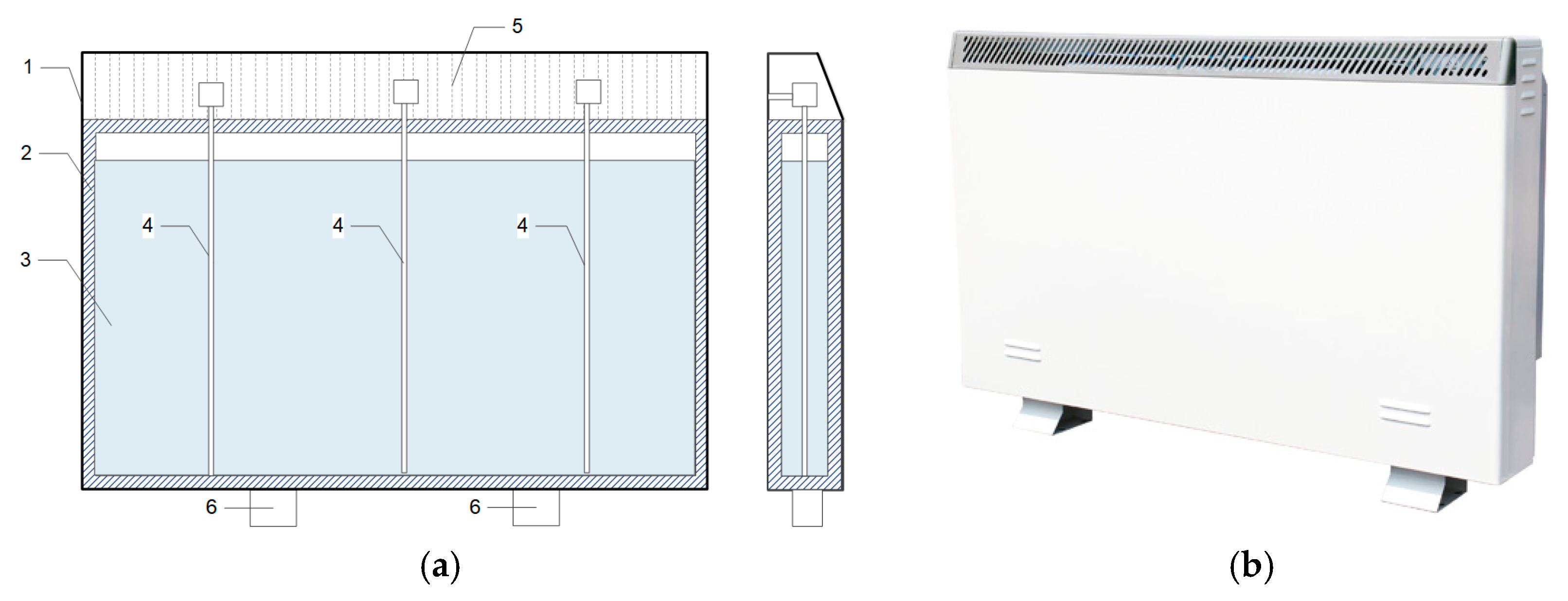
2.1.2. Electric Radiator Combined with PCM Storage
2.1.3. Selection of Salt Hydrates
2.2. Numerical Method and Model Validation
2.2.1. Governing Equations and Boundary Conditions
- the PCM is homogeneous and isotropic;
- the phase change temperature of the PCM is constant, ignoring the volume change during the charging/discharging process and the phenomenon of subcooling;
- the melted PCM is an incompressible fluid;
- the thermophysical properties of the PCM in the solid phase and in the liquid phase are constant, and they are independent of the temperature.
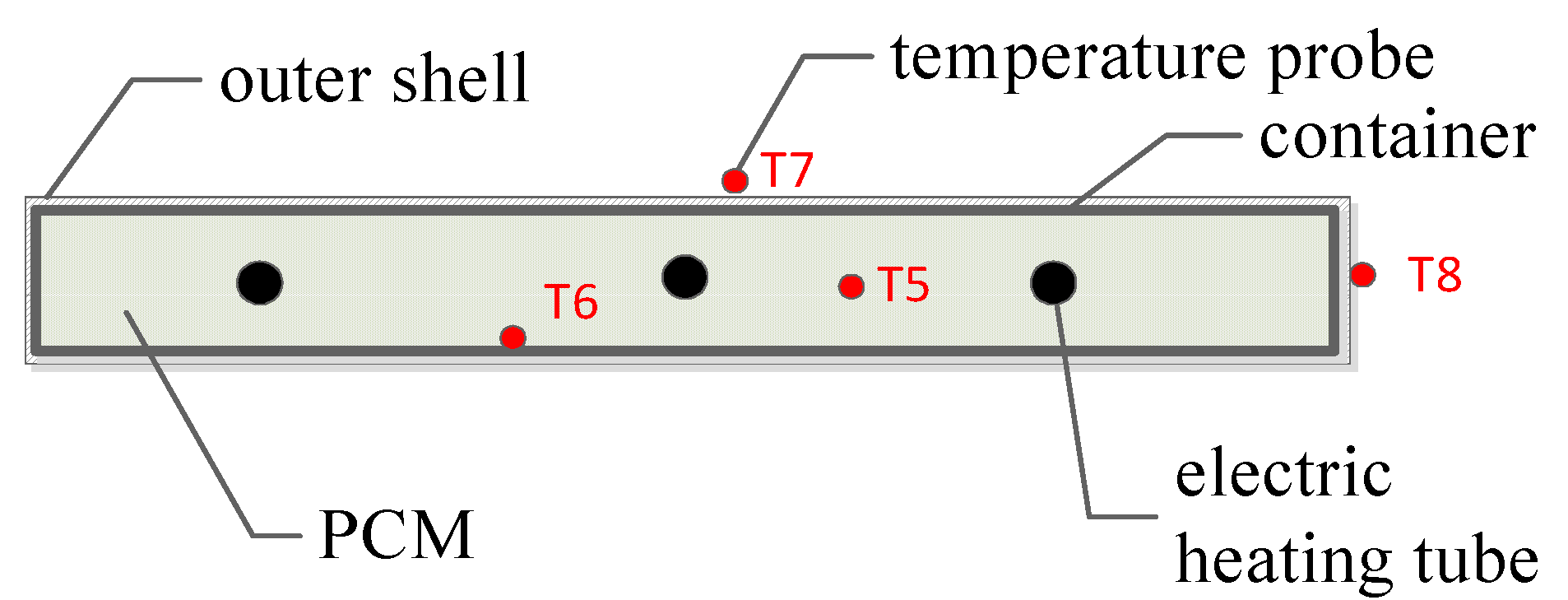
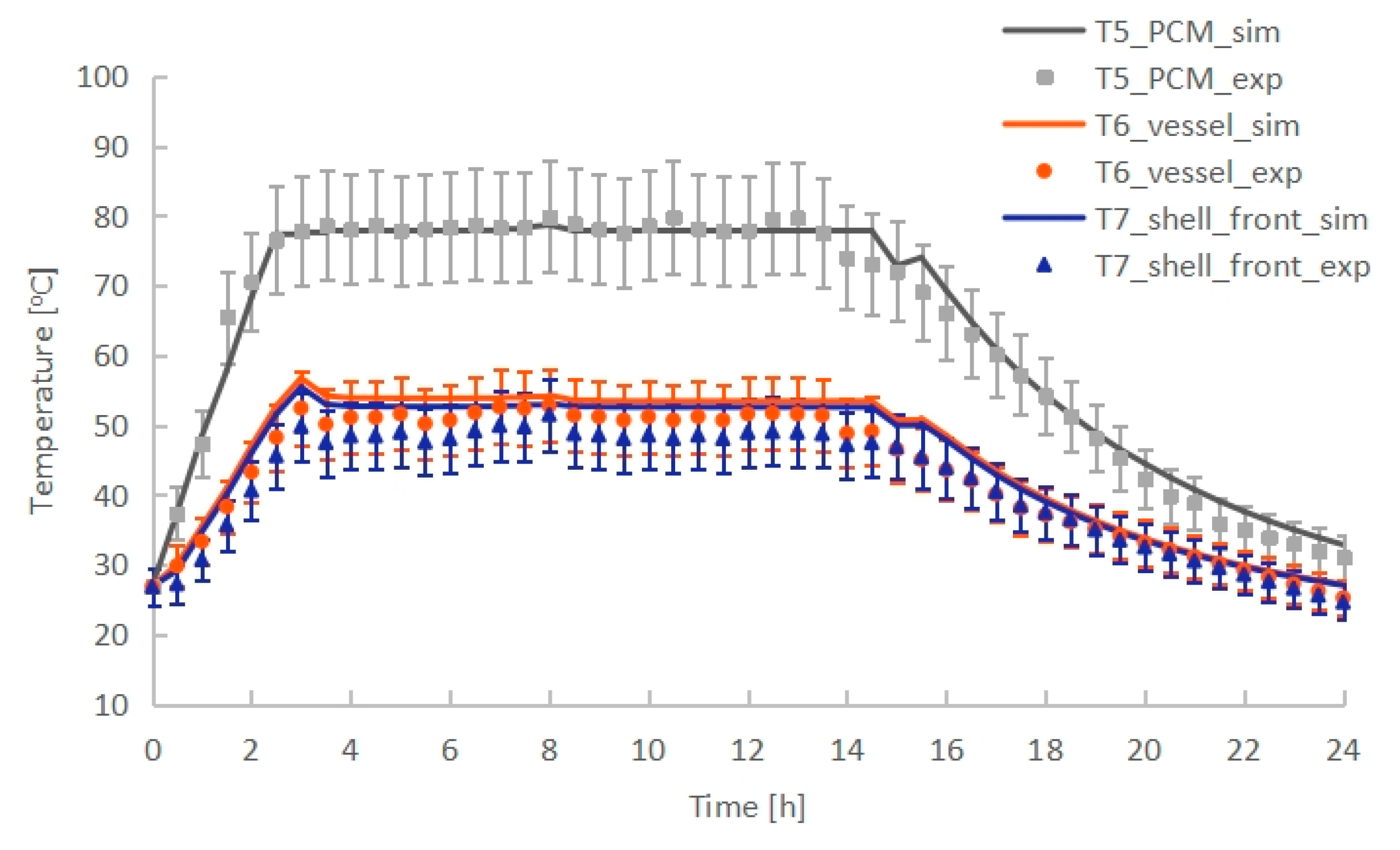
2.2.2. Model Validation
3. Results
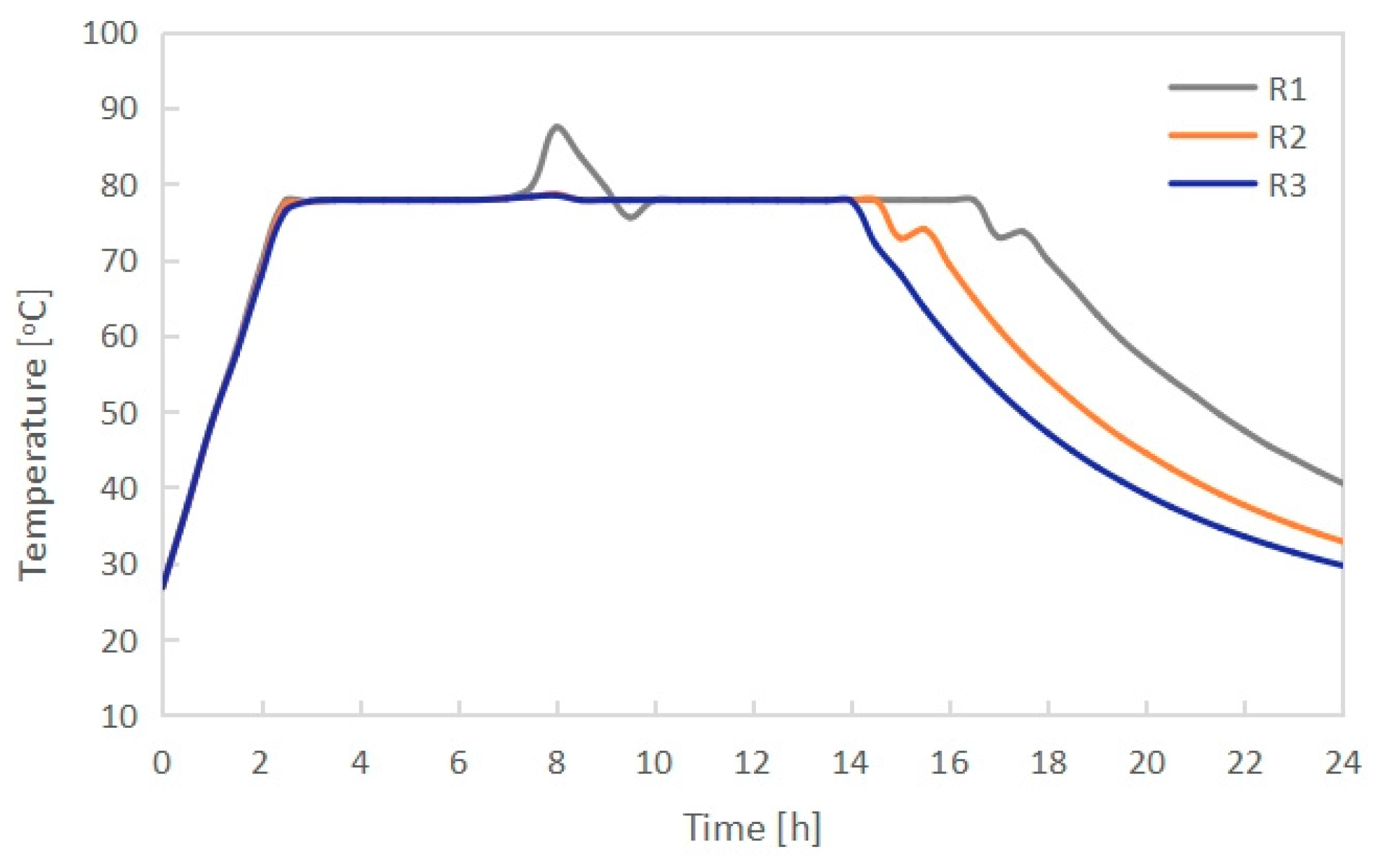
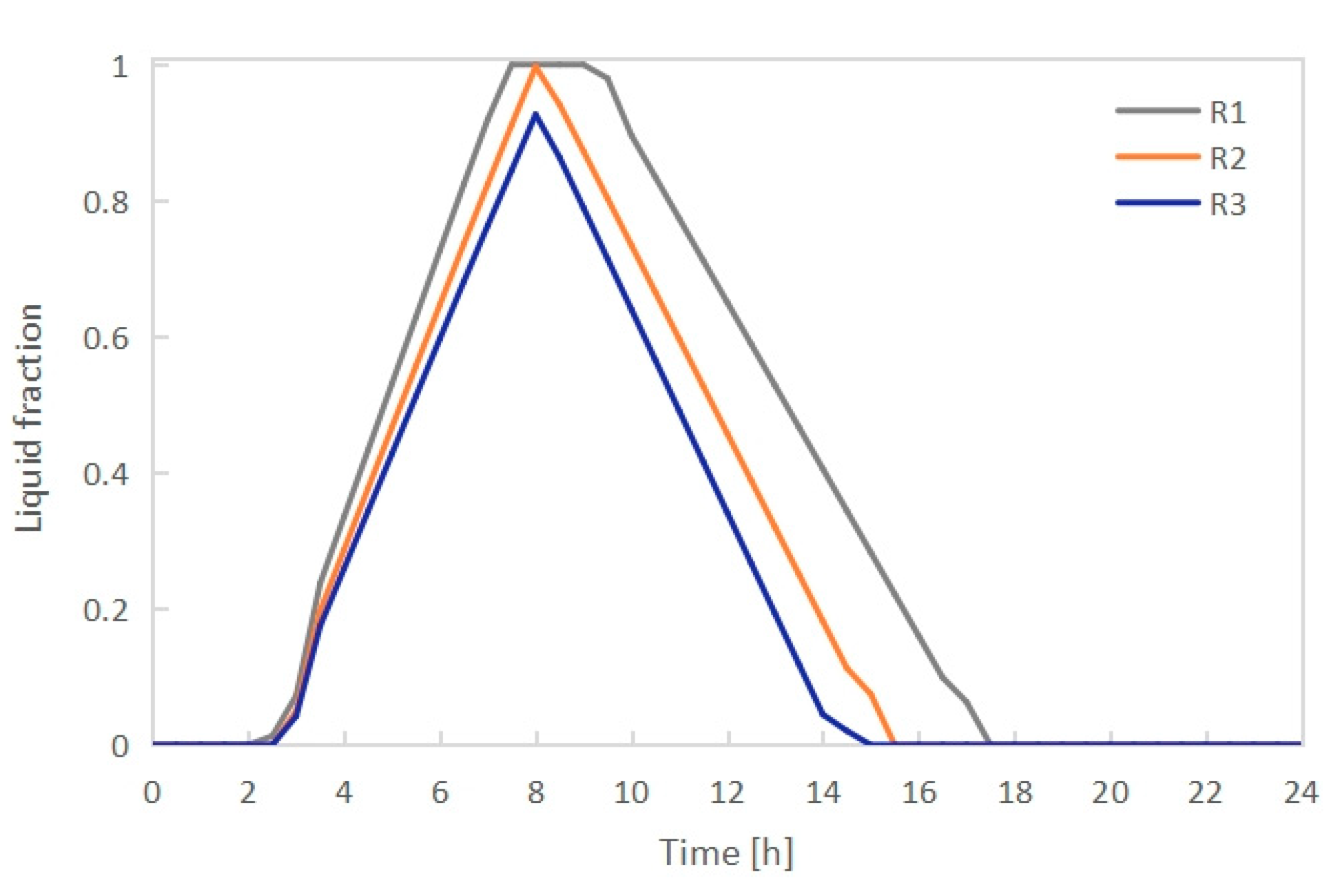
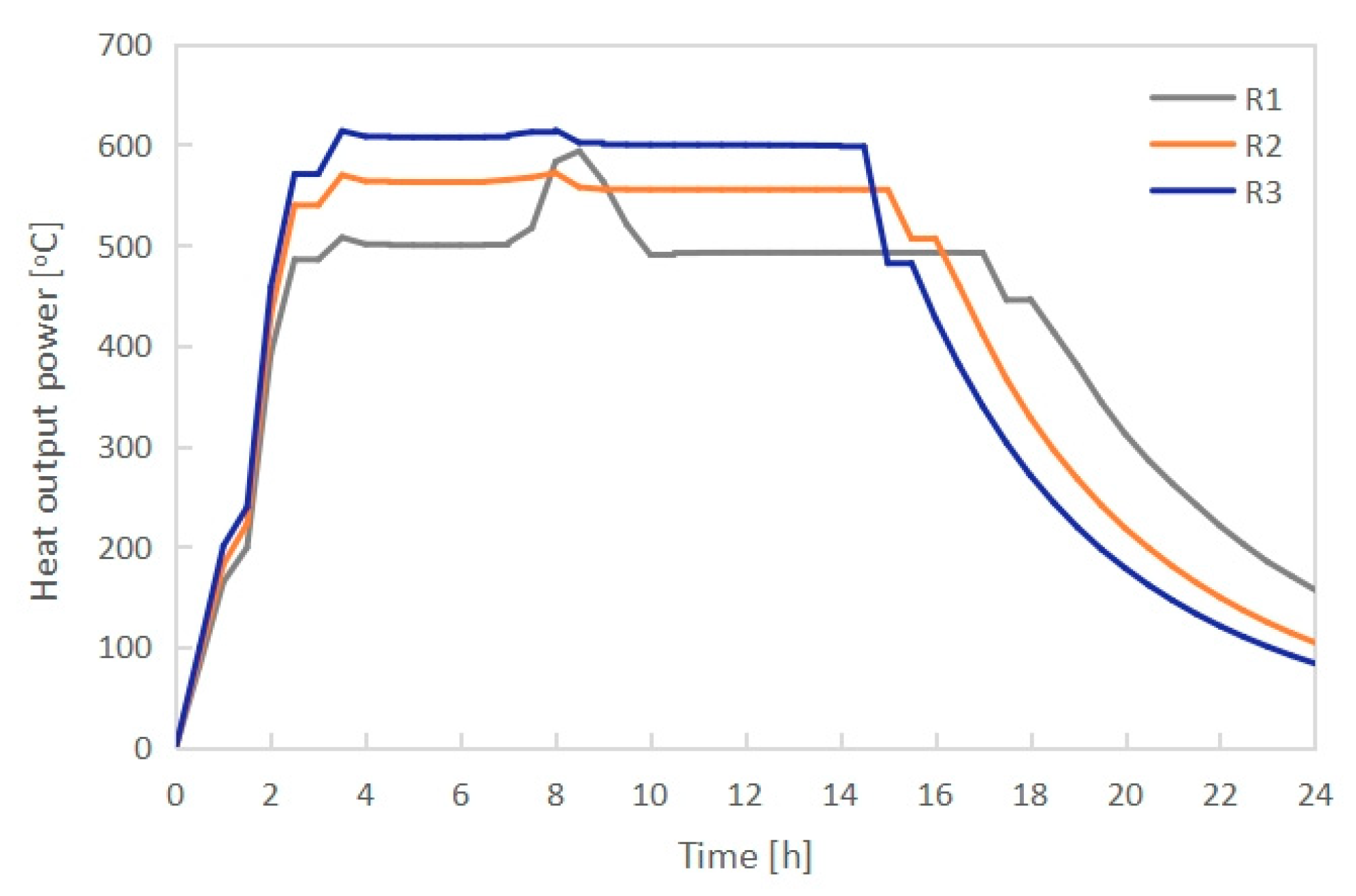
3.1. Effect of Radiator Configuration
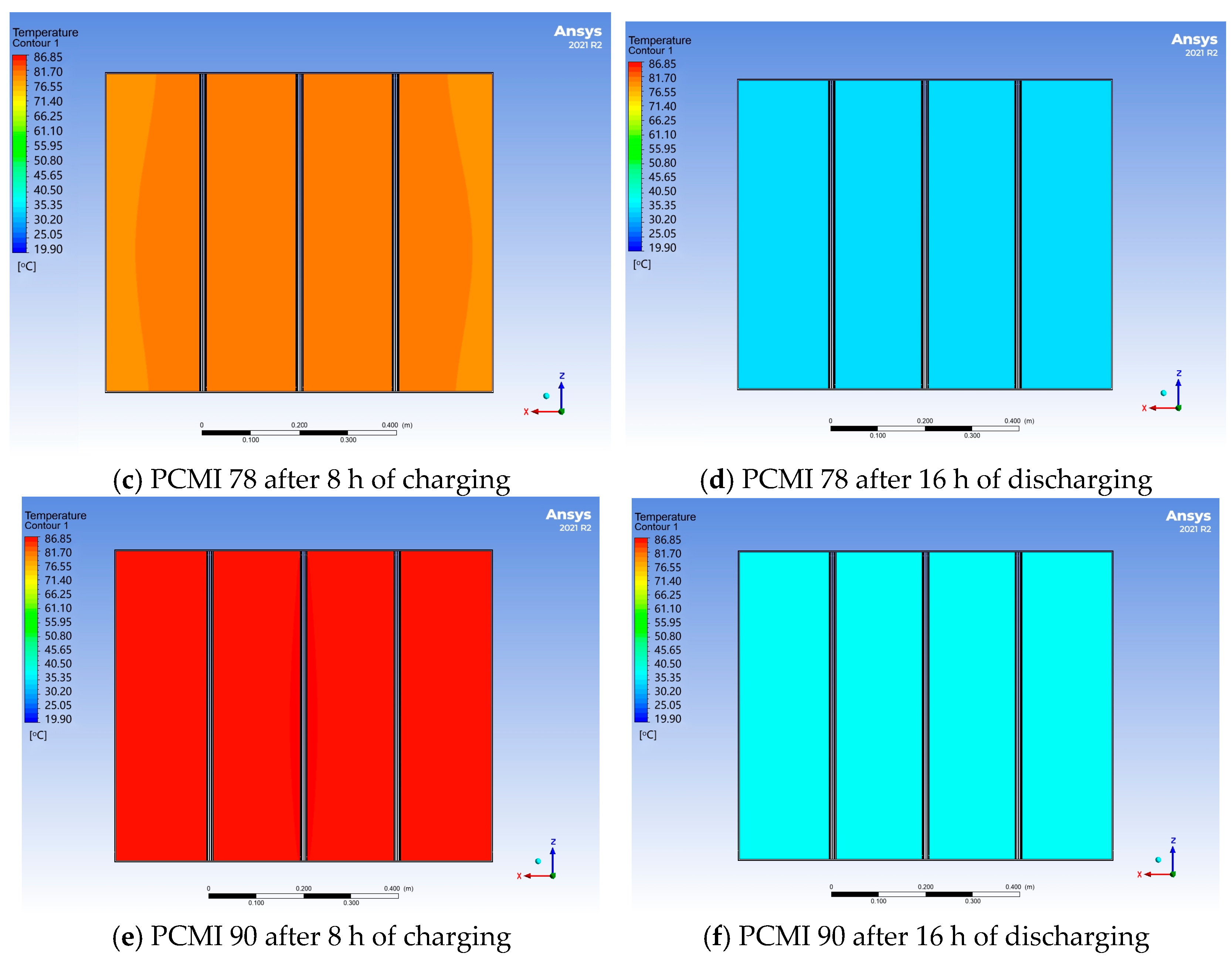
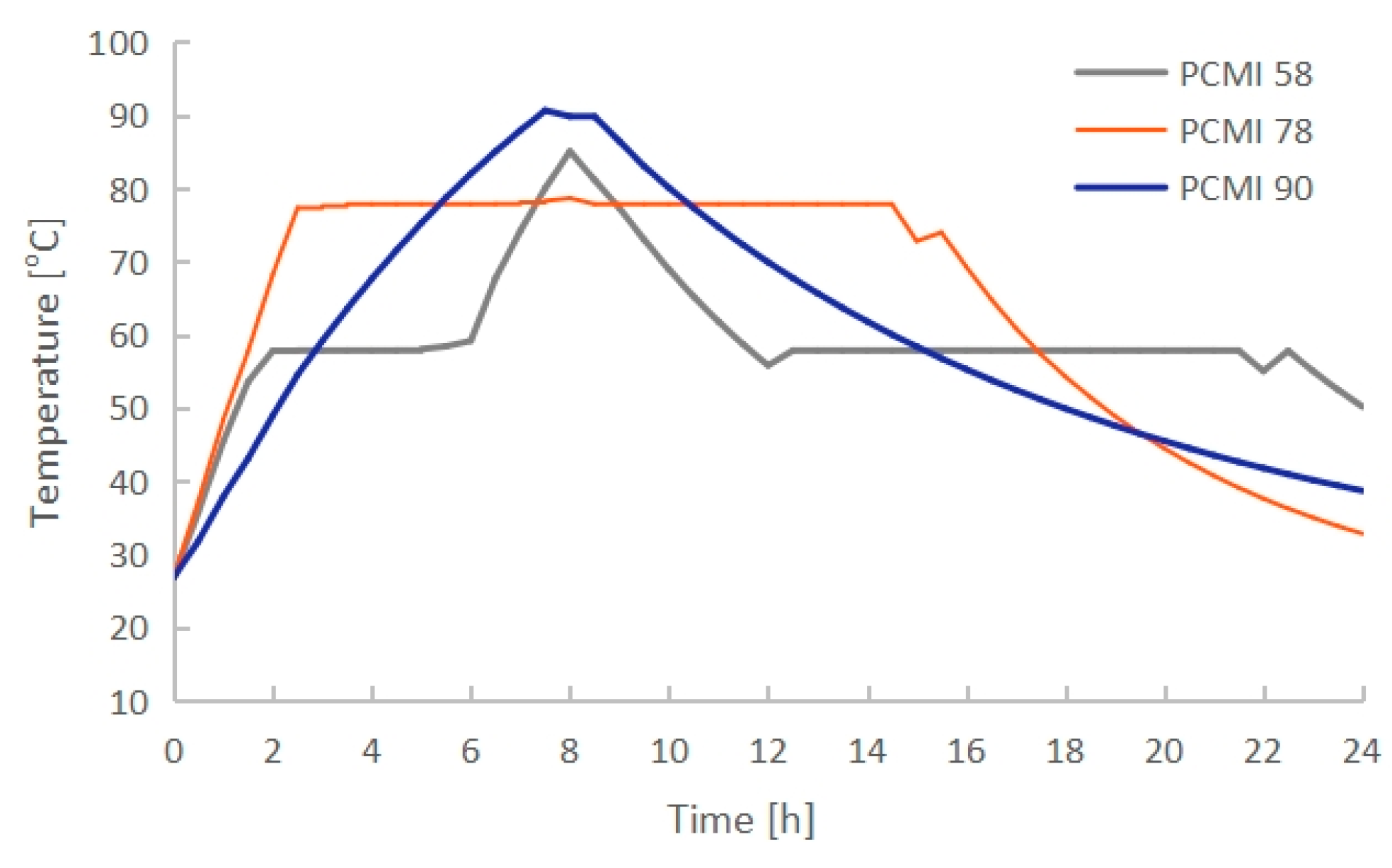
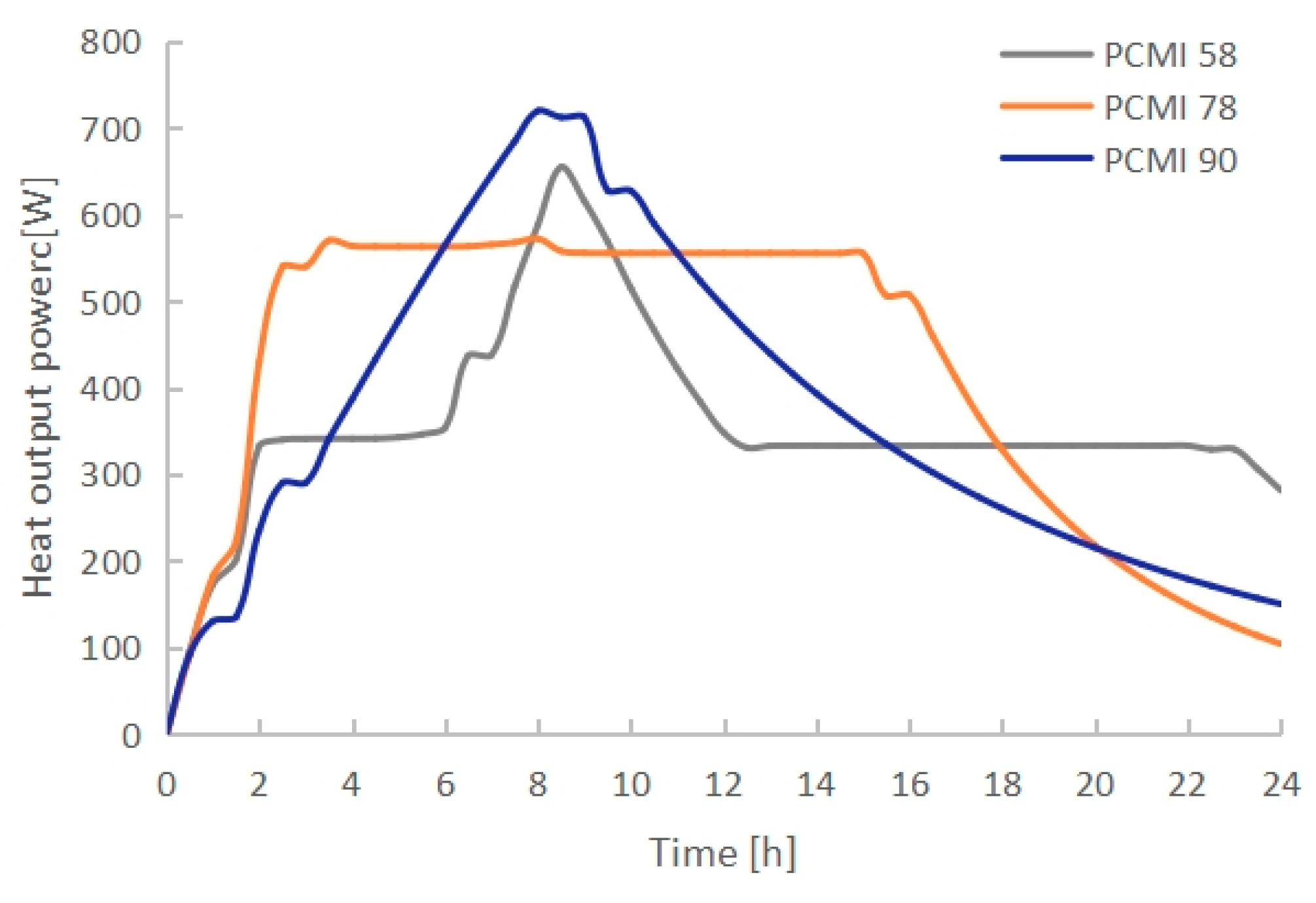
3.2. Effect of PCM Thermal Properties
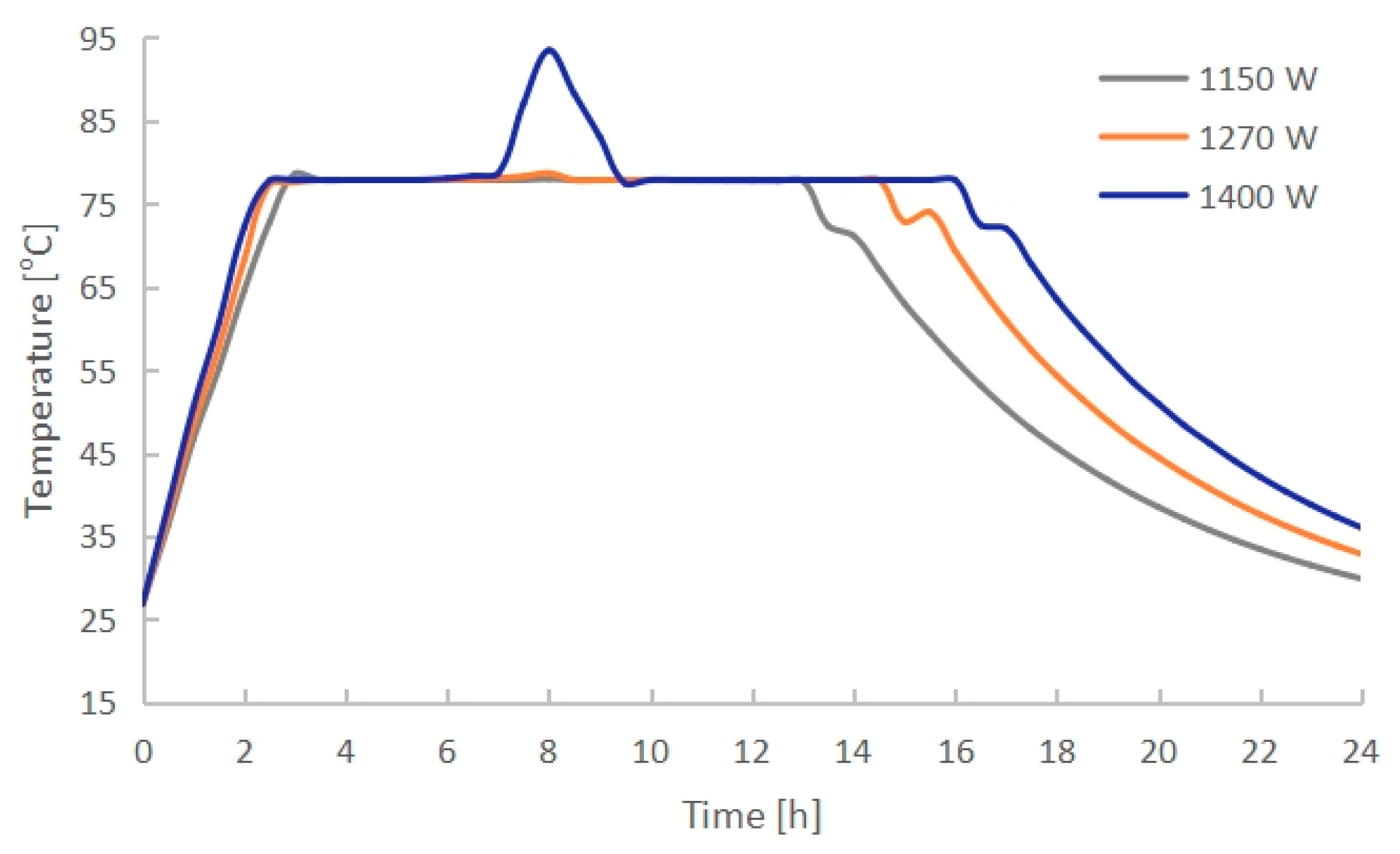
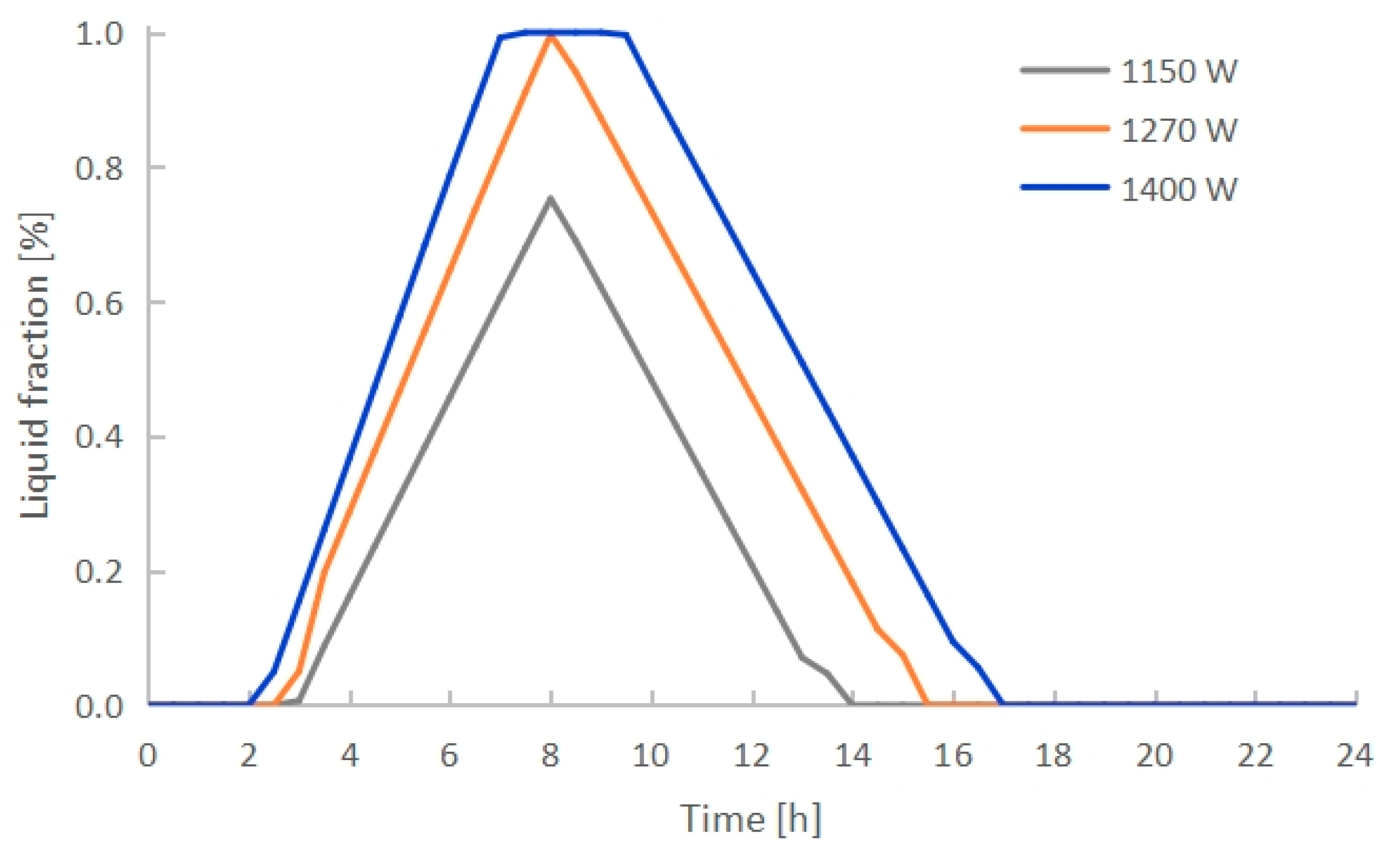
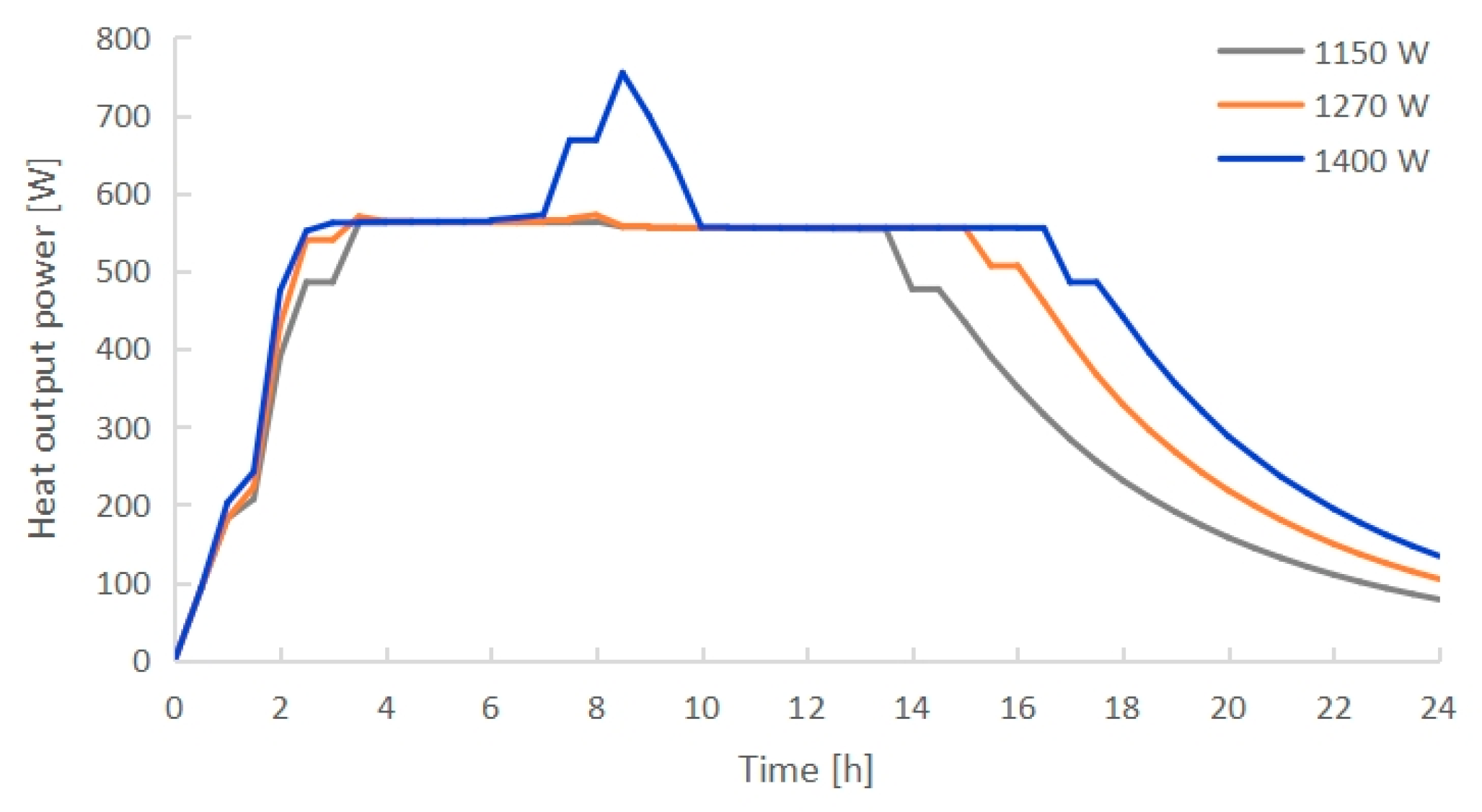
3.3. Effect of Electric Heating Power
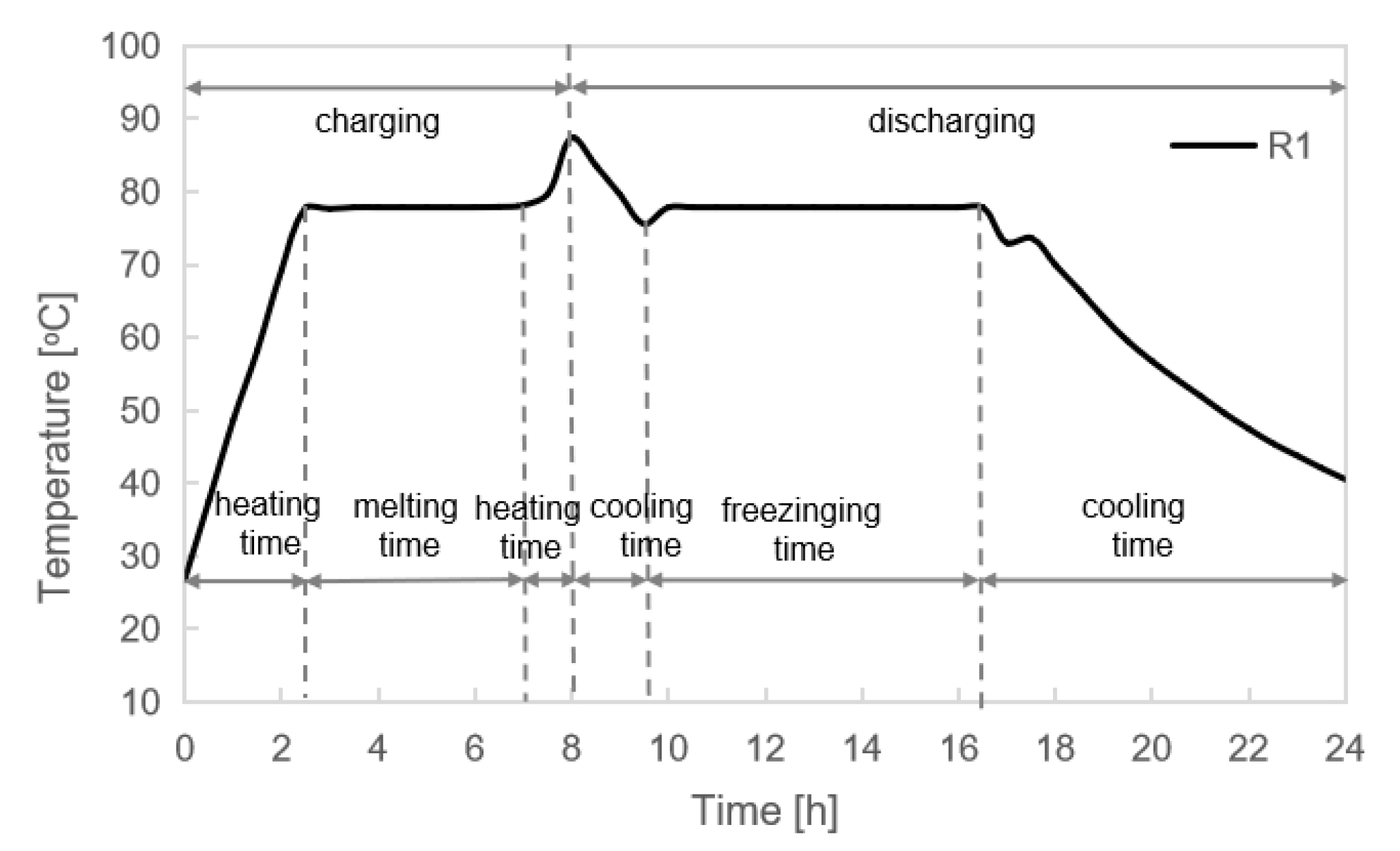
3.4. Room Test Results
4. Discussion and Conclusions
- The PCM melting time increased with growing length-width ratio (L/B) of the radiator when keeping the height H unchanged. PCMI 78 with a high L/B ratio of 9.3 could not be completely melted during the charging process. Conversely, the average heat output of the electric radiator rose with increasing L/B ratio. In consideration of both the PCM melting/freezing behaviors and the radiator heat output, the radiator having the external dimension L × B × H of 796 × 106 × 656 mm and the L/B ratio of 7.5 presented the best thermal performance.
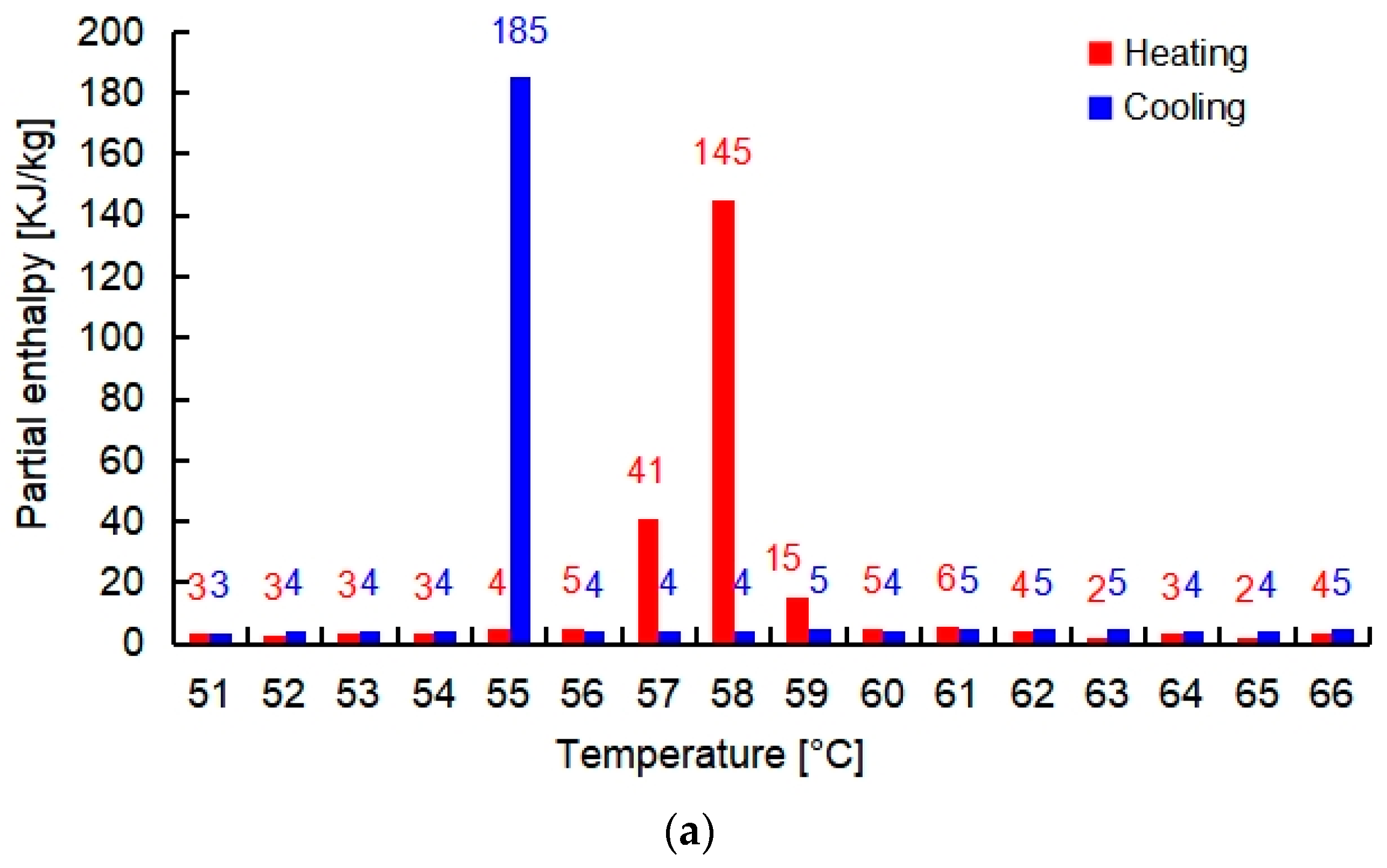
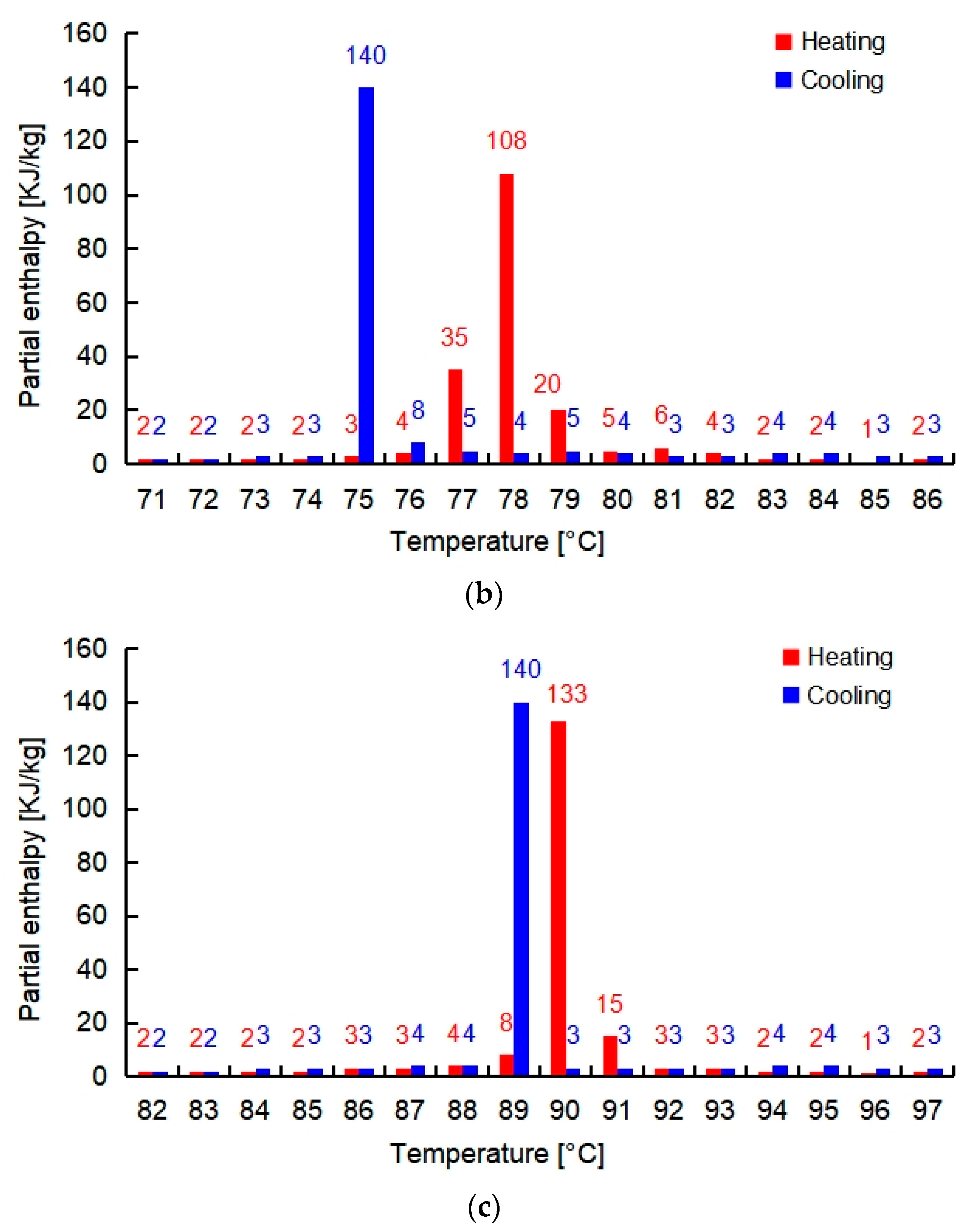
- The PCM melting time increased with the rising melting temperature. PCMI 58 and PCMI 78 were completely melted after 8 h of heating, while only 11.6% of PCMI 90 was melted. However, a large amount of heat stored in PCMI 58 could not be released after a charging/discharging cycle, due to the small temperature difference between the radiator surfaces and ambient air. The average heat output of the radiator with PCMI 58, PCMI 78 and PCMI 90 were 355 W, 412 W and 366 W, respectively. Therefore, PCMI 78 is suitable for applying in the electric radiator.
- The PCM melting time decreased with increasing electric heating power. PCMI 78 was completely melted after exactly 8 h of heating with 1270 W, while only 75.3% of the material was melted with 1150 W, and it was overheated with 1400 W. Conversely, both the heat output and thermal storage efficiency grew with the increasing electric heating power. The average heat output in 24 h arrived 412 W with 1270 W, which could cover the heating demand of a 10 m2 floor area with a total heating load of 400 W.
- The room test results indicated the designed heating requirement could be met by using the electric radiator combined with PCMI 78. During the three test days in February 2023 with an average outdoor temperature of 5.2 °C, the indoor air temperature was kept at 20.0 °C, with a maximum of 23.5 °C and a minimum of 18.2 °C.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| cp | specific heat at constant pressure, kJ/kg·K |
| C | value measured or simulated, - |
| F | area, m2 |
| h | sensible enthalpy, kJ/kg |
| H | total enthalpy, kJ/kg |
| latent enthalpy, kJ/kg | |
| K | total heat transfer coefficient, W/m2·K |
| l | length, m |
| L | latent heat, kJ/kg |
| m | mass, kg |
| n | coefficient, - |
| P | electrical |
| q | heat power, W |
| Q | heat, kJ |
| S | source term, - |
| t | time, h |
| T | temperature, K |
| velocity, m/s | |
| correction coefficient, - | |
| emissivity, - | |
| thermal storage efficiency, - | |
| effective thermal conductivity, W/m·K | |
| density, kg/m3 | |
| Stefan-Boltzmann constant | |
| liquid fraction, % | |
| Subscripts | |
| air | air |
| e | electrical |
| env | envelope |
| f | freezing |
| i | instance |
| in | indoor |
| m | melting |
| mush | mushy zone |
| off | off-peak time |
| on | on-peak time |
| out | outdoor |
| ref | reference |
| s | stored heat |
| t | total |
| Acronyms | |
| Cv(RMSE) | the coefficient of root-mean-square error |
| PCM | phase change material |
| MBE | mean bias error |
References
- Jiang, Y.; Tang, X.Y.; Ni, W.D.; Yue, G.; Wang, J.; Hu, S. The relevance between PM2.5 in Beijing and winter heating systems and control measures. Chin. Energy 2014, 36, 7–13,28. [Google Scholar]
- Zhang, J.G. Promotion of low-carbon heat supply under the background of carbon emissions peak and carbon neutrality. Energy Ind. 2021, 9, 32–37. [Google Scholar]
- Administration of the People’s Republic of China. Statement on Winter Clean Heating Planning in Northern Regions (2017–2021); Administration of the People’s Republic of China: Beijing, China, 20 December 2017. Available online: http://www.gov.cn/xinwen/2017-12/20/5248855/files/7ed7d7cda8984ae39a4e9620a4660c7f.pdf (accessed on 10 September 2023).
- Climate Change and Energy Transition Program. China Dispersed Coal Management Report 2022; Institute of Energy, Peking University: Beijing, China, 20 September 2022; Available online: https://www.ccetp.cn/newsinfo/4371839.html (accessed on 10 September 2023).
- Xu, G.; Wang, C.L.; Xu, C.; Bai, P. Evaluation of air pollutant emissions from scattered coal burning and electric heating in Beijing-Tianjin-Heibei region. Res. Environ. Sci. 2016, 29, 1735–1742. [Google Scholar]
- Lin, K.; Zhang, Y.; Xu, X.; Di, H.; Yang, R.; Qin, P. Modeling and simulation of under-floor electric heating system with shape-stablized PCM plates. Build. Environ. 2004, 39, 1427–1434. [Google Scholar] [CrossRef]
- Lin, K.; Zhang, Y.; Xu, X.; Di, H.; Yang, R.; Qin, P. Experimental study of under-floor electric heating system with shape-stablized PCM plates. Build. Environ. 2005, 37, 215–220. [Google Scholar] [CrossRef]
- Barzin, R.; Chen, J.J.J.; Young, B.R.; Farid, M.M. Application of PCM underfloor heating in combination with PCM wallboards for space heating using price based control system. Appl. Energy 2015, 148, 39–48. [Google Scholar] [CrossRef]
- Devaux, P.; Farid, M.M. Benefits of PCM underfloor heating with PCM wallboards for space heating in winter. Appl. Energy 2017, 191, 593–602. [Google Scholar] [CrossRef]
- Faraj, K.; Faraj, J.; Hachem, F.; Bazzi, H.; Khaled, M.; Castelain, C. Analysis of underfloor electrical heating system integrated with coconut oil-PCM plates. Appl. Therm. Eng. 2019, 158, 113778. [Google Scholar] [CrossRef]
- Ma, G.Y.; Wang, Z.H.; Yan, R.; Cao, H. Making and capability testing of electric heater with phase change accumulator. J. Fushun Pet. Inst. 2003, 23, 50–53. [Google Scholar]
- Chen, G.S.; Zhang, R.Y.; Ke, X.F. Thermal efficiency modelling and experimental research for electric heating units with phase change materials. HVAC 2006, 36, 23–26. [Google Scholar]
- Liu, J.; Liu, S.; Wang, X.; Zahng, Y.; Di, H. Research and development of a high-temperature phase change storage electric heater and test of its thermal performance. Build. Sci. 2007, 23, 58–61, 86. [Google Scholar]
- Long, K. Experimental and Simulation Study on Heat Transfer Characteristics of Solid Regenerative Electric Heating Device. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021. [Google Scholar]
- Wang, P.; Wang, X.; Huang, Y.; Li, C.; Peng, Z.; Ding, Y. Thermal energy charging behaviour of a heat exchange device with a zigzag plate configuration containing multi-phase-change-materials (m-PCMs). Appl. Energy 2015, 142, 328–336. [Google Scholar] [CrossRef]
- Sardari, P.T.; Giddings, D.; Grant, D.; Gillott, M.; Walker, G.S. Discharge of a composite metal foam/phase change material to air heat exchanger for a domestic thermal storage unit. Renew. Energy 2020, 148, 987–1001. [Google Scholar] [CrossRef]
- Sardari, P.T.; Babaei-Mahani, R.; Giddings, D.; Yasseri, S.; Moghimi, M.A.; Bahai, H. Energy recovery from domestic radiators using a compact composite metal Foam/PCM latent heat storage. J. Clean. Prod. 2020, 257, 120504. [Google Scholar] [CrossRef]
- Sardari, P.T.; Grant, D.; Giddings, D.; Walker, G.S.; Gillott, M. Composite metal foam/PCM energy store design for dwelling space air heating. Energy Convers. Manag. 2019, 201, 112151. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical modeling of nano enhanced PCM solidification in an enclosure with metallic fin. J. Mol. Liq. 2018, 259, 424–438. [Google Scholar] [CrossRef]
- Pereira da Cunha, J.; Eames, P. Thermal energy storage for low and medium temperature applications using phase change materials e a review. Appl. Energy 2016, 177, 227–238. [Google Scholar] [CrossRef]
- DB33/1038-2007; Design Standard for Energy Efficiency of Public Buildings in Zhejing Provice. Zhejiang Provincial Department of Construction: Hangzhou, China, 2007.
- GB50736-2012; Chinese Design Code for Heating Ventilation and Air Conditioning of Civil Buildings. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China: Beijing, China, 2012.
- Sharma, S.D.; Kitano, H.; Sagara, K. Phase change materials for low temperature solar thermal applications. Res. Rep. Fac. Eng. Mie Univ. 2004, 29, 31–64. [Google Scholar]
- Lidy Energy Technology Co., Ltd. Available online: http://www.lidy.net.cn/en/col.jsp?id=112 (accessed on 10 September 2023).
- W&a Wärme- und Anwendungstechnische Prüfungen. Available online: http://www.xn--wrmeprfung-q5a70a.de/projekte_messsystem_kalorimeter.html (accessed on 10 September 2023).
- Voller, V.R. Modeling solidification processes, technical report. In Proceedings of the Mathematical Modeling of Metals Processing Operations Conference; American Metallurgical Society: Palm Desert, CA, USA, 1987. [Google Scholar]
- Voller, V.R.; Brent, A.D.; Reid, K.J. A computational modeling framework for the analysis of metallurgical solidification process and phenomena, technical report. In Proceedings of the Conference for Solidification Processing, Ranmoor House, Sheffield, UK, 21–24 September 1987. [Google Scholar]
- Voller, V.R.; Prakash, C. A Fixed-Grid numerical modeling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1720. [Google Scholar] [CrossRef]
- Wang, B.X. Engineering Heat and Mass Transfer; Science Publishing House: Beijing, China, 2015; Volume 2, p. 378. [Google Scholar]
- ASHRAE. ASHRAE Guideline 14–2014: Measurement of Energy Demand and Savings; American Society of Heating, Refrigerating and Air Conditioning Engineers: Atlanta, GA, USA, 2014. [Google Scholar]






| Parameter | Value | |
|---|---|---|
| Total heat transfer coefficient K (W/m2·K) | roof | 0.70 |
| external walls | 1.38 | |
| door | 3.00 | |
| window | 2.53 | |
| Dimension B × H (mm) | door | 800 × 2100 |
| window | 1200 × 1600 | |
| Type of window | frame | PVC-U |
| glass | double clear (5/9/5) | |
| g-value window (-) | 0.8 | |
| Air change (1/h) | 1.0 | |
| Salt Hydrate | Specific Heat Solid (kJ/kg·K) [24] | Thermal Conductivity Solid (W/m·K) [24] | Density Solid (kg/m3) [24] | Melting Point (°C) | Total Enthalpy in 15 K (kJ/kg) |
|---|---|---|---|---|---|
| PCMI 58 | 2.40 | 0.61 | 1400 | 58 | 250 |
| PCMI 78 | 1.46 | 0.70 | 1890 | 78 | 200 |
| PCMI 90 | 3.80 | Not available | 1630 | 90 | 187 |
| Number of Elements | Melting Time (h) | Freezing Time (h) |
|---|---|---|
| 297,422 (mesh size on the shell &vessel: 10 mm, on the PCM: 6 mm) | 8.5 | 6.5 |
| 836,542 (mesh size on the shell &vessel: 10 mm, on the PCM: 4 mm) | 8.0 | 7.0 |
| 1,932,417 (mesh size on the shell &vessel: 10 mm, on the PCM: 3 mm) | 8.0 | 7.0 |
| MEB (%) | Cv (RMSE) (%) | |
| PCM temperature (T5) | −0.71 | 3.30 |
| Vessel temperature (T6) | −5.47 | 6.38 |
| Shell front temperature (T7) | −7.63 | 8.61 |
| R 1 | R 2 | R 3 | |
|---|---|---|---|
| L × B × H (mm) | 664 × 126 × 656 | 796 × 106 × 656 | 887 × 96 × 656 |
| L/B | 5.3 | 7.5 | 9.3 |
| l (mm) | 105.9 | 93.5 | 86.6 |
| Electric Heating Power | 1150 W | 1270 W | 1400 W |
|---|---|---|---|
| PCM heating time before melting (h) | 2.5 | 2.5 | 2.0 |
| PCM melting time (h) | 5.5 | 5.5 | 5.0 |
| PCM heating time after melting (h) | 0.0 | 0.0 | 1.0 |
| PCM cooling time before freezing (h) | 0.0 | 0.0 | 1.5 |
| PCM freezing time (h) | 5.5 | 7.0 | 7.0 |
| PCM cooling time after freezing (h) | 10.5 | 9.0 | 7.5 |
| Average heat output power (W) during the charging process | 375 | 412 | 469 |
| Average heat output power (W) during the discharging process | 422 | 450 | 432 |
| Average heat output power (W) in 24 h | 334 | 392 | 451 |
| Thermal storage efficiency (%) | 63.2 | 65.6 | 66.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Piontek, U.; Zhuang, L.; Zheng, R.; Zou, D. Study on Thermal Performance of Electric Heating System with Salt Hydrate-PCM Storage. Energies 2023, 16, 7108. https://doi.org/10.3390/en16207108
Huang L, Piontek U, Zhuang L, Zheng R, Zou D. Study on Thermal Performance of Electric Heating System with Salt Hydrate-PCM Storage. Energies. 2023; 16(20):7108. https://doi.org/10.3390/en16207108
Chicago/Turabian StyleHuang, Li, Udo Piontek, Lulu Zhuang, Rongyue Zheng, and Deqiu Zou. 2023. "Study on Thermal Performance of Electric Heating System with Salt Hydrate-PCM Storage" Energies 16, no. 20: 7108. https://doi.org/10.3390/en16207108
APA StyleHuang, L., Piontek, U., Zhuang, L., Zheng, R., & Zou, D. (2023). Study on Thermal Performance of Electric Heating System with Salt Hydrate-PCM Storage. Energies, 16(20), 7108. https://doi.org/10.3390/en16207108








