Development of the Kinetic Equation of the Groove Corrosion Process for Predicting the Residual Life of Oil-Field Pipelines
Abstract
1. Introduction
- -
- An impact from a galvanic couple (bare metal-metal) coated with iron sulfide or, at low flow rates, promoting the deposition of mechanical impurities in pipelines, corrosion due to the operation of concentration cells in which surface areas with deposits are anodes;
- -
- An increased stress state in the area of the initial metal thinning, which initiates the mechanism of brittle destruction due to general and localized mechanochemical corrosion.
- According to the first scheme, the abrasives destroy the diffusion layer at the “pumped medium–steel” boundary;
- According to the second scheme, the passivating films formed as a result of corrosion processes are destroyed;
- The third scheme is a plasticizing effect due to the mechanical deformation of metal with subsequent depolarization.
2. Materials and Methods
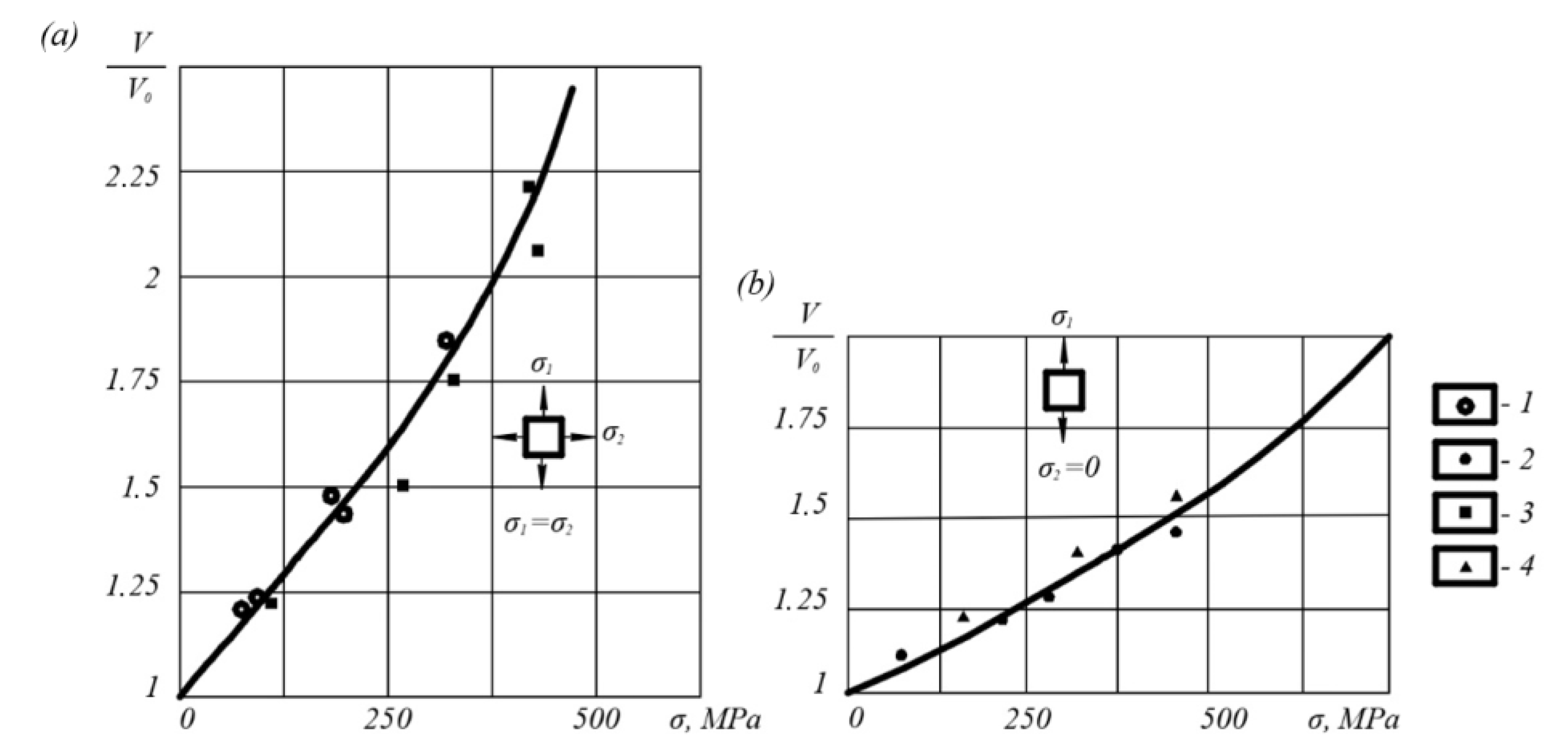
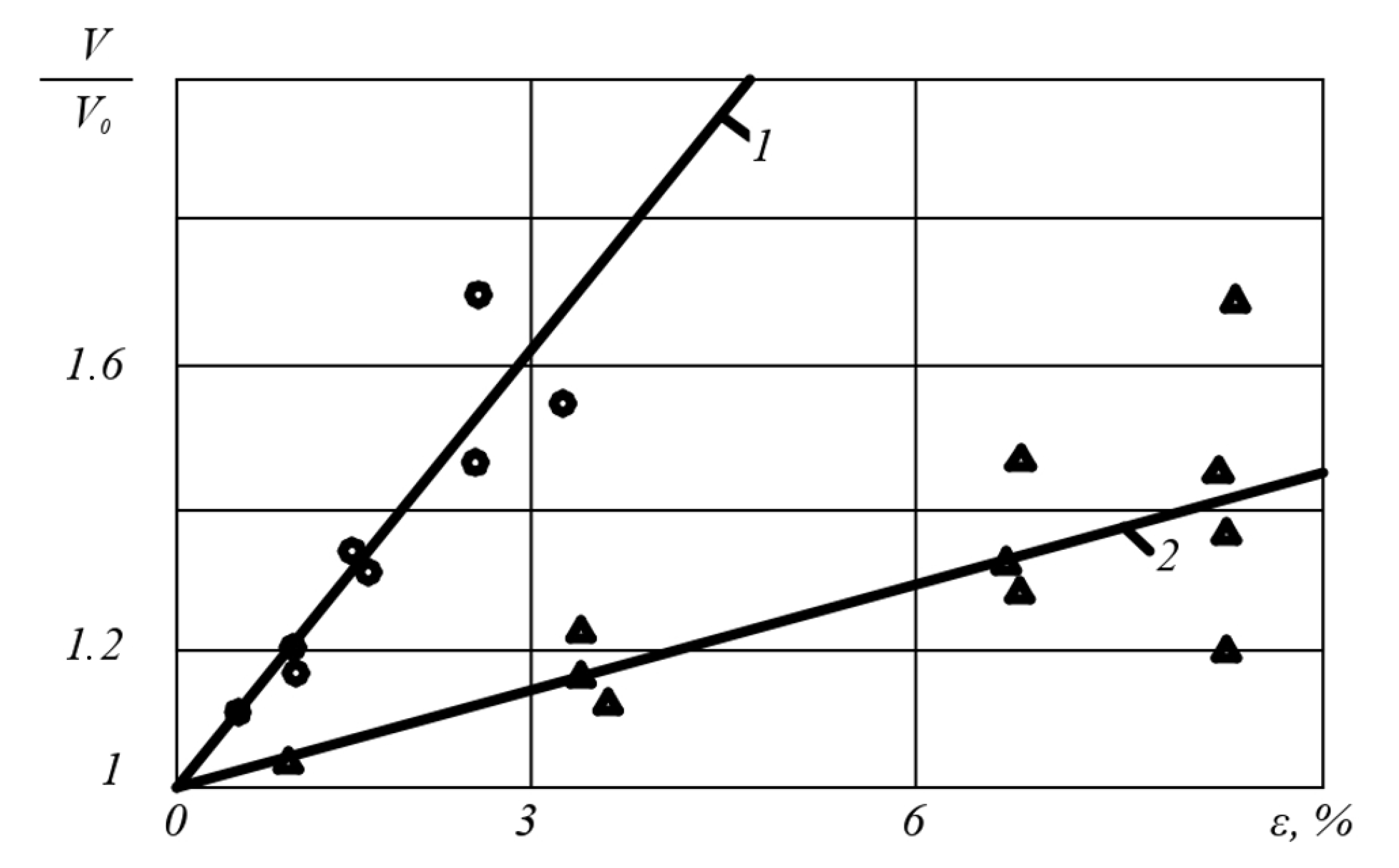
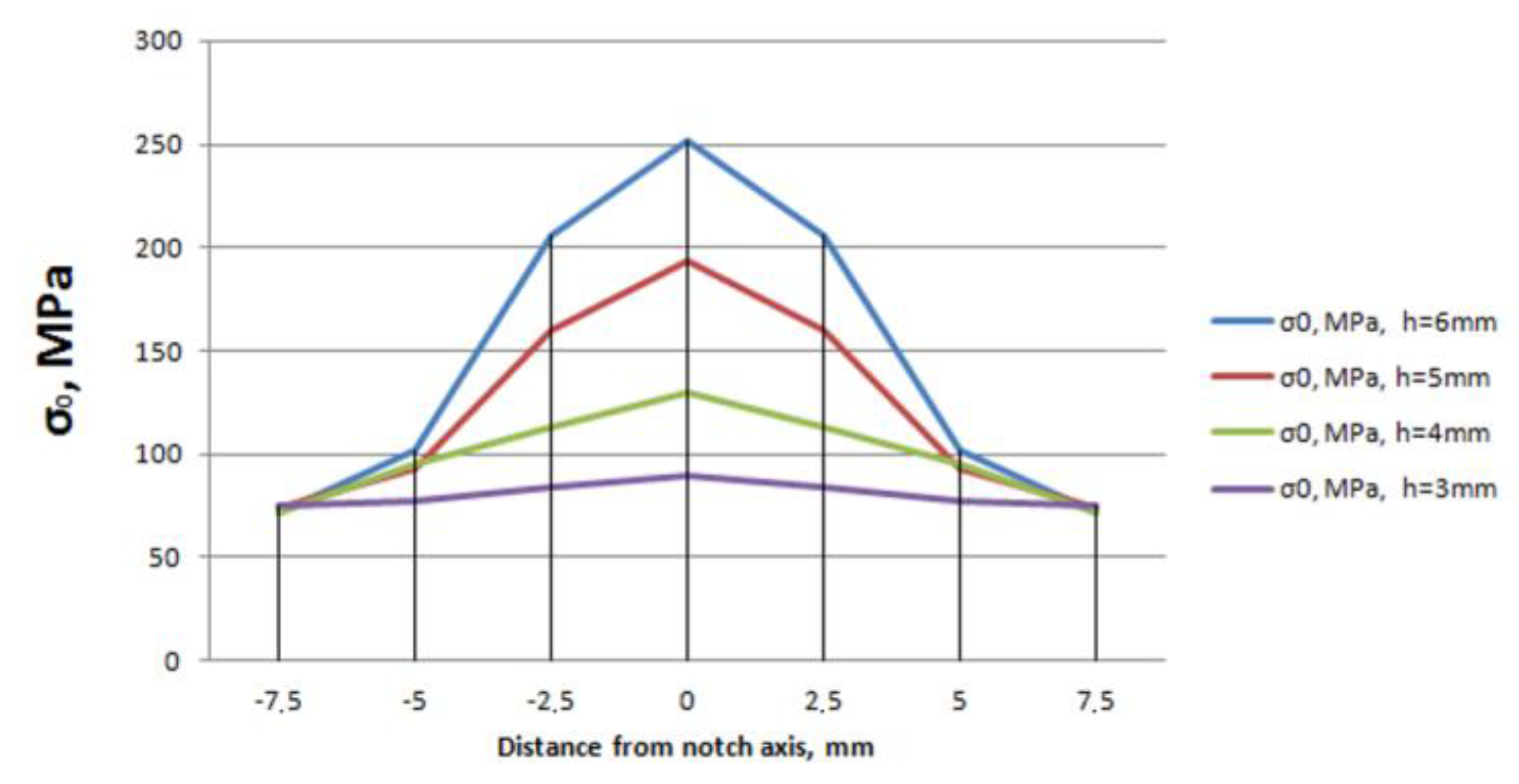
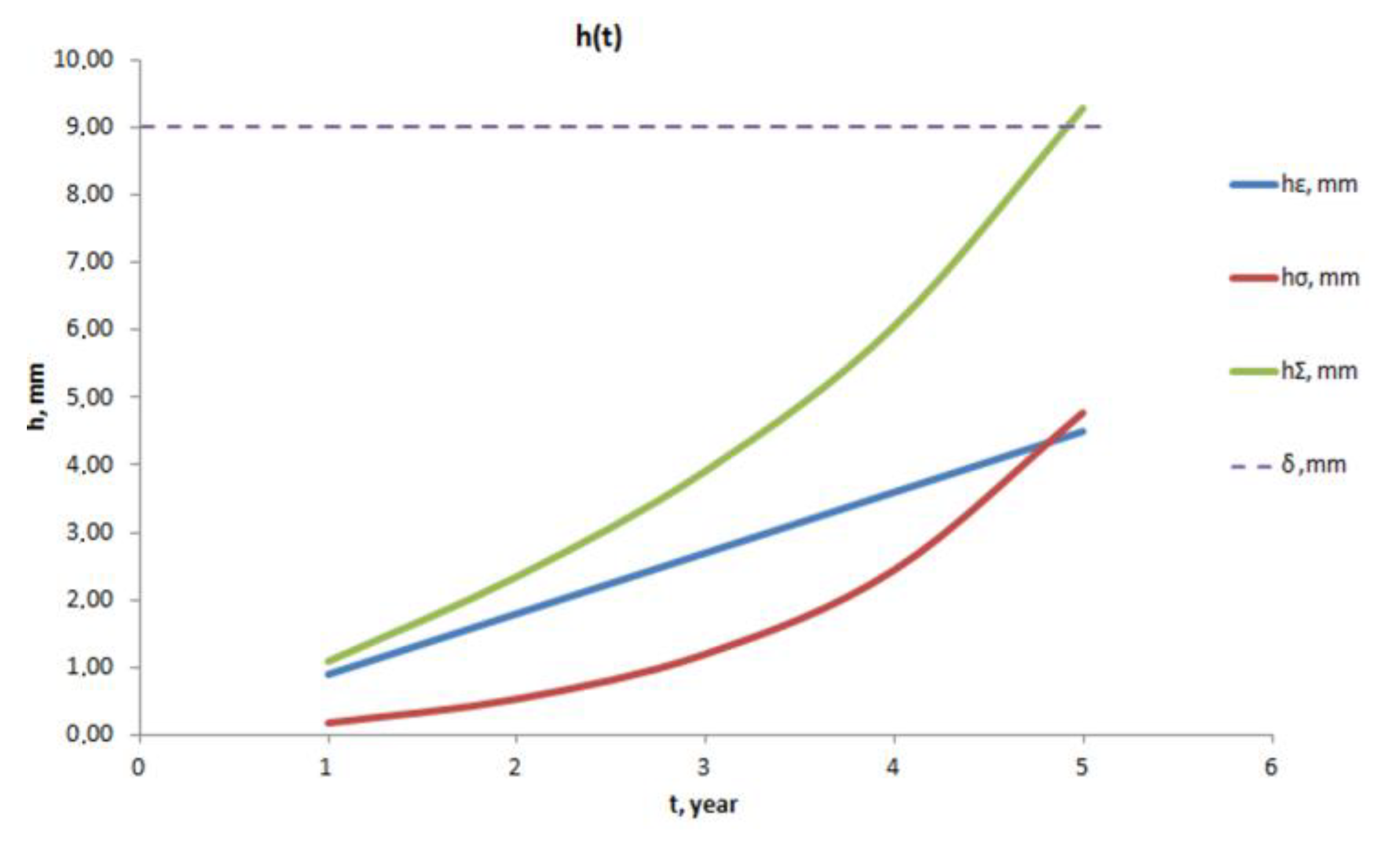
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goldobina, L.A.; Orlov, P.S. Analysis of the Corrosion Destruction Causes in Underground Pipelines and New Solutions for Increasing Corrosion steel’s Resistance. J. Min. Inst. 2016, 219, 459. [Google Scholar] [CrossRef]
- Lyubchik, A.N.; Krapivskii, E.I.; Bolshunova, O.M. Prediction of the technical status of pipeline based on analysis. J. Min. Inst. 2011, 192, 153–156, (In Russian, Abstract in English). [Google Scholar]
- Sultanbekov, R.R.; Nazarova, M.N. The influence of total sediment of petroleum products on the corrosiveness of the metal of the tanks during storage. In Proceedings of the E3S Web Conference—I International Conference «Corrosion in the Oil and Gas Industry», Saint Petersburg, Russia, 22–24 May 2019; E3S Web of Conferences: Les Ulis, France, 2019; Volume 121, p. 01015. [Google Scholar] [CrossRef]
- Shammazov, I.; Dzhemilev, E.; Sidorkin, D. Improving the Method of Replacing the Defective Sections of Main Oil and Gas Pipelines Using Laser Scanning Data. Appl. Sci. 2023, 13, 48. [Google Scholar] [CrossRef]
- Bolobov, V.I.; Latipov, I.U.; Zhukov, V.S.; Popov, G.G. Using the Magnetic Anisotropy Method to Determine Hydrogenated Sections of a Steel Pipeline. Energies 2023, 16, 5585. [Google Scholar] [CrossRef]
- Vinogradov, S.N.; Volchihin, V.I.; SHirina, E.V.; Meshcheryakov, A.S. Issledovanie korrozionnoj stojkosti konstrukcionnyh stalej v plastovoj vode [Investigation of corrosion resistance of structural steels in reservoir water]. Izv. Vyss. Uchebnyh Zaved. [News High. Educ. Inst.] 2008, 4, 139–144. (In Russian) [Google Scholar]
- Medvedev, A.P. Kompleksnaya Sistema Obespecheniya Bezopasnosti Promyslovyh Truboprovodov Zapadnoj Sibiri [An Integrated Safety System for West Siberian Field Pipelines]. Ph.D. Thesis, Institute of Problems of Transport of Energy Resources of the Republic of Bashkortostan, Ufa, Russia, 2004; p. 44. (In Russian). [Google Scholar]
- Medvedev, A.P.; Markin, A.N. Ob usilennoj korrozii truboprovodov sistem sbora nefti NGDU «Belozerneft’» [About increased corrosion of pipelines of oil collection systems NGDU «Belozerneft»]. Neft. Hozyajstvo [Oil Gas Ind.] 1995, 11, 23–24. (In Russian) [Google Scholar]
- Burkov, P.V.; Burkov, V.P.; Fat’yanov, D.S.; Timofeev, V.Y. Studying the stress-strain state of oilfield pipelines exposed to rill corrosion. Vestn. Kuzbasskogo Gos. Tekhnicheskogo Univ. [Bull. Kuzbass State Tech. Univ.] 2018, 3, 5–12, (In Russian, Abstract in English). [Google Scholar] [CrossRef]
- Abdullin, I.G.; Davydov, S.N.; Hudyakov, M.A. The mechanism of groove destruction of the lower forming pipes of oil collectors. Oil Gas Ind. 1984, 3, 51–53. (In Russian) [Google Scholar]
- Zajnullin, R.S. Kinetika mekhanohimicheskogo razrusheniya i resurs truboprovodnyh sistem [Kinetics of mechanochemical destruction and resource of pipeline systems]. Probl. Sbora Podgot. Transp. Neft. Nefteprod. [Probl. Collect. Prep. Transp. Oil Pet. Prod.] 2005, 65, 44–63. (In Russian) [Google Scholar]
- Klisenko, L.B.; Lapshin, A.P.; Kudrin, D.V. Probable reasons for the formation of ribbed corrosion in oilfield pipelines detected during technical diagnosis. Mod. Sci. Curr. Probl. Solut. 2015, 9, 58–61. (In Russian) [Google Scholar]
- Popod’ko, D.V. Ocenka Bezopasnoj Ekspluatacii Obolochek s «Kanavochnym Iznosom» Metodom Konechnyh Elementov [Evaluation of the Safe Operation of Shells with “Groove Wear” by the Finite Element Method]. Ph.D. Thesis, Ufa State Petroleum Technological University (USPTU), Ufa, Russia, 2004; p. 24. (In Russian). [Google Scholar]
- Bolobov, V.I.; Popov, G.G. Methodology for testing pipeline steels for resistance to grooving corrosion. J. Min. Inst. 2021, 252, 854–860. [Google Scholar] [CrossRef]
- Gutman, E.M.; Zajnullin, R.S.; Zaripov, R.A. Kinetika mekhanohimicheskogo razrusheniya i dolgovechnost’ rastyanutyh konstruktivnyh elementov pri uprugo-plasticheskih deformaciyah [Kinetics of mechanochemical destruction and durability of stretched structural elements under elastic-plastic deformations]. Fiz.-Him. Mekhanika Mater. [Phys.-Chem. Mech. Mater.] 1984, 2, 14–17. (In Russian) [Google Scholar]
- Zajnullin, R.S. K metodike korrozionnyh ispytanij metalla pri dvuhosnom napryazhennom sostoyanii [To the method of corrosion testing of metal in a biaxial stress state]. Fiz.-Him. Mekhanika Mater. [Phys.-Chem. Mech. Mater.] 1983, 9, 683–695. (In Russian) [Google Scholar]
- Mansour, M.A.; Alfantazi, A.M.; Elboujdaini, M. Sulfide stress cracking resistance of API-X100 high strength low alloy steel. Mater. Des. 2009, 30, 4088–4094. [Google Scholar] [CrossRef]
- Dergach, T.O.; Sukhomlin, G.D. Methods for the Improvement of Corrosion Resistance of Low-Alloy Steel Pipes for the Oil-And-Gas Extraction Industry. Mater. Sci. 2021, 56, 684–690. [Google Scholar] [CrossRef]
- Sultanbekov, R.; Islamov, S.; Mardashov, D.; Beloglazov, I.; Hemmingsen, T. Research of the Influence of Marine Residual Fuel Composition on Sedimentation Due to Incompatibility. J. Mar. Sci. Eng. 2021, 9, 1067. [Google Scholar] [CrossRef]
- Askari, M.A.; Aliofkhazraei, M.; Afroukhteh, S. Comprehensive review on internal corrosion and cracking of oil and gas pipelines. J. Nat. Gas Sci. Eng. 2019, 71, 102971. [Google Scholar] [CrossRef]
- Hasan, F.; Iqbal, J.; Ahmed, F. Stress corrosion failure of high-pressure gas pipeline. Eng. Fail. Anal. 2007, 14, 801–809. [Google Scholar] [CrossRef]
- Saleem, B.; Ahmed, F.; Rafiq, M.A.; Ajmal, M.; Ali, L. Stress corrosion failure of an X52 grade gas pipeline. Eng. Fail. Anal. 2014, 46, 157–165. [Google Scholar] [CrossRef]
- Abaev, Z.K.; Galachieva, S.V. Mathematical model elaboration in terms of baking time influence on the resistance to stress corrosion cracking under tension. In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Chelyabinsk, Russia, 19–20 May 2016; IEEE: Manhattan, NY, USA, 2016; Volume 2, pp. 1–4. [Google Scholar] [CrossRef]
- Darowicki, K.; Orlikowski, J.; Arutunow, A. Dynamic electrochemical impedance spectroscopy measurements of passive layer cracking under static tensile stresses. Solid State Electrochem. 2004, 8, 352–359. [Google Scholar] [CrossRef]
- Griggs, J.; Gamboa, E.; Lavigne, O. A review of modelling high pH stress corrosion cracking of high-pressure gas pipelines. Mater. Corros. 2015, 67, 251–263. [Google Scholar] [CrossRef]
- Kundyanova, U.P. Modelirovanie ruchejkovoj korrozii polosti truboprovoda [Modeling of rivulet corrosion of the pipeline cavity]. In Sovremennye Tekhnika i Tekhnologii: Sbornik Trudov XX Mezhdunarodnoj Nauchno-Prakticheskoj Konferencii Studentov, Aspirantov i Molodyh Uchenyh [Modern Equipment and Technologies: Proceedings of the XX International Scientific and Practical Conference of Students, Postgraduates and Young Scientists], Tomsk, Russia, 14–18 April 2014; The National Research Tomsk Polytechnic University: Tomsk, Russia, 2014; Volume 2, pp. 49–50. (In Russian) [Google Scholar]
- Kolikov, A.P.; Leletko, A.S.; Matveev, D.B.; Kulyutin, S.A.; Kadil’nikov, S.V. Investigation of residual stresses in welded pipes. Izv. Ferr. Metall. 2014, 57, 48–53, (In Russian, Abstract in English). [Google Scholar] [CrossRef][Green Version]
- Shinkin, V.N. Residual stresses during expansion of a steel pipe. Molod. Uchenyi [Young Sci.] 2015, 20, 88–93. (In Russian) [Google Scholar]
- Shchipachev, A.M.; Gorbachev, S.V. Influence of post-welding processing on continuous corrosion rate and microstructure of welded joints of steel 20 and 30KHGSA. J. Min. Inst. 2018, 231, 307–311. [Google Scholar] [CrossRef]
- Ren, R.K.; Zhang, S.; Pang, X.L.; Gao, K.W. A novel observation of the interaction between the macroelastic stress and electrochemical corrosion of low carbon steel in 3.5 wt.% NaCl solution. Electrochim. Acta 2012, 85, 283–294. [Google Scholar] [CrossRef]
- Wang, X.; Tang, X.; Wang, L.; Wang, C.; Zhou, W. Synergistic effect of stray current and stress on corrosion of API X65 steel. J. Nat. Gas Sci. Eng. 2014, 21, 474–480. [Google Scholar] [CrossRef]
- Ovchinnikov, I.G.; Ovchinnikov, I.I.; Bashirzade, S.R. Prognozirovanie povedeniya truboprovodnyh konstrukcij v slozhnyh gruntovo-geologicheskih usloviyah. CHast’ 1. Obobshchennaya model’ deformirovaniya truboprovoda [Predicting the behavior of pipeline structures in difficult ground-geological conditions. Part 1. Generalized model of pipeline deformation]. Naukoved. [Sci. Stud.] 2016, 8, 99. (In Russian) [Google Scholar]
- Shaymuhametov, M.R. Tensions in the Area of Groove Destruction of Pipelines. Oil Gas Bus. 2009, 2, 115–120, (In Russian, Abstract in English). [Google Scholar]
- Chen, Z.F.; Wang, W.; Yang, H.; Yan, S.T.; Jin, Z.J. On the effect of long corrosion defect and axial tension on the burst pressure of subsea pipelines. Appl. Ocean Res. 2021, 111, 102637. [Google Scholar] [CrossRef]
- Zlotin, V.A.; Popov, G.G.; Bolobov, V.I. Raschyotnyj analiz raspredeleniya napryazhenij v stenke truboprovoda pri nalichii na eyo poverhnosti nadreza razlichnoj glubiny [Computational analysis of the stress distribution in the pipeline wall in the presence of an incision of various depths on its surface]. In Sovremennye Obrazovatel’nye Tekhnologii v Podgotovke Specialistov Dlya Mine-Ral’no-Syr’evogo Kompleksa [Modern Educational Technologies in the Training of Specialists for the Mineral Resource Complex], Saint-Petersburg, Russia, 5–6 March 2020; Saint Petersburg Mining University: Saint-Petersburg, Russia, 2020; pp. 1324–1329. (In Russian) [Google Scholar]
- Firstov, A.A.; Kapachinskih, Z.Y.; Seredenok, V.A. Obosnovanie vozmozhnosti ocenki urovnya izgibnyh napryazhenij v stenkah trub magistral’nyh gazonefteprovodov opredeleniem ego prostranstvennogo polozheniya s poverhnosti grunta [Substantiation of the possibility of assessing the level of bending stresses in the walls of pipes of main gas and oil pipelines by determining its spatial position from the ground surface]. Nauka Tekhnika Gazov. Promyshlennosti [Sci. Technol. Gas Ind.] 2020, 2, 89–98. (In Russian) [Google Scholar]
- Aginey, R.V.; Firstov, A.A.; Kapachinskikh, Z.Y. To the question of determining bending stress of a buried pipeline from the ground surface. In Proceedings of the International Conference on Innovations, Physical Studies and Digitalization in Mining Engineering (IPDME 2020), Saint-Petersburg, Russia, 23–24 April 2020; IOP: Bristol, UK, 2020; Volume 1753, p. 012068. [Google Scholar] [CrossRef]


| Deterministic (Phenomenological) | Stochastic (Probabilistic) | Unclear (Linguistic) |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, G.; Bolobov, V.; Zhuikov, I.; Zlotin, V. Development of the Kinetic Equation of the Groove Corrosion Process for Predicting the Residual Life of Oil-Field Pipelines. Energies 2023, 16, 7067. https://doi.org/10.3390/en16207067
Popov G, Bolobov V, Zhuikov I, Zlotin V. Development of the Kinetic Equation of the Groove Corrosion Process for Predicting the Residual Life of Oil-Field Pipelines. Energies. 2023; 16(20):7067. https://doi.org/10.3390/en16207067
Chicago/Turabian StylePopov, Grigory, Victor Bolobov, Ilia Zhuikov, and Vladimir Zlotin. 2023. "Development of the Kinetic Equation of the Groove Corrosion Process for Predicting the Residual Life of Oil-Field Pipelines" Energies 16, no. 20: 7067. https://doi.org/10.3390/en16207067
APA StylePopov, G., Bolobov, V., Zhuikov, I., & Zlotin, V. (2023). Development of the Kinetic Equation of the Groove Corrosion Process for Predicting the Residual Life of Oil-Field Pipelines. Energies, 16(20), 7067. https://doi.org/10.3390/en16207067








