Lithium-Ion Battery State of Health Estimation Using Simple Regression Model Based on Incremental Capacity Analysis Features
Abstract
:1. Introduction
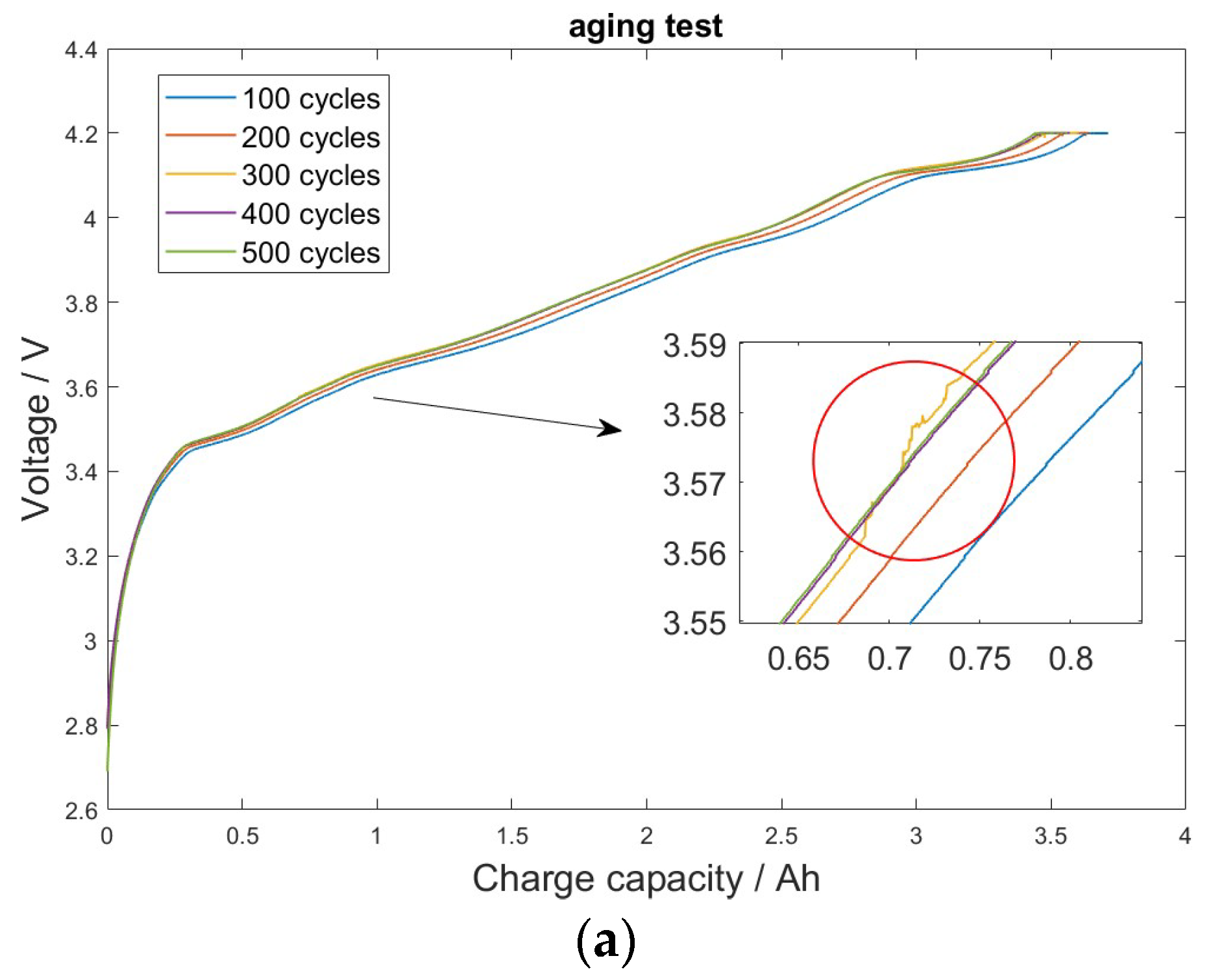
2. Acquisition and Smoothing of ICA Curve
2.1. Construction of the ICA Curve
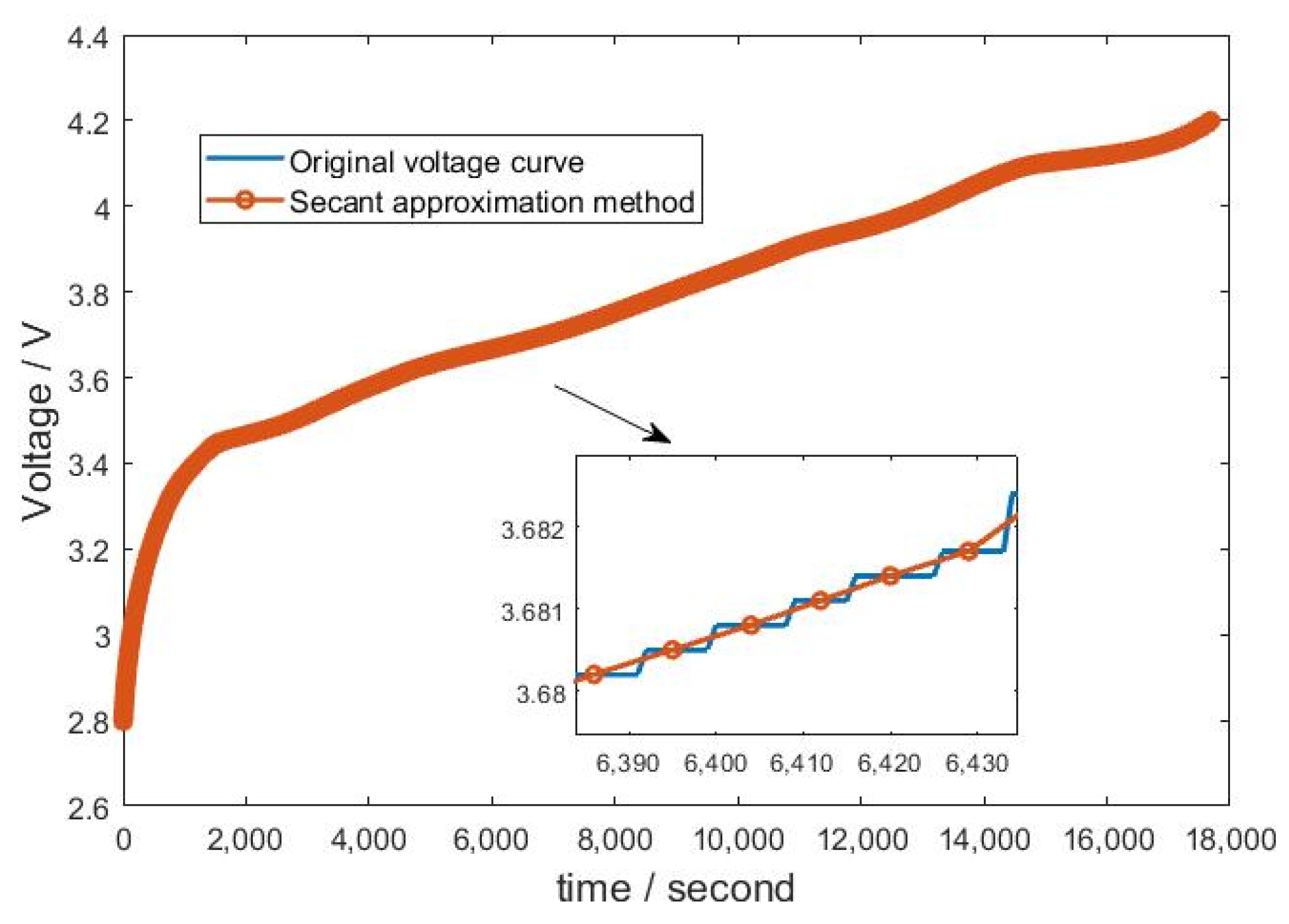
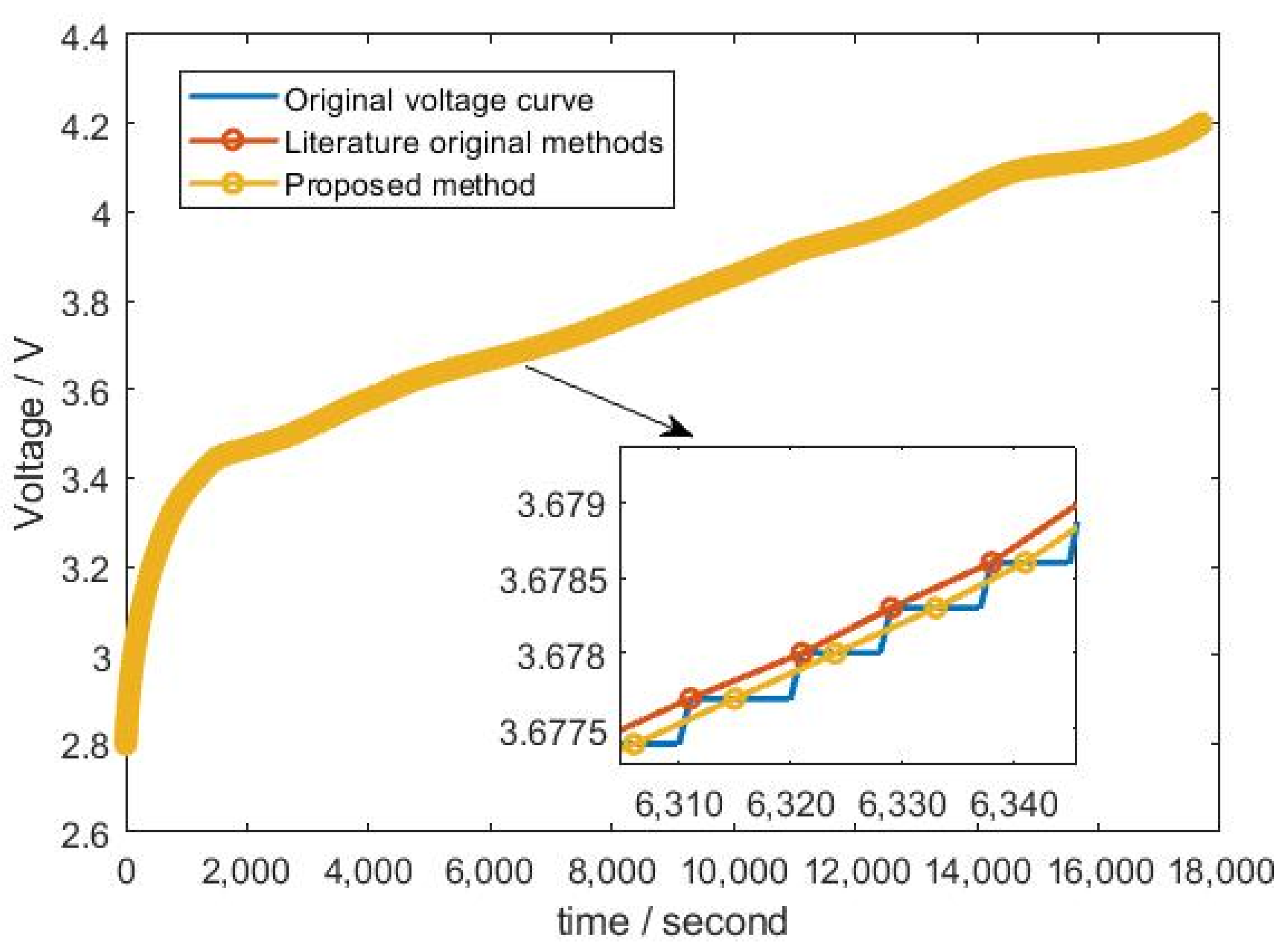
2.2. Voltage Curve Smoothing
| Algorithm 1. Secant approximation method algorithm. |
| 1: Initial value i = 1, j = 1, k = 0, p = 2, l = 0 |
| 2: V(i) = V(j) and Record(i) = V(j) and j = j + 1 |
| 3: while j ≤ jfinal do |
| 4: if |V(j) − V(i)| < δ then |
| 5: k = 0 |
| 6: l = l + 1 |
| 7: else |
| 8: k = k + 1 |
| 9: if k = 1 then |
| 10: B1 = V(j) |
| 11: ID1 = j |
| 12: B2 = V(j − round(l/2) − 1) |
| 13: ID2 = j − round(l/2) − 1 |
| 14: else |
| 15: if k = p then |
| 16: I = i + 1 |
| 17: V(i) = B1 |
| 18: Record(i) = B2 |
| 19: j = ID1 |
| 20: ix(i) = ID2 |
| 21: l = 0 |
| 22: k = 0 |
| 23: end if |
| 24: end if |
| 25: end if |
| 26: j = j + 1 |
| 27: end while |
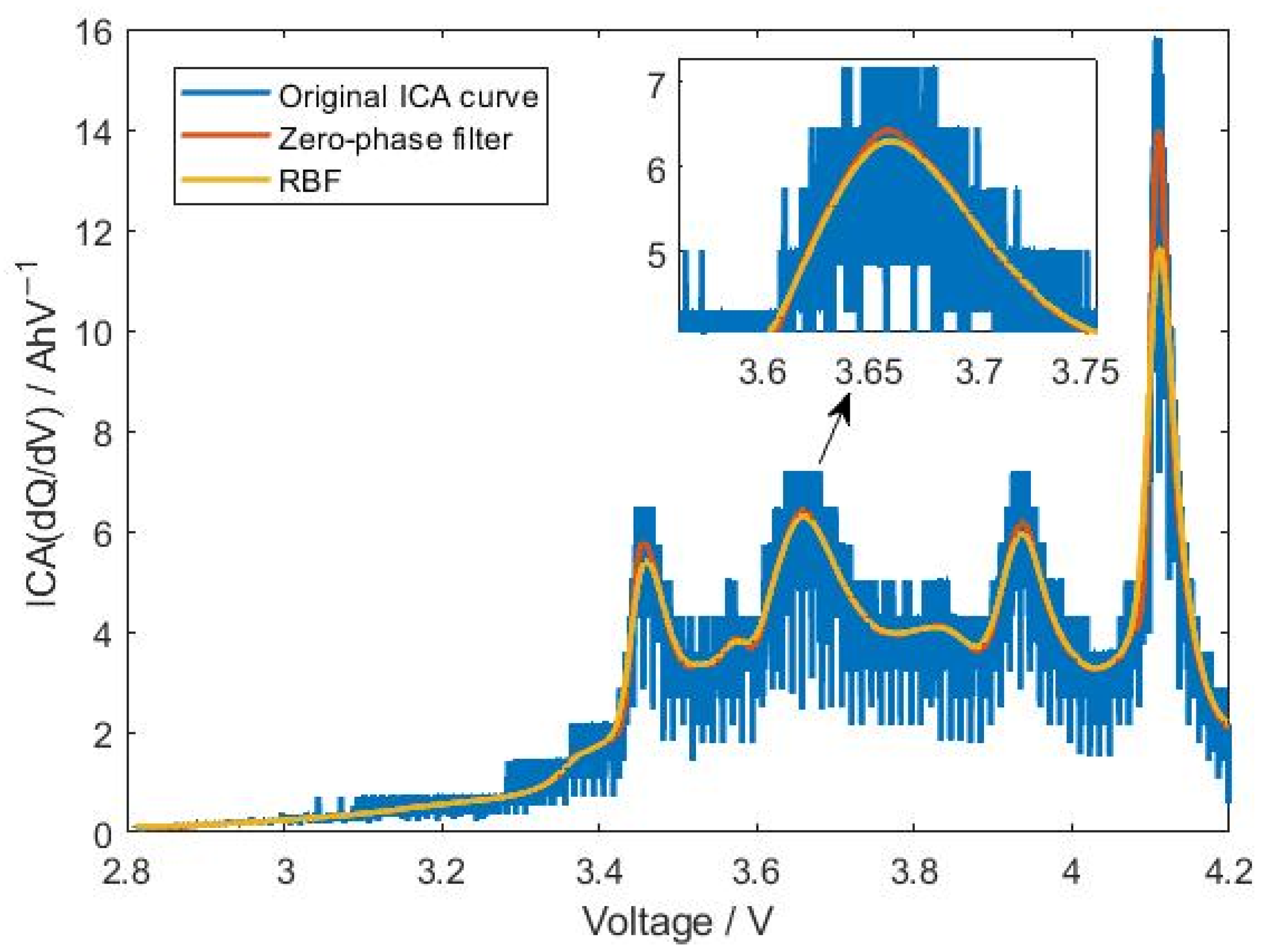
2.3. ICA Curve Smoothing
Effect of ICA Curve Smoothing
3. Aging Feature Parameter Extraction
4. SOH Estimation Methods
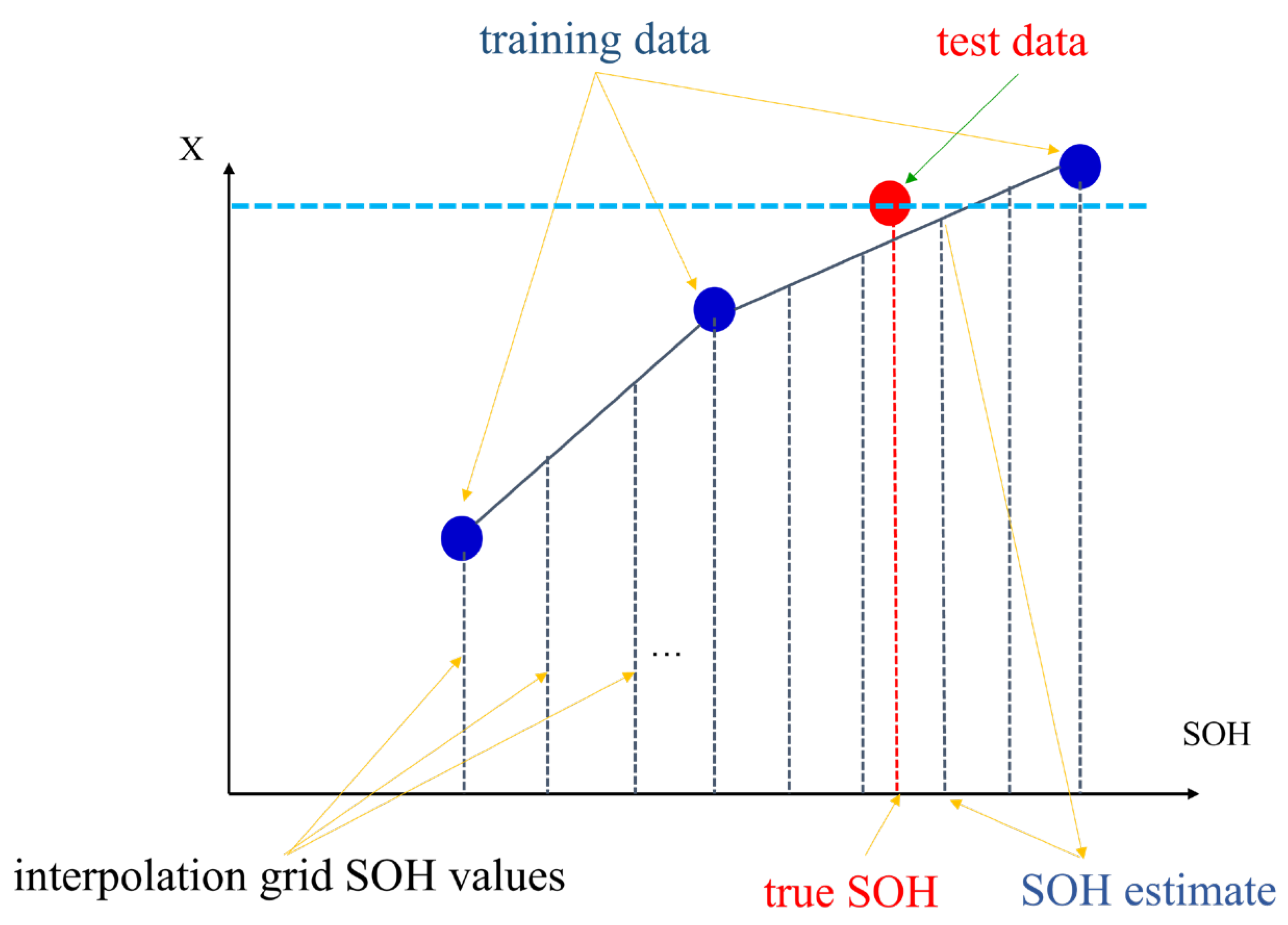
4.1. Piecewise Linear Regression Function
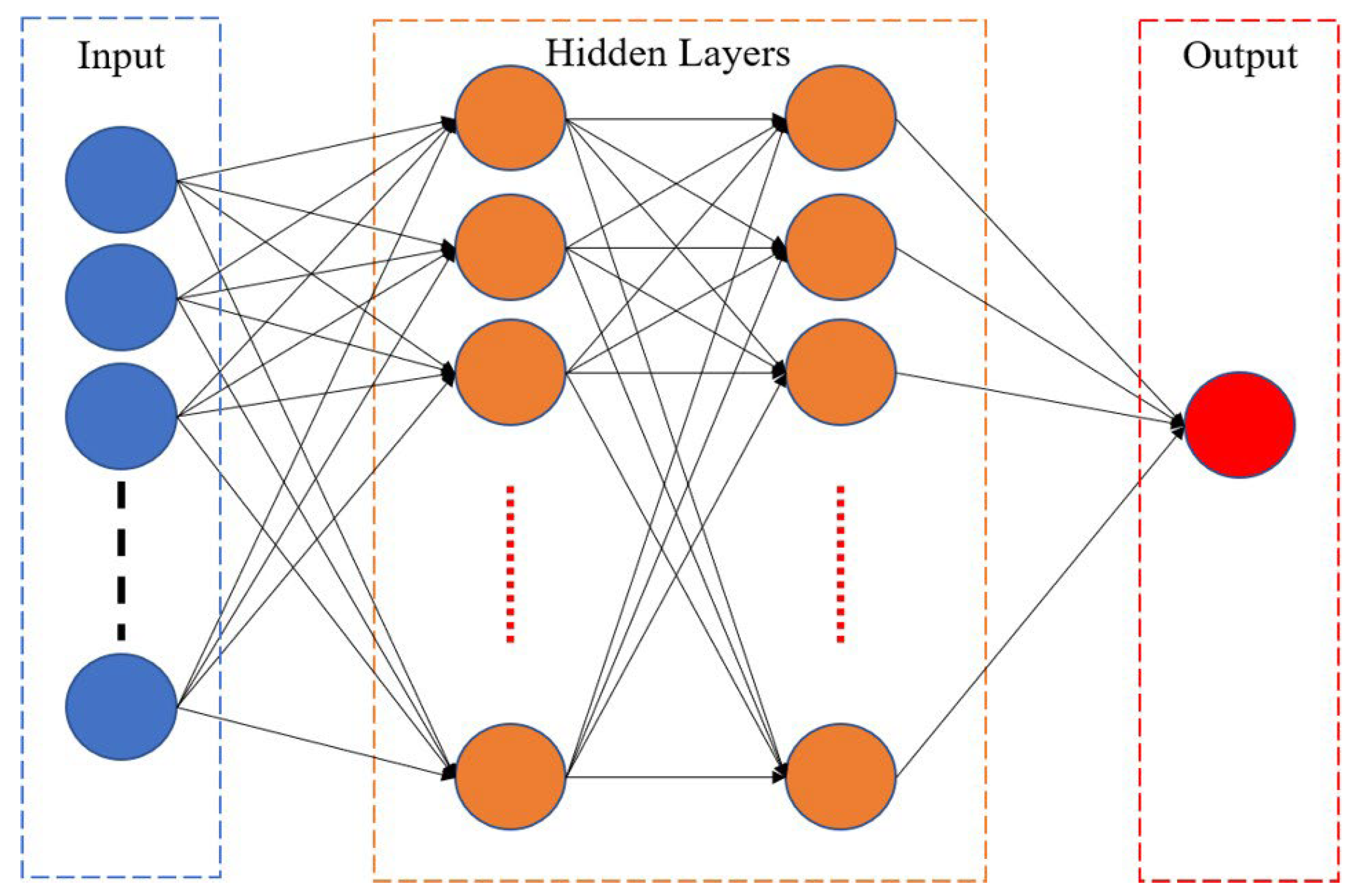
4.2. Back-Propagation Neural Network
- Neural input:wx + b
- Neural output:y = f (wx + b)
5. Test Results and Discussions
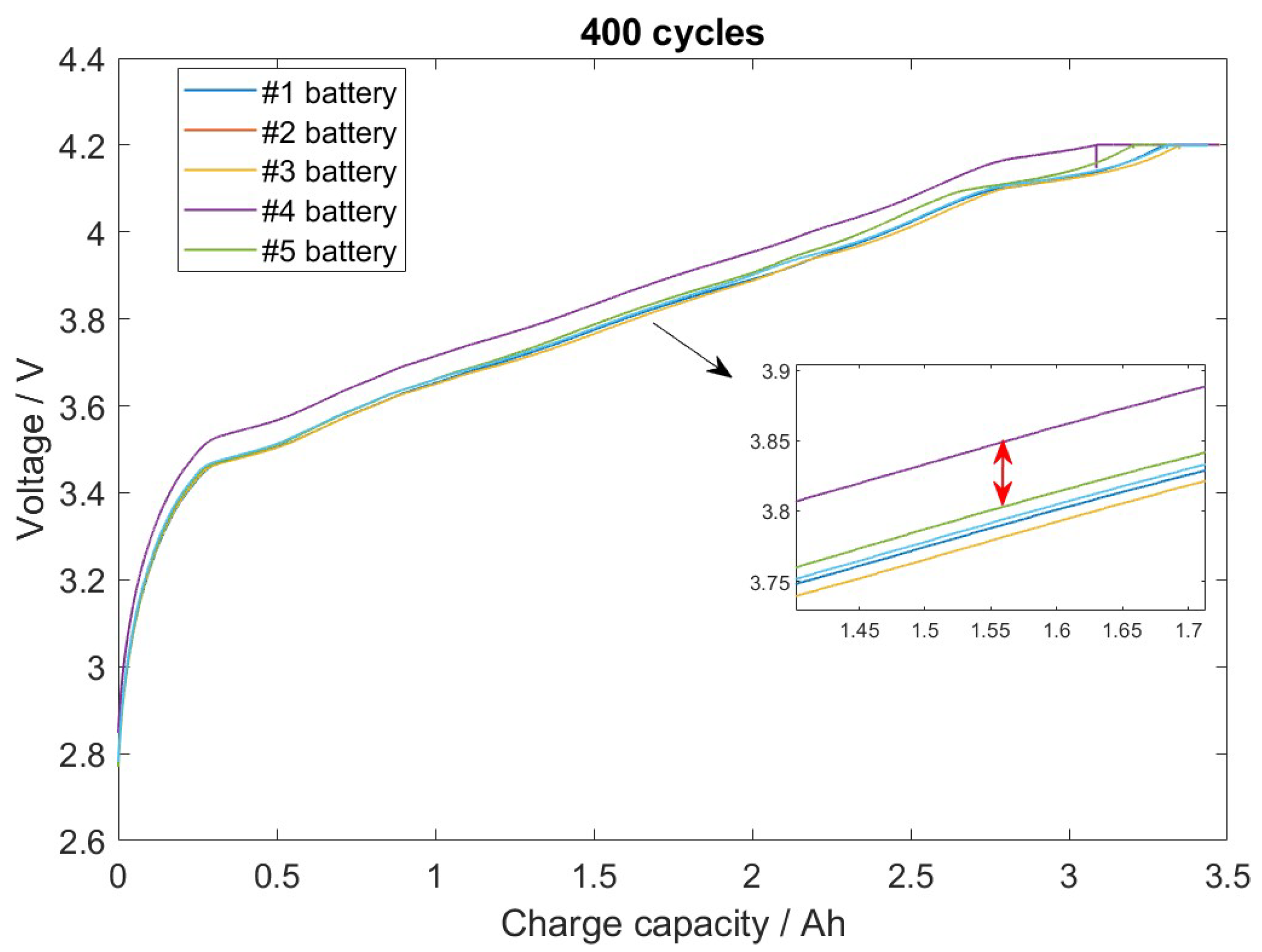
5.1. Physical Experiment Settings
5.2. SOH Estimation Computational Experiment Settings
- (a)
- ICA with piecewise linear interpolation regression:
- (b)
- ICA with BPNN regression:
- (c)
- Piecewise linear interpolation regression using voltage measurements:
- (d)
- BPNN regression using voltage measurements:
5.3. Error Metrics
5.4. Results: Comparing Combinations of Smoothing and Regression Techniques
5.5. Results: Comparing Choices of Aging Feature Parameters
5.6. Discussions on Robustness against Data Anomalies and Truncation Error
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EV | Electric vehicle |
| ESS | Energy storage system |
| ICA | Incremental capacity analysis |
| BPNN | Back-propagation neural network |
| LIBs | Lithium-ion batteries |
| BMS | Battery management system |
| SOH | State of health |
| SOC | State of charge |
| EIS | Electrochemical impedance spectroscopy |
| EM | Electrochemical model |
| LAM | Loss of active material |
| LLI | Loss of lithium inventory |
| MA | Moving average |
| GS | Gaussian smoothing |
| SVR | Support vector regression |
| CC-CV | Constant current and constant voltage |
| CC | Constant current |
| RBF | Radial basis function |
| MRE | Mean relative error |
| RMSRE | Root mean squared relative error |
References
- Silvestri, L.; De Santis, M.; Mendecka, B.; Bella, G. Identification of the Best Vehicle Segment for e-Taxis from a Life Cycle Assessment Perspective (No. 2022-24-0020); SAE Technical Paper; SAE: Byron Bay, Australia, 2022. [Google Scholar]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. ETransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; Van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Wei, X.; Zhu, B.; Xu, W. Internal resistance identification in vehicle power lithium-ion battery and application in lifetime evaluation. In Proceedings of the 2009 International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, Hunan, 11–12 April 2009; Volume 3, pp. 388–392. [Google Scholar]
- Andre, D.; Meiler, M.; Steiner, K.; Walz, H.; Soczka-Guth, T.; Sauer, D.U. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. II: Modelling. J. Power Sources 2011, 196, 5349–5356. [Google Scholar] [CrossRef]
- Chayambuka, K.; Cardinaels, R.; Gering, K.L.; Raijmakers, L.; Mulder, G.; Danilov, D.L.; Notten, P.H. An experimental and modeling study of sodium-ion battery electrolytes. J. Power Sources 2021, 516, 230658. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar] [CrossRef]
- Remmlinger, J.; Buchholz, M.; Meiler, M.; Bernreuter, P.; Dietmayer, K. State-of-health monitoring of lithium-ion batteries in electric vehicles by on-board internal resistance estimation. J. Power Sources 2011, 196, 5357–5363. [Google Scholar] [CrossRef]
- Prasad, G.K.; Rahn, C.D. Model based identification of aging parameters in lithium ion batteries. J. Power Sources 2013, 232, 79–85. [Google Scholar] [CrossRef]
- Luo, Y.F.; Lu, K.Y. An online state of health estimation technique for lithium-ion battery using artificial neural network and linear interpolation. J. Energy Storage 2022, 52, 105062. [Google Scholar] [CrossRef]
- Chen, R.J.; Hsu, C.W.; Lu, T.F.; Teng, J.H. Rapid SOH estimation for retired lead-acid batteries. In Proceedings of the 2021 IEEE International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 16–19 November 2021; pp. 1–4. [Google Scholar]
- Teng, J.H.; Chen, R.J.; Lee, P.T.; Hsu, C.W. Accurate and Efficient SOH Estimation for Retired Batteries. Energies 2023, 16, 1240. [Google Scholar] [CrossRef]
- Dubarry, M.; Liaw, B.Y.; Chen, M.S.; Chyan, S.S.; Han, K.C.; Sie, W.T.; Wu, S.H. Identifying battery aging mechanisms in largeformat Li ion cells. J. Power Sources 2011, 196, 3420–3425. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation diagnostics for lithium ion cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Dubarry, M.; Anseán, D. Best practices for incremental capacity analysis. Front. Energy Res. 2022, 10, 1023555. [Google Scholar] [CrossRef]
- Fly, A.; Chen, R. Rate dependency of incremental capacity analysis (dQ/dV) as a diagnostic tool for lithium-ion batteries. J. Energy Storage 2020, 29, 101329. [Google Scholar] [CrossRef]
- Wu, J.; Su, H.; Meng, J.; Lin, M. State of Health Estimation for Lithium-Ion Battery via Recursive Feature Elimination on PartialCharging Curves. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 11, 131–142. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L.; Zou, C.; Dorrell, D.D. State-of-health estimation for Li-ion batteries by combing the incrementalcapacity analysis method with grey relational analysis. J. Power Sources 2019, 410, 106–114. [Google Scholar] [CrossRef]
- Li, X.; Jiang, J.; Chen, D.; Zhang, Y.; Zhang, C. A capacity model based on charging process for state of health estimation of lithium ion batteries. Appl. Energy 2016, 177, 537–543. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Nanini-Maury, E.; Omar, N.; van den Bossche, P.; Van Mierlo, J. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Li, X.; Wang, Z. State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression. Energy 2020, 190, 116467. [Google Scholar] [CrossRef]
- Schaltz, E.; Stroe, D.I.; Nørregaard, K.; Ingvardsen, L.S.; Christensen, A. Incremental capacity analysis applied on electric vehiclesfor battery state-of-health estimation. IEEE Trans. Ind. Appl. 2021, 57, 1810–1817. [Google Scholar] [CrossRef]
- Tang, X.; Liu, K.; Lu, J.; Liu, B.; Wang, X.; Gao, F. Battery incremental capacity curve extraction by a two-dimensional Luenberger–Gaussian-moving-average filter. Appl. Energy 2020, 280, 115895. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Wang, J.; Zhang, T. State-of-health estimation for lithium-ion batteries by combining model-based incrementalcapacity analysis with support vector regression. Energy 2022, 239, 121986. [Google Scholar] [CrossRef]
- Lin, H.; Kang, L.; Xie, D.; Linghu, J.; Li, J. Online State-of-Health Estimation of Lithium-Ion Battery Based on Incremental Capacity Curve and BP Neural Network. Batteries 2022, 8, 29. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Li, X.; Lu, L.; Li, J.; Zhou, L.; Zhang, Z. Recording frequency optimization for massive battery data storage in battery management systems. Appl. Energy 2016, 183, 380–389. [Google Scholar] [CrossRef]
- Wanhammar, L.; Saramäki, T. Frequency-Selective Filters. In Digital Filters Using MATLAB; Springer International Publishing: Cham, Switzerland, 2020; pp. 40–55. [Google Scholar]
- Becker, M.; Zhao, W.; Pagani, F.; Schreiner, C.; Figi, R.; Dachraoui, W.; Grissa, R.; Kühnel, R.-S.; Battaglia, C. Understanding the Stability of NMC811 in Lithium-Ion Batteries with Water-in-Salt Electrolytes. ACS Appl. Energy Mater. 2022, 5, 11133–11141. [Google Scholar] [CrossRef]
- Molicel Co., Ltd. Lithium-ion Rechargeable Battery Product Data Sheet. 2019. Available online: https://www.molicel.com/wp-content/uploads/INR21700P42A-V4-80092.pdf (accessed on 30 January 2022).
- IndiaMART. INR-21700-P42A 3.6v Molicel Lithium-ion Battery. Available online: https://www.indiamart.com/proddetail/molicel-lithium-ion-battery-22854981788.html (accessed on 30 January 2022).



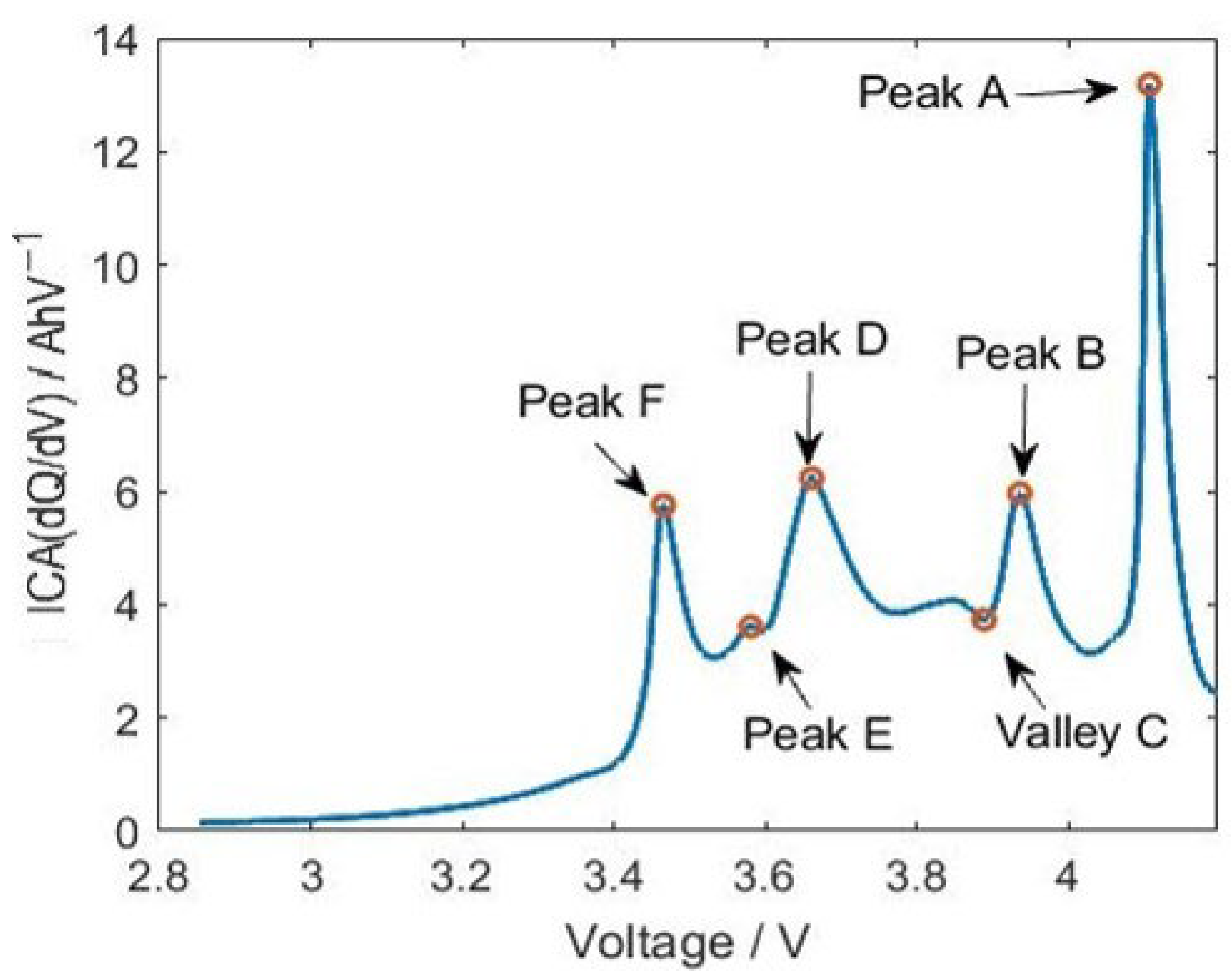
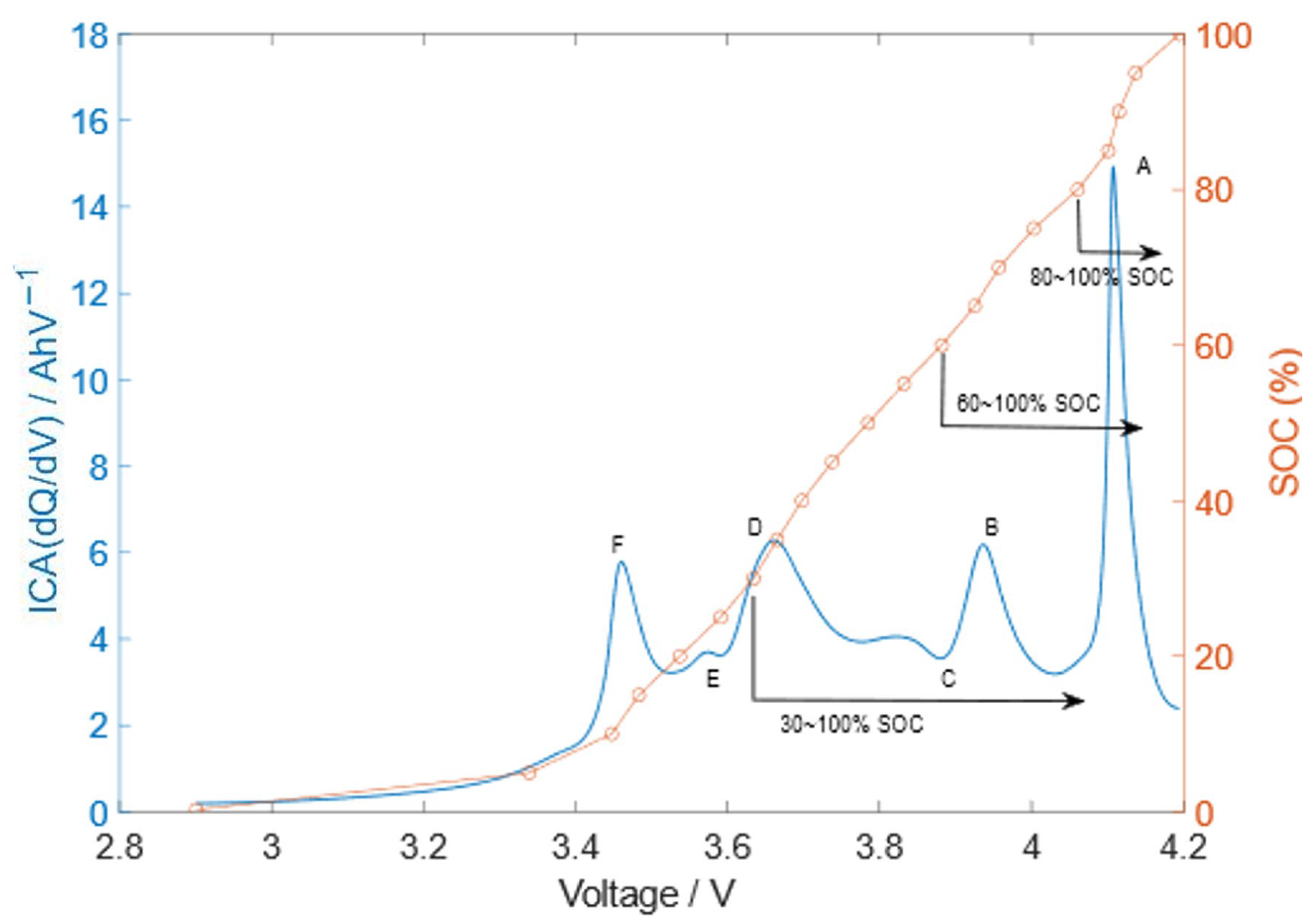

| Feature Parameter | Peak or Valley Name | Correlation Coefficient |
|---|---|---|
| Peak A | −0.10301 | |
| Peak B | −0.73225 | |
| Position | Valley C | −0.84532 |
| Peak D | −0.75366 | |
| Peak E | −0.52812 | |
| Peak F | −0.64102 | |
| Peak A | 0.9636 | |
| Peak B | 0.9519 | |
| Height | Valley C | 0.17517 |
| Peak D | 0.94085 | |
| Peak E | 0.88985 | |
| Peak F | 0.77354 |
| Temperature | Charge Current (C-Rate) | Discharge Current (C-Rate) |
|---|---|---|
| 25 °C | 0.2 C | 0.2 C, 0.5 C, 1 C, 2 C |
| 45 °C | 0.2 C | 0.2 C, 0.5 C, 1 C, 2 C |
| Voltage Smoothing Method | MRE (%) | RMSRE (%) | MAX (%) |
|---|---|---|---|
| MA | 0.6327 | 0.917 | 4.978 |
| Wavelet filtering | 0.6548 | 0.9338 | 4.975 |
| Secant approximation | 0.6028 | 0.8848 | 4.862 |
| Voltage Smoothing Method | MRE (%) | RMSRE (%) | MAX (%) |
|---|---|---|---|
| MA | 0.6331 | 0.923 | 4.988 |
| Wavelet filtering | 0.6483 | 0.9334 | 4.9881 |
| Secant approximation | 06211 | 0.9198 | 5.264 |
| Voltage Smoothing Method | MRE (%) | RMSRE (%) | MAX (%) |
|---|---|---|---|
| MA | 0.547 | 0.729 | 12.096 |
| Wavelet filtering | 0.5773 | 0.7721 | 17.897 |
| Secant approximation | 0.5246 | 0.704 | 11.88 |
| Voltage Smoothing Method | MRE (%) | RMSRE (%) | MAX (%) |
|---|---|---|---|
| MA | 0.5481 | 0.773 | 14.598 |
| Wavelet filtering | 0.5753 | 0.7753 | 16.189 |
| Secant approximation | 0.5479 | 0.7405 | 16.307 |
| Estimation Method | Input | MRE (%) | RMSRE (%) | MAX (%) |
|---|---|---|---|---|
| Piecewise linear interpolation | X1 | 0.6028 | 0.8848 | 4.862 |
| Piecewise linear interpolation | X2 | 1.2742 | 1.697 | 8.5536 |
| BPNN | X1 | 0.5246 | 0.704 | 11.88 |
| BPNN | X2 | 1.0255 | 1.291 | 10.523 |
| Estimation Method | MRE (%) | RMSRE (%) | MAX (%) | |
|---|---|---|---|---|
| Measurement error included | Piecewise linear interpolation | 0.6028 | 0.8848 | 4.862 |
| BPNN | 0.5246 | 0.704 | 11.88 | |
| Measurement error not included | Piecewise linear interpolation | 0.6025 | 0.8856 | 4.862 |
| BPNN | 0.523 | 0.7086 | 8.462 |
| Estimation Precision | MRE (%) | RMSRE (%) | MAX (%) |
|---|---|---|---|
| Piecewise linear high precision | 0.6028 | 0.8848 | 4.862 |
| interpolation low precision | 0.6022 | 0.8834 | 4.864 |
| BPNN high precision | 0.5246 | 0.704 | 11.88 |
| low precision | 0.5282 | 0.7094 | 10.925 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, K.-R.; Huang, C.-C.; Sou, K.-C. Lithium-Ion Battery State of Health Estimation Using Simple Regression Model Based on Incremental Capacity Analysis Features. Energies 2023, 16, 7066. https://doi.org/10.3390/en16207066
Lin K-R, Huang C-C, Sou K-C. Lithium-Ion Battery State of Health Estimation Using Simple Regression Model Based on Incremental Capacity Analysis Features. Energies. 2023; 16(20):7066. https://doi.org/10.3390/en16207066
Chicago/Turabian StyleLin, Kai-Rong, Chien-Chung Huang, and Kin-Cheong Sou. 2023. "Lithium-Ion Battery State of Health Estimation Using Simple Regression Model Based on Incremental Capacity Analysis Features" Energies 16, no. 20: 7066. https://doi.org/10.3390/en16207066
APA StyleLin, K.-R., Huang, C.-C., & Sou, K.-C. (2023). Lithium-Ion Battery State of Health Estimation Using Simple Regression Model Based on Incremental Capacity Analysis Features. Energies, 16(20), 7066. https://doi.org/10.3390/en16207066







