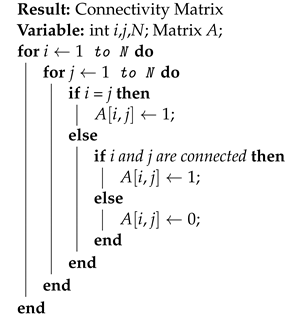Optimal Placement of μPMUs in Distribution Networks with Adaptive Topology Changes
Abstract
:1. Introduction
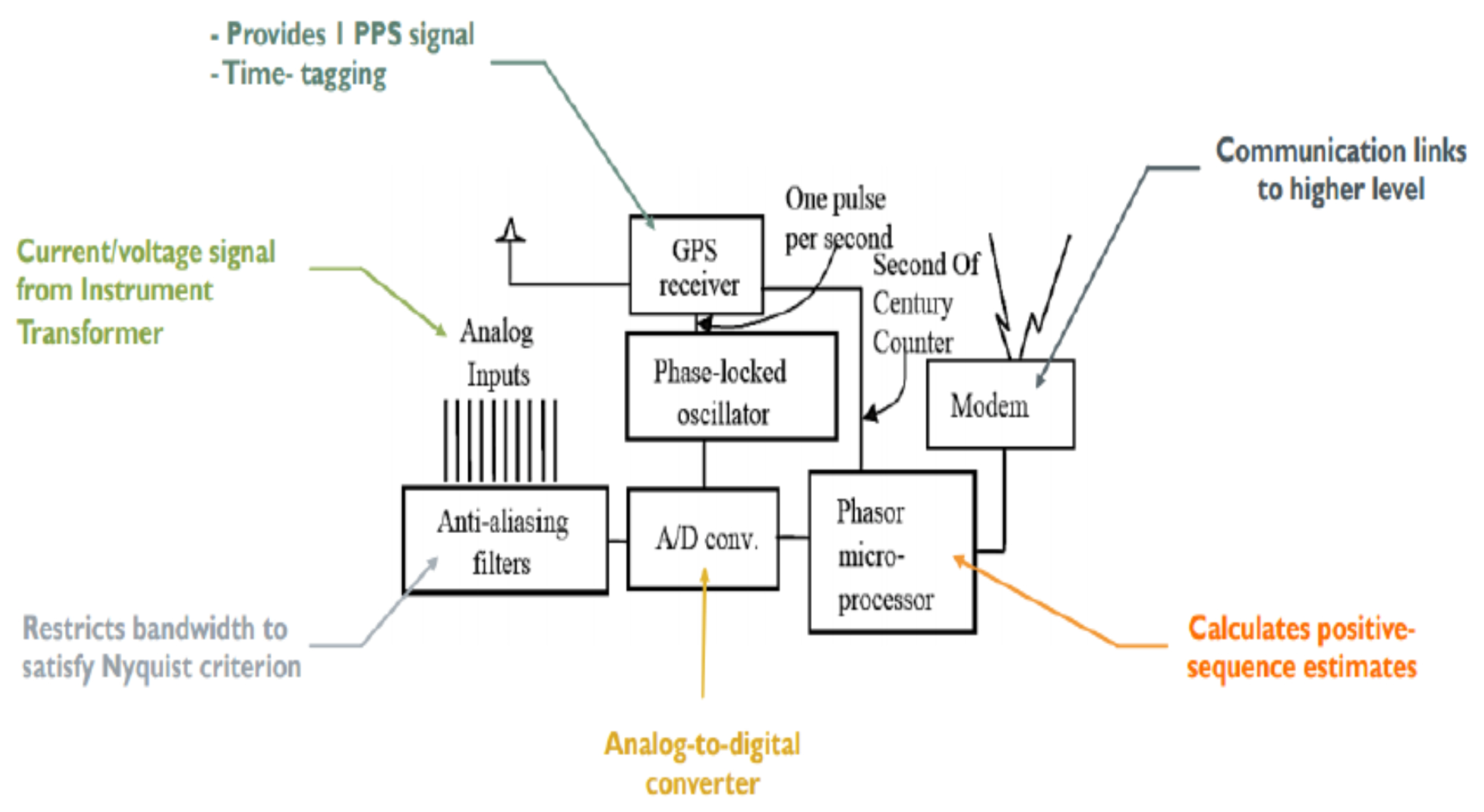
2. Micro Phasor Measurement Unit in Distribution Networks
- Proper Voltage: Ensuring stable voltage levels at consumers’ terminals is essential for the proper functioning of electrical devices and equipment. Voltage variations should remain within acceptable limits, typically ±6% of the rated voltage. This minimizes the risk of equipment damage and malfunction due to voltage fluctuations.
- Availability of Power on Demand: The distribution network should be designed to meet consumers’ varying power demands promptly. Whether consumers need a small amount of power or a larger supply, the network should be capable of delivering it without interruption.
- Reliability: The dependence of various industries and services on electrical power underscores the importance of a reliable distribution network. Interruptions in power supply can lead to production halts, loss of revenue, and inconvenience to consumers. A reliable network is crucial to prevent such disruptions and maintain consistent service.
3. State of the Art of Optimal Placement
4. Placement Algorithms: Parameters and Challenges
- High cost of measuring devices.
- High implementation costs of the communication infrastructure.
- 1.
- Key Parameters
- ObservabilityThe optimization method attempts to find out the places with the highest observation. Observability is defined as the ability to uniquely estimate the states of a bus in a power system using certain measurements. Observability analysis is necessary for deciding on the location of the device in order to maintain the solvability of the observation equations under different conditions. An observability constraint vector is used to store information about the observability of the network. Observability can be classified into Numerical Observability and Topological Observability. Observability is evaluated by the Bus Observability Index BOI () which presents the number of devices that are able to observe a given bus. A bus is said to be observable if its voltage and branch currents are measurable. Consequently, the maximum bus observability index is limited to the maximum connectivity () of a bus plus one as presented in (4).where mc is the maximum connectivity and i is the number of the bus.
- Number of placed devicesOne of the criteria that must be considered in the placement problem is the number of placed devices. The goal of a placement problem is to accomplish this task with as few devices as possible [42].
- System Observability Redundancy Index (SORI)SORI is the total count of observability of a bus by different measuring devices either directly or indirectly. It refers to the number of buses, which achieve observability. Increasing the SORI value helps reduce the uncertainty in measurements. When multiple measurements corroborate each other, it enhances the confidence in the accuracy and reliability of the data, contributing to better observability [42]. The System Observability Redundancy Index for all the busses of a system is presented in (5).When the SORI value is higher, it indicates that more of the system will remain visible and more reliable in the event of a device failure [15].
- 2.
- Distribution Network ChallengesMany of the placement algorithms have been previously used for transmission systems. Because of the clear difference between transmission and distribution systems in terms of topology and the number of nodes, these algorithms would not lead to optimal results in distribution systems because they did not take into consideration the specifications of distribution networks. In addition, the distribution network is a dynamic system due to the existence of switches in it, which makes the network topology changeable. The placement algorithms of the distribution network should be improved for the following three reasons:
- Computing time: Distribution systems contain more nodes than transmission systems, resulting in higher compute time in the network.
- Topology: A radial network is a common configuration in electrical power distribution.
- Switches: Distribution systems contain switches that make the system structure subject to change.
Placement algorithms should be optimized by making them consider these characteristics of the distribution system, in order to solve its complexities [38].
5. Proposed Solution
- Greedy algorithms are relatively simple to implement and computationally efficient. They often have low time complexity, which is essential for solving optimization problems in large-scale power systems with real-time requirements.
- While greedy algorithms do not guarantee finding the global optimum, they can often find solutions that are near-optimal or good enough for practical purposes. In many cases, near-optimal solutions are sufficient to improve the observability and control of the power system.
- The placement of PMUs can be a combinatorial optimization problem, which can be computationally intensive. Greedy algorithms can reduce the combinatorial complexity by making incremental decisions based on a local criterion. This can significantly speed up the solution process compared to exhaustive search methods.
- Greedy algorithms can be adapted to incorporate different criteria and constraints, allowing for flexibility in addressing specific power system objectives. For example, we can modify the greedy algorithm to consider cost constraints or communication network limitations.
- The nature of µPMU placement problems may make greedy strategies particularly effective. Depending on the specific problem formulation and objectives, a greedy algorithm may produce solutions that meet the power system’s observability and control requirements.
- 1.
- AssumptionsThe proposed algorithm was developed based on several assumptions concerning both the distribution network and the Phasor Measurement Units. These assumptions serve as foundational principles for the algorithm’s design:
- The distribution networks under consideration are balanced and are modeled as single-phase power systems.
- Each PMU is equipped with multiple channels, enabling them to be connected to all the incident lines. This configuration enables a PMU to measure the voltage phasor of its own node and the current phasors of the lines connected to it.
- The impedances of the lines in the distribution network are known. This knowledge of line impedances facilitates the calculation of voltage values for nodes that are not equipped with PMUs, ensuring a comprehensive understanding of the entire network.
Modeling distribution networks as balanced and single-phase power systems is indeed more suitable for certain types of applications, particularly residential areas where loads are predominantly single-phase and relatively small. It may be particularly well-suited for apartment buildings or blocks of flats where individual apartments are typically supplied with single-phase electricity. PMUs can have applications in various settings, including apartment buildings or blocks of flats, although their deployment in such environments may differ from larger-scale power systems. PMUs can monitor the voltage quality within apartment buildings. They can detect issues such as voltage sags, swells, or harmonics, which can affect the operation of sensitive electronic equipment in residential units. In addition, in areas with distributed energy resources like rooftop solar panels, PMUs can help assess the stability of the local grid and ensure that energy generation and consumption are balanced.These assumptions provide a structured framework upon which the proposed algorithm is built, allowing it to effectively optimize the placement of PMUs while accounting for the distribution network’s characteristics and the capabilities of the measurement units themselves. - 2.
- ObjectivesThe developed algorithm aims to achieve the following objectives:
- Achieving full network observability: full network observability entails the installation of PMUs strategically throughout the distribution network. This strategic placement ensures the measurement and observation of all voltage and current values across the network, resulting in a comprehensive monitoring system. This approach facilitates the accurate analysis and understanding of the behavior of voltage and current quantities at every node within the network.
- Minimize the number of PMUs: optimize the deployment of PMUs in such a way that the total count of these units utilized is minimized. This objective seeks to ensure an efficient and cost-effective solution by strategically selecting only the essential locations for installing PMUs across the distribution network. By achieving this objective, the monitoring system can effectively capture critical data points while keeping the infrastructure investment and operational costs to a minimum.
- Achieve a high redundancy index: as indicated by the System Overall Redundancy Index value, this emphasis on SORI underscores the importance of enhancing system reliability and robustness. By attaining a high SORI value, the distribution network becomes better equipped to handle potential failures, ensuring uninterrupted operation even in the presence of disturbances or faults.
- 3.
- ConsiderationsIn order to face the real challenges of the distribution network, certain constraints have been taken into account in this algorithm, they are listed below:
- Topology Change: The existence of switches in the distribution network makes the network dynamic by switching their status from open to close or vice versa. This fact makes the topology of the distribution network changeable, that some nodes of the network could be totally disconnected from the rest of the nodes. This challenge affects directly the placement problem. In fact, PMUs need to be placed in such a way that complete observability is achieved regardless of the switch (es) status.
- Devices Failure: Device failure is a possible event that could occur at PMUs placed on the distribution network for technical or environmental reasons. This event could also affect the complete observability of the system. The goal is to find a location, which has the minimum number of unobserved nodes in the event of a device failure. The key parameter that depends on the number of unobserved nodes in the event of a device failure is the SORI value. The higher the SORI value, the fewer unobserved nodes are reached in the event of a device failure. Taking this constraint into account improves the reliability of the system.
- 4.
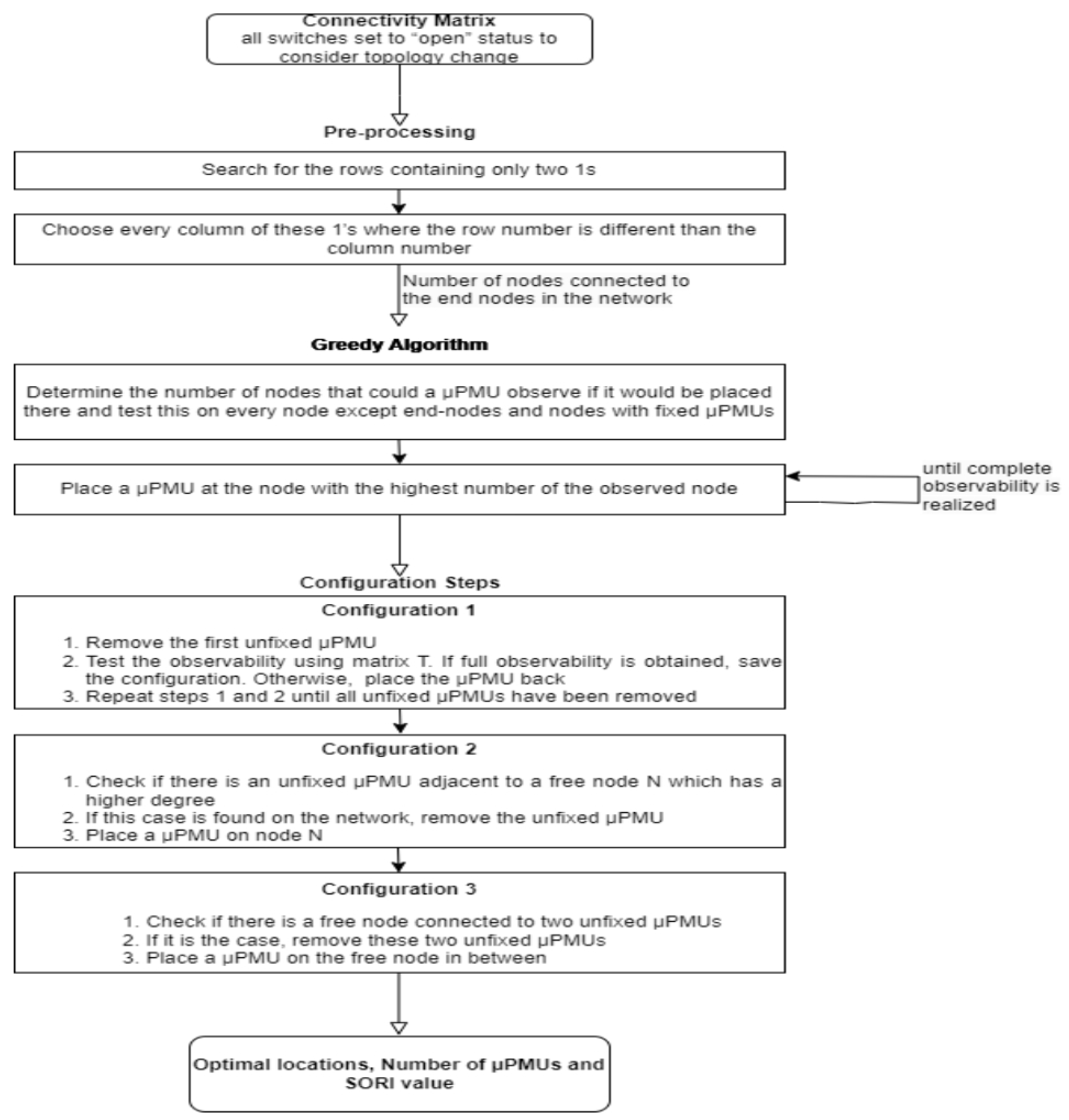
- Functioning of the AlgorithmThe proposed algorithm has the connectivity matrix of the network as input. To consider the topology change of the network, this matrix is built with all switches set to “open” status, which is the worst case.To avoid the manual creation of the connectivity matrix, a user interface is used to draw the graph of the desired network and an algorithm would automatically generate the connectivity matrix into an Excel file. This Excel file will be the input of the algorithm.The algorithm is composed of a pre-processing step and a greedy algorithm followed by three configurations. The result of this algorithm is the placement of the PMUs on the network graph as well as the number of, the SORI values, and the nodes where the PMUs have been optimally placed. The algorithm also detects the location of switches on the network. The block diagram of this algorithm is presented in Figure 3.A greedy algorithm, by nature, focuses on making locally optimal decisions at each step of a problem-solving process without considering the global consequences. While it may not inherently prioritize data quality assurance. Consider adding redundancy to the placement by placing multiple PMUs in critical areas. The greedy algorithm can distribute PMUs strategically to maximize both data quality and redundancy. In each step of the greedy algorithm, select the next µPMU location based on the scoring function. The algorithm should prioritize locations with the highest scores, indicating better data quality and lower noise interference.Connectivity MatrixThe connectivity matrix is the binary admittance matrix of a power system network and essentially shows which buses are connected to one another (see Algorithm 1). Usually gets the variable A, and its mathematical definition is defined in (6).
Algorithm 1: Connectivity Matrix Pre-processingThe aim of this step is to place PMUs on nodes connected to the final nodes and eliminate the placement on the end nodes because a PMU placed on an end node could observe only two nodes and a failure of a device, in this case, increase the number of unobserved nodes.Otherwise, a PMU placed on nodes connected to an end node would observe three or more nodes. This step improves the SORI value and reduces the search space of the network to provide a faster search for the next steps (see Algorithm 2). As the connectivity matrix is the input of this step, end-nodes and nodes connected to end-nodes must be identified from it.Greedy AlgorithmOnce the PMUs have been placed on the nodes connected to the end nodes, the greedy algorithm runs.In the first step of the greedy algorithm, the number of observed nodes of each node except fixed and end nodes is determined. Then the results are presented in the observability matrix O. The fixed and end-nodes get the number 0 in this matrix because no PMU would be placed on them. The greedy algorithm always takes the first best solution it encounters. The algorithm will therefore place a PMU on this node then the observability will be tested using the matrix T presented in (7). If the observability is reached, the results will be saved and the greedy algorithm stops here. Otherwise, the algorithm will continue to place on the other nodes that have the greatest number of nodes observed in the matrix O as in Algorithm uid51.After placing the PMU on the node and calculating the matrix T, the complete observability of the system can be easily tested by following these steps:- Verification of each row of matrix T.
- Calculate the number of 1 in each row.
- If the number of 1s in each row equals at least 1, then the system is completely observable. The PMUs placed from the greedy algorithm are unfixed PMUs and could change their placement in the following steps.
Algorithm 2: Preprocessing
Configuration stepsAfter performing the pre-processing and greedy algorithm, placement is done and observability is obtained. Otherwise, this is not enough, as other key parameters such as the number of PMU and the SORI value have not yet achieved their best results, compared to the results of other algorithms [35,36,37]. The configuration steps are performed in order to improve these parameters by achieving the minimum number of PMUs as possible and the highest value of SORI possible to ensure system workability and minimize implementation costs see Algorithm uid52.- Configuration 1The objective of this configuration is to reduce the number of PMUs installed without affecting the complete observability of the network.
- Configuration 2The goal of this configuration is to improve the system observability redundancy index (SORI) value. This step gives priority to free nodes that have a higher degree than nodes with unfixed PMUs because a node with a higher degree can observe more nodes and as a result, the SORI value will increase.
- Configuration 3This configuration search also for a placement situation where it is possible to remove a PMU without affecting the complete observability of the system.
Algorithm 3: Greedy Algorithm 4: Configuration - 5.
- ApplicationsThe proposed method for optimal placement of PMUs in distribution networks has several practical applications in real-world power system operations and management.Enhanced Fault Detection and Localization: By strategically placing PMUs in critical locations, the proposed method improves the observability of the distribution network. This enables rapid detection and precise localization of faults when they occur. With accurate fault information, utilities can quickly dispatch crews to the affected areas, reducing outage durations and improving overall system reliability.Grid Stability and Resilience: The proposed method ensures better observability of the distribution system, which is crucial for maintaining grid stability and resilience. With the number of PMUs strategically placed, operators can detect voltage fluctuations, frequency deviations, and other system dynamics promptly, enabling them to take corrective actions to prevent instability or cascading failures.Distribution Network Planning and Expansion: The placement results obtained from the proposed algorithm can be used for long-term distribution network planning. Utilities can use this information to identify areas with inadequate observability and plan for future expansions or upgrades to ensure grid reliability as the demand for electricity and distributed generation resources increases.Integration of Renewable Energy Sources: As renewable energy sources (e.g., solar, wind) are integrated into distribution networks, their intermittent nature poses challenges for grid management. The proposed method optimizes the placement of PMUs to monitor the impact of renewable energy generation, enabling utilities to balance supply and demand efficiently and maintain power quality.Grid Restoration and Blackout Prevention: In the event of a major grid disruption or blackout, the high observability provided by the optimal placement of PMUs allows for faster restoration and post-event analysis. Utilities can identify affected areas and assess the system’s response during the event, aiding in grid restoration and learning from such incidents for future grid resilience.
6. Results and Analysis
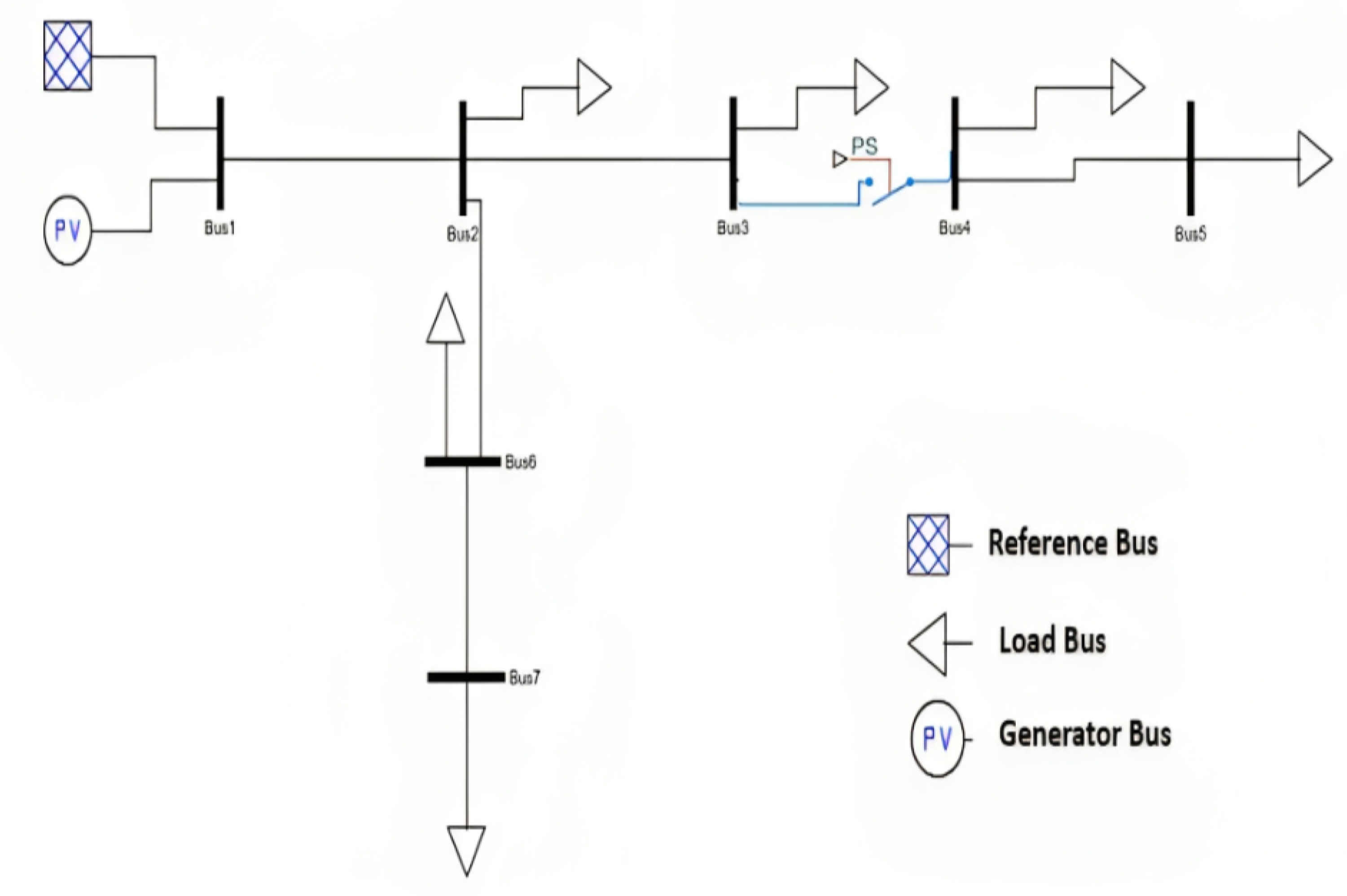
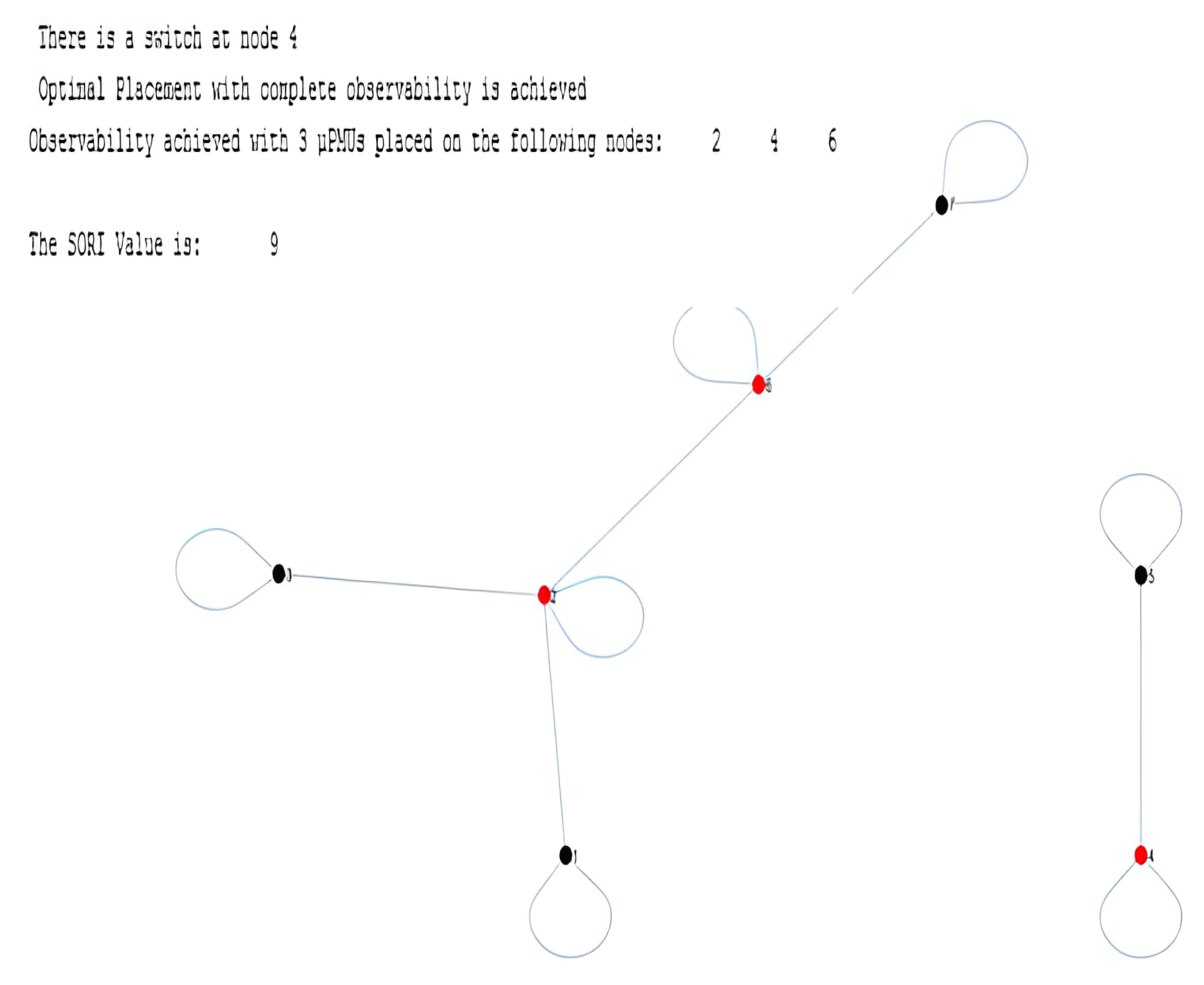
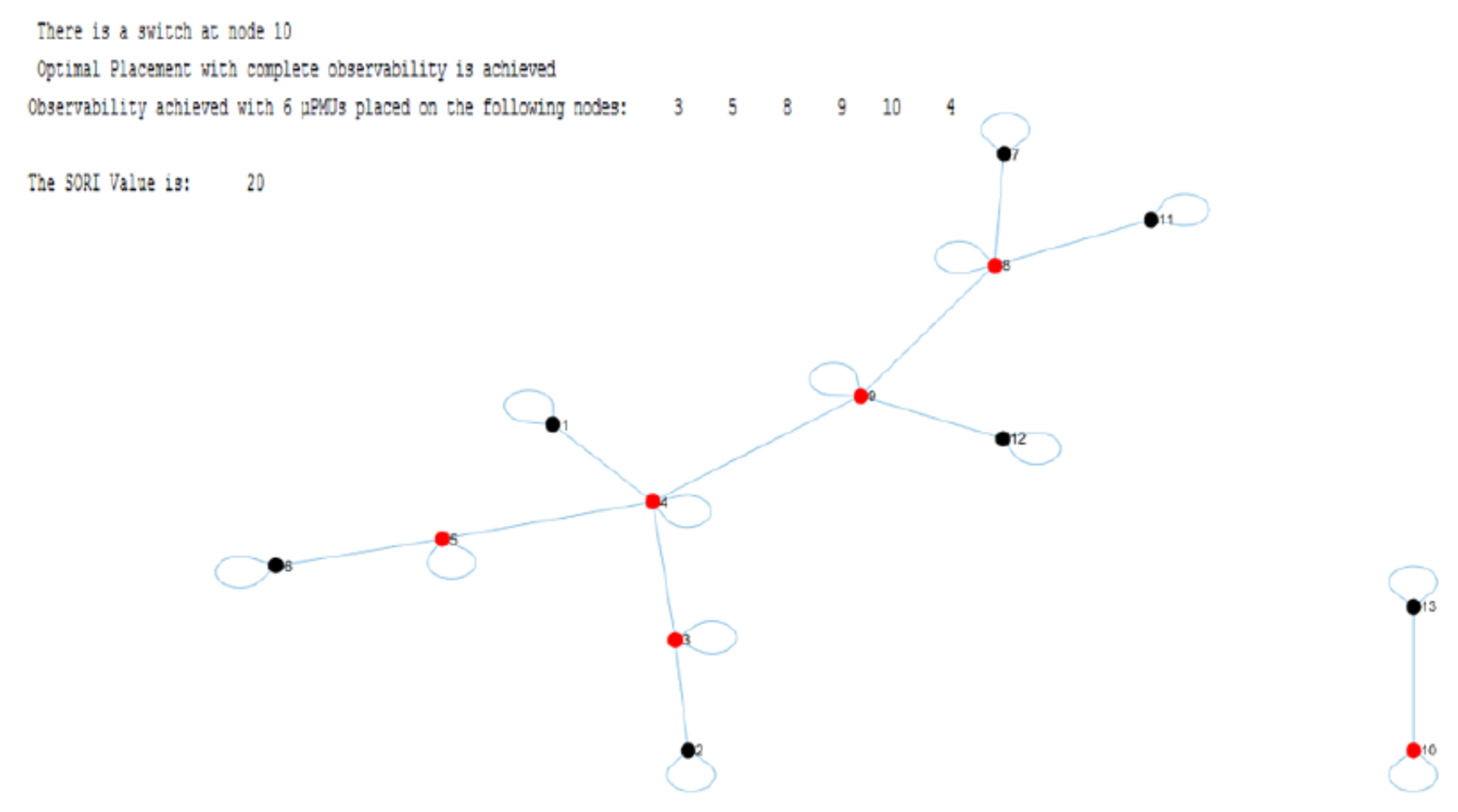
6.1. IEEE 7-Node Network
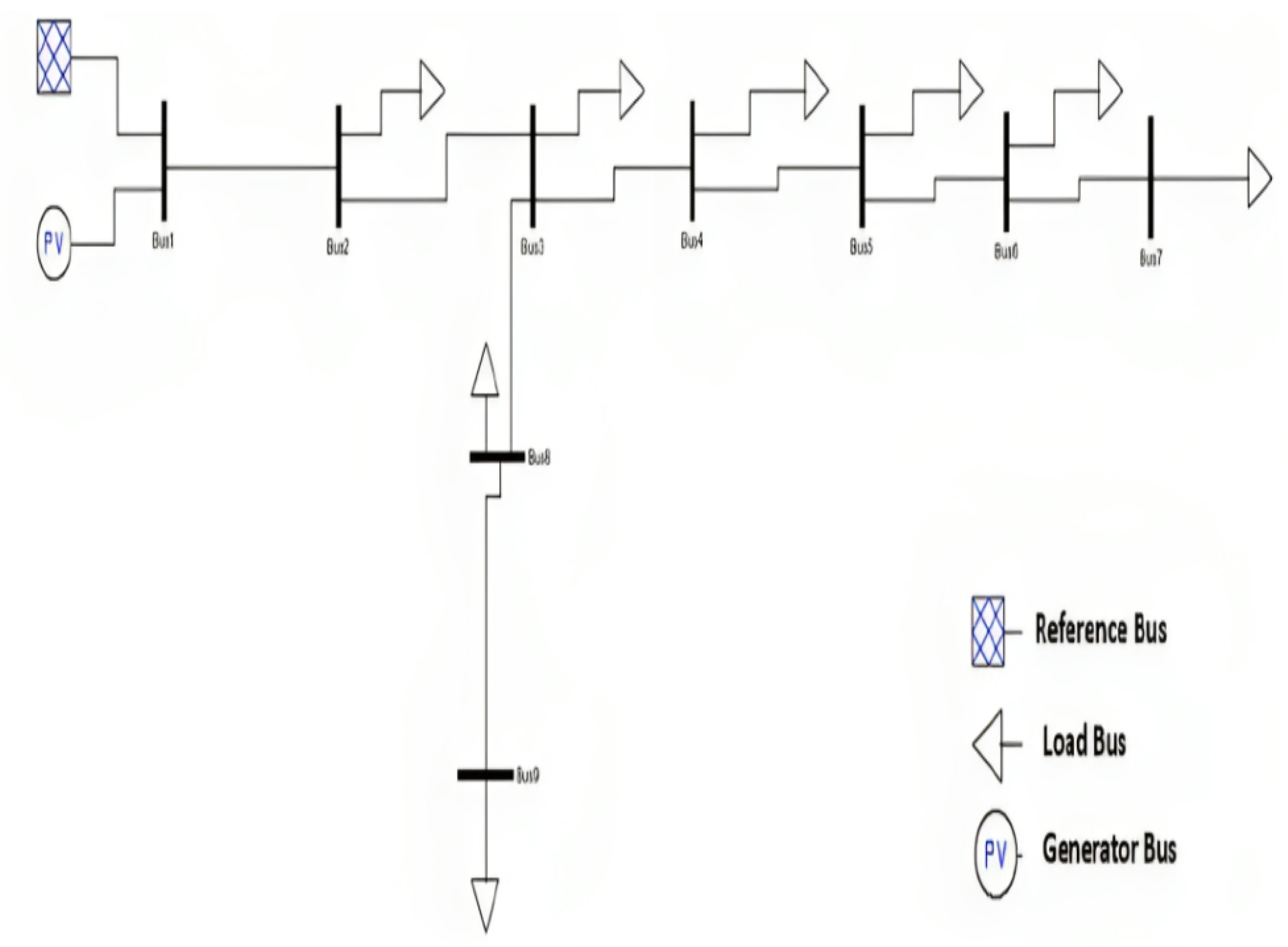
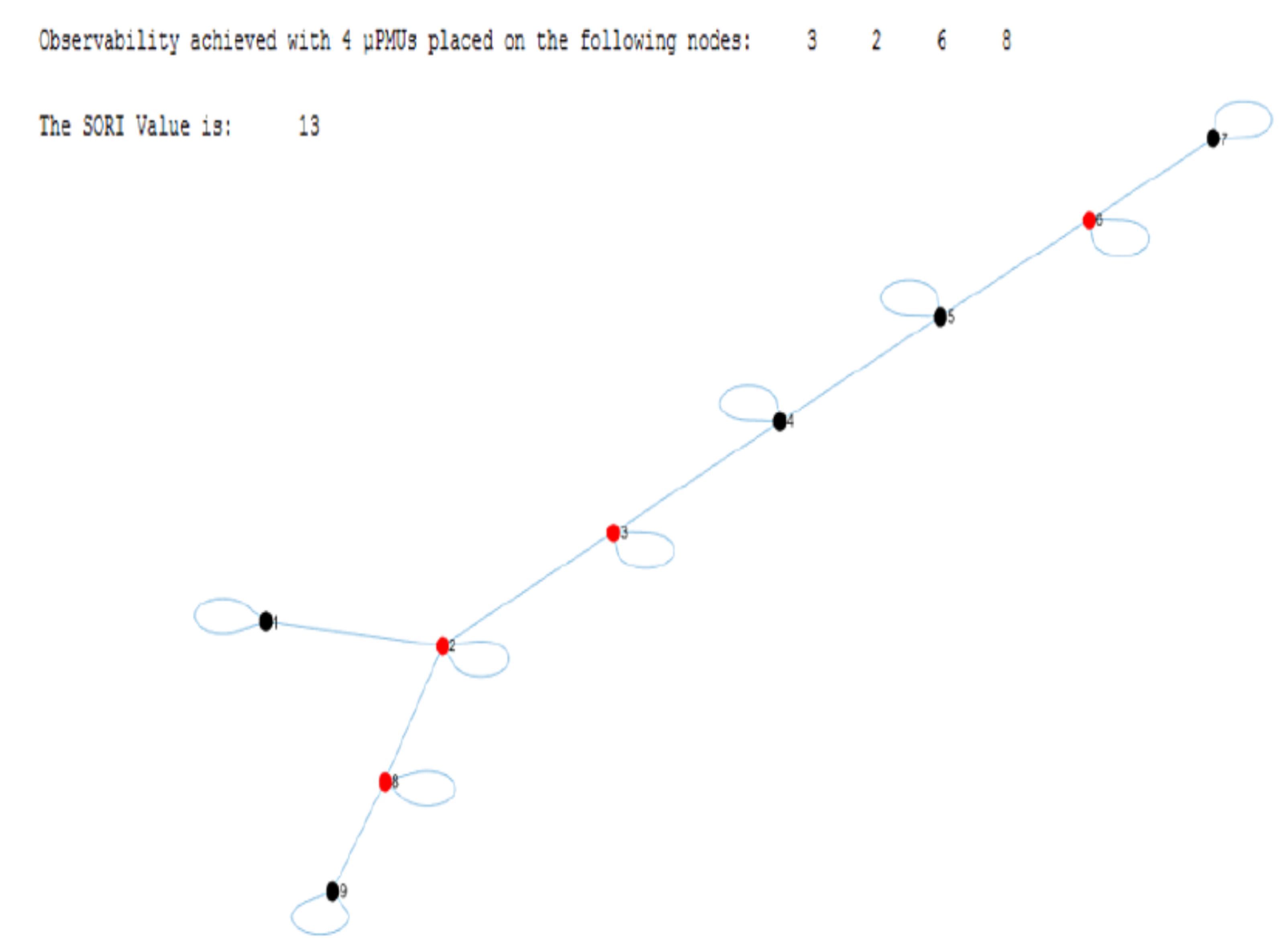
6.2. IEEE 9-Node Network
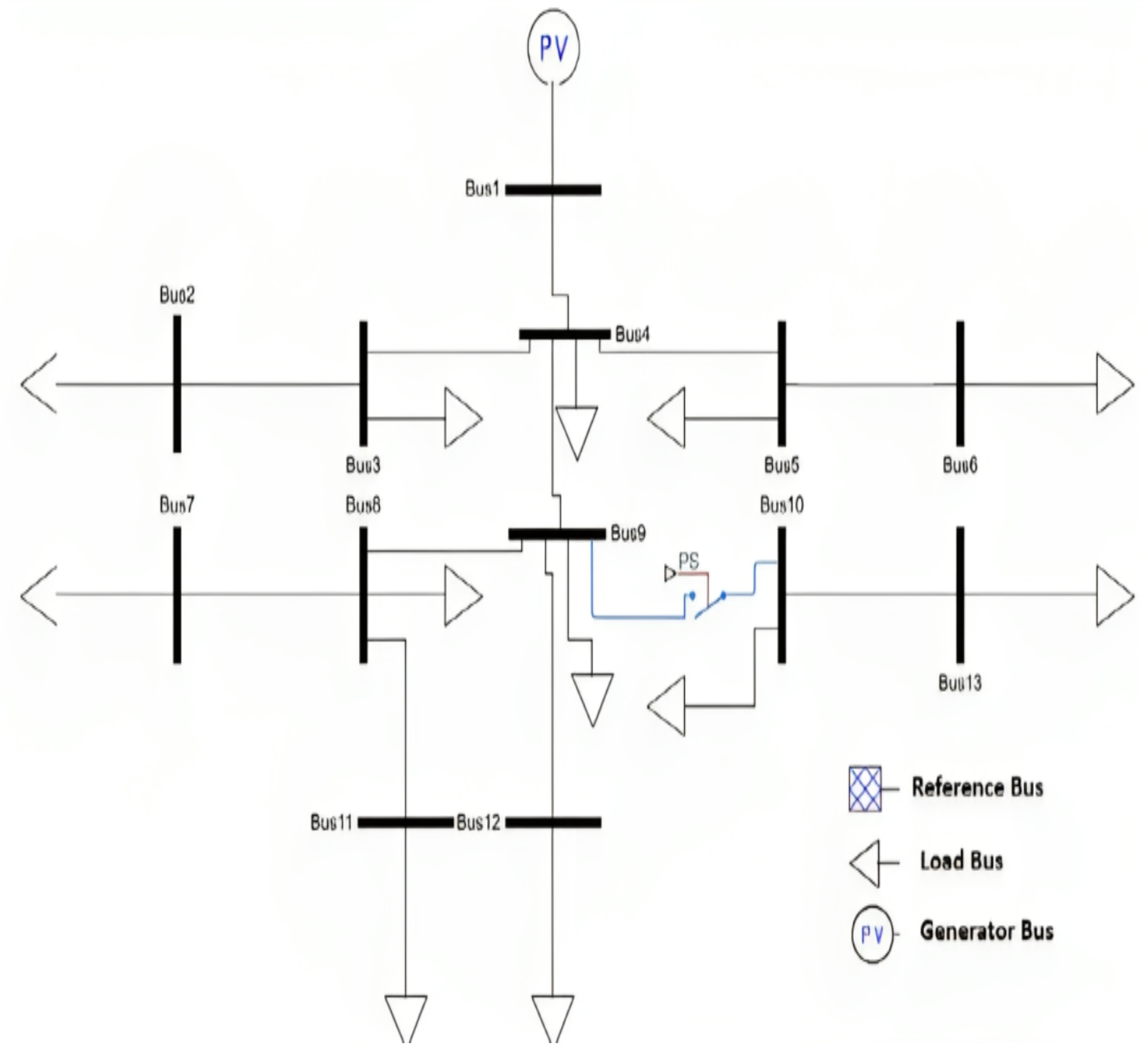
IEEE 13-Node Network
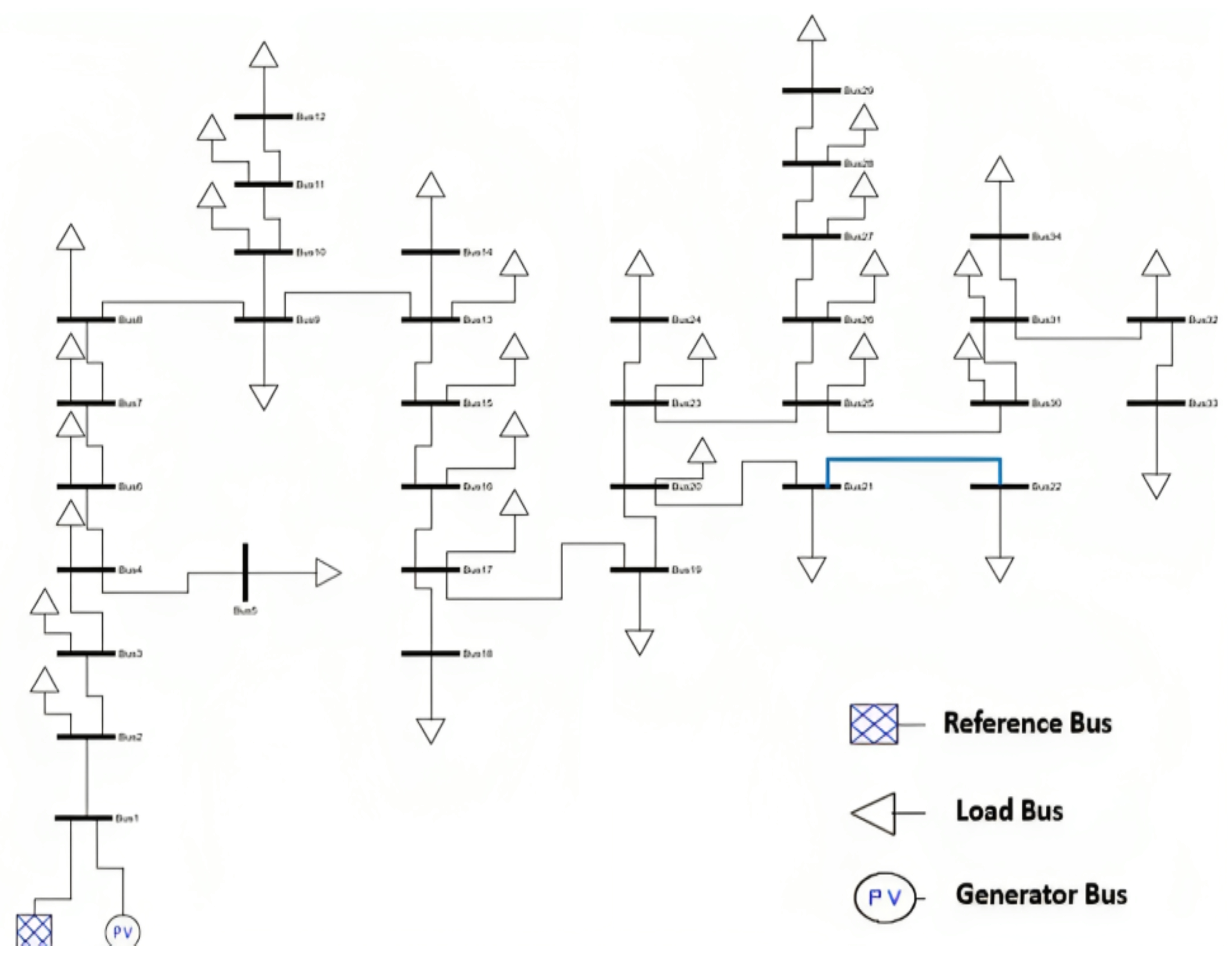
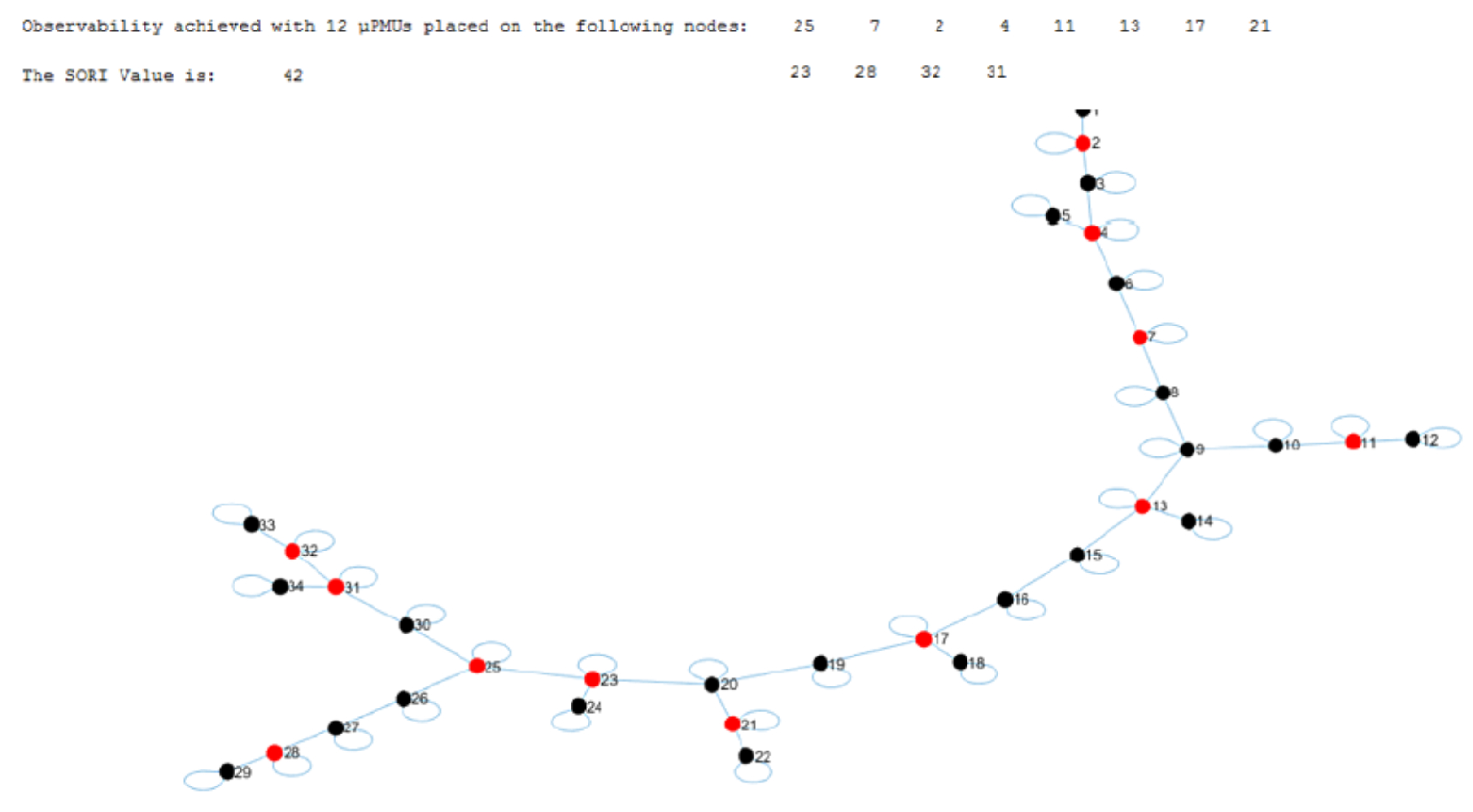
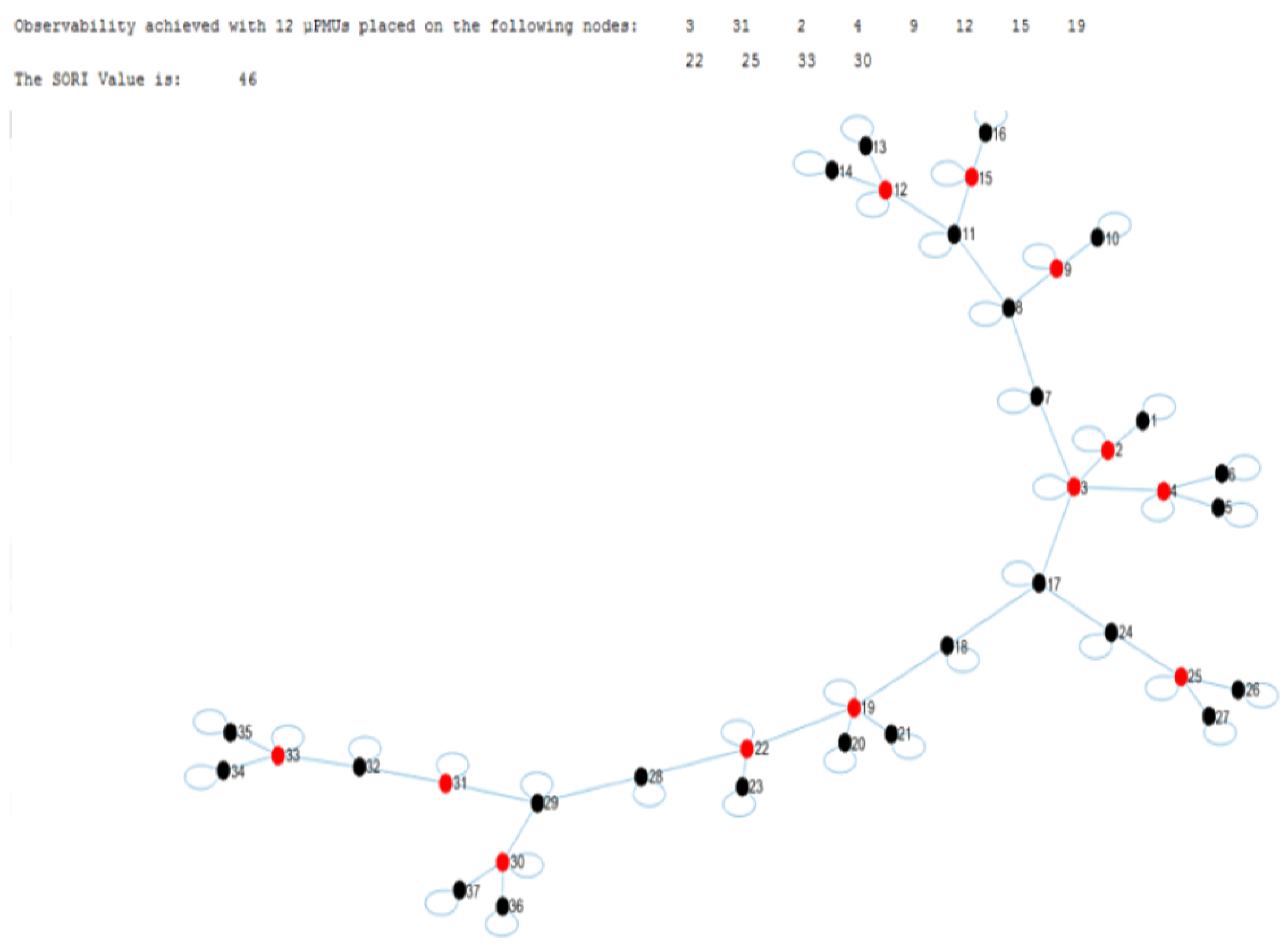
6.3. IEEE 34-Node Network
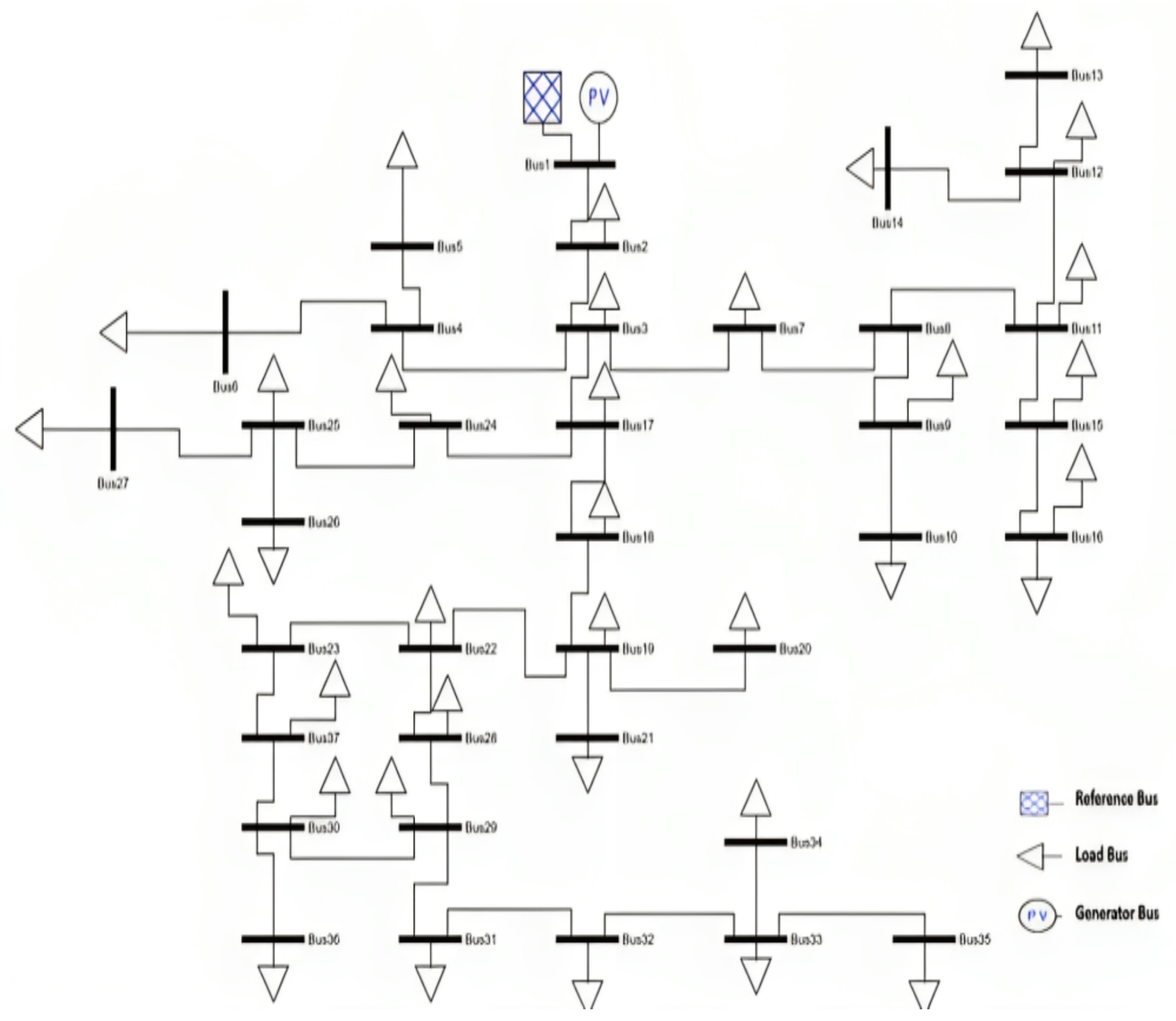
IEEE 37-Node Network
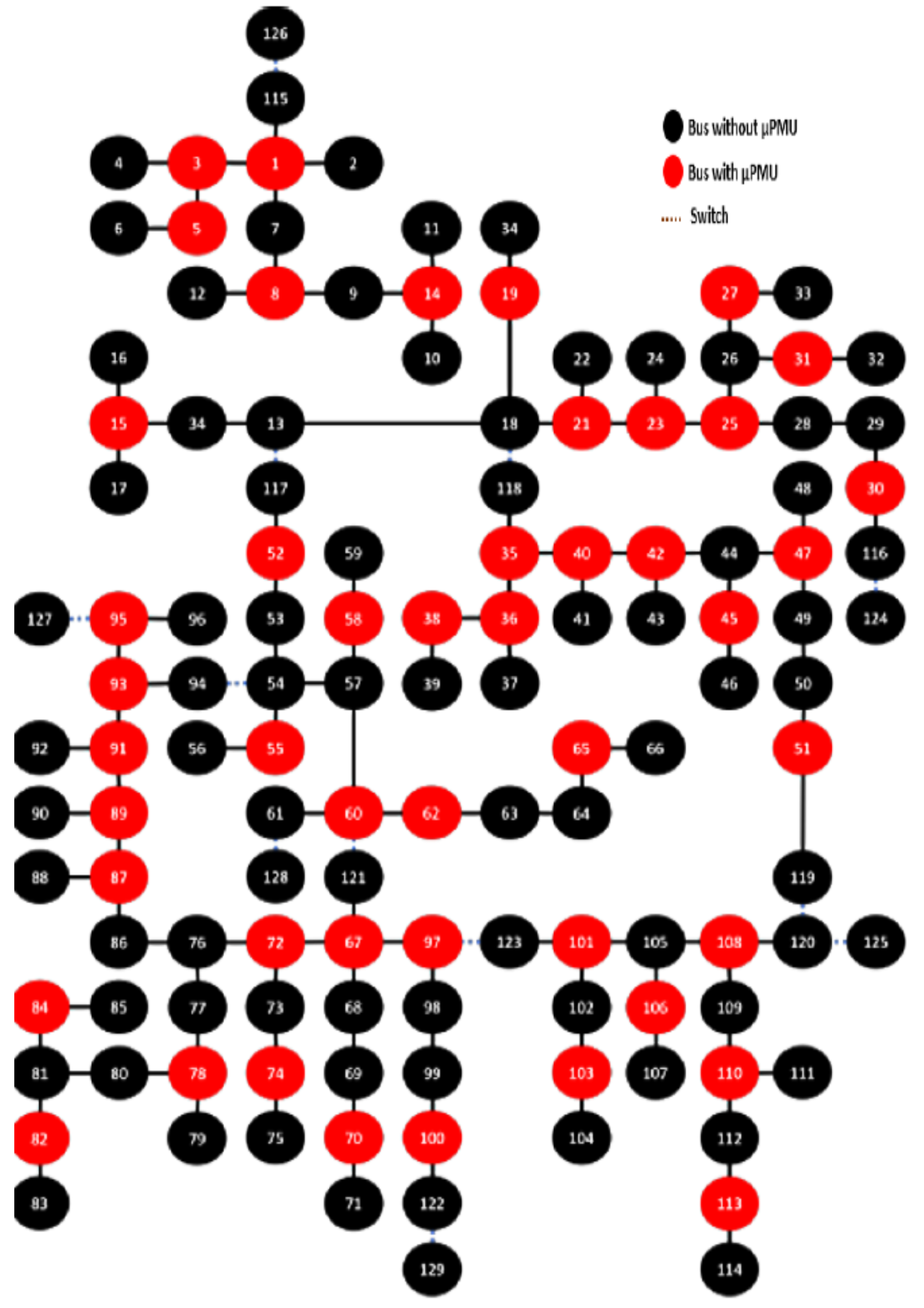
6.4. IEEE 123-Node Network
- Observability: Achieved
- Number of PMUs: 48
- Locations of PMUs: 18, 25, 72, 63, 98, 1, 3, 5, 14, 8, 15, 19, 21, 23, 31, 27, 36, 38, 40, 42, 45, 47, 55, 58, 60, 65, 70, 74, 78, 82, 84, 87, 89, 91, 93, 95, 103, 106, 110, 113, 30, 52, 35, 51, 108, 67, 100, 101
- SORI value: 171
6.5. Comparison with Previous Algorithms
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PMU | Phasor Measuring Unit |
| REG | Renewable Energy-based Generator |
| DNs | Distribution Networks |
| DER | Distributed Energy Resource |
| SORI | System Observed Repeat Index |
| LV | Low Voltage |
| MV | Medium Voltage |
| PQ | Power Quality |
| RES | Renewable Energy Sources |
| EVs | Electric Vehicle |
| RES | Renewable Energy Sources |
| ADC | Analog-to-Digital Converter |
| DSP | Digital Signal Processor |
| DG | Distributed Generator |
| SPI | Serial Peripheral Interface |
| RQP | Recursive Quadratic Programming |
| GPS | Generalized Pattern Search |
References
- Theodorakatos, N.P.; Lytras, M.; Babu, R. Towards Smart Energy Grids: A Box-Constrained Nonlinear Underdetermined Model for Power System Observability Using Recursive Quadratic Programming. Energies 2020, 13, 1724. [Google Scholar] [CrossRef]
- Joshi, P.M.; Verma, H.K. Synchrophasor measurement applications and optimal PMU placement: A review. Electr. Power Syst. Res. 2021, 199, 107428. [Google Scholar] [CrossRef]
- Bikiran, G.; Flueck, A.J. Real-Time Wide-Area Fault Locator for Power Transmission Networks Using Sparse PMU Measurements. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Koochi, M.H.R.; Dehghanian, P.; Esmaeili, S. PMU Placement with Channel Limitation for Faulty Line Detection in Transmission Systems. IEEE Trans. Power Deliv. 2020, 35, 819–827. [Google Scholar] [CrossRef]
- Rahman, N.H.A.; Zobaa, A.F. Optimal PMU Placement Using Topology Transformation Method in Power Systems. J. Adv. Res. 2016, 7, 625–634. [Google Scholar] [CrossRef] [PubMed]
- Manousakis, N.M.; Korres, G.N.; Georgilakis, P.S. Optimal placement of phasor measurement units: A literature review. In Proceedings of the 2011 16th International Conference on Intelligent System Applications to Power Systems, Hersonissos, Greece, 25–28 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–6. [Google Scholar]
- More, K.K.; Jadhav, H.T. A literature review on optimal placement of phasor measurement units. In Proceedings of the 2013 International Conference on Power, Energy and Control (ICPEC), Dindigul, India, 6–8 February 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 220–224. [Google Scholar]
- Tholomier, D.; Kang, H.; Cvorovic, B. Phasor measurement units: Functionality and applications. In Proceedings of the 2009 Power Systems Conference, Kharagpur, India, 27–29 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–12. [Google Scholar]
- Noureen, S.S.; Roy, V.; Bayne, S.B. Phasor measurement unit integration: A review on optimal PMU placement methods in power system. In Proceedings of the 2017 IEEE Region 10 Humanitarian Technology Conference (R10-HTC), Dhaka, Bangladesh, 21–23 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 328–332. [Google Scholar]
- Dusabimana, E.; Yoon, S.-G. A survey on the micro-phasor measurement unit in distribution networks. Electronics 2020, 9, 305. [Google Scholar] [CrossRef]
- Usai, L.; Lamb, J.J.; Hertwich, E.; Burheim, O.S.; Strømman, A.H. Analysis of the Li-ion battery industry in light of the global transition to electric passenger light-duty vehicles until 2050. Environ. Res. Infrastruct. Sustain. 2022, 2, 011002. [Google Scholar] [CrossRef]
- Lakervi, E.; Holmes, E.J. Electricity Distribution Network Design; IET: London, UK, 1995. [Google Scholar]
- Zuhaib, M.; Khair, A.; Rihan, M. An objective analysis of micro-synchrophaosrs technology for monitoring and control of active distribution network. J. Inst. Eng. (India) Electr. Eng. Div. 2019, 3, 27–36. [Google Scholar]
- Menezes, T.S.; Barra, P.H.A.; Dizioli, F.A.S.; Lacerda, V.A.; Fernandes, R.A.S.; Coury, D.V. A Survey on the Application of Phasor Measurement Units to the Protection of Transmission and Smart Distribution Systems. Electr. Power Compon. Syst. 2023, 1–18. [Google Scholar] [CrossRef]
- Tahabilder, A.; Ghosh, P.K.; Chatterjee, S.; Rahman, N. Distribution system monitoring by using micro-pmu in graph-theoretic way. In Proceedings of the 2017 4th International Conference on Advances in Electrical Engineering (ICAEE), Dhaka, Bangladesh, 28–30 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 159–163. [Google Scholar]
- Prasad, B.R.V.; Sai, B.S.; Vijaychandra, J.; Babu, R. A Review on the Micro-Phasor Measurement Unit in Distribution Networks. In Recent Advances in Power Systems; Springer: Berlin/Heidelberg, Germany, 2022; pp. 93–104. [Google Scholar]
- Hojabri, M.; Dersch, U.; Papaemmanouil, A.; Bosshart, P. A comprehensive survey on phasor measurement unit applications in distribution systems. Energies 2019, 12, 4552. [Google Scholar] [CrossRef]
- Das, H.P.; Pradhan, A.K. Development of a micro-phasor measurement unit for distribution system applications. In Proceedings of the 2016 National Power Systems Conference (NPSC), Bhubaneswar, India, 19–21 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Chen, X.; Chen, T.; Tseng, K.J.; Sun, Y.; Amaratunga, G. Customized optimal μpmu placement method for distribution networks. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 135–140. [Google Scholar]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B. Application of Heuristic Algorithms to Optimal PMU Placement in Electric Power Systems: An Updated Review. Renew. Sustain. Energy Rev. 2015, 50, 214–228. [Google Scholar] [CrossRef]
- Anas, A.; Fan, L. Optimal PMU Placement for Modeling Power Grid Observability with Mathematical Programming Methods. Int. Trans. Electr. Energy Syst. 2020, 30, e12182. [Google Scholar] [CrossRef]
- Berghout, T.; Benbouzid, M.; Amirat, Y. Towards Resilient and Secure Smart Grids against PMU Adversarial Attacks: A Deep Learning-Based Robust Data Engineering Approach. Electronics 2023, 12, 2554. [Google Scholar] [CrossRef]
- Kou, L.; Wu, J.; Zhang, F.; Ji, P.; Ke, W.; Wan, J.; Liu, H.; Li, Y.; Yuan, Q. Image encryption for offshore wind power based on 2D-LCLM and Zhou Yi eight trigrams. Int. J. Bio-Inspired Comput. 2023, 22, 53–64. [Google Scholar] [CrossRef]
- Al-Hazaimeh, O.M.; Al-Jamal, M.F.; Alomari, A.K.; Bawaneh, M.J.; Tahat, N. Image encryption using anti-synchronisation and Bogdanov transformation map. Int. J. Comput. Sci. Math. 2022, 15, 43–59. [Google Scholar] [CrossRef]
- Pinto, S.J.; Siano, P.; Parente, M. Review of Cybersecurity Analysis in Smart Distribution Systems and Future Directions for Using Unsupervised Learning Methods for Cyber Detection. Energies 2023, 16, 1654. [Google Scholar] [CrossRef]
- Gupta, A. Integration Challenges of Wind Power on Power System Grid A Review. In Proceedings of the 2018 International Conference on Advanced Computation and Telecommunication (ICACAT), Bhopal, India, 28–29 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–7. [Google Scholar]
- Hassini, K.; Fakhfakh, A.; Derbel, F. μpmu based on wireless ieee 1588 ptp. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Tunis, Tunisia, 28 September–1 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1030–1034. [Google Scholar]
- Ochoa, L.F.; Dent, C.J.; Harrison, G.P. Distribution network capacity assessment: Variable DG and active networks. IEEE Trans. Power Syst. 2009, 25, 87–95. [Google Scholar] [CrossRef]
- Ambrosino, D.; Scutella, M.G. Distribution network design: New problems and related models. Eur. J. Oper. Res. 2005, 165, 610–624. [Google Scholar] [CrossRef]
- Kumar, S.; Soni, M.K.; Jain, D.K. Power quality monitoring using pmu. Int. J. Comput. Appl. 2016, 135, 1–5. [Google Scholar] [CrossRef]
- Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M. Optimal location of electric vehicle charging station and its impact on distribution network: A review. Energy Rep. 2022, 8, 2314–2333. [Google Scholar] [CrossRef]
- Priyadarshini, S.; Panigrahi, C.K. Application of heuristic methods for optimal placement of phasor measurement unit. In Applications of Robotics in Industry Using Advanced Mechanisms: Proceedings of International Conference on Robotics and Its Industrial Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 223–233. [Google Scholar]
- Hassini, K.; Fakhfakh, A.; Derbel, F. Iot devices in smart grids. In Proceedings of the 2020 17th International Multi-Conference on Systems, Signals & Devices(SSD), Sfax, Tunisia, 20–26 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1086–1091. [Google Scholar]
- Ahmed, M.M.; Amjad, M.; Qureshi, M.A.; Imran, K.; Haider, Z.M.; Khan, M.O. A Critical review of state-of-the-art optimal PMU placement techniques. Energies 2022, 15, 2125. [Google Scholar] [CrossRef]
- Tran, V.-K.; Zhang, H.-S.; Nguyen, V.-N. Optimal pmu placement in multi-configuration power distribution networks. In Proceedings of the 2016 4th In-ternational Conference on Electrical & Electronics Engineering and Computer Science (ICEEECS 2016), Jinan, China, 15–16 October 2016; Atlantis Press: Amsterdam, The Netherlands, 2016; pp. 508–514. [Google Scholar]
- Jamil, E.; Rihan, M.; Anees, M. Towards optimal placement of phasor measurement units for smart distribution systems. In Proceedings of the 2014 6th IEEE Power India International Conference (PIICON), Delhi, India, 5–7 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Abdelaziz, A.Y.; Ibrahim, A.M.; Salem, R.H. Optimal pmu placement for complete observability using heuristic methods. In Proceedings of the 15th International Middle East Power Systems Conference, Alexandria, Egypt, 23–25 December 2012; pp. 23–25. [Google Scholar]
- Yuill, W.; Edwards, A.; Chowdhury, S.; Chowdhury, S. Optimal pmu placement: A comprehensive literature review. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–8. [Google Scholar]
- Theodorakatos, N.P.; Lytras, M.; Babu, R. A Generalized Pattern Search Algorithm Methodology for Solving an Under-Determined System of Equality Constraints to Achieve Power System Observability Using Synchrophasors. J. Phys. Conf. Ser. 2021, 2090, 012125. [Google Scholar] [CrossRef]
- Redstone, J.; Ruzzo, W.L. Algorithms for a simple point placement problem. In Proceedings of the Algorithms and Complexity: 4th Italian Conference, CIAC 2000, Rome, Italy, 1–3 March 2000; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2000; pp. 32–43. [Google Scholar]
- Xie, N.; Torelli, F.; Bompard, E.; Vaccaro, A. A graph theory based methodology for optimal pmus placement and multiarea power system state estimation. Electr. Power Syst. Res. 2015, 119, 25–33. [Google Scholar] [CrossRef]
- Aydin, B.E.; Hagedooren, H.; Rutten, M.M.; Delsman, J.; Essink, G.H.O.; van Giesen, N.; Abraham, E. A greedy algorithm for optimal sensor placement to estimate salinity in polder networks. Water 2019, 11, 1101. [Google Scholar] [CrossRef]
- Teimourzadeh, S.; Aminifar, F.; Shahidehpour, M. Contingency constrained optimal placement of micro-pmus and smart meters in microgrids. IEEE Trans. Smart Grid 2017, 10, 1889–1897. [Google Scholar]
- Carta, D.; Benigni, A.; Muscas, C. Model order reduction for pmu- based state estimation in distribution grids. IEEE Syst. Journal 2017, 12, 2711–2720. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassini, K.; Fakhfakh, A.; Derbel, F. Optimal Placement of μPMUs in Distribution Networks with Adaptive Topology Changes. Energies 2023, 16, 7047. https://doi.org/10.3390/en16207047
Hassini K, Fakhfakh A, Derbel F. Optimal Placement of μPMUs in Distribution Networks with Adaptive Topology Changes. Energies. 2023; 16(20):7047. https://doi.org/10.3390/en16207047
Chicago/Turabian StyleHassini, Khaoula, Ahmed Fakhfakh, and Faouzi Derbel. 2023. "Optimal Placement of μPMUs in Distribution Networks with Adaptive Topology Changes" Energies 16, no. 20: 7047. https://doi.org/10.3390/en16207047
APA StyleHassini, K., Fakhfakh, A., & Derbel, F. (2023). Optimal Placement of μPMUs in Distribution Networks with Adaptive Topology Changes. Energies, 16(20), 7047. https://doi.org/10.3390/en16207047