1. Introduction
1.1. HVAC Systems
Amid the paradigm shift in the energy industry from traditional energy supply systems to low-carbon power sources, such as renewable energy, in recent years, digital technologies, such as big data and artificial intelligence (AI), have been rapidly applied to the electric power industry, increasing its efficiency. While pursuing demand management and energy efficiency improvements as major policies in achieving a Green New Deal and carbon neutrality, plans have been established to expand distributed resources (DR) and foster various new power industries. Energy transition has now become an important issue that cannot be rejected. Renewable energy, such as photovoltaics (PV) and wind turbines (WT), that does not emit greenhouse gas for a substantial portion of energy consumption is necessary to achieve carbon neutrality for greenhouse gas reduction. This requires developing vast resources; however, renewable energy is volatile because power generation cannot be controlled. The increase in renewable energy resources requires major changes in traditional power grids and power markets, which have been operated mainly on nuclear power, coal, and liquefied natural gas (LNG). Furthermore, measures must be taken to minimize output variability on the grid side and prevent frequency, voltage, and inertia from degrading.
Renewable energy is attracting attention as an alternative solution to climate change and greenhouse gas and technology, which will lead to new growth engines and sustain-able growth in the future. As the number of DR connected to power distribution systems continues to increase yearly, various technical solutions are imperatively needed to expand the DR accommodation capacity of power distribution systems. Since the increase in DR threatens the efficiency and stability of power grid operation, the need for VPP has increased, which is operated as one power plant by connecting and controlling various DR based on information and communication technology (ICT) and automatic control technology.
A VPP is a virtual system that does not occupy physical space or exists in a specific place but is integrated and managed as a single power plant through cloud-based AI software [
1]. ICT and automatic control technology are used to connect and control various DR and operate them like power plants, showing the same effect as physical power plants supplying electricity. DR are integrated on a cloud-based platform, connected to the power grid operating system, and controlled remotely using sensors. Through the VPP, the optimal amount of power can be supplied from DR according to information to minimize wasted power. Energy efficiency can be improved by supplying power without a shortage of supply and demand. If the use of VPP is expanded, replacing current large-scale fossil fuel power plants that emit carbon, renewable energy can be supplied constantly, contributing to reducing carbon generation. Furthermore, VPP is expected to contribute to stable grid operation environments by securing grid flexibility [
2,
3,
4].
1.2. Literature Review
The goal of heating, ventilation, and air conditioning (HVAC) is to maintain indoor temperature, humidity, and air conditioning in a state appropriate for the intended use of the indoor space. HVAC research trends, modeling, and control technologies applying various techniques were reviewed. McKoy reviews the historical advances in HVAC technology and the current state of HVAC systems in [
5] and provides key concepts on the usefulness of AI use in previous studies conducted in this field. Based on the latest research trends, Kim reviews the latest updates of building energy modeling technology and MPC in HVAC applications, and presents the importance of building energy modeling in implementing MPC-based control and operation design to reduce building energy consumption and costs [
6]. Ye Yao [
7] discussed extensive information on modeling techniques and optimization algorithms by applying MPC to building HVAC systems. A systematic literature review was conducted based on a database search to provide in-depth insight into key challenges related to modeling, control, and optimization of HVAC systems in [
8] and to improve energy performance by focusing on data-driven model functions.
As HVAC control technology develops, various methods such as machine learning and reinforcement learning are applied. The importance of precise operation of advanced HVAC systems was emphasized by studying existing research and technological advancements in the latest techniques of computer vision and neural networks for application to HVAC control systems in [
9]. In the model-based approach, a thermal resistance–capacitance (RC) model of HVAC is formulated to capture the thermodynamic behavior of the building, and a distributed solution algorithm is applied to determine day-ahead HVAC behavior. The data-driven approach presents a control method that can be used for subsequent online decision making through a neural network training process [
10]. Learning the optimal control strategy from the optimized operation dataset is a way to improve the operation efficiency of HVAC systems in [
11]. A scenario reduction method was proposed that dramatically reduces the number of optimization calculations by clustering similar operation scenarios. This significantly increases the speed of generating optimal control strategy datasets while ensuring that the scenario reduction method achieves energy savings. It provides a case study of how the thermal comfort of a building can be controlled and improved through integrated solutions, in [
12], that collect from the Internet of Things (IoT). The accuracy of machine learning routines for building optimization control and their ability to control various systems and learn optimized data were investigated using CNN, LSTM, RNN-GRU, and RNN-attention [
13]. Then, by comparing the difference between single output generation and multiple output generation to determine the best preempted input, the control solution can be improved through preprocessing and various configuration operations. An automated approach is presented to identify important parameters of HVAC systems in building energy use in [
14] and to identify HVAC operation characteristics and corresponding energy profiles. In [
15], It develops a data-driven approach that leverages the deep reinforcement learning technique, to intelligently learn the effective strategy for operating the building HVAC systems. To minimize the energy cost of HVAC systems, the energy cost minimization problem was reorganized into a Markov game in [
16]. The HVAC control algorithm to solve the Markov game was proposed based on multi-agent deep reinforcement learning.
1.3. Main Feature and Contributions
In this paper, we built a VPP, which included PV, WT, energy storage systems (ESS), load, HVAC, and EV, to secure grid flexibility according to the expansion of renewable energy. For its efficient operation, we integrated and configured the actual DR system and the virtual DR system, which was created by applying digital twin technology. HVAC, one of the components of the VPP, is a control technology for maintaining the indoor environment with comfortable air conditions, and HVAC modeling is essential for efficient energy management. Sufficiently understanding the characteristics of BIM while continuously responding to changes in the external environment is necessary to increase the understanding of HVAC. Since information can be obtained only by participating in the building design stage, it is difficult to perform the modeling of HVAC accurately; we propose data-based modeling as a solution to this problem. We modeled an actual HVAC system and 29 virtual HVAC systems, 30 systems in total, with slightly different characteristics, and comparatively analyzed the performance of the models through the case study. Currently, HVAC system modeling implements models mostly based on equations [
17,
18]. Although some studies have used machine learning (ML) methods to perform modeling for HVAC operation [
19,
20,
21,
22], very few studies have used virtual models of HVAC for the optimal operation of VPP. For HVAC research, we used an HVAC system used at the test site and constructed virtual models to implement ML-based modeling [
23].
For data-based modeling, we used past operation data obtained from the energy management system (EMS) of the VPP and weather data, which are external environment variables. The model was implemented by reducing errors through numerous iterative learnings based on the data. The similarity between the results measured through the case study and the results obtained through modeling was verified.
This study aimed to contribute to the stable operation of VPP and improve the convenience of model implementation without knowing the HVAC system’s characteristics. The results obtained by modeling using ML were compared with the operational results of the actual system, and similarity with the system was verified through model performance indicators. This was achieved by determining the physical characteristics of HVAC with only past operation data and then implementing the model that sufficiently reflects those characteristics.
2. Data-Driven Modeling of HVAC Systems
2.1. HVAC Systems
HVAC [
24] is a technology that controls the maintenance of temperature and humidity conditions and air purification according to the user’s needs. Since it can respond to demands by controlling the amount of power consumption while maintaining user comfort with the load that uses the heat capacity of the building, it is considered a major resource for improving the stability of power grid operation. To secure efficient operation and grid flexibility using DR, a VPP was built, and a VPP operation platform was developed. The DR included in the VPP were PV, WT, ESS, load, HVAC, and EV, but this paper focuses on HVAC systems. It does not consider other types of DR. By collecting and analyzing response characteristics data for each resource of VPP, we developed a virtual HVAC model using ML-based digital technology.
Digital twin technology refers to a technology that combines physical equipment (e.g., power generators, ESS, and PV) and life-cycle elements of equipment operations (e.g., design, operation, and preventive maintenance) with AI, IoT, and big data technologies to represent them in a digital space. The key to digital twin technology is that a virtual model and the real-world system are interconnected with communication technology to influence each other, and real-time monitoring and simulation functions can be implemented. Digital twins are attracting attention while being actively applied in various fields, led by the manufacturing sector. They have the advantage of not being bound by time and space.
We used 30 HVAC systems by configuring 1 actual HVAC system and 29 virtual HVAC systems. The actual system, HVAC29, was an HVAC system that was built and operated at the test site. As for the virtual HVAC systems, we built 29 ML-based models that can respond within about 9% error by designing virtual resources using the characteristics of the actual HVAC resource learned and deriving the relationship between temperature setting and power consumption based on the historical data learned.
Figure 1 shows the real EMS of HVAC systems and
Figure 2 shows the configuration for virtual HVAC systems using a digital twin.
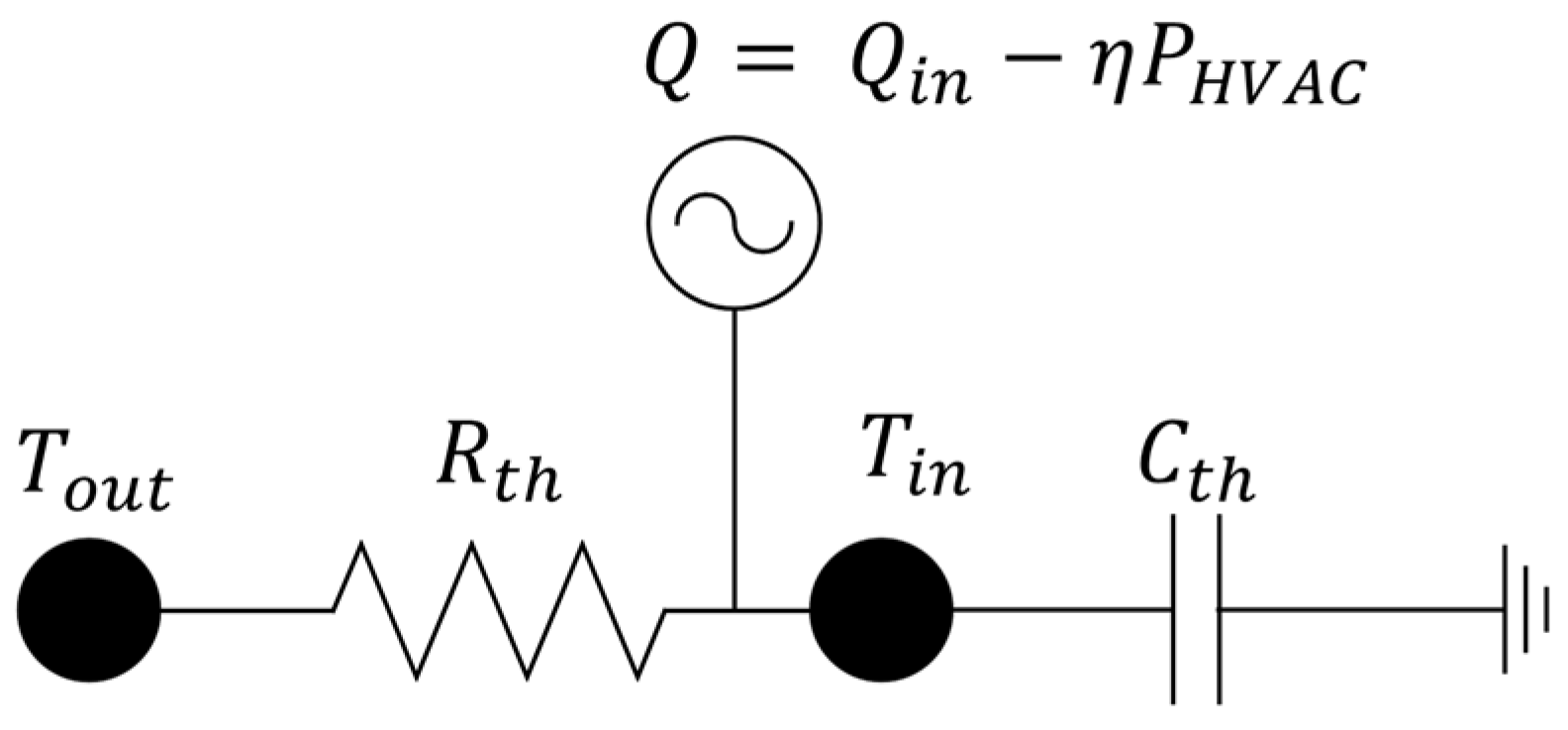
Figure 3 shows the first Equivalent Thermal Model of an HVAC system with a resistance–capacitance circuit. The model represents the change in the indoor temperature of a building according to the HVAC system [
7,
19] power, indoor temperature, and outdoor temperature as Equations (1) and (2).
Table 1 shows parameters of First equivalent thermal model.
Figure 4 shows a graph for the operation data of HVAC29, an actual HVAC system.
Figure 5 shows the process of virtual HVAC modeling.
2.2. HVAC Modeling Using ANN
Artificial neural network (ANN)-based HVAC modeling [
25,
26,
27] was performed according to the procedure shown in
Figure 5 to design the models. First, we collected HVAC operation data through the VPP’s EMS and gathered weather data that will be used as variables affecting the external environment. The collected data underwent preprocessing, including outlier removal and missing value processing, and the results were divided into a training dataset and a validation dataset. The HVAC models were designed and repeatedly trained using ANN to minimize the error of the learning result obtained through the models. The test dataset was applied to the trained models to obtain the results of the HVAC models.
To avoid overfitting the models and generate more generalized models, we performed cross-validation (CV) and chose the commonly used k-fold CV (KFCV) method as the CV method. CV refers to cross-selecting data for training and testing when training a model. The KFCV method divides data into k sets for cross-validation to use k − 1 sets for training and the remaining dataset for validation. By repeating the cross-validation process k times, this method cross-changes the datasets to use all datasets for training and validation. In this study, we set k to 5 and performed the validation by changing the validation set (1/5) and training sets (4/5) five times. This process was applied to 29 virtual models and 1 actual system to model 30 systems. For ANN, we used the nonlinear autoregressive network with exogenous inputs (NARX) [
28,
29], a recurrent dynamic network with exogenous inputs and feedback connections enclosing several layers;
Figure 6 shows its architecture.
Here, the next indoor temperature value, which is the output, regresses in the input signal, independent of the previous values. The NARX model was implemented by approximating the function using a two-layer feed-forward neural network. NARX is normally used for modeling nonlinear dynamic systems. As shown in the figure, it has the characteristic that the output value is fed back as an input value to the feed-forward neural network. The training is performed using the open feedback loop, in which the output is fed back as an input to the network through a delay. Since the input value to the feed-forward network is more accurate, and the resulting network has a pure feed-forward structure, the model can be trained more efficiently. The training is performed using the Levenberg–Marquardt Method (LMM). In the case of training, by combining the Gauss–Newton Method (GNM) and the gradient descent (GD) method, the LMM obtained the solution using GD when the parameters were far from the solution and using GNM when close to the solution. With the LMM, the probability of finding the solution is high even if the initial value is far from the solution. Furthermore, the GNM can be improved, thereby reducing the risk of divergence and finding the solution more stably, and its result can converge to the solution relatively quickly. NARX is suitable for nonlinear dynamic system modeling because it can be used as a predictor for predicting the next value of the input signal and can also be applied to nonlinear filtering, where the result of removing noise from the input signal is the target output value.
3. Case Study
This section describes the data collection and configuration for HVAC modeling and the model establishment. To design data-based HVAC models, we propose implementing it as a black box using ML without equation-based definitions. We used actual HVAC operation data collected from the implemented VPP’s EMS from 10 August 2022 to 4 September 2022. Data measured in 15 min intervals were collected. The information used included the date, day of the week, temperature setting, on/off work, power consumption, indoor temperature, outdoor temperature, indoor humidity, outdoor humidity, solar radiation, and on/off status. The size of the collected data is (2496, 12), of which the mean, variance, and standard deviation of indoor temperature to be used as dependent variables are shown in
Table 2.
The learning model was trained repeatedly in 15 min cycles, and for the learning period, the training data of each training cycle were accumulated and used. As the data size increased, the results estimated through the data-based model became quite similar to the actual measurement results, thus improving the model’s accuracy.
To comparatively analyze the performance of the model proposed in this paper, we created a model using the supervised learning method. The linear regression (LR) method, commonly used in modeling, and SVM [
30,
31,
32,
33], one of the ML techniques, were used. The results of the HVAC model created with each method were compared and analyzed. The kernel functions of the SVM-based HVAC model used Gaussian, and Bayesian optimization was utilized to implement the model. The ANN-based HVAC model was set to input layer sizes 12, hidden layer sizes 10, input delay and feedback delay (1:2), Lambda 0, and an iteration limit of 1000.
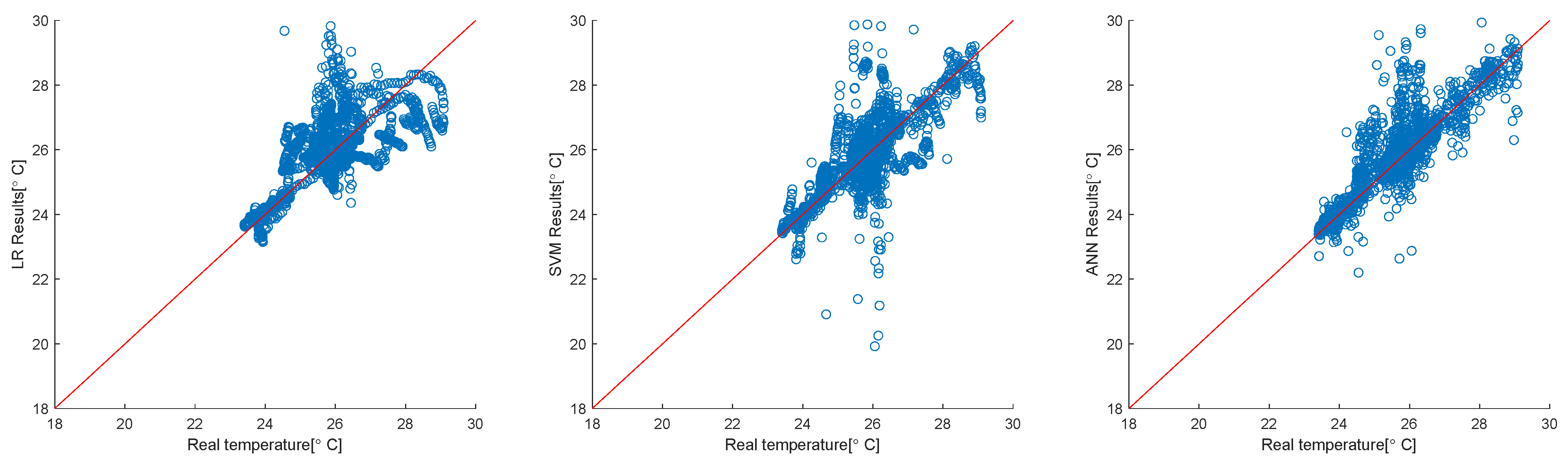
Figure 7,
Figure 8 and
Figure 9 show the accuracy of modeling, and the results obtained through data-based modeling and the HVAC results obtained from the VPP EMS can be compared at a glance.
Figure 9 compares the results of HVAC 29, the actual system at the test site, and the results obtained through data-based modeling. The results obtained using ANN show that the model’s performance is superior.
In
Figure 7,
Figure 8 and
Figure 9, the results of the HVAC models and the results obtained through the case study are analyzed. The horizontal axis represents the temperature of HVAC obtained through the VPP EMS, and the vertical axis represents the temperature obtained through data-based modeling. Although the graph is linear, outliers showing large errors compared to the actual data occurred the most in LR.
Table 3 shows the R-Squared of the HVAC model for Data 1, Data 17, and Data 29. ANN had the least errors.
4. Performance Evaluation of Data-Based HVAC Models
We used the mean squared error (MSE), root mean squared error (RMSE), mean ab-solute error (MAE), and mean absolute percent error (MAPE) as performance evaluation metrics of the HVAC models implemented using LR, SVM, and ANN, and quantitatively evaluated the fitness of each model [
34,
35]. In the case of MAE, the same weight is assigned to all errors, assuming that the errors are relatively unaffected by outliers. Then, the mean of the absolute values of the errors is calculated. If there is a small number of outliers in the data, it is appropriate to use MAE when establishing a model with little effect of the outliers. The equation for MAE is as follows.
For the MAPE, the difference between the actual measurement value and the predicted value in MAE is divided by the predicted value. Then, the sum of the absolute value of the result is converted into a percentage. MAPE has a limited maximum size, and since MAE is vulnerable to outliers, MAPE can be seen as an improvement over MAE. It is easy to compare the error with other models, but if the actual value is less than 1, there is the disadvantage that it can converge to an infinite value.
MSE is sensitive to outliers because the difference between the predicted value and the actual measured value is squared. The difference is reflected significantly when the predicted value is very different from the actual measured value. Furthermore, since the error value is squared, the error is reflected as smaller than the original when it is between 0 and 1, and it is reflected as greater when the error is greater than 1.
Since RMSE is the root of MSE, the distortion of the value caused by squaring the error is reduced, supplementing the drawback of MSE. Furthermore, RMSE is less sensitive to outliers than MSE, thus having the advantage of being more robust. The equations for MSE and RMSE are shown in Equations (5) and (6), respectively.
As shown in
Table 4,
Table 5 and
Table 6, when the performance of each model was evaluated, ANN performed the best, followed by SVM and LR. However, while the SVM model performed more similarly to the ANN model than the LR model when the performance was evaluated based on MAE and MAPE, it performed more similarly to the LR model when evaluated based on MSE and RMSE. This means that the error obtained through SVM modeling the difference between the value predicted through modeling and the actual measured value is often quite different. When there are some outliers, and one wants to create a model with small effects of the outliers, modeling can be performed by considering the performance metrics of MAE and MAPE. When creating a model considering the outliers, modeling can be performed appropriately by considering the MSE and RMSE results. Since the ANN model is superior in all metrics, it is concluded that the ANN model performs the best.
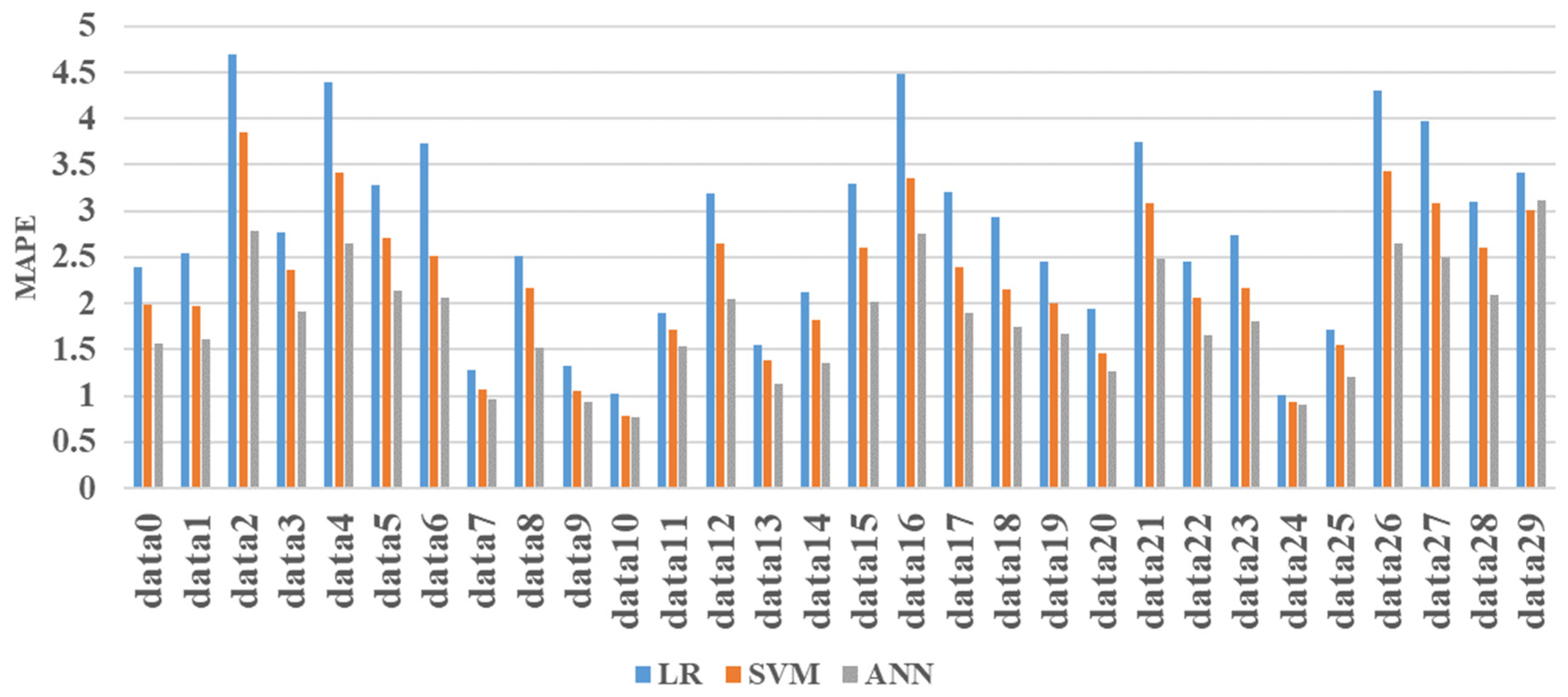
As shown in
Figure 10 and
Figure 11, the performance of the models was evaluated with MAE and MAPE for each HVAC system. From Data 0 to 29, LR was the largest for MAE and MAPE, and for Data 29, SVM had the smallest by a slight difference. However, except for Data 29, it was confirmed that ANN had the smallest error.
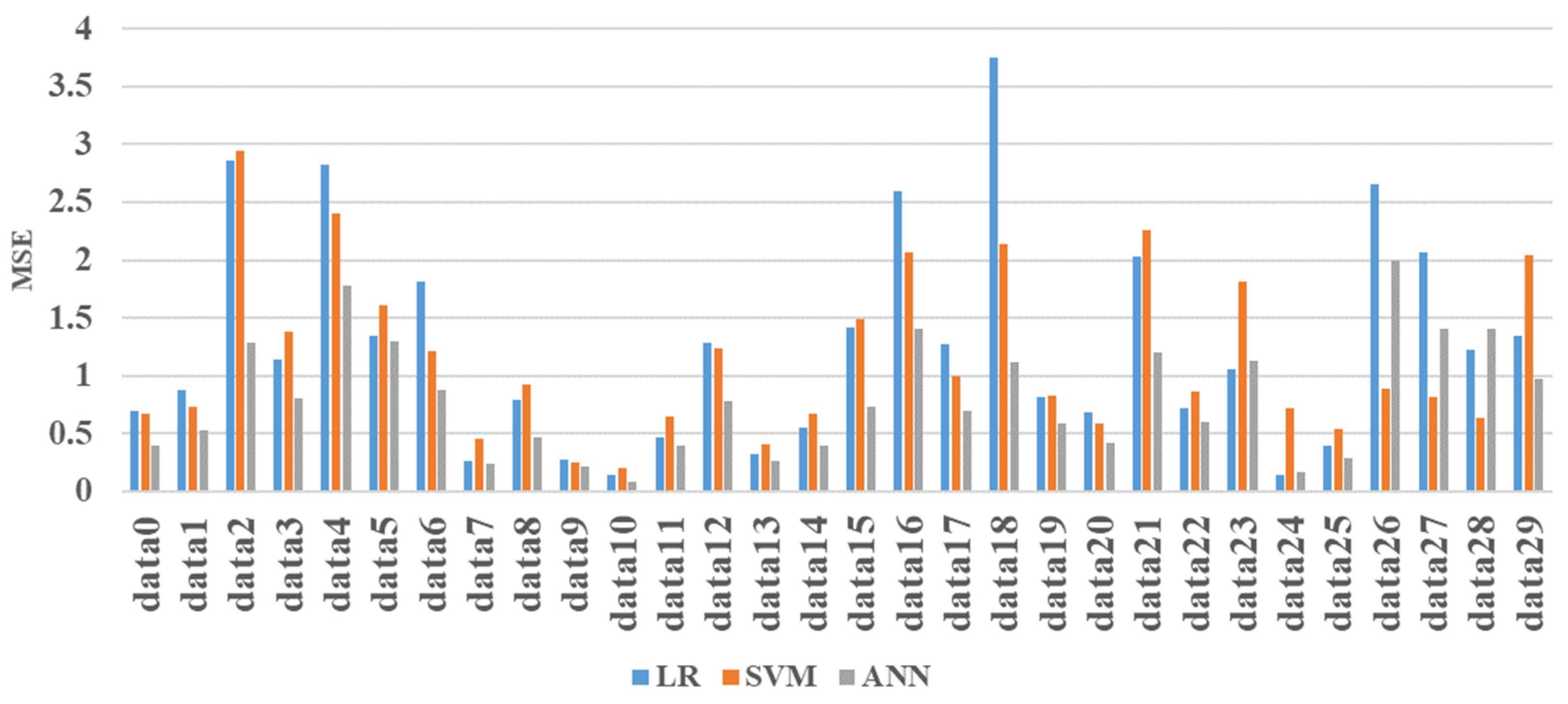
Figure 12 and
Figure 13 show the performance evaluation of the models for each system using MAE and RMSE. Some of the model RMSEs had the largest errors in LR, but most had similar errors in LR and SVM, and overall, ANN had the least error. Since the difference between the indoor temperature of the actual building and the indoor temperature obtained through the HVAC model is 0.41 on average, it is expected that the proposed model can be used in actual HVAC operation.
5. Conclusions
In this study, a data-based modeling method was proposed. We proposed data-based modeling using past operation data instead of conventional equation-based modeling. Then, we implemented a model using ANN and comparatively analyzed the prediction results of the model with the measurement results of the actual system, showing that they were similar. The model’s performance was measured using the metrics of MAE, MAPE, MSE, and RMSE to evaluate the model’s fitness quantitatively. The ANN-based HVAC model performed the best, and the LR-based model performed the worst. In short, a model similar to the actual HVAC system can be created based on past operation data through data-based modeling, even if the HVAC system’s physical characteristics and BIM are not known in detail. Therefore, our proposed data-based modeling method provides convenience and solves the difficulty of establishing an HVAC model. We expect the VPP’s operation efficiency to be improved when applied to virtual HVAC through digital twin technology.
After extracting, collecting, and preprocessing the HVAC system’s operation data and performing modeling, the model can be applied to optimal DR command allocation technology for ultimate grid flexibility and the VPP’s efficient operation, thereby maximizing the benefits of resources. In the future, we plan to use it for predictive maintenance algorithms of HVAC.
When ML is used to perform data-based modeling, the accumulation of past data for a sufficient period is required, unlike conventional equation-based HVAC modeling. If there is not enough data to be used for learning, the accuracy of modeling is poor, so there is a disadvantage that several types of sufficient periods of operational data are essential. We expect to build a convenient, accurate, and efficient model through a strategic accumulation of more HVAC operation data. In the future, we will further improve the model’s performance by changing the model’s independent variables and implementing other re-sources in the VPP, such as PV, and EV, through data-based modeling.
Author Contributions
H.-A.P. performed the research and wrote the paper; G.B. and J.K. led the project and advised on the whole process of manuscript preparation; H.-A.P. and W.S. analyzed the data; S.K. provided guidance for the research and revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP), granted financial resource from the Ministry of Trade, Industry & Energy, Republic of Korea (No. 23A02059).
Data Availability Statement
The data are not publicly available due to privacy.
Acknowledgments
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP), granted financial resource from the Ministry of Trade, Industry & Energy, Republic of Korea. (No. 23A02059).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bhuiyan, E.A.; Hossain, M.Z.; Muyeen, S.M.; Fahim, S.R.; Sarker, S.K.; Das, S.K. Towards next generation virtual power plant: Technology review and frameworks. Renew. Sustain. Energy Rev. 2021, 150, 111358. [Google Scholar] [CrossRef]
- Yu, S.; Fang, F.; Liu, Y.; Liu, J. Uncertainties of virtual power plant: Problems and countermeasures. Appl. Energy 2019, 239, 454–470. [Google Scholar] [CrossRef]
- Baringo, A.; Baringo, L.; Arroyo, J.M. Day-ahead self-scheduling of a virtual power plant in energy and reserve electricity markets under uncertainty. IEEE Trans. Power Syst. 2018, 34, 1881–1894. [Google Scholar] [CrossRef]
- Gong, H.; Jones, E.S.; Alden, R.E.; Frye, A.G.; Colliver, D.; Ionel, D.M. Virtual power plant control for large residential communities using hvac systems for energy storage. IEEE Trans. Ind. Appl. 2021, 58, 622–633. [Google Scholar] [CrossRef]
- Mckoy, D.R.; Tesiero, R.C.; Acquaah, Y.T.; Gokaraju, B. Review of HVAC Systems History and Future Applications. Energies 2023, 16, 6109. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J.; Do, S.; Mago, P.J.; Lee, K.H.; Cho, H. Energy modeling and model predictive control for HVAC in buildings: A review of current research trends. Energies 2022, 15, 7231. [Google Scholar] [CrossRef]
- Yao, Y.; Shekhar, D.K. State of the art review on model predictive control (MPC) in Heating Ventilation and Air-conditioning (HVAC) field. Build. Environ. 2021, 200, 107952. [Google Scholar] [CrossRef]
- Ala’raj, M.; Radi, M.; Abbod, M.F.; Majdalawieh, M.; Parodi, M. Data-driven based HVAC optimisation approaches: A Systematic Literature Review. J. Build. Eng. 2022, 46, 103678. [Google Scholar] [CrossRef]
- Borodinecs, A.; Zemitis, J.; Palcikovskis, A. HVAC System Control Solutions Based on Modern IT Technologies: A Review Article. Energies 2022, 15, 6726. [Google Scholar] [CrossRef]
- Kou, X.; Du, Y.; Li, F.; Pulgar-Painemal, H.; Zandi, H.; Dong, J.; Olama, M.M. Model-based and data-driven HVAC control strategies for residential demand response. IEEE Open Access J. Power Energy 2021, 8, 186–197. [Google Scholar] [CrossRef]
- Tian, Z.; Ye, C.; Zhu, J.; Niu, J.; Lu, Y. Accelerating Optimal Control Strategy Generation for HVAC Systems Using a Scenario Reduction Method: A Case Study. Energies 2023, 16, 2988. [Google Scholar] [CrossRef]
- Tanasiev, V.; Pluteanu, Ș.; Necula, H.; Pătrașcu, R. Enhancing monitoring and control of an HVAC system through IoT. Energies 2022, 15, 924. [Google Scholar] [CrossRef]
- Abida, A.; Richter, P. HVAC control in buildings using neural network. J. Build. Eng. 2023, 65, 105558. [Google Scholar] [CrossRef]
- Yu, X.; Ergan, S.; Dedemen, G. A data-driven approach to extract operational signatures of HVAC systems and analyze impact on electricity consumption. Appl. Energy 2019, 253, 113497. [Google Scholar] [CrossRef]
- Wei, T.; Wang, Y.; Zhu, Q. Deep reinforcement learning for building HVAC control. In Proceedings of the 54th Annual Design Automation Conference, Austin, TX, USA, 18–22 June 2017; pp. 1–6. [Google Scholar]
- Yu, L.; Sun, Y.; Xu, Z.; Shen, C.; Yue, D.; Jiang, T.; Guan, X. A Review of Reinforcement Learning Applications to Control of Heating, Ventilation and Air Conditioning Systems. IEEE Trans. Smart Grid 2020, 12, 407–419. [Google Scholar] [CrossRef]
- Zhang, W.; Lian, J.; Chang, C.Y.; Kalsi, K. Aggregated modeling and control of air conditioning loads for demand response. IEEE Trans. Power Syst. 2013, 28, 4655–4664. [Google Scholar] [CrossRef]
- Jung, W.; Jazizadeh, F. A Comparative assessment of HVAC control strategies using personal thermal comfort and sensitivity models. Build. Environ. 2019, 158, 104–119. [Google Scholar] [CrossRef]
- Jang, Y.-E.; Kim, Y.-J.; Catalão, J.P. Optimal HVAC system operation using online learning of interconnected neural networks. IEEE Trans. Smart Grid 2021, 12, 3030–3042. [Google Scholar] [CrossRef]
- Yoon, A.-Y. A Study on Price-based Demand Response of an HVAC System in a Commercial Building using Online Supervised Learning. Trans. Korean Inst. Electr. Eng. 2021, 70, 1812–1819. [Google Scholar] [CrossRef]
- Satrio, P.; Mahlia, T.M.I.; Giannetti, N.; Saito, K. Optimization of HVAC system energy consumption in a building using artificial neural network and multi-objective genetic algorithm. Sustain. Energy Technol. Assess. 2019, 35, 48–57. [Google Scholar]
- Yang, Y.; Hu, G.; Spanos, C.J. Stochastic optimal control of HVAC system for energy-efficient buildings. IEEE Trans. Control Syst. Technol. 2021, 30, 376–383. [Google Scholar] [CrossRef]
- Park, H.-A.; Jo, H.-C.; Kim, J.Y. A Study on the Optimal Parameters Estimation of Data-driven HVAC System. Trans. Korean Inst. Electr. Eng. 2022, 346–347. [Google Scholar]
- Liu, B.; Akcakaya, M.; McDermott, T.E. Automated control of transactive hvacs in energy distribution systems. IEEE Trans. Smart Grid 2020, 12, 2462–2471. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Sharshir, S.W.; Abd Elaziz, M.; Kabeel, A.E.; Guilan, W.; Haiou, Z. Modeling of solar energy systems using artificial neural network: A comprehensive review. Sol. Energy 2019, 180, 622–639. [Google Scholar] [CrossRef]
- Golbayani, P.; Florescu, I.; Chatterjee, R. A comparative study of forecasting corporate credit ratings using neural networks, support vector machines, and decision trees. N. Am. J. Econ. Financ. 2020, 54, 101251. [Google Scholar] [CrossRef]
- Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Lin, T.; Horne, B.G.; Tino, P.; Giles, C.L. Learning long-term dependencies in NARX recurrent neural networks. IEEE Trans. Neural Netw. 1996, 7, 1329–1338. [Google Scholar]
- Diaconescu, E. The use of NARX neural networks to predict chaotic time series. WSEAS Trans. Comput. Res. 2008, 3, 182–191. [Google Scholar]
- Dai, Y.; Zhao, P. A hybrid load forecasting model based on support vector machine with intelligent methods for feature selection and parameter optimization. Appl. Energy 2020, 279, 115332. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Sikinioti-Lock, A.; Shah, N. Machine-learning methods for integrated renewable power generation: A comparative study of artificial neural networks, support vector regression, and Gaussian Process Regression. Renew. Sustain. Energy Rev. 2019, 108, 513–538. [Google Scholar] [CrossRef]
- Zendehboudi, A.; Baseer, M.A.; Saidur, R. Application of support vector machine models for forecasting solar and wind energy resources: A review. J. Clean. Prod. 2018, 199, 272–285. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
Figure 1.
Energy Management System(EMS) of HVAC systems.
Figure 1.
Energy Management System(EMS) of HVAC systems.
Figure 2.
Virtual HVAC systems using digital twin.
Figure 2.
Virtual HVAC systems using digital twin.
Figure 3.
1st Equivalent Thermal Model for HVAC Systems.
Figure 3.
1st Equivalent Thermal Model for HVAC Systems.
Figure 4.
Correlation between power and temperature of HVAC29.
Figure 4.
Correlation between power and temperature of HVAC29.
Figure 5.
Modeling Process of HVAC systems.
Figure 5.
Modeling Process of HVAC systems.
Figure 6.
Architecture of NARX.
Figure 6.
Architecture of NARX.
Figure 7.
Comparison of results for HVAC model for Data 1.
Figure 7.
Comparison of results for HVAC model for Data 1.
Figure 8.
Comparison of results for HVAC model for Data 17.
Figure 8.
Comparison of results for HVAC model for Data 17.
Figure 9.
Comparison of results for HVAC model for Data 29.
Figure 9.
Comparison of results for HVAC model for Data 29.
Figure 10.
Performance (MAE) of HVAC modeling.
Figure 10.
Performance (MAE) of HVAC modeling.
Figure 11.
Performance (MAPE) of HVAC modeling.
Figure 11.
Performance (MAPE) of HVAC modeling.
Figure 12.
Performance (MSE) of HVAC modeling.
Figure 12.
Performance (MSE) of HVAC modeling.
Figure 13.
Performance (RMSE) of HVAC modeling.
Figure 13.
Performance (RMSE) of HVAC modeling.
Table 1.
First Equivalent Thermal Model Parameters.
Table 1.
First Equivalent Thermal Model Parameters.
| Parameter | Unit | Explanation |
|---|
| °C | Indoor Temperature |
| °C | Outdoor Temperature |
| kW | Quantity of Heat Transfer from Indoor Loads |
| | Coefficient of Performance (COP) |
| kW | HVAC Power |
| °C/kW | Building Heat Resistance |
| kW/°C | Building Heat Capacity |
| 15 min | Unit Time Step |
Table 2.
Mean, Variance, and Standard deviation of Data.
Table 2.
Mean, Variance, and Standard deviation of Data.
| Data | Mean | Var | Std | Data | Mean | Var | Std |
|---|
| Data 0 | 24.2078 | 0.5393 | 0.7344 | Data 15 | 26.1434 | 1.0889 | 1.0435 |
| Data 1 | 26.1232 | 0.905 | 0.9513 | Data 16 | 25.4575 | 2.8702 | 1.6942 |
| Data 2 | 26.2141 | 2.7305 | 1.6524 | Data 17 | 25.4702 | 1.073 | 1.0359 |
| Data 3 | 26.8644 | 0.9038 | 0.9507 | Data 18 | 26.8512 | 0.7386 | 0.8594 |
| Data 4 | 26.3598 | 2.3491 | 1.5327 | Data 19 | 26.9247 | 0.7391 | 0.8597 |
| Data 5 | 24.5551 | 1.3647 | 1.1682 | Data 20 | 27.7886 | 0.3461 | 0.5883 |
| Data 6 | 27.3584 | 2.1787 | 1.476 | Data 21 | 27.4411 | 2.0333 | 1.4259 |
| Data 7 | 28.0311 | 0.2762 | 0.5256 | Data 22 | 24.1919 | 0.54 | 0.7349 |
| Data 8 | 24.3353 | 0.6838 | 0.8269 | Data 23 | 26.8915 | 1.0564 | 1.0278 |
| Data 9 | 27.9208 | 0.1941 | 0.4405 | Data 24 | 26.8739 | 0.1592 | 0.399 |
| Data 10 | 25.8623 | 0.1679 | 0.4098 | Data 25 | 24.2478 | 0.3024 | 0.5499 |
| Data 11 | 25.0469 | 0.478 | 0.6914 | Data 26 | 26.2327 | 2.5465 | 1.5958 |
| Data 12 | 24.5574 | 1.2897 | 1.1356 | Data 27 | 26.5061 | 2.2516 | 1.5005 |
| Data 13 | 25.9853 | 0.2893 | 0.5378 | Data 28 | 24.4787 | 1.2856 | 1.1338 |
| Data 14 | 24.2583 | 0.4008 | 0.6331 | Data 29 | 23.4063 | 3.0321 | 1.7413 |
Table 3.
R-Squared of HVAC Model for Data 1, Data 17, and Data 29.
Table 3.
R-Squared of HVAC Model for Data 1, Data 17, and Data 29.
| Method | Data 1 | Data 17 | Data 29 |
|---|
| LR | 0.486 | 0.434 | 0.701 |
| SVM | 0.580 | 0.368 | 0.802 |
| ANN | 0.692 | 0.536 | 0.766 |
Table 4.
Performance Evaluation of HVAC Modeling for Data 1.
Table 4.
Performance Evaluation of HVAC Modeling for Data 1.
| Method | MAE | MAPE | MSE | RMSE |
|---|
| LR | 0.664 | 2.553 | 0.8572 | 0.934 |
| SVM | 0.512 | 1.975 | 0.729 | 0.854 |
| ANN | 0.414 | 1.610 | 0.531 | 0.729 |
Table 5.
Performance Evaluation of HVAC Modeling for Data 17.
Table 5.
Performance Evaluation of HVAC Modeling for Data 17.
| Method | MAE | MAPE | MSE | RMSE |
|---|
| LR | 0.815 | 3.211 | 1.268 | 1.126 |
| SVM | 0.607 | 0.699 | 0.986 | 0.993 |
| ANN | 0.478 | 2.396 | 0.687 | 0.829 |
Table 6.
Performance Evaluation of HVAC Modeling for Data 29.
Table 6.
Performance Evaluation of HVAC Modeling for Data 29.
| Method | MAE | MAPE | MSE | RMSE |
|---|
| LR | 0.756 | 3.416 | 1.341 | 1.158 |
| SVM | 0.654 | 3.010 | 2.043 | 1.429 |
| ANN | 0.677 | 3.107 | 1.041 | 1.020 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).