Improving Directional Overcurrent Relay Coordination in Distribution Networks for Optimal Operation Using Hybrid Genetic Algorithm with Sequential Quadratic Programming

Abstract

In recent years, with the growing popularity of smart microgrids in distribution networks, the effective coordination of directional overcurrent relays (DOCRs) has presented a significant challenge for power system operators due to the intricate and nonlinear nature of their optimization model. Hence, this study proposes a hybrid GA-SQP algorithm to enhance the coordination of directional overcurrent relays (DOCRs) in radial and non-radial interconnected distributed power networks. The proposed approach combines the advantages of both the genetic algorithm (GA) and sequential quadratic programming (SQP) methods to optimize the objective function of relay coordination in the best manner. Thus, the proposed hybrid techniques improved the convergence of the problem and increased the likelihood of obtaining a globally optimal solution. Finally, to validate the effectiveness of the proposed algorithm, it was tested through three case studies involving the IEEE 3-Bus, 8-Bus, and modified 30-Bus distribution networks. In addition, the results were compared to those obtained using previous methods. The results obtained from the comparison of the proposed method and recent advanced research indicate that the proposed optimization approach is preeminent in terms of accuracy and total operating time as well as the continuity of the minimum margin time requirements between the primary/backup relay pairs.

1. Introduction

1.1. Importance

Currently, electric power systems require robust and reliable protection measures to ensure safe and stable operation owing to their complex network structures. An integral part of a protection system is the implementation of protective relays that detect and isolate faults within the system in order to prevent equipment damage, power outages, and potentially catastrophic incidents. Among various types of protective relays, directional overcurrent relays (DOCRs) are commonly used in power systems. Coordinating DOCRs is a critical step in designing protection systems because it guarantees appropriate and prompt functioning of protective relays. Numerous researchers have proposed various computational approaches to achieve the optimal coordination of protective relays. However, the integration of non-conventional distributed generation (DG) into the distribution system has introduced both advantages and challenges for power system engineers as it plays a vital role in delivering electricity from both conventional and non-conventional sources such as wind, geothermal, biomass, and solar energy, most of which are renewable [1]. Incorporating non-conventional DG into a distribution system has transformed its topology from a radial and unidirectional structure to a loop system, posing a significant challenge to power system distribution networks. This alteration can result in improper coordination and configuration of the protective relays, potentially affecting the overall efficiency and effectiveness of the power system [2]. Therefore, it is crucial to deploy an innovative optimization method for relay coordination in distributed networks, including DGs, to address the limitations and challenges identified in previous studies. This plays a significant role in achieving high-precision power network protection. Therefore, a comprehensive study focusing on these aspects has been conducted.

1.2. Literature Review

In the past, relay coordination was typically accomplished using a trial-and-error approach, resulting in a slow convergence rate. This was mainly due to the substantial number of iterations required to identify suitable relay settings [3]. The optimization of coordinating OCRs in distribution networks with both single-loop and multi-loop structures has been regarded as a matter of optimization [4]. Various optimization techniques, including both conventional methods and heuristic approaches, have been utilized to calculate the optimal time dial and pick-up current settings for the DOCRs. These settings guarantee coordination among the relays and minimize the overall operating time [5,6,7,8,9,10]. As an example, the coordination of directional overcurrent relays was successfully achieved in [11] by employing a modified particle swarm optimization (MPSO) technique along with a local search algorithm. Linear programming was used to determine the optimal time multiplier setting (TMS) for these relays. Similarly, in [12], the optimal coordination of DOC relays was attained using a multi-verse optimization (MVO) algorithm, which demonstrated preeminent performance compared to the particle swarm optimization (PSO) algorithm. Recently, scholars have investigated hybrid approaches to tackle the problem of the optimal coordination of DOCRs [13,14,15,16,17]. The authors in [13] proposed a hybrid technique known as the simulated annealing-linear programming (SA-LP) to attain optimal coordination of DOCRs. Similarly, in another study [14], a hybrid algorithm called HHO-SQP was introduced by combining Harris hawks’ optimization with sequential quadratic programming. This hybrid approach aims to enhance the accuracy of the HHO method for optimizing the coordination of the directional overcurrent relays. In [15], optimization algorithms such as grey wolf optimization (GWO), grey wolf optimization (GWO-PSO), and interior point optimization were employed to optimize the operational time of a hybrid protection scheme. Additionally, in [16], a hybrid differential evolution–genetic algorithm (DE-GA) was utilized to optimize the settings of DOCRs by utilizing phasor measurement unit (PMU) data from a real-time wide-area measurement system. In [17], several algorithms including grey wolf optimization (GWO), enhanced grey wolf optimization (EGWO), hybrid whale and grey wolf optimization (HWGO), evolutionary optimization (EO), and flow direction algorithm (FDA) were employed to address the coordination problem. This problem was treated as a single-objective function. Another study [18] utilized particle swarm optimization to coordinate the directional overcurrent relays in distribution systems. The objective function aims to minimize the operating time of all main DOCRs while considering both near/far-end fault scenarios. Additionally, ref. [19] introduced an enhanced grey wolf optimizer (EGWO) to improve DOCR coordination. Other research efforts have focused on specific aspects of relay coordination. For instance, ref. [20] proposed a quaternary protection scheme for microgrids, incorporating dual-directional overcurrent relays (dual-DOCRs) and a protection control strategy. In [21], a genetic algorithm was employed to optimize the limits of the maximum plug-setting multiplier (PSM) for OCR coordination, considering the upper limit of PSM as a variable. Furthermore, ref. [22] introduced a novel optimization strategy called hybrid fractional computing with a gravitational search strategy (FPSOGSA) to enhance DOCR coordination in power systems. This strategy combines the concept of fractional calculus with a normative particle swarm, and gravitational search algorithm, to improve the performance of the optimizer. Although heuristic algorithms have been extensively utilized, they may struggle to accurately represent the optimal and global minima, resulting in difficult convergence towards satisfactory solutions [23]. Different types of intelligent optimization techniques have been proposed to solve optimization problems in different contexts, such as particle swarm optimization (PSO) [24], improved differential evolution (IDE) [25,26,27,28], the improved Kriging-based hierarchical collaborative approach (IK-HC) [29], the deep learning regression-stratified strategy (DLR-SS) [30], extreme gradient boosting (XGB) algorithm [31], the multivariate ensembles-based hierarchical linkage strategy (ME-HL) [32], and the slime mould algorithm (SMA) [33].

Table 1. Comparison of the features of the proposed and previous methods.

Features	[3,4]	[5,6,7,8,9,10]	[11,12]	[13,14,15,16,17]	[18,19,20]	[21,22,23]	Proposed Method
Interconnected non-radial power networks	✓	✗	✓	✗	✓	✓	✓
Consideration of the DG effect	✗	✓	✗	✓	✗	✗	✓
No getting stuck in local optimal points	✗	✗	✗	✓	✗	✓	✓
Optimal coordination using hybrid algorithm frame	✗	✗	✗	✓	✗	✓	✓
Mid-point faults facility	✗	✗	✗	✗	✗	✗	✓
Forming relay numbers automatically	✗	✗	✗	✗	✓	✗	✓

summarizes the shortcomings identified in previous schemes, aiming to offer a thorough comprehension of their limitations. The main features and advantages of the proposed approach are emphasized in this table, illustrating how it stands out from the existing methodologies. The benefits encompassed by these advantages involve enhancing the coordination of the DOCRS in both interconnected radial and non-radial power networks, which considers the impact of distributed generators (DGs), enabling smooth system operation and effective coordination of overcurrent relays (DOCRs) even when fault locations vary, without getting stuck in the local optimal location. Furthermore, the proposed methodology introduces an automated procedure within the protection manager (PM) to establish coordination pairs, thereby eliminating the requirement for manual intervention. This distinctive characteristic distinguishes the proposed approach from previous schemes and substantially enhances the overall efficiency of the protection scheme. By addressing these distinguished research gaps, the PM makes a valuable contribution to the existing body of literature.

1.3. Contributions

Hybrid algorithms that combine heuristic and traditional methods have shown the potential to address the limitations and shortcomings of previous research. These hybrid algorithms leverage the strengths of both approaches to provide enhanced performance and more reliable optimization results. This study aims to resolve the issue of the optimal coordination of directional overcurrent relays (DOCRs) in interconnected power networks, including distributed generators (DGs), and overcome the shortcomings of previous research. To achieve this, we propose a hybrid GA-SQP algorithm that utilizes both a genetic algorithm (GA) and sequential quadratic programming (SQP). The proposed methodology aims to improve the convergence and increase the probability of finding a globally optimal solution. Finally, a comprehensive assessment was conducted on three standard case studies involving IEEE 3-Bus, 8-Bus, and 30-Bus systems to validate the effectiveness of the proposed algorithm. These case studies serve as practical examples to demonstrate the preeminent performance of the proposed optimization approach in terms of the total operating time and continuity of the minimum margin time requirements between the primary and backup relay pairs compared to previous methods. Furthermore, the superiority of the proposed optimization approach in achieving the optimal coordination of protective relays can be established by comparing the simulation results of the proposed method with those of state-of-the-art methods.

In summary, the present paper makes the following contributions:

• It introduces a robust hybrid optimization algorithm that efficiently tackles the coordination problem of DOCRs by integrating the global exploration capabilities of genetic algorithms with the local refinement abilities of sequential quadratic programming.
• It implements the suggested GA-SQP method, which can result in a significant reduction in the operation times of primary/backup (P/B) relays for mid-point faults in power networks with DGs. This decrease guarantees that such networks are protected in a timely and effective manner.

1.4. Organization

The rest of this paper is structured in the following manner. Section 2 provides a comprehensive explanation of the methodology and the intricacies of the proposed hybrid GA-SQP algorithm. In Section 3, case studies are discussed and the results are presented. Finally, in Section 4 we conclude the study and outline potential directions for future research.

2. Methodology

In this section, practical and efficient mathematical tools and formulas are introduced to address the limitations and deficiencies of previous methods. In the initial stage, the objective function is defined to achieve the optimal coordination of DOCRs in both radial and non-radial power networks, considering the inclusion of DGs and the automatic determination of forming relay numbers. To this end, a novel formulation of the objective function is devised to minimize the coordination time interval (CTI). Subsequently, a hybrid optimization algorithm that combines a genetic algorithm (GA) and sequential quadratic programming (SQP) is proposed. This algorithm aims to enhance the accuracy and speed of convergence while eliminating local optimal points.

2.1. Problem Formulation

The formulation of coordinating distribution operation and control relays (DOCRs) in a network is presented as an optimization challenge. The goal is to reduce the overall operating time of all the relays installed during a specific fault occurrence, as shown in (1) [16]. Mathematically, this problem can be represented as follows:

$$\mathrm{OF}=min\sum _{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{t}}_{\mathrm{op},\mathrm{i}}$$

(1)

Typically, restrictions on the operating times of the relays are expressed as the upper and lower limits of inequality constraints. The lower limit signifies the minimum duration required for the relay to activate, while the upper limit signifies the maximum acceptable duration for the relay to activate. These limits are determined according to the specific demands of the system and protection strategy employed. Failure to adhere to these inequality constraints can result in the malfunctioning of the protection system. For instance, if a relay requires an excessive amount of time to activate, it may fail to offer adequate protection to the system. Conversely, if the system operates too swiftly, unnecessary tripping may be triggered. Hence, it is crucial to consider these inequality constraints when the designing and evaluating protection systems. The problem is influenced by various factors, including the coordination time interval between relay pairs, potential errors in relay operations, safety margins, and the operating time of circuit breakers. Equation (2) [14] introduces the variables ${\mathrm{t}}_{\mathrm{op},\mathrm{i}}$ and ${\mathrm{t}}_{\mathrm{ob},\mathrm{j}}$, which represent the activation times of the primary and secondary relays, respectively. These two components play a crucial role in relay operations. The coordination time interval is calculated by considering the operating times of the backup and main relays. In this scenario, the CTI value was designated as 0.2 s.

$${\mathrm{t}}_{\mathrm{ob},\mathrm{j}}-{\mathrm{t}}_{\mathrm{op},\mathrm{i}}\ge \mathrm{CTI}$$

(2)

By utilizing (3) [4,5,6], it is possible to ascertain the maximum and minimum values for a relay’s time-multiplier setting, represented as ${\mathrm{TMS}}_{\mathrm{i},\min }$ and ${\mathrm{TMS}}_{\mathrm{i},\max }$, respectively. The specified values for these variables are 0.01 and 1.1 s, respectively.

$${\mathrm{TMS}}_{\mathrm{i},\min }\le {\mathrm{TMS}}_{\mathrm{i}}\le {\mathrm{TMS}}_{\mathrm{i},\max }$$

(3)

Figure 1 shows a visual representation of the permissible range of the pickup setting PS for a relay. To ensure proper functioning, the lower limit ${\mathrm{PS}}_{\mathrm{i},\min }$ must be set to match or exceed the maximum overload current ${\mathrm{I}}_{\mathrm{OL}}^{\max }$. This precaution is taken to guarantee that the relay will activate and interrupt the circuit in the event of overload. Conversely, the upper limit ${\mathrm{PS}}_{\mathrm{i},\max }$ should be configured as either equal to or lower than the minimum fault current to ensure that the relay will trip and disconnect the system in the event of fault occurrence. The expression ${\mathrm{I}}_{\mathrm{OL}}^{\max }$ refers to the highest possible current associated with an overload condition and can be calculated using (4) [34].

$${\mathrm{I}}_{\mathrm{OL}}^{\max }=\mathrm{OLF}\times {\mathrm{I}}_{\mathrm{L}}^{\max }$$

(4)

where ${\mathrm{I}}_{\mathrm{L}}^{\max }$ denotes the maximum permissible current rating. The overload factor OLF, typically chosen within the range of 1.25 to 1.5 [34], was employed. The minimum fault current ${\mathrm{I}}_{\mathrm{f}}^{\min }$ is utilized to ascertain the upper limit of the pickup setting ${\mathrm{PS}}_{\mathrm{i},\max }$ according to (5) [34].

$${\mathrm{PS}}_{\mathrm{i},\max }=\frac{2}{3}{\mathrm{I}}_{\mathrm{f}}^{\min }$$

(5)

In a general sense, the mathematical representation of the constraint for the ith pickup setting (PS) can be expressed as depicted in (6) [5].

$${\mathrm{PS}}_{\mathrm{i},\min }\le {\mathrm{PS}}_{\mathrm{i}}\le {\mathrm{PS}}_{\mathrm{i},\max }$$

(6)

Equation (7) [5,6] defines the upper and lower boundaries of the relay operation time, denoted as ${\mathrm{t}}_{\mathrm{i},\max }$ and ${\mathrm{t}}_{\mathrm{i},\min }$, respectively:

$${\mathrm{t}}_{\mathrm{i},\min }\le {\mathrm{t}}_{\mathrm{op},\mathrm{i}}\le {\mathrm{t}}_{\mathrm{i},\max }$$

(7)

The primary and backup relays simultaneously detect the fault occurrence. The distribution operation and control relay (DOCR) exhibits an inverse time-current behavior, which is influenced by the values of TMS and PS, as depicted through a collection of curves. The operating time of the relay was directly proportional to the fault current, resulting in longer operating times as the fault current decreased. The mathematical formulation of the inverse-time overcurrent characteristic can be derived by following the guidelines outlined in the IEC [35] and the IEEE [36] standards.

$${\mathrm{t}}_{\mathrm{op},\mathrm{i}}=\frac{\mathrm{A}\times {\mathrm{TMS}}_{\mathrm{i}}}{{\left(\frac{{\mathrm{I}}_{\mathrm{F},\mathrm{i}}}{{\mathrm{PS}}_{\mathrm{i}}}\right)}^{\mathrm{B}}-1}$$

(8)

Equation (8) introduces the variables A and B, which are characteristic constants specific to the relays. ${\mathrm{I}}_{\mathrm{F},\mathrm{i}}$ represents the fault current flowing through the operating coil of the relay ${\mathrm{R}}_{\mathrm{i}}$. ${\mathrm{TMS}}_{\mathrm{i}}$ and ${\mathrm{PS}}_{\mathrm{i}}$ are the two adjustable parameters of relay ${\mathrm{R}}_{\mathrm{i}}$ that are subject to optimization. For standard inverse definite minimum time (IDMT) relays, the values of A and B are typically set to 0.14 and 0.02, respectively. The DOCRs feature two control variables: TMS, which determines the operating time of the relay, and PS, which represents the current value at which the DOCR is activated. The calculation of the PS value is based on the maximum load current and fault current.

2.2. Enhancing Objective Function (OF) to Minimize Coordination Time Interval (CTI)

Ensuring effective coordination between primary and backup relays is vital for guaranteeing selectivity and reliability in safeguarding power systems. Although it is advantageous to minimize the coordination time interval to maintain proper selectivity, excessively delayed activation of the backup relays can compromise the efficiency of relay coordination. To address this issue, the study presents a new approach that involves modifying the expression of the objective function’s expression. The expression for the proposed (OF) approach is given in (9).

$$\underset{({\mathrm{PS}}_{\mathrm{i}},{\mathrm{TMS}}_{\mathrm{i}})}{min}\mathrm{OF}=\sum _{\mathrm{i}=1}^{\mathrm{N}}\sum _{\mathrm{k}}{\mathrm{T}}_{\mathrm{ik}}+{\alpha }_1\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{Penalty}}^2$$

(9)

The initial double summation as seen in (9) serves the purpose of calculating the total operating times of all DOCRs in response to a three-phase fault current scenario. Subsequently, the following summation of square the penalty calculates the aggregate penalties associated with each relay state. These penalties are introduced to address specific constraints within the objective function, ensuring that it is consistently met and aligned with the desired system behavior. The new penalty expressions introduced in Equations (10) and (11) are integral to maintaining the integrity of the objective function by enforcing the required constraints.

$$\mathrm{Penalty}={\alpha }_2\sum _{\mathrm{p}=1}^{{\mathrm{N}}_{\mathrm{p}}}\left(\left|\Delta {\mathrm{T}}_{\mathrm{Nbp}}<0\right|+\beta \left|\sum _{\mathrm{p}=1}^{{\mathrm{N}}_{\mathrm{p}}}{\mathrm{T}}_{\mathrm{Nbp}}<0.2\right|\right)$$

(10)

$$\Delta {\mathrm{T}}_{\mathrm{Nbp}}={\mathrm{T}}_{\mathrm{jk}}-{\mathrm{T}}_{\mathrm{ik}}-\mathrm{CTI}$$

(11)

When discussing relay coordination, the term $\Delta {\mathrm{T}}_{\mathrm{Nbp}}$ pertains to the disparity in the operating time between the primary and backup relays within the pth relay pair. The variable ${\mathrm{N}}_{\mathrm{p}}$ signifies the overall count of the primary/backup relay pairs, whereas p signifies each distinct primary/backup relay pair spanning from 1 to ${\mathrm{N}}_{\mathrm{p}}$. By adjusting the control weighting factors ${\alpha }_1$, ${\alpha }_2$, and $\beta$, it is possible to assign varying degrees of significance to the sum of operating times and penalty terms. This flexibility allows for controlling the balance between minimizing the total operating time and imposing penalties for violations of coordination constraints, as well as for operating times that fall below a specified threshold. Fine tuning these factors enables the management of trade-offs in the optimization process.

2.3. GA-SQP Hybrid Algorithm

2.3.1. GA Algorithm

The (GA) is a popular metaheuristic approach extensively employed by researchers to address intricate optimization problems. Similar to other metaheuristic techniques, the GA draws inspiration from the principles of natural selection and genetics. In the context of the genetic algorithm (GA) methodology, a collection of potential solutions, known as individuals or chromosomes, undergoes evolutionary processes using genetic operators such as selection, crossover, and mutation. These operators imitate the biological mechanisms of reproduction, recombination, and mutation [37]. The fitness function plays a crucial role in assessing the effectiveness of each potential solution and guiding the search process towards the optimal solution. When applying GA optimization to coordinate the distribution operation and control relays (DOCRs), it becomes possible to determine the optimal configurations of the relay parameters, including the pick-up current, time delay, and minimum total operating time.

2.3.2. SQP Algorithm

The sequential quadratic programming (SQP) method is a well-known technique used to solve nonlinear programming problems involving constraints. It is widely regarded as one of the most efficient methods for constrained optimization, delivering exceptional accuracy and a high success rate for producing solutions to a diverse range of test problems. Within the SQP framework, the constraints are explicitly integrated into the optimization procedure. During each iteration of the SQP algorithm, an estimation of the Hessian matrix represented by x was generated using the Broyden Fletcher (Goldfarb) Shannon quasi-Newton updating method [38]. Subsequently, the estimated Hessian matrix is employed to construct a quadratic programming (QP) subproblem. The QP subproblem was solved to determine the search direction for the line search procedure. The optimal step length along the search direction is determined through a line search, which minimizes the objective function while adhering to the imposed constraints. This iterative process continued until the convergence criterion was satisfied. The algorithm begins by evaluating the gradients of objective variables. Next, the gradient is projected onto the null space of the Jacobian matrix of constraints. The resulting vector was subsequently rescaled to ensure an appropriate step length, thereby effectively reducing the infeasibility of the process.

2.3.3. Hybrid Algorithm Based on GA and SQP

This paper proposes a hybrid GA-SQP algorithm that combines the strengths of both GA and SQP methods while mitigating their limitations. GA employs a probabilistic search approach across multiple points, which can potentially converge to suboptimal solutions. On the other hand, SQP is a single-point search method that may become stuck in local optima. By integrating SQP and the GA, the hybrid algorithm enhances convergence and increases the likelihood of discovering the global optimal solution. In cases in which a GA iteration yields an invalid result, the best fitness values are utilized in the SQP phase, which incorporates a probability-based local search. This further enhances the fitness of the solution. Figure 2 shows a flowchart summarizing the GA-SQP algorithm.

3. Case Studies (Result and Discussions)

To assess and demonstrate the efficacy of the proposed GA-SQP hybrid optimization algorithm, three distinct case studies were conducted. These case studies are referred to as the IEEE 3-bus, 8-bus, and 30-bus configurations, as shown below.

3.1. Case Study 1 (3-Bus System)

As shown in Figure 3, the initial case study revolved around a power system configuration comprising three generators, three transmission lines, and six protection relays. The detailed information and data for this specific test case can be found in [34]. The aim of the optimization problem in this particular model was to coordinate the configurations of all six protection relays, giving rise to a sum of 12 decision variables, ${\mathrm{TMS}}_1$ to ${\mathrm{TMS}}_6$, and ${\mathrm{PS}}_1$ to ${\mathrm{PS}}_6$.

Table 2. P/B relays and fault currents for case 1.

Primary Relay	Fault Current (A)	Backup Relay	Fault Current (A)
R1	1961.2	R6	172.7
R2	1515.4	R4	544.9
R3	1678.9	R1	611.8
R4	1816.5	R5	467.4
R5	1765.1	R2	144.6
R6	1499.8	R3	385.3

lists the short-circuit currents recorded by the primary and the backup relays.

Table 3. Operating times and coordination time interval (CTI) for case 1.

Relay Pairs		GA			GA-SQP
Primary	Backup	Tp (s)	Tb (s)	CTI (s)	Tp (s)	Tb (s)	CTI (s)
R1	R6	0.225	0.425	0.200	0.223	0.423	0.200
R2	R4	0.201	0.401	0.200	0.200	0.400	0.200
R3	R1	0.201	0.399	0.198	0.200	0.400	0.200
R4	R5	0.231	0.431	0.200	0.230	0.430	0.200
R5	R2	0.236	0.436	0.200	0.235	0.436	0.200
R6	R3	0.237	0.437	0.200	0.236	0.436	0.201

provides information on the operating times of the primary and backup relay pairs along with their respective CTI values.

Case Study 1 Discussion:

Table 4. Optimal relay settings for case 1.

Relay No.	GA		GA-SQP
	TMS (s)	PS (pu)	TMS (s)	PS (pu)
R1	0.090	0.156	0.088	0.161
R2	0.133	0.021	0.133	0.021
R3	0.081	0.128	0.081	0.127
R4	0.098	0.120	0.097	0.123
R5	0.104	0.106	0.103	0.106
R6	0.179	0.012	0.177	0.012
OF (s)	1.330		1.324

presents the optimal values of the TMS and PS settings for the relays, which were obtained using both the standalone GA and hybrid GA-SQP algorithm. The objective function value is determined as the cumulative operating time of each relay when a fault occurs within the primary protection zone. The findings indicate that the proposed approach successfully achieves a reduced operating time of 1.324 s, which is faster than the minimum operating time of 1.330 s achieved using the standalone GA method for this specific relay coordination problem in the given case study. Figure 4 illustrates the enhanced coordination time for all six relay pairs when the GA-SQP algorithm is utilized. Notably, the CTI for all relay pairs remains consistently at a minimum of 0.2 s.

Table 5. Comparing GA-SQP with other methods for case 1.

Ref.	Method	The Algorithm’s Parameters for 3-Bus Test System							Objective Function
		TMSmin	TMSmax	PSmin	PSmax	PS Mode	CTI	NFE
[39]	TLBO (MOF)	0.025	1.2	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.3	N/A	6.972
[39]	TLBO	0.025	1.2	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.3	N/A	5.335
[40]	MDE	0.05	1.1	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.3	38250	4.781
[41]	MINLP	0.1	1.1	1.5	2.5	discrete	0.3	85	1.727
[41]	SA	0.1	1.1	1.5	3	discrete	0.3	85	1.599
[42]	MSPO	0.1	1.1	1.5	5	discrete	0.2	200	1.926
[43]	BBO-LP	0.1	1.1	1.5	3	discrete	0.2	20	1.599
[44]	WOA	0.05	1.1	1.5	5	continuous	0.3	130	1.526
[44]	HWOA	0.05	1.1	1.5	5	continuous	0.3	50	1.503
Proposed GA-SQP		0.05	1.1	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.2	100	1.324

shows the distinguished advancements achieved by the proposed GA-SQP algorithm in coordinating directional overcurrent relays for the IEEE 3-bus system, surpassing the results obtained by other evolutionary algorithms documented in the literature. The results clearly indicate the preeminent performance of the GA-SQP algorithm in minimizing the operating time of (primary/backup) relay pairs for mid-point faults while simultaneously maintaining the required discrimination time between them. These findings strongly suggest that the proposed GA-SQP algorithm has the potential to provide high-quality and efficient solutions for coordinating directional overcurrent relays in meshed power networks. In addition, Table 5 includes the algorithm parameters, the number of function of evaluation (NFE), and the objective function (OF) values of our proposed method with those compared to the references. In Figure 5, we can see how the GA-SQP approach (on IEEE-3-Bus) outperforms techniques mentioned in the literature by achieving the total operating time.

3.2. Case Study 2 (8-Bus System)

The second case study revolves around an 8-bus, 9-line network, as shown in Figure 6. Notably, at bus 4 there exists a connection to another network denoted by a short-circuit capacity of 400 MVA. The optimization problem in this case study centers on coordinating the settings of all 14 overcurrent relays, resulting in 28 decision variables, ranging from ${\mathrm{TMS}}_1$ to ${\mathrm{TMS}}_{14}$ and ${\mathrm{PS}}_1$ to ${\mathrm{PS}}_{14}$. The parameters used in this case study can be found in [34].

Table 6. P/B relays and fault currents for case 2.

Primary Relay	Fault Current (A)	Backup Relay	Fault Current (A)
R1	3500.5	R6	638.4
R2	1710.0	R8	1704.2
R3	3521.6	R2	533.2
R3	3521.6	R6	1009.0
R4	1892.0	R10	1948.8
R5	2883.8	R2	11.2
R5	2883.8	R4	847.0
R6	2905.6	R7	3.8
R6	2905.6	R13	886.0
R7	1622.5	R1	1616.5
R8	3660.4	R5	697.6
R8	3660.4	R13	1014.0
R9	2104.5	R3	2015.9
R10	3294.0	R12	1015.9
R11	3242.1	R9	961.4
R12	2197.8	R14	2104.4
R13	1901.2	R11	1956.3
R14	3615.3	R5	1041.2
R14	3615.3	R7	550.5

lists the short-circuit currents measured by both the (primary/backup) relays, whereas

Table 7. Operating times and coordination time interval (CTI) for case 2.

Relay Pairs		GA			GA-SQP
Primary	Backup	Tp (s)	Tb (s)	CTI (s)	Tp (s)	Tb (s)	CTI (s)
R1	R4	0.322	0.523	0.200	0.287	0.487	0.200
R1	R6	0.322	0.401	0.200	0.287	1.184	0.896
R2	R8	0.204	0.404	0.200	0.200	0.400	0.200
R3	R2	0.466	0.666	0.200	0.323	0.627	0.304
R3	R6	0.466	0.666	0.200	0.323	0.523	0.200
R4	R10	0.340	0.540	0.200	0.310	0.513	0.203
R5	R2	0.349	-	-	0.256	-	-
R5	R4	0.349	0.572	0.223	0.256	0.537	0.281
R6	R7	0.316	-	-	0.226	-	-
R6	R13	0.316	0.613	0.297	0.226	0.562	0.336
R7	R1	0.277	0.477	0.200	0.207	0.407	0.200
R8	R5	0.348	1.013	0.665	0.299	0.894	0.595
R8	R13	0.348	0.548	0.200	0.299	0.499	0.200
R9	R3	0.396	0.596	0.200	0.246	0.446	0.200
R10	R12	0.425	0.625	0.200	0.370	0.570	0.200
R11	R9	0.446	0.646	0.200	0.362	0.563	0.201
R12	R14	0.386	0.586	0.200	0.250	0.450	0.200
R13	R11	0.365	0.565	0.200	0.326	0.528	0.202
R14	R5	0.462	0.662	0.200	0.327	0.527	0.200
R14	R7	0.462	0.662	0.200	0.327	0.598	0.271

lists the operating times of the B/P relay pairs and their corresponding CTI values. From Table 7, it is evident that specific primary relays (R5 and R6) do not have backup protection (R2 and R7, respectively), owing to the network topology.

Case Study 2 Discussion:

The optimization of relay coordination in an IEEE 8-bus distribution system was performed in this case study using the GA-SQP algorithm implemented in MATLAB. The goal was to minimize the time required for the operation while ensuring efficient coordination among the relays. A summary of the results obtained through the optimization process is presented in

Table 8. Optimal relay settings for case 2.

Relay No.	GA		GA-SQP
	TMS (s)	PS (pu)	TMS (s)	PS (pu)
R1	0.114	0.808	0.113	0.621
R2	0.050	0.821	0.050	0.796
R3	0.179	0.666	0.097	1.173
R4	0.099	0.665	0.087	0.719
R5	0.111	0.845	0.075	1.014
R6	0.094	0.991	0.062	1.151
R7	0.076	0.646	0.050	0.799
R8	0.304	0.030	0.137	0.426
R9	0.118	0.706	0.050	1.346
R10	0.156	0.699	0.103	1.260
R11	0.159	0.741	0.085	1.665
R12	0.115	0.741	0.050	1.434
R13	0.102	0.732	0.087	0.784
R14	0.176	0.695	0.096	1.262
OF (s)	5.101		3.989

. The findings indicated that the GA-SQP approach achieved a minimum operating time of 3.989 s, whereas the GA method resulted in 5.101 s, resulting in a 21.8% improvement. Figure 7 shows the improvement in the coordination time achieved by the GA-SQP algorithm for a set of 20 relay pairs. The graph clearly shows how the algorithm enhances coordination time, highlighting its effectiveness in achieving efficient relay coordination. Additionally, it is noteworthy that the coordination time interval (CTI) values for all relay pairs remained consistently at or above 0.2 s. This ensures maintenance of the necessary coordination time, ultimately leading to effective fault detection and isolation.

Table 9. Comparing GA-SQP with other methods for case 2.

Ref.	Method	The Algorithm’s Parameters for 8Bus Test System							Objective Function
		TMSmin	TMSmax	PSmin	PSmax	PS Mode	CTI	NFE
[45]	LM	0.05	1.1	0.5	2	discrete	N/A	N/A	11.065
[46]	GA	0.1	1.1	0.5	2.5	discrete	0.3	100000	11.001
[46]	HGA-LP	0.1	1.1	0.5	2.5	discrete	0.3	30	10.950
[43]	BBO-LP	0.1	1.1	0.5	2.5	discrete	0.3	30	8.756
[41]	SA	0.1	1.1	1.5	2.5	discrete	0.3	169	8.427
[9]	MILP	0.1	1.1	0.5	2.5	discrete	0.3	N/A	8.006
[47]	FA	0.05	1.1	1.25	1.5	discrete	0.2	49980	6.646
[45]	NLP	0.05	1.1	0.5	2	discrete	N/A	N/A	6.412
[48]	MEFO	0.05	1.1	0.5	2	discrete	0.3	11213	6.349
[44]	WOA	0.1	1.2	1.25	2.5	continuous	0.3	120	5.954
[44]	HWOA	0.1	1.2	1.25	2.5	continuous	0.3	115	5.857
Proposed GA-SQP		0.05	1.1	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.2	100	3.989

presents a comprehensive analysis, including the algorithm parameters, the number of function evaluations (NFE), and the objective function (OF) values, showcasing the preeminent performance of the proposed GA-SQP algorithm on the IEEE 8-bus system. This performance comparison is made against other evolutionary algorithms documented in the existing literature. The table provides a clear and detailed insight into how our proposed method outperforms the references, taking into account algorithm settings, NFE, and OF values. In the graph provided as in Figure 8, for (IEEE-8Bus), we can observe how the algorithm we propose achieves an operating time. This comparison considers algorithms mentioned in the existing literature.

3.3. Case Study 3 (30-Bus System)

To ensure the effectiveness of the proposed method, it is crucial to assess its performance within a larger system. For this purpose, we utilize the IEEE 30-Bus system distribution network. Specifically, Figure 9 provides an illustration of the 33 kV part of the IEEE 30-bus network. The power grid relies on three 50 MVA, 132/33 kV transformers, each connected to buses 1, 6, and 14 [34]. In addition to these three sources, there are also four distributed generators (DGs) linked to buses 3, 7, 11, and 16 that contribute power in the same manner. This distribution network has 21 lines and is protected by 42 DOCRs. The optimization problem involves 84 variables, namely, ${\mathrm{TMS}}_1$ to ${\mathrm{TMS}}_{42}$ and ${\mathrm{PS}}_1$ to ${\mathrm{PS}}_{42}$.

Table 10. P/B relays and fault currents for case 3.

Primary Relay	Fault Current (A)	Backup Relay	Fault Current (A)	Primary Relay	Fault Current (A)	Backup Relay	Fault Current (A)	Primary Relay	Fault Current (A)	Backup Relay	Fault Current (A)
R1	11607.3	R4	724.0	R14	2386.1	R17	457.0	R31	6173.6	R37	1520.8
R1	11607.3	R20	1835.9	R15	4879.0	R11	756.2	R31	6173.6	R42	1122.5
R1	11607.3	R22	1953.9	R15	4879.0	R14	83.2	R32	3458.8	R28	3459.7
R2	5334.1	R6	5316.6	R16	1467.1	R18	1466.0	R33	9323.1	R30	1479.9
R3	8416.0	R2	1836.5	R17	1937.0	R15	1936.3	R33	9323.1	R36	499.1
R3	8416.0	R20	1513.7	R18	2961.1	R13	964.3	R34	5167.9	R32	2032.0
R3	8416.0	R22	1613.0	R19	12710.9	R2	1877.2	R34	5167.9	R37	1534.8
R4	6017.0	R5	2017.5	R19	12710.9	R4	1226.5	R34	5167.9	R42	1598.3
R4	6017.0	R8	1972.9	R19	12710.9	R22	1761.3	R35	6877.4	R30	1160.9
R5	7071.5	R1	7050.5	R20	2890.3	R25	2878.3	R35	6877.4	R34	521.6
R6	8843.0	R3	3355.3	R21	8401.6	R2	1210.3	R36	3875.0	R38	1602.0
R6	8843.0	R8	2644.0	R21	8401.6	R4	792.5	R37	4449.1	R35	2093.6
R7	7461.8	R3	2244.6	R21	8401.6	R20	1008.6	R38	5485.2	R32	1515.5
R7	7461.8	R5	3431.3	R22	3673.9	R23	3673.1	R38	5485.2	R33	2798.2
R8	3674.5	R10	1862.6	R23	5630.6	R27	2639.7	R38	5485.2	R42	1191.5
R8	3674.5	R39	1804.3	R24	4758.2	R21	4756.5	R39	3235.7	R41	3236.4
R9	4157.0	R7	2806.8	R25	4048.8	R29	4048.7	R40	4494.0	R7	3028.6
R9	4157.0	R39	1352.2	R26	6113.7	R19	6113.8	R40	4494.0	R10	1468.8
R10	3219.9	R12	3223.8	R27	3569.0	R31	83.6	R41	6594.1	R32	1475.1
R11	2403.8	R9	2400.5	R28	5820.0	R24	3205.2	R41	6594.1	R33	3612.4
R12	7288.1	R14	630.3	R29	10286.5	R34	1483.5	R41	6594.1	R37	1538.6
R12	7288.1	R16	437.0	R29	10286.5	R36	983.1	R42	2587.7	R40	2583.2
R13	3670.5	R11	629.1	R30	3421.7	R26	3417.6
R13	3670.5	R16	458.2	R31	6173.6	R33	3560.7

lists the short-circuit currents recorded by the primary and the backup relay pairs.

Table 11. Operating times and coordination time interval (CTI) for case 3.

Relay Pairs		GA			GA-SQP			Relay Pairs		GA			GA-SQP
Primary	Backup	Tp (s)	Tb (s)	CTI (s)	Tp (s)	Tb (s)	CTI (s)	Primary	Backup	Tp (s)	Tb (s)	CTI (s)	Tp (s)	Tb (s)	CTI (s)
R1	R4	0.700	1.322	0.622	0.337	0.746	0.409	R21	R4	1.048	1.249	0.202	0.485	0.688	0.202
R1	R20	0.700	0.939	0.239	0.337	0.537	0.200	R21	R20	1.048	1.251	0.203	0.485	0.881	0.396
R1	R22	0.700	0.901	0.201	0.337	0.537	0.200	R22	R23	0.517	0.730	0.213	0.279	0.479	0.200
R2	R6	0.704	0.905	0.200	0.194	0.394	0.200	R23	R27	0.647	0.853	0.206	0.323	0.523	0.200
R3	R2	0.743	1.032	0.289	0.252	0.484	0.232	R24	R21	0.994	1.238	0.244	0.462	0.662	0.200
R3	R20	0.743	1.021	0.278	0.252	0.614	0.362	R25	R29	0.857	1.058	0.201	0.453	0.653	0.200
R3	R22	0.743	1.159	0.416	0.252	0.745	0.493	R26	R19	0.596	0.802	0.205	0.281	0.481	0.200
R4	R5	0.553	1.331	0.778	0.247	1.148	0.901	R27	R31	0.750	0.951	0.201	0.402	0.602	0.200
R4	R8	0.553	1.096	0.543	0.247	0.540	0.293	R28	R24	0.916	1.139	0.223	0.461	0.662	0.201
R5	R1	0.701	0.906	0.206	0.257	0.457	0.200	R29	R34	0.804	1.057	0.253	0.330	0.557	0.227
R6	R3	0.756	0.958	0.202	0.273	0.473	0.200	R29	R36	0.804	1.057	0.253	0.330	0.574	0.245
R6	R8	0.756	0.958	0.203	0.273	0.473	0.200	R30	R26	0.574	0.775	0.201	0.250	0.450	0.200
R7	R3	0.764	1.094	0.330	0.267	0.762	0.494	R31	R33	0.817	1.092	0.275	0.403	0.603	0.200
R7	R5	0.764	0.966	0.201	0.267	0.467	0.200	R31	R37	0.817	1.089	0.272	0.403	0.606	0.203
R8	R10	0.839	1.041	0.202	0.415	0.615	0.200	R31	R42	0.817	1.084	0.267	0.403	0.949	0.546
R8	R39	0.839	1.040	0.201	0.415	0.615	0.200	R32	R28	0.808	1.017	0.209	0.371	0.571	0.200
R9	R7	0.554	1.042	0.488	0.247	0.646	0.399	R33	R30	0.713	0.912	0.200	0.255	0.455	0.200
R9	R39	0.554	1.123	0.569	0.247	0.856	0.609	R33	R36	0.713	1.493	0.780	0.255	1.071	0.816
R10	R12	0.872	1.080	0.207	0.359	0.559	0.200	R34	R32	0.707	0.961	0.254	0.351	0.551	0.200
R11	R9	0.486	0.686	0.200	0.169	0.369	0.200	R34	R37	0.707	1.086	0.379	0.351	0.597	0.245
R12	R14	0.623	0.824	0.201	0.285	0.485	0.200	R34	R42	0.707	0.907	0.200	0.351	0.551	0.200
R12	R16	0.623	0.825	0.201	0.285	0.508	0.223	R35	R30	0.802	1.098	0.296	0.176	0.595	0.418
R13	R11	0.525	0.779	0.254	0.233	0.501	0.268	R35	R34	0.802	1.778	0.975	0.176	1.070	0.894
R13	R16	0.525	0.807	0.282	0.233	0.475	0.242	R36	R38	0.660	0.869	0.209	0.293	0.494	0.201
R14	R17	0.635	0.835	0.200	0.372	0.572	0.200	R37	R35	0.802	1.002	0.200	0.209	0.459	0.250
R15	R11	0.519	0.720	0.201	0.194	0.395	0.201	R38	R32	0.660	1.073	0.413	0.374	0.750	0.377
R15	R14	0.519	1.465	0.947	0.194	0.877	0.683	R38	R33	0.660	1.258	0.598	0.374	0.911	0.537
R16	R18	0.524	0.728	0.204	0.181	0.391	0.209	R38	R42	0.660	1.049	0.389	0.374	0.846	0.473
R17	R15	0.552	0.756	0.203	0.206	0.408	0.201	R39	R41	0.904	1.107	0.203	0.390	0.613	0.223
R18	R13	0.618	0.821	0.202	0.217	0.417	0.200	R40	R7	0.809	1.014	0.205	0.383	0.583	0.200
R19	R2	0.633	1.022	0.389	0.269	0.469	0.200	R40	R10	0.809	1.135	0.326	0.383	0.889	0.506
R19	R4	0.633	0.986	0.353	0.269	0.499	0.230	R41	R32	0.885	1.084	0.200	0.351	0.776	0.425
R19	R22	0.633	1.024	0.391	0.269	0.633	0.363	R41	R33	0.885	1.084	0.199	0.351	0.591	0.240
R20	R25	0.788	0.991	0.203	0.413	0.613	0.200	R41	R37	0.885	1.085	0.200	0.351	0.594	0.243
R21	R2	1.048	1.257	0.209	0.485	1.142	0.656	R42	R40	0.742	0.944	0.202	0.350	0.550	0.200

lists the operating times of the B/P relay pairs, along with their respective CTI values.

Case Study 3 Discussion:

The relay coordination of the IEEE 30-Bus distribution system was optimized using GA-SQP in MATLAB. The results presented in

Table 12. Optimal relay settings for case 3.

Relay No.	GA		GA-SQP		Relay No.	GA		GA-SQP
	TMS (s)	PS (pu)	TMS (s)	PS (pu)		TMS (s)	PS (pu)	TMS (s)	PS (pu)
R1	0.227	0.717	0.094	0.971	R22	0.112	0.470	0.053	0.560
R2	0.358	0.098	0.051	0.508	R23	0.376	0.065	0.062	0.858
R3	0.470	0.069	0.073	0.659	R24	0.468	0.112	0.088	0.725
R4	0.303	0.085	0.117	0.140	R25	0.324	0.175	0.087	0.617
R5	0.276	0.275	0.061	0.799	R26	0.225	0.266	0.064	0.729
R6	0.353	0.212	0.067	0.943	R27	0.281	0.159	0.077	0.544
R7	0.427	0.099	0.065	0.796	R28	0.757	0.014	0.186	0.213
R8	0.333	0.140	0.167	0.136	R29	0.479	0.107	0.091	0.879
R9	0.239	0.127	0.060	0.442	R30	0.192	0.198	0.068	0.299
R10	0.450	0.057	0.069	0.490	R31	0.489	0.063	0.098	0.659
R11	0.262	0.036	0.050	0.180	R32	0.410	0.064	0.089	0.381
R12	0.177	0.591	0.070	0.776	R33	0.296	0.317	0.062	0.995
R13	0.296	0.047	0.106	0.096	R34	0.406	0.062	0.179	0.093
R14	0.588	0.003	0.338	0.003	R35	0.765	0.007	0.050	0.561
R15	0.230	0.138	0.050	0.471	R36	0.365	0.053	0.123	0.129
R16	0.263	0.028	0.050	0.126	R37	0.502	0.038	0.050	0.490
R17	0.362	0.014	0.069	0.114	R38	0.532	0.015	0.295	0.017
R18	0.452	0.013	0.050	0.344	R39	0.630	0.018	0.092	0.368
R19	0.336	0.201	0.066	1.356	R40	0.485	0.046	0.103	0.406
R20	0.336	0.091	0.120	0.224	R41	0.478	0.099	0.086	0.704
R21	0.593	0.106	0.153	0.552	R42	0.294	0.100	0.067	0.391
OF (s)						30.099		13.017

demonstrate that the minimum operating time achieved by the proposed method was 13.017 s. Consequently, the GA-SQP method outperformed the GA method by a margin of 17.082 s in this specific relay coordination problem. Figure 10 illustrates the enhancement in coordination time achieved by employing the GA-SQP algorithm for a set of 70 relay pairs. The CTI values for all the pairs consistently remained equal to or greater than 0.2 s.

Table 13. Comparing GA-SQP with other methods for case 3.

Ref.	Method	The Algorithm’s Parameters for 30-Bus Test System							Objective Function
		TMSmin	TMSmax	PSmin	PSmax	PS Mode	CTI	NFE
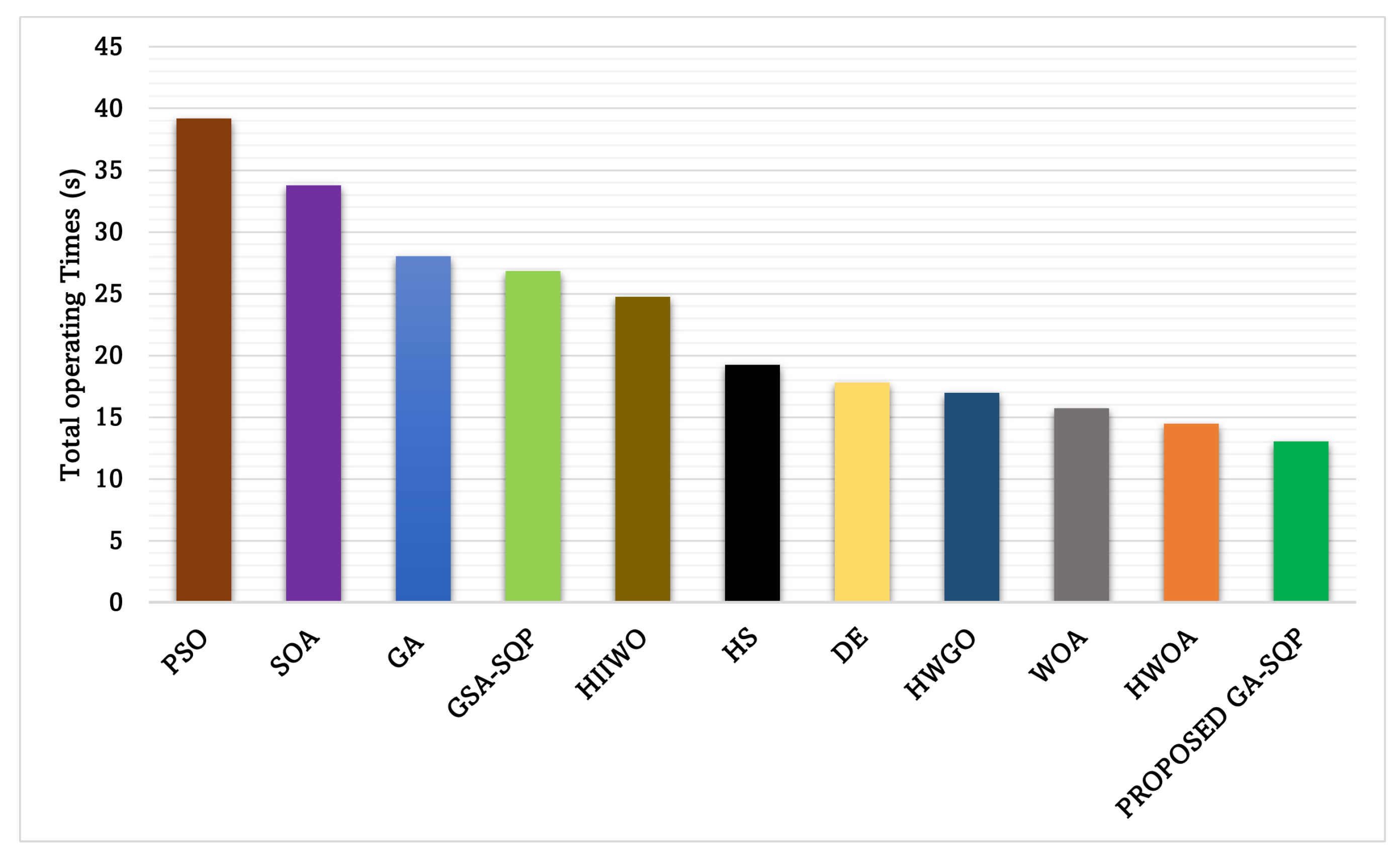
[49]	PSO	0.1	1.1	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.2	100	39.1834
[49]	SOA	0.1	1.1	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.2	100	33.7734
[49]	GA	0.1	1.1	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.2	100	28.0195
[50]	GSA-SQP	0.1	1.1	1.5	6	continuous	0.3	200	26.8258
[51]	HIIWO	0.1	1.1	1.5	6	continuous	0.3	200	24.759
[49]	HS	0.1	1.1	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.2	100	19.2133
[49]	DE	0.1	1.1	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.2	100	17.8122
[17]	HWGO	0.1	1.1	1.5	6	continuous	0.3	3489	16.96
[44]	WOA	0.1	1.2	1.5	2.5	continuous	0.3	320	15.7139
[44]	HWOA	0.1	1.2	1.5	2.5	continuous	0.3	250	14.4649
Proposed GA-SQP		0.05	1.1	$I_{OL}^{max}$	$I_f^{min}$	continuous	0.2	300	13.017

provides a comprehensive comparison of the proposed GA-SQP algorithm’s performance on the IEEE 30-bus system with that of other evolutionary algorithms documented in the existing literature. This comparison includes crucial details such as algorithm parameters, the number of function evaluations (NFE), and the objective function (OF) values. The table highlights the excellent performance of our proposed method, offering a comprehensive view of how it excels over the references in terms of algorithm settings, NFE, and OF values. In Figure 11, as shown for the IEEE-30-Bus, we can observe the efficiency of our proposed algorithm in terms of operating time. This comparison encompasses algorithms mentioned in the existing literature.

4. Conclusions

In this study, a novel and potent hybrid optimization method was introduced to tackle the coordination issue in distributed overcurrent relay coordination (DOCR) systems. Our approach harnessed the strengths of genetic algorithms (GA) and sequential quadratic programming (SQP), allowing for a combination of global exploration and local refinement. Following thorough testing across multiple systems, including the IEEE3-Bus, 8-Bus, and 30-Bus systems, our proposed method exhibited remarkable results. The utilization of our GA-SQP algorithm resulted in a significant reduction in the operating times of P/B relays for mid-point faults, ensuring effective and swift protection. Furthermore, the protection mechanism (PM) effectively maintained the necessary time intervals between the P/B relay pairs, thus enhancing the dependability and efficiency of protective systems. Compared to other conventional GA algorithms and advanced techniques as documented in the existing literature, the GA-SQP algorithm introduced in this study has displayed preeminent performance in terms of solution quality, resilience, and efficiency when evaluated in the past. By harnessing the combined advantages of genetic algorithms and sequential quadratic programming, the method presented in this study offered a comprehensive and reliable solution for optimizing the coordination of distributed overcurrent relays (DOCRs) within distribution systems. The effective implementation and validation of the proposed algorithm on various test systems in previous experiments provide compelling evidence of its effectiveness and potential for practical adoption. It is worth noting that our algorithm had the potential for further improvement and customization to accommodate additional constraints and complexities of power systems, thereby increasing its applicability in real-world scenarios. This study has made a significant contribution to the field of protective relay coordination by introducing a unique and efficient approach that outperforms current methodologies. The incorporation of both global and local optimization techniques within the GA-SQP algorithm demonstrated the effectiveness of hybrid algorithms in addressing complex and constrained optimization problems in the past. Potential avenues for future research could include assessing the applicability of the suggested algorithm to different protection coordination issues and evaluating its performance under various system conditions and fault scenarios. Additionally, the inclusion of uncertainty analysis and real-time data integration could enhance the resilience and reliability of the proposed algorithm, which warrants further investigation in these areas.