Self- and Mutual-Inductance Cross-Validation of Multi-Turn, Multi-Layer Square Coils for Dynamic Wireless Charging of Electric Vehicles
Abstract
1. Introduction
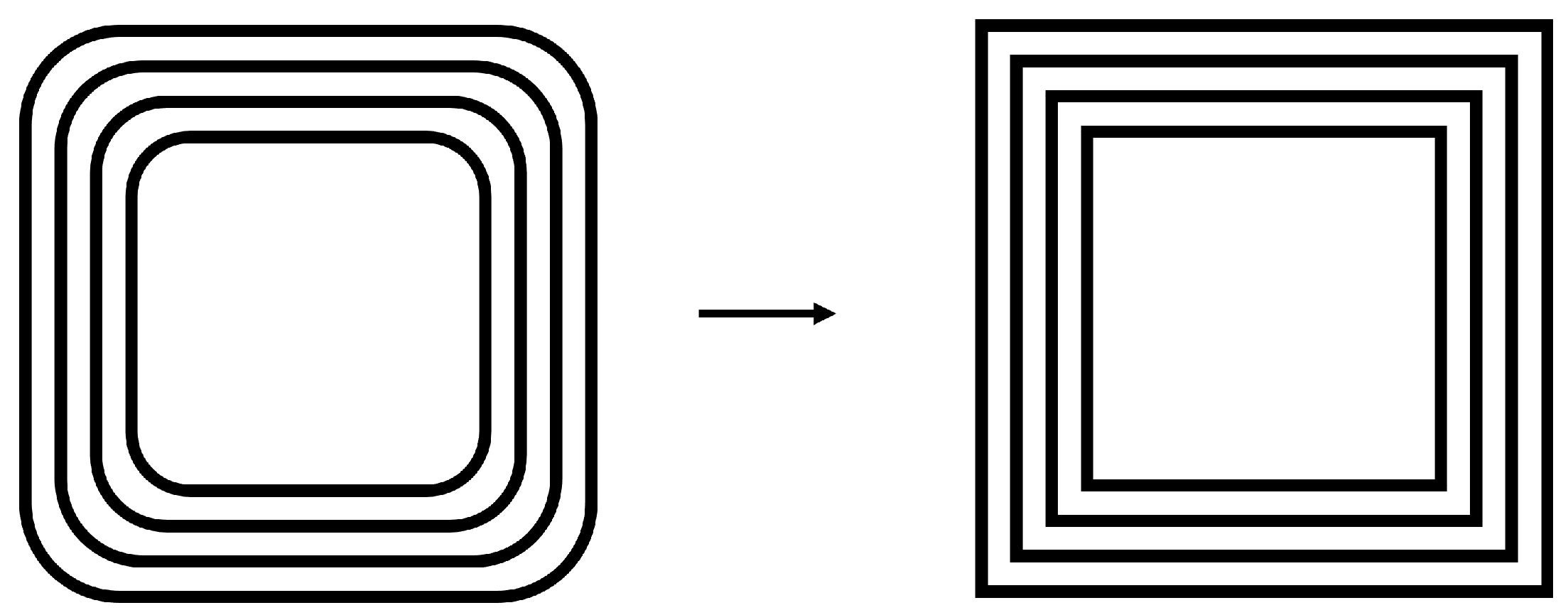
2. A Multi-Turn, Multi-Layer Square Coil
3. Theoretical Calculation
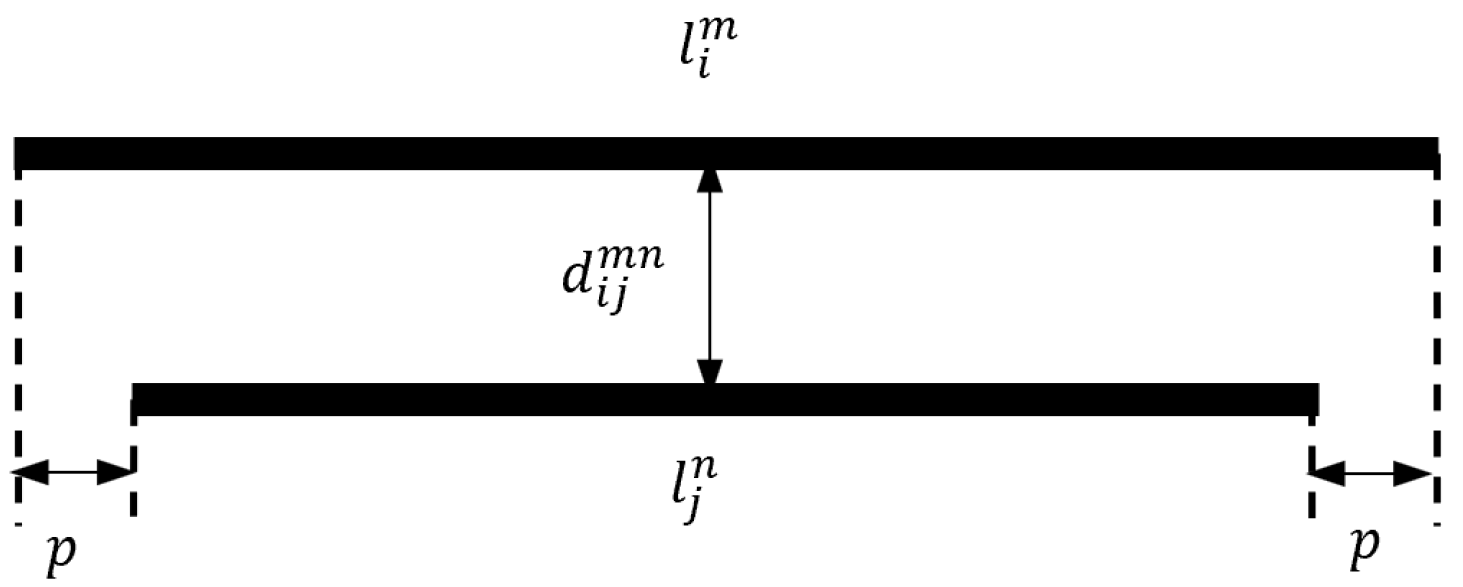
3.1. Self Inductance
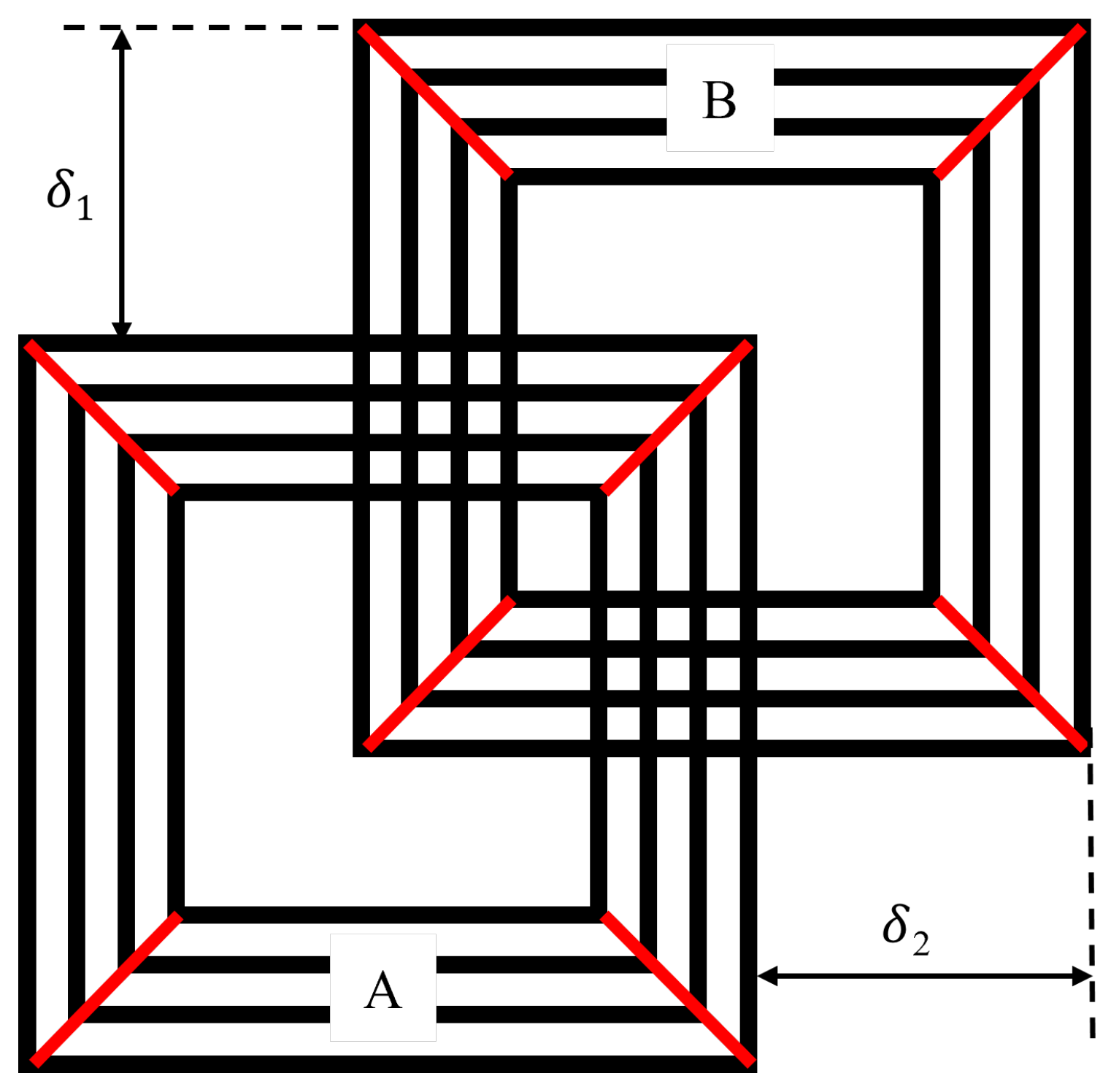
3.2. Mutual-Inductance
4. 3D Coil Modelling and Simulation
4.1. Model Development
4.2. Self Inductance
4.3. Mutual Inductance
5. Practical Measurement
5.1. Self Inductance
5.2. Mutual Inductance
5.2.1. Voltage Measurement Method
5.2.2. Leakage Inductance Measurement Method
6. Cross-Validation
6.1. Self Inductance
6.2. Mutual-Inductance
7. Theoretical–Experimental Verification
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DWPT | Dynamic Wireless Power Transfer |
| EV | Electric Vehicle |
| FEM | Finite Element Method |
| IoT | Internet of Things |
| WPT | Wireless Power Transfer |
| ZPA | Zero Phase Angle |
References
- Tesla, N. Apparatus for Transmitting Electrical Energy. US Patent 1119732, 1 December 1914. [Google Scholar]
- Si, P.; Hu, A.P.; Malpas, S.; Budgett, D. A Frequency Control Method for Regulating Wireless Power to Implantable Devices. IEEE Trans. Biomed. Circuits Syst. 2008, 2, 918284. [Google Scholar] [CrossRef] [PubMed]
- Bakula, M.; Pelgrims, P.; Puers, R. A Wireless Powering and Communication System for Implantable Devices Based on a Royer Oscillator with Radio and Near-field Communication Links. Procedia Eng. 2015, 120, 306–309. [Google Scholar] [CrossRef][Green Version]
- Han, S.; Wentzloff, D.D. Wireless power transfer using resonant inductive coupling for 3D integrated ICs. In Proceedings of the 2010 IEEE International 3D Systems Integration Conference (3DIC), Munich, Germany, 16–18 November 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Riehl, P.S.; Satyamoorthy, A.; Akram, H.; Yen, Y.C.; Yang, J.C.; Juan, B.; Lee, C.M.; Lin, F.C.; Muratov, V.; Plumb, W.; et al. Wireless Power Systems for Mobile Devices Supporting Inductive and Resonant Operating Modes. IEEE Trans. Microw. Theory Tech. 2015, 63, 780–790. [Google Scholar] [CrossRef]
- Kuo, R.C.; Riehl, P.; Satyamoorthy, A.; Plumb, W.; Tustin, P.; Lin, J. A 3D resonant wireless charger for a wearable device and a mobile phone. In Proceedings of the 2015 IEEE Wireless Power Transfer Conference (WPTC), Boulder, CO, USA, 13–15 May 2015; pp. 1–3. [Google Scholar] [CrossRef]
- Shinohara, N. Trends in Wireless Power Transfer: WPT Technology for Energy Harvesting, Mllimeter-Wave/THz Rectennas, MIMO-WPT, and Advances in Near-Field WPT Applications. IEEE Microw. Mag. 2021, 22, 46–59. [Google Scholar] [CrossRef]
- Azad, A.; Teeneti, C.R.; Zane, R.; Pantic, Z. DAB-based WPT Charger with Integrated Battery Management System for Fast Charging of Mobility Devices. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Shoki, H. Issues and Initiatives for Practical Deployment of Wireless Power Transfer Technologies in Japan. Proc. IEEE 2013, 101, 1312–1320. [Google Scholar] [CrossRef]
- Hamam, R.E.; Karalis, A.; Joannopoulos, J.; Soljačić, M. Efficient weakly-radiative wireless energy transfer: An EIT-like approach. Ann. Phys. 2009, 324, 1783–1795. [Google Scholar] [CrossRef]
- Karalis, A.; Joannopoulos, J.; Soljačić, M. Efficient wireless non-radiative mid-range energy transfer. Ann. Phys. 2008, 323, 34–48. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless Power Transfer via Strongly Coupled Magnetic Resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef]
- Imura, T.; Okabe, H.; Hori, Y. Basic experimental study on helical antennas of wireless power transfer for Electric Vehicles by using magnetic resonant couplings. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–10 September 2009; pp. 936–940. [Google Scholar] [CrossRef]
- Mou, X.; Gladwin, D.T.; Zhao, R.; Sun, H. Survey on magnetic resonant coupling wireless power transfer technology for electric vehicle charging. IET Power Electron. 2019, 12, 3005–3020. [Google Scholar] [CrossRef]
- Li, S.; Liu, Z.; Zhao, H.; Zhu, L.; Shuai, C.; Chen, Z. Wireless Power Transfer by Electric Field Resonance and Its Application in Dynamic Charging. IEEE Trans. Ind. Electron. 2016, 63, 6602–6612. [Google Scholar] [CrossRef]
- Cai, C.; Wang, J.; Fang, Z.; Zhang, P.; Hu, M.; Zhang, J.; Li, L.; Lin, Z. Design and Optimization of Load-Independent Magnetic Resonant Wireless Charging System for Electric Vehicles. IEEE Access 2018, 6, 17264–17274. [Google Scholar] [CrossRef]
- Aydin, E.; Aydemir, M.T.; Aksoz, A.; El Baghdadi, M.; Hegazy, O. Inductive Power Transfer for Electric Vehicle Charging Applications: A Comprehensive Review. Energies 2022, 15, 4962. [Google Scholar] [CrossRef]
- Feng, H.; Cai, T.; Duan, S.; Zhao, J.; Zhang, X.; Chen, C. An LCC-Compensated Resonant Converter Optimized for Robust Reaction to Large Coupling Variation in Dynamic Wireless Power Transfer. IEEE Trans. Ind. Electron. 2016, 63, 6591–6601. [Google Scholar] [CrossRef]
- Panchal, C.; Stegen, S.; Lu, J. Review of static and dynamic wireless electric vehicle charging system. Eng. Sci. Technol. Int. J. 2018, 21, 922–937. [Google Scholar] [CrossRef]
- Barsari, V.Z.; Thrimawithana, D.J.; Covic, G.A. An Inductive Coupler Array for In-Motion Wireless Charging of Electric Vehicles. IEEE Trans. Power Electron. 2021, 36, 9854–9863. [Google Scholar] [CrossRef]
- Song, B.; Cui, S.; Li, Y.; Zhu, C. A Fast and General Method to Calculate Mutual Inductance for EV Dynamic Wireless Charging System. IEEE Trans. Power Electron. 2021, 36, 2696–2709. [Google Scholar] [CrossRef]
- Budhia, M.; Covic, G.A.; Boys, J.T. Design and Optimization of Circular Magnetic Structures for Lumped Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2011, 26, 3096–3108. [Google Scholar] [CrossRef]
- Choi, Y.; Kwak, B.; Kim, M. 4kW magnetic resonance wireless power transfer system. In Proceedings of the 2016 IEEE International Conference on Power System Technology (POWERCON), Wollongong, Australia, 28–30 September 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Mahesh, A.; Chokkalingam, B.; Mihet-Popa, L. Inductive Wireless Power Transfer Charging for Electric Vehicles—A Review. IEEE Access 2021, 9, 137667–137713. [Google Scholar] [CrossRef]
- Budhia, M.; Boys, J.T.; Covic, G.A.; Huang, C.Y. Development of a Single-Sided Flux Magnetic Coupler for Electric Vehicle IPT Charging Systems. IEEE Trans. Ind. Electron. 2013, 60, 318–328. [Google Scholar] [CrossRef]
- Liang, M.; Khamlichi Drissi, K.E.; Pasquier, C. Optimal frequency for Dynamic Wireless Power Transfer. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hanover, Germany, 5–9 September 2022; pp. 1–10. [Google Scholar]
- Patil, D.; McDonough, M.K.; Miller, J.M.; Fahimi, B.; Balsara, P.T. Wireless Power Transfer for Vehicular Applications: Overview and Challenges. IEEE Trans. Transp. Electrif. 2018, 4, 3–37. [Google Scholar] [CrossRef]
- Grover, F.W. Inductance Calculations; Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Maxwell, J.C. A Treatise on Electricity and Magnetism. In Cambridge Library Collection—Physical Sciences; Cambridge University Press: Cambridge, UK, 2010; Volume 1. [Google Scholar] [CrossRef]
- Rosa, E.B.; Frederick, W.G. Formulas and Tables for the Calculation of Mutual and Self-Inductance, Number 169, 3rd ed.; US Department of Commerce and Labor, Bureau of Standards: Washington, DC, USA, 1948. [Google Scholar]
- NIST. Circular of the Bureau of Standards C74: Radio Instruments and Measurements. NBS Circulars; National Institute of Standards and Technology (NIST), Commerce Department: Washington, DC, USA, 1937; p. 242.
- Rosa, E.B. The self and mutual inductance of linear conductors. Bull. Bur. Stand. 1908, 4, 301–344. [Google Scholar] [CrossRef]
- López-Alcolea, F.J.; Real, J.V.d.; Roncero-Sánchez, P.; Torres, A.P. Modeling of a Magnetic Coupler Based on Single- and Double-Layered Rectangular Planar Coils With In-Plane Misalignment for Wireless Power Transfer. IEEE Trans. Power Electron. 2020, 35, 5102–5121. [Google Scholar] [CrossRef]
- Kushwaha, B.K.; Rituraj, G.; Kumar, P. 3-D Analytical Model for Computation of Mutual Inductance for Different Misalignments With Shielding in Wireless Power Transfer System. IEEE Trans. Transp. Electrif. 2017, 3, 332–342. [Google Scholar] [CrossRef]
- Raju, S.; Wu, R.; Chan, M.; Yue, C.P. Modeling of Mutual Coupling Between Planar Inductors in Wireless Power Applications. IEEE Trans. Power Electron. 2014, 29, 481–490. [Google Scholar] [CrossRef]
- Rohde & Schwarz GmbH & Co. KG. R&S® HM8118 LCR Bridge User Manual; Rohde & Schwarz GmbH & Co. KG.: Muhich, Germany, 2016. [Google Scholar]
- Su, Y.P.; Liu, X.; Hui, S.Y.R. Mutual Inductance Calculation of Movable Planar Coils on Parallel Surfaces. IEEE Trans. Power Electron. 2009, 24, 1115–1123. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T. Modern Trends in Inductive Power Transfer for Transportation Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 28–41. [Google Scholar] [CrossRef]
- Jiang, J.; Dai, X.; Hu, A.P. A Dynamic Tuning Method for ZPA Frequency Operation of MEU-WPT System by DC Input Voltages Regulation. IEEE Trans. Power Electron. 2022, 37, 11369–11381. [Google Scholar] [CrossRef]
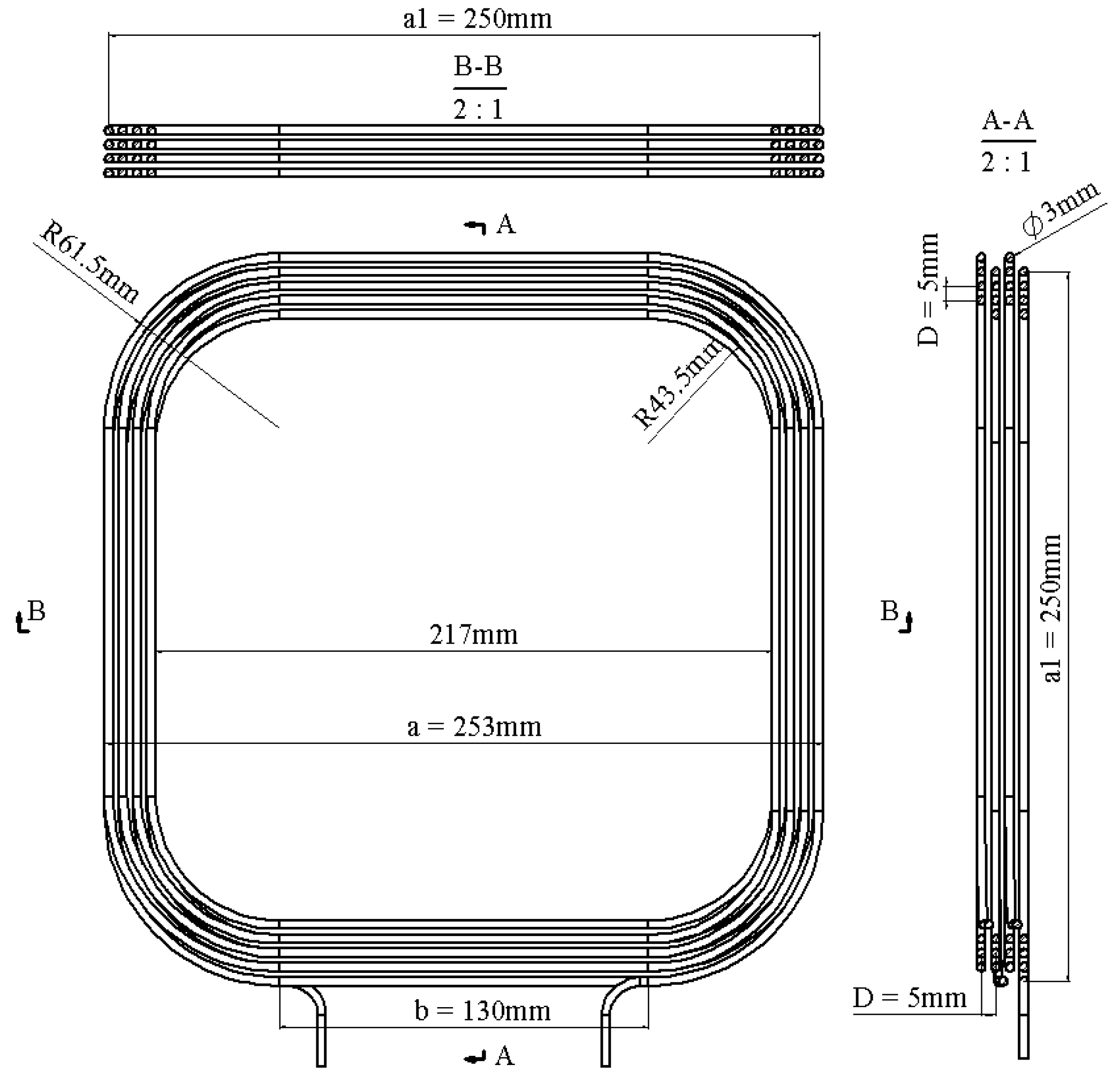


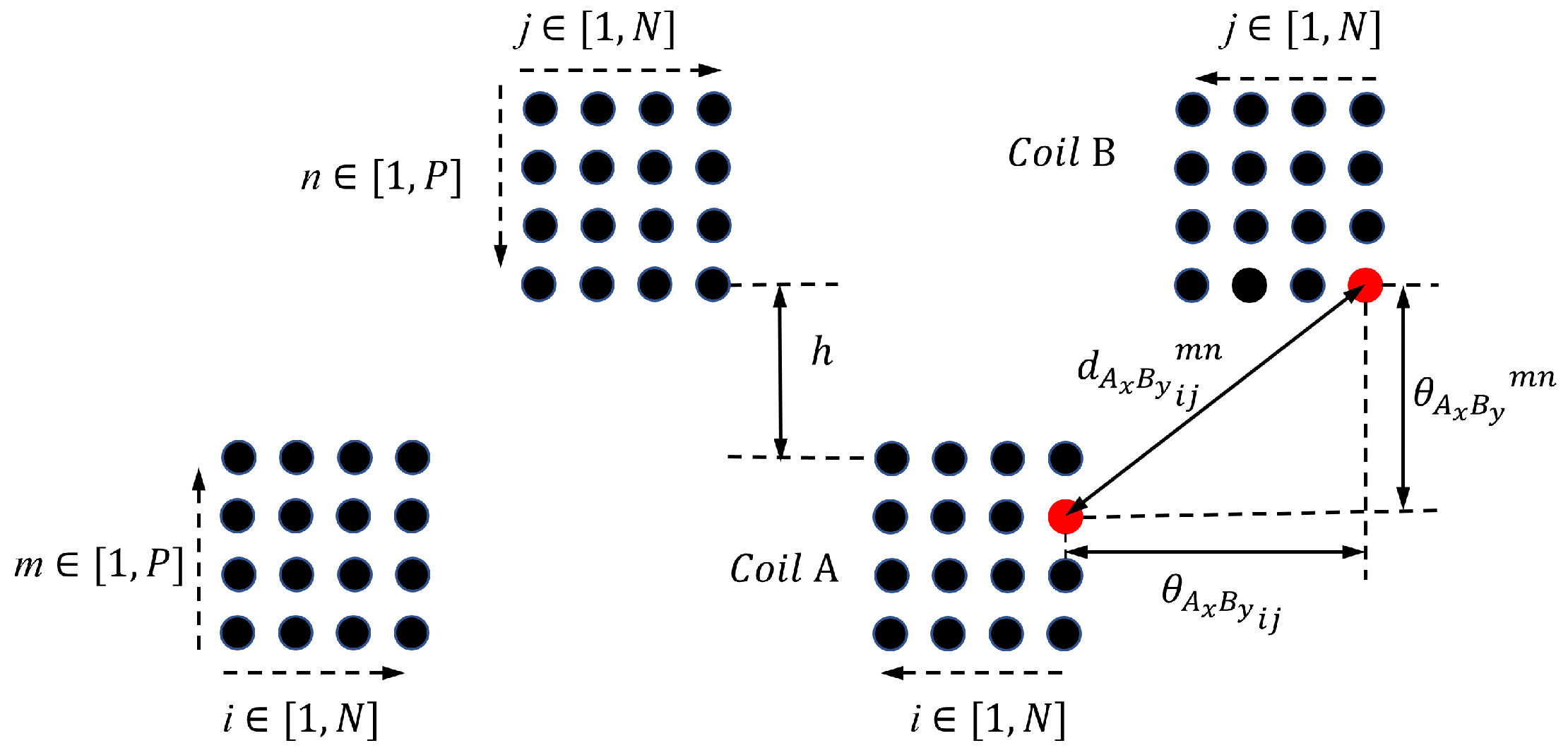

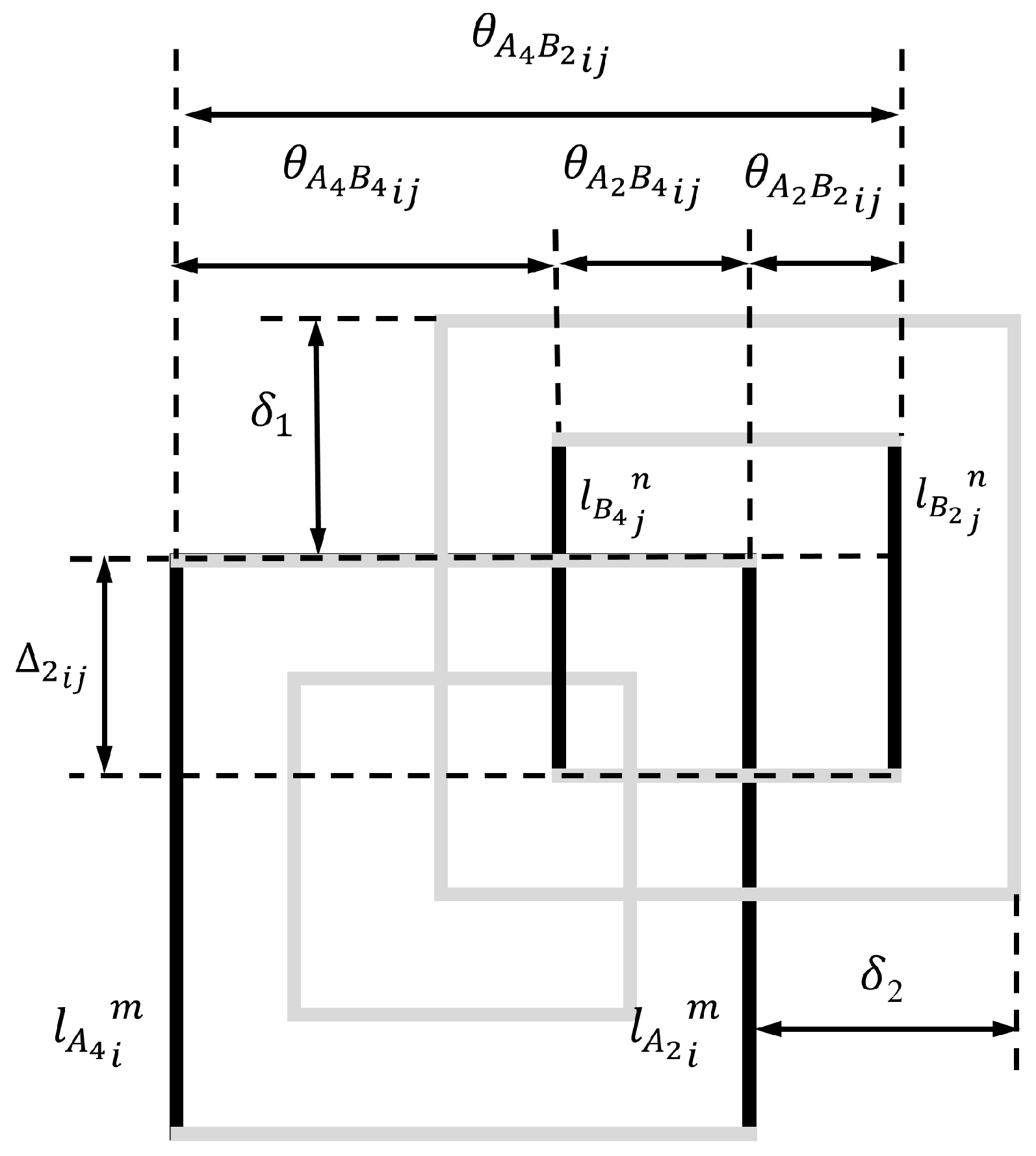
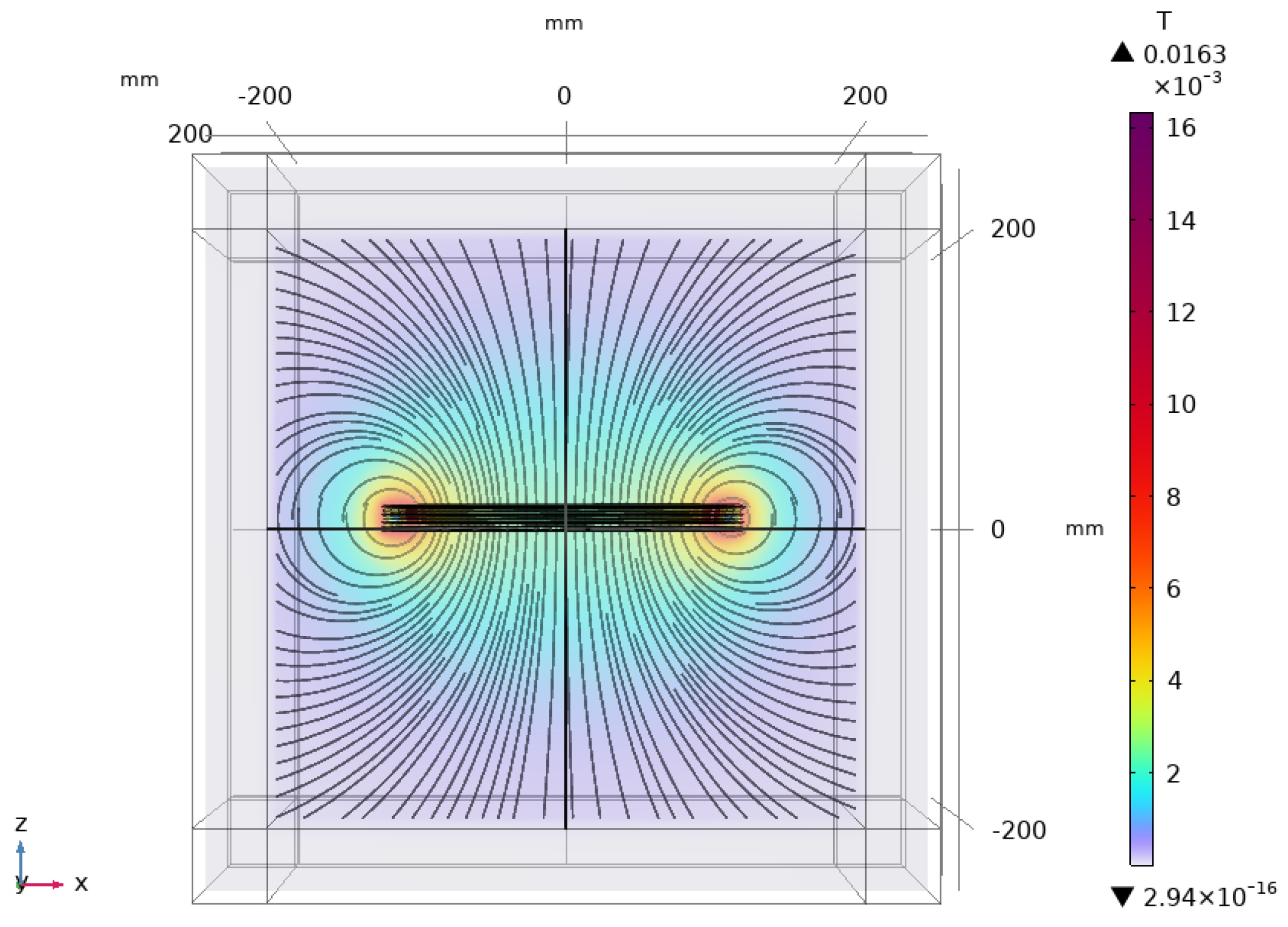
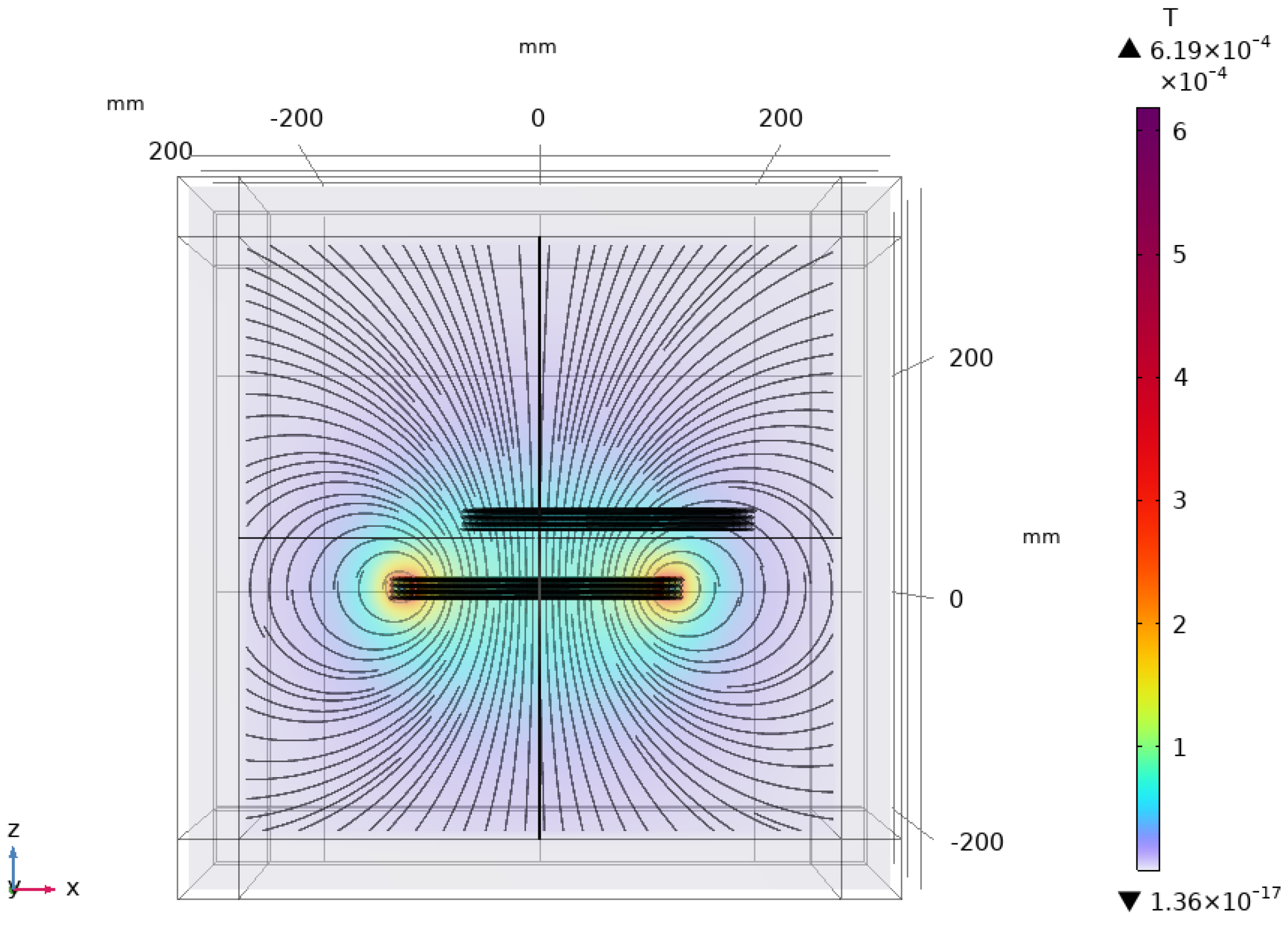




| (cm) | r (cm) | D (cm) | (H) | ||
|---|---|---|---|---|---|
| 25.00 | 0.15 | 0.50 | 4 | 4 | 113.76 |
| Results | Theoretical Model | Simulation | Measurement |
|---|---|---|---|
| 113.76 | 111.48 | 117.34 | |
| NRMSE (%) | 0.51 | 2.57 | 3.02 |
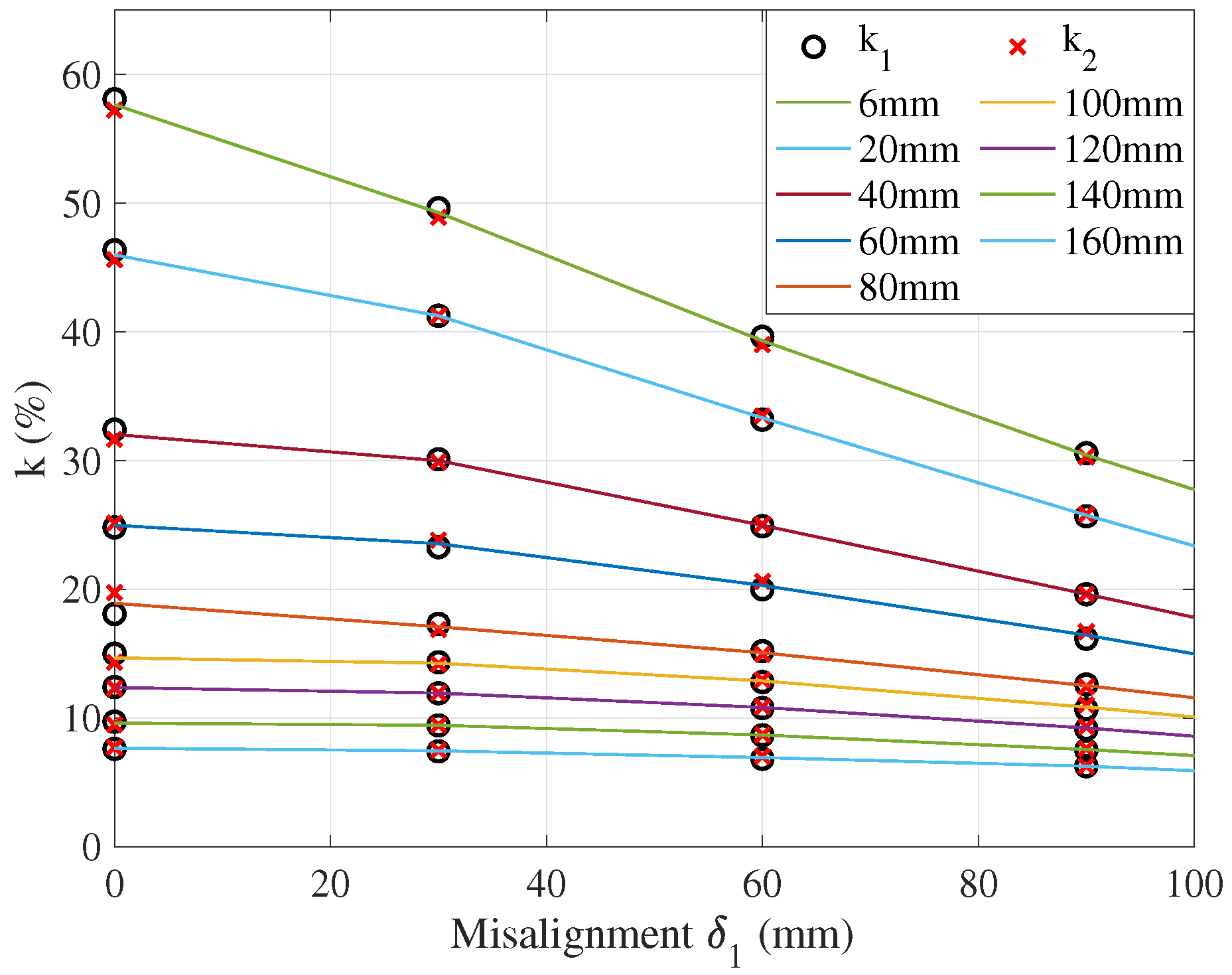
| VD * (mm) | Misalignment 0 mm | Misalignment 30 mm | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M-1 * (%) | M-2 * (%) | T * (%) | S * (%) | M-1 (%) | M-2 (%) | T (%) | S (%) | |||||||||
| * | ||||||||||||||||
| 6 | 58.08 | 3.30 | 57.23 | 4.71 | 62.53 | 4.11 | 62.41 | 3.90 | 49.62 | 3.46 | 48.91 | 4.84 | 54.19 | 5.45 | 52.89 | 2.85 |
| 20 | 46.35 | 1.09 | 45.61 | 2.65 | 48.82 | 4.19 | 46.65 | 0.45 | 41.25 | 1.97 | 41.25 | 1.98 | 44.13 | 4.87 | 41.69 | 0.92 |
| 40 | 32.40 | 2.65 | 31.65 | 4.92 | 35.79 | 7.52 | 33.30 | 0.04 | 30.10 | 3.12 | 29.90 | 23.76 | 33.40 | 7.51 | 30.87 | 0.64 |
| 60 | 24.81 | 2.87 | 25.13 | 1.61 | 27.19 | 6.45 | 25.04 | 1.97 | 23.27 | 3.54 | 23.81 | 1.29 | 25.79 | 6.90 | 23.63 | 2.07 |
| 80 | 18.08 | 7.80 | 19.74 | 0.68 | 21.15 | 7.87 | 19.46 | 0.76 | 17.31 | 5.13 | 16.86 | 7.58 | 20.26 | 11.05 | 18.55 | 1.66 |
| 100 | 15.00 | 2.52 | 14.33 | 6.86 | 16.74 | 8.79 | 15.48 | 0.59 | 14.33 | 3.68 | 14.18 | 4.65 | 16.13 | 8.44 | 14.86 | 0.12 |
| 120 | 12.40 | 2.14 | 12.33 | 2.76 | 13.43 | 5.95 | 12.54 | 1.05 | 11.92 | 0.44 | 11.94 | 0.30 | 13.00 | 8.55 | 11.04 | 7.81 |
| 140 | 9.71 | 3.88 | 9.48 | 6.12 | 10.90 | 7.89 | 10.32 | 2.11 | 9.42 | 4.43 | 9.44 | 4.26 | 10.59 | 7.40 | 9.99 | 1.29 |
| 160 | 7.60 | 7.48 | 7.71 | 6.12 | 8.94 | 8.89 | 8.60 | 4.71 | 7.40 | 7.26 | 7.48 | 6.26 | 8.70 | 8.98 | 8.35 | 4.54 |
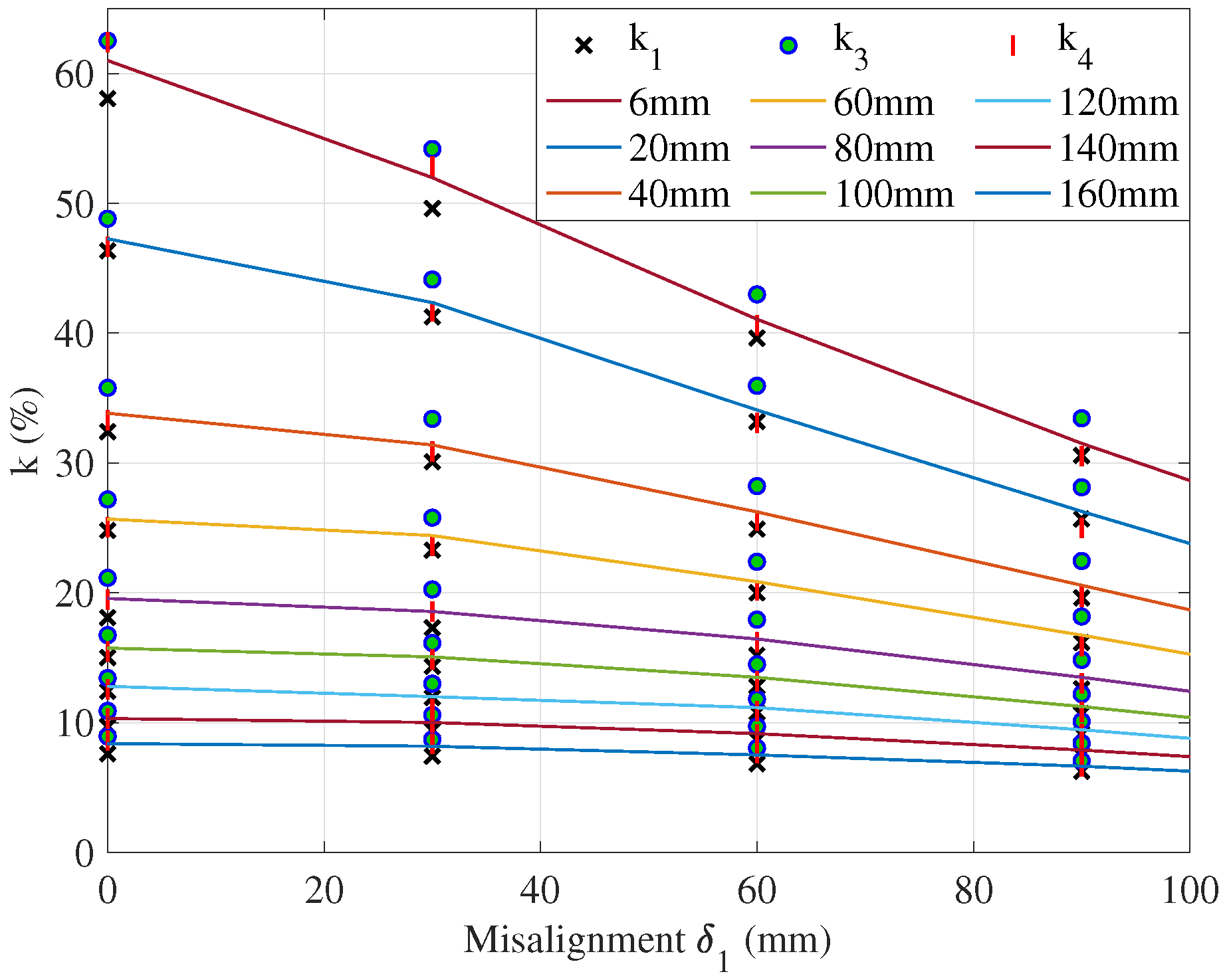
| VD (mm) | Misalignment 60 mm | Misalignment 90 mm | ||||||||||||||
| M-1 (%) | M-2 (%) | T (%) | S (%) | M-1 (%) | M-2 (%) | T (%) | S (%) | |||||||||
| 6 | 39.62 | 2.32 | 39.01 | 3.82 | 42.99 | 6.00 | 40.61 | 0.14 | 30.58 | 2.00 | 30.28 | 2.95 | 33.44 | 7.17 | 30.51 | 2.22 |
| 20 | 33.17 | 2.21 | 33.47 | 1.34 | 35.95 | 5.98 | 33.10 | 2.42 | 25.67 | 1.86 | 25.83 | 1.24 | 28.13 | 7.53 | 25.00 | 4.43 |
| 40 | 24.90 | 3.95 | 25.03 | 3.47 | 28.22 | 8.84 | 25.56 | 1.41 | 19.62 | 3.56 | 19.63 | 3.48 | 22.45 | 10.37 | 19.66 | 3.32 |
| 60 | 20.00 | 3.80 | 20.60 | 0.91 | 22.39 | 7.70 | 20.17 | 2.99 | 16.15 | 3.44 | 16.71 | 0.11 | 18.17 | 8.61 | 15.88 | 5.06 |
| 80 | 15.19 | 5.42 | 14.94 | 6.99 | 17.93 | 11.62 | 16.19 | 0.78 | 12.60 | 4.75 | 12.43 | 6.02 | 14.83 | 12.14 | 13.04 | 1.38 |
| 100 | 12.79 | 4.24 | 12.96 | 2.94 | 14.49 | 8.50 | 13.18 | 1.31 | 10.67 | 4.54 | 11.02 | 1.47 | 12.19 | 9.02 | 10.85 | 3.14 |
| 120 | 10.77 | 2.79 | 10.86 | 1.96 | 11.81 | 6.60 | 10.87 | 1.85 | 9.13 | 2.94 | 9.30 | 1.14 | 10.09 | 7.21 | 9.12 | 3.14 |
| 140 | 8.65 | 4.19 | 8.69 | 3.78 | 9.71 | 7.50 | 9.08 | 0.48 | 7.50 | 3.98 | 7.60 | 2.74 | 8.41 | 7.68 | 7.74 | 0.96 |
| 160 | 6.83 | 7.55 | 7.02 | 4.99 | 8.04 | 8.88 | 7.65 | 3.65 | 6.25 | 4.47 | 6.25 | 4.50 | 7.05 | 7.76 | 6.62 | 1.21 |
| NRMSE | NRMSE | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 58.08 | 0.7924 | 0.7944 | 0.85 | 1.5097 | 1.5167 | 3.28 |
| 30 | 49.62 | 0.8241 | 0.8183 | 0.73 | 1.3730 | 1.3823 | 3.60 |
| 60 | 39.62 | 0.8560 | 0.8498 | 0.71 | 1.2159 | 1.2605 | 0.68 |
| 90 | 30.58 | 0.8901 | 0.8826 | 0.25 | 1.1348 | 1.1726 | 0.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, M.; El Khamlichi Drissi, K.; Pasquier, C. Self- and Mutual-Inductance Cross-Validation of Multi-Turn, Multi-Layer Square Coils for Dynamic Wireless Charging of Electric Vehicles. Energies 2023, 16, 7033. https://doi.org/10.3390/en16207033
Liang M, El Khamlichi Drissi K, Pasquier C. Self- and Mutual-Inductance Cross-Validation of Multi-Turn, Multi-Layer Square Coils for Dynamic Wireless Charging of Electric Vehicles. Energies. 2023; 16(20):7033. https://doi.org/10.3390/en16207033
Chicago/Turabian StyleLiang, Mincui, Khalil El Khamlichi Drissi, and Christopher Pasquier. 2023. "Self- and Mutual-Inductance Cross-Validation of Multi-Turn, Multi-Layer Square Coils for Dynamic Wireless Charging of Electric Vehicles" Energies 16, no. 20: 7033. https://doi.org/10.3390/en16207033
APA StyleLiang, M., El Khamlichi Drissi, K., & Pasquier, C. (2023). Self- and Mutual-Inductance Cross-Validation of Multi-Turn, Multi-Layer Square Coils for Dynamic Wireless Charging of Electric Vehicles. Energies, 16(20), 7033. https://doi.org/10.3390/en16207033






