Estimation of 3D Permeability from Pore Network Models Constructed Using 2D Thin-Section Images in Sandstone Reservoirs
Abstract
:1. Introduction
- (i)
- To establish a PNM using two-dimensional thin-section slices.
- (ii)
- To achieve fluid simulation using PNM and reduce the input dimensions of MLP with simulation results.
- (iii)
- To compare the predictive performance of the network after fluid calculation with that of the original network.
- (iv)
- To attempt to change the number of layers in the MLP to obtain the best prediction results.
2. Methodology
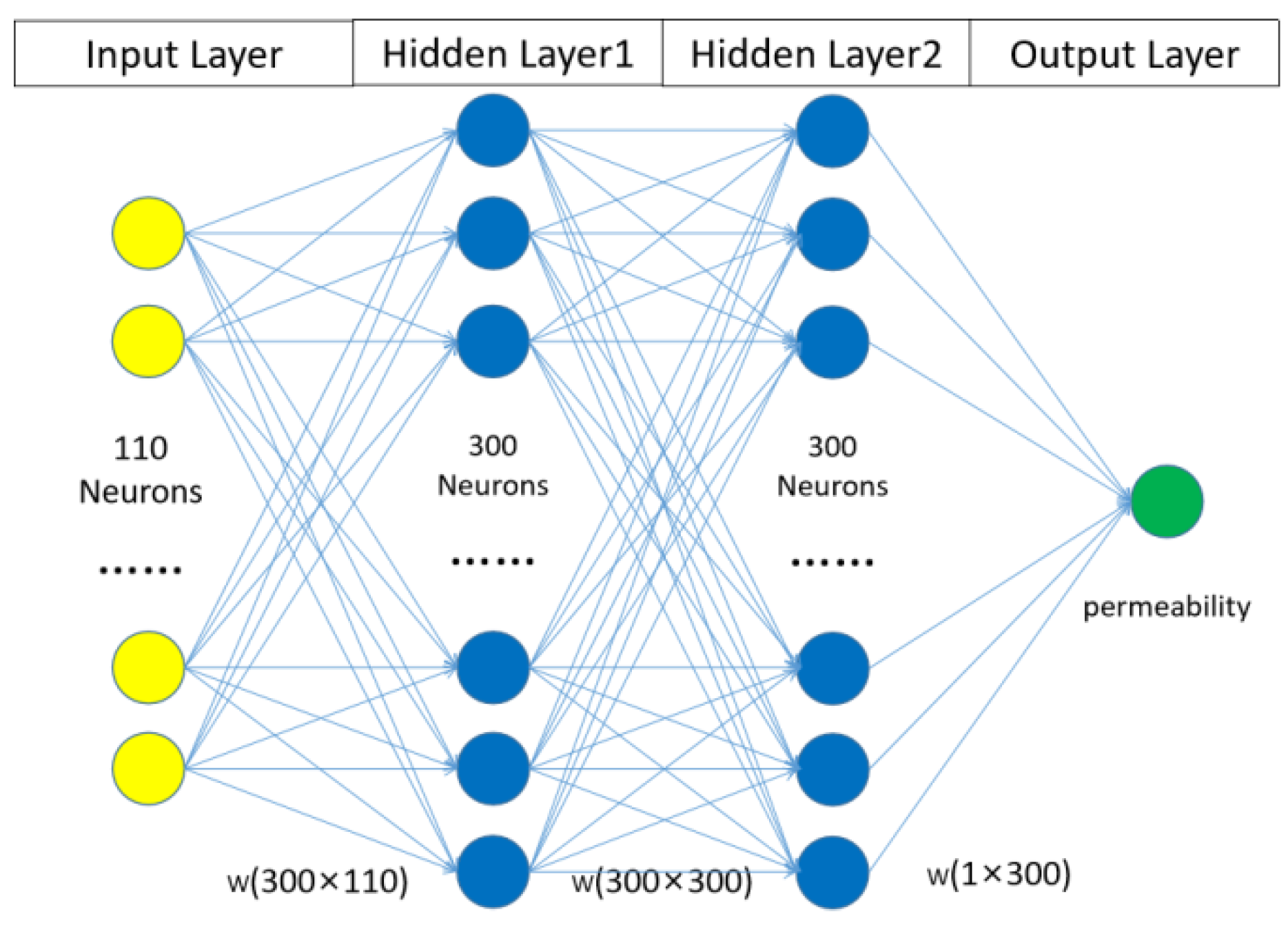
2.1. Classic MLP Network Method
2.2. Fluid–MLP Network Method
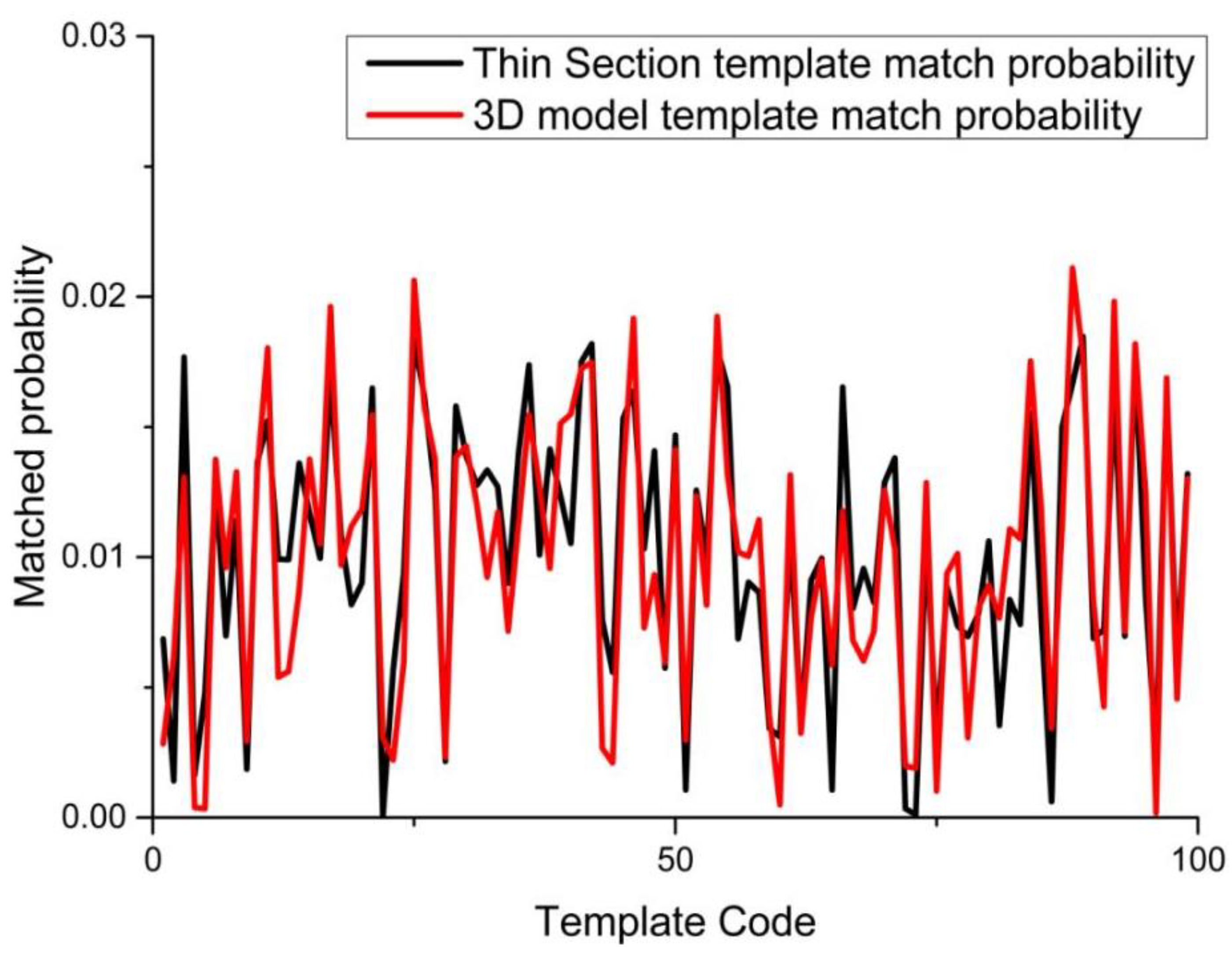
3. Results and Discussion
4. Conclusions
- 1.
- It is proposed that the characteristic parameters obtained from two-dimensional reservoir rock thin-section images can be used to construct an equivalent PNM.
- 2.
- A drop-out input experiment was conducted using the Fluid–MLP network model, in which the input dimensions were reduced from 112 to 6. The average accuracy of permeability prediction on the training samples was around 92%. The reduced number of input dimensions and hidden layer neurons significantly improved training time efficiency, with a slight improvement in accuracy.
- 3.
- Compared to the original MLP network, the Fluid–MLP network achieved an average improvement in prediction accuracy of approximately 4%. We also compared different training sample sizes and found that the Fluid–MLP network outperformed the original MLP network by over 1% in terms of prediction accuracy.
- 4.
- Our comparison with the results obtained when adding hidden layers showed that the addition of hidden layers did not effectively improve the original MLP network or the prediction accuracy of the Fluid–MLP network.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Øren, P.-E.; Bakke, S. Process Based Reconstruction of Sandstones and Prediction of Transport Properties. Transp. Porous Media 2002, 46, 311–343. [Google Scholar] [CrossRef]
- Miele, R.; Grana, D.; Varella, L.E.S.; Barreto, B.V.; Azevedo, L. Iterative geostatistical seismic inversion with rock-physics constraints for permeability prediction. Geophysics 2023, 88, M105–M117. [Google Scholar] [CrossRef]
- Raghavan, R. Some observations on the scale dependence of permeability by pumping tests. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Heap, M.J.; Kennedy, B.M. Exploring the scale-dependent permeability of fractured andesite. Earth Planet. Sci. Lett. 2016, 447, 139–150. [Google Scholar] [CrossRef]
- Shabani, M.; Ghanizadeh, A.; Clarkson, C.R. Gas relative permeability evaluation in tight rocks using rate-transient analysis (RTA) techniques. Mar. Pet. Geol. 2023, 152, 106207. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, X.; Tahmasebi, P.; Luo, C.; Cai, J. NMR-data-driven prediction of matrix permeability in sandstone aquifers. J. Hydrol. 2023, 618, 129147. [Google Scholar] [CrossRef]
- Medici, G.; West, L.J. Reply to discussion on ‘Review of groundwater flow and contaminant transport modelling approaches for the Sherwood Sandstone aquifer, UK; insights from analogous successions worldwide’ by Medici and West (QJEGH, 55, qjegh2021-176). Q. J. Eng. Geol. Hydrogeol. 2023, 56, qjegh2022-097. [Google Scholar] [CrossRef]
- Martyushev, D.A.; Ponomareva, I.N.; Chukhlov, A.S.; Davoodi, S.; Osovetsky, B.M.; Kazymov, K.P.; Yang, Y. Study of void space structure and its influence on carbonate reservoir properties: X-ray microtomography, electron microscopy, and well testing. Mar. Pet. Geol. 2023, 151, 106192. [Google Scholar] [CrossRef]
- Dong, S.; Zeng, L.; Xu, C.; Dowd, P.; Gao, Z.; Mao, Z.; Wang, A. A novel method for extracting information on pores from cast thin-section images. Comput. Geosci. 2019, 130, 69–83. [Google Scholar] [CrossRef]
- Rabbani, A.; Assadi, A.; Kharrat, R.; Dashti, N.; Ayatollahi, S. Estimation of carbonates permeability using pore network parameters extracted from thin section images and comparison with experimental data. J. Nat. Gas Sci. Eng. 2017, 42, 85–98. [Google Scholar] [CrossRef]
- Chen, X.; Yao, G.; Luo, C.; Jiang, P.; Cai, J.; Zhou, K.; Herrero-Bervera, E. Capillary pressure curve determination based on a 2-D cross-section analysis via fractal geometry: A bridge between 2-D and 3-D pore structure of porous media. J. Geophys. Res. Solid Earth 2019, 124, 2352–2367. [Google Scholar] [CrossRef]
- Keehm, Y.; Mukerji, T.; Nur, A. Permeability prediction from thin sections: 3D reconstruction and Lattice-Boltzmann flow simulation. Geophys. Res. Lett. 2004, 31, L04606. [Google Scholar] [CrossRef]
- Okabe, H.; Blunt, M.J. Prediction of permeability for porous media reconstructed using multiple-point statistics. Phys. Rev. E 2004, 70, 066135. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Ahmad, R.; Cai, W.; Mukerji, T. Hierarchical Homogenization With Deep-Learning-Based Surrogate Model for Rapid Estimation of Effective Permeability From Digital Rocks. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025378. [Google Scholar] [CrossRef]
- Neto IA, L.; Misságia, R.M.; Ceia, M.A.; Archilha, N.L.; Oliveira, L.C. Carbonate pore system evaluation using the velocity–porosity–pressure relationship, digital image analysis, and differential effective medium theory. J. Appl. Geophys. 2014, 110, 23–33. [Google Scholar] [CrossRef]
- He, J.; Ding, W.; Li, A.; Sun, Y.; Dai, P.; Yin, S.; Chen, E.; Gu, Y. Quantitative microporosity evaluation using mercury injection and digital image analysis in tight carbonate rocks: A case study from the Ordovician in the Tazhong Palaeouplift, Tarim Basin, NW China. J. Nat. Gas Sci. Eng. 2016, 34, 627–644. [Google Scholar] [CrossRef]
- Mollajan, A.; Ghiasi-Freez, J.; Memarian, H. Improving pore type identification from thin section images using an integrated fuzzy fusion of multiple classifiers. J. Nat. Gas Sci. Eng. 2016, 31, 396–404. [Google Scholar] [CrossRef]
- Pal, A.K.; Garia, S.; Ravi, K.; Nair, A.M. Pore scale image analysis for petrophysical modelling. Micron 2022, 154, 103195. [Google Scholar] [CrossRef]
- Payton, R.L.; Chiarella, D.; Kingdon, A. The upper percolation threshold and porosity–permeability relationship in sandstone reservoirs using digital image analysis. Sci. Rep. 2022, 12, 11311. [Google Scholar] [CrossRef]
- Rabbani, A.; Fernando, A.M.; Shams, R.; Singh, A.; Mostaghimi, P.; Babaei, M. Review of Data Science Trends and Issues in Porous Media Research With a Focus on Image-Based Techniques. Water Resour. Res. 2021, 57, e2020WR029472. [Google Scholar] [CrossRef]
- Ghiasi-Freez, J.; Soleimanpour, I.; Kadkhodaie-Ilkhchi, A.; Ziaii, M.; Sedighi, M.; Hatampour, A. Semi-automated porosity identification from thin section images using image analysis and intelligent discriminant classifiers. Comput. Geosci. 2012, 45, 36–45. [Google Scholar] [CrossRef]
- Zaitoun, N.M.; Aqel, M.J. Survey on Image Segmentation Techniques. Procedia Comput. Sci. 2015, 65, 797–806. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Chanussot, J.; Benediktsson, J.A. Segmentation and classification of hyperspectral images using watershed transformation. Pattern Recognit. 2010, 43, 2367–2379. [Google Scholar] [CrossRef]
- Zhao, F.; Liu, H.; Fan, J. A multiobjective spatial fuzzy clustering algorithm for image segmentation. Appl. Soft Comput. 2015, 30, 48–57. [Google Scholar] [CrossRef]
- Pun, T. A new method for grey-level picture thresholding using the entropy of the histogram. Signal Process. 1980, 2, 223–237. [Google Scholar] [CrossRef]
- Izadi, H.; Sadri, J.; Mehran, N.A. A new intelligent method for minerals segmentation in thin sections based on a novel incremental color clustering. Comput. Geosci. 2015, 81, 38–52. [Google Scholar] [CrossRef]
- Chen, X.; Yao, G. An improved model for permeability estimation in low permeable porous media based on fractal geometry and modified Hagen-Poiseuille flow. Fuel 2017, 210, 748–757. [Google Scholar] [CrossRef]
- Zhang, M.; Ye, G.; van Breugel, K. Microstructure-based modeling of permeability of cementitious materials using multiple-relaxation-time lattice Boltzmann method. Comput. Mater. Sci. 2013, 68, 142–151. [Google Scholar] [CrossRef]
- Al-Mahrooqi, S.; Grattoni, C.; Muggeridge, A.; Zimmerman, R.; Jing, X. Pore-scale modelling of NMR relaxation for the characterization of wettability. J. Pet. Sci. Eng. 2006, 52, 172–186. [Google Scholar] [CrossRef]
- Rabbani, A.; Jamshidi, S. Specific surface and porosity relationship for sandstones for prediction of permeability. Int. J. Rock Mech. Min. Sci. 2014, 71, 25–32. [Google Scholar] [CrossRef]
- Rabbani, A.; Jamshidi, S.; Salehi, S. An automated simple algorithm for realistic pore network extraction from micro-tomography images. J. Pet. Sci. Eng. 2014, 123, 164–171. [Google Scholar] [CrossRef]
- Houston, A.N.; Schmidt, S.; Tarquis, A.M.; Otten, W.; Baveye, P.C.; Hapca, S.M. Effect of scanning and image reconstruction settings in X-ray computed microtomography on quality and segmentation of 3D soil images. Geoderma 2013, 207–208, 154–165. [Google Scholar] [CrossRef]
- Arand, F.; Hesser, J. Accurate and efficient maximal ball algorithm for pore network extraction. Comput. Geosci. 2017, 101, 28–37. [Google Scholar] [CrossRef]
- Al-Kharusi, A.S.; Blunt, M.J. Network extraction from sandstone and carbonate pore space images. J. Pet. Sci. Eng. 2007, 56, 219–231. [Google Scholar] [CrossRef]
- Aghaei, A.; Piri, M. Direct pore-to-core up-scaling of displacement processes: Dynamic pore network modeling and experimentation. J. Hydrol. 2015, 522, 488–509. [Google Scholar] [CrossRef]
- Politis, M.; Kikkinides, E.; Kainourgiakis, M.; Stubos, A. A hybrid process-based and stochastic reconstruction method of porous media. Microporous Mesoporous Mater. 2008, 110, 92–99. [Google Scholar] [CrossRef]
- Liu, X.; Sun, J.; Wang, H. Reconstruction of 3-D digital cores using a hybrid method. Appl. Geophys. 2009, 6, 105–112. [Google Scholar] [CrossRef]
- Zhao, X.; Yao, J.; Yi, Y. A new stochastic method of reconstructing porous media. Transp. Porous Media 2006, 69, 1–11. [Google Scholar] [CrossRef]
- Hajizadeh, A.; Safekordi, A.; Farhadpour, F.A. A multiple-point statistics algorithm for 3D pore space reconstruction from 2D images. Adv. Water Resour. 2011, 34, 1256–1267. [Google Scholar] [CrossRef]
- Ju, Y.; Huang, Y.; Zheng, J.; Qian, X.; Xie, H.; Zhao, X. Multi-thread parallel algorithm for reconstructing 3D large-scale porous structures. Comput. Geosci. 2017, 101, 10–20. [Google Scholar] [CrossRef]
- Wu, K.; Nunan, N.; Crawford, J.W.; Young, I.M.; Ritz, K. An efficient Markov chain model for the simulation of heterogeneous soil structure. Soil Sci. Soc. Am. J. 2004, 68, 346–351. [Google Scholar] [CrossRef]
- Quiblier, J.A. A new three-dimensional modeling technique for studying porous media. J. Colloid Interface Sci. 1984, 98, 84–102. [Google Scholar] [CrossRef]
- Tahmasebi, P.; Hezarkhani, A.; Sahimi, M. Multiple-point geostatistical modeling based on the cross-correlation functions. Comput. Geosci. 2012, 16, 779–797. [Google Scholar] [CrossRef]
- Straubhaar, J.; Walgenwitz, A.; Renard, P. Parallel Multiple-Point Statistics Algorithm Based on List and Tree Structures. Math. Geosci. 2013, 45, 131–147. [Google Scholar] [CrossRef]
- Strebelle, S. Conditional Simulation of Complex Geological Structures Using Multiple-Point Statistics. J. Int. Assoc. Math. Geol. 2002, 34, 1–21. [Google Scholar] [CrossRef]
- Bakhshian, S.; Hosseini, S.A.; Shokri, N. Pore-scale characteristics of multiphase flow in heterogeneous porous media using the lattice Boltzmann method. Sci. Rep. 2019, 9, 3377. [Google Scholar] [CrossRef]
- Tölke, J. Lattice Boltzmann simulations of binary fluid flow through porous media. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2002, 360, 535–545. [Google Scholar] [CrossRef] [PubMed]
- Ahrenholz, B.; Tölke, J.; Lehmann, P.; Peters, A.; Kaestner, A.; Krafczyk, M.; Durner, W. Prediction of capillary hysteresis in a porous material using lattice-Boltzmann methods and comparison to experimental data and a morphological pore network model. Adv. Water Resour. 2008, 31, 1151–1173. [Google Scholar] [CrossRef]
- Küntz, M.; Mareschal, J.C.; Lavallée, P. Numerical estimation of electrical conductivity in saturated porous media with a 2-D lattice gas. Geophysics 2000, 65, 766–772. [Google Scholar] [CrossRef]
- Andrä, H.; Combaret, N.; Dvorkin, J.; Glatt, E.; Han, J.; Kabel, M.; Keehm, Y.; Krzikalla, F.; Lee, M.; Madonna, C.; et al. Digital rock physics benchmarks—Part I: Imaging and segmentation. Comput. Geosci. 2013, 50, 25–32. [Google Scholar] [CrossRef]







| Pore and Throat Parameter | Include Data Content | Number of Parameters | Can be Used to Reconstruct PNM |
|---|---|---|---|
| Pore type | Pore type rank: 1~6 | 1 | no |
| Lithology | Lithology rank: 1~14 | 1 | no |
| 2D porosity | Porosity % | 1 | yes |
| Average coordination number | Decimal number | 1 | yes |
| Reservoir code | Integer | 1 | no |
| Well number | Well name code: 1~2000 | 1 | no |
| Tortuosity | Decimal number | 1 | yes |
| Pore shape factor distribution | Range (0~1.0) | 13 | yes |
| Average pore–throat ratio | Decimal number | 1 | yes |
| Max throat count | Integer | 1 | no |
| Pore diameter distribution | Range (2 μm~2000 μm) | 40 | yes |
| Throat diameter distribution | Range (2 μm~2000 μm) | 40 | yes |
| Coordination number distribution frequency | Range (0~8.0) | 8 | yes |
| Permeability | The same depth core analysis permeability | 1 | no |
| Network Structure | Number of Hidden Nodes | Training Average Relative Error (after 1 × 107 iterations) | Proportion of Correct Predictions (Error within ±10% Measured Permeability) |
|---|---|---|---|
| Original MLP | 300 | <1 × 10−5 | 89% (training time 671s) |
| Original MLP | 300 + 300 | <1 × 10−5 | 90% (training time 1950s) |
| Fluid–MLP | 100 | <1 × 10−6 | 93% (training time 101s) |
| Fluid–MLP | 300 | <1 × 10−6 | 93% (training time 324s) |
| Fluid–MLP | 300 + 300 | <1 × 10−6 | 94% (training time 1560s) |
| Dropped Parameter | Proportion of Correct Predictions with All 110 and with 6 Parameters | Proportion of Correct Predictions after Dropping 1 Parameter | Difference with 6 Parameters |
|---|---|---|---|
| Pore type rank | 89%, 93% | 70% | 23% |
| Lithology rank | 89%, 93% | 56% | 37% |
| 2D porosity | 89%, 93% | 84% | 9% |
| Average pore–throat ratio | 89%, 93% | 70% | 24% |
| Average throat diameter | 89%, 93% | 78% | 15% |
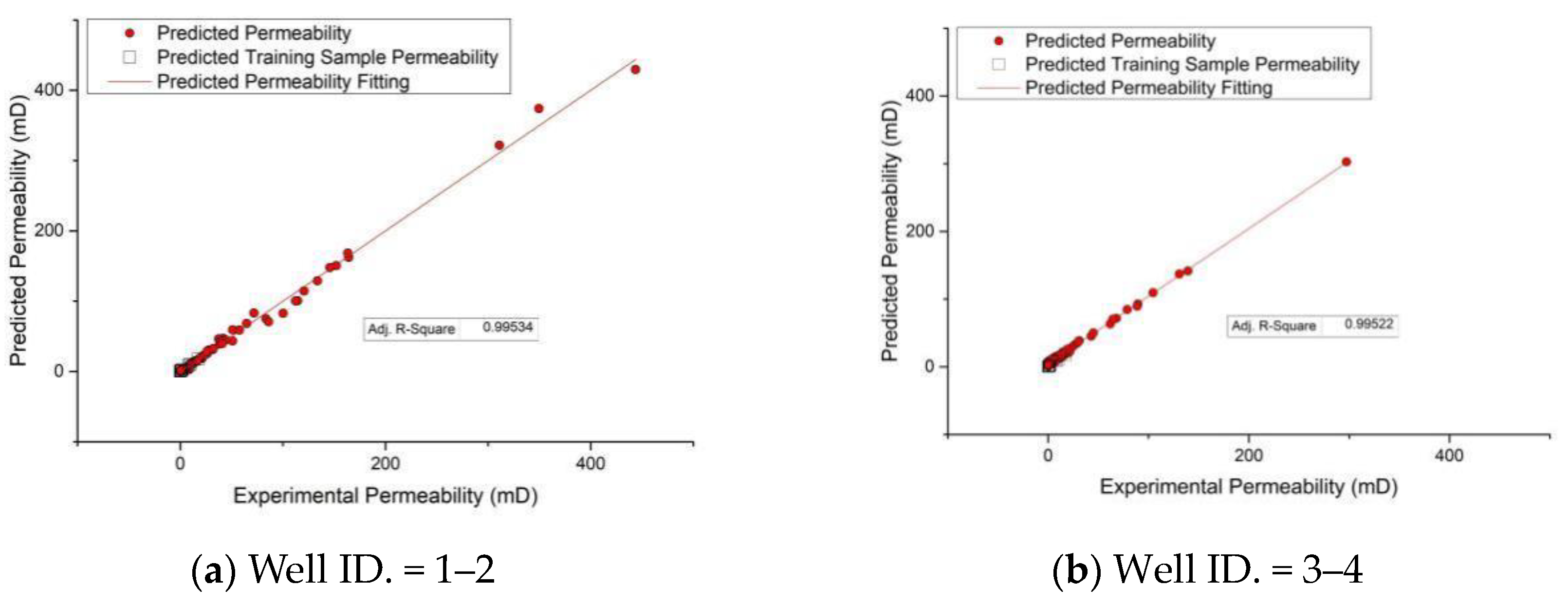
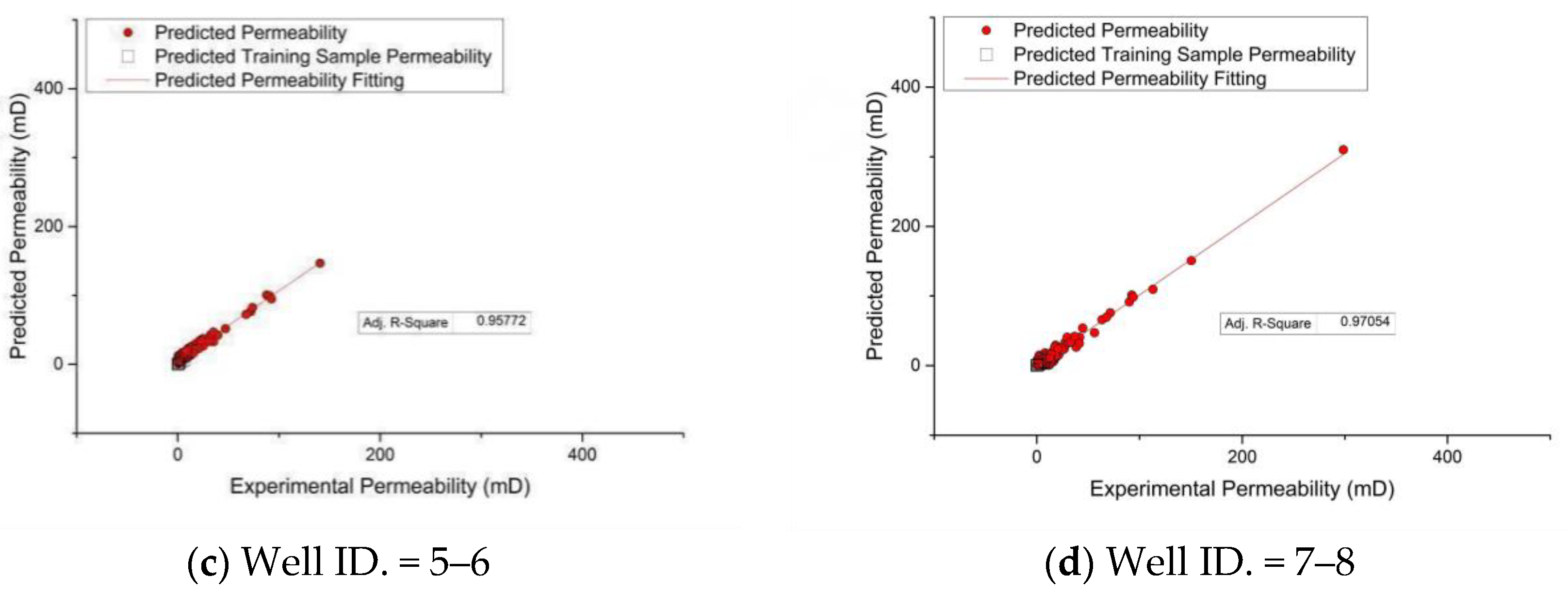
| Well Number | Basin Number | Number of Samples | Proportion of Correct Predictions |
|---|---|---|---|
| 1–2 | 1 | 287 | 92% |
| 3–4 | 1 | 210 | 92% |
| 5–6 | 2 | 181 | 90% |
| 7–8 | 2 | 322 | 94% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Wan, H.; Chen, J.; Huang, X.; Cui, S.; Qin, J.; Yan, Z.; Qiao, D.; Shi, Z. Estimation of 3D Permeability from Pore Network Models Constructed Using 2D Thin-Section Images in Sandstone Reservoirs. Energies 2023, 16, 6976. https://doi.org/10.3390/en16196976
Luo C, Wan H, Chen J, Huang X, Cui S, Qin J, Yan Z, Qiao D, Shi Z. Estimation of 3D Permeability from Pore Network Models Constructed Using 2D Thin-Section Images in Sandstone Reservoirs. Energies. 2023; 16(19):6976. https://doi.org/10.3390/en16196976
Chicago/Turabian StyleLuo, Chengfei, Huan Wan, Jinding Chen, Xiangsheng Huang, Shuheng Cui, Jungan Qin, Zhuoyu Yan, Dan Qiao, and Zhiqiang Shi. 2023. "Estimation of 3D Permeability from Pore Network Models Constructed Using 2D Thin-Section Images in Sandstone Reservoirs" Energies 16, no. 19: 6976. https://doi.org/10.3390/en16196976
APA StyleLuo, C., Wan, H., Chen, J., Huang, X., Cui, S., Qin, J., Yan, Z., Qiao, D., & Shi, Z. (2023). Estimation of 3D Permeability from Pore Network Models Constructed Using 2D Thin-Section Images in Sandstone Reservoirs. Energies, 16(19), 6976. https://doi.org/10.3390/en16196976





