Research on the Modulation and Control Strategy for a Novel Single-Phase Current Source Inverter

Abstract

Compared to the voltage source inverter, the current source inverter (CSI) can boost voltage and improve filtering performance. However, the DC side of CSI is not a real current source, and the DC input current comprises a DC power supply and an inductor. In the switching process, the DC-link inductor is charged or discharged and is in an uncontrollable state. This paper proposes a novel CSI topology containing five switching tubes and a modulation strategy based on the hysteresis control strategy of the DC-link current. Due to the conduction and switching loss being positive to the DC-link current, the calculation method for the least reference value of the DC-link current is derived to meet power requirements. By constructing a virtual axis, we then present the control strategy of the output voltage in a two-phase rotating reference frame. Finally, we carry out the simulation and experiment are to validate the proposed topology, modulation, and control strategy.

1. Introduction

Inverters can be categorized as voltage source inverters (VSI) [1] and current source inverters (CSI) [2] according to the characteristics of input power supplies. Some unique advantages of CSIs have been discovered [3], such as their boost capacity, inherent short-circuit protection capacity, and AC filtering structure. CSI, therefore, has potential applications [4] in the solar photovoltaic industry, wind energy power generation, motor drive systems, and HVDC transmission systems.

In recent years, various control and modulation strategies for CSI have been proposed [5], such as decoupling methods, low common voltage modulation, and digital vector control strategy. However, the DC-link current is considered a constant value in the above studies in which the charging or discharging process of the DC-link inductor has been ignored, leading to the DC-link current being discontinuous or continuously increasing.

Unlike VSI, the DC-link current of CSI is formed by the DC input voltage DC-link inductor, and constant DC-link current output is a necessary condition for high performance operation of CSI [6]. In [7,8,9,10,11], several novel CSI topologies are proposed to achieve control of the DC-link current. In [7], a three-phase current source rectifier (CSR) is introduced to adjust the DC-link current, but this topology is very complex and only suitable for AC-DC-AC applications. A buck converter is added to the DC side to regulate the DC-link current in [8]. In [6], the buck converter is replaced with a bi-directional converter that can control the current, and the buck operation can also be realized. However, the switching and conduction losses increase as the converter is introduced. In [9], a buck-boost CSI is proposed, which has the advantages of a simple structure and large voltage output range, but the control strategy is difficult to implement. The current-fed quasi-Z-source inverter is proposed in [10]. However, with the addition of many passive components, both efficiency and power density are greatly reduced.

In [11], an additional switching tube and diode are connected in parallel with the DC-side inductor of the three-phase CSI. The DC-side inductor can self-continuate when the switch is turned on. During the zero vector period, the continuous current mode is used to replace the traditional magnetizing mode, which can prevent the increase of the DC-link current. On this basis, a novel single-phase five-switch CSI topology is proposed in this paper. The modulation and control strategies are studied to obtain the constant DC-link current and high-quality AC voltage output. Finally, the simulation and experimental verification are carried out.

2. Topology and Operating Modes of the Proposed Single-Phase CSI

2.1. Analysis of the Proposed Single-Phase CSI’s Operating Modes

The topology of the proposed single-phase CSI is shown in Figure 1. The DC side is composed of a DC voltage source and DC-link inductance L_dc. The inverter part is composed of switching tubes (S₁, S₂, S₃, S₄) and diodes (D₁, D₂, D₃, D₄). The AC side contains the filter capacitor C and the resistive load R. The switching tube S₀ and diode D₀ are parallel with L_dc.

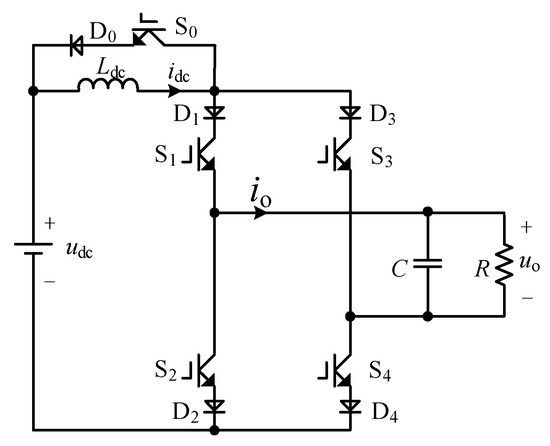
Figure 1. The topology of the proposed single-phase CSI.

There are four operating modes of the proposed single-phase CSI. The corresponding switching states are shown in Table 1.

Table 1. The operating modes, switching state, and switching function.

Operating Modes	Switching State	Switching Function p and q
magnetizing mode	S1 and S2 ON, S0, S3, and S4 OFF	p = 0, q = 1
energy-supplying mode I	S1 and S4 ON, S0, S2, and S3 OFF	p = 1, q = 0
energy-supplying mode II	S2 and S3 ON, S0, S1, and S4 OFF	p = −1, q = 0
freewheeling model	S0 ON, S1, S2, S3, and S4 OFF	p = 0, q = 0

(1) Magnetizing mode: S₁ and S₂ are turned on, and the equivalent circuit under magnetizing mode is shown in Figure 2a. At this moment, i_o is equal to 0 A, the u_dc is charging to L_dc, and C provides energy for the load separately.

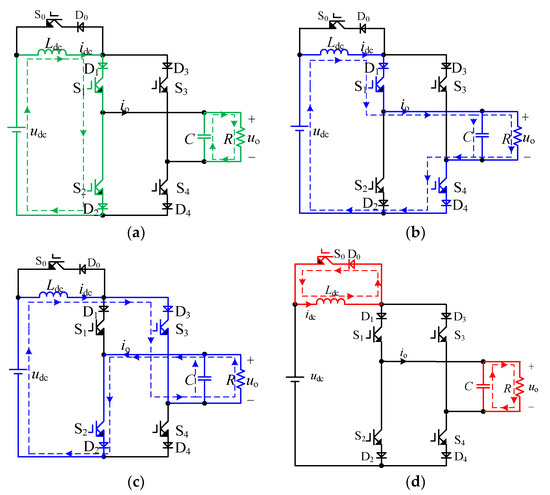
Figure 2. The operating modes of the proposed single-phase CSI: (a) magnetizing mode; (b) energy-supplying mode I; (c) energy-supplying mode II; (d) freewheeling model.

(2) Energy-supplying mode I: S₁ and S₄ are turned on, and the equivalent circuit under this operating mode is shown in Figure 2b. At this moment, i_o is equal to i_dc, and the u_dc and L_dc provide energy to the AC load together.

(3) Energy-supplying mode II: S₂ and S₃ are turned on, and the equivalent circuit under this operating mode is shown in Figure 2c. Different from energy-supplying mode I, the polarity of the output current is negative; i_o is equal to −i_dc.

(4) Freewheeling model: Only S₀ is turned on, and the equivalent circuit under the freewheeling model is shown in Figure 2d. The i_dc freewheels through S₀, and C provides energy for the load separately.

Two switching functions (p and q) are defined and shown in Table 1. The p is used to indicate whether the CSI is operating in energy-supplying mode, and the math relationship between i_dc and i_o can be expressed as

$$i_{\mathrm{o}}=i_{\mathrm{dc}}p$$

(1)

The state equation of u_o follows:

$$C\frac{\mathrm{d}{u}_{\mathrm{o}}}{\mathrm{d}t}=p{i}_{\mathrm{dc}}-\frac{u_{\mathrm{o}}}{R}$$

(2)

q is used to indicate whether the CSI is operating in magnetizing mode. The state equation of i_o follows:

$$L_{\mathrm{dc}}\frac{\mathrm{d}{i}_{\mathrm{dc}}}{\mathrm{d}t}=q{u}_{\mathrm{dc}}-p{u}_{\mathrm{o}}$$

(3)

Since the conduction current of all switching tubes is i_dc, the current stresses of all switching tubes are equal to the DC-link current. The voltage stresses can be derived according to Figure 2, and the voltage stresses of all switching tubes under different operating modes are summarized in Table 2.

Table 2. Voltage stresses of all switching tubes under different operating modes.

Operating Mode	Withstand Voltage S0	Withstand Voltage S1	Withstand Voltage S2	Withstand Voltage S3	Withstand Voltage S4
Magnetizing mode	udc	0	0	−uo	uo
Energy-supplying mode	udc − uo	0	−uo	−uo	0
Freewheeling model	0	uo	−udc − uo	0	−udc

2.2. Comparison of Different CSI Topologies

The recent literature presents many CSI structures comprising distinct tradeoffs among different topologies, as shown in Figure 3. According to [12,13], a cost function (CF) is established in (4) to carry out a fair comparison of different CSI topologies:

$$CF=N_V(N_{\mathrm{US}}+2N_{\mathrm{BS}}+N_D+N_C+N_{\mathrm{drv}}+N_T)/N_l$$

(4)

where N_V is the number of DC voltages, N_US is the number of unidirectional switches, N_BS is the number of bidirectional switches, N_D is the number of diodes, N_C is the number of capacitors, N_drv is the number of individual drivers, N_T is the number of transformers, and N_l is the number of output current levels.

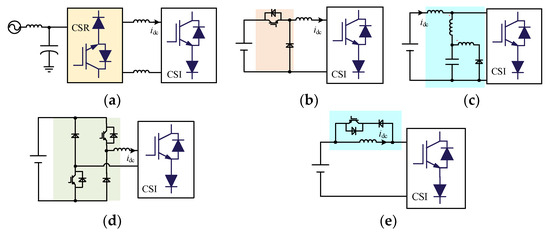
Figure 3. The topologies of different CSI: (a) current source rectifier; (b) buck converter; (c) quasi-Z source network; (d) bidirectional DC chopper; (e) proposed single-phase CSI.

The comparison result is presented in Table 3. Although the quasi-Z source network receives the lowest CF, it contains numerous passive components, and its control system is too complex. The proposed single-phase CSI and the buck converter have the same CF. However, the buck converter contains more switches than the proposed single-phase CSI. The bidirectional DC chopper’s CF is slightly higher than the proposed one because of the additional two diodes and switching tubes. The current source rectifier rates the worst CF because it includes too many components.

Table 3. Comparison of different CSI topologies.

Parameter	Current Source Rectifier	Buck Converter	Quasi-Z Source Network	Bidirectional DC Chopper	Proposed Single-Phase CSI
NV	1	1	1	1	1
NUS	0	0	0	0	0
NBS	8	5	4	6	5
ND	8	5	5	6	5
NC	2	1	2	1	1
Ndrv	8	5	4	6	5
NT	0	0	1	0	0
Nl	3	3	3	3	3
CF	11.33	7	6.67	8.33	7
Input H Bridge	Yes	No	No	Yes	No
Modulation	PWM	PWM	PWM	PWM	PWM

3. Modulation Strategy Based on DC-Link Current Control

Unlike VSI, switching signals cannot be directly generated by comparing modulated signals with carrier waves [14]. In [15], a logic conversion circuit is adopted to convert the switching signals, which will delay them. In this section, a novel modulation strategy is presented which can be implemented by the DSP without a logic conversion circuit. Three logic signals (p₁, p₂, and p₃) are set, where p₁ represents the comparison result between the modulation wave and carrier wave, as shown in Figure 4, and where d is the duty cycle and is defined as

$$d=\frac{\left|i_{\mathrm{o}}\right|}{i_{\mathrm{dc}}}$$

(5)

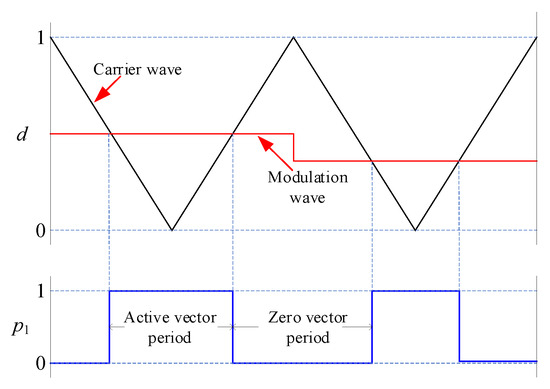
Figure 4. The diagram of p₁, carrier wave, and modulation wave.

p₁ = 1 represents the active vector period, and the CSI operates at energy-supplying mode I or II, which is determined by the polarity of i_o. p₂ represents the polarity of i_o. If i_o > 0, p₂ = 1; otherwise, p₂ = 0.

p₁ = 0 represents the zero vector period, and the CSI operates on either the magnetizing mode or freewheeling model, which is determined by i_dc. If i_dc > the reference value $i_{\mathrm{dc}}^{*}$, the freewheeling model will be selected to prevent i_dc from increasing in the zero vector period. Otherwise, the magnetizing mode will be implemented to charge L_dc in the zero vector period. p₃ is defined to represent the math relationship between i_dc and $i_{\mathrm{dc}}^{*}$. If i_dc > $i_{\mathrm{dc}}^{*}$, p₃ = 1; else, p₃ = 0. The changing process of i_dc and p₃ is described in Figure 5. i_dc can be adjusted according to p₃. This approach belongs to a hysteresis control method [16].

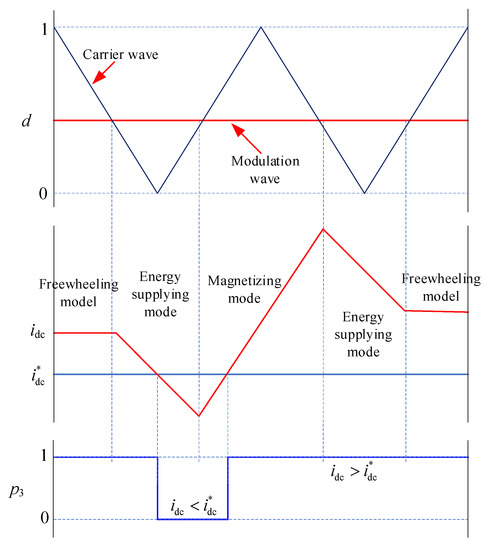
Figure 5. The changing process of i_dc and p₃.

Based on the above settings and analysis, the production logic of the five switching signals is shown in Figure 6. The specific logic expression for each switching is described as follows:

$$\left\{\begin{array}{l}{p}_{\mathrm{S}1}={\overline{p}}_1\&{\overline{p}}_3|p_2\\ p_{\mathrm{S}2}={\overline{p}}_1\&{\overline{p}}_3|{\overline{p}}_2\\ p_{\mathrm{S}3}=p_1\&{\overline{p}}_2\\ p_{\mathrm{S}4}=p_1\&p_2\\ p_{\mathrm{S}0}={\overline{p}}_2\&p_3\end{array}\right.$$

(6)

where p_S1, p_S2, p_S3, p_S4, and p_S5 represent the driving logic of switch S₁, S₂, S₃, S₄, and S₅, respectively.

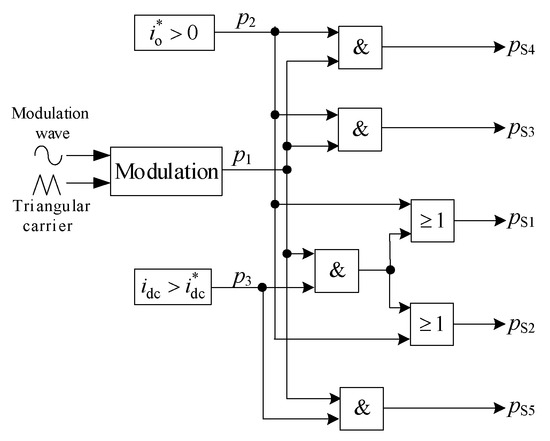
Figure 6. Logical conversion for the proposed single-phase CSI.

4. Calculation for the Optimal Reference of DC-Link Current

In Section 3, a DC-link current hysteresis control is introduced into the modulation scheme. However, the reference of the DC-link current must be determined for the following reasons [17]. If $i_{\mathrm{dc}}^{*}$ is set too small, the DC-link current is unable to provide sufficient power to the AC load. If $i_{\mathrm{dc}}^{*}$ is set too great, the conduction loss, switching loss, and harmonic distortion will increase. Thus, the DC-link current should be reduced to satisfy the current requirements. The calculation method for the optimal reference of the DC-link current is derived in this section.

It is assumed that u_o remains in a constant state in a switching period. Under energy-supplying mode, the reduction ∆i_{dc_down} of i_dc can be expressed as follows:

$$\Delta i_{\mathrm{dc}\_\mathrm{down}}=\frac{T_{\mathrm{s}}}{L_{\mathrm{dc}}}d(t)\left[u_{\mathrm{o}}(t)-u_{\mathrm{dc}}\right]$$

(7)

The increment of ∆i_{dc_up} under magnetizing mode can be expressed as

$$\Delta i_{\mathrm{dc}\_\mathrm{up}}=\frac{u_{\mathrm{dc}}{T}_{\mathrm{s}}}{L_{\mathrm{dc}}}\left[1-d(t)\right]$$

(8)

According to (7) and (8), the total reduction ∆i_dc of i_dc in a switching period can be expressed as

$$\Delta i_{\mathrm{dc}}=\Delta i_{\mathrm{dc}\_\mathrm{down}}-\Delta i_{\mathrm{dc}\_\mathrm{up}}=\frac{T_s}{L_{\mathrm{dc}}}\left[u_{\mathrm{o}}(t)d(t)-u_{\mathrm{dc}}\right]$$

(9)

By substituting (5) with (9), ∆i_dc can be rewritten as

$$\Delta i_{\mathrm{dc}}=\frac{T_s}{L_{\mathrm{dc}}}\left[\frac{u_{\mathrm{o}}(t)i_{\mathrm{o}}^{}(t)}{i_{\mathrm{dc}}(t)}-u_{\mathrm{dc}}\right]$$

(10)

Ignoring the harmonic component and initial phase, u_o is expressed as

$$u_{\mathrm{o}}(t)=U\sin \omega t$$

(11)

where U represents the fundamental amplitude of u_o, and ω represents the fundamental frequency. i_o is expressed as

$$i_{\mathrm{o}}(t)=I\sin (\omega t+\theta )$$

(12)

where I represents the amplitude of i_o, and θ represents the initial phase of i_o. Due to the load of the inverter consisting of the resistance and the capacitance paralleling with the load, the following relations are satisfied:

$$\left\{\begin{array}{l}I=U\sqrt{1+{(\omega CR)}^2}/R\\ \theta =\arctan (\omega CR)\end{array}\right.$$

(13)

Substituting (11) and (12) with (10), the following can be obtained:

$$\Delta i_{\mathrm{dc}}=\frac{T_s}{L}\left[\frac{UI\sin (\omega t)\sin (\omega t+\theta )}{i_{\mathrm{dc}}(t)}-u_{\mathrm{dc}}\right]$$

(14)

Formula (14) is simplified as follows:

$$\Delta i_{\mathrm{dc}}=\frac{T_{\mathrm{s}}}{2L}\left\{\frac{UI\left[\cos \theta -\cos (2\omega t+\theta )\right]}{i_{\mathrm{dc}}(t)}-2u_{\mathrm{dc}}\right\}$$

(15)

The maximum reduction ∆i_dcmax of i_dc in a switching period is shown as follows:

$$\Delta i_{dc\max }=\frac{T_{\mathrm{s}}}{2L}\left[\frac{UI(\cos \theta +1)}{i_{\mathrm{dc}}(t)}-2u_{\mathrm{dc}}\right]$$

(16)

If ∆i_dcmax < 0, i_dc can continue increasing in any switching period, which consists of magnetizing mode and energy-supplying mode. Thus, i_dc needs to be satisfied as follows:

$$i_{\mathrm{dc}}^{}>\frac{UI(\cos \theta +1)}{2u_{\mathrm{dc}}}$$

(17)

Substituting (13) with (17), and replacing i_dc with $i_{\mathrm{dc}}^{*}$, Formula (17) can be rewritten as follows:

$$i_{\mathrm{dc}}^{*}>\frac{U_{}^2\left[1+\sqrt{1+{(\omega CR)}^2}\right]}{2u_{\mathrm{dc}}R}$$

(18)

The theoretical waveforms in a fundamental period, including i_dc, u_o, and switching signals are presented in Figure 7. Based on the operation mode, switching signals, DC-link current optimal reference, and control strategy, the theoretical waveform is divided into eight stages:

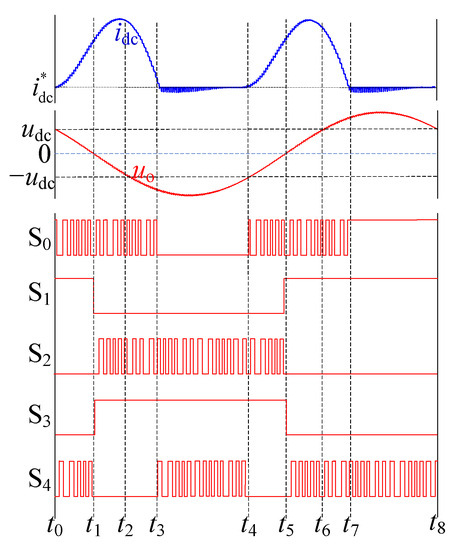
Figure 7. The theoretical waveforms in a fundamental period.

(1) Stage 1 (t₀ − t₁): 0 < u_o < u_dc, L_dc is charged in energy-supplying mode I; S₁ remains on-state; S₀ is turned on in the zero vector period to prevent i_dc from continuously increasing.

(2) Stage 2 (t₁ − t₂): −u_dc < u_o < 0, L_dc is charged in energy-supplying mode II; S₃ remains on-state; S₀ is turned on in the zero vector period to prevent i_dc from continuously increasing.

(3) Stage 3 (t₂ − t₃): u_o < −u_dc; L_dc discharges in energy-supplying mode II due to i_dc being still greater than $i_{\mathrm{dc}}^{*}$; S0 is also turned on in the zero vector period; i_dc begins to decrease.

(4) Stage 4 (t₃ − t₄): u_o < −u_dc and i_dc < $i_{\mathrm{dc}}^{*}$; to prevent i_dc further decrease, S4 is turned on in the zero vector period, since $i_{\mathrm{dc}}^{*}$ is the optimal reference of the DC-link current; i_dc will be clamped near $i_{\mathrm{dc}}^{*}$.

(5) Stage 5 (t₄ − t₅), Stage 6 (t₅ − t₆), Stage 7 (t₆ − t₇), and Stage 8 (t₇ − t₈) are similar to Stage 1 (t₀ − t₁), Stage 2 (t₁ − t₂), Stage 3 (t₂ − t₃), and Stage 4 (t₃ − t₄), respectively.

5. Control Strategy of the Output Voltage

Since the PI controller is not suitable for AC models, the math model of the singe phase CSI is established in d-q frame. The fundamental component of u_o is represented as follows:

$$u_{\mathrm{o}}(t)=u_{\mathrm{od}}\sin (\omega t)+u_{\mathrm{oq}}\cos (\omega t)$$

(19)

where u_od = U, and u_oq = 0. The quadrature virtual component of u_o is introduced, which is shown as follows:

$${u^{\prime }}_{\mathrm{o}}(t)=-U_{\mathrm{o}}\sin (\omega t-\frac{\pi }{2})$$

(20)

The d-q frame components u_od and u_oq can be obtained as follows:

$$\left\{\begin{array}{l}{u}_{\mathrm{od}}(t)=u_{\mathrm{o}}(t)\sin \left(\omega t\right)+u_{\mathrm{o}}^{\prime }(t)\cos \left(\omega t\right)\\ u_{\mathrm{oq}}(t)=u_{\mathrm{o}}(t)\cos \left(\omega t\right)-u_{\mathrm{o}}^{\prime }(t)\sin \left(\omega t\right)\end{array}\right.$$

(21)

The same representation for i_o is shown as follows:

$$i_{\mathrm{o}}(t)=i_{\mathrm{od}}\sin \left(\omega t\right)+i_{\mathrm{oq}}\cos \left(\omega t\right)$$

(22)

where i_od and i_oq are the DC component. Substituting Equations (21) and (22) with (2), it yields the following:

$$\left\{\begin{array}{l}C\frac{d{u}_{\mathrm{od}}}{dt}+\frac{u_{\mathrm{od}}}{R}=\omega C{u}_{\mathrm{oq}}+i_{\mathrm{od}}\\ C\frac{d{u}_{\mathrm{oq}}}{dt}+\frac{u_{\mathrm{oq}}}{R}=-\omega C{u}_{\mathrm{od}}+i_{\mathrm{oq}}\end{array}\right.$$

(23)

u_od and u_oq are adjusted by the PI controller, and feedback decoupling is adopted to cancel out the coupling terms ωCu_od and ωCu_oq. The control strategy of u_o is shown in Figure 8, where $u_{\mathrm{od}}^{*}$ and $u_{\mathrm{oq}}^{*}$ are the reference of u_od and u_oq, and $i_{\mathrm{od}}^{*}$ and $i_{\mathrm{oq}}^{*}$ are the reference of i_od and i_oq, respectively. $i_{\mathrm{od}}^{*}$ and $i_{\mathrm{oq}}^{*}$ are expressed as follows:

$$\left\{\begin{array}{l}{i}_{\mathrm{od}}^{*}=\frac{k_{\mathrm{p}}s+k_{\mathrm{i}}}{s}(u_{\mathrm{od}}^{*}-u_{\mathrm{od}})-\omega C{u}_{\mathrm{oq}}\\ i_{\mathrm{oq}}^{*}=\frac{k_{\mathrm{p}}s+k_{\mathrm{i}}}{s}(u_{\mathrm{oq}}^{*}-u_{\mathrm{oq}})+\omega C{u}_{\mathrm{od}}\end{array}\right.$$

(24)

where k_p and k_i are the proportional coefficient and integral coefficient, respectively.

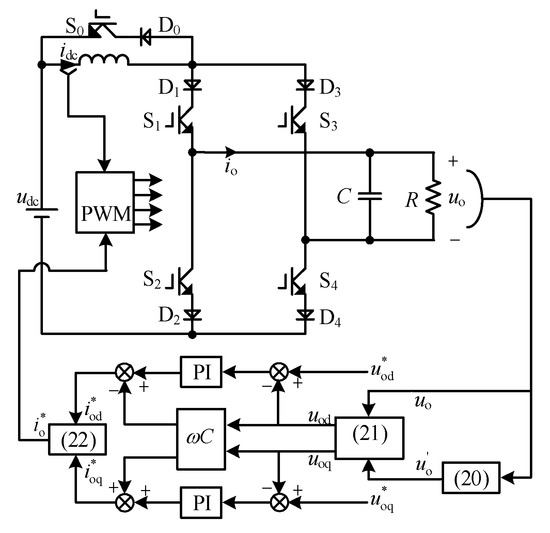
Figure 8. Control strategy diagram of output voltage.

Considering the digital delay, the open-loop transfer function G_open(s) can be derived as follows:

$$G_{\mathrm{open}}(s)=\frac{k_{\mathrm{p}}s+k_{\mathrm{i}}}{s(1+T_{\mathrm{s}}s)(1+RCs)}$$

(25)

where T_s is the switching period and is equal to 100 μs. Zero point is set to offset the pole, and the cutoff frequency is set at 1 kHz. k_p and k_i are set as 2000πRC and 2000π. The Bode plot of G_open(s) is shown in Figure 9a, and the Bode plot of the closed-loop transfer function G_close(s) is shown in Figure 9b. Good track performance and fast dynamic response can thus be achieved.

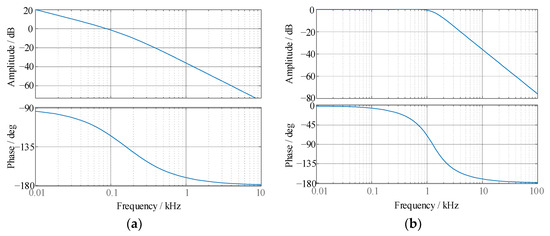
Figure 9. The Bode-plots of the output voltage control: (a) G_open(s), (b) G_close(s).

6. Experimental Results

An experimental prototype of a single-phase CSI is established and shown in Figure 10. The corresponding soft simulation is presented in the Supplementary Material. The algorithm of modulation and control are implemented by TMS320F28335, and the IGBT and diode are PM400HSA120 and RM300HA-24F, respectively. u_dc is supplied by a DC power supply. The parameters of the passive components are consistent with Table 4.

Figure 10. Experimental prototype of proposed single-phase CSI.

Table 4. Parameters of experiment.

Name	Value
DC input voltage (V)	25
AC output voltage (V)	30~150
Load power (W)	≤103
Output frequency (Hz)	≤500 Hz
Switching frequency (Hz)	10 k
Sampling frequency (Hz)	10 k
Ldc (mH)	4
C (μF)	265
R (Ω)	25

6.1. Experimental Results of Steady-State

The amplitude and frequency of the reference of u_o are 50 V and 50 Hz. $i_{\mathrm{dc}}^{*}$ is set to 13.5 A. The experimental waveforms of i_dc and u_o are shown in Figure 11a, where the amplitude and frequency of u_o are consistent with the reference, and i_dc is maintained in the range of 13.5 A to 15 A. Figure 11b shows that u_o’s THD is only 0.61%, and its harmonics are limited.

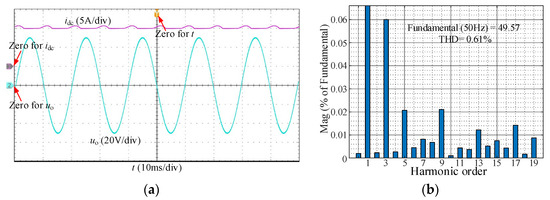
Figure 11. Experimental results under $i_{\mathrm{dc}}^{*}$ = 13.5 A: (a) experimental waveforms of i_dc and u_o; (b) FFT results.

In order to verify that $i_{\mathrm{dc}}^{*}$ = 13.5 A is the optimal reference of the DC-link current, a steady-state experiment is carried out in Figure 12, where $i_{\mathrm{dc}}^{*}$ is set to 11.5 A. A large fluctuation occurs in i_dc, which cannot maintain above 11.5 A. In some switching periods, i_dc cannot meet the requirement of current for the AC load. Therefore, significant low-order harmonic distortion occurs in u_o, whose THD is 23.88%, and fundamental amplitude is 38.5 V, lower than the reference 50 V.

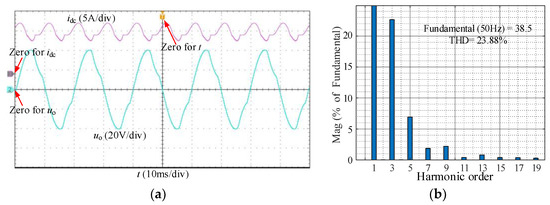
Figure 12. Experimental results under $i_{\mathrm{dc}}^{*}$ = 11.5 A: (a) experimental waveforms of i_dc and u_o; (b) FFT results.

In Figure 13, $i_{\mathrm{dc}}^{*}$ is set to 20 A, and i_dc maintains above 20 A with small fluctuation. Since i_dc is higher than the amplitude of i_o, u_o can track the reference. u_o’s THD is 1.38%, greater than the one when $i_{\mathrm{dc}}^{*}$ = 13.5 A. Meanwhile, the switching loss and conduction loss of IGBT and diode are positively related to i_dc. The above experimental results show that the calculation method for the optimal reference of DC-link current is correct and feasible.

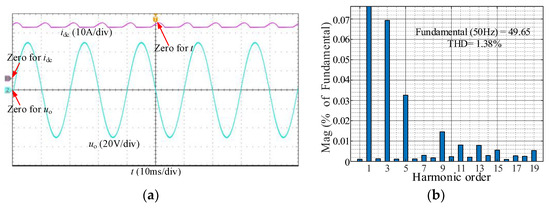
Figure 13. Experimental results under $i_{\mathrm{dc}}^{*}$ = 20 A: (a) Experimental waveforms of i_dc and u_o; (b) FFT results.

6.2. Experimental Results of Dynamic-State

The dynamic performance of the output voltage control strategy will be verified in this section. The frequency remains 50 Hz, and the amplitude of the reference voltage is adjusted from 40 V to 60 V. According to Formula (18), $i_{\mathrm{dc}}^{*}$ is set to 9 A and 17.5 A, respectively. The experimental waveforms of i_dc and u_o are shown in Figure 14. i_dc reaches the steady state again after 2 ms and remains above 17.5 A. In Figure 14, the u_o‘s amplitude is adjusted to 60 V with smooth changing.

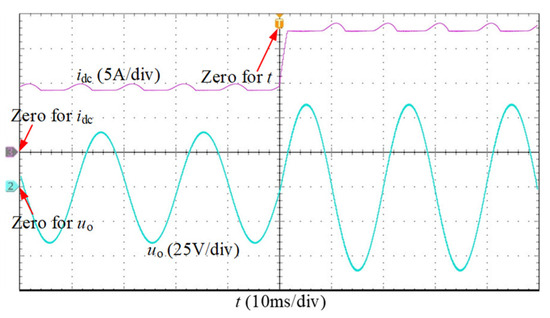
Figure 14. The dynamic-state experimental waveforms under amplitude changing.

Figure 15 shows the experimental waveforms when the amplitude is set to 50 V, and the frequency ω changes from 50 Hz to 100 Hz. According to (18), $i_{\mathrm{dc}}^{*}$ is related to ω, so it should be adjusted from 13.5 A to 16.5 A. In Figure 15, i_dc and u_o can track the reference quickly. In conclusion, the superior steady-state and dynamic-state performance of the output voltage control strategy can be fully proved, and the DC-link current reference from the proposed calculation method is the minimum value that can meet the power demand.

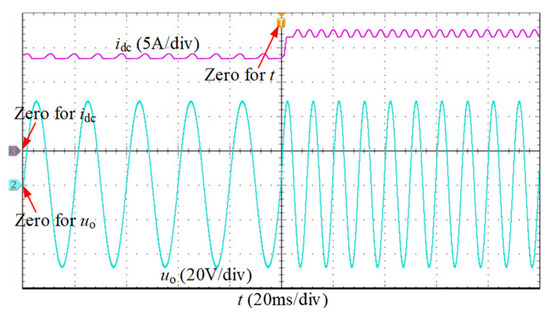
Figure 15. The dynamic-state experimental waveforms under frequency changing.

Finally, the CSI’s efficiency has been tested under different load powers from 100 W to 500 W. A curve map of the CSI’s efficiency is illustrated in Figure 16. When the load power increases, the power loss in the conduction and switching increases relatively more slowly than the load power, so the CSI’s efficiency rises with the increased load power.

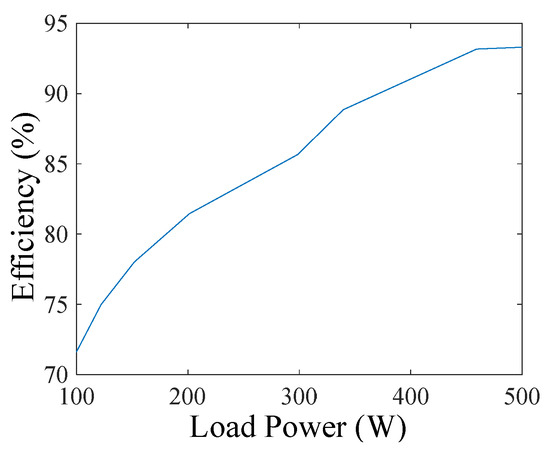
Figure 16. The efficiency map of the proposed single-phase CSI.

7. Conclusions

This paper proposes a novel PWM modulation method to control DC-link current for the improved topology of single-phase CSI; the corresponding operating modes and modulation strategy with DC-link current hysteresis control are also introduced in detail. The relationship between the optimal reference of DC-link current and output voltage is derived. A voltage control strategy based on d-q frame components is discussed. A series of simulations and experiments is set up to demonstrate the feasibility of the proposed method. The conclusions are summarized as follows:

(1) DC-link current can remain in the expected range by adopting the improved PWM modulation, and the number of switching activities is the same as the traditional modulation.

(2) The calculation method of optimal reference for DC-link current can meet the AC side load demand, improving current utilization and reducing loss.

(3) The control of DC-link current is implemented by switching magnetizing mode and freewheeling mode, which is separated from output voltage control. Thus, the DC-side model can be considered a controlled current source.