Applications of Machine Learning in Subsurface Reservoir Simulation—A Review—Part II
Abstract
:1. Introduction
2. Machine Learning Strategies for Production Forecast and Optimization Applications
2.1. Production Optimization of Conventional Oil Reservoirs
2.1.1. Production Optimization Based on ANNs
2.1.2. Production Optimization Based on Other Methods Other Than ANNs
2.2. Production Forecasting of Conventional Reservoirs
2.2.1. Static Machine Learning Models
2.2.2. Dynamic Machine Learning Models
2.3. Machine Learning Methods for PFO Applications in Unconventional Reservoirs
2.3.1. Static Machine Learning Models
2.3.2. Dynamic Machine Learning Models
2.4. Machine Learning Methods for EOR/Sequestration Projects
2.4.1. Machine Learning Models for the MMP Calculation
2.4.2. Machine Learning Models for EOR PFO Applications
2.4.3. Machine Learning Models for EOR Trapping Performance Metrics
2.4.4. Machine Learning Models for WAG-EOR Applications
Static Machine Learning Models
Dynamic Machine Learning Models
2.5. Machine Learning Methods for Heavy Oil Production Applications
2.5.1. Machine Learning Models for Thermal EOR Applications
Static Machine Learning Models
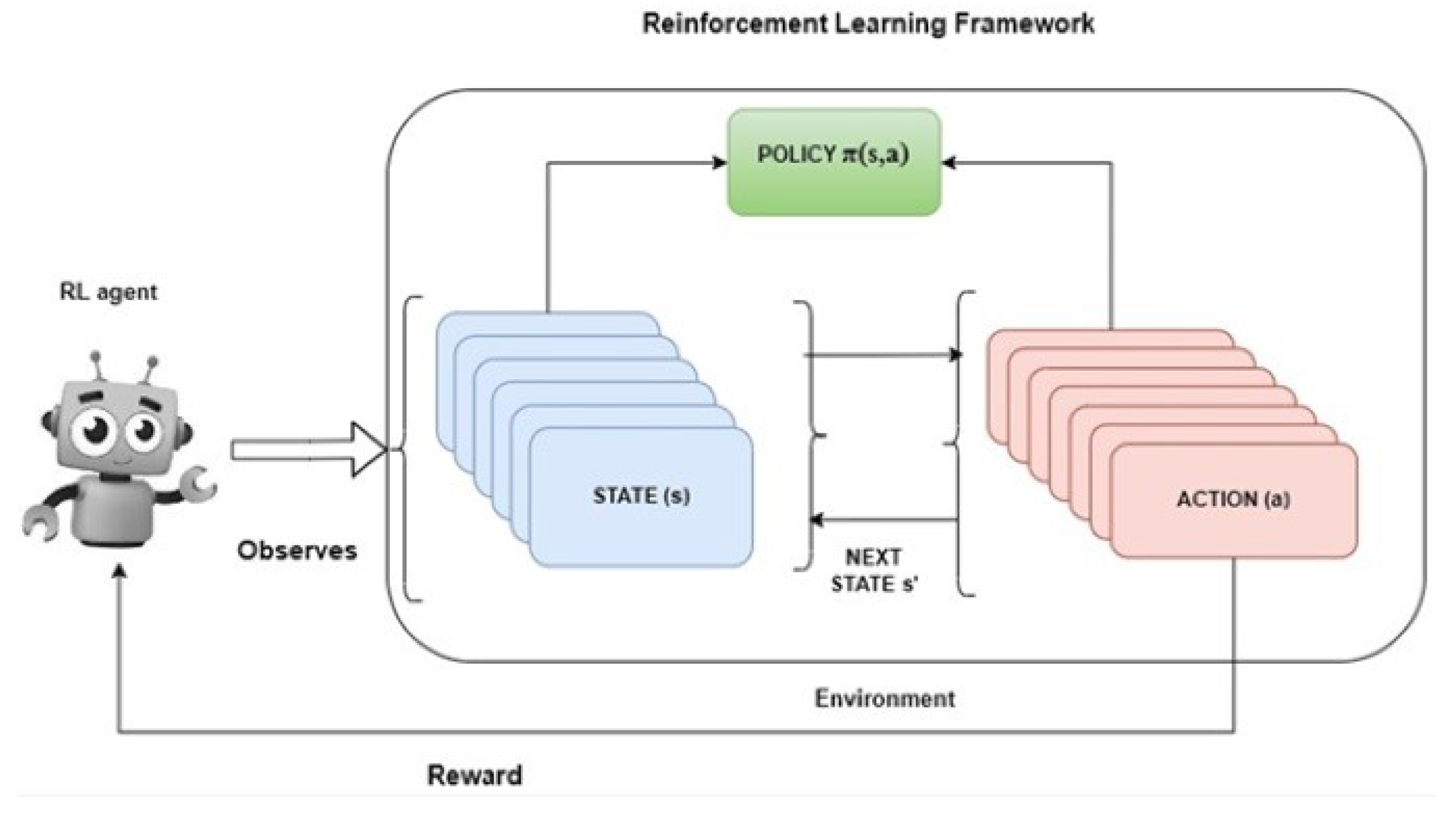
Dynamic Machine Learning Models
2.5.2. Machine Learning Models for Non-Thermal (Chemical) EOR Applications
Static Machine Learning Models
Dynamic Machine Learning Models
2.6. Machine Learning Methods for Gas Condensate Reservoirs
2.7. Machine Learning Methods for Flow Assurance Problems
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | Meaning |
| ML | Machine Learning |
| EOR | Enhanced Oil Recovery |
| EoS | Equation of State |
| HM | History Matching |
| PFO | Production Forecast and Optimization |
| SL | Supervised Learning |
| UL | Unsupervised Learning |
| RL | Reinforcement Learning |
| NPV | Net Present Value |
| DCA | Decline Curve Analysis |
| BHP | Bottom Hole Pressure |
| ANN | Artificial Neural Network |
| GA | Genetic Algorithm |
| XGB | Extreme Gradient Boosting |
| MVR | MultiVariate Regression |
| PSO | Particle Swarm Optimization |
| GSO | Genetical Swarm Optimization |
| LSSVR | Least Square Support Vector Regression |
| LH | Latin Hypercube |
| StoSAG | Stochastic Simplex Approximate Gradient |
| SVR | Support Vector Regression |
| GOR | Gas to Oil Ratio |
| RF | Random Forest |
| GBR | Gradient Boosting Regressor |
| SVM | Support Vector Machine |
| CNN | Convolutional Neural Network |
| DL | Deep Learning |
| RNN | Recurrent Neural Network |
| PCA | Principal Component Analysis |
| GAN | Generative Adversarial Network |
| TgNN | Theory-guided Neural Network |
| LSTM | Long Short-Term Memory |
| EMD | Empirical-Mode Decomposition |
| MDI | Mean Decrease Impurity |
| ARIMA | Autoregressive Integrated Moving Average |
| EnKF | Ensemble Kalman Filter |
| ICA | Imperialist Competitive Algorithm |
| MTS | Multivariate Time Series |
| VAR | Vector Auto-Regressive |
| HONN | Higher Order Neural Network |
| ACF | Auto-Correlation Function |
| CCF | Cross-Correlation Function |
| MLMVN | MultiLayer network with Multi-Valued Neurons |
| FNN | Fuzzy Neural Network |
| DT | Decision Tree |
| AdaBoost | Adaptive Boosting |
| LSSVM | Least Square Support Vector Machines |
| HFK | Hybrid Fuzzy Kalman filter |
| ROM | Reduced Order Model |
| MMP | Minimum Miscibility Pressure |
| MW | Molecular Weight |
| RBFNN | Radial Basis Function Neural Network |
| SA | Sensitivity Analysis |
| WAG | Water alternating gas |
| SCG | Scaled Conjugate Gradient |
| MARS | Multivariate Adaptive Regression Splines |
| CCS | Carbon Capture Sequestration |
| SMAC | Sequential Model-based Algorithm Configuration |
| GPR | Gaussian Process Regression |
| GMDH | Group Method of Data Handling |
| MADS | Mesh Adaptive Direct Search |
| ACO | Ant Colony Optimization |
| MLP | Multi-Layer Perceptron |
| LM | Levenberg–Marquardt |
| GWO | Grey Wolf Optimization |
| SAGD | Steam-Assisted Gravity Drainage |
| CSS | Cyclic Steam Stimulation |
| DACE | Design and Analysis of Computer Experiment |
| SP | Surfactant–Polymer |
| WAT | Wax Appearance Temperature |
| ABC | Artificial Bee Colony |
| CSA | Coupled Simulated Annealing |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ERT | Extremely Randomized Tree |
| GP | Genetic Programming |
References
- Samnioti, A.; Gaganis, V. Applications of Machine Learning in Subsurface Reservoir Simulation—A Review—Part I. Energies 2023, 16, 6079. [Google Scholar] [CrossRef]
- Alenezi, F.; Mohaghegh, S.A. Data-Driven Smart Proxy Model for a Comprehensive Reservoir Simulation. In Proceedings of the 4th Saudi International Conference on Information Technology (Big Data Analysis) (KACSTIT), Riyadh, Saudi Arabia, 6–9 November 2016; pp. 1–6. [Google Scholar]
- Ghassemzadeh, S. A Novel Approach to Reservoir Simulation Using Supervised Learning. Ph.D. Dissertation, University of Adelaide, Australian School of Petroleum and Energy Resources, Faculty of Engineering, Computer & Mathematical Sciences, Docklands, VIC, Australia, November 2020. [Google Scholar]
- Abdelwahhab, M.A.; Radwan, A.A.; Mahmoud, H.; Mansour, A. Geophysical 3D-static reservoir and basin modeling of a Jurassic estuarine system (JG-Oilfield, Abu Gharadig basin, Egypt). J. Asian Earth Sci. 2022, 225, 105067. [Google Scholar] [CrossRef]
- Abdelwahhab, M.A.; Abdelhafez, N.A.; Embabi, A.M. 3D-static reservoir and basin modeling of a lacustrine fan-deltaic system in the Gulf of Suez, Egypt. Pet. Res. 2022, 8, 18–35. [Google Scholar] [CrossRef]
- Radwan, A.A.; Abdelwahhab, M.A.; Nabawy, B.S.; Mahfouz, K.H.; Ahmed, M.S. Facies analysis-constrained geophysical 3D-static reservoir modeling of Cenomanian units in the Aghar Oilfield (Western Desert, Egypt): Insights into paleoenvironment and petroleum geology of fluviomarine systems. Mar. Pet. Geol. 2022, 136, 105436. [Google Scholar] [CrossRef]
- Danesh, A. PVT and Phase Behavior of Petroleum Reservoir Fluids; Elsevier: Amsterdam, The Netherlands, 1998; ISBN 9780444821966. [Google Scholar]
- Gaganis, V.; Marinakis, D.; Samnioti, A. A soft computing method for rapid phase behavior calculations in fluid flow simulations. J. Pet. Sci. Eng. 2021, 205, 108796. [Google Scholar] [CrossRef]
- Voskov, D.V.; Tchelepi, H. Comparison of nonlinear formulations for two-phase multi-component EoS based simulation. J. Pet. Sci. Eng. 2012, 82–83, 101–111. [Google Scholar] [CrossRef]
- Wang, P.; Stenby, E.H. Compositional simulation of reservoir performance by a reduced thermodynamic model. Comput. Chem. Eng. 1994, 18, 75–81. [Google Scholar] [CrossRef]
- Gaganis, V.; Varotsis, N. Machine Learning Methods to Speed up Compositional Reservoir Simulation. In Proceedings of the EAGE Annual Conference & Exhibition incorporating SPE Europe, Copenhagen, Denmark, 4–7 June 2012. [Google Scholar]
- Aminian, K. Modeling and simulation for CBM production. In Coal Bed Methane: Theory and Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 9780128159972. [Google Scholar]
- Jaber, A.K.; Al-Jawad, S.N.; Alhuraishawy, A.K. A review of proxy modeling applications in numerical reservoir simulation. Arab. J. Geosci. 2019, 12, 701. [Google Scholar] [CrossRef]
- Sircar, A.; Yadav, K.; Rayavarapu, K.; Bist, N.; Oza, H. Application of machine learning and artificial intelligence in oil and gas industry. Pet. Res. 2021, 6, 379–391. [Google Scholar] [CrossRef]
- Bao, A.; Gildin, E.; Zalavadia, H. Development of Proxy Models for Reservoir Simulation by Sparsity Promoting Methods and Machine Learning Techniques. In Proceedings of the 16th European Conference on the Mathematics of Oil Recovery, Barcelona, Spain, 3–6 September 2018. [Google Scholar]
- Denney, D. Pros and cons of applying a proxy model as a substitute for full reservoir simulations. J. Pet. Technol. 2010, 62, 41–42. [Google Scholar] [CrossRef]
- Ibrahim, D. An overview of soft computing. In Proceedings of the 12th International Conference on Application of Fuzzy Systems and Soft Computing, ICAFS, Vienna, Austria, 29–30 August 2016. [Google Scholar]
- Samnioti, A.; Anastasiadou, V.; Gaganis, V. Application of Machine Learning to Accelerate Gas Condensate Reservoir Simulation. Clean Technol. 2022, 4, 153–173. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7139-4. [Google Scholar]
- Bao, A.; Gildin, E.; Huang, J.; Coutinho, E.J. Data-Driven End-To-End Production Prediction of Oil Reservoirs by EnKF-Enhanced Recurrent Neural Networks. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Virtual, 27–31 July 2020. [Google Scholar]
- Wang, P.; Litvak, M.; Aziz, K. Optimization of Production Operations in Petroleum Fields. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar]
- Sun, Q.; Ertekin, T. Screening and optimization of polymer flooding projects using artificial-neural-network (ANN) based proxies. J. Pet. Sci. Eng. 2020, 185, 106617. [Google Scholar] [CrossRef]
- Koray, A.M.; Bui, D.; Ampomah, W.; Kubi, E.A.; Klumpenhower, J. Application of Machine Learning Optimization Workflow to Improve Oil Recovery. In Proceedings of the SPE Oklahoma City Oil and Gas Symposium, Oklahoma City, OK, USA, 17–19 April 2023. [Google Scholar]
- Zangl, G.; Graf, T.; Al-Kinani, A. Proxy Modeling in Production Optimization. In Proceedings of the SPE Europec/EAGE Annual Conference and Exhibition, Vienna, Austria, 12–15 June 2006. [Google Scholar]
- Andersen, M.G. Reservoir Production Optimization Using Genetic Algorithms and Artificial Neural Networks. Master’s Thesis, Norwegian University of Science and Technology Department of Computer and Information Science, Trondheim, Norway, July 2019. [Google Scholar]
- Pershin, I.M.; Papush, E.G.; Kukharova, T.V.; Utkin, V.A. Modeling of Distributed Control System for Network of Mineral Water Wells. Water 2023, 15, 2289. [Google Scholar] [CrossRef]
- Raji, S.; Dehnamaki, A.; Somee, B.; Mahdiani, M.R. A new approach in well placement optimization using metaheuristic algorithms. J. Pet. Sci. Eng. 2022, 215 Part A, 110640. [Google Scholar] [CrossRef]
- Centilmen, A.; Ertekin, T.; Grader, A.S. Applications of Neural Networks in Multiwell Field Development. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA 3–6 October 1999. [Google Scholar]
- Doraisamy, H.; Ertekin, T.; Grader, A.S. Field development studies by neuro-simulation: An effective coupling of soft and hard computing protocols. Comput. Geosci. 2000, 26, 963–973. [Google Scholar] [CrossRef]
- Min, B.H.; Park, C.; Kang, J.M.; Park, H.J.; Jang, I.S. Optimal well placement based on artificial neural network incorporating the productivity potential. Energy Sources Part A 2011, 33, 1726–1738. [Google Scholar] [CrossRef]
- Teixeira, A.F.; Secchi, A.R. Machine learning models to support reservoir production optimization. IFAC-Pap. 2019, 52, 498–501. [Google Scholar] [CrossRef]
- Amjad, M.; Ahmad, I.; Ahmad, M.; Wróblewski, P.; Kaminski, P.; Amjad, U. Prediction of Pile Bearing Capacity Using XGBoost Algorithm: Modeling and Performance Evaluation. Appl. Sci. 2022, 12, 2126. [Google Scholar] [CrossRef]
- Chai, Z.; Nwachukwu, A.; Zagayevskiy, Y.; Amini, S.; Madasu, S. An integrated closed-loop solution to assisted history matching and field optimization with machine learning techniques. J. Pet. Sci. Eng. 2021, 198, 108204. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Grimaccia, F.; Mussetta, M.; Zich, R.E. Genetical Swarm Optimization: Self-Adaptive Hybrid Evolutionary Algorithm for Electromagnetics. IEEE Trans. Antennas Propag. 2007, 55, 781–785. [Google Scholar] [CrossRef]
- Guo, Z.; Reynolds, A.C. Robust Life-Cycle Production Optimization with a Support-Vector-Regression Proxy. SPE J. 2018, 23, 2409–2427. [Google Scholar] [CrossRef]
- Xu, J.; Zhou, W.; Li, H.; Wang, X.; Liu, S.; Fan, L. Stochastic simplex approximation gradient for reservoir production optimization: Algorithm testing and parameter analysis. J. Pet. Sci. Eng. 2022, 209, 109755. [Google Scholar] [CrossRef]
- Lawati, M.; Thatcher, J.; Rehman, A.; Gee, I.; Eldred, M. AI for Production Forecasting and Optimization of Gas Wells: A Case Study on a Gas Field in Oman. In Proceedings of the SPE Symposium: Artificial Intelligence—Towards a Resilient and Efficient Energy Industry, Virtual, 18–19 October 2021. [Google Scholar]
- Shirangi, M.G. Applying Machine Learning Algorithms to Oil Reservoir Production Optimization; Research Report; Stanford University: Stanford, CA, USA, 2012. [Google Scholar]
- Gu, J.; Liu, W.; Zhang, K.; Zhai, L.; Zhang, Y.; Chen, F. Reservoir production optimization based on surrogate model and differential evolution algorithm. J. Pet. Sci. Eng. 2021, 205, 108879. [Google Scholar] [CrossRef]
- Gupta, A. Spearman’s Rank Correlation: The Definitive Guide to Understand. 2023. Available online: https://www.simplilearn.com/tutorials/statistics-tutorial/spearmans-rank-correlation (accessed on 29 April 2023).
- Mannon, R.W. Oil production forecasting by decline curve analysis. In Proceedings of the Fall Meeting of the Society of Petroleum Engineers of AIME, Denver, CO, USA, 3–6 October 1965. [Google Scholar]
- Chahar, J.; Verma, J.; Vyas, D.; Goyal, M. Data-driven approach for hydrocarbon production forecasting using machine learning techniques. J. Pet. Sci. Eng. 2022, 217, 110757. [Google Scholar] [CrossRef]
- Liu, W.; Liu, W.D.; Gu, J. Forecasting oil production using ensemble empirical model decomposition based Long Short-Term Memory neural network. J. Pet. Sci. Eng. 2020, 189, 107013. [Google Scholar] [CrossRef]
- Gharbi, R.; Karkoub, M.; ElKamel, A. An artificial neural network for the prediction of immiscible flood performance. Energy Fuels 1995, 9, 894–900. [Google Scholar] [CrossRef]
- Weiss, W.W.; Balch, R.S.; Stubbs, B.A. How Artificial Intelligence Methods Can Forecast Oil Production. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 13–17 April 2002. [Google Scholar]
- Chen, S.J.; Hwang, C.L. Fuzzy Ranking Methods. In Fuzzy Multiple Attribute Decision Making. Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1992; ISBN 978-3-540-54998-7. [Google Scholar]
- Cao, Q.; Banerjee, R.; Gupta, S.; Li, J.; Zhou, W.; Jeyachandra, B. Data Driven Production Forecasting Using Machine Learning. In Proceedings of the SPE Argentina Exploration and Production of Unconventional Resources Symposium, Buenos Aires, Argentina, 1–3 June 2016. [Google Scholar]
- Fan, L.; Zhao, M.; Yin, C.; Peng, X. Analysis method of oilfield production performance based on BP neural network. Fault-Block Oil Gas Field 2013, 20, 204–206. [Google Scholar]
- Elmabrouk, S.; Shirif, E.; Mayorga, R. Artificial Neural Network Modeling for the Prediction of Oil Production. Pet. Sci. Technol. 2014, 32, 1123–1130. [Google Scholar] [CrossRef]
- Sun, L.; Bi, Y.; Lu, G. Application of BP Neural Network in Oil Field Production Prediction. In Proceedings of the 2nd World Congress on Software Engineering, Wuhan, China, 19–20 December 2010. [Google Scholar]
- Park, M.; Jung, D.; Lee, S.; Park, S. Heatwave Damage Prediction Using Random Forest Model in Korea. Appl. Sci. 2020, 10, 8237. [Google Scholar] [CrossRef]
- Masui, T.; Towards Data Science. All You Need to Know about Gradient Boosting Algorithm—Part 1. Regression. 2022. Available online: https://towardsdatascience.com/all-you-need-to-know-about-gradient-boosting-algorithm-part-1-regression-2520a34a502 (accessed on 3 May 2023).
- Martyushev, D.A.; Ponomareva, I.N.; Zakharov, L.A.; Shadrov, T.A. Application of machine learning for forecasting formation pressure in oil field development. Izv. Tomsk. Politekh. Univ. Inz. Georesursov. 2021, 332, 140–149. [Google Scholar]
- Han, B.; Bian, X. A hybrid PSO-SVM-based model for determination of oil recovery factor in the low-permeability reservoir. Petroleum 2017, 4, 43–49. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N. Bayesian deep convolutional encoder–decoder networks for surrogate modeling and uncertainty quantification. J. Comput. Phys. 2018, 366, 415–447. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, D. Stein Variational Gradient Descent: A General-Purpose Bayesian Inference Algorithm. arXiv 2016. [Google Scholar] [CrossRef]
- Cornelio, J.; Razak, S.M.; Jahandideh, A.; Jafarpour, B.; Cho, Y.; Liu, H.; Vaidya, R. Investigating Transfer Learning for Characterization and Performance Prediction in Unconventional Reservoirs. In Proceedings of the SPE Middle East Oil & Gas Show and Conference, Sanabis, Bahrain, 28 November–1 December 2021. [Google Scholar]
- Illarionov, E.; Temirchev, P.; Voloskov, D.; Kostoev, R.; Simonov, M.; Pissarenko, D.; Orlov, D.; Koroteev, D. End-to-end neural network approach to 3D reservoir simulation and adaptation. J. Pet. Sci. Eng. 2022, 208, 109332. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, X.; Ma, X.; Wang, J.; Yang, Y.; Zhang, L.; Yao, J.; Wang, J. The prediction of reservoir production-based proxy model considering spatial data and vector data. J. Pet. Sci. Eng. 2022, 208, 109694. [Google Scholar] [CrossRef]
- Tang, M.; Liu, Y.; Durlofsky, L.J. A deep-learning-based surrogate model for data assimilation in dynamic subsurface flow problems. J. Comput. Phys. 2020, 413, 109456. [Google Scholar] [CrossRef]
- Zhong, Z.; Sun, A.Y.; Wang, Y.; Ren, B. Predicting field production rates for waterflooding using a machine learning-based proxy model. J. Pet. Sci. Eng. 2020, 194, 107574. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, D.; Chang, H.; Li, H. Deep learning of subsurface flow via theory-guided neural network. J. Hydrol. 2020, 584, 124700. [Google Scholar] [CrossRef]
- Wang, H.; Mu, L.; Shi, F.; Dou, H. Production prediction at ultra-high water cut stage via Recurrent Neural Network. Petrol. Explor. Develop. 2020, 47, 1084–1090. [Google Scholar] [CrossRef]
- Fan, H.; Jiang, M.; Xu, L.; Zhu, H.; Cheng, J.; Jiang, J. Comparison of Long Short Term Memory Networks and the Hydrological Model in Runoff Simulation. Water 2020, 12, 175. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Dong, Z.; Wang, R.; Qu, B. Reservoir production prediction with optimized artificial neural network and time series approaches. J. Pet. Sci. Eng. 2022, 215, 110586. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Liu, W.; Liu, W.D.; Gu, J. Petroleum Production Forecasting Based on Machine Learning. In Proceedings of the 3rd International Conference on Advances in Image Processing (ICAIP), New York, NY, USA, 8–10 November 2019. [Google Scholar]
- Lee, C. Feature Importance Measures for Tree Models—Part I. VeriTable. 2017. Available online: https://medium.com/the-artificial-impostor/feature-importance-measures-for-tree-models-part-i-47f187c1a2c3 (accessed on 2 May 2023).
- Zhang, J.; Towards Data Science. Dynamic Time Warping—Explanation and Code Implementation. 2020. Available online: https://towardsdatascience.com/dynamic-time-warping-3933f25fcdd (accessed on 2 May 2023).
- Song, X.; Liu, Y.; Xue, L.; Wang, J.; Zhang, J.; Wang, J.; Jiang, L.; Cheng, Z. Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model. J. Pet. Sci. Eng. 2019, 186, 106682. [Google Scholar] [CrossRef]
- Huang, R.; Wei, C.; Wang, B.; Yang, J.; Xu, X.; Wu, S.; Huang, S. Well performance prediction based on Long Short-Term Memory (LSTM) neural network. J. Pet. Sci. Eng. 2022, 208, 109686. [Google Scholar] [CrossRef]
- Fan, D.; Sun, H.; Yao, J.; Zhang, K.; Yan, X.; Sun, Z. Well production forecasting based on ARIMA-LSTM model considering manual operations. Energy 2021, 220, 119708. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Regression and ARIMA Models. In Time Series Analysis and Its Applications; Springer: New York, NY, USA, 2013; ISBN 978-1-4757-3263-4. [Google Scholar]
- Sagheer, A.; Kotb, M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing 2019, 323, 203–213. [Google Scholar] [CrossRef]
- He, Z.; Yang, L.; Yen, Y.; Wu, C. Neural-Network Approach to Predict Well Performance Using Available Field Data. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 26–30 March 2001. [Google Scholar]
- Ahmadi, M.A.; Ebadi, M.; Shokrollahi, A.; Mohammad, S.; Majidi, J. Evolving artificial neural network and imperialist competitive algorithm for prediction oil flow rate of the reservoir. Appl. Soft Comput. 2013, 13, 1085–1098. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007. [Google Scholar]
- Berneti, S.M.; Shahbazian, M. An Imperialist Competitive Algorithm Artificial Neural Network Method to Predict Oil Flow Rate of the Wells. Int. J. Comput. Appl. 2011, 26, 47–50. [Google Scholar]
- Zhang, R.; Jia, H. Production performance forecasting method based on multivariate time series and vector autoregressive machine learning model for waterflooding reservoirs. Pet. Explor. Dev. 2021, 48, 201–211. [Google Scholar] [CrossRef]
- Singh, A.; Analytics Vidhya. Multivariate Time Series Analysis with Python for Forecasting and Modeling. 2018. Available online: https://www.analyticsvidhya.com/blog/2018/09/multivariate-time-series-guide-forecasting-modeling-python-codes/ (accessed on 9 May 2023).
- Prabhakaran, S. Vector Autoregression (VAR)—Comprehensive Guide with Examples in Python. 2019. Available online: https://www.machinelearningplus.com/time-series/vector-autoregression-examples-python/?utm_content=cmp-true (accessed on 9 May 2023).
- Madan, M.; Gupta, M.M.; Bukovsky, I.; Homma, N.; Solo, A.M.G.; Hou, Z. Fundamentals of Higher Order Neural Networks for Modeling and Simulation. In Artificial Higher Order Neural Networks for Modeling and Simulation; IGI Global: Pennsylvania, PA, USA, 2012; ISBN 1466621753. [Google Scholar]
- Chakra, C.; Song, K.Y.; Saraf, D.N.; Gupta, M.M. Production Forecasting of Petroleum Reservoir applying Higher-Order Neural Networks (HONN) with Limited Reservoir Data. Int. J. Comput. Appl. 2013, 72, 23–35. [Google Scholar]
- Prasetyo, J.N.; Setiawan, N.A.; Adji, T.B. Forecasting Oil Production Flowrate Based on an Improved Backpropagation High-Order Neural Network with Empirical Mode Decomposition. Processes 2022, 10, 1137. [Google Scholar] [CrossRef]
- López-Yáñez, I.; Sheremetov, L.; González-Sánchez, A.; Ponomarev, A. Time Series Forecasting: Applications to the Upstream Oil and Gas Supply Chain. In Proceedings of the 7th IFAC Conference on Manufacturing Modeling, Management, and Control, Saint Petersburg, Russia, 19–21 June 2013. [Google Scholar]
- López-Yáñez, I.; Sheremetov, L.; Yáñez-Márquez, C. A novel associative model for time series data mining. Pattern Recognit. Lett. 2014, 41, 23–33. [Google Scholar] [CrossRef]
- Lopez-Martin, C.; López-Yáñez, I.; Yáñez-Márquez, C. Application of Gamma Classifier to Development Effort Prediction of Software Projects. Appl. Math. Inf. Sci. 2012, 6, 411–418. [Google Scholar]
- Aizenberg, I.; Sheremetov, L.; Villa-Vargas, L.; Martinez-Muñoz, J. Multilayer Neural Network with Multi-Valued Neurons in time series forecasting of oil production. Neurocomputing 2016, 175, 980–989. [Google Scholar] [CrossRef]
- Aizenberg, I. Complex-Valued Neural Networks with Multi-Valued Neurons. In Studies in Computational Intelligence; Springer: New York, NY, USA, 2011; Volume 353, ISBN 978-3-642-20352-7. [Google Scholar]
- Lizhe, L.; Fujian, Z.; You, Z.; Zhuolin, C.; Bo, W.; Yingying, Z.; Yutian, L. The prediction and optimization of Hydraulic fracturing by integrating the numerical simulation and the machine learning methods. Energy Rep. 2022, 8, 15338–15349. [Google Scholar] [CrossRef]
- Yu, T.; Xie, X.; Li, L.; Wu, W. Comparison of Candidate-Well Selection Mathematical Models for Hydraulic Fracturing. Adv. Intell. Syst. Comput. 2015, 367, 289–299. [Google Scholar]
- Oberwinkler, C.; Ruthammer, G.; Zangl, G.; Economides, M.J. New Tools for Fracture Design Optimization. In Proceedings of the SPE International Symposium and Exhibition Formation Damage Control, Lafayette, LA, USA, 18–20 February 2004. [Google Scholar]
- Clar, F.H.; Monaco, A. Data-Driven Approach to Optimize Stimulation Design in Eagle Ford Formation. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar]
- Carpenter, C. Geology-Driven Estimated-Ultimate-Recovery Prediction with Deep Learning. J. Pet. Technol. 2016, 68, 74–75. [Google Scholar] [CrossRef]
- Ockree, M.; Brown, K.G.; Frantz, J.; Deasy, M.; John, R. Integrating big data analytics into development planning optimization. In Proceedings of the SPE/AAPG Eastern Regional Meeting, Pittsburgh, PA, USA, 7–11 October 2018. [Google Scholar]
- Cabana, E.; Lillo, R.E.; Laniado, H. Multivariate outlier detection based on a robust Mahalanobis distance with shrinkage estimators. Stat. Pap. 2021, 62, 1583–1609. [Google Scholar] [CrossRef]
- Natras, R.; Soja, B.; Schmidt, M. Ensemble Machine Learning of Random Forest, AdaBoost and XGBoost for Vertical Total Electron Content Forecasting. Remote Sens. 2022, 14, 3547. [Google Scholar] [CrossRef]
- Xue, H.; Malpani, R.; Agrawal, S.; Bukovac, T.; Mahesh, A.L.; Judd, T. Fast-Track Completion Decision Through Ensemble-Based Machine Learning. In Proceedings of the SPE Reservoir Characterization and Simulation Conference and Exhibition, Abu Dhabi, United Arab Emirates, 17–19 September 2019. [Google Scholar]
- Wang, S.; Chen, S. Insights to fracture stimulation design in unconventional reservoirs based on machine learning modeling. J. Pet. Sci. Eng. 2019, 174, 682–695. [Google Scholar] [CrossRef]
- Park, J.; Datta-Gupta, A.; Singh, A.; Sankaran, S. Hybrid physics and data-driven modeling for unconventional field development and its application to US onshore basin. J. Pet. Sci. Eng. 2021, 206, 109008. [Google Scholar] [CrossRef]
- Panja, P.; Velasco, R.; Pathak, M.; Deo, M. Application of artificial intelligence to forecast hydrocarbon production from shales. Petroleum 2018, 4, 75–89. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Ebadi, M.; Hosseini, S.M. Prediction breakthrough time of water coning in the fractured reservoirs by implementing low parameter support vector machine approach. Fuel 2014, 117, 579–589. [Google Scholar] [CrossRef]
- Chen, G.; Xie, Q.; Shieh, L.S. Fuzzy Kalman filtering. Inf. Sci. 1998, 109, 197–209. [Google Scholar] [CrossRef]
- Pal, M. On application of machine learning method for history matching and forecasting of times series data from hydrocarbon recovery process using water flooding. Pet. Sci. Technol. 2021, 39, 519–549. [Google Scholar] [CrossRef]
- Srinivasan, S.; O’Malley, D.; Mudunuru, M.K.; Sweeney, M.R.; Hyman, J.D.; Karra, S.; Frash, L.; Carey, W.; Gross, M.R.; Guthrie, G.D.; et al. A machine learning framework for rapid forecasting and history matching in unconventional reservoirs. Sci. Rep. 2021, 11, 21730. [Google Scholar] [CrossRef]
- Pan, Y.; Bi, R.; Zhou, P.; Deng, L.; Lee, J. An effective physics-based deep learning model for enhancing production surveillance and analysis in unconventional reservoirs. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Bian, X.Q.; Han, B.; Du, Z.M.; Jaubert, J.N.; Li, M.J. Integrating support vector regression with genetic algorithm for CO2-oil minimum miscibility pressure (MMP) in pure and impure CO2 streams. Fuel 2016, 182, 550–557. [Google Scholar] [CrossRef]
- Shokrollahi, A.; Arabloo, M.; Gharagheizi, F.; Mohammadi, A.H. Intelligent model for prediction of CO2—Reservoir oil minimum miscibility pressure. Fuel 2013, 112, 375–384. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Zahedzadeh, M.; Shadizadeh, S.R.; Abbassi, R. Connectionist model for predicting minimum gas miscibility pressure: Application to gas injection process. Fuel 2015, 148, 202–211. [Google Scholar] [CrossRef]
- Huang, Y.F.; Huang, G.H.; Dong, M.Z.; Feng, G.M. Development of an artificial neural network model for predicting minimum miscibility pressure in CO2 flooding. J. Pet. Sci. Eng. 2003, 37, 83–95. [Google Scholar] [CrossRef]
- Nezhad, A.B.; Mousavi, S.M.; Aghahoseini, S. Development of an artificial neural network model to predict CO2 minimum miscibility pressure. Nafta 2011, 62, 105–108. [Google Scholar]
- Mousavi, S.M.; Sefti, M.V.; Ameri, A.; Kaveh, N.S. Minimum miscibility pressure prediction based on a hybrid neural genetic algorithm. Chem. Eng. Res. Des. 2008, 86, 173–185. [Google Scholar]
- Ahmadi, M.A. WITHDRAWN: Prediction of minimum miscible pressure by using neural network-based hybrid genetic algorithm and particle swarm optimization. J. Pet. Sci. Eng. 2012. [Google Scholar] [CrossRef]
- Sayyad, H.; Manshad, A.K.; Rostami, H. Application of hybrid neural particle swarm optimization algorithm for prediction of MMP. Fuel 2014, 116, 625–633. [Google Scholar] [CrossRef]
- Chen, G.; Fu, K.; Liang, Z.; Sema, T.; Li, C.; Tontiwachwuthikul, P.; Idem, R. The genetic algorithm based back propagation neural network for MMP prediction in CO2-EOR process. Fuel 2014, 126, 202–212. [Google Scholar] [CrossRef]
- Thanh, H.V.; Sugai, Y.; Sasaki, K. Application of artificial neural network for predicting the performance of CO2 enhanced oil recovery and storage in residual oil zones. Sci. Rep. 2020, 10, 18204. [Google Scholar] [CrossRef]
- Ampomah, W.; Balch, R.S.; Cather, M.; Will, R.; Gunda, D.; Dai, Z.; Soltanian, M.R. Optimum design of CO2 storage and oil recovery under geological uncertainty. Appl. Energy 2017, 195, 80–92. [Google Scholar] [CrossRef]
- Parada Minakowski, C.H.; Ertekin, T. A New Screening Tool for Improved Oil Recovery Methods Using Artificial Neural Networks. In Proceedings of the SPE Western Regional Meeting, Bakersfield, CA, USA, 21–23 March 2012. [Google Scholar]
- Parada Minakowski, C.H. An Artificial Neural Network Based Tool-Box for Screening and Designing Improved Oil Recovery Methods. Ph.D. Dissertation, Energy and Geo-Environmental Engineering, The Pennsylvania State University, University Park, PA, USA, January 2007. [Google Scholar]
- Surguchev, L.; Li, L. IOR Evaluation and Applicability Screening Using Artificial Neural Networks. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 3–5 April 2000. [Google Scholar]
- Talapatra, A. A study on the carbon dioxide injection into coal seam aiming at enhancing coal bed methane (ECBM) recovery. J. Pet. Explor. Prod. Technol. 2020, 10, 1965–1981. [Google Scholar] [CrossRef]
- Mohammadpoor, M.; Qazvini Firouz, A.R.; Torabi, F. Implementing Simulation and Artificial Intelligence Tools to Optimize the Performance of the CO2 Sequestration in Coalbed Methane Reservoirs. In Proceedings of the Carbon Management Technology Conference, Orlando, FL, USA, 7–9 February 2012. [Google Scholar]
- Odusote, O.; Ertekin, T.; Smith, D.H.; Bromhal, G.; Sams, W.N.; Jikich, S. Carbon Dioxide Sequestration in Coal Seams: A Parametric Study and Development of a Practical Prediction/Screening Tool Using Neuro-Simulation. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. [Google Scholar]
- Gorucu, F.B.; Ertekin, T.; Bromhal, G.S.; Smith, D.H.; Sams, W.N.; Jikich, S.A. A Neurosimulation Tool for Predicting Performance in Enhanced Coalbed Methane and CO2 Sequestration Projects. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Ahmed, A.A.M.; Deo, R.C.; Ghimire, S.; Downs, N.J.; Devi, A.; Barua, P.D.; Yaseen, Z.M. Introductory Engineering Mathematics Students’ Weighted Score Predictions Utilizing a Novel Multivariate Adaptive Regression Spline Model. Sustainability 2022, 14, 11070. [Google Scholar] [CrossRef]
- Chen, B.; Pawar, R.J. Capacity assessment and co-optimization of CO2 storage and enhanced oil recovery in residual oil zones. J. Pet. Sci. Eng. 2019, 182, 106342. [Google Scholar] [CrossRef]
- Kuk, E.; Stopa, J.; Kuk, M.; Janiga, D.; Wojnarowski, P. Petroleum Reservoir Control Optimization with the Use of the Auto-Adaptive Decision Trees. Energies 2021, 14, 5702. [Google Scholar] [CrossRef]
- Artun, Ε.; Ertekin, T.; Watson, R.; Miller, B. Designing cyclic pressure pulsing in naturally fractured reservoirs using an inverse looking recurrent neural network. Comput. Geosci. 2012, 38, 68–79. [Google Scholar] [CrossRef]
- Mo, S.; Zhu, Y.; Zabaras, N.; Shi, X.; Wu, J. Deep Convolutional Encoder-Decoder Networks for Uncertainty Quantification of Dynamic Multiphase Flow in Heterogeneous Media. Water Resour. Res. 2018, 55, 703–728. [Google Scholar] [CrossRef]
- Thanh, H.V.; Lee, K.K. Application of machine learning to predict CO2 trapping performance in deep saline aquifers. Energy 2022, 239, 122457. [Google Scholar] [CrossRef]
- Kim, Y.; Jang, H.; Kim, J.; Lee, J. Prediction of storage efficiency on CO2 sequestration in deep saline aquifers using artificial neural network. Appl. Energy 2017, 185, 916–928. [Google Scholar] [CrossRef]
- Al-Nuaimi, M.M. Application of Artificial Intelligence for CO2 Storage in Saline Aquifer (Smart Proxy for Snap-Shot In Time). Ph.D. Dissertation, College of Engineering and Mineral Resources, West Virginia University, Morgantown, WV, USA, 2022. [Google Scholar]
- Wen, G.; Tang, M.; Benson, S.M. Towards a predictor for CO2 plume migration using deep neural networks. Int. J. Greenh. Gas Control 2021, 105, 103223. [Google Scholar] [CrossRef]
- Zhong, Z.; Sun, A.Y.; Jeong, H. Predicting CO2 Plume Migration in Heterogeneous Formations Using Conditional Deep Convolutional Generative Adversarial Network. Water Resour. Res. 2019, 55, 5830–5851. [Google Scholar] [CrossRef]
- You, J.; Ampomah, W.; Sun, Q.; Kutsienyo, E.J.; Balch, R.S.; Dai, Z.; Cather, M.; Zhang, X. Machine learning based co-optimization of carbon dioxide sequestration and oil recovery in CO2-EOR project. J. Clean. Prod. 2020, 260, 120866. [Google Scholar] [CrossRef]
- You, J.; Ampomah, W.; Sun, Q. Development and application of a machine learning based multi-objective optimization workflow for CO2-EOR projects. Fuel 2020, 264, 116758. [Google Scholar] [CrossRef]
- Van, S.L.; Chon, B.H. Evaluating the critical performances of a CO2–Enhanced Oil Recovery process using artificial neural network models. J. Pet. Sci. Eng. 2017, 157, 207–222. [Google Scholar] [CrossRef]
- Anastasakis, L.; Mort, N. The Development of Self-Organization Techniques in Modeling: A Review of the Group Method of Data Handling (GMDH); Research Report 813; Department of Automatic Control & Systems Engineering, The University of Sheffield: Sheffield, UK, 2011. [Google Scholar]
- Belazreg, L.; Mahmood, S.M.; Aulia, A. Novel approach for predicting water alternating gas injection recovery factor. J. Pet. Explor. Prod. Technol. 2019, 9, 2893–2910. [Google Scholar] [CrossRef]
- Belazreg, L.; Mahmood, S.M. Water alternating gas incremental recovery factor prediction and WAG pilot lessons learned. J. Pet. Explor. Prod. Technol 2020, 10, 249–269. [Google Scholar] [CrossRef]
- Belazreg, L.; Mahmood, S.M.; Aulia, A. Random Forest algorithm for CO2 water alternating gas incremental recovery factor prediction. Int. J. Adv. Sci. Technol. 2020, 29, 168–188. [Google Scholar]
- Li, H.; Gong, C.; Liu, S.; Xu, J.; Imani, G. Machine Learning-Assisted Prediction of Oil Production and CO2 Storage Effect in CO2-Water-Alternating-Gas Injection (CO2-WAG). Appl. Sci. 2022, 12, 10958. [Google Scholar] [CrossRef]
- Nwachukwu, A.; Jeong, H.; Pyrcz, M.; Lake, L.W. Fast evaluation of well placements in heterogeneous reservoir models using machine learning. J. Pet. Sci. Eng. 2018, 163, 463–475. [Google Scholar] [CrossRef]
- Nwachukwu, A.; Jeong, H.; Sun, A.; Pyrcz, M.; Lake, L.W. Machine Learning-Based Optimization of Well Locations and WAG Parameters under Geologic Uncertainty. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 14–18 April 2018. [Google Scholar]
- Alizadeh, M.; Moshirfarahi, M.M.; Rasaie, M.R. Mathematical and neural network prediction model of three-phase immiscible recovery process in porous media. J. Nat. Gas Sci. Eng. 2014, 20, 292–311. [Google Scholar] [CrossRef]
- You, J.; Ampomah, W.; Tu, J.; Morgan, A.; Sun, Q.; Wei, B.; Wang, D. Optimization of Water-Alternating-CO2 Injection Field Operations Using a Machine-Learning-Assisted Workflow. SPE Res. Eval. Eng. 2022, 25, 214–231. [Google Scholar] [CrossRef]
- Amar, M.; Zeraibi, N.; Redouane, K. Optimization of WAG Process Using Dynamic Proxy, Genetic Algorithm and Ant Colony Optimization. Arab. J. Sci. Eng. 2018, 43, 6399–6412. [Google Scholar] [CrossRef]
- Rahman, A.; Towards Data Science. Introduction to Ant Colony Optimization (ACO). A Probabilistic Technique for Finding Optimal Paths. 2020. Available online: https://towardsdatascience.com/the-inspiration-of-an-ant-colony-optimization-f377568ea03f (accessed on 18 May 2023).
- Amar, M.N.; Zeraibi, N.; Ghahfarokhi, A.J. Applying hybrid support vector regression and genetic algorithm to water alternating CO2 gas EOR. Greenh. Gases Sci. Technol. 2020, 10, 613–630. [Google Scholar] [CrossRef]
- Amar, M.N.; Ghahfarokhi, A.J.; Wui, C.S.; Zeraibi, N. Optimization of WAG in real geological field using rigorous soft computing techniques and nature-inspired algorithms. J. Pet. Sci. Eng. 2021, 206, 109038. [Google Scholar] [CrossRef]
- Ranganathan, A. The Levenberg-Marquardt Algorithm. Tutoral LM Algorithm 2004, 11, 101–110. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Wikipedia, the Free Encyclopedia. Heavy Oil Production. Available online: https://en.wikipedia.org/wiki/Heavy_oil_production (accessed on 22 May 2023).
- Ahmad, M.A.; Samsuri, S.; Amran, N.A. Methods for Enhancing Recovery of Heavy Crude Oil. In Processing of Heavy Crude Oils—Challenges and Opportunities; Intechopen: London, UK, 2019; ISBN 978-1-83968-410-4. [Google Scholar]
- Kam, D.; Park, C.; Min, B.; Kang, J.M. An Optimal Operation Strategy of Injection Pressures in Solvent-aided Thermal Recovery for Viscous Oil in Sedimentary Reservoirs. Pet. Sci. Technol. 2013, 31, 2378–2387. [Google Scholar] [CrossRef]
- Sun, Q.; Ertekin, T. The Development of Artificial-neural-network-based Universal Proxies to Study Steam Assisted Gravity Drainage (SAGD) and Cyclic Steam Stimulation (CSS) Processes. In Proceedings of the SPE Western Regional Meeting, Garden Grove, CA, USA, 27–30 April 2015. [Google Scholar]
- Sun, Q.; Ertekin, T. Structuring an artificial intelligence-based decision-making tool for cyclic steam stimulation processes. J. Pet. Sci. Eng. 2016, 154, 564–575. [Google Scholar] [CrossRef]
- Shafiei, A.; Dusseault, M.B.; Zendehboudi, S.; Chatzis, I. A new screening tool for evaluation of steam flooding performance in naturally fractured carbonate reservoirs. Fuel 2013, 108, 502–514. [Google Scholar] [CrossRef]
- Queipo, N.V.; Goicochea, J.V.; Pintos, S. Surrogate modeling-based optimization of SAGD processes. J. Pet. Sci. Eng. 2002, 35, 83–93. [Google Scholar] [CrossRef]
- Queipo, N.V.; Pintos, S.; Rincón, N.; Contreras, N.; Colmenares, J. Surrogate modeling-based optimization for the integration of static and dynamic data into a reservoir description. J. Pet. Sci. Eng. 2002, 35, 167–181. [Google Scholar] [CrossRef]
- Santner, T.J.; Williams, B.J.; Notz, W.I. The Design and Analysis of Computer Experiments; Springer: New York, NY, USA, 2014; ISBN 978-1-4419-2992-1. [Google Scholar]
- Amirian, E.; Leung, J.Y.; Zanon, S.; Dzurman, P. Integrated Cluster Analysis and Artificial Neural Network Modeling for Steam-Assisted Gravity Drainage Performance Prediction in Heterogeneous Reservoirs. Expert Syst. Appl. 2015, 42, 723–740. [Google Scholar] [CrossRef]
- Alolayan, O.S.; Alomar, A.O.; Williams, J.R. Parallel Automatic History Matching Algorithm Using Reinforcement Learning. Energies 2023, 16, 860. [Google Scholar] [CrossRef]
- Guevara, J.L.; Patel, R.G.; Japan, J.T. Optimization of Steam Injection for Heavy Oil Reservoirs Using Reinforcement Learning. In Proceedings of the SPE International Heavy Oil Conference and Exhibition, Kuwait City, Kuwait, 10–12 December 2018. [Google Scholar]
- Sivamayil, K.; Rajasekar, E.; Aljafari, B.; Nikolovski, S.; Vairavasundaram, S.; Vairavasundaram, I. A Systematic Study on Reinforcement Learning Based Applications. Energies 2023, 16, 1512. [Google Scholar] [CrossRef]
- Panjalizadeh, H.; Alizadeh, N.; Mashhadi, H. A workflow for risk analysis and optimization of steam flooding scenario using static and dynamic proxy models. J. Pet. Sci. Eng. 2014, 121, 78–86. [Google Scholar] [CrossRef]
- Fedutenko, E.; Yang, C.; Card, C.; Nghiem, L.X. Time-Dependent Neural Network Based Proxy Modeling of SAGD Process. In Proceedings of the SPE Heavy Oil Conference-Canada, Calgary, AB, Canada, 10–12 June 2014. [Google Scholar]
- Klie, H. Physics-Based and Data-Driven Surrogates for Production Forecasting. In Proceedings of the SPE Reservoir Simulation Symposium, Houston, TX, USA, 23–25 February 2015. [Google Scholar]
- Kamari, A.; Gharagheizi, F.; Shokrollahi, A.; Arabloo, M.; Mohammadi, A.H. Integrating a robust model for predicting surfactant–polymer flooding performance. J. Pet. Sci. Eng. 2016, 137, 87–96. [Google Scholar] [CrossRef]
- Alghazal, M. Development and Testing of Artificial Neural Network-Based Models for Water Flooding and Polymer Gel Flooding in Naturally Fractured Reservoirs. Master’s Thesis, The Pennsylvania State University, Energy and Mineral Engineering, University Park, PA, USA, August 2015. [Google Scholar]
- Al-Dousari, M.M.; Garrouch, A.A. An artificial neural network model for predicting the recovery performance of surfactant polymer floods. J. Pet. Sci. Eng. 2013, 109, 51–62. [Google Scholar] [CrossRef]
- Van, S.L.; Chon, B.H. Optimization study on chemical flooding for viscous oil reservoirs by an artificial neural network with the support of the response surface methodology. Int. J. Appl. Eng. Res. 2017, 12, 15644–15658. [Google Scholar]
- Van, S.L.; Chon, B.H. Artificial Neural Network Model for Alkali-Surfactant-Polymer Flooding in Viscous Oil Reservoirs: Generation and Application. Energies 2016, 9, 1081. [Google Scholar] [CrossRef]
- Ahmadi, M.A. Developing a Robust Surrogate Model of Chemical Flooding Based on the Artificial Neural Network for Enhanced Oil Recovery Implications. Math. Probl. Eng. 2015, 2015, 1–9. [Google Scholar] [CrossRef]
- Karambeigi, M.S.; Zabihi, R.; Hekmat, Z. Neuro-simulation modeling of chemical flooding. J. Pet. Sci. Eng. 2011, 78, 208–219. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Pournik, M. A predictive model of chemical flooding for enhanced oil recovery purposes: Application of least square support vector machine. Petroleum 2016, 2, 177–182. [Google Scholar] [CrossRef]
- Larestani, A.; Mousavi, S.P.; Hadavimoghaddam, F.; Ostadhassan, M.; Hemmati-Sarapardeh, A. Predicting the surfactant-polymer flooding performance in chemical enhanced oil recovery: Cascade neural network and gradient boosting decision tree. Alex. Eng. J. 2022, 61, 7715–7731. [Google Scholar] [CrossRef]
- Amirian, E.; Dejam, M.; Chen, Z. Performance forecasting for polymer flooding in heavy oil reservoirs. Fuel 2018, 216, 83–100. [Google Scholar] [CrossRef]
- Sun, Q. The Development of an Artificial-Neural-Network-Based Toolbox for Screening and Optimization of Enhanced Oil Recovery Projects. Ph.D. Dissertation, The Pennsylvania State University, Energy and Mineral Engineering, University Park, PA, USA, December 2017. [Google Scholar]
- Abdullah, M.; Emami-Meybodi, H.; Ertekin, T. Development and Application of an Artificial Neural Network Tool for Chemical EOR Field Implementations. In Proceedings of the SPE Europec featured at 81st EAGE Conference and Exhibition, London, UK, 3–6 June 2019. [Google Scholar]
- Aihara, K. Chaotic Neural Networks. Phys. Lett. A 1990, 144, 333–340. [Google Scholar] [CrossRef]
- Jiang, J.; Shao, K.; Wei, Y.; Tian, T. Chaotic neural network model for output prediction of polymer flooding. In Proceedings of the International Conference on Mechatronics and Automation, Harbin, China, 5–8 August 2007. [Google Scholar]
- Ayala, L.F.; Ertekin, T. Neuro-simulation analysis of pressure maintenance operations in gas condensate reservoirs. J. Pet. Sci. Eng. 2007, 58, 207–226. [Google Scholar] [CrossRef]
- Ahmed, T. Equations of State and PVT Analysis; Gulf Publishing Company: Houston, TX, USA, 2007; ISBN 978-1-933762-03-6. [Google Scholar]
- Ilyshin, Y.V. Development of a Process Control System for the Production of High-Paraffin Oil. Energies 2022, 15, 6462. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Ahmadi, M.A.; Mohammadzadeh, O.; Bahadori, A.; Chatzis, I. Thermodynamic Investigation of Asphaltene Precipitation during Primary Oil Production: Laboratory and Smart Technique. Ind. Eng. Chem. Res. 2013, 52, 6009–6031. [Google Scholar] [CrossRef]
- Ahmadi, M.A. Prediction of asphaltene precipitation using artificial neural network optimized by imperialist competitive algorithm. J. Pet. Explor. Prod. Technol. 2011, 1, 99–106. [Google Scholar] [CrossRef]
- Ahmadi, M.A. Neural network based unified particle swarm optimization for prediction of asphaltene precipitation. Fluid Phase Equilibria 2011, 314, 46–51. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Shadizadeh, S.R. New approach for prediction of asphaltene precipitation due to natural depletion by using evolutionary algorithm concept. Fuel 2012, 102, 716–723. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Golshadi, M. Neural network-based swarm concept for prediction asphaltene precipitation due to natural depletion. J. Pet. Sci. Eng. 2012, 98–99, 40–49. [Google Scholar] [CrossRef]
- Ashoori, S.; Abedini, A.; Abedini, R.; Nasheghi, K.Q. Comparison of scaling equation with neural network model for prediction of asphaltene precipitation. J. Pet. Sci. Eng. 2010, 72, 186–194. [Google Scholar] [CrossRef]
- Kamari, A.; Safiri, A.; Mohammadi, A.H. Compositional Model for Estimating Asphaltene Precipitation Conditions in Live Reservoir Oil Systems. J. Dispers. Sci. Technol. 2015, 36, 301–309. [Google Scholar] [CrossRef]
- Ghorbani, M.; Zargar, G.; Jazayeri-Rad, H. Prediction of asphaltene precipitation using support vector regression tuned with genetic algorithms. Petroleum 2016, 2, 301–306. [Google Scholar] [CrossRef]
- Amar, M.N.; Ghahfarokhi, A.J.; Wui, C.S. Predicting wax deposition using robust machine learning techniques. Petroleum 2022, 8, 167–173. [Google Scholar] [CrossRef]
- Benamara, C.; Gharbi, K.; Amar, M.N.; Hamada, B. Prediction of Wax Appearance Temperature Using Artificial Intelligent Techniques. Arab. J. Sci. Eng. 2020, 45, 1319–1330. [Google Scholar] [CrossRef]
- Benamara, C.; Amar, M.N.; Gharbi, K.; Hamada, B. Modeling Wax Disappearance Temperature Using Advanced Intelligent Frameworks. Energy Fuels 2019, 33, 10959–10968. [Google Scholar] [CrossRef]
- Karaboga, D. Artificial bee colony algorithm. Scholarpedia 2010, 5, 6915. [Google Scholar] [CrossRef]
- Bian, X.Q.; Huang, J.H.; Wang, Y.; Liu, Y.B.; Kasthuriarachchi, T.K.; Huang, L.J. Prediction of Wax Disappearance Temperature by Intelligent Models. Energy Fuels 2019, 33, 2934–2949. [Google Scholar] [CrossRef]
- Obanijesu, E.O.; Omidiora, E.O. Artificial Neural Network’s Prediction of Wax Deposition Potential of Nigerian Crude Oil for Pipeline Safety. Pet. Sci. Technol. 2008, 26, 1977–1991. [Google Scholar] [CrossRef]
- Kamari, A.; Khaksar-Manshad, A.; Gharagheizi, F.; Mohammadi, A.H.; Ashoori, S. Robust Model for the Determination of Wax Deposition in Oil Systems. Ind. Eng. Chem. Res. 2013, 52, 15664–15672. [Google Scholar] [CrossRef]
- Chu, Z.Q.; Sasanipour, J.; Saeedi, M.; Baghban, A.; Mansoori, H. Modeling of wax deposition produced in the pipelines using PSO-ANFIS approach. Pet. Sci. Technol. 2017, 35, 1974–1981. [Google Scholar] [CrossRef]
- Kamari, A.; Mohammadi, A.H.; Bahadori, A.; Zendehboudi, S. A Reliable Model for Estimating the Wax Deposition Rate During Crude Oil Production and Processing. Pet. Sci. Technol. 2014, 32, 2837–2844. [Google Scholar] [CrossRef]
- Stefenon, S.F.; Freire, R.Z.; Coelho, L.S.; Meyer, L.H.; Grebogi, R.B.; Buratto, W.G.; Nied, A. Electrical Insulator Fault Forecasting Based on a Wavelet Neuro-Fuzzy System. Energies 2020, 13, 484. [Google Scholar] [CrossRef]
- Xie, Y.; Xing, Y. A prediction method for the wax deposition rate based on a radial basis function neural network. Petroleum 2017, 3, 237–241. [Google Scholar] [CrossRef]
- Yu, Z.; Tian, H. Application of Machine Learning in Predicting Formation Condition of Multi-Gas Hydrate. Energies 2022, 15, 4719. [Google Scholar] [CrossRef]
- Qasim, A.; Lal, B. Machine Learning Application in Gas Hydrates. In Machine Learning and Flow Assurance in Oil and Gas Production; Springer: Cham, Switzerland, 2019; ISBN 978-3-031-24230-4. [Google Scholar]
- Suresh, S.D.; Lal, B.; Qasim, A.; Foo, K.S.; Sundramoorthy, J.D. Application of Machine Learning Models in Gas Hydrate Mitigation. In Proceedings of the International Conference on Artificial Intelligence for Smart Community, Seri Iskandar, Malaysia, 17–18 December 2020. [Google Scholar]
- Kumari, A.; Madhaw, M.; Pendyala, V.S. Prediction of Formation Conditions of Gas Hydrates Using Machine Learning and Genetic Programming. In Machine Learning for Societal Improvement, Modernization, and Progress; IGI Global: Hershey, PA, USA, 2022; ISBN 1668440458. [Google Scholar]
- Hosseini, M.; Leonenko, Y. A Reliable Model to Predict the Methane-Hydrate Equilibrium: An Updated Database and Machine Learning Approach. Renew. Sustain. Energy Rev. 2023, 173, 113103. [Google Scholar] [CrossRef]
- Wright, B. Chevron Work Flow Reinforces Importance of Simulation to Predictive Behaviors. J. Pet. Technol. 2021. Available online: https://jpt.spe.org/chevron-workflow-reinforces-importance-of-simulation-to-predictive-behaviors (accessed on 10 August 2023).
- Larsen, P.F.; Tønnessen, T.; Schuchert, F.; Khamassi, A.; Jarraya, H.; Aarrestad, H.D.; Imsland, V.; Johan, V.L. Sverdrup: The Digital Flagship. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 4–7 May 2020. [Google Scholar]
- NVIDIA. NVIDIA Success Story: Shell. Using AI and HPC to Improve the Efficiency, Safety, and Sustainability of the Energy Sector. Available online: https://images.nvidia.com/data-center/nvidia-shell-dgx-case-study.pdf (accessed on 10 August 2023).
- Gryzlov, A.; Mironova, L.; Safonov, S.; Arsalan, M. Evaluation of Machine Learning Methods for Prediction of Multiphase Production Rates. In Proceedings of the SPE Symposium: Artificial Intelligence—Towards a Resilient and Efficient Energy Industry, Virtual, 18–19 October 2021. [Google Scholar]
- Aramco. Al and Big Data. Available online: https://www.aramco.com/en/creating-value/technology-development/in-house-developed-technologies/digitalization/ai-and-big-data (accessed on 10 August 2023).
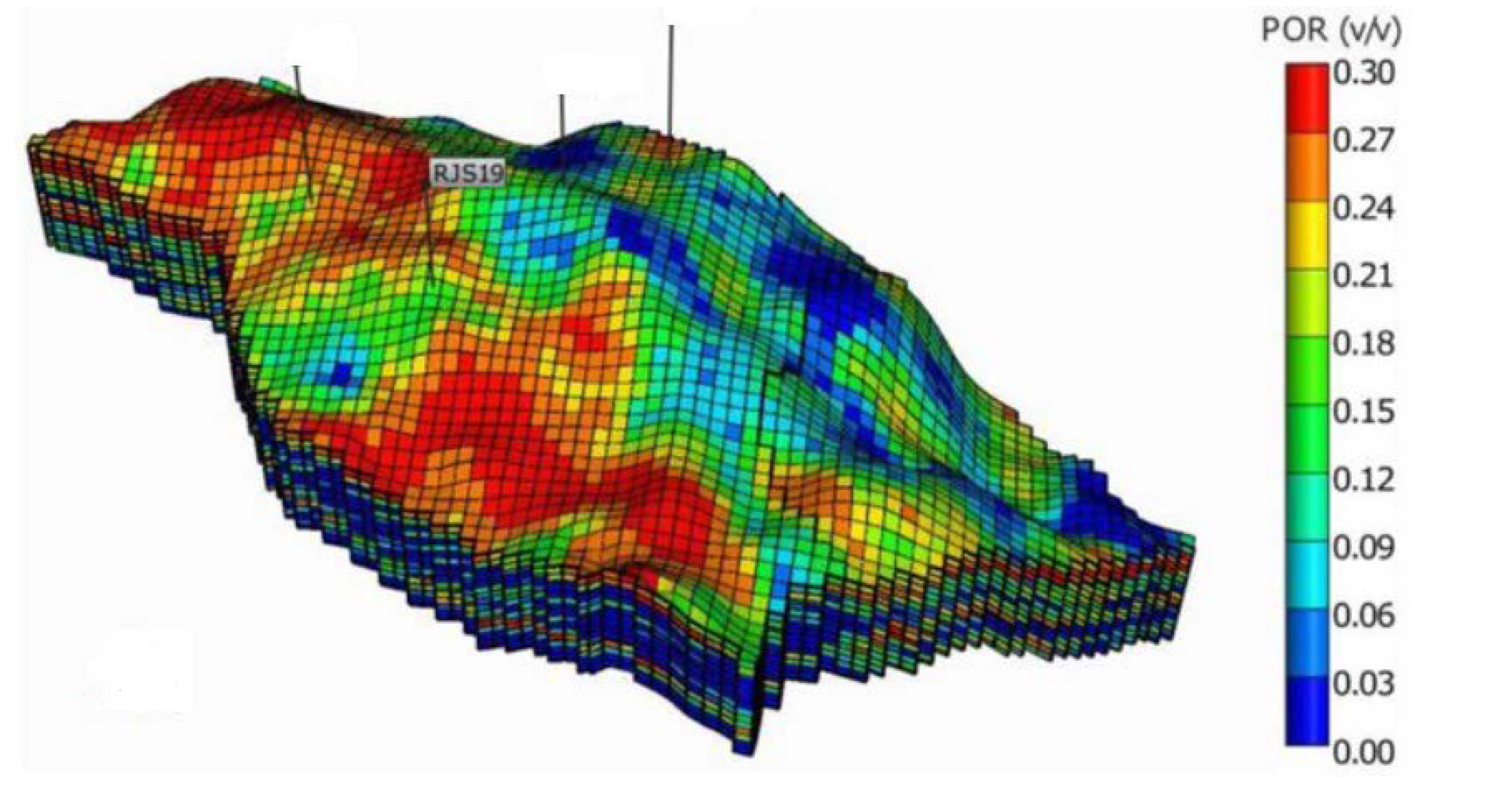
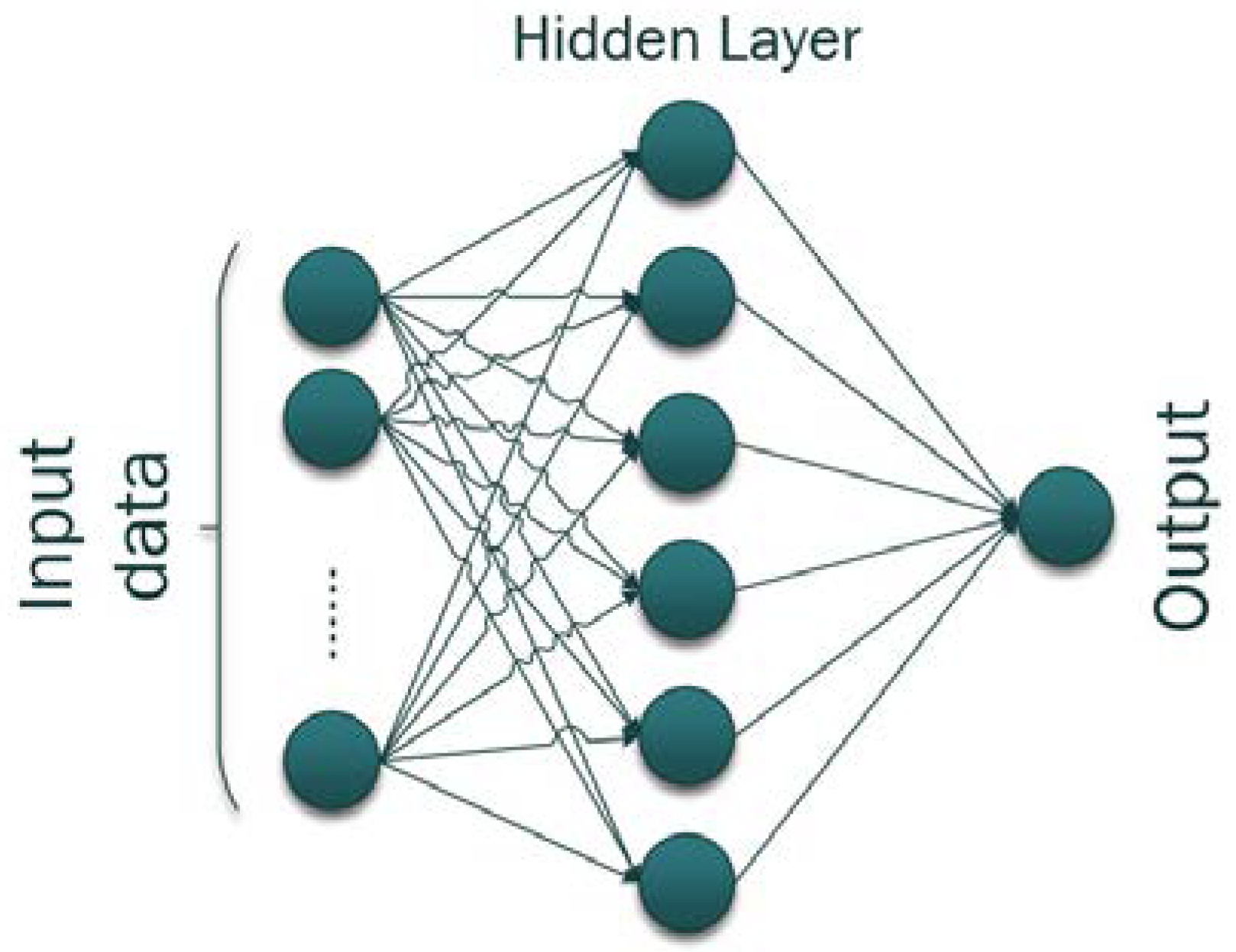
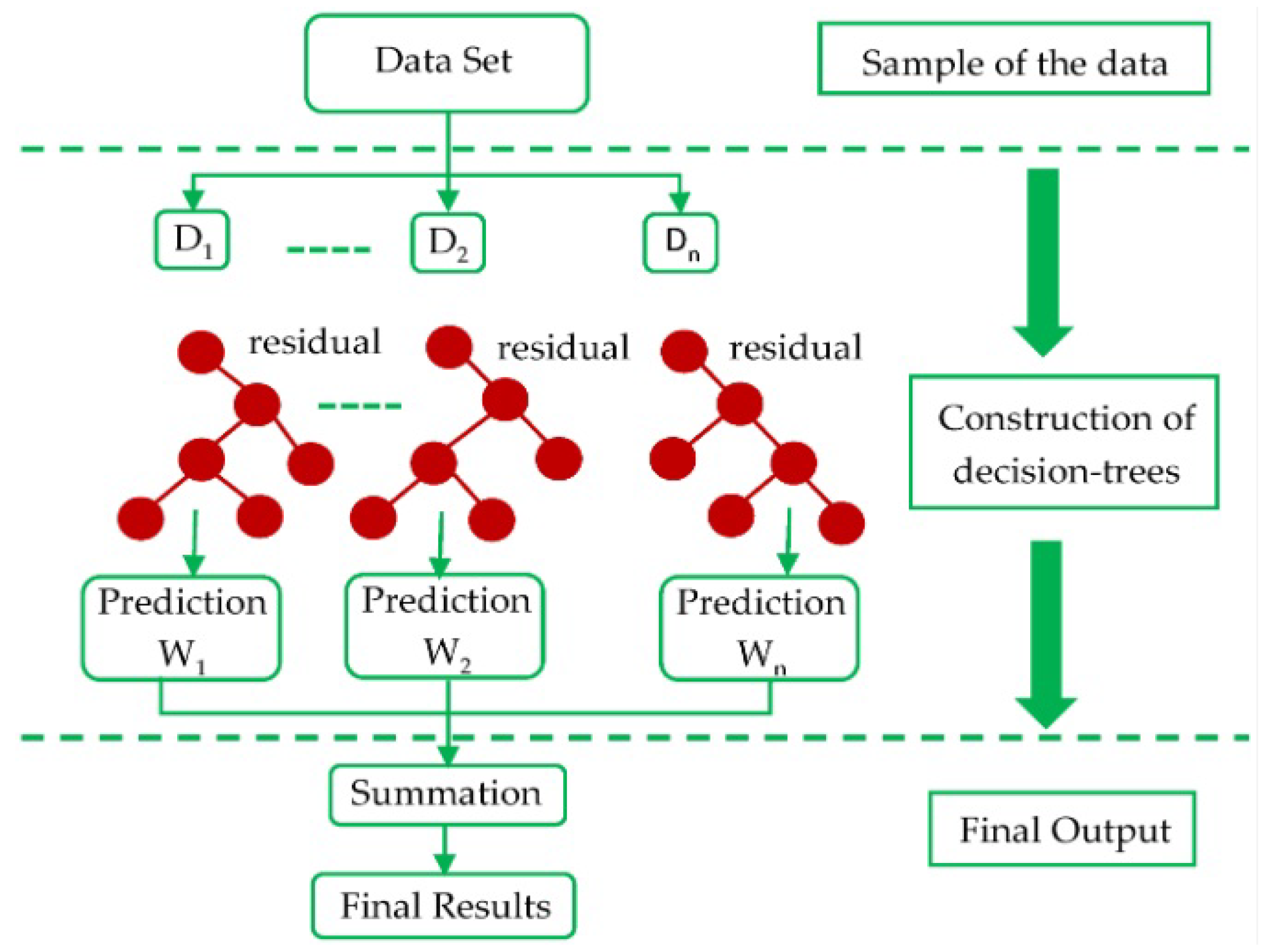
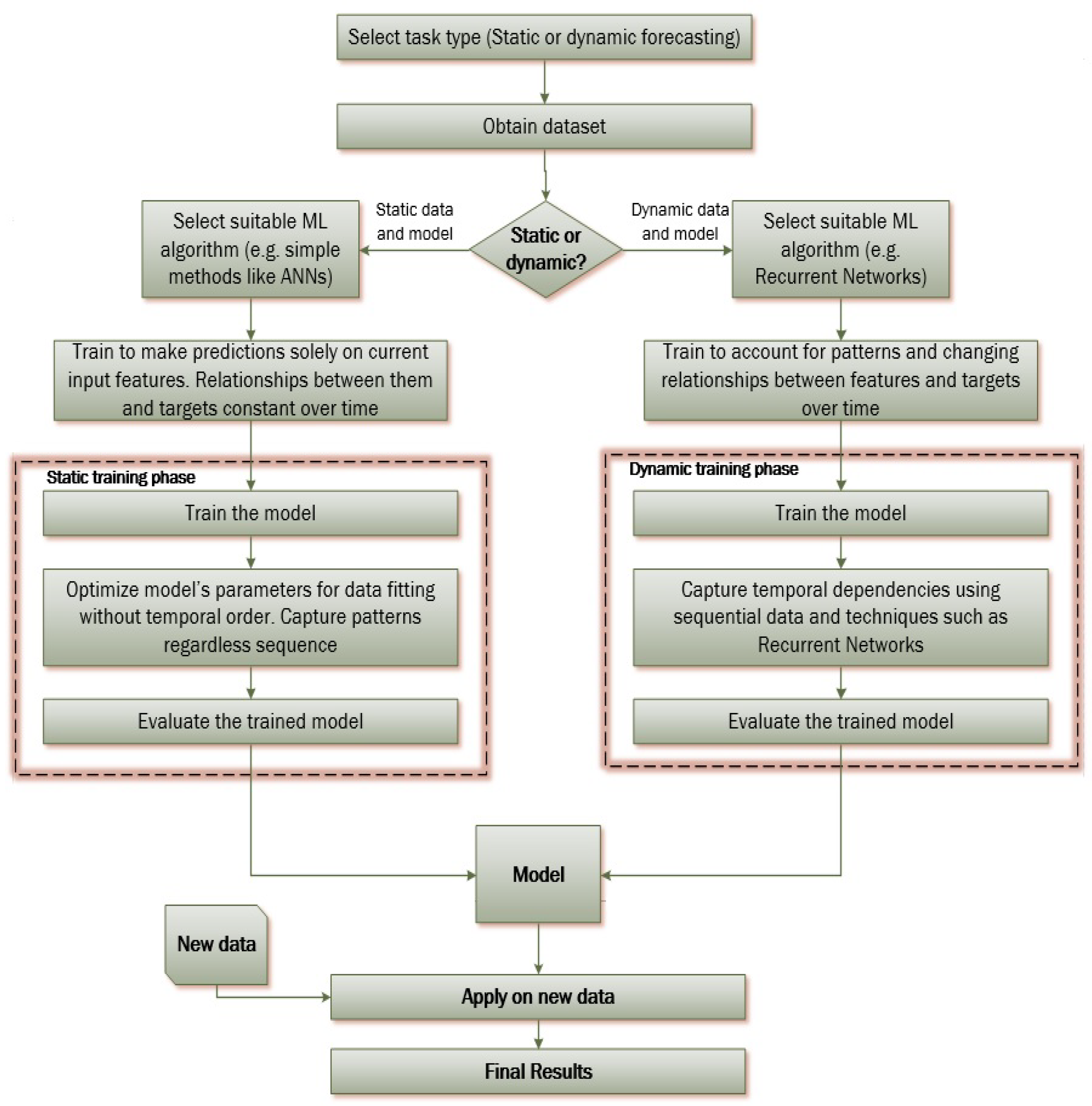
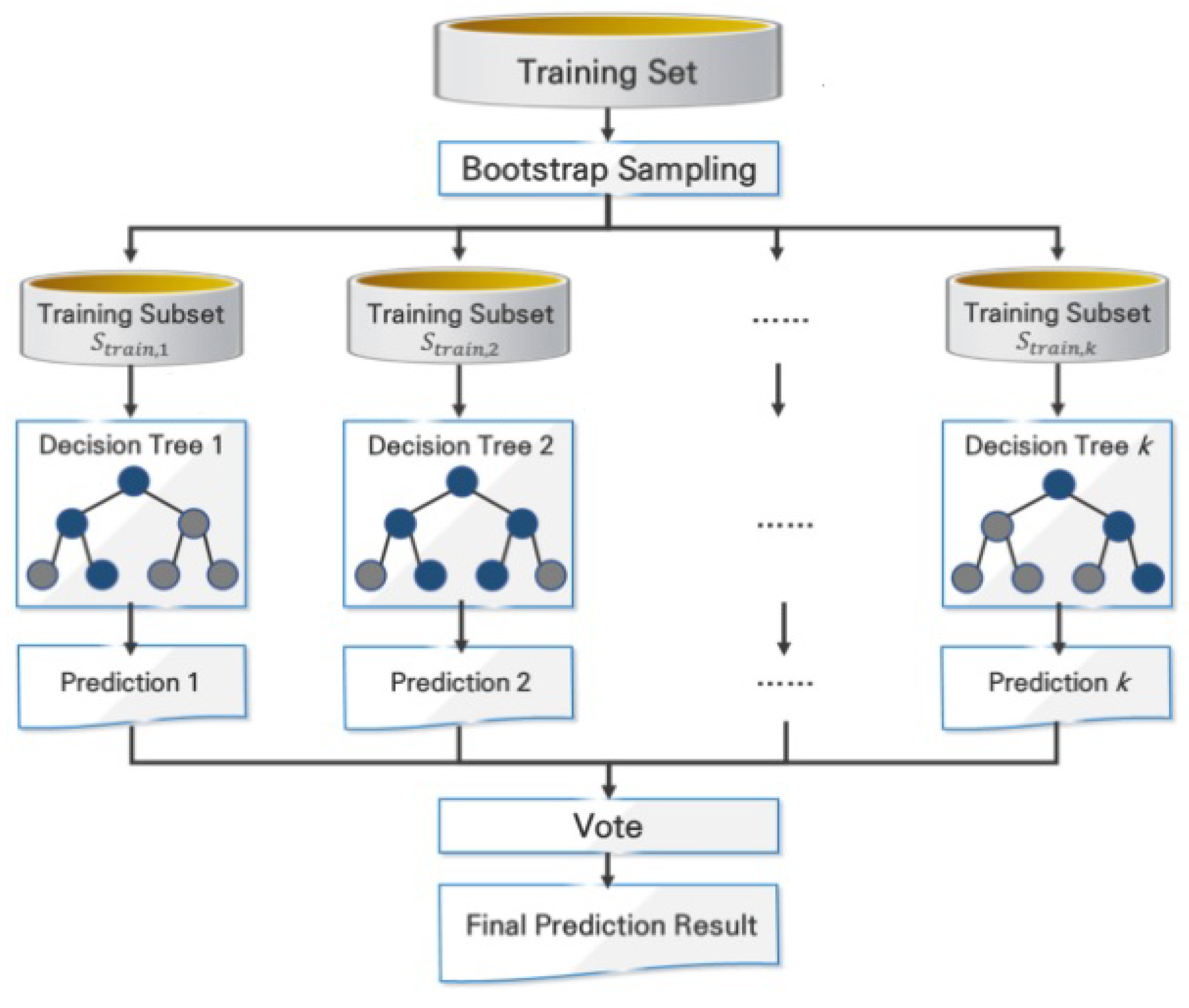

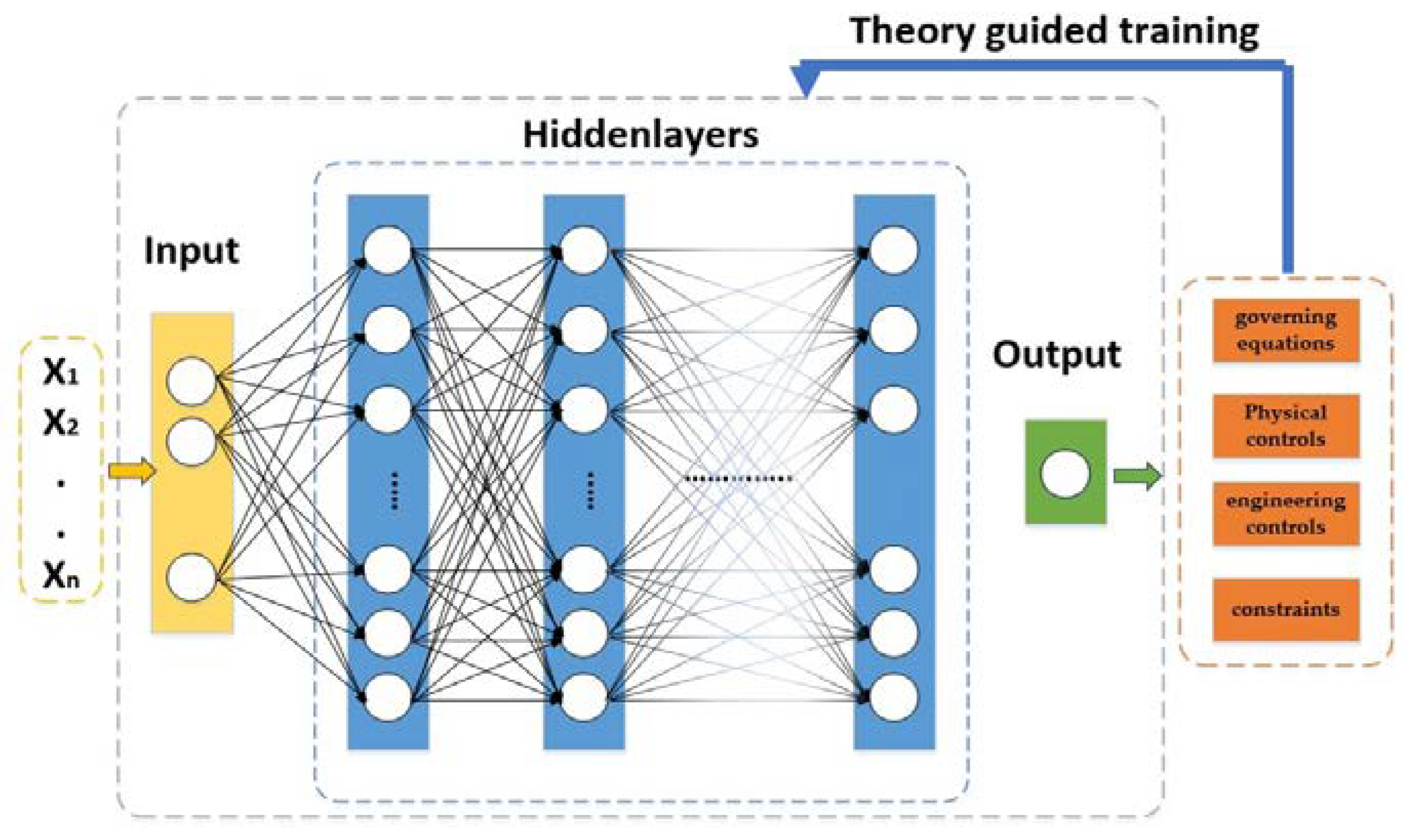
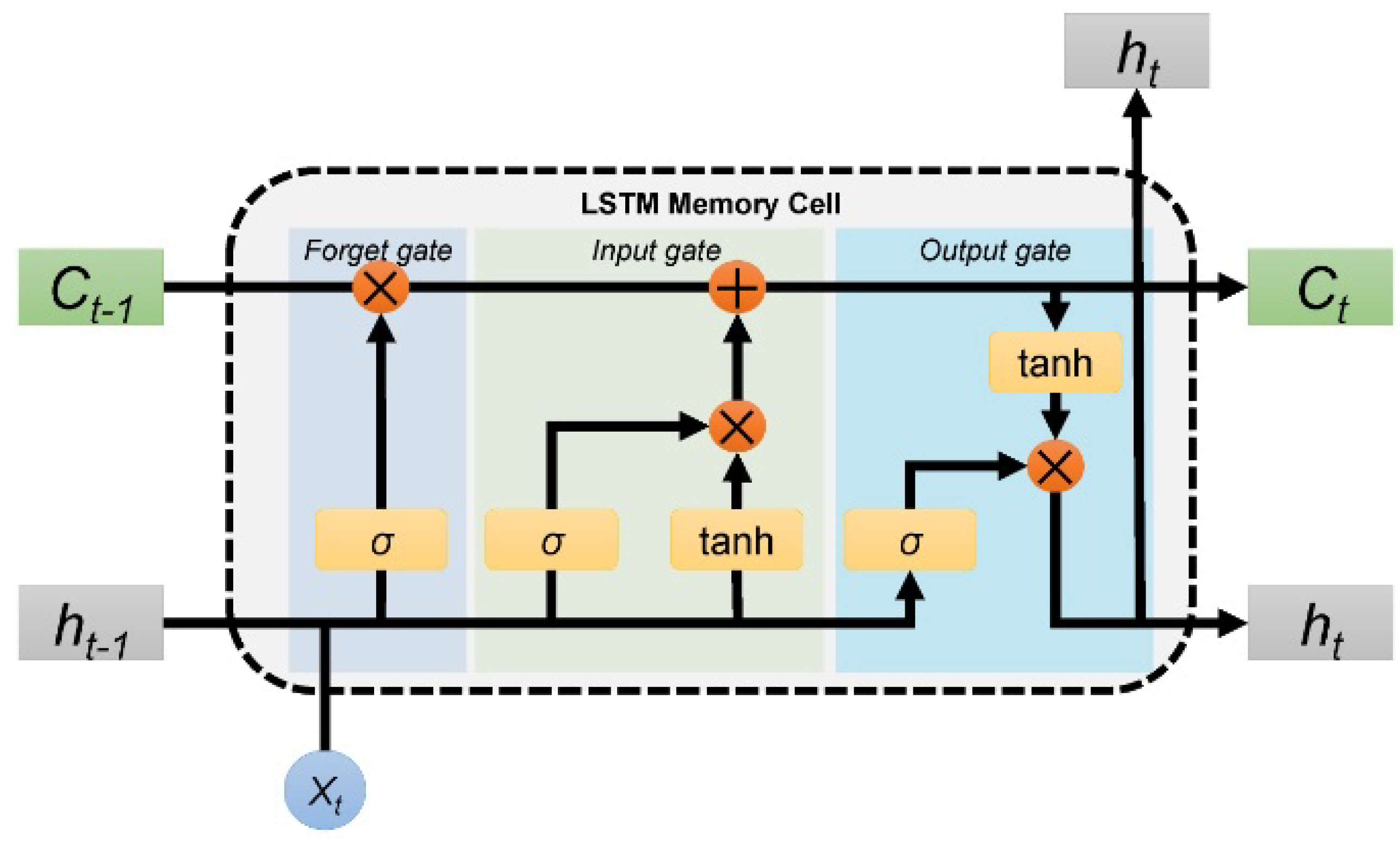
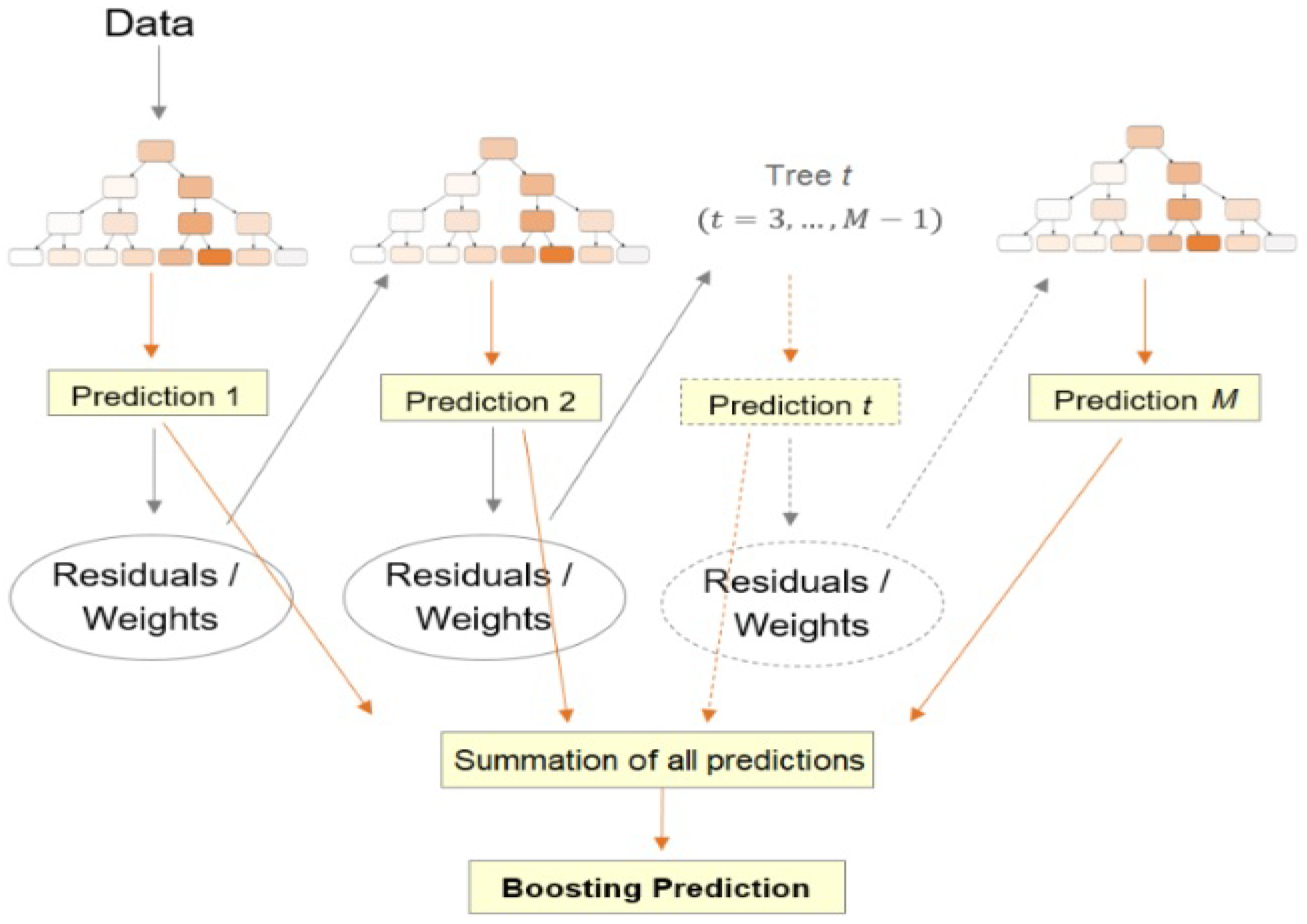
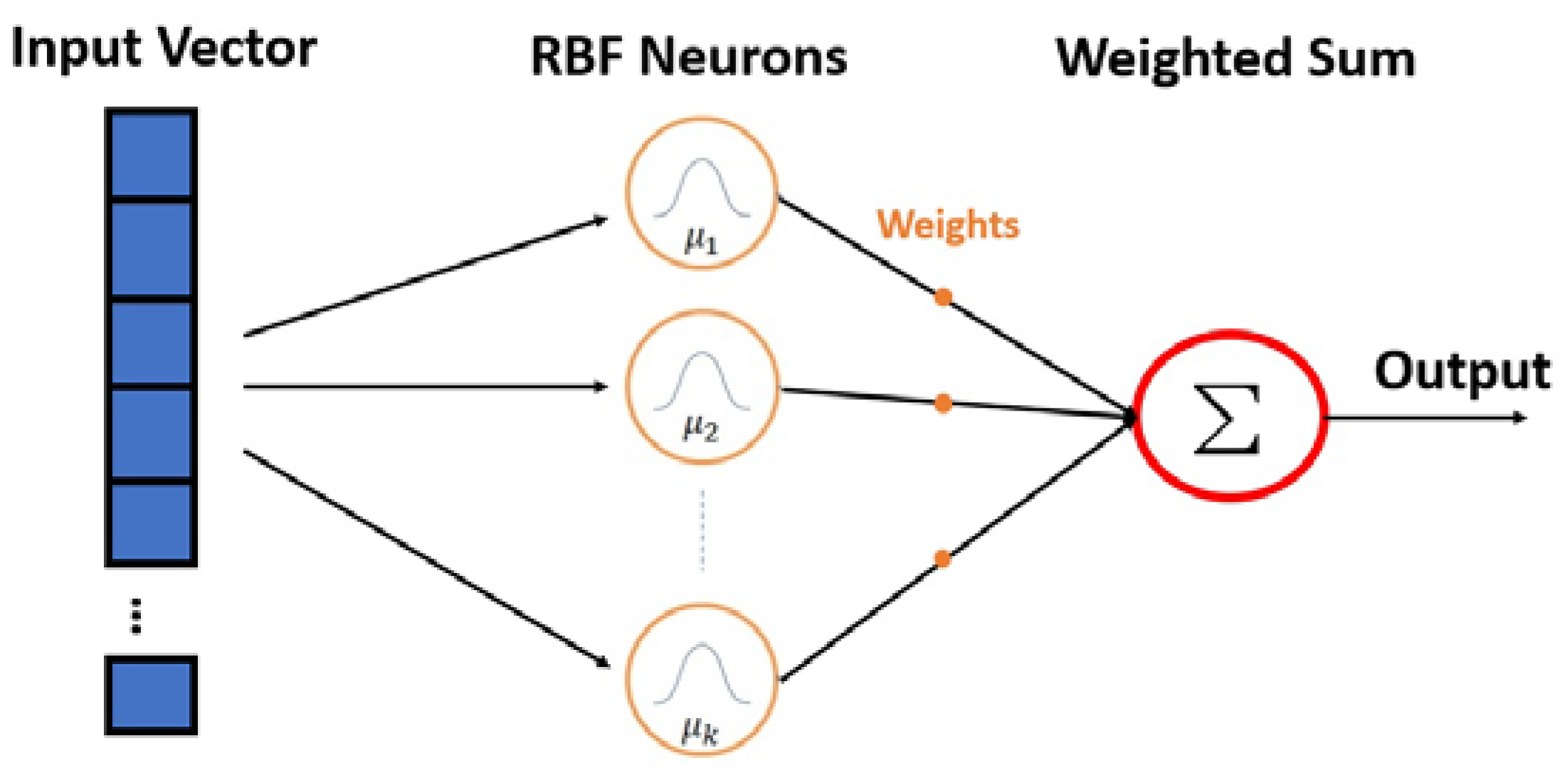
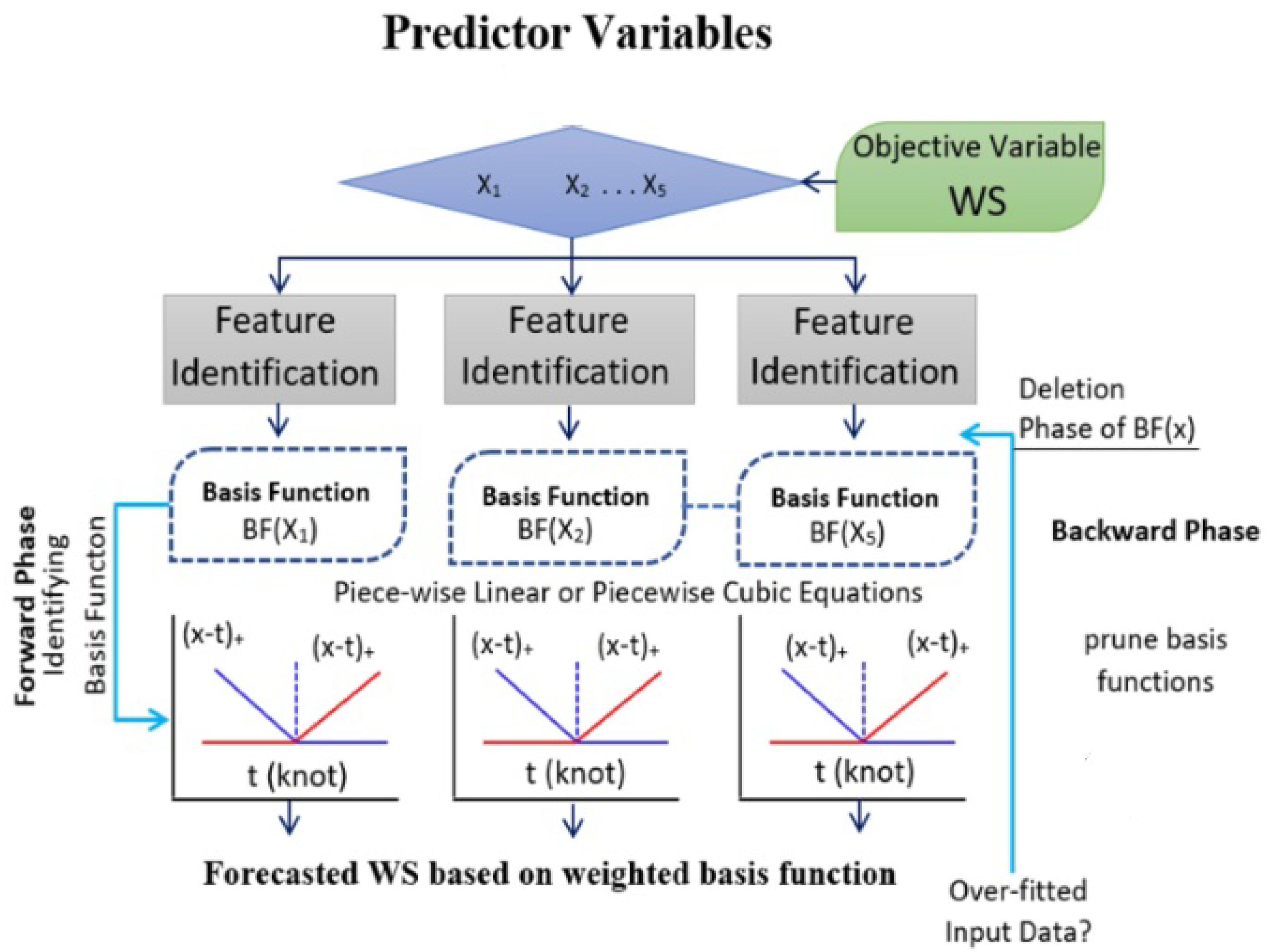
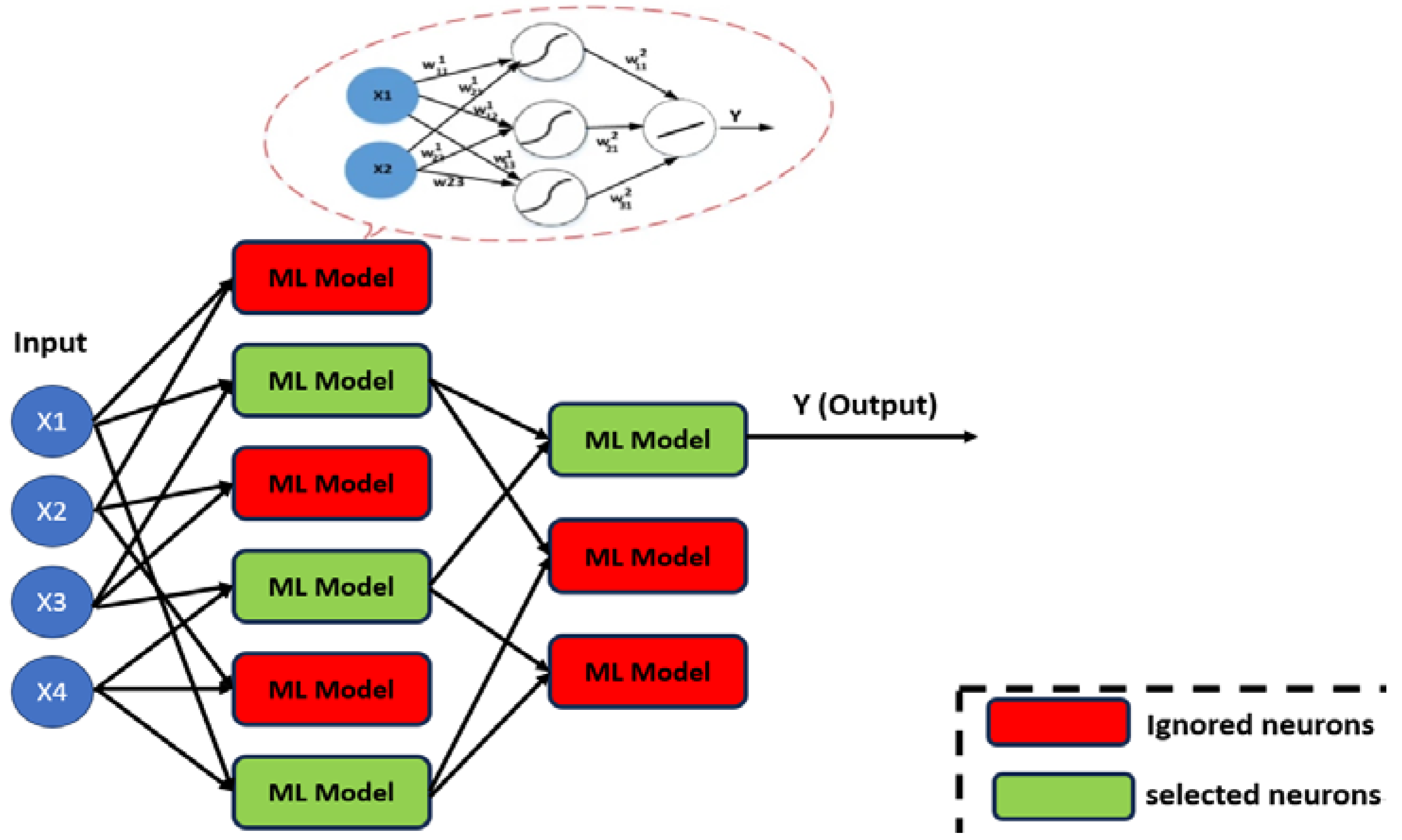
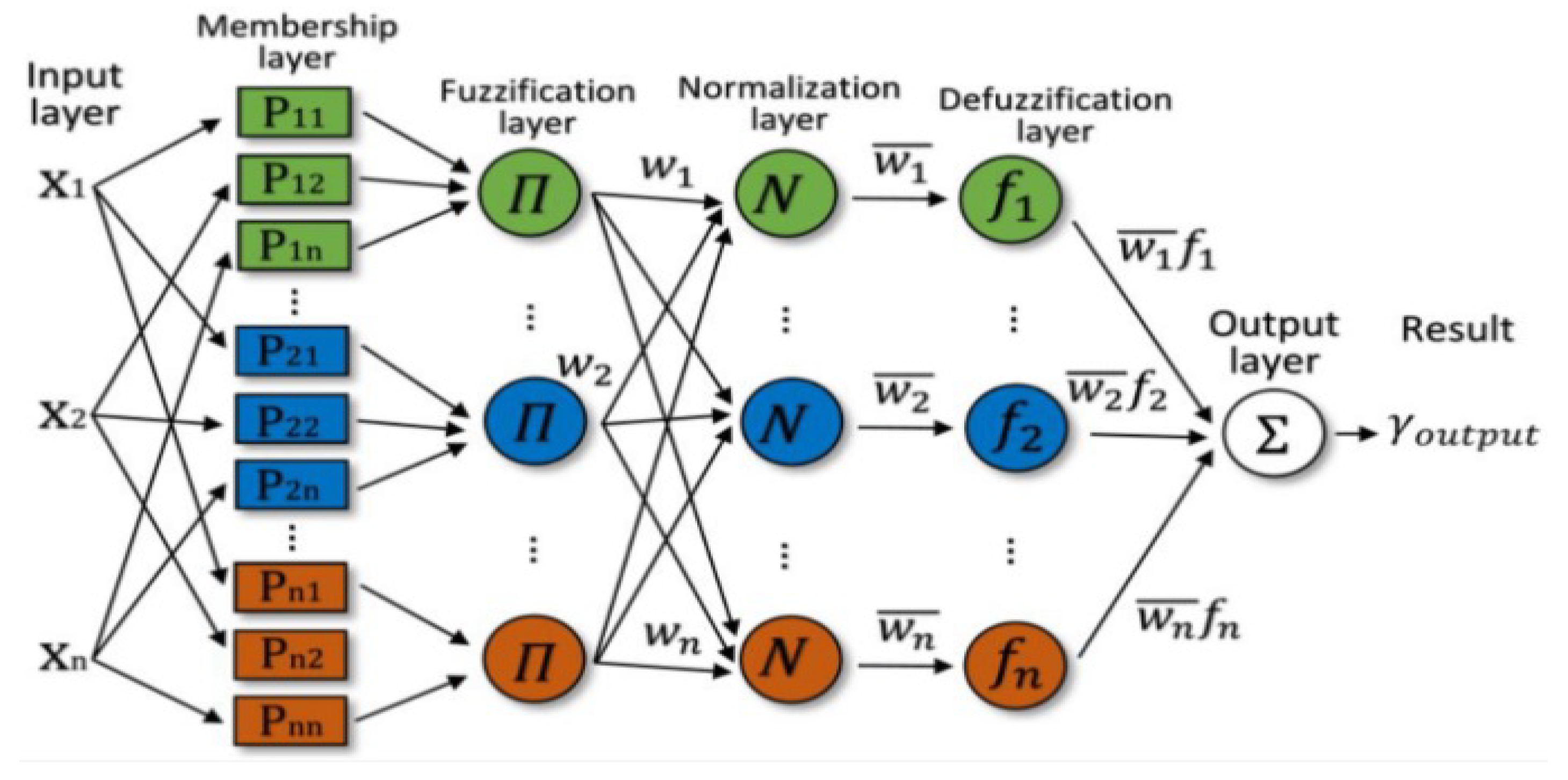
| ML Application | ML Training Scheme | Main Objective | ML Method | Reviewed Studies (Reference List Number) |
|---|---|---|---|---|
| Optimization | Supervised | Production optimization | ANNs or ANNs with optimization techniques | [23,24,25,31,33,93,101] |
| DTs and Ensemble methods (e.g., XGB, GBR, RF) | [33,40,101] | |||
| SVMs and their variations (e.g., LSSVMs, SVRs) | [36] | |||
| Well placement optimization | ANNs or ANNs with optimization techniques | [28,30,92,162] | ||
| DTs and Ensemble methods (e.g., XGB, GBR, RF) | [99] | |||
| Unsupervised | Production optimization | Clustering techniques | [38,39] | |
| Forecasting | Supervised | Static predictions | ANNs or ANNs with optimization techniques | [45,46,48,49,50,51,91,94,100,102,104,113,115,116,117,118,119,120,121,122,123,125,126,127,131,134,140,148,158,159,160,161,163,165,173,174,175,176,177,180,181,189,190,191,192,194,202,210,211] |
| RBFNN | [114,180,199,207] | |||
| DTs and Ensemble methods (e.g., XGB, GBR, RF) | [43,54,96,100,130,133,145,146,147,180,208,210,212] | |||
| SVMs and their variations (e.g., LSSVM, SVRs) | [55,92,100,102,104,110,111,112,133,149,172,179,180,195,196,201,203,205,208,210,211] | |||
| Deep Learning (ANN, encoder- decoder CNN, RNN, etc.) | [56,58,59,60,61,95,132,136,138,139,178,197,198,212] | |||
| Theory guided networks | [63] | |||
| MARS | [129] | |||
| ANFIS | [204] | |||
| GMDH | [142,143,144] | |||
| Unsupervised | GAN | [62,137] | ||
| Reinforcement Learning | Reinforcement algorithm | [167] | ||
| Supervised | Dynamic predictions | RNNs (mostly LSTMs) | [20,44,54,66,71,72,73,75,106,108] | |
| ANNs or ANNs with optimization techniques | [22,76,77,79,86,87,107,135,150,153,169,171,182,183] | |||
| RBFNN | [153,170] | |||
| SVMs and their variations (e.g., LSSVM, SVRs) | [152] | |||
| MTS and VAR | [80] | |||
| HONNs | [84,85] | |||
| Gamma regression | [86,87] | |||
| MLMVN | [89] | |||
| Chaotic Neural Networks | [185] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samnioti, A.; Gaganis, V. Applications of Machine Learning in Subsurface Reservoir Simulation—A Review—Part II. Energies 2023, 16, 6727. https://doi.org/10.3390/en16186727
Samnioti A, Gaganis V. Applications of Machine Learning in Subsurface Reservoir Simulation—A Review—Part II. Energies. 2023; 16(18):6727. https://doi.org/10.3390/en16186727
Chicago/Turabian StyleSamnioti, Anna, and Vassilis Gaganis. 2023. "Applications of Machine Learning in Subsurface Reservoir Simulation—A Review—Part II" Energies 16, no. 18: 6727. https://doi.org/10.3390/en16186727
APA StyleSamnioti, A., & Gaganis, V. (2023). Applications of Machine Learning in Subsurface Reservoir Simulation—A Review—Part II. Energies, 16(18), 6727. https://doi.org/10.3390/en16186727







