Abstract
Profit maximization is critical in the control of power system networks for both power providers and users. Electrical energy is freely accessible in the electrical grid during off-peak hours, with storage units helping to store excess energy and assist the electrical grid during high-demand situations. Such techniques promote grid stability and ensure safe operation. Because renewable resources are intermittent, energy storage technologies are especially significant in renewable-associated power systems. Vehicle-to-grid (V2G) technology has recently acquired popularity in preserving power grid stability in the presence of renewable resources.V2G technology employs automobiles as mobile storage devices and focuses on the efficient utilization of extra power available during off-peak hours. The goal of this work is to improve the functioning of a V2G system in a power network to reduce energy production costs while increasing system profitability. This study for deregulated power environments also depicts the influence of V2G mixing on system voltage profile and locational marginal pricing (LMP), as well as the performance of the Unified Power Flow Controller (UPFC) on system economics. The MiPower simulation program is used in the study to find the best placement of the power storage unit for the modified IEEE 14-bus system.
1. Introduction
At present, thermal energy is the most common type of energy produced in power systems. The market’s major source of electricity is fossil fuel-based energy. However, because of worries about CO2 emissions and global warming, international leaders are pressing people to switch to renewable energy sources to limit the depletion rate of nonrenewable energy sources. Wind power is regarded as one of the most efficient renewable energy sources. However, renewable energy sources are frequently intermittent, necessitating the use of energy storage devices to manage surplus energy output during periods of availability. This method enables energy saving during low peak demand periods and utilization during high peak demand periods. Furthermore, determining the best location for renewable energy sources and storage facilities is critical to increasing overall efficiency. The regulated electricity environment is shifting to a competitive one, known as the deregulated system, to increase financial gains for power producers and customers. Because customers have no option under a controlled system, a single corporation dominates the electrical market, inflicting a burden on consumers. However, with the deregulation of the energy sector, customers have been able to choose from several attractive solutions. Customers in a competitive electrical system can choose their power producers depending on parameters such as power production cost or quality.
In the renewable integrated deregulated system, the combined operation of wind farms and thermal power plants poses a substantial problem due to their volatile nature. This may aggravate system instability and security issues. In this scenario, vehicle-to-grid (V2G) technology can provide a feasible alternative by supplying additional power to the electric grid when renewable sources are unavailable. V2G technology works by discharging electric vehicles (EVs) and transferring electricity to the grid. This procedure can boost system voltage to keep it at a safe level and sustain grid frequency by supplying extra power to the power network. This technology involves feeding power to an EV’s battery and returning it to the grid while the vehicle is in motion. This approach is part of a smart grid that uses information technology to manage energy use. EVs have two distinct advantages. For starters, bidirectional charging and V2G allow a building’s energy management system to be raised and intelligently managed without the need for large, expensive infrastructure expenditures. Second, bidirectional charging lowers the cost of operating power.
Recent studies have been undertaken in the fields of renewable energy and storage technologies. The fluctuating nature of renewable energy sources poses considerable challenges to the integration of renewable energy into power networks. Wind energy is the most important and fastest-growing form of renewable energy [1]. Currently, the grid energy storage system can provide around 125 GW or approximately 3% of the world’s energy generating capacity. Pumped storage hydropower plants are the most frequent and widely used type of energy storage equipment [2]. The battery-based energy storage transport (BEST) technology has been introduced in the power network to improve the usage of variable renewable energy (VRE) and load shifting. BEST is also a promising approach for dealing with transmission line congestion [3]. As renewable energy sources such as wind and solar power become more prevalent, the need for ancillary services to manage their increased variability and unpredictability becomes increasingly essential [4]. Developing countries have set lofty goals to assess the impact of large-scale renewable energy on economic growth and fulfill rising power demand [5]. The authors of the paper [6] focused on optimizing societal welfare and profit by lowering generation costs in a renewable energy system. The study investigated the notion of double-sided bidding, as well as its influence on local marginal pricing and system congestion. Furthermore, the viability of the suggested technique was assessed using thyristor-controlled series capacitors (TCSC) and unified power flow controllers (UPFC).
As indicated by the emergence of new battery technologies for power grid deployment [7], the present trend toward power grid energy storage solutions has grown increasingly crucial. This study provides a multiyear transmission planning model that takes four distinct grid charge methods to reduce system expenses. The model accounts for variations in solar and wind generation [8]. Despite their economic appeal in comparison to alternative storage systems and conventional frequency control methods, lithium-ion batteries represent a significant obstacle to their usage in this setting [9]. Only a few windy locations can compete economically with conventional power generation. This article examines wind turbine cost structures, including turbine life and operating, and maintenance expenses [10]. The researchers of [11] suggest that the effectiveness of V2G systems is around 60–70%, although this number is affected by a variety of circumstances. Paper [12] suggests combining energy storage devices with renewable energy sources in a competitive power system to deliver electricity to thermal power plants at the lowest possible cost while maximizing societal benefits. The existing scenario, multiple problems, regulatory measures, and incentives for developing renewable energy in a competitive electrical system are all discussed in this paper [13]. The research looks towards developing an optimization model that takes into account both the load scheduling on the EV consumer side and routing on the generator side [14].
According to the study, running an alternative power system during an emergency, and using local resources to meet local power demand can influence the course of events. PEVs can serve as mobile power producers, although distributed generators (DGs) such as solar panels or wind farms can also create electricity [15]. With the depletion of nonrenewable resources and the growth in environmental degradation, the use of renewable energy sources has increased significantly in recent years. The lead–acid battery, which is extensively used in electric cars throughout the world, is being abandoned at an alarming rate of 99% in the United States and Europe [16]. The authors [17] debate the design of a supercapacitor energy storage system (SCESS) in the work and discover that the PEV is the only energy storage system that can be recycled and has a larger energy storage capacity [18]. FACTS devices have been utilized to satisfy energy demands while lowering voltage variation, power losses, and operational expenses. These devices are well-known for their outstanding control and ability to increase power transfer capabilities via power electronic converters. Gandoman [19] conducted a literature review on the use of FACTS devices and power quality applications in renewable energy systems to improve efficiency and effectiveness. In his research, Hossain [20] investigated many control theories for FACTS devices. It is critical to determine the best place for putting FACTS devices to maximize their advantages. Benabid [21] used a nondominated sorting particle swarm optimization (PSO) method in his research to discover the optimal location of SVC and TCSC to overcome this issue. Shehata [22] suggested a unique hybrid heuristic method in a multiobjective framework that combines Autonomous Groups Particle Swarm and Grey Wolf optimizers (AGPSO-GWO). This technique is used in power grids to allocate FACTS controllers to reduce active power system losses, voltage variation, and total operating expenses.
Dawn [23] developed an optimization approach for determining the appropriate location and parameter settings of TCSCs in a deregulated power market that includes wind power producers in the system. In the study, Luburi [24] conducted an in-depth examination of the influence of energy storage and FACTS devices on the economic performance of power systems and the exploitation of renewable energy sources. Sulaiman [25] proposed using several metaheuristic algorithms to tackle optimum power flow issues in power systems using FACTS devices. Transmission loss and generating cost were the objective functions considered. Shashank [26] showed in his research that TCSCs may improve transmission line transient stability and Available Transfer Capability (ATC). Paper [27] provides a three-level intelligent framework based on gameplay to evaluate individual and joint tactics of power makers while taking network and physical restrictions into consideration. Ref. [28] describes a simulation model that was used in the design of transactive energy system (TES) architecture. The suggested technique provides for the integration of diverse domains connected with smart grids, while the combined usage of simulation tools that comprise a multidomain system allows for the evaluation of control actions, optimization algorithms, load flow, and communication infrastructure. The study [29] takes the solar PV prediction and the likelihood of EV arrival to improve the operation of an off-grid, solar PV-based commercial CS with a battery energy storage system (BESS) to maximize profit. Work [30] provides a profit maximization model for a Decentralized Electric Vehicle Supply Equipment (D-EVSE) outfitted with a renewable energy system, such as a solar energy system. The authors have developed a Decentralized Profit Maximization Algorithm (DPMA) to assist D-EVSEs in profiting from variations in power prices during the day while selling or purchasing electricity to EVs or from the grid or EVs as discharging procedures. Lai et al. [31] describe a unique deep reinforcement learning-based power scheduling technique for BESS in an active distribution network. The network incorporates quick EV charging demand, PV power generation, and main grid electricity arbitrage. Electricity import from the grid is reduced by recognizing the optimal combination of DG resources such as photovoltaic (PV), wind energy resources, batteries and microturbines, and incorporation of demand response (DR) programs with optimal scheduling of plug-in hybrid electric vehicles (PHEVs) [32]. The proposed DR program minimizes imported power during peak hours by transferring nonemergency loads, known as controlled loads here, to off-peak hours, resulting in lower import costs.
Using vehicle-to-grid (V2G) systems, a strategy for smoothing the volatility of large-scale wind generation is examined in [33]. First, a system for energy management and optimization is created and modeled. The desired grid-connected wind power, necessary electric vehicle (EV) power, and supercapacitor power are calculated using the wavelet packet decomposition method. Paper [34] presents a simple and comprehensive technique for determining the best investment and operation of residential building tenants while moving from automobile ownership to an e-car-sharing system. The research models in [35] present an electric vehicle (EV)-based battery storage as a V2G system for use in long-term dynamic power system simulations. It is also examined for power system control services in the Western Danish power system on typical days with high and low wind output. Work [36] proposes a method for implementing electric vehicles and stationary battery storage in optimization problems using linear relationships, and it is applied to a real-world use case with measurable data to demonstrate its efficacy. The influence of power exchange between EV load aggregators and all-producing businesses in single and multiple strategic corporations on electricity market equilibria is investigated in [37]. To study this method, two levels are put into the power market: the wholesale layer and the EV layer.
Following a thorough review of the literature, it was determined that several studies in the fields of renewable energy and competitive power systems have been conducted in recent years by researchers. There is, however, a research gap that has been filled in this work. The following are the key considerations of this research:
- The prime goal of this research is to optimize the system profit of a wind-associated competitive power system while accounting for imbalanced pricing.
- Profitability in the electrical system may be increased by using renewable energy, and profitability differs between regulated and deregulated contexts. This tendency is caused by the competitiveness that exists in a deregulated economy.
- Because wind energy is unpredictable, it generates a pricing imbalance in the system, which directly affects the system’s profit.
- The goal of this research is to lower the imbalance price while increasing profit by applying optimal V2G operation and UPFC placement.
- V2G technology is used to alleviate pricing imbalances by executing bidirectional power operations between electric cars and the grid based on power demand. Furthermore, UPFC has been included in the system to optimize system profit by lowering congestion expenses.
- The primary goal of this strategy is to supply the greatest possible green electricity at the best possible price while pleasing both power producers and customers.
This paper is organized into various sections by topic. Section 1 focuses on the background research and emphasizes the most important aspects of this study. Section 2 describes the mathematical technique used to validate the work given. Section 3 presents the objective functions in conjunction with the relevant limitations. Section 4 describes the planned work’s step-by-step methods. Section 5 and Section 6 show V2G integration technology and the results gained by including EVs and UPFC, both singly and in combination. The final section presents the results of this investigation.
The work includes both regulated and deregulated environments. Different market participants, including market controllers, are present in the deregulated electricity environment. The whole scheme was completed for the IEEE 14-bus system. When the system was transformed from regulated to deregulated, the system data were converted. Following that, the optimal power flow was solved using the MiPower program, and the remaining work was completed based on the optimal value obtained from the OPF solution.
2. Mathematical Modeling
This section presents comprehensive analyses regarding the mathematical modeling of wind farms, the V2G system, and the UPFC static model.
2.1. Wind Farm
The wind farm is in operation and functions based on wind speed in a specific location. Initially, Vijayawada in Andhra Pradesh, India, the home of Velagapudi Ramakrishna Siddhartha Engineering College, was selected for data collection on wind speed. To carry out this process, information on current wind speeds (CWSs) and estimated wind speeds (EWSs) was gathered at a height of 10 m in real time. Furthermore, the analysis took into account that the hub height of wind turbines (h) in India is generally 120 m. Equation (1) can be utilized to calculate the wind speed at 120 m.
The wind velocity at a height h can be denoted as Wsh, where Ws10 represents the wind velocity at a height of 10 m. Additionally, N is representative of the Hellman coefficient, which is equivalent to 0.143. Measuring the power generated by the wind farm, denoted as WP, can be achieved as elucidated in (2).
In this particular context, the symbol ‘AD’ represents air density while ‘a’ pertains to the swept area of a wind turbine, and ‘e’ represents wind farm efficiency. For this discussion, ‘AD’ has been established to be equivalent to 1.226 kg/m3, ‘e’ has been assumed to be 0.51, and the rotor radius (r) of the turbine has been established as 40 m. According to a report from [6], the wind farm’s investment cost is estimated to be 3.75 $/MWh.
2.2. V2G System
In a vehicle-to-grid (V2G) system, power can flow in a bidirectional fashion, necessitating the use of controlled converters in most V2G systems. The total power output of a V2G system is expounded upon in the following subsections.
- Charging Mode:
During the charging process, the electric vehicle’s battery receives power from the grid. The charging station, which offers a low locational marginal pricing (LMP), can significantly improve the economic sustainability of the system, as stated in (3).
Herein, PDi refers to the aggregate power demand of the ith bus, while pdi denotes the power demand of the ith bus. Additionally, C represents the capacity of the electric vehicle battery that necessitates charging.
- Discharging Mode:
During the process of discharging, the electrical power is transferred from the electric vehicle battery towards the electrical grid. It is imperative to note that, to ensure optimal functionality, the battery should not be fully discharged. The constraints of efficiency ought to be adhered to stringently, not only concerning the internal efficiency of the electric vehicle battery but also for the stable operation of the converters that are present within the system. The average efficiency emanating from both the electric vehicle battery and the converter will have a direct impact on the discharge of the battery toward the grid. This relationship has been explicitly expounded in (4).
Here, E is the overall battery efficiency. Different types of batteries are used in EVs. Table 1 shows some parameters related to different types of batteries that can be used for V2G applications [16]. In the mentioned paper, lead–acid and lithium-ion batteries have been compared in terms of performance and profit maximization for both the utility and the consumers. In addition, supercapacitors have also been used for comparison since they have an efficiency of 97.94% [17]. Here, the overall efficiency has been obtained by averaging the efficiencies of the V2G system (efficiency of 70%) [11] and the efficiencies of different batteries.

Table 1.
Parameters of EV Batteries.
2.3. Locatioaln Marginal Price (LMP)
Locational Marginal Price (LMP) is a pricing mechanism utilized in electricity markets worldwide to determine the cost of electricity at specific locations within the grid. This method takes into consideration various factors, such as the expense associated with transporting electricity from the point of generation to the point of consumption, demand, and available capacity. It allows for the establishment of the market clearing price for multiple nodes on the transmission grid. The marginal price at a particular node is essentially the sum of the variable supply cost, transmission losses, and congestion within the system. Typically, in an LMP system, electricity prices are determined individually for each location on the grid, based on the cost of delivering power to that specific location. Therefore, electricity prices may differ in various parts of the grid, even if they are supplied by the same power plant. LMP is a widely used pricing method in electricity markets globally, including the United States, Europe, and Australia. It efficiently promotes the optimal use of the grid and encourages investment in new transmission infrastructure.
2.4. Sequential Quadratic Programming (SQP)
The optimal power flow problem is generally solved using the SQP method in MiPower. The constrained nonlinear problem can be solved using the sequential quadratic programming (SQP) iterative approach. SQP techniques are capable of resolving mathematical issues where the objective function and limitations are twice continuously differentiable. These techniques are utilized in popular numerical settings such as MATLAB and GNU Octave. Among the most frequently used algorithms is Sequential Quadratic Programming (SQP), which has robust theoretical underpinnings and a broad range of algorithmic capabilities.
2.5. Unified Power Flow Controller (UPFC)
The Unified Power Flow Controller (UPFC) is a popular FACTS device utilized for managing and regulating the flow of power and voltage in electrical transmission systems. Unlike TCSC, the static model of the UPFC is more elaborate and consists of various components, including a series transformer, a shunt transformer, and a voltage source converter. The UPFC can function as capacitive or inductive compensation by modifying the series reactance of the transmission line and shunt reactive power injections or extractions at the connected bus. The reactance of the UPFC is determined by the reactance of the transmission line where it is located. As a result, the UPFC is vital in improving the stability and reliability of power systems and ensuring more efficient use of electrical energy. With its excellent capabilities, the UPFC has become an indispensable device for power utilities and grid operators, contributing to the seamless interconnection and integration of different power systems and grids worldwide. The reactance value of the UPFC is dependent on the reactance value of the transmission line where the UPFC is intended to be installed. Concurrently or independently, the UPFC can modify the amplitude and phase angle of the series-injected voltage as well as the reactive current drawn by the shunt-connected voltage source converter. UPFC is composed of two voltage source converters connected back-to-back through a direct current connection. The UPFC static model is depicted in Figure 1, which is considered for this work.
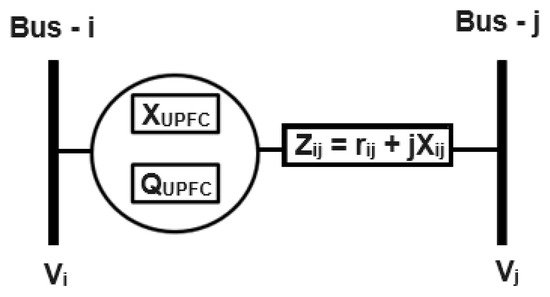
Figure 1.
Static model of UPFC.
The determination of the total reactance of a transmission line () requires the combination of the line’s reactance () and that of the UPFC, to which it is connected (). The equation incorporates a variable () that represents the compensation level of the UPFC. To obtain the reactance of the connected UPFC, it is necessary to multiply the constant by the line’s reactance. The compensation level of the UPFC is limited to a specific range, meaning that it should not exceed 20% of the line’s reactance or fall below 70% of it.
The injected or extracted reactive power through the shunt converter of UPFC is represented by . The considered operational range of (MVAr) for this work is as follows:
To determine the ideal UPFC position and rating, the values of and were changed simultaneously within the considered limits, and the objective function values (i.e., system generation cost) were calculated for all instances. The ideal position and rating of UPFC have been determined based on the minimal objective function values conditions.
3. Objective Function
In a regulated system, market controllers are nonexistent, thus requiring customers to pay energy prices determined by power producers. However, in a deregulated system, an independent system operator serves as the market controller to oversee the entire power market. This results in customers receiving various benefits, such as reduced power prices, improved power quality, and stable voltage profiles. In a renewable added system, the electrical network’s operation follows the power scheduling concept. The renewable power plant must provide future generation scenarios to market operators, initiating power scheduling based on the data submitted. However, the unpredictable nature of renewable sources means that the renewable power plant cannot always follow the submitted power generation, leading to the imbalance price concept. This concept harms system profits. The positive imbalance price indicates awards given to renewable power producers for supplying extra power to the grid compared to the submitted data. Conversely, the negative imbalance price happens due to the shortage of power supply from the renewable plant to the grid. The system profit SP(p) relies on the revenue RC(p), generation cost GC(p), and imbalance price IP(p) at time p. This paper considers the expansion problem in (8) as the objective function for profit maximization.
The overall cost of revenue comprises two distinct sections, namely the revenue generated from the thermal plant () and the revenue from the wind farm (), both of which are illustrated in (9) and (10).
represents the thermally generated power at a given time p, while LMP(m,p) refers to the LMP of the mth thermal generator at the same time. The total number of generators in the system is denoted by N. The current wind power (CWP) and estimated wind power (EWP) are the determining factors for the imbalance price in the system. The imbalance price for an electrical network with wind incorporation can be expressed using Equation (11).
where ER(p) and DR(p) represent the surplus and shortfall rates of the wind power facility at a given moment p. Moreover, the generated wind power for the mth unit is determined based on the estimated and current wind velocity. Additionally, the imbalance price coefficient is denoted by . It should be noted that the system’s generation cost is defined as stated in (14).
At time p, one must consider both the thermal production cost () and the investment cost of wind farms (). The price coefficient of the thermal plant is represented by am, bm, and cm. The analysis of integrating wind generators at different locations in the power grid on voltage, LMP, generation costs, and profits in regulated systems has been carried out using the IEEE 14-bus system. The integration of renewable energy generation has increased the system’s profit. The profitability of the energy system can be enhanced by introducing a deregulated environment. Competitive power systems with demand-side bidding have higher returns compared to regulated systems. In this case, renewable energy sources are chosen to maximize the benefits of the power system.
Constraints for solving of OPF problem:
In the realm of power transmission, and denote transmission loss and power demand, respectively. In addition, , which refers to the line conductance of the line that connects buses ‘x’ and ‘y’, is important. Furthermore, the voltage magnitude of bus ‘x’ and bus ‘y’, denoted as ‘|Vx|’ and ‘|Vy|’, respectively, and the voltage angle of bus ‘x’ and bus ‘y’, represented as ‘δx’ and ‘δy’. To execute Optimal Power Flow (OPF) solutions, it is imperative to consider a variety of continuous and discrete constraints. These constraints serve the purpose of preserving the system’s security and operational limits, and are as follows:
The voltage limits for bus ‘m’ comprise both the lower and upper limits denoted by ‘’ and ‘’, respectively. In addition, the corresponding phase angle limits for voltages at the same bus are represented by ‘’ and ‘’. The total number of transmission lines within the system is commonly referred to as ‘NTL’. The actual power limits of bus ‘m’ are bounded by lower and upper limits, indicated by ‘’ and ‘’, respectively. Lastly, the minimum and maximum limits of reactive power at bus ‘m’ are ‘’ and ‘’, respectively.
4. Flow Chart of the Proposed Method
The fundamental parameters of an IEEE 14-bus system have been meticulously examined, and the earned revenue, production expenditures, and net income have been accurately computed using advanced Mipower software 7.0. The systematic approach of the recommended methodology is elegantly illustrated in Figure 2. The proposed work involves multiple steps for its completion. Various load buses of the IEEE 14-bus system were used to determine the ideal placement of the wind farm and calculate the profit for each scenario. The optimal position of the wind farm was recommended based on the maximum profit achieved by the system post-placement. The wind farm’s capacity was randomly set at 7MW. The primary goal of this work is to enhance the system’s profit by utilizing V2G technology while considering the imbalance price. Additionally, the placement of UPFC was conducted to minimize transmission line congestion and further maximize system profit. The proposed approach involves a step-by-step process as outlined below:
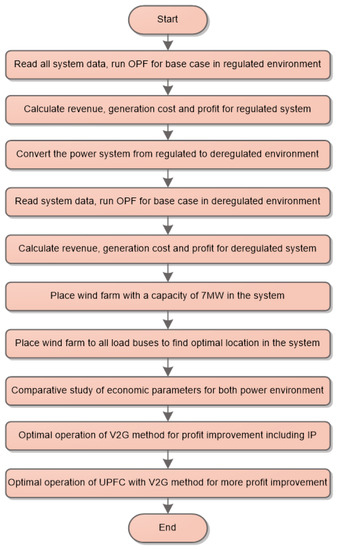
Figure 2.
Flowchart of the proposed method for maximizing profit.
- Firstly, the system data of the considered system are read and analyzed.
- Next, the economic parameters of the system, including revenue, generation cost, and profit, are calculated for a regulated power environment.
- The power system is then converted from a regulated to a deregulated environment, and the economic parameters are recalculated.
- A wind farm with a fixed capacity of 7 MW is added to the system, and an optimal placement strategy is suggested. The wind farm is placed at all load buses simultaneously, and the system profit is calculated for each case. Based on the highest values of profit, the optimal location for the wind farm is identified.
- A comparison study of all economic parameters is conducted for both regulated and deregulated environments.
- Imbalance cost measurement is performed to account for any mismatches between actual and predicted wind speed data.
- V2G placement is then implemented in the system to reduce the adverse effects of imbalance cost and boost system profit.
- Finally, UPFC placement is utilized to further maximize system profit by reducing system congestion.
The proposed methodology can apply to any small, large, or hybrid power system.
5. V2G Integration Technology
The uprising of cardinal and the deployment of advanced technologies across societies have facilitated the widespread implementation of intricate solutions. One such solution is V2G technology, which effectively resolves the issues associated with power quality, voltage instability, and stable grid frequency maintenance. The V2G system functions through communication between the EV charging location and the power grid. In a deregulated market environment, electricity prices are lower during off-peak periods, while they are significantly higher during peak periods. The block diagram of the V2G system is illustrated in Figure 3. The bidirectional flow illustrates the power transfer process from the grid to vehicles and from vehicles to the grid. This shows how an EV battery storage system works in charging and discharging modes. Power flows from vehicles to the grid (V2G) during peak load situations and from the grid to vehicles (G2V) during off-peak load conditions. This preserves the grid’s stability as well as improves the system’s economics. The V2G mechanism is utilized to return the EV’s stored energy to the power grid. During charging, electricity goes from the electric grid to the EV’s battery, and during discharge, power flows from the EV’s battery to the electric grid. The AC–DC bidirectional converter, the DC–AC bidirectional converter, and the control and management system are the three basic functional components of the V2G system.
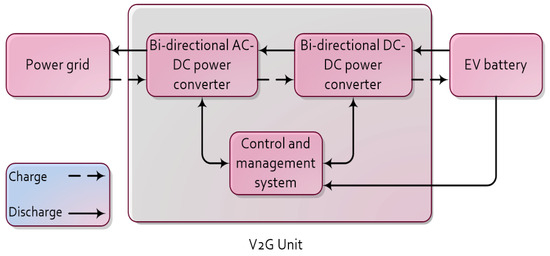
Figure 3.
Block diagram of V2G system.
6. Results and Discussions
A selected IEEE 14-bus test system has been utilized to authenticate the effectiveness, sustainability, and feasibility of the proposed approach. This system comprises 14 buses, five generators, and 20 lines, with Bus No. 1 defined as the slack bus. The system data have been obtained from [38]. The study and analyses have been executed in the following sequential steps:
- Step 1:
- Determining the optimal placement of the wind farm;
- Step 2:
- Comparing the economic factors between regulated and deregulated power systems;
- Step 3:
- Measuring the imbalance price and evaluating its impact on the system profit;
- Step 4:
- Implementing V2G technology to enhance the profit margin;
- Step 5:
- Strategically placing UPFC to further improve the profit margin.
- Step 1:
- Determining the optimal placement of the wind farm
The wind farm incurs no running costs, but there are investment and labor costs that wind power producers must consider to optimize profit placement within the system. To determine the optimal location of the wind farm within the system, it has been placed at different load buses and the system’s profit has been calculated for each case. The wind farm’s optimal position has been selected based on the maximum system profit achieved after placement. The wind farm’s capacity within the system has been set at 7 MW, chosen at random. To verify the proposed method’s applicability, a total of nine cases, including the base case, have been selected and listed in Table 2. The impact of wind farm allocation on economic parameters is assessed for all cases considered, both in regulated and deregulated power environments.

Table 2.
Scenario Details.
Table 3 presents an insightful comparative analysis of the revenues, generation costs, and profits of a regulated system. The system has installed wind energy at several load collection points, with due consideration given to the system’s thermal revenues, generation costs, and profits. Furthermore, the power generated by the generated buses and the corresponding Locational Marginal Prices (LMP) have been meticulously recorded. It has been discerned that the placement of the wind farm at bus number 9, also known as Case-4 in Table 2, offers the most substantial profit.

Table 3.
Economic Factors in Regulated System ($/h).
Currently, the system has undergone a transformation from a regulated to a deregulated environment, which was achieved by taking load-side bidding along with generator-side bidding in the electrical market. The demand-end bidding procedure is executed specifically from bus number 6. Similar to the regulated system, in this case, wind energy has been established at distinct load buses. Thermal revenues, generation costs, and profit have been meticulously computed based on the generated power capacity and LMP of the system. As indicated in Table 4, the placement of the wind farm at bus number 14 provides the optimal system profit, which is known as Case-9. Additionally, Figure 4 showcases the single-line diagram of the optimal power flow solution for the base case by utilizing MiPower software 7.0.

Table 4.
Economic Factors in Deregulated System ($/h).
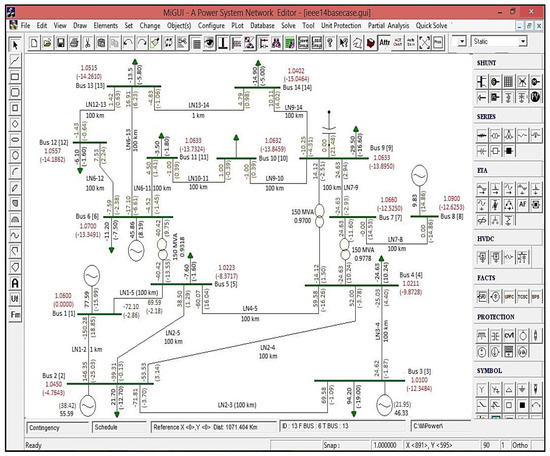
Figure 4.
Single-line diagram of OPF problem solution using MiPower for the base case.
- Step 2:
- Comparing the economic factors between regulated and deregulated power systems
Currently, there has been a significant increase in the utilization of deregulated systems worldwide, which can be attributed to the economic support given to its players. This surge is further influenced by the economic benefits associated with deregulation. To this effect, a comparative analysis has been conducted to examine the revenue, generation cost, and profit of both regulated and deregulated systems. As depicted in Figure 5, the comparison of revenue between the two systems shows that the regulated system generates more revenue than the deregulated system. It is important to note that the revenue mentioned here refers to the income of power producers. Therefore, the reduction of revenue implies a lesser burden on consumers in terms of energy costs, which is the primary objective of the deregulated system.
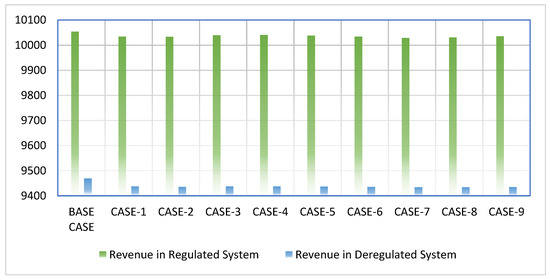
Figure 5.
Revenue comparison for regulated and deregulated power systems ($/h).
The amalgamation of investment disbursed towards the creation of electric power, in addition to the combined expenses of transmission and distribution, is commonly referred to as the system generation cost. This comprises the expenses incurred on the procurement of machinery, raw materials, installation costs, wages of the workers, and miscellaneous expenses. It is noteworthy that the generation cost of the regulated system surpasses that of the deregulated system, as is evident from Figure 6. This phenomenon can be attributed to the intense competition prevailing among the power producers, which compels them to assimilate modern technologies to ensure the maintenance of power quality while simultaneously minimizing the generation cost with the ultimate goal of improving their customer base.
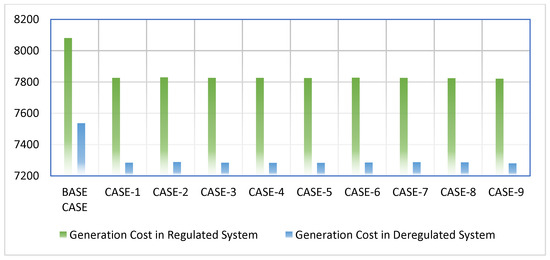
Figure 6.
Generation Cost comparison for regulated and deregulated power systems ($/h).
The remnant funds ensuing from the subtraction of the expenses incurred in the process of production from the revenue collected are commonly referred to as profit. In this paper, profit is denoted in the currency of dollars per hour. The comparative analysis of the profitability of regulated and deregulated systems is presented in Figure 7, which unequivocally establishes that the regulated system yields higher profits when juxtaposed with the deregulated system. This clearly indicates that power producers garner profits, thereby enabling customers to reap the rewards of the deregulated system’s implementation. From Figure 7, it can be concluded that wind farm deployment offers superior profits for both regulated and competitive power systems, in contrast to systems that lack such deployment. This outcome is bound to stimulate power providers to invest significant capital in renewable power plants as it will procure greater economic paybacks.
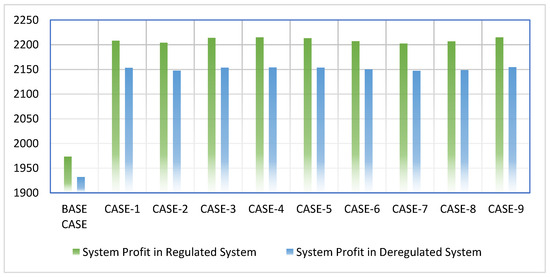
Figure 7.
System profit comparison for regulated and deregulated power systems ($/h).
In the present paper, a wind farm consisting of a fixed amount of 7 MW has been meticulously selected to demonstrate the significant impact of wind farms on both the regulated and the deregulated systems. After conducting a comprehensive comparative study, it has been conclusively determined that a larger volume of wind power placement can result in better profits for market participants, particularly for customers, which can be referred to as social benefits. The electrical system performance in the competitive power system is determined by two key factors, namely, the locational marginal price (LMP) and the system voltage profile. While the LMP directly influences the system economy, the voltage profile can exercise control over the system’s stability and power quality. Upon thoroughly analyzing all the case studies, it has been observed that Case-4 and Case-9 offer the maximum profits for both the deregulated and regulated systems. Therefore, comparative studies of LMP and voltage profiles have been precisely executed for these two cases. As can be seen from Figure 8 and Figure 9, the comparison of locational marginal prices in the regulated and deregulated systems for Case-4 and Case-9, respectively, reveal intriguing insights into the workings of the system.
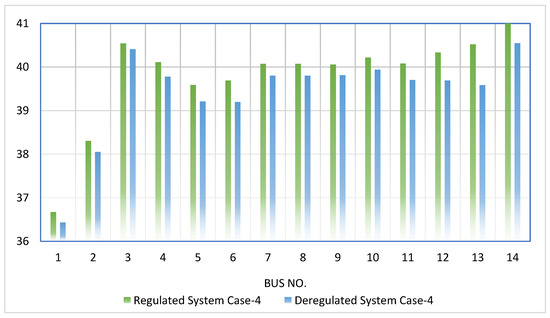
Figure 8.
Comparison for Case-4 (in $/MWh) in regulated and deregulated power systems.
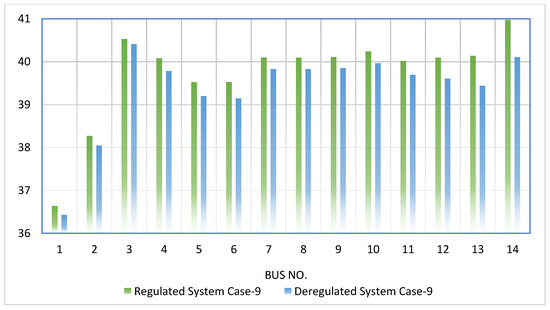
Figure 9.
LMP comparison for Case-9 (in $/MWh) in regulated and deregulated power systems.
The LMP, which refers to the locational marginal price, possesses the ability to exert direct control over the system revenue, given that it represents the selling price of the power that is generated. As evidenced in both Figure 8 and Figure 9, the value of the LMP for each bus has undergone a reduction in the deregulated system, which in turn causes a decrease in the selling price of the produced power. Consequently, customers pay a lesser amount for their utilized energy. In such a setting, it becomes crucial to examine the system voltage profile, which can be seen in Figure 10 and Figure 11 when comparing the regulated and deregulated systems for Case-4 and Case-9, respectively. It is essential to note that the acceptable range for the bus voltage is situated between 0.95 p.u. to 1.05 p.u. and that it is always desirable to maintain the same voltage for all buses to enhance the system’s security and stability. The obtained results reveal that the overall system voltage profile has undergone an improvement following the implementation of the deregulated environment.
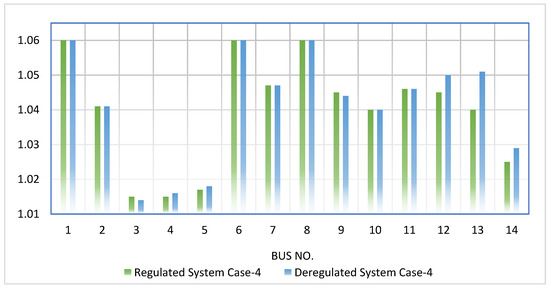
Figure 10.
Voltage comparison for Case-4 (in p.u.) in regulated and deregulated power systems.
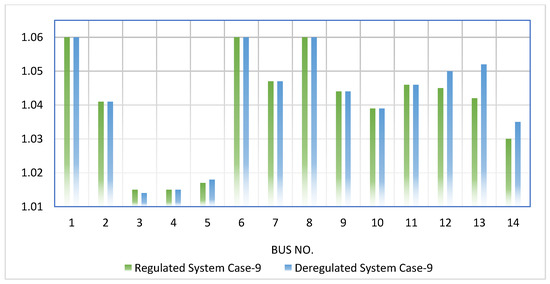
Figure 11.
Voltage comparison for Case-9 (in p.u.) in regulated and deregulated power systems.
The change of the electricity system from a regulated to a deregulated environment provides more economic profit to the consumer. The profit for the producing stations will be lower, which will increase the profits of the consumers because they will pay less for their power use. The deregulated environment also delivers superior voltage profiles for the system, as demonstrated in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. These findings demonstrate that the deregulated environment outperforms the regulated system in all facets of system stability.
- Step 3:
- Measuring the imbalance price and evaluating its impact on the system profit
When conducting an economic assessment of a renewable power network, it is crucial to take into account the impact of imbalanced prices. The characteristics of renewable sources are often ambiguous, leading to power plants being unable to meet scheduled power demands, which poses a significant threat to the electrical network. To mitigate the risk of economic loss, there are two primary solutions available: efficient forecasting technologies and the use of energy storage devices. However, the former has its own set of limitations that may make it less effective. Therefore, the use of energy storage devices is a viable option to ensure scheduled power delivery and reduce the chances of economic loss.
During the survey, the data collected on the day of the assessment are categorized as current wind speed (CWS), while the previous day’s data are considered as estimated wind speed (EWS). The difference between the two speeds has a direct impact on wind generation, leading to a disparity between expected power generation and actual profits. This difference, commonly referred to as the generation of an imbalance price, is a crucial factor that should be considered when assessing renewable power networks. Real-time current and estimated wind speed data were collected for the city of Vijayawada [39] (as shown in Table 5). Due to the unpredictable nature of wind speed, hourly intervals were taken into account. The collected wind speeds were measured at a height of 10 m, and probable wind speeds at a height of 120 m (wind turbine’s hub height) were calculated to determine wind generation at different hours.

Table 5.
Real-time Wind Speed Data of Vijayawada (Km/h).
If the current velocity of the wind surpasses the estimated velocity of the wind, the generating corporations shall receive remuneration in the form of an award. Conversely, if the current velocity of the wind falls below the estimated velocity of the wind, the generation corporations shall receive a penalty for their inability to provide the promised electricity. Upon analysis of the amassed wind speeds, it has been noted that certain repetitive situations have occurred, thus the repetitive scenarios were not taken into consideration (i.e., hours—5, 8, 15, 18, 19, 21, and 23). The wind farm has been situated on bus number 14, which was determined during Step Two, and the cost of the imbalance has been measured by considering the current and estimated wind power. Table 6 displays the impact of imbalance prices on profit, where the estimated profit signifies the system profit exclusive of imbalance prices, whereas the actual profit indicates the profit that takes into account the imbalance price.

Table 6.
Effect of imbalance prices on profit for Deregulated System.
Figure 12, as presented in the following, depicts a comprehensive analysis of the profit that has been attained without considering the imbalance prices and the profit that has been achieved whilst taking into account the imbalance prices for the deregulated system. Upon close examination, it becomes evident that in numerous instances, the actual profit has been diminished in comparison to the estimated profit. This occurrence can be attributed to the fact that negative imbalance prices are the root cause of this decrement.
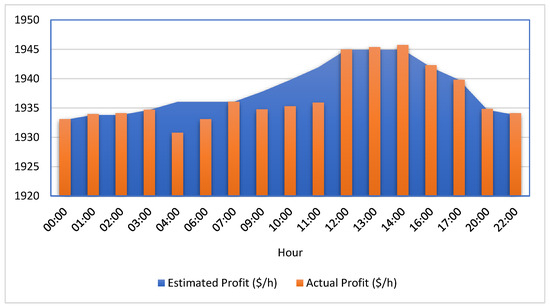
Figure 12.
Profit comparison without and with imbalance prices (in $/h) for a deregulated system.
- Step 4:
- Implementing V2G technology to enhance the profit margin
To evade such circumstances and eliminate the unsteadiness cost that was discussed in the third step, the utilization of Vehicle-to-Grid (V2G) technology can be executed. V2G technology is a technique whereby the power that is stored in Electric Vehicles (EVs) is utilized by the grid to prevent difficulties during high-demand intervals. In instances where there is low demand, the EVs consume power from the grid. However, when the demand escalates, the energy that is stored inside the EVs can be retrieved from the grid to fulfill the requirement.
As demonstrated in Table 6, the influence of the unbalanced prices on the factual profit is displayed. The method was performed over 24 h. After eradicating any duplicates or analogous wind speed scenarios, 17 distinct cases remained. In this particular scenario, the wind farm has been installed at the most profitable bus in the deregulated system, which is bus number 14, as stated earlier. The transformation in the profit that is caused due to the imbalance can be observed in this scenario. The penalty that is associated with the imbalance is higher than the profit itself. This emphasizes the importance of eliminating the cost of the imbalance, as a larger penalty leads to more losses. The utilization of the V2G system helps in circumventing this issue. It should be noted that the V2G technology is operated on batteries. The capacity of the electric vehicle (EV) fleet that we are considering in this analysis is a substantial 3 megawatts (MW). It is important to note that the final efficiency of each battery utilized in the EV fleet will vary. The amount of output power that can be generated by the EV is heavily reliant on how much capacity we have at our disposal. It is an unequivocal fact that the higher the efficiency, the more output power we can generate, and in turn, the higher our profits will be. In situations where there is an imbalance in prices, the EV fleet will need to step in and supply the missing power to prevent this imbalance from persisting. In such scenarios, the power supplied by the EV fleet is subtracted, and the profit is calculated based on the remaining power that is generated.
It is well known that the power system’s profit can be maximized by utilizing the latest and greatest vehicle-to-grid (V2G) technology that is currently available. The current iteration of V2G technology is based on the use of lithium-ion batteries. In this detailed analysis, we have compared the impact of lithium-ion, lead–acid, and supercapacitor batteries on system profits after they have been integrated into the power system. The results of our analysis are found in Table 7, which demonstrates the impact of each type of battery on the power grid’s overall profitability. It should be noted that the system we have examined in this analysis is deregulated because it is more profitable when compared to a regulated system.

Table 7.
System economic factor with V2G but without Imbalance Price for deregulated system.
Herein, we can discern that the gain in the charging scenario remains consistent across all cases, as the battery here is fully charged. On the other hand, the gain in discharging for the various cases varies, because the output efficiency differs for each battery. Notably, amongst the three battery options considered, the supercapacitor exhibits the highest efficiency. However, it is imperative to note that the supercapacitor carries a rather exorbitant installation cost. In this particular scenario, the electric vehicle is discharged close to the generator bus. This V2G concept is intricately linked to the electric vehicle’s battery storage unit. It can charge itself from a bus and subsequently discharge in alternative buses. Hence, this method serves as an effective measure to ensure that the electrical grid is safeguarded from potential severe faulty conditions.
From the data presented in Table 8, it is evident that the incorporation of the Vehicle-to-Grid (V2G) system leads to remarkable gains in the power system, despite the presence of system imbalances. As observed, the integration of V2G technology elevates the system’s performance and improves its overall gains. The relative gains are succinctly illustrated in Figure 13, which provides a better comprehension of the system’s performance. The aforementioned figure displays the system’s profitability clearly and concisely. Based on the results obtained, it can be unequivocally inferred that the inclusion of V2G technology in the power system has a significant impact, particularly when the V2G system is powered by an efficient battery or an energy storage system. In both scenarios, with or without an imbalance in the pricing, the V2G system’s successful operation leads to a noticeable increase in the profit margin.

Table 8.
System economic factor with V2G and Imbalance Price for deregulated system.
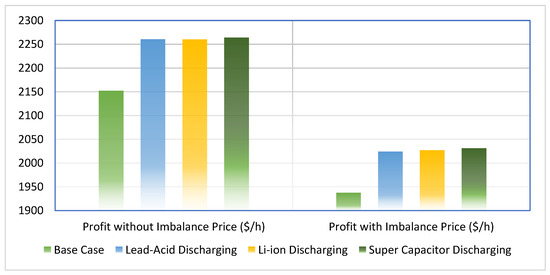
Figure 13.
Profit comparison without and with imbalance prices for the V2G method.
- Step 5:
- Strategically place UPFC to further improve the profit margin
In a vast and complex power network, there are always opportunities for the occurrence of transmission line congestion, which can occur due to the failure or abnormalities of buses, generators, or lines. This congestion places an additional burden on the power customer because of the congestion charges added to the energy selling prices, thereby causing significant economic challenges. In this scenario, the Unified Power Flow Controller (UPFC) can be implemented to flexibly manage the transmission line thermal limit and minimize the congestion problem in the transmission channel.
In this research study, the UPFC placement has been performed to maximize the system profit and give economic benefit to the market players. To find out the optimal position of the UPFC placement in the system, a comprehensive approach has been adopted. The UPFC has been placed in all the transmission lines by changing the compensation level between −0.7 to 0.2 and changing the reactive power injection or absorption (−100 to 100) to the bus simultaneously and finding the system generation cost for all cases. Based on the lower generation cost, the optimal position of UPFC has been decided. It was found that UPFC placement at line no. 6 with a compensation level of −0.35 and reactive power absorption of 44.36 (MVAr) provides the lowest system generation cost. So, this condition has been taken as the optimal placement scenario of UPFC in the considered system. Now, the system profit has been calculated along with the Vehicle to Grid (V2G) method and the placement of the UPFC in the system. Figure 14 shows the profit comparison without and with imbalance prices for the V2G method after the placement of UPFC in the system. From the result, it is found that the UPFC placement along with the V2G method can boost the system profit again. By incorporating the UPFC, the transmission line congestion can be eliminated, and the power network can operate efficiently. Therefore, the proposed method can be a potential solution to the existing challenges of power systems and can ensure a reliable and sustainable energy supply.
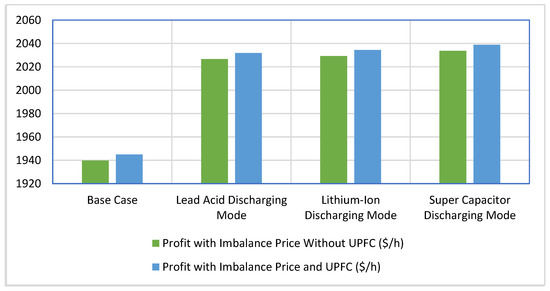
Figure 14.
Profit comparison with imbalance prices for V2G and UPFC placement.
The entirety of this work has been executed with the utilization of specialized MiPower software. The preliminary two phases of this endeavor have been systematically arranged to cater to both the regulated and deregulated system environments. Once determined that the deregulated system surpasses the regulated system in economic facets, the remainder of the study was solely conducted in the deregulated environment.
Only the V2G system is capable of maximizing system profits by avoiding the negative impact of pricing imbalance. Furthermore, we have added UPFC placement to optimize profits once again. Storage devices and other types of FACTS controllers can be employed to improve system efficiency once again.
7. Conclusions
Renewable energy sources, as opposed to traditional power plants, are highly recommended for increasing profitability due to lower operating and maintenance costs. Renewable energy is readily available, inexpensive, and easily accessible. The intermittent nature of renewable energy sources might cause inconsistencies in the system, manifesting as an uneven pricing. This, however, may be effectively avoided by using Electric Vehicles (EVs). As noted in the current research, vehicle-to-grid (V2G) technology is a realistic option that may effectively boost the profit of the power system by decreasing the imbalance price. EVs may be discharged at any needed time during peak hours, reducing the danger of grid blackouts. The battery of an EV may be charged at a low LMP and drained at a high LMP, guaranteeing that the system profit is automatically raised. It is critical to stress that the idea of distinct LMPs applies only in a deregulated environment. Furthermore, UPFC placement has been carried out, and it has been shown that the profit is maximized in all circumstances. The UPFC placement has been efficiently used to reduce system congestion costs, resulting in economic advantages for energy customers. The findings of this study show that wind farms may be efficiently used to reduce the percentage of fossil fuels in electricity networks. Furthermore, other technologies, such as V2G and UPFC, can be used efficiently to maintain grid stability by minimizing system congestion. The suggested method is universal and may be used to power networks of any scale, integrated or deregulated. This proposed strategy is a generic one that may be applied to any small, large, or hybrid system that involves several types of storage devices to maximize the system’s profit. Storage devices and other FACTS controllers can be used in the future to boost the system economy once again.
Author Contributions
Conceptualization, S.D. and G.S.R.; methodology, M.L.N.V.; software, K.D.R.; validation, S.D., F.A. and M.H.A.; formal analysis, S.D.; investigation, G.S.R. and K.D.R.; resources, M.L.N.V.; data curation, F.A. and M.H.A.; writing—original draft preparation, S.D. and K.D.R.; writing—review and editing, F.A. and M.H.A.; visualization, G.S.R.; supervision, M.H.A.; project administration, S.D.; funding acquisition, F.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is unavailable.
Acknowledgments
This work was supported by the Researchers Supporting Project number (RSPD2023R646), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Karanja, J.M.; Hinga, P.K.; Ngoo, L.M.; Muriithi, C.M. Optimal Battery Location for Minimizing the Total Cost of Generation in a Power System. In 2020 IEEE PES/IAS PowerAfrica; IEEE: Nairobi, Kenya, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Lawder, M.T.; Suthar, B.; Northrop, P.W.C.; DE, S.; Hoff, C.M.; Leitermann, O.; Crow, M.L.; Santhanagopalan, S.; Subramanian, V.R. Battery Energy Storage System (BESS) and Battery Management System (BMS) for Grid-Scale Applications. Proc. IEEE 2014, 102, 1014–1030. [Google Scholar] [CrossRef]
- Pulazza, G.; Zhang, N.; Kang, C.; Nucci, C.A. Transmission Planning with Battery-Based Energy Storage Transportation for Power Systems with High Penetration of Renewable Energy. IEEE Trans. Power Syst. 2021, 36, 4928–4940. [Google Scholar] [CrossRef]
- Bhatnagar, D.; Currier, A.; Hernandez, J.; Ma, O.; Kirby, B. Market and Policy Barriers to Energy Storage Deployment: A Study for The Energy Storage Systems Program, Sandia National Laboratories, SAND2013-7606, Release on September 2013. Available online: https://www.sandia.gov/ess-ssl/publications/SAND2013-7606.pdf (accessed on 22 June 2023).
- Lee, N.; Flores-Espino, F.; De Oliveira, R.P.C.; Roberts, B.J.; Brown, T.; Katz, J.R. Exploring Renewable Energy Opportunities in Select Southeast Asian Countries: A Geospatial Analysis of the Levelized Cost of Energy of Utility-Scale Wind and Solar Photo-Voltaics; No. NREL/TP-7A40-71814; National Renewable Energy Lab (NREL): Golden, CO, USA, 2019. [Google Scholar]
- Dawn, S.; Tiwari, P.K. Improvement of economic profit by optimal allocation of TCSC & UPFC with wind power generators in double auction competitive power market. Int. J. Electr. Power Energy Syst. 2016, 80, 190–201. [Google Scholar] [CrossRef]
- Versteeg, T.; Baumann, M.; Weil, M.; Moniz, A. Exploring emerging battery technology for grid-connected energy storage with Constructive Technology Assessment. Technol. Forecast. Soc. Chang. 2016, 115, 99–110. [Google Scholar] [CrossRef]
- Bravo, D.; Sauma, E.; Contreras, J.; de la Torre, S.; Aguado, J.A.; Pozo, D. Impact of network payment schemes on transmission expansion planning with variable renewable generation. Energy Econ. 2016, 56, 410–421. [Google Scholar] [CrossRef]
- MaciejŚwierczyński; IoanStroe, D.; RasmusLærke; Stan, A.I.; Kjær, P.C.; Teodorescu, R.; Kær, S.K. Field Experience from Li-Ion BESS Delivering Primary Frequency Regulation in the Danish Energy Market. ECS Trans. 2014, 61, 37. [Google Scholar]
- Morthorst, P.E. Wind Energy; The facts, Risoe National Lab.: Roskilde, Denmark; The European Wind Energy Association: Brussels, Belgium, 2004; Volume 2, pp. 95–110. [Google Scholar]
- Apostolaki-Iosifidou, E.; Codani, P.; Kempton, W. Measurement of power loss during electric vehicle charging and discharging. Energy 2017, 127, 730–742. [Google Scholar] [CrossRef]
- Chakraborty, M.R.; Dawn, S.; Saha, P.K.; Basu, J.B.; Ustun, T.S. A Comparative Review on Energy Storage Systems and Their Application in Deregulated Systems. Batteries 2022, 8, 124. [Google Scholar] [CrossRef]
- Singh, R.; Sood, Y.R.; Padhy, N.P. Development of renewable energy sources for indian power sector moving towards competitive electricity market. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- He, J.; Hu, Z. Hourly coordinated operation of Electric vehicles charging/discharging and wind-thermal power generation. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Hussain, S.S.; Aftab, M.A.; Ali, I.; Ustun, T.S. IEC 61850 based energy management system using plug-in electric vehicles and distributed generators during emergencies. Int. J. Electr. Power Energy Syst. 2020, 119, 105873. [Google Scholar] [CrossRef]
- May, G.J.; Davidson, A.; Monahov, B. Lead batteries for utility energy storage: A review. J. Energy Storage 2018, 15, 145–157. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, J.; Li, G.; Liu, A. Research on Energy Efficiency of Supercapacitor Energy Storage System. In Proceedings of the Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–4. [Google Scholar] [CrossRef]
- Lakshmi, G.S.; Divya, G.; Sravani, G. V2G Transfer of Energy to Various Applications. E3S Web Conf. 2019, 87, 01019. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Ahmadi, A.; Sharaf, A.M.; Siano, P.; Pou, J.; Hredzak, B.; Agelidis, V.G. Review of FACTS technologies and applications for power quality in smart grids with renewable energy systems. Renew. Sustain. Energy Rev. 2018, 82, 502–514. [Google Scholar] [CrossRef]
- Hossain, J.; Pota, H.R. Robust Control for Grid Voltage Stability: High Penetration of Renewable Energy. In Power Systems; Springer Science: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Benabid, R.; Boudour, M.; Abido, M. Optimal location and setting of SVC and TCSC devices using non-dominated sorting particle swarm optimization. Electr. Power Syst. Res. 2009, 79, 1668–1677. [Google Scholar] [CrossRef]
- Shehata, A.A.; Tolba, M.A.; El-Rifaie, A.M.; Korovkin, N.V. Power system operation enhancement using a new hybrid methodology for optimal allocation of FACTS devices. Energy Rep. 2021, 8, 217–238. [Google Scholar] [CrossRef]
- Basu, J.B.; Dawn, S.; Saha, P.K.; Chakraborty, M.R.; Alsaif, F.; Alsulamy, S.; Ustun, T.S. Risk Mitigation & Profit Improvement of a Wind-Fuel Cell Hybrid System with TCSC Placement. IEEE Access 2023, 11, 39431–39447. [Google Scholar] [CrossRef]
- Luburić, Z.; Pandžić, H. FACTS devices and energy storage in unit commitment. Int. J. Electr. Power Energy Syst. 2019, 104, 311–325. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z. Optimal placement and sizing of FACTS devices for optimal power flow using metaheuristic optimizers. Results Control. Optim. 2022, 8, 100145. [Google Scholar] [CrossRef]
- Singh, S.; Jaiswal, S.P. Enhancement of ATC of micro grid by optimal placement of TCSC. Mater. Today Proc. 2020, 34, 787–792. [Google Scholar] [CrossRef]
- Moafi, M.; Ardeshiri, R.R.; Mudiyanselage, M.W.; Marzband, M.; Abusorrah, A.; Rawa, M.; Guerrero, J.M. Guerrero, Optimal coalition formation and maximum profit allocation for distributed energy resources in smart grids based on co-operative game theory. Int. J. Electr. Power Energy Syst. 2023, 144, 108492. [Google Scholar] [CrossRef]
- Melo, L.S.; Tofoli, F.L.; Issicaba, D.; Monteiro, M.E.P.; Barroso, G.C.; Sampaio, R.F.; Leão, R.P.S. Co-simulation platform for the assessment of transactive energy systems. Electr. Power Syst. Res. 2023, 223, 109693. [Google Scholar] [CrossRef]
- Dukpa, A.; Butrylo, B. MILP-Based Profit Maximization of Electric Vehicle Charging Station Based on Solar and EV Arrival Forecasts. Energies 2022, 15, 5760. [Google Scholar] [CrossRef]
- Alghamdi, T.G.; Said, D.; Mouftah, H.T. Profit Maximization for EVSEs-Based Renewable Energy Sources in Smart Cities with Different Arrival Rate Scenarios. IEEE Access 2021, 9, 58740–58754. [Google Scholar] [CrossRef]
- Lai, C.S.; Chen, D.; Zhang, J.; Zhang, X.; Xu, X.; Taylor, G.A.; Lai, L.L. Profit maximization for large-scale energy storage systems to enable fast EV charging infrastructure in distribution networks. Energy 2022, 259, 124852. [Google Scholar] [CrossRef]
- Senthilkumar, P.; Samidurai, S.; Nedunchezian, V.; Krishnan, N.; Sharma, G.; Senjyu, T. Profit maximization in hybrid microgrid system incorporating demand response and plug in EV. Int. Trans. Electr. Energy Syst. 2021, 31, e13260. [Google Scholar] [CrossRef]
- Wang, W.; Liu, L.; Liu, J.; Chen, Z. Energy Management and Optimization of Vehicle-to-grid Systems for Wind Power Integration. CSEE J. Power Energy Syst. 2021, 7, 172–180. [Google Scholar]
- Corinaldesi, C.; Lettner, G.; Auer, H. On the characterization and evaluation of residential on-site E-car-sharing. Energy 2022, 246, 123400. [Google Scholar] [CrossRef]
- Pillai, J.R.; Bak-Jensen, B. Integration of Vehicle-to-Grid in the Western Danish Power System. IEEE Trans. Sustain. Energy 2010, 2, 12–19. [Google Scholar] [CrossRef]
- Corinaldesi, C.; Lettner, G.; Schwabeneder, D.; Ajanovic, A.; Auer, H. Impact of Different Charging Strategies for Electric Vehicles in an Austrian Office Site. Energies 2020, 13, 5858. [Google Scholar] [CrossRef]
- Tavakoli, A.; Morton, T. Energy Exchange Between Unidirectional Vehicle- to-Grid Aggregators, and Wind and Conventional Generating Companies in the Electricity Market. In Proceedings of the 2019 9th International Conference on Power and Energy Systems (ICPES), Perth, WA, Australia, 10–12 December 2019; pp. 1–6. [Google Scholar]
- Das, S.S.; Das, A.; Dawn, S.; Gope, S.; Ustun, T.S. A Joint Scheduling Strategy for Wind and Solar Photovoltaic Systems to Grasp Imbalance Cost in Competitive Market. Sustainability 2022, 14, 5005. [Google Scholar] [CrossRef]
- Time and Date Website. Available online: https://www.timeanddate.com (accessed on 10 April 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).