Abstract
It is indisputable that power systems are being transformed around the world to increase the use of RES and reduce the use of fossil fuels in overall electricity production. This year, the EU Parliament adopted the Fit for 55 package, which should significantly reduce the use of fossil fuels in the energy balance of EU countries while increasing the use of RES. At the end of 2022, the total number of prosumer installations in Poland amounted to about one million two hundred thousand. Such a high saturation of prosumer micro-installations in the power system causes many threats resulting from their operation. These threats result, among others, from the fact that photovoltaics are classified as unstable sources and the expected production of electricity from such installations is primarily associated with highly variable weather conditions and is only dependent on people to a minor extent. Currently, there is a rapid development of topics related to forecasting the volume of energy production from unstable sources such as wind and photovoltaic power plants. This issue is being actively developed by research units around the world. Scientists use a whole range of tools and models related to forecasting techniques, from physical models to artificial intelligence. According to our findings, the use of machine learning models has the greatest chance of obtaining positive prognostic effects for small, widely distributed prosumer installations. The present paper presents the research results of two energy balance prediction algorithms based on machine learning models. For forecasting, we proposed two regression models, i.e., regularized LASSO regression and random forests. The work analyzed scenarios taking into account both endogenous and exogenous variables as well as direct multi-step forecasting and recursive multi-step forecasting. The training was carried out on real data obtained from a prosumer micro-installation. Finally, it was found that the best forecasting results are obtained with the use of a random forest model trained using a recursive multi-step method and an exogenous scenario.
1. Introduction
1.1. New Challenges in the Energy Sector—Towards Clean Energy
One of the reasons for the accelerated economic development of the world observed since the beginning of the 19th century was the use of new energy sources. These new energy sources enabled the development of further industries or new means of transport and have also indirectly improved the working and living conditions of the population. This quantum leap is referred to in the field of industry as the first industrial revolution.
The following decades brought further stages of industrialization, which were inextricably linked to the spread of new energy sources around the world. The global energy sector is changing, and this is an indisputable fact. Currently, conventional energy sources, i.e., hard coal, crude oil, and natural gas, are also of great importance in the global structure of electricity. However, according to a report prepared by BloombgergNEF [1], it is estimated that in 2050, the share of primary energy from RES will be 62%, including 48% wind and solar energy, and only 31% will be fossil fuels. As can be seen in Figure 1, the forecasted dynamics of the increase in wind and solar sources is very high.
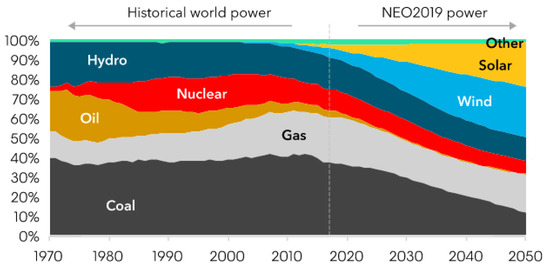
Figure 1.
Forecast of the percentage share of various energy carriers in the global energy mix by 2050. Source: own study based on [1].
Energy from the sun is the basis of life on Earth. Even fossil energy resources, which were created millions of years ago, were created thanks to solar energy, without which organic matter could not be created as a starting material for the creation of, e.g., coal. Therefore, humanity is increasingly trying to use solar energy for its own purposes, i.e., to generate electricity and heat.
According to the sources of the Energy Development Agency [2], the development of solar PV in Poland, especially in recent years, has clearly accelerated. This is clearly illustrated in Figure 2. At the end of December 2022, the power of photovoltaics installed in Poland exceeded 12 GW and amounted to exactly 12,189 MW. This is a significant increase compared to December 2021, when the total installed capacity of Polish photovoltaics was only 7681 MW.
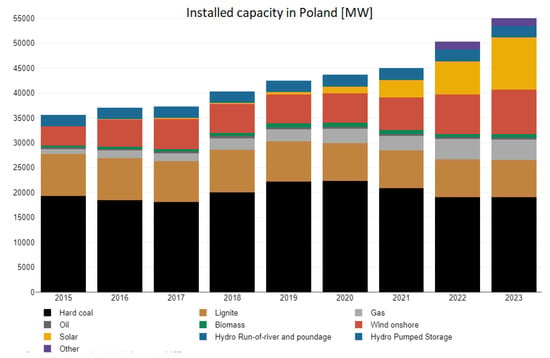
Figure 2.
Installed capacity in Poland broken down by individual energy sources. Source: own study based on [2].
This dynamic development of micro-installations resulted in the fact that 362,159 new photovoltaic (PV) installations with a total capacity of 4269.8 MW were built in 2022 alone. At the end of 2022, the total number of prosumer installations in Poland amounted to about one million two hundred thousand. In December 2022 alone, 14,245 new photovoltaic installations with a capacity of 334.56 MW [2] were installed. This shows that the most frequently built and most dynamically developing type of (PV) installation in Poland is a photovoltaic micro-installation, i.e., one whose total installed capacity in accordance with the provisions of the RES Act in Poland [3] is below 50 kW.
Polish photovoltaics, unlike many countries in Europe, have a very prosumer, dispersed character, which results from the interest of citizens in the self-production of energy and the establishment of many small installation companies that meet these expectations. Such a dynamic development of prosumer micro-installations (PV) has resulted in the emergence of new organizational structures and concepts regarding the functioning energy market. One of them is the concept of a microgrid as a complementary component of the energy market in Poland, ensuring the diversification of energy supplies. Generally, many authors [4,5,6,7] define them as subsystems in which power and electricity are generated, stored, and consumed similarly as in virtual power plants (VPP) [8]. The main criterion for identifying and describing the key microgrid processes is to ensure its controllable continuity of operation. This is a feature of the processes that ensures a stable power flow on the line of energy source–reception–storage–distribution–consumer, which is controlled by the Operator, including in the case of a large number of power sources located in the vicinity of consumption points and for the coordinated island operation of various RES energy sources (wind, sun) and receiving devices.
The high level of saturation of prosumer micro-installations in the power system causes many threats resulting from their operation. In the articles [9,10,11], the authors indicated that one of these threats may be the bidirectional power flow from the source to the supply network. In a conventional power system, the flow moves in one way from supply to load. In the case of the high saturation of prosumer installations, the phenomenon of reverse power flow should be anticipated.
The authors of the publications [12,13,14] pointed out a very important problem, which is the voltage instability that can be caused by local oscillations resulting from the interaction of the control system with microsources. This implies the search for new effective control methods at the low voltage level. In the case of very good insolation, the operation of individual prosumer (PV) installations is combined, and therefore, too much power (P, Q) is sent to the distribution network. Such a transmission causes additional losses of power and energy, as indicated by the authors of [15,16,17,18] in their publications.
In the publications [19,20,21,22,23,24,25], the authors also raised the problem of low system inertia (PV) caused by low power generation sources and their distraction. This can cause large deviations from the main frequency. Each photovoltaic inverter, although it works independently of the DSO, constantly monitors the parameters of electricity in the grid and adapts to them. Therefore, the inverter will not start or stop operation if the voltage or frequency is outside the set range. This phenomenon is practically absent in a conventional power system, where the vast majority of power is generated by large generators that have high inertia.
Summarizing the above considerations, it should be emphasized that all the above-mentioned problems during the operation of micro-installations (PV) depend on the correct prediction of the energy production of these installations. This value depends on many factors related to the generation and processing of energy, but above all, on weather conditions, which are highly variable and to a small extent dependent on humans. Over time, the nominal parameters of the panels themselves also change. Currently, there is a rapid development of topics related to forecasting the volume of energy production, especially in wind and photovoltaic power plants. This issue is being actively developed by research units around the world. Researchers use a range of tools and models related to forecasting techniques ranging from physical [26,27,28] and statistical [29,30,31,32,33,34] to models based on artificial intelligence and hybrids combining many techniques [35,36,37,38,39,40].
Analyzing the above-mentioned topics, we chose to focus this article on the problem of correctly determining the forecast of the electricity demand balance of a facility with its own photovoltaic micro-installation. The balance takes into account the production of electricity from PV panels, which is periodic/seasonal, and electricity consumption, which is also largely random and does not depend on these trends. Forecasting this balance may be an important factor in the process of short-term forecasting the demand for energy storage capacity, taking into account economic indicators (e.g., energy prices). Most of the prosumer installations built so far did not take into account the hybrid operation of such installations with electricity storage due to the very high costs of these storage facilities. Until now, the role of such electricity storage was played by the grid supplying the PV installation, the so-called “web storage”. The dynamically growing number of prosumer PV micro-installations caused the inefficiency of such a solution and, as a result, due to the overproduction of electricity in the power system, these installations were shut down. In the environmental conditions in Poland, other variants of storage not only for electricity but also for heat energy should be considered. The demand for energy storage in the Polish power system will grow due to the current state of the power system, as well as future challenges of the energy market, including the increasingly visible dynamic increase in the share of generation from prosumer RES installations. Therefore, the authors of the present article propose short-term forecasting of the balance of electricity in prosumer micro-installations, which can help to predict the amount of a necessary electricity storage volume. We propose that the amount subject to forecasting should be the balance of electricity.
The rest of this article is organized as follows. The Section 1.2 and Section 2 describes the methodology of obtaining and processing data sets used for modeling and forecasting the prosumer demand for th energy of a given photovoltaic installation and describes the machine learning model used for the forecast. The Section 3 presents the results of the obtained forecasts. The article ends with a summary in which the authors present their conclusions.
1.2. Forecasting Time Series Using Regressive Machine Learning Models
Time series forecasting consists of determining the future values of a variable in time on the basis of a model and the values of this quantity measured in the past [41]. In their first forecasting attempts dedicated to various RES installations, the authors of various studies in the literature [41,42,43,44,45] used various forecasting models, e.g., those based on econometric models (creeping trend models, exponential smoothing models, etc.) [46] or autoregressive and moving averages [47]. In the case of Holt–Winters exponential smoothing models, the time series were decomposed into a trend component (expressed by the growth level and conditions) and seasonal components, which were combined additively or muttiplicatively. This model allows us to model nonlinear and heteroscedastic time series, but exogenous variables cannot be introduced into the model. Another important disadvantage of these models is their excessive parameterization and the large number of initial values to be estimated.
Many other econometric models have also been used and positively applied to forecasting processes in publications [48,49,50]; however, all these attempts, apart from their very high labor consumption, did not lead to satisfactory results, and the accuracy of forecasting models dedicated to RES installations was consistent with what had already been generally published [51,52,53,54]. After analyzing the literature [55,56,57,58,59,60] and based on a number of their own experimental experiences, the authors of the present paper could thus see the solution to the problems described above in machine learning algorithms and various hybrids combining the best properties of classical econometric methods with artificial intelligence [61]. This paper proposes a different approach: known regression models such as random forests and linear model with a regularization term (LASSO) have been used to forecast energy balances [62]. One of the goals of this research was to check how purely regression-based models behave when used for time series forecasting. For this reason, the authors tested both a simple regression model (LASSO) and a more complicated random forest (RF) model on real data. Moreover, the RF forecasting model was closely related to the specificity of the problem. Namely, it contained multidimensional dependencies with a limited number of training data. In such a case, the RF models cited in the literature provided by the authors worked very well. Thanks to their structure, they allowed for high prediction accuracy on test data while reducing the risk of overfitting.
Regression is one type of supervised learning that enables input–output relationships to be modelled in the case of a continuous explanatory variable. The regression model can therefore be treated as a function that approximates the multivariate relationship between the explanatory variables (model inputs) and the explained variable (model output). In this paper, the problem of energy balance forecasting is presented using a regression scheme built on the basis of the SkForecast library. The LASSO penalized regression model and the random forest model were used to solve the problem.
The LASSO regression model is a linear model that enables regression coefficients to be estimated while penalizing (limiting) their absolute values. For this reason, this model prefers solutions with a smaller number of non-zero coefficients, effectively reducing the number of features on which a given solution depends. The LASSO model minimizes the following goal function [63]:
where represents the number of training samples, represents the learning data matrix of a size of the number of observations × number of features, y represents the vector of output training data, and − is the norm of the parameter vector.
In the regression case, the random forest model allows the construction of a set of decision trees for which the predicted average of this collection is then determined [64]. The basic component of a random forest is the decision tree. It enables one to record decisions and related probabilities relating to the classification or regression task. The most popular algorithm for building a decision tree used in machine learning is the CART (classification and regression tree) algorithm. In the first step, it separates the learning data into left and right subsets, thus minimizing the following MSE cost function:
where represents the left set count, represents the right set count, and m represents the total number of training samples, while the error in the selected node is defined as follows:
The next steps of the algorithm lead to further divisions of the training dataset. The number of consecutive divisions (tree depth) can be controlled using one of the model’s hyperparameters. Machine learning algorithms based on Equations (1)–(4) were used to build and train models forecasting the balance of electricity in a prosumer installation. The results of our investigations of these models are described in the latter part of this work.
The open-source package Skforecast, version 0.10.0, developed in Python, enables time series forecasting using the regression algorithms of the Scikit-learn library, which is the global standard in the field of machine learning in Python [63]. The main purpose of the procedures implemented within the SkForecast library is to transform the time series written in the form of a vector into a matrix form, which can be processed by regression algorithms. The diagram of the transformation is shown in Figure 3.
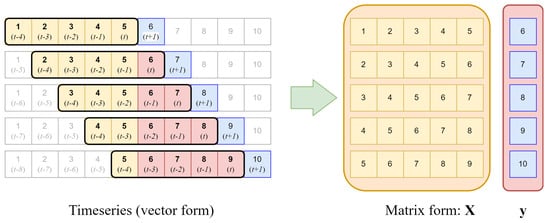
Figure 3.
Scheme of transforming a time series vector into a matrix form suitable for regression models.
According to the diagram shown in Figure 3, the input time series is represented by a 10-element vector of the measurement samples. During the operation of the transformation algorithm, the values of vector elements are rewritten to the next rows of the learning data input matrix and the vector of the output data learning . In the rows of matrix , there are further multidimensional observations stored in the columns of features. These features represent the delayed values of the time series. The operation of the algorithm can be illustrated by moving a fixed-length time window over the input vector and rewriting the values of samples from to t matrix , where n is the number of window samples (e.g., for the vector from Figure 3, ). In addition, in each step of the algorithm, the sample , treated as the current forecast, is written into a column vector representing the target output values. Thanks to this data transformation, it is possible to forecast time series using regression machine learning algorithms.
This paper proposes two forecasting scenarios: recursive multi-step forecasting and direct multi-step forecasting. In the first scenario, a recursive process is used, which enables one to determine a new prediction based on the previous one. For the second scenario, separate models are created for individual steps of the forecast horizon, e.g., if it is necessary to predict the next 24 steps, 24 models are created for each of the 24 steps.
Time series forecasting using regression algorithms can only take place on the basis of past values of the forecasted variable (endogenous case) and with regard to the values of additional variables (exogenous case). In this paper, both cases were investigated. Thus, forecasting algorithm studies were examined for both of these cases.
2. Materials and Methods
2.1. Experimental Setup
The research was carried out on the basis of real measurement data obtained from an individual farm in the south of Poland.
The household is equipped with a photovoltaic installation with a capacity of 10.1 kWp located on the ground, consisting of 22 bi-facial panels, each with a nominal power of 455 Wp. The installation is directed to the south (azimuth ) and inclined at an angle of 26 C to the horizontal. Each two panes are connected to an HM-1200 micro-inverter (made by Hoymiles Power Electronics Inc.) with a nominal power of 1200 W. Thanks to this configuration, each panel works individually. Problems with one of the panels (dirt, damage) do not affect the work of the others. In Figure 4, a diagram of the electrical connection of the photovoltaic power plant is shown. It confirms that each of the panels works individually.
Figure 4.
Diagram of the connections of a photovoltaic power plant.
Individual inverters are connected to the power supply phases according to the following scheme: 4 inverters are connected to the L1 phase, 4 inverters are connected to the L2 phase, and 3 inverters are connected to the L3 phase. Through the communication module, data on the operation of the photovoltaic installation are transferred to the servers of the inverter manufacturer. They are then made available through a website or mobile application. Thanks to this, the prosumer has the ability to view on-line the parameters of the panels (voltage, amperage, power) and micro-inverters (voltage and frequency in the grid, temperature), as well as the total power generated in the installation and the amount of energy produced at a given time. Through the web portal, it is also possible to download data on the energy produced with a minimum resolution of 1 day and data on the average power produced in 15 min intervals. The average power in the next quarter of an hour, after conversion into the amount of energy produced, was one of the input elements used in conducting our research. The prosumer has the ability to check the most important parameters in a clear and transparent way by examining the current power of the virtual power plant and the electricity produced. The basic dashboard is shown in Figure 5.
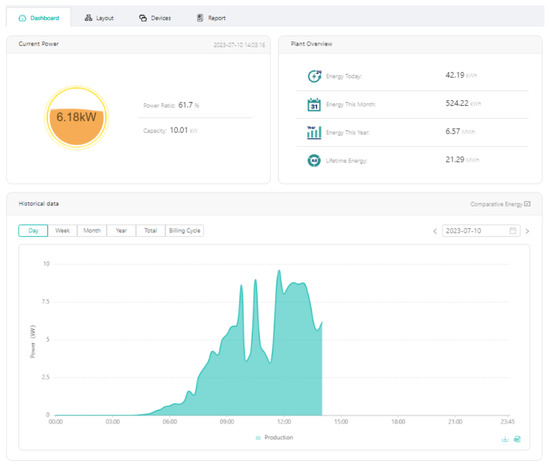
Figure 5.
The application for monitoring the photovoltaic power plant.
The photovoltaic installation is connected to the switchboard located in the building via a 5 × 10 mm copper cable with a length of 36 m. A cable with such a large cross-section was used to reduce losses associated with energy transmission.
Near the pv installation there is a Renkforce WH2600 weather station equipped with an outdoor WH24 sensor. The ranges of basic parameters measured by the station were as follows: temperature range, C ± 60 C; humidity(relative), 1–99%; wind velocity, –; and light, 0–400,000 lux. To determine solar radiation, a conversion factor of 126.7 was assumed according to the default calibration setting at the weather station. The sampling interval was 16 s. Access to weather data is provided via the website on which the user account has been registered and the weather data has been made available. Historical values were retrieved using a dedicated API. Data on the average hourly value of solar radiation and temperature were collected and used for the study. An example of a weather station dashboard is shown in Figure 6.
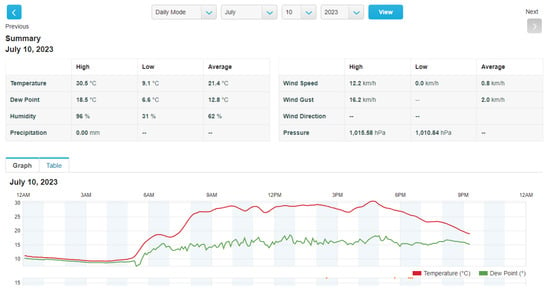
Figure 6.
Weather station start screen.
The building was built on the basis of the WT 2021 energy standard, which assumes that the value of the maximum annual demand of the building for non-renewable, primary energy for heating, ventilation, cooling, domestic hot water preparation, and lighting () does not exceed 70 kWh/myear. At the design stage, materials were used that allowed us, in this particular case, to attain the value of the coefficient kWh/myear. The entire energy demand of the building and its users comes from electricity. The source of heating for central heating and hot water is an air source heat pump. Underfloor heating is installed in the building, and water is heated and kept in a tank with a capacity of 300 liters. Importantly, due to energy consumption, the kitchen uses an electric hob to prepare meals. The energy-intensive devices indicated above indicate that electricity consumption is stochastic in nature. However, a detailed analysis of the meter readings for electricity consumed (P+) in the summer (the heat pump only works for DHW heating) indicates that other devices that are permanently switched on (routers, pumps, sensors) generate a constant daily consumption of 5–6 kWh. This estimation was carried out on the basis of the analysis of energy consumption in night periods between 1:00 and 5:00, where the impact of electricity production from the photovoltaic installation and additional consumption resulting from the prosumer’s activity was not noted.
The prosumer settles its electricity consumption based on measurements from a three-phase S34U18 smart meter. The meter allows remote reading of electrical parameters over time. The prosumer can locally (directly from the meter) read the current values of active and reactive energy and collected and returned energy (P+, P−, Q+, Q−) and check the current energy flow (consumption, production). In addition, the electricity distributor (the owner of the electricity meter) allows access to historical data via an online portal. The website allows one to view historical values, including readings of the active energy given and consumed as recorded at 23:59:59 each day, access to ten maximum power records in a given month, and an overview of hourly values from electric energy production and consumption. A graph of electric energy produced and consumed in subsequent hours in the indicated period is presented in Figure 7. Unfortunately, the application is only available in Polish.
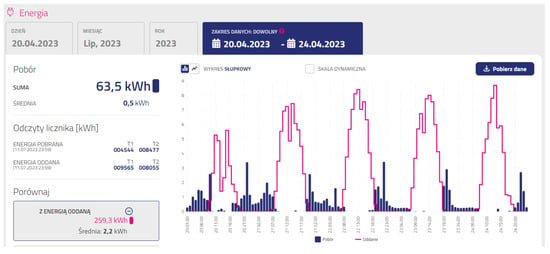
Figure 7.
Values of energy produced and consumed in hourly time intervals.
The value of electricity taken and returned was obtained through the portal and used to determine the balance sheet. The individual values of the time series were obtained according to the formula
where , in kWh, represents the active energy balance, , in kWh, represents the produced active energy, and , in kWh, represents the consumed active energy.
The time series was used in subsequent stages for the research and preparation of forecasts.
2.2. Research Methodology
The research carried out as part of this work was aimed at forecasting the energy balance in the prosumer micro-installation along with providing an assessment of accuracy. Forecasting was carried out using time series recorded using the position described in Section 2.1 and two regression models (i.e., the LASSO regression model and the random forest model described in Section 1.2). A workflow diagram illustrating the research methodology described above is shown in Figure 8.

Figure 8.
Research methodology workflow diagram.
The methodology of the research included the following stages:
- 1.
- Preliminary analysis and processing of data: at this stage, data cleaning was performed, including filling in missing data as well as removing outliers. The numerical procedures included in the open source Python libraries Numpy and Pandas were used to perform the analysis.
- 2.
- The next stage was to divide the time series into the training and test sets. In the case of the LASSO model, standardization of the training data was additionally applied according to the following scaling formula:where x represents a single value of the training sample, represents the mean value of the training set, and represents the standard deviation of the training set.The training and testing of the models was conducted on time series recorded in November 2022 (training data: hourly balance, 10–13 November 2022, testing data: hourly balance, 13 November 2022) and April 2023 (training data: hourly balance, 20–23 April 2023, testing data: hourly balance, 24 April 2023).
- 3.
- Training machine learning models and tuning hyperparameters. During tuning, for both model types tested, a parameter grid and a lags grid were created. For each combination of parameter values and number of lags, the model was trained and evaluated using a backtesting procedure with the MSE (mean squared error) and MAE (mean absolute error) metrics. For the LASSO model, two values for the number of delays were adopted: and 300 hyperparameter values ranging from to , as a result of which 600 models were created. For the random forest model, we utilized , and 15 tree count values (), resulting in 15 values for the maximum depth of the tree (). In addition, the models were tested for three parameter values, with determining the maximum number of features taken into account during the learning of trees. Three possible values of this parameter were assumed in our studies: = (all features), = (the square root of the maximum number of features (rounded to the nearest integer)), and = (the base 2 logarithm of the maximum number of features). Hyperparameters were tuned for both the endogenous case (forecasting only on the basis of previous values of the forecasted variable) and exogenous (taking into account the day of additional variables). In the second case, the models were trained on three variants:
- Using the balance and average hourly air temperature ;
- Using the balance and maximum hourly intensity of solar radiation ;
- Using the balance of and .
All models were trained for recursive multi-step forecasting and direct multi-step forecasting. The selection of the hyperparameters of the models using the above-described methodology provided models that offered the best performance. - 4.
- Testing the models on testing datasets.
- 5.
- Evaluating the models on the basis of test data. Both the metric used as a loss function in training regression models (MSE) and the MAE criterion used to evaluate forecasting models were used for this evaluation.
- 6.
- Discussion of the results and conclusions.
3. Forecasting Results
3.1. Results for Time Series Representing Energy Balance Recorded in April 2023
3.1.1. LASSO Model
The results of forecasting the balance sheet (5) registered in April 2023 in the prosumer microinstallation using the LASSO model (1) are presented in Figure 9, Figure 10, Figure 11 and Figure 12. Figure 9 and Figure 10 show the results of forecasting using recursive multi-step forecasting, while Figure 11 and Figure 12 show the results of direct multi-step forecasting. Figure 9 and Figure 11 illustrate forecasting using an endogenous scenario. Figure 10 and Figure 12 show the forecasts obtained in the exogenous scenario.
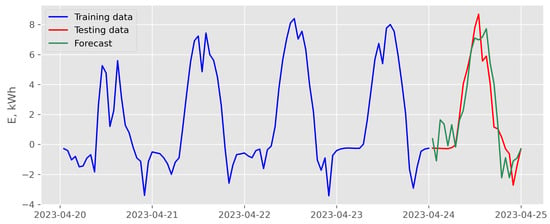
Figure 9.
Results of recursive multi-step forecasting with LASSO model and endogenous scenario for data recorded in April 2023 (case of the best backtesting MSE).
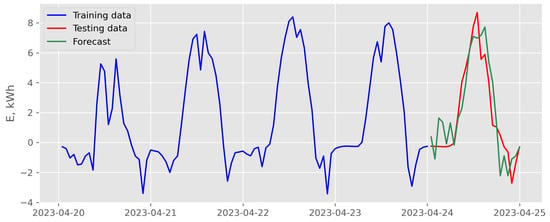
Figure 10.
Results of recursive multi-step forecasting with LASSO model and exogenous variables scenario for data recorded in April 2023 (case of the best backtesting MSE).
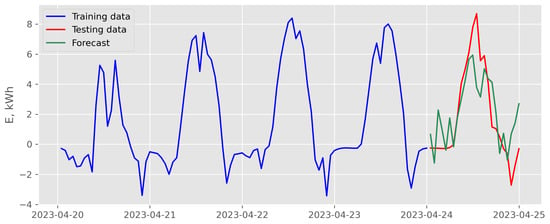
Figure 11.
Results of direct multi-step forecasting with LASSO model and endogenous scenario for data recorded in April 2023 (case of the best backtesting MSE).
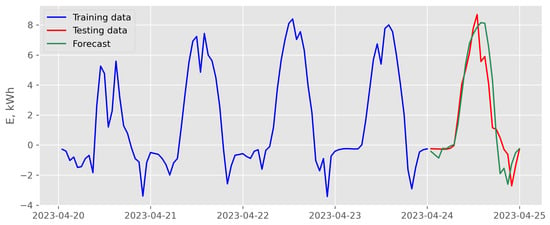
Figure 12.
Results of direct multi-step forecasting with LASSO model and exogenous variables scenario for data recorded in April 2023 (case of the best backtesting MSE).
Table 1, Table 2, Table 3 and Table 4 summarize the values of forecasting accuracy measures on test data and the values of the hyperparameter and the number of lags l for the LASSO model. The results were sorted in terms of the mean squared error values obtained in the backtesting process. Each table contains the results of the evaluation of three models (i.e., the best, intermediate, and worst in terms of ). The results of the evaluation of the LASSO model for the endogenous scenario are presented in Table 1 and Table 3. In turn, Table 2 and Table 4 show the results of model evaluation for the exogenous scenario.

Table 1.
Evaluation results of LASSO model for data recorded in April 2023 (case of recursive multi-step forecasting with endogenous scenario).

Table 2.
Evaluation results of LASSO model for data recorded in April 2023 (case of recursive multi-step forecasting with exogenous variables scenario).

Table 3.
Evaluation results of LASSO model for data recorded in April 2023 (case of direct multi-step forecasting with endogenous scenario).

Table 4.
Evaluation results of LASSO model for data recorded in April 2023 (case of direct multi-step forecasting with exogenous variables scenario).
3.1.2. Random Forest Model
The results of forecasting the balance (5) registered in April 2023 in the prosumer micro-installation using the random forest model (2)–(4) are presented in Figure 13, Figure 14, Figure 15 and Figure 16. Figure 13 and Figure 14 show the results of recursive multi-step forecasting, while Figure 15 and Figure 16 show the results of direct multi-step forecasting. Figure 13 and Figure 15 illustrate forecasting using an endogenous scenario. Figure 14 and Figure 16 present forecasts obtained in the exogenous scenario.
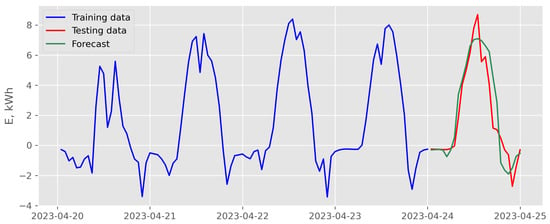
Figure 13.
Results of recursive multi-step forecasting with random forest model and endogenous scenario for data recorded in April 2023 (case of the best backtesting MSE).
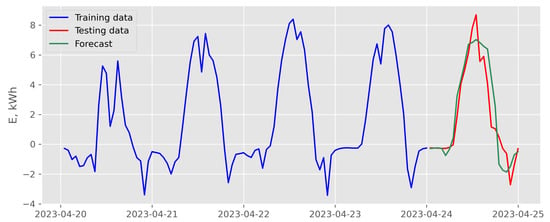
Figure 14.
Results of recursive multi-step forecasting with random forest model and exogenous variables scenario for data recorded in April 2023 (case of the best backtesting MSE).
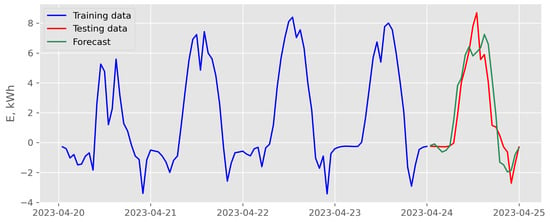
Figure 15.
Results of direct multi-step forecasting with random forest model and endogenous scenario for data recorded in April 2023 (case of the best backtesting MSE).
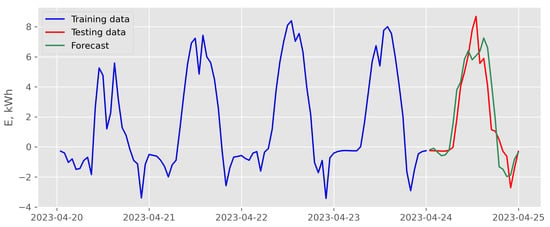
Figure 16.
Results of direct multi-step forecasting with random forest model and exogenous variables scenario for data recorded in April 2023 (case of the best backtesting MSE).
Table 5, Table 6, Table 7 and Table 8 summarize the values for forecasting accuracy measures on test data and the values of the hyperparameters , , and the number of lags l for the random forest model. In addition, the tables also present the values of the parameter determining the maximum number of features taken into account during tree learning.

Table 5.
Evaluation results of random forest model for data recorded in April 2023 (case of recursive multi-step forecasting with endogenous scenario).

Table 6.
Evaluation results of random forest model for data recorded in April 2023 (case of recursive multi-step forecasting with exogenous variables scenario).

Table 7.
Evaluation results of random forest model for data recorded in April 2023 (case of direct multi-step forecasting with endogenous scenario).

Table 8.
Evaluation results of random forest model for data recorded in April 2023 (case of direct multi-step forecasting with exogenous variables scenario).
The results were sorted in terms of the value of the mean squared error obtained in the backtesting process. Each table contains the results of the evaluation of three models (i.e., the best, intermediate, and worst in terms of ). The results of the evaluation of the random forest model for the endogenous scenario are presented in Table 5 and Table 7. In turn, in Table 6 and Table 8, we show the results of the model evaluation for the exogenous scenario.
3.2. Results for Time Series Representing Energy Balance Recorded in November 2022
3.2.1. LASSO Model
The results of forecasting the balance sheet (5) registered in November 2022 in the prosumer micro-installation using the LASSO model (1) are shown in Figure 17, Figure 18, Figure 19 and Figure 20. Figure 17 and Figure 18 show the results of forecasting using recursive multi-step forecasting, while Figure 19 and Figure 20 show the results of direct multi-step forecasting. Figure 17 and Figure 19 illustrate forecasting using an endogenous scenario. Figure 18 and Figure 20 show forecasts obtained in the exogenous scenario.
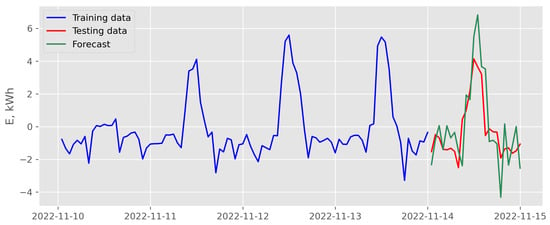
Figure 17.
Results of recursive multi-step forecasting with LASSO and endogenous scenario for data recorded in November 2022 (case of the best backtesting MSE).
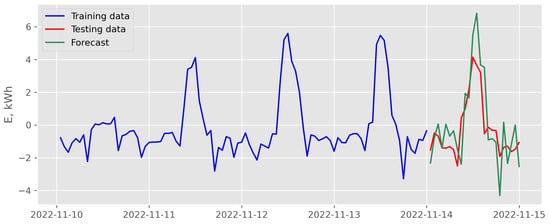
Figure 18.
Results of recursive multi-step forecasting with LASSO and exogenous variables scenario for data recorded in November 2022 (case of the best backtesting MSE).
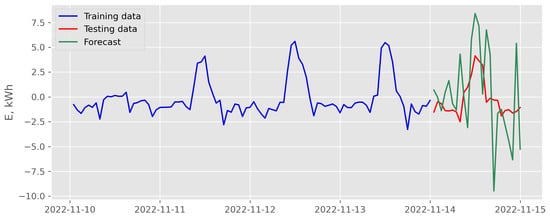
Figure 19.
Results of direct multi-step forecasting with LASSO and endogenous scenario for data recorded in November 2022 (case of the best backtesting MSE).
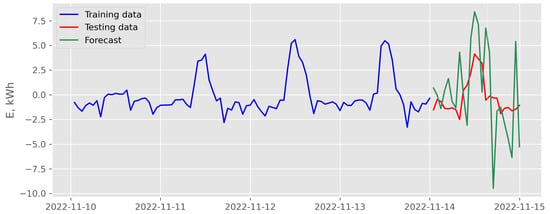
Figure 20.
Results of direct multi-step forecasting with LASSO and exogenous variables scenario for data recorded in November 2022 (case of the best backtesting MSE).
Table 9, Table 10, Table 11 and Table 12 summarize the values of the forecasting accuracy measures on the test data and the values of the hyperparameter and the number of lags l for the LASSO model. The results were sorted in terms of the value of the mean squared error obtained in the backtesting process. Each table contains the results of the evaluation of three models (i.e., the best, intermediate, and worst in terms of ). The results of the evaluation of the LASSO model for the endogenous scenario are shown in Table 9 and Table 11. In turn, Table 10 and Table 12 show the results of the model evaluation for the exogenous scenario.

Table 9.
Evaluation results of LASSO model for data recorded in November 2022 (case of recursive multi-step forecasting with endogenous scenario).

Table 10.
Evaluation results of LASSO model for data recorded in November 2022 (case of recursive multi-step forecasting with exogenous variables scenario).

Table 11.
Evaluation results of LASSO model for data recorded in November 2022 (case of direct multi-step forecasting with endogenous scenario).

Table 12.
Evaluation results of LASSO model for data recorded in November 2022 (case of direct multi-step forecasting with exogenous variables scenario).
3.2.2. Random Forest Model
The results of forecasting the balance (5) registered in November 2023 in the prosumer micro-installation using the random forest model (2)–(4) are shown in Figure 21, Figure 22, Figure 23 and Figure 24. Figure 21 and Figure 22 show the results of forecasting using recursive multi-step forecasting, while Figure 23 and Figure 24 show the results of direct multi-step forecasting. Figure 21 and Figure 23 illustrate forecasting using an endogenous scenario. Figure 22 and Figure 24 show the forecasts obtained in the exogenous scenario.
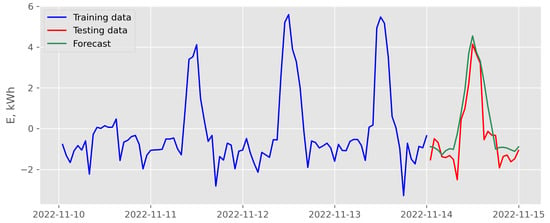
Figure 21.
Results of recursive multi-step forecasting with random forest and endogenous scenario for data recorded in November 2022 (case of the best backtesting MSE).
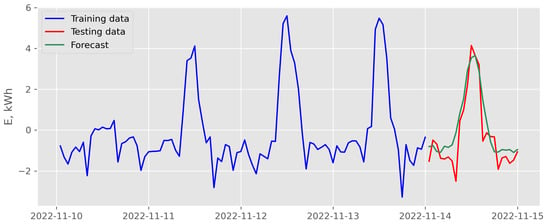
Figure 22.
Results of recursive multi-step forecasting with random forest and exogenous variables scenario for data recorded in November 2022 (case of the best backtesting MSE).
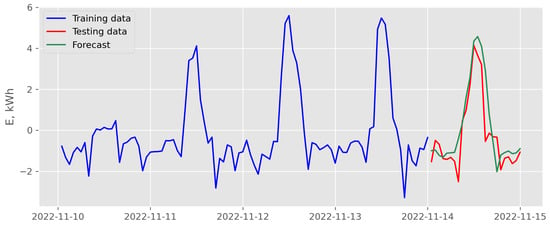
Figure 23.
Results of direct multi-step forecasting with random forest and endogenous scenario for data recorded in November 2022 (case of the best backtesting MSE).
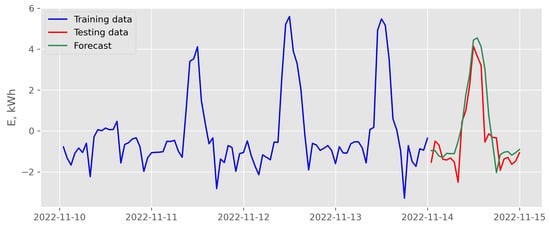
Figure 24.
Results of direct multi-step forecasting with random forest and exogenous variables scenario for data recorded in November 2022 (case of the best backtesting MSE).
Table 13, Table 14, Table 15 and Table 16 summarize the values of the forecasting accuracy measures on the test data and the values of the hyperparameters , , and number of lags l for the random forest model. In addition, the tables present the values of the parameter for the decision on the maximum number of features taken into account during the learning of trees.

Table 13.
Evaluation results of random forest model for data recorded in November 2022 (case of recursive multi-step forecasting with endogenous scenario).

Table 14.
Evaluation results of random forest model for data recorded in November 2022 (case of recursive multi-step forecasting with exogenous variables scenario).

Table 15.
Evaluation results of random forest model for data recorded in November 2022 (case of direct multi-step forecasting with endogenous scenario).

Table 16.
Evaluation results of random forest model for data recorded in November 2022 (case of direct multi-step forecasting with exogenous variables scenario).
The results were sorted in terms of the squared mean error value obtained in the backtesting process. Each of the tables contains the results of the evaluation of three models (i.e., the best, intermediate and worst in terms of MSEbck dem). The results of the evaluation of the random forest model for the endogenous scenario are presented in Table 13 and Table 15. In turn, Table 14 and Table 16 show the results of the model evaluation for the exogenous scenario.
For better clarity of presentation, the best results obtained for both the analyzed months are presented below in Table 17 and Table 18.

Table 17.
Best results for April.

Table 18.
Best results for November.
While analyzing the forecasts made for April 2023, in the case of the LASSO model, the backtesting error ranged from 1.05 to 18.0, while for the model based on random forest, it ranged from 0.88 to 3.49.
Such a significant difference in the magnitude of maximum errors translates into forecast error values. The worst models based on random forest show error values ranging from 1.02 to 1.49 for and from 0.77 to 0.80 for . In the case of the LASSO model, the respective values range from 8.27 to 9.58 for and from 2.52 to 2.74 for . In the case of the intermediate and best variants, it can be found that the differences in forecast error values are similar to each other. Hence, it can be concluded that the use of the random forest model, which is a much more complex model requiring more computing power than the LASSO model, is ineffective.
In the case of forecasts made for November 2022, the dispersion of the error value of the backtesting ranged from 0.61 to 40.8 for the LASSO model and from 1.52 to 5.48 for models using random forest. The increase in the maximum values of backtesting errors for both models is due to the increased importance in the overall energy balance of variable random nature related to electricity consumption. In the case of forecasts made in April, the periodic component related to electricity production was more important. This is visible in the charts: in April, the maximum balance values reach 8 kWh; in November, these values do not exceed 6 kWh.
Comparing the best cases shown in Table 17 and Table 18, it can be concluded that the forecasts prepared using the random forest model are more accurate for April data. In the case of November, the situation is not so clear-cut, but by comparing the corresponding variants, it can be concluded that the LASSO model is better.
4. Conclusions
The research we carried out was aimed at developing a forecast model for the electricity balance of a prosumer household. The preparation of such forecasts can help to choose the appropriate energy storage capacity to increase the self-consumption of electricity on the one hand and to reduce the costs of installed storage on the other. Making such a forecast is difficult due to the random factor of predicting the electricity consumption behavior of household members. The greater the importance of this factor, the more difficult it is to build a suitable forecasting model. In [8], one of the research goals described was to optimize the operation of Virtual Power Plant. In this work, the authors used the Prophet model for the short-term forecasting of the PV farm’s electricity production. This forecast helped adjust autoconsumption in Virtual Power Plant. In the current article, the authors tried to approach the problem globally, taking into account the production and consumption of electricity by the prosumer.
A comparison of endogenous and exogenous scenarios shows that the introduction of additional variables does not significantly improve the quality of the forecast. Indeed, in some cases, it even causes an increase in the error value for the forecast.
It should also be noted that the error value is not always an indicator of the quality of the forecast as measured by the and error values. This particularly applies to the intermediate and best variants and can be seen in Table 1, Table 3, and Table 15, for example. In addition, by annotating the results of the research carried out in this work, it can be confirmed that:
- 1.
- Prediction errors using the random forest model and the LASSO model are similar, but the LASSO model is a less complicated model, which makes the required training period much shorter. Moreover, this model requires much less hardware.
- 2.
- 3.
- In the case of data used to train the LASSO model, in the research presented in this paper, it can be concluded that the smallest error was obtained for relatively small values of the -factor. The smaller the value, the smaller the impact of the regularisation factor. Therefore, it can be concluded that the LASSO model could be replaced by the OLS (ordinary least squares) model in this case.
- 4.
- In this work, research was carried out according to two scenarios: endogenous and exogenous. An analysis of the results showed that adding exogenous variables to the forecast model does not improve the accuracy of the forecast in relation to the and metrics, as shown in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15 and Table 16. In algorithms that train regression models, it is important to maintain a balance between the number of inputs (the size of the training vector) and the amount of learning data. The amount of data must be many times larger than the size of the learning vectors. The addition of exogenous variables, such as and , significantly increases the size of the training vectors. Unfortunately, the amount of training data remains constant. This leads to a limitation in the generalization capability of the model. Therefore, in some cases, it may even increase the error value on the testing data set.
- 5.
- When analyzing the results shown in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15 and Table 16, it can be concluded that much higher forecasting accuracy in both models was obtained for the time series recorded in April. If we consider the time series as a composition of the periodic, random, and trend components, then in the case of the balance sheet, the periodic component is mainly the energy produced by the photovoltaic micro-installation. It can also be observed that, in November, this component was smaller than it was in April. In turn, electricity consumption (the random component) was higher in November. Regression models look for correlations between input and output. Therefore, increasing the content of the random component adversely affects the model training process and, consequently, the accuracy of forecasting.
A significant limitation of the scope of the method presented is the limited number of learning and test samples. In this paper, the authors used a small dataset for model learning, with 96 learning data samples and 24 test data samples. According to the authors, an optimal selection of the number of learning and test samples is necessary for further research. Another limitation is the use of a prosumer installation for the study, understood in Polish legislation as an installation with a capacity of up to 10 kWp. In addition, the research results presented are dependent on individual human behavior and are very difficult to generalize to a wider class of models. The aim of the presented research was to predict the balance in a prosumer micro-installation for electricity storage. Future research is planned to develop methods for selecting energy storage capacity based on the machine learning algorithms described above.
Author Contributions
Conceptualization, T.P., S.D. and P.S.; methodology, T.P., S.D. and P.S.; validation, investigation, S.D. and P.S.; analysis, S.D. and P.S.; data curation, P.S.; writing—original draft preparation, T.P., S.D. and P.S.; writing—review and editing, T.P.; theoretical modelling, S.D.; software, S.D. and P.S.; visualization, T.P., S.D. and P.S.; supervision, T.P.; project administration, T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- BloombergNEF, New Energy Outlook 2022. Available online: https://about.bnef.com/new-energy-outlook/#toc-download (accessed on 28 April 2023).
- Energy Development Agency (ARE) and ENTSO-E. Creative Commons Attribution 4.0 International (CC BY 4.0). Available online: https://energy.instrat.pl/installed_power (accessed on 28 April 2023).
- Act of February 20, 2015 on Renewable Energy Sources. Act and Certain Other Acts; Sejm of the Republic of Poland: Warsaw, Poland, 2022. (In Polish)
- Parol, M.; Wójtowicz, T.; Księżyk, K.; Wenge, C.; Balischewski, S.; Arendarski, B. Optimum management of power and energy in low voltage microgrids using evolutionary algorithms and energy storage. Electr. Power Energy Syst. 2020, 119, 105886. [Google Scholar] [CrossRef]
- Lasseter, R.; Akhil, A.; Marnay, C.; Stephens, J.; Dagle, J.; Guttromson, R.; Meliopoulous, A.S.; Yinger, R.; Eto, J. White paper on integration of distributed energy resources: The CERTS microgrid concept, Lawrence Berkeley National Laboratory. Available online: https://escholarship.org/uc/item/9w88z7z1 (accessed on 5 September 2023).
- Hatziargyriou, N.D.; Asano, A.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energe Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Kroposki, B.; Lasseter, R.; Ise, T.; Morozumi, S.; Papathanassiou, S.; Hatziargyriou, N.D. Making microgrids work. IEEE Power Energe Mag. 2008, 6, 41–53. [Google Scholar] [CrossRef]
- Popławski, T.; Dudzik, S.; Szela˛g, P.; Baran, J. A Case Study of a Virtual Power Plant (VPP) as a Data Acquisition Tool for PV Energy Forecasting. Energies 2021, 14, 6200. [Google Scholar] [CrossRef]
- Sysko-Romańczuk, S.; Kluj, G. Microgrids as an innovative component of energy market diversification in Poland. Organ. Manag. 2019, 9, 19–24. (In Polish) [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhao, Z. Grid-Connected Photovoltaic Power Systems: Technical and Potential Problems—A Review. Renew. Sustain. Energy Rev. 2010, 14, 112–129. [Google Scholar] [CrossRef]
- Lucas, A. Single-Phase PV Power Injection Limit Due to Voltage Unbalances Applied to an Urban Reference Network Using Real-Time Simulation. Appl. Sci. 2018, 8, 1333. [Google Scholar] [CrossRef]
- Brinkel, N.B.G.; Gerritsma, M.K.; AlSkaif, T.A.; Lampropoulos, I.; van Voorden, A.M.; Fidder, H.A.; van Sark, W.G.J.H.M. Impact of Rapid PV Fluctuations on Power Quality in the Low-Voltage Grid and Mitigation Strategies Using Electric Vehicles. Int. J. Electr. Power Energy Syst. 2020, 118, 105741. [Google Scholar] [CrossRef]
- De Silva, H.H.H.; Jayamaha, D.K.J.S.; Lidula, N.W.A. Power Quality Issues Due to High Penetration of Rooftop Solar PV in Low Voltage Distribution Networks: A Case Study. In Proceedings of the 2019 IEEE 14th International Conference on Industrial and Information Systems: Engineering for Innovations for Industry 4.0, ICIIS 2019—Proceedings 2019, Peradeniya, Sri Lanka, 18–20 December 2019; pp. 395–400. [Google Scholar]
- Kharrazi, A.; Sreeram, V.; Mishra, Y. Assessment Techniques of the Impact of Grid-Tied Rooftop Photovoltaic Generation on the Power Quality of Low Voltage Distribution Network—A Review. Renew. Sustain. Energy Rev. 2020, 120, 109643. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Kang, W.; Li, T.; Zhou, H.; Hu, X.; Sun, K. Distributed Nodal Voltage Regulation Method for Low-Voltage Distribution Networks by Sharing PV System Reactive Power. Energies 2022, 16, 357. [Google Scholar] [CrossRef]
- Almeida, D.; Pasupuleti, J.; Ekanayake, J. Comparison of Reactive Power Control Techniques for Solar PV Inverters to Mitigate Voltage Rise in Low-Voltage Grids. Electronics 2021, 10, 1569. [Google Scholar] [CrossRef]
- Ghasemi, M.A.; Parniani, M. Prevention of Distribution Network Overvoltage by Adaptive Droop-Based Active and Reactive Power Control of PV Systems. Electr. Power Syst. Res. 2016, 133, 313–327. [Google Scholar] [CrossRef]
- Ucar, M.; Ozdemir, E.; Kale, M. An Analysis of Three-Phase Four-Wire Active Power Filter for Harmonic Elimination Reactive Power Compensation and Load Balancing under Non-Ideal Mains Voltage. In Proceedings of the PESC Record—IEEE Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; Volume 4, pp. 3089–3094. [Google Scholar]
- Shivashankar, S.; Mekhilef, S.; Mokhlis, H.; Karimi, M. Mitigating methods of power fluctuation of photovoltaic (PV) sources—A review. Renew. Sustain. Energy Rev. 2016, 59, 1170–1184. [Google Scholar] [CrossRef]
- Kakimoto, N.; Takayama, S.; Satoh, H.; Nakamura, K. Power modulation of photovoltaic generator for frequency control of power system. IEEE Trans. Energy Convers 2009, 24, 943–949. [Google Scholar] [CrossRef]
- Yan, R.; Marais, B.; Saha, T.K. Impacts of residential photovoltaic power fluctuation on on-load tap changer operation and a soluation using DSTATCOM. Electr. Power Syst. Res. 2014, 111, 185–193. [Google Scholar] [CrossRef]
- Liu, X.; Cramer, A.M.; Liao, Y. Reactive power control methods for photovoltaic inverters to mitigate short-term voltage magnitude fluctuations. Electr. Power Syst. Res. 2015, 127, 213–220. [Google Scholar] [CrossRef]
- Lave, M.; Kleissl, J.; Arias-Castro, E. High-frequency irradiance fluctuations and geographic smoothing. Solar Energy 2012, 86, 2190–2199. [Google Scholar] [CrossRef]
- Hoff, T.E.; Perez, R. Quantifying PV power output variability. Sol. Energy 2010, 84, 1782–1793. [Google Scholar] [CrossRef]
- Senjyu, T.; Datta, M.; Yona, A.; Sekine, H.; Funabashi, T. A new method for smoothing output power fluctuations of PV system connected to small power utility. In Proceedings of the 7th IEEE Internatonal Conference on Power Electronics, Daegu, Republic of Korea, 22–26 October 2007; pp. 829–834. [Google Scholar]
- Asmine, M.; Brochu, J.; Fortmann, J.; Gagnon, R.; Kazachkov, Y.; Langlois, C.E.; Larose, C.; Muljadi, E.; MacDowell, J.; Pourbeik, P.; et al. Model validation for wind turbine generator models. IEEE Trans. Power Syst. 2011, 26, 1769–1782. [Google Scholar] [CrossRef]
- Xu, M.; Gu, T.; Xu, J.; Wang, K.; Li, G.; Guo, F. Electromechanical modeling of the direct-driven wind turbine generator considering the stochastic component of wind speed. In Proceedings of the 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; p. 185. [Google Scholar]
- Silva, E.A.; Bradaschia, F.; Cavalcanti, M.C.; Nascimento, A.J.; Michels, L.; Pietta, L.P. An eight-parameter adaptive model for the singlediode equivalent circuit based on the photovoltaicmodule’s physics. IEEE J. Photovoltaics 2017, 7, 1115–1123. [Google Scholar] [CrossRef]
- Carvalho, L.M.; Teixeira, J.; Matos, M. Modeling wind power uncertainty in the long-term operational reserve adequacy assessment: A comparative analysis between the naive and the arima forecasting models. In Proceedings of the 2016 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16–20 October 2016. [Google Scholar]
- Li, J.F.; Zhang, B.H.; Xie, G.L.; Li, Y.; Mao, C.X. Grey predictor models for wind speed-wind power prediction. Power Sysem Prot. Control. 2010, 38, 152–159. [Google Scholar]
- Hua, S.; Wang, S.; Jin, S.; Feng, S.; Wang, B. Wind speed optimisation method of numerical prediction for wind farm based on Kalman filter method. J. Eng. 2017, 2017, 1146–1149. [Google Scholar] [CrossRef]
- Gao, S.; He, Y.; Chen, H. Wind speed forecast for wind farms based on ARMAARCH model. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009. [Google Scholar]
- Nair, K.R.; Vanitha, V.; Jisma, M. Forecasting of wind speed using ANN, ARIMA and hybrid models. In Proceedings of the International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, Kerala, India, 6–7 July 2017; pp. 170–175. [Google Scholar]
- Tian, S.; Fu, Y.; Ling, P.; Wei, S.; Liu, S.; Li, K. Wind power forecasting based on arima-lgarch model. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–9 November 2018. [Google Scholar]
- Sahay, K.B.; Srivastava, S. Short-term wind speed forecasting of lelystad wind farm by using ANN algorithms. In Proceedings of the 2018 International Electrical Engineering Congress (iEECON), Krabi, Thailand, 7–9 March 2018. [Google Scholar]
- Khodayar, M.; Wang, J. Spatio-temporal graph deep neural network for short-term wind speed forecasting. IEEE Trans. Sustain. Energy 2019, 10, 670–681. [Google Scholar] [CrossRef]
- Xu, A.; Yang, T.; Ji, J.; Gao, Y.; Gu, C. Application of cluster analysis in short-term wind power forecasting model. J. Eng. 2019, 2019, 5423–5426. [Google Scholar] [CrossRef]
- Perveen, G.; Rizwan, M.; Goel, N. Comparison of intelligent modelling techniques for forecasting solar energy and its application in solar PV based energy system. IET Energy Syst. Integr. 2019, 1, 34–51. [Google Scholar]
- Liu, Y.; Sun, Y.; Infield, D.; Zhao, Y.; Han, S.; Yan, J. A hybrid forecasting method for wind power ramp based on orthogonal test and support vector machine (ot-svm). IEEE Trans. Sustain. Energy 2017, 8, 451–457. [Google Scholar] [CrossRef]
- Xu, A.; Yang, T.; Ji, J.; Gao, Y.; Gu, C. Forecasting short-term wind speed based on iewt-lssvm model optimized by bird swarm algorithm. J. Eng. 2019, 7, 5423–5426. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Tyass, I.; Bellat, A.; Raihani, A.; Mansouri, K.; Khalili, T. Wind Speed Prediction Based on Seasonal ARIMA model. In Proceedings of the The International Conference on Energy and Green Computing (ICEGC’2021), Meknes, Morocco, 9–10 December 2021; 2022. [Google Scholar] [CrossRef]
- Weron, R. Modeling and Forecasting Electricity Loads and Prices; Wiley: Chichester, UK, 2006. [Google Scholar]
- Taylor, J.W. Short-term load forecasting with exponentially weighted methods. IEEE Trans. Power Syst. 2012, 27, 458–464. [Google Scholar] [CrossRef]
- Lee, C.-M.; Ko, C.-N. Short-term load forecasting using lifting scheme and ARIMA models. Expert Syst. Appl. 2011, 38, 5902–5911. [Google Scholar]
- Popławski, T.; Weżgowiec, M. IT implementation of the creeping trend model for wind farm power forecasting. Available online: http://pe.org.pl/articles/2017/2/54.pdf (accessed on 5 September 2023). (In Polish).
- Poplawski, T.; Szelag, P. Use the similarity of processes to predict the power output of wind turbines. Energy Mark. 2011, 92, 103–107. (In Polish) [Google Scholar]
- Percival, D.B.; Walden, A.T. Spectral Analysis for Physical Applications; Cambridge University: Cambridge, UK, 1993. [Google Scholar]
- Nespoli, A.; Ogliari, E.; Leva, S.; Massi, P.A.; Mellit, A.; Lughi, V.; Dolara, A. Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques. Energies 2019, 12, 1621. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. PeerJ 2017, 5, e3190v2. [Google Scholar] [CrossRef]
- Ozbek, A.; Yildirim, A.; Bilgili, M. Deep learning approach for one-hour ahead forecasting of energy production in a solar-PV plant. Energy Sources Part Recover. Util. Environ. Eff. 2022, 44, 10465–10480. [Google Scholar] [CrossRef]
- Bezerra Menezes Leite, H.; Zareipour, H. Six Days Ahead Forecasting of Energy Production of Small Behind-the-Meter Solar Sites. Energies 2023, 16, 1533. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Lu, S.; Hamann, H.F.; Hodge, B.M.; Lehman, B. A Solar Time Based Analog Ensemble Method for Regional Solar Power Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 268–279. [Google Scholar] [CrossRef]
- Ramesh, G.; Logeshwaran, J.; Kiruthiga, T.; Lloret, J. Prediction of Energy Production Level in Large PV Plants through AUTO-Encoder Based Neural-Network (AUTO-NN) with Restricted Boltzmann Feature Extraction. Future Internet 2023, 15, 46. [Google Scholar] [CrossRef]
- Dudek, G. A Comprehensive Study of Random Forest for Short-Term Load Forecasting. Energies 2022, 15, 7547. [Google Scholar] [CrossRef]
- Bojer, C.S.; Meldgaard, J.P. Kaggle forecasting competitions: An overlooked learning opportunity. Int. J. Forecast. 2021, 37, 587–603. [Google Scholar] [CrossRef]
- Patel, A.; Swathika, O.V.G.; Subramaniam, U.; Sudhakar, B.T.; Alok, T.A.; Samriddha, N.S.; Karthick, A.; Muhibbullah, M. A Practical Approach for Predicting Power in a Small-Scale Off-Grid Photovoltaic System using Machine Learning Algorithms. Int. J. Photoenergy 2022, 2022, 9194537. [Google Scholar] [CrossRef]
- Zazoum, B. Solar photovoltaic power prediction using different machine learning methods. Energy Rep. 2022, 8 (Suppl. 1), 19–25. [Google Scholar] [CrossRef]
- Ullah, I.; Liu, K.; Yamamoto, T.; Al Mamlook, R.E.; Jamal, A. A comparative performance of machine learning algorithm to predict electric vehicles energy consumption: A path towards sustainability. Energy Environ. 2022, 33, 1583–1612. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y.; Hammou Ou Ali, I. CNN-LSTM: An efficient hybrid deep learning architecture for predicting short-term photovoltaic power production. Electr. Pow. Syst. Res. 2022, 208, 107908. [Google Scholar] [CrossRef]
- Popławski, T.; Szelag, P.; Bartnik, R. Adaptation of models from determined chaos theory to short-term power forecasts for wind farms. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 1491–1501. [Google Scholar] [CrossRef]
- Kim, S.J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An Interior-Point Method for Large-Scale L1-Regularized Least Squares. IEEE J. Sel. Top. Signal Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2826–2830. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).