Meta In-Context Learning: Harnessing Large Language Models for Electrical Data Classification

Abstract

The evolution of communication technology has driven the demand for intelligent power grids and data analysis in power systems. However, obtaining and annotating electrical data from intelligent terminals is time-consuming and challenging. We propose Meta In-Context Learning (M-ICL), a new approach that harnesses large language models to classify time series electrical data, which largely alleviates the need for annotated data when adapting to new tasks. The proposed M-ICL consists of two stages: meta-training and meta-testing. In meta-training, the model is trained on various tasks that have an adequate amount of training data. The meta-training stage aims to learn the mapping between electrical data and the embedding space of large language models. In the meta-testing stage, the trained model makes predictions on new tasks. By utilizing the in-context learning ability of large language models, M-ICL adapts models to new tasks effectively with only a few annotated instances (e.g., 1–5 training instances per class). Our contributions lie in the new application of large language models to electrical data classification and the introduction of M-ICL to improve the classification performance with the strong in-context learning ability of large language models. Furthermore, we conduct extensive experiments on 13 real-world datasets, and the experimental results show that the proposed M-ICL improves the average accuracy over all datasets by 19.06%, 12.06%, and 6.63% when only one, two, and five training instances for each class are available, respectively. In summary, M-ICL offers a promising solution to the challenges of electrical data classification.

1. Introduction

With the rapid evolution of communication technology [1,2,3], the demand for intelligent power grid systems is on a steady rise [4]. In recent years, studying and mining the information behind electricity data has become an emerging field of research [5]. For example, Yan and Wen [6] proposed an electricity theft detector using metering data based on extreme gradient boosting. Wang et al. [7] proposed a method to evaluate power systems’ real-time state and evolution direction. Zhang et al. [8] focused on collaborative techniques between cloud and end devices for modern power systems. The goal is to achieve real-time analysis of extensive power time series data.

This paper is motivated by the challenge of expensive data collection and annotation processes in harnessing evolving time series data from users’ intelligent terminals [9,10]. This research aims to classify electrical data collected in the form of time series with less annotation. Specifically, in practical scenarios, collecting and annotating time series data by intelligent terminals within power grids is often time-consuming and laborious [11,12]. On one hand, the process of data collection itself introduces challenges. The intelligent terminals might be spread across geographically dispersed locations, each with its unique communication infrastructure and potential signal interference. This diversity further complicates the uniformity and accuracy of data collection. Consequently, electrical companies often allocate substantial resources to manage and maintain these terminals regularly.

On the other hand, the process of annotation of these electrical data is laborious. For example, assume that an electrical company aims to monitor the fluctuations in electricity demand across a diverse set of consumers. It requires meticulous annotation to identify patterns linked to consumption behaviors, anomalies, or even potential faults. Converting raw voltage and current readings into meaningful insights requires domain knowledge and human expertise. Human annotators must distinguish between regular load variations and irregular spikes that might signify an issue requiring immediate attention. Therefore, in the practical scenarios of collaborative cloud–end technology for power grids, obtaining a large number of annotated data for data mining is challenging.

Recently, large language models have found extensive applications in various fields such as finance and banking, healthcare, retail and e-commerce, media and entertainment, and education. More recently, generative pre-trained large language models, such as ChatGPT [13] and GPT-4 [14], have demonstrated remarkable performance in human–computer dialogues, igniting a frenzy of large-scale practical implementations.

As it is known, large language models empower general knowledge during pre-training [15]. Furthermore, large language models show remarkable ability of in-context learning, i.e., learning and inference with the provided samples without updating model parameters [16]. The in-context learning ability stems from the process of general pre-training [17,18,19,20], and existing studies [21,22] show that the large language models achieve superior performance in downstream tasks through in-context learning.

More importantly, recent advances [23] show that transformer-based models exhibit in-context learning ability even on a synthetic dataset. Furthermore, transformer-based models also show in-context learning ability in the linear regression task. In other words, transformer-based models can perform in-context learning when the input is not natural language. This motivated us to utilize large language models for classifying electrical data. To our knowledge, we are the first to utilize the in-context learning ability of large language models for electrical data classification.

As mentioned above, collecting and annotating electrical data is time-consuming and laborious. Therefore, it is necessary to devise new learning algorithms to learn useful patterns from electrical data from only a few annotated samples. Since large language models have learned general knowledge from various domain data, it is natural to introduce large language models for modeling electrical data. Furthermore, the in-context learning ability dramatically reduces the demand for collecting and annotating electrical data since large language models learn to adapt to target tasks with only a few (e.g., 5) annotated samples. For example, if an electrical power company aims to identify abnormal customer behavior, only a few abnormal instances need to be collected and annotated.

Furthermore, meta learning [24], i.e., learning-to-learn, has also been a hot research topic in recent years. Unlike conventional supervised learning algorithms, meta learning aims to improve the learning algorithm itself, given the learning experience in previous tasks. Meta learning alleviates the demand for data collection and annotation since it transfers the knowledge from previous tasks to unseen tasks.

Motivated by this, we propose an improved method called Meta In-Context Learning (M-ICL) to utilize the extensive knowledge in large language models for modeling electrical data. There are two main components in M-ICL: a pre-trained large language model and a randomly initialized fully connected layer. The large language model can be regarded as a knowledge base with knowledge from various domains, such as the electrical domain and edge computing domain. Since the large language model uses natural language as the medium, we need to convert the raw electrical data to the embedding space of large language models. To achieve this, we introduce a trainable, fully connected layer which takes electrical data as input and outputs the embedding of it. The output embedding has the same hidden dimensions as the large language model so that the electrical data elicit the pre-trained knowledge in the large language model.

There are two stages in the proposed M-ICL: meta-training and meta-testing. In the meta-training stage, the large language model is parameters are frozen, and the fully connected layer has parameters that are trainable. More specifically, M-ICL fine-tunes the model using an extensive range of tasks. We sample K+1 training instances for each task and construct the input using a predefined template (also known as prompt [15]). Then, the model is optimized to predict the (K+1)-th sample with the rest of the K samples. Since the large language model is not updated in the process, it encourages the fully connected layer to learn the best mapping from the input space of electrical data to the embedding space of the large language model. We utilize cross-entropy loss to optimize the model prediction of the (K+1)-th sample. In the meta-testing stage, we collect K annotated instances from a new task and construct the input using the predefined template with K annotated instances as well as test samples. We note that the tasks used in the meta-training stage can be different from the tasks in the meta-testing stage. For example, the meta-training tasks can classify whether an electrical load is balanced, and the meta-testing task can classify whether the customer’s electricity consumption behavior is abnormal.

In summary, the contributions of this paper are as follows:

• In electrical power edge–end interaction classification, we are the first to utilize the internal pre-trained knowledge in large language models for classifying time-series data. Combining large language models with electrical power edge–end interaction classification is an under-explored research question.
• We introduce a target method called M-ICL, which employs extensive tasks to fine-tune a pre-trained language model. This process enhances the model’s in-context learning ability, allowing it to adapt effectively to new tasks.
• Extensive experiments conducted on 13 electrical datasets collected in real-world scenarios demonstrate that our proposed M-ICL achieves superior classification performance in various settings. In addition, the ablation study further demonstrates the effectiveness of different components in M-ICL.

2. Related Work

2.1. Electrical Power Edge–End Interaction Modeling

Extensive scholarly interest has been directed towards the exploration of interaction methods between cloud systems and end systems within the context of power systems. This research foundation is firmly established [25,26]. For instance, Wang et al. [27] applied the classical federated learning approach to create an authentication system for users’ power consumption patterns. Similarly, Taïk et al. [28] employed federated learning to forecast power loads, developing efficient deployable cloud–end models. Lv and Kumar [29] analyzed the dual-channel architecture defined by the wireless sensor software in 6G/IoE and proposed a reasonable solution to reduce the signal interference to transmit the related signals better. Xiong et al. [30] proposed a transferable scheduling strategy for home energy management systems with different tasks utilizing a Meta-Reinforcement Learning framework. Zhao et al. [31] proposed a learning-based method for surviving critical loads in microgrids during sequential extreme events.

Real-world power scenarios introduce challenges like the high cost associated with data collection and annotation, giving rise to the obstacle of few-shot learning [32]. However, ongoing explorations [33,34] primarily focus on optimizing collaboration between cloud and end systems, with relatively less emphasis on effectively extracting meaningful patterns from sparsely labeled samples within the cloud–end interaction framework.

In summary, the challenge of learning from limited samples remains significant, hampering the practical utility of pertinent models in power-side end-interaction modeling.

2.2. Large Language Models

GPT models [13,15] undergo a training process in two distinct stages. Initially, these models are exposed to a comprehensive dataset of text collected from the Internet. Their primary objective during this phase is to predict the next word in a given context, thus establishing their foundational linguistic competence. Following this foundational training, a subsequent stage known as fine-tuning is executed. This stage involves incorporating additional data and employing an algorithm called reinforcement learning from human feedback (RLHF). Fine-tuning aims to enhance the models’ outputs by aligning them with human preferences, which are indicated by skilled human labelers.

Using extensive text datasets for training language models has enabled impressive capabilities, including but not limited to few-shot learning, where models can learn new tasks with minimal examples. These language models have demonstrated proficiency across a wide range of natural language tasks spanning various domains. Noteworthy applications include question-answering, arithmetic operations, and classification tasks. However, the subsequent fine-tuning process has significantly advanced these models in terms of control and practical usefulness, making them more skilled at generating desired outcomes.

2.3. In-Context Learning

The concept introduced by [15] revolves around utilizing a language model (LM) conditioned on a concatenation of training examples for few-shot learning, all without necessitating parameter updates. Subsequent research has built upon this concept, with [22] refining the approach and showcasing promising results across various tasks. Nonetheless, the effectiveness of LM-based in-context learning encounters challenges when confronted with markedly dissimilar tasks or when utilizing inadequately large LMs. Moreover, this approach displays notable variability and superior performance in worst-case scenarios, as emphasized by [35]. Our work is deeply rooted in the core principle of in-context learning through the conditioning of training examples. By explicitly training with an in-context learning objective, we demonstrate that M-ICL achieves noteworthy improvements, even in situations involving smaller LMs.

3. Method

In this section, we delve into the components of the proposed approach, structured into three subsections. We present M-ICL, a method leveraging the in-context learning capabilities inherent in large language models to amplify model performance in few-shot learning. The overview is in Figure 1.

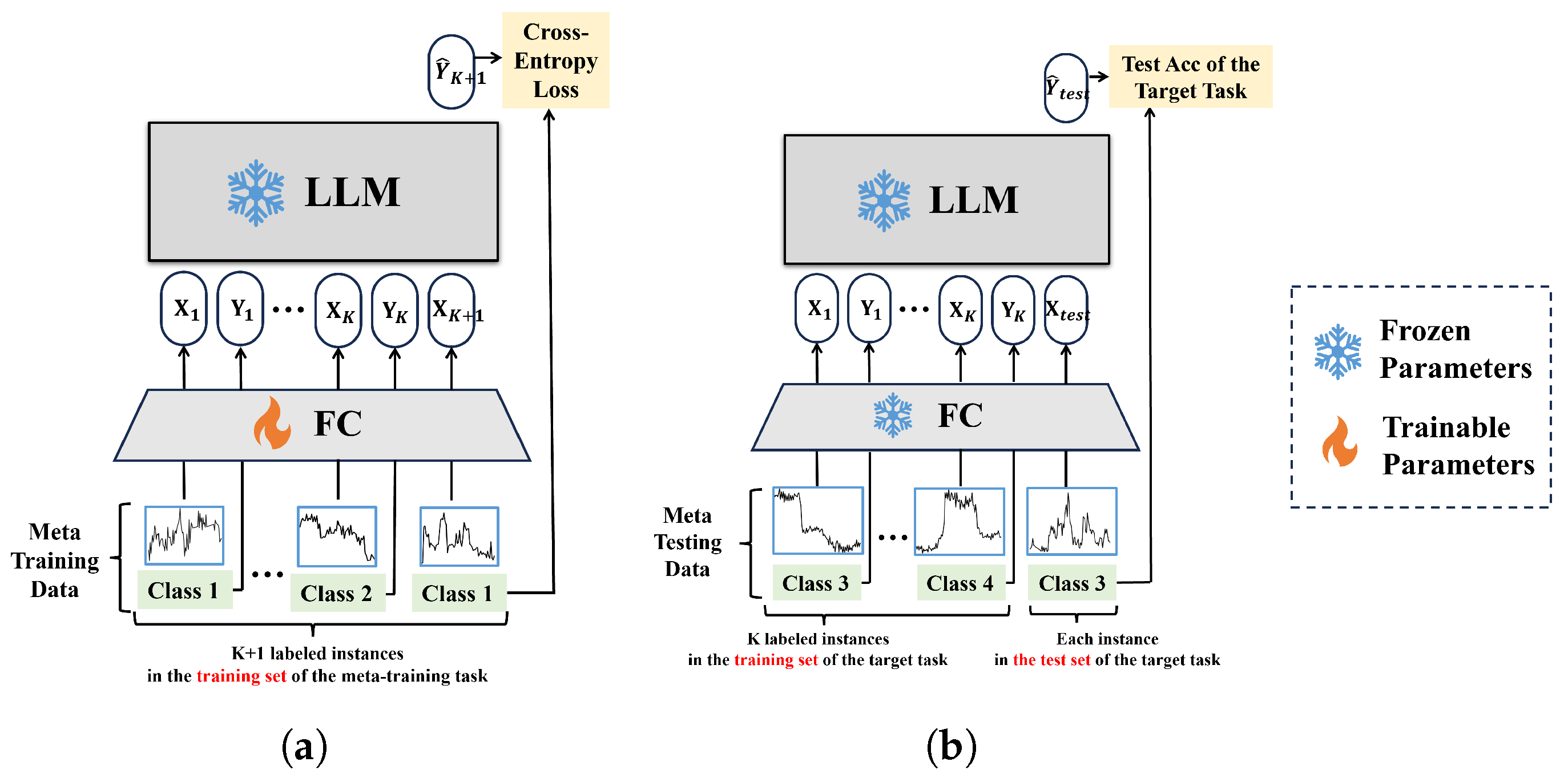
3.1. Overview of M-ICL

In practical scenarios, some electrical data are easy to collect and annotate, while others are expensive. Ideally, we expect models to learn transferable knowledge from tasks where annotated samples are abundant and to adapt to target tasks when only a few annotated instances are provided. Motivated by this, we proposed M-ICL, which first trains a large language model on tasks where annotated instances are abundant (i.e., meta-training) and then adapts models to the target task with only a few annotated instances using the in-context learning ability of large language models (i.e., meta-testing).

M-ICL comprises two key components: a pre-trained expansive language model $\mathcal{G}$ and an arbitrarily initialized fully connected layer $\mathcal{F}$. The expansive language model functions as a repository of knowledge spanning diverse domains, including but not limited to the electrical and edge computing realms. As this language model operates through natural language, converting raw electrical data into the language model’s embedding space becomes necessary. To facilitate this transformation, we introduce a trainable, fully connected layer. This layer takes raw electrical data as input and generates the corresponding embedding. Remarkably, this output embedding shares identical hidden dimensions with the large language model so that the electrical data elicit the pre-trained knowledge in the large language model.

3.2. Meta-Training with Time-Series Data

The tasks in the meta-training stage are called meta-training tasks. In each iteration, a meta-training task is randomly selected, and a set of $K+1$ training examples $(X_1,Y_1),(X_2,Y_2),\cdots ,(X_K,Y_K),(X_{K+1},Y_{K+1})$ is drawn from the chosen task’s training examples. Here, $X_i$ and $Y_i$ represent the input and the label of the i-th sample, respectively. Since we focus on electrical data classification, $X_i$ is one sample of electrical data, and $Y_i$ is the annotated label. Subsequently, the model is supervised by inputting the concatenation of $X_1$,$Y_1$,$X_2$,$Y_2$,⋯,$X_K$,$Y_K$,$X_{K+1}$ and training it to generate $y_{K+1}$, utilizing the cross-entropy loss. We summarize the process in the following:

$$filled\_template=template(\mathcal{F}\left(X_1\right),Y_1,\mathcal{F}\left(X_2\right),Y_2,\cdots ,\mathcal{F}\left(X_K\right),Y_K,\mathcal{F}\left(X_{K+1}\right))$$

(1)

$$\widehat{Y_{K+1}}=\mathcal{G}(filled\_template)$$

(2)

$$training\_loss=CrossEntropyLoss(\widehat{Y_{K+1}},Y_{k+1})$$

(3)

where $\widehat{Y_{K+1}}$ represents the model prediction of the $(K+1)$-th sample, $template(\cdots )$ represents concatenating the input data using the predefined template, and $CrossEntropyLoss(·,·)$ represents the cross-entropy loss. In Equation (8), we fill the template in Algorithm 1 with $K+1$ training instances. In the template in Algorithm 1, $\{·\}$ represents the placeholder. For example, if there are three categories in the meta-training phase, {the label set of the meta-training/testing data} represents 0,1,2. {$Y_1$} represents the label of $X_1$ (e.g., 1). the embedding of $X_1$ represents the embedding of $X_1$ extracted by the fully connected layer. In Equation (2), the large language model predicts the next token of the filled_template (i.e., the prediction of $X_{k+1}$) and the prediction is denoted as $\widehat{Y_{K+1}}$. In Equation (3), we minimize the cross-entropy loss between the prediction $\widehat{Y_{K+1}}$ and the ground-truth label $Y_{k+1}$. We note that this procedure simulates the in-context learning during inference, where the initial set of k examples acts as training instances, and the last example (K + 1)-th is used as the test instance.

Algorithm 1: The template for meta-training or meta-testing in the proposed M-ICL.

1  Please classify the time series data into the following categories: {the label set of the meta-training/testing data}. 2  Examples: 3  ### Input: {the embedding of $X_1$} 4  ### Label: {$Y_1$} 5  ### Input: {the embedding of $X_2$} 6  ### Label: {$Y_2$} 7  ⋮ 8  ### Input: {the embedding of $X_K$} 9  ### Label: {$Y_K$} 10  ### Input: {the embedding of $X_{test}$/$X_{K+1}$} 11  ### Label:

3.3. Meta-Testing on Target Tasks

After training the model in the meta-training stage, the fully connected layer learns to map the time-series data into the embedding space of the large language model. Then, the model only requires K annotated training samples, denoted as $(X_1,Y_1),(X_2,Y_2),\cdots ,$$(X_K,Y_K)$, to adapt to the target task. More specifically, given a test sample $X_{test}$, we fill the template in Algorithm 1 with K training samples as well as $X_{test}$. We note that the label set of the target task is given in the template. Therefore, the model uses the internal knowledge as well as the K training instances to choose the best answer in the label set $\mathcal{C}$, where $\mathcal{C}$ represents the label set of the target task.

Furthermore, inspired by the work of Min et al. [36], we improve the prediction process in M-ICL. Concretely, the model predicts the label $\widehat{Y_{test}}$ directly in the conventional prediction. In other words, the model selects the label with the largest probability as follows:

$$\widehat{Y_{test}}=argma{x}_{Y\in \mathcal{C}}\mathbb{P}\left(Y\right|X_1,Y_1,\cdots ,X_K,Y_K,X_{K+1})$$

(4)

However, this prediction is inaccurate because it only considers the conditional probability of each label given the input [36]. Using the Bayes rule, we have the following relationship:

$$\mathbb{P}\left(Y\right|X_1,Y_1,\cdots ,X_K,Y_K,X_{K+1})=\frac{\mathbb{P}\left(X_{K+1}\right|Y,X_1,Y_1,\cdots ,X_K,Y_K)\mathbb{P}\left(Y\right)}{{\sum }_{Y\in \mathcal{C}}\mathbb{P}(X_{K+1},Y|X_1,Y_1,\cdots ,X_K,Y_K)}$$

(5)

Since the evidence term in Equation (5) is a constant when the K training data are sampled, we have the following relationship:

$$\mathbb{P}\left(Y\right|X_1,Y_1,\cdots ,X_K,Y_K,X_{K+1})\propto \mathbb{P}\left(X_{K+1}\right|Y,X_1,Y_1,\cdots ,X_K,Y_K)\mathbb{P}\left(Y\right)$$

(6)

Following [36], we assume that each category has the same prior probability. Therefore, in Equation (6), we find that the posterior probability is proportional to the likelihood term. Therefore, we predict the following:

$$\widehat{Y_{test}}=argma{x}_{Y\in \mathcal{C}}\mathbb{P}\left(X_{K+1}\right|Y,X_1,Y_1,\cdots ,X_K,Y_K)$$

(7)

Different from [36], the input of $X_{K+1}$ is a continuous vector $\mathcal{F}\left(X_{K+1}\right)$ in the embedding space instead of a discrete word in the vocabulary. Therefore, we compute the Euclidean distance between $\mathcal{F}\left(X_{K+1}\right)$ and the last hidden feature (i.e., the feature output by the last transformer layer before mapped to the vocabulary) of large language models (denoted as ${\mathcal{G}}^{(-1)}\left(X_{K+1}\right)$). Formally, the prediction is as follows:

$$filled\_template\_test=template(\mathcal{F}\left(X_1\right),Y_1,\mathcal{F}\left(X_2\right),Y_2,\cdots ,\mathcal{F}\left(X_K\right),Y_K,Y)$$

(8)

$$\widehat{Y_{test}}=argmi{n}_{Y\in \mathcal{C}}Euclidean\_Distance(\mathcal{F}\left(X_{test}\right),{\mathcal{G}}^{(-1)}(filled\_template\_test))$$

(9)

where $X_{test}$ and $\widehat{Y_{test}}$ are the input and the predicted label of the test sample, $filled\_template\_test$ represents the template filled with the K pairs of input and label. The candidate labels Y, $Euclidean\_Distance(·,·)$ represents the Euclidean distance between two vectors. We note that, in the meta-testing stage, we slightly adjust the template in Algorithm 1 by swapping the last two rows to enable obtaining the last hidden feature of the next token given K annotated instances and the candidate label Y. Finally, we summarize the meta-training and meta-testing stage of M-ICL in Algorithm 2 and Algorithm 3, respectively.

Algorithm 2: The meta-training phase in the proposed M-ICL framework.

Algorithm 3: The meta-testing phase in the proposed M-ICL framework.

4. Experiments

This section compares the proposed method, M-ICL, with other classification methods. Section 4.1 describes the experimental settings. Section 4.2 presents the comparison results of all methods. Section 4.3 demonstrates the results of ablation experiments.

4.1. Experiment Settings

4.1.1. Datasets Collection

To verify the effectiveness of the proposed M-ICL in the practical scenario, we collected active electrical load data from three companies, including a semiconductor materials company (denoted as C1), an electrical appliance manufacturing company (denoted as C2), and a technology company (denoted as C3). For each company, we collected data from different metering points (e.g., S1, S2, S3). For example, C3S2 represents the dataset constructed by the S2 metering point of the C3 company. More specifically, the value of the active electrical load was recorded every 15 min, and each sample contains the data in one day (i.e., from 0 a.m. to 12 p.m.). Therefore, each sample has $(60/15)\times 24=96$ points. We classified each dataset into two categories, including regular electricity consumption behavior (normal) and abnormal electricity consumption behavior (abnormal). The former category represents the normal electricity consumption of customers, while the latter category represents the abnormal electricity consumption of customers. We divided each dataset into a training set and a test set at a scale of 4:1. According to the above data collection process, we collected a total of 13 datasets and 4028 samples. We summarize the data statistics in

Table 1. The data statistics of the collected datasets.

Company	Dataset	# Categories	# Training Samples	# Testing Samples	# Points in Each Sample
C1	C1S1	2	50	13	96
	C1S2	2	77	20	96
	C1S3	2	111	28	96
C2	C2S1	2	176	44	96
	C2S2	2	78	20	96
C3	C3S1	2	404	101	96
	C3S2	2	376	95	96
	C3S3	2	422	106	96
	C3S4	2	416	104	96
	C3S5	2	410	103	96
C4	C4S1	2	329	83	96
	C4S2	2	33	9	96
	C4S3	2	336	84	96

.

We show some examples in Figure 2. Figure 2a is an example in C1S1 labeled as normal electricity consumption behaviors. Figure 2b is an example in C1S1 labeled as abnormal electricity consumption behaviors (abnormal fluctuation around noon).

To obtain the test performance on one dataset, we used the remaining datasets as the meta-training datasets and calculated the test accuracy on the test set of that dataset.

4.1.2. Architecture

We consider three large language models for experiments: GPT2-large (GPT2) [37], bert-base-cased (BERT) [38], and RoBERTa-large (RoBERTa) [39].

GPT-2 is a pre-trained model developed by OpenAI, which is pre-trained in English using a causal language modeling objective. GPT-2 is part of the GPT series of models and is designed to generate human-like text based on the input it receives. GPT-2 is built upon the transformer architecture, a deep learning model designed explicitly for sequence-to-sequence tasks, such as language translation and text generation.

BERT is a pre-trained transformers model for English text, trained in a self-supervised manner on a large dataset. It learns from raw text without human labeling, using two main objectives. First, it predicts masked words in sentences where 15% of words are randomly masked. This enables bidirectional understanding, unlike sequential models. Second, it predicts whether pairs of masked sentences are consecutive or not. BERT’s learned representation can be utilized as features for downstream tasks like classification when labeled data are available.

RoBERTa has the same architecture as BERT except that the training hyper-parameters and the training data are carefully selected. More specifically, RoBERTa builds upon BERT’s pre-training methodology by extending the model’s training duration, utilizing larger batches across a broader dataset. It omits the task of predicting the next sentence and instead focuses on training with longer sequences. Additionally, RoBERTa introduces the concept of dynamically altering the masking pattern applied to the training data.

4.1.3. Baselines

We compare state-of-the-art fine-tuning methods which adapt large language models to downstream tasks. We combine each fine-tuning method with a trainable, fully connected layer to map the electrical data into the embedding space of large language models. Unlike the proposed M-ICL, these fine-tuning methods directly train the fully connected layer and the large language model on the K annotated instance of target tasks. In contrast, M-ICL only requires training the fully connected layer and better utilizes the in-context learning ability. The competitive methods are described below:

• Vanilla Fine-Tuning: Demonstrated as a straightforward and effective technique, fine-tuning adapts large pre-trained language models to specific downstream tasks.
• BSS (Batch Spectral Shrinkage) [40] (https://github.com/thuml/Batch-Spectral-Shrinkage accessed on 1 September 2022): BSS mitigates negative transfer by penalizing small singular values in the feature matrix. The minimum singular value is penalized, with a recommended regularization weight of $1\times {10}^{-3}$.
• ChildTune-F and ChildTune-D [41] (https://github.com/alibaba/AliceMind/tree/main/ChildTuning accessed on 1 September 2022): ChildTune-F & ChildTune-D train a subset of parameters (referred to as the child network) of large language models during the backward process. ChildTune-D leverages the pre-trained model’s Fisher Information Matrix to identify the child network, while ChildTune-F employs a Bernoulli distribution for this purpose.
• Mixout (https://github.com/bloodwass/mixout accessed on 1 September 2022) [42]: Mixout introduces randomness by blending parameters from the pre-trained and fine-tuned models, thereby regularizing the fine-tuning process. The mixing probability, denoted as p, is set to 0.9 in the experiments.
• NoisyTune [43]: NoisyTune introduces uniform noise to pre-trained model parameters based on their standard deviations. The scaling factor $\lambda$, which controls noise intensity, is set at 0.15.
• R3F (https://github.com/facebookresearch/fairseq/tree/main/\examples/rxf accessed on 1 September 2022) [44]: R3F addresses representational collapse by introducing parametric noise. Noise is generated from normal or uniform distributions.
• RecAdam (https://github.com/Sanyuan-Chen/RecAdam accessed on 1 September 2022) [45]: RecAdam optimizes a multi-task objective, gradually transitioning the objective from pre-training to downstream tasks using an annealing coefficient.
• ReInit [46]: The authors of [46] found that transferring the top pre-trained layers hampers learning and performance. ReInit re-initializes the top layers of large language models during adaptation to new tasks. In our experiments, the top three transformer blocks are re-initialized.

4.1.4. Implementation Details

In the meta-training stage, each model is trained for 100 epochs. We employed PyTorch [47] and Huggingface [48] frameworks for our model implementations. Our approach follows the Huggingface implementation, using the default hyper-parameters of the GPT-2, BERT, and RoBERTa models. We selected the best batch size within {8,16,32} and adjusted the learning rate for the backbone model within the set {$5\times {10}^{-5}$, $2\times {10}^{-5}$, $1\times {10}^{-5}$}. We utilized the RAdam optimizer [49] with a constant learning rate scheduler to optimize our models. Our configuration also encompassed a weight decay $1\times {10}^{-2}$ and a maximum gradient norm of 1.0. For a fair comparison, the training hyper-parameters remained consistent for all methods across each dataset. All experiments were conducted on GeForce RTX 3090 GPUs.

4.2. Comparison with State-of-the-Art Methods

We validate the effectiveness of our method in the scenario where only limited annotated samples of the target task are available. Specifically, we consider three settings: K = 1, K = 2, and K = 5, representing K annotated samples provided for each class. We evaluate all the baselines, and our methods on all 13 datasets with different K are selected. We use GPT-2 as the large language model; its hidden dimension is 1280. Accordingly, the input and output dimensions of the fully connected layer are 96 and 1280, respectively. We use uniform distribution to initialize the parameters in the fully connected layer. The experiment results of K = 1, K = 2, and K = 5 are summarized in

Table 2. Comparison with state-of-the-art methods when K = 1. The backbone model is GPT-2.

	C1S1	C1S2	C1S3	C2S1	C2S2	C3S1	C3S2	C3S3	C3S4	C3S5	C4S1	C4S2	C4S3	Average
Vanilla Fine-tuning	15.38	25.00	7.14	47.73	35.00	96.04	84.21	18.87	18.27	69.90	15.66	66.67	0.00	38.45
BSS	15.38	45.00	10.71	40.91	35.00	95.05	84.21	38.68	28.85	70.87	13.25	33.33	0.00	39.33
ChildTune-F	38.46	25.00	7.14	47.73	50.00	95.05	97.90	30.19	36.54	69.90	25.30	33.33	46.43	46.38
ChildTune-D	7.69	40.00	42.86	47.73	50.00	95.05	84.21	36.79	74.04	69.90	26.51	33.33	46.43	50.35
Mixout	15.38	45.00	46.43	47.73	50.00	96.04	97.90	38.68	51.92	70.87	43.37	55.56	45.24	54.16
NoisyTune	46.15	45.00	53.57	47.73	50.00	96.04	97.90	66.04	70.19	71.84	51.81	66.67	46.43	62.26
R3F	61.54	75.00	53.57	47.73	60.00	98.02	98.95	67.92	80.77	71.84	38.55	88.89	53.57	68.95
RecAdam	61.54	75.00	96.43	40.91	35.00	98.02	97.90	67.92	74.04	70.87	51.81	55.56	45.24	66.94
ReInit	53.85	60.00	50.00	40.91	50.00	98.02	84.21	68.87	51.92	70.87	59.04	77.78	98.81	66.48
M-ICL (Ours)	69.23	80.00	100.00	65.91	60.00	98.02	98.95	87.74	99.04	88.35	81.93	88.89	100.00	86.00

,

Table 3. Comparison with state-of-the-art methods when K = 2. The backbone model is GPT-2.

	C1S1	C1S2	C1S3	C2S1	C2S2	C3S1	C3S2	C3S3	C3S4	C3S5	C4S1	C4S2	C4S3	Average
Vanilla Fine-tuning	46.15	15.00	53.57	31.82	35.00	97.03	94.74	39.62	62.50	75.73	27.71	77.78	100.00	58.20
BSS	23.08	20.00	53.57	45.45	40.00	97.03	94.74	20.76	18.27	72.82	20.48	77.78	88.10	51.70
ChildTune-F	53.85	15.00	46.43	45.45	45.00	98.02	94.74	37.74	39.42	72.82	55.42	77.78	100.00	60.13
ChildTune-D	38.46	70.00	21.43	45.45	40.00	98.02	94.74	33.96	62.50	70.87	55.42	88.89	100.00	63.06
Mixout	53.85	15.00	21.43	43.18	40.00	97.03	97.90	66.98	42.31	75.73	50.60	88.89	100.00	60.99
NoisyTune	46.15	70.00	46.43	43.18	40.00	97.03	94.74	66.98	42.31	72.82	57.83	100.00	88.10	66.58
R3F	46.15	90.00	46.43	43.18	35.00	98.02	97.90	53.77	76.92	70.87	71.08	100.00	88.10	70.57
RecAdam	84.62	70.00	100.00	50.00	45.00	97.03	94.74	68.87	76.92	75.73	69.88	100.00	100.00	79.45
ReInit	76.92	75.00	92.86	45.45	40.00	98.02	97.90	52.83	83.65	72.82	60.24	88.89	88.10	74.82
M-ICL (Ours)	84.62	90.00	100.00	77.27	60.00	99.01	98.95	88.68	100.00	92.23	98.80	100.00	100.00	91.50

, and

Table 4. Comparison with state-of-the-art methods when K = 5. The backbone model is GPT-2.

	C1S1	C1S2	C1S3	C2S1	C2S2	C3S1	C3S2	C3S3	C3S4	C3S5	C4S1	C4S2	C4S3	Average
Vanilla Fine-tuning	61.54	55.00	100.00	56.82	35.00	97.03	97.90	56.60	42.31	85.44	77.11	100.00	100.00	74.21
BSS	61.54	50.00	100.00	50.00	35.00	97.03	97.90	85.85	41.35	87.38	60.24	100.00	100.00	74.33
ChildTune-F	76.92	50.00	96.43	45.46	35.00	97.03	97.90	85.85	32.69	85.44	60.24	100.00	100.00	74.07
ChildTune-D	53.85	45.00	100.00	45.46	40.00	98.02	97.90	85.85	42.31	85.44	60.24	100.00	100.00	73.39
Mixout	76.92	45.00	100.00	45.46	40.00	97.03	97.90	87.74	58.65	85.44	71.08	100.00	100.00	77.32
NoisyTune	76.92	50.00	96.43	56.82	45.00	97.03	98.95	85.85	65.38	90.29	60.24	88.89	100.00	77.83
R3F	61.54	55.00	100.00	45.46	45.00	98.02	100.00	87.74	50.00	85.44	96.39	88.89	100.00	77.96
RecAdam	61.54	95.00	100.00	56.82	40.00	98.02	97.90	58.49	58.65	92.23	71.08	100.00	100.00	79.21
ReInit	92.31	80.00	100.00	56.82	35.00	97.03	98.95	88.68	75.00	85.44	96.39	100.00	100.00	85.05
M-ICL (Ours)	92.31	95.00	100.00	68.18	60.00	99.01	100.00	88.68	100.00	92.23	96.39	100.00	100.00	91.68

, respectively.

In Table 2, Table 3 and Table 4, the proposed M-ICL outperforms all other competitive baselines consistently. Existing methods easily overfit the training samples, and overfitting becomes severe when fewer training samples are available. More specifically, when K = 1, the proposed M-ICL achieves 86.00% average accuracy, which is 19.52% higher than ReInit, 19.06% higher than RecAdam, 17.05% higher than R3F, 23.75% higher than NoisyTune, 31.84% higher than Mixout, 35.66% higher than ChildTune-D, 39.62% higher than ChildTune-F, 46.68% higher than BSS, and 47.55% higher than Vanilla Fine-Tuning. When K = 2, the proposed M-ICL achieves 91.50% average accuracy, which is 16.68% higher than ReInit, 12.06% higher than RecAdam, 20.93% higher than R3F, 24.92% higher than NoisyTune, 30.51% higher than Mixout, 28.45% higher than ChildTune-D, 31.38% higher than ChildTune-F, 39.81% higher than BSS, and 33.30% higher than Vanilla Fine-Tuning. When K = 5, the proposed M-ICL achieves 91.68% average accuracy, which is 6.63% higher than ReInit, 12.47% higher than RecAdam, 13.72% higher than R3F, 13.85% higher than NoisyTune, 14.35% higher than Mixout, 18.29% higher than ChildTune-D, 17.60% higher than ChildTune-F, 17.35% higher than BSS, and 17.47% higher than Vanilla Fine-Tuning.

4.3. Ablation Analysis

To further verify the proposed M-ICL’s effectiveness, we consider the following four ablated versions of M-ICL. (1) M-ICL w/o Meta-Training: we do not train the model on the meta-training tasks and directly test the model on the target task. In other words, M-ICL w/o Meta-Training uses the in-context learning ability of large language models. (2) M-ICL w/o Predefined Template: We do not use the predefined template as shown in Algorithm 1. Instead, we simply concatenate all the input embeddings and labels sequentially. In this case, the model does not have the information about the label set and needs to infer that according to the given instances. (3) M-ICL w/o Posterior Prediction: We select the candidate label according to the likelihood term instead of the posterior term in Equation (5). (4) M-ICL w/o Fixing LLM: We do not fix the parameters of the large language model during the meta-training phase. We use GPT-2 as the backbone model, and the experimental results are summarized in

Table 5. The ablation study of the proposed M-ICL. The average test accuracy on all datasets is reported. The backbone model is GPT-2.

	K = 1	$\mathsf{\Delta }$	K = 2	$\mathsf{\Delta }$	K = 5	$\mathsf{\Delta }$
M-ICL (Ours)	86.00	/	91.50	/	91.68	/
M-ICL w/o Meta-Training	41.75	−44.25	42.61	−48.89	45.94	−45.74
M-ICL w/o Predefined Template	84.43	−1.57	87.95	−3.55	90.84	−0.84
M-ICL w/o Posterior Prediction	85.14	−0.86	90.43	−1.07	90.75	−0.93
M-ICL w/o Fixing LLM	69.65	−16.35	76.11	−15.39	87.48	−4.20

.

Table 5 shows that all ablated versions significantly degrade performance. Specifically, when K = 1, M-ICL w/o Meta-Training degrades the performance by 44.25%, M-ICL w/o Predefined Template degrades the performance by 1.57%, M-ICL w/o Posterior Prediction degrades the performance by 0.86%, and M-ICL w/o Fixing LLM degrades the performance by 16.35%. When K = 2, M-ICL w/o Meta-Training degrades the performance by 48.89%, M-ICL w/o Predefined Template degrades the performance by 3.55%, M-ICL w/o Posterior Prediction degrades the performance by 1.07%, and M-ICL w/o Fixing LLM degrades the performance by 15.39%. When K = 5, M-ICL w/o Meta-Training degrades the performance by 45.74%, M-ICL w/o Predefined Template degrades the performance by 0.84%, M-ICL w/o Posterior Prediction degrades the performance by 0.93%, and M-ICL w/o Fixing LLM degrades the performance by 4.20%.

We find that M-ICL w/o Meta-Training performs worse, indicating that meta-training is the key step in the proposed M-ICL. With the meta-training phase, the electrical data can be properly mapped into the embedding space of the large language model. Moreover, M-ICL w/o Fixing LLM also presented bad performance. Therefore, fixing the parameters of the large language model is also crucial to the performance. The reason may be that the large language model easily overfits the training data when only limited training instances are available. In contrast, fixing the large language model avoids the overfitting problem. Moreover, it encourages the large language model to use the in-context learning ability to make a prediction on target tasks. Both M-ICL w/o Predefined Template and M-ICL w/o Posterior Prediction slightly degrade the performance. This indicates that both the predefined template (Algorithm 1) and the proposed prediction process (Algorithm 3) are effective.

4.4. The Analysis of Using Different Large Language Models

In the previous experiments, we used GPT-2 as the large language model. In fact, we can use other popular large language models in the proposed M-ICL. We consider three large language models, GPT-2, BERT, and RoBERTa, for the experiments in this subsection. The results are summarized in

Table 6. The average accuracy on all datasets when using different large language models.

	K = 1	$\mathsf{\Delta }$	K = 2	$\mathsf{\Delta }$	K = 5	$\mathsf{\Delta }$
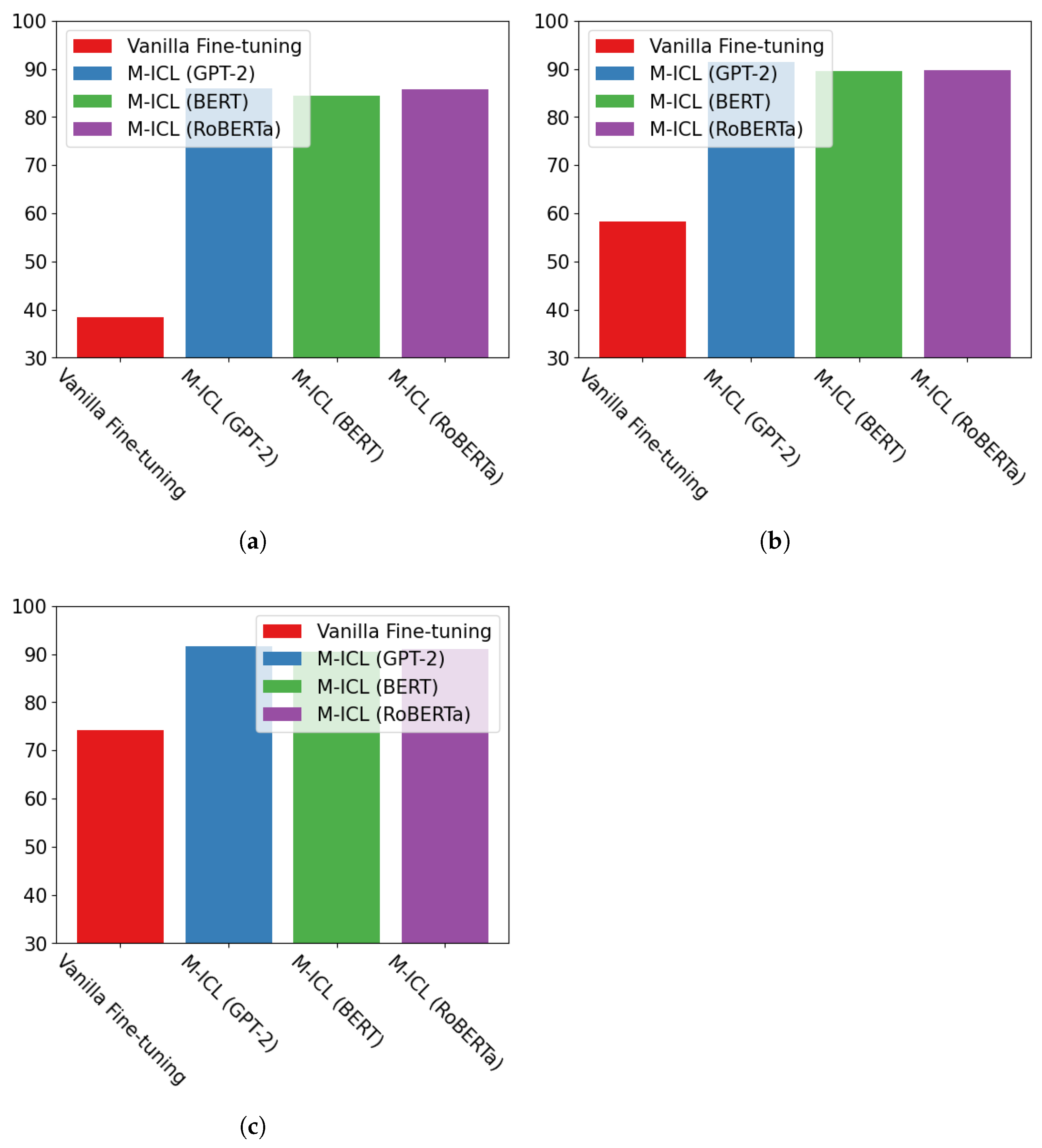
Vanilla Fine-Tuning	38.45	/	58.20	/	74.21	/
M-ICL (GPT-2)	86.00	+47.55	91.50	+33.30	91.68	+17.47
M-ICL (BERT)	84.37	+45.92	89.63	+31.43	90.54	+16.33
M-ICL (RoBERTa)	85.71	+47.26	89.80	+31.60	91.06	+16.85

and Figure 3.

The results in Table 6 and Figure 3 show that, when K = 1, M-ICL (GPT-2) improves Vanilla Fine-Tuning by 47.55%, M-ICL (BERT) improves Vanilla Fine-Tuning by 45.92%, and M-ICL (RoBERTa) improves Vanilla Fine-Tuning by 47.26%. When K = 2, M-ICL (GPT-2) improves Vanilla Fine-Tuning by 33.30%, M-ICL (BERT) improves Vanilla Fine-Tuning by 31.43%, and M-ICL (RoBERTa) improves Vanilla Fine-Tuning by 31.60%. When K = 5, M-ICL (GPT-2) improves Vanilla Fine-Tuning by 17.47%, M-ICL (BERT) improves Vanilla Fine-Tuning by 16.33%, and M-ICL (RoBERTa) improves Vanilla Fine-Tuning by 16.85%.

From the result above, we find that using different large language models improves Vanilla Fine-Tuning significantly. The improvement is the largest when K = 1. It shows that the proposed M-ICL avoids the overfitting issue and benefits from the strong in-context learning ability.

4.5. The Analysis of Using Different K for In-Context Learning

In the previous experiments, we consider three values of K. In this subsection, we consider more possible values of K, including {1,2,5,10,20,50,100,200}. The result is summarized in Figure 4.

The result in Figure 4 shows that the gap between M-ICL and Vanilla Fine-Tuning becomes smaller when K becomes large. The result shows that M-ICL performs better when the training instances are inadequate. Specifically, on the C1S1 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 50. On the C1S2 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 50. On the C1S3 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 5. On the C2S1 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 100. On the C2S2 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 50. On the C3S1 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 100. On the C3S2 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 200. On the C3S3 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 100. On the C3S4 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 20. On the C3S5 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 100. On the C4S1 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 200. On the C4S2 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 50. On the C4S3 dataset, M-ICL outperforms Vanilla Fine-Tuning when K ≤ 2.

5. Discussion and Conclusions

In conclusion, as the demand for intelligent power grid systems continues to grow in the ever-evolving communication technology landscape, the need for efficient data analysis methods within the realm of electrical power edge–end interaction classification becomes increasingly apparent. This paper has explored a new approach by harnessing the extensive knowledge embedded within large language models, such as ChatGPT and GPT-4, to address the challenges associated with annotating and classifying electrical data.

In the practical context of power grid management, collecting and annotating electrical data have traditionally been laborious and resource-intensive tasks. However, our proposed method, Meta In-Context Learning (M-ICL), capitalizes on the in-context learning ability of large language models. By leveraging the general knowledge acquired during pre-training and adapting to new tasks with only a few annotated samples, M-ICL offers a promising solution to streamline the process of understanding complex electrical data.

Through extensive experimentation on real-world electrical datasets, this paper has demonstrated the effectiveness of M-ICL in various classification scenarios. By fine-tuning a pre-trained language model on a diverse range of tasks, we have shown that M-ICL can adapt quickly and achieve superior classification performance. Furthermore, our ablation studies have shed light on the specific contributions of different components within the M-ICL framework.

In summary, this research not only pioneers the application of large language models in the domain of electrical power edge–end interaction classification but also introduces a practical and efficient method, M-ICL, to empower the analysis of electrical data. As technology continues to advance and the demands on power grid systems increase, our work contributes to the development of intelligent, data-driven solutions that can enhance the stability and efficiency of modern power grids. This paper opens up new avenues for future research in the intersection of artificial intelligence and electrical engineering, with the potential to revolutionize the way we manage and optimize power distribution systems.