Abstract
The growing demand for electricity in long-duration space missions has become a pressing concern. The space nuclear closed-Brayton-cycle (CBC) power generation system offers advantages in power output, operational lifespan, and range. However, a significant speed disparity exists between its compressor and alternator. To address this challenge, this paper proposes a double-rotor CBC configuration. A corresponding dynamic model that couples the nuclear reactor and radiator is formulated, and dynamic analysis is conducted to facilitate system control. The study delves into the dynamic start-up process of the double-rotor CBC system and examines how various component parameters impact its power generation performance. The findings indicate that through the introduction of suitable reactivity to regulate reactor power and the incorporation of a PID controller to manage flow distribution between two turbines, the system can achieve start-up within 5200 s. Moreover, the innovative double-rotor structure suggested in this paper enables the separation of compressor and alternator speeds. Consequently, the compressor and alternator can operate within their optimal speed ranges independently, which is a feature that holds potential benefits for the system’s practical implementation. In addition, the steady-state operation of the system showcases the recuperator’s heat transfer power at around 1127.60 kW, a parameter of significant importance. Following steady-state operation, the double-rotor CBC system demonstrated an electrical power output of 175.99 kW and a thermal efficiency of 32.38%.
1. Introduction
The advancement of science and technology has propelled humanity’s foray into the cosmos. Spacecraft stand as indispensable vessels for human space endeavors, space missions, and the exploration of extraterrestrial realms. Prolonged space missions have elevated spacecraft’s energy requirements to unparalleled heights, demanding energy sources characterized by utmost reliability, high energy density, extended service life, and ecological neutrality [1]. As conventional energy sources like chemical or solar power increasingly fall short in meeting these demands, the space nuclear power generation system based on atomic fission emerges as a compelling choice. This system boasts robust environmental resilience, impressive energy and power densities, elevated heat source temperatures, and prolonged longevity. Consequently, advanced space nuclear reactor power becomes the predestined, if not sole, option for missions like deep space exploration [2,3,4]. The core objective of the power conversion system is the transformation of the reactor’s thermal output into electrical energy. The efficiency of this conversion process is intrinsically tied to the operational efficacy of the space nuclear power generation system, exerting influence over its compact structure and overall quality. Dynamic conversion systems, which are revered for their superior efficiency and power density, find widespread application in the space domain. Among them, the closed Brayton cycle (CBC) boasts heightened energy conversion efficiency, enhanced mass-specific power, and a reduced number of moving components [5,6]. Research findings [7,8] highlight that coupling the CBC with a reactor holds pronounced benefits, especially when the space nuclear reactor operates at elevated outlet temperatures and the power demand spans the kilowatt to megawatt range. This integration emerges as an ideal technical configuration for high-power deep space nuclear power detection initiatives [3,4,9].
The closed Brayton cycle (CBC) employs various primary working fluids, including supercritical carbon dioxide (S-CO2), helium, and air, among others. The use of inert gases such as helium as the circulating working fluid boasts favorable thermodynamic attributes and chemical stability, mitigating potential corrosion issues. This approach allows for the controlled elevation of inlet temperatures during operation, thereby yielding heightened efficiency. In comparison to helium’s use in space operations, the utilization of a helium-xenon mixture (He-Xe) presents superior chemical stability, elevated heat transfer capabilities, and improved compressibility. The incorporation of xenon gas into helium effectively reduces the aerodynamic load imposed on turbine machinery and minimizes turbomachinery requirements, consequently reducing system mass. This helium-xenon mixture stands as the prevailing choice for working fluids within space-based Brayton cycle power generation systems [10]. The He-Xe Brayton cycle has emerged as a pivotal area of study for future high-power space energy applications due to its exceptional energy efficiency, robust output performance, and favorable mass ratio power [8].
El-Genk et al. [11] pointed out that when helium (He) forms binary mixtures with inert gases like krypton (Kr) and xenon (Xe), the resultant heat transfer coefficient marginally surpasses that of pure helium. Specifically, this phenomenon occurs when the combined molar mass is less than 22 g/mol for krypton and 40 g/mol for xenon. Moreover, these mixtures yield a notable reduction in the size of turbomachinery. In a separate study, Malik et al. [12,13,14] conducted an evaluation of He-Xe as a working fluid in the axial compressor of terrestrial nuclear power plants. With a molecular weight of 15 g/mol, the He-Xe mixture demonstrated its potential. Interestingly, incorporating xenon into helium up to a molecular weight of less than 40 g/mol not only increased the coefficient of heat transfer but also significantly elevated the compressor’s loading. Examining the effects of different working fluids He-Xe, helium, argon, and air on radial turbine performance, Yuan et al. [15,16] made noteworthy observations. As the working conditions deviated from the design point, the efficiency disparity between helium and the other fluids grew wider, mirroring the increase in the magnitude of the working condition deviation. Exploring the influence of non-ideal gas characteristics on the efficiency of a 3 MWth lithium-cold fast reactor power system, Xu et al. [17] developed a robust thermodynamic model. This model, founded on the distinctive properties of non-ideal gases, sheds light on the system’s efficiency dynamics. Miao et al. [18,19] used an innovative approach to improve the thermal efficiency of CBC systems by utilizing a new working fluid component, a mixture of nitrous oxide and helium (N2O-He). The concept of an integrated gas-cooled space nuclear reactor (IGCR-200), introduced by Li et al. [20], derives its foundation from the TRISO particle fuel design. This groundbreaking concept seamlessly integrates with a potent He/Xe CBC generator, which is capable of delivering an impressive 200 kW of output power.
El-Genk et al. [2] developed an intricate dynamic simulation model for a space reactor power system encompassing multiple CBCs for energy conversion. They validated the model by assessing its start-up transients. In their subsequent research [21], they expanded the program to encompass transient operations and start-up scenarios for the reactor system. This entailed the incorporation of the CBC system module and PID controller. This enhanced model established a dynamic simulation framework for a power system featuring a gas-cooled reactor coupled with three autonomous CBCs. This same framework was also employed to simulate the behavior of the subcritical reactor (S^4). Li et al. [22], in a parallel effort, formulated a cycle model and deduced three independent variables with corresponding constraint conditions. This served as the foundation for conceptualizing control strategies, namely, inventory control, bleed control, and rotating speed control, grounded in the theoretical model. Moving forward, Ma et al. [23,24,25] constructed a comprehensive thermal-hydraulic model for the space nuclear power system with multi Brayton loops (SNPS-MBL). Their work includes the development of two different start-up methods, simultaneous start-up and sequential start-up, for SNPS with double Brayton loops (SNPS-DBL). A performance comparison of these two schemes was conducted. Additionally, they devised four diverse cooling configurations for bearings and generators within the space closed Brayton cycle (SBC). The analysis encompassed the impact of bleeding gas on critical component performance and circulation dynamics. In a different vein, Romano et al. [26] proposed a comprehensive thermodynamic model for the recuperated closed Brayton cycle (CBC). Their approach included a thermal model aimed at predicting the comprehensive attributes of the cold side of the system (including heat pipes and radiators) under varied CBC conditions. Lucia [27,28,29,30] et al. introduced an innovative approach rooted in irreversible thermodynamics to enhance the Human Development Index (HDI). This novel metric, known as the Thermodynamic Human Development Index (THDI), is established through a thermodynamic optimization methodology. The THDI is intricately linked to socio-economic considerations as well as ecological assessments, thereby offering a comprehensive framework for evaluating the thermoeconomics of the closed-Brayton-cycle power generation system.
Presently, within the context of space closed-Brayton-cycle (CBC) systems, a coherent turbine-alternator-compressor (TAC) configuration has been adopted. This integration of the compressor, alternator, and hydraulic turbine onto a single shaft is designed to enhance system cohesion and efficiency. It is worth noting that the TAC structure necessitates synchronized operation of the turbine and compressor at identical speeds. Notably, the compressor’s efficiency is profoundly influenced by its operating speed, within a specified range, and higher speeds correspond to heightened design efficiency. Moreover, the compressor’s efficiency bears a significant impact on the overall efficiency of the CBC system. A diminished compressor efficiency can dramatically compromise system performance. However, challenges arise due to the relatively low operating speeds of high-power alternators. Integrating these elements constrains the shaft’s speed to align with the alternator’s typical operational pace. For instance, high-power alternators may peak at around 30,000 r/min. Yet, the optimal speed range for compressor efficiency is notably higher, typically falling between 80,000 to 100,000 r/min. This scenario results in a quandary that adhering to the alternator’s speed limit curtails the compressor’s potential efficiency, consequently dampening the system’s overall performance. To address the incongruity between the most effective operating speeds of the compressor and the alternator, this paper introduces a solution: the double-rotor CBC configuration. This novel approach, which is based on the traditional gas turbine and turboshaft engine structure consisting of a gas generator and a power turbine, employs an additional turbine to disentangle the speeds of the compressor and the alternator. Consequently, both components can operate independently within their respective optimal speed ranges, mitigating the efficiency limitations posed by the TAC structure and enhancing the overall system performance.
Considering that the CBC system in the context of space applications predominantly treats the reactor as a fundamental heat source, the intricate heat transfer coupling calculations among CBC components are somewhat subdued. In order to propel deeper exploration into the potential of the CBC power generation system, a dynamic model has been developed for the double-rotor CBC configuration. This model delves into the dynamic interplay within the system, conducting a thorough analysis and culminating in the establishment of a comprehensive control simulation framework. This study employs a configuration wherein liquid lithium serves to cool the reactor core and facilitate heat exchange with He-Xe. The intricate process of heat exchange within the CBC is meticulously examined, leading to the identification and implementation of an enhanced control scheme. This deliberate choice ensures the seamless initiation of the dynamic system, ultimately realizing the desired power output. Guided by the selected control strategy, this study delves deep into the interplay among various system components and their collective impact on overall performance. The outcome is an optimization process that yields a dynamic system model characterized by swifter start-up and heightened power generation efficiency.
2. Double-Rotor CBC Configuration
As illustrated in Figure 1, an innovative double-rotor CBC configuration has been proposed, which introduces an additional power turbine to enable the independent operation of the compressor and alternator speeds. This configuration establishes a connection between the turbine and compressor, forming a turbine and compressor (T&C) module. This T&C module revolves at high speeds, ensuring optimal efficiency for both the compressor and the turbine. The power turbine serves the purpose of driving the alternator to generate electricity. This component maintains a lower speed range, guaranteeing the efficient operation of the alternator. Notably, the turbine and compressor are joined on the same shaft, facilitating their synchronized rotation. This cohesive operation ensures that the alternator operates efficiently while generating power. During the start-up phase, a clutch mechanism connects the T&C module, alternator, and power turbine, causing them to rotate at uniform speeds driven by the alternator. Once the system is successfully initiated, a pivotal shift occurs; when the turbine’s output power surpasses the power consumed by the compressor, the T&C module becomes disconnected from both the alternator and the power turbine. As a result, the T&C module can then operate within an elevated speed range, maximizing compressor efficiency. Simultaneously, the alternator and power turbine operate within a lower speed range to ensure the consistent operation of the high-power alternator.
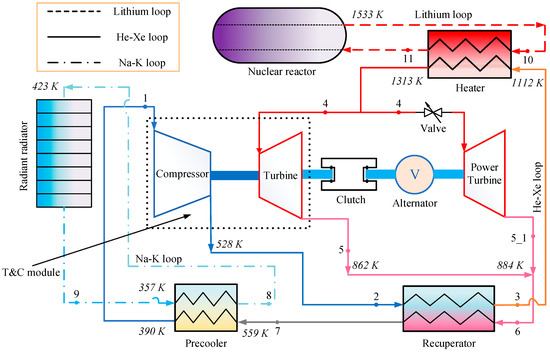
Figure 1.
Configuration sketch of double-rotor CBC.
In this paper, the double-rotor CBC system consists of three loops: high-temperature liquid lithium loop, He-Xe loop and low-temperature Na-K alloy loop. Liquid metal lithium is a vital heat transfer medium for reactors because of its good heat transfer capacity, low density and high specific heat capacity. The lithium absorbs heat from the reactor and cools the core, then enters the heater to transfer heat to the He-Xe, and finally enters the reactor to complete the cycle; part of the high-temperature He-Xe at the heater outlet enters the turbine to drive the compressor to do work, and the other part enters the power turbine to drive the alternator to rotate and generate electricity, and then enters the precooler to be cooled by the Na-K to the initial temperature of the cycle. The helium-xenon working fluid at the heater outlet is divided into two turbines, that is, it works in parallel. Compared with the series configuration (all helium-xenon working fluid first enters the turbine of the T&C module to expand and do work and then enters the power turbine), the thermal efficiency of the parallel configuration is slightly lower than that of the series configuration, but its regulation is simpler and easier to calculate. Therefore, the parallel configuration is adopted in this paper; the cooling system mainly adopts the form of the liquid metal cooling loop, usually using Na-K alloy as the circulating working fluid [31]. The Na-K absorbs heat in the precooler and then enters the radiant radiator to stabilize the system temperature.
Within the scope of this study, the double-rotor CBC system encompasses three distinct loops: the high-temperature liquid lithium loop, the He-Xe loop, and the low-temperature Na-K alloy loop. The inclusion of liquid metal lithium as a pivotal heat transfer medium underscores its remarkable heat transfer capacity, low density, and impressive specific heat capacity. This versatile medium absorbs heat from the reactor, effectively cooling the core. Subsequently, it traverses to the heater, facilitating heat transfer to the He-Xe loop, before culminating in its journey back to the reactor to complete the cycle. Simultaneously, a segment of the high-temperature He-Xe mixture, emanating from the heater outlet, embarks on two distinct paths. One stream enters the turbine, energizing the compressor to perform mechanical work. The other stream takes a divergent course, propelling the power turbine to rotate and generate electricity. Following this, it moves through the precooler, undergoing cooling by the Na-K loop, and is subsequently restored to the cycle’s initial temperature. Of note, the helium-xenon working fluid exiting the heater finds itself divided between two turbines, thereby functioning in parallel, whereas the turbine of the gas generator and the power turbine are connected in series in traditional gas turbine and turboshaft engines. This parallel configuration, though slightly reducing thermal efficiency compared to the series arrangement, is preferred due to its simpler regulation and calculation process, as well as better system start-up characteristics, mainly due to a higher inlet temperature of the power turbine. This choice reflects the pragmatism pursued within this study. Within the realm of cooling, the system predominantly adopts a liquid metal cooling loop, often leveraging the Na-K1 alloy as the circulating working fluid. Specifically, the Na-K alloy operates as a heat absorber within the precooler, subsequently transitioning to the radiant radiator, thereby contributing to the stabilization of system temperature. The melting and boiling points of the liquid metals employed in the loops are outlined in Table 1.

Table 1.
Physical properties of some liquid metals (at 1 bar) [32,33,34].
3. Mathematic Modeling
3.1. Reactor Calculation Model
The calculation of the point kinetics equation centers on simplifying the reactor’s transient behavior and assessing its evolution across time [35]. For the purpose of deducing dynamic system characteristics, this study deliberately sidesteps the spatial variations within the reactor. Formulas (1) to (3) provide the means to calculate the point kinetics equation. The reactor model, in this context, operates on the premise that the distribution of reactor power and the configuration of neutron flux remain constant and are linked solely to the magnitude of core power. This model employs a six-group delayed neutron population while integrating a negative feedback term to account for reactivity shifts stemming from fuel expansion or other consequential factors.
where PNu represents the core power of the nuclear reactor, l denotes the average lifetime of neutrons, ρ stands for the reactivity of the reactor, β represents the effective fraction of delayed neutrons precursors, λ denotes the decay constant of the delayed neutron group, and C represents the concentration of delayed neutron precursors. The subscript ‘i’ corresponds to the classification of the six groups of delayed neutron groups. The implicit Runge–Kutta method has been employed to discretize the point kinetics equations.
For ease of computation, the convective heat transfer process over time is streamlined through the incorporation of a time constant. Furthermore, the interaction between core fuel and temperature evolution is evaluated through the application of Formulas (4) to (6).
where Cp represents the average heat capacity and Pth represents the thermal power from the core to the liquid lithium.
3.2. Turbine and Compressor Dynamic Model
The characteristic curve of the compressor is established using the following equation [36,37]:
where nC,cor represents the relative rotational speed, WC,cor corresponds to the relative mass flow rate, πC denotes the pressure ratio, and ηC signifies the isentropic efficiency.
The characteristic curve of the turbine bears resemblance to that of the compressor and is determined using the following equation [38]:
where nT,cor represents the relative rotational speed, WT,cor corresponds to the relative mass flow rate, πT denotes the pressure ratio, and ηT signifies the isentropic efficiency.
The coordination of mass flow rate adjustment guarantees the power equilibrium of the T&C rotor at its designated speed. Consequently, the surplus power of the T&C module is ascertained, i.e., this denotes the disparity between the power generated by the turbine (PT) and the power absorbed by the compressor (PC).
The T&C model amalgamates the surplus power with the moment of inertia of the rotating shaft to compute the rate of change in shaft speed. This yields the correlation between rotational speed and time, which is depicted in the ensuing formula [39]:
where N represents the rotational speed in both the turbine and compressor, I denotes the rotor’s moment of inertia, and P signifies the component load.
3.3. Heat-Exchanger Dynamic Model
The high-temperature and low-temperature channels, along with the heat exchange wall of the heat exchanger, are individually subjected to modeling and calculations. Both sides of the heat exchange channel operate in the liquid phase, maintaining consistent inlet and outlet mass flow rates, thus adhering to the principles of the continuity equation. The energy equations governing distinct channels employ a temperature-based approach, and the equation models, along with their simplified expressions, are presented as follows.
where h refers to the convective heat transfer coefficient, and A represents the heat transfer area.
The energy equations pertaining to the aforementioned three flow channels can be solved to derive the dynamic variations in the inlet and outlet temperatures of these distinct channels over time. Subsequently, the integration of the CBC with the nuclear reactor and radiant radiator forms the foundation for constructing a dynamic simulation and computational system model. This model serves to replicate the start-up progression of the double-rotor CBC system.
4. Results and Analysis
4.1. Model Validation of Heat Exchanger
The dynamic heat transfer model constitutes a pivotal component of the circulation system. To ensure the model’s precision, the heat exchanger calculation process outlined in a prior publication underwent meticulous review [40]. Subsequently, the outcomes of this paper’s calculations were juxtaposed with the data presented in the referenced literature, thereby confirming the accuracy of the established model.
The obtained outcomes are illustrated in Figure 2. It is evident that the calculated values in this paper closely align with the reference values obtained from the literature’s recuperator data. The discrepancy between the temperature at the low-temperature channel outlet and the literature’s maximum reference value is approximately 33.07 K. Meanwhile, the highest temperature difference at the high-temperature channel outlet reaches 26.13 K. Admittedly, a notable relative error exists, and the maximal relative error within the calculated results stands at 4.77%. Nevertheless, this discrepancy remains within an acceptable margin of error, affirming the precision of the recuperator’s calculation model employed in this study.
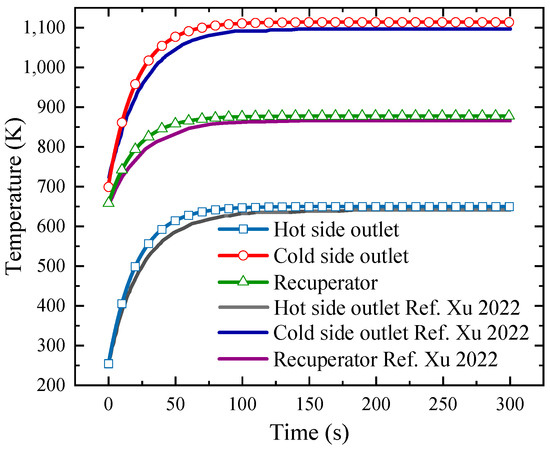
Figure 2.
Verification of the recuperator [40].
4.2. Dynamic System Start-Up Scheme
The alterations in introduced reactivity and reactor power are graphically presented in Figure 3. During the start-up sequence, the reactor is initiated initially, followed by the activation of the CBC once a specific temperature threshold is attained. Subsequently, the system’s operation is propelled by the rotational shaft. The reactor is launched to initiate heat generation, with the lithium cycle circuit set into motion upon reaching a reactor core temperature of 400 K. Throughout the reactor’s temperature start-up phase, reactivity modulation is implemented to achieve predetermined reactor power parameters, effectively concluding the power generation scheme for the circulating system. Notably, the introduced reactivity in this project undergoes linear modification. Given the intricate nature of the dynamic system’s adjustment process, the temporary omission of negative feedback regulation by nuclear fuel on reactor reactivity as temperature rises is acknowledged, and instead, a gradual introduction of reactivity over an extended timeframe is implemented.
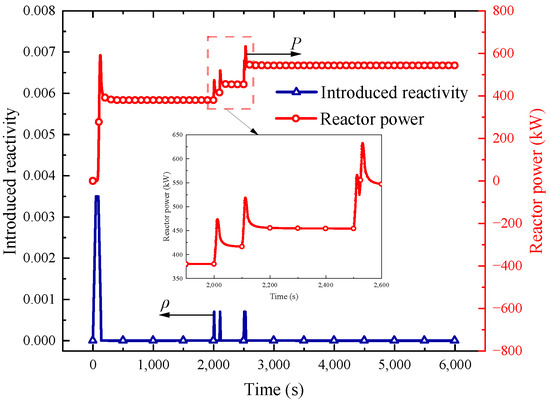
Figure 3.
Variation of reactor power.
When the liquid lithium temperature reaches 450 K, the initiation of the He-Xe cycle ensues. Given the initially low temperature of the reactor core, elevating the liquid lithium and He-Xe to higher temperatures becomes challenging, thus hindering the effective activation of the alternator’s functionality. Consequently, the pathway of He-Xe to the rotating components is sealed off. Instead, the He-Xe is propelled by a bypass fluid pump for heat transfer. As the He-Xe’s temperature gradually ascends, its heat is dissipated through the Na-K cycle, which commences at a He-Xe temperature of 400 K, thereby facilitating space heat release via the radiant radiator. Continuing with the temperature increase of He-Xe, the alternator’s ignition is deferred until the temperature achieves 800 K. Following the maximization of the alternator’s speed, the He-Xe inlet valve is unsealed. Here, the alternator propels both turbines and the compressor in synchronized rotation. In this configuration, He-Xe is pressurized in the compressor before entering the turbine for expansion and work. Notably, the inlet valve of the power turbine remains sealed. Throughout the heating process, the fluctuation of turbine and compressor power is vigilantly monitored. As the turbine inlet temperature surges, turbine power surpasses that of the compressor. At this juncture, the linkage between the T&C module and the alternator is disconnected.
The divergence between the target flow rate and the actual flow rate of the turbine is depicted in Figure 4. In this study, a PID controller is employed to oversee the flow balance between both turbines, thereby achieving system stability. Under conditions where turbine output power aligns with compressor energy consumption, surplus flow is channeled into the power turbine to stimulate alternator-driven electricity generation. During flow regulation, the turbine’s expansion ratio is determined by the pressure differential across the system’s front and back.
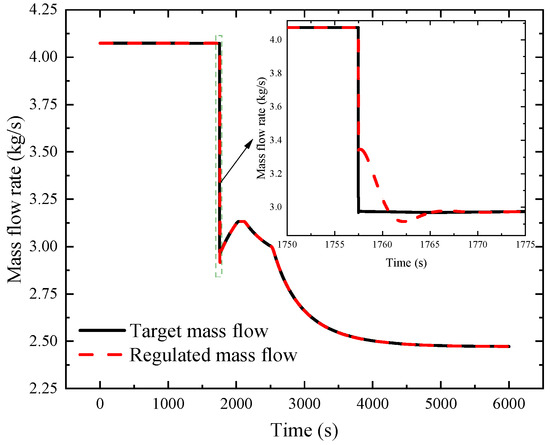
Figure 4.
Flow regulation of the turbine.
The calculation of the mass flow rate, which satisfies the compressor power requirement, relies on the compressor’s dynamic power and the enthalpy variation before and after He-Xe’s expansion within the turbine. This mass flow rate difference is then employed to control the turbine’s mass flow rate towards the target value, taking into account the discrepancy between the previous He-Xe flow rate in the turbine and the current target value. Concurrently, as the turbine inlet temperature increases, timely adjustments are made to the flow distribution between the two turbines. As depicted in Figure 4, following the separation of the clutch, the turbine’s target mass flow rate undergoes rapid fluctuations, eventually stabilizing around the target value after minor oscillations. This meticulous regulation process ensures sensitivity and maintains equilibrium within the T&C module. Subsequently, as the turbine inlet temperature fluctuates, the turbine’s flow rate initially rises, gradually peaks, and subsequently declines, ultimately converging towards a constant value. This pattern signifies the system’s transition into a stable operational state, effectively indicating the successful completion of the start-up process.
4.3. Results of Dynamic System Simulation
The variation of the reactor core temperature over time is illustrated in Figure 5. Evidently, the core temperature experiences a gradual ascent in tandem with the increase in reactor power. Upon reaching 400 K, the initiation of the liquid lithium circulation loop facilitates the dissipation of some of the core’s heat by the liquid lithium. Consequently, the pace of core temperature elevation decelerates. The regulation of reactor power is achieved through the modulation of core reactivity, ultimately leading to system stabilization as the core temperature persists in its ascent, reaching approximately 2000 K. To avert abrupt fluctuations in core temperature, a substantial liquid lithium mass flow rate is configured. In a stable state, the core power attains 543.86 kW with the reactor’s liquid lithium temperature witnessing a 16.73 K temperature increase.
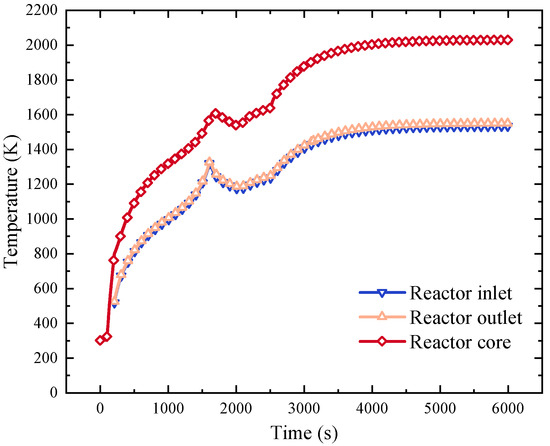
Figure 5.
Variation of the reactor core temperature.
The temperature change of He-Xe within each component during the start-up process is shown in Figure 6. Through the heater, liquid lithium imparts heat to He-Xe, and the initiation of the CBC cycle system commences once the He-Xe attains a specific temperature threshold. As the temperature of He-Xe continues to ascend, the turbine’s power surpasses that of the compressor. Consequently, the T&C module disengages from the alternator, causing the T&C module’s speed to ascend to the target condition. After a duration of 5200 s, equilibrium is reached between the alternator’s output power, the heat dissipation power of the radiating cooling plate, and the thermal power emitted by the reactor core.
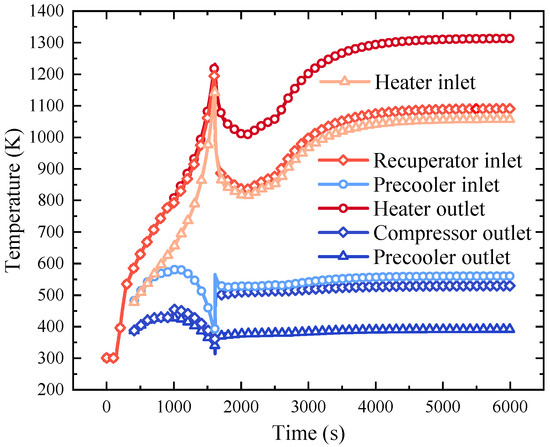
Figure 6.
Variation of the He-Xe temperature.
The temporal variation of Na-K temperature is illustrated in Figure 7. When the temperature within the precooler reaches 460 K, the Na-K cycle initiates, serving to cool down the He-Xe. Once the He-Xe attains a cooler temperature, the temperature discrepancy between both sides of the recuperator facilitates its operation. The stored state of Na-K is maintained at 300 K. Given the substantial temperature contrast between Na-K and He-Xe, upon cycle commencement, heat is absorbed from He-Xe, resulting in a gradual temperature elevation within Na-K. This temperature change is then systematically regulated to achieve a stable equilibrium state.
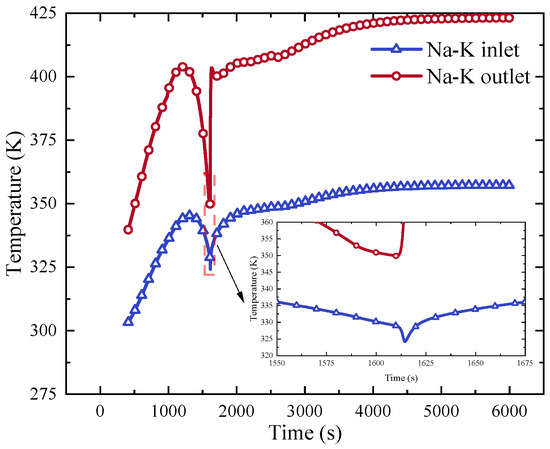
Figure 7.
Variation of the Na-K temperature.
Analyzing the power variations of each heat exchange component during the cycle transition of the working fluid offers valuable insights into the dynamic system’s heat exchange performance. By leveraging the inlet and outlet parameters of mass within the heat exchanger component, the CBC power change diagram, as depicted in Figure 8a,b, is obtained. Upon initiating different working fluid cycles, the energy transfer process occurring on both sides of the heat exchanger sheds light on the dynamic characteristics of the circulation system. It is evident from the graph that the system’s power variation is notably influenced by the regulation approach, ultimately stabilizing in an operational equilibrium. The heater contributes a power input of 543.56 kW to the CBC system, which operates alongside a reactor power of 543.56 kW, and the radiant radiator releases 365.05 kW of power. The majority of the heat absorbed by the Brayton cycle is effectively dissipated into space through the radiant radiator. As is evident from Figure 8c,d, after the 1800 s mark, a power equilibrium is reached between the turbine and compressor. Electrical energy generation primarily relies on the power turbine, with the system yielding 175.99 kW of electrical energy after accounting for alternator losses. Most of the heat generated by the reactor is efficiently expelled into space via the radiant radiator. Notably, the recuperator exhibits a maximum heat transfer power of nearly 1750 kW, and under stable conditions, its power output stands at 1127.60 kW. This underscores the pivotal role the recuperator plays in maintaining the dynamic system’s functionality. Having gleaned the evolving trends within the dynamic system, subsequent analysis focuses on parameter shifts at the control node.
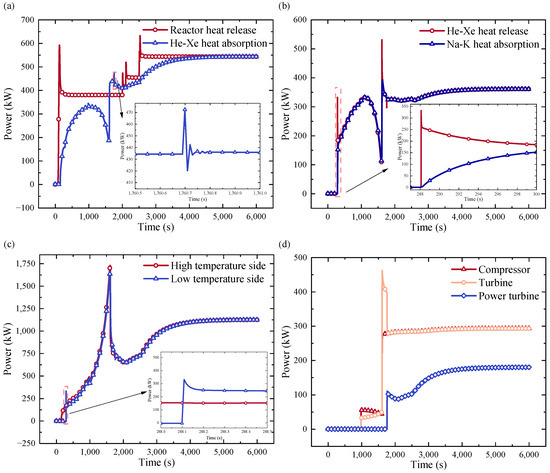
Figure 8.
Variation of the power of each component of the CBC system: (a) nuclear reactor; (b) Na-K; (c) recuperator; (d) turbomachine.
4.4. Impact of Regulation Schemes on the System
In this study, well-devised schemes are implemented for both the cycle medium and motor start-up procedures. These measures contribute to the achievement of a more stable and seamless transition into the operational state of the dynamic cycle system. Moreover, the alterations in cycle medium parameters vividly reflect the distinct control strategies employed at various system nodes. Initiating the liquid lithium cycle occurs when the reactor core temperature reaches 400 K, corresponding to a time of t = 100.80 s. Subsequently, the He-Xe cycle is activated at t = 144.80 s. The inherent thermal energy generated by the system is efficiently converted into electrical energy through the operation of the CBC system. This progression is well depicted in Figure 9, which outlines the temporal changes in the outlet temperature of the heater. Following the separation of the clutch, the power turbine propels the alternator, effectively transforming a portion of the thermal energy into electrical output. Initially, the temperatures of both the liquid lithium and He-Xe experience a rapid decline, followed by a subsequent increase. This temperature behavior is attributed to the introduction of reactivity, which prompts the core to release heat. Consequently, the temperatures of both working fluids commence an ascent, leading to a stabilization of the system after approximately 5200 s.
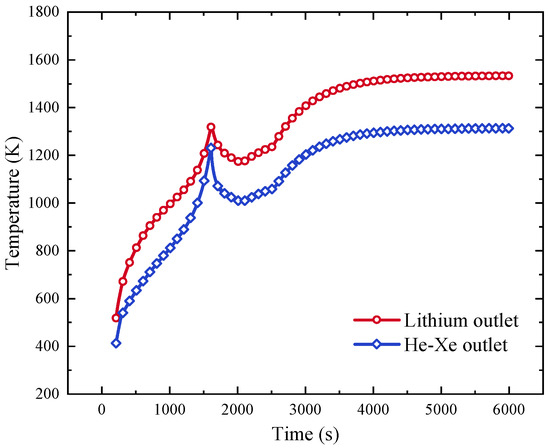
Figure 9.
Variation of heater outlet temperature.
The initiation of the Na-K cycle is synchronized with the attainment of a He-Xe inlet temperature of 450 K at the precooler, marked at t = 288.10 s. The implications of the Na-K loop on the system are illustrated in Figure 10. An examination of the graph reveals that upon the commencement of the Na-K cycle, an intricate heat exchange transpires between Na-K and He-Xe within the precooler. This interplay induces a swift reduction in the outlet temperature of He-Xe at the precooler, causing it to rapidly drop to around 300 K within a concise interval. Subsequent to this phase, the heat exchange involving He-Xe undergoes amplification within the heater and the recuperator. Consequently, the inlet temperature of He-Xe at the precooler begins a gradual ascent, and the Na-K temperature also experiences a gradual elevation. Figure 10b highlights the distinctive impact of the precooler’s operation on the temperature distribution within the various components. Notably, the temperature within the low-temperature flow channel of the recuperator significantly diverges from the inlet temperature of the high-temperature flow channel. This temperature contrast optimizes the heat transfer efficiency of the recuperator. However, this effect remains relatively inconsequential concerning the temperature of the lithium loop and the nuclear reactor’s core. As the Na-K temperature ascends into a higher range, the radiative cooling in the radiant radiator surpasses the heat absorbed during the precooler phase. This causes both the He-Xe and Na-K temperatures to decrease. Subsequently, the temperature of the He-Xe at the heater outlet escalates in tandem with the nuclear reactor core temperature and the liquid lithium temperature. Upon the He-Xe heater temperature surpassing 800 K, the alternator becomes primed for activation and poised to initiate rotor system operation. At t = 982.60 s, meticulous control prompts the alternator to attain its maximum speed, facilitating the passage of He-Xe into the turbine for productive work output.
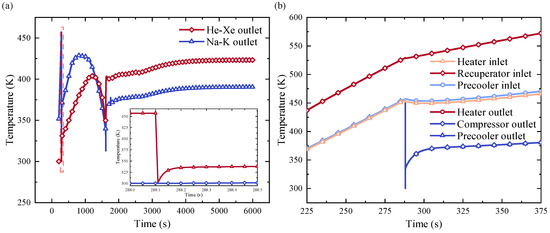
Figure 10.
Effect of Na-K loop on the system: (a) variation of the precooler outlet; (b) variation of He-Xe temperature.
The impact of initiating the alternator on the system is meticulously depicted in Figure 11. Upon closer inspection, it becomes apparent that once the alternator is set in motion, discernible temperature changes occur in the He-Xe subsequent to its passage through the turbine. Owing to the initially low rotor speed, the transformation of He-Xe temperature following its traversal through the turbine and compressor is comparatively restrained. Nevertheless, the temperature at the turbine outlet remains on an ascending trajectory. The pronounced radiative heat dissipation attributed to Na-K engenders a notable reduction in the outlet temperature of He-Xe at the cooler, whereas the diminished temperature emanating from the compressor outlet contributes to a subsequent decline in the high-temperature flow channel’s He-Xe outlet temperature. In the aftermath of the alternator’s commencement, the thermal energy absorbed by He-Xe in the heater experiences an exponential surge, mirroring the rapid escalation of energy liberated in the cooler. Over the course of a predefined timeframe, the heat absorption by He-Xe begins to lag behind the heat release within the precooler. This resultant discrepancy precipitates a gradual transition in the He-Xe and Na-K temperatures within the precooler, shifting from an ascending trend to a descending one.
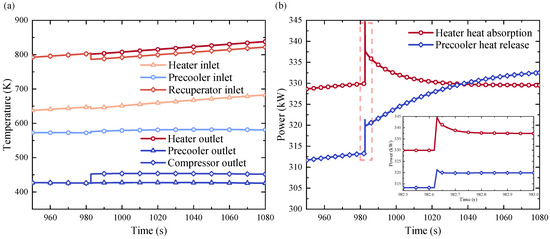
Figure 11.
Effect of alternator start-up on the system: (a) variation of the He-Xe temperature; (b) variation of thermal power.
The transformations in speed, efficiency, and expansion ratios are vividly portrayed in Figure 12. Evidently, the temperature at the compressor outlet experiences a drop, juxtaposed with the increment in the inlet temperature to the turbine. This occurrence precipitates a gradual reduction in the power discrepancy between the primary turbine and the compressor, ultimately culminating in a scenario where the turbine’s output power surpasses the compressor’s power consumption. At t = 1611 s, the T&C module and alternator become disengaged, enabling the He-Xe to generate residual work within the T&C module, thereby fostering an escalation in the T&C rotor speed. Once the maximum speed is attained, the rotor’s velocity is confined to a controlled increment, thus ensuring the T&C module functions in line with the target operating conditions. Notably, subsequent to the speed augmentation, the efficiencies and expansion ratios of both the compressor and turbine witness an accelerated ascent.
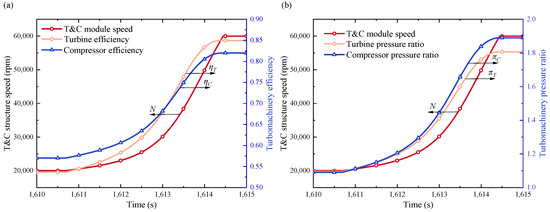
Figure 12.
Dynamic characteristics of the T&C module: (a) T&C module speed and efficiency; (b) T&C module speed and pressure ratio.
The variations in He-Xe temperature and turbomachine power are vividly presented in Figure 13. The augmentation of operational speed triggers a marked reduction in the turbine outlet temperature, even as the compressor outlet temperature exhibits an increase, consequently precipitating a decline in the temperature of the He-Xe preceding its entry into the heater. In concert, the liquid lithium and core temperature follow a pattern of decrease followed by gradual ascent. This temperature reduction within the working fluid stems from the lower work consumption by the compressor prior to the speed increment, coupled with the alternator’s exertion of work on the system to elevate the overall temperature of the He-Xe. With the He-Xe temperature’s elevation, the turbine’s work output surpasses the compressor’s work consumption, prompting the alternator to curtail energy input. The elevation of the T&C module’s speed engenders a substantial augmentation in the turbine’s work capacity. Consequently, the power turbine propels the alternator into generating power, thus driving an accelerated surge in the He-Xe’s work amount. This vigorous alteration in the work amount leads to a conspicuous temperature decrease, thereby culminating in a swift decline in the temperature differential between the liquid lithium and the core within a brief interval.
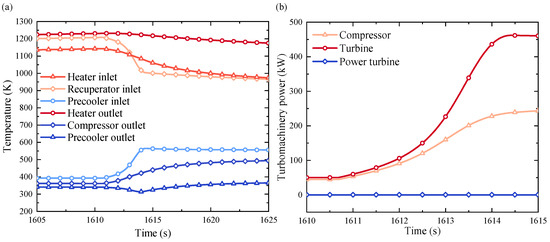
Figure 13.
Effect of T&C module speed on the system: (a) variation of the He-Xe temperature; (b) turbomachinery power.
Upon attaining a substantial power discrepancy, the inflow of He-Xe gas into the turbine undergoes modification, with the PID controller orchestrating adjustments to align the turbine’s power with that of the compressor. The He-Xe gas then enters the power turbine, where both turbines undergo expansion at identical pressures, ensuring an equivalent expansion ratio. Nevertheless, owing to variances in turbine efficiency, the temperature of the He-Xe gas upon entering the high-temperature flow channel of the recuperator displays fluctuations. This, in turn, introduces a degree of lag in the flow adjustment process, thereby contributing to the temperature shifts observed. Given that the temperature fluctuation of the He-Xe gas primarily stems from the operations of the turbines and compressors, the temperature alteration within the outlet of the rotating machinery between t = 1760.65 s and 1760.85 s is depicted in Figure 14. The graphical representation illustrates that the process of regulating the mass flow rate within both turbines engenders flow oscillations, thereby inducing temperature vacillations in the He-Xe gas at the entrance of the recuperator. Consequently, the temperature fluctuations extend to the precooler, giving rise to abrupt alterations in the temperature of individual system components. These fluctuations gradually converge as the system components collectively stabilize, resulting in an overall temperature transition in the wake of the fluctuation.
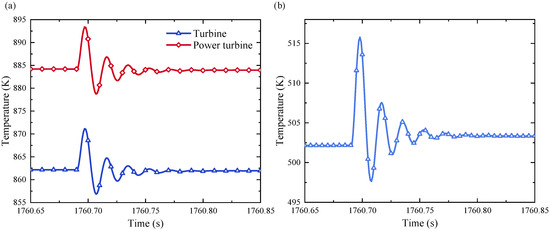
Figure 14.
Variation of the turbomachinery outlet temperature: (a) turbine; (b) compressor.
The impact of controlled flow on the system’s power dynamics is elucidated in Figure 15. Once the power attains the intended level, the initiation of flow regulation engenders power oscillations, causing transient fluctuations within the system that subsequently coalesce for a brief interval. Following this initial convergence, the flow regulation introduces a more gradual oscillatory pattern. The power output of the T&C module eventually achieves equilibrium through this incremental stabilization process. With the system components now in operational mode post-start-up, the reactor temperature undergoes a gradual transition, eventually settling into an initial state of stability. However, considering that the initial power generation does not align with the prescribed targets, adjustments to reactor reactivity are made to sustain ongoing core heating. As a result, the He-Xe gas temperature across various components of the double-rotor CBC system continues to ascend, ultimately culminating in a gradual yet consistent stabilization phase that fulfills the designated power generation requisites.
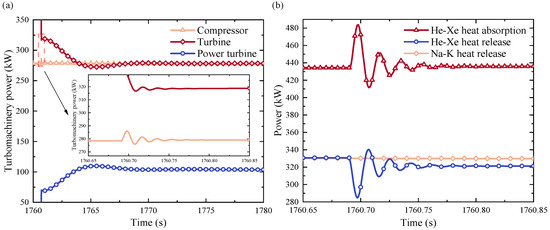
Figure 15.
Effect of the regulated flow on system power: (a) turbomachinery power; (b) thermal power.
This phenomenon is depicted in Figure 16a. As the temperature of the He-Xe gas entering the turbine’s front inlet rises incrementally, the turbine’s output power experiences a gradual surge. Once the turbine’s power surpasses that of the compressor, the coupling between the T&C module and the alternator is severed, subsequently boosting the T&C module’s rotational speed. Following this phase of stable operation, fine-tuned adjustments to the remaining flow direct it into the power turbine for electricity generation. Consequently, the system’s power generation experiences a rapid upsurge post the time point of 1760.69 s. Subsequently, in response to the escalating reactor power, the electrical output continues to climb, gradually achieving a state of equilibrium.
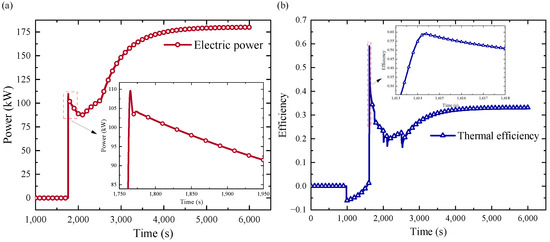
Figure 16.
Performance parameters of the system: (a) electric power; (b) thermal efficiency.
The temporal evolution of the system’s thermal efficiency is portrayed in Figure 16b. Upon introducing He-Xe into the turbine, the thermal efficiency of the system initially exhibits a negative trend. This phenomenon emerges because, during instances of low turbine inlet temperatures, the compressor’s power consumption surpasses the turbine’s power output. The initiation of the system relies on an external power source, with the utilization of power devices like nickel-metal hydride batteries at present. The alternator effectively functions as an engine driving the rotor system in such cases. Subsequently, a substantial peak in thermal efficiency is observed. This surge is attributed to the rapid escalation of the system’s operational capacity due to the elevated speed of the T&C module. The system experiences an excess power generation phase, primarily originating from substantial heat absorption via the heater. This excessive power generation, however, promptly wanes as the temperature at the turbine’s inlet initiates a decline. Furthermore, a subsequent peak in thermal efficiency follows this initial surge. This peak is attributable to the enhanced matching between the power turbine and the alternator. However, because the alternator’s efficiency is inferior to that of the turbine, the overall system efficiency diminishes. In the subsequent phases, as the temperature at the turbine’s inlet gradually ascends, the system’s thermal efficiency progressively stabilizes. In terms of specific values, the double-rotor CBC system attains an electrical power output of 175.99 kW with a thermal efficiency of 32.38%.
5. Conclusions
To propel further explorations into the application of space closed-Brayton-cycle power generation systems, this paper introduced a novel configuration, a double-rotor closed Brayton power generation system employing helium-xenon as the working fluid. The investigation delved into the dynamic coupling of each component within the double-rotor CBC system, culminating in the establishment of a comprehensive control simulation model. The principal findings are encapsulated as follows:
- Reactor power can be judiciously tailored to predetermined parameters through the incorporation of reactivity. The efficacy of the PID controller in regulating the flow between both turbines is noteworthy, with the regulation process exhibiting heightened sensitivity. Post-initiating the reactor for approximately 5200 s, the system attains a state of stable operation, thereby successfully completing the start-up phase.
- The double-rotor configuration adeptly achieves the disentanglement of compressor and alternator speeds. Notably, the separation between the T&C module and the alternator transpires at t = 1611 s. Following this, the T&C module’s speed escalates to 60 krpm. The augmentation of efficiency and pressure ratios in both the turbine and compressor manifests as an elevation in system efficiency.
- At t = 1800 s, a power equilibrium emerges between the turbine and compressor. Electrical energy predominantly emanates from the power turbine. After accounting for alternator losses, the system’s net power generation clocks in at 175.99 kW.
- A substantial portion of the heat originating from the reactor is released into space by means of the radiant radiator, facilitating a heat dissipation of 365.05 kW. The recuperator, meanwhile, experiences peak heat transfer power nearing 1750 kW. Operating in steady-state mode, the recuperator manifests as a pivotal component within the system.
- The culmination of the analysis reveals that the double-rotor CBC system’s steady-state operation boasts an electrical power output of 175.99 kW, coupled with a commendable thermal efficiency of 32.38%.
Author Contributions
Conceptualization, J.Q.; Methodology, K.C. and J.Y.; Software, J.L.; Validation, J.L.; Investigation, K.C.; Writing—original draft, K.C.; Writing—review & editing, W.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant numbers 52006044 and 52076051.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A | Area (m2) | 5_1 | Outlet of the power turbine |
| C | delayed neutron precursor (m−3) | 6 | Hot side inlet of recuperator |
| Cp | specific heat capacity (J/kg/K) | 7 | Hot side inlet of precooler |
| I | Moment of Inertia (kg·m2) | 8 | Inlet of radiant radiator |
| N | The rotating speed (rpm) | 9 | Cold side inlet of precooler |
| P | Power (kW) | 10 | Hot side inlet of heater |
| T | Temperature (K) | 11 | Inlet of nuclear reactor |
| W | Mass flow rate (kg/s) | C | Compressor |
| h | Convection heat transfer coefficient (W/(m2·K)) | CBC | Closed-Brayton-cycle |
| l | The average lifetime of neutrons (s) | He-Xe | Helium-xenon mixture |
| m | Mass (kg/s) | Li | Lithium |
| n | Converted rotating speed (rpm) | Na-K | Sodium-potassium alloy |
| p | Pressure (Pa) | Nu | Nuclear reactor |
| t | Time (s) | S-CO2 | Supercritical carbon dioxide |
| Greek | T | Turbine | |
| β | Delayed neutron fraction dimensionless | ave | Average |
| η | Efficiency dimensionless | c | Cold end |
| λ | Decay constant (s−1) | d | Design point |
| π | Pressure ratio dimensionless | ex | Heat exchanger |
| ρ | Reactivity of the reactor ($) | f | Core fuel |
| Subscript | h | Hot end | |
| 1 | Inlet of compressor | i | Corresponding groups |
| 2 | Cold side inlet of recuperator | in | Inlet |
| 3 | Cold side inlet of heater | out | Outlet |
| 4 | Inlet of turbine | s | Inner surface of the core |
| 5 | Outlet of the turbine | w | Wall |
References
- Hall, S.J.; Florenz, R.E.; Gallimore, A.; Kamhawi, H.; Brown, D.L.; Polk, J.E.; Goebel, D.M.; Hofer, R.R. Implementation and Initial Validation of a 100-KW Class Nested-Channel Hall Thruster. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar]
- El-Genk, M.S.; Tournier, J.-M.P.; Gallo, B.M. Dynamic Simulation of a Space Reactor System with Closed Bray-ton Cycle Loops. J. Propuls. Power 2010, 26, 394–406. [Google Scholar] [CrossRef]
- Adamantiades, A.; Kessides, I. Nuclear Power for Sustainable Development: Current Status and Future Pro-spects. Energy Policy 2009, 37, 5149–5166. [Google Scholar] [CrossRef]
- Koroteev, A.S.; Oshev, Y.A.; Popov, S.A.; Karevsky, A.V.; Solodukhin, A.Y.; Zakharenkov, L.E.; Semenkin, A.V. Nuclear Power Propulsion System for Spacecraft. Therm. Eng. 2015, 62, 971–980. [Google Scholar] [CrossRef]
- Biondi, A.; Toro, C. Closed Brayton Cycles for Power Generation in Space: Modeling, Simulation and Exergy Analysis. Energy 2019, 181, 793–802. [Google Scholar] [CrossRef]
- Ribeiro, G.B.; Guimarães, L.N.F.; Filho, F.A.B. Design-Based Model of a Closed Brayton Cycle for Space Power Systems; American Nuclear Society: Washington, DC, USA, 2016. [Google Scholar]
- Mazzetti, A.; Gianotti Pret, M.; Pinarello, G.; Celotti, L.; Piskacev, M.; Cowley, A. Heat to Electricity Conversion Systems for Moon Exploration Scenarios: A Review of Space and Ground Technologies. Acta Astronaut. 2019, 156, 162–186. [Google Scholar] [CrossRef]
- Mason, L.S.; Schreiber, J.G. A Historical Review of Brayton and Stirling Power Conversion Technologies for Space Applications. In Proceedings of the Space Nuclear Conference 2007, Boston, MA, USA, 24–28 June 2007. [Google Scholar]
- Longhurst, G.R.; Schnitzler, B.G.; Parks, B.T. Multi-Megawatt Power System Trade Study. In Proceedings of the AIP Conference Proceedings, Washington, DC, USA, 3–6 February 2002; AIP: Albuquerque, NM, USA, 2002; Volume 608, pp. 1075–1083. [Google Scholar]
- Van Den Braembussche, R.A.; Brouckaert, J.F.; Paniagua, G.; Briottet, L. Design and Optimization of a Multi-stage Turbine for Helium Cooled Reactor. Nucl. Eng. Des. 2008, 238, 3136–3144. [Google Scholar] [CrossRef]
- El-Genk, M.; Tournier, J.-M. Selection of Noble Gas Binary Mixtures for Brayton Space Nuclear Power Systems. In Proceedings of the 4th International Energy Conversion Engineering Conference and Exhibit (IECEC), San Diego, CA, USA, 26 June 2006. [Google Scholar]
- Malik, A.; Zheng, Q.; Lin, A. The Design and Performance Analysis of Highly Loaded Compressor of Closed Brayton Cycle HTGR Power Plant with Helium Xenon Gas Mixture as Working Fluid. Prog. Nucl. Energy 2019, 117, 103084. [Google Scholar] [CrossRef]
- Malik, A.; Zheng, Q.; Qureshi, S.R.; Zaidi, A.A. Effect of Helium Xenon as Working Fluid on the Compressor of Power Conversion Unit of Closed Brayton Cycle HTGR Power Plant. Int. J. Hydrogen Energy 2020, 45, 10119–10129. [Google Scholar] [CrossRef]
- Malik, A.; Zheng, Q.; Qureshi, S.R.; Zaidi, A.A.; Yaqoob, T.; Aziz, A. Effect of Helium Xenon as Working Fluid on Centrifugal Compressor of Power Conversion Unit of Closed Brayton Cycle Power Plant. Int. J. Hydrogen Energy 2021, 46, 7546–7557. [Google Scholar] [CrossRef]
- Yuan, Z.; Zheng, Q.; Yue, G.; Jiang, Y. Performance Evaluation on Radial Turbines with Potential Working Flu-ids for Space Closed Brayton Cycle. Energy Convers. Manag. 2021, 243, 114368. [Google Scholar] [CrossRef]
- Yuan, Z.; Zheng, Q.; Jiang, Y.; Jiang, B.; Luo, M. Review on Power Conversion Unit of Noble Gas Closed Bray-ton Cycle for Space and Underwater Applications. Appl. Therm. Eng. 2023, 223, 119981. [Google Scholar] [CrossRef]
- Xu, C.; Kong, F.; Yu, D.; Yu, J.; Khan, M.S. Influence of Non-Ideal Gas Characteristics on Working Fluid Proper-ties and Thermal Cycle of Space Nuclear Power Generation System. Energy 2021, 222, 119881. [Google Scholar] [CrossRef]
- Miao, X.; Zhang, H.; Sun, W.; Wang, Q.; Zhang, C. Optimization of a Recompression Supercritical Nitrous Ox-ide and Helium Brayton Cycle for Space Nuclear System. Energy 2022, 242, 123023. [Google Scholar] [CrossRef]
- Miao, X.; Zhang, H.; Wang, Q.; Sun, W.; Xia, Y. Mass Optimization of a Recompression Supercritical Nitrous Oxide and Helium Power System for Space Exploration. Prog. Nucl. Energy 2023, 158, 104606. [Google Scholar] [CrossRef]
- Li, Z.; Sun, J.; Liu, M.; Lang, M.; Shi, L. Design of a Hundred-Kilowatt Level Integrated Gas-Cooled Space Nu-clear Reactor for Deep Space Application. Nucl. Eng. Des. 2020, 361, 110569. [Google Scholar] [CrossRef]
- El-Genk, M.; Tournier, J.-M. DynMo-CBC: Dynamic Simulation Model of a Space Reactor Power System with Multiple CBC Loops. In Proceedings of the 7th International Energy Conversion Engineering Conference, Denver, CO, USA, 2 August 2009. [Google Scholar]
- Li, Z.; Yang, X.; Wang, J.; Zhang, Z. Off-Design Performance and Control Characteristics of Space Reactor Closed Brayton Cycle System. Ann. Nucl. Energy 2019, 128, 318–329. [Google Scholar] [CrossRef]
- Ma, W.; Ye, P.; Zhao, G.; Yang, X.; Wang, J. Effect of Cooling Schemes on Performance of MW-Class Space Nu-clear Closed Brayton Cycle. Ann. Nucl. Energy 2021, 162, 108485. [Google Scholar] [CrossRef]
- Ma, W.; Ye, P.; Gao, Y.; Yang, X. Comparative Study on Sequential and Simultaneous Startup Performance of Space Nuclear Power System with Multi Brayton Loops. Acta Astronaut. 2022, 199, 142–152. [Google Scholar] [CrossRef]
- Ma, W.; Ye, P.; Gao, Y.; Yang, X. Study on the Load Loss Characteristics of a Space Nuclear Power System with Multi Brayton Loops. Ann. Nucl. Energy 2023, 185, 109702. [Google Scholar] [CrossRef]
- Romano, L.F.R.; Ribeiro, G.B. Optimization of a Heat Pipe-Radiator Assembly Coupled to a Recuperated Closed Brayton Cycle for Compact Space Power Plants. Appl. Therm. Eng. 2021, 196, 117355. [Google Scholar] [CrossRef]
- Lucia, U.; Grisolia, G. The Gouy-Stodola Theorem—From Irreversibility to Sustainability—The Thermodynamic Human Development Index. Sustainability 2021, 13, 3995. [Google Scholar] [CrossRef]
- Lucia, U.; Grisolia, G. Irreversible Thermodynamics and Bioeconomy: Toward a Human-Oriented Sustainability. Front. Phys. 2021, 9, 659342. [Google Scholar] [CrossRef]
- Lucia, U.; Grisolia, G. Biofuels Analysis Based on the THDI Indicator of Sustainability. Front. Energy Res. 2021, 9, 794682. [Google Scholar] [CrossRef]
- Umberto, L.; Debora, F.; Giulia, G. A Thermoeconomic Indicator for the Sustainable Development with Social Considerations. Environ. Dev. Sustain. 2022, 24, 2022–2036. [Google Scholar]
- Tournier, J.-M.P.; El-Genk, M.S. Liquid Metal Loop and Heat Pipe Radiator for Space Reactor Power Systems. J. Propuls. Power 2006, 22, 1117–1134. [Google Scholar] [CrossRef]
- Foust, O. Sodium-Nak Engineering Handbook. Volume I. Sodium Chemistry and Physical Properties; Science Publishers Inc.: New York, NY, USA, 1972. [Google Scholar]
- Bobkov, V.; Fokin, L.; Petrov, E.; Popov, V.; Rumiantsev, V.; Savvatimsky, A. Thermophysical Properties of Materials for Nuclear Engineering: A Tutorial and Collection of Data; IAEA Vienna: Wien, Austria, 2008. [Google Scholar]
- Ohse, R.W. Others Handbook of Thermodynamic and Transport Properties of Alkali Metals; Blackwell Scientific Oxford: Oxford, UK, 1985. [Google Scholar]
- Wright, S.A.; Lipinski, R.J.; Vernon, M.E.; Sanchez, T. Closed Brayton Cycle Power Conversion Systems for Nu-Clear Reactors: Modeling, Operations, and Validation; Sandia National Laboratories: Albuquerque, New Mexico; Livermore, CA, USA, 2006. [Google Scholar]
- Guo, F.; Qin, J.; Ji, Z.; Liu, H.; Cheng, K.; Zhang, S. Performance Analysis of a Turbofan Engine Integrated with Solid Oxide Fuel Cells Based on Al-H2O Hydrogen Production for More Electric Long-Endurance UAVs. Energy Convers. Manag. 2021, 235, 113999. [Google Scholar] [CrossRef]
- Wang, C.; Yu, X.; Ha, C.; Liu, Z.; Fang, J.; Qin, J.; Shao, J.; Huang, H. Thermodynamic Analysis for a Novel Chemical Precooling Turbojet Engine Based on a Multi-Stage Precooling-Compression Cycle. Energy 2023, 262, 125352. [Google Scholar] [CrossRef]
- Cihangir, S.A.; Aygun, H.; Turan, O. Energy and Performance Analysis of a Turbofan Engine with the Aid of Dynamic Component Efficiencies. Energy 2022, 260, 125085. [Google Scholar] [CrossRef]
- Litchford, R.J.; Harada, N. Multi-MW Closed Cycle MHD Nuclear Space Power Via Nonequilibrium He/Xe Working Plasma. In Proceedings of the Nuclear and Emerging Technologies for Space 2011, Albuquerque, NM, USA, 7–10 February 2011. [Google Scholar]
- Xu, C. Optimization Design and Operational Characteristics Analysis of Space Lithium Cryocooler He-Xe Brayton Cycle Power Generation System; University of Science and Technology of China: Hefei, China, 2022. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).