Analysis of Residential Electricity Usage Characteristics and the Effects of Shifting Home Appliance Usage Time under a Time-of-Use Rate Plan
Abstract
:1. Introduction
2. Analysis of Electricity Usage, Peak-Hour Usage Ratio, and TOU Rate Plan
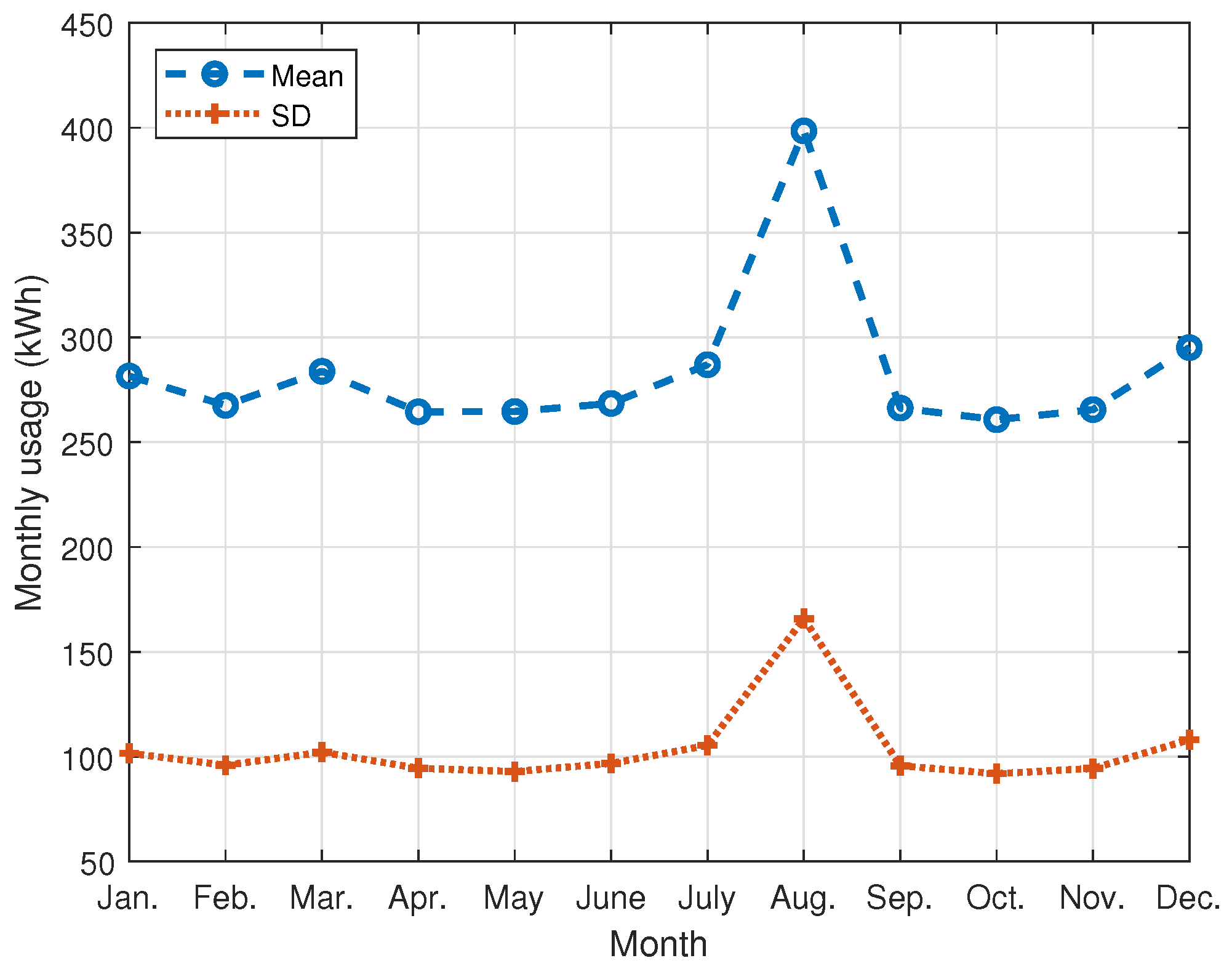
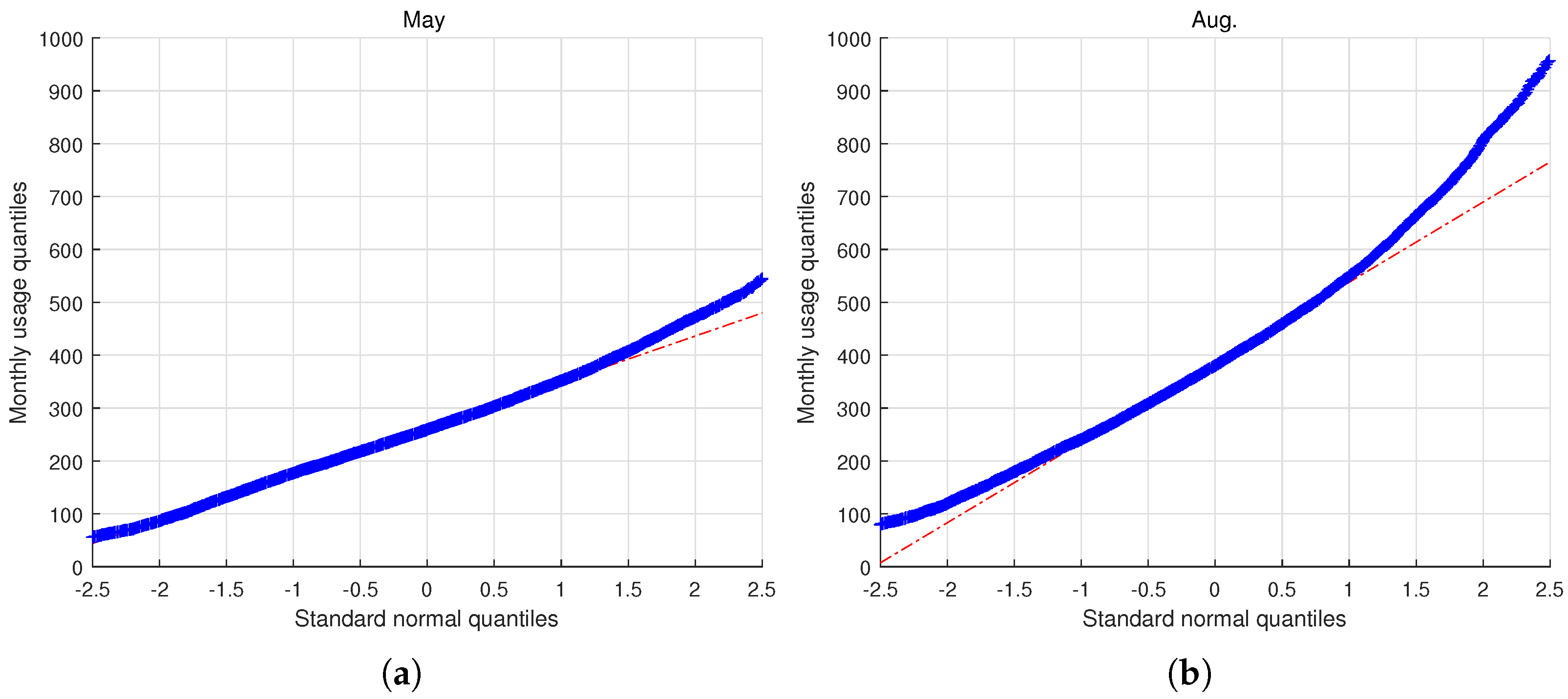
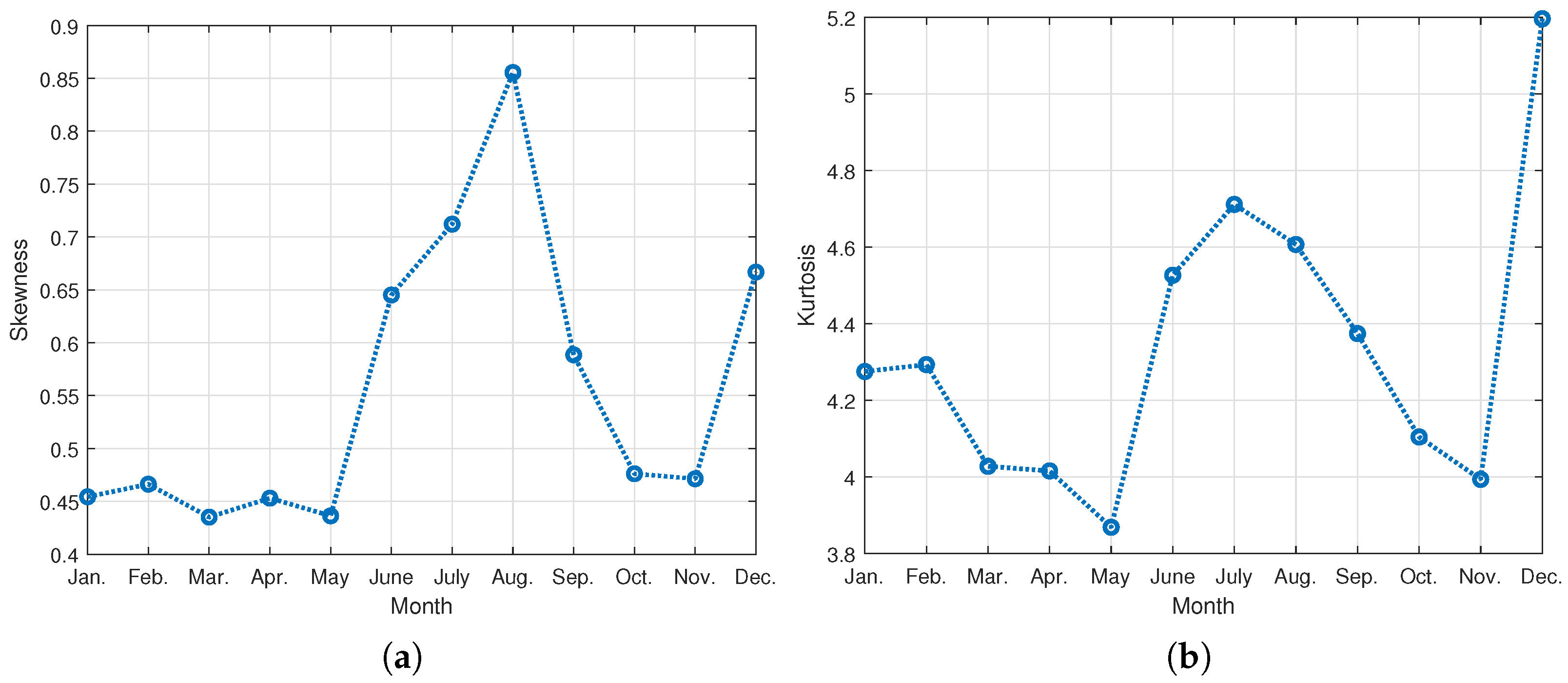
2.1. Analysis of Monthly Electricity Usage of Households
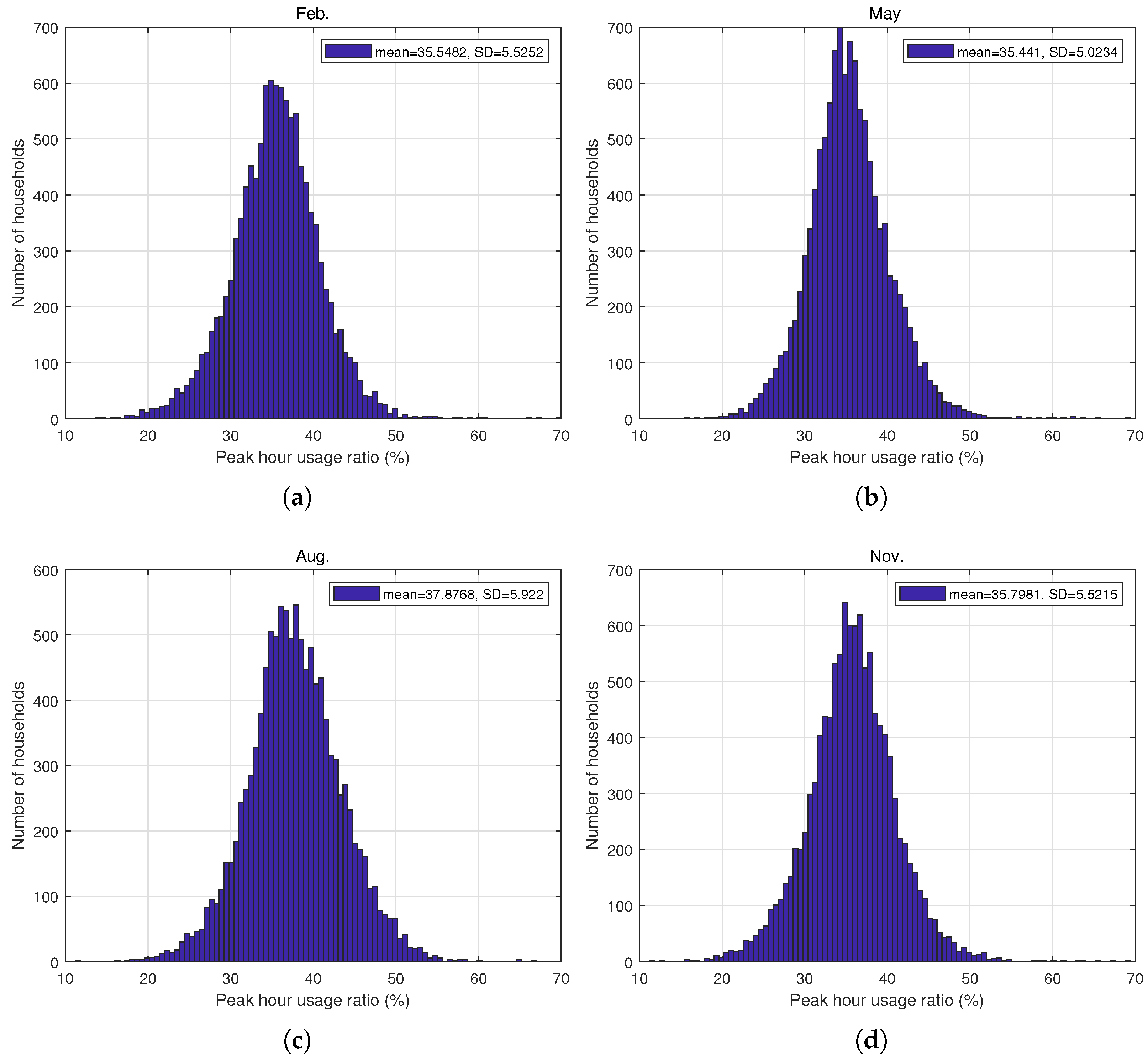
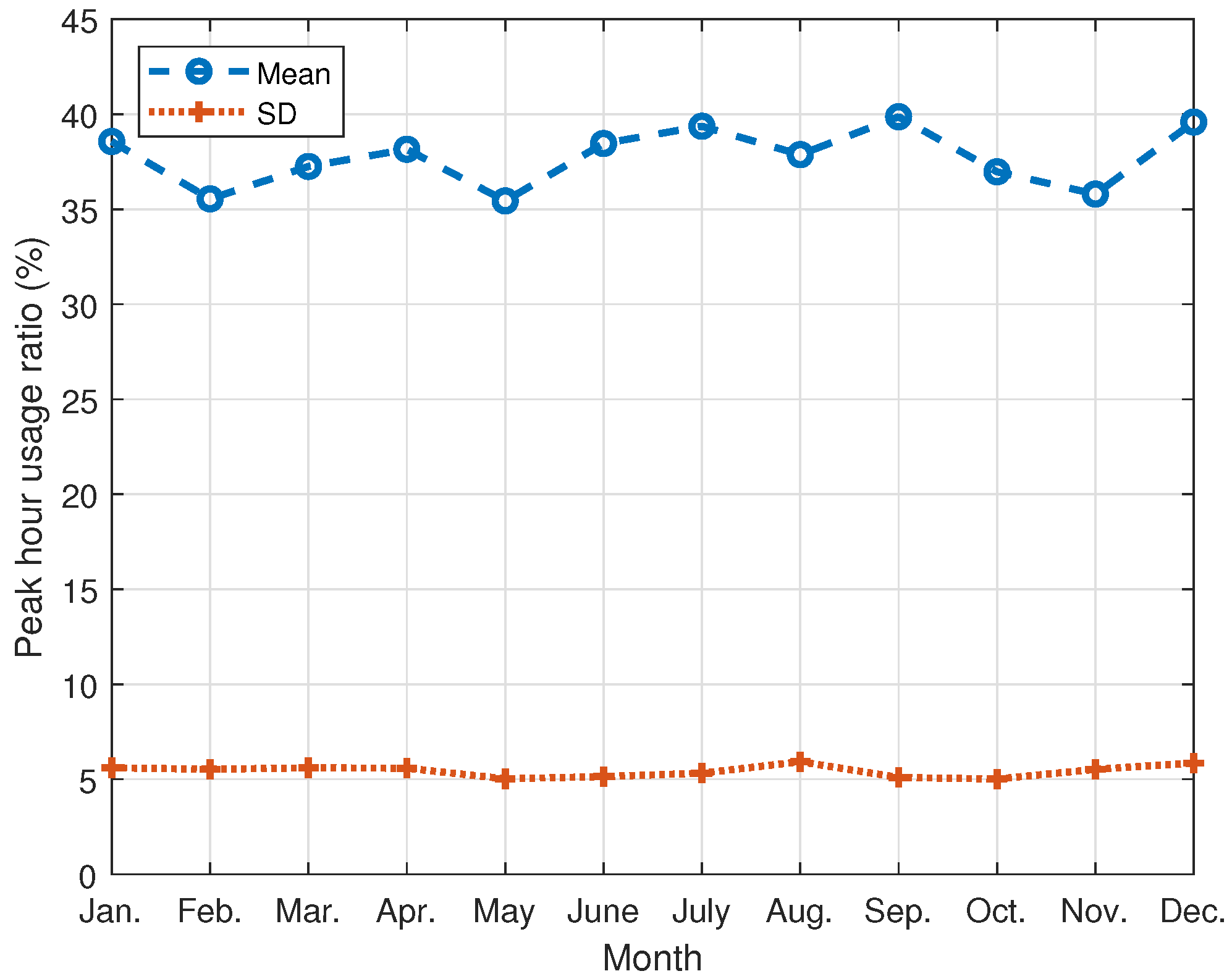
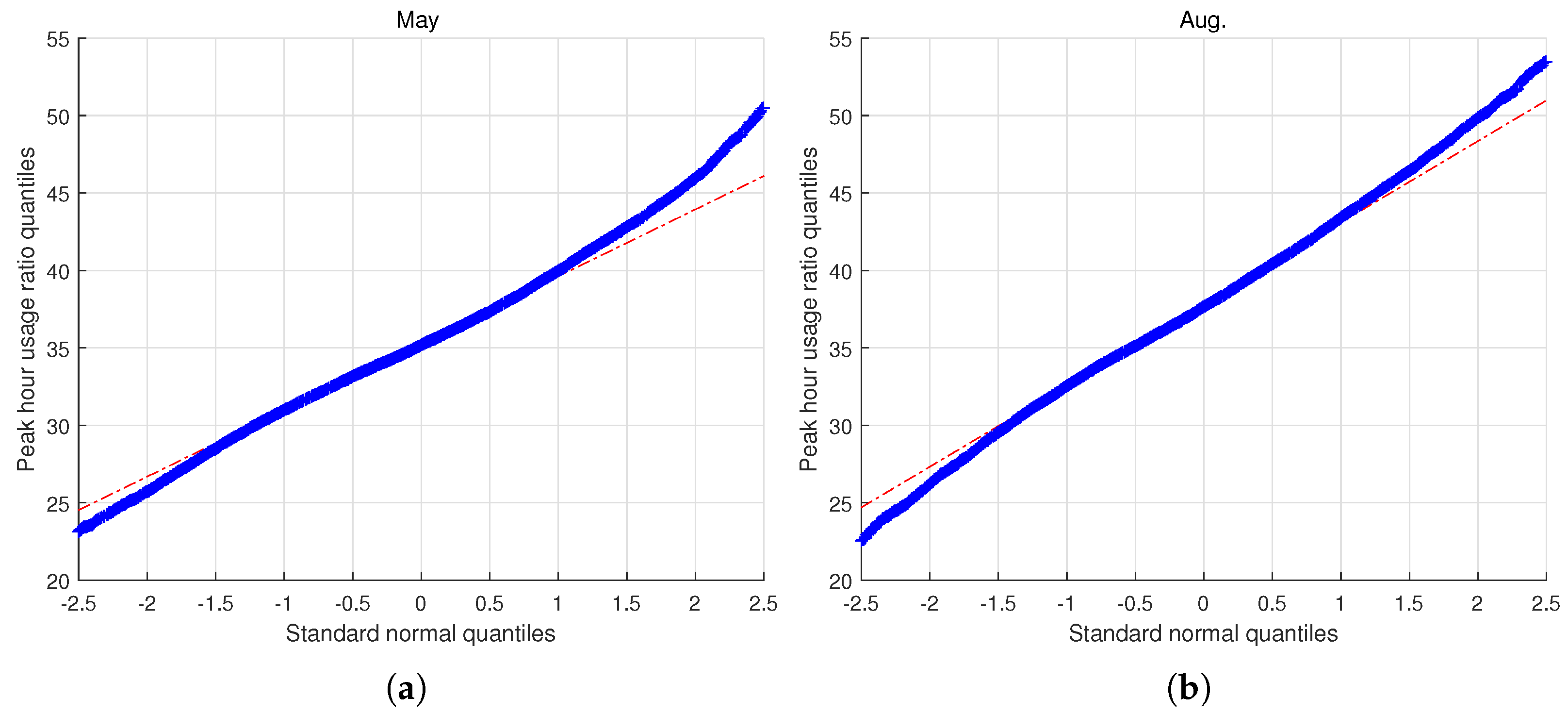
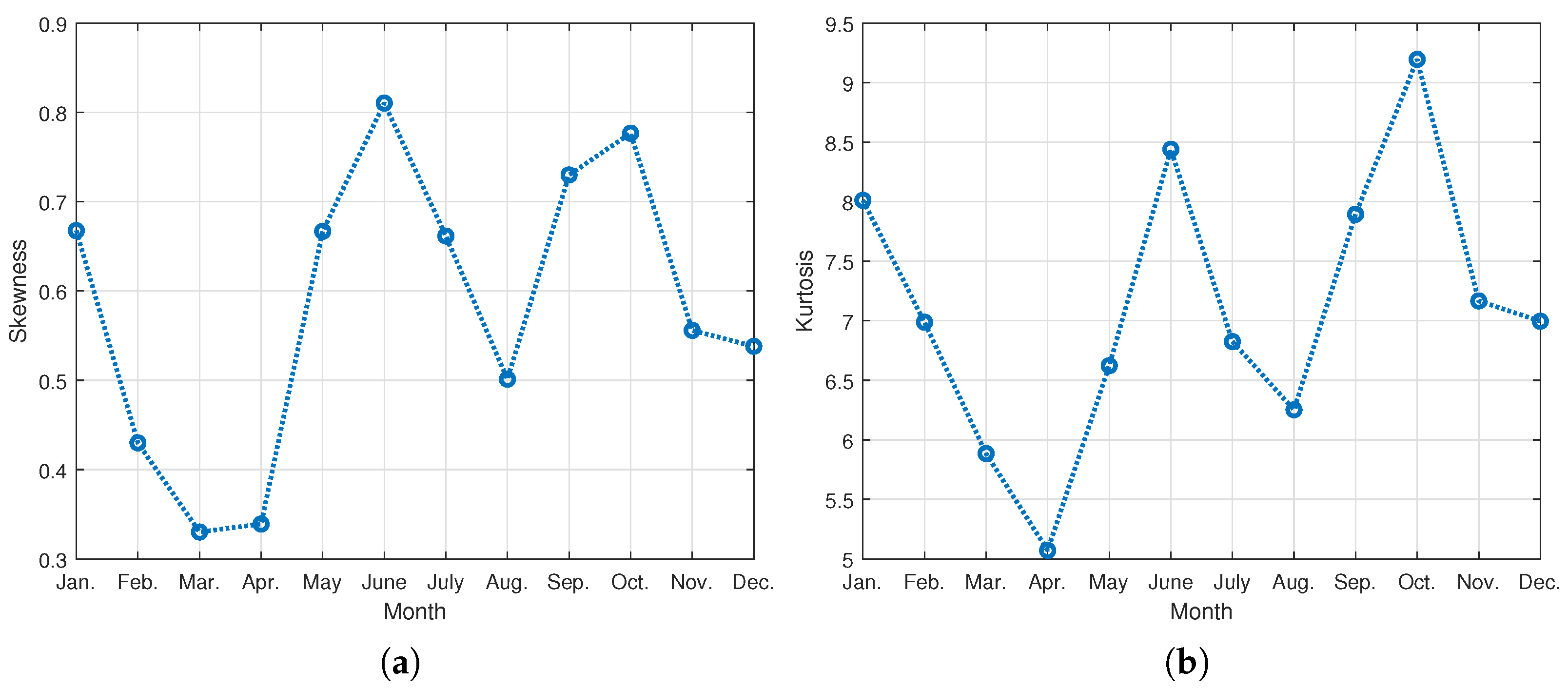
2.2. Analysis of Peak-Hour Usage Ratio of Households
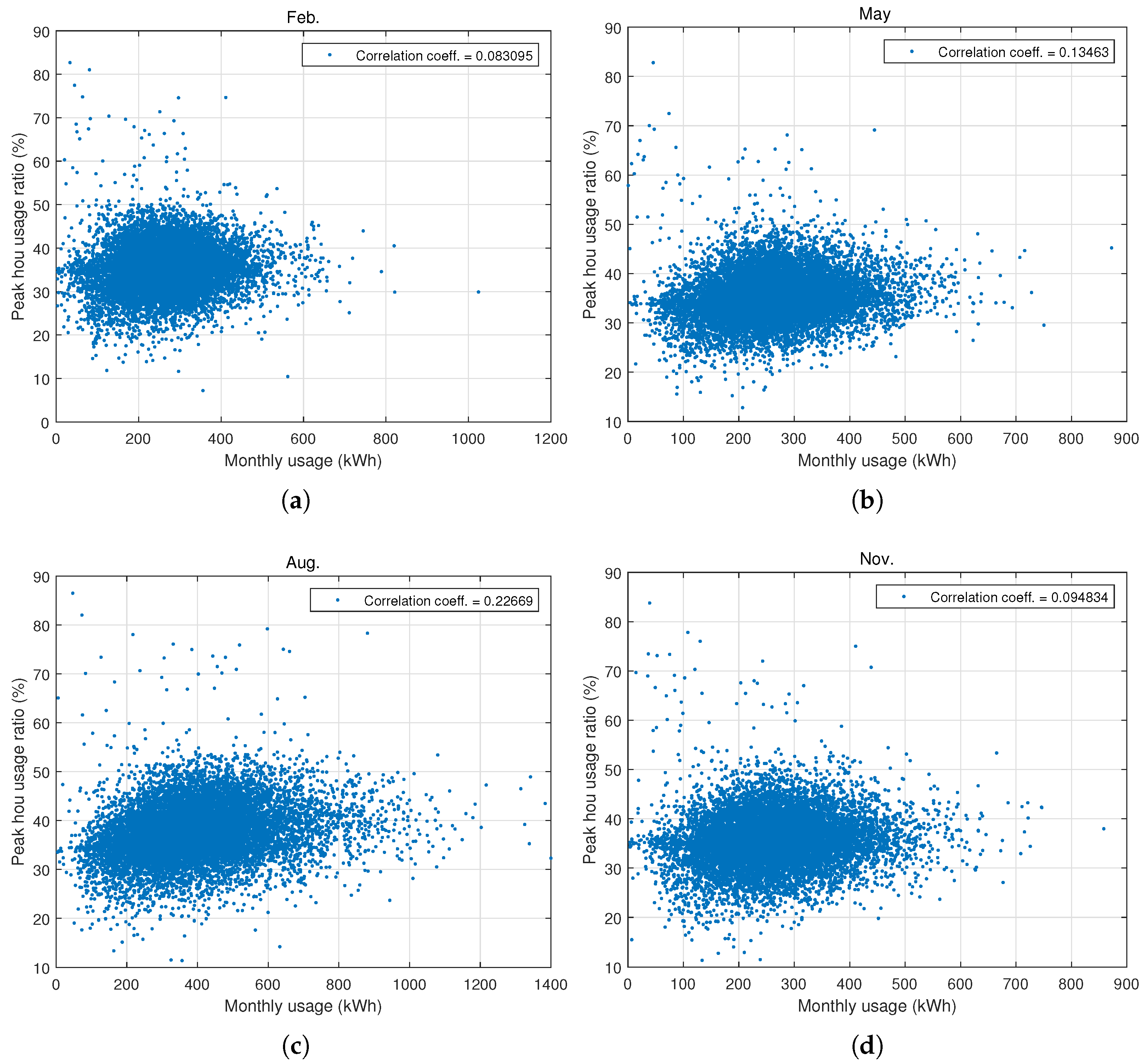
2.3. Correlation between Electricity Usage and peak-hour usage Ratio
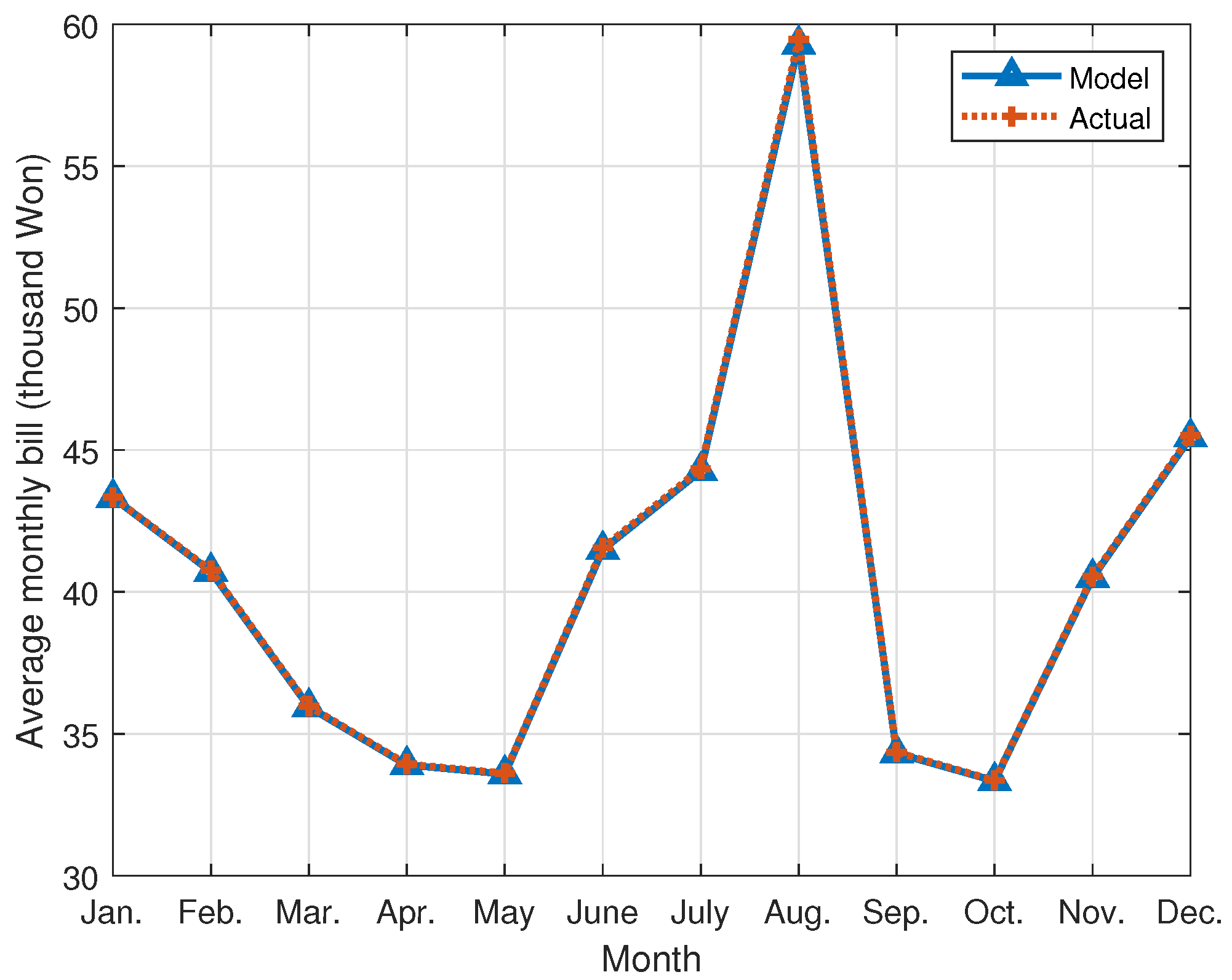
2.4. Analysis for Average Monthly Bill by TOU Rate Plan
2.5. Analysis of Bill Savings Obtained from Shifting Electricity Usage from Peak Hours to Off-Peak Hours
3. Simulation Analysis on Shifting Home Appliance Usage Time
- Electric washing machines (normal and drum washing machines);
- Clothes dryers.
3.1. Usage Time Shift on Electric Washing Machines
3.1.1. Shift of the Washing Machine Usage from the Perspective of Households
3.1.2. Shift of the Washing Machine Usage from the Perspective of Apartment Complexes
3.2. Usage Time Shift on Clothes Dryers
3.2.1. Shift of the Clothes Dryer Usage from the Perspective of Households
3.2.2. Shift of the Clothes Dryer Usage from the Perspective of Apartment Complexes
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMI | Advanced metering infrastructure |
| DR | Demand response |
| KCA | Korea Consumer Agency |
| KEA | Korea Energy Agency |
| LP | Load profile |
| Q-Q | quantile-quantile |
| TOU | Time-of-use |
References
- Alberini, A.; Filippini, M. Response of residential electricity demand to price: The effect of measurement error. Energy Econ. 2011, 33, 889–895. [Google Scholar] [CrossRef]
- Torriti, J. A review of time use models of residential electricity demand. Renew. Sustain. Energy Rev. 2014, 37, 265–272. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, S.; Li, J.; Zhang, X.P. Real-Time Scheduling of Residential Appliances via Conditional Risk-at-Value. IEEE Trans. Smart Grid 2014, 5, 1282–1291. [Google Scholar] [CrossRef]
- Agnetis, A.; de Pascale, G.; Detti, P.; Vicino, A. Load Scheduling for Household Energy Consumption Optimization. IEEE Trans. Smart Grid 2013, 4, 2364–2373. [Google Scholar] [CrossRef]
- Kohlhepp, P.; Harb, H.; Wolisz, H.; Waczowicz, S.; Müller, D.; Hagenmeyer, V. Large-scale grid integration of residential thermal energy storages as demand-side flexibility resource: A review of international field studies. Renew. Sustain. Energy Rev. 2019, 101, 527–547. [Google Scholar] [CrossRef]
- Yahia, Z.; Pradhan, A. Multi-objective optimization of household appliance scheduling problem considering consumer preference and peak load reduction. Sustain. Cities Soc. 2020, 55, 102058. [Google Scholar] [CrossRef]
- Sadeghianpourhamami, N.; Demeester, T.; Benoit, D.; Strobbe, M.; Develder, C. Modeling and analysis of residential flexibility: Timing of white good usage. Appl. Energy 2016, 179, 790–805. [Google Scholar] [CrossRef]
- Mckenna, E.; Higginson, S.; Grunewald, P.; Darby, S. Simulating residential demand response: Improving socio-technical assumptions in activity-based models of energy demand. Energy Effic. 2018, 11, 1583–1597. [Google Scholar] [CrossRef]
- Mammoli, A.; Robinson, M.; Ayon, V.; Martínez-Ramón, M.; Chen, C.F.; Abreu, J.M. A behavior-centered framework for real-time control and load-shedding using aggregated residential energy resources in distribution microgrids. Energy Build. 2019, 198, 275–290. [Google Scholar] [CrossRef]
- Yilmaz, S.; Weber, S.; Patel, M. Who is sensitive to DSM? Understanding the determinants of the shape of electricity load curves and demand shifting: Socio-demographic characteristics, appliance use and attitudes. Energy Policy 2019, 133, 110909. [Google Scholar] [CrossRef]
- Verbong, G.P.; Beemsterboer, S.; Sengers, F. Smart grids or smart users? Involving users in developing a low carbon electricity economy. Energy Policy 2013, 52, 117–125. [Google Scholar] [CrossRef]
- Thimmapuram, P.R.; Kim, J. Consumers’ Price Elasticity of Demand Modeling With Economic Effects on Electricity Markets Using an Agent-Based Model. IEEE Trans. Smart Grid 2013, 4, 390–397. [Google Scholar] [CrossRef]
- Sergici, S.; Faruqui, A.; Powers, N. PC44 Time of Use Pilots: Year One Evaluation; Brattle Group: Baltimore, MD, USA, 2020. [Google Scholar]
- Yu, T.; Kim, D.S.; Son, S.Y. Optimization of scheduling for home appliance in conjunction with renewable and energy storage resources. Int. J. Smart Home 2013, 7, 261–272. [Google Scholar]
- Zhang, L.; Tang, Y.; Zhou, T.; Tang, C.; Liang, H.; Zhang, J. Research on flexible smart home appliance load participating in demand side response based on power direct control technology. Energy Rep. 2022, 8, 424–434. [Google Scholar] [CrossRef]
- Chung, Y.M.; Kang, S.; Jung, J.; Chung, B.J.; Kim, D.S. Residential electricity rate plans and their selections based on statistical learning. IEEE Access 2022, 10, 74012–74022. [Google Scholar] [CrossRef]
- Kim, D.S.; Jung, W.; Chung, B.J. Analysis of the Electricity Supply Contracts for Medium-Voltage Apartments in the Republic of Korea. Energies 2021, 14, 293. [Google Scholar] [CrossRef]
- Thode, J.C., Jr. Testing for Normality; Marcel-Dekker: New York, NY, USA, 2002. [Google Scholar]
- Doane, D.P.; Seward, L.E. Measuring skewness: A forgotten statistics? J. Stat. Educ. 2011, 19, 1–18. [Google Scholar] [CrossRef]
- Hair, J.F., Jr.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis, 7th ed.; Pearson Education Limited: Essex, UK, 2014. [Google Scholar]
- George, D.; Mallery, P. IBM SPSS Statistics 26 Step by Step: A Simple Guide and Reference, 16th ed.; Routledge: New York, NY, USA, 2020. [Google Scholar]
- Byrne, B.M. Structural Equation Modeling wih AMOS: Basic Concepts, Applications, and Programming, 2nd ed.; Routledge: New York, NY, USA, 2010. [Google Scholar]
- Electrical and Electronics Team. Drum Washing Machine Quality Comparison Test Result. Korea Consumer Agency. 2020. Available online: www.kca.go.kr (accessed on 1 October 2020).
- Electrical and Electronics Team. Efficiency Rating System. Korea Energy Agency. 2023. Available online: www.energy.or.kr (accessed on 27 April 2022).




| Cases | Basic Rate (KRW) | Usage Rate (KRW/kWh) | |
|---|---|---|---|
| Peak (9 a.m.–9 p.m. on Weekdays) | Off-Peak (9 p.m.–9 a.m. on Weekdays, All Day on Weekends) | ||
| Spring/autumn (March–May, September–October) | 4310 | 140.7 | 94.1 |
| Summer/winter (November–February, June–August) | 4310 | 188.8 | 107.0 |
| Apartment Complex | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of households | 595 | 1294 | 470 | 1035 | 1638 | 433 | 2048 | 1966 | 780 | 1263 | 11,522 |
| Month k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 281.56 | 267.56 | 283.81 | 264.49 | 264.63 | 268.50 | 286.98 | 398.48 | 266.28 | 260.74 | 265.55 | 295.13 | |
| 101.67 | 95.92 | 102.12 | 94.47 | 92.92 | 96.80 | 105.40 | 165.85 | 95.67 | 91.89 | 94.38 | 108.11 |
| Month k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 38.568 | 35.548 | 37.253 | 38.158 | 35.441 | 38.462 | 39.372 | 37.877 | 39.871 | 36.974 | 35.798 | 39.590 | |
| 5.603 | 5.525 | 5.603 | 5.580 | 5.023 | 5.141 | 5.320 | 5.922 | 5.096 | 5.012 | 5.522 | 5.853 |
| Energy Consumption per Wash (Wh) | ||||
|---|---|---|---|---|
| Manufacturer | Washing Capacity | 40 Standard | Cold Standard | Futon |
| Samsung | Large (21 kg) | 262 | 84 | 488 |
| LG | Large (21 kg) | 224 | 72 | 294 |
| Samsung | Medium (14 kg) | 389 | 66 | 362 |
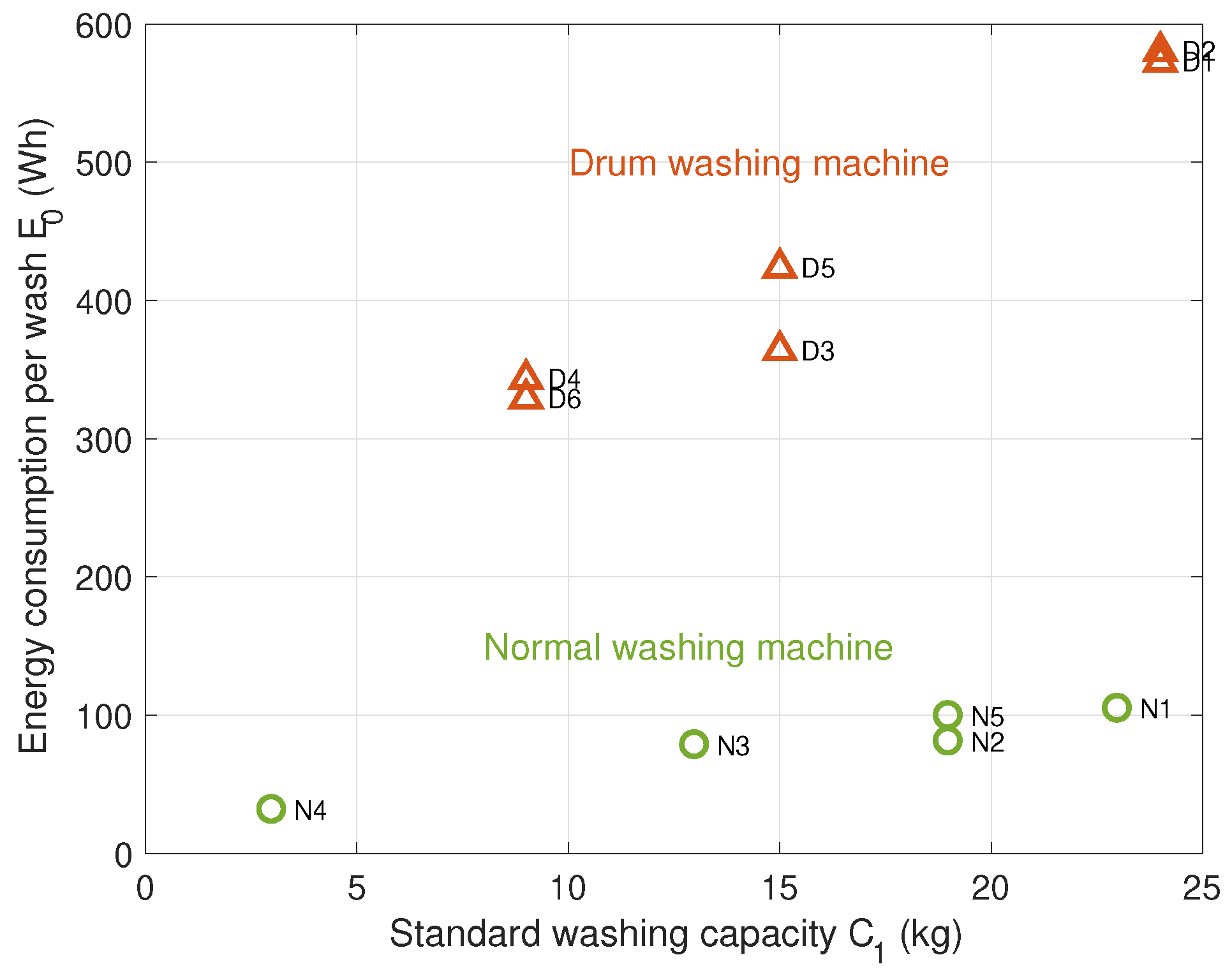
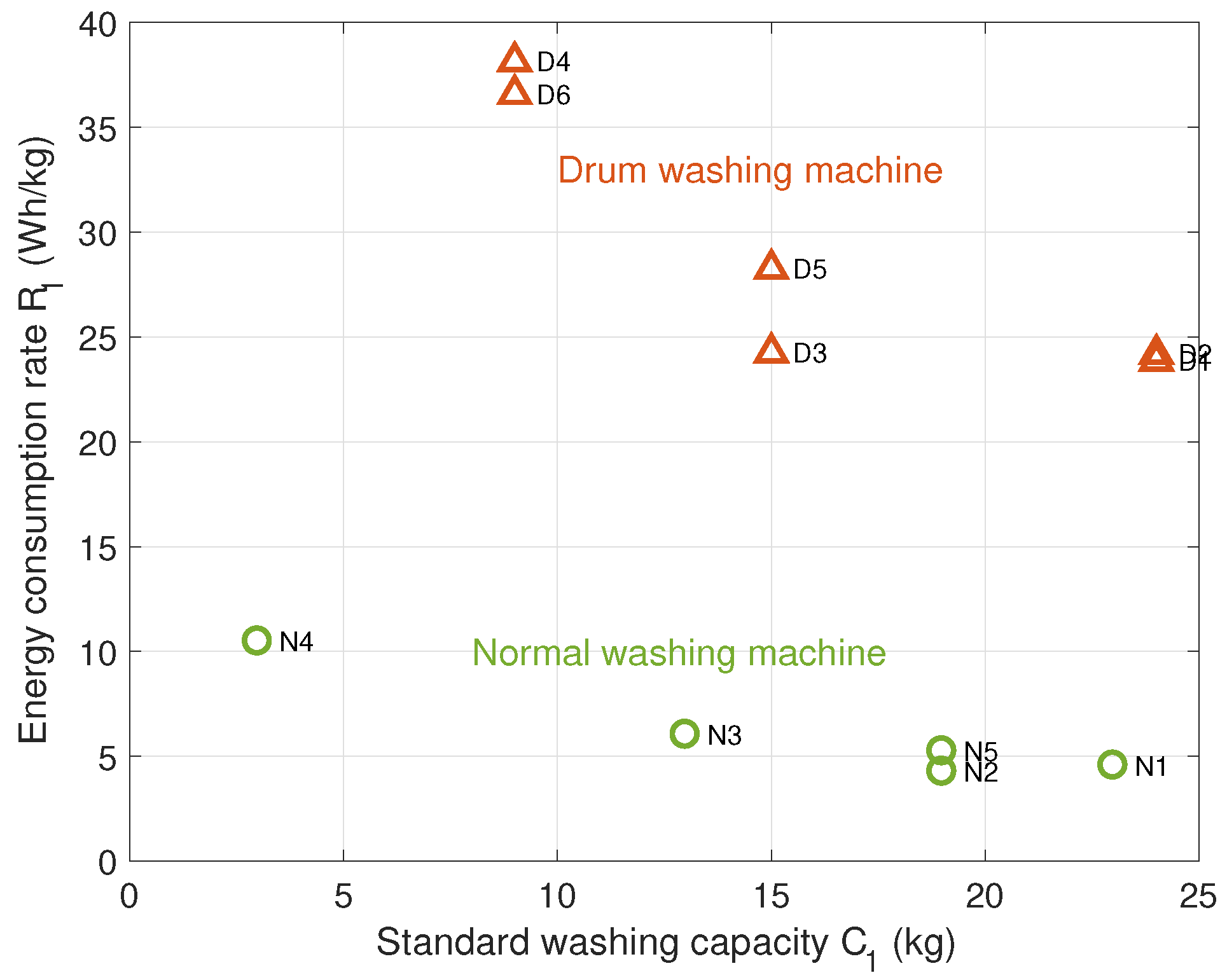
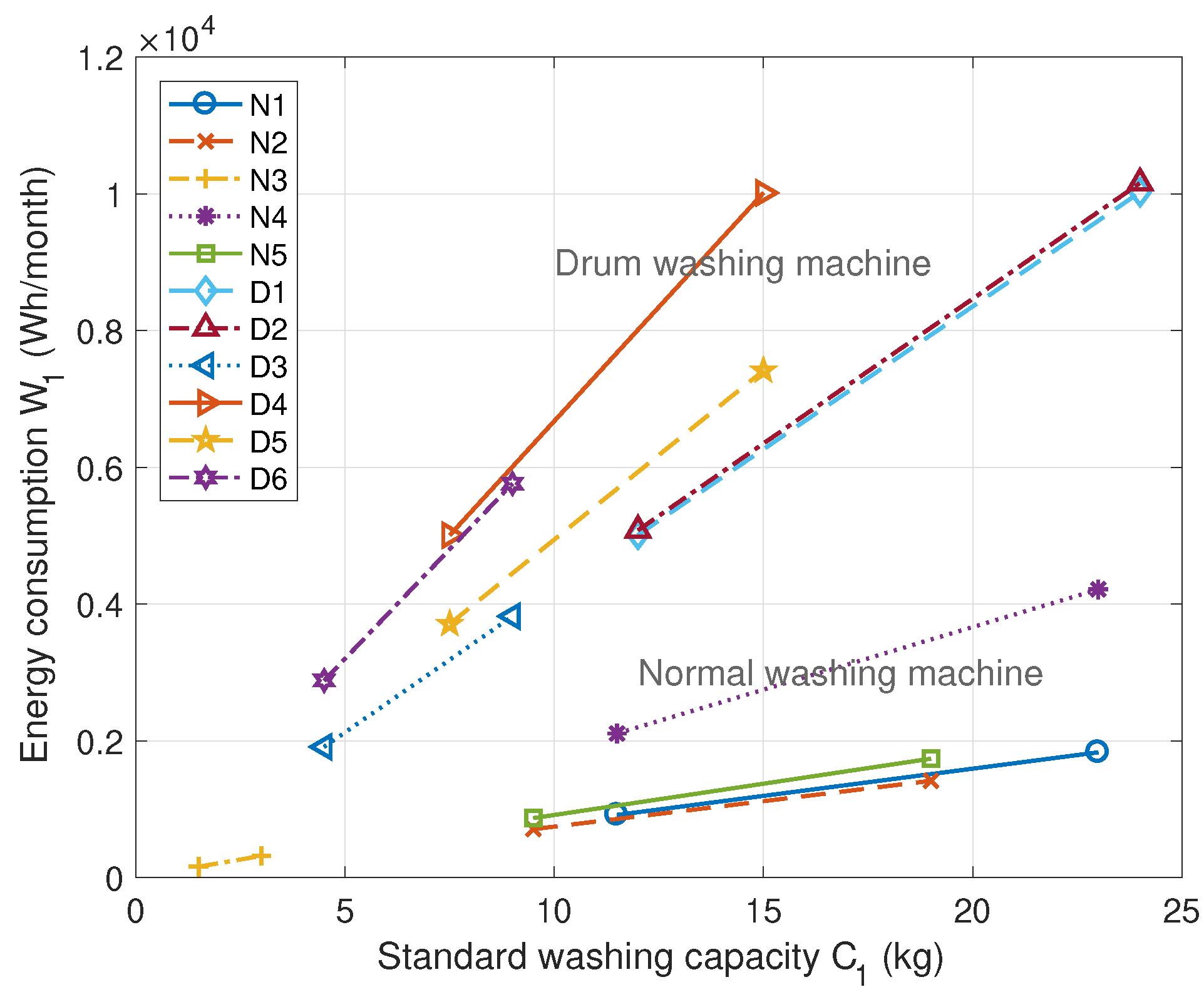
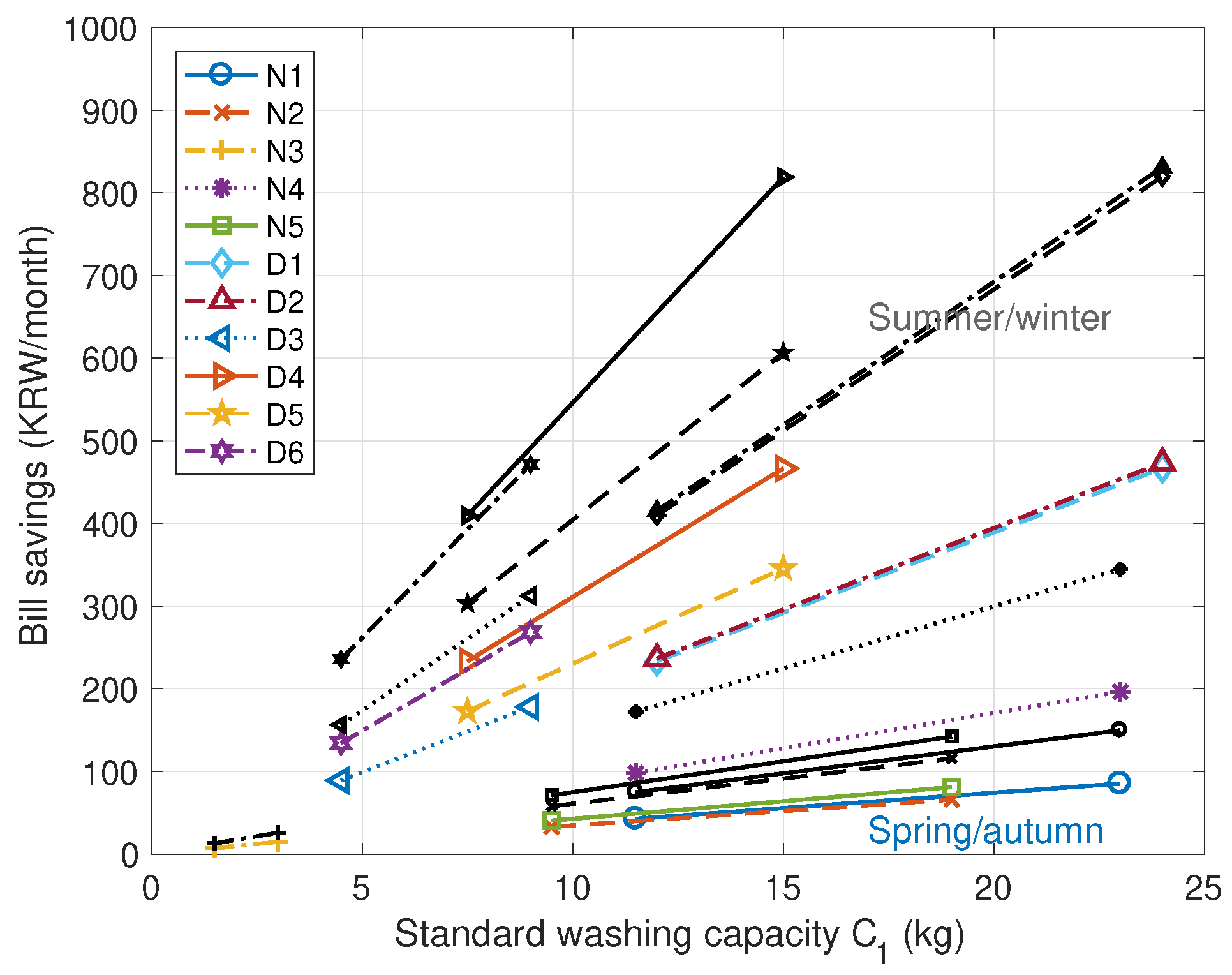
| Washing Machine | Type | Standard Washing Capacity (kg) | Energy per Wash (Wh) | Manufacturer | Efficiency Class | Energy per 1 kg (Wh/kg) |
|---|---|---|---|---|---|---|
| N1 | Normal | 23 | 104.6 | Samsung | 1 | 4.5478 |
| N2 | Normal | 19 | 80.8 | LG | 2 | 4.2526 |
| N3 | Normal | 13 | 78.2 | LG | 3 | 6.0154 |
| N4 | Normal | 3 | 31.4 | Winia | 1 | 10.467 |
| N5 | Normal | 19 | 99.3 | Winia | 2 | 5.2263 |
| D1 | Drum | 24 | 572.7 | Samsung | 1 | 23.8625 |
| D2 | Drum | 24 | 580.4 | LG | 1 | 24.1833 |
| D3 | Drum | 15 | 363.9 | LG | 1 | 24.26 |
| D4 | Drum | 9 | 343.3 | LG | 3 | 38.1444 |
| D5 | Drum | 15 | 423.7 | Winia | 1 | 28.2467 |
| D6 | Drum | 9 | 329.2 | Winia | 3 | 36.5778 |
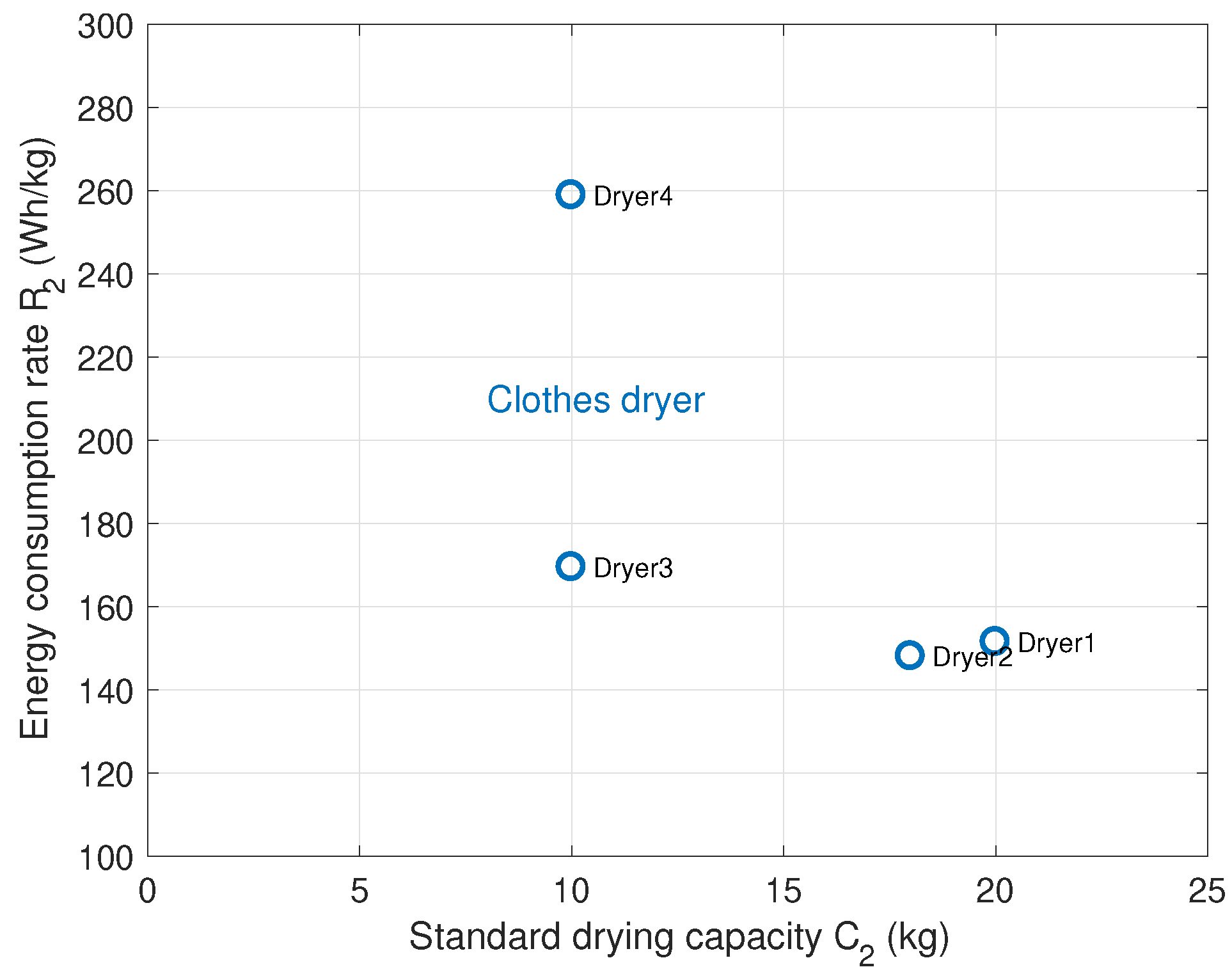
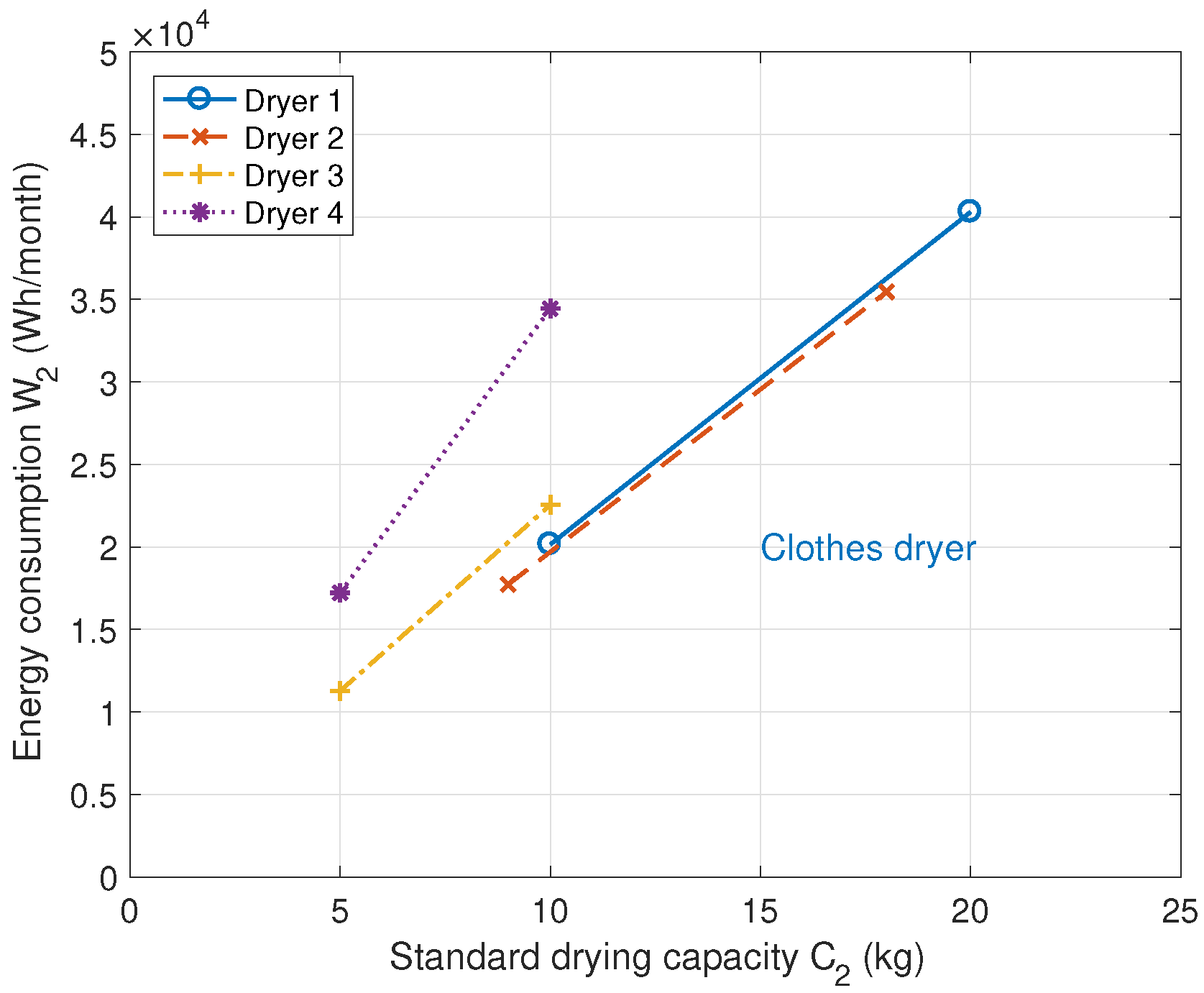
| Clothes Dryer | Standard Drying Capacity (kg) | Manufacturer | Efficiency Class | Energy per 1 kg (Wh/kg) |
|---|---|---|---|---|
| Dryer 1 | 20 | Samsung | 1 | 151.5 |
| Dryer 2 | 18 | LG | 2 | 148.1 |
| Dryer 3 | 10 | Samsung | 3 | 169.5 |
| Dryer 4 | 10 | Winia | 3 | 258.9 |
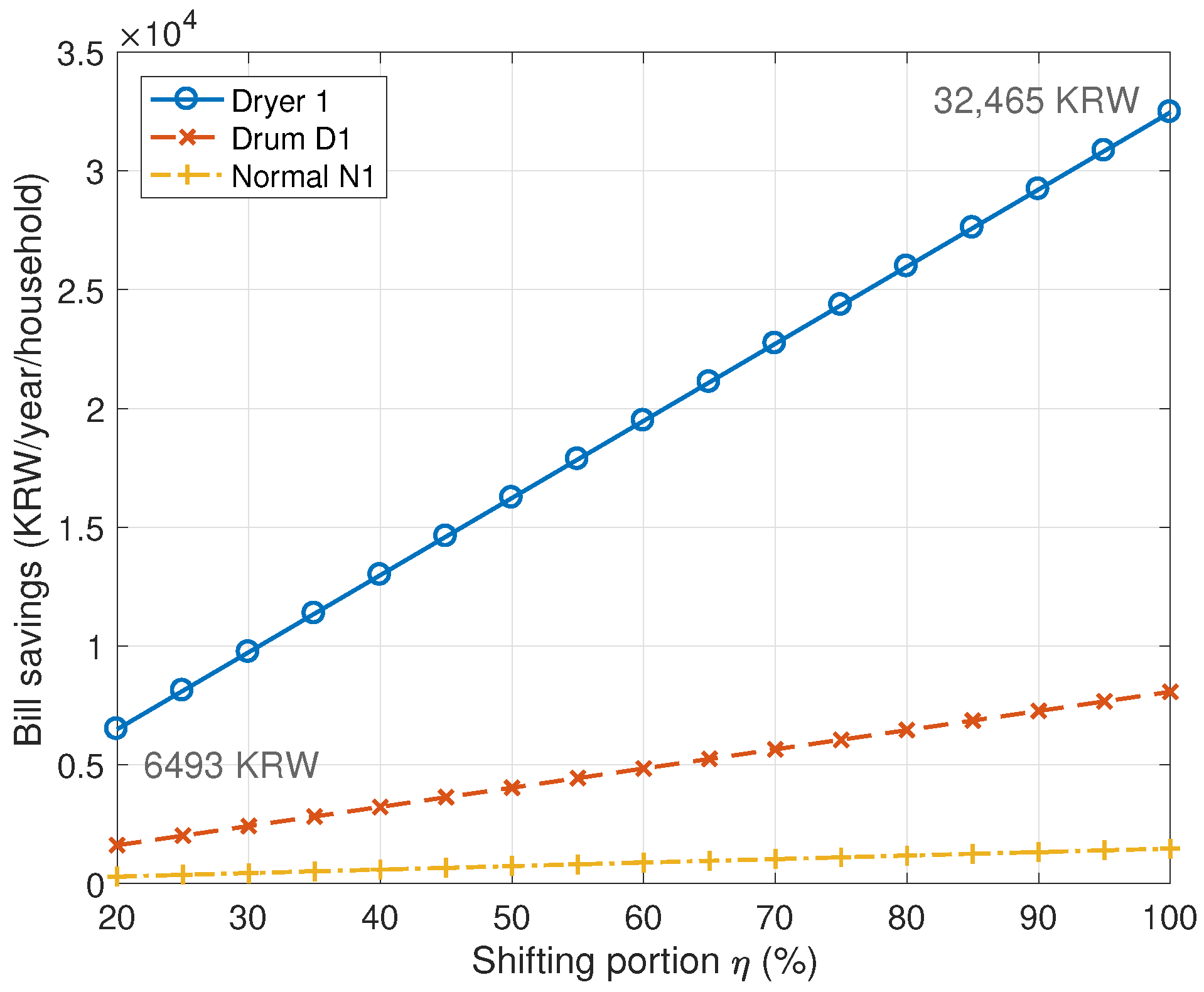
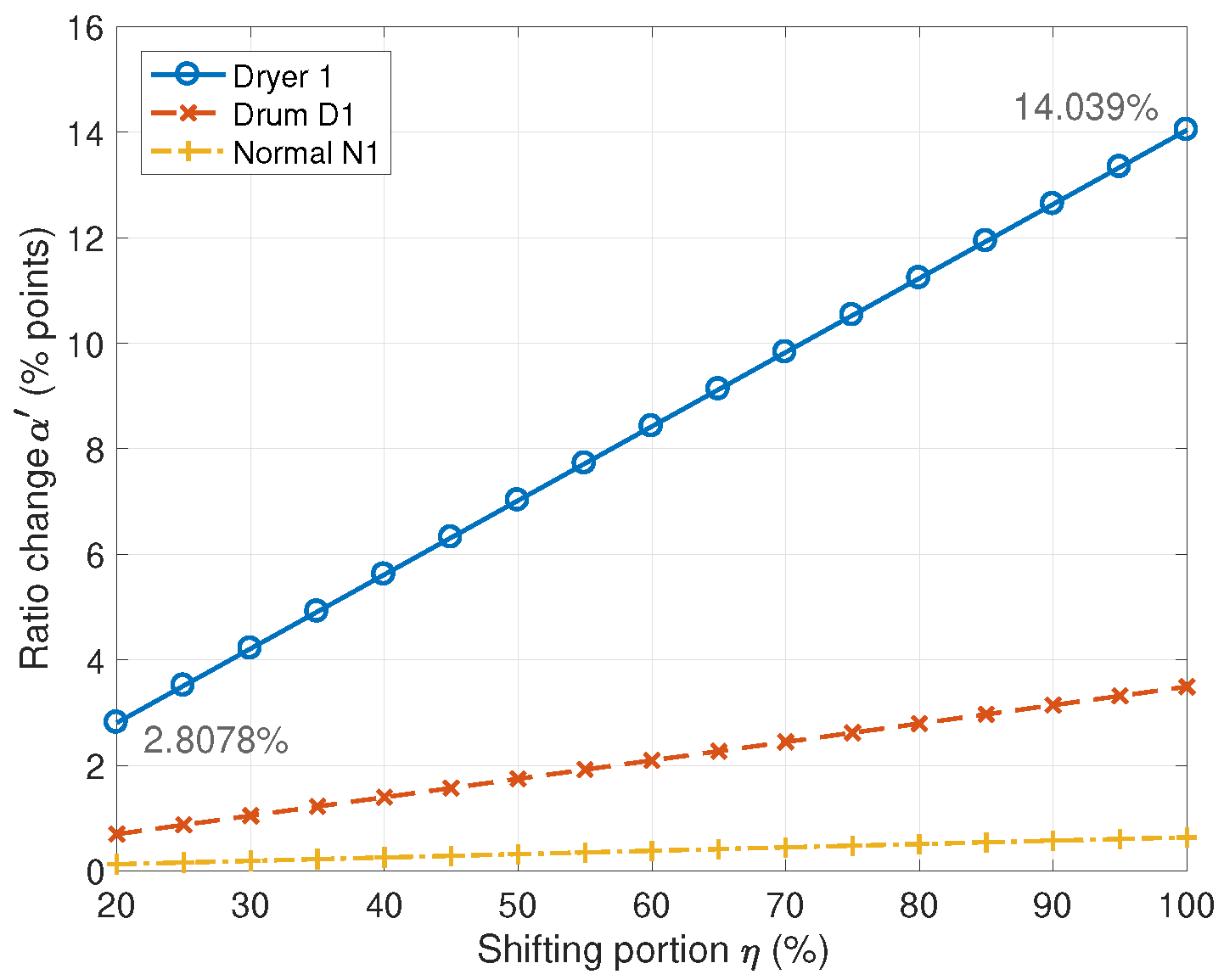
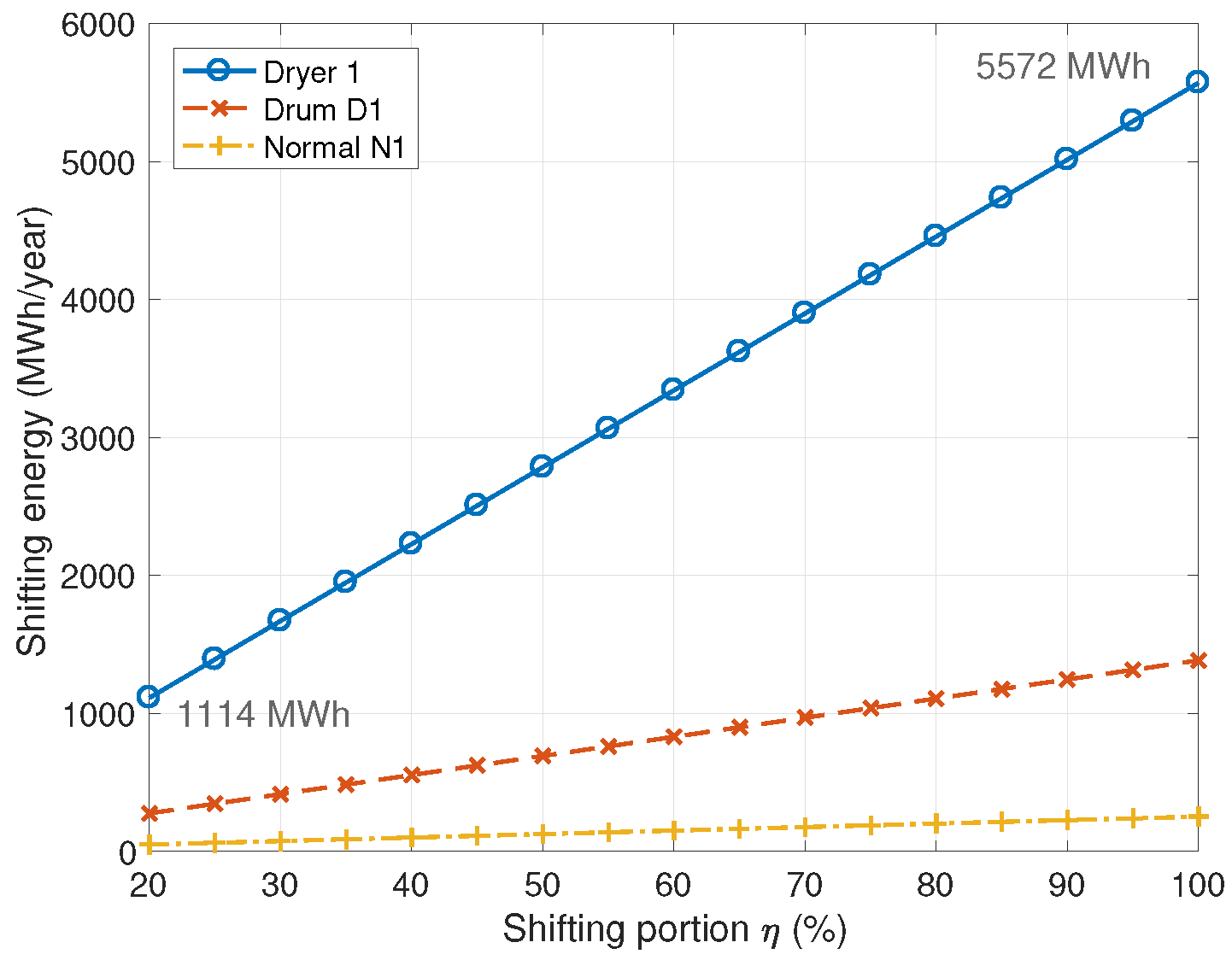
| Home Appliance | Bill Savings (KRW/Year) Energy Shift (kWh/Year) | Energy Ratio Change (%) (10 Complexes) | Conditions | ||
|---|---|---|---|---|---|
| Normal washing machine | 295 | 1470 | 0.128 | 0.638 | Capacity 23 kg 4.55 Wh/kg |
| 4.40 | 22.0 | ||||
| Drum washing machine | 1610 | 8070 | 0.698 | 3.49 | Capacity 24 kg 23.9 Wh/kg |
| 24.0 | 120 | ||||
| Clothes dryer | 6490 | 32,500 | 2.80 | 14.0 | Capacity 20 kg 151.5 Wh/kg |
| 96.8 | 484 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, Y.M.; Chung, B.J.; Kim, D.S. Analysis of Residential Electricity Usage Characteristics and the Effects of Shifting Home Appliance Usage Time under a Time-of-Use Rate Plan. Energies 2023, 16, 6602. https://doi.org/10.3390/en16186602
Chung YM, Chung BJ, Kim DS. Analysis of Residential Electricity Usage Characteristics and the Effects of Shifting Home Appliance Usage Time under a Time-of-Use Rate Plan. Energies. 2023; 16(18):6602. https://doi.org/10.3390/en16186602
Chicago/Turabian StyleChung, Young Mo, Beom Jin Chung, and Dong Sik Kim. 2023. "Analysis of Residential Electricity Usage Characteristics and the Effects of Shifting Home Appliance Usage Time under a Time-of-Use Rate Plan" Energies 16, no. 18: 6602. https://doi.org/10.3390/en16186602
APA StyleChung, Y. M., Chung, B. J., & Kim, D. S. (2023). Analysis of Residential Electricity Usage Characteristics and the Effects of Shifting Home Appliance Usage Time under a Time-of-Use Rate Plan. Energies, 16(18), 6602. https://doi.org/10.3390/en16186602






