An Overview of Strengths and Weaknesses in Using MOSFET Experience for Modeling GaN HEMT
Abstract
:1. Introduction
2. Power Electronics Devices Modeling
3. Comparison between MOSFET and GaN HEMT
- (A)
- Output Characteristic (OC) expressed in terms of drain current, ID, vs. drain-source voltage, VDS. Figure 1A shows typical output characteristics of Si MOSFET (Tj = 125 °C, VGS = 10 V), SiC MOSFET (Tj = 175 °C, VGS = 20 V) and GaN HEMT (Tj = 150 °C, VGS = 4 V).
- Dissimilarity—None in terms of shape.
- Similarity—The shape of the curves is analogous.
- (B)
- Transfer Characteristic (TC, ID vs. gate-source voltage, VGS)—Figure 1B shows typical transfer characteristics of Si MOSFET, SiC MOSFET, and GaN HEMT at ambient temperature (Tj = 25 °C) and Tj = 150 °C.
- Dissimilarity—When the MOSFET is considered, the effect of the temperature on ID depends on VGS. The drain currents of Si and SiC MOSFETs are independent of Tj for a specific VGS, known as the zero temperature coefficient (ZTC) point (see Figure 1B). Another difference is the behavior of the MOSFET below the ZTC point, where ID increases with Tj. There is not any ZTC point in GaN HEMT, and ID never increases with increasing Tj. The shape of the GaN HEMT curve (blue in Figure 1B) is different from the MOSFET’s one.
- Similarity—In MOSFETs and GaN HEMTs, ID increases with VGS at any temperature. Above ZTC, the MOSFET current decreases with increasing Tj. This behavior also occurs in GaN HEMT, whatever the VGS.
- (C)
- Threshold Voltage (VTH, VTH vs. Tj)—Figure 1C shows typical trends of the threshold voltage for increasing junction temperature.
- Dissimilarity—In Si and SiC MOSFETs, VTH decreases with increasing Tj, while GaN HEMT presents a temperature-independent threshold.
- Similarity—None.
Figure 1. Comparison among Si, SiC MOSFET, and GaN HEMT. The datasheet is the data source. (A) Output characteristic (B) Transfer characteristic (C) Threshold voltage (D) Conduction resistance (E) Third-quadrant (F) COSS.Figure 1. Comparison among Si, SiC MOSFET, and GaN HEMT. The datasheet is the data source. (A) Output characteristic (B) Transfer characteristic (C) Threshold voltage (D) Conduction resistance (E) Third-quadrant (F) COSS. - (D)
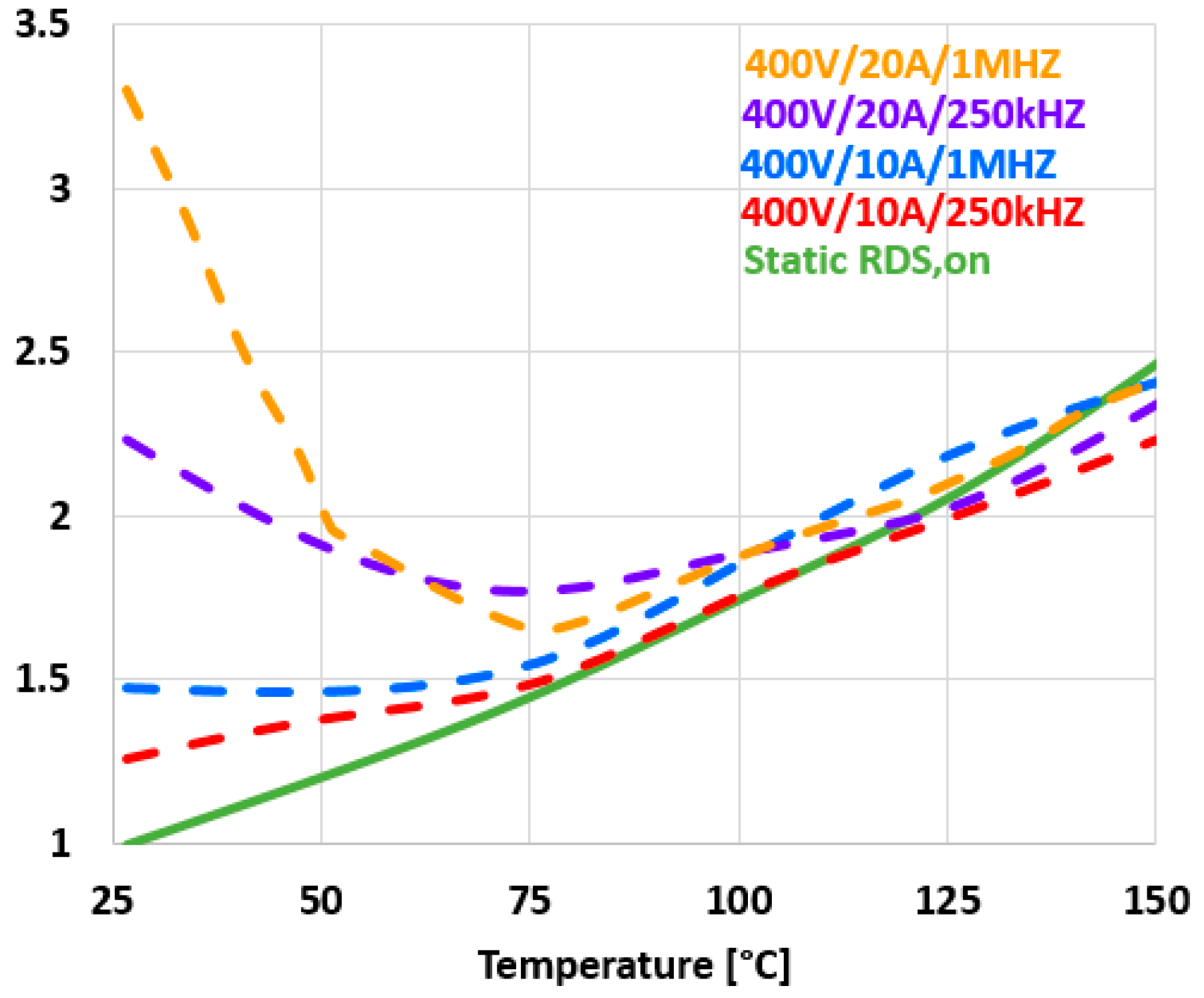
- Conduction Resistance (RDS,on, normalized on-state resistance vs. Tj). Figure 1D shows typical curves for MOSFETs and GaN HEMTs.
- Dissimilarity—SiC MOSFET presents a “U-shape” curve, then, below the room temperature, the conduction resistance decreases with increasing temperature, while in GaN HEMT the resistance always increases when the temperature increases.
- Similarity—The curves of Si MOSFETs and GaN HEMTs are analogous, whatever the temperature. The curves of SiC MOSFETs and GaN HEMTs are analogous above room temperature.
- (E)
- Third-Quadrant (TQ, ID flowing in opposite direction vs. negative VDS). The physical structure of Si and SiC MOSFETs presents a parasitic diode that enables third-quadrant operations, but it introduces issues, especially in Si MOSFETs, related to the reverse recovery current.
- Dissimilarity—GaN HEMT does not present any reverse recovery current thanks to the absence of a parasitic diode.
- Similarity—MOSFETs and GaN HEMTs present analogous curve shapes of the third quadrant current (Figure 1E).
- (F)
- Parasitic Capacitances (CISS, CRSS, COSS vs. VDS). Any technology presents parasitic capacitance, although the GaN HEMT capacitance is widely lower than in MOSFET technologies, as shown in Figure 1F.
- Dissimilarity—None in terms of shape.
- Similarity—The shape is analogous.
4. GaN HEMT Circuit Models
4.1. GMOS
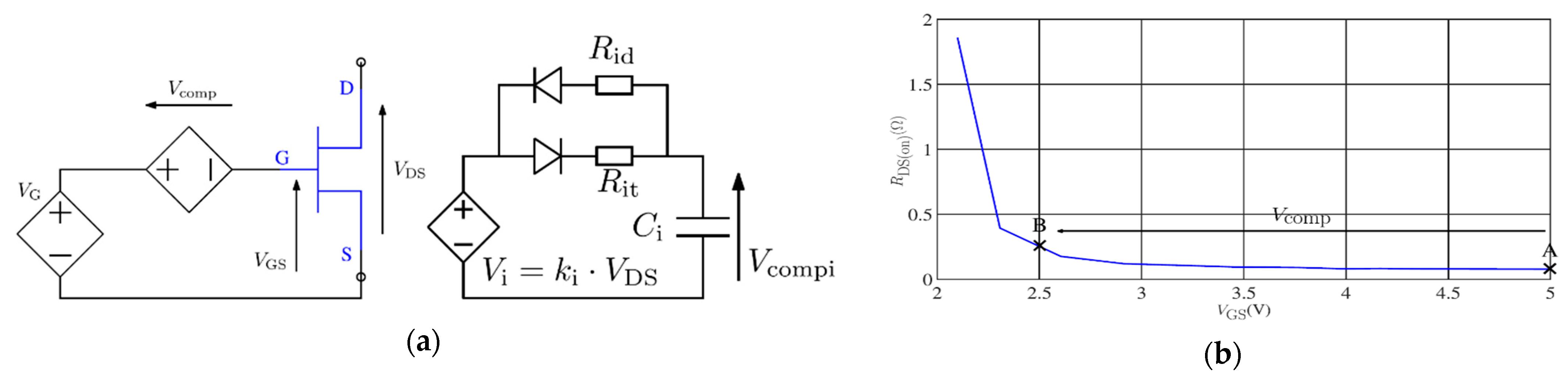
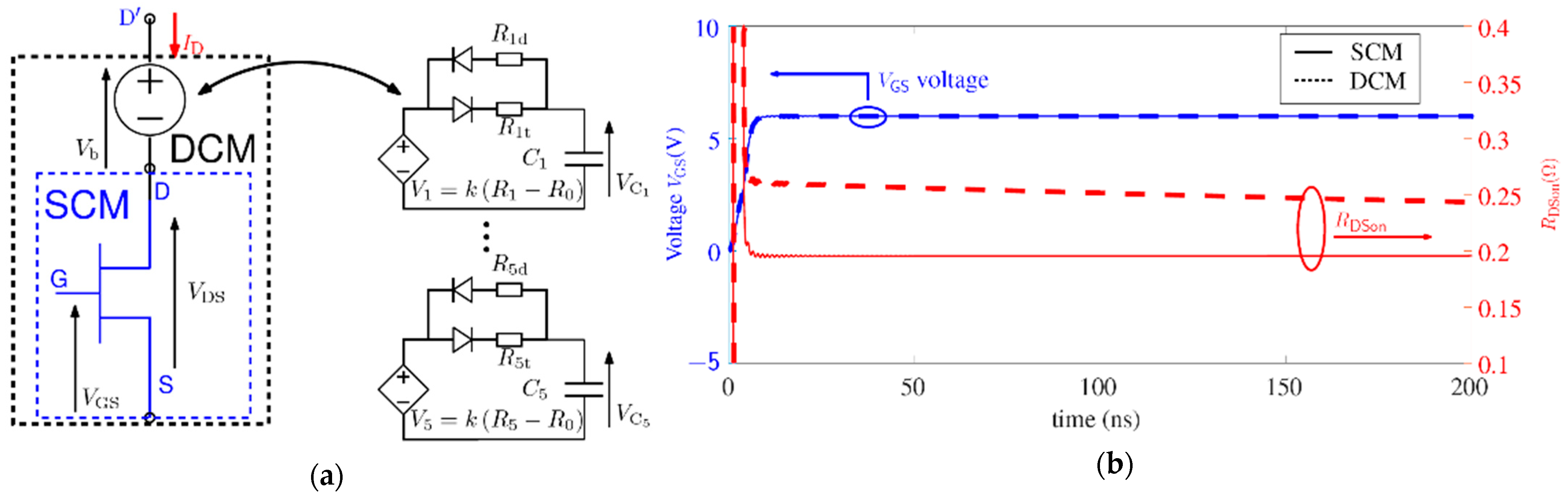
4.2. RVAR
4.3. Third-Quadrant Conduction
4.4. Parasitic Capacitance
5. Problems in GaN HEMT Modeling
5.1. On-State Power Loss
5.2. Large Signal Parasitic Capacitance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Van Do, T.; Trovao, J.P.F.; Li, K.; Boulon, L. Wide-Bandgap Power Semiconductors for Electric Vehicle Systems: Challenges and Trends. IEEE Veh. Technol. Mag. 2021, 16, 89–98. [Google Scholar] [CrossRef]
- Luo, D.; Gao, Y.; Mok, P.K.T. A GaN Driver for a Bi-Directional Buck/Boost Converter with Three-Level VGS Protection and Optimal-Point Tracking Dead-Time Control. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 2212–2224. [Google Scholar] [CrossRef]
- Marzoughi, A.; Burgos, R.; Boroyevich, D. Characterization and Performance Evaluation of the State-of-the-Art 3.3 kV 30 A Full-SiC MOSFETs. Trans. Ind. Appl. 2019, 55, 575–583. [Google Scholar] [CrossRef]
- Hazra, S.; De, A.; Cheng, L.; Palmour, J.; Schupbach, M.; Hull, B.A.; Allen, S.; Bhattacharya, S. High switching performance of 1700-V, 50-A SiC Power MOSFET over Si IGBT/BiMOSFET for advanced power conversion applications. IEEE Trans. Power Electron. 2016, 31, 4742–4754. [Google Scholar]
- Matocha, K.; Dunne, G.; Soloviev, S.; Beaupre, R. Time-Dependent Dielectric Breakdown of 4H-SiC MOS Capacitors and DMOSFETs. IEEE Tran. Electron Dev. 2008, 55, 1830–1834. [Google Scholar] [CrossRef]
- Ni, Z.; Lyu, X.; Yadav, O.P.; Singh, B.N.; Zheng, S.; Cao, D. Overview of Real-Time Lifetime Prediction and Extension for SiC Power Converters. IEEE Trans. Power Electron. 2019, 35, 7765–7794. [Google Scholar] [CrossRef]
- Lidow, A. GaN as a displacement technology for silicon in power management. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 1–6. [Google Scholar]
- Talikoti, N.; Rao, K.U.; Ghosh, R. GAN versus CoolMOS: A theoretical comparison of performances. In Proceedings of the Fifth International Conference on Advances in Recent Technologies in Communication and Computing (ARTCom 2013), Bangalore, India, 20–21 September 2013; pp. 409–414. [Google Scholar]
- Musumeci, S.; Mandrile, F.; Barba, V.; Palma, M. Low-Voltage GaN FETs in Motor Control Application; Issues and Advantages: A Review. Energies 2021, 14, 6378. [Google Scholar] [CrossRef]
- Kulkarni, A.; Gupta, A.; Mazumder, S.K. Resolving Practical Design Issues in a Single-Phase Grid-Connected GaN-FET-Based Differential-Mode Inverter. IEEE Trans. Power Electron. 2018, 33, 3734–3751. [Google Scholar] [CrossRef]
- Khandelwal, S.; Chauhan, Y.S.; Fjeldly, T.A.; Ghosh, S.; Pampori, A.; Mahajan, D.; Dangi, R.; Ahsan, S.A. ASM GaN: Industry Standard Model for GaN RF and Power Devices—Part 1: DC, CV, and RF Model. IEEE Trans. Power Electron. 2019, 66, 80–86. [Google Scholar] [CrossRef]
- Cucak, D.; Vasic, M.; Garcia, O.; Oliver, J.A.; Alou, P.; Cobos, J.A.; Wang, A.; Martin-Horcajo, S.; Romero, M.F.; Calle, F. Physics-Based Analytical Model for Input, Output, and Reverse Capacitance of a GaN HEMT With the Field-Plate Structure. IEEE Trans. Power Electron. 2017, 32, 2189–2202. [Google Scholar] [CrossRef]
- Albahrani, S.A.; Mahajan, D.; Hodges, J.; Chauhan, Y.S.; Khandelwal, S. ASM GaN: Industry Standard Model for GaN RF and Power Devices—Part-II: Modeling of Charge Trapping. IEEE Trans. Electron Devices 2019, 66, 87–94. [Google Scholar] [CrossRef]
- Hontz, M.R.; Chu, R.; Khanna, R. Effect of Substrate Choice on Transient Performance of Lateral GaN FETs. IEEE J. Electron Devices Soc. 2020, 8, 331–335. [Google Scholar] [CrossRef]
- Hontz, M.R.; Cao, Y.; Chen, M.; Li, R.; Garrido, A.; Chu, R.; Khanna, R. Modeling and Characterization of Vertical GaN Schottky Diodes With AlGaN Cap Layers. IEEE Trans. Electron Devices 2017, 64, 2172–2178. [Google Scholar] [CrossRef]
- Wang, K.; Yang, X.; Li, H.; Ma, H.; Zeng, X.; Chen, W. An Analytical Switching Process Model of Low-Voltage eGaN HEMTs for Loss Calculation. IEEE Trans. Power Electron. 2016, 31, 635–647. [Google Scholar] [CrossRef]
- Huang, X.; Li, Q.; Liu, Z.; Lee, F.C. Analytical Loss Model of High Voltage GaN HEMT in Cascode Configuration. IEEE Trans. Power Electron. 2014, 29, 2208–2219. [Google Scholar] [CrossRef]
- Wu, X.; Wong, S.C.; Tse, C.K.; Lu, J. Bifurcation behavior of SPICE simulations of switching converters: A systematic analysis of erroneous results. IEEE Trans. Power Electron. 2007, 22, 1743–1752. [Google Scholar] [CrossRef]
- The Power MOSFET Application Handbook—Design Engineer’s Guide, NXP Semiconductors, Manchester, United Kingdom. Available online: https://www.nxp.com/docs/en/user-guide/MOSFET-Application-Handbook.pdf (accessed on 7 September 2023).
- Mantooth, H.A.; Peng, K.; Santi, E.; Hudgins, J.L. Modeling of Wide Bandgap Power Semiconductor Devices—Part I. IEEE Trans. Electron Devices 2014, 62, 423–433. [Google Scholar] [CrossRef]
- Kotecha, R.M.; Hossain, M.; Rashid, A.U.; Emon, A.I.; Zhang, Y.; Mantooth, H.A. Compact Modeling of High-Voltage Gallium Nitride Power Semiconductor Devices for Advanced Power Electronics Design. IEEE Open J. Power Electron. 2021, 2, 75–87. [Google Scholar] [CrossRef]
- Wu, L.; Saeedifard, M. A Simple Behavioral Electro-Thermal Model of GaN FETs for SPICE Circuit Simulation. IEEE J. Emerg. Sel. Top. Power Elec. 2016, 4, 730–737. [Google Scholar] [CrossRef]
- Bazzano, G.; Raffa, A.; Rizzo, S.A.; Salerno, N.; Susinni, G.; Veneziano, P. Optimization of a SiC MOSFET behavioural circuit model by using a multi-objective genetic algorithm. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020. [Google Scholar]
- Yazgi, M.; Kuntman, H. A new approach for the extraction of SPICE MOSFET Level-3 static model parameters. In Proceedings of the 1998 IEEE International Conference on Electronics, Circuits and Systems. Surfing the Waves of Science and Technology (Cat. No.98EX196), Lisboa, Portugal, 7–10 September 1998. [Google Scholar]
- Jadli, U.; Mohd-Yasin, F.; Moghadam, H.A.; Pande, P.; Chaturvedi, M.; Dimitrijev, S. Modeling Power GaN-HEMTs Using Standard MOSFET Equations and Parameters in SPICE. Electronics 2021, 10, 130. [Google Scholar] [CrossRef]
- Curtice, W.R.; Ettenberg, M. A Nonlinear GaAs FET Model for Use in the Design of Output Circuits for Power Amplifiers. Trans. Micro. Th. Technol. 1985, 33, 1383–1394. [Google Scholar] [CrossRef]
- Endruschat, A.; Novak, C.; Gerstner, H.; Heckel, T.; Joffe, C.; Marz, M. A Universal SPICE Field-Effect Transistor Model Applied on SiC and GaN Transistors. IEEE Trans. Power Electron. 2019, 34, 9131–9145. [Google Scholar] [CrossRef]
- Angelov, I.; Zirath, H.; Rosman, N. A new empirical nonlinear model for HEMT and MESFET devices. IEEE Trans. Microw. Theory Tech. 1992, 40, 2258–2266. [Google Scholar] [CrossRef]
- Hsu, F.J.; Hung, C.C.; Chu, K.T.; Lee, L.S.; Lee, C.Y. A Dynamic Switching Response Improved SPICE Model for SiC MOSFET with Non-linear Parasitic Capacitance. In Proceedings of the 2020 IEEE Workshop on Wide Bandgap Power Devices and Applications in Asia (WiPDA Asia), Suita, Japan, 23–25 September 2020. [Google Scholar]
- Hsu, F.-J.; Yen, C.-T.; Hung, C.-C.; Lee, C.-Y.; Lee, L.-S.; Chu, K.-T.; Li, Y.-F. High accuracy large-signal SPICE model for silicon carbide MOSFET. In Proceedings of the 2018 IEEE 30th International Symposium on Power Semiconductor Devices and ICs (ISPSD), Chicago, IL, USA, 13–17 May 2018; pp. 403–406. [Google Scholar]
- Li, K.; Evans, P.L.; Johnson, C.M.; Videt, A.; Idir, N. A GaN-HEMT Compact Model Including Dynamic RDSon Effect for Power Electronics Converters. Energies 2021, 14, 2092. [Google Scholar] [CrossRef]
- Peng, K.; Santi, E. Characterization and modeling of a gallium nitride power HEMT. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 113–120. [Google Scholar]
- Bottaro, E.; Cacciato, M.; Raffa, A.; Rizzo, S.A.; Salerno, N.; Veneziano, P.P. Development of a SPICE modelling strategy for power devices in GaN technology. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021. [Google Scholar]
- Li, H.; Zhao, X.; Su, W.; Sun, K.; You, X.; Zheng, T.Q. Nonsegmented PSpice Circuit Model of GaN HEMT with Simulation Convergence Consideration. IEEE Trans. Ind. Electron. 2017, 64, 8992–9000. [Google Scholar] [CrossRef]
- Bouchour, A.A.M.; Dherbécourt, P.; Echeverri, A.; El Oualkadi, A.; Latry, O. Modeling of power GaN HEMT for switching circuits applications using Levenberg-Marquardt algorithm. In Proceedings of the 2018 International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Rabat, Morocco, 21–23 November 2018. [Google Scholar]
- Wu, C.; Jeng, S. Comparing and modeling power GaN FETs for switching converter applications. In Proceedings of the 2017 International Conference on Applied System Innovation (ICASI), Sapporo, Japan, 13–17 May 2017; pp. 740–743. [Google Scholar]
- Okamoto, M.; Toyoda, G.; Hiraki, E.; Tanaka, T.; Hashizume, T.; Kachi, T. Loss evaluation of an AC-AC direct converter with a new GaN HEMT SPICE model. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 1795–1800. [Google Scholar]
- Datasheet GaNSystem GS-065-030-2-L. Available online: https://gansystems.com/gan-transistors/gs-065-030-2-l/ (accessed on 8 September 2023).
- Yeo, H.L.; Tseng, K.J. Modelling technique utilizing modified sigmoid functions for describing power transistor device capacitances applied on GaN HEMT and silicon MOSFET. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 3107–3114. [Google Scholar]
- Yang, S.; Han, S.; Sheng, K.; Chen, K.J. Dynamic On-Resistance in GaN Power Devices: Mechanisms, Characterizations, and Modeling. J. Em. Sel. Topics Power El. 2019, 7, 1425–1439. [Google Scholar] [CrossRef]
- Li, K.; Evans, P.L.; Johnson, C.M. Characterisation and Modeling of Gallium Nitride Power Semiconductor Devices Dynamic On-State Resistance. Trans. Power El. 2018, 33, 5262–5273. [Google Scholar] [CrossRef]
- Zulauf, G.; Guacci, M.; Kolar, J.W. Dynamic on-Resistance in GaN-on-Si HEMTs: Origins, Dependencies, and Future Characterization Frameworks. Tr. Power El. 2020, 35, 5581–5588. [Google Scholar] [CrossRef]
- Badawi, N.; Hilt, O.; Bahat-Treidel, E.; Bocker, J.; Wurfl, J.; Dieckerhoff, S. Investigation of the Dynamic On-State Resistance of 600V Normally-Off and Normally-On GaN HEMTs. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Kohlhepp, B.; Kübrich, D.; Dürbaum, T. Measuring and Modeling of Dynamic On-State Resistance of GaN-HEMTs. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019. [Google Scholar]
- Mauromicale, G.; Rizzo, S.A.; Salerno, N.; Susinni, G.; Raciti, A.; Fusillo, F.; Palermo, A.; Scollo, R. Analysis of the impact of the operating parameters on the variation of the dynamic on-state resistance of GaN power devices. In Proceedings of the 2020 2nd IEEE International Conference on Industrial Electronics for Sustainable Energy Systems (IESES), Cagliari, Italy, 1–3 September 2020; pp. 101–106. [Google Scholar]
- Li, Y.; Zhao, Y.; Huang, A.Q.; Zhang, L.; Lei, Y.; Yu, R.; Ma, Q.; Huang, Q.; Sen, S.; Jia, Y.; et al. Evaluation and Analysis of Temperature-Dependent Dynamic RDS,on of GaN Power Devices Considering High-Frequency Operation. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 111–123. [Google Scholar] [CrossRef]
- Bottaro, E.; Rizzo, S.A.; Salerno, N. Circuit Models of Power MOSFETs Leading the Way of GaN HEMT Modelling—A Review. Energies 2022, 15, 3415. [Google Scholar] [CrossRef]
- Tong, Z.; Roig-Guitart, J.; Neyer, T.; Plummer, J.D.; Rivas-Davila, J.M. Origins of Soft-Switching Coss Losses in SiC Power MOSFETs and Diodes for Resonant Converter Applications. IEEE J. Emerg. Sel. Top. Power Electronics 2021, 9, 4082–4095. [Google Scholar] [CrossRef]
- Perera, N.; Kampitsis, G.; van Erp, R.; Ancay, J.; Jafari, A.; Nikoo, M.S.; Matioli, E. Analysis of Large-Signal Output Capacitance of Transistors Using Sawyer–Tower Circuit. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3647–3656. [Google Scholar] [CrossRef]
- Perera, N.; Jafari, A.; Nela, L.; Kampitsis, G.; Nikoo, M.S.; Matioli, E. Output-Capacitance Hysteresis Losses of Field-Effect Transistors. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 9–12 November 2020. [Google Scholar]


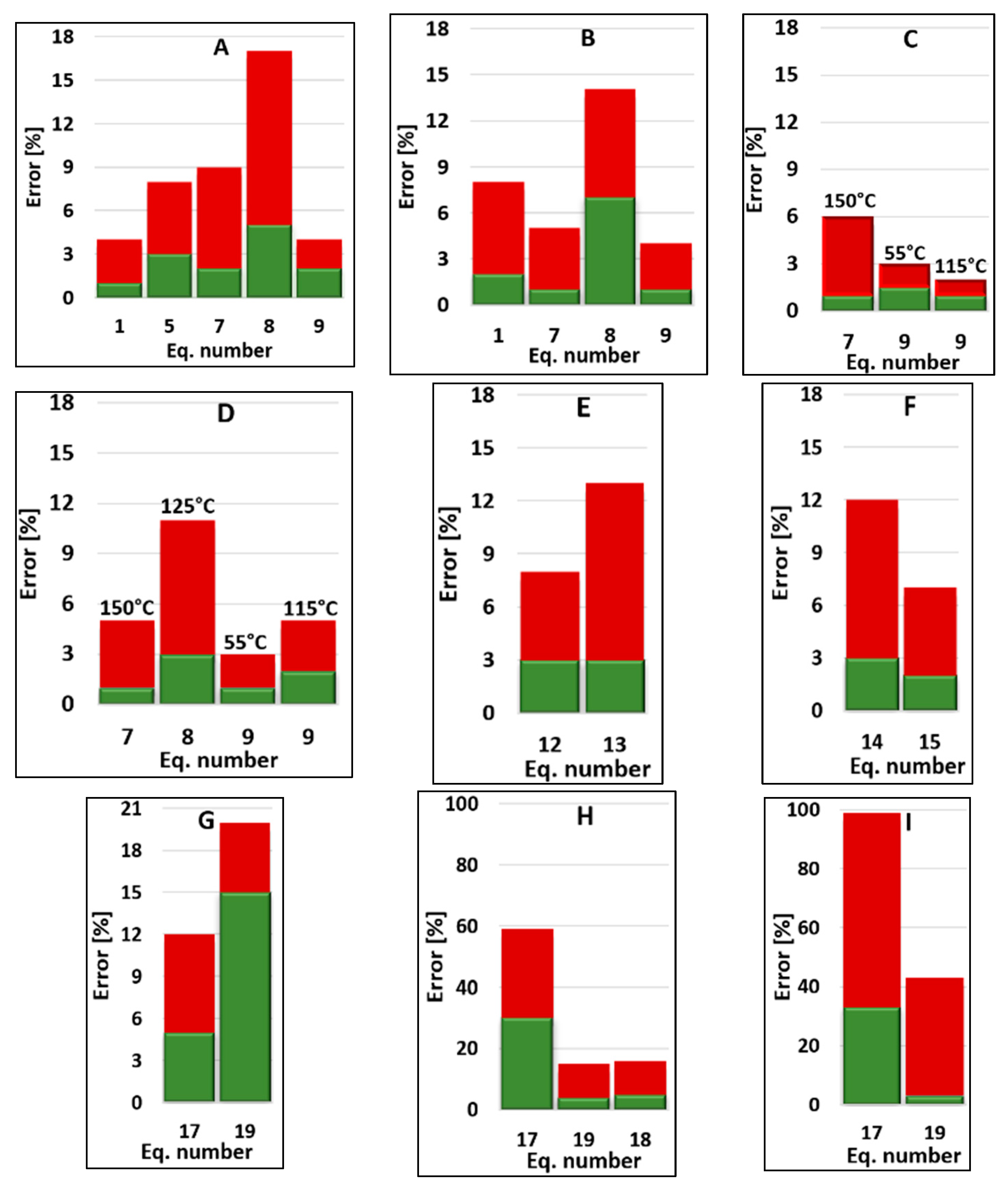
| Characteristic | Si MOSFET | SiC MOSFET | GaN HEMT |
|---|---|---|---|
| OC | IPW65R150CFD | SCTH35N65G2V-7 | GS66516T |
| TC | IPB60R360P7 | IMW65R027M1H | GS-065-004-1-L |
| VTH | STW48N60M2 | SCTH35N65G2V-7 | GAN190-650FBE |
| RDS,on | IPB60R360P7 | SCTH35N65G2V-7 | GS-065-004-1-L |
| TQ | IPB60R360P7 | IMW65R027M1H | GPI65060DFN |
| COSS | STB30N65M5 | IMZA65R072M1H | GPI65007DF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bottaro, E.A.; Rizzo, S.A. An Overview of Strengths and Weaknesses in Using MOSFET Experience for Modeling GaN HEMT. Energies 2023, 16, 6574. https://doi.org/10.3390/en16186574
Bottaro EA, Rizzo SA. An Overview of Strengths and Weaknesses in Using MOSFET Experience for Modeling GaN HEMT. Energies. 2023; 16(18):6574. https://doi.org/10.3390/en16186574
Chicago/Turabian StyleBottaro, Enrico Alfredo, and Santi Agatino Rizzo. 2023. "An Overview of Strengths and Weaknesses in Using MOSFET Experience for Modeling GaN HEMT" Energies 16, no. 18: 6574. https://doi.org/10.3390/en16186574
APA StyleBottaro, E. A., & Rizzo, S. A. (2023). An Overview of Strengths and Weaknesses in Using MOSFET Experience for Modeling GaN HEMT. Energies, 16(18), 6574. https://doi.org/10.3390/en16186574








