Abstract
Prior to switching operations, the dispatch automation system is required to be able to search for closed-loop paths quickly in real time. In order to improve the efficiency of closed-loop path search, this paper proposes a multi-stage real-time fast search method for closed-loop paths based on the characteristics of power grid hierarchical partitioning. First, we divide the closed-loop judgement process into three phases: initialization, acceptance of the closed-loop judgement command, and post-operation. Then, we define three types of nodes, including root nodes, same-layer contact nodes, and common nodes, and construct path data models for each type of node in accordance with the node liaison relationship in grid hierarchical zoning. In the initialization phase, we design a method for the automatic generation of real-time nodal path data models and study a hierarchical partitioned closed-loop path search method based on a nodal path data model for the phase of accepting closed-loop judgement commands. Next, we design a fast local correction method for nodal path models after the switch closure and disconnection operations in the post-operation idle phase are performed. Finally, a real power grid model is used as an example to test the above closed-loop path search method, which improves the search efficiency by eight times compared with the conventional breadth-first search method. The method is applicable to real large and complex power grids.
1. Introduction
The normal operation of the power system and the accident handling process requires closing and disconnecting operations of switching electrical equipment, which will change the topology of the grid and change the operation of equipment. Before operating switchgear, it is necessary to determine whether it will cause personal injury or death, equipment damage, unplanned power outages, or other safety hazards. In order to prevent the occurrence of misoperation, a number of anti-misoperation rules have been established in accordance with the severity of the consequences.
In the substation automation system, the anti-misoperation system will be deployed to determine whether the operation of each switchgear complies with all the anti-misoperation rules, and the operation can only be executed when the calibration passes.
The rules of anti-misoperation are usually expressed in logical formulas, where the variables in the formulas are the operating states of the switches at the same intervals as the operating equipment [1]. However, with the old anti-misoperation rules, it is difficult to achieve cross-interval, cross-voltage level, and cross-station rule checking; the rule base is huge, and the error rate of manual maintenance is high.
The State Grid Corporation of China’s latest trial of anti-misoperation rules (July 2022) covers six major categories of equipment, including twenty-five electrical rules and twenty-one administrative rules. For the new anti-misoperation rules, we propose a real-time online fast topology analysis technique, which achieves per-rule checking based on the judgement of dynamic attributes, where dynamic attributes refer to power system operation information, specifically charged/uncharged, loaded, grounded, parallel/disaggregated, closed loop/unlooping, no-load, running, hot standby, cold standby, and maintenance.
The focus of this paper is on the judgement of the closed-loop attribute in the dynamic attribute, which specifically determines whether the switching operation will lead to the loop closure of the grid and gives the loop closure path, which is used to assess the impact caused by the loop closure, and ultimately decides whether the calibration can be passed or not [2].
The judgement of the closed loop of any switch operation requires finding connectivity paths starting from nodes on both sides of the switchgear. Taking the municipal scale power grid as an example, the network has many components and complex wiring, generally according to the “closed-loop design, open-loop operation”, which contains tens of thousands of nodes [3]. Moreover, each operation verification of the anti-misoperation system requires dozens of rule judgements in a short period of time. This requires high efficiency of the closed-loop path search algorithm to meet real-time requirements.
Therefore, the specific performance requirements for the closed-loop judgement function in an anti-misoperation system are:
- Determine whether it results in a closed loop, and if it does, the relevant equipment that forms the closed-loop path should be given to assist manual decision-making;
- The judgement is fast and suitable for large and complex power grids [4].
According to the above requirements, the closed-loop judgement function in the anti-misoperation system needs a fast closed-loop path search method that can be adapted to large-scale power grids and can meet the requirements of the closed-loop judgement function module in the anti-misoperation verification.
Currently, closed-loop judgements for distribution networks mostly rely on experience [5], and there is very little literature on the search methods for closed-loop judgment. The existing topological path search methods are mainly used to generate equivalent circuits for grid computation, grid fault routes, post-fault power supply paths, and so on [6,7]. The topological path search methods are generally based on the graph theory tree search method and the adjacency matrix method [8].
The adjacency matrix method uses a matrix to express the connectivity relationship between two nodes, which is intuitively better, but when applied to the actual complex power grid with tens of thousands of nodes, it is computationally intensive and cannot give the specific path of the closed loop [9].
In the application of the tree search method, the literature [10] proposes a distance vector-based power supply path search algorithm to search for power supply paths to lost power islands by establishing a routing table between electrical islands. This method does not search for connected paths between nodes and cannot give a closed-loop path. The literature [11] proposes a topological path search method based on undirected graphs, but its essence is still matrix traversal and computationally intensive. The literature [12] proposes a path search method based on vertex splitting. In the process of searching each node, the paths are eliminated according to different constraints, which leads to the constant change in topology and reduces the search efficiency. The literature [13] first simplifies the distribution network model based on CIM (public information model) and then gives a depth-first path search algorithm for the distribution network. When the topology is changed, the whole network model optimization needs to be redone.
In summary, all the above methods require a large computational effort when performing a network-wide topology search. The closed-loop path searches for routes between two points, which can be made more efficient if the search is narrowed down and restricted from a global search to a local search.
The literature [14] proposes a local search method for closed-loop judgement based on the structural characteristics of power grid hierarchy. Layers are stratified according to the voltage level, a path search is performed in each layer using the foreground backtracking search algorithm, and the paths between the layers are combined. This method reduces the search range compared with the breadth-first algorithm.
The method in the literature [14] only focuses on the hierarchical structure of the grid and does not consider the characteristics of the grid partition structure. In addition, the search pattern of this method is not different from the previous search methods, and the topology search workload at each layer is not reduced. If the number of nodes at the same layer is too high in real large and complex grids, the real-time search performance will be affected. In this paper, in addition to using the grid stratification feature, the grid partitioning feature is also utilized to make the search scope smaller, and the search pattern is improved to achieve a phased search.
To reduce the search scope, this paper takes advantage of the characteristics of the grid’s hierarchical partitioned operation mode to construct the closed-loop path data model and design the closed-loop path search method.
To achieve a better real-time performance of the closed-loop judgement, the idea of this paper is to implement this function in the following stages:
- In the initialization phase of the closed-loop judgement function, topological path search work is carried out for the whole network according to the current real-time state of the switch to establish the nodal path data model. This process is computationally intensive and time consuming, and after initialization, it enters the idle phase before operation;
- When receiving a closed-loop judgement command, the current nodal path data model is used to obtain the closed-loop path after the operation in the fewest possible steps and the shortest possible time;
- During the idle time after operation, if there is a switch dislocation, a local closed-loop path search is performed, and the nodal path data model is corrected. This process is computationally minimal and takes less time compared to the initialization phase.
After the search work is staged as described above, the most time-consuming topology search work is no longer performed at the stage of receiving the closed-loop judgement command, which enhances real-time performance.
The main innovations of this paper are:
- Proposing a node path data model and its automatic generation method based on the characteristics of grid hierarchical partitioning;
- With the goal of minimizing the real-time response time for closed-loop judgement, a phased closed-loop judgement model is proposed;
- A loop path search method for hierarchical partitioning at the stage of receiving the closed-loop judgement command is proposed;
- A nodal path model correction method for the case of switch closing and disconnecting operation in the idle phase after operation is proposed.
Finally, a simplified model of a real power grid is used as an example to test the above closed-loop path search method, and its search efficiency is analyzed compared with the conventional breadth-first search method.
2. Nodal Path Data Model and Its Automatic Generation Method
2.1. Closed-Loop Path Grid Model Based on Grid Hierarchical Zoning Characteristics
Actual large and complex grids are operated and managed using a hierarchical zoning model, which is characterized by:
- Equipment of different voltage levels is under the management of different dispatchers. Each voltage level is called a layer, and the layers are connected to each other by transformer branch circuits;
- To limit the short-circuit currents, each layer of the grid is split to operate in multiple partitions. Each node within the same partition has a connectivity relationship with the rest of the nodes. Some of the partitions have alternate contact lines between them, and when the alternate contact line is in operation, the partitions on both sides of the contact line have the same level of connectivity and merge into a single partition island.
Based on the above characteristics of the hierarchical partitioning of the grid and the liaison relationship between the nodes, this paper classifies the nodes in the grid into the following three categories:
- Root nodes: nodes within the partition that are directly connected to the upper layer of the grid, i.e., nodes on both sides of the transformer branches;
- Same-layer contact nodes: nodes within the partition that are directly connected to other partitions on the same level, i.e., nodes on both sides of the alternate contact line;
- Common nodes: nodes in the partition other than the root node and the same layer of contact nodes.
For ease of presentation, the relevant names and symbols are labelled in Figure 1, and the relevant descriptions are as follows:
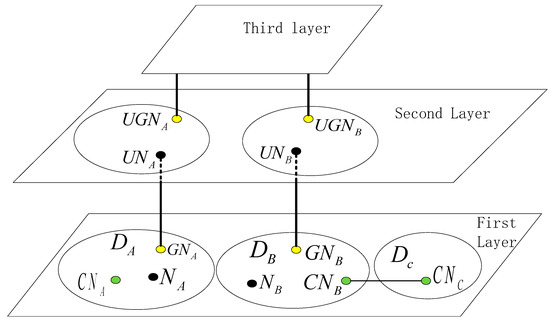
Figure 1.
Schematic diagram of the hierarchical zoning structure of the power grid.
- The three partitions of the first layer of the grid are , , and ;
- and are common nodes within partitions and ;
- , , and are same-layer contact nodes in partitions , , and , respectively;
- The root nodes of partitions and are and ;
- The upper-level grid nodes connected to the root nodes and are and ;
- The root nodes of the partitions in which and are located are and ;
- There are operational liaison lines between partitions and , and there is a same-level liaison relationship between these two partitions to form a partitioned island.
2.2. Nodal Path Data Model
In order to speed up the closed-loop path search, the idea of this paper is as follows:
- In the initialization phase, the paths between each node and other nodes are searched and saved;
- During a real-time closed-loop path search, only the saved node paths in the model are searched and combined, and the shortest closed-loop path between any two nodes can be found quickly, without the need for a topology search.
In this paper, a nodal path table is created for each node to save the path data between this node and other nodes, and the designed node path table format is as follows:
- Path origin node;
- Path: a directed chain of nodes on a path from the start to the end node;
- Path end node;
- Type of node at the end of the path: used for quick search.
There are multiple paths between each node and other nodes of the same subsystem, and the nodal path data model should meet the search demand of closed-loop judgement under the condition of saving as few paths as possible. Therefore, according to the node type, this paper establishes the following three kinds of nodal path tables, with the same data table structure and different saved data contents. The specific contents and principles are described as follows.
2.2.1. Common Node Path Table
Save the connectivity paths of each common node to the rest of the nodes in the same partition.
2.2.2. Same-Layer Contact Node Path Table
The same-layer contact node is a node directly connected to other partitions in this partition, and in the subsequent search process, it needs to obtain the path information with other partitions from the path table of the same-layer contact node. Therefore, the path table of same-layer contact nodes not only has the function of a common node path table but also needs to save the paths between each same-layer contact node and the rest of the same-layer contact nodes belonging to the same partition island.
2.2.3. Root Node Path Table
Within the same layer, there are few connectivity relationships between the various partitions of the grid. However, the grid structure is generally radial [15]; the higher the nodes are connected more closely, so the nodes in different partitions can often find their connection paths in the topology model of the previous layer of the grid.
If it is possible to pre-find the connection paths between individual partitions in the upper grid through the topology model of the upper grid in the initialization phase, this will substantially reduce the search difficulty during the closed-loop path search phase.
Since the root node is the node in the partition that directly connects to the upper layer of the grid, the idea of this paper is as follows.
Search for the path relationship between each root node in this layer in the topological model of the upper layer of the grid and save these paths in the root node path table.
Since the paths between the root node and the rest of the nodes in this partition have been saved in the path table of the rest of the nodes in this partition, in order to reduce the amount of path data stored, only the paths between each root node and the other root nodes of the same level layer are saved in the root node path table.
In summary, the node path table for each type, which is equivalent to the topology analysis result before the closed-loop judgement, should be automatically generated according to the current switching state.
2.3. Automatic Generation Method for Common Node Path Data Table
The breadth-first method is used to automatically generate the common node path table, which is implemented in the following steps:
- From the starting node, the breadth-first search method is used to expand the search nodes outwards, and the search scope involves only the nodes in the same partition;
- Every time a new node is searched, the path table creates new path data, saving the path from the initial node to that node;
- Repeat step 2 until all nodes in the same partition as the starting node have been searched, ending the search.
The breadth-first algorithm flow is shown in Figure 2.
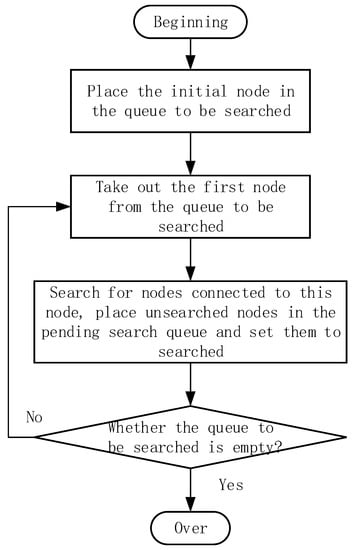
Figure 2.
Breadth-first algorithm flow.
2.4. Automatic Generation Method for Same-Layer Contact Node Path Data Table
The first search establishes the paths between the same-layer contact node and the other nodes in this partition, as described in Section 2.3.
Then, search to establish the path between the same-layer contact node and the rest of the same-layer contact nodes in the same partition island. In this paper, we use the bilaterally forward probing backtracking search method, so that the initial same-layer contact node and the target same-layer contact node are simultaneously extended outward for searching, which accelerates the search efficiency. Among them, the flow of the bilateral forward probing backtracking search algorithm is shown in Figure 3.
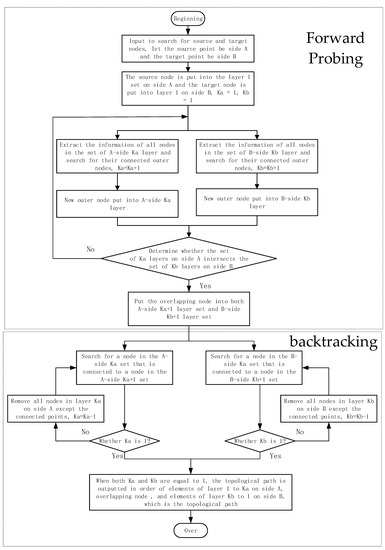
Figure 3.
Bilateral forward probing backtracking search algorithm flow.
Take Figure 1 as an example. is the initial same-layer contact node and is the target same-layer contact node, and the steps to search the path between these two nodes are as follows:
- Search for nodes connected to and put the unsearched connected nodes into the outermost set of the A side;
- Search for nodes connected to and put the unsearched connected nodes into the outermost set of the B side;
- Take the intersection of the outermost set of nodes on A side and B side, and if it is empty, return step 1, until the same node is found in both sets;
- Find and by backtracking from the same node;
- The path table creates new path data; save the path “-same node-”.
2.5. Automatic Generation Method for Root Node Path Data Table
The overall idea is as follows. First, the initial root node and the target root node find their respective directly connected upper layer nodes, and then the two upper layer nodes are searched in the upper layer topology model using the bilateral forward probing backtracking method, which extends the search outward at the same time bilaterally.
Take Figure 1 as an example. is the initial root node and is the target root node; the steps to search the path between these two nodes are as follows:
- Find the upper nodes and of and ;
- If and do not belong to the same partition island, then there is no connected path in the previous layer of and , and the process ends;
- Search for the nodes connected to and put the unsearched connected nodes into the outermost set of nodes on the A side;
- Search for the nodes connected to and put the unsearched connected nodes into the outermost set of nodes on the B side;
- Take the intersection of the set of outermost nodes on side A and the set of outermost nodes on side B. If it is empty, return step 3 until the same node in both sets is found;
- Find and by backtracking from the same node;
- The path table creates new path data; save the path “--same node--”.
3. Closed-Loop Path Search Process and Rules
Based on the characteristics of the grid’s hierarchical partitioning, the priority principle of the closed-loop path search is to prioritize the search at this layer and then search upwards. Therefore, the priority order of the search is in the following order: same partition → same-layer contact node of the same partition island → same layer root node → upper layer node → upper layer root node. In this way, the closed-loop search will only search one or several layers of the relevant partition, and the search scope is small, which improves the search efficiency.
The path search has been completed in the initialization phase, and the results are saved. In the real-time path search process, there is no need to perform a topology search, but searching and combining the existing paths to generate the final path should be performed, which greatly improves the search efficiency.
Take Figure 1 as an example. If the two end nodes of the operation switch are and , the search for the closed-loop path starts from these two end nodes, and the specific judgement process is as follows:
- If nodes and belong to the same partition, save the path from “ to ”, to the path set, and the process ends;
- Otherwise, if nodes and belong to the same partition island, take the same-layer contact nodes, and , and save the paths from “-, -, and -” to the set of paths, and the process ends;
- Otherwise, if there is a connected path between root nodes and in the same layer, save the paths from “-, -, -” to the path set, and the process ends;
- Otherwise, take the upper-level nodes and connected to the same level root nodes and and the upper-level partition root nodes and ;
- If there is a path from to , save the path from “-, -, -, -, and -” to the set of paths, and the process ends;
- Otherwise, return to step 4 until you search upwards to the highest level.
4. Method for Modifying Path Library Data Model after Switchgear Operation
The topology of the grid changes when the switch is operated. This process is time-consuming if the nodal path data model is regenerated for the entire grid. When a switching device is operated, it only affects the topology locally, and only the affected nodal path data need to be corrected.
4.1. Related Nodes Affected by Grid Topology Changes
Topology changes caused by switching operations can result in branching in or out, affecting the path data of related nodes. Therefore, the relationship data between the branch and the related nodes (branch-correlation node table) should be established, and only the path data of these related nodes need to be corrected when the switching operation causes a change in the branch state.
Before the switching operation, if the branch is in the input state, it is called a connected branch, and if the branch is out of the state, it is called an unconnected branch.
- The principle for determining the related nodes of a connected branch is that a node is related if any path in its path table contains this connected branch;
- The principle for determining the related nodes of an unconnected branch is that a node is related if any of the paths in its path table contains nodes at both ends of this unconnected branch.
Following the above principles, data on the relationship between branches and related nodes (branch-correlation node table) can be automatically generated.
4.2. Nodal Path Correction Method after Switch Disconnection
When disconnecting the switching device, the nodal path correction process is as follows:
- Determine whether the nodes on both sides of the switch belong to different partitions. If they belong to different partitions, proceed to step 2; if they belong to the same partition, jump to step 3;
- Modify the node attributes of both nodes to common nodes, update the path tables of both nodes, re-run the partition island analysis for this layer, and update the path tables of all same-layer contact nodes in this layer;
- According to the relationship data between the branch and the related node, find out the related node of the branch between two nodes, and update the path table of the related node; update the data content of this branch in the branch-correlation node table.
4.3. Nodal Path Correction Method after Switch Closure
When the switching device is closed, the process of nodal path correction is as follows:
- Determine whether the nodes on both sides of the switch belong to different partitions. If they belong to different partitions, proceed to step 2; if they belong to the same partition, jump to step 5;
- Modify the node attributes of both nodes to same-layer contacts and update the path tables of both nodes;
- Determine whether the partition where the two nodes are located belongs to the same partition island. If it belongs to a different partition island, proceed to step 4; if it belongs to the same partition island, jump to step 5;
- Redo the partition island analysis for this layer, update the path table for all same-layer contact nodes in this layer, and update the path table for lower-level nodes (all root nodes) connected to all nodes within the two partition islands;
- According to the relationship data between the branch and the related node, find out the related node of the branch between two nodes, and update the path table of the related node; update the data content of this branch in the branch-correlation node table.
5. Case Study Results and Analysis
In order to verify whether the proposed method can be applied to large and complex grid models, a real grid model is used as an example for testing. Due to the large size of the actual grid, each voltage level is only taken locally, constituting a grid model as shown in Figure 4. There are three voltage levels in the model (110 kV, 220 kV, 500 kV), and the extent of each partition is delineated by dotted lines; there are forty-five partitions in the 110 kV layer, three partitions in the 220 kV layer, and one partition in the 500 kV layer, and the 500 kV and 220 kV partition numbers are labelled in Figure 4, the red nodes represent 500 kV, the blue nodes represent 220 kV, the black nodes represent 110 kV, green highlights in figure represent same-layer contact node, yellow highlights in figure represent root node. Due to the large number of nodes and branches at 110 kV, nodes connecting to the 220 kV layer have been added at the 110 kV layer. The dotted lines between the partitions are the backup lines.
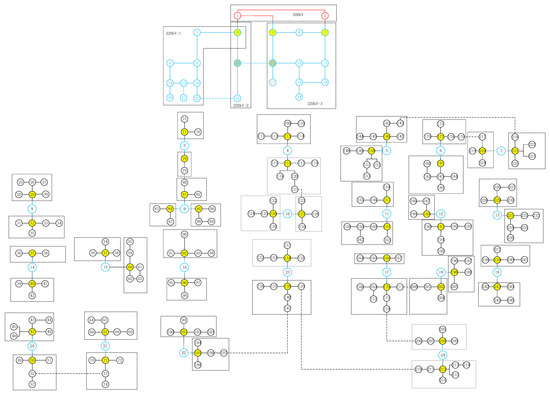
Figure 4.
Grid topology model.
It is known that the partitioning of each voltage level, the common nodes, the same-layer contact nodes and the root nodes in each partition, and the nodal path tables and branch-correlation node tables are created by following the steps in Section 2.3, Section 2.4 and Section 2.5. By analyzing the linkage relationship of each partition, the partitioned island is established.
Assuming a switch closure operation, the node numbers at the ends of the branch where the switch is located are 139 and 210; both located at the 110 kV level, and the closed-loop path search process is tested. The data content are huge, and only the data related to this search are shown.
Node 139 is a common node, and the root node of the partition in which it is located is node 138, and the upper (220 kV layer) node of this partition is 23.
Node 210 is a common node, and the root node of the partition in which it is located is node 212, and the upper (220 kV level) node of this partition is 24.
The node path tables for 139, 210, and 138 are shown in Table 1, Table 2, and Table 3, respectively. Among them, the value of “type of node at the end of the path” means the following.: Zero means common node type, one means root node type, and two means same-layer contact node type.

Table 1.
Path table of node 139.

Table 2.
Path table of node 210.

Table 3.
Path table of node 138.
According to Section 3, the closed-loop path search procedure is as follows:
- Nodes 139 and 210 are not in a partition and are not in a partition island;
- Search the 139 node path table to find the path between 139 and the root node 138 of this partition, i.e., 139-138;
- Search the 210 node path table to find the path between 210 and the root node 212 of this partition, i.e., 210-211-212;
- Search the node path table for 138 (the root node of the partition where 139 is located) and find the path between 138 and 212 (the root node of the partition where 210 is located), i.e., 138-23-10-11-12-18-24-212;
- The three paths add up to the final path, which is 139-138-23-10-11-12-18-24-212-211-210.
The metrics used to evaluate the complexity of the search algorithm are generally the number of nodes involved in the search process, the number of branches involved in the search process, and the number of searches [6,14]. The number of searches is recorded for every time a device and its node information were searched for.
Using this case, the complexity evaluation data of this paper’s method and the breadth-first algorithm were counted, as shown in Table 4.

Table 4.
Algorithm complexity comparison.
It can be seen that compared with the breadth-first search method, in the method proposed in this paper, the number of nodes and the number of branches involved are significantly reduced, and the search efficiency is improved by eight times according to the number of searches.
6. Conclusions
In this paper, we propose a real-time fast search method for closed-loop paths. The method is characterized by the following:
- Based on the characteristics of power grid hierarchical partitioning, three types of nodes are defined: the corresponding node path data model is constructed, the hierarchical search priority principle is formulated, and the fast search method for the closed-loop path is designed. Compared with the graph search, the characteristics of the power grid are considered, the search directionality is clearer, and the search scope is much reduced;
- The closed-loop judgement process is divided into three phases: initialization, receiving the closed-loop judgement command, and post-operation. In the initialization phase, the whole network nodal path data model is established in real time, which takes the longest time; in the receiving the closed-loop judgement command phase, the nodal path model of the current state is used to obtain the closed-loop path after the operation, which takes the shortest time; and in the post-operation phase, the model is corrected locally, which takes a shorter time. By configuring the tasks in this way, real-time performance is improved.
The method is applicable to real large and complex power grids.
The disadvantages of this method compared to conventional graph search methods are the following. Additional modelling of the nodal path data is required, and the model needs to be corrected locally when the switch changes position.
Author Contributions
Conceptualization, D.Z. and K.Y.; methodology, D.Z. and K.Y.; validation, D.Z. and K.Y.; resources, W.W., X.H., T.L., K.S. and Y.Z.; writing—original draft preparation, K.Y.; writing—review and editing, D.Z.; supervision, D.Z. and W.W.; funding acquisition, D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the State Grid Corporation of China Headquarters Science and Technology Project Funding (project No. 5200-202140365A).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, B.; Zhao, D.; Li, B.; Zhang, H. Key Technologies of Online Error Prevention System in Smart Substation. Smart Power 2020, 48, 73–78+111. [Google Scholar]
- Sha, L.; Li, G.; Xie, M.; Lv, Y.; Shan, L. Optimal Search and Operation Security Correction of the Closed-loop Switches in the Distribution Network. Electr. Autom. 2020, 42, 82–84+88. [Google Scholar]
- Qin, Q.; Zhou, Q.; Zhang, Y.; Guo, Q. Influencial Factors Analysis of Receiving Power Flow Capacity and Countermeasures. Electr. Power Constr. 2017, 38, 120–126. [Google Scholar]
- Yu, J.; Xia, Y.; Dong, Y.; Su, Z.; Liao, H. Online Real-time Loop Closing Analysis System for Main Distribution Network Integration Based on CIM/SVG. Power Capacit. React. Power Compens. 2020, 41, 157–163. [Google Scholar]
- Wu, Y.; Wang, H.; Yang, L. A hybrid aided decision-making algorithm of distribution network loop closing based on priority. Power Syst. Prot. Control. 2020, 48, 57–67. [Google Scholar]
- Zhou, Y.; Yan, Z.; Li, N.; Feng, D.; Dai, S. A New System Restoration Path Search Algorithm and Its Applicability Research. Proc. CSEE 2016, 36, 4152–4161. [Google Scholar]
- Huang, C. Research on Cascading Failure Path Search and Critical Line Identification in AC/DC Hybrid System. Master’s Thesis, South China University of Technology, Beijing, China, June 2022. [Google Scholar]
- Su, Y.; Qiu, T.; Qiu, J. Study on Topology Analysis for Distribution Network. Zhejiang Electr. Power 2001, 5, 10–14. [Google Scholar]
- Guo, S.; Yan, Y.; Jiang, J.; Ma, M.; Bao, W. Network topology identification algorithm based on adjacency matrix. Power Syst. Prot. Control. 2018, 46, 50–56. [Google Scholar]
- Yu, K.; Xie, L.; Jin, R. Recent Development and Application Prospects of IGBT in Flexible HVDC Power System. Autom. Electr. Power Syst. 2016, 40, 65–70+143. [Google Scholar]
- Zhou, H.; Sun, F. Topology Path Search Method of Active Distribution Network Based on Undirected Graph. Autom. Electr. Power Syst. 2014, 38, 64–71. [Google Scholar]
- Zhang, X.; Cheng, X.; Zhao, D.; Su, L. A Path Searching Method Based on Vertex Splitting for Online Power Grid Fault Restoration. Guangdong Electr. Power 2022, 35, 71–77. [Google Scholar]
- Xu, C.; Dong, S.; Sun, Z.; Li, C.; Sun, M. A Path Searching Algorithm for Distribution Network Based on Network Simplification and Depth First Traversal. Autom. Electr. Power Syst. 2017, 41, 170–176. [Google Scholar]
- Cui, J.; Hai, D.; Fang, Q.; Yang, C.; Xu, W.; Huang, C. A Closing-Loop Topology Analysis Based on Hierarchical Forward-Probing and Backward-Tracking Search Algorithm. Mod. Electr. Power 2022, 39, 143–150. [Google Scholar]
- Ji, Y.; Zhao, J. Design and research on the loop closing operation analysis system medium voltage in radial distribution network. Power Syst. Prot. Control. 2009, 37, 58–61+69. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).