Selection of the Winding Type of Solid-State Transformers in Terms of Transmitting the Greatest Possible Power in the Frequency Range from 500 Hz to 6000 Hz
Abstract
:1. Introduction
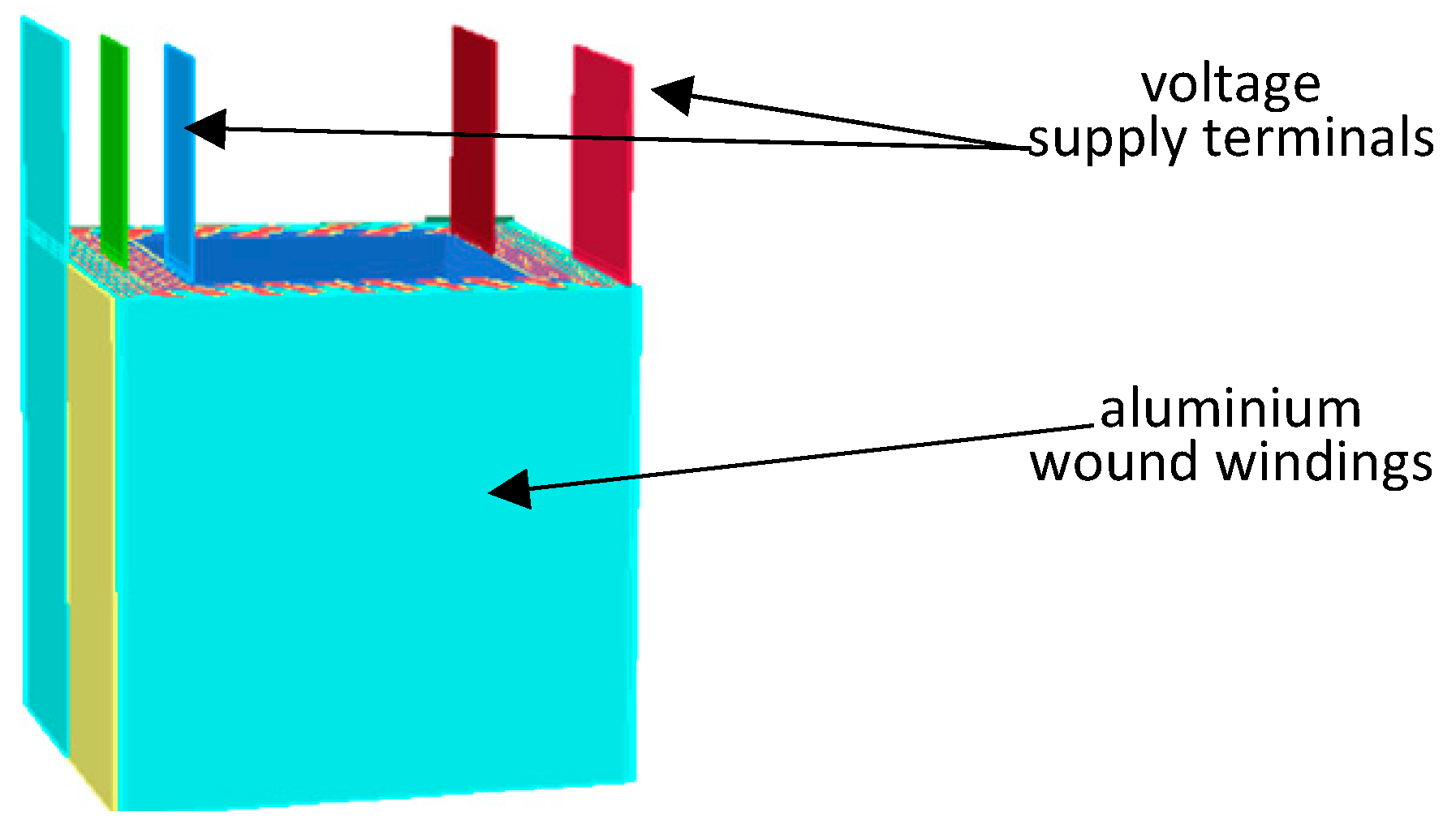
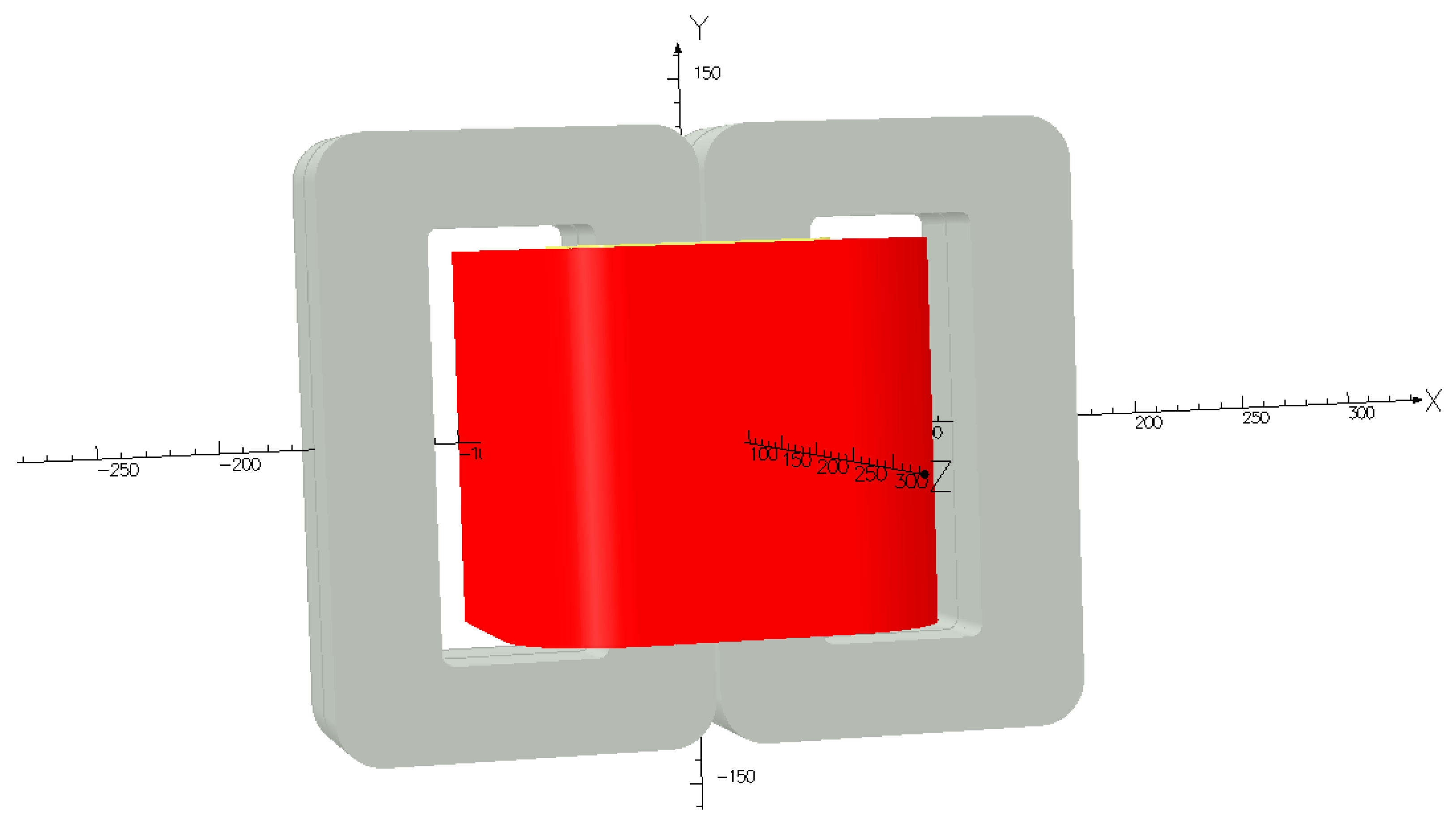
2. Construction of Medium Frequency Transformer
- wire diameter—0.2 mm
- number of copper wires in a bundle—100
- cross-sectional area of copper in a bundle—3.14 mm2
- bundle outer diameter 2.89 mm.
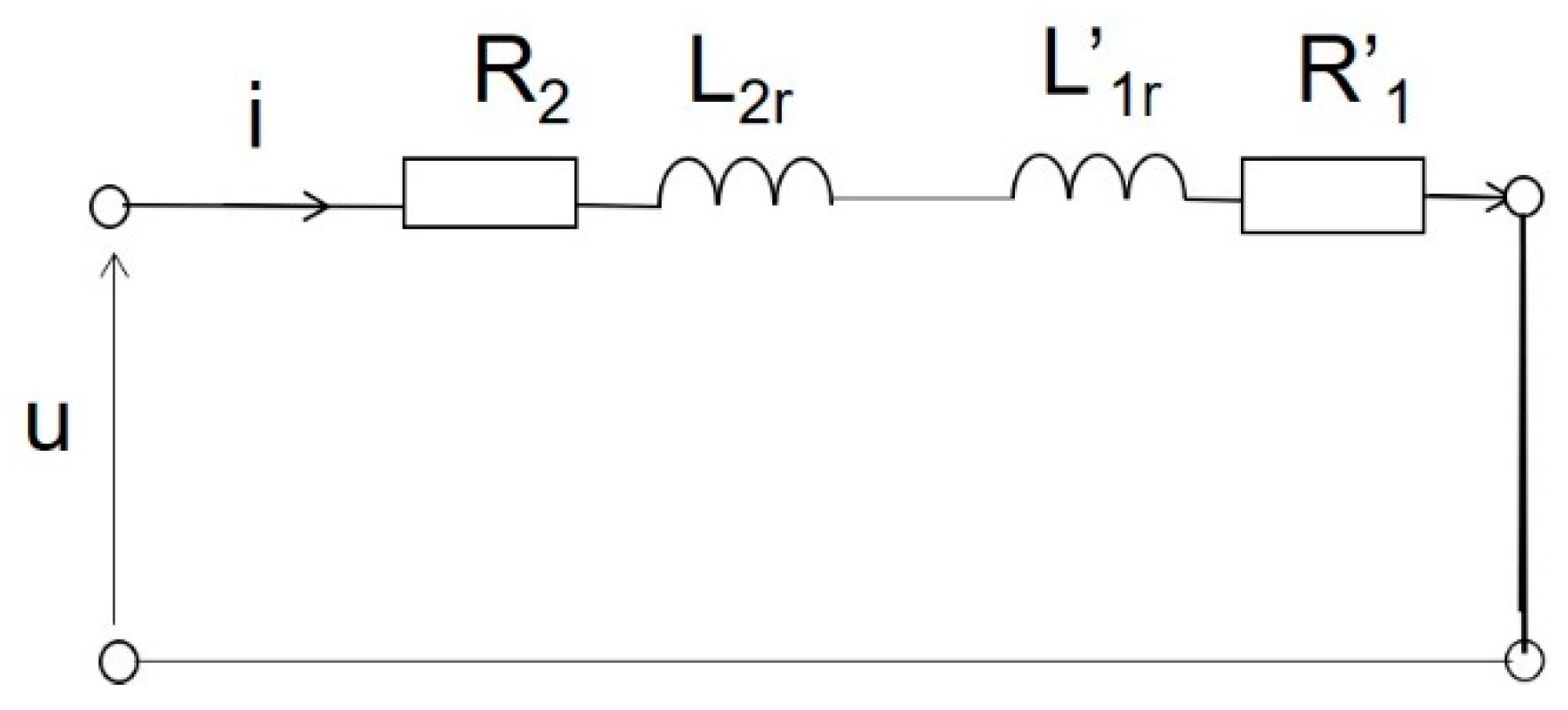
3. Mathematical Model of the Medium Frequency Transformer
4. The Result of the Computation
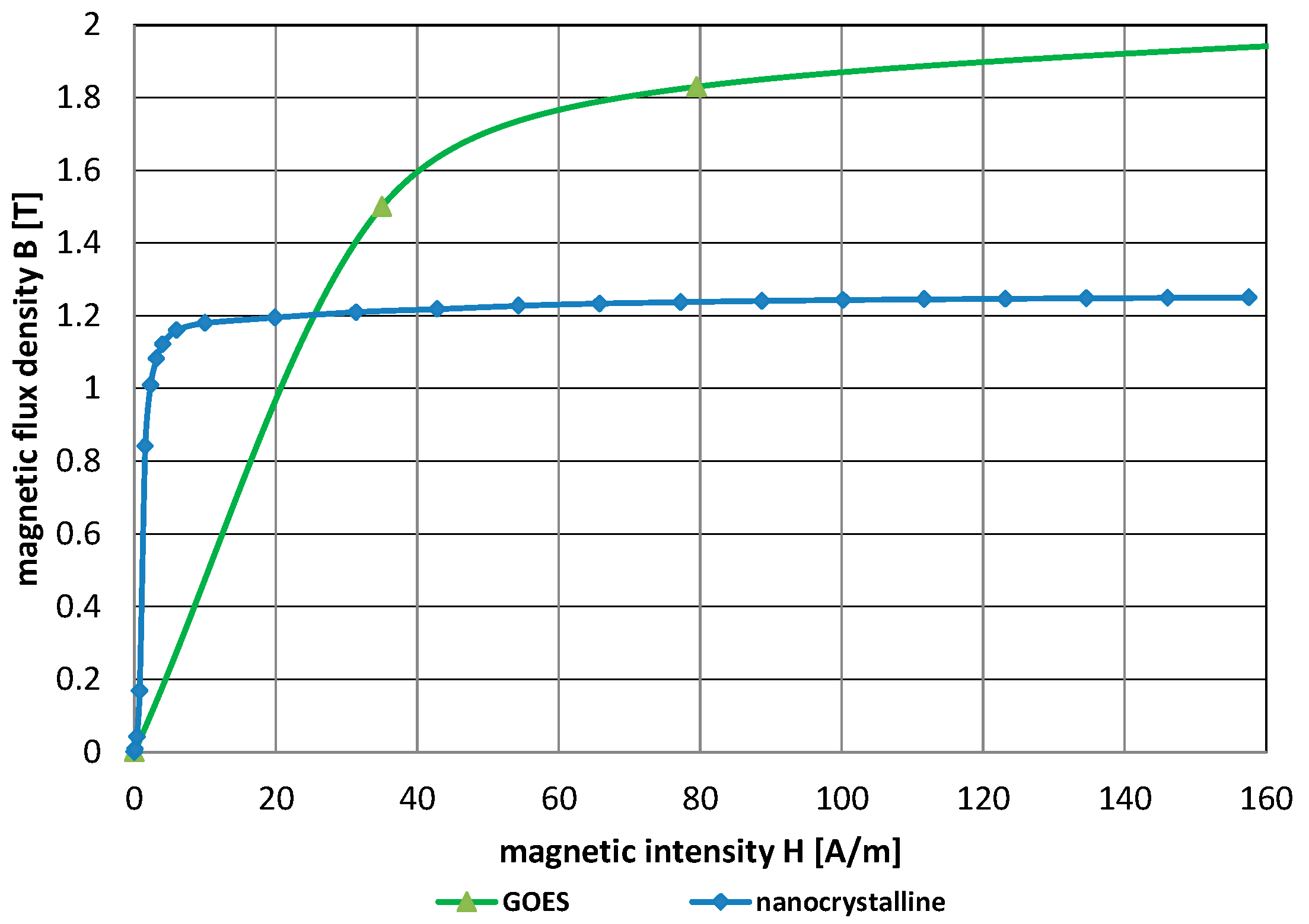
4.1. Comparison of the Materials Used for the Core
4.2. Comparison of the Use of Aluminum Foil Windings or Litz Windings
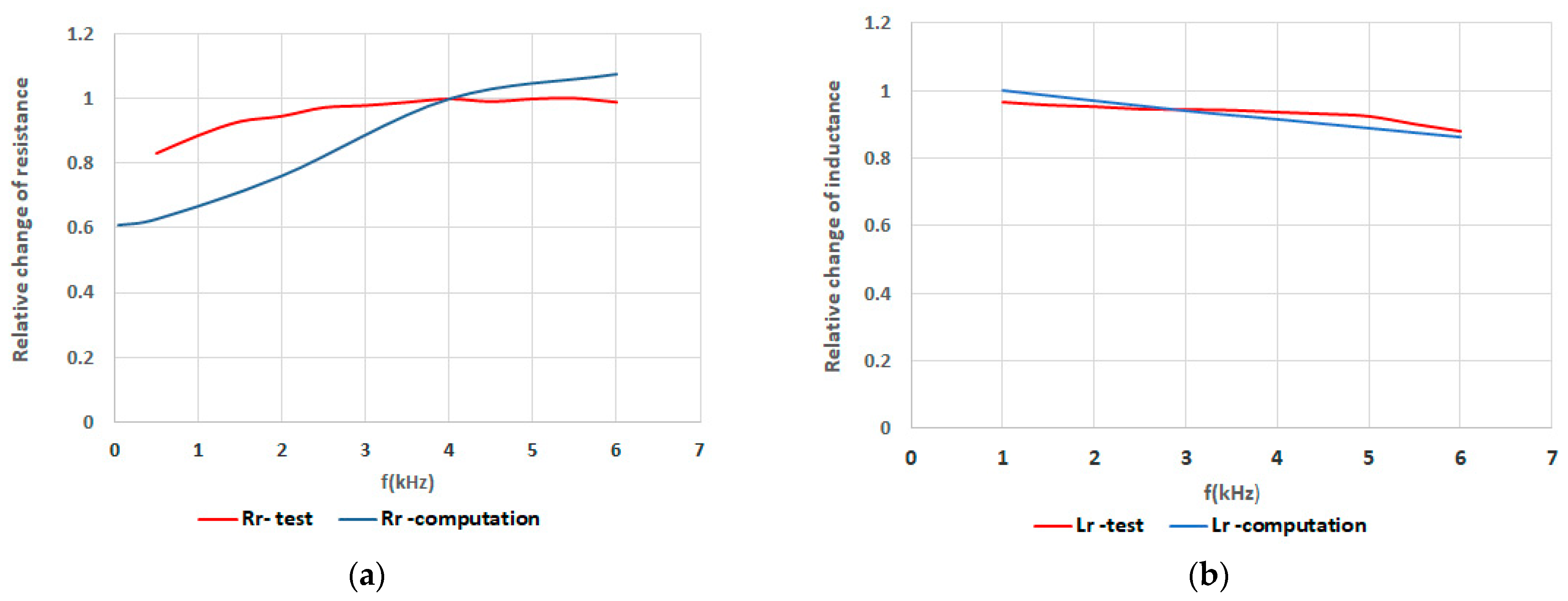
4.3. Influence of Power Frequency on the Short-Circuit Reactance and Inductance of Transformers with GOES Core and Interleaved Foil Coils
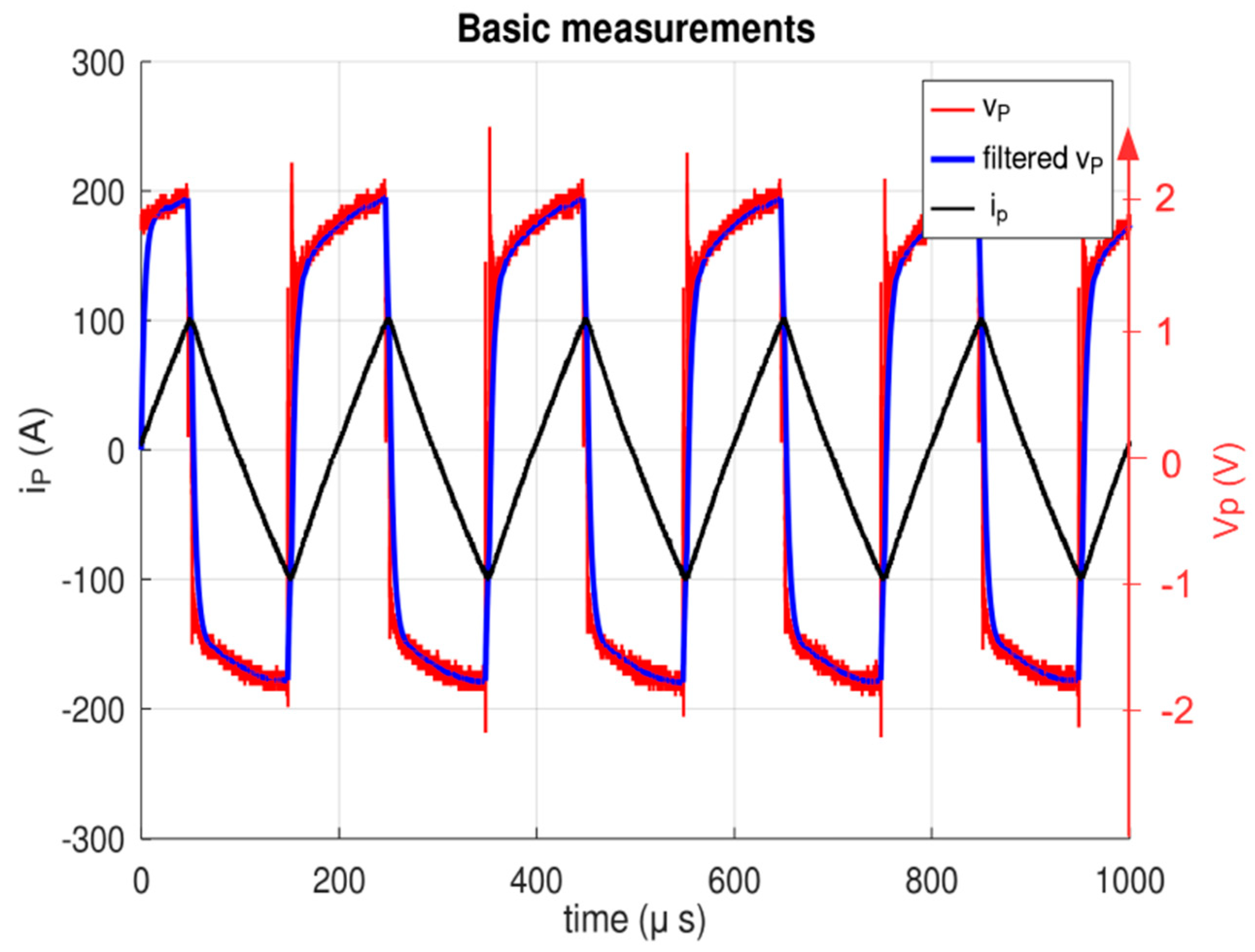
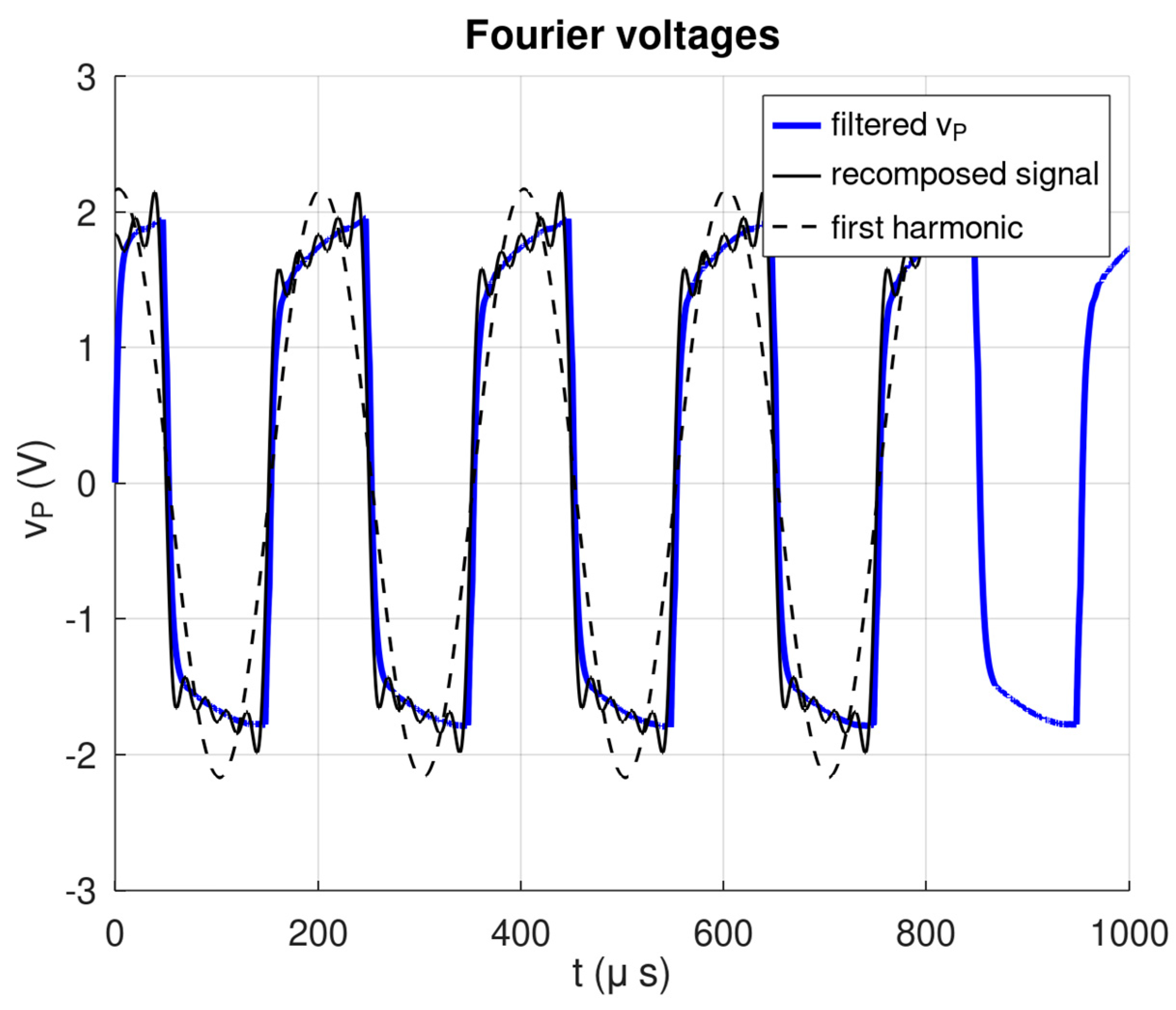
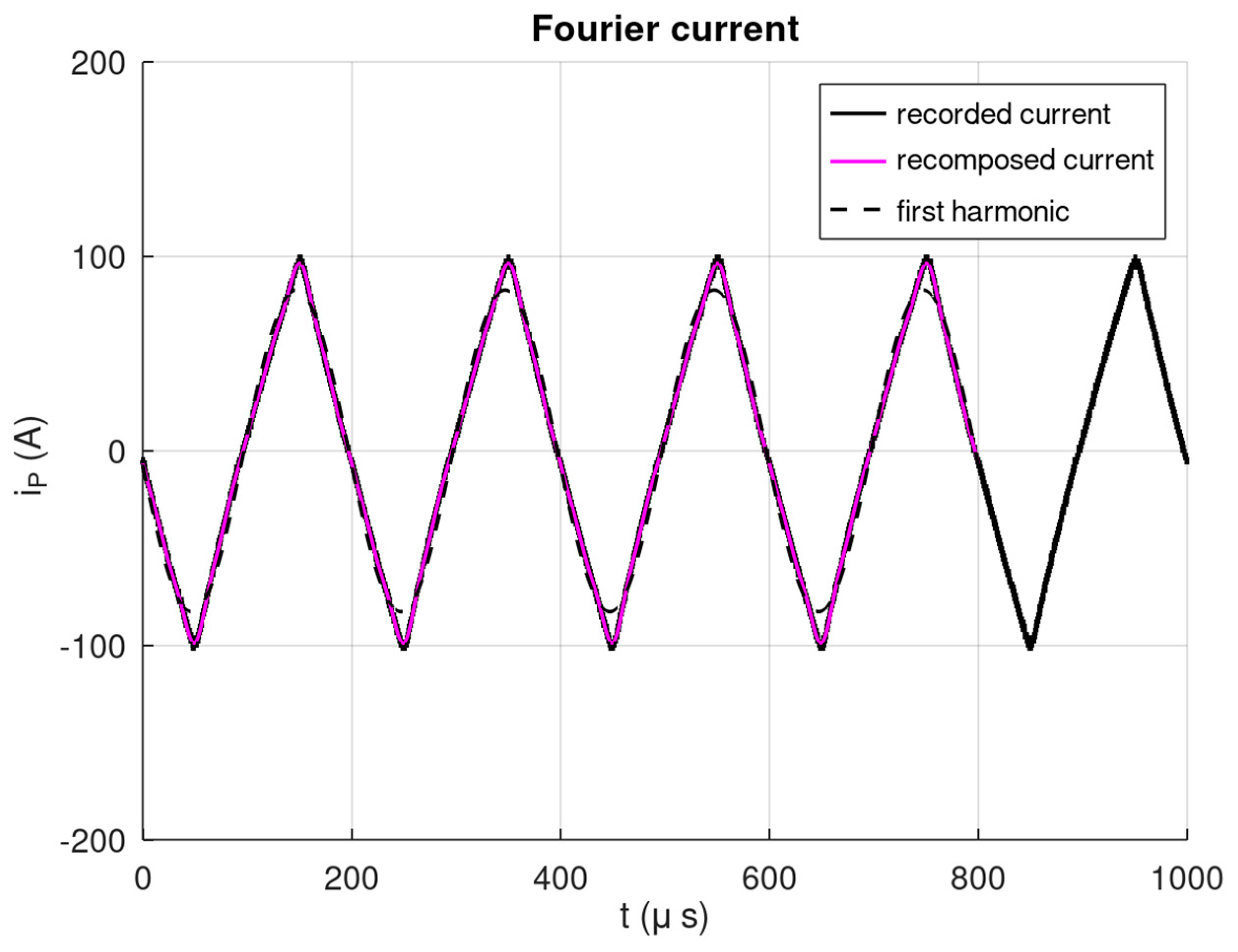
5. Prototype Description and Measurements
6. Comparison of Simulation and Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ortiz, G.; Leibl, M.; Kolar, J.W.; Apeldoorn, O. Medium Frequency Transformers for Solid-State-Transformer Applications—Design and Experimental Verification. In Proceedings of the IEEE 10th International Conference on Power Electronics and Drive Systems (PEDS), Kitakyushu, Japan, 22–25 April 2013; pp. 1285–1290. [Google Scholar] [CrossRef]
- Chen, B.; Liang, X.; Wan, N. Design Methodology for Inductor-Integrated Litz-Wired High-Power Medium-Frequency Transformer with the Nanocrystalline Core Material for Isolated DC-Link Stage of Solid-State Transformer. IEEE Trans. Power Electron. 2020, 35, 11557–11573. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ker, P.J.; Lipu, M.S.H.; Choi, Z.H.; Rahman, M.S.A.; Muttaqi, K.M.; Blaabjerg, F. Blaabjerg State of the Art of Solid-State Transformers: Advanced Topologies, Implementation Issues, Recent Progress and Improvements. IEEE Access 2020, 8, 19113–19132. [Google Scholar] [CrossRef]
- Bahmani, M.A.; Thiringer, T.; Kharezy, M. Design Methodology and Optimization of a Medium-Frequency Transformer for High-Power DC–DC Applications. IEEE Trans. Ind. Appl. 2016, 52, 4225–4233. [Google Scholar] [CrossRef]
- Rylko, M.; Hartnett, K.; Hayes, J.; Egan, M. Magnetic material selection for high power high frequency inductors in dc-dc converters. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 2043–2049. [Google Scholar] [CrossRef]
- Dujic, D.; Kieferndorf, F.; Canales, F.; Drofenik, U. Power electronic traction transformer technology. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, China, 2–5 June 2012; Volume 1, pp. 636–642. [Google Scholar] [CrossRef]
- Bahmani, M.A.; Thiringer, T.; Ortega, H. An accurate pseudo empirical model of winding loss calculation in HF foil and round conductors in switchmode magnetics. IEEE Trans. Power Electron. 2014, 29, 4231–4246. [Google Scholar] [CrossRef]
- Meier, S.; Kjellqvist, T.; Norrga, S.; Nee, H.-P. Design considerations for medium-frequency power transformers in offshore wind farms. In Proceedings of the 2009 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–12. [Google Scholar]
- Villar, I. Multiphysical Characterization of Medium-Frequency Power Electronic Transformers. Ph.D. Thesis, École Polytechnique Fédérale De Lausanne, Lausanne, Switzerland, 2010. [Google Scholar] [CrossRef]
- Kumar, B.M.; Kumar, A.; Bhat, A.H.; Agarwal, P. Comparative study of dual active bridge isolated DC to DC converter with single phase shift and dual phase shift control techniques. In Proceedings of the 2017 Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 26–27 October 2017; pp. 453–458. [Google Scholar] [CrossRef]
- Ruiz-Robles, D.; Ortíz-Marín, J.; Venegas-Rebollar, V.L.; Moreno-Goytia, E.; Granados-Lieberman, D.R.; Rodríguez-Rodriguez, J. Nanocrystalline and Silicon Steel Medium-Frequency Transformers Applied to DC-DC Converters: Analysis and Experimental Comparison. Energies 2019, 12, 2062. [Google Scholar] [CrossRef]
- Roger, D.; Rossi, M.; Ichou, H.; Blaszkowski, J. Magnetic behavior of GOES wound cores of transformers fed by square or sine voltages. J. Magn. Magn. Mater. 2022, 564, 170032. [Google Scholar] [CrossRef]
- Roger, D.; Napieralska, E.; Komeza, K.; Napieralski, P. Design of High−Power Solid−State Transformers with Grain−Oriented Electrical Steel Cores. Electronics 2022, 11, 2398. [Google Scholar] [CrossRef]
- Diaz, G.A.; Mombello, E.E.; Venerdini, G.D.G. Calculation of Leakage Reactance in Transformers with Constructive Deformations in Low Voltage Foil Windings. IEEE Trans. Power Deliv. 2018, 33, 3205–3210. [Google Scholar] [CrossRef]
- Ichou, H.; Roger, D.; Rossi, M. Thermal behavior of grain-oriented electrical steel wound core solid-state transformer. COMPEL 2022, 41, 732–751. [Google Scholar] [CrossRef]
- Jezierski, E. Power Transformer; WNT: Warsow, Poland, 1983; pp. 1–650. ISBN 5905279053229. (In Polish) [Google Scholar]
- Wiszniewski, A. Instrument Transformers in the Power Industry; WNT: Warsow, Poland, 1983; pp. 1–302. ISBN 8320403707. (In Polish) [Google Scholar]
- Koszmider, A.; Olak, J.; Piotrowski, Z. Current Transformers; WNT: Warsow, Poland, 1985; pp. 1–283. ISBN 8320407109. (In Polish) [Google Scholar]
- Asghari, B.; Dinavahi, V.; Rioual, M.; Martinez, J.A.; Iravani, R. Interfacing Techniques for Electromagnetic Field and Circuit Simulation Programs IEEE Task Force on Interfacing Techniques for Simulation Tools. IEEE Trans. Power Deliv. 2009, 24, 939–950. [Google Scholar] [CrossRef]
- Amoiralis, E.I.; Georgilakis, P.S.; Tsili, M.A.; Kladas, A.G. Global transformer optimization method using evolutionary design and numerical field computation. IEEE Trans. Magn. 2009, 45, 1720–1723. [Google Scholar] [CrossRef]
- Tong, Z.; Braun, W.D.; Rivas-Davila, J. Design and Fabrication of Three-Dimensional Printed Air-Core Transformers for High-Frequency Power Applications. IEEE Trans. Power Electron. 2020, 35, 8472–8489. [Google Scholar] [CrossRef]
- Konrad, A.; Brudny, J.F. Virtual air gap length computation with the finite-element method. IEEE Trans. Magn. 2007, 43, 1829–1832. [Google Scholar] [CrossRef]
- Lesniewska, E. Applications of the Field Analysis during Design Process of Instrument Transformers. In Transformers. Analysis, Design, and Measurement; Lopez-Fernandez, X.M., Ertan, B.H., Turowski, J., Eds.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA; London, UK; New York, NY, USA, 2012; pp. 349–380. [Google Scholar]
- Dems, M.; Komeza, K.; Kubiak, W.; Szulakowski, J. Impact of Core Sheet Cutting Method on Parameters of Induction Motors. Energies 2020, 13, 1960. [Google Scholar] [CrossRef]
- Lesniewska, E.; Olak, J. Analysis of the Operation of Cascade Current Transformers for Measurements of Short-Circuit Currents with a Non-Periodic Component with a Large Time Constant of Its Decay. Energies 2022, 15, 2925. [Google Scholar] [CrossRef]
- Lesniewska, E.; Kaczmarek, M.; Stano, E. 3D Electromagnetic Field Analysis Applied to Evaluate the Accuracy of a Voltage Transformer under Distorted Voltage. Energies 2021, 14, 136. [Google Scholar] [CrossRef]
- Lesniewska, E.; Olak, J. Improvement the Insulation System of Unconventional Combined Instrument Transformer Using 3D Electric Field Analysis. IEEE Trans. Power Deliv. 2018, 33, 2582–2589. [Google Scholar] [CrossRef]
- KING MAGNETICS Catalogue; Zhuhai King Magnetics Technology Co., Ltd.: Zhuhai, China, 2018; Available online: http://www.kingmagnetics.com/kingmagnetics_catalog.pdf (accessed on 31 July 2023).
- Isolectra Martin Company Catalogue. Available online: https://www.isolectra.fr/catalogue_isolectra_en (accessed on 31 July 2023).
- Markovic, M.; Perriard, Y. Eddy current power losses in a toroidal laminated core with rectangular cross section. In Proceedings of the 12th International Conference on Electrical Machines and Systems, Tokyo, Japan, 15–18 November 2009; pp. 1–4. [Google Scholar]
- Zirka, S.E.; Moroz, Y.I.; Marketos, P.H.; Moses, A.J. Evolution of the loss components in ferromagnetic laminations with induction level and frequency. J. Magn. Magn. Mater. 2008, 320, e1039–e1043. [Google Scholar] [CrossRef]
- Roger, D.; Napieralska, E.; Komeza, K.; Napieralski, P. Solid-state transformers of smart high-power battery charger for electric vehicles. IEEE Trans. Ind. Appl. 2023, 1–10. [Google Scholar] [CrossRef]


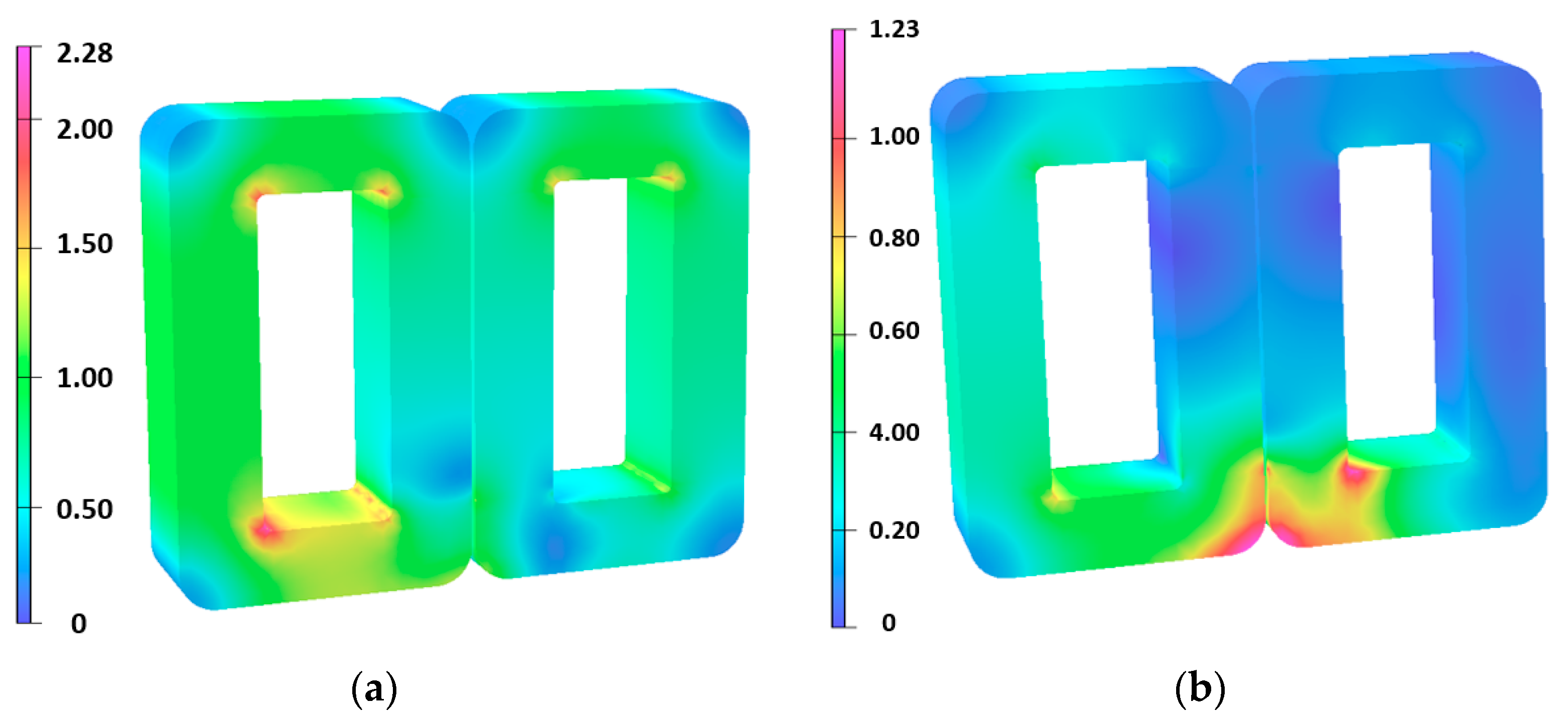
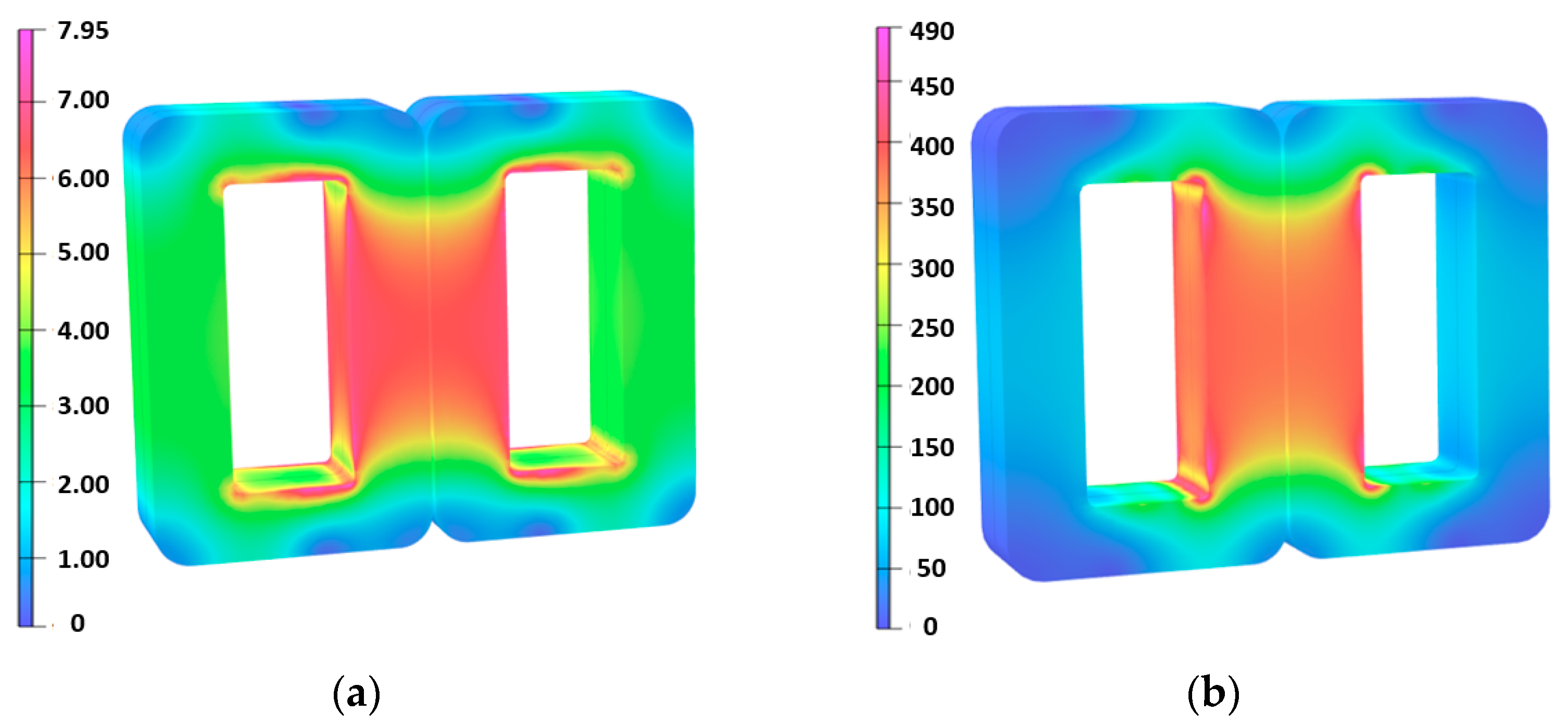
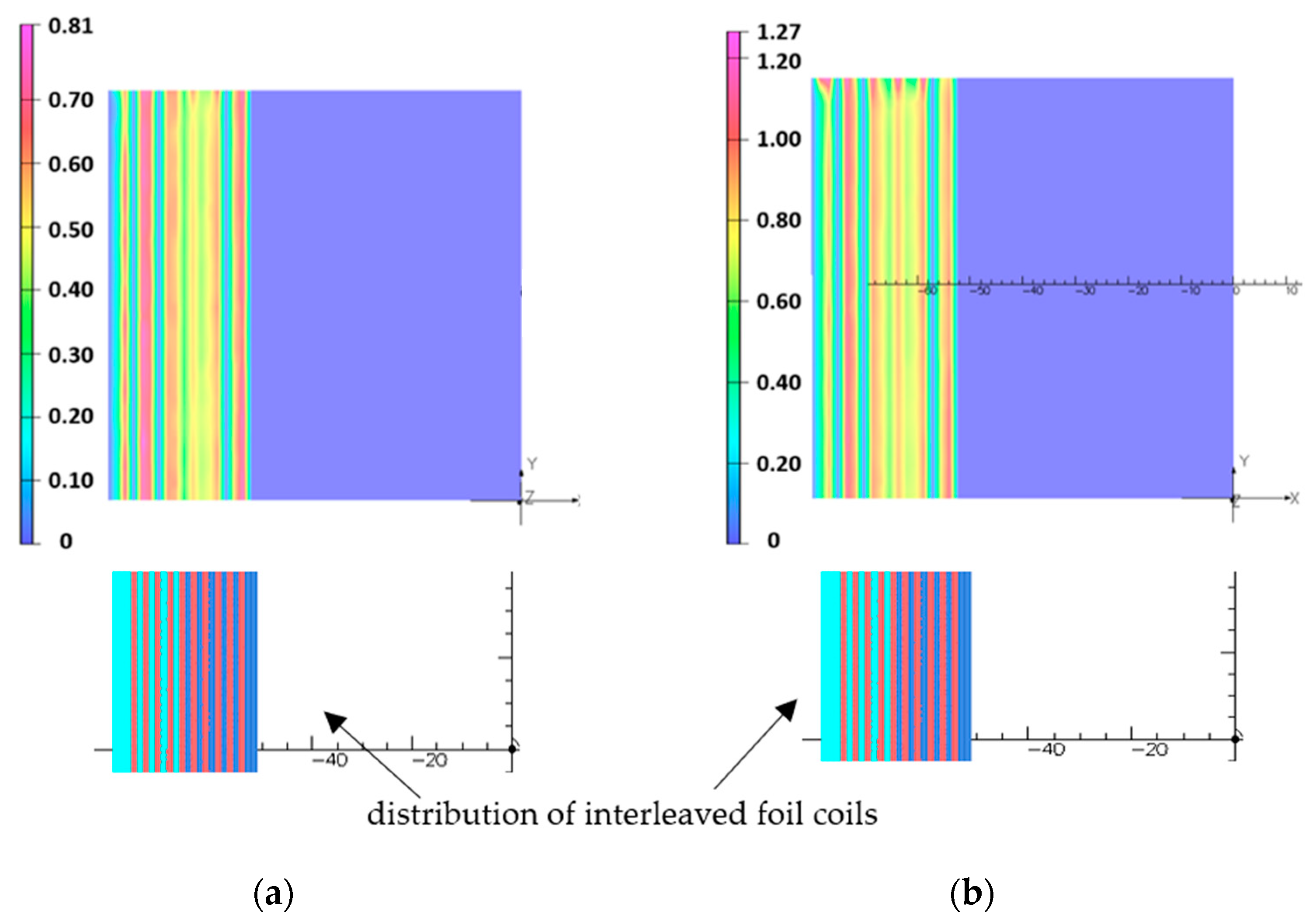


| Frequency | GOES | Nanocrystalline Material |
|---|---|---|
| 6000 Hz | 0.1987 μH | 0.1965 μH |
| 4000 Hz | 0.2308 μH | 0.2080 μH |
| 3000 Hz | 0.2739 μH | 0.2468 μH |
| 2000 Hz | 0.2732 μH | 0.2459 μH |
| 500 Hz | 0.3101 μH | 0.2804 μH |
| Litz Windings | Foil Windings | |
|---|---|---|
| Without Interleaving | With Interleaving | With Interleaving |
| 9.1056 μH | 3.8245 μH | 0.1987 μH |
| Frequency | 500 Hz | 2000 Hz | 3000 Hz | 4000 Hz | 6000 Hz | 8000 Hz | 10,000 Hz |
|---|---|---|---|---|---|---|---|
| Inductance | 0.31015 μH | 0.27323 μH | 0.27395 μH | 0.23082 μH | 0.19873 μH | 0.17670 μH | 0.16176 μH |
| Reactance | 3.4603 mΩ | 4.1988 mΩ | 4.8324 mΩ | 5.5133 mΩ | 5.9340 mΩ | 7.4873 mΩ | 8.0932 mΩ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lesniewska, E.; Roger, D. Selection of the Winding Type of Solid-State Transformers in Terms of Transmitting the Greatest Possible Power in the Frequency Range from 500 Hz to 6000 Hz. Energies 2023, 16, 6528. https://doi.org/10.3390/en16186528
Lesniewska E, Roger D. Selection of the Winding Type of Solid-State Transformers in Terms of Transmitting the Greatest Possible Power in the Frequency Range from 500 Hz to 6000 Hz. Energies. 2023; 16(18):6528. https://doi.org/10.3390/en16186528
Chicago/Turabian StyleLesniewska, Elzbieta, and Daniel Roger. 2023. "Selection of the Winding Type of Solid-State Transformers in Terms of Transmitting the Greatest Possible Power in the Frequency Range from 500 Hz to 6000 Hz" Energies 16, no. 18: 6528. https://doi.org/10.3390/en16186528
APA StyleLesniewska, E., & Roger, D. (2023). Selection of the Winding Type of Solid-State Transformers in Terms of Transmitting the Greatest Possible Power in the Frequency Range from 500 Hz to 6000 Hz. Energies, 16(18), 6528. https://doi.org/10.3390/en16186528








